Identification of geometric and mechanical factors predictive of bird-beak configuration in thoracic endovascular aortic repair using computational models of stent graft deployment

Abstract

Objective

Formation of a bird-beak configuration in thoracic endovascular aortic repair (TEVAR) has been shown to be influenced by various factors. However, the main cause of bird-beak formation remains poorly understood. The hypothesis has been that the geometric and mechanical properties of both the aorta and the stent graft contribute to the formation and extent of a bird-beak configuration. The goal of the present study was to use parameter-based computational simulations of TEVAR to predict for bird-beak formation and identify its most significant contributing factors.

Methods

In the present study, we considered five parameters for the computational simulations of TEVAR, including aortic curvature, aortic arch angle, age as a surrogate for thoracic aortic tissue properties, TEVAR landing zone, and stent graft oversizing. Using an experimental design approach, computational models for 160 TEVAR scenarios were developed by varying the values of the simulation parameters within clinically relevant ranges. The bird-beak length and angle were used as metrics to evaluate the simulation results. Statistical analysis of the simulation data using a random forest model was conducted to identify significant parameters and interactions.

Results

The mean ± standard deviation of the bird-beak length and angle across 160 simulations were 4.32 ± 4.87 mm and 9.16° ± 12.21°, respectively. The largest mean bird-beak length and angle were found in the most distal location in zone 0 (10.04 mm) and zone 2 (21.48°), respectively. An inverse correlation was found between the aortic arch angle and the bird-beak length and angle. In ∼75% of the scenarios, increased stent graft oversizing either fully resolved the presence of the bird-beak configuration or had reduced its size. In the remaining 25%, oversizing minimally changed the bird-beak length and enlarged the bird-beak angle, which mainly occurred in cases with a smaller aortic arch angle and landing zones near the arch apex. This was justified by the mechanism of stent graft bending in the arch angulation. The aortic curvature and tissue properties were shown to be statistically insignificant in relation to bird-beak formation.

Conclusions

Significant parameters predictive of a bird-beak configuration in TEVAR were identified, and the trends in which each parameter influenced the bird-beak size were determined. The findings from the present study can inform the surgical planning and device selection process with the goal of minimizing bird-beak formation.

Clinical Relevance

The presence of a bird-beak configuration after thoracic endovascular aortic repair (TEVAR) has been correlated with the risk of type Ia endoleaks. The underlying cause of bird-beak formation remains poorly understood. In the present study, parameter-based computational models of TEVAR were used to identify the most significant mechanical and geometric factors contributing to bird-beak formation. Our findings have suggested that the aortic arch angle, landing zone, and stent graft oversizing are statistically significant in relation to the formation and extent of bird-beak configurations. With proper validation, these findings could be useful in the identification of patients with a greater risk of bird-beak formation preoperatively, optimal stent graft selection, and procedure modifications to minimize bird-beak formation.

Article Highlights.

• •Type of Research: Basic science
• •Key Findings: Aortic arch angle, TEVAR landing zone, and stent-graft oversizing are statistically significant in relation to bird-beak configuration formation.
• •Take Home Message: The findings of these parameter-based TEVAR computational simulations show that smaller aortic arch angles and landing zones near the arch apex are more prone to bird-beak. In patient cases with these characteristics, additional emphasis must be placed on selecting the optimal stent-graft design and oversizing, with the goal of minimizing bird-beak occurrence.

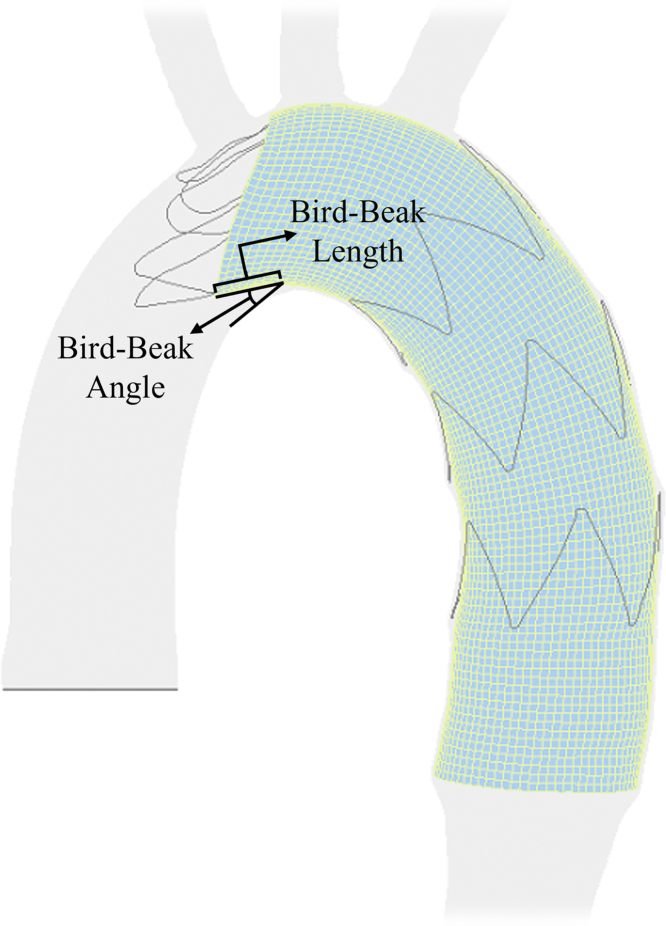
A complete seal of the proximal landing zone is essential for successful thoracic endovascular aortic repair (TEVAR).¹ Stent graft stiffness and increased angulation of the aortic arch can make achieving a complete seal challenging.² Failure to achieve a complete proximal seal on the inner curvature of the aorta will result in a wedge-shaped gap between the stent graft and the aortic wall, referred to as a bird-beak deformity.³ The presence of a bird-beak configuration is highly correlated with the risk of a type Ia endoleak.3, 4, 5, 6, 7, 8 A bird-beak configuration can also lead to other postoperative complications, such as stent graft migration, infolding, or collapse.^6,7,9,10 In a recent meta-analysis, the frequency of bird-beak formation was reported to be 4% to 100% in various studies, depending on how it was defined.⁶ Also, the rate of postoperative complications was higher for the patients with a bird-beak configuration than for patients without (14.7% vs 6.3%). Several studies have correlated the geometric parameters of bird-beak configurations (ie, bird-beak length and angle; Fig 1), with the risk of bird-beak adverse events, providing evidence for their clinical significance.^3,7,8,10 Different studies have identified various factors that contribute to the bird-beak formation. Pasta et al^10,11 have identified the high angulation and curvature of the aortic arch as a cause of bird-beak formation. Similarly, Ueda et al³ found a correlation between the bird-beak length and the degree of aortic curvature. Frohlich et al¹² determined that bird-beak occurrence and geometries correlated with the product of the aorta inner curvature and diameter. However, Sze et al⁸ found a weak association between the bird-beak length and degree of curvature. Hsu et al¹³ found that a preoperative distal arch angle <151° can be considered a predictor of bird-beak formation. Boufi et al¹⁴ determined that a cutoff value of 51° for the aortic angle at the deployment zone is predictive of a bird-beak configuration. In a review by Nauta et al,⁹ they reported that stent graft deployment in TEVAR landing zones 2 or 3 increased the risk of bird-beak formation. In a retrospective study, Kudo et al¹⁵ found that TEVAR landing zone 0 will be advantageous compared with landing zone 1 or 2 in terms of bird-beak formation risk and the length of the formed bird-beaks.

Fig 1.

Definition of bird-beak configuration length and angle.

Although the exact underlying cause of bird-beak formation remains poorly understood, it is evident that its mechanism of formation is multifactorial. In a commentary, Boufi and Alexandru⁷ identified the need for model-based computational simulations to better understand bird-beak configurations and investigate the effects of changing anatomic parameters.

In the present study, we hypothesized that the geometric and material properties of the aorta and stent graft would contribute to the formation of a bird-beak configuration. We tested this hypothesis using parameter-based computational models of TEVAR representative of a range of patient anatomies. The primary objective was to predict and assess the formation of a bird-beak configuration after stent graft deployment in TEVAR focused on aneurysms using computational finite element simulations. The secondary objective was to use the bird-beak length and angle as metrics to analyze and identify the stent graft and thoracic aorta (TA) geometric and material properties considered risk factors for bird-beak formation.

Methods

In silico computational models of stent graft deployment in TEVAR were developed using five parameters as variables for the simulations: aortic curvature (β), α, TA tissue mechanical properties as a function of age, TEVAR landing zone, and stent graft oversizing. Clinically relevant ranges of aortic geometry and tissue properties based on population studies were used. Several TEVAR scenarios were simulated with different combinations of these variables. In the simulation results, the length and angle of the formed bird-beaks (Fig 1) were measured and statistically analyzed with respect to the variables to characterize their effects on bird-beak formation.

TA and stent graft computational models

In silico three-dimensional computer aided design models of the TA and Zenith Alpha stent grafts (Cook Medical, Inc, Bloomington, IN) were created in SolidWorks (Dassault Systèmes Solid Works Corp, Waltham, MA). Models of the aorta were adopted from idealized models proposed previously using nonaneurysmal patient population data from the literature.¹⁶ These models span the distance from the aortic valve to the descending aorta adjacent to the diaphragm and included an aortic arch type I.¹⁷ As shown in a previous study, the presence of an aneurysm with a minimum landing zone length of 20 mm had negligible effects on bird-beak formation.¹⁶ Therefore, it was neglected in the aortic geometries to eliminate the need for several models with different aneurysm locations in the simulations of the different TEVAR landing zones. The arch profile was modeled as a semiellipse using the arch width w and height h as the ellipse axes with a constant radius r and wall thickness throughout the TA. The α was defined in a parasagittal plane as the angle between the lines that connect the arch apex to the centerline of the ascending and descending aorta at the level of the bifurcation of the pulmonary trunk (Fig 2). With a constant r, α can be defined as a function of w and h. These values were previously defined based on several population studies.16, 17, 18, 19 The three values used for α were 56.4°, 65.8°, and 75.2°.

Fig 2.

Representation of aortic arch dimensions for thoracic aortic geometry construction.¹⁶α, aortic arch angle; β, aortic curvature.

The β was defined along the lumen centerline as the angle between the coronal plane and the aortic arch in the axial view (angle between lines AD and AC in Fig 2). A center of rotation for the arch curvature angle was estimated at the centerline of the descending aorta in the axial plane. The three values used for β were 49.8°, 58.1°, and 66.4°.¹⁶

Zenith Alpha thoracic endovascular stent grafts (Cook Medical, Inc) with constant diameters and lengths of 26 and 105 mm, 28 and 109 mm, and 30 and 109 mm were used in the simulations. The 28-mm diameter is the manufacturer’s recommended sizing for aneurysms for the generated TA geometries (with a 25-mm outer diameter). The 26- and 30-mm diameters are the next available smaller and larger configurations. These stent grafts provided 4%, 12%, and 20% oversizing for our TA geometries. Because 0% oversizing is more often used for cases of aortic dissection, it was considered clinically irrelevant in the context of aneurysms and was not included in our study.

Material models of TA tissue

To define the mechanical properties of TA tissue, an age-dependent five-parameter Mooney-Rivlin model was adopted,¹⁶ which was developed based on the biaxial tensile testing data of cadaver, nonaneurysmal TA tissue from subjects aged 13 to 78 years.²⁰ Satisfactory computational results were obtained in several studies of stent graft deployment in the aorta using isotropic tissue models.21, 22, 23, 24, 25, 26 Additionally, it was shown previously that although an anisotropic four-fiber-family Holzapfel-Gasser-Ogden model exhibited a better fit than the selected isotropic model with respect to experimental data, it was too complex for computational implementation.¹⁶ The Mooney-Rivlin model, however, had a very similar fit to an anisotropic two-fiber-family Holzapfel-Gasser-Ogden model and was, hence, selected for computational simplicity. The material parameters were defined for four age groups of 41 to 50, 51 to 60, 61 to 70, and 71 to 78 years. In a previous study, the age of diagnosis for TA aneurysms for women and men was 75.9 ± 12.7 years and 62.8 ± 17.3 years, respectively, confirming the clinical relevance of the selected age ranges.²⁷

TEVAR landing zones

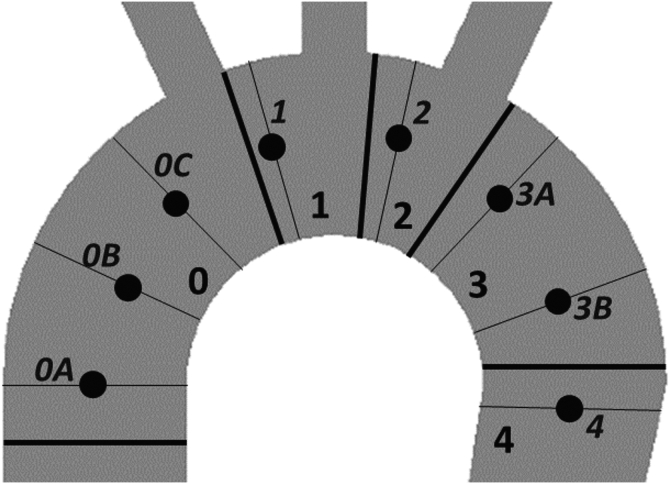
Eight locations along TEVAR landing zones 0 to 4 were selected (Fig 3).¹ Owing to the larger lengths of zones 0 and 3, multiple landing locations along them were assigned, denoted as zones 0A, 0B, and 0C and 3A and 3B.

Fig 3.

Classification of landing zones for thoracic endovascular aortic repair (TEVAR) and eight landing positions used in the simulations.

Computational models

Mesh generation of the computer aided design models of the aorta, stent grafts, and a Lunderquist guidewire (Cook Medical, Inc) was performed in HyperMesh (Altair, Troy, MI), and the simulations were performed in LS-DYNA (Livermore Software Technology, Livermore, CA). A mesh independence study was performed before running the simulations. The simulations of stent graft deployment during TEVAR were developed using a previously proposed framework.^16,21 In brief, the prestressed aorta was pressurized at the mean physiologic blood pressure of 93 mm Hg. The stent graft was crimped, tied to the guidewire, and positioned on the TA centerline. After the guidewire had reached equilibrium, the stent graft was expanded and deployed. The length and angle of the formed bird-beaks were measured using their two-dimensional projection on a plane passing through the protruded graft midline and normal to the graft surface. Numerical damping was applied during the simulations to reduce the unrealistic contact vibrations and mimic the damping properties of the surrounding tissues. Additional boundary conditions were used to constrain the translational movement of the nodes at the proximal and distal ends of the TA. An explicit time integration scheme was selected because of the nonlinearity of the problem and the large number of contacts in the computational models. Tied contacts were used between the graft and stents, and penalty-based contacts were used between all simulation parts.

Design of experiment

To understand the effects of the simulation parameters, they were considered as variables using ranges of their values. Simulations with different combinations of these variables were performed using a fractional factorial design of experiment (DOE). For β and α, three levels were considered as their mean and mean ± standard deviation (SD). Five TA geometric configurations were developed by combining the two extremes of β and α (four configurations) and their mean values (one configuration). To understand whether the aortic tissue properties will have a significant effect on bird-beak formation, only the tissue properties of the first and last age groups (41-50 years and 71-78 years) were used in the simulations. Such selections were useful in maximizing the effect of different tissue properties in the simulation results. All eight identified landing zones (along zones 0-4) and three stent graft oversizing values (4%, 12%, and 20%) were used.

The simulation scenarios were divided into three parts according to stent graft oversizing (Table I). For 4% oversizing (Table I), all combinations of the other parameters were used, which resulted in 80 scenarios. A preliminary statistical analysis of these 80 simulation results (data not shown) determined that the effect of the tissue properties for age groups 41 to 50 years and 71 to 78 years were statistically insignificant in relation to the bird-beak size. Hence, to minimize the number of simulations, only the tissue properties for age group 41 to 50 years were used in simulations with 12% and 20% oversizing, which resulted in 80 additional scenarios, for a total of 160 simulations. More details about the selection of the DOE levels and simulation scenarios are provided in the Supplementary Methods.

Table I.

Calculation of simulation scenario numbers^a

Stent graft oversizing, %	Geometric configurations (combination of α and β), No.	Age groups for thoracic aortic tissue properties, years	Landing zones, No.	Simulation scenarios, No.
4	5	41-50 and 71-78	8	80
12	5	41-50	8	40
20	5	41-50	8	40

α, Aortic arch angle; β, aortic curvature.

^aTotal number of simulation scenarios, 160.

Testing the effect of larger aortic arch diameter/width ratios

The effect of the aortic diameter was not considered in the DOE scenarios. Although using different stent graft oversizing values considers the relative effects of the aortic diameter, the arch diameter/width ratio could be significant for bird-beak formation. To test this hypothesis, additional TA geometries were developed. Because larger arch widths have been associated with larger aortic diameters, three previously defined TA geometric configurations with the largest w values were modified to increase their outer arch diameter from 25 mm to 30 mm, with maintenance of their w, h, and β values.²⁸ These modifications decreased the value of α.

For simulations with a 30-mm arch diameter, a Zenith Alpha thoracic stent graft (Cook Medical, Inc) with 34-mm diameter and 113-mm length was used (the manufacturer’s recommended oversizing). Stent graft deployment was simulated in zones 0C, 1, and 2, which had been previously shown to be more prone to bird-beak formation. The results of these nine simulations were compared with the simulation with the 25-mm arch diameter using the stent graft with a 28-mm diameter (the manufacturer’s recommended oversizing).

Results

Main effects

The bird-beak length and angle were measured and recoded for each simulation. The mean ± SD of the bird-beak length and angle across 160 simulations was 4.32 ± 4.87 mm and 9.16° ± 12.21°, respectively. For each parameter, the main effects were calculated by determining the mean of the bird-beak length and angle for every parameter level to show the overall effect of a parameter independently without considering the potential interactions (Table II). The large SD values reported in Table II resulted from the large variance in the bird-beak data. In many scenarios, no bird-beak formation occurred and in several other scenarios, the bird-beak length and angle were relatively large. The main effects did not show a consistent pattern between the β and bird-beak size. The mean bird-beak length and angle decreased as the α increased. In the simulations with 4% stent graft oversizing, the aortic tissue properties for the age groups of 41 to 50 years and 71 to 78 years were both used, resulting in 40 simulations per age group (80 scenarios in Table I). For the remaining 80 scenarios (40 with 12% and 40 with 20% oversizing), only the tissue properties of the younger age group (41-50 years) were used (Table I). To directly compare the results of the two age groups under equal conditions, the results of aortic tissue properties were grouped by their respective oversizing values (Table II). The mean bird-beak length and angle were slightly smaller in the older age group. Similarly, the results of the different oversizing values are presented by age group (Table II). For the younger age group, the mean bird-beak length decreased by oversizing and the mean bird-beak angle increased. Finally, the simulation results in the different landing zones showed that no bird-beak formations had occurred in landing zones 0A and 4. The largest mean bird-beak length and angle were found in zones 0C and 2, respectively. The calculated mean bird-beak length and angle in zone 0 (including zones 0A, 0B, and 0C) was 5.8 mm and 5.2°, respectively. The mean bird-beak length in zone 0 was smaller than that in zone 1 and was minimally larger (by 0.6 mm) than that in zone 2. The mean bird-beak angle was smaller in zone 0 than those in zones 1 and 2.

Table II.

Bird-beak length and angle at different levels of design of experiment (DOE) parameters

Variable	Bird-beak length, mm	Bird-beak angle, °
DOE parameter
β, °
49.8	4.00 ± 5.00	8.91 ± 13.17
58.1	4.76 ± 4.73	6.94 ± 8.91
66.4	3.72 ± 4.77	7.90 ± 12.59
α, °
56.4	5.46 ± 5.45	13.97 ± 15.82
65.8	4.76 ± 4.73	6.94 ± 8.91
75.2	2.26 ± 3.60	2.84 ± 4.47
Aortic tissue properties (age group)
Simulations with 4% stent graft oversizing
41-50 years	5.78 ± 5.58	9.12 ± 11.32
71-78 years	4.42 ± 4.46	6.19 ± 6.94
Simulations with 12% stent graft oversizing
41-50 years	3.85 ± 4.75	9.10 ± 13.98
Simulations with 20% stent graft oversizing
41-50 years	2.12 ± 3.78	8.04 ± 14.80
Zone
0A	0 ± 0	0 ± 0
0B	7.32 ± 5.63	3.49 ± 3.02
0C	10.04 ± 4.17	12.11 ± 4.23
1	7.25 ± 4.18	17.38 ± 14.04
2	5.20 ± 3.01	21.48 ± 18.51
3A	2.26 ± 2.19	9.96 ± 11.36
3B	0.24 ± 0.73	0.47 ± 1.41
4	0 ± 0	0 ± 0
Oversizing
Simulations with aortic tissue properties
Age 41-50 years
4%	5.78 ± 5.58	9.12 ± 11.32
12%	3.85 ± 4.75	9.10 ± 13.98
20%	2.12 ± 3.78	8.04 ± 14.80
Age 71-78 years
4%	4.42 ± 4.46	6.19 ± 6.94

α, Aortic arch angle; β, aortic curvature; SD, standard deviation.

Data presented as mean ± standard deviation.

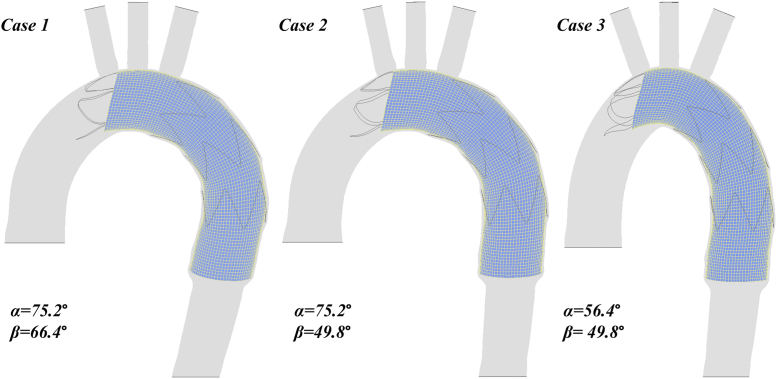
Bird-beak formation in three simulation scenarios with varying values of α and β is shown in Fig 4. Changes in β between cases 1 and 2 resulted in a minor change in the bird-beak size; however, the decrease in α from case 2 to 3 resulted in a noticeable enlargement of the bird-beak configuration.

Fig 4.

Comparison of bird-beak size in three simulation scenarios with varying aortic arch angle (α) and aortic curvature (β) values.

Statistical analysis of DOE

Regression modeling was used to analyze the DOE results and investigate the correlations between the bird-beak size and simulation parameters. The dataset was normalized before regression modeling. The DOE results were fit into several regression models and compared by their adjusted coefficient of determination. The tested linear regression models exhibited a poor fit owing to their inability to predict for cases without a formed bird-beak (bird-beak lengths and angles equal to zero). Considering the nonlinearity of the problem and the poor predictability of the investigated regression models, the random forest regression modeling method was used, which has a great predictive performance for nonlinear and high-dimensional datasets.

To fit the bird-beak dataset to a random forest model, the dataset was first split into training and test sets.²⁹ The best random forest model was found for the training dataset. The test dataset was then used to evaluate the prediction error of the model, which resulted in a coefficient of determination of 0.75 and 0.89 for the bird-beak angle and length, respectively. The reader is referred to the Supplementary Methods and the study by Breiman³⁰ for detailed descriptions of random forest regression models.

For any given regression model, a measure of the relative importance (RI) of each variable can be calculated using a permutation procedure, which involves creating a new auxiliary dataset by randomly permuting the values of the variable under consideration and maintaining the other variables unmodified. The importance of the variable is calculated as the difference in the predictive performance of the model with the original and permuted data. After normalizing the mean values of the RI for easier comparison, the SD of the normalized values can be calculated to test the hypothesis for the significance of the importance metric, as reported by Mentch and Hooker.³¹ A P value of <10% was considered statistically significant. The landing zone and α value (Table III) were the most important variables for the prediction of the bird-beak angle and length, although the bird-beak length was also influenced by oversizing.

Table III.

Relative importance for each independent variable calculated using permutation method

Variable	Bird-beak length		Bird-beak angle
	Normalized RI	P value	Normalized RI	P value
β	0.011098 ± 0.003952	1.00	0.008942 ± 0.003257	1.00
α	0.154564 ± 0.054885	2.515693e-21	0.384650 ± 0.076892	1.464670e-30
Tissue properties	0.054885 ± 0.015497	1.00	0.005301 ± 0.001016	1.00
Landing zones	0.641460 ± 0.088382	8.062982e-41	0.552169 ± 0.070040	6.583712e-42
Oversizing	0.137993 ± 0.024266	4.399582e-15	0.048938 ± 0.010615	1.00

α, Aortic arch angle; β, aortic curvature; RI, relative importance.

Data presented as mean ± standard deviation.

An alternative analysis is the calculation of the Sobol sensitivity indexes, which can provide a measure of variable interactions.³² The first-order and total sensitivity indexes for each variable and their error bars are shown in Fig 5. The first-order indexes were used to quantify the main effect. The total indexes included the main effects and total effects of all interactions involving that variable. A difference between the first-order and total indexes indicated the presence of interactions. The Sobol first-order indexes coincided with the permutation importance values (Fig 5; Table III). Additionally, the only interactions were between the α and the landing zone for the bird-beak angle. All interactions for the bird-beak length were negligible in comparison (note the vertical scale).

Fig 5.

Sobol first-order (S_1) sensitivity indexes for bird-beak length (1A) and bird-beak angle (1B), and Sobol sensitivity indexes for two-way interactions for bird-beak length (2A) and bird-beak angle (2B). α, Aortic arch angle; β, aortic curvature; S_T, total sensitivity index.

Results of simulations with increased aortic diameters

The results of nine simulations using the 30-mm outer aortic diameter were compared with those using the 25-mm aortic diameter. In all simulations with the 30-mm diameter, the size of the bird-beak configuration had increased compared with that using the 25-mm diameter.

Discussion

DOE outcomes

Statistical analysis showed that the most significant contributors to the bird-beak length and angle were the landing zone, α, and oversizing. The tissue properties and β were statistically insignificant in the prediction of bird-beak formation. For the bird-beak length, a significant interaction was found between α and the landing zone, which refers to enlargement of the bird-beak in landing zones near the arch apex that was more prominent with smaller α values. However, these results only correspond to the Zenith Alpha stent graft (Cook Medical, Inc) and should not be generalized to other devices without further investigation.

Aortic geometry

Analysis of the DOE results with respect to the aortic geometries showed an inverse relation between the α and the bird-beak size, although β had insignificant effects on the bird-beak configuration. Previous literature has shown similar findings because deployment of a stent graft in a small α will require larger stent graft bending. The spring back force, defined as the force applied to the greater wall of the aorta by the stent graft, results from poor flexibility of the stent graft.³³ The large bending of the stent graft in an aorta with a smaller α will generate a greater spring-back force, leading to straightening of the stent graft inside the aorta and enlarging the bird-beak gap.

Age and aortic tissue properties

A comparison of the mean bird-beak size between the two age groups showed that the bird-beak geometries were minimally larger in the younger age group. This might have resulted from the increased radial forces induced by the stiffer aortic tissue in the older age group and the inability of the stent graft to straighten inside the stiffer artery walls. However, the difference between the two age groups was minor, and the statistical analysis demonstrated that the role of the aortic tissue properties in bird-beak formation was insignificant.

TEVAR landing zone

The mean bird-beak angle was smaller in zone 0 than that in zones 1 and 2. These results are similar to the early postoperative results of a population study, in which the mean bird-beak length and angle were smaller in zone 0 than in zones 1 and 2.¹⁵ In addition, the largest formed bird-beaks in these three zones were found in geometries with the smallest α, consistent with the observations from two previous studies.^13,34 In those studies, the bird-beak formation in zone 2 was significantly associated with the aortic arch geometries with a steep arch curvature change between zones 2 and 3, characteristic of aortic arch geometries with a small α.^13,34 Future advances in stent graft design and device modifications for the landing zones prone to bird-beak formation might be beneficial in reducing bird-beak occurrence.

Oversizing

To evaluate the effect of oversizing, the simulations with the smallest oversizing (4%) were used as the baseline. Oversizing had different effects on the bird-beak size with the different landing zones and TA geometries. In landing zones 0A, 0B, 3B, and 4, no bird-beak configuration had formed in 75% of the baseline simulations. In the remaining 25% with bird-beak configurations, oversizing either fully resolved the presence of the bird-beak or reduced the bird-beak length and angle size, likely owing to the increased radial forces. In landing zones 0C, 1, 2, and 3A, oversizing either resolved the presence of the bird-beak or reduced the length and angle of the formed bird-beaks in ∼50% of the scenarios. In the remaining 50%, oversizing minimally reduced the bird-beak length but increased the bird-beak angle. The enlargement of the bird-beak angle mainly occurred in landing zones 0C, 1, and 2 and was more prominent in scenarios with a smaller α.

A factor that contributes to bending resistance is the second moment of inertia I, which is a geometric characteristic of the bending body’s cross-section.³⁵ For thin-walled cylinders, I can be defined as follows:

$$I=\pi {r_C}^{3}t\text{,}$$ (1)

where r_C is the cylinder radius, and t is the cylinder wall thickness. Because t is constant across all used stent grafts, oversizing would increase I. In TEVAR scenarios with a smaller α and landing zone closer to the arch apex, effective stent graft conformation will require greater proximal stent graft bending. In such scenarios, a stent graft with a larger diameter could pose a disadvantage owing to its larger I and, thus, reduced bending ability. A study by Demanget et al³⁶ also confirmed that the stent graft design parameters will significantly affect its bending flexibility.

Modeling the protruded portion of the stent graft adjacent to the bird-beak configuration as a fixed-end cantilever, a simplified relationship for the bending deflection δ and the angle of deflection φ for the proximal end of the deployed stent graft (Fig 6) can be defined as follows³⁵:

$$\delta =\frac{F{L}^3}{3EI}\text{,}$$ (2)

$$\phi =\frac{F{L}^2}{2EI}\text{,}$$ (3)

where F is the load acting on the bending part, L is the length of the bending part, and E is the Young’s modulus of the stent graft. Assuming t (Eq 1), F, and E (Eq 2 and Eq 3) to be constant across all scenarios and L to be equal to the bird-beak length (Fig 6), it can be concluded that at the proximal end of the stent graft, δ and φ would correlate, respectively, with the following:

$$\frac{L^3}{r^3}\text{,}$$ (4)

$$\frac{L^2}{r^3}\text{.}$$ (5)

Fig 6.

Representation of protrusion (bird-beak) length L and the protruded part of the stent graft (dashed area) modeled as a cantilever. δ, Bending deflection; φ, angle of deflection.

In most of the scenarios in which oversizing resulted in enlargement of the bird-beak angle, the bird-beak length L did not change significantly with oversizing. Considering the similarity of L among these cases, Eq 4 and Eq 5 justify that a larger stent graft radius r_C would result in smaller values of δ and φ during bending, which would translate into poor stent graft bending and an increased bird-beak angle. A similar observation was reported by Hsu et al¹³ for stent grafts landing in the distal arch. Hsu et al¹³ hypothesized that the inner curvature of the arch acts as a fulcrum and that the rigidity of the stent graft, along with the blood flow wind-sock effect, can lead to protrusion of the proximal stent graft and bird-beak formation. The bird-beak angle can be further enlarged by the blood flow force applied to the stent graft's protruded undersurface.¹³

Effect of larger aortic diameter

Increasing the aortic arch diameter from 25 mm to 30 mm in nine simulations enlarged the bird-beak size. Increasing r, with h and w maintained, decreased α. Considering the similarity of the stent graft oversizing in the two sets of simulations (12% vs 13.3%), the decrease in α in simulations with a larger r might be the reason for the enlarged bird-beak sizes. This is consistent with the DOE findings showing that α was inversely correlated with the bird-beak length and angle.

Effect of bird-beak length and angle on hemodynamics

Several studies have investigated the hemodynamics of blood flow in the bird-beak configuration site. In a postoperative TEVAR study, the aortic hemodynamics in the presence of a bird-beak were analyzed and a transmural pressure gradient of ∼10 mm Hg was found between the luminal surface of the stent graft and its undersurface at the bird-beak gap.² In a similar hemodynamics study, the effects of the bird-beak length and angle were analyzed independently in eight scenarios, in which the maximum transmural pressure load was found in the case with the largest bird-beak length.²³ Although both the bird-beak length and the angle had an effect on increasing the transmural pressure gradient, the bird-beak length played a primary role. In another computational study, a high transmural pressure gradient and stent graft displacement were observed with bird-beak lengths >21 mm.³⁷ In a postoperative TEVAR study, longer lengths of bird-beak were associated with a greater risk of type Ia endoleaks.³ From these studies, it can be concluded that the bird-beak length plays a more significant role than does the bird-beak angle in increasing the transmural pressure gradient and, hence, the risk of stent graft infolding and type Ia endoleaks. Although the effect of a bird-beak deformity on hemodynamics has been widely studied, to the best of our knowledge, at present, no finite element studies have focused on the initial formation of bird-beaks. The findings from the present studies complement those from previous studies by investigating the underlying mechanism of bird-beak formation and its contributing geometric and mechanical factors during stent graft deployment. Hence, the hemodynamics of blood flow were neglected, and only static blood pressure was applied.

Advantages of parameter-based in silico models

In silico models of TA have been used in several computational studies and achieved satisfactory numerical results.38, 39, 40, 41, 42, 43, 44, 45 In the present study, several sources for population-based data were used to obtain realistic and clinically relevant ranges for the TA geometric parameters. The advantage of the proposed parameter-based approach was that it allowed for developing TEVAR scenarios that are not easily attainable with patient-specific data. These models have provided valuable insight into the factors that are predictive of bird-beak formations. As a part of future studies, the accuracy of the developed models in predicting the bird-beak size will be validated using patient-specific data. Nonetheless, the size of the formed bird-beaks in the present study can be considered a relative value, and our results show the trends in which the bird-beak length and angle were affected by each simulation parameter. The findings from our study can inform the surgical planning and device selection process for each patient to minimize bird-beak formation, reducing bird-beak–related complications and improving patient outcomes. These findings have confirmed that a smaller α and smaller landing zones near the arch apex are more hostile in terms of bird-beak formation. In such cases, additional emphasis must be placed on selecting the optimal stent graft design and oversizing and potentially moving the landing zone to a straighter area within the TA. Although the initial focus of the present study was the repair of thoracic aortic aneurysms, this approach can be extended to other pathologies treated with TEVAR to create a more comprehensive TEVAR surgical planning tool.

Study limitations

Although the simplified TA computational models provided the possibility for testing a wide range of aortic geometries, they had some limitations. First, the two extreme cases of aortic geometries developed comprised the maximum w combined with the minimum h, and vice versa. These two TA configurations might be less clinically relevant, although their h/w ratios were within realistic ranges. Second, owing to the unavailability of other population-based data sources, the study data used for the ranges of β and α only included the north Indian population.¹⁷ Patient demographics can pose a limitation for defining realistic ranges for these parameters. Third, in the present study, only aortic arch type I was considered. In two previous population studies, no association was found between the arch type and bird-beak formation.^46,47 Therefore, the inclusion of other arch types likely would not have influenced the results of our study. The fourth geometric limitation was the use of a constant arch diameter, although, in reality, its diameter will vary along its length. A tapered shape of the arch might have required a tapered stent graft that varies in the proximal and distal diameters. This effect was considered by the testing of different stent grafts oversizing values. In addition, testing the effects of different aortic diameters demonstrated that the decrease in α, caused by enlarging r, was the main reason for the enlarged bird-beaks. Finally, instead of modeling the helical shape of the aorta, a center of rotation was considered for the aortic curvature. Although this is a simplification, in the simulations with landing zones adjacent to this center of rotation (zones 3B and 4), which possess a sharp local curvature, the bird-beak size was either small or did not occur. These results did not change significantly when varying the value of β from 49.8° to 66.4°. This suggests that modeling the helical shape of the aorta would likely have insignificant effects on bird-beak formation.

For the tissue properties, using the youngest age group (41-50 years) for most of the simulations might be less clinically relevant for patients with aneurysms compared with the older age group. However, such a selection was made to develop more cases with bird-beak configurations for data analysis, because bird-beak formation was eliminated in the older age group in some scenarios. Despite the minor variance between the different age groups, the tissue properties were shown to be statistically insignificant. Therefore, using the tissue properties of the younger age group potentially did not affect the overall study results. Finally, results are only specific to the Cook Zenith Alpha stent graft (Cook Medical, Inc).

In the present study, application of TEVAR methods such as chimney, periscope, or sandwich techniques, were not considered, which might have affected the bird-beak configuration. In all the simulations, only Cook Zenith Alpha thoracic stent grafts were used. This is because in a subsequent patient-specific study, Cook Zenith Alpha stent grafts were used in most of our patient cohort, which provided an opportunity for comparison and validation of the idealized simulation results. Other stent graft designs could affect these results and will be considered in a future study.

Some of the inherent limitations of the computational algorithm include neglecting the hemodynamic effects of blood flow and pulsatile movement of the vessel, which can affect the stent graft deployed position. In addition, the surrounding tissues and structures were not included in the computational models. Instead, boundary conditions were imposed to estimate their effects. A method was used to pre-stress the vessel to a zero pressure configuration before applying blood pressure. However, in this method, residual stresses were not considered. Homogeneous tissue properties were used throughout the TA, although these properties vary axially and circumferentially.

Conclusions

A lack of proximal stent graft apposition to the lesser curvature of the TA during TEVAR can lead to the formation of bird-beak configuration. The bird-beak length and angle have been shown to directly correlate with the risk of type Ia endoleaks and were used in the present study as metrics to investigate the role of aortic geometry, tissue properties, landing zone, and stent graft oversizing on bird-beak formation in a set of parameter-based TEVAR computational simulations. A designed simulation experiment was conducted, followed by statistical analysis of the simulation data, which identified the α, landing zone, and oversizing as the most significant contributors to bird-beak formation and size. The proposed method could be useful in the selection of the optimal stent graft design and procedure modifications to minimize bird-beak formation in patients undergoing TEVAR.

Author Contributions

Conception and design: NS, DR, TF, CA

Analysis and interpretation: NS, DR, TF, CA

Data collection: NS

Writing the article: NS, DR

Critical revision of the article: NS, DR, TF, CA

Final approval of the article: NS, DR, TF, CA

Statistical analysis: NS, DR

Obtained funding: TF, CA

Overall responsibility: NS

Supplementary Methods

Material models of thoracic aorta tissue

The Mooney-Rivlin model used in the present study was defined as follows:

$$W=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)+C_{20}{\left(I_1-3\right)}^2+C_{11}\left(I_1-3\right)\left(I_2-3\right)+C_{02}{\left(I_2-3\right)}^2$$ (1)

where W, I_i, and C_ij are the strain energy density function, strain invariants, and constitutive material parameters, respectively. The constitutive material parameters for C_ij were defined for four age groups: 41 to 50 years, 51 to 60 years, 61 to 70 years, and 71 to 78 years.

Thoracic endovascular aortic repair landing zones

To ensure the consistency of the landing locations in the simulations with different thoracic aortic geometries, each of the eight identified landing zones (along zones 0-4) were defined numerically as the arc length of the vessel centerline between the aortic root and the respective proximal landing location, normalized by the total centerline arc length from the aortic root to the descending aorta at the level of the aortic root. The normalized values corresponding to landing zones 0A, 0B, 0C, 1, 2, 3A, 3B, and 4 were 0.14, 0.27, 0.41, 0.51, 0.59, 0.68, 0.81, and 0.95, respectively.

Additional details on mesh generation and the mesh independence study

Because the thickness of the vessel and graft fabric is significantly smaller than their other axes, they were meshed using 1-mm triangular and 1-mm quadratic shell elements, respectively. Similarly, owing to the significantly small ratio of the guidewire and stent diameters compared with their other dimensions, they were meshed using 1-mm and 0.6-mm circular beam elements, respectively. The mesh independence study was performed, with emphasis on the displacements and stresses, in particular, near the proximal attachment site of the stent graft and the bird-beak configuration. The average number of nodes for the vessels, grafts, and stents was 8318, 6160, and 1870, respectively, and their average number of elements was 16,495, 6090, and 1870, respectively.

Design of experiment

To determine the various simulation scenarios with different values of the simulation parameters, a fractional factorial design of experiment (DOE) was used. This statistical method allows for the analysis and prediction of the output response of experiments using only a subset of all possible combination of variables. In the present study, the DOE was used to effectively select the minimum number of possible parameter combinations and simulation scenarios and still obtain the required information.

Additional details on the selection of DOE levels

With the assumption of a constant arch radius r, the aortic arch angle α can be defined as a function of the arch width w and height h. The parameter values w and h corresponding to each value of α used in the present study are listed in the Supplementary Table. These values corresponded to a 25-mm thoracic aortic diameter. Five thoracic aortic geometric configurations for the simulations obtained from combining different values of β and α are also presented in the Supplementary Table. The two extremes of aortic curvature (β = 49.8° or 66.4°) and aortic arch angle (α = 56.4° or 75.2°) were combined. In addition, a geometric configuration with their middle values (β = 58.1° and α = 65.8°) was selected to obtain information about potential interactions between β and α in relation to bird-beak formation.

Statistical analysis of 80 simulations with 4% stent graft oversizing (using both age groups for aortic tissue properties) determined that the tissue properties were statistically insignificant in relation to the bird-beak length and angle. The tissue properties of the older age group reduced or eliminated bird-beak formation. Hence, the younger age group was selected for simulations with 12% and 20% oversizing to generate more cases with formed bird-beak configurations for data analysis purposes. The simulations with 4% oversizing (using two age groups) allowed for the analysis of the effect of the tissue properties on bird-beak formation and any interactions between the tissue properties and other simulation parameters.

Additional details on DOE statistical analysis

For regression modeling, the aortic tissue properties were considered as the only categorical parameter. All other parameters were considered as continuous numerical values. The landing zone was presented as the normalized value of the arc length from the aortic root, previously calculated. In addition, the values of stent graft oversizing were replaced by the diameters of the used stent grafts (26, 28, and 30 mm). To scale the data using different units and ranges before regression modeling, the dataset was normalized using the z-score method (also known as standardization), such that the mean and standard deviation of the dataset were 0 and 1, respectively.

Regression models

During the regression modeling, initially, linear regression models were tested, which exhibited a poor fit with a adjusted coefficient of determination value of 0.27 and 0.18 for bird-beak length and angle, respectively. A major shortcoming of such linear models is their inability to predict bird-beak lengths and angles equal to zero, which represent cases without a formed bird-beak configuration. An acceptable regression model would be one that could predict bird-beak length and angle values equal to zero in a large number of scenarios and predict nonzero values in other cases. Owing to the nonlinearity of the problem and the poor predictability of the analyzed regression models for cases without bird-beak formation, the random forest regression modeling method was used.

Random forest model

Given the poor predictability of the linear regression models for cases without bird-beak formation, random forest regression modeling was investigated. Random forests are a part of the family of ensemble methods. A random forest is a collection of shallow decision trees and can be used for either regression or classification tasks. Decision tree regression models split the data set recursively, using a different independent variable and threshold value in each node to maximize the similarity (ie, minimize the impurity) of the data in each child node. A decision tree is fit to a given data set by modifying the maximum depth of the tree, minimum number of samples allowed in a terminal node, and minimum number of samples allowed in an internal node. In a random forest, instead of using a single decision tree for prediction, a collection of trees is used, and their predictions are averaged. It has been shown that by averaging the predictions of many shallow trees, each fitted to a different subset of the data, the predictive accuracy will improve and the predictive variance will decrease.²⁵ The reader is referred to the study by Breiman for detailed descriptions of the underlying theory (Breiman L. Random forests. Machine Learning 2001;45:5-32).

In the present study, a random forest model was fit to the bird-beak data set using a grid search cross-validation procedure, as implemented in the open-source Python library scikit-learn (Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: machine learning in Python. arXiv:12010490 [cs]. Published June 5, 2018). In brief, the dataset is first split into training and test sets. The training data set is split into five folds, a random forest model with the given parameters is fit using data from four folds, and its error is measured using the hold out data. This procedure is repeated five times, and the average cross-validation error is calculated for this model. By repeating this procedure for different combinations of model parameters, the best random forest model will be found for the training data. Once fit to the training data set, the test data set can be used to evaluate the prediction error of the model.

Supplementary Table.

Values of w and h for each target α and definition of α and β values for five thoracic aorta geometric configurations using 25-mm outer aortic diameter

TA geometric configuration	β Level, °	α Level, °	w and h Level corresponding to each α, mm
			w	h
1	58.1°	65.8°	76	46.36
2	66.4°	75.2°	86	43
3	66.4°	56.4°	66	49.5
4	49.8°	75.2°	86	43
5	49.8°	56.4°	66	49.5

α, Aortic arch angle; β, aortic curvature; h, arch height; TA, thoracic aorta; w, arch width.