Near real time monitoring and forecasting for COVID-19 situational awareness

Abstract

In the opening months of the pandemic, the need for situational awareness was urgent. Forecasting models such as the Susceptible-Infectious-Recovered (SIR) model were hampered by limited testing data and key information on mobility, contact tracing, and local policy variations would not be consistently available for months. New case counts from sources like John Hopkins University and the NY Times were systematically reliable. Using these data, we developed the novel COVID County Situational Awareness Tool (CCSAT) for reliable monitoring and decision support. In CCSAT, we developed a retrospective seven-day moving window semantic map of county-level disease magnitude and acceleration that smoothed noisy daily variations. We also developed a novel Bayesian model that reliably forecasted county-level magnitude and acceleration for the upcoming week based on population and new case count data. Together these formed a robust operational update including county-level maps of new case rate changes, estimates of new cases in the upcoming week, and measures of model reliability. We found CCSAT provided stable, reliable estimates across the seven-day time window, with the greatest errors occurring in cases of anomalous, single day spikes. In this paper, we provide CCSAT details and apply it to a single week in June 2020.

1. Introduction

The outbreak of COVID-19 in the United States in late February 2020 created a public health maelstrom with complex economic, security, and communication crises in its wake. Initial uncertainty surrounding modes of transmission and certain population dynamics that might expedite or abate progression created considerable concern, and even panic, across virtually every sector of the U.S.. There was an urgent need to characterize and project the growth of COVID-19 with a focus on the timing and location of new case spikes that could overwhelm healthcare systems and lead to catastrophic death and suffering. Mechanistic epidemiological models, such as the Susceptible-Infected-Recovered (SIR) model or its variants SEIR (exposed) and SEIRS (return to susceptible) have a successful history of responding to this kind of need and are a natural first choice for modeling the spread of infectious disease; Brauer (Brauer, 2008) provides a detailed overview. These models do require adequate data on susceptible, exposed, and recovered populations as well as infection disease rate estimates. Unfortunately, the COVID-19 data landscape was widely varied, uncertain, and constantly changing. These conditions severely hampered the use of these models in the early months.

Early aggregation efforts by John Hopkins University (Johns Hopkins, University of Medicine, 2020) and The New York Times (NY Times) (The New York Times, 2020) focused on developing daily new case updates by aggregating open source public health data at the state and county level. This was possible because new case data was fairly consistent in delivery and definition across U.S. public health portals. A deeper look, however, revealed this was not the norm. The data landscape was actually a rich and rapidly evolving ecosystem of state and local strategies fielding a wide variety of data types, data definitions, schema, reporting strategies, and delivery mechanisms. As the weeks unfolded, the increase in volume and variety of data across these portals was matched only by the speed in which schema and delivery solutions were changed without notice. For example, Knox County, Tennessee defines a recovered case as “a person released from isolation” (Knox County Tennessee Health Department, 2020). However, the state of Tennessee requires a recovered case to “(1) have been confirmed to be asymptomatic by their local or regional health department and have completed their isolation period or (2) are at least 21 days beyond the first test confirming their illness” (TN Department of Health, 2020). Under this scenario an individual could be classified as recovered in Knox County but not be included in Tennessee's state recovery total. This was not an isolated case. This lack of a common data standard meant that harmonizing and integrating county-level data into a consistent view across the U.S. was an extraordinary effort for most other attributes, often incurring heuristic conflation solutions. There is a clear need for public health data standards that serve research and public health communities alike. Efforts by these authors to curate and harmonize the data at scale are well beyond the scope of this work but will be published in a forthcoming paper.

Against this backdrop, producing stable, long range forecasts at scale was very difficult. Attention was given to shorter term capabilities that could reliably support decision making on a one-to two-week cycle. This capability would greatly benefit near-term decision making by allowing authorities to be informed and intentionally react to imminent trends at the county, state, and federal level. Pressing questions include:

• ●How bad is the situation in my jurisdiction and is it getting worse or better?
• ●Are things getting better or worse overall across the nation?
• ●How many new cases should I anticipate next week?
• ●How well do the weekly predictions match reality?

Answering these questions at the county scale was particularly hampered by two prevailing factors. First, visualizing the daily disease dimensions of severity and growth over 3000+ counties required a careful visualization and monitoring strategy. Secondly, predicting future case counts in an uncertain data environment is further challenged by the presence of numerous counties with small populations and sparse daily new case counts. This can lead to rates based on small numbers which can be unreliable.

In March 2020, enabled by the CARES Act, the U.S. Department of Energy (DOE) established the National Virtual Biotechnology Laboratory (NVBL) to address key challenges associated with the COVID-19 crisis (Buchanan & Streiffer, 2020). The broad scientific and technical expertise and resources of DOE's 17 national laboratories were organized under NVBL to address a range of issues including monitoring and modeling of the COVID-19 pandemic. Under NVBL the COVID County Situational Awareness Tool (CCSAT) was developed as a data-driven solution, leveraging robust spatio-temporal techniques in statistics, visualization, and decision support. The aim of CCSAT was to inform decision makers about county-level disease progression within the past seven days, to forecast progression in the upcoming seven days, and to assess the larger fine-scale (i.e., county) national trends. The model was developed and deployed in the opening months of the pandemic. Results from the model were submitted weekly to the U.S. DOE to inform situational awareness and a web tool implementation of a Bayesian nowcast model ultimately adopted by the Tennessee State Data Center (Tennessee State Data Center, 2021).

1.1. Literature review

The volume of literature on characterizing and predicting the spread of COVID-19 is significant and continues to grow even at the time of this writing. Here we provide a brief synopsis of recent and ongoing work and situate the CCSAT model within this larger context.

Historically, the epidemic curve is used to understand disease growth and has long been used as a metric (Wilson & Burke, 1942). However, most works estimate the curve under the assumption of a fixed number of susceptible individuals (Blackwood & Childs, 2018; Lanzas et al., 2020), an unknown quantity in the early stage of this pandemic. More recently, for ongoing epidemics such as SARS and measles, people began to calculate the time derivative of epidemic curves, which yields the number of new cases over a time interval (Rozema, 2007). Looking at the first derivative of the data provides a useful metric because its calculation does not require knowledge of the total number of susceptible individuals. Similarly, research on the epidemic curve's second derivative has helped identify inflection points during the SARS epidemic (Chen et al., 2008), which provides a basis measurement for when case counts are accelerating or decelerating. One of the most notable works Wu et al. (2020) warned of the potential for an epidemic after estimating R ₀ values in Wuhan. Later work Calvetti et al. (2020) estimated county-level transmission rates of COVID-19 as well as ratios of asymptomatic to symptomatic individuals. Unlike our tool, this work was localized to less than 40 counties. Similar county-level work was done in NYC and tried to predict the effectiveness of COVID-19 control strategies using an adapted SIR model Albani et al. (2021c). Some work, took a similar hierarchical Bayesian pure spatiotemporal modeling approach and looked at estimating the relative risk of COVID-19 Jaya and Folmer (2021). Zhou et al. (2020) represents mechanistic modeling work most closely related in resolution and scale to CCSAT. The authors developed a rich model that accounted mechanistically for several factors including mobility, travel, infection rates, this that and the other. The authors note that those factors were not typically available at the county-level and so various assumptions and application of state values for county-level parameters were required impacting objectivity and creating unusual artifacts in the modeling output. Nonetheless the model is well positioned for expansion and inclusion of these data as it becomes available. It is worth noting that agent based modeling approaches have also been explored (Faucher et al., 2022; Kerr et al., 2021; Kumar et al., 2021; Wang et al., 2021). However, agent based approaches are typically aimed at targeted scenarios, spatially limited, or even theoretical (e.g. Wang et al., 2021) and are beyond the scope of the CCSAT effort.

Under-reporting (UR) is a common problem in the COVID-19 pandemic. An excellent survey on methods for dealing with under-reporting is available in Gibbons et al. (2014) including community-based studies such as seroprevelance surveys, returning traveller studies, capture-recapture studies for European incidence of salmonellellosis and campylobacteriosis. Recent papers apply and expand on these approaches in the case of COVID-19 including Albani et al. (2021a); Angulo et al. (2021); Lau et al. (2021); Whittaker et al. (2021). Since these data were largely unavailable or unreliable at the time at county-level we elected to move forward without addressing this challenge in the current version, focusing entirely on the prediction of new cases as reported by the NY Times.

Newly accessible mobility data in 2020 from companies such as SafeGraph (2020), Google (2020), and Apple (2020) facilitated important research in the relationship between mobility, social distancing, and COVID-19. Recent literature shows promising efficacy for mobility especially in the estimation of lagged effects (two to five weeks) between mobility changes and COVID-19 progression differences (e.g. Bushman et al., 2020; Cot et al., 2021; Sulyok & Walker, 2020). Hu et al. (2021) provide an excellent overview and comparison of recent publications. There are a number of challenges and concerns in using this kind of mobility data. For example, Hu et al. (2021) points to a number of open challenges and concerns with mobility data including privacy concerns and how to choose and integrate multi-source mobility data properly. Coston et al. (2021) show that these data are biased and can disproportionately harm high-risk elderly and minority groups. Additional caveats exist in using these data at the county-level. For example, Google warns against long study periods as their understanding of facility use has changed over time. Google further warns that counties and categories with insufficient data are omitted. For example, in a Google report dated 5/29/2022, of Tennessee's 95 counties, 44 are missing 50% of mobility data, 25 are missing 83%, and two have none at all. These problems are prevalent and led authors to postpone their use in CCSAT.

In the main, mechanistic approaches were unduly hampered by poor local information without a significant number of assumptions and approaches that rely on mobility, death rates, vaccinations, hospitalization, death rate, and seroprevelance data where too incomplete at the county-level to serve a weekly operational tempo and be included in CCSAT. Instead, we took a different approach for nowcasting; we developed an entirely data driven model requiring only county-level, new case data to provide operational answers to the those primary questions (previously mentioned). While this may miss opportunities in small areas where detailed data do exist, we show that the approach scales well to 3300+ counties producing reliably accurate results on a weekly tempo.

Specifically, CCSAT brings forward three fundamental capabilities for supporting decision makers at an operational cadence under conditions of data scarcity.

• ●A bivariate mapping approach for conveying stable, near term measures of county-level growth and growth acceleration
• ●A straightforward approach for assessing national county and population disease dynamics over time
• ●A statistical near-term forecasting model for producing stable estimates of upcoming new case totals at the county-level

We now develop the details of the CCSAT and demonstrate its use during June 2020, an early and unstable month of the pandemic. Details on how to access source code and data are available in the Supporting Information section.

2. Materials and methods

The aim for CCSAT was to provide both a retrospective analysis of disease progression and a statistical prediction of future progression for each of the 3000+ U.S. counties. From there, aggregations and analyses at the state and federal level are also possible. The decision was made to choose a seven-day interval for both prospective and retrospective analysis. This was motivated by the need to balance the pace and variability of COVID-19 progression with the ability of policy-makers and crisis managers to engage with measured responses. Monitoring and predictions over a shorter time interval (e.g., daily) were possible but had higher variations and did not align with the pace of decision making. The seven-day window also provided several beneficial analytical properties. For example, data collected daily could be noisy especially in regions with small populations. In other cases, public health portals would sporadically upload multiple days of new cases on a single day (Monday was popular for batch weekend updates). Aggregation over seven-day blocks (both past and future) tends to produce smoother data that is more easily interpreted and predicted. Within this moving window two seven-day models were utilized. For a retrospective analysis of the previous seven days we developed the Velocity and Acceleration (V&A) cartographic model. Prediction of new cases in the upcoming seven days is handled by a novel Bayesian nowcast model (nowcasting refers to very near-term predictions). We continue now with a description of each.

2.1. Velocity and acceleration maps

We define velocity as simply the current cumulative new case load for a seven-day period. Acceleration is how much faster (or slower) the current case load is over the previous seven-day total (i.e., this week's new cases vs last week's new cases). It is simply the ratio of the most recent seven-day new case count with the previous seven. Using data from the NY Times, the number of new case counts for all 3000+ U.S. counties was tracked and normalized by county population. To report velocity, a county is labeled as low, middle, or high based on whether it falls respectively into the lower, middle, or upper third of new county cases per capita nationally. The acceleration of a given county is the ratio of this week's growth to last week's growth. A county is labeled as decelerating, constant, or accelerating if the ratio falls within the intervals [0–0.9], [0.9–1.1], or [ > 1.1], respectively. Through experimentation we found a 10% interval around a constant value of 1 struck a practical balance between the need for interpretable results and the need to detect small but real growth patterns. We found that using smaller intervals (e.g., 1%) produced chaotic county-level oscillations between deceleration and acceleration, obscuring larger trends with small scale noise. Choosing a larger percentage (e.g., 20%) tended to obscure smaller important trends. Ultimately, the percentage is only a parameter and can easily be modified to suit different conditions.

In the next step, we convey these two within a bivariate map legend that allows decision makers to jointly observe COVID-19 velocity and acceleration behaviors. While adaptations to the number of categories is easily done, choosing three each for velocity and acceleration has appealing cartographic qualities. First, the bivariate legend will present 9 joint categories, a recognized upper limit for human interpretability that can be traced back as far as Miller's formal cognitive work (Miller, 1956). Secondly, choosing labels of (low, middle, upper) and (decelerating, constant, accelerating) provides a nice symmetry that responds to the need to understand conditions “bettering, unchanging, or worsening” along separate and joint metrics. Choosing more categories will likely put pressure on human interpretabilty. Choosing fewer will break with the need to understand caseload dynamics at their simplest semantic level. Using the velocity and acceleration rules above, each county is semantically tagged with velocity and acceleration and mapped using the joint 3 × 3 bivariate legend. In this manner, it is easy to visualize counties with high velocity and high acceleration, low velocity and low acceleration, and so forth. Ultimately this responds to the need to simultaneously know “How bad is this and are things getting worse?” at the county-level. Two important properties arise from this approach that proved valuable in our experience. First, the computation is straightforward and well understood by a less technical decision maker, an important confidence feature in an uncertain and changing environment. Secondly, as a seven-day approach, the results were relatively stable with transitions from week to week that were consumable and interpretable.

2.2. Acceleration graphs

In addition to the map, we temporally characterize the national outlook by computing a daily V&A map providing a continuous seven-day moving window. On each day, the number of counties that fall into the decelerating, accelerating, or constant velocity categories were represented as a stacked area graph over time. This provided a visualization of the national status as a whole allowing easy inspection of national disease progression at finer county-level scales.

2.3. Bayesian nowcast model

At the time of development and writing of this paper, between March and June of 2020, the combination of an uncertain and evolving data environment with a pressing demand for useable predictions motivated the development of a forecasting model based only on the underlying population and the temporal progression of new cases. Indeed because of the tight linkage between COVID-19 and population as both a target and mode of transmission, we reasoned that a model based only on these two inputs might quickly produce and operationalize viable near-term estimates. In parallel to our model development, sparse data constraints elsewhere also motivated other researchers to develop and apply Bayesian disease models that could operate with little data, such as Jaya and Folmer (2021), who develop and apply a Bayesian spatiotemporal forecasting model for the identification of COVID-19 hotspots in West Java Province, Indonesia. For a recent and extensive review on the history and development of the field of Bayesian disease mapping see MacNab (2022).

It is worth noting that as time moved forward other information on mobility, policy, and more demographic insights became available. Interesting future work may focus on the value of these other inputs in improving near-term predictions of our models in cases where transmission dynamics are better known and reliable data is available. The goal of the present nowcast model is to estimate the total number of new cases in the upcoming week for each U.S. county.

We approach this challenge by estimating the number of daily expected new cases, E[Y _it], for each county i and day t, then aggregating the total across all seven days. Conceptually this is a straightforward modeling task, however, three main challenges needed to be addressed to ensure a single robust model with reliable new estimates for each day for every county in the U.S. regardless of population size or the size of previously observed outbreaks.

• 1.How to appropriately capture the day-to-day variation of observed new cases within a county?
• 2.How to characterize the shifting temporal dynamics of this variation as new cases grew and declined at different rates across the U.S.?
• 3.How to do so in a manner that is flexible enough to provide useful uncertainty bounds for all counties in the U.S., regardless of how sparsely populated or limited their previous new case counts had been?

The first challenge was addressed by taking advantage of an alternative formulation of the negative binomial distribution, called the Negative Binomial-1 (NB-1) that was able to better capture the variation of new cases observed in the data. The second was addressed by using temporally smoothing splines that allowed the slope of each county's estimated new cases to flexibly and continuously adapt over time by allowing previous estimated cases to influence the current days estimate. The third issue was handled by defining a multi-level hierarchical relationship between counties and then using partial pooling to borrow information across counties when estimating new case counts. We now cover each of these in detail.

2.4. Negative Binomial-1 (NB-1)

Counts are often modeled as random variables from a Poisson distribution, which requires variance and the expected value to be equal. Inspecting histograms of daily new case counts quickly revealed they had a relatively large variance and were dispersed more widely than a Poisson distribution would tolerate. A common correction to this is to use a Negative Binomial model instead (Cameron & Trivedi, 2013). The Negative Binomial model NB(μ, θ) is parameterized in terms of the mean, μ, and the overdispersion parameter θ. Initial experiments, however, showed this model also did not fit the count data, producing extremely large count predictions relative to the mean.

The standard Negative Binomial distribution has a variance equal to $Var(Y)=\mu +\frac{{\mu }^2}{\theta }$ (Greene, 2008). Because of the quadratic mean-variance relation, Cameron and Trivedi (Cameron & Trivedi, 1986) call this the Negative Binomial-2 model (NB-2) and specify an alternative model with a linear mean-variance relation, referred to as the Negative Binomial-1 model. This linear mean-variance relationship can be achieved by using the NB-2 model when θ = μφ. Substituting μφ for θ in the above variance equation simplifies the NB-1 variance to $Var(Y)=\mu +\frac{\mu }{\phi }$. Hence, the NB-1 model is equivalent to an NB-2 when θ = μφ. This adaptation to provided a much better fit between the model predictions and the observed data and NB-1 was used as the basis for nowcast estimates. Specifically, We define a county's daily new case count, Y _it, as being generated from an NB-1 distribution and adopt the following model:

$$Y_{it}\sim NegativeBinomial({\mu }_{it},{\mu }_{it}{\phi }_i),$$ (1)

This formulation implies that the case counts Y on day t in county i are modeled to have a Negative Binomial-1 distribution, however we have specified it using the NB2-NB1 transformation with mean μ _it and dispersion parameter θ = μ _it φ _i. To get the outputs for that county's daily distribution we must provide values for two input parameters. One that determines where the center of that distribution is located, μ _it. This is what we expect the number new cases to be for that county on that day. This parameter represents the modeled estimation of the true but unknown value E[Y _it]. The second, μ _it φ _i, controls how confident we are in this estimate. Estimating the value of these parameters requires the formulation of a link function.

Typically, the main concern of constructing this function is around determining which independent variables will be used to help estimate the dependent variable. Also included in this function, whether explicitly defined or implicitly assumed, is the relationship each observation in the dataset has to the others. Because independent and identically distributed (iid) observations are uncommon, particularly in spatio-temporal data, it is often helpful to include variables in the link function that attempt to capture the nature of this relationship and quantify the influence each observation has on the others.

This is especially true when modeling a phenomenon that progresses across space and time like the spread of COVID-19 across the U.S.. Strong spatial and temporal autocorrelation can introduce difficulties if the goal of a model is one of inference. However, if prediction is the goal, then these strong autocorrelations are often one of the most valuable features to include in the structure of the model. In fact, for the task of forecasting a county's near-term daily new case counts, exploiting the spatio-temporal autocorrelation in the data turned out to be a more reliable source of prediction than attempting to include external independent variables, such as a county's median income or measures of mobility. Therefore, the focus of our efforts when constructing the link function was not on finding external independent variables, but on constructing parameters that were flexible and robust enough to make predictions of county-level new case counts based solely on the temporal and spatial autocorrelations observed in the new case and underlying population data. We accomplished this by constructing the link function around a temporally auto-regressive parameter, α _k,i,t.

Each α _k,i,t parameter, defined further below, captures the day to day changing rate of growth in previously observed new case counts in county, i, on date, t, across three levels of a spatial hierarchy, k. The three levels of spatial hierarchy correspond to the individual county k = 0, the Combined Metropolitan Statistical Area (CMSA) that the county is a part of (if metropolitan) k = 1, and a binary metropolitan/non-metropolitan level k = 2. These rates are then used in the estimation of each county's daily new case counts. How much influence the temporal trend at each level of the spatial hierarchy has on a county's estimate is determined by the partial pooling structure described later in the section. Using a log-linear specification for the link function, we model the center of each county's daily NB-1 distribution, μ _it, as

$$\log ({\mu }_{it})=\log ({Population}_i)+({\alpha }_{0,i,t}+{\alpha }_{1,i,t}+{\alpha }_{2,i,t})$$ (2)

The three α _k,i,t parameters act together as a robust, temporally and spatially smoothed, composite estimate of the infection rate county i is experiencing on date t. Additionally, including log(Population _i) allows log(μ _it) to be proportional to a county's population. When these values are exponentiated through the inverse link function to arrive back at μ _it, it has the effect of multiplying this composite infection rate by the county's population, thus putting μ _it into the desired units of expected number of daily new cases.

County-level population counts were developed from the 2019 LandScan USA population distribution data (Bhaduri et al., 2007; Weber et al., 2019). LandScan USA is part of the Homeland Infrastructure Foundation-Level Data (HIFLD) Open Data GeoPlatform (U.S. Department of Homeland Security, 2020) which uses a multi-variable dasymetric modeling approach to generate a mid-year population estimate model by spatially distributing official Census counts using information such as land cover and building footprints.

2.5. Temporally smoothing splines

To take advantage of the temporal autocorrelation observed in the data, the α _k,i,t parameters treat the next day's value, α _k,i,t+1, as a function of the previously observed new case counts plus an error term. Since infectious diseases follow an exponential (i.e., log-linear) growth model, the splines were constructed to be linear functions of each other from one time step to the next, mathematically represented by a second-order random walk (Fahrmeir & Wagenpfeil, 1996). In a second-order random walk, the expected value of each new observation is a continuation of the trend from the previous day. Resulting in the following formulation:

$${\alpha }_{k,i,t+1}={\alpha }_{k,i,t}+({\alpha }_{k,i,t}-{\alpha }_{k,i,t-1})+{\epsilon }_{k,i,t};{\epsilon }_{k,i,t}\sim Normal(0,{\sigma }^2)$$ (3)

The advantage of using this stochastic approach is that the error term ε can account for changes in the underlying disease rate that are not explicitly accounted for in the model formulation. As changing conditions on the ground lead to changes in the rate of new cases, these are captured by the splines as changes in the slope of the log-linear link function.

Capturing the autocorrelation present in the data leads high correlation among individual elements that make up the α _k,i,t. This high correlation causes the Markov Chain Monte Carlo simulations to become inefficient as it tries to attribute a specific amount of variation to every individual element of α _k,i,t. To handle these posterior correlations and improve overall model efficiency singular value decomposition was used to create a low-rank approximation of the full second-order random walk process. Switching to matrix notation this leads to the following:

$${\alpha }_{k,i,t}=a_{k,i}+{\mathbf{Z}}_{i,t}{\mathbf{b}}_{k,i};k=\{0,1,2\}$$ (4)

Where Z _i,t is the matrix of singular values and b _k,i the vector of error terms. Further details are provided in the Supporting Information.

2.6. Partial pooling

The nowcast model creates partial pooling by using Bayesian prior distributions at each of the three levels of the defined spatial hierarchy. The use of hierarchical Bayesian priors to partially pool modeling estimates is a long-established method that performs well when modeling a phenomenon that occurs within or across clusters (e.g., counties or states) especially when those observations are highly imbalanced (Gelman et al., 2013; Gelman & Hill, 2006; Lemoine, 2019). The use of partial pooling balances fitting the daily county-level data with a prior assumption that counties at each hierarchical level share the same trends in the spread of COVID-19. In large counties, the Bayesian model favors data fit within that county. However, in counties with low counts, the prior distributions become important because they encourage the trend in each county to be similar to the trend in other counties within the hierarchy. Bayesian priors allow a data-driven smoothing of county-level trends, enabling estimates to borrow more strength if the amount of data is low and less strength if the number of cases in the county is large. In contrast, if a county has enough data to detect deviations from state or metropolitan region-level trends, then the model enables this. In this way, the model allows a smooth, data-driven level of flexibility between small and large counties, enabling the single model to provide robust, stable estimates for counties of all sizes.

2.7. Computation

The Bayesian nowcast model is fit using Stan (Carpenter et al., 2017), which uses Bayesian Markov Chain Monte Carlo simulation to estimate the model coefficients. Weakly informative priors (Lemoine, 2019) were necessary for making the model computationally feasible on a daily update schedule and for the model to be fit as automatic and hands-free as possible. With each run, thousands of new parameters had to be estimated, taking much too long (days) to complete on commodity compute resources. Timely completion was made possible by using the Compute and Data Environment for Science (CADES) platform at Oak Ridge National Laboratory. Using 320 CPU cores and 640 GB of available RAM the CCSAT model could be run in about 12 h. At this pace, the model could be comfortably run every day producing a constant fourteen-day moving window if needed.

3. Results

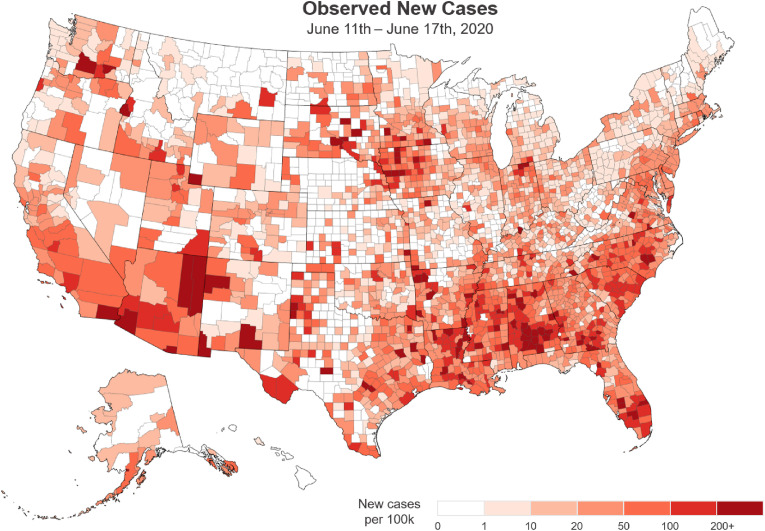
We demonstrate the CCSAT's ability to support a decision maker requiring new case count situational awareness on June 18th, 2020 (CCSAT output was actually produced on weekly basis and sent to the U.S. DOE for continued situational awareness). We begin with a map of NY Times new case counts for June 11–17 in Fig. 1 . This map shows the higher number of cases occurring in the southeast, southwest, and parts of Iowa. Using the CCSAT model we supply the decision maker with greater context on severity (velocity), whether things are getting worse or not (acceleration), and what can be expected over the next seven days (nowcast).

Fig. 1.

Observed per capita new cases. US county-level map of new COVID-19 cases during the week of June 11–17, 2020. The darker shades indicate higher numbers of per capita cases for the week, and the lighter shades represent few to no new cases.

3.1. V&A results

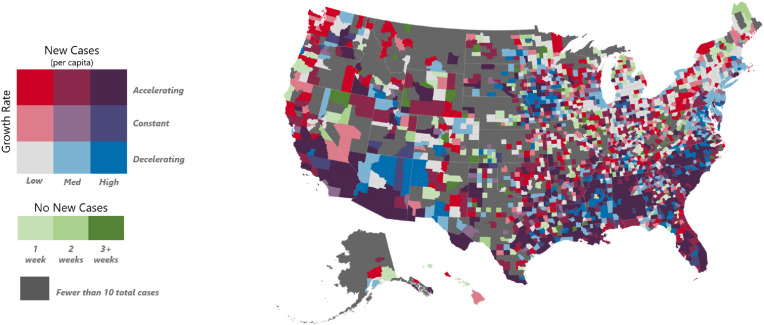
We produced a V&A map (Fig. 2 ) showing the velocity and acceleration of new case totals compared to the previous week of June 4–10. This informs the decision makers about the relative severity of each county and whether conditions are improving, constant, or worsening.

Fig. 2.

V&A county map. V&A map for week of June 11–17, 2020.

From a decision-makers standpoint, several interesting features become apparent. For example:

Worst and getting worse: The deep purple regions in the southern and western U.S. indicate the worst scenario: the highest new case per capita rates in the country with an acceleration in those rates. In particular southern California, southern Arizona, southern Florida, the Carolinas, and most of Alabama have large persistent regions with high and accelerating case rates.

Still Unaffected: A roughly contiguous strip of counties with fewer than 10 total cases persists from central Texas, western Oklahoma, Kansas, Nebraska, and extending farther north toward the Canadian border.

Highly Variable: A region of high variability exists beginning roughly in the Atlanta area and streaming through Tennessee, Kentucky, Indiana, Ohio, running west of the Appalachians all the way into upstate New York. Here we have a heterogeneous mixture of nearly every one of the V&A classifications.

Low and Accelerating Everywhere: Many counties with currently low number of cases (bright red) are now beginning to accelerate virtually everywhere indicating COVID-19 is gaining ubiquitous footing throughout the country.

We further summarize the impact to the U.S. population. Comparing new confirmed COVID-19 cases from last week (June 11–17, 2020) to that of the previous week (June 4–10, 2020) reveals the following statistics:

• ●785 counties or county equivalents, home to 111 million residents (34.1%), saw a decelerating growth rate.
• ●330 counties or county equivalents, home to 46 million residents (14.2%), saw a relatively constant growth rate.
• ●1079 counties or county equivalents, home to 157 million residents (47.9%), saw an accelerating growth rate.
• ●161 counties or county equivalents, home to 4.8 million residents (1.5%), have seen no new cases over the past week.
• ●51 counties or county equivalents, home to 1.3 million residents (0.38%), have seen no new cases over the past 2 weeks.
• ●50 counties or county equivalents, home to 867 thousand residents (0.26%), have seen no new cases over the past 3+ weeks.
• ●682 counties or county equivalents, home to 5.7 million residents (1.8%), remain at less than 10 total reported cases.

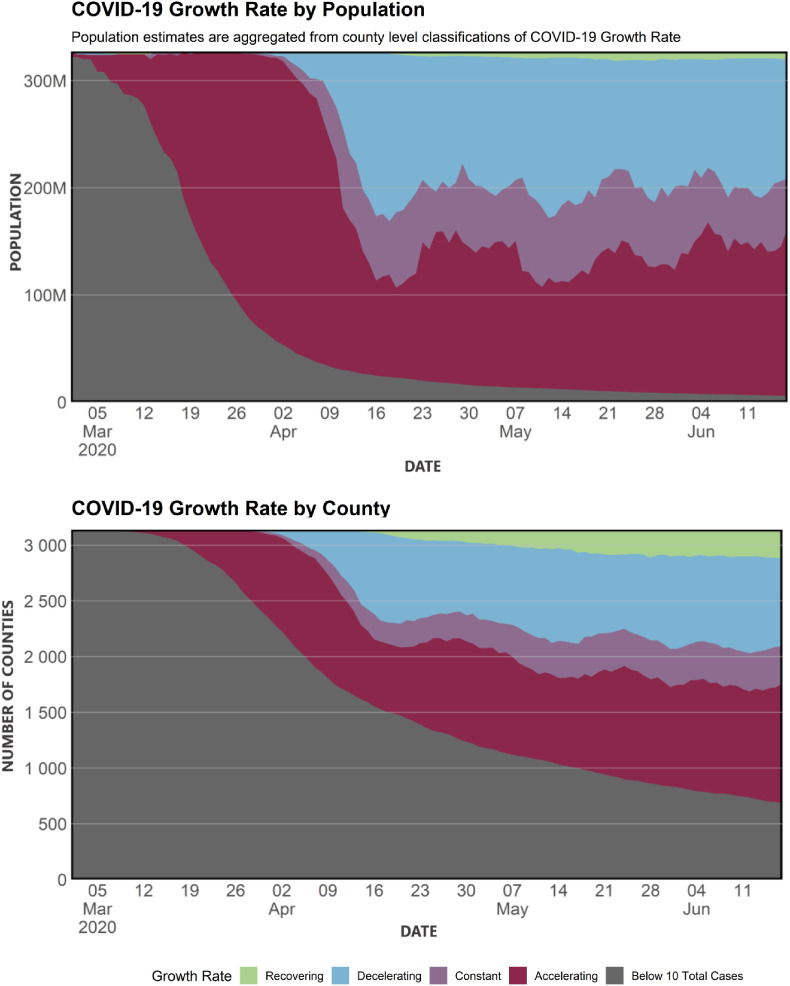
These population based summaries indeed can be viewed over time to see overall experiences back to the beginning of the pandemic. Fig. 3 shows these trends for both population and number of counties. The upper figure shows that by March 12th, most Americans lived in a county with too few cases to even measure growth. By April 2nd, the majority of Americans lived in a county with accelerating growth. Between April 9th and April 16th more Americans lived in counties with decelerating growth. This may be due to public policy changes, improving weather, and behavioral adjustments to the pandemic. The national trend that followed was a rather consistent, undulating pattern of worsening and improving.

Fig. 3.

COVID-19 temporal acceleration by population (top) and county (bottom). In the top stacked area chart shows the daily percentage of the national population living in each type of growth rate during March 1st-June 17th. The bottom graph shows what percentage of US counties are experiencing these growth rates.

In the bottom figure, we see a slightly different pattern with about a quarter of counties still having too few cases to monitor. Like the population perspective, beginning about April 16th, we see an undulating pattern in the number of improving counties. Unfortunately, the number of counties observing an accelerating growth is increasing over time as more counties convert from the category of ”too few cases to assess growth” into the ”acceleration” category.

These graphs serve as a top level view about the spatial and temporal dynamics of the disease and the impact of those dynamics on the population. As weeks go by, individual counties can leave one category and enter another. For example, one county is high and accelerating one week and the next week high and constant. Populations in those counties follow suit. Progression as measured by Fig. 3 provides a national county metric that absorbs these exchanges and enables an interpretable view of disease progression at the county population level. As the pandemic recedes due to policy intervention or vaccine distribution, the inventory of counties and their populations will begin converting to decelerating growth. As the pandemic ends the inventory will be largely classified as ”no new cases in recent weeks.”

3.2. Bayesian nowcast results

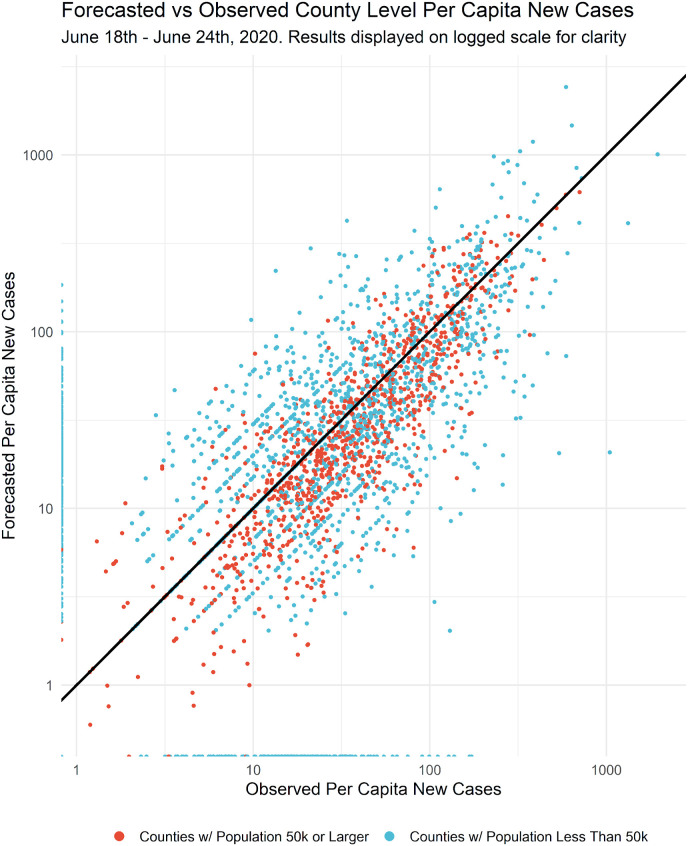
Overall, forecasts for the week of June 18–24, 2020 were well-aligned with the net number of new cases across all states (Fig. 4 ). Excluding counties with no previous new cases, 53.6% of the daily count of county-level new COVID-19 case totals were within the model's 50% prediction interval, 73.3% within the 70% prediction interval, and 92.3% within the 90% prediction interval. The strong agreement between the model's prediction interval and the actual observed data indicates that the prediction intervals are well-calibrated and not overly restrictive or excessively encompassing.

Fig. 4.

Forecasted and observed new cases per capita June 18–24, 2020. The predicted growth rate of the number of new COVID-19 cases per capita was estimated based on known cases the prior week.

Given the initial goal of stable predictions for both urban and rural counties we further break out the comparison by county population (Fig. 5 ). Counties with a population of less than 50,000 demonstrated a larger range of outcomes than those with 50,000 or more but the model performed consistently across both groups. The larger range of outcomes for counties with a population of less than 50,000 was expected given the smaller population (denominator) and small number problems associated with lower counts of new cases in more rural areas.

Fig. 5.

Forecasted vs Observed Per Capita New Cases By Population Groups Counties with a population of less than 50,000 demonstrated a larger range of outcomes than those with 50,000 or more but the model performed consistently across both groups.

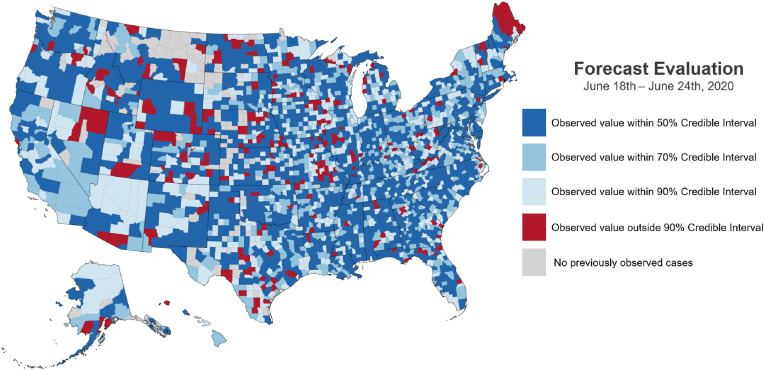
In Fig. 6 , we map the prediction credibility intervals in which observed new case count data falls. In this spatial view, there do not seem to be any systemic errors with values outside the 90% credibility showing no to have apparent spatial clustering.

Fig. 6.

Map showing the spatial location of model forecast deviations for June 18–24, 2020. The map shows which model quantiles new case observations fall within by county.

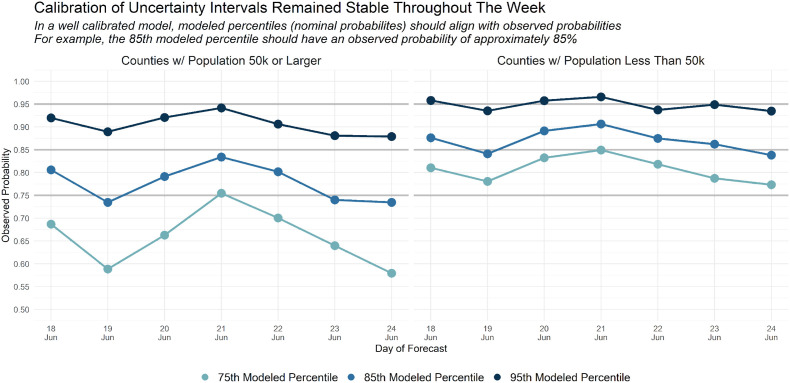
To further assess model validation we introduce some useful diagnostics at the daily level. These deeper looks can help illuminate reasons for problematic weekly count estimates. Fig. 7 shows the daily nominal credibility intervals with the observed outcomes. Overall the model performs relatively well even on a daily basis with observed and nominal probabilities within a few percentage points of one another. Deviations such as those on the 2nd (June 19th) and 7th day (June 24th) for larger counties can prompt deeper analysis into what may be occurring there.

Fig. 7.

Posterior Predictive Coverage Intervals. These charts show the actual and nominal 75, 85 and 95 percent credible regions for the Bayesian model predictions.

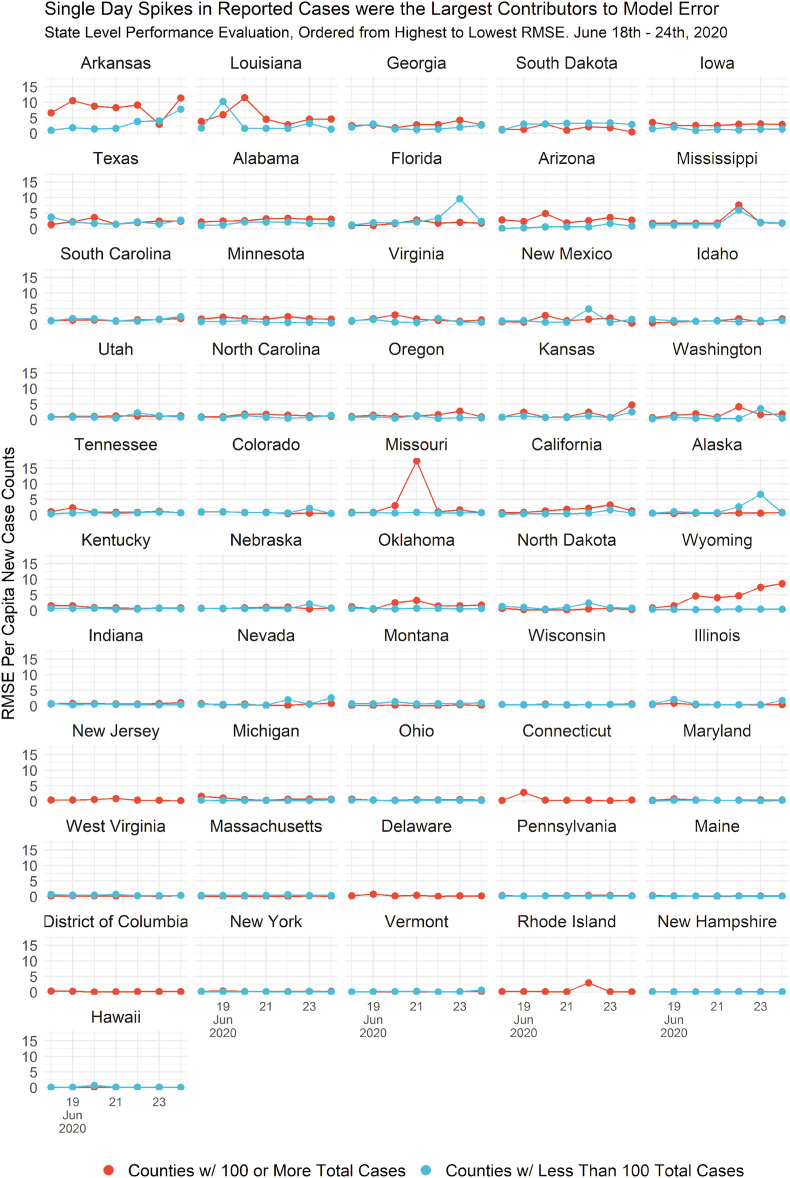
In Fig. 8 we partitioned counties into those with $<$100 and ≥ 100 confirmed cases, and the daily root mean squared error (RMSE) was examined for those partitions each day during June 18–24. The results are ordered from largest average RMSE to smallest. Arkansas and Louisiana have the highest overall differences between forecasts and observed data, driven by counties with ≥100 cases. Observing states near the bottom of the graph with the lowest average RMSE, we see areas that performed well include Hawaii, New Hampshire, Rhode Island, Vermont, New York, District of Columbia, Maine, Pennsylvania and so forth. It's noteworthy that the states with the lowest RMSE had a more aggressive COVID response than Arkansas and Louisiana, which performed poorly in our prediction. Also interestingly we see specific days in specific states where error spikes emerge, such as day 6 in Florida and day 4 in Missouri. This means that overall error rates may be attributable to those specific days. On the other hand, Wyoming saw an consistently increasing error rate over the seven-day period, for counties with a total number of cases greater than 100. This indicates that overall error are not attributable to single day instances but a divergent trend may be occurring there warranting further investigation.

Fig. 8.

Error analysis of model forecasts by confirmed case counts. For counties with $<$100 and ≥ 100 confirmed cases, the RMSE of model forecasts are presented by state for the period of June 18–24, 2020.

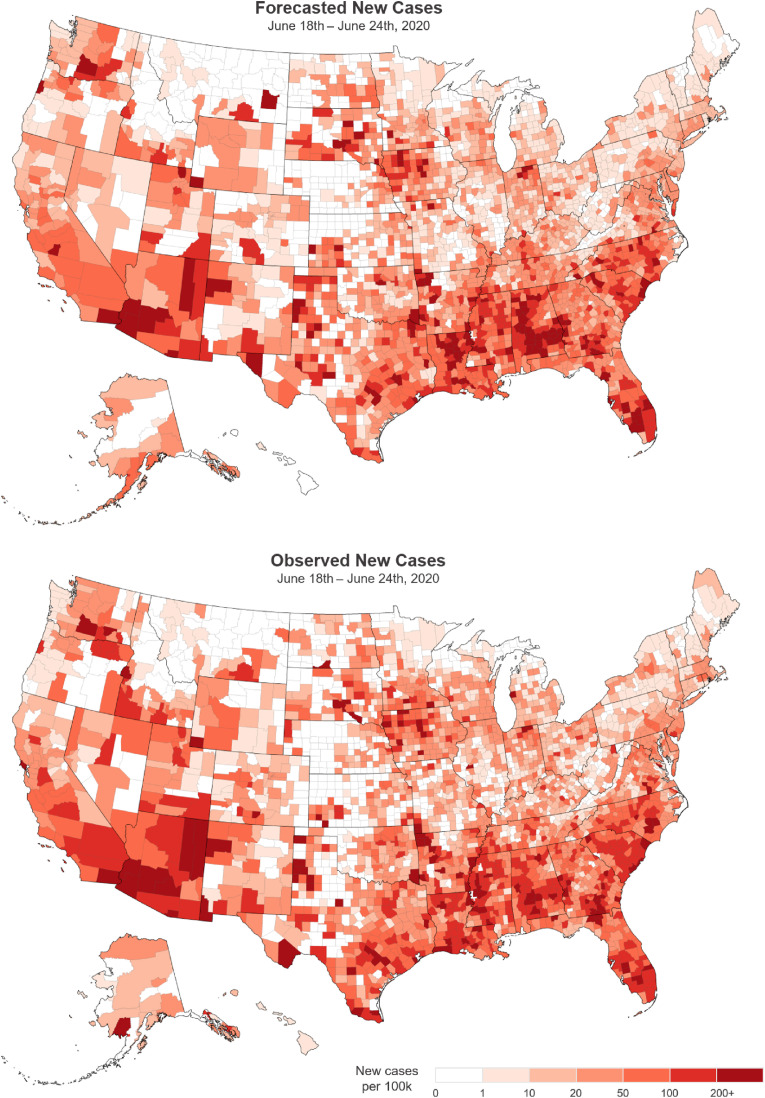
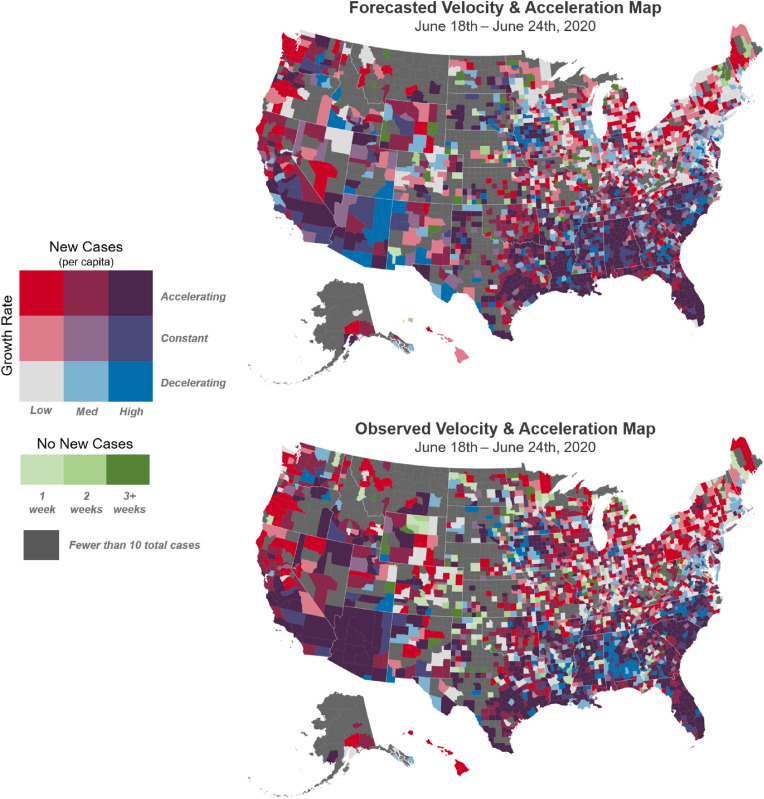
Another way to present nowcast results is to apply V&A maps to predicted values. V&A maps were constructed by using model predictions for the June 18–24 period and compared with V&A maps for the subsequently observed data, as shown in Fig. 9 . These V&A maps show similarities between the model forecasts and observed data. Most strikingly, forecasted and observed V&A maps for the coastal states appear largely consistent; Florida, North Carolina, South Carolina, southern Louisiana, eastern Texas, and southern California show similar patterns of high new case rates combined with accelerating growth.

Fig. 9.

Forecasted and observed V&A maps June 18–24, 2020. A V&A map constructed with model predictions (top) is compared with subsequent observed data (bottom), showing strong concordance.

Notable exceptions to this trend are Alabama and Arizona. Cases in Alabama were predicted to accelerate, however Alabama saw a deceleration of new cases state wide during the June 18–24 period. In Arizona, many counties were predicted to decelerate or remain constant, however in the end, they accelerated significantly. Departures such as these from predictions can potentially alert decision makers to check for local changes in governance for public health approaches that may be mitigating (or promoting) disease progression.

4. Discussion

4.1. Key outcomes

With these results in hand, we return to the motivating questions first posed in the introduction and indicate how CCSAT provides salient answers.

How bad is the situation in my jurisdiction and is it getting worse or better? The CCSAT V&A map provides a simultaneous view of the relative severity (velocity) and growth in that severity (acceleration) over the past week. The map can be used by county, state, and federal authorities in understanding the greater pandemic context and where their particular jurisdiction is situated in that context.

Are things getting better or worse overall across the nation? The two stacked time series charts show the number of counties and persons living in those counties that are experiencing decelerating, constant, or accelerating growth. This shows an overall fine-scale (county-level) impact of COVID dynamics back to the start of the pandemic.

How many new cases should I anticipate next week? The Bayesian nowcast model predicts the number of new cases each county can expect seven days ahead of time. This allows prediction of new case maps as well as projected V&A maps that can be interpreted at county, state, and federal levels.

How well do the weekly predictions match reality? By comparing the actual number of new cases for each county to the prediction, the performance of the Bayesian nowcast model can be easily assessed in a variety of ways. Here we compare actual data to predicted values and evaluate how well those fall into expected percentiles at the county and state level. This assessment is conducted across large and small populations and large and small case counts alike.

In addition to these, we note the following key outcomes.

• ●Within an urgent, operational pandemic environment with limited information, CCSAT can be executed quickly (within a few hours on CADES) providing near-term public health information on the spread of disease.
• ●The V&A retrospective analysis allows decision makers to simultaneously consider both disease severity and growth enabled by familiar terms of velocity and acceleration and to interpret maps with accessible cartographic representation.
• ●The national new case rate stacked graphs trace the population and counties falling into each V&A category back to the start of the pandemic. This provided a national perspective on the county-level progression of the disease. Major trends (e.g., flattening, growth) were easily visualized.
• ●The Bayesian nowcast model provided robust estimates of new case counts expected over the next seven days. The performance of the model could be constantly evaluated by comparing predictions with actual values on a weekly basis.

4.2. Future work

In some sense, the model is agnostic to the type of variable that authorities wish to trace as long as the variable is time based and is meaningful as a rate over population at the county, state, and national scale. Hence, CCSAT is well positioned for new variants of COVID-19 or entirely new future pandemics with similarly limited information. Here the target source was new case count. Future scenarios may have, for example, a more reliable death count and CCSAT could be used to estimate the velocity, acceleration, and projected growths of there as well.

In other future work, we aim to develop a more agile CCSAT that could deal with more heterogeneous and richer data surfaces in those counties where it is available. For example, methods for under-reporting (Albani et al., 2021c; Angulo et al., 2021; Gibbons et al., 2014; Lau et al., 2021; Whittaker et al., 2021), mobility (Hu et al., 2021), vaccination effects (Albani et al., 2021b; Amaku et al., 2021), and mechanistic modeling approaches (Zhou et al., 2020) could be implemented where the data are available under an architecture that can dynamically respond to variations in data detail and richness at operational tempo. Cross-comparison and benchmarking of different model architectures and ensembles will be a critical part of that work.

5. Conclusion

In the early stages of the pandemic, understanding the spatio-temporal progression of COVID-19 through traditional SIR models and their variants was severely hampered by a sparse and uncertain data environment. In addition to data variation, massive societal behaviour changes occurred such as school closures and mask mandates. This made long term prediction very difficult but also clouded situational awareness about near-term severity and progression at a time when it was greatly needed. Against this backdrop, a pressing need remained for a fine-scale, national perspective on the immediate and near-term severity and growth of the COVID-19 pandemic across the U.S.

The DOE's NVBL pandemic modeling initiative responded with development of CCSAT, a novel data driven framework for providing reliable measures of near-term severity and growth as well as near-term projections across all 3000+ U.S. counties. Focusing on the most recent and upcoming seven-day periods, the 14-day moving window utilized a bivariate cartographic model (V&A) to convey immediate conditions while a Bayesian nowcast model estimated likely conditions over the next seven days. Results were operationally reliable as model diagnostics (e.g, predicted-actual scatter plots, RMSE, and credibility intervals) showed strong and stable alignment between projected and actual disease distributions throughout time window. With this new capability, it was now possible to understand and reliably predict near-term spatio-temporal progression of COVID-19 across the U.S. at the federal, state, and county-level.

Author contributions

Robert Stewart: Conceptualization, Methodology, Supervision, Visualization, Writing – original draft, Funding acquisition. Samantha Erwin: Conceptualization, Formal Analysis, Methodology, Visualization, Writing – original draft. Jesse Piburn: Conceptualization, Methodology, Formal Analysis, Visualization, Software, Validation, Writing – original draft. Nicholas Nagle: Conceptualization, Methodology, Formal Analysis, Visualization, Software, Validation, Writing – original draft. Jason Kaufman: Data Curation. Alina Peluso: Formal Analysis. Blair Christian: Supervision, Writing – original draft. Joshua Grant: Data Curation, Software. Alexandre Sorokine: Methodology, Visualization, Writing – original draft. Budhendra Bhaduri: Funding Acquisition, Supervision.

Funding and Acknowledgements

We would like to thank our Compute and Data Environment for Science (CADES) colleagues at the Oak Ridge National Laboratory, for supplying the computational resources needed to carry out this work. CADES is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. Research was supported by the DOE Office of Science through the National Virtual Biotechnology Laboratory, a consortium of DOE national laboratories focused on response to COVID-19, with funding provided by the Coronavirus CARES Act.

Appendix A. Supplementary data

The following is the Supplementary data to this article: