Highly Scalable Bayesian Geostatistical Modeling via Meshed Gaussian Processes on Partitioned Domains

Abstract

We introduce a class of scalable Bayesian hierarchical models for the analysis of massive geostatistical datasets. The underlying idea combines ideas on high-dimensional geostatistics by partitioning the spatial domain and modeling the regions in the partition using a sparsity-inducing directed acyclic graph (DAG). We extend the model over the DAG to a well-defined spatial process, which we call the Meshed Gaussian Process (MGP). A major contribution is the development of a MGPs on tessellated domains, accompanied by a Gibbs sampler for the efficient recovery of spatial random effects. In particular, the cubic MGP (Q-MGP) can harness high-performance computing resources by executing all large-scale operations in parallel within the Gibbs sampler, improving mixing and computing time compared to sequential updating schemes. Unlike some existing models for large spatial data, a Q-MGP facilitates massive caching of expensive matrix operations, making it particularly apt in dealing with spatiotemporal remote-sensing data. We compare Q-MGPs with large synthetic and real world data against state-of-the-art methods. We also illustrate using Normalized Difference Vegetation Index (NDVI) data from the Serengeti park region to recover latent multivariate spatiotemporal random effects at millions of locations. The source code is available at github.com/mkln/meshgp.

1. Introduction

Collecting large quantities of spatial and spatiotemporal data is now commonplace in many fields. In ecology and forestry, massive datasets are collected using satellite imaging and other remote sensing instruments such as LiDAR that periodically record high-resolution images. Unfortunately, clouds frequently obstruct the view resulting in large regions with missing information. Figure 1 shows this phenomenon in Normalized Difference Vegetation Index (NDVI) data from the Serengeti region. Filling such gaps in the data is an important goal as is quantifying uncertainty in predictions. This goal is achieved through stochastic modeling of the underlying phenomenon, which involves the specification of a spatial or spatiotemporal process characterizing dependence from a finite realization. Gaussian processes (GP) are a customary choice to characterize spatial dependence, but their implementation is notoriously burdened by their O(n³) computational complexity. Consequently, intense research has been devoted in recent years to developing scalable models for large spatial datasets – see detailed reviews by Sun et al. (2011) and Banerjee (2017).

Figure 1:

Left: NDVI in the Serengeti region on 2016-12-17. White areas correspond to missing data due to cloud cover. Right: elevation data for the same region.

Computational complexity can be reduced by considering low-rank models; among these, knot-based methods motivated by “kriging” ideas enjoy some optimality properties but over-smooth the estimates of spatial random effects unless the number of knots is large, and require corrections to avoid overestimation of the nugget (Banerjee et al., 2008; Cressie and Johannesson, 2008; Banerjee et al., 2010; Guhaniyogi et al., 2011; Finley et al., 2012). Other methods reduce the computational burden by introducing sparsity in the covariance matrix; strategies include tapering (Furrer et al., 2006; Kaufman et al., 2008) or partitioning of the spatial domain into regions with a typical assumption of independence across regions (Sang and Huang, 2012; Stein, 2014). These can be improved by considering a recursive partitioning scheme, resulting in a multi-resolution approximation (MRA; Katzfuss 2017). Other assumptions on conditional independence assumptions also have a good track record in terms of scalability to large spatial datasets: Gaussian random Markov random fields (GMRF; Rue and Held, 2005), composite likelihood methods (Eidsvik et al., 2014), and neighbor-based likelihood approximations (Vecchia, 1988) belong to this family.

The recent literature has witnessed substantial activity surrounding the so called Vecchia approximation (Vecchia, 1988). This approximation can be regarded as a special case of the GMRF approximations with a simplified neighborhood structure motivated from a directed acyclic graphical (DAG) representation of a Gaussian process likelihood. Extensions leading to well-defined spatial processes to accommodate inference at arbitrary locations by extending the DAG representation to the entire domain include Nearest neighbor Gaussian processes (NNGP; Datta et al. 2016a,b) and further generalizations by constructing DAGs over the augmented space of outcomes and spatial effects (Katzfuss and Guinness, 2017). These approaches render computational scalability by introducing sparsity in the precision matrix. The DAG relies upon a specific topological ordering of the locations, which also determine the construction of neighborhood sets, and certain orderings tend to deliver improved performance of such models (Katzfuss and Guinness, 2017; Guinness, 2018).

When inference on the latent process is sought, Bayesian inference has the benefits of providing direct probability statements based upon the posterior distribution of the process. Inference based on asymptotic approximations are avoided, but there remain challenges in computing the posterior distribution given that inference is sought on a very high-dimensional parameter space (including the realizations of the latent process). One possibility, available for Gaussian first-stage likelihoods, is to work with a collapsed or marginalized likelihood by integrating out the spatial random effects. However, Gibbs samplers and other MCMC algorithms for the collapsed models can be inexorably slow and are impractical when data are in the millions. A sequential Gibbs sampler that updates the latent spatial effects (Datta et al., 2016a) is faster in updating the parameters but suffers from high autocorrelation and slow mixing. Another possibility emerges when interest lies in prediction or imputation of the outcome variable only and not the latent process. Here, a so called “response” model that models the outcome itself using an NNGP can be constructed. This model is much faster and enjoys superior convergence properties, but we lose inference on the latent process and its predictive performance tends to be inferior to the latent process model. Furthermore, these options are unavailable in non-Gaussian first-stage hierarchical models or when the focus is not uniquely on prediction. A detailed comparison of different approaches for computing Bayesian NNGP models is presented in Finley et al. (2019).

Our current contribution introduces a class of Meshed Gaussian Process (MGP) models for Bayesian hierarchical modeling of large spatial datasets. This class builds upon the aforementioned works that build upon Vecchia (1988) and other DAG based models. The inferential focus remains within the context of massive spatial datasets over very large domains. We exploit the demonstrated benefits of the DAG based models, but we now adapt them to partitioned domains. We describe dependence across regions of a partitioned domain using a small, patterned DAG which we refer to as a mesh. Within each region, some locations are selected as reference and collectively mapped to a single node in the DAG. Relationships among nodes are governed by kriging ideas. In the resulting MGP, regions in the spatial domain depend on each other through the reference locations. Realizations at all other locations are assumed independent, conditional upon the reference locations. This construction leads to a valid standalone spatial process.

As a particular subclass of MGPs, we propose a novel partitioning and graph design based on domain tessellations. Unlike methods that build sparse DAGs by limiting dependence to m nearest neighbors, our approach shapes the underlying DAG with a known, repeating pattern corresponding to the chosen tessellation geometry. The underlying sparse DAG enables scaling computations to large data settings and its known pattern guarantees the availability of block-parallel sampling schemes; furthermore, large computational savings can be achieved at no additional approximation cost if data are collected on patterned lattices. Finally, extensions to spatiotemporal and/or multivariate data are straightforward once a suitable covariance function has been defined. We use axis-parallel domain partitioning and the corresponding cubic DAG – resulting in cubic MGPs or Q-MGPs – to show substantial improvements in computational time and inferential performance relative to other models with data sizes ranging from the thousands to the several millions, for both spatial and spatiotemporal data and using multivariate spatial processes.

The present work may appear to share similarities with the block-NNGP model of Quiroz et al. (2019), who advocate building sparse DAGs on grouped locations based on their ordering and subsequent identification of m “past” neighbors. Unlike block-NNGPs, our tessellated GPs consider the domain tessellation as generating the DAG; the number of parents of any node is thus fixed and depends on the geometry of the chosen tessellation rather than on a user-defined parameter. Inclusion of more distant locations in the parent set of any location will, therefore, not proceed by increasing the number of neighbors m, but rather by increasing the regions’ size and/or modifying their shape. Central to tessellated GPs is the idea of forcing a DAG with known coloring on the data, resulting in guaranteed efficiencies when recovering the latent spatial effects. This strategy is analogous in spirit to multi-resolution approximations (Katzfuss, 2017; Gramacy and Lee, 2008), which also force a DAG on the data, resulting in conditional independence patterns that are known in advance and that can be used to improve computations. However, while multi-resolution approximations are defined by branching graphs associated to recursive domain partitioning, tessellated GPs use a single domain partition, with each region connected in the DAG only to its immediate neighbors. Compared to treed graphs, tessellated GPs are associated to DAGs with fewer conditionally-independent groups and whose repeated patterns facilitate the identification of redundant matrix operations arising when one or more coordinate margins are gridded. We also note that while the idea of partitioning domains to create approximations is not new, construction of the DAG-based approximation over partitioned domains has received considerably less attention. Finally, our focus here is in developing tessellated GPs as a methodology that enables the efficient recovery of the latent spatial random effects and the Bayesian estimation of covariance parameters via MCMC; we are thus not focusing on alternative computational algorithms (see e.g. Finley et al. 2019), which have been developed for NNGPs but can nonetheless all be adapted to general MGP models.

The balance of this paper proceeds as follows. Section 2 introduces our general framework for hierarchical Bayesian modeling of spatial processes using networks of grouped spatial locations. The MGP is outlined in Section 3, where we provide a general, scalable computing algorithm in Section 3.1. Tessellation-based schemes and the specific case of Q-MGPs are outlined in Section 4, which highlights their properties and computational advantages. We illustrate the performance of our proposed approach in Section 5 using simulation experiments and an application on a massive dataset with millions of spatiotemporal locations. We conclude the paper with a discussion and pointers to further research. Supplementary material accompanying this manuscript as an Appendix is available online and contains further comparisons of Q-MGPs with several state-of-the-art methods for spatial data.

2. Spatial processes on partitioned domains

A q × 1 spatial process assigns a probability law on $\left\{w(\mathit{\ell }):\mathit{\ell }\in \mathcal{D}\right\}$, where w(ℓ) is a q × 1 random vector with elements w_i(ℓ) for i = 1,2,…,q. In the following general discussion we will not distinguish between spatial $\left(\mathcal{D}\subset {\Re }^d\right)$ and spatiotemporal domains $\left(\mathcal{D}\subset {\Re }^{d+1}\right)$, and denote spatial or spatiotemporal locations as ℓ,s, or u.

For any finite set of spatial locations $\left\{{\mathit{\ell }}_1,{\mathit{\ell }}_2,\dots ,{\mathit{\ell }}_{n_{\mathcal{L}}}\right\}=\mathcal{L}\subset \mathcal{D}$ of size $n_{\mathcal{L}}$, let P(·) denote the probability law of the $n_{\mathcal{L}}q\times 1$ random vector $w_{\mathcal{L}}={\left(w{\left({\mathit{\ell }}_1\right)}^{\top },w{\left({\mathit{\ell }}_2\right)}^{\top },\dots ,w{\left({\mathit{\ell }}_{n_{\mathcal{L}}}\right)}^{\top }\right)}^{\top }$ with probability density p(·). The joint density of $w_{\mathcal{L}}$ can be expressed as a DAG (or a Bayesian network model) with respect to the ordered set of locations $\mathcal{L}$ as

$$p\left(w_{\mathcal{L}}\right)=\prod _{i=1}^{n_{\mathcal{L}}}p\left(w\left({\mathit{\ell }}_i\right)\mid w\left({\mathit{\ell }}_1\right),\dots ,w\left({\mathit{\ell }}_{i-1}\right)\right),$$ (1)

where the conditional set for each w(ℓ_i) can be interpreted as the set of its parents in a large, dense Bayesian network. Defining a simplified valid joint density on $\mathcal{L}$ by reducing the size of the conditioning sets is a popular strategy for fast likelihood approximations in the context of large spatial datasets. One typically limits dependence to “past” neighboring locations with respect to the ordering in (1) (Vecchia, 1988; Gramacy and Apley, 2015; Stein et al., 2004; Datta et al., 2016a; Katzfuss and Guinness, 2017). The neighbors are defined and fixed and model performance may benefit from the addition of some distant locations (Stein et al., 2004). The ordering in $\mathcal{L}$ is also fixed and inferential performance may benefit from the use of some fixed permutations (Guinness, 2018). The result of shrinking the conditional sets to a smaller set of neighbors from the past yields a sparse DAG or Bayesian network, which yields potentially massive computational gains.

We proceed in a similar manner, but instead of defining a sparse DAG at the level of each individual location, we map entire groups of locations to nodes in a much smaller graph; the same graph will be used to model the dependence between any location in the spatial domain and, therefore, to define a spatial process. Let $\mathcal{P}=\left\{{\mathcal{D}}_1,\dots ,{\mathcal{D}}_M\right\}$ be a partition of $\mathcal{D}$ into M mutually exclusive subsets so that $\mathcal{D}={\cup }_{i=1}^M{\mathcal{D}}_i$ and ${\mathcal{D}}_i\cap {\mathcal{D}}_j=\varnothing$ whenever i ≠ j. Similar to the nomenclature in the NNGP, we fix a reference set $\mathcal{S}=\left\{{\mathit{s}}_1,\dots ,{\mathit{s}}_{n_{\mathcal{S}}}\right\}\subset \mathcal{D}$, which itself is partitioned using $\mathcal{P}$ by letting ${\mathcal{S}}_j={\mathcal{D}}_j\cap \mathcal{S}$. The set of non-reference locations is similarly partitioned with ${\mathcal{U}}_j={\mathcal{D}}_j\backslash {\mathcal{S}}_j$ so that ${\mathcal{D}}_j={\mathcal{S}}_j\cup {\mathcal{U}}_j$ for each j = 1,2,…,M. We now construct a DAG to model dependence within and between $\mathcal{S}$ and $\mathcal{U}$. Let $\mathcal{G}=\left\{V,E\right\}$ be a graph with nodes V = A ∪ B, where we refer to A = {a₁,…,a_M} as the reference nodes and to B = {b₁,…,b_M} as the non-reference, or simply “other”, nodes. Let A ∩ B = ∅. We introduce a map $\eta :\mathcal{D}\to V$ such that

$$\eta (\mathit{\ell })=\{\begin{array}{l}{a}_j\in A\text{ if }\mathit{\ell }\in {\mathcal{S}}_j\hfill \\ b_j\in B\text{ if }\mathit{\ell }\in {\mathcal{U}}_j\hfill \end{array}.$$ (2)

This surjective many-to-one map links each location in ${\mathcal{S}}_j$ and ${\mathcal{U}}_j$ to a node in $\mathcal{G}$. The edges connecting nodes in $\mathcal{G}$ are E = {Pa[v₁],…,Pa[v_2M]} where Pa[v] ⊂ V denotes the set of parents of any v ∈ V and, hence, identifies the directed edges pointing to v. We let $\mathcal{G}$ be acyclic, i.e., there is no chain $\left\{v_{i_1}\to v_{i_2}\to \cdots \to v_{i_t}\right\}$ of elements of V such that $v_{i_j}\in \text{Pa}\left[v_{i_{j+1}}\right]$ and $v_{i_{j+1}}\in \text{Pa}\left[v_{i_1}\right]$. Crucially, we assume that Pa[v] ⊂ A for all v ∈ V, i.e., that only reference nodes have children, to distinguish the reference nodes A from the other nodes B. Apart from the assumption that a_j ∈ Pa[b_j], we refrain from defining the parents of a node, thereby retaining flexibility. In general, however, all locations in ${\mathcal{U}}_j$ will share the same parent set. In Section 4 we will consider meshes associated to domain tessellations.

Consider the enumeration ${\mathcal{S}}_i=\left\{{\mathit{s}}_{i_1},\dots ,{\mathit{s}}_{i_{n_i}}\right\}$, where $\left\{i_1,i_2,\dots ,i_{n_i}\right\}\subset \left\{1,2,\dots ,n_{\mathcal{S}}\right\}$, and let $w_i={\left(w{\left(s_{i_1}\right)}^{\top },w{\left(s_{i_2}\right)}^{\top },\dots ,w{\left(s_{i_{n_i}}\right)}^{\top }\right)}^{\top }$ be the n_iq × 1 random vector listing elements of w(s) for each $s\in {\mathcal{S}}_i$. We now rewrite (1) as a product of M conditional densities

$$p\left(w_{\mathcal{S}}\right)=p\left(w_1,w_2,\dots ,w_M\right)=\prod _{i=1}^{M}p\left(w_i\mid w_1,\dots ,w_{i-1}\right).$$ (3)

The conditioning sets are then reduced based on the graph $\mathcal{G}$:

$$\tilde{p}\left(w_{\mathcal{S}}\right)=\prod _{i=1}^{M}p\left(w_i\mid w_{[i]}\right),$$ (4)

where we denote w_[i] = {w_j : a_j ∈ Pa[a_i]}, and Pa[a_i] ⊂ {a₁,…,a_i−1} ⊂ A. This is a proper multivariate joint density since the graph is acyclic (Lauritzen, 1996). It is instructive to note how the above approximation behaves when the size of the parent set shrinks, for a given domain partitioning scheme. To this end, we adapt a result in Banerjee (2020) and show that sparser DAGs correspond to a larger Kullback-Leibler (KL) divergence from the base density p. This result has been proved earlier for Gaussian likelihoods by Guinness (2018), but the argument given below is free of distributional assumptions and is linked to the submodularity of entropy and the “information never hurts” principle (see e.g. Cover and Thomas, 1991).

Consider random vector w and some partition of the domain $\mathcal{P}$ corresponding to nodes V = {v₁,…,v_M} via map η. Let the base process correspond to graph ${\mathcal{G}}_0=\left\{V,E_0\right\}$ where E₀ = {Pa₀[v₁],…,Pa₀[v_M]}. Then, let ${\mathcal{G}}_1=\left\{V,E_1\right\}$ where E₁ = {Pa₁[v₁],…,Pa₁[v_M]} and Pa₁[v_i] ⊆ Pa₀[v_i] for all i ∈ {1,…,M}. Finally construct ${\mathcal{G}}_2=\left\{V,E_2\right\}$ by letting Pa₂[v_i*] = Pa₁[v_i*] \ {v*} for some v* ∈ Pa₁[v_i*]. In other words, graph ${\mathcal{G}}_2$ is obtained by removing the directed edge v* → v_i* from ${\mathcal{G}}_1$. We approximate p using densities p₁ and p₂ based on ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$, respectively, obtaining

$$\frac{p_1(w)}{p_2(w)}=\prod _{i=1}^M\frac{p\left(w_i\mid w_{{[i]}_1}\right)}{p\left(w_i\mid w_{{[i]}_2}\right)}=\frac{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_1}\right)}{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_2}\right)}.$$ (5)

Considering the Kullback-Leibler divergence of each density from p, and denoting V * = V \ {{i*} ∪ Pa₁[i*]}, we find

$$\begin{gathered} KL\left(p_2\Vert p\right)-KL\left(p_1\Vert p\right)=\int \left\{\text{log}\left(\frac{p(w)}{p_2(w)}\right)-\text{log}\left(\frac{p(w}{p_1(w}\right)\right\}p(w)dw \\ =\int \text{log}\left(\frac{p_1(w)}{p_2(w)}\right)p(w)dw=\int \text{log}\left(\frac{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_1}\right)}{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_2}\right)}\right)p(w)dw \\ =\int \text{log}\left(\frac{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_1}\right)}{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_2}\right)}\right)p\left(w_{i^{*}},w_{{\left[i^{*}\right]}_1}\right)d{w}_{i^{*}}d{w}_{{\left[i^{*}\right]}_1} \\ =\int \left\{\int \text{log}\left(\frac{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_1}\right)}{p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_2}\right)}\right)p\left(w_{i^{*}}\mid w_{{\left[i^{*}\right]}_1}\right)d{w}_{i^{*}}\right\}p\left(w_{{\left[i^{*}\right]}_1}\right)d{w}_{{\left[i^{*}\right]}_1}\ge 0, \end{gathered}$$ (6)

where we use (5), the fact that V * and {i*} ∪ Pa₁[i*] are disjoint, and Jensen’s inequality. This result implies that larger parent sets are preferrable as they correspond to better approximations to the full model; the choice of sparser graphs will be driven by computational considerations – see Section 3.2.

We construct the spatial process over arbitrary locations by enumerating other locations as $\mathcal{U}=\left\{u_1,\dots ,u_{n_{\mathcal{U}}}\right\}\subset \mathcal{D}\backslash \mathcal{S}$ and extending (4) to the non-reference locations. Given the partition of $\mathcal{U}$ defined earlier with components ${\mathcal{U}}_j$ for j = 1,2,…,M, for each $u\in {\mathcal{U}}_j$ we set η(u) = b_j and recall that Pa[b_i] ⊂ A by construction. For each $i=1,\dots ,n_{\mathcal{U}}$, we denote $w_{\left[u_i\right]}=\left\{w_j:a_j\in \text{Pa}\left[\eta \left(u_i\right)\right]\right\}\subset w_{\mathcal{S}}$ and define the conditional density of ${\mathit{w}}_{\mathcal{U}}$ given ${\mathit{w}}_{\mathcal{S}}$ as

$$\tilde{p}\left(w_{\mathcal{U}}\mid w_{\mathcal{S}}\right)=\prod _{u_i\in \mathcal{U}}p\left(w\left(u_i\right)\mid w_{\left[{\mathit{u}}_i\right]}\right)=\prod _{j=1}^{M}p\left(w_{{\mathcal{U}}_j}\mid w_{\left[{\mathit{b}}_j\right]}\right).$$ (7)

Therefore, for any finite subset of spatial locations $\mathcal{L}\subset \mathcal{D}$ we can let $\mathcal{U}=\mathcal{L}\backslash \mathcal{S}$ and obtain

$$\tilde{p}\left(w_{\mathcal{L}}\right)=\int \tilde{p}\left(w_{\mathcal{U}}\mid w_{\mathcal{S}}\right)\tilde{p}\left(w_{\mathcal{S}}\right)\prod _{s_i\in \mathcal{S}\backslash \mathcal{L}}d\left(w\left(s_i\right)\right).$$

We show (see Appendix A, available online) that this is a well-defined process by verifying the Kolmogorov consistency conditions. This new process can be built starting from a base process, a fixed reference set, domain partition $\mathcal{P}$ and a graph $\mathcal{G}$. Next, we elucidate with Gaussian processes.

3. Meshed Gaussian Processes

Let $\left\{w(\mathit{\ell }):\mathit{\ell }\in \mathcal{D}\right\}$ be a q-variate multivariate Gaussian process, denoted as w(ℓ) ~ GP(0, C(·, · | θ)). The cross-covariance C(·,· | θ) indexed by parameters θ is a function $C:\mathcal{D}\times \mathcal{D}\to {\mathcal{M}}_{q\times q}$, where ${\mathcal{M}}_{q\times q}$ is a subset of ${\Re }^{q\times q}$ (the space of all q × q real matrices) such that the (i, j)-th entry of C(ℓ, ℓ′ | θ) evaluates the covariance between the i-th and j-th elements of w(ℓ) at ℓ and ℓ′, respectively, i.e., cov(w_i(ℓ), w_j(ℓ′)). We omit dependence on θ to simplify notation. The cross-covariance function itself needs to be neither symmetric nor positive-definite, but must satisfy the following two properties: (i) C(ℓ, ℓ′) = C(ℓ′, ℓ)^⊤; and (ii) ${\sum }_{i=1}^n{\sum }_{j=1}^n{z}_i^{\top }C\left({\mathit{\ell }}_i,{\mathit{\ell }}_j\right)z_j>0$ for any integer n and any finite collection of points {ℓ₁, ℓ₂, …, ℓ_n} and for all $z_i\in {\Re }^q\backslash \left\{0\right\}$. See Genton and Kleiber (2015) for a review of cross-covariance functions for multivariate processes. The (partial) realization of the multivariate process over any finite set $\mathcal{L}$ has a multivariate normal distribution $w_{\mathcal{L}}~N\left(0,C_{\mathcal{L}}\right)$ where $w_{\mathcal{L}}$ is the $q{n}_{\mathcal{L}}\times 1$ column vector and $C_{\mathcal{L}}$ is the $q{n}_{\mathcal{L}}\times q{n}_{\mathcal{L}}$ block matrix with the q×q matrix C(ℓ_i, ℓ_j) as its (i, j) block for $i,j=1,\dots ,n_{\mathcal{L}}$.

We construct the MGP from a base, or parent, multivariate GP for w(ℓ) and then, using the graph $\mathcal{G}$ defined in Section 2, represent the joint density at the reference set $\mathcal{S}$ as

$$\tilde{p}\left(w_{\mathcal{S}}\right)=\prod _{j=1}^{M}N\left(w_j\mid H_j{w}_{[j]},R_j\right),$$ (8)

where $H_1=O_{n_1\times 1}$, $R_1=C_{{\mathcal{S}}_j}$ and for j > 1, $H_j=C_{{\mathcal{S}}_j,{\mathcal{S}}_{[j]}}{C}_{{\mathcal{S}}_{[j]}}^{-1}$ and $R_j=C_{{\mathcal{S}}_j}-C_{{\mathcal{S}}_j,{\mathcal{S}}_{[j]}}{C}_{{\mathcal{S}}_{[j]}}^{-1}{C}_{{\mathcal{S}}_{[j]},{\mathcal{S}}_j}$. The resulting joint density $\tilde{p}\left(w_{\mathcal{S}}\right)$ is multivariate normal with covariance ${\tilde{C}}_{\mathcal{S}}$ and a precision matrix ${\tilde{C}}_{\mathcal{S}}^{-1}$. The precision matrix for Gaussian graphical models is easily derived using customary linear model representations for each conditional regression. Consider the DAG in (4). Each w_i is n_iq × 1 and let J_i = |Pa[a_i]| be the number of parents for a_i in the graph $\mathcal{G}$. Furthermore, let C_i,j be the n_iq × n_jq covariance matrix between w_i and w_j, C_i,[i] be the n_iq × J_iq covariance matrix between w_i and w_[i], and C_[i],[i] be the J_iq × J_iq covariance matrix between w_[i] and itself. Representing each conditional density in (4) as a linear regression on w_i, we get

$$w_1={\omega }_1~N\left(0,R_1\right);w_i=\sum _{\left\{j:a_j\in \text{Pa}\left[a_i\right]\right\}}{H}_{ij}{w}_j+{\omega }_i,i=2,3,\dots ,M,$$ (9)

where each H_ij is an n_iq×n_jq is a coefficient matrix representing the multivariate regression of w_j given w_[i], ${\omega }_i\stackrel{ind}{~}N\left(0,R_i\right)$ for i = 1,2,…,M, and each R_i is an n_iq × n_iq residual covariance matrix. We set H_ii = O and H_ij = O, where O is the matrix of zeros, whenever j ∈ {j : a_j ∉ Pa[a_i]}. For j ∈ {j : a_j ∈ Pa[a_i]}, let $\left\{j_1,j_2,\dots ,j_{J_i}\right\}$ be the indices in Pa[a_i] and let $H_{i,[i]}=\left[H_{i,j_1},H_{i,j_2},\dots ,H_{i,j_{J_i}}\right]$ be the $n_{i}q\times \left({\sum }_{k=1}^{J_i}{n}_{j_k}\right)q$ block matrix formed by stacking $H_{i,j_k}$ side by side for each $a_{j_k}\in \text{Pa}\left[a_i\right]$. Since $\text{E}\left[w_i\mid w_{[i]}\right]=H_{i,[i]}{w}_{[i]}=C_{i,[i]}{C}_{[i][i]}^{-1}{w}_{[i]}$, we obtain $H_{i,[i]}=C_{i,[i]}{C}_{[i][i]}^{-1}$ and each $H_{i{j}_K}$ can be obtained from the respective submatrix of H_i[i]. We also obtain $R_i=\text{var}\left\{w_i\mid w_{[i]}\right\}=C_{i,i}-C_{i,[i]}{C}_{[i][i]}^{-1}{C}_{[i],i}$. Therefore, all the H_ij’s and R_i’s can be computed from the base cross-covariance function.

The distribution of $w={\left[w_1^{\top },w_2^{\top },\dots ,w_M^{\top }\right]}^{\top }$ can be obtained by noting that w = Hw+ ω, where H = {H_ij} is the $\left({\sum }_{i=1}^M{n}_{i}q\right)\times \left({\sum }_{i=1}^M{n}_{i}q\right)$ block matrix with {H_ij} as (i, j)-th block. Therefore, ${\tilde{C}}_{\mathcal{S}}=\text{var}(w)={(I-H)}^{-1}R{(I-H)}^{-\top }$, where R is block-diagonal with R_i as the (i, i)-th block. Note that I − H is block lower-triangular with 1’s on the diagonal, hence non-singular. Also, the precision matrix ${\tilde{C}}_{\mathcal{S}}^{-1}={(I-H)}^{\top }{R}^{-1}(I-H)$ is sparse because of H_ij = O whenever a_j ∉ Pa[a_i]. Block-sparsity of ${\tilde{C}}_{\mathcal{S}}^{-1}$ can be induced by building $\mathcal{G}$ with few, carefully placed directed edges among nodes in A; Appendix B, available online, contains a more in-depth treatment. We extend (8) to the collection of non-reference locations $\mathcal{U}\subset \mathcal{D}\backslash \mathcal{S}$:

$$\tilde{p}\left(w_{\mathcal{U}}\mid w_{\mathcal{S}}\right)=\prod _{j=1}^{M}N\left(w_{{\mathcal{U}}_j}\mid H_{{\mathcal{U}}_j}{w}_{\left[{\mathit{b}}_j\right]},R_{{\mathcal{U}}_j}\right)=N\left(w_{\mathcal{U}}\mid H_{\mathcal{U}}{w}_{\mathcal{S}},R_{\mathcal{U}}\right),$$ (10)

where $H_{{\mathcal{U}}_j}=C_{{\mathcal{U}}_j,{\mathcal{S}}_{\left[{\mathit{b}}_j\right]}}{C}_{{\mathcal{S}}_{\left[{\mathit{b}}_j\right]}}^{-1}$ and $R_{{\mathcal{U}}_j}=C_{{\mathcal{U}}_j}-C_{{\mathcal{U}}_j,{\mathcal{S}}_{\left[{\mathit{b}}_j\right]}}{C}_{{\mathcal{S}}_{\left[{\mathit{b}}_j\right]}}^{-1}{C}_{{\mathcal{S}}_{\left[{\mathit{b}}_j\right]},{\mathcal{U}}_j}$, analogously to (8), while $H_{\mathcal{U}}$ and $R_{\mathcal{U}}$ are analogous to $H_{\mathcal{S}}$ and $R_{\mathcal{S}}$. Clearly, given that all the $\tilde{p}$ densities are Gaussian, all finite dimensional distributions will also be Gaussian. We have constructed a Gaussian process with the following cross-covariance function for any two locations ${\mathit{\ell }}_1,{\mathit{\ell }}_2\in \mathcal{D}$

$$Co{v}_{\tilde{p}}\left(w\left({\mathit{\ell }}_1\right),w\left({\mathit{\ell }}_2\right)\right)=\{\begin{array}{ll}{\tilde{C}}_{s_i,s_j}\hfill & \text{ if }{\mathit{\ell }}_1=s_i,{\mathit{\ell }}_2=s_j\text{ and }{s}_i,s_j\in \mathcal{S}\hfill \\ H_{{\mathit{\ell }}_1}{\tilde{C}}_{{\mathcal{S}}_{\left[{\mathit{\ell }}_1\right]},s_j}\hfill & \text{ if }{\mathit{\ell }}_1\in \mathcal{D}\backslash \mathcal{S},{\mathit{\ell }}_2=s_j\text{ and }{s}_j\in \mathcal{S}\hfill \\ {\delta }_{\left({\mathit{\ell }}_1={\mathit{\ell }}_2\right)}{R}_{{\mathit{\ell }}_1}+H_{{\mathit{\ell }}_1}{\tilde{C}}_{{\mathcal{S}}_{\left[{\mathit{\ell }}_1\right]},{\mathcal{S}}_{\left[{\mathit{\ell }}_2\right]}}{H}_{{\mathit{\ell }}_2}^{\top }\hfill & \text{ otherwise. }\hfill \end{array}$$

For a given base Gaussian covariance function C, domain partitioning $\mathcal{P}$, mesh $\mathcal{G}$, and reference set $\mathcal{S}$, we denote the corresponding meshed Gaussian process as MGP($\mathcal{G}$, $\mathcal{P}$, $\mathcal{S}$,C).

3.1. Bayesian hierarchical model and Gibbs sampler

Meshed GPs produce block-sparse precision matrices that are constructed cheaply from their block-sparse Cholesky factors by solving small linear systems. General purpose sparse-Cholesky algorithms (Davis, 2006; Chen et al., 2008) can then be used to obtain collapsed samplers as in Finley et al. (2019). Unfortunately, these algorithms can only be used on Gaussian first stage models and are computationally impracticable for data in the millions. Hence, we develop a more general scalable Gibbs sampler for the recovery of spatial random effects in hierarchical MGP models that entirely circumvents large matrix computations.

Consider a multivariate spatiotemporally-varying regression model at $\mathit{\ell }\in \mathcal{D}\subset {\Re }^{d+1}$,

$$y(\mathit{\ell })=X{(\mathit{\ell })}^{\top }\beta +Z{(\mathit{\ell })}^{\top }w(\mathit{\ell })+\epsilon (\mathit{\ell }),$$ (11)

where $y(\mathit{\ell })\in {\Re }^l$ is the multivariate point-referenced outcome, $X{(\mathit{\ell })}^{\top }=\text{blockdiag}{\left\{x_i{(\mathit{\ell })}^{\top }\right\}}_{i=1}^l$ is a l × p = l × ∑p_i matrix of spatially referenced predictors linked to constant coefficients β, w(ℓ) is the spatial process, Z(ℓ) is a l × q design matrix, ε(ℓ) is measurement error such that $\epsilon (\mathit{\ell })\stackrel{iid}{~}N(0,D)$ and $D=\text{diag}\left({\tau }_1^2,\dots ,{\tau }_l^2\right)$. A simple univariate regression model with a spatially-varying intercept can be obtained with l = 1, Z(ℓ) = 1. For observed locations $\mathcal{T}=\left\{{\mathit{\ell }}_1,\dots ,{\mathit{\ell }}_n\right\}$, we write the above model compactly y = Xβ + Zw + ε, where y = (y(ℓ₁)^⊤, …, y(ℓ_n)^⊤)^⊤, w and ε are similarly defined, X = [X(ℓ₁) : ⋯ : X(ℓ_n)]^⊤, $Z=\text{ blockdiag }\left({\left\{Z{\left({\mathit{\ell }}_i\right)}^{\top }\right\}}_{i=1}^n\right)$, and $D_n=\text{ blockdiag }\left({\left\{D\right\}}_{i=1}^n\right)$.

For subsets $\left\{{\mathit{\ell }}_1,\dots ,{\mathit{\ell }}_{n_{\mathcal{A}}}\right\}=\mathcal{A}\subset \mathcal{T}$, let $y(\mathcal{A})={\left(y{\left({\mathit{\ell }}_1\right)}^{\top },\dots ,y{\left({\mathit{\ell }}_{n_{\mathcal{A}}}\right)}^{\top }\right)}^{\top }$, with analogous definitions for $w(\mathcal{A})$ and $\epsilon (\mathcal{A})$, $X(\mathcal{A})={\left[X\left({\mathit{\ell }}_1\right):\dots :X\left({\mathit{\ell }}_{n_{\mathcal{A}}}\right)\right]}^{\top }$, $Z_{\mathcal{A}}=\text{blockdiag}\left({\left\{Z{\left({\mathit{\ell }}_i\right)}^{\top }\right\}}_{i=1}^{n_{\mathcal{A}}}\right)$ and $D_{\mathcal{A}}=\text{blockdiag}\left({\left\{D\right\}}_{i=1}^{n_{\mathcal{A}}}\right)$. After fixing a reference set $\mathcal{S}$, we obtain ${\mathcal{S}}^{*}=\mathcal{T}\cap \mathcal{S}$ and $\mathcal{U}=\mathcal{T}\backslash \mathcal{S}$. We partition the domain as above to obtain ${\mathcal{S}}_j$, ${\mathcal{S}}_j^{*}$, ${\mathcal{U}}_j$ for j = 1, …, M and model w(ℓ) using the MGP which yields $w~N\left(0,{\tilde{C}}_{\mathcal{S}}^{-1}\right)$. We complete the model specification by assigning β ~ N(β | μ_β, Σ_β), ${\tau }_j^2~Inv.\mathit{\text{Gamma}}\left({\tau }_j^2\mid a_{{\tau }_j},b_{{\tau }_j}\right)$, θ ~ p(θ).

The resulting full conditional distribution for β is $N\left({\Sigma }_{\beta }^{*}{\mathit{\mu }}_{\beta }^{*},{\Sigma }_{\beta }^{*}\right)$, where ${\Sigma }_{\beta }^{*}=({\Sigma }_{\beta }^{-1}+{X^{\top }{D}_n^{-1}X)}^{-1}$, ${\mu }_{\beta }^{*}={\Sigma }_{\beta }^{-1}{\mu }_{\beta }+X^{\top }{D}_n^{-1}(y-Zw)$. For ${\tau }_r^2$, r = 1, …, q, the full conditional is Inverse-Gamma with parameters $a_{{\tau }_r}+n/2$ and $b_{{\tau }_r}+\frac{1}{2}{E}_r^{\top }{E}_r$ where E_r = y_·r −X_·rβ−Z_·rw and y_·r,X_·r,Z_·r are the subsets of y,X,Z corresponding to outcome r (out of q).

The Gibbs update of the $w_{\mathcal{U}}$ components can proceed simultaneously as all blocks in $\mathcal{U}$ have no children and their parents are in $\mathcal{S}$. The full conditional for $w_{{\mathcal{U}}_j}$ for j = 1,…,M is thus $N\left({\Sigma }_{{\mathcal{U}}_j}^{*}{\mathit{\mu }}_{{\mathcal{U}}_j}^{*},{\Sigma }_{{\mathcal{U}}_j}^{*}\right)$ where ${\Sigma }_{{\mathcal{U}}_j}^{*}={\left(Z\left({\mathcal{U}}_j\right)D^{-1}Z{\left({\mathcal{U}}_j\right)}^{\top }+R_{{\mathcal{U}}_j}^{-1}\right)}^{-1}$ and ${\mathit{\mu }}_{{\mathcal{U}}_j}^{*}=Z\left({\mathcal{U}}_j\right)D^{-1}\left(y\left({\mathcal{U}}_j\right)-X{\left({\mathcal{U}}_j\right)}^{\top }\beta \right)+R_{{\mathcal{U}}_j}^{-1}{H}_{{\mathcal{U}}_j}{w}_{\left[{\mathit{b}}_j\right]}$, where $w_{\left[{\mathit{b}}_j\right]}$ is the spatial process at locations corresponding to the parents of b_j ∈ B ⊂ V.

We update $w_{{\mathcal{S}}_j}=w_j$ for j = 1,…,M via its full conditional $N\left({\Sigma }_j^{*}{\mu }_j^{*},{\Sigma }_j^{*}\right)$. Let $1_j={\left(In\left(s_1\in {\mathcal{S}}_j^{*}\right),\dots ,In\left(s_{n_j}\in {\mathcal{S}}_j^{*}\right)\right)}^{\top }$ be the vector of indicators that identify locations with non-missing outputs, and let a_j ∈ V be the node in $\mathcal{G}$ corresponding to ${\mathcal{S}}_j$. Then,

$$\begin{gathered} {\Sigma }_j^{*-1}=Z_j^{\top }{\tilde{D}}_{n_j}^{-1}{Z}_j+R_j^{-1}+\sum _{i=1}^{\left|\text{Ch}\left[{\mathit{a}}_j\right]\right|}{H}_i^{[j]\top }{R}_i^{[j]-1}{H}_i^{[j]} \\ {\mu }_j^{*}=R_j^{-1}{H}_j{w}_{[j]}+Z_j^{\top }{\tilde{D}}_{n_j}^{-1}{\tilde{y}}_j+\sum _{i=1}^{\left|\text{Ch}\left[{\mathit{a}}_j\right]\right|}{H}_i^{[j]\top }{R}_i^{[j]-1}{w}_i^{[j]}, \end{gathered}$$ (12)

where ${\tilde{D}}_{n_j}^{-1}=I_j\odot D_{n_j}^{-1}$ with $I_j=1_j{1}_j^{\top }$, and ${\tilde{y}}_j=1_j\odot \left(y_j-X_j\beta \right)$ and ⊙ denotes the Hadamard or Schur (element-by-element) product. Finally, θ is updated via a Metropolis step with target density $p(\theta )N\left(w_{\mathcal{S}}\mid 0,{\tilde{C}}_{\mathcal{S}}\right)N\left(w_{\mathcal{U}}\mid H_{\mathcal{U}}{w}_{\mathcal{S}},R_{\mathcal{U}}\right)$ using (8) and (10). The Gibbs sampling algorithm will iterate across the above steps and, upon convergence, will produce samples from $p\left(\beta ,{\left\{{\tau }_j^2\right\}}_{j=1}^q,w\mid y\right)$.

We obtain posterior predictive inference at arbitrary $\mathit{\ell }\in \mathcal{D}$ by evaluating p(y(ℓ) | y). If $\mathit{\ell }\in \mathcal{S}\cup \mathcal{U}$, then we draw one sample of y(ℓ) ~ N(X(ℓ)^⊤β + Z(ℓ)^⊤w(ℓ), D) for each draw of the parameters from $p\left(\beta ,{\left\{{\tau }_j^2\right\}}_{j=1}^q,w\mid y\right)$. Otherwise, considering that $\mathit{\ell }\in {\mathcal{D}}_j$ for some j and thus η(ℓ) = b_j, with parent nodes Pa[b_j] and children Ch[b_j] = ∅, we sample w(ℓ) from the full conditional $N\left({\Sigma }_{\mathit{\ell }}^{*}{\mu }_{\mathit{\ell }}^{*},{\Sigma }_{\mathit{\ell }}^{*}\right)$, where ${\Sigma }_{\mathit{\ell }}^{*}={\left(Z(\mathit{\ell })D^{-1}Z{(\mathit{\ell })}^{\top }+R_{\mathit{\ell }}^{-1}\right)}^{-1}$ and ${\mu }_{\mathit{\ell }}^{*}=Z(\mathit{\ell })D^{-1}\left(y(\mathit{\ell })-X{(\mathit{\ell })}^{\top }\beta \right)+R_{\mathit{\ell }}^{-1}{H}_{\mathit{\ell }}{w}_{\left[{\mathit{b}}_j\right]}$, then draw y(ℓ) ~ N(X(ℓ)^⊤β + Z(ℓ)^⊤w(ℓ), D).

3.2. Non-separable multivariate spatiotemporal covariances

We provide an account of the computational cost of general MGPs as a starting point to motivate the introduction of more efficient tessellated MGPs, and specifically Q-MGPs, in Section 4. We consider (11) and take l = 1 to simplify our exposition. In the resulting model, β is the regression coefficient on the p point-referenced regressors with a static effect on the outcome, whereas the q-variate spatiotemporal process w(·) captures the dynamic effect of the Z regressors. Typically in geostatistical modeling p and q are small, hence sampling β and τ² carries a negligible computational cost. The cost of each Gibbs iteration is dominated by updates of θ and w. Let us assume, solely for expository purposes, that each of the M blocks comprise the same number of locations, i.e. $\left|{\mathcal{S}}_j\right|=\left|{\mathcal{U}}_j\right|=m$, for all j = 1,…,M. Thus, $m=\frac{n}{2M}$ and the graph nodes have J or fewer parents and L or fewer children.

The evaluation of $N\left(w_{\mathcal{S}}\mid 0,{\tilde{C}}_{\mathcal{S}}\right)={\prod }_{j=1}^{M}N\left(w_j\mid H_j{w}_{[j]},R_j\right)$ and $N\left(w_{\mathcal{U}}\mid H_{\mathcal{U}}{w}_{\mathcal{S}},R_{\mathcal{U}}\right)={\prod }_{j=1}^{M}N\left(w_{{\mathcal{U}}_j}\mid H_{{\mathcal{U}}_j}{w}_{[{\mathit{b}}_j]},R_{{\mathcal{U}}_j}\right)$ dominates the computation. Each term in the product entails $R_j^{-1}$ and $R_{{\mathcal{U}}_j}^{-1}$, both of size qm×qm, and their determinants. These require $C_{[j]}^{-1}$ of size Jqm×Jqm or less, resulting in $O\left(2M\left(q^3{m}^3+J^3{q}^3{m}^3\right)\right)=O\left(2M{q}^3{m}^3\left(J^3+1\right)\right)\approx O\left(2M{q}^3{m}^3{J}^3\right)=O\left(\frac{n^3{q}^3{J}^3}{M^2}\right)$ flops via Cholesky decomposition. Reasonably, J and m are fixed so M may grow linearly with sample size and the cost is O(nq³J³) considering M ∝ n. The total computing time is $~O\left(\frac{n{q}^3{J}^3}{K}\right)$ with K processors for computing the 2M densities. Sampling $w_{\mathcal{S}}$ and $w_{\mathcal{U}}$ from their full conditional distributions requires O(2Mq³m³ +MLq²m² +Mq²m²) flops, assuming $R_j^{-1}$ and $R_{{\mathcal{U}}_j}^{-1}$ are stored in the previous step. The first term in the complexity order is due to the Cholesky decomposition of covariance matrices, the second is due to sampling the reference nodes, and the third comes from sampling other nodes. Without further assumptions, parallelization reduces complexity to $O\left(\frac{2M{q}^3{m}^3}{K}+\frac{M{q}^2{m}^2}{K}+ML{q}^2{m}^2\right)$, since the covariances can be computed beforehand and the M components of $w_{\mathcal{U}}$ are independent given $w_{\mathcal{S}}$. With fixed block size m, the overall complexity for a Gibbs iteration is $O\left(\frac{2}{K}M{q}^3{m}^3\left(J^3+1\right)+\frac{1}{K}2M{q}^3{m}^3+\frac{1}{K}M{q}^2{m}^2+ML{q}^2{m}^2\right)\approx O\left(\frac{1}{K}{J}^3{q}^{3}n+q^{2}n\right)\approx O(n)$, linear in the sample size and cubic in J, highlighting the computational speedup of sparse graphs (J small), the negative impact of large q, and the serial sampling of $w_{\mathcal{S}}$.

In terms of storage, H_j and R_j correspond to a storage requirement of O(4Mq²m²) = O(q²n). The matrix Z of size qn×qn can be represented as a list of 2M block-diagonal (hence sparse) Z_j matrices. Furthermore, computing Zw (dimension n×1) can be vectorized as the row-wise sum of Z* ⊙ w* where Z* and w* are n×q matrices with jth column representing the jth space-time varying predictor. The cost of storing Z is thus O(2qn).

Complexity is further reduced by considering a graph with small J or a finer partition resulting in large M and small m, whereas the overall time can be reduced by distributing computations on K processors. Possible choices for $\mathcal{G}$ include nearest-neighbor graphs and multiresolution trees. In settings with large q, adjusting J and M may be insufficient to reduce the computational burden. Covariance functions that are separable in the variables (but perhaps non-separable in space and time) bring the cost of Choesky factorizations of Jqm × Jqm matrices from O(J³q³m³) to O(J³m³ + q³) because $C^{-1}={\left(C_{\mathit{h},\mathit{u}}\otimes C_{\mathit{v}}\right)}^{-1}=C_{\mathit{h},\mathit{u}}^{-1}\otimes C_{\mathit{v}}^{-1}$, where C_h,u is the Jm×Jm space-time component of the cross-covariance, and C_v the q × q variable component. Savings accrue when evaluating the likelihood and in sampling from the full-conditionals at the cost of realism in describing the spatial process.

The next section develops a novel MGP design based on domain tessellations or tiling – i.e. partitions of the domain forming repeated patterns – to which we associate similarly patterned meshes. If observations are also located in patterns, the bulk of the largest linear solvers will be redundant, resulting in a significant reduction in computational time. In either scenario, sampling $w_{\mathcal{S}}$ will also proceed in parallel with improved mixing.

4. MGPs based on domain tessellation or tiling

We construct MGPs based on a tessellation or tiling of the domain. For spatial domains (d = 2, Figure 2), regular tiling results in triangular, quadratic, or hexagonal tessellations; mixed designs are also possible. These partition schemes can be linked to a DAG $\mathcal{S}$ by drawing directed outgoing edges starting from an originating node/tile. The same fixed pattern can be repeated over a surface of any size. In dimensions d > 2, which may include time, space-filling tessellations or honeycombs can be constructed analogously, along with their corresponding meshes. Constructions of MGPs based on these ideas simply requires partitioning the locations $\mathcal{S}$ into subsets based on the chosen tessellation.

Figure 2:

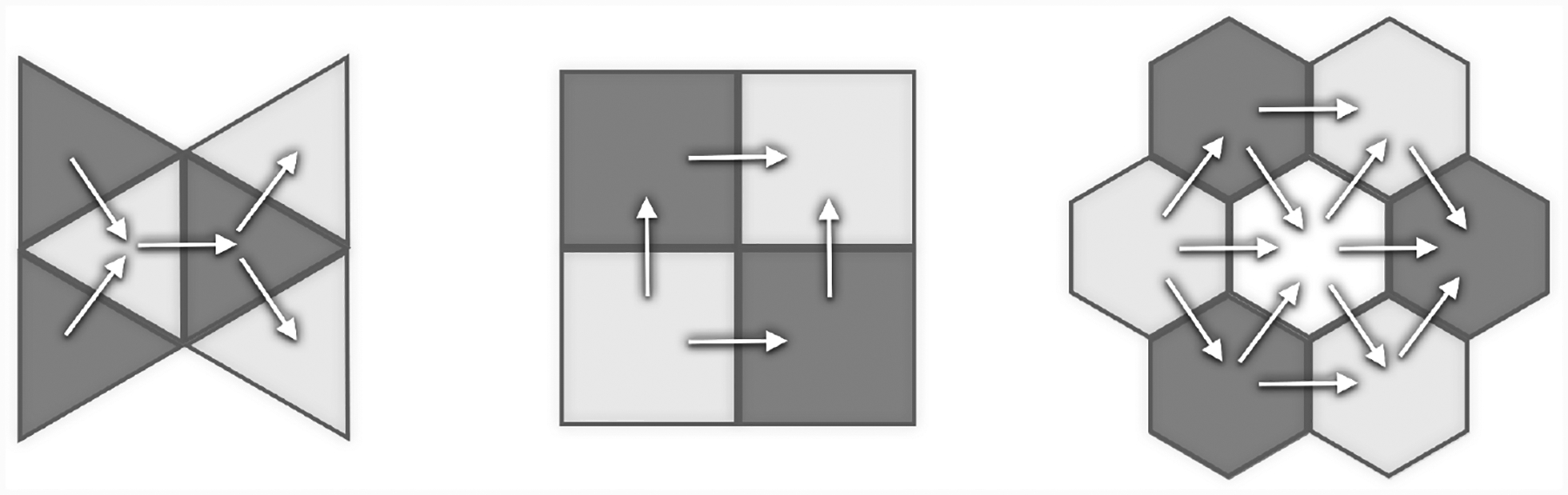
Regular tessellation base units and corresponding MGP graphs for spatial domains.

This subclass of MGP models corresponds by design to graphs with known coloring, with each color linked to a subgraph conditionally independent of all nodes of other colors, regardless of the dimension of the domain. This feature enables large-scale parallel sampling of $w_{\mathcal{S}}$ and improves mixing without the need to implement heuristic graph-coloring algorithms. Furthermore, regions in a tessellated domain are typically translations and/or rotations of a single geometric shape. Carefully choosing $\mathcal{S}$, it will be possible to avoid computing the bulk of linear solvers, resulting in substantial computational gains. Subsequently, we focus on axis-parallel partitioning (quadratic or cubic tessellation) and cubic meshes, but analogous constructions and the same properties hold with other tessellation schemes.

A cubic MGP (Q-MGP) is constructed by partitioning each coordinate axis into intervals. In d + 1 dimensions, splitting each axis into L intervals results in L^d+1 regions. Consider a spatiotemporal domain $\mathcal{D}={\times }_{r=1}^{d+1}{\mathcal{D}}^{(r)}$, where ${\mathcal{D}}^{(d+1)}$ is the time dimension. We partition each coordinate axis into L_r disjoint sets: ${\mathcal{D}}^{(r)}={\mathcal{I}}_{r,1}\cup \cdots \cup {\mathcal{I}}_{r,L_r}$, where ${\mathcal{I}}_{r,j}\cap {\mathcal{I}}_{r,k}=\varnothing$ if j ≠ k and ${\mathcal{I}}_{r,s}$ denotes the sth interval in the rth coordinate axis. Solely for exposition, and without loss of generality, assume that ${\mathcal{D}}^{(r)}=\mathcal{I}=[0,1]$ and L_r = L for r = 1,…,d + 1. Any location $\mathit{\ell }=\left({\ell }_1,\dots ,{\ell }_{d+1}\right)\in \mathcal{D}$ will be such that $\mathit{\ell }\in {\mathcal{I}}_{1,i_1}\times \cdots \times {\mathcal{I}}_{d+1,i_{d+1}}={\mathcal{D}}_j$ for some i₁,…,i_d+1 and with j = 1,…,M, where M = L^d+1. We refer to this axis-parallel partition scheme as a cubic tessellation and denote it by $T={\left\{{\mathcal{I}}_{r,s}\right\}}_{r=1,\dots ,d+1}^{s=1,\dots ,L}$. We use T to partition the reference set $\mathcal{S}$ as ${\mathcal{S}}_j={\mathcal{D}}_j\cap \mathcal{S}$ for j = 1,…,L^d+1.

Next, we define η(ℓ) = (η₁(ℓ), …,η_L(ℓ)) ∈ {1, …, L}^d+1, where η_j = η_j(ℓ) = r if ${\ell }_j\in {\mathcal{I}}_{j,r}$. Then, let $\mathcal{Q}=(V,E)$ be a directed acyclic graph with V = A∪B and reference nodes $A=\left\{a_1,\dots ,a_{L^{d+1}}\right\}$. Therefore, for any j = 1,…,L^d+1 if $s\in {\mathcal{S}}_j$ then η(s) = a_j ∈ A ⊂ V. We write each node v ∈ V as $v=\left(v_{{\eta }_1},\dots ,v_{{\eta }_L}\right)\in {\left\{1,\dots ,L\right\}}^{d+1}$. The directed edges are constructed using a “line-of-sight” strategy. Suppose Pa[v] = {x⁽¹⁾,…,x^(d+1)}. The hth parent of v is defined as $x^{(h)}=\left(a_{{\eta }_1},\dots ,a_{{\eta }_h}-k,\dots ,a_{{\eta }_L}\right)\cap {\left\{1,\dots ,d+1\right\}}^{d+1}$, where k ≥ 1 is the smallest integer such that x^(h) ∈ A. Consequently x^(h) = ∅ if a_h = 1. Thus, the parents of node v = η(ℓ) are the ones that precede it along each of the d + 1 coordinates. If $\mathit{\ell }\in {\mathcal{D}}_j\backslash {\mathcal{S}}_j$, then η(ℓ) = b_j ∈ B and Pa[b_j] = {a_j} ∪ Pa[a_j] where a_j ∈ A is a reference node. To avoid Pa[b_j] = ∅ we set $\text{Pa}\left[b_j\right]=\left\{x_1^{(1)},x_2^{(1)},\dots ,x_1^{(d+1)},x_2^{(d+1)}\right\}$. The two parents along the hth dimension are $x_1^{(h)}=a_{{\eta }_h}+k_1,x_2^{(h)}=a_{{\eta }_h}-k_2$ where k_i is the smallest positive integer such that $x_i^{(h)}\in A$, i = 1,2. In this setting J = 2(d + 1). The construction is finalized by fixing the cross-covariance function C(ℓ, ℓ′); Figure 3 shows that the same basic structure can be immediately extended to higher dimensions, including time.

Figure 3:

Q-MGP meshes used for spatial data on d = 2 (left) can be extended for use on spatiotemporal data d = 3 (right). Node colors correspond to Gibbs sampler blocks.

4.1. Caching redundant expensive matrix operations

The key computational bottleneck for the Gibbs sampler in Section 3.2 is calculating, for j = 1,…,2M, of (i) $C_{[j]}^{-1}$ (2MJ³q³m³ flops) and (ii) $R_j^{-1}$, ${\Sigma }_j^{*-1}$ 4Mq³m³ flops). The former is costlier than the latter by a factor of J³/2. Q-MGPs are designed to greatly reduce this cost. We start with an axis-parallel tessellation of the domain in equally-sized regions ${\mathcal{D}}_1,\dots ,{\mathcal{D}}_M$, storing observed locations in $\mathcal{U}$ to create ${\mathcal{U}}_1,\dots ,{\mathcal{U}}_M$, which we assume, for simplicity, to be no larger than m in size. Taking a stationary base-covariance function C, implies that $C\left({\mathcal{L}}_1,{\mathcal{L}}_2\right)=C\left({\mathcal{L}}_1+h,{\mathcal{L}}_2+h\right)$, where $h\in {\Re }^{d+1}$ is used to shift all locations in the sets. Recall that the reference set $\mathcal{S}$ of MGPs can include unobserved locations. Hence, we can build $\mathcal{S}$ on a lattice of regularly spaced locations. Since domain partitions have the same size, we have ${\mathcal{S}}_j={\mathcal{S}}^{*}+h_j$ for j = 1,…,M, where ${\mathcal{S}}^{*}$ is a single “prototype set” using which one can locate all other reference subsets. Also, since Pa[a_j] ⊂ Pa[b_j], there will be 4(d + 1) prototype sets for parents, i.e. ${\mathcal{S}}_{\text{Pa}\left[{\mathit{v}}_j\right]}={\mathcal{S}}_r^{*}+h_j$ for some r ∈ {1,…,4(d + 1)} and j = 1,…,2M. Then, we can build maps ${\xi }_{\mathcal{S}}:\left\{1,\dots ,M\right\}\to \left\{1,\dots ,4(d+1)\right\}$ and ${\xi }_{\mathcal{U}}:\left\{1,\dots ,M\right\}\to \left\{1,\dots ,4(d+1)\right\}$ linking each of ${\mathcal{S}}_j$ and ${\mathcal{U}}_j$ to a parent prototype. This ensures that $C_{[j]}^{-1}=C_{{\mathcal{S}}_r^{*}}^{-1}$ for each j = 1,…,2M. One only needs the maps ${\xi }_{\mathcal{S}}$ and ${\xi }_{\mathcal{U}}$, cache the r unique inverses, and reuse them. The same method applies to cache $R_{{\mathcal{S}}_j}^{-1}=R_{{\mathcal{S}}_r^{*}}^{-1}$ on reference sets, but not on other locations since no redundancy arises in $C_{{\mathcal{U}}_j}$ for j = 1,…,M. See Figure 4 for an illustration. Compared to general MGPs (see Table 1), the number of large linear system solvers is now constant with sample size and (d + 1) ≪ M significantly reduces computational cost.

Figure 4:

Visualizing redundancies: a spatial domain is partitioned in M = 25 regions and linked to a quadratic mesh. The reference set $\mathcal{S}$ is fixed on a regular grid, with m = 9. Parent locations of the orange (resp. purple) are in green (resp. blue). Using a stationary covariance, C_blue,blue = C_green,green. Therefore only one inversion is necessary; this can be replicated at no cost across 9 of the 16 regions.

Table 1:

Summary of computational cost of general MGPs and Q-MGPs. Rows are sorted from most expensive (top) to least expensive (bottom).

	$C_{[j],[j]}^{-1}$	$R_{{\mathcal{S}}_j}^{-1}$	$R_{{\mathcal{U}}_j}^{-1}$	${\sum }_{{\mathcal{S}}_j}^{*-1}$	${\sum }_{{\mathcal{U}}_j}^{*-1}$	Sampling $w_{\mathcal{S}}$, $w_{\mathcal{U}}$
MGPs (all cases)	2MJ3q3m3	Mq 3 m 3	Mq 3 m 3	Mq 3 m 3	Mq 3 m 3	MLq2m2 + Mq2m2
Q-MGPs
— Irregular locations	4(d + 1)J3q3m3	4(d + 1)q3m3	Mq 3 m 3	Mq 3 m 3	Mq 3 m 3	MLq2m2 + Mq2m2
— Pattern lattice w/missing	2M*J3q3m3	2M*q3m3		Mq 3 m 3		MLq 2 m 2
— Lattice w/missing	4(d + 1)J3q3m3	4(d + 1)q3m3		Mq 3 m 3		MLq 2 m 2
— Full lattice and Z(ℓ) = Iq	4(d + 1)J3q3m3	4(d + 1)q3m3		2(d + 2)(d + 1)q3m3		MLq 2 m 2

Furthermore, Q-MGPs automatically adjust to settings where observed locations $\mathcal{T}$ are on partly regular lattices, i.e., they are located at patterns repeating in space or time which emerge after initial inspections of the data. Appendix G, available online, outlines a simple algorithm to identify such patterns and create maps ${\xi }_{\mathcal{S}}$ and ${\xi }_{\mathcal{U}}$. In such cases, we fix $\mathcal{S}\supseteq \mathcal{T}$ and $\mathcal{U}=\varnothing$. In addition to the above mentioned savings, we now do not have to compute $R_{{\mathcal{U}}_j}^{-1}$ and ${\Sigma }_{{\mathcal{U}}_j}^{*-1}$. If $\mathcal{T}$ is not a regular lattice over the whole domain, 4(d + 1) is a lower bound and in general there are M* ≪ M inverses to compute. If $\mathcal{T}$ is a fully observed regular lattice and if Z(ℓ) = I (a varying intercept model), then we save in computing the full conditional covariances as well, since all D_j = I. See Appendix C, available online, for details on choosing $\mathcal{S}$ and $\mathcal{U}$.

4.2. Improved mixing via parallel sampling

With caching, a much larger proportion of time is spent on sampling; parallelization may in general be achieved via appropriate node coloring algorithms (see e.g. Molloy and Reed, 2002; Gonzalez et al., 2011; Lewis, 2016), but this step is unnecessary in Q-MGPs as the colors in $\mathcal{Q}$ are set in advance independently of the data and result in efficient parallel sampling of the latent effects. Reference nodes A of $\mathcal{Q}$ are colored to achieve independence conditional on realizations of nodes of all other colors. For example, we partition spatial domains (d = 2) into M₁ × M₂ regions and link each region to a reference node in a quadratic mesh. A “central” reference node v₊ will have two parents and two children, i.e. Pa[v₊] = {v_l, v_b} and Ch[v₊] = {v_r, v_t}, with l, b, r, t respectively denoting left, bottom, right, top – refer to Figure 3 (left). We have Pa[v_t] = {v₊, v_tl} and Pa[v_r] = {v₊, v_br}. The Markov blanket of v₊, denoted as mb(v₊), is the set of neighbors of v₊ in the undirected “moral” graph $Q^{\mathcal{M}}$, hence mb(v₊) = Pa[v₊] ∪ Ch[v₊] ∪ {v_tl, v_br}. The corresponding spatial process is such that $p\left(w_{+}\mid w\backslash w_{+}\right)=p\left(w_{+}\mid w_{\text{mb}\left({\mathit{v}}_{+}\right)}\right)$. Denoting v_bl = Pa[v_l] ∩ Pa[v_b] and v_tr = Ch[v_r] ∩ Ch[v_t], we note that {v_bl, v_tr} ∩ mb(v₊) = ∅. We partition reference nodes A into four groups {A⁽¹⁾,A⁽²⁾,A⁽³⁾,A⁽⁴⁾}, such that {v₊} ⊂ A⁽¹⁾, {v_b, v_t} ⊂ A⁽²⁾, {v_l, v_r} ⊂ A⁽³⁾, and {v_tl,v_tr, v_bl, v_br} ⊂ A⁽⁴⁾. This 3 × 3 pattern is repeated over the whole graph. Then, if v ∈ A^(j), mb(v) ∩ A^(j) = ∅. Denoting by $\mathcal{D}$ the other variables in the Gibbs sampler, we get:

$$p\left(w_j\mid w_{-j},\mathcal{D}\right)=p\left(w_j\mid w_{\mathfrak{m}\mathfrak{b}\left(v_j\right)},\mathcal{D}\right)=\prod _{v_i\in A^{(j)}}p\left(w_i\mid w_{A^{(-j)}},\mathcal{D}\right).$$

Since parallelization is possible within each of the groups, only be four serial steps are needed; time savings are due to M/4 typically being orders of magnitude larger than the number of available processors. Extensions to other tessellation schemes and higher dimensional domains and the associated graphs follow analogously.

5. Data analysis

Satellite imaging and remote sensing data are nowadays frequently collected in large quantities and processed to be used in geology, ecology, forestry, and other fields, but clouds and atmospheric conditions obstruct aerial views and corrupt the data creating gaps. Recovery of the underlying signal and quantification of the associated uncertainty are thus the major goals to enable practitioners in the natural sciences to fully exploit these data sources. Several scalable geostatistical models based on Gaussian processes have been implemented on tens or hundreds of thousands of data points, with few exceptions. In considering larger data sizes, one must either have a large time budget – usually several days – or reduce model flexibility and richness. Scalability concerns become the single most important issue in multivariate spatiotemporal settings. In fact, repeated collection of aerial images and multiple spatially-referenced predictors modeled to have a variable effect on the outcome have a multiplicative effect on data size. With no separability assumptions, the dimension of the latent spatial random effects that one may wish to recover will be huge even when individual images would be manageable when considered individually.

The lack of software to implement scalable models for spatiotemporal data makes it difficult to compare our proposed approach with others in these settings. On the other hand, a recent article (Heaton et al., 2019) pins many state-of-the-art models against each other in a spatial (d = 2) prediction contest. On the same data, we show in Appendix E, available online, that Q-MGPs can outperform all competitors in terms of predictive performance and coverage while using a similar computational budget.

5.1. Non-separable multivariate spatiotemporal base covariance

In our analyses, we choose a class of multivariate space-time cross-covariances that models the covariance between variables i and j at the $(h,u)\in {\Re }^{d+1}$ space-time lags as:

$$C_{ij}(h,u)=\frac{{\sigma }^2}{{\left({\psi }_1\left(\frac{|u{|}^2}{{\psi }_2\left({\delta }_{ij}^2\right)}\right)\right)}^{d/2}{\left({\psi }_2\left({\delta }_{ij}^2\right)\right)}^{1/2}}{\varphi }_1\left(\frac{\Vert h{\Vert }^2}{{\psi }_1\left(\frac{|u{|}^2}{{\psi }_2\left({\delta }_{ij}^2\right)}\right)}\right),$$ (13)

where δ_ij > 0 (and with δ_ij = δ_ji) is the latent dissimilarity between variables i and j. In the resulting cross-covariance function C(h, u, v) in ${\Re }^{d+1+k}$, each component of the q-variate spatial process is represented by a point in a k-dimensional latent space, k ≤ q. Refer to Apanasovich and Genton (2010) for a more in-depth discussion. We set ϕ₁(x) = exp(−cx) and ψ_j(x) = (a_jx^αj + 1)^βj, j = 1,2; see Gneiting (2002) for alternatives. We also fix ${\alpha }_1={\alpha }_2=\frac{1}{2}$, and seek to estimate θ = (σ², c, a₁, β₁, a₂, β₂, {δ_ij}_{i<j,j=1,…,q}) a posteriori. The usual exponential covariance arises in univariate spatial settings.

5.2. Synthetic data

We mimick real world satellite imaging data analyzed later in Section 5.3 at a much smaller scale by generating 81 datasets from the model y(ℓ) = Z(ℓ)^⊤w(ℓ) + ε(ℓ), where ε(ℓ) ~ N(0, τ²) with $\mathit{\ell }\in \mathcal{T}$ and $\mathcal{T}$ is a regular grid of size 40×40×10, resulting in n_all = 16,000 total locations. We take w ~ GP(0,C) where C is as in (13), ψ₂ ≡ 1 and σ² = 1. We generate one dataset for each combination of τ² ∈ {1/1000,1/20,1/10}, temporal range α ∈ {5,50,500}, space-time separability $\beta \in \left\{1/20,1/2,1-\frac{1}{20}\right\}$, and spatial range c ∈ {1,5,25}.

We compare Q-MGPs with the similarly-targeted Gapfill method of Gerber et al. (2018) as implemented in the R package gapfill. We create “synthetic clouds” of radius $\sqrt{0.1}$ and with center (c_1,t, c_2,t) ∈ [0,1/20]² where $c_{1,t},c_{2,t}\stackrel{iid}{~}U[0,1]$ to cover the outcomes at six randomly selected times for each of the 81 datasets. Outcomes at two of the remaining four time periods were then randomly selected to be completely unobserved at all but 10 locations in order to avoid errors from gapfill. Refer to Figure 5 for an illustration.

Figure 5:

Artificial cloud coverin in synthetic data.

A Q-MGP model with M = 500 was fit by partitioning each spatial axis into 10 intervals and the time axis into 5 intervals. The priors were τ² ~ Inv.G.(2,1), σ² ~ Inv.G.(2,1), β ~ U(0,1), α ~ U(0,10⁴), c ~ U(0,10⁴); 7000 iterations of Gibbs sampling were run, of which 5000 used for burn-in and thinning the remaining 2000 to obtain a posterior sample of size 1000. For each of the 81 datasets we calculate the mean absolute prediction error (MAE) and the root mean squared prediction error (RMSE). Figure 6 compares Gapfill’s 90% intervals with 90% posterior equal-tailed credible intervals for the Q-MGP predictions obtained from 1000 posterior samples. In terms of MAE, the Q-MGP model outperformed Gapfill in all datasets; in terms of RMSE, it outperformed Gapfill in all but one dataset. The average MAE of Q-MGP was 0.4094 against Gapfill’s 0.5366; the average RMSE was 0.5308 against Gapfill’s 0.6820. The Q-MGP also yielded improved coverage of the prediction intervals, although some under-coverage was observed possibly due to the large M. This comparison may favor Q-MGPs as the data were generated from a Gaussian process. Appendix K, available online, confirms similar findings on non-Gaussian data (a GIF image).

Figure 6:

Performance of Q-MGP and Gapfill in out-of-sample predictions in 81 spatiotemporal datasets, at the three tested levels of noise variance τ².

5.3. NDVI data from the Serengeti ecosystem

Time series of Normalized Difference Vegetation Index (NDVI) derived from satellite imagery are used to understand spatial patterns in vegetation phonology. For such studies, image pixel-level NDVI values are observed over time to assess seasonal trends in vegetation green-up, growing season length and peak, and senescence. These analyses typically require NDVI values for all pixels over the region and time period of interest. As noted in the beginning of this section, atmospheric conditions, e.g., cloud cover, and sensor malfunction cause missing NDVI pixel values and hence predicting such values, i.e., gap-filling, is of key interest to the remote sensing community. Here, we consider NDVI data derived from the LandSat 8 sensor (which provides a ~30×30 m spatial resolution pixel) taken over Serengeti National Park, Tanzania, Africa. These data were part of a larger study conducted by Desanker et al. (2019) that looked at environmental drivers in vegetation phonology change. The data cover an area of 30×30km and 34 months, and correspond to 64 images of size 1000×1000 collected at 16-day intervals. Data on NDVI are complemented with elevation and soil moisture data, for a total of three spatially referenced predictors. We are thus interested in understanding their varying effect in space and time, in addition to predicting NDVI output at missing locations. We achieve both these goals by implementing model (11), where Z(ℓ) = X(ℓ) includes the intercept and three predictors; their varying effect will be represented by w(ℓ), which we recover by implementing Q-MGP models. Storing posterior samples of the multivariate spatially-varying coefficients for the full data with q = 4 is impossible using our computing resources as each sample would be of size 1000×1000×64×4 = 2.56e+8. For this reason, we consider two feasible setups. Denote by n_all the number of observed and missing locations. In model (1), we subsample each image to obtain 64 frames of size 500 × 500, and fit a regression model with Z(ℓ) = 1 resulting in a spatially-varying intercept model on n_obs = 12,582,484 observed locations, a total of n_all = 16,000,000 locations for prediction, and a latent spatial random effect w of the same size. The Q-MGP was fit using M = 328,125 space-time regions of size ~48.

The base covariance of (13) becomes a univariate non-separable spatiotemporal covariance as in Gneiting (2002). In model (2), we aim to estimate the varying effect of elevation on NDVI. We subsample each image to obtain 64 frames of size 278 × 278, each covering an area of 25×25km, and take Z(ℓ) = (1 X_elev(ℓ)) resulting in q = 2 and targeting the recovery of latent effects of size 9,892,352. Considering the additional computational burden of the multivariate latent effects, in this case we used M = 156,800, corresponding to smaller space-time regions of average size ~31. In this model there is a single unknown δ_ij in (13) which corresponds to the latent dissimilarity between the intercept and elevation. We thus consider ψ₂ = (a₂δ_ij + 1)^β2 as the unknown parameter. We assign priors β_r ~ N(0,100) for r = 1,…,q, σ² ~ Inv.G.(2,1), τ² ~ Inv.G(2,1), and uniform priors to other covariance parameters (their support is reported in Table 2).

Table 2:

Posterior summaries of Q-MGP models implemented on the Serengeti data.

	Q-MGP Model (1)	Q-MGP Model (2)
n all	16, 000, 000	4, 946, 176
n obs	12, 755,856	3, 961, 715
M	328125	156800
q	1	2
β elevation	0.0017(0.0014,0.0021)	0.0415(0.0398,0.0432)
β topoindex	5.54e-4(4.72e-4,6.30e-4)	−0.0011(−0.0012,−0.0008)
β accum	−4.84e-4(−5.66e-4,−4.02e-4)	7.88e-4(6.94e-4,9.06e-4)
σ 2	0.0585(0.0583,0.0587)	0.0728(0.0711,0.0749)
τ 2	1.05e-4(1.05e-4, 1.05e-4)	1.27e-4(1.21e-4,1.32e-4)
c ~ U(0, 1e+6)	7.0331(7.0146,7.0519)	3.0710(3.0562,3.0846)
a1 ~ U(0, 1e+6)	433.98(429.67,439.50)	3857.6(3492.6,4154.7)
β1 ~ U(0,1)	0.0694(0.0690,0.0697)	0.1058(0.1043,0.1080)
ψ2 ~ U(0, 1e+6)	–	221.36(198.09,240.57)
95% coverage	94.96	95.66
RMSE	0.0175	0.0253
Time/it. (s)	6.18	4.53
Time (hours)	42.9	31.5

In both cases, approximate posterior samples of the latent random effects and the other unknown parameters were obtained by running the proposed Gibbs sampler for a total of 25,000 iterations. A posterior sample of size 500 was obtained by using the first 22,000 iterations as burn-in, and thinning the remaining 3,000 by a factor of 6. Additional computational details are at Appendix F, available online. Posterior summaries of the unknown parameters for these models are reported in Table 2, along with RMSE in predicting NDVI at 10,000 left-out locations, 95% posterior coverage at those locations, and run times. Both models achieved similar out-of-sample predictive performance and coverage. Figure 7 shows the NDVI predictions of model (2) at one of the 64 time points. This reveals that the varying effect of elevation on NDVI output (see e.g. Figure 8) is credibly different from zero at 42.54% of the space-time locations (95% c. i.). In particular, it highlights the extent to which higher elevation reduces vegetation. The spatial range is approximately 4km; the time range is about 8 days. The large estimated ψ₂ indicates that the correlation between the two covariates of the latent random process is very small at all spatial and temporal lags. The predicted NDVI and latent spatiotemporal effects are supplied as animated GIF images in the supplement.

Figure 7:

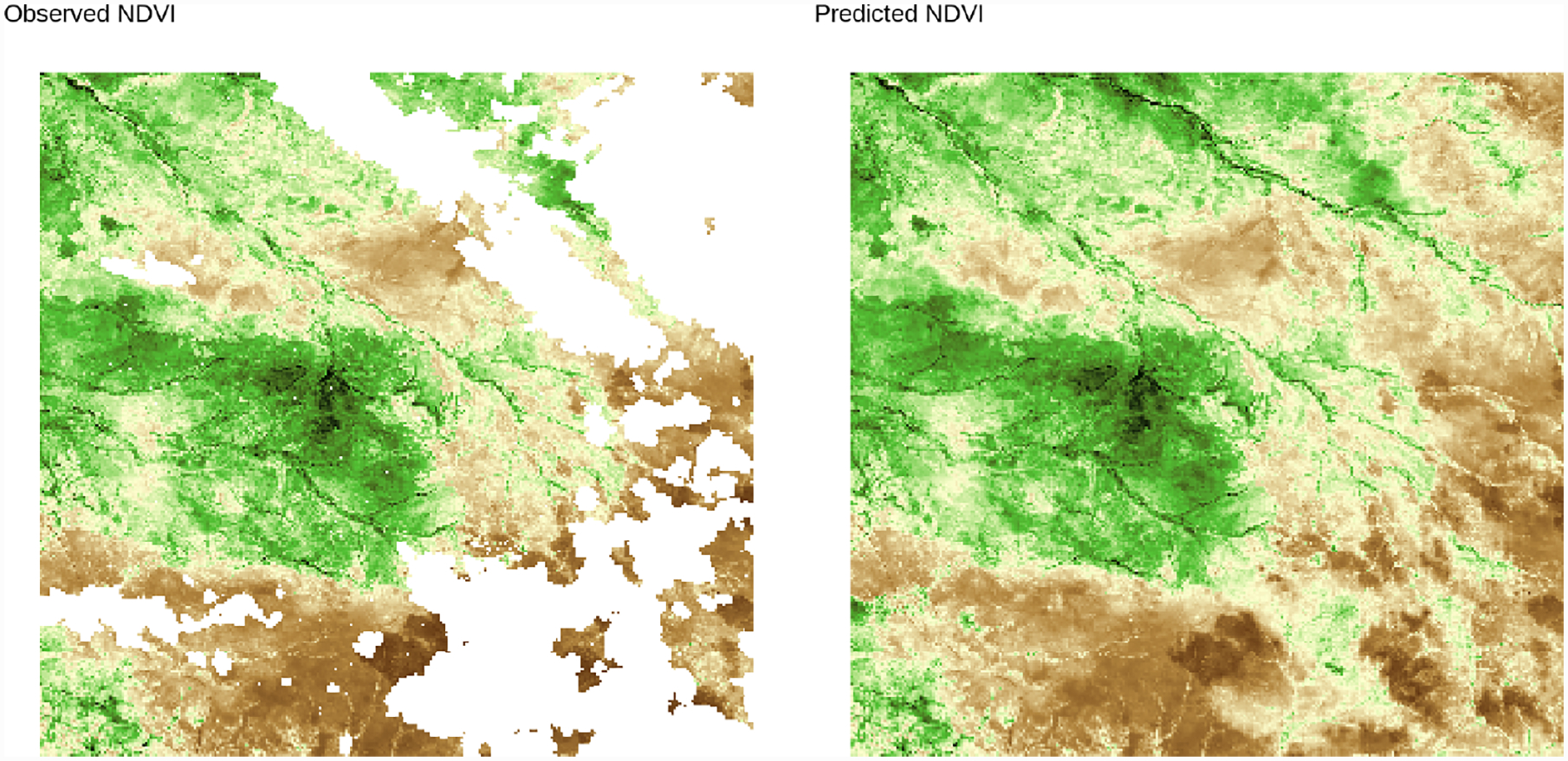
NDVI predictions from Q-MGP model (2) at time 60 (2016-12-17).

Figure 8:

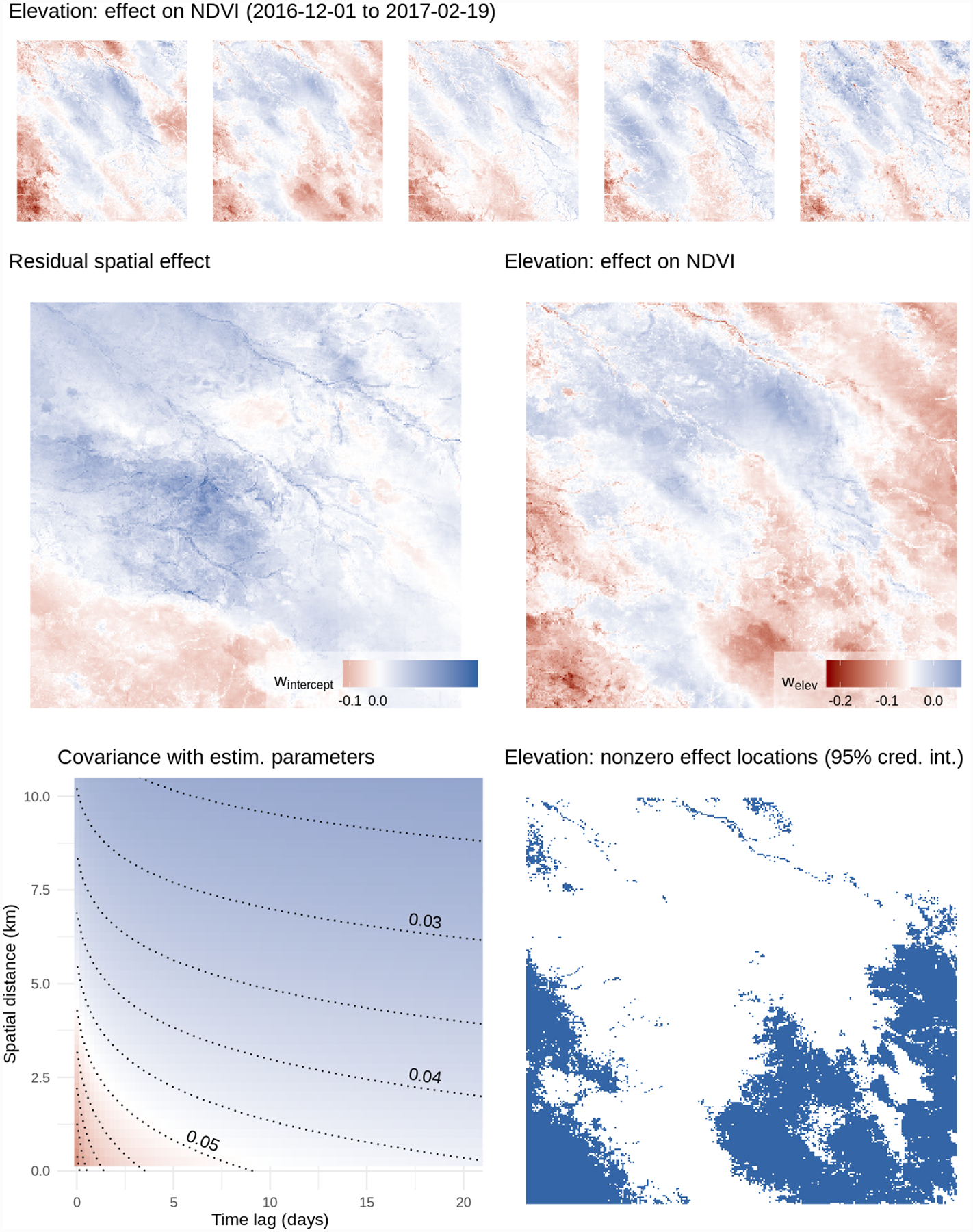
Top: the effect of elevation on NDVI output, evolving over five time periods. Middle left: effect on NDVI not explained by elevation; right: effect on NDVI attributable to elevation. Bottom left: estimated covariance at different space-time lags; right, in blue: locations with credibly nonzero effect of elevation on NDVI output.

6. Discussion

We have developed a class of Bayesian hierarchical models for large spatial and spatiotemporal datasets based on linking domain partitions to directed acyclic graphs. These models can be tailored for specific algorithmic needs, and we have demonstrated the advantages of using a cubic tessellation scheme (Q-MGP) when targeting the efficient recovery of spatial random effects in Bayesian hierarchical models using Gibbs samplers.

When considering alternative computational strategies, the proposed Q-MGP may not be optimal. For example, Gaussian first stage models enable marginalization of the latent spatial effects; posterior sampling of unknown covariance parameters via MCMC is typically associated by better mixing. Future research may thus focus on identifying “optimal” DAGs for collapsed samplers. Furthermore, the blocked conditional independence structure of Q-MGPs may be suboptimal as it corresponds to possibly restrictive conditional independence assumptions in neighboring locations. While we have not focused on the effect of different tessellations or partitioning choices in this article, alternative tessellation schemes (e.g. hexagonal) may be associated to less stringent assumptions and possibly better performance, while retaining all the desirable features of Q-MGP.

Other natural extensions to high-dimensional spatiotemporal statistics include settings where there are a very large number of spatiotemporal outcomes in addition to a large number of spatial and temporal locations. Here there are a few different avenues. One approach is in the same spirit of joint modeling pursued here, but instead of modeling the cross-covariance functions explicitly, as has been done here, we pursue dimension reduction using factor models (see, e.g., Christensen and Amemiya, 2003; Lopes et al., 2008; Ren and Banerjee, 2013; Taylor-Rodriguez et al., 2019). The aforementioned references have attempted to model the factor models using spatial processes some of which have used scalable low-rank predictive processes or the NNGP. We believe that modeling latent factors using spatiotemporal MGPs will impart some of the computational and inferential benefits seen here. However, this will need further development especially with regard to identifiability of loading matrices (Lopes et al., 2008; Ren and Banerjee, 2013) and process parameters.

A different approach to multivariate spatial modeling has relied upon conditional or hierarchical specifications. This has been well articulated in the text by Cressie and Wikle (2011); see also Royle and Berliner (1999) and the recent developments in Cressie and Zammit-Mangion (2016). An advantage of the hierarchical approach is that the multivariate processes are valid stochastic processes, essentially by construction and without requiring spectral representations, and can also impart considerable computational benefits. It will be interesting to extend the ideas in Cressie and Zammit-Mangion (2016) to augmented spaces of DAGs to further introduce conditional independence, and therefore sparsity, in MGP models with high-dimensional outcomes.

Finally, it is worth pointing out that alternate computational algorithms, particularly tuned for high-dimensional Bayesian models, should also be explored. Recent developments on algorithms based upon classes of piecewise deterministic Markov processes (see e.g., Fearnhead et al., 2018; Bierkens et al., 2019, and references therein) that avoid Gibbs samplers and even reversible MCMC algorithms are being shown to be increasingly effective for high-dimensional Bayesian inference. Adapting such algorithms to MGP and Q-MGP for scalable Bayesian spatial process models will constitute natural extensions of our current offering.