Academic Acceleration in Gifted Youth and Fruitless Concerns Regarding Psychological Well-Being: A 35-Year Longitudinal Study

Abstract

Academic acceleration of intellectually precocious youth is believed to harm overall psychological well-being even though short-term studies do not support this belief. Here we examine the long-term effects. Study 1 involves three cohorts identified before age 13, then longitudinally tracked for over 35 years: Cohort 1 gifted (top 1% in ability, identified 1972–1974, N = 1,020), Cohort 2 highly gifted (top 0.5% in ability, identified 1976–1979, N = 396), and Cohort 3 profoundly gifted (top 0.01% in ability, identified 1980–1983, N = 220). Two forms of educational acceleration were examined: 1. Age at high school graduation, and 2. Quantity of advanced learning opportunities pursued prior to high school graduation. Participants were evaluated at age 50 on several well-known indicators of psychological well-being. Amount of acceleration did not covary with psychological well-being. Study 2, a constructive replication of Study 1, utilized a different high-potential sample—elite science, technology, engineering, and mathematics graduate students (N = 478) identified in 1992. Their educational histories were assessed at age 25 and they were followed up at age 50 using the same psychological assessments. Again, the amount of educational acceleration did not covary with psychological well-being. Further, the psychological well-being of participants in both studies was above the average of national probability samples. Concerns about long-term social/emotional effects of acceleration for high-potential students appear to be unwarranted, as has been demonstrated for short-term effects.

Educational Impact and Implications Statement

Best practices suggest that acceleration in one of its many forms is educationally efficacious for meeting the advanced learning needs of intellectually precocious youth. Yet, parents, teachers, academic administrators, and psychological theorists worry that this practice engenders negative psychological effects. A three-cohort study of intellectually precocious youth followed for 35 years suggests that there is no cause for concern. These findings were replicated on a sample of elite STEM graduates whose educational histories were assessed at age 25 and tracked for 25 years.

Educational acceleration has enjoyed decades of empirical support as an effective intervention for meeting the advanced learning needs of intellectually precocious youth. It has received positive endorsements from international teams of experts (Assouline, Colangelo, & Vantassel-Baska, 2015; Colangelo, Assouline, & Gross, 2004), meta-analytic inquiry (Kulik & Kulik, 1984, 1992; Rogers, 2004; Steenbergen-Hu & Moon, 2011), and was deemed as one of the best practices by the National Mathematics Advisory Panel (2008). More recently, two 100-year reviews (Lubinski, 2016; Steenbergen-Hu, Makel, & Olszewski-Kubilius, 2016), both published in the Review of Educational Research to showcase cumulative knowledge advances on the centennial anniversary of the American Educational Research Association (AERA), reinforced the educational efficacy of academic acceleration for students who learn complex and abstract material at rapid rates. Beyond assimilating knowledge in formal learning settings (Benbow & Stanley, 1996; Stanley, 2000), two large scale 25-year longitudinal studies revealed that intellectually precocious youth who had experienced more acceleration produced greater creative output years later relative to their intellectual peers (Park, Lubinski, & Benbow, 2013; Wai, Lubinski, Benbow, & Steiger, 2010).

Although the educational efficacy of this practice is clear, administrators, parents, and teachers still worry about possible negative outcomes associated with acceleration. These concerns focus on the ultimate social and emotional development of adolescents who experience rapid-pace learning environments. Even though positive short-term appraisals by the students themselves have been documented repeatedly (Assouline et al., 2015; Bleske-Rechek, Lubinski, & Benbow, 2004; Colangelo et al., 2004), speculation continues in the educational and counseling literature on the harmful short- and long-term psychological effects that this practice might engender (Cross, Cross, & O’Reilly, 2018; Dare et al., 2016; Laine, Hotulainen, & Tirri, 2019; Siegle, Wilson, & Little 2013; Wood, Portman, Cigrand, & Colangelo, 2010) including how undesirable outcomes are possibly moderated by gender (Kretschmann, Vock, Ludtke, & Gronostaj, 2016). In a recent Annual Review of Psychology chapter, “Gifted Students,” Worrell, Subotnik, Olszewski-Kubilius, & Dixson (2019, p. 552) observe “[a]lthough research strongly supports accelerated programming for gifted students (Assouline et al., 2015; Steenbergen-Hu et al., 2016), even support for acceleration is not universal.”

Concerns about acceleration are fueled by mainstream psychological theorizing and popular writing. For example, recently, in the Journal of Personality and Social Psychology, Pekrun, Murayama, Marsh, Goetz, and Frenzel (2019, p. 169) speculated that “… Being in a low-achieving group relates to better emotional well-being compared with being in a group of high achievers… (it is better to be a happy fish in a little pond than an unhappy fish in a big pond of high achievers)…” and “…placing individuals in high-achievement groups may incur emotional costs.” The idea is that being in a high-achieving group makes it more difficult to succeed and experience the positive emotions associated with achievement motivation.¹ Malcolm Gladwell (2013) has expressed similar opinions despite empirical evidence casting doubt on the generalizability and verisimilitude of the happy fish, little pond theory (e.g., Makel, Lee, Olszewski-Kubilius, & Putallaz, 2012; Meehl, 1990).

This study examines whether academic acceleration of intellectually talented youth is associated with negative psychological consequences later in life (at age 50). Study 1 longitudinally tracked three cohorts of intellectually talented young adolescents for over 35 years. They were identified before age 13, between 1972–1983. Same-age intellectual peers who had experienced different degrees of acceleration were assessed to determine if differing amounts of educational acceleration were related to psychological well-being at age 50. Measures of psychological well-being included well-known measures of flourishing, life satisfaction, and positive emotionality, which are routinely incorporated in cross cultural assessments of global well-being (Diener, Oishi, & Tay, 2018), as well as core self-evaluations, which are frequently employed in industrial/organizational psychology (Judge, 2009; Judge, Erez, Bono, & Thoresen, 2003).

Study 2 involved a generalization probe to ascertain whether the findings in Study 1 would replicate in a different high-potential population. Participants in Study 2 were also unquestionably of high-potential, but they were identified at a different age, using different procedures, and during a more recent decade. Given the contemporary concern in the social sciences regarding the importance of replication (Camerer et al., 2018; Open Science Collaboration, 2015), conducting such appraisals of generalizability and robustness is essential (Makel & Plucker, 2014; Makel, Plucker, & Hegarty, 2012).

In 1992, a cohort of elite science, technology, engineering, and math (STEM) graduate students (48.5% female) attending one of the top 15 STEM graduate training programs in the United States were psychologically profiled (Lubinski, Benbow, Shea, Eftekhari-Sanjani, & Halvorson, 2001a); extensive information also was collected on their educational experiences prior to high school graduation. Among other things, this cohort was secured to evaluate the validity of procedures developed by the Study of Mathematically Precocious Youth (SMPY) for identifying early-adolescent potential for STEM innovation and impactful careers (Bernstein, Lubinski, & Benbow, 2019; Clynes, 2016; Lubinski & Benbow, 2006; McCabe, Lubinski, & Benbow, in press; Stanley, 1996). The elite STEM graduate students in Study 2 were recently surveyed with the same age-50 instruments utilized in Study 1. Like Study 1, Study 2 focused on participants’ pre-collegiate accelerative educational experiences and their psychological well-being at age 50. Because this high-potential sample was identified at an older age, using different procedures, and during a different decade, but the same focal predictor/criterion constructs were preserved, Study 2 constitutes a constructive replication of Study 1 (Lykken, 1968, 1991).

Study 1

Method

Participants and Surveys.

In total 1,636 participants from three SMPY cohorts were surveyed (Lubinski & Benbow, 2006).

Cohort 1 consists of individuals who were identified between 1972 and 1974 as 13-year-olds within the top 1% of cognitive ability (according to above-level assessments: SAT-M ≥ 390 or SAT-V ≥ 370). This sample came largely from Maryland and includes 420 females and 600 males; the sample is 94.8% White or Caucasian, 0.5% Hispanic, 0.9% Black or African-American, 1.8% Asian-American, and 1.9% other.

Cohort 2 consists of individuals who were identified between 1976 and 1979 as 13-year-olds within the top 0.5% of cognitive ability (SAT-M ≥ 500 or SAT-V ≥ 430). This sample came from throughout the mid-Atlantic states and includes 129 females and 267 males; the sample is 89.6% White or Caucasian, 0.8% Hispanic, 0.5% Black or African-American, 6.8% Asian-American, and 2.3% other.

Cohort 3 consists of individuals who were identified between 1980 and 1983 as 13-year-olds within the top 0.01% of cognitive ability (SAT-M ≥ 700 or SAT-V ≥ 630). This sample came from throughout the United States and includes 49 females and 171 males; the sample is 75.5% White or Caucasian, 0.5% Hispanic, 0.9% Black or African-American, 18.6% Asian-American, and 4.5% other.

Each participant completed an age-13 (identification) survey and two relevant follow-up surveys: an age-18 (after high school) survey and an age-50 (mid-life) survey. The identification survey was completed by participants at the time they qualified for SMPY. To assess the socioeconomic status (SES) of their early adolescence home environment, information was collected on the highest degree obtained by each parent as well as their occupation. Occupations were then coded according to the Stevens and Hoisington (1987) occupational coding system.

The after high school survey (administered at age 18) collected information regarding the acceleration opportunities participants utilized prior to obtaining their high school degree. Participants were contacted shortly after high school graduation in order to complete their age-18 survey (Lubinski & Benbow, 2006).

The mid-life (age-50) surveys were conducted online and in two phases: during 2012–2013 for Cohorts 1 and 2 (Lubinski, Benbow, & Kell, 2014) and, using this same survey, in 2017–2018 for Cohort 3. Response rates for these three cohorts were 88.5%, 88.6, and 75.9% for Cohorts 1, 2, 3, respectively; of these participants, 84.0%, 77.0%, 65.9% also responded to the after high school follow-up with complete data or we were able to triangulate the needed information for them to qualify for this study. Participants either received an amazon.com incentive of $20 to complete the survey or were given the opportunity to donate this amount to summer residential academic programs for intellectually precocious youth from economically challenged homes (67% chose to donate).

Measures of Acceleration.

Academic acceleration was assessed in two ways, and equivalent analyses were conducted for both assessments. The first indicator was an acceleration composite computed as a weighted sum of three different types of acceleration modalities:

$$AccelerationComposite=\mathit{1}\times APCourses+\mathit{1}\times CollegeCourses+\mathit{4}\times GradesSkipped$$ (1)

The relative weights in Equation 1 (1, 1, and 4) were chosen rationally to represent the relative intensities of these types of acceleration. Although reasonable minds may differ with respect to the weighting of these constituents, the three authors derived these weights independently.

The age at which participants graduated from high school, measured to the nearest month, was used to assess types of acceleration not captured by the acceleration composite. For example, many participants in SMPY entered kindergarten or first grade early or graduated high school early without technically skipping any grades at all; age of high school graduation captures some of these nuances that the construct of educational acceleration embodies.

The average age of high school graduation was for Cohort 1: M = 17.8 years (SD = 0.62); for Cohort 2: M = 17.7 years (SD = 0.76); and for Cohort 3: M = 17.2 years (SD = 1.02). The ages were relatively normally distributed with negative skew (i.e., a few individuals graduated very early). Combining across cohorts, the correlation between the acceleration composite and the age of high school graduation was sizeable (r(1,620) = −.58, p < .001), but the two indicators are by no means redundant and likely capture different aspects of acceleration.

Measures of Psychological Well-Being.

Psychological well-being was conceptualized in this study according to the eudaimonic and hedonic perspectives (Ryff, Singer, & Love, 2004). The eudaimonic perspective of well-being originated with Aristotle and posits that achieving well-being is a matter of achieving personal growth, purpose in life, autonomy, and self-acceptance. The hedonic perspective, on the other hand, posits that well-being is a function of life satisfaction, positive affect, and lack of negative affect. As part of their mid-life survey, participants completed five well known, reliable, and construct valid assessments for making inferences about psychological well-being. Each of these five measures asked questions related to either the eudaimonic or hedonic conceptualization of well-being (or both).

Core Self-Evaluations (12 items; Judge et al., 2003) assesses participants’ evaluation of themselves and their abilities. This scale contains four personality dimensions (locus of control, neuroticism, generalized self-efficacy, and self-esteem). Alpha reliabilities were .86, .88, and .90 for Cohorts 1, 2, and 3, respectively.

Psychological Flourishing (8 items; Diener et al., 2010) measures self-perceived success in relationships, self-esteem, purpose, and optimism. The scale was designed to measure social-psychological prosperity and also to complement other measures of well-being. Alpha reliabilities were .85, .89, and .88 for Cohorts 1, 2, and 3, respectively.

Positive Affect (5 items; Diener et al., 2010), from the Scale of Positive and Negative Experience, asks participants about the extent to which they experience positive feelings. The feelings participants were asked to rate were Positive, Good, Pleasant, Contented, and Happy. Alpha reliabilities were .90, .90, and .89 for Cohorts 1, 2, and 3, respectively.

Life Satisfaction (5 items; Diener, Emmons, Larsen, & Griffin, 1985; Pavot & Diener, 1993) measures global judgements of satisfaction with one’s life. The scale does not ask participants about certain aspects of their lives with which they are satisfied (e.g., finances); rather, the scale allows participants to evaluate their lives holistically, giving differential weight to each aspect of their lives as they see fit. Alpha reliabilities were .90, .90, and .91 for Cohorts 1, 2, and 3, respectively.

Negative Affect (10 items; Goldberg, 1992) was drawn from the IPIP Big-Five 50-item inventory. This scale is in the public domain and asks participants to rate on a Likert type scale the extent to which a series of statements describes them. This results in scores on each of the Big Five personality dimensions, but only that reflecting Negative Affect was used here. Alpha reliabilities were .88, .89, and .92 for Cohorts 1, 2, and 3, respectively.

Software.

Analyses were performed using SPSS, AMOS, and basic functions in R (R Core Team, 2019). Moreover, structural equation modeling was employed using the lavaan package in R (Rosseel, 2012), and parallel analysis was performed using Revelle’s (2018) psych package.

Results

Bivariate results.

Because findings across all three cohorts were commensurate in all important respects, we aggregated results across them to distill an efficient and clear Results section. Findings on each individual cohort are provided in an online supplement, which reveals a three-sequence series of operational replications (Lykken, 1968, 1991) across successively more able cohorts. Table 1 summarizes the bivariate correlations between five measure of psychological well-being and the two indices of academic acceleration. All correlations hover around zero.

Table 1.

Correlations between Acceleration Indicators and Measures of Psychological Well-Being for Study 1

Measure	Age of High School Graduation	Acceleration Composite
Core Self-Evaluations	.02	−.07
Positive Affect	.01	−.03
Life Satisfaction	.00	.00
Negative Affect (Reversed)	.03	−.06
Psychological Flourishing	.02	−.05

Note. All correlations fall below Cohen’s (1988) threshold for “small”.

For more nuanced analyses, Appendix A shows each of the five indicators of psychological well-being as a function of each of the two indicators of academic acceleration, by gender, utilizing box-and-whisker plots (Tukey, 1977). This approach was applied because psychological concerns about academic acceleration for intellectually precocious youth tend to focus on those students who experience more extreme forms of acceleration. Across all five indicators, there were no substantive relationships between academic acceleration and psychological well-being for either males or females.

Moreover, Appendix A paints a picture of participants who are above average, according to norms, for the indicators of psychological well-being. Benchmarked against normative standards (Diener et al., 1985; Diener et al., 2010; Judge et al., 2003; Pavot & Diener, 1993), the typical participant in Study 1 scored about the average on the Core Self-Evaluations scale, and above average on Psychological Flourishing, Positive Affect, and Life Satisfaction.

An Aggregated Approach: Principal Components Analysis.

Although the five indicators of psychological well-being are well known and each is intended to capture slightly different aspects of psychological well-being, it is natural to ask about the extent to which there is redundancy between the five measures and whether some simpler structure underlies them (Dawis, 1992; Judge, Erez, Bono, & Thoresen, 2002; Lubinski, 2004; Lucas, Diener, & Suh, 1996). Table 2 shows the intercorrelations for the five measures of psychological well-being, with their alpha reliabilities in the diagonal. This revealed a relatively strong and uniform covariance pattern (positive manifold). Because of this, a principal component analysis was conducted to reduce the dimensionality of these measures.

Table 2.

Reliabilities and Intercorrelations of Psychological Well-Being Measures for Study 1

	Core Self-Evaluations	Positive Affect	Life Satisfaction	Negative Affect (Reversed)	Psychological Flourishing
Core Self-Evaluations	(.87)
Positive Affect	.58	(.90)
Life Satisfaction	.60	.60	(.90)
Negative Affect (Reversed)	.63	.54	.42	(.89)
Psychological Flourishing	.62	.61	.66	.45	(.87)

Note. Coefficient alpha reliabilities are given in the diagonal.

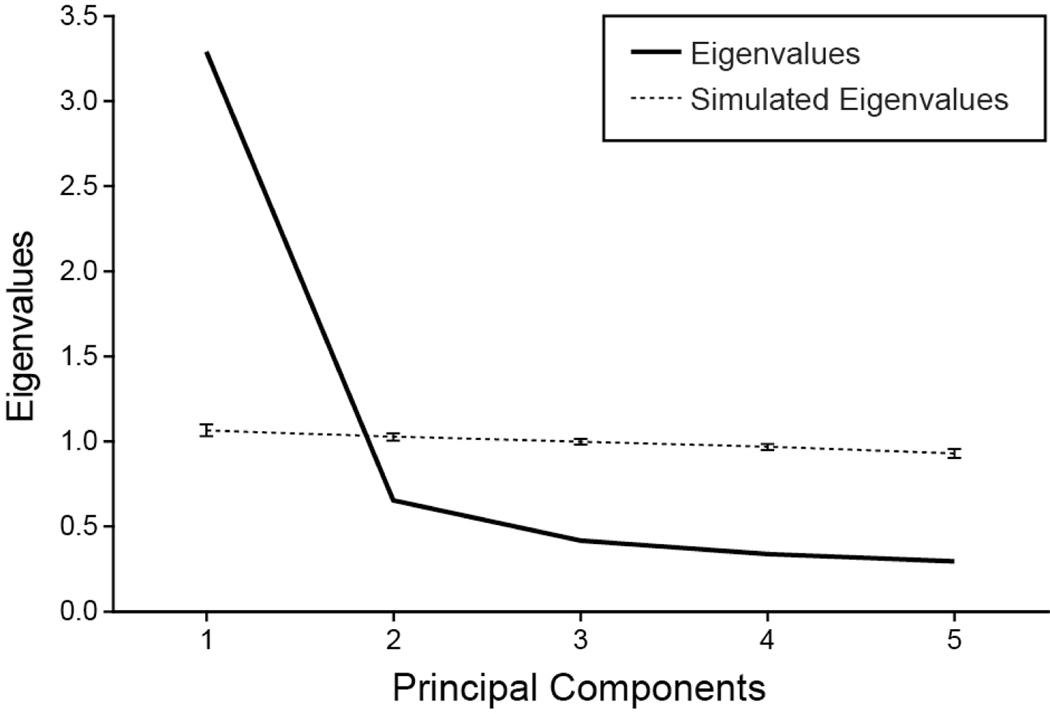
Figure 1 shows the scree plot of eigenvalues and a parallel analysis of these intercorrelations (Horn, 1965; Revelle, 2018). A one-component solution was unambiguously supported by this procedure; therefore, we performed principle component analysis and retained the first component. Table 3 shows the loading matrix. The loadings are large and uniform across the five measures, and the first component is readily interpretable as a general measure of psychological well-being.

FIGURE 1.

Scree plot and parallel analysis on the correlation matrix of the indicators of psychological well-being for Study 1 using Revelle’s (2018) psych package in R. Only the first eigenvalue is above what would be expected by chance.

Table 3.

Loading Matrix for Study 1

	Component Loading	h2 (communality)	u2 (uniqueness)
Core Self-Evaluations	.85	.72	.28
Positive Affect	.82	.68	.32
Life Satisfaction	.81	.66	.34
Negative Affect (Reversed)	.74	.55	.45
Psychological Flourishing	.83	.69	.31

Note. All indicators had relatively strong and uniform loadings on the first principle component, suggesting relatively equal weighting in the computation of the first principle component.

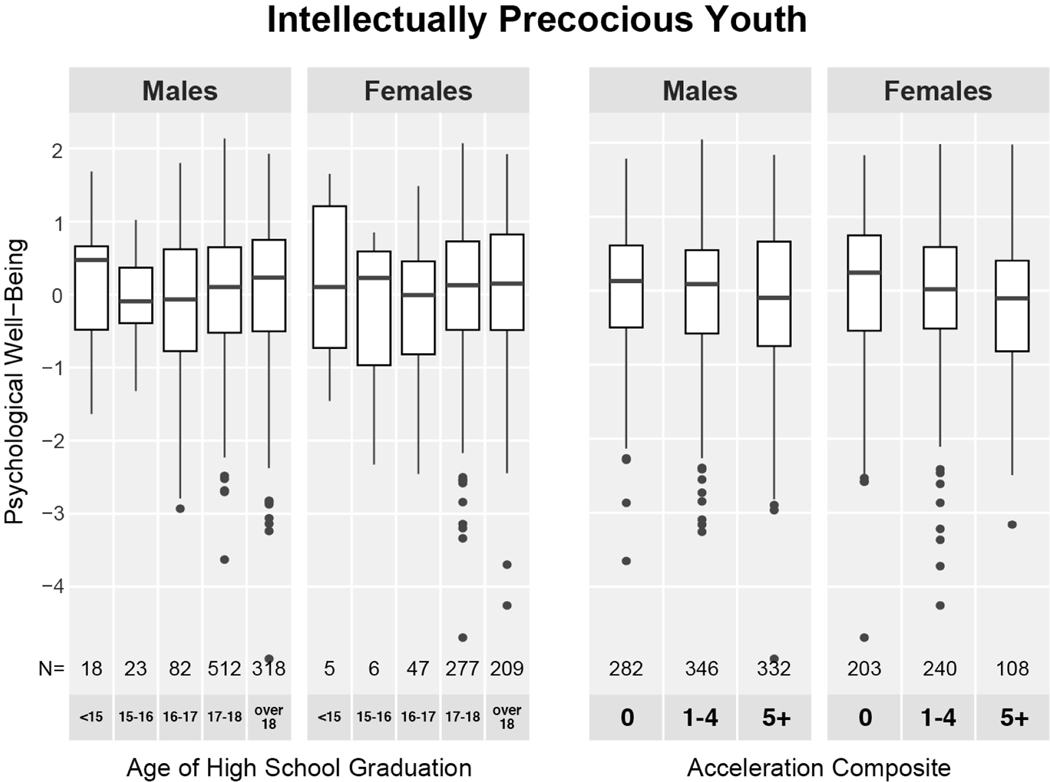
Using box-and-whisker plots, Figures 2a and 2b show the first component (psychological well-being) as a function of age of high school graduation and the acceleration composite by gender. Across both indices of acceleration and across gender, there is no substantive relationship between acceleration and age-50 psychological well-being. Overall, the correlation between psychological well-being and the acceleration composite was r(1,495) = −.06, p = .02; the correlation between psychological well-being and age of high school graduation was r(1,495) = .03, p = .207.

FIGURE 2.

Box-and-whisker plots of the relationship between psychological well-being and age of high school graduation (2a) and the acceleration composite (2b) in Study 1. Sample sizes appear below the box. Horizontal lines represent medians; hinges represent the interquartile range (IQR); upper and lower whiskers extend to the furthest point within 1.5 × IQR from the median; all other data points are outliers.

Latent Model Approach: Structural Equation Modeling.

For many investigators, the question of controlling for nuisance variables arises naturally at this point. That little relationship was found between measures of psychological well-being and each indicator of academic acceleration is clear. However, readers might wonder if this lack of relationship would hold if controls (for example, SES) were taken into account.

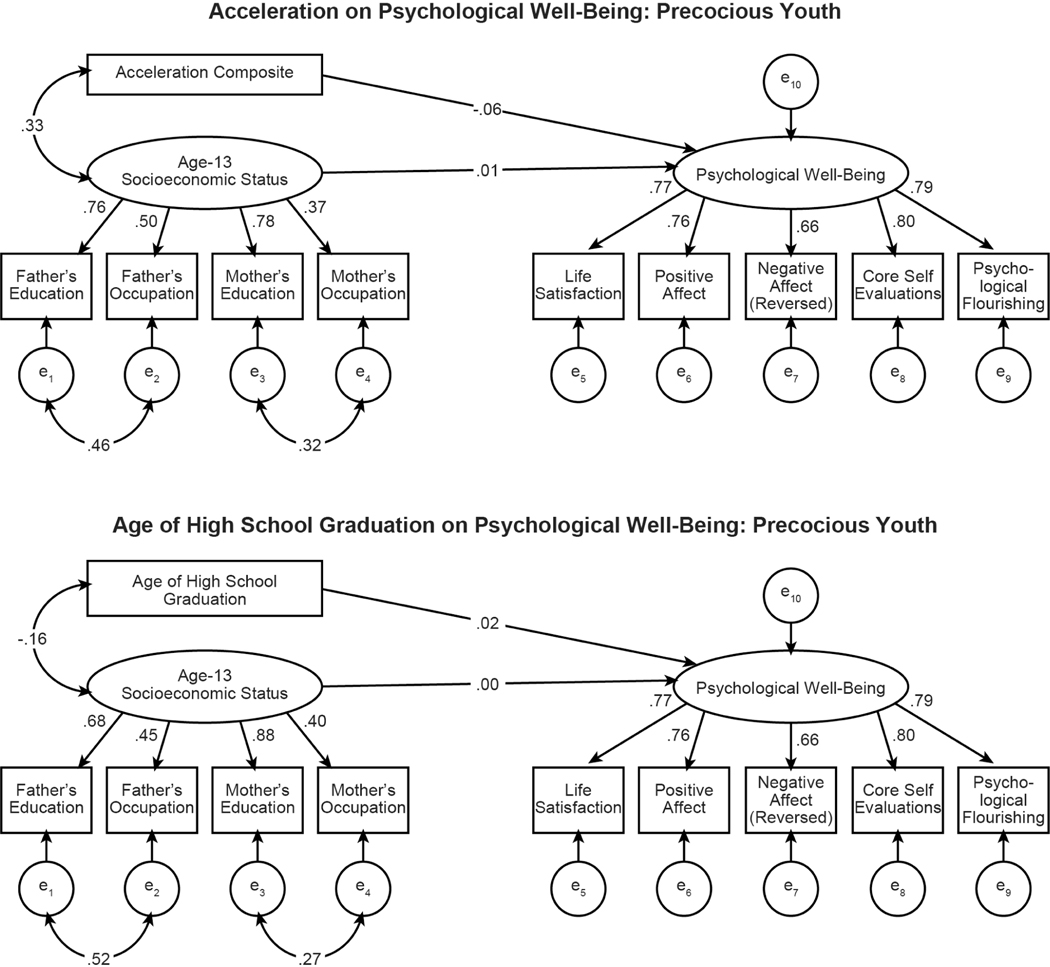
Including controls in designs of this types has become something of an automatic reaction in the social sciences (Gottfredson, 2004; Lubinski, 2009), but it is not always advisable (Gordon, 1968). Following Meehl (1970), controlling or matching on nuisance variables can often have unintended consequences and distort estimates of the focal relationships of interest. Statistically equating quasi-experimental and control groups is frequently offset by the creation of status differences on other unmeasured individual differences, which are relevant to the outcome of interest. So, when quasi-experimental differences are found, it is difficult to infer a causal relation. Appendix C provides a brief discussion of some complex issues involving matching and partialling applications. Nevertheless, this section incorporates SES as a statistical control and brings the model into a latent framework, while being vigilant of these concerns (Gordon, 1968; Meehl, 1970).

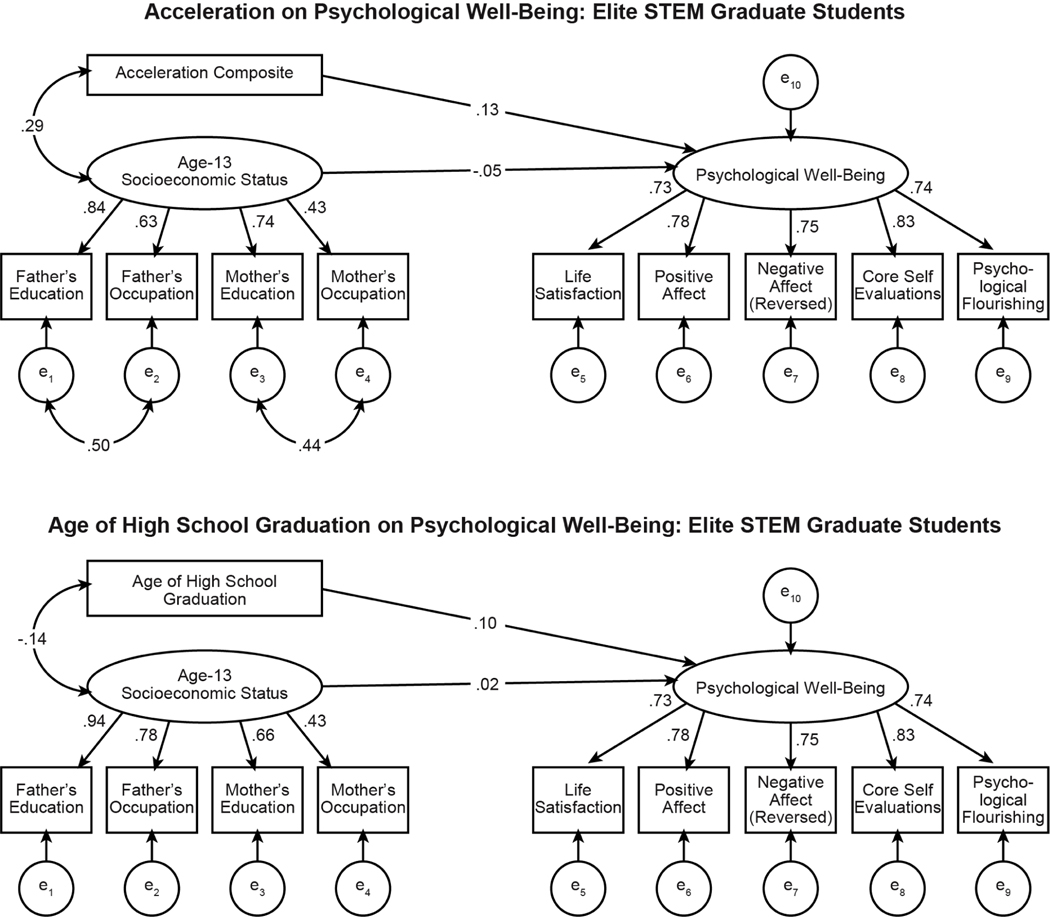
We show the relation of latent SES, latent psychological well-being, and the educational composite (Figure 3, top) and age of high school graduation (Figure 3, bottom). Fit indices for each of the two models were good. Model 1 (top) has a CFI = .959, SRMR = .030, and RMSEA = .067 (90% CI: [.060, .075]). Model 2 (bottom) has a CFI = .958, SRMR = .030, and RMSEA = .067 (90% CI: [.060, .075]). In each model, using SES as a control, the path coefficient of interest, namely, from the indicator of academic acceleration to psychological well-being, was trivial: −.06 (p = .03) in Model 1 and .02 (p = .491) in Model 2.

FIGURE 3.

Structural equation modeling results for the relationships between psychological well-being, SES, and acceleration composite (top) or age of high school graduation (bottom) for Study 1.

Discussion

In Study 1 we found a pattern that replicated across three cohorts of intellectually precocious youth: participants who received more acceleration did not suffer from a decrement in psychological well-being at age 50. This result was consistent across two indicators of acceleration (age of high school graduation and an acceleration composite), five indicators of psychological well-being (Core Self-Evaluations, Positive Affect, Life Satisfaction, Negative Affect, and Psychological Flourishing), and a principal component of these indicators. Moreover, the results remained substantively unchanged when controlling for SES in a latent framework.

The results do not support the concerns frequently voiced when intellectually precocious youth seek out and express a desire for advanced learning opportunities. These results are consistent with the previous literature on acceleration evaluated under less protracted time frames (e.g., Gross, 2004; Robinson, 2004), which indicates that intellectually precocious youth by and large enjoy atypically fast paced learning environments (cf. Assouline et al., 2015; Benbow, Lubinski, Shea, & Eftekhari-Sanjani, 2000, Figures 4 & 5, p. 479; Benbow, Lubinski, & Suchy, 1996; Bleske-Rechek et al., 2004; Colangelo et al., 2004; Lubinski, Webb, Morelock, & Benbow, 2001b, Figure 1, p. 720; Pressey, 1949).

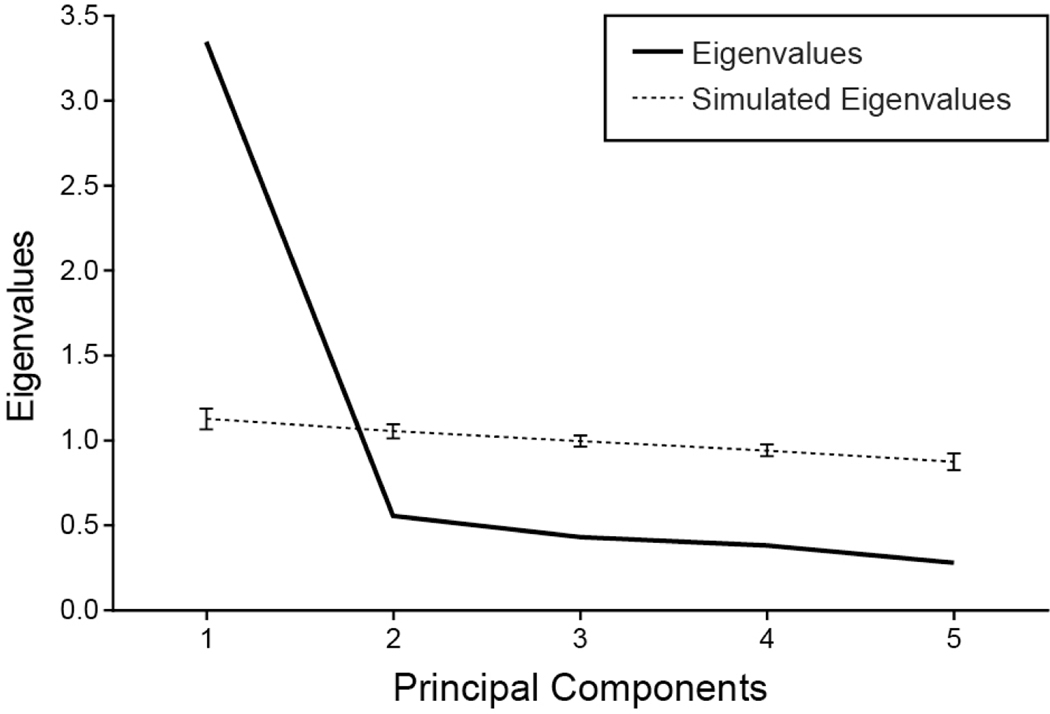
FIGURE 4.

Scree plot and parallel analysis on the correlation matrix of the indicators of psychological well-being for Study 2 using Revelle’s (2018) psych package in R. Only the first eigenvalue is above what would be expected by random chance.

FIGURE 5.

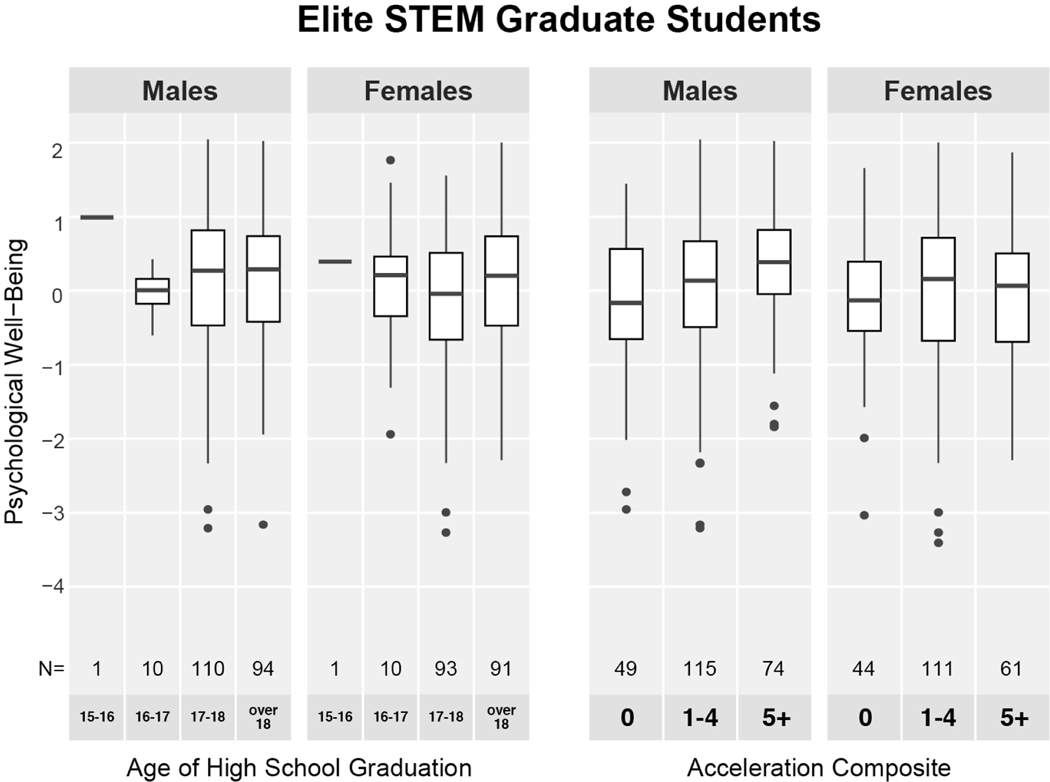
Box-and-whisker plots of the relationship between psychological well-being and age of high school graduation (5a) and the acceleration composite (5b) in Study 2. Sample sizes appear below the box. Horizontal lines represent medians; hinges represent the interquartile range (IQR); upper and lower whiskers extend to the furthest point within 1.5 × IQR from the median; all other data points are outliers.

Study 2

Study 2 was designed to constructively replicate (Lykken, 1968, 1991) Study 1 with a distinct high-potential sample. The idea behind constructive replication is the same as that behind systematic heterogeneity in test construction (Hulin & Humphreys, 1980; Humphreys, 1962) and with how the nature of psychological constructs is explicated through the construct validation process (Cronbach, 1989; Meehl, 1999). Simply stated, the idea is to vary as many of the construct-irrelevant design features as possible in a preexisting study (or class of studies), while preserving the integrity of the focal constructs. For purposes here, a cohort of elite STEM graduate students would meet these criteria. They are unquestionably of high potential and have demonstrated the ability to learn complex, abstract material at atypically fast rates. Moreover, they were identified at a different age, during a different decade, and using different procedures. If such a sample of young adults were assessed 25 years after their initial identification using the same age 50 outcome measures employed in Study 1, a compelling test of the generalizability and robustness of the findings in Study 1 would be possible. Would the psychological well-being of these participants covary with the amount of educational acceleration they experienced prior to high school graduation?

Method

Participants.

Study 2 consisted of 478 participants (230 females, 248 males; 84.0% White or Caucasian, 2.0% Hispanic, 1.0% Black or African-American, 9.0% Asian-American, and 4.0% other) from Cohort 5 of SMPY (Lubinski et al., 2001a). These participants were identified at age 25 in 1992 as first- or second-year graduate students seeking doctoral training at one of the top 15 STEM graduate programs in the United States.

Each participant included in Study 2 completed two relevant surveys: an age-25 (identification) survey and an age-50 (mid-life) survey. The time-1 survey collected information regarding acceleration opportunities that participants utilized prior to high school graduation (see Lubinski et al., 2001a, Tables 2 and 3). In addition, it also collected information on their parents’ education and occupation (retrospectively, when the participant was 13). Occupational prestige was again coded according to Stevens and Hoisington (1987), and SES was defined by these four measures in a structural equation model.

Finally, in addition to completing this identification survey, participants submitted university transcripts, from which age of high school graduation was obtained; for those without transcripts, age of high school graduation was discernable from triangulating other information in their survey. Scores on the acceleration composite were again computed according to Equation 1 in Study 1. The correlation between the acceleration composite and the age of high school graduation was modest (r(427) = −.30, p < .001), indicating that each captured different aspects of the acceleration construct.

The mid-life survey, which occurred between 2017 and 2018, utilized the same questionnaire, measures of psychological well-being, and procedures described in Study 1 (Lubinski et al., 2014). This survey was launched simultaneously with SMPY’s Cohort 3 follow-up, as reported in Study 1, and had a response rate of 77.1%. Incentives were also the same as in Study 1, and 70% of participant chose to donate $20 to summer residential academic programs for intellectually precocious youth from economically challenged homes, rather than to receive their amazon.com incentive.

Results

Bivariate results.

Table 4 summarizes the bivariate correlations between measures of psychological well-being and academic acceleration. These range from .02 to .10, with an average correlation coefficient of .07 (age of high school graduation) and .09 (acceleration composite). Despite multiple hypothesis testing, only two of these correlations break the threshold to be considered small (.10 in magnitude), and they both suggest that more acceleration leads to greater well-being.

Table 4.

Correlations between Acceleration Indicators & Psychological Well-Being Measures for Study 2

Measure	Age of High School Graduation	Acceleration Composite
Core Self-Evaluations	.09	.09
Positive Affect	.07	.08
Life Satisfaction	.02	.10
Negative Affect (Reversed)	.08	.08
Psychological Flourishing	.09	.10

Note. Despite the fact that multiple hypothesis testing was performed, only two correlations met Cohen’s (1988) threshold for “small” (≤.10 in magnitude); both indicate that more acceleration is associated with better outcomes at age 50.

For more nuanced analyses, Appendix B shows each of the five indicators of psychological well-being as a function of each of the two indicators of academic acceleration, by gender, using box-and-whisker plots. These plots reveal no substantive relationships between academic acceleration and psychological well-being. Even at extreme levels of acceleration, psychological well-being appears unperturbed. Using normative probability samples as benchmarks (Diener et al., 1985; Diener et al., 2010; Judge et al., 2003; Pavot & Diener, 1993), the data in Appendix B reflect that this group had scores that were above-average on psychological well-being, about average on the Core Self-Evaluations, and above average on Psychological Flourishing, Positive Affect, and Life Satisfaction scales.

An Aggregated Approach: Principal Components Analysis.

Table 5 shows the correlation matrix for each of the five measures of psychological well-being and their alpha reliabilities. The correlation matrix again reveals a positive manifold between the measures of psychological well-being: large, positive, and relatively uniform correlations between each pair of measures.

Table 5.

Reliabilities and Intercorrelations of Psychological Well-Being Measures for Study 2

	Core Self-Evaluations	Positive Affect	Life Satisfaction	Negative Affect (Reversed)	Psychological Flourishing
Core Self-Evaluations	(.86)
Positive Affect	.61	(.90)
Life Satisfaction	.59	.61	(.88)
Negative Affect (Reversed)	.69	.58	.49	(.88)
Psychological Flourishing	.61	.60	.57	.51	(.83)

Note. Coefficient alpha reliabilities are given in the diagonal.

The scree plot and parallel analysis (Figure 4) again support a one-component solution. Principle component analysis was performed and one component was retained. Table 6 shows the loading matrix of the first principle component. The loadings are again large and uniform across the five measures. The first component is again interpretable as a general measure of psychological well-being.

Table 6.

Loading Matrix for Study 2

	Component Loading	h2 (communality)	u2 (uniqueness)
Core Self-Evaluations	.86	.74	.26
Positive Affect	.83	.69	.31
Life Satisfaction	.79	.63	.37
Negative Affect (Reversed)	.80	.64	.36
Psychological Flourishing	.80	.64	.36

Note. All indicators had relatively strong and uniform loadings on the first principle component, suggesting relatively equal weighting in the computation of the first principle component.

Using box-and-whisker plots, Figures 5a and 5b show the first component (psychological well-being) as a function of age of high school graduation and the acceleration composite by gender. Across both indices of acceleration, there is essentially zero covariance between the two measures within each gender. Overall, the correlation between psychological well-being and age of high school graduation was r(408) = .08, p = .09; the correlation between psychological well-being and the acceleration composite was r(452) = .11 p = .02. The correlation between psychological well-being and the acceleration composite can be considered small but significant—yet, it indicates a positive relation between acceleration and psychological well-being.

Latent Model Approach: Structural Equation Modeling.

As in Study 1, we conducted a latent analysis of the relation between educational acceleration and psychological well-being while controlling for SES (Figure 6). Fit indices for each of the two models were good. Model 3 (top) has a CFI = .969, SRMR = .034, and RMSEA = .063 (90% CI: [.048, .078]). Model 4 (bottom) has a CFI = .928, SRMR = .055, and RMSEA = .092 (90% CI: [.079, .106]). In each model, the coefficient of interest (from the indicator of academic acceleration to psychological well-being) was small: .13 (p = .015) in Model 3 and .10 (p = .065) in Model 4. These results mirror the findings reported in Study 1 in all important respects.

FIGURE 6.

Structural equation modeling results for the relationships between psychological well-being, SES, and acceleration composite (top) and age of high school graduation (bottom) for Study 2. The latter does not include correlated residuals due to a Heywood case.

Discussion

Study 2 constituted a constructive replication of Study 1’s results with a distinct high-potential population. For these elite STEM graduate students, educational acceleration, indexed in the same two ways as in Study 1, did not covary with measures of psychological well-being at age 50. Moreover, the overall status of participants on measures of psychological well-being was above average when benchmarked against national probability samples. The lack of an acceleration/psychological well-being relationship was also observed in a latent framework in which SES was controlled. Jointly, these results suggest that findings observed on intellectually precocious youth in Study 1 extend to elite STEM graduate students. We hypothesize that they will generalize to other high-potential populations in future investigations.

General Discussion

The results of Study 1 demonstrate that across three cohorts of intellectually precocious youth identified over the course of an 11-year period (1972–1983), academic acceleration did not covary with age-50 psychological well-being. Using Lykken’s (1968, 1991) nomenclature for conducting replications in psychological research, this amounted to a series of three operational replications. In Study 2, using a different population identified in a later decade and at an older age, conceptually equivalent findings were observed among elite STEM graduate students. Because the construct-irrelevant design features of Study 2 were appreciably different from Study 1, Study 2 constitutes a constructive replication of Study 1’s findings, which is even more scientifically compelling (Lykken, 1968, 1991).

Overall, academic acceleration does not appear to be associated with deficits in psychological well-being later in life among high-potential populations. No appreciable negative relation appeared between academic acceleration and indicators of psychological well-being.² Moreover, this generalization held when structural equation modeling was employed and SES was controlled.

These findings are consistent with research on the effects of academic acceleration on psychological well-being. That is, there is little evidence that academic acceleration has negative consequences on the psychological well-being of intellectually talented youth (Assouline et al., 2015; Benbow & Stanley, 1996; Colangelo et al., 2004; Gross, 2006; Robinson, 2004). Previous studies have shown this null relationship in terms of short-term psychological well-being (Assouline et al., 2015; Colangelo et al., 2004; Pressey, 1949). This study, however, is the first to examine the relationship over an extensive time frame (35 years).

These findings do not support the frequently expressed concerns about the possible long-term social and emotional costs of acceleration by counselors, parents, and administrators (Assouline et al., 2015; Colangelo et al., 2004; Wood et al., 2010). Our findings also question the tenability of the Happy-Fish-Little-Pond theory (Pekrun et al., 2019), namely, that gifted children would be happier if they had remained with age-matched peers rather than with their intellectual peers. In support of this idea, see the idiographic data collected by Bleske-Rechek et al. (2004), as well as Benbow et al. (2000, p. 479, Figure 5) and Lubinski et al. (2001b, p. 720, Figure 1). This literature suggests that those who were accelerated had few regrets for doing so. Indeed, if anything, they tended to wish that they had accelerated more.

However, that the participants of Study 1 were not a random sample of all intellectually precocious youth is a limitation of this study. All participants had a parent sign them up for a talent search, and thus participants tended to come from families that were more knowledgeable about the educational system. In addition, spatially gifted youth are underrepresented in our samples, and they are more likely to come from economically challenged homes relative to mathematically and verbally talented students. The literature suggests that approximately half of the top 1% in spatial ability are missed by talent searches restricted to mathematical and verbal reasoning measures (Wai, Lubinski, & Benbow, 2009; Wai & Worrell, 2016). Our demographic categories also fell short of being ideal, which we readily acknowledge. So, our samples were not representative of the full scope of intellectually precocious youth. Nevertheless, we believe our findings will be found to generalize to more representation samples. Finally, our time-1 assessment did not included measures of psychological well-being. This would have enabled us to assess temporal changes in psychological well-being as a function of acceleration to garner more informative results. This would be a worthy endeavor for future researchers to consider.

Many fear negative possibilities of moving a gifted child to a more advanced class. Yet it also is important to consider the negative possibilities of holding children back in classes aiming to teach subject matter that they have already mastered (Benbow & Stanley, 1996; Gross, 2006; Stanley, 2000). Choosing not to accelerate is as much of a decision as choosing to do so; both have costs and benefits, which must be weighed (Bleske-Rechek et al., 2004, pp. 219–223). Both findings reported here and the preexisting literature suggest little reason to anticipate negative effects on psychological well-being for intellectually able accelerants who wish to experience learning environments tailored to the rate at which they learn. This is particularly important given the extensive empirical literature showing positive effects of acceleration on academic achievement (Kulik & Kulik, 1984, 1992; Lubinski, 2016; Rogers, 2004; Steenbergen-Hu et al., 2016) and creativity (Park et al., 2013; Wai et al., 2010).³ When counselors, parents, or administrators encounter precocious students who desire more advanced subject matter, students should be allowed the freedom to choose to pursue their passions (Assouline et al., 2015; Colangelo et al., 2004; National Mathematics Advisory Panel, 2008; Pressey, 1949, 1955).

Finally, the modalities of acceleration used in this study are but a few examples of a broader class of educational interventions for intellectually precocious youth. There are many ways in which to meet the educational needs of precocious learners and several are likely functionally equivalent (Southern & Jones, 2004; Wai et al., 2010). The concept of acceleration itself is best conceptualized as a location on a developmental continuum of best practices, which focus on the region for intellectually precocious youth. The more general dimension is the continuum for what all students require, that is, appropriate developmental placement (Lubinski & Benbow, 2000). Presenting students with an educational curriculum at the depth and pace with which they assimilate new knowledge is beneficial. For intellectually talented students, above-level assessments (for precocity) are useful in determining when an above-level curriculum (for acceleration) is needed. The current study provides evidence to suggest that, when these best practices are implemented for gifted youth, neither social nor emotional development is compromised. Other studies have shown that academic acceleration tends to enhance professional and creative achievements before age 50 (Park et al., 2013; Wai et al., 2010). Together these conclusions are not all that different from the way in which Pressey (1949, 1955) conceptualized meeting the needs of gifted youth years ago. This evidence demonstrates, rather definitively, the effectiveness of this conceptualization.

Appendix A.

Box-and-whisker plots of the relationship between indicators of psychological well-being and age of high school graduation (first column pair) and the acceleration composite (second column pair) in Study 1. Sample sizes appear below the box. Horizontal lines represent medians; hinges represent the interquartile range (IQR); upper and lower whiskers extend to the furthest point within 1.5 × IQR from the median; all other data points are outliers.

Appendix B.

Box-and-whisker plots of the relationship between indicators of psychological well-being and age of high school graduation (first column pair) and the acceleration composite (second column pair) in Study 2. Sample sizes appear below the box. Horizontal lines represent medians; hinges represent the interquartile range (IQR); upper and lower whiskers extend to the furthest point within 1.5 × IQR from the median; all other data points are outliers.

Appendix C. Discussion of Meehl’s (1970) Ex Post Facto Design

It is often assumed (particularly in quasi-experimental designs such as this one) that, in order to make valid causal inferences about the relation between a predictor of interest (X) and an outcome of interest (Y), some sort of control or match must be made on a third nuisance variable (Z). In this design, for example, many researchers would automatically assume that a proper inference on the relation between academic acceleration (X) and age-50 psychological well-being (Y) requires controlling for a nuisance variable such as socioeconomic status (Z).

However, Meehl (1970), complementing Kahneman’s (1965) contribution, noted several issues with this ex post facto design. Specifically, Meehl warns that the matching, partialling, and ANCOVA designs often lead to systematic unmatching on a fourth, unmeasured or unconsidered variable (W) or vector of such variables (W_{1, 2, …, k −1, k}), resulting in unrepresentative groups, which distort the accuracy of causal inferences. Two examples clarify the issue.

Imagine a researcher who is interested in inferring a causal relationship between years of education (X) and job success (Y). The researcher collects job performance ratings on a number of employees and also information on whether they graduated from high school. The researcher finds a positive correlation between high school graduation and job success and concludes that the two indeed positively covary in the general population and a causal relationship (high school graduation → job success) is inferred.

A critic, however, points out that a third factor, intelligence (Z), may be responsible for the relation between high school graduation and job success. It is possible that there is no causal relationship between graduation and job success (X and Y); that there is a positive relation between intelligence and graduation (Z and X); and that there is a positive relation between intelligence and job success (Z and Y). The scenario sets the stage for a spurious causal inference between graduation and job success (X and Y).

Therefore, the researcher uses a matching paradigm in order to control for the effects of intelligence. A researcher takes participants with IQ test scores centered around 80 and compares those who graduated high school (Group A) to those who did not (Group B). This can be done for any arbitrary level of IQ.

By matching for intelligence (confound Z), the researcher has unwittingly unmatched the two groups on a fourth confound that was either not considered or not measured in the design. In this example, those individuals who graduated high school with an IQ score around 80 (the cutoff for the bottom 10% of the distribution) are not a representative sample of individuals around the first decile of IQ. They are individuals who differ from their intellectual peers on unmeasured variables (e.g., conscientiousness, need for achievement, impulse control, interpersonal charm), which serve as compensatory facilitators to enhance the likelihood of high school graduation. Many individuals scoring at the first decile of IQ do graduate from high school due to a host of compensatory attributes, just as many individuals with average IQs fail to graduate because their status on these attributes are liabilities. The result of matching high school graduates and dropouts on an important “confound” such as intelligence is to systematically mismatch the groups on a host of unmeasured variables. This results in making the groups unrepresentative of the populations of interest on personal attributes that enhance the likelihood of graduating from high school.

Another way in which erroneous inferences could occur is through the related issue of unambiguous exogeneity. When inferring the relation between X and Y and controlling for confound Z, researchers often behave as if X and Z were both unambiguously exogenous (that is, there is nothing “upstream” that is causing these variables to covary; rather, they are pure inputs in the causal pathway).

Consider this example from agronomy. In inferring the effects of fertilizer (X) on plant growth (Y), one might control for soil quality (Z). No one would complain about this design; it is clear that fertilizer and soil quality are exogenous inputs in the design, and one would be hard pressed to think of a fourth variable that directly is the cause of the two of them. (It is no coincidence that Ronald Fisher, from whom many of these designs originated, was working within the relatively simple designs of agronomy, e.g., the “split plot” design.)

However, the social sciences rarely deal with such unambiguous designs (Meehl, 1978, 1990). Consider the research design presented in this article. In inferring the relation between academic acceleration (X) and age-50 psychological well-being (Y), we control for socioeconomic status (Z). This would be fine if academic acceleration and childhood socioeconomic status were both pure inputs and not a result of some common-upstream input, but that is not the case. Amount of acceleration is related to intelligence, and childhood intelligence is in turn related to parents’ intelligence; childhood socioeconomic status is related to the education and occupation of one’s parents, and the parents’ education and occupation are related to the parents’ intelligence. Thus, parental intelligence is an upstream variable that was not included in this design (cf. Gottfredson, 2004; Judge, Jackson, Shaw, Scott, & Rich, 2007; Lubinski, 2010).

The result of matching for nuisance variables such as socioeconomic status is to match, as a function of their covariation, for all further-upstream covariates (e.g., parental intelligence), and all of the variables downstream that covary with them (including the focal construct: educational acceleration). To control for a nuisance variable is to also control somewhat for the construct of interest; this results in an underestimate of its potency for influencing the outcome of interest. Further, to the extent that the inputs in the design emanate in part from genetic antecedents (Plomin, DeFries, Knopik, & Neiderhiser, 2016), upstream variables partially cause the “inputs” in one’s design; as such, these sources of variation need to be factored in when making causal inferences, which require biometrically informed procedures (Bouchard, 2009; Jensen, 1980; Lubinski, 2004; Plomin, DeFries, Knopik, & Neiderhiser, 2013).

Controlling for purported confounds in correlational and quasi-experimental designs involves many assumptions about the causal antecedents giving rise to the phenomenon under analysis. As our conceptual and empirical knowledge base develops more fully, the extent to which more informed modeling decisions can be made to enhance the accuracy of causal inferences becomes greater.