A network Data Envelopment Analysis to estimate nations’ efficiency in the fight against SARS-CoV-2

Abstract

The ongoing outbreak of SARS-CoV-2 has been deeply impacting health systems worldwide. In this context, it is pivotal to measure the efficiency of different nations’ response to the pandemic, whose insights can be used by governments and health authorities worldwide to improve their national COVID-19 strategies. Hence, we propose a network Data Envelopment Analysis (DEA) to estimate the efficiencies of fifty-five countries in the current crisis, including the thirty-seven Organisation for Economic Co-operation and Development (OECD) member countries, six OECD prospective members, four OECD key partners, and eight other countries. The network DEA model is designed as a general series structure with five single-division stages – population, contagion, triage, hospitalisation, and intensive care unit admission –, and considers an output maximisation orientation, denoting a social perspective, and an input minimisation orientation, denoting a financial perspective. It includes inputs related to health costs, desirable and undesirable intermediate products related to the use of personal protective equipment and infected population, respectively, and desirable and undesirable outputs regarding COVID-19 recoveries and deaths, respectively. To the best of the authors’ knowledge, this is the first study proposing a cross-country efficiency measurement using a network DEA within the context of the COVID-19 crisis. The study concludes that Estonia, Iceland, Latvia, Luxembourg, the Netherlands, and New Zealand are the countries exhibiting higher mean system efficiencies. Their national COVID-19 strategies should be studied, adapted, and used by countries exhibiting worse performances. In addition, the observation of countries with large populations presenting worse mean efficiency scores is statistically significant.

1. Introduction

The ongoing outbreak of SARS-CoV-2 is deeply impacting modern societies, increasing the interest of scientific researchers worldwide. At the beginning of February 2021, a search in the ScienceDirect online platform using “SARS-CoV-2” as the only keyword returned more than twenty-four thousand published studies, with more than three thousand review articles and three times that value of research articles. Most of the publications are classified in the subject “Medicine and Dentistry” (nearly 74%), while only a small share of 2.4% is devoted to “Social Sciences”. When searching for terms like “efficiency” and “SARS-CoV-2” together as keywords, the number of publications drops to 15% of the original search. Nonetheless, most of them deal with the efficiency of medical treatments against the virus; only a handful of studies deals with the subject of countries’ efficiency in fighting the pandemic. Thus, there is plenty of room for research on this subject.

Characterised by symptoms such as fever, difficulty in breathing, cough, and dyspnoea and respiratory stress syndrome in more severe cases (Zhu et al., 2020), the resulting disease from SARS-CoV-2 infection, known as COVID-19, presents relatively high admission rates for patients, particularly those requiring treatment in intensive care units (ICUs) (Remuzzi & Remuzzi, 2020). Treatment for these patients may include advanced respiratory, cardiovascular, renal, liver, or neurological support (Flynn et al., 2020). A total length of stay in the hospital reaching up to nearly two months, from which a median of three weeks can be spent in the ICU, has been reported in the literature (Rees et al., 2020). It drastically diminishes the response capacity of health services to provide consistent and appropriate care for COVID-19 patients, as the installed capacity of hospital ICU beds and staffing can easily be overwhelmed (Sen-Crowe et al., 2020). Moreover, health services for other illnesses are also affected, including declines in emergency departments attendance, primary care utilisation, and cancer and inpatient/outpatient referrals (Flynn et al., 2020).

The pandemic forced institutions to issue recommendations about the use of face masks, hygiene, and social distancing,1 as well as governments, to impose strict limitations on individual freedom at an unprecedented scale (Benítez et al., 2020, Desson, Weller et al., 2020, Hasnain et al., 2020). These measures have been taken to limit the spread of the virus and its consequences on the response capacity of health systems (Flynn et al., 2020). However, despite the efforts, the impact of COVID-19 has been profound in health systems worldwide (Berardi et al., 2020, Bergquist et al., 2020, Ibrahim et al., 2020, Xu et al., 2020). Uneven responses to the health crisis have been given, with necessarily different results. The responses have been motivated by factors such as political leadership, legislative control, and differences in health systems (Lee et al., 2020), but also demographic and economic ones.

Countries such as Germany, Austria, and Switzerland have been identified as having particularly successful strategies in coping with the pandemic during the early stages of 2020 (Desson, Lambertz et al., 2020). Effective tracking, testing and containment of cases are indicated as some of the successful measures taken in preventing the spread of the virus. In addition, the nature and the response of the health systems resulted in relatively low to moderate case fatality rates for these countries (peaks of 5%, 4%, and 6% for Germany, Austria, and Switzerland, respectively).2 Particularly, only 10% of ICU beds were occupied in Germany and Austria during the first demand peak in April 2020 (Desson, Lambertz et al., 2020).

Portugal was originally identified as another successful example in dealing with the COVID-19 crisis in the early stages of the pandemic.3 This country has a public and universal national health service, which witnessed important budgetary constraints in the aftermath of the 2008 financial crisis, particularly during the Bailout Programme and the Memorandum of Understanding (2011–2014) (Ferreira & Marques, 2019). The health budget shrank from 7.5% of the gross domestic product (GDP) in 2010, to little more than 6% in 2018.4 Nonetheless, low infection and case fatality rates were observed at the beginning of the health crisis (peak of 4%)2. However, by the end of 2020, the scenario quickly switched. The country was considered one of the world’s worst COVID-19 hotspots, setting records in one of the world’s worst pandemic surges. This indicates that a country can easily become a cautionary tale if its policies on preventing the widespread of the disease are soft and more restrictive ones are not followed by the population.

On the contrary, Italy faced a major impact from the pandemic on its health system. High case fatality rates were observed in the country (peak of 15%)2, partially due to the saturation of ICUs (Berardi et al., 2020). Spain was another country severely hit by the pandemic, despite having a public and universal health service. After drastic cuts to the health budgets, as a result of the 2008 financial crisis, the current expenditure on health is 8.9% of the GDP, higher than the Organisation for Economic Co-operation and Development (OECD) average (8.8%) and that in 2008 (8.3%). The country is above the OECD average for health resources such as doctors, nurses, and beds per 1000 population (Henríquez et al., 2020). Nonetheless, during the first peak of the crisis, the country registered high case fatality rates (peak of 12%)2 and twice as many deaths as those for the same period in the previous year (Henríquez et al., 2020). Other countries were highly affected by the SARS-CoV-2 crisis during the early stages of 2020. The United Kingdom (UK) has observed high infection rates, as well as case fatality rates (peak of 15%)2, despite also having a well-funded public, free, and universal health service (Flynn et al., 2020).

The United States of America (USA) has been one of the most affected countries by the SARS-CoV-2 crisis with a total of 319,364 recorded deaths by December 21, 2020.5 Unlike most of the European countries, the health system in the USA is predominantly private and insurance-based, where enrolment is voluntary (Bergquist et al., 2020). Poor coordination between the federal and state governments and limited testing resulted in high infection rates in the early stages of the pandemic (Cornwall et al., 2020). Moderate case fatality rates have also been recorded (peak of 6%).2

Given this context, it is particularly important to measure the efficiency of different countries in responding to the ongoing SARS-CoV-2 pandemic. By doing so, it is possible to assess which health systems perform better and should be regarded as benchmarks, and which need to improve their performance. Insights can, thus, be obtained on the factors contributing to the best/worst performances, allowing governments to take the necessary measures in improving their respective health systems.

Therefore, we propose an approach based on network Data Envelopment Analysis (DEA) to estimate the efficiency of health systems in responding to the current crisis at the end of 2020. Our analysis comprises fifty-five countries, including the thirty-seven OECD member countries, six OECD prospective members, four OECD key partners, and eight other counties, ensuring a credible representation of worldwide responses. By using network DEA instead of conventional DEA, it is possible to evaluate the internal efficiencies of entities, in this case, national health systems. In our work, the network is modelled through a general series structure with five single-division stages – Population, Contagion, Triage, Hospitalisation, and ICU admission. We also consider two model orientations: output orientation, denoting a Social perspective, and input orientation, denoting a Financial perspective. The model includes inputs related to health expenditure and specific health costs associated with the pandemic, desirable and undesirable intermediate products related to the use of personal protective equipment (PPE) and infected population, respectively, and desirable and undesirable outputs such as COVID-19 recoveries and deaths, respectively. To the best of our knowledge, this is the first study using network DEA to estimate cross-country efficiency within the context of the SARS-CoV-2 pandemic.

The remainder of the paper is organised as follows. In Section 2, a literature review is pursued on the application of DEA, particularly network DEA, to similar problems. In Section 3, the reasoning behind the methodology is detailed. In Section 4, the case study is described, and the results are presented and discussed. Finally, in Section 5, conclusions are drawn.

2. Literature review

As previously mentioned, network DEA was used in this paper to measure the efficiency of health systems worldwide in dealing with the COVID-19 pandemic. DEA is the preeminent non-parametric method for measuring the efficiency of different entities – the so-called decision-making units (DMUs) –, using multiple inputs to produce multiple outputs (Kao, 2017). Nonetheless, conventional DEA does not consider the internal structure of DMUs, taking into account only the inputs and outputs. Thus, the efficiencies of the internal components of a DMU cannot be assessed, nor can they be compared with those of other DMUs. Network DEA extends the conventional DEA method to address this limitation.

Since the seminal work of Charnes et al. (1978), DEA has been applied to a broad range of sectors, such as banking (Lin et al., 2009, Tsolas and Charles, 2015), culture (Van Puyenbroeck et al., 2021), manufacturing (Jain et al., 2011), the military (Sutton & Dimitrov, 2013), portfolio selection (Amin & Hajjami, 2021), supply chains (Álvarez-Rodríguez et al., 2020, Tajbakhsh and Hassini, 2015), sustainability (Shabanpour et al., 2019, Tsaples and Papathanasiou, 2021), transport (Mahmoudi et al., 2020), and urban systems (Ai et al., 2019, Pozo et al., 2019). Moreover, since the appearance of the term ‘network DEA’ in the original work of Färe and Grosskopf (2000), recent examples of its applications include, e.g., Henriques et al. (2020) and Izadikhah et al. (2018) in banking, Xu et al. (2021) in environmental governance, Peykani et al. (2021) in financing, Kou et al. (2016) in innovation systems, and Ferreira et al. (2021) in water and sanitation.

Health is another sector that has widely used DEA, particularly to measure the efficiency of hospitals. Some examples are presented subsequently. Chen et al. (2005) argue that only measuring the overall efficiency of hospitals may be of limited value, as insights about the inefficiencies of individual inputs may be lost. The overall inefficiency score is decomposed into different individual input inefficiencies and variables on organisation, management, demographics, and market competition of a set of hospitals in California are used to identify which factors are associated with the overall operational inefficiency. Ancarani et al. (2009) use DEA to measure the technical efficiency of wards in an Italian hospital and study how these efficiencies are related to organisational and managerial factors. Mitropoulos et al. (2015) propose an integrated approach between Bayesian analysis and Chance Constrained DEA (CCDEA) and apply it to Greek public hospitals. CCDEA is said to overcome the limitation of traditional DEA in requiring all input and output values to be known, allowing such values to be represented by probability distributions, while Bayesian techniques allow the parameters for these distributions to be inferred from data. Cinaroglu (2020) use DEA to assess the relationship between size and efficiency in Turkish hospitals. Kao et al. (2021) study how economies of scope can be exploited by Chinese hospitals. The degree of economies of scope is measured as efficiency gains through DEA.

However, instead of considering hospitals or hospital departments as DMUs, DEA can be used in higher decision-making levels to assess the efficiency of entire health systems, or applied to other aspects of the sector. Ippoliti and Falavigna (2012) study the effect of pharmaceutical clinical research on the efficiency of the regional medical care industry in Italy. Cheng and Zervopoulos (2014) develop a DEA model to measure the efficiency of health systems in 171 countries, which considers desirable and undesirable outputs. Together with super-efficiency DEA, the authors make use of a generalised directional distance function that, unlike other studies, acknowledges the significance of undesirable outputs. Shwartz et al. (2016) use DEA to develop a composite measure of quality in pay-for-performance programmes of health care providers. Top et al. (2020) measure the efficiency of health systems in 36 African countries through DEA. The study used the health expenditure, the number of physicians, nurses, and hospital beds per 1,000 population, the unemployment rate, and the Gini coefficient as inputs, and the life expectancy at birth and the inverse of the infant mortality rate as outputs.

Furthermore, studies in the health sector using network DEA are quite scarce. Kawaguchi et al. (2014) were the first to do such an application, by evaluating the policy effect of Japan’s municipal hospitals’ reforms using a dynamic network DEA model. Later, Gong et al. (2019) used network DEA and Tobit regression to understand if China’s healthcare system improved after the country’s healthcare reform. More recently, Gavurova et al. (2021) and Pereira, Ferreira et al. (2021) published their respective studies on the efficiency of the health systems of OECD countries and the Portuguese public hospitals while employing variants of network DEA. Nonetheless, Hamzah et al. (2021) and Mariano et al. (2021) were the only authors to address the issue of the response of countries to COVID-19 using network DEA, but both studies only considered the scope of Brazil and Malaysia, respectively. To the best of the authors’ knowledge, there are no published works that employ some type of network DEA model to measure the efficiency of a large set of nations in the fight against SARS-CoV-2.

Besides, in terms of desirable and undesirable outputs, the literature has been giving some attention to the subject in the works of Tone and Tsutsui (2014) and their dynamic slacks-based DEA model with a network structure, Khalili-Damghani and Shahmir (2015) and their uncertain network DEA model, and Yu et al. (2020) and their matrix-type network DEA model, for instance. Indeed, Ferreira et al. (2021) and Yu et al. (2020) had already stated that omitting undesirable outputs and undesirable intermediate products in a network DEA model leads to biased efficiency scores; thus, it is unreasonable to ignore them in efficiency measurements. Nonetheless, as far as the authors are aware, studies that address desirable and undesirable outputs and desirable and undesirable intermediate products simultaneously are lacking (see, e.g., Ferreira et al., 2021), with no publications in the health sector.

Our study includes the OECD member countries, whose health systems have been extensively compared in the literature, particularly through DEA approaches. Examples include Cetin and Bahce, 2016, Önen and Sayın, 2018, and Retzlaff-Roberts et al. (2004). Gearhart (2016) studies the robustness of cross-country healthcare efficiency comparisons in OECD countries, namely those made with DEA, and Varabyova and Müller (2016) present a literature review on the same subject. The work of Zanakis et al. (2007) has used DEA to assess the efficiency of countries in battling the HIV/AIDS pandemic. The authors collected information from 151 countries and used the percentage of adults living with HIV/AIDS, HIV/AIDS cases per capita, and AIDS-related death rate as outputs of the DEA model, and the health system performance index, health private expenditure, health public expenditure, adult literacy rate, and doctors, nurses, GDP, and ratios per capita as inputs. In the context of the current SARS-CoV-2 pandemic, Aydin and Yurdakul (2020) develop a DEA model called “weighted stochastic imprecise DEA” to assess the performances of 142 countries. The authors establish as inputs the sum of total deaths, the “stringency index”, reflecting the severity of containment policies, extreme poverty rate, heart attack death rate, diabetes prevalence, female smokers, and male smokers, and as outputs the population, GDP, hospital beds per 100,000 population, total recoveries from COVID-19, and total tests. The sum of total cases and active cases are used as “flexible data”, i.e. the result of the model determines if the variable is considered an input or an output. Additionally, Nepomuceno et al. (2020) used DEA to estimate the reallocation of hospital beds for urgent COVID-19 hospitalisations in Brazil and Ibrahim et al. (2020) used two-stage DEA to evaluate the relative efficiency of the response management system of 58 countries fighting the COVID-19 pandemic.

Therefore, we argue that DEA, particularly network DEA, considering undesirable outputs and undesirable intermediate products is an important tool for political and health decision-makers to devise effective strategies for health systems worldwide in battling the current SARS-CoV-2 pandemic. Nonetheless, to the best of the authors’ knowledge, no studies exist presenting a cross-country healthcare efficiency measurement using such a tool within the context of the current crisis, especially taking into account a social and a financial perspective.

3. Methodology

There are numerous real-world systems with a multi-stage structure (Kao, 2017). Although such a statement is quite vague, since a stage can be comprised of many divisions with distinct structures, the fact is that conventional network DEA sees a multi-stage system as being composed of various single-division stages connected in series.

Three types of series structures are usually addressed in the literature. First, the basic series structure considers that not only all outputs of a certain division are the inputs of the following one, but also that only the first division consumes exogenous inputs. Second, the general series structure allows all divisions to consume exogenous inputs, as well as some of their outputs to be exogenous ones. Third, the series structure with reversal links acknowledges that the outputs of a certain division can be sent back to a previous division. Among these types of series structures, the second one is the most prevalent in the literature (Kao, 2017).

In the end, for a DMU $j=1,\dots ,n$, we model the country-wide pandemic response according to:

• –Inputs $x_{ij}$, with $i=1,\dots ,m$;
• –Desirable and undesirable intermediate products $z_j^{(p,p^{\prime })}$ and $q_j^{(p,p^{\prime })}$, respectively, for a relationship between divisions $p$ and $p^{\prime }$;
• –Desirable outputs $y_{rj}$, with $r=1,\dots ,s$; and
• –Undesirable outputs $b_{lj}$, with $l=1,\dots ,t$.

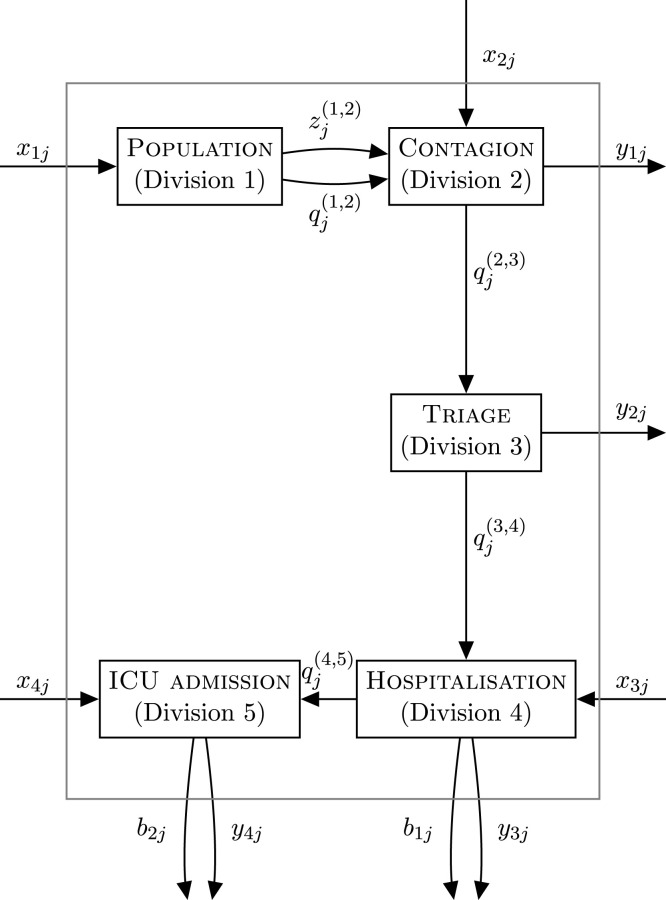
Table 1 presents these variables and their corresponding indicators. Moreover, we consider each division available for the 55 countries described in Section 1 at the end of 2020. Based on that, we structure the network as a general series structure with five single-division stages: Population, Contagion, Triage, Hospitalisation, and ICU admission. These details are shown in Fig. 1, where:

Table 1.

Inputs, intermediate products, and outputs, and respective indicators per division $p$ of DMU $j$.

Type	Indicator	Description	Primary source (s)	Division (s)
Input ($m=4$)	Health expenditure, $x_{1j}$	Reports the amount of funds (in M€) spent by each country in health.	OECD $+$ WHO $+$ World Bank	1
	Costs with instruments used in COVID-19 diagnostic testing, $x_{2j}$	Corresponds to amount (in €) spent in instruments used for testing the existence of the SARS-CoV-2 in an individual in 2020.	Eurostat $+$ World Bank	2
	Costs with disinfection and sterilisation products, $x_{3j}$	Concerns the amount (in €) spent in products for disinfecting and sterilising activities in 2020.	Eurostat $+$ World Bank	4
	Costs with oxygen therapy equipment, $x_{4j}$	Relates to the amount (in €) spent in equipment used for oxygen therapy in 2020.	Eurostat $+$ World Bank	5
Desirable intermediate product ($h=1$)	Population that uses PPE, $z_j^{(1,2)}$	Matches the population that wears specialised equipment that protects the user against health risks in 2020.	Institute for Health Metrics and Evaluation $+$ Worldometer	1,2
	Population that does not use PPE, $q_j^{(1,2)}$	Matches the population that does not wear specialised equipment that protects the user against health risks in 2020.	Institute for Health Metrics and Evaluation $+$ Worldometer	1,2
Undesirable intermediate product ($k=4$)	Infected population, $q_j^{(2,3)}$	Counts the number of active infected individuals on 31/12/2020.	Our World in Data $+$ Worldometer	2,3
	Infected population that needs hospitalisation, $q_j^{(3,4)}$	Measures the number of infected individuals that required hospital care on 31/12/2020.	European Centre for Disease Prevention and Control	3,4
	Hospitalised population that needs treatment in the ICU, $q_j^{(4,5)}$	Measures the number of hospitalised individuals that required treatment in the ICU on 31/12/2020.	European Centre for Disease Prevention and Control $+$ Worldometer	4,5
	Non-infected population, $y_{1j}$	Counts the number of individuals on 31/12/2020 that have never been infected.	Our World in Data $+$ Worldometer	2
Desirable output ($s=4$)	Home recoveries, $y_{2j}$	Details the number of individuals on 31/12/2020 that recovered from COVID-19 at home.	European Centre for Disease Prevention and Control $+$ Our World in Data $+$ Worldometer	3
	Hospitalisation recoveries, $y_{3j}$	Details the number of individuals on 31/12/2020 that recovered from COVID-19 in non-ICU facilities.	–	4
	ICU recoveries, $y_{4j}$	Details the number of individuals on 31/12/2020 that recovered from COVID-19 in ICU facilities.	–	5
Undesirable output ($t=2$)	Hospitalisation deaths, $b_{1j}$	Details the number of individuals that perished from COVID-19 in non-ICU facilities on 31/12/2020.	–	4
	ICU deaths, $b_{2j}$	Details the number of individuals that perished from COVID-19 in ICU facilities on 31/12/2020.	–	5

Fig. 1.

Series structure of the network system of a country $j$ with five divisions.

• –$z_j^{(1,2)}=z_{fj}^{(1,2)}=z_{gj}^{(2,1)}$;
• –$q_j^{(1,2)}=q_{aj}^{(1,2)}=q_{dj}^{(2,1)}$;
• –$q_j^{(2,3)}=q_{aj}^{(2,3)}=q_{dj}^{(3,2)}$;
• –$q_j^{(3,4)}=q_{aj}^{(3,4)}=q_{dj}^{(4,3)}$;
• –$q_j^{(4,5)}=q_{aj}^{(4,5)}=q_{dj}^{(5,4)}$; and

$f$ denotes the $f$th desirable intermediate product produced by division $p$, $g$ denotes the $g$th desirable intermediate product used by division $p$, $a$ denotes the $a$th undesirable intermediate product produced by division $p$, and $d$ denotes the $d$th undesirable intermediate product used by division $p$. Vaccination against COVID-19 was not considered, since less than a third of the selected 55 nations had began their respective vaccination campaigns by 31/12/2020.

Note that $q_j^{(2,3)}$ corresponds to the number of active infected individuals in 31/12/2020 rather than the number of individuals that have been infected until 31/12/2020, which constitutes a limitation of this study due to data unavailability. Additionally, some of the values of indicators $x_{1j}$, $x_{2j}$, $x_{3j}$, $x_{4j}$, $q_j^{(3,4)}$, $q_j^{(4,5)}$, and $y_{1j}$ had to be estimated by means of a linear regression to account for the missing data. These estimations were conducted based on their corresponding analogous from 2019 with a statistically significant positive strong correlation. For instance, to estimate $x_{1j}$, we conducted a linear regression of the health expenditure of 2019 and the available health expenditure values of 2020 to estimate the remaining values of 2020, ending up with a regression model that fits 99.69% of the input data.

Furthermore, due to understandable data constraints, the values of the outputs $y_{3j}$, $y_{4j}$, $b_{1j}$, and $b_{2j}$ were not available. Hence, we adapted the work of Pereira, Ferreira et al. (2021) to estimate the sample distribution of the outputs using the Monte Carlo method. Accordingly, we rewrote them as a function of the intermediate products that generated them in a certain division $p$, weighted by a simulated value given by ${\alpha }_{rj}^{(p,o)}$ or ${\alpha }_{lj}^{(p,o)}$ (where $o$ denotes the operational environment), depending on whether the output being estimated is desirable or undesirable:

$$\left\{\begin{array}{c}{y}_{3j}={\alpha }_{3j}^{(4,o)}{q}_j^{(3,4)},\hfill \\ b_{1j}={\alpha }_{1j}^{(4,o)}{q}_j^{(3,4)},\hfill \\ y_{4j}={\alpha }_{4j}^{(5,o)}{q}_j^{(4,5)},\hfill \\ b_{2j}={\alpha }_{2j}^{(5,o)}{q}_j^{(4,5)},\hfill \end{array}\right)$$ (1)

where:

$${\alpha }_{3j}^{(4,o)}+{\alpha }_{1j}^{(4,o)}+\frac{q_j^{(4,5)}}{q_j^{(3,4)}}=1$$ (2)

$${\alpha }_{4j}^{(5,o)}+{\alpha }_{2j}^{(5,o)}=1$$ (3)

The Monte Carlo simulated values $\alpha$ followed a uniform probability distribution limited between a certain range according to the literature, as shown in Table 2. The remaining simulated values can be computed based on these in line with Eqs. (2) and (3).

Table 2.

Lower and upper bounds of the simulated values.

Simulated value	Interval	Reference
${\alpha }_{1j}^{(4,0)}$	$\left[0.12,0.22\right]$	Piroth et al. (2020)
${\alpha }_{2j}^{(5,o)}$	$\left[0.72,0.82\right]$	Rahim et al. (2020)

Moreover, amidst the several models that measure the efficiency of network structures, we chose the relational model (Kao & Liu, 2009), under variable returns-to-scale (VRS) to depict the efficiency of a country $j$ with the structure depicted in Fig. 1. This choice is due to the distinct scale size of each country and the fact that constant returns-to-scale efficiency scores already include VRS efficiency scores and scale efficiencies, which are not within the scope of this work. In particular, a step-by-step reasoning behind the model is presented below:

Division 1 Population —

At this stage, country $j$ has a certain health expenditure $x_{1j}$ to serve its population, while some individuals use PPE for protection against the virus, $z_j^{(1,2)}$, and others do not, $q_j^{(1,2)}$. Therefore, the constraint associated with Population is:

$$v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}-{\hat{w}}^{\left(1_z\right)}{z}_j^{(1,2)}-\left(-{\hat{w}}^{\left(1_q\right)}{q}_j^{(1,2)}\right)⩾0,$$ (4)

where the multipliers ${\hat{w}}^{\left(1_z\right)}$ and $v_1^{\left(1\right)}$ should be greater than or equal to a non-Archimedean number $\varepsilon$; the other multiplier, ${\hat{w}}^{\left(1_q\right)}$, associated with an undesirable intermediate product, is unrestricted in sign. Indeed, multipliers can be either nonnegative (for desirable variables) or unrestricted in sign (for undesirable variables). In particular, since undesirable variables are part of the production process, their multipliers need to reflect their negative impact on performance by being unrestricted in sign, thus working as penalties (Ferreira et al., 2021). Furthermore, the partial efficiency of country $j$ in Division 1 is given by:

$$E_j^{\left(1\right)}=\frac{{\hat{w}}^{\left(1_z\right)}{z}_j^{(1,2)}}{v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}+{\hat{w}}^{\left(1_q\right)}{q}_j^{(1,2)}}.$$ (5)

Division 2 Contagion —

Here, to identify the infected individuals among those that use and do not use PPE ($z_j^{(1,2)}$ and $q_j^{(1,2)}$, respectively), investment in COVID-19 diagnostic testing $x_{2j}$ is required. It returns the infected ($q_j^{(2,3)}$) and non-infected population ($y_{1j}$). Hence, the constraint concerning Contagion is:

$$w^{\left(2_z\right)}{z}_j^{(1,2)}+\left(-w^{\left(2_q\right)}{q}_j^{(1,2)}\right)+v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}-\left(-{\hat{w}}^{\left(2\right)}{q}_j^{(2,3)}\right)-u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}⩾0,$$ (6)

where $w^{\left(2_z\right)}$, $u_1^{\left(2\right)}$, and $v_2^{\left(2\right)}$ are greater than or equal to $\varepsilon$, and $w^{\left(2_q\right)}$ and ${\hat{w}}^{\left(2\right)}$ are unrestricted in sign. The partial efficiency of country $j$ in Division 2 is computed as follows:

$$E_j^{\left(2\right)}=\frac{w^{\left(2_q\right)}{q}_j^{(1,2)}+u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}}{w^{\left(2_z\right)}{z}_j^{(1,2)}+v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}+{\hat{w}}^{\left(2\right)}{q}_j^{(2,3)}}.$$ (7)

Division 3 Triage —

The infected population $q_j^{(2,3)}$ must undergo triage. Afterwards, depending on the severity of the disease, individuals are either sent home ($y_{2j}$) or hospitalised ($q_j^{(3,4)}$). The constraint related to Triage is given by:

$$-w^{\left(3\right)}{q}_j^{(2,3)}-\left(-{\hat{w}}^{\left(3\right)}{q}_j^{(3,4)}\right)-u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}⩾0,$$ (8)

where $u_2^{\left(3\right)}$ is greater than or equal to $\varepsilon$, and ${\hat{w}}^{\left(3\right)}$ and $w^{\left(3\right)}$ are unrestricted in sign. Division 3’s partial efficiency can be obtained via:

$$E_j^{\left(3\right)}=\frac{w^{\left(3\right)}{q}_j^{(2,3)}+u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}}{{\hat{w}}^{\left(3\right)}{q}_j^{(3,4)}}.$$ (9)

Division 4 Hospitalisation —

Among the infected population that needs hospitalisation $q_j^{(3,4)}$, some individuals may recover or die ($y_{3j}$ and $b_{1j}$, respectively), and others may require treatment at the ICU ($q_j^{(4,5)}$). There are also costs with disinfection and sterilisation procedures $x_{3j}$ that need to be taken into consideration. The constraint regarding Hospitalisation is then formulated as:

$$-w^{\left(4\right)}{q}_j^{(3,4)}+v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}-\left(-{\hat{w}}^{\left(4\right)}{q}_j^{(4,5)}\right)-u_3^{\left(4\right)}{y}_{3j}^{\left(4\right)}-\left(-{\hat{u}}_1^{\left(4\right)}{b}_{1j}^{\left(4\right)}\right)⩾0,$$ (10)

where $u_3^{\left(4\right)}$ and $v_3^{\left(4\right)}$ are greater than or equal to $\varepsilon$, and ${\hat{w}}^{\left(4\right)}$, ${\hat{u}}_1^{\left(4\right)}$, and $w^{\left(4\right)}$ are unrestricted in sign. The partial efficiency of Division 4 corresponds to:

$$E_j^{\left(4\right)}=\frac{w^{\left(4\right)}{q}_j^{(3,4)}+u_3^{\left(4\right)}{y}_{3j}^{\left(4\right)}}{v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}+{\hat{w}}^{\left(4\right)}{q}_j^{(4,5)}+{\hat{u}}_1^{\left(4\right)}{b}_{1j}^{\left(4\right)}}.$$ (11)

Division 5 ICU admission —

In ICU admission, the hospitalised individuals that need ICU treatment $q_j^{(4,5)}$ are considered, as well as the costs with oxygen therapy equipment $x_{4j}$. Naturally, two outputs are generated by Division 5 - ICU recoveries ($y_{4j}$) and ICU deaths ($b_{2j}$), which results in the following constraint:

$$-w^{\left(5\right)}{q}_j^{(4,5)}+v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}-u_4^{\left(5\right)}{y}_{4j}^{\left(5\right)}-\left(-{\hat{u}}_2^{\left(5\right)}{b}_{2j}^{\left(5\right)}\right)⩾0,$$ (12)

where $u_4^{\left(5\right)}$ and $v_4^{\left(5\right)}$ are greater than or equal to $\varepsilon$, and ${\hat{u}}_2^{\left(5\right)}$ and $w^{\left(5\right)}$ are unrestricted in sign. Therefore, the partial efficiency of this division is given by:

$$E_j^{\left(5\right)}=\frac{w^{\left(5\right)}{q}_j^{(4,5)}+u_4^{\left(5\right)}{y}_{4j}^{\left(5\right)}}{v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}+{\hat{u}}_2^{\left(5\right)}{b}_{2j}^{\left(5\right)}}.$$ (13)

System. Globally, four inputs ($x_{ij}$, with $i=1,\dots ,4$) enter the system, producing six outputs ($y_{rj}$, with $r=1,\dots ,4$, and $b_{lj}$, with $l=1,\dots ,2$). The constraint associated with this relation is modelled as:

$$v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}+v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}+v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}+v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}-u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}-u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}-u_3^{\left(4\right)}{y}_{3j}^{\left(4\right)}-\left(-{\hat{u}}_1^{\left(4\right)}{b}_{1j}^{\left(4\right)}\right)-u_4^{\left(5\right)}{y}_{4j}^{\left(5\right)}-\left(-{\hat{u}}_2^{\left(5\right)}{b}_{2j}^{\left(5\right)}\right)⩾0,$$ (14)

where the multipliers have the same restrictions in sign as described divisionwise. Finally, the system efficiency is given by:

$$E_j=\frac{u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}+u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}+u_3^{\left(4\right)}{y}_{3j}^{\left(4\right)}+u_4^{\left(5\right)}{y}_{4j}^{\left(5\right)}}{v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}+v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}+v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}+v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}+{\hat{u}}_1^{\left(4\right)}{b}_{1j}^{\left(4\right)}+{\hat{u}}_2^{\left(5\right)}{b}_{2j}^{\left(5\right)}}.$$ (15)

Note that, although we have adopted a notation that seems to depict different multipliers for the same specific intermediate products in different divisions, we have indeed considered the linkage between divisions. In fact, according to Kao (2017), any intermediate product produced by a certain division can be used by another division as long as, in multiplier network DEA formulations such as the one proposed here, the multiplier of an intermediate product as the output of the previous division is the same as the multiplier of that intermediate product as the input of the current division. Although this subject is not very discussed in the literature, there are a few studies that use the same multipliers in different divisions while considering their respective undesirable intermediate products as inputs (Ferreira et al., 2021, Huang et al., 2019, Kiani Mavi et al., 2019, Lopes et al., 2018, Nematizadeh et al., 2019). In particular:

• –${\hat{w}}^{\left(1z\right)}=w^{\left(2z\right)}$ and ${\hat{w}}^{\left(1q\right)}=w^{\left(2q\right)}$ between Population and Contagion;
• –${\hat{w}}^{\left(2\right)}=w^{\left(3\right)}$ between Contagion and Triage;
• –${\hat{w}}^{\left(3\right)}=w^{\left(4\right)}$ between Triage and Hospitalisation; and
• –${\hat{w}}^{\left(4\right)}=w^{\left(5\right)}$ between Hospitalisation and ICU admission.

This linkage takes into account the fact that multipliers must be consistently either nonnegative (${\hat{w}}^{\left(1z\right)}$ and $w^{\left(2z\right)}$) or unrestricted in sign (${\hat{w}}^{\left(1q\right)}$ and $w^{\left(2q\right)}$, ${\hat{w}}^{\left(2\right)}$ and $w^{\left(3\right)}$, ${\hat{w}}^{\left(3\right)}$ and $w^{\left(4\right)}$, and ${\hat{w}}^{\left(4\right)}$ and $w^{\left(5\right)}$).

Finally, we use Model (16), which presents the complete modelling of the problem at hand for the DMU under assessment $j_0$ while considering all the assumptions mentioned above:

$$min{v}_1^{\left(1\right)}{x}_{1j_0}^{\left(1\right)}+v_2^{\left(2\right)}{x}_{2j_0}^{\left(2\right)}+v_3^{\left(4\right)}{x}_{3j_0}^{\left(4\right)}+v_4^{\left(5\right)}{x}_{4j_0}^{\left(5\right)}+c_0$$ (16)

$$\text{subject to:}{u}_1^{\left(2\right)}{y}_{1j_0}^{\left(2\right)}+u_2^{\left(3\right)}{y}_{2j_0}^{\left(3\right)}+u_3^{\left(4\right)}{\alpha }_{3j_0}^{(4,o)}{q}_{j_0}^{(3,4)}-{\hat{u}}_1^{\left(4\right)}{\alpha }_{1j_0}^{(4,o)}{q}_{j_0}^{(3,4)}$$

$$+u_4^{\left(5\right)}{\alpha }_{4j_0}^{(5,o)}{q}_{j_0}^{(4,5)}-{\hat{u}}_2^{\left(5\right)}{\alpha }_{2j_0}^{(5,o)}{q}_{j_0}^{(4,5)}=1$$ (16.1)

$$v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}+v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}+v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}+v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}$$

$$-u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}-u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}-u_3^{\left(4\right)}{\alpha }_{3j}^{(4,o)}{q}_j^{(3,4)}+{\hat{u}}_1^{\left(4\right)}{\alpha }_{1j}^{(4,o)}{q}_j^{(3,4)}$$

$$-u_4^{\left(5\right)}{\alpha }_{4j}^{(5,o)}{q}_j^{(4,5)}+{\hat{u}}_2^{\left(5\right)}{\alpha }_{2j}^{(5,o)}{q}_j^{(4,5)}+c_0⩾0j=1,\dots ,n$$ (16.2)

$$v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}-{\hat{w}}^{\left(1_z\right)}{z}_j^{(1,2)}+{\hat{w}}^{\left(1_q\right)}{q}_j^{(1,2)}+c_0⩾0,j=1,\dots ,n$$ (16.3)

$$w^{\left(2_z\right)}{z}_j^{(1,2)}-w^{\left(2_q\right)}{q}_j^{(1,2)}+v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}+{\hat{w}}^{\left(2\right)}{q}_j^{(2,3)}$$

$$-u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}+c_0⩾0,j=1,\dots ,n$$ (16.4)

$$-w^{\left(3\right)}{q}_j^{(2,3)}+{\hat{w}}^{\left(3\right)}{q}_j^{(3,4)}-u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}+c_0⩾0,j=1,\dots ,n$$ (16.5)

$$-w^{\left(4\right)}{q}_j^{(3,4)}+v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}+{\hat{w}}^{\left(4\right)}{q}_j^{(4,5)}-u_3^{\left(4\right)}{\alpha }_{3j}^{(4,o)}{q}_j^{(3,4)}$$

$$+{\hat{u}}_1^{\left(4\right)}{\alpha }_{1j}^{(4,o)}{q}_j^{(3,4)}+c_0⩾0,j=1,\dots ,n$$ (16.6)

$$-w^{\left(5\right)}{q}_j^{(4,5)}+v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}-u_4^{\left(5\right)}{\alpha }_{4j}^{(5,o)}{q}_j^{(4,5)}+{\hat{u}}_2^{\left(5\right)}{\alpha }_{2j}^{(5,o)}{q}_j^{(4,5)}$$

$$+c_0⩾0,j=1,\dots ,n$$ (16.7)

$$c_0,{\hat{w}}^{\left(1_q\right)},w^{\left(2_q\right)}{\hat{w}}^{\left(2\right)},{\hat{w}}^{\left(3\right)},w^{\left(3\right)},{\hat{w}}^{\left(4\right)},{\hat{u}}_1^{\left(4\right)},w^{\left(4\right)},{\hat{u}}_2^{\left(5\right)},$$

$$\text{and}{w}^{\left(5\right)}\text{are free}$$

$${\hat{w}}^{\left(1_z\right)},v_1^{\left(1\right)},w^{\left(2_z\right)},u_1^{\left(2\right)},v_2^{\left(2\right)},u_2^{\left(3\right)},u_3^{\left(4\right)},v_3^{\left(4\right)},u_4^{\left(5\right)},v_4^{\left(5\right)}⩾\varepsilon$$

where $c_0$ is the intercept and $\varepsilon =0.001$. Bear in mind that the equations presented in the step-by-step reasoning correspond to the division and system efficiencies, which had to be slightly adjusted to fit the DEA formulation. For example, since Model (16) is output-oriented, only the input variables of Expression (14) are part of the objective function. Besides, we have adopted an additive model since it not only assumes that there is no competition among outputs for the inputs, but also is more common in the literature, which typically mentions the use of additive models instead of multiplicative models, with the latter being more common in works studying non-convex production possibility sets (Kao, 2017).

The output orientation of Model (16) fixes the input level and seeks to increase output generation, which, in the context of the COVID-19 pandemic, implies an estimation of efficiency that aims for an increase in the number of recoveries and a decrease in the number of deaths while holding the costs constant. It can be interpreted as a Social Perspective model since it aims to improve social well-being for the same amount of financial resources. However, an input orientation, where the received input is sought to be reduced for the same output level, is also relevant. In the context of COVID-19 pandemic outbreaks, this model results in estimating efficiencies while holding the numbers of recoveries and deaths and seeking the reduction of resource consumption. In this case, we have a Financial Perspective model given the aim to reduce resource consumption for the same level of social well-being, which is mathematically formulated for DMU $j_0$ through Model (17) as follows:

$$max{u}_1^{\left(2\right)}{y}_{1j_0}^{\left(2\right)}+u_2^{\left(3\right)}{y}_{2j_0}^{\left(3\right)}+u_3^{\left(4\right)}{\alpha }_{3j_0}^{(4,o)}{q}_{j_0}^{(3,4)}-{\hat{u}}_1^{\left(4\right)}{\alpha }_{1j_0}^{(4,o)}{q}_{j_0}^{(3,4)}$$

$$+u_4^{\left(5\right)}{\alpha }_{4j_0}^{(5,o)}{q}_{j_0}^{(4,5)}-{\hat{u}}_2^{\left(5\right)}{\alpha }_{2j_0}^{(5,o)}{q}_{j_0}^{(4,5)}+c_0$$ (17)

$$\text{subject to:}{v}_1^{\left(1\right)}{x}_{1j_0}^{\left(1\right)}+v_2^{\left(2\right)}{x}_{2j_0}^{\left(2\right)}+v_3^{\left(4\right)}{x}_{3j_0}^{\left(4\right)}+v_4^{\left(5\right)}{x}_{4j_0}^{\left(5\right)}=1$$ (17.1)

$$-v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}-v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}-v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}-v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}$$

$$+u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}+u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}+u_3^{\left(4\right)}{\alpha }_{3j}^{(4,o)}{q}_j^{(3,4)}-{\hat{u}}_1^{\left(4\right)}{\alpha }_{1j}^{(4,o)}{q}_j^{(3,4)}$$

$$+u_4^{\left(5\right)}{\alpha }_{4j}^{(5,o)}{q}_j^{(4,5)}-{\hat{u}}_2^{\left(5\right)}{\alpha }_{2j}^{(5,o)}{q}_j^{(4,5)}+c_0⩽0j=1,\dots ,n$$ (17.2)

$$-v_1^{\left(1\right)}{x}_{1j}^{\left(1\right)}+{\hat{w}}^{\left(1_z\right)}{z}_j^{(1,2)}-{\hat{w}}^{\left(1_q\right)}{q}_j^{(1,2)}+c_0⩽0,j=1,\dots ,n$$ (17.3)

$$-w^{\left(2_z\right)}{z}_j^{(1,2)}+w^{\left(2_q\right)}{q}_j^{(1,2)}-v_2^{\left(2\right)}{x}_{2j}^{\left(2\right)}-{\hat{w}}^{\left(2\right)}{q}_j^{(2,3)}$$

$$+u_1^{\left(2\right)}{y}_{1j}^{\left(2\right)}+c_0⩽0,j=1,\dots ,n$$ (17.4)

$$w^{\left(3\right)}{q}_j^{(2,3)}-{\hat{w}}^{\left(3\right)}{q}_j^{(3,4)}+u_2^{\left(3\right)}{y}_{2j}^{\left(3\right)}+c_0⩽0,j=1,\dots ,n$$ (17.5)

$$w^{\left(4\right)}{q}_j^{(3,4)}-v_3^{\left(4\right)}{x}_{3j}^{\left(4\right)}-{\hat{w}}^{\left(4\right)}{q}_j^{(4,5)}+u_3^{\left(4\right)}{\alpha }_{3j}^{(4,o)}{q}_j^{(3,4)}$$

$$-{\hat{u}}_1^{\left(4\right)}{\alpha }_{1j}^{(4,o)}{q}_j^{(3,4)}+c_0⩽0,j=1,\dots ,n$$ (17.6)

$$w^{\left(5\right)}{q}_j^{(4,5)}-v_4^{\left(5\right)}{x}_{4j}^{\left(5\right)}+u_4^{\left(5\right)}{\alpha }_{4j}^{(5,o)}{q}_j^{(4,5)}-{\hat{u}}_2^{\left(5\right)}{\alpha }_{2j}^{(5,o)}{q}_j^{(4,5)}$$

$$+c_0⩽0,j=1,\dots ,n$$ (17.7)

$$c_0,{\hat{w}}^{\left(1_q\right)},w^{\left(2_q\right)}{\hat{w}}^{\left(2\right)},{\hat{w}}^{\left(3\right)},w^{\left(3\right)},{\hat{w}}^{\left(4\right)},{\hat{u}}_1^{\left(4\right)},w^{\left(4\right)},{\hat{u}}_2^{\left(5\right)},$$

$$\text{and}{w}^{\left(5\right)}\text{are free}$$

$${\hat{w}}^{\left(1_z\right)},v_1^{\left(1\right)},w^{\left(2_z\right)},u_1^{\left(2\right)},v_2^{\left(2\right)},u_2^{\left(3\right)},u_3^{\left(4\right)},v_3^{\left(4\right)},u_4^{\left(5\right)},v_4^{\left(5\right)}⩾\varepsilon .$$

4. Case study

The application of the network DEA models is further detailed here. Section 4.1 describes the gathering and processing of data, Section 4.2 explains additional details of the models, and Section 4.3 discusses the main findings of their implementation. Section 4.4 mentions some policy implications from the key benchmarks.

4.1. Data and sample

With an OECD-focus, due to issues with data availability from other nations, fifty-five countries were selected as DMUs, including:

• –The organisation’s thirty-seven member countries;
• –Six prospective members (Argentina, Brazil, Bulgaria, Croatia, Peru, and Romania); and
• –Four key partners (China, India, Indonesia, and South Africa).

Eight other countries were added to the set, given their relevance in a wider scope, ensuring a comprehensive and reliable representation of worldwide responses: Algeria, Egypt, Morocco, Russia, Thailand, Tunisia, Ukraine, and Vietnam.

Moreover, the key fundamental statistics of the ten available indicators for the sample at the end of 2020 are exhibited in Table 3. Note that there is considerable variability among all indicators, derived from the distinct scale size of each country. For instance, nations like Iceland and New Zealand typically have the minimum values of the sample, while countries like China and India have the maximum values of the sample.

Table 3.

Descriptive statistics of the available indicators.

Indicators	Average	Standard deviation	Minimum	Maximum
$x_{1j}$ (M€)	123,447	415,134	1,764	3,017,112
$x_{2j}$ (€)	2,600,849,323	4,974,551,976	11,635,269	2,9036,229,752
$x_{3j}$ (€)	234,017,589	395,991,994	13,316,280	2,505,707,645
$x_{4j}$ (€)	477,753,640	773,360,577	9,225,565	4,975,291,796
$z_j^{(1,2)}$	64,463,704	165,860,132	192,889	897,002,850
$q_j^{(1,2)}$	33,376,536	101,392,442	119,435	590,122,748
$q_j^{(2,3)}$	296,877	1,117,458	55	8,035,801
$q_j^{(3,4)}$	11,224	20,827	5	125,379
$q_j^{(4,5)}$	1,726	4,125	1	29,179
$y_{1j}$	96,495,080	264,351,979	335,489	1,439,236,705
$y_{2j}$	285,653	1,100,397	50	7,910,422

4.2. Software

The methodology presented here was implemented using MATLAB version R2020a software alongside IBM ILOG CPLEX Optimisation Studio version 12.8.

4.3. Results and discussion

Here, results are presented and discussed in line with the two perspectives derived from the modelling stage: Section 4.3.1 addresses the Social perspective and Section 4.3.2 the Financial perspective. Section 4.3.3 summarises the main findings from both perspectives.

4.3.1. Social perspective : produce the largest amount of output for the same amount of input

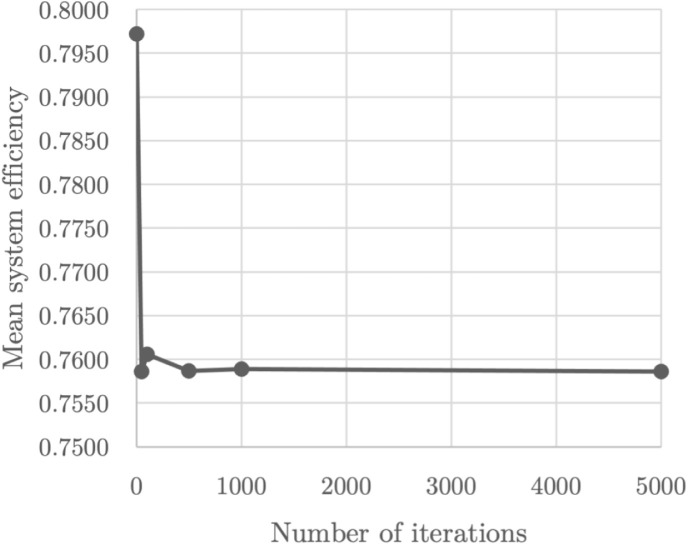
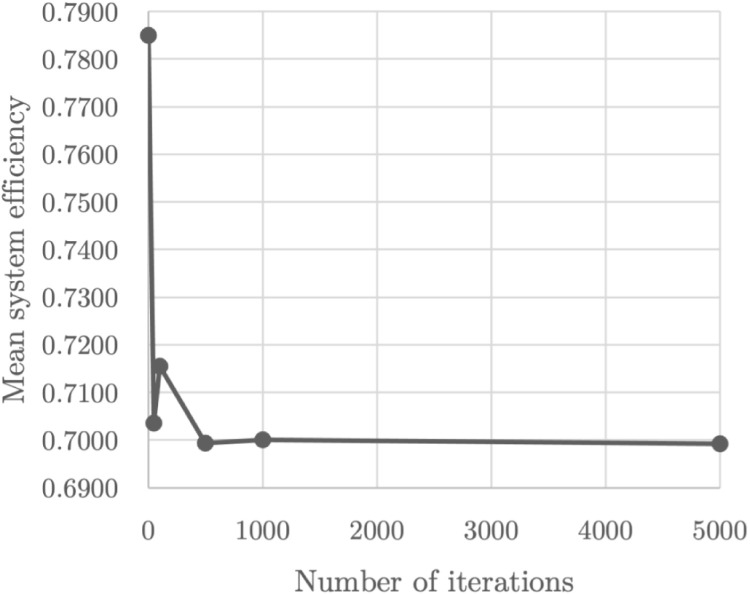
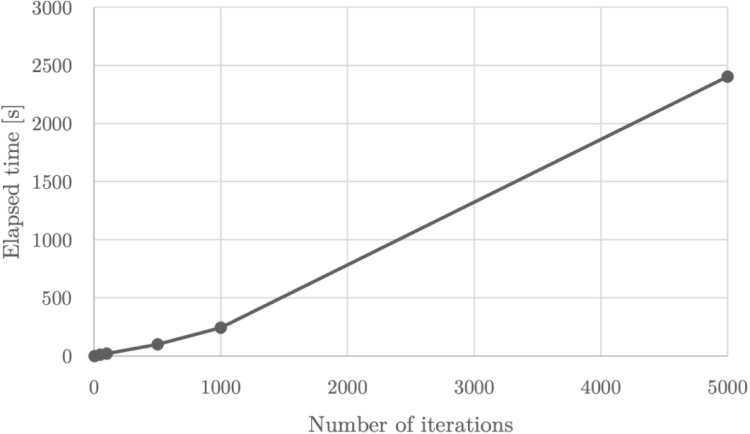
First, it is vital to establish the number of iterations of the Monte Carlo simulation in order to smooth out the effect of any potential outliers — one of DEA’s weaknesses. In the literature, only (Pereira, Ferreira et al., 2021) use this method to generate the sampling distribution for the simulated values of some indicators of a network DEA model. However, unlike these authors, we intended to generate the simulated values of a few outputs rather than the intermediate products. For this reason, we found that 1,000 iterations were the minimum threshold of stabilisation instead of 5,000. In fact, we ran our model for 1, 50, 100, 500, 1,000, and 5,000 iterations using a 2.7 GHz Quad-Core Intel Core i7 processor, but the mean system efficiency remained at a relatively stable value from 1,000 iterations onwards (see Fig. 2) at the expense of the considerable growth in computational complexity (see Fig. 3).

Fig. 2.

Global mean system efficiency as a function of the number of iterations of the Monte Carlo simulation for the Social perspective.

Fig. 3.

Elapsed model solving time as a function of the number of iterations of the Monte Carlo simulation for the Social perspective.

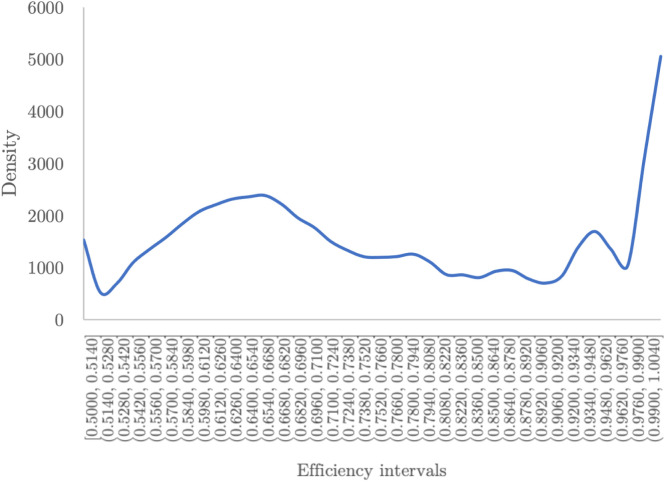
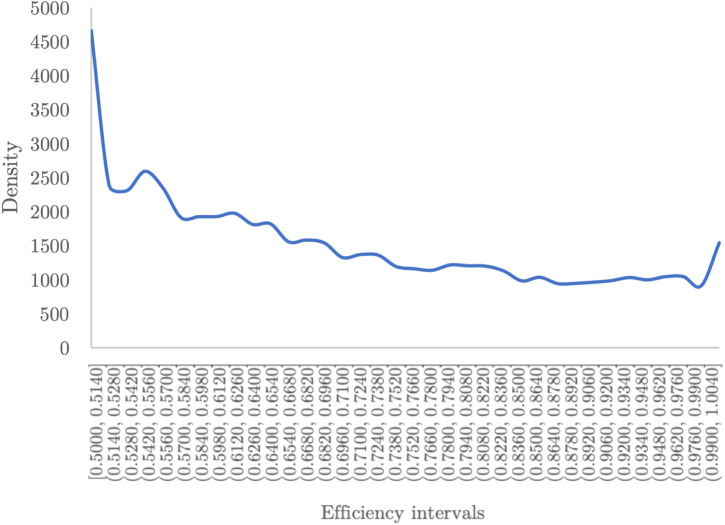
Second, with the number of iterations ascertained, the probability distribution of the global system efficiency was plotted (see Fig. 4). There is a clear peak for relatively high efficiencies. However, there is also a substantial share of countries exhibiting less-than-average performance against COVID-19.

Fig. 4.

Probability distribution of global efficiency after 1000 iterations for the Social perspective.

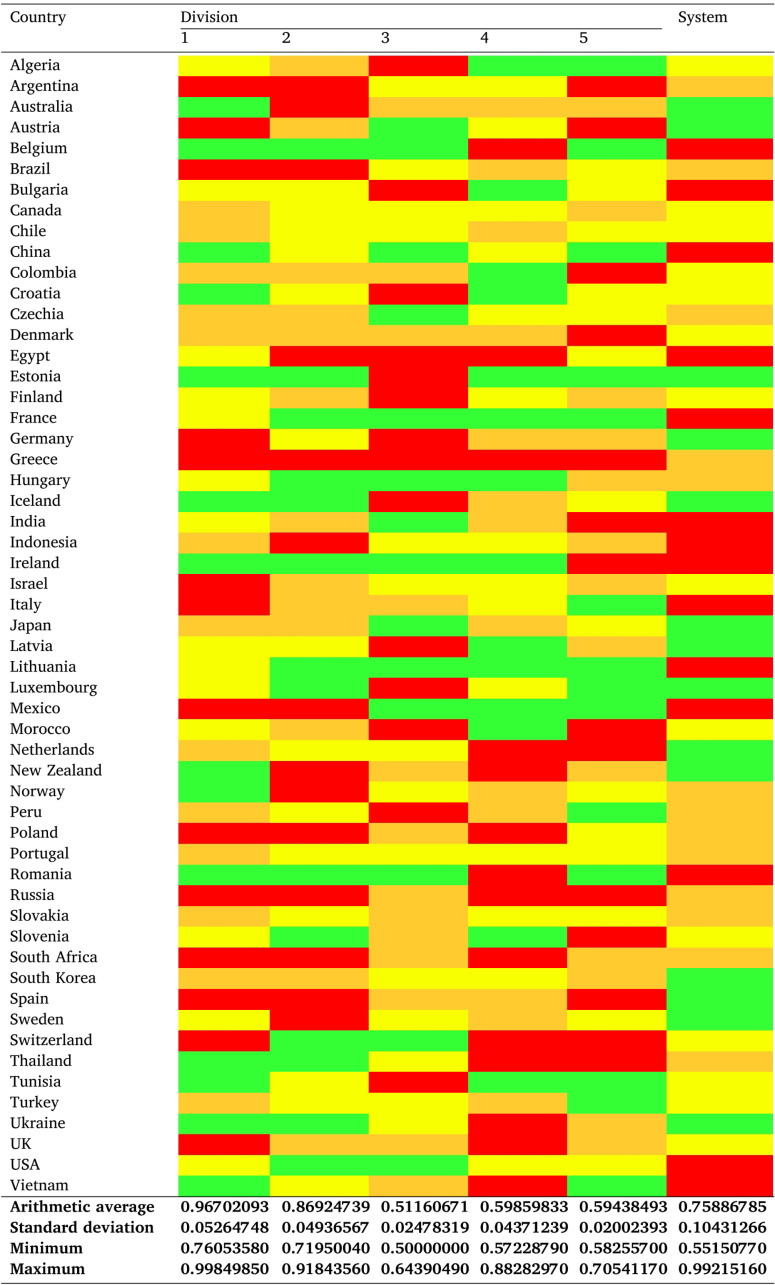
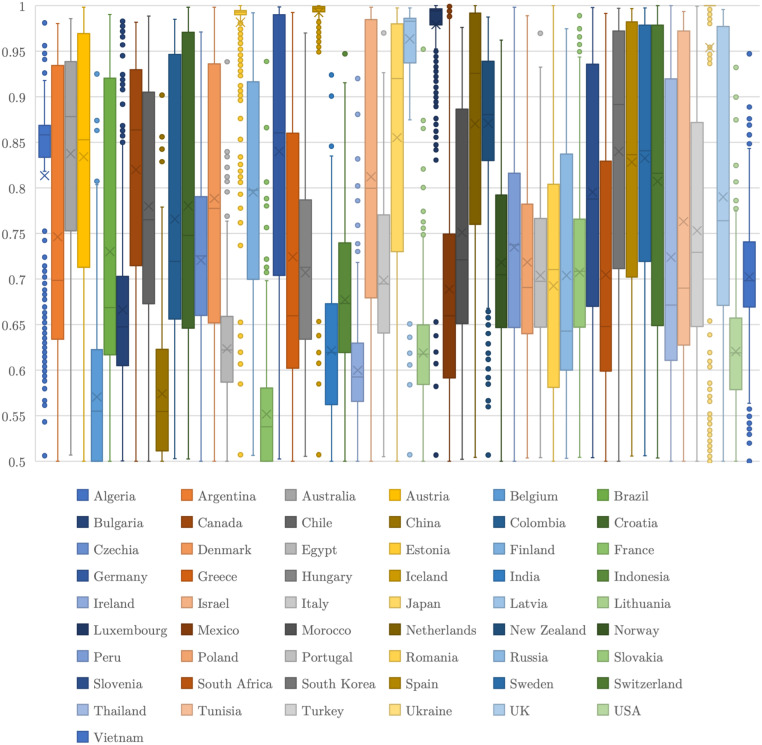
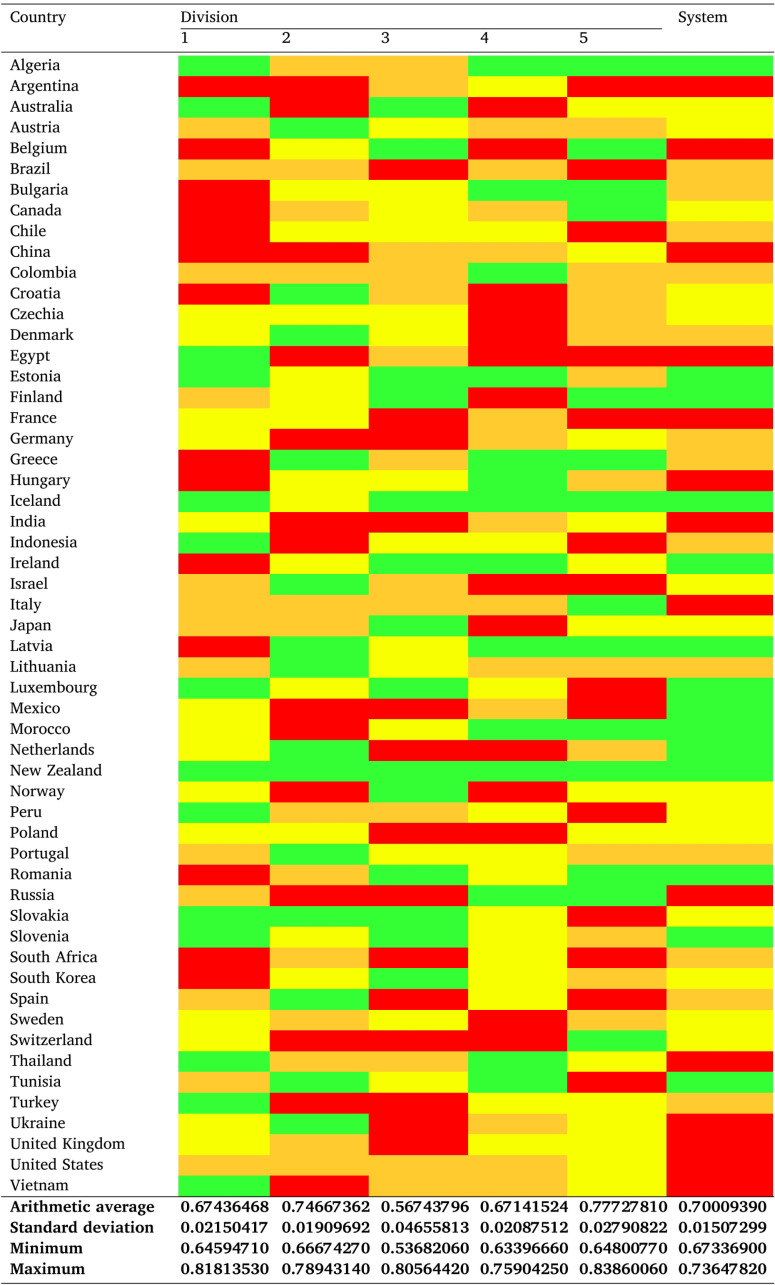
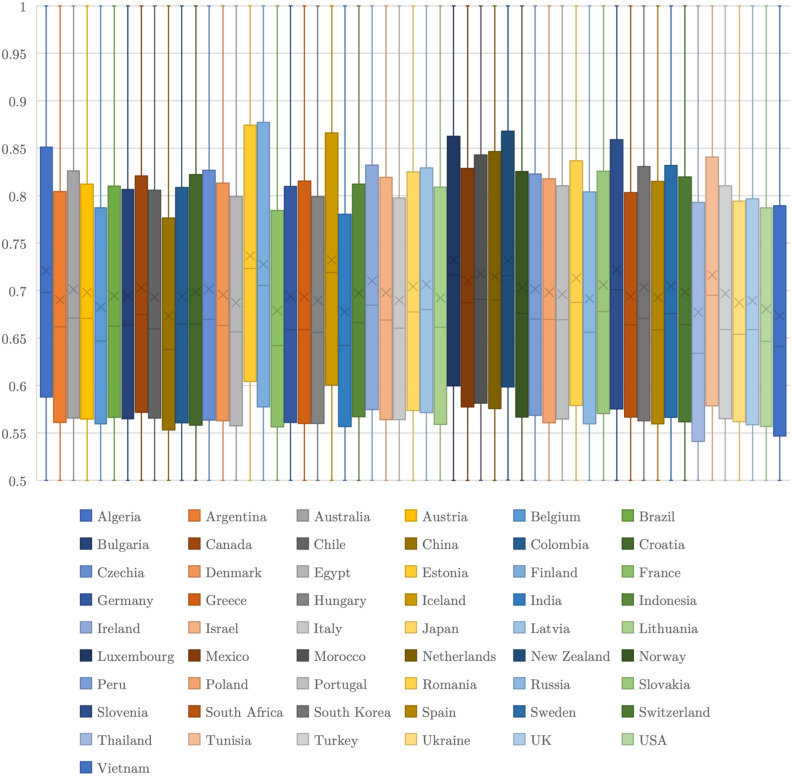
Finally, considering the number of DMUs and iterations, it is more useful to look at the key mean results of the Social perspective using Table 4, even with the box plots per country depicting their respective system efficiency set (see Fig. 5). Note that averagely inefficient DMUs belong to Q1,6 Q2, Q3, or Q4 and are portrayed in green, yellow, orange, or red colour, respectively, since averagely efficient DMUs are nonexistent.

Table 4.

Mean system efficiency and corresponding descriptive statistics for the Social perspective.

Fig. 5.

Box plots of all system efficiencies per country for the Social perspective.

There is no doubt that none of the assessed fifty-five DMUs is systemically efficient on average. Still, Australia, Austria, Estonia, Germany, Iceland, Japan, Latvia, Luxembourg, the Netherlands, New Zealand, South Korea, Spain, Sweden, and Ukraine (approximately 25% of the sample) are positioned in Q1, generating the largest amount of COVID-19 recoveries and the least amount of COVID-19 deaths while consuming the same amounts of resources. Note that all of these nations are considered to be developed economies, apart from Ukraine’s economy in transition and South Korea’s developing economy (United Nations, 2020). On the opposite end, we find Belgium, Bulgaria, China, Egypt, France, India, Indonesia, Ireland, Italy, Lithuania, Mexico, Romania, the USA, and Vietnam as the nations with Q4 performances, i.e., the worst performers regarding an increase in COVID-19 recoveries and a decrease in COVID-19 deaths for the same amount of inputs. These are either developed or developing economies (United Nations, 2020).

Similarly to system efficiency, a division-by-division analysis is unable to identify a single country as averagely efficient. On the one hand, Belgium, Estonia, France, Ireland, and Lithuania are the nations that have the most Q1 performances per division, even though Estonia is in Q1 and the other four countries are in Q4 in terms of mean system efficiency. On the other hand, twenty-one countries have no Q1 performances in any division, with Germany, the Netherlands, South Korea, Spain, and Sweden performing at a Q1 level regarding the mean system efficiency. This can be explained by the way that the partial and global efficiencies are computed — unlike the equations for divisionwise efficiencies, which take into account the intermediate products, Eq. (14) only considers inputs and outputs. In the end, the Population division is the one in which all nations have a higher mean partial efficiency, followed by Contagion and Hospitalisation. ICU admission and then Triage are the divisions with the lowest mean partial efficiency scores.

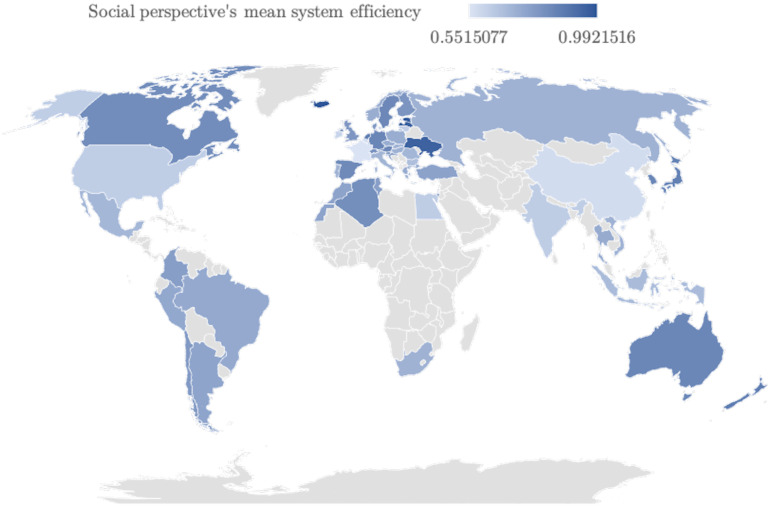
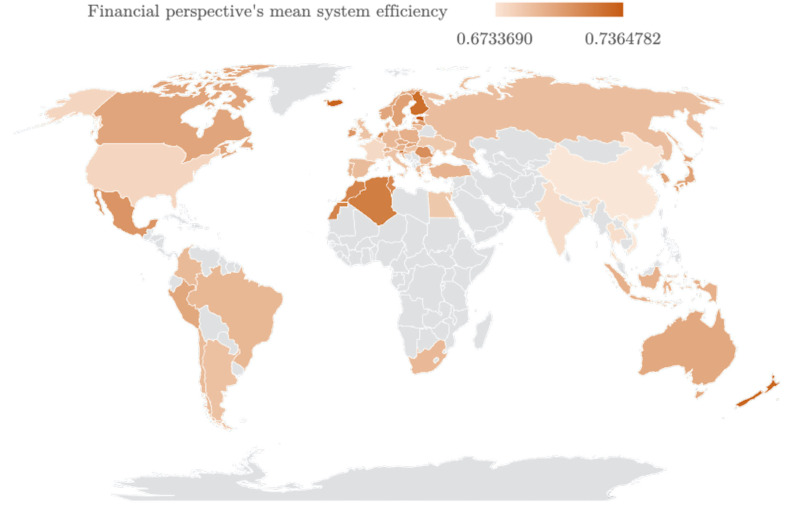
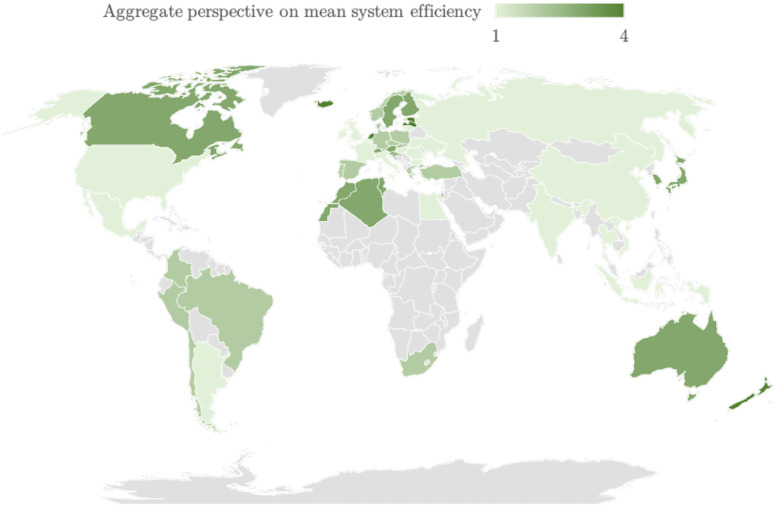
Additionally, the mean system efficiency results can be shown geographically in Fig. 6. Bear in mind that a gradient blue colour scheme was employed (the countries that were not included in the sample are exhibited in light grey colour).

Fig. 6.

Geographical dispersion of the assessed nations in terms of their mean system efficiency in the fight against SARS-CoV-2 on 31/12/2020 for the Social perspective.

Finally, despite the absence of averagely efficient countries systemwise, there is a trend for European countries to perform in Q1, namely Central European ones (Ukraine may be an outlier, but, given the current crisis that the country is undergoing,7 the country is being able to do more with the resources it has). Island nations also seem to have higher efficiencies, among which Australia, Iceland, Japan, and New Zealand are the prominent cases. Moreover, the majority of the larger countries in the world (either by area or by population) appear to have lower mean system efficiencies, such as Argentina, Brazil, China, India, Indonesia, Mexico, Russia, and the USA, given their performances in Q3 or Q4. In fact, to investigate the connection between the efficiencies of the Social perspective and the area and population of a country, we have conducted two Mann–Whitney $U$ tests using MATLAB’s ranksum function, as in Pereira, Camanho et al. (2021), where:

• –The null hypothesis declares that countries with small and large areas have the same distribution for the efficiencies of the Social perspective and the alternative hypothesis declares that countries with small and large areas have different distributions for the efficiencies of the Social perspective, for the former; and
• –The null hypothesis declares that countries with small and large populations have the same distribution for the efficiencies of the Social perspective and the alternative hypothesis declares that countries with small and large populations have different distributions for the efficiencies of the Social perspective, for the latter;

Since the tests were conducted assuming a 5% significance level, the null hypotheses are rejected for a $p$-value lower than 0.05 and not rejected otherwise. Additionally, we establish that: countries with a small area have an area below the average of the sample, and countries with a large area have an area above the average of the sample; and countries with a small population have a population below the average of the sample, and countries with a large population have a population above the average of the sample. This means that 11 DMUs have large areas and 9 DMUs have large populations. Summarily, given the $p$-values of 0.1075 and 0.0075, the first null hypothesis cannot be rejected and the second is rejected. These results suggest an asymmetric response in fighting COVID-19 pandemic outbreaks between countries with a relatively small population and countries with a relatively large population.

4.3.2. Financial perspective : produce the same amount of output using the least amount of input

First, ascertaining the number of iterations of the Monte Carlo simulation is important yet again in the interest of freeing the model of the effect of any possible outliers. Similarly to the previous perspective, 1,000 iterations were the minimum threshold of stabilisation after running the model for 1, 50, 100, 500, 1,000, and 5,000 iterations using the same processor (see Fig. 7). The computational complexity of the model is displayed in Fig. 8.

Fig. 7.

Global mean system efficiency as a function of the number of iterations of the Monte Carlo simulation for the Financial perspective.

Fig. 8.

Elapsed model solving time as a function of the number of iterations of the Monte Carlo simulation for the Financial perspective.

Second, once again, the probability distribution of the mean system efficiency was drawn, as shown in Fig. 9. The increase in lower efficiencies is immediately apparent.

Fig. 9.

Probability distribution of global efficiency after 1000 iterations for the Financial perspective.

Finally, Table 5 presents the key mean results of the Financial perspective, again with box plots per country denoting their respective system efficiency set (see Fig. 10). The colour scheme of Table 4 applies.

Table 5.

Mean system efficiency and corresponding descriptive statistics for the Financial perspective.

Fig. 10.

Box plots of all system efficiencies per country for the Financial perspective.

Once more, no DMU was deemed as averagely system efficient. Nonetheless, Algeria, Estonia, Finland, Iceland, Ireland, Latvia, Luxembourg, Mexico, Morocco, the Netherlands, New Zealand, Romania, Slovenia, and Tunisia are in Q1 in a way that sees them using the least amount of financial resources to produce the same amount of COVID-19 recoveries and deaths, when compared with other peers. On the contrary, Argentina, Belgium, China, Egypt, France, Hungary, India, Italy, Russia, Thailand, Ukraine, the UK, the USA, and Vietnam comprise the set of DMUs in Q4, being unable to use lower amounts of financial resources to generate the same amount of COVID-19 recoveries and deaths. This time, both sets contain a mix between developed economies, economies in transition, and developing economies (United Nations, 2020).

Regarding partial efficiencies, no nations are averagely efficient. On the one hand, New Zealand is the only nation with Q1 performances across all divisions, followed immediately by Iceland with four partial efficiencies in Q1. On the other hand, fourteen countries have no Q1 performances in any division, with Mexico performing at a Q1 level regarding the mean system efficiency. Ultimately, ICU admission and Contagion are the divisions in which all nations have higher mean partial efficiencies, succeeded by Population and Hospitalisation. Triage is the division with the lowest mean partial efficiency scores. This division was also the one with the poorest performance worldwide according to the Social Perspective, which seems to suggest that not only many countries have faced difficulties controlling the disease’s spread, increasing the number of infected citizens (upstream), but also that many of those infections developed into more severe cases, demanding more hospital admissions (downstream). From those inpatients, in general, there are not many requiring ICU admission, helping to justify a fair efficiency of this later stage according to the Financial Perspective. However, recalling the efficiency results of the Social Perspective, this stage was among the worst divisions, which can result from a high level of mortality of critically ill inpatients due to COVID-19.

Moreover, the geographical point of view of the results regarding the mean system efficiency can be seen in Fig. 11. Note that a gradient orange colour scheme was employed (the countries that were not included in the sample are exhibited in light grey colour). Performances at the Q1 level are mostly located in Europe and Northern Africa. Indeed, Algeria, Morocco, and Tunisia are developing economies that are more efficient in reducing the costs to obtain the same results rather than producing more from the same resources in the fight against the COVID-19 pandemic. The same happens with Mexico. Additionally, many of the larger countries in the world by area and/or by population exhibit lower mean system efficiencies, such as Argentina, China, India, Russia, and the USA. Note that many countries performing at a Q4 level are also located in Europe, with developed economies like Belgium, France, Italy, and the UK as the most worrying cases. As a matter of fact, to explore the link between the efficiencies of the Financial perspective and the area and population of a country, we have conducted two Mann–Whitney $U$ tests under the same conditions as the previous perspective. Essentially, given the $p$-values of 0.2429 and 0.0575, both null hypotheses cannot be rejected.

Fig. 11.

Geographical dispersion of the assessed nations in terms of their mean system efficiency in the fight against SARS-CoV-2 on of 31/12/2020 for the Financial perspective.

4.3.3. Summary

An all-encompassing look at the results of both perspectives can be achieved by means of a map that follows the reasoning implicit in Table 6. Indeed, Fig. 12 presents the mean system efficiency of the sample using a gradient green colour scheme, bearing in mind their positioning according to the quartiles in both perspectives, where a higher score is given to the higher combination of quartiles and vice versa. For example, by looking at Table 4, Table 5, we can see that Czechia has a mean system efficiency in Q3 according to the Social perspective and Q2 according to the Financial perspective; following Table 6, this means that the nation’s aggregate system efficiency is equal to 2 (essentially, it implies that Czechia’s aggregate system efficiency is in Q2).

Table 6.

Scoring logic behind Fig. 12.

Social perspective\Financial perspective	Q1	Q2	Q3	Q4
Q1	4	3	2	1
Q2	3	3	2	1
Q3	2	2	2	1
Q4	1	1	1	1

Fig. 12.

Geographical dispersion of the assessed nations in terms of their mean system efficiency in the fight against SARS-CoV-2 on of 31/12/2020 for the aggregate perspective.

Interestingly, even though there are no averagely systemically efficient DMUs, six nations perform at a Q1 level: Estonia, Iceland, Latvia, Luxembourg, the Netherlands, and New Zealand. They are followed by Algeria, Australia, Austria, Canada, Croatia, Finland, Israel, Japan, Morocco, Slovenia, South Korea, Sweden, Switzerland, and Tunisia. Nevertheless, 36% of the countries are in Q4 from the aggregate perspective.

To survey the relationship between the scores of the aggregate perspective and the area, population, type of economy, and type of health system of a country, we have conducted four Mann–Whitney $U$ tests following the assumptions set for each perspective. In the end, the only statistically significant $p$-value (0.0105) implied that the second null hypothesis was rejected, suggesting only an asymmetric response in fighting COVID-19 pandemic outbreaks between countries with a relatively small population and countries with a relatively large population, regardless of the point of view.

From another perspective, the bivariate correlation between the efficiencies of the Social perspective and the efficiencies of the Financial perspective indicates that both variables move in the same direction, i.e., when one increases, the other increases, and vice versa. This is due to the positive value of Pearson’s correlation coefficient ($r\left(53\right)=0.615,p<0.001$), which denotes a statistically significant moderate correlation. Additionally, since each country faces different resource and environmental conditions, it is also important to understand the relationship and the impact of the aggregate system efficiency scores and those contextual factors. For this reason, we have conducted a bivariate correlation and a truncated double bootstrap regression analysis — to avoid the finite sample bias, following (Simar & Wilson, 2007) - based on eleven key variables. They contemplate health expenditure per capita, GDP per capita, population density, the percentage of the population that uses PPE, the percentage of the infected population, the percentage of the infected population that needs hospitalisation, the percentage of the hospitalised population that needs treatment in the ICU, the Human Development Index (HDI) and its components (namely life expectancy at birth, expected years of schooling, and mean years of schooling), and are commonly used in the literature (see, e.g., Pereira and Marques, 2021, Pereira and Marques, 2022a). Given the presence of outliers and heteroscedasticity in the sample, the dependent variables of the truncated double bootstrap regression were replaced using a log transformation (see, e.g., Pereira & Marques, 2022b). First, the bivariate correlation analysis denoted statistically significant results in terms of the GDP per capita ($r\left(53\right)=0.389,p=0.003$), the percentage of the population that uses PPE ($r\left(53\right)=-0.305,p=0.024$), the percentage of the infected population ($r\left(53\right)=-0.301,p=0.026$), and the HDI and all its components ($r\left(53\right)=0.368,p=0.006$, $r\left(53\right)=0.421,p=0.001$, $r\left(53\right)=0.313,p=0.020$, and $r\left(53\right)=0.303,p=0.025$, respectively). All these correlations are either low positive or negative, with the GDP per capita and the HDI and its components moving in the same direction of the aggregate system efficiency and the percentage of the population that uses PPE and the percentage of the infected population moving in an opposite direction regarding the aggregate system efficiency. Second, the truncated double bootstrap regression analysis returned bias-adjusted coefficients within the 95% bootstrap confidence interval, on account of the log transformation, as shown in Table 7. Bear in mind that, due to the possible existence of collinearity or the return of a local optimum, we have simplified the truncated double bootstrap regression by removing the variables that did not show a statistically significant bivariate correlation with the global efficiency. In essence, GDP per capita, the percentage of the infected population, and life expectancy at birth are statistically significant predictors of nations’ efficiency in the fight against SARS-CoV-2, unlike the remaining variables that showed no statistically significant results. These statistically significant predictors had already displayed statistically significant correlations. Ultimately, this implies that governments need to seriously consider the use of PPE and the implementation of measures to avoid population infections (such as testing-and-tracing systems and lockdowns) as the main drivers of their health system’s efficiency in the fight against COVID-19, without jeopardising their respective economic output in order to pursue human development.

Table 7.

Results of the truncated double bootstrap regression.

Variable	Bias-adjusted coefficient	95% bootstrap confidence interval
		Lower bound	Upper bound
GDP per capita	1.17⁎	0.18	2.37
Percentage of the population that uses PPE	0.05	−0.02	0.11
Percentage of the infected population	−4.77⁎	−7.76	−1.02
HDI	−0.19	−1.41	0.91
Life expectancy at birth	0.01⁎	0.00	0.02
Expected years of schooling	0.01	−0.01	0.02
Mean years of schooling	0.01	−0.01	0.03

^*Significance at the 5% level.

Besides, bridging our results with the prospects presented in Section 1, Austria and Switzerland have indeed been identified as having relatively successful COVID-19 national strategies, with Germany showing a slightly lower mean system efficiency from the aggregate perspective (Desson, Lambertz et al., 2020). However, Southern European countries like Portugal, Spain, and Italy have some of the lowest mean system efficiency scores, emerging from the aggregate perspective with scores of 1 or 2, which confirms the major impact that the pandemic has had on their health systems (Moros et al., 2021, Sanfelici, 2020). As for the Anglo-Saxon nations, both the UK and the USA are found at the bottom of the ranking, something that is in line with the fact that they are two of the most affected countries by the SARS-CoV-2 crisis (Gurdasani et al., 2020).

At last, some notes on other noticeable cases must be provided. On the one hand, Iceland and New Zealand present high mean efficiencies and constant Q1 performances, which are in line with the literature (Fouda et al., 2020). Northern African nations also present high performances, particularly Q2 in the Social perspective and Q1 in the Financial perspective. Furthermore, Sweden, and the Swedish enigma (Claeson & Hanson, 2021), whose liberal COVID-19 national strategy has been heavily criticised, presents Q1 and Q2 performances in the Social perspective and the Financial perspective, respectively. On the other hand, the apparent Chinese success (He et al., 2020) is not evident in this study, with the country performing at a Q4 level in both perspectives.

4.4. Policy implications

Among the six countries with a score of 4 in the aggregate perspective, we must address the national COVID-19 strategies according to three pairings: Baltic Republics (Estonia and Latvia), Low Lands (Luxembourg and the Netherlands), and Islands (Iceland and New Zealand). Note that these countries have distinct populations, cultures, and governance structures, which influence not only policy-making, but also policy implementation.

First, the reasons behind the success of Baltic Republics in fighting against SARS-CoV-2 reside in8 :

• –The rapid response in declaring a state of emergency one day after the WHO’s announcement of COVID-19 reaching pandemic proportions;
• –The adaptation to a “new normal” through reasonable and achievable solutions to constantly emerging problems. For instance, Latvia resorted to its Ministry of Defence’s State Central Reserve Procurement Group to take advantage of the entity’s experience in large-scale procurement to solve the issue concerning the lack of funding for PPE for health professionals;
• –The effort to counteract misinformation and disinformation via enormous information campaigns and additional funding to journalists and accurate pandemic reports, as well as to provide free of charge communication between their populations and medical experts regarding mental health;
• –The enforcement of physical-distancing requirements and the enablement of alternative ways to continue daily activities, such as the closure of supermarkets and the implementation of distance-learning at schools and universities before the majority of other countries; massive population testing was also adopted.

Second, the Low Lands’ success is due to:

• –The Netherlands’ decentralised “intelligent lockdowns” that alleviated the pressure on the health system and the lessons learned from experience9 ;
• –Luxembourg’s massive testing regime and testing-and-tracing system.10

Third, despite their differences, the Islands succeeded in the war on COVID-19 because of11 :

• –Iceland’s COVID-19 mitigation strategy aimed at preventing the overwhelmment of the health system, given the easy access to COVID-19 testing and mass screening;
• –New Zealand’s COVID-19 elimination strategy with a nationwide shutdown after the appearance of the first community transmission and consequent implementation of managed quarantine facilities and strict border controls;
• –Both countries use of contact-tracing and isolation systems, as well as science-based decision-making and informed communication with the population.

In essence, these three pairings of countries have had different approaches in fighting the threat posed by SARS-CoV-2, namely the rapid, practical, and informed measures of the Baltic Republics, the liberal standpoint of the Low Lands, and the contact-tracing and well-founded decision-making of the Islands. Bottom line, although the six aforementioned countries are relatively small and two are isolated, it is clear that science-based decision-making for the sake of the early adoption of physical-distancing measures, national shutdowns, and, if possible, systems of testing-and-tracing, alongside a transparent and intelligible communication with the population, are fundamental for their success and partially explains the collapse of other countries. Note that these results are in line with the statistically significant findings obtained in Section 4.3.3. Further research on this topic is encouraged, as it could be paramount for future national COVID-19 strategy reforms towards proper management of the pandemic.

5. Conclusion

The general series structure network DEA models with simulation devised in this paper were applied to the estimation of nations’ efficiency in the fight against SARS-CoV-2. Indeed, those efficiencies were analysed under two perspectives: one that concerns the production of the largest amount of output for the same amount of input and the other the production of the same amount of output using the least amount of input. Ultimately, the results were valid and credible, in the sense that they were capable of answering the research question and they rely on sound data and methods, respectively.

According to our approach, Estonia, Iceland, Latvia, Luxembourg, the Netherlands, and New Zealand present the higher mean system efficiency scores, performing at the Q1 level. They are followed by Algeria, Australia, Austria, Canada, Croatia, Finland, Israel, Japan, Morocco, Slovenia, South Korea, Sweden, Switzerland, and Tunisia. Nevertheless, 36% of the countries perform at Q4 from the aggregate perspective. Besides, it is statistically significant that countries with a large population have worse mean efficiency scores, which may derive from more complex national COVID-19 strategies, regarding planning and execution. There is no apparent relation between better or worse mean efficiency scores in terms of developed economies, economies in transition, or developing economies for the Social perspective or the Financial perspective; as a whole, the fifty-five assessed nations are less efficient from the Financial perspective. Moreover, there is also no apparent relation between better or worse mean efficiency scores regarding the different types of health systems. However, there are statistically significant low positive correlations between the aggregate system efficiency and the GDP per capita and the HDI and its components, and low negative correlations between the aggregate system efficiency and the percentage of the population that uses PPE and the percentage of the infected population. These variables were also found to be statistically significant predictors of nations’ efficiency in the fight against SARS-CoV-2 via a truncated double bootstrap regression.

In terms of limitations, the absence of credible data concerning some outputs leads to their estimation via the Monte Carlo method. Although we were able to find an acceptable solution with a minimum stabilisation threshold for the number of iterations from which the mean system efficiency remains constant, even taking into account computational complexity, using the actual data would be preferable. The same issue resulted in the selection of 55 countries as the DMUs, thus preventing a more comprehensive analysis. Furthermore, including migratory data in terms of flows and restrictions would have been an interesting feature, but difficult to incorporate in this context, especially due to data constraints. Finally, there is no doubt that the 55 considered nations are not entirely homogeneous, as one can expect from countries found across all continents. However, they are homogeneous regarding a common goal — mitigating the effect of SARS-CoV-2. Therefore, despite not all of them adopting the same specific COVID-19 mitigation policies, they all shared the implementation of, e.g., lockdowns, social distancing, and the mandatory use of PPE, to some degree. This assumption was on the foundation of our benchmarking exercise.

In the future, these results can be useful to understand how each country’s national COVID-19 strategy behaved in a worldwide scenario, in order to redesign public policy towards a certain benchmark. Moreover, the feedback of decision-making actors could be incorporated into the model to improve the network structure, the data set, and, possibly, the simulated values. At last, the use of a multiplicative model could overcome the “overcompensatory” nature of the additive model and would be an interesting prospect in terms of comparison of results.

CRediT authorship contribution statement

Miguel Alves Pereira: Conceptualisation, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing – original draft, Writing – review & editing, Visualisation. Duarte Caldeira Dinis: Conceptualisation, Validation, Investigation, Data curation, Writing – original draft, Writing – review & editing. Diogo Cunha Ferreira: Conceptualisation, Methodology, Validation, Resources, Writing – review & editing, Supervision, Project administration. José Rui Figueira: Validation, Resources, Writing – review & editing, Supervision, Project administration, Funding acquisition. Rui Cunha Marques: Validation, Resources, Writing – review & editing, Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.