Enhancing Cosinor Analysis of Circadian Phase Markers Using the Gamma Distribution

Abstract

The cosinor model, in which a cosine curve is fitted to periodic data within a regression model, is a frequently used method for describing patterns of cyclical activity such as circadian rhythms. For circadian variables of interest (e.g., melatonin and heart rate) that do not take on negative values, the assumption of normally distributed residuals required by the general linear model, which is most commonly used for cosinor analysis, may not be appropriate. Alternatively, a generalized linear model with the gamma distribution (GZLM-gamma) is specifically defined to accommodate non-negative outcomes. Herein, we demonstrate the improved fit and gains of efficiency in detection of circadian rhythm afforded by using the GZLM-gamma in cosinor models of heart rate, actigraphic activity, and urinary 6-sulfatoxymelatonin. Notably, this improved detection of circadian rhythm allows retention of additional patients for downstream analyses, further improving study power.

Introduction

The cosinor model, in which a cosine curve is fitted to periodic data within a regression model, is a commonly used method for describing cyclical variation. Recent examples in the sleep and circadian literature include the modelling of diurnal variation in urinary metabolites during normal and abnormal sleep (Giskeødegård et al., 2015), the impact of blue light on peak urinary 6-sulfatoxymelatonin (aMT6s) (Sletten et al., 2017), and evaluation of the association between heart rate and activity with variation in mood and bipolar disorder (Carr et al., 2018). In most studies using cosinor analysis, a general linear model (GLM) is employed. However, many outcome variables of interest are constrained to be non-negative. If such outcome variables are modeled with a GLM, residuals are frequently non-normally distributed, thereby violating an essential model assumption.

In non-cosinor models, a generalized linear model with gamma distribution (GZLM-gamma) is commonly used to model outcomes which are continuous and constrained to be positive. In our own work such outcomes include heart rate, actigraphic activity, and urinary 6-sulfatoxymelatonin (aMT6s). It is reasonable to expect that cosinor analysis of each of these circadian phase markers might benefit from the improved fit that the GZLM-gamma could provide versus the more commonly used GLM. A tangible advantage of such improved fit would be greater power to detect diurnal variation of circadian phase markers. Downstream analyses of fitted cosinor parameters is generally restricted to individuals who meet significance criteria vis a vis testing for diurnal variation; thus, increased power to detect diurnal variation might additionally increase power for subsequent stages of analysis. Circadian studies are resource intensive, implying that techniques which extract maximum information from modest sample sizes are extremely valuable.

To test our hypothesis that the GZLM-gamma will provide better fit than the GLM, we have modeled three 3 circadian phase markers: heart rate, actigraphic activity and urine aMT6s with both models. We describe herein the results of these analyses.

Methods

Data for these analyses come from three patient populations. In all analyses data for an individual patient were excluded if a period of longer than 6 hours existed during which no data was recorded.

Heart rate data in the form of beats per minute every 5 seconds was obtained during the first 24 hours of medical intensive care unit (MICU) admission from a cohort (n=56) of critically ill patients as previously described (Knauert et al., 2020) (HIC #1508016346). Heart rate values less than 10 beats per minute were considered device artifact and removed from the dataset (0.003% of all measures).

Actigraphic activity data in the form of activity counts per 30 seconds was obtained from a second cohort (n=32) of critically ill patients enrolled in an observational study March to June of 2011. This study included patients older than 18 years of age admitted to the MICU. Exclusion criteria included terminal illness, coma or deep sedation, and severe agitation. Recordings were initiated within 72 hours of MICU admission and continued for 24 hours (HIC #0709003048). Because the gamma distribution requires that outcomes be positive, 0 values found in 30 second actigraphy measurements were changed to 0.01 prior to analysis.

Finally, urine aMT6s data, sampled every 1-, 2- or 4-hours, was obtained from a cohort (n=18) of critically ill patients enrolled in a randomized controlled trial of daytime bright light from December 2018 to August 2021. This study included patients older than 50 years of age admitted to the MICU for less than 30 hours at the time of study initiation. We excluded patients with a high risk of pre-existing circadian disorders and paralyzed patients (HIC #2000023033).

Statistical Analysis

In the cosinor model, data of period X units of time is modeled as Y = M + A* cos (2πt/X−Φ) (1). In this equation, Y represents the modeled outcome in the units of the circadian variable of interest. M represents the mesor, Φ represents the acrophase, and A represents the curve amplitude (Halberg et al., 1967).

By applying the trigonometric identity cos(a−b) = cos(a)*cos(b) + sin(a)*sin(b), the series can instead be expressed as Y = M+ β1*cos(2π t/X) + β2*sin(2π t/X) (2), where β1= A cos(Φ) and β2= Asin(Φ). This transformation linearizes the model, facilitating its modeling by either GLM or GZLM-gamma (A. G. Barnett et al., 2012).

We fit both GLM and GZLM-gamma cosinor models to each patient’s data and output measures of goodness of fit. These measures included the Akaike Information Criteria both with (AICC) and without (AIC) correction for small sample sizes and the Bayesian Information Criteria (BIC). In addition, we output a bivariate test for the presence of significant circadian rhythm which we have defined per Barnett (A. A. Barnett et al., 2020) if the p-value from either β1 or β2 in equation 2 above was less than 0.05.

To assess the impact of data frequency on model fit, data for heart rate and actigraphy were also modeled using hourly averages to determine how reducing the total number of measurements for an individual impacted our results. All analyses were performed in SAS 9.4, using a previously published macro written to perform such analyses (Doyle et al., 2021).

Results

Analysis using GZLM-gamma (versus the GLM) improved the fit for a dominant majority of patients in the three circadian phase markers (Table 1). GZLM-gamma was especially beneficial in analysis of actigraphic activity every 30 seconds in which many observations sit at the lower bound of zero; 100% of these patients demonstrated better model fit under GZLM-gamma. Otherwise, the proportion of patients with better model fit under GZLM-gamma varied between 63 and 78%. Figure 1 illustrates an example of improved model fit for one patient’s hourly actigraphic activity counts. In addition, detection of rhythm was increased with GZLM-gamma for all circadian phase markers other than heart rate every 5 seconds, for which the GLM normal model already detected rhythm in 100% of patients.

Table 1:

Model fit and detection of diurnal variation in circadian phase markers

	Percentage of Patients with Improved Model Fit for Gamma Distribution			Percentage of Patients with Diurnal Variation Meeting Significance Criteria
Sample	AIC	AICC	BIC	GLM: Normal Distribution	GZLM: Gamma Distribution
Number of Patients
Heart rate every 5 sec	70%	70%	70%	100%	100%
N=56
Heart rate Hourly	63%	63%	63%	89%	91%
N=56
Actigraphy every 30 sec	100%	100%	100%	94%	100%
N=32
Actigraphy, Hourly	78%	78%	78%	44%	47%
N=32
Urinary aMT6s	78%	78%	78%	83%	89%
N=18

Abbreviations: AIC, Akaike Information Criteria without correction for small sample sizes; AICC, Akaike Information Criteria with correction for small sample sizes aMT6s, 6-sulfatoxymelatonin; BIC, Bayesian Information Criteria; sec, seconds; GLM, general linear model with normal distribution; GZLM, generalized linear model with gamma distribution.

Figure 1:

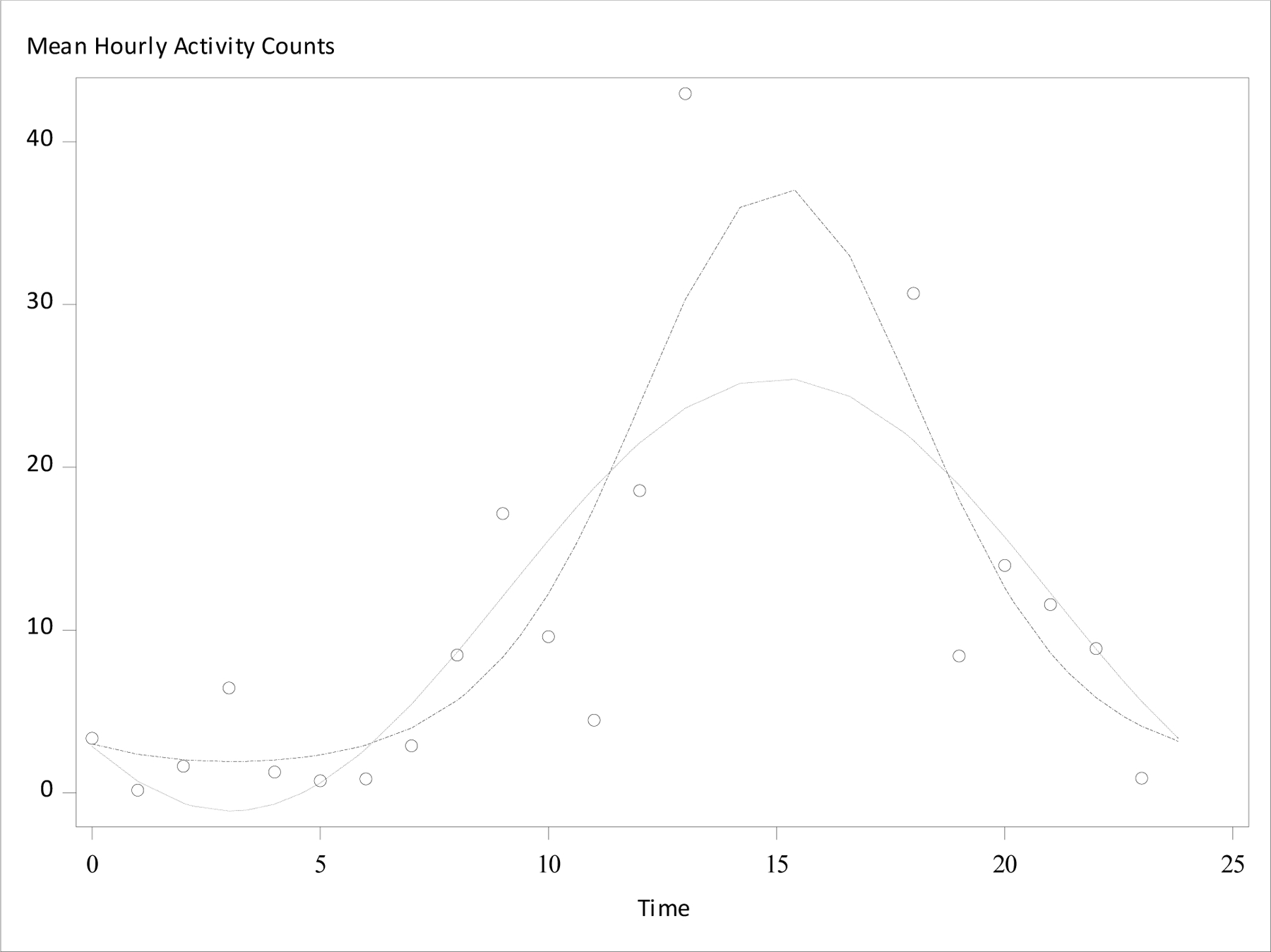
Graphical output of hourly actigraphy data and fitted cosinor models. Average hourly activity counts were modeled for a single patient. Dot-dot-dash line indicates fitted cosinor curve under a generalized linear model with gamma distribution (GZLM-gamma), dotted line indicated fitted cosinor curve under a general linear model (GLM). Open circles indicate observed average hourly activity count.

Discussion

Many outcome variables of interest in sleep and circadian research, such as the common circadian phase markers of heart rate, activity, and melatonin, can only take on non-negative values. We have demonstrated that use of GZLM-gamma resulted in improved fit in all three circadian phase markers analyzed. In addition, we found that the use of the GZLM-gamma improved efficiency of detection of circadian rhythm in all datasets where improvement was possible, thus increasing sample size for any downstream analyses restricted to patients with significant diurnal variation.

Though the GZLM-gamma is designed specifically for the modeling of outcomes which are continuously and positively distributed, most researchers employ GLM-based cosinor analyses. The novel GZLM-gamma technique represents an opportunity to improve analysis of circadian data. The GZLM-gamma may be particularly useful in describing diurnal variation in measures which normally include a high proportion of near-zero or zero values such as actigraphic activity, blood or salivary melatonin, or urine aMT6s. Circadian studies are highly challenging, requiring significant resources to oversee iterative, longitudinal sampling under tightly controlled patient conditions. Therefore, analytic techniques that minimize required sample size, optimize retention of data for subsequent analyses and that improve fit are critically important.

Some caveats should be noted. The acute care population is clinically atypical, and the results of our models in this population may not generalize to healthy or non-hospitalized patients. In addition, the sample sizes presented are small and from a single hospital, suggesting they may not be reflective of all intensive care unit patients.

Nevertheless, we believe that many users might benefit from adopting the GZLM-gamma as a means of improving fit and increasing the utility of cosinor model in circadian research.