Dynamic prediction of mortality in COVID-19 patients in the intensive care unit: A retrospective multi-center cohort study

Abstract

Background

The COVID-19 pandemic continues to overwhelm intensive care units (ICUs) worldwide, and improved prediction of mortality among COVID-19 patients could assist decision making in the ICU setting. In this work, we report on the development and validation of a dynamic mortality model specifically for critically ill COVID-19 patients and discuss its potential utility in the ICU.

Methods

We collected electronic medical record (EMR) data from 3222 ICU admissions with a COVID-19 infection from 25 different ICUs in the Netherlands. We extracted daily observations of each patient and fitted both a linear (logistic regression) and non-linear (random forest) model to predict mortality within 24 h from the moment of prediction. Isotonic regression was used to re-calibrate the predictions of the fitted models. We evaluated the models in a leave-one-ICU-out (LOIO) cross-validation procedure.

Results

The logistic regression and random forest model yielded an area under the receiver operating characteristic curve of 0.87 [0.85; 0.88] and 0.86 [0.84; 0.88], respectively. The recalibrated model predictions showed a calibration intercept of −0.04 [−0.12; 0.04] and slope of 0.90 [0.85; 0.95] for logistic regression model and a calibration intercept of −0.19 [−0.27; −0.10] and slope of 0.89 [0.84; 0.94] for the random forest model.

Discussion

We presented a model for dynamic mortality prediction, specifically for critically ill COVID-19 patients, which predicts near-term mortality rather than in-ICU mortality. The potential clinical utility of dynamic mortality models such as benchmarking, improving resource allocation and informing family members, as well as the development of models with more causal structure, should be topics for future research.

1. Introduction

The COVID-19 pandemic has put a lot of pressure on intensive care units (ICUs) worldwide. Risk stratification of critically ill COVID-19 patients would be of value in decision making in the ICU setting. Well-known scoring systems like APACHE II [1] and SAPS II [2] provide static predictions for hospital mortality among the general ICU population based on measurements obtained during the first 24 h of admission in the ICU. These static prediction models leave events unconsidered that occur later during ICU admission and potentially influence the prognosis. In contrast, a dynamic mortality model (i.e. one that enables repeated mortality predictions throughout the ICU stay) enables predictions based on all information available up to the moment of prediction. Recent works [[3], [4], [5]] have shown that dynamic mortality prediction for ICU patients is feasible. However, these models were developed for the general ICU population. Given the heterogeneity of this patient group, model prediction may benefit from focusing on specific patient’s subgroups. Several mortality models specifically for COVID-19 patients have also been developed e.g. for mortality predictions at ICU admission [6], mortality predictions on day 1, 7 and 14 after ICU admission [7] and dynamic mortality predictions throughout the whole hospitalization [8]. In contrast, we present a dynamic mortality model specifically for COVID-19 patients admitted to the ICU. Moreover, most developed mortality models use relatively long prediction horizons, i.e. to predict ‘long-term’ mortality. Such models tend to identify patients who are generally more likely to die after ICU admission. Instead, we present a model that predicts the patient’s mortality within 24 h from the moment of prediction, i.e. ‘near-term mortality’. This can offer a more precise patient prognosis and is less dependent on a patient’s prior risk of not surviving ICU admission (e.g. due to high age). To compare near-term and long-term mortality predictions in our setting, we also carried out long-term mortality modeling based on the same data and model development procedure.

In this work, we report on the development and validation of a dynamic mortality model, specifically for critically ill COVID-19 patients, and discuss its potential utility in the ICU.

2. Methods

2.1. Data sources

We used data from the Dutch Data Warehouse (DDW) [9,10] which contains data from 25 ICUs of collaborating academic, general or teaching hospitals in the Netherlands, collected between February 2020 and March 2021. This database is available to researchers upon request within ethical and legal boundaries. Included patients had proven or a high clinical suspicion of COVID-19 (defined as: positive real-time reverse-transcriptase polymerase chain reaction assay or a COVID-19 Reporting and Data System [11] score and clinical suspicion with no obvious other cause of respiratory distress). We extracted demographic information, vital signs, laboratory test results and blood gasses. High frequency measurements were down-sampled by taking one value every 30 min. For each patient admission, we collected multiple observation sets, or ‘samples’, at different time points during admission, starting at 24 h after admission and adding one every 24 h until either discharge or death occurred. Loss to follow-up occurred for patients who were transferred to other ICUs (that were not included in the DDW) and for patients who were still admitted at moment of data collection. In both cases, we assumed uninformative censoring.

2.2. Predictors

A reduced set of candidate predictors was selected a priori (Supplementary Table 1) and we selected predictors for model fitting based on availability. To describe the availability of the different predictors in the EMR, we quantified the availability of each predictor per patient in terms of entry density, that is, the fraction of ICU days for a patient in which at least one value of this predictor is available. We judged a median entry density >0.33 (i.e., at least one measurement per patient every third day) as sufficient. Given the respiratory nature of COVID-19, we included an extra candidate predictor similar to the PaO₂/FiO₂ ratio, the SpO₂/FiO₂ ratio, by dividing SpO₂ by FiO₂ measurements with matching measurement times. To model the influence of the duration of ICU admission on mortality risk, we added the (current) length of ICU stay as a predictor.

Each sample consists of the most recent predictors available (last observation carried forward). We used a K-Nearest-Neighbour (KNN) imputation algorithm to impute missing values occurring before the first actual measurement. This algorithm imputes missing predictors using values from the five nearest neighbours (i.e., the shortest Euclidean distance regarding the remaining predictors) that have a value for that predictor, averaging these uniformly. We fitted the KNN imputer using the development set and used it for imputation in both development and validation sets. After imputation, predictors were centered and scaled by the standard deviation, based on the distributions of the individual predictors in the development set.

2.3. Model development

To model near-term mortality, we chose a prediction horizon of 24 (Supplementary Fig. 1a). To achieve this, we fitted classification models using the collected daily samples (section 2.1). We labeled samples as ‘event samples’ if death occurred within 24 h from the time of sampling and as ‘non-event samples’ otherwise (Supplementary Fig. 2a). To compare this with long-term mortality prediction, we also fitted models to predict in-ICU mortality (Supplementary Fig. 1b) following the same procedure, but labeling each sample as an ‘event sample’ if death occurred before ICU discharge (Supplementary Fig. 2b).

To examine the added value of modeling non-linear dependencies in the data, we fitted both linear and non-linear models for both near-term mortality and in-ICU mortality. For linear modeling, we fitted logistic regression models using L2 regularization (LR) and for non-linear modeling, we fitted random forest (RF) models. Additionally, we benchmarked these results against other linear and non-linear models, i.e. a logistic regression models using L1 regularization (LASSO), a Gradient Boosting (XGBoost) model and a multilayer perceptron (MLP). A more detailed description of the MLP can be found in appendix C. Model hyperparameters were optimized using an exhaustive gridsearch in a stratified 5-fold cross-validation procedure optimizing the area under the receiver operating curve (AUROC). Supplementary Table 2 shows the hyperparameter grids which were searched for the different models.

2.4. Model re-calibration

To improve the calibration of predictions, we re-calibrated the original model predictions using isotonic regression [12]. Here, model estimates are transformed by passing the predictions through a calibrator function (a monotonically increasing step-function), which results from fitting an isotonic regressor on a left-out set of samples. To fit the calibrator function based on samples disjoint from the samples used for fitting the classification model, we made an extra stratified split in the development set by randomly assigning one third of the samples to the calibration fold and two thirds to the training fold. First, we fitted the imputation algorithm, optimized the model hyperparameters (as described in section 2.3) and fitted the logistic regression or random forest classifier using the samples in the training fold. Then, we fitted the calibrators using the predictions by the fitted classifiers and the labels of the samples in the calibration fold. These calibrators re-map the predictions of the fitted models.

2.5. Model performance

To examine the model’s ability to generalize over different ICUs as efficient as possible, we evaluated the models in a leave-one-ICU-out (LOIO) cross-validation procedure. In this procedure, models are fitted and validated in 25 iterations. In each iteration, patient samples from one ICU formed the test set which we used to evaluate the models that were fitted (and re-calibrated with the fitted calibrators) using the patient samples from the 24 remaining ICUs (forming the development set). Thus, both for near-term mortality and in-ICU mortality, we fitted 25 LR and 25 RF models and evaluated these on the unseen data from the left-out ICUs. This process is visualized in Supplementary Fig. 3.

To evaluate model discrimination, we determined the overall AUROC (combining the predictions of all iterations in the LOIO procedure) and the AUROC yielded in each ICU individually. We estimated the uncertainty around this metric by calculating the bootstrap percentile-t 95% confidence intervals (CIs) [13]. Following the hierarchy formulated by Van Calster and colleagues [14], we evaluated overall model calibration in the ‘weak’ and ‘moderate’ sense. For calibration in the weak sense, we determined the calibration intercept and slope [15]. Here, an intercept of 0 and slope of 1 indicate perfect calibration. For calibration in the moderate sense, we plotted smoothed flexible calibration curves [14], in which deviations of points from a diagonal line with unit slope indicate lack of calibration.

2.6. Explainable predictions

To gain insight in the influence of different predictors on the model predictions of near-term mortality and in-ICU mortality, we assessed the importance of the individual predictors by fitting an extra LR and RF model using the complete cohort (all 25 ICUs). We applied the Shapley additive explanations (SHAP) algorithm [16] to obtain SHAP values for each predictor and for each prediction, which serves as a surrogate for predictor importance. The SHAP value can be interpreted as the change in mortality risk in the expected model prediction when conditioning on that predictor (and in case of non-linear models, averaging these changes in risk across all possible predictor orderings). Global importance of the individual predictors was obtained by averaging the magnitudes of all obtained SHAP values, i.e. the mean SHAP magnitude.

2.7. Model performance in subgroups

Previous studies have shown that the performance of medical prediction models can vary widely depending patient characteristics such as sex, age, race, and socioeconomic status [17,18]. As the DDW does not contain information about race or socioeconomic status, we examined the model performance for near-term and in-ICU mortality prediction between the sexes and among different age groups. For the latter, we defined three age groups by splitting the full cohort in patients aged 50 or younger, patients aged between 50 and 70, and patients aged 70 or older.

3. Results

3.1. Data characteristics

We collected data from 3222 ICU admissions of patients with COVID-19, coming from 25 ICUs in the Netherlands. 667 patients died in the ICU (20.7%), and in-ICU mortality varied among the different ICUs between 7% and 41%. Table 1 shows the summary statistics of the included patient admissions.

Table 1.

Summary statistics of the included patient admissions.

	In-ICU mortality (N = 667)	Non In-ICU mortality (N = 2555)	All (N = 3222)
Age, years: mean (sd)	68.7 (9.2)	61.8 (11.8)	63.2 (11.6)
Sex, male: N (%)	514 (77.1)	1817 (71.1)	2331 (72.3)
Length-of-stay: N (%)
0–24 h	37 (5.5)	154 (6.0)	191 (5.9)
1–7 days	167 (25.0)	709 (27.7)	876 (27.2)
7–14 days	179 (26.8)	334 (13.1)	513 (15.9)
14–21 days	133 (19.9)	58 (2.3)	191 (5.9)
>21 days	151 (22.6)	264 (10.3)	415 (12.9)
Still admitted	0 (0.0)	171 (6.7)	171 (5.3)

3.2. Model performance

Overall, i.e. by combining the predictions of all iterations in the LOIO procedure, the LR and RF models yielded

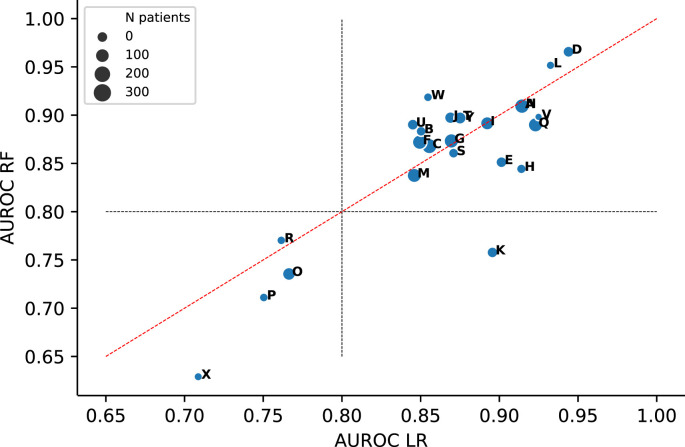
an AUROC of 0.87 [0.85; 0.88] and 0.86 [0.84; 0.88], respectively. The LASSO, XGBoost and MLP models yielded similar overall AUROCs (Supplementary Fig. 4). Point estimates of the AUROCs yielded in the individual ICUs are depicted in Fig. 1 and Table 2 shows the corresponding 95% CIs. Whether the LR model yielded a slightly higher AUROC than the RF model or vice versa varied for the different ICUs. The LR and RF models yielded an AUROC >0.80 in respectively 21 and 20 ICUs. We observed wide CIs for the models validated on ICUs with relatively small sample sizes Supplementary Fig. 5).

Fig. 1.

Areas under the receiver operating characteristic curve (AUROCs) yielded by the logistic regression (LR) and random forest (RF) models in the different ICUs.

Table 2.

AUROCs with 95% CI yielded by the logistic regression (LR) and random forest (RF) models in the different left-out ICUs (sorted by sample size). Prevalence is the fraction of patients who experience in-ICU mortality per ICU.

ICU	N patients	Prevalence in-ICU mortality	LR AUROC [95% CI]	RF AUROC [95% CI]
V	21	0.33	0.92 [0.87,0.97]	0.90 [0.79,0.98]
X	39	0.41	0.71 [0.55,0.85]	0.63 [0.49,0.77]
L	44	0.20	0.93 [0.87,0.98]	0.95 [0.90,0.99]
R	51	0.31	0.76 [0.59,0.89]	0.77 [0.66,0.87]
Y	53	0.13	0.88 [0.75,0.99]	0.90 [0.84,0.94]
P	53	0.25	0.75 [0.61,0.88]	0.71 [0.55,0.86]
W	54	0.07	0.85 [0.57,1.00]	0.92 [0.85,0.98]
H	71	0.14	0.91 [0.85,0.96]	0.84 [0.73,0.94]
B	79	0.30	0.85 [0.74,0.94]	0.88 [0.79,0.95]
S	81	0.35	0.87 [0.80,0.93]	0.86 [0.78,0.92]
K	107	0.11	0.90 [0.83,0.95]	0.76 [0.59,0.89]
N	109	0.18	0.91 [0.82,0.98]	0.91 [0.84,0.97]
E	110	0.19	0.90 [0.83,0.96]	0.85 [0.74,0.94]
U	113	0.18	0.85 [0.79,0.90]	0.89 [0.83,0.94]
D	114	0.23	0.94 [0.90,0.98]	0.97 [0.94,0.99]
J	134	0.14	0.87 [0.82,0.92]	0.90 [0.81,0.96]
T	153	0.29	0.88 [0.81,0.92]	0.90 [0.84,0.95]
O	177	0.18	0.77 [0.68,0.86]	0.74 [0.66,0.81]
I	193	0.33	0.89 [0.84,0.93]	0.89 [0.85,0.93]
M	230	0.10	0.85 [0.79,0.90]	0.84 [0.76,0.90]
Q	234	0.14	0.92 [0.88,0.97]	0.89 [0.83,0.94]
F	240	0.30	0.85 [0.81,0.90]	0.87 [0.83,0.91]
G	242	0.18	0.87 [0.82,0.92]	0.87 [0.82,0.93]
A	248	0.25	0.91 [0.87,0.95]	0.91 [0.86,0.95]
C	272	0.16	0.86 [0.79,0.91]	0.87 [0.81,0.92]

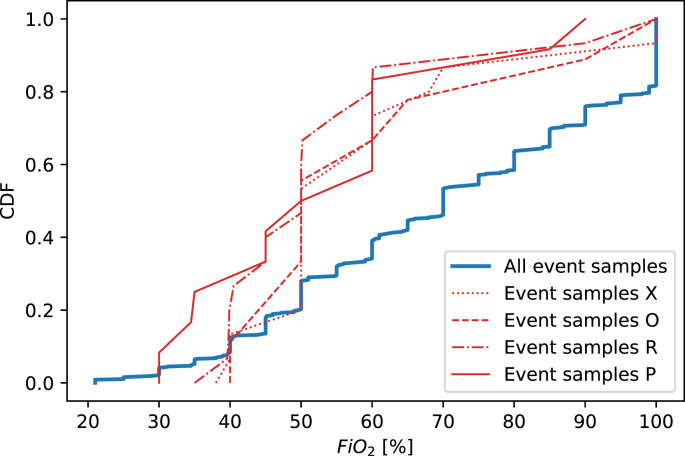
Both LR and RF models validated on ICUs O, P, R and X yielded an AUROC <0.80 (Fig. 1). In terms of patient demographics (age and sex) and length-of-stay in the ICU, we did not observe notable differences in these ICUs compared to the other ICUs (Supplementary Fig. 6). To check for notable deviations for any predictors in patients from these ICUs compared to the remaining ICUs, we examined the cumulative distributions for all predictors based on the samples taken within 24 h before death (‘event samples’) of patients from ICU O, P, R and X (see Supplementary Fig. 7). The FiO₂ distributions in these ICUs appear notably low (Fig. 2 ). In each of these four ICUs, we found the FiO₂ distribution to be significantly (P < 0.05) different from the complete distribution of event samples, based on a two-sided Kolmogorov-Smirnov (KS) test.

Fig. 2.

Cumulative distributions for F iO2 of the samples taken within 24 h before death (i.e. ‘event samples’) of patients from ICU O(N = 31), P(N = 13), R(N = 16) and X(N = 16). The cumulative distribution of event samples of patients from all ICUs (N = 667) is plotted as references. Distributions were found significantly different (P < 0.05) from the reference based on a two-sided Kolmogorov-Smirnov (KS) test in ICU O (KS-statistic = 0.32, P = 0.011), P (KS-statistic = 0.43, P = 0.012), R (KS-statistic = 0.46, P = 0.002) and X (KS-statistic = 0.33, P = 0.046).

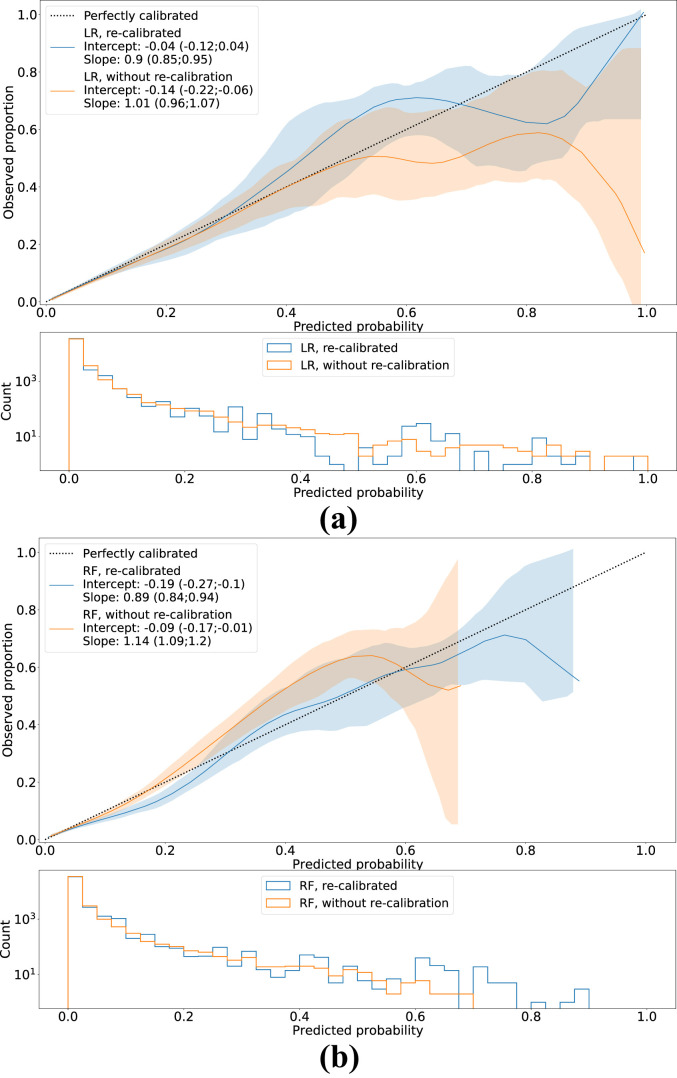
Fig. 3 shows the flexible calibration curves for both models with and without re-calibration, including the corresponding calibration intercepts and slopes. Without re-calibration, both models slightly overestimated the mortality risk (calibration intercept<0) and the RF model yielded too moderate predictions calibration slope>1). After re-calibration, the LR model shows good calibration in the large, while the RF model still shows slight overestimation (calibration intercept<0). Both models show slightly too extreme predictions (calibration slope<1). Calibration curves for the LASSO, XGBoost and MLP models are depicted in Supplementary Fig. 8.

Fig. 3.

Smoothed flexible calibration curves for (a) the logistic regression (LR) and (b) the random forest (RF) models, with and without re-calibration using isotonic regression. Shaded areas around the curves represent the 95%CIs. In the bottom plots, histograms of the predictions are shown.

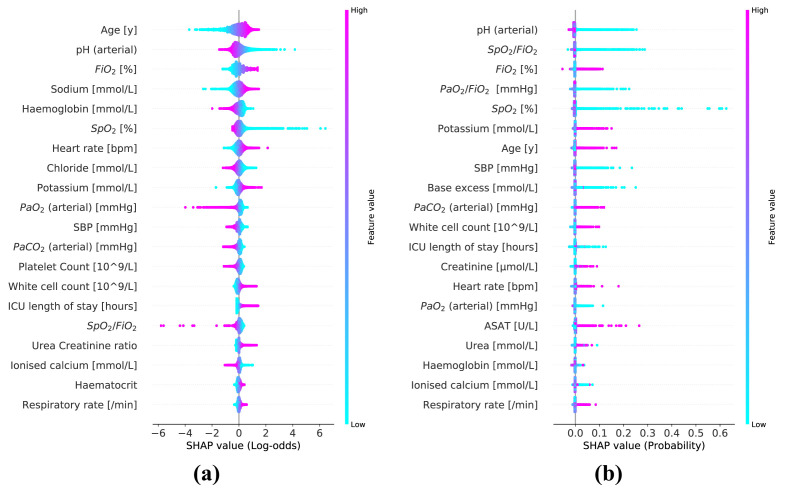
Table 3 shows the 20 most important predictors ranked based on the mean SHAP magnitude. The corresponding summary plots for the SHAP values for the LR and RF models are depicted in Fig. 4 .

Table 3.

Global importance of the top 20 most important predictors for the logistic Regression (LR) and random forest (RF) model, ranked based on mean SHAP magnitude.

Predictor	Predictor importance LR model (mean |SHAP|, log-odds scale)	Predictor	Predictor importance RF model (mean |SHAP|, probability scale)
Age [y]	0.453	pH (arterial)	0.0044
pH (arterial)	0.333	SpO2/FiO2	0.0037
FiO2 [%]	0.332	FiO2 [%]	0.0034
Sodium [mmol/L]	0.257	PaO2/FiO2 [mmHg]	0.0026
Haemoglobin [mmol/L]	0.211	SpO2 [%]	0.0017
SpO2 [%]	0.207	Potassium [mmol/L]	0.0016
Heart rate [bpm]	0.181	Age [y]	0.0014
Chloride [mmol/L]	0.175	SBP [mmHg]	0.0013
Potassium [mmol/L]	0.160	Base excess [mmol/L]	0.0011
PaO2 (arterial) [mmHg]	0.131	PaCO2 (arterial) [mmHg]	0.0010
SBP [mmHg]	0.130	White cell count [109/L]	0.0008
PaCO2 (arterial) [mmHg]	0.116	ICU length of stay [hours]	0.0008
Platelet Count [109/L]	0.116	Creatinine [μmol/L]	0.0006
White cell count [109/L]	0.114	Heart rate [bpm]	0.0006
ICU length of stay [hours]	0.112	PaO2 (arterial) [mmHg]	0.0006
SpO2/FiO2	0.111	ASAT [U/L]	0.0006
Urea Creatinine ratio	0.092	Urea [mmol/L]	0.0006
Ionised calcium [mmol/L]	0.078	Haemoglobin [mmol/L]	0.0005
Haematocrit	0.069	Ionised calcium [mmol/L]	0.0005
Respiratory rate [/min]	0.068	Respiratory rate [/min]	0.0005

Fig. 4.

Summary plots for the SHAP values constructed from both logistic regression (a) and random forest model (b). Each SHAP value is represented by a single dot on each predictor row. Color is used to display the corresponding value of the predictor. Predictors are ordered by the mean SHAP magnitude. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

3.3. Predictors

To give an overview of the role of different predictors during the 24 h preceding patient death, the cumulative distributions for the different predictors of samples taken within 24 h before death (‘event samples’) compared to all other (‘non-event’) samples are depicted in Supplementary Fig. 9. The daily data availability is visualized by boxplots showing the distributions of daily entry densities (i.e. fractions of non-empty daily measurements) across all patient samples for the candidate predictors (Supplementary Fig. 10). All candidate predictors showed a median entry density >0.33, except for lactate (arterial), which was excluded for model fitting. We plotted the correlations between the included predictors (before imputation) in a clustered heatmap (Supplementary Fig. 11).

3.4. In-ICU mortality prediction

The LR and RF models both yielded an overall AUROC of 0.79 [0.78; 0.79]. Validation of the LR models yielded an AUROC >0.80 in 13 out of the 25 ICUs and in 15 out of 25 ICUs for validation of the RF models. Again, we observed notably wide confidence intervals for the models validated on ICUs with relatively small sample sizes. Without recalibration, the LR models overestimated the mortality risk (intercept<0) and the RF models yielded slightly too moderate predictions (slope>1). After re-calibration, both models show good calibration in the large, with a calibration intercept of 0.00 [−0.03; 0.02] and 0.00 [−0.03; 0.03], but slightly too extreme predictions, with a calibration slope of 0.87 [0.84; 0.89] and 0.55 [0.54; 0.57], for the LR and RF model respectively.

In comparison with near-term mortality modeling, the patient’s age acted as a relatively more important predictor (in terms of mean SHAP magnitude) in both the LR and RF model. We report on the results for in-ICU mortality modeling in more detail in appendix D.

3.5. Model performance in subgroups

Supplementary Figs. 12 and 13 respectively show the model performances for near-term and in-ICU mortality prediction for the LR and RF models. Both models show slightly better discrimination for both near-term and in-ICU mortality prediction in female patients and in patients within the lower age group (i.e. <50 years). Moreover, for the LR model, we observed mortality underestimation for both near-term and in-ICU mortality in the lower age group. However, there is relatively large uncertainty due to the small number of patients aged 50 or younger and, therefore, care should be taken interpreting these results.

4. Discussion

We developed both a linear and non-linear model for to predict near-term mortality, based on a mixture of static information (e.g. age and sex) and dynamic information (e.g., vital signs and laboratory values). Overall, the discriminative performance of the LR model was similar the RF model and other non-linear models (i.e. XGBoost and MLP). These empirical results suggest that modeling non-linear predictor-outcome relations does not improve model performance for the task of dynamic mortality prediction.

While we evaluated model discrimination both overall (i.e. by combining the predictions of all iterations in the LOIO procedure) and separately for each ICU, we did not evaluate model calibration in the individual ICUs as the sample sizes were too small to enable good judgement of model calibration.

The low F iO2 distributions we observed in samples taken within 24 h before death (‘event samples’) of patients from ICUs O, P, R and X compared to the event samples from the complete cohort may have influenced the predictive performance of the models validated on these ICUs. As the F iO2 is set by the physician, this observation may be explained by local differences in protocols concerning discontinuation of treatment. However, since we are dealing with relatively small numbers of (deceased) patients in these ICUs, care has to be taken in interpreting these findings.

As expected for a respiratory illness like COVID-19, predictors related oxygenation such as F iO2, oxygen saturation (SpO2) and arterial pH appeared in the top 10 most important predictors for both the LR and RF model.

The severity of missingness varies widely between the included predictors (Supplementary Table 1). The imputation algorithm we chose (i.e. the KNN imputation algorithm) could have been influenced by the pattern of missingness among the predictors and therefore, influencing the model performance. We performed an additional analysis to examine the data missingness pattern (appendix E) and observed clusters of predictors with similar missingness patterns. The most important predictors (based on mean SHAP magnitude) are not strongly concentrated within these clusters, making it unlikely that the pattern in the predictor importance we observed are due to the missingness pattern. Whether different imputation techniques would lead to even better model performance was beyond the scope of the current analysis.

Both traditional ‘static’ mortality models [1,2] and more recent works on dynamic mortality models [3,5] focus on the ICU population as a whole. In contrast, we presented a model specifically developed for COVID-19 patients. Given the heterogeneity among ICU patients, improved mortality prediction may be achieved by focusing on sub-populations. This study may serve as a proof of concept to move from ‘one-size-fits-all’ modeling towards modeling for subgroups in the ICU population.

4.1. Clinical applications

Meyer and colleagues [4] noted that the mortality predictions do not target a specific pathological entity but suggest that these may serve to draw attention of the care team, such that subtle changes that could develop into a critical state will not be missed. However, in most cases a COVID-19 patient dies within the ICU (especially later during an ICU course), this is the result of a well-considered shared clinical decision, rather than a sudden event that could have been avoided by drawing more attention. The model presented here may thus predict the physician’s decision to discontinue treatment rather than a patient’s deterioration. Thorsen-Meyer and colleagues [3] question the clinical utility of their presented mortality model mainly because of its lack of causality, which is true for the model presented in this study as well. Based on the prediction of a model which lacks a causal structure, one cannot know if any action based on this will affect the outcome. Therefore, we doubt the clinical utility of mortality models when simply implemented as a ‘red flag model’, e.g. triggering an alarm for high mortality risk. Instead, non-causal mortality models like those presented here may serve as a guidance in the development of models with more causal structure, which could provide decision support for the clinician as these models could suggest which actions lead to a lower risk of patient death.

We foresee three other potential clinical utilities for non-causal mortality models in the ICU. First, a dynamic mortality model could improve resource allocation in the ICU, e.g. by assigning more nurses per patient for those with high risk of mortality. However, it remains to be determined whether (near-term or long-term) mortality risk is a good surrogate for clinical workload. Second, a dynamic mortality model can be used for benchmarking purposes throughout the whole ICU journey, contrasting to static mortality models like SAPS II [2] and APACHE II [1]. As static mortality models are based on measurements from the admission day, they represent disease severity before a patient receives any ICU care and may only serve as a good benchmark for patients when entering ICU. Predictions by the dynamic model enable benchmarking of patients at any moment during admission. Third, as suggested by Schmidt and colleagues [7], a dynamic mortality model could help informing family members of likely prognosis. This could be a prognosis of the patient’s survival in the coming 24 h (i.e. near-term mortality) or the likelihood of eventually being discharged alive (i.e. long-term mortality).

4.2. Study limitations

First, several potentially relevant predictors, such as comorbidities or medical history, were not available for modeling. Inclusion of these variables could have improved the predictive performance and enabled correction for potential confounding. Second, not all included predictors were daily available for all patients and missingness was especially high for certain laboratory test results. The degree of data missingness may be associated with the predicted outcome, as demonstrated in previous work on in-ICU sepsis prediction [19]. Thus, not including predictors derived from missingness may have introduced a bias to the predictions. Third, the number of admissions per month included in the Dutch Data Warehouse (DDW) varied widely between different ICUs Supplementary Fig. 14). Numbers peak during two time-periods coinciding with the first March–April 2020) and second (November 2020–January 2021) COVID-19 ‘waves’ in the Netherlands. All the ICU data sets contain admissions during the first wave, but roughly half of them contain none (or very few) admissions during the second wave. Advances in COVID-19 research have improved the patient care during the pandemic, for instance the start of widespread usage of dexamethasone [20] in July 2020. Therefore, models evaluated on ICUs that only contain patients admitted during the first wave may have underestimated mortality risks compared to models evaluated on ICUs that contain admissions during both waves. Fourth, clinical machine learning models can experience significantly degraded performance in datasets not seen during model fitting (i.e. a domain shift) [21]. Although our results suggest that the models generalize well over different ICUs, the model robustness for other domain shifts (e.g. predicting mortality in a later stage of the pandemic) remains unknown. Finally, we drew repeated observations (samples) on the same patient at different points in time, resulting in highly correlated sample clusters. The methods to estimate uncertainty of the performance we used falsely assume these samples to be independent of previous and next ones (IID assumption), which may have resulted in too optimistic uncertainty estimations. It would be an interesting topic for future research to examine the added value of modeling the dependency between samples, e.g. by using recurrent neural networks (RNNs), which are often used in dynamic mortality modeling studies [[3], [4], [5]]. On the other hand, we doubt the added value of more complex modeling, as more complex non-linear models did not improve discriminative performance compared to linear modeling using logistic regression.

4.3. Conclusion

In this study, we developed dynamic mortality models for COVID-19 patients admitted to the ICU. Our contribution to traditional mortality models [1,2] and more recently published dynamic mortality models [[3], [4], [5]] is twofold. First, we focused on a sub-population of patients (i.e. COVID-19 patients) instead of the ICU population as a whole. Second, we introduced near-term mortality predictions instead long-term mortality prediction. Further research is required to examine its possible applications, such as guidance in resource allocation and real-time benchmarking. Finally, interpretable mortality models may pave the way for the development ICU models with a more causal structure which may provide actionable advice on patient treatment in the future.

Ethics approval and consent to participate

The Medical Ethics Committee at Amsterdam UMC, location VUmc waived the need for patient informed consent and approved of an opt-out procedure for the collection of COVID-19 patient data during the COVID-19 crisis.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: