Multi-layer sequential network analysis improves protein 3D structural classification

Abstract

Protein structural classification (PSC) is a supervised problem of assigning proteins into pre-defined structural (e.g., CATH or SCOPe) classes based on the proteins’ sequence or 3D structural features. We recently proposed PSC approaches that model protein 3D structures as protein structure networks (PSNs) and analyze PSN-based protein features, which performed better than or comparable to state-of-the-art sequence or other 3D structure-based PSC approaches. However, existing PSN-based PSC approaches model the whole 3D structure of a protein as a static (i.e., single-layer) PSN. Because folding of a protein is a dynamic process, where some parts (i.e., sub-structures) of a protein fold before others, modeling the 3D structure of a protein as a PSN that captures the sub-structures might further help improve the existing PSC performance. Here, we propose to model 3D structures of proteins as multi-layer sequential PSNs that approximate 3D sub-structures of proteins, with the hypothesis that this will improve upon the current state-of-the-art PSC approaches that are based on single-layer PSNs (and thus upon the existing state-of-the-art sequence and other 3D structural approaches). Indeed, we confirm this on 72 datasets spanning ~44,000 CATH and SCOPe protein domains.

1 |. INTRODUCTION

1.1 |. Background and motivation

Protein structural classification (PSC) uses sequence or 3D structural features of proteins and pre-defined structural classes to perform a supervised learning of a classification model, which can then be used to predict classes of currently unclassified proteins based on their features. Because structural similarity of proteins often indicates their functional similarity, PSC can help understand functions of proteins. That is, the predicted structural class of a protein can be used to predict functions of the protein based on functions of other proteins that have the same class as the protein of interest.

Traditional PSC approaches rely heavily on sequence-based protein features¹. However, it has been argued that proteins with low (high) sequence similarity can have high (low) 3D structural similarity^2;3. Hence, 3D-structural features offer complementary insights to sequence features in the task of PSC. Traditional 3D-structural protein features are extracted directly from 3D structures of proteins⁴. In contrast, one can first model the 3D structure of a protein using a protein structure network (PSN), where nodes are amino acids and two nodes are joined by an edge when the corresponding amino acids are close enough to each other in the protein’s 3D structure. Then, one can use PSN (i.e., network) features of proteins in the task of PSC. Modeling 3D structures of proteins as PSNs could help gain novel insights about protein folding because it opens up opportunities to apply an arsenal of approaches from the network science field to study 3D protein structures⁵.

We already proposed a PSN-based PSC approach called NETPCLASS⁶ that performed better than or comparable to existing state-of-the-art sequence or other 3D structure-based (i.e., non-PSN-based) approaches in the task of PSC, i.e., when classifying protein domains from two established databases, i.e., Class, Architecture, Topology, and Homology (CATH)⁷ and Structural Classification of Proteins (SCOP)^8;9. Thus, PSN analysis is a state-of-the-art in the task of PSC; note that the same holds in the task of 3D structure-based protein function prediction as well¹⁰. NETPCLASS relies on ordered PSNs, where nodes in a PSN have order based on positions of the corresponding amino acids in the protein sequence. Following NETPCLASS, we proposed an improved PSC approach that relies on weighted PSNs instead of ordered PSNs, where each edge in a PSN is assigned a weight that quantifies distances between amino acids in terms of both sequence and 3D structure¹¹. Intuitively, a higher edge weight signifies that the two amino acids are close in the 3D space even though they are far apart in the sequence, while a low edge weight signifies that the two amino acids are close in the 3D space only because they are also close in the sequence.

Both of the above existing PSN-based PSC approaches rely on static or single-layer PSNs, which capture the final (i.e., native) 3D structure of a protein; henceforth, we refer to the above two PSN types as single-layer unweighted ordered PSNs and single-layer weighted unordered PSNs, respectively. However, folding of a protein is a temporal process, as some parts of the protein fold earlier than others before the protein acquires its native 3D structure¹². Hence, using this dynamic 3D structural information of a protein, which captures the 3D sub-structural (or intermediate) configurations of the protein as the protein undergoes folding to attain its native structure, can be more informative.

Unfortunately, only a few kind of experimental methods exist that can determine such folding intermediates^13;14, and such methods are not scalable, i.e., they are restricted to studying only a few 3D sub-structural configurations of a single protein¹⁵. So, experimental data on intermediate sub-structures resulting from such a dynamic protein folding process are lacking. Because there is abundant availability of experimental data for the native structures of proteins, can we use this information to approximate the 3D sub-structural configurations of proteins? If so, this is the best anyone could do at this point in time, until large-scale experimental data on folding intermediates potentially becomes available in the future.

Indeed, existing computational, simulation-based methods do exactly this – they rely on the native 3D structure as a proxy to predict folding intermediates of a protein^16;17;18. This includes protein folding models according to which only the amino acid interactions present in the native structure of a protein (i.e., native contacts) are important for the folding of the protein and other transient (i.e., non-native) contacts can be ignored^{19;20;21;22;23}. However, even such computational studies that “only” approximate the dynamics of the folding process are limited to a few proteins (e.g., nine¹⁷), and typically rely on small, model proteins, rather than a representative selection of proteins that appear in nature¹⁶.

1.2 |. Our contributions

Here, we propose to approximate 3D sub-structural configurations of proteins using multi-layer sequential (or simply multi-layer) PSNs, with the hypothesis that this will improve PSC performance compared to single-layer PSNs that only capture native 3D structures of proteins. If our proposed multi-layer PSN-based PSC approach outperforms existing single-layer PSN-based PSC approaches, then it would open up opportunities to explore protein folding-related research questions using multi-layer, rather than single-layer, PSNs. One such research question is to explore the effect of synonymous codon usage on co-translational protein folding²⁴, which has significance in heterologous protein expression for drug discovery²⁵. Because co-translational protein folding leads to partial folds of a protein during translation before the protein acquires its final 3D structure, a multi-layer PSN-based analysis as opposed to the current single-layer PSN-based analysis⁵ could provide more insights.

Given the 3D native structure of a protein, we model it as a multi-layer PSN. Intuitively, our multi-layer PSN consists of multiple PSN “snapshots”, where the final snapshot captures the native 3D structure of the protein, while the earlier snapshots approximate 3D sub-structural views of the protein as it attains its final 3D structure via the folding process (Fig. 1). Specifically, by “approximate”, we mean that given information about the native (final, as available in the Protein Data Bank (PDB)²⁶) 3D structure of a protein, we convert it into a multi-layer PSN by forming incremental cumulative groups of amino acids (i.e., sub-sequences) of the protein starting from the amino- or N-terminus (i.e., start of the protein sequence) up to the carboxyl- or C-terminus (i.e., end of the protein sequence). Then, we construct a PSN snapshot corresponding to each incremental sub-sequence. We refer to the sequential collection of all PSN snapshots of a protein as a multi-layer PSN. Currently, our multi-layer PSNs are unweighted and unordered. To emphasize again, because of the reasons outlined before, each snapshot in a multi-layer PSN captures the native 3D sub-structure (i.e., the native contacts as available in the final PDB structure) of the corresponding sub-sequence of a protein, rather than the actual intermediate 3D sub-structure formed during the folding process. The latter, in theory, could contain native as well as non-native contacts and could thus differ from the PSN snapshots of our multi-layer PSN. However, just as with the existing approaches discussed above, this is the best anyone can do at this point in time, until large-scale experimental data on folding intermediates potentially becomes available in the future.

FIGURE 1.

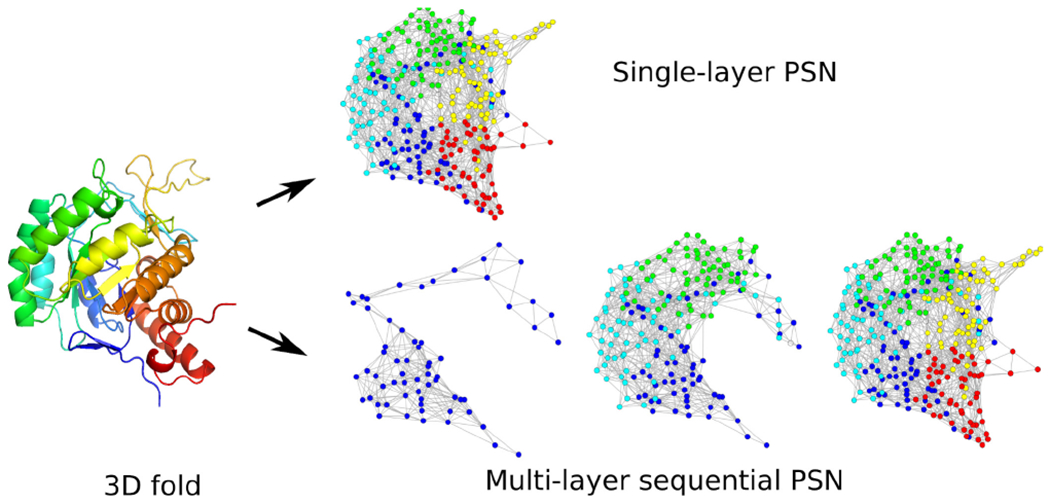
Illustration of the single-layer vs. multi-layer PSN of a protein 3D structure.

Our proposed multi-layer PSNs are multi-layer (and thus more detailed) versions of existing single-layer unweighted unordered PSNs⁶. Hence, to show that capturing (native) 3D sub-structural information helps in the task of PSC, it is sufficient to show that our multi-layer PSNs outperform single-layer unweighted unordered PSNs. Consequently, we compare our proposed multi-layer PSNs with single-layer unweighted unordered PSNs in the task of PSC. Additionally, we compare our multi-layer PSNs with each of the other existing, more advanced notions of single-layer weighted unordered PSNs¹¹ and single-layer unweighted ordered PSNs⁶, in the task of PSC. Note that we do not propose multi-layer versions of the above two existing single-layer PSN types (weighted and ordered) because of the lack of computational approaches that can extract meaningful information (i.e., features) from the corresponding multi-layer versions. Instead, we propose a multi-layer version of single-layer unweighted unordered PSNs because there exist advanced computational approaches using which we can extract meaningful features from this multi-layer version. We hope to explore in our future work both adding weights and node order to our multi-layer PSNs as well as developing novel approaches for analyzing such multi-layer weighted ordered PSNs.

We extract features from our proposed multi-layer PSNs as follows. In the network science sense, our multi-layer PSNs are dynamic or temporal networks (i.e., collections of network snapshots arranged in some ordered manner), but we avoid the use of the term “dynamic” in this paper as to not confuse the dynamic nature of the networks with the dynamics of the protein folding process, which we are unable to capture for the reasons stated above. So, we can rely on features that have been proposed for dynamic networks. Namely, we rely on graphlets; small subgraphs of a large network²⁷. Specifically, we use the concepts of dynamic graphlets²⁸ and graphlet orbit transitions (GoTs)²⁹. Despite having different mathematical definitions, intuitively, both dynamic graphlets and GoTs capture changes in local network neighborhoods of nodes in a dynamic network, including a multi-layer PSN.

To extract features from the considered existing PSN types, i.e., single-layer unweighted unordered PSNs, single-layer weighted unordered PSNs, and single-layer unweighted ordered PSNs, we use the concepts of original graphlets³⁰, weighted graphlets ¹¹, and ordered graphlets ³¹, respectively, which we again note have been shown to be among state-of-the-art features in the task of PSC^6;11.

We compare our proposed multi-layer PSNs (i.e., the corresponding features) with each of the existing single-layer PSNs (i.e., the corresponding features) in the task of PSC. Note that we do not compare our proposed multi-layer PSNs with other non-PSN-based protein features because we already showed that existing single-layer PSNs perform better than or are comparable to existing state-of-the-art non-PSN-based protein features in the task of PSC⁶. Hence, if we show that our proposed multi-layer PSNs outperform existing single-layer PSNs, then by transitivity, this would mean that our proposed multi-layer PSNs also outperform existing non-PSN-based protein features.

Specifically, we evaluate the considered PSN types under the same classification algorithm, i.e., logistic regression (LR), for a fair comparison. For a given input protein, the output of an LR classifier is a set of likelihoods with which the protein belongs to the considered structural classes. Note that previously we explored other conventional classifiers, e.g., support vector machine, but this did not yield improvement, i.e., LR performed better in our considered task of PSC ⁶. Also, note that we use LR as opposed to a non-conventional (i.e., deep learning-based) classification algorithm because our proposed multi-layer PSNs already perform very well under LR (see below), and because a non-conventional classification algorithm would also come at a cost of much larger computational time. However, one of our recent works showed an encouraging PSC performance boost when the single-layer weighted unordered PSNs were used with a deep learning-based algorithm compared to when they were used with a conventional algorithm¹¹. So, we plan to test whether this holds for our proposed multi-layer PSNs in our future work.

We evaluate the considered PSN types in the task of classifying ~44,000 protein domains from CATH⁷ and Structural Classification of Proteins–extended (SCOPe)⁹ databases. We transform protein domains to PSNs with labels corresponding to CATH and SCOPe structural classes, where we study each of the four hierarchy levels of CATH and SCOPe, resulting in 72 protein domain datasets. Our performance evaluation is based on quantifying the misclassification rate, i.e., the fraction of PSNs in the test data for which the trained models give incorrect structural class predictions, using 5-fold cross-validation.

Over all of the 72 considered datasets, our proposed multi-layer PSNs statistically significantly outperform their single-layer counterpart, i.e., single-layer unweighted unordered PSNs, in the task of PSC. Additionally, our multi-layer PSNs statistically significantly outperform the other PSN types, i.e., single-layer weighted unordered and single-layer unweighted ordered PSNs. Moreover, our multi-layer PSNs not “only” outperform all of the existing PSN types, but also, for most of the datasets, their performance is exemplary. Namely, for 66 out of 72 (i.e., 92%) of the datasets, our proposed multi-layer PSNs show a misclassification rate of only 0.1 or less.

2 |. METHODS

2.1 |. Data

We use all of the 145,219 currently available Protein Data Bank (PDB) IDs²⁶ that have sufficient 3D crystal structure resolution (i.e., resolution values of 3 Angstrom (Å) or lower). This set of PDB IDs contains 408,404 unique protein sequences (i.e., chains). To identify protein domains within these protein chains, we rely on two protein domain structural classification databases: CATH⁷ and SCOPe⁹.

Because protein chains that are almost sequence identical can affect our downstream PSC analysis, as is typically done⁶, we only keep a set of protein chains such that each chain in the set is less than 90% sequence identical to any other chain in the set, using the procedure from Supplementary Section S1. This procedure results in 35,131 sequence non-redundant protein chains, where each chain has at least one CATH- or SCOPe-based protein domain, resulting in a total of 60,434 CATH and 25,864 SCOPe protein domains.

Both CATH and SCOPe classify protein domains based on four hierarchical levels of protein 3D structural classes. The lower the hierarchy level of a class, the higher the structural similarity of protein domains within the class. Because we aim to perform supervised protein structural classification at each hierarchy level, including the fourth, to have enough statistical power³², we only consider those fourth-level CATH and SCOPe protein structural classes where each class has at least 30 protein domains. Thus, we only consider those protein domains that belong to any one such class, which results in 34,791 CATH and 9,394 SCOPe domains.

For each of the 34,791 CATH and 9,394 SCOPe domains, we create a single-layer unweighted unordered protein structure network (PSN) (Section 2.2). Then, as is typically done⁶, we only keep those domains whose corresponding PSNs have a single connected component. Additionally, we keep only those domains that have at least 30 amino acids. This results in 34,630 CATH and 9,329 SCOPe domains. These are the final sets of CATH and SCOPe domains that we use in our study.

Given all of the 34,630 CATH domains, we test the ability of the considered features to distinguish between the first-level classes of CATH, i.e., mainly alpha (α), mainly beta (β), and alpha/beta (α/β), which have at least 30 domains each. Hence, we consider all 34,630 CATH domains as a single dataset, where the protein domains have labels corresponding to three first-level CATH classes: α, β, and α/β. Second, we compare the features on their ability to distinguish between the second-level classes of CATH, i.e., within each of the first-level classes, we classify domains into their sub-classes. To ensure enough training data, we focus only on those first-level classes that have at least two sub-classes with at least 30 domains each. All three first-level classes satisfy this criteria. For each such class, we take all of the domains belonging to that class and form a dataset, which results in three datasets. Third, we compare the approaches on their ability to distinguish between the third-level classes of CATH, i.e., within each of the second-level classes, we classify domains into their sub-classes. Again, we focus only on those second-level classes that have at least two sub-classes with at least 30 domains each. 16 classes satisfy this criteria. For each such class, we take all of the domains belonging to that class and form a dataset, which results in 16 datasets. Fourth, we compare the approaches on their ability to distinguish between the fourth-level classes of CATH, i.e., within each of the third-level classes, we classify PSNs into their sub-classes. We again focus only on those third-level classes that have at least two sub-classes with at least 30 domains each. 28 classes satisfy this criteria. For each such class, we take all of the domains belonging to that class and form a dataset, which results in 28 datasets.

Thus, in total, we analyze 1+3+16+28=48 CATH datasets. We follow the same procedure for SCOPe and obtain 1+6+5+10=22 SCOPe datasets. In addition to the above 48+22=70 CATH and SCOPe datasets, as is typically done⁶, we use two additional datasets because of the following reason. Typically, high sequence similarity of proteins indicates their high 3D structural similarity. Consequently, given a set of proteins, if proteins that belong to the same 3D structural class have high sequence identity (typically > 40%), then a sequence-based protein feature might be sufficient to compare them³³. So, we aim to evaluate how well our considered PSN (i.e., 3D structural) features can identify protein domains that belong to the same structural class when all of the domains (within and across structural classes) come from protein sequences that show low (≤ 40%) sequence identity. To do this, first, we download an existing popular dataset from the SCOPe database called Astral that has 14,666 protein domains, where the pairwise identities of the corresponding protein sequences are ≤ 40% and the label of a domain indicates the protein family (i.e., the fourth-level structural class) to which it belongs. We follow the same filtering criteria for the Astral dataset that we do above for the CATH and the other SCOPe datasets, which results in a single dataset with 729 domains and 18 structural classes. Second, we evaluate the consider PSC approaches on a more constrained criterion of ≤ 25% sequence identity. To do this, we create a dataset named Scop25% that contains all of those domains from our final set of 9,394 SCOPe domains (see above) whose corresponding protein sequences show ≤ 25% pairwise sequence identities (Supplementary Section S1). We follow the same filtering criteria for Scop25% that we do for Astral, CATH, and the other SCOPe datasets, which results in a single dataset with 531 domains and nine structural classes, where the label of a domain indicates the protein family to which it belongs. Hence, including all of the CATH, SCOPe, Astral, and Scop25% datasets, in total, we use 72 datasets in this study.

2.2 |. PSN types and their corresponding features

For each protein domain, we construct four types of PSNs, out of which three are existing notions of single-layer PSN types and one is our proposed notion of multi-layer PSN type. The three existing single-layer PSN types cover all of the types of PSNs that currently exist in the literature. These existing PSN types are (i) single-layer unweighted unordered PSN (named original), (ii) single-layer weighted unordered PSN (named weighted), and (iii) single-layer unweighted ordered PSN (named ordered). The fourth PSN type, i.e., our proposed multi-layer PSN (named multi-layer), is the multi-layer version of the single-layer unweighted unordered PSN type (Table 1).

TABLE 1.

Summary of the four considered PSN types, i.e., our proposed multi-layer PSN type and three existing single-layer PSN types. Each row (except the first) corresponds to a PSN type, and each column (except the first) outlines the corresponding PSN characteristic. Note that original PSNs differ from multi-layer PSNs in a single aspect and the two are thus fairly comparable. On the other hand, weighted PSNs and ordered PSNs differ from multi-layer PSNs in two aspects.

PSN type	Single-layer or multi-layer?	Unweighted or weighted?	Unordered or ordered?
Multi-layer	Multi-layer	Unweighted	Unordered
Original	Single-layer	Unweighted	Unordered
Weighted	Single-layer	Weighted	Unordered
Ordered	Single-layer	Unweighted	Ordered

Below, we provide details of how we create each PSN type, as well as how we extract graphlet features from each PSN type. The latter is explained only briefly in the main paper due to space constraints, and it is explained in detail in Supplementary Section S2.

Existing single-layer unweighted unordered PSNs (i.e., original).

Given a protein domain, we first obtain the corresponding Crystallographic Information File (CIF) from the PDB ²⁶ that contains information about the 3D coordinates of the heavy atoms (i.e., carbon, nitrogen, oxygen, and sulphur) of the amino acids in the domain. Then, we create the single-layer unweighted unordered PSN for the given domain using an established criteria^34;6;11;35: (i) we consider amino acids as nodes, and (ii) we define an edge between two amino acids if the spatial distance between any of their heavy atoms is within 6Å. To extract features from this PSN type, we rely on edge-based graphlet degree vector matrix (eGDVM)³⁶, which is based on the concept of original graphlets³⁰. For details, see Supplementary Sections S2 and S3.

Existing single-layer weighted unordered PSNs (i.e., weighted).

Given a protein domain, we first create the single-layer unweighted unordered PSN as described above. Then, using an established approach¹¹, we assign weights to edges of the PSN, where an edge weight is the geometric mean of two types of distances between the corresponding amino acids, i.e., their sequential distance and the inverse of their spatial distance. To extract features from the resulting single-layer weighted unordered PSN type, we rely on an existing measure called weighted edge-based graphlet degree vector matrix (weGDVM), which is based on the concept of weighted graphlets and has been successfully used in the task of PSN-based PSC¹¹ (Supplementary Section S2).

Existing single-layer unweighted ordered PSNs (i.e., ordered).

Given a protein domain, we first create the single-layer unweighted unordered PSN as described above. Then, using an established approach³¹, we add a node order to the PSN, such that the node order represents the positions of the nodes (i.e., amino acids) in the sequence of the corresponding protein domain. To extract features from the resulting single-layer unweighted ordered PSN type, we rely on an existing measure called ordered graphlet feature vector (oGFV), which is based on the concept of ordered graphlets³¹ and has been successfully used in the task of PSN-based PSC⁶ (Supplementary Section S2).

Our proposed multi-layer unweighted unordered PSNs (i.e., multi-layer).

Given a protein domain, starting from the first amino acid (i.e., the amino acid closest to the N-terminus) of the domain sequence, we define multiple incremental sub-sequences of the protein domain, where each sub-sequence i + 1 includes all of the amino acids from the previous sub-sequence i. Then, for each sub-sequence, i.e., using the amino acids in the given sub-sequence, we create a single-layer unweighted unordered PSN using the same procedure as we describe in subsection “Existing single-layer unweighted unordered PSN (i.e., original)”. We identify this PSN corresponding to a protein sub-sequence as a PSN snapshot. The collection of all PSN snapshots corresponding to all of the sub-sequences for the given domain forms the multi-layer unweighted unordered PSN of that domain. We create two types of multi-layer unweighted unordered PSNs using two strategies to create PSN snapshots, i.e., to define protein domain sub-sequences, as follows.

Strategy 1:

Given a protein domain of length S (i.e., containing S amino acids), we create S/5 sub-sequences (i.e., PSN snapshots) as follows. Starting from the first amino acid of the sequence, the first snapshot has first 5 amino acids, the second snapshot has first 10 amino acids, the third snapshot has first 15 amino acids, and so on, until we include all of the S amino acids of the protein domain in the last (i.e., (S/5)^th) PSN snapshot. We use an increment of five amino acids per snapshot because it intuitively mimics addition of individual 3D secondary structural elements (i.e., α-turns or β-strands that are usually 3 to 7 amino acids long) as the domain folds into its final 3D structure.

Strategy 2:

With the above strategy, different domains might have different numbers of PSN snapshots. However, it might be beneficial to consider the same number of PSN snapshots over all domains, for consistency. So, here, given all of the protein domains that we analyze, we first identify the length of the smallest domain. We find that the smallest domain is 30 amino acids long. Second, we define PSN snapshots of the smallest domain using the same approach as described above in strategy 1, which results in six PSN snapshots. Then, for each of the other considered protein domains, we create a multi-layer PSN with six PSN snapshots. That is, given a protein domain, we define incremental snapshots in the increments of 100/6 ~ 17% of amino acids in the corresponding protein domain.

To extract features of multi-layer PSNs created using each of the above two strategies, we rely on two existing measures, i.e., dynamic graphlet degree vector matrix (dGDVM)²⁸ and graphlet orbit transition matrix (GoTM)^29;37. Thus, we consider 2×2 = 4 combinations of multi-layer PSNs and their features. For more details, see Supplementary Section S2. Again, recall that we can use dynamic network features on our multi-layer PSNs because these PSNs are actually dynamic networks, per discussion in Section 1.2.

2.3 |. The classification framework

For each of the 72 datasets (Section 2.1), we train a logistic regression (LR) classifier for each of the considered PSN features (Section 2.2). Specifically, for a given dataset and a given feature, we perform 5-fold cross-validation. That is, first, we divide the dataset into five equal-sized folds (or subsets), where in each subset we keep the same proportion of different protein structural classes as present in the initial dataset. Second, for each such subset, we use the PSNs in the subset as the test data and the union of PSNs in the remaining four subsets as the training data.

But before we train an LR model using a training data and use it to predict classes of PSNs in a test data, we use the training data itself in a 5-fold cross validation manner^38;39 to perform hyper-parameter tuning, i.e., to choose an “optimal” value for the regularization hyper-parameter. We perform linear search on 10 equally-spaced log-scaled values between 2⁻⁸ and 2⁸ to find an optimal value. After we choose the “best” hyper-parameter value, we use it and all of the training data to train an LR model (Supplementary Section S4).

After training an LR model, we evaluate its performance on the test data using misclassification rate – the percentage of all PSNs from the test data that are not classified into their correct protein structural classes. We compute both aggregate and average misclassifiation rate. Aggregate misclassification rate is a single misclassification rate over all five folds, while average misclassification rate is the per-fold misclassification rate averaged over the five folds. For any of the considered features, for any of the considered datasets, we find negligible performance differences between the two measures. Hence, for each feature, for each dataset, we only report the corresponding aggregate misclassification rate for simplicity.

3 |. RESULTS AND DISCUSSION

We hypothesize that modeling (native, final, as available in the PDB) protein 3D structures using multi-layer, as opposed to single-layer, PSNs will capture more information about the 3D structural organization of proteins in the task of PSC. To confirm this hypothesis, it is necessary and sufficient for our proposed multi-layer unweighted unordered PSNs to outperform existing single-layer unweighted unordered PSNs. If additionally our multi-layer PSNs outperform the other, more advanced notions of single-layer weighted unordered PSNs and single-layer unweighted ordered PSNs (Section 2.2), then that would only further strengthen the importance of multi-layer PSN-based modeling of protein 3D structures. For each PSN type, we extract graphlet-based features from the corresponding PSNs (Section 2.2) and use the features in the task of PSC (Section 2.3). Because we consider four combinations of multi-layer PSN construction strategies and features (Section 2.2), in Section 3.1, we first evaluate the four combinations to choose the best one. Then, we compare the best combination, i.e., the best multi-layer PSN approach, to original PSNs (Section 3.2), weighted PSNs (Section 3.3), and ordered PSNs (Section 3.3), in the task of PSC. Finally, in Section 3.4, we summarize the overall performance of multi-layer PSNs compared to all existing PSN types combined.

3.1 |. Selection of the best multi-layer PSN approach

Recall that we use four combinations of multi-layer PSN construction strategies and features (or four multi-layer PSN approaches): strategy 1 with dGDVM, strategy 2 with dGDVM, strategy 1 with GoTM, and strategy 2 with GoTM (Section 2.2). We evaluate each multi-layer PSN approach on each of the 72 considered datasets in the task of PSC and obtain the corresponding 72 misclassification rates (Section 2.3). Then, we compare all four multi-layer PSN approaches to each other to check whether a given multi-layer PSN approach outperforms each of the other three multi-layer PSN approaches. Specifically, for each pair of approaches, we evaluate whether the misclassification rates of the given approach are significantly better (i.e., have lower values) than the corresponding misclassification rates of the other approach, using paired Wilcoxon rank sum test. Because we perform three pairwise comparisons for each of the four approaches, in total, we perform 3 × 4 = 12 pairwise comparisons. Thus, we obtain 12 p-values, which we correct using False Discovery Rate (FDR)⁴⁰ to obtain the corresponding adjusted p-values (i.e., q-values). We find that the multi-layer PSN approach based on strategy 1 with dGDVM significantly (q-value ≤ 10⁻⁶) outperforms the other three approaches (Supplementary Fig. S1). For this reason, in the following sections, we report results only for this multi-layer PSN approach.

In more detail, our results show that, if we keep the feature (i.e., dGDVM or GoTM) constant, then there are negligible performance differences between the two PSN construction strategies for each of the considered datasets (Supplementary Fig. S1). That is, dGDVM with strategy 1 works as well as dGDVM with strategy 2, and GoTM with strategy 1 works as well as GoTM with strategy 2. However, if we keep the PSN construction strategy the same, then there are significant performance differences between the two considered features. That is, dGDVM with strategy 1 outperforms GoTM with strategy 1, and dGDVM with strategy 2 outperforms GoTM with strategy 2, where we consider dGDVM with strategy 1 the best because it outperforms all others in a significant number of datasets. While it is desirable to explain exactly why a given feature (here, dGDVM) works better than the other (here, GoTM), this is often difficult because these approaches are heuristics. Consequently, more often than not, the performance of a heuristic feature (or in general, a heuristic computational approach) is dependent on the data/task in the consideration. For example, for our task of protein structural classification, dGDVM always outperforms GoTM irrespective of the dataset and irrespective of the PSN construction strategy that we consider. However, in the past, the two approaches have been used in another domain, i.e., for comparing different social networks to each other or different biological networks to each other³⁷, where dGDVM worked better than GoTM in about a half of the considered evaluation tests while GoTM worked better than dGDVM in the remaining half of the evaluation tests.

3.2 |. Multi-layer PSNs outperform original PSNs

To check whether multi-layer PSNs outperform original PSNs or vice versa, we compare the two PSN types by comparing their misclassification rates over all 72 datasets. That is, we check whether misclassification rates of multi-layer PSNs are better than original PSNs and vice versa, using the paired Wilcoxon rank-sum test (Section 3.1). Hence, we obtain two p-values, which we correct using FDR to obtain the corresponding q-values. We find that multi-layer PSNs significantly (q-value ≤ 10⁻⁶) outperform original PSNs (Figs. 2 and 3a).

FIGURE 2.

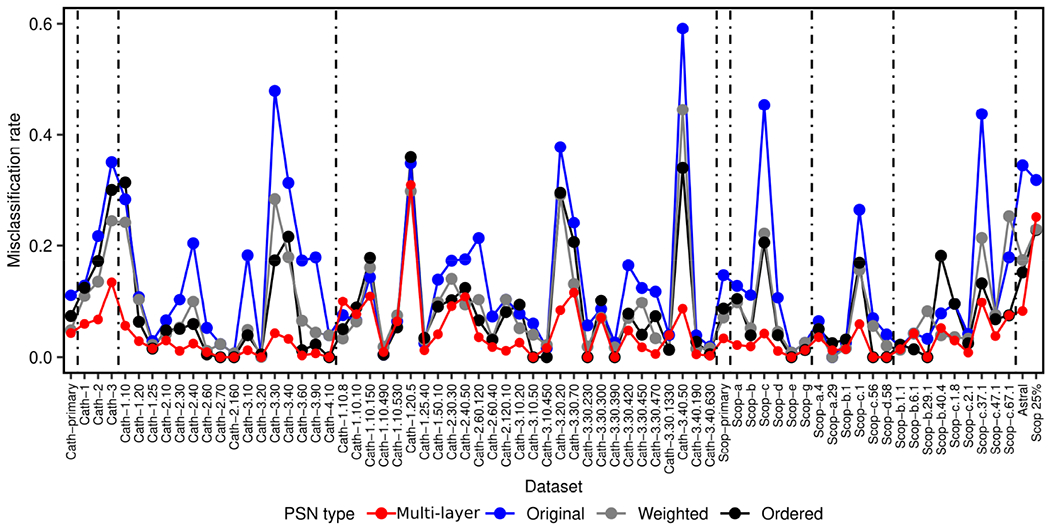
Misclassification rates of all four PSN types for each of the 72 datasets (48 from CATH, 22 from SCOPe, Astral, and Scop25%; Section 2.1). In red are results for our proposed multi-layer PSNs. In blue, gray, and black are results for the existing single-layer PSN types.

FIGURE 3.

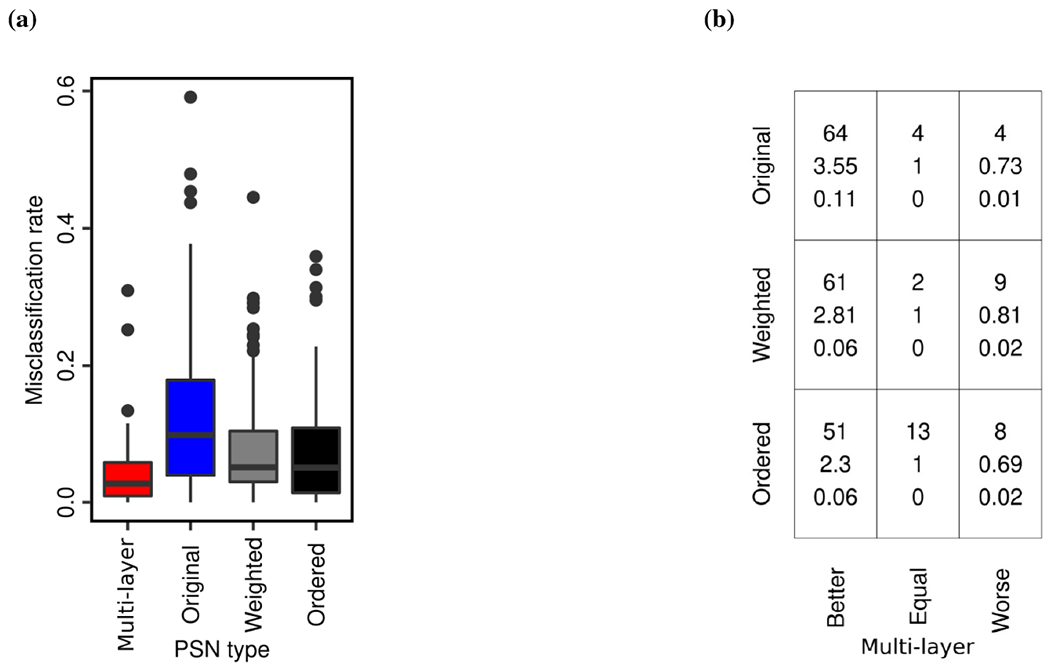
Performance summary of the four PSN types over all 72 datasets. Panel (a) compares distributions of the 72 misclassification rates between the four PSN types. Panel (b) compares multi-layer PSNs (x-axis) with each of the original, weighted, and ordered PSNs (y-axis). In a given cell in panel (b), the three numbers mean the following. The top number indicates the number of datasets in which multi-layer PSNs perform better than, the same as, or worse than the corresponding original, weighted, or ordered PSNs. The middle number indicates the relative increase (if greater than 1) or decrease (if less than 1) in the performance of multi-layer PSNs compared to original, weighted, or ordered PSNs. The bottom number indicates the absolute increase or decrease in the performance of multi-layer PSNs compared to original, weighted, or ordered PSNs.

In more detail (Fig. 3b), multi-layer PSNs are superior to original PSNs for 64 of the 72 datasets (i.e., ~89% of them). The two PSN types are tied for four of the 72 datasets (i.e., ~6% of them). Multi-layer PSNs are inferior to original PSNs for only four of the 72 datasets (i.e., ~6% of them). Thus, the 72 datasets can be partitioned into three groups, depending on whether multi-layer PSNs perform better than, the same as, or worse than original PSNs. Given a group of datasets, we quantify the increase or decrease in performance of multi-layer PSNs compared to original PSNs using relative change and absolute change between misclassification rates of the two PSN types. To compute relative change, we divide original PSNs’ average misclassification rate over all considered datasets with multi-layer PSNs’ average misclassification rate over all considered datasets. Hence, a relative change of more than one means that multi-layer PSNs are superior to original PSNs. A relative change of less than one means that multi-layer PSNs are inferior to original PSNs. A relative change of one means that the two PSN types perform the same. To compute absolute change, we take the absolute difference between original PSNs’ average misclassification rate over all considered datasets and multi-layer PSNs’ average misclassification rate over all considered datasets. We find that multi-layer PSNs are superior to original PSNs with a relative increase of 3.55 and an absolute increase of 0.11 in performance, while multi-layer PSNs are inferior to original PSNs with a relative decrease of 0.73 and an absolute decrease of 0.01 in performance (Fig. 3b). That is, multi-layer PSNs are not only superior for many more datasets than original PSNs, but also, multi-layer PSNs improve more on average upon original PSNs than the latter improve on average upon the former.

In particular, it is important to note that for the Astral dataset, multi-layer PSNs show a relative increase of 4.18 in performance over original PSNs, decreasing the misclassification rate from 0.344 to 0.082, which is close to “ideal” performance (i.e., to misclassification rate of 0). This is important because all domains in the Astral dataset come from a set of proteins with low (≤ 40%) sequence identities (Section 2.1). Hence, the likelihood of a sequence-based protein feature to work well for such dataset is low, and proposing a good 3D structure- or PSN-based protein feature for such dataset is important. Additionally, for the Scop25% dataset, multi-layer PSNs show relative and absolute increases of 1.30 and 0.074 over original PSNs, respectively, indicating superior performance of multi-layer PSNs over original PSNs even when we further decrease the sequence identities to ≤ 25% (Section 2.1).

3.3 |. Multi-layer PSNs outperform weighted PSNs and ordered PSNs

Next, we compare our multi-layer PSNs, which are unweighted and unordered, against each of the remaining two existing single-layer PSN types, i.e., weighted PSNs and ordered PSNs. We perform each comparison (multi-layer PSNs against weighted PSNs and multi-layer PSNs against ordered PSNs) the same way we have performed the comparison of our multi-layer PSNs against original PSNs in Section 3.2. We find that multi-layer PSNs significantly outperform both weighted PSNs (q-value ≤ 10⁻⁶) and ordered PSNs (q-value ≤ 10⁻⁶).

Similar to the way we quantify the performance increase or decrease of multi-layer PSNs against original PSNs in Section 3.2, we use relative and absolute changes to quantify the performance increase or decrease of multi-layer PSNs against weighted PSNs and against ordered PSNs. Regarding performance comparison of multi-layer PSNs against weighted PSNs, multi-layer PSNs are superior to weighted PSNs for 61 of the 72 datasets (i.e., ~85% of them), with a relative increase of 2.81 and an absolute increase of 0.06 in performance. The two PSN types are tied for two of the 72 datasets (i.e., ~3% of them). Multi-layer PSNs are inferior to weighted PSNs for only nine out of the 72 datasets (i.e., ~12% of them), with a relative decrease of 0.81 and an absolute decrease of 0.02 in performance (Fig. 3b). Regarding performance comparison of multi-layer PSNs against ordered PSNs, multi-layer PSNs are superior to ordered PSNs for 51 of the 72 datasets (i.e., ~71% of them), with a relative increase of 2.3 and an absolute increase of 0.06 in performance. The two PSN types are tied for 13 of the 71 datasets (i.e., ~18% of them). Multi-layer PSNs are inferior to ordered PSNs for only eight out of the 72 datasets (i.e., ~11% of them), with a relative decrease of 0.69 and an absolute decrease of 0.02 in performance (Fig. 3b). That is, multi-layer PSNs are not only superior for many more datasets than weighted and ordered PSNs, but also, multi-layer PSNs improve more on average upon weighted and ordered PSNs than the latter two improve on average upon the former.

Similar to the results in Section 3.2, multi-layer PSNs show a decent performance boost for the Astral dataset compared to each of the weighted PSNs and ordered PSNs. That is, for the Astral dataset, multi-layer PSNs show a relative increase of 2.12 in performance over weighted PSNs and a relative increase of 1.85 in performance over ordered PSNs, decreasing the misclassification rate of 0.174 for weighted PSNs and of 0.152 for ordered PSNs to 0.082. However, for the Scop25% data, multi-layer PSNs show a relative decrease of 0.94 and 0.89 compared to weighted PSNs and ordered PSNs, respectively, with the corresponding (minor) absolute decreases of 0.016 and 0.026.

3.4 |. Summary of the performance of multi-layer PSNs

So far, we compared multi-layer PSNs against each of the existing three single-layer PSN types individually. Here, we compare multi-layer PSNs against all of the existing single-layer PSN types at the same time, in order to evaluate the performance of multi-layer PSNs against the best of the existing PSN types for each of the 72 datasets. Consequently, we find that multi-layer PSNs perform strictly better than all existing PSN types for 44 datasets, while they are tied with the best of the existing PSN types for 14 datasets. That is, for 44 + 14 = 58 of the 72 datasets (i.e., ~81% of them), multi-layer PSNs perform the best. For the remaining 14 of the 72 datasets (i.e., ~19% of them), at least one of the existing single-layer PSN types is better than multi-layer PSNs.

Given the above two groups of datasets (the 58 datasets where multi-layer PSNs are the best and the 14 datasets where multi-layer PSNs are not the best), we examine whether any of the two groups are biased towards any of the four hierarchy levels of CATH or SCOPe. We do this to understand whether multi-layer PSNs are more likely to perform better or worse for datasets from a certain hierarchy level of CATH or SCOPe. Specifically, given a group of datasets and a hierarchy level of CATH or SCOPe, we evaluate whether the given group contains a statistically significantly high number of (i.e., is enriched in) datasets from the given hierarchy level, and we do so by using the hypergeometric test⁴¹ (Supplementary Section S5). Because there are two groups of datasets and 4 + 4 = 8 CATH and SCOPe hierarchy levels, in total, we perform 16 hypergeometric tests and obtain the corresponding 16 p-values. We correct the p-values using FDR to obtain the corresponding q-values. We find that the group of datasets where multi-layer PSNs perform the best is statistically significantly (q-values < 0.05) enriched in each of the four hierarchy levels of CATH and SCOPe, or equivalently that the group of datasets where multi-layer PSNs do not perform the best is not enriched in any of the hierarchy levels. This shows that multi-layer PSNs perform consistently well for all four hierarchy levels of CATH and SCOPe.

4 |. CONCLUSION

We propose to capture the (native, final, as available in the PDB) 3D structural organization of a protein using a multi-layer PSN. We hypothesize that our multi-layer PSNs should capture more of 3D structural information than existing single-layer PSNs in the task of protein structural classification (PSC), where the latter have already been established as a state-of-the-art compared to traditional sequence and 3D structural PSC approaches. We evaluate our hypothesis on protein domains and corresponding 3D structural labels from CATH and SCOPe databases. We show that our multi-layer PSNs significantly outperform all existing single-layer PSN types in the task of PSC. Our results are thus expected to guide future development of PSC approaches. Additionally, because we show that multi-layer PSNs capture more complete 3D structural information of proteins than single-layer PSNs, our study opens up opportunities to explore protein folding-related research questions using multi-layer, rather than single-layer, PSNs.

We believe that our multi-layer PSNs outperform the existing single-layer PSNs because the former are a more detailed model of the 3D structural organization of a protein than the latter. That is, in a multilayer PSN, going from one PSN snapshot to another clearly highlights how the (native, final, as available in the PDB) protein structure changes with the subsequent addition of amino acids of the protein in a sequential order, which is reflected in the network structural changes of the corresponding PSN snapshots. Intuitively, these inter-snapshot network structural changes is exactly what is captured by the dynamic graphlet approach that we use in our work to extract features from multi-layer PSNs. Hence, multi-layer PSNs, together with the dynamic graphlet approach, help in capturing more detailed protein 3D structural information than single-layer PSNs.

There is a room for further improvement in our approach to create a multi-layer PSN. Namely, we create a multi-layer PSN of a protein in a step-wise manner, where we add subsequent native sub-structure of the protein starting from the N-terminus to the C-terminus to imitate the protein folding process, which is motivated by several theoretical^42;20, simulation²³, and experimental^43;12 studies. More specifically, given information about the native 3D structure of a protein, we convert it into a multi-layer PSN by forming PSN snapshots corresponding to incremental cumulative groups of amino acids (i.e., sub-sequences) of the protein, where we add a fixed number of amino acids (that approximates individual secondary structural elements) at each subsequent snapshot. However, adding a fixed number of amino acids in subsequent snapshots (or “folding steps”) of a protein might not be ideal because for some proteins it has been shown that the folding occurs by adding protein sub-structures called “foldons”¹², where the length of a foldon is not fixed and can span from one to multiple secondary structural elements. Hence, creating a multi-layer PSN of a protein by using known foldons of the protein, instead of a fixed number of amino acids as we do, to define PSN snapshots might be more biochemically meaningful. Similar holds for using actual folding intermediates (as defined in Section 1) to define PSN snapshots. However, there is no large-scale experimental data available about foldons of different proteins, besides a few experimental studies that cover a limited number of proteins^12;43. Similarly, per discussion in Section 1, there is no large-scale experimental data about folding intermediates. So, our multi-layer PSN model is the best that currently can be done. And while potentially imperfect, as we have shown in this study, the current model is the new state-of-the-art in the task of PSC. In the future, as more experimental data on foldons or folding intermediates might be collected, incorporating such data into the multi-layer PSN model might only further increase its biochemical meaningfulness.

Data availability

The data and code are available at https://nd.edu/~cone/MultilayerPSN/.