Summary
Animals adaptively integrate sensation, planning, and action to navigate toward goal locations in ever-changing environments, but the functional organization of cortex supporting these processes remains unclear. We characterized encoding in approximately 90,000 neurons across mouse posterior cortex during a virtual-navigation task with rule-switching. The encoding of task and behavioral variables was highly distributed across cortical areas but differed in magnitude, resulting in three spatial gradients encoding visual cue, spatial position plus dynamics of choice formation, and locomotion, with peaks respectively in visual, retrosplenial, and parietal cortices. Surprisingly, the conjunctive encoding of these variables in single neurons was similar throughout posterior cortex, creating high-dimensional representations in all areas instead of revealing computations specialized for each area. We propose that, for guiding navigating decisions, posterior cortex operates in parallel rather than hierarchically, and collectively generates a state representation of the behavior and environment, with each area specialized in handling distinct information modalities.
In Brief
In mice navigating in dynamic environments, Tseng, Chettih et al. find highly distributed but specialized encoding of visual, cognitive, and locomotor signals in posterior cortex with similar conjunctive codes across areas. They propose posterior cortex integrates distinct information modalities to form a general-purpose state representation of the environment and behavior.
Introduction
As an animal navigates an ever-changing environment, it adaptively incorporates acquired sensory information into a navigation plan to guide its movements. The neural circuits supporting this behavior must integrate sensory processing, navigation planning, and motor execution, and furthermore adapt the rules governing their integration in response to experience. Evidence in rodents suggests densely interconnected dorsal-posterior cortical areas are critical for visually guided and navigation-based decision-making, including primary (V1) and secondary visual cortices, retrosplenial cortex (RSC), and posterior parietal cortex (PPC) (Zingg et al., 2014). However, it remains uncertain how the set of processes for navigation-based decision-making are represented across posterior cortex, and what principles specify the functional organization of these areas.
A longstanding view is that cortex is organized as anatomically and functionally distinct modules that encode different information, reflecting their specialized functions. Accordingly, many studies have aimed to identify how specific areas contribute to behavior by identifying the variables each area encodes. For example, visual areas in posterior cortex encode visual features with increasing complexity between primary and secondary areas and are proposed to serve distinct functions in visual processing (Andermann et al., 2011; Glickfeld and Olsen, 2017; Marshel et al., 2011; Siegle et al., 2021). PPC has roles in accumulating sensory evidence and history-dependent signals (Hanks et al., 2015; Hattori et al., 2019; Hwang et al., 2017; Morcos and Harvey, 2016; Pinto et al., 2019), transforming stimuli into motor outputs (Goard et al., 2016; Harvey et al., 2012; Licata et al., 2017; Pho et al., 2018; Raposo et al., 2014), and monitoring navigation route progression (Nitz, 2006), often in egocentric coordinates (Nitz, 2012; Wilber et al., 2014). In RSC, information for navigation and spatial memory is prevalent, including for heading direction (Cho and Sharp, 2001; Jacob et al., 2017), landmark cues (Fischer et al., 2020), and goal locations (Miller et al., 2019; Vale et al., 2020), and is often represented as conjunctions of variables in an allocentric reference frame (Alexander and Nitz, 2017).
Recent studies have observed that the encoding of actions and spatial position is distributed widely across posterior cortex and, relatedly, that individual areas encode many variables (Allen et al., 2017, 2019; Kauvar et al., 2020; Minderer et al., 2019; Musall et al., 2019; Steinmetz et al., 2019; Stringer et al., 2019). Furthermore, even sensory areas like V1 exhibit conjunctive, multi-modal tuning (Keller et al., 2012; Saleem et al., 2018; Shuler and Bear, 2006). It is unclear how to reconcile this highly distributed encoding in posterior cortex with evidence for specialized functions in distinct areas. One possibility is that studies proposing specialized functions typically examined only one or two cortical areas with different experimental designs, and thus underemphasized the commonalities in encoding across areas. Another possibility is that some variables are encoded in a distributed manner and others more modularly. In particular, distributed encoding of bodily movements observed during spontaneous or simple behaviors might contrast with modular encoding of cognitive variables in more complex tasks.
Functional organization is determined not only by the “distributedness” of encoding for individual variables but also the pattern of variable combinations in single neurons and the resulting population geometry of encoding for multiple variables. For instance, given distributed encoding of two variables, one area may encode each variable in separate neurons and relay them to distinct downstream targets, whereas another area may perform arithmetic manipulation of the two to generate new quantities useful for specialized computations. Areas may build increasingly complex multi-modal, high-dimensional population codes along a functional hierarchy (Bernardi et al., 2020; Rigotti et al., 2013). Alternatively, even if areas specialize in which variables they encode, variables may be combined in similar ways across areas, suggesting general rules of integration that underlie shared computational goals. Thus, a quantitative analysis of functional organization must look beyond the “distributedness” of encoding for single variables to consider the “conjunctive structure”, namely the way variables are integrated by single neurons and the resulting geometry of population representations.
Here we determine how the various processes underlying flexible, navigation-based decision-making are functionally organized, using a single experimental and analysis framework for quantitative comparison of the encoding of ~90,000 neurons across posterior cortex. We find that encoding of all variables is more distributed than modular, despite significant differences in encoding strength across areas for visual, locomotor, position, and choice variables. Surprisingly, each area does not create unique conjunctions of variables, as would be expected for areas performing distinct computations. Instead, all areas combine variables similarly, resulting in a high-dimensional representation of variable conjunctions that is shared across areas. We propose that posterior cortical areas integrate qualitatively distinct input modalities to form a general-purpose state representation of the environment and behavior, which is used by downstream circuits to guide flexible navigation decisions.
Results
Mice learned flexible cue-choice associations in a virtual reality decision-making task
We designed a behavioral task to study how sensation, planning, movement, and recent experience are integrated during navigation decisions. Mice were trained to navigate a virtual reality Y-maze using visual cues (black or white walls) to make decisions to run toward rewarded locations (left or right arms), based on learned and changing rules (Figure 1A, 1B and S1A). We switched the rule determining the rewarded cue-choice associations every 100–175 trials in a session, without explicitly signaling the rule or rule switch. To maximize reward, the mouse had to combine the visual cue with an estimate of the current rule to generate a choice and update its rule estimate following reward.
Figure 1. Diverse decision-making strategies during flexible navigation decisions and photoinhibition in posterior cortex.
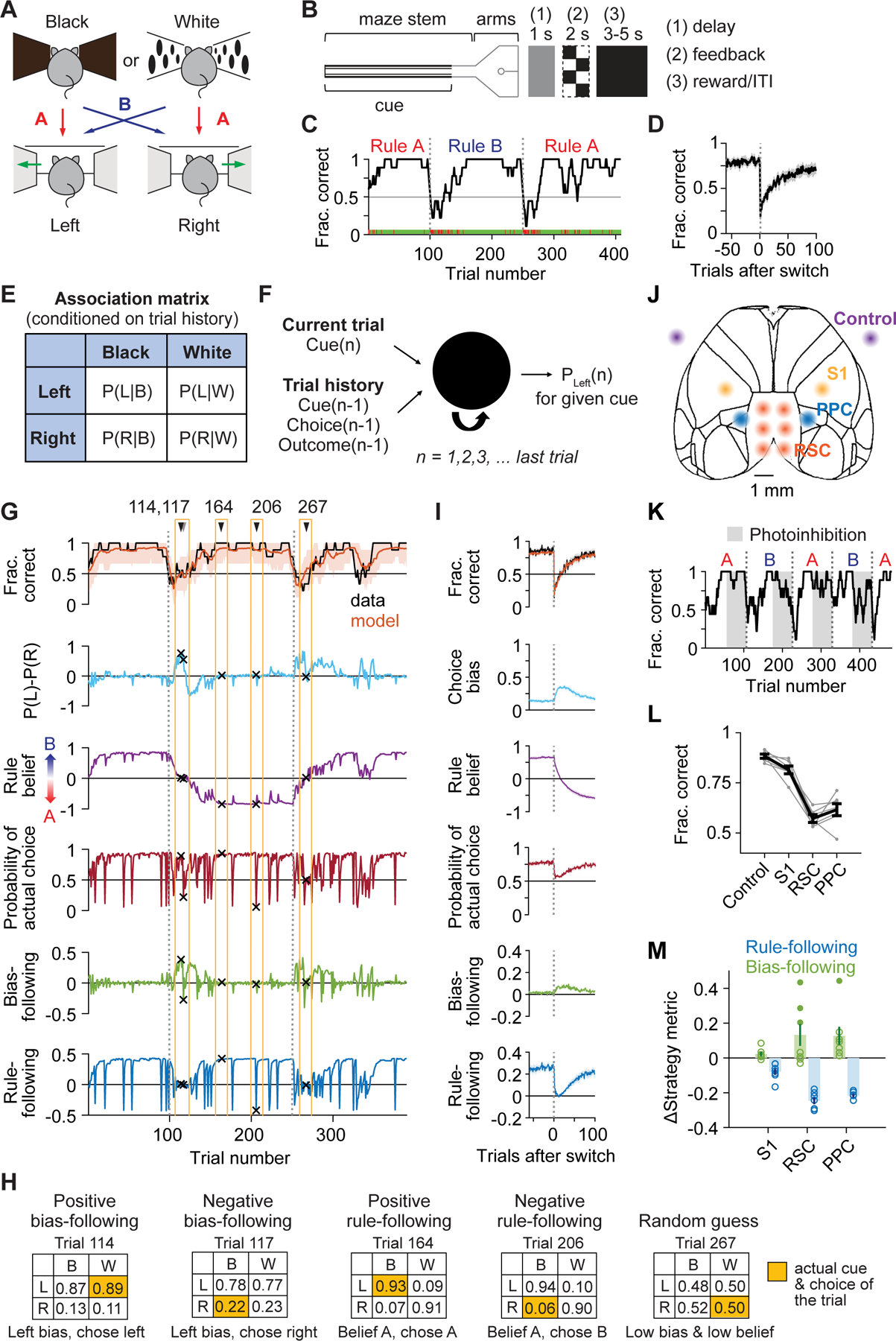
(A) Rewarded cue-choice associations for rules A and B.
(B) Maze configuration and structure of trial epochs. At the trial end, after a delay, mice received visual feedback about the correctness before a reward and inter-trial interval.
(C) Task performance for an example session. Green ticks, correct trials; red ticks, incorrect trials; black line, smoothed performance (boxcar of 9 trials); gray dashed line, rule switches.
(D) Switch-aligned performance. n = 513 switches from 8 mice.
(E) Association matrix used to quantify strategy variables: the probability of choosing left or right given a black or white cue for a given trial, conditioned on its trial history.
(F) Schematic of LSTM for deriving the association matrix on each trial.
(G) Modeled fraction correct and strategy variables for an example session. Orange shading, 90% CI from 1000 simulations of task performance from the model.
(H) Association matrices for the 5 example trials in (G).
(I) Switch-aligned modeled fraction correct and strategy variables. n = 265 switches.
(J) Bilateral inhibition sites in VGAT-ChR2 mice.
(K) Task performance of an example session during photoinhibition.
(L) Effects of photoinhibition on task performance. Gray lines, individual mice; black line, all mice. Control vs. RSC or PPC: p < 10−4; control vs. S1: p = 0.0002; S1 vs. RSC or PPC: p < 10−4; RSC vs. PPC: p = 0.058. n = 164 sessions from 7 mice.
(M) Effects of photoinhibition on strategy variables, measured as differences from control. Open circles, average for individual mice. For bias-following, p = 0.025 for S1, p = 0.018 for RSC, p < 10−4 for PPC; for rule-following, p < 10−4 for all targets. Filled circles indicate mice with large increase in bias-following (greater than 0.2; 3 mice for RSC and one mouse for PPC).
Data and statistics in (D), (I), (L), (M) are presented as hierarchical bootstrap mean ± SEM.
See also Figure S1.
After training, mice learned both rules and adapted to rule switches over tens of trials multiple times within a single session (Figure 1C). Their behavioral performance was high before rule switches and typically dropped below chance after switches before gradually recovering to high accuracy by the end of a block, without signs of anticipating rule switches (Figure 1D and S1B–S1F). This task encouraged behavioral variability driven by trial-and-error even in expert mice, particularly following rule switches, as we characterize below.
Decision-making strategy varied between rule-guided, biased, and random modes
The performance of the mouse varied greatly within a session, including high performance before rule switches and many errors immediately after rule switches. A mouse’s choice might reflect a variety of time-varying strategies such as following a specific cue-choice mapping based on a rule, or repeatedly making the same choice regardless of the cue identity, or making random choices. We modeled decision-making strategy on each trial by estimating the conditional probability that the mouse would select a choice given a specific cue and its trial history using a long short-term memory recurrent neural network (LSTM) (Figure 1E and 1F). The LSTM accurately predicted a mouse’s choices in held-out sessions (80.2% ± 5.1%, mean ± SD) and served as a simple descriptive model, in contrast to more interpretable but less accurate reinforcement learning models (Figure S1G and S1H).
We extracted a set of strategy variables using the model to describe a wide range of behaviors exhibited during flexible decision-making (STAR Methods – Decision-making strategy variables). From model predictions, we computed “rule belief” as the probability that the cues informed choices consistent with one rule versus the other, and “choice bias” as the tendency to choose left versus right independent of the cue. In individual sessions, we observed periods of strong rule belief (Figure 1G and 1H, example trials 164, 206), choice bias (trials 114, 117), and unpredictable choices or “random guessing” (trial 267). We also compared model predictions to the mouse’s actual choice to determine the degree to which individual decisions were influenced by bias (bias-following) or rule belief (rule-following). These metrics were positive when actual choices followed a bias (example trial 114) or rule belief (trial 164), negative when choices were opposite a bias (trial 117) or rule belief (trial 206), and near zero for random guessing.
On average, prior to a rule switch, mice performed with little choice bias and followed the correct rule (Figure 1I and S1I). After a rule switch, the randomness of choices increased rapidly, as seen by near chance levels of the model’s probability of the actual choice, and bias-following increased moderately. Then, rule-following recovered gradually for the new rule belief. Although behavior on individual rule blocks and sessions was highly variable around these average trends (Figure S1J), our strategy variables quantified these variations at a single-trial level. This task and behavioral modeling thus dissociated both cue and choice from the diverse decision-making strategies on a trial-by-trial basis.
Photoinhibition of posterior cortical areas impaired rule-following
Previous studies have indicated that various areas of posterior cortex are necessary for navigation and decision-making, including RSC and PPC (Harvey et al., 2012; Licata et al., 2017; Pinto et al., 2019). We tested the necessity of these areas using transcranial optogenetic excitation of GABAergic interneurons, leading to inhibition of nearby excitatory cells (Figure 1J) (Guo et al., 2014; Li et al., 2019). Inhibition was performed throughout maze traversal on randomized trials after mice reached high performance between rule switches (Figure 1K). Inhibiting either RSC or PPC led to markedly lower task performance compared to control trials or trials in which part of primary somatosensory cortex (S1) was inhibited (Figure 1L).
We analyzed the behavioral changes underlying impaired task performance by including the inhibition sites as an input to our LSTM model of decision-making strategy. PPC and RSC inhibition decreased rule-following compared to control trials and S1 inhibition (Figure 1M, S1K and S1L). Inhibition also caused large increases in bias-following in a subset of mice (Figure 1M, filled green dots), but this was inconsistent across mice and uncorrelated with effects on rule-following (Figure S1M). Our results are consistent with and extend previous work using tasks with static rules in which inhibition of PPC did not disrupt basic sensory or motor function but prevented abstract sensory cues from appropriately guiding actions (Harvey et al., 2012), which in our study was quantified as rule-following.
Running trajectories reflected the within-trial dynamics of choice formation
Mice used the presented cue and their rule belief to report their choice at the end of the maze. However, the choice might develop at any point in the trial and with different time courses from trial to trial, potentially depending on the mouse’s decision-making strategy. We reasoned that choice formation might be reflected in the running of the mouse during navigation. For example, early in a trial, mice might exhibit movements in preparation to report their choice when confident (Figure 2B; right panel, trials 1 and 2) but may delay such movements (trial 3) or alternate between options (trial 4) when uncertain. Indeed, mice exhibited diverse running trajectories in the maze stem which were typically predictive of the choice reported at the end of the trial, even though the virtual heading and lateral position in the maze were fixed by task design until the end of the maze stem (Figure 2A; 2B, left panel; Figure S2A). This variability in running trajectories increased following a rule switch, suggesting that running variability reflected differences in underlying decision-making strategies (Figure 2C and S2B).
Figure 2. Choice formation estimated from running trajectories.
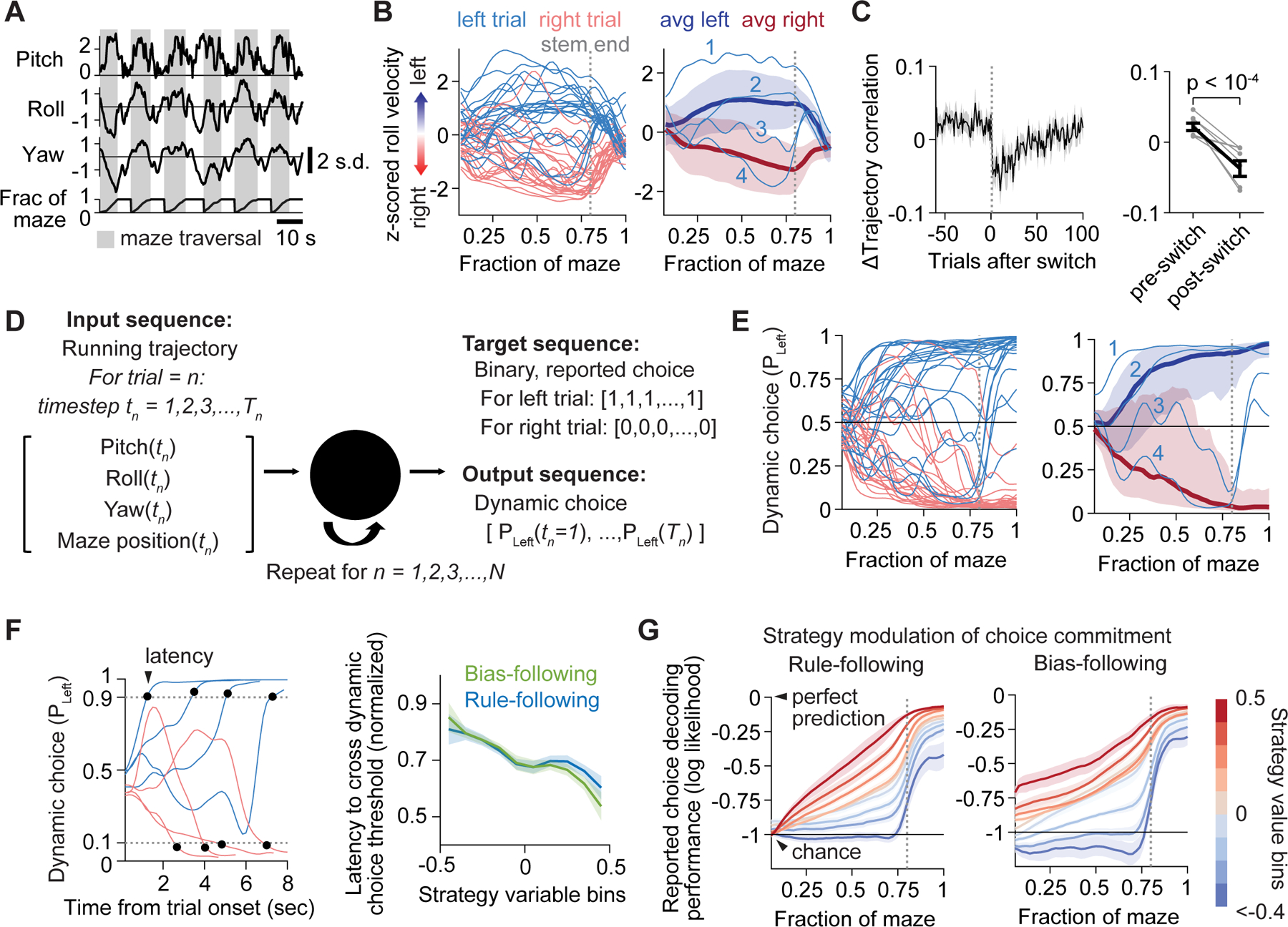
(A) Example normalized treadmill velocities and position in the maze.
(B) Roll velocity aligned to maze position. Left: example single trials from one session. Right: four example left trials compared to average left and right trials; mean ± SD.
(C) Correlation of running trajectories for choice-matched trials, measured as difference from session average, aligned to the switch (left; n = 265 switches) or averaged for 20 trials before vs. after switches (right; gray lines, individual mice).
(D) Schematic of LSTM for decoding reported choice from running trajectories. The output is dynamic choice (Pleft).
(E) Dynamic choice for same data shown in (B).
(F) Left: latency to dynamic choice crossing a threshold (dashed line) for example trials. Right: relationship between latency (normalized by session-averaged trial duration, 8.95 ± 2.04 sec, mean ± SD) and strategy variables. n = 85,463 trials.
(G) Time course of choice commitment (LSTM decoding performance for reported choice, calculated as log likelihood with log base 2), binned by values of rule-following (left) and bias-following (right). n = 68,249 trials.
Data and statistics in (C), (F), (G) are presented as hierarchical bootstrap mean ± SEM.
See also Figure S2.
To estimate choice formation from running, we quantified how well the running trajectory in a single trial predicted the mouse’s reported choice on that trial with an LSTM (Figure 2D). At each timepoint, the model used all previous timepoints to estimate the probability that the mouse eventually chose left or right. This estimate evolved with varying time courses and settled on correct predictions at different maze positions in different trials, recapitulating the variability seen in running trajectories (Figure 2E). We termed this quantity “dynamic choice”, to distinguish it from the binary, reported choice, and interpret it as a real-time estimate of the mouse’s choice formation. We also observed running trajectories that reflected the identity of the cue early in a trial, which we refer to as “cue-biased running”; however, this behavior was variable across mice and sessions and was uncorrelated with task performance and the time course of dynamic choice (Figure S2C–S2K).
We validated our interpretation of dynamic choice by demonstrating that it varied in an expected manner with differences in decision-making strategy. In particular, when a mouse is confident in its choice, due to high rule- or bias-following, it will select its choice more rapidly than trials with random or unpredictable choices (rule- or bias-following ≤ 0). As expected, the latency to dynamic choice crossing a threshold was shorter on trials with higher rule- or bias-following (Figure 2F). We then analyzed how strategy shaped the within-trial time course of dynamic choice by calculating how accurately dynamic choice at each timepoint predicted the actual reported choice (“choice commitment”). On trials with high rule-following, choice commitment started near chance but increased rapidly during maze traversal (Figure 2G). In contrast, when rule-following was low, choice commitment was low until late in the trial, consistent with indecisiveness or changes of mind when mice were uncertain of the rule. Furthermore, when mice followed a bias, choice commitment was high at trial onset, reflecting a choice formed early and irrespective of the cue. Bias-following and rule-following thus both affected choice commitment with distinct and sensible dynamics (Figure S2L), and consistent effects were observed in photoinhibition experiments (Figure S2M). Our findings support the interpretation that running trajectories reveal nuances of decision-making beyond the reported choice.
Calcium imaging of neural activity across posterior cortex
The task and behavioral modeling allowed for the study of neural representations of visual, motor, and a variety of cognitive variables, including choice and decision-making strategy. To determine the functional organization of posterior cortex, we aimed to quantify the spatial distribution of the encoding for these variables and their conjunctive structure. We used two-photon calcium imaging to measure the activity of hundreds of neurons simultaneously in a local region as mice performed the task and tiled imaging windows across posterior cortex over multiple sessions (Figure 3A and 3B). Within each mouse, we sampled neurons across V1, areas adjacent and medial to V1 (anteromedial, or AM, and posteromedial, or PM), areas between V1 and S1 (anterior, or A, and a small portion of rostrolateral, or RL), RSC, and an area adjacent and lateral to RSC (mediomedial, or MM) (Gămănuț et al., 2018; Paxinos and Franklin, 2013). Using surface vasculature patterns and retinotopic mapping, we registered all fields-of-view into the Allen Institute Mouse Common Coordinate Framework (CCF) and assigned coordinates to 93,881 layer 2/3 neurons imaged from 141 sessions of 8 mice (Figure 3C, 3D and S3A–S3C). This registration permitted analysis of neural activity as a function of cortical location, without assuming pre-defined area boundaries.
Figure 3. Calcium imaging in posterior cortex and encoding of instantaneous movement and task variables.
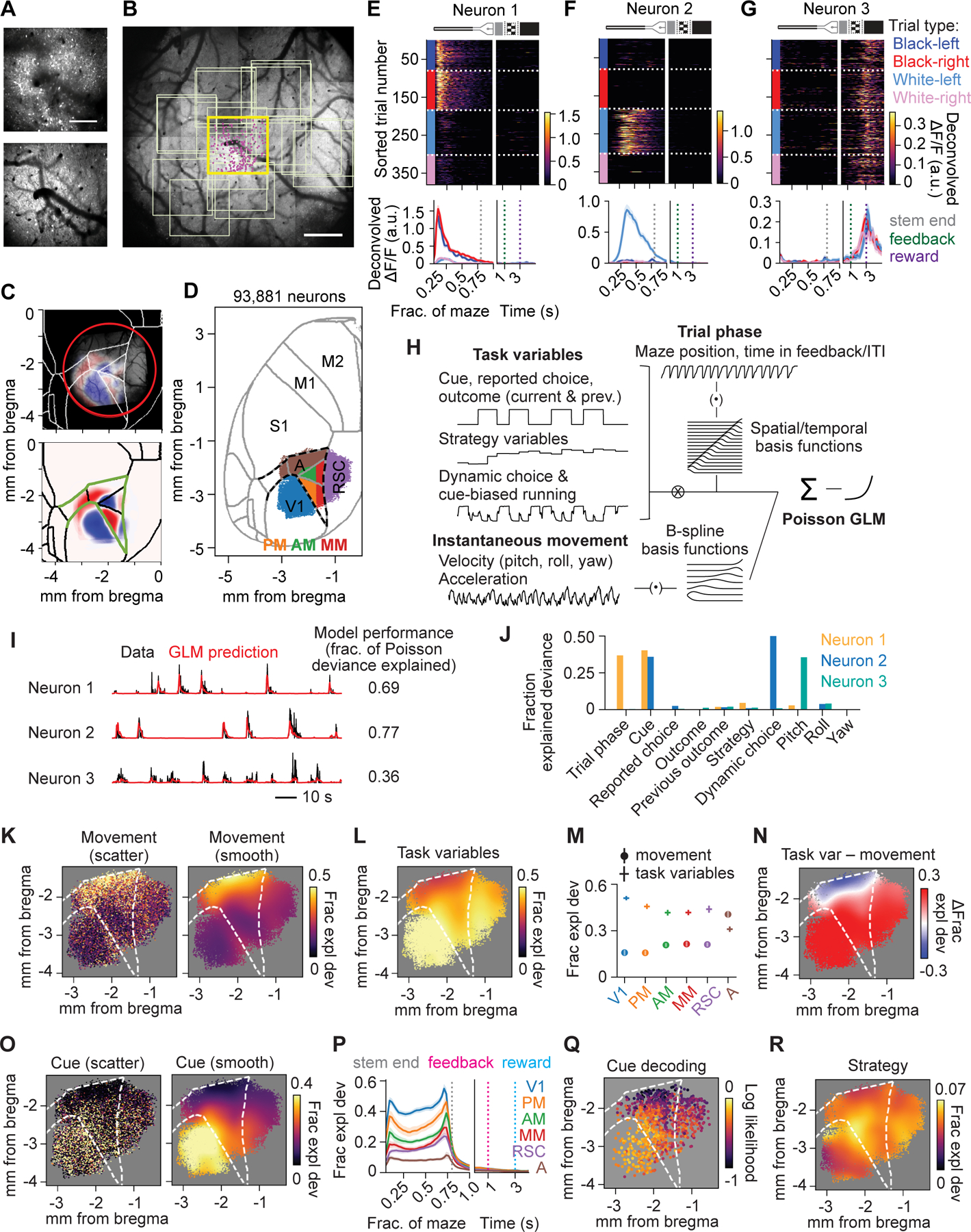
(A) Example mean GCaMP6s image (top) and overlying vasculature pattern near the brain surface (bottom) for an example field of view (FOV).
(B) Overview image of the vasculature pattern within the cranial window. Yellow box, location of the FOV in (A); pink dots, locations of neurons recorded in that FOV; light yellow boxes, other FOVs.
(C) Top: Registered field sign map overlaid with the vasculature pattern in (B). White lines, area contours from Allen Institute Mouse CCF; red circle, cranial window location. Bottom: Mean field sign map of 8 mice. Green lines: anterior medial border of V1, lateral border of RSC, and posterior border of S1; used as anatomical landmarks in subsequent figures.
(D) Parcellation of all recorded neurons into 6 discrete areas, overlaid with area borders from CCF. n = 93,881 neurons from 141 sessions from 8 mice.
(E-G) Deconvolved activity of three example RSC neurons. Top: heatmap of single trial activity sorted by trial types. Bottom, trial-type average activity; mean ± SEM. The x-axis is in spatial units during maze traversal and in time units during feedback period/ITI.
(H) Schematic of the GLM.
(I) Example traces of deconvolved activity and GLM prediction on held-out data for the three neurons shown in (E-G).
(J) Encoding profiles (fraction explained deviance for individual variables) of the three neurons in (E-G).
(K) Left: encoding magnitude of instantaneous movement for single neurons (individual dots) at their cortical locations. Right: smoothed encoding map (Gaussian filter, SD = 150 μm). n = 42,998 well-fit neurons from 8 mice.
(L) Smoothed encoding map for task variables.
(M) Average encoding magnitude of instantaneous movement and task variables for 6 areas. Hierarchical bootstrap mean ± SEM. (error bars for movement are contained in the symbols). Area A had higher encoding for movement and lower encoding for task variables than every other area (p < 10−3), while V1 had higher encoding for task variables than every other area (p < 10−3).
(N) Smoothed map showing difference between encoding magnitude of task variables and movement.
(O) Left: encoding magnitudes of cue for individual neurons during stem traversal at their cortical locations. Right: smoothed encoding map.
(P) Time course of cue encoding for 6 areas for sessions with cue offset at 0.76 of maze length. Hierarchical bootstrap mean ± SEM.
(Q) Decoding performance for cue from population activity, quantified as log likelihood with log base 2. Each point represents one population decoder consisting of ~100 nearby neurons, plotted at the mean location of all member neurons. n = 974 decoders.
(R) Encoding map of strategy variables, including individual strategy variables and their interactions with task variables.
Single neurons had diverse responses across trial types, and many were seemingly selective for specific maze positions or time points within a trial (“trial phase”) (Figure 3E–3G). To systematically quantify and distinguish the contributions of many visual, cognitive, and motor components, we built a generalized linear model (GLM) to fit and predict the activity of single neurons (Figure 3H). Predictors of neural activity included task variables like cue, strategy variables and dynamic choice, as well as variables of instantaneous movement, measured as rotational velocities and accelerations of the treadmill around three axes.
The GLM explained a substantial amount of moment-to-moment variability in a neuron’s activity (fraction of Poisson deviance explained: 0.25 ± 0.17, mean ± SD; Figure 3I and S3D–S3F), and for subsequent analyses, we focused on well fit neurons although results were robust to this criterion (Figure S8K–S8O). To build an encoding profile for each neuron, we quantified the fraction of explained deviance accounted for by each individual variable by measuring the decrease in cross-validated prediction performance after zeroing the variable’s coefficients or by refitting the GLM after excluding a given variable (Figure 3J, S3G and S3H).
Distinct encoding gradients for task variables and instantaneous movement
To examine the distribution of encoding, we constructed encoding maps by plotting each neuron’s fraction of explained deviance for selected variables at the neuron’s cortical location and smoothed these maps to show trends over space. We observed that the encoding of both task variables and instantaneous movement was present throughout all areas (Figure 3K and 3L). However, the encoding of task variables exhibited an anterior-posterior gradient with highest strength in V1, intermediate in RSC, and lowest in area A, whereas movement encoding strength exhibited a gradient in the opposite direction (Figure 3M, 3N and S4A–S4I). Posterior cortex therefore had widespread encoding of both task variables and instantaneous movement, consistent with previous literature (Musall et al., 2019; Stringer et al., 2019), but with distinct quantitative gradients.
Encoding of the visual cue identity was strongest in V1 and neighboring areas AM and PM, weaker in RSC, and weakest in area A (Figure 3O, S4J and S4K), which was corroborated with decoding of these variables from the activity of ~100 simultaneously recorded neurons (Figure 3Q). Cue encoding increased rapidly after cue onset and decreased after the cue disappeared, without major differences in the average time course between areas (Figure 3P). Variables related to the decision-making strategy, including their interactions with other task variables, collectively exhibited a moderate encoding strength distributed evenly across posterior cortex (Figure 3R and S4L–S4O). Strategy variables reflect a complex function of trial history, but we also examined direct representations of the previous trial’s cue, choice, and outcome (Akrami et al., 2018; Hattori et al., 2019; Hwang et al., 2019; Koay et al., 2021; Morcos and Harvey, 2016). The previous trial’s outcome was much more strongly encoded than the previous trial’s cue or choice, which may relate to the task demands imposed by rule-switching, and its encoding was evenly distributed over space (Figure S4P–S4S). In summary, whereas cue encoding showed a gradient with enrichment in visual areas, decision-making strategy had modulatory and widespread effects on activity in posterior cortex.
Encoding of dynamic choice was enriched in RSC and distinct from instantaneous movement
We next examined where and how choice was encoded across posterior cortex. We considered that, as mice traversed the maze, neural activity may be more related to dynamic choice than the eventual reported choice because dynamic choice approximates the actual time course of the mouse’s choice formation within a trial. Indeed, during traversal of the maze stem, encoding of dynamic choice was distributed across all areas but enriched in RSC and adjacent medial areas, accounting for a substantial amount of neural activity compared to near-zero encoding of reported choice (Figure 4A, 4B and S5A, S5D, S5E). In contrast, during the feedback and ITI periods, we observed greater encoding of reported choice than dynamic choice (Figure 4C and S5B–S5E). This is sensible since choice encoding during the feedback epoch is a memory of a recent decision, rather than an evolving variable linked to ongoing movements. The magnitude and spatial distribution of choice encoding was similar between the maze stem and feedback epochs, with a medial-to-lateral gradient distinct from cue and movement.
Figure 4. Encoding of choice and maze position.
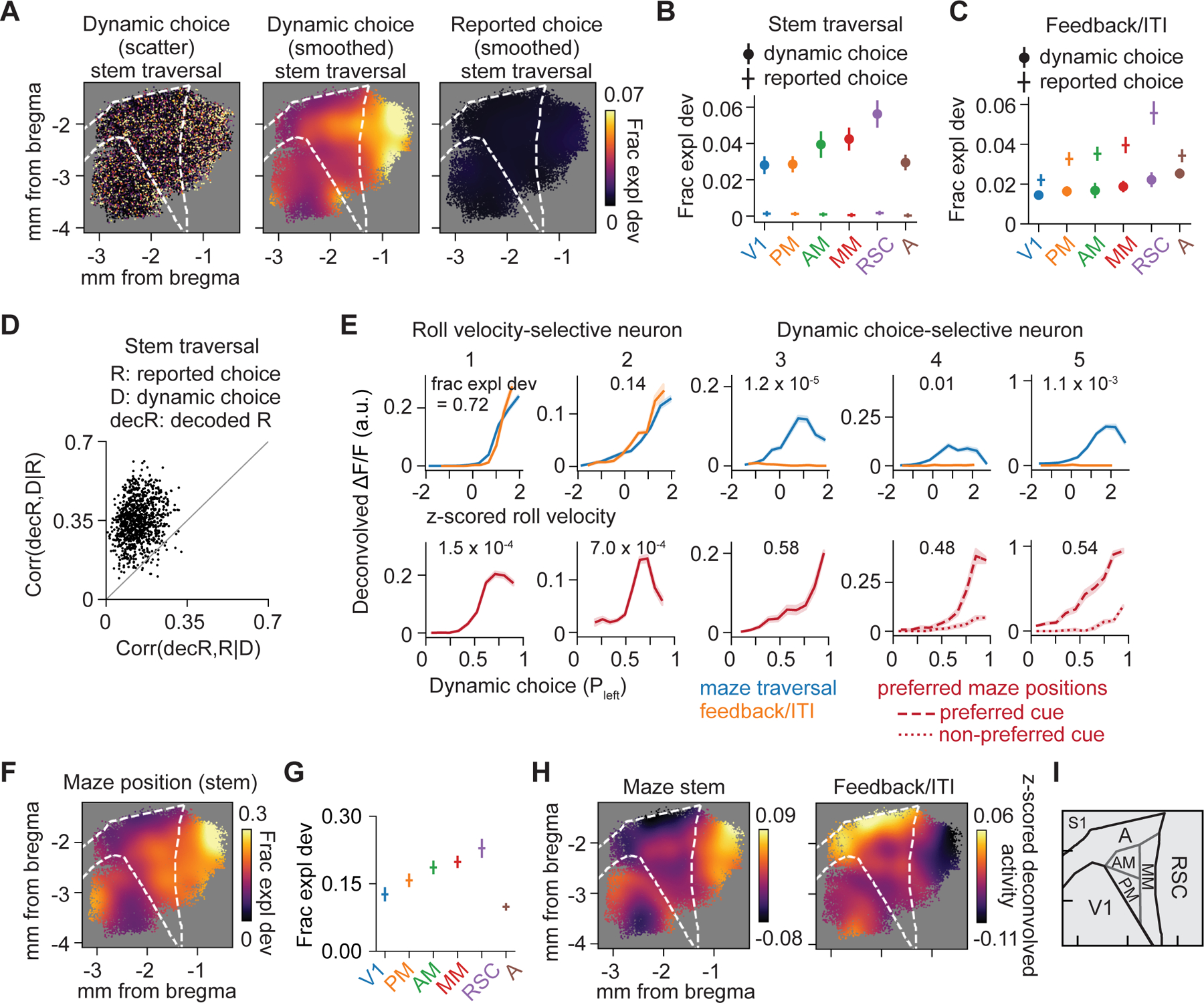
(A) Encoding magnitude (left) and smoothed map of dynamic choice (middle) and smoothed map of reported choice (right) during stem traversal.
(B) Average encoding magnitude of dynamic choice and reported choice during stem traversal for 6 areas. All 6 areas: dynamic choice vs. reported choice, p < 10−3. Dynamic choice: RSC vs. V1, PM or A, p < 10−3; RSC vs. AM or MM, p > 0.05. Reported choice: each area vs. zero, p > 0.05.
(C) Same as (B), but in feedback period/ITI. All 6 areas: reported choice vs. dynamic choice, p < 10−3. Reported choice, RSC vs. each other area, p < 0.05.
(D) Partial correlation (Spearman) of decoded reported choice (decR) with dynamic choice (D), conditioned on reported choice (R) (bootstrap mean ± SEM, 0.35 ± 0.02) vs. partial correlation of decR with R, conditioned on D (bootstrap mean ± SEM, 0.14 ± 0.02) during stem traversal. Each point represents one population decoder consisting of ~100 nearby neurons. Mean difference between the two partial correlations is greater than 0 (bootstrap mean difference ± SEM, 0.21 ± 0.02, p < 10−3). n = 974 decoders.
(E) Tuning curves for roll velocity (top; plotted during maze traversal and feedback period/ITI) and dynamic choice (bottom; plotted at each neuron’s preferred maze position) for two roll velocity-selective neurons (neuron 1 and 2) and three dynamic choice-selective neurons (neuron 3–5). The GLM-derived encoding magnitude (fraction explained deviance) for that variable is indicated on each panel.
(F) Smoothed encoding map of maze position during stem traversal.
(G) Average encoding magnitude for maze position during stem traversal for 6 areas. RSC vs. V1, PM, or A, p < 10−3; RSC vs. AM or MM, p > 0.05.
(H) Smoothed maps of average z-scored deconvolved activity during the maze stem (left) and feedback period/ITI (right).
(I) Schematic of area parcellation.
Data and statistics in (B), (C), (G) are presented as hierarchical bootstrap mean ± SEM.
See also Figure S5.
Our finding of near-zero encoding of reported choice during stem traversal suggests posterior cortex contained little information about upcoming choice beyond that embodied in behavior. We more closely examined this by training neural decoders to predict the mouse’s reported choice based on population activity (Figure S5F) and examined whether reported choice decoding contained information that was not accounted for by dynamic choice. We calculated the partial correlation between the reported choice decoder’s output and either the reported choice it was designed to predict or the dynamic choice, conditioned on the value of the other. Partial correlations were greater for dynamic choice than reported choice, revealing that even decoders trained to predict reported choice were more closely related to dynamic choice (Figure 4D and S5G). Thus choice-related activity in posterior cortex closely reflected the embodied process summarized by dynamic choice.
Our finding of distinct encoding gradients for instantaneous movement and dynamic choice may seem surprising given that dynamic choice was derived from running trajectories. To clarify the distinction, we generated model-free tuning curves for single neurons identified by the GLM as selective to left-right running (roll velocity) or dynamic choice (Figure 4E and S5H). The activity of roll velocity-selective neurons (neurons 1 and 2) closely tracked instantaneous movement, importantly both during maze traversal and the feedback period/ITI, and their activity was thus somewhat correlated with dynamic choice. Dynamic choice-selective neurons had weak and inconsistent activity correlations with roll velocity and were instead most active at specific positions in the maze with strong choice (neuron 3) and often cue (neurons 4 and 5) selectivity. Dynamic choice encoding, and its enrichment in RSC, was not explained by more complex or temporally integrated movement encoding (Figure S5I–S5N).
Because choice in this task corresponded to a navigation goal in the maze, we also considered whether RSC and medial areas encoded other navigation-related signals. Encoding of maze position was present in all areas, but strongest in RSC, with a similar medial-to-lateral gradient as choice encoding (Figure 4F and 4G). RSC was also most active in the maze stem and least active during feedback and ITI periods, when area A was more active (Figure 4H and S5O). Together, these differences justify a distinction between the anterior-posterior movement encoding gradient and a medial-lateral choice and position encoding gradient.
Encoding of most variables is highly distributed
Our results show that specializations in encoding coincide with widely distributed encoding, and we sought to quantify where each variable’s encoding lies on the spectrum of distributedness. We first quantified the mutual information between encoding strength and area identity, with higher values indicating encoding that is more modular, i.e. specialized to specific locations in posterior cortex (Figure 5A and S6A). We then compared these values to two intuitive models that we used to generate synthetic encoding strength distributions spanning the entire spectrum from “fully distributed” to “fully modular” (Figure 5B–5D; STAR Methods – Quantification of distributedness). One model mixed encoding strengths from modular and distributed distributions according to a “random fraction”, while the other added gaussian “jitter” to a modular encoding strength distribution. By varying each model’s underlying parameter to produce encoding strength distributions with equivalent mutual information as the empirical data (Figure S6B and S6C), we obtained “equivalent” random fraction and jitter parameters, which summarize the distributedness of encoding for a single variable along an intuitive quantitative spectrum.
Figure 5. Distributedness of encoding across posterior cortical areas.
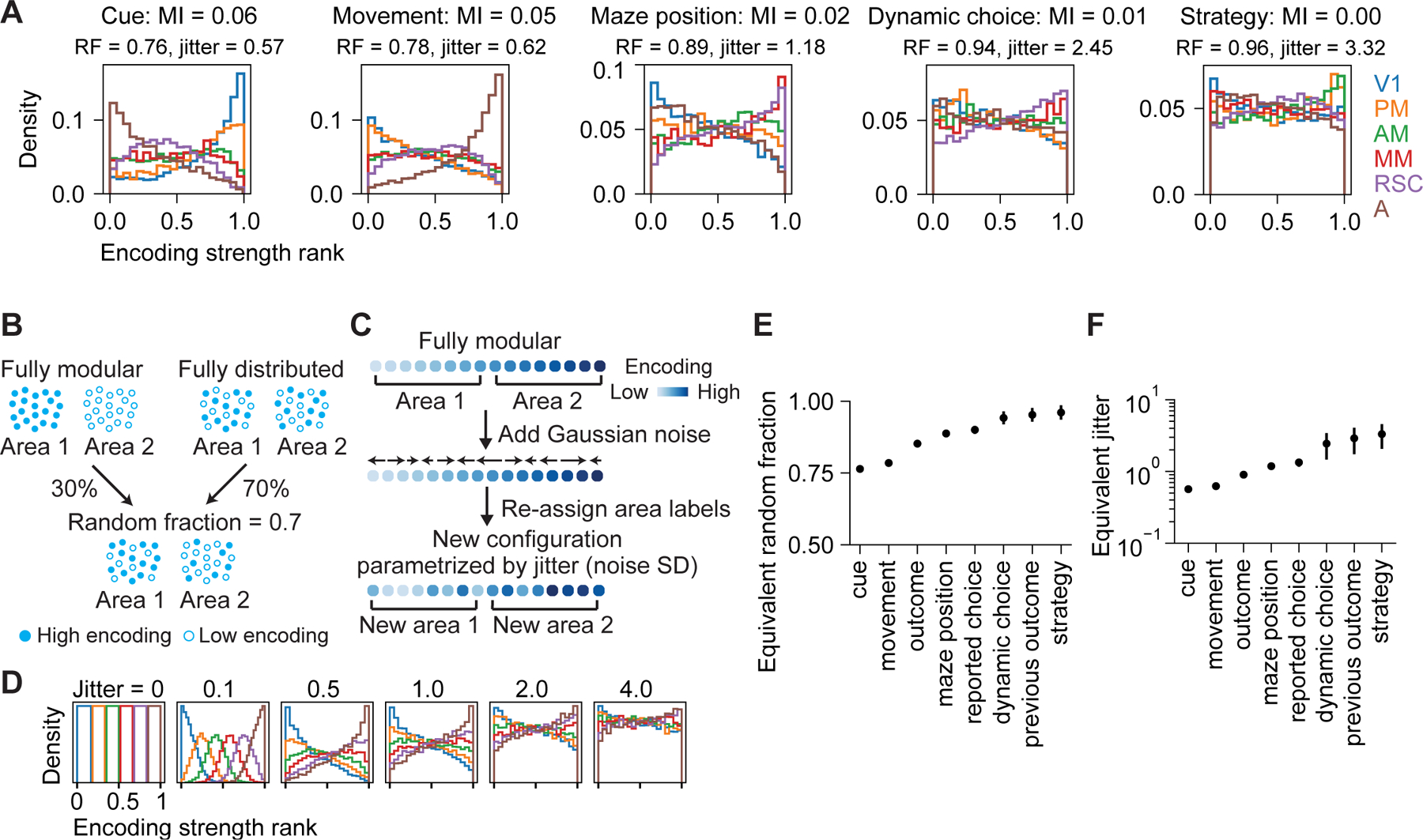
(A) Distribution of encoding strength rank of single neurons in 6 areas for various variables. MI, normalized mutual information between encoding strength and area identity; RF: equivalent random fraction; jitter, equivalent jitter; see (B) and (C).
(B) Schematic of toy models generated by mixing fully modular and fully distributed configurations with random faction = 0.7.
(C) Schematic of toy models generated by perturbing the encoding strength rank of the fully modular configurations by adding Gaussian noise (parametrized by jitter, or Gaussian noise SD) to the rank.
(D) Distribution of encoding strength rank for toy models in (C) generated with different jitter values.
(E-F) Equivalent random fraction and jitter for various variables. Bootstrap mean ± SEM.
See also Figure S6.
Cue and movement were the two variables with the highest mutual information between encoding strength and posterior cortical area. However, their equivalent random fractions were greater than 0.75, implying that the representations were closer to “fully distributed” (random fraction = 1) than “fully modular” (random fraction = 0) (Figure 5E). Similarly, their equivalent jitters were near 0.6, which is large relative to the normalized encoding strength range of 0–1 (Figure 5F). The encoding of maze position and choice were even more distributed than cue and movement, with equivalent random fractions near 0.9. All other variables were also highly distributed, with decision-making strategy being the most distributed (random fraction near one). These results are consistent with studies showing distributed movement encoding across mouse cortex, as all variables were closer to a fully distributed than modular organization. Interestingly, however, many cognitive variables are even more widely distributed than movement encoding, at least for posterior cortex.
Single-neuron encoding profiles confirm functional gradients and distributed representations
We have so far analyzed the distributedness of encoding only for single variables, but it is possible that a more modular picture of cortical organization emerges if we consider multiple variables at once. We designed analyses to identify the patterns of encoding that best distinguish between cortical areas when considering multiple variables and to visualize the distributedness of these patterns across posterior cortex. We first identified location-informative encoding by training decoders to predict the probability that each neuron was located at each site in a grid across cortex based on the neuron’s encoding strengths for multiple variables, which we termed a neuron’s “encoding profile” (Figure 6A, S6E and S6F). Neurons in V1, A, and RSC were typically predicted to reside in their actual areas of origin, indicating that these neurons had distinctive encoding profiles, in contrast to neurons from AM and MM that were predicted to reside in all sites across posterior cortex (Figure 6B).
Figure 6. Distinct spatial gradients of encoding in posterior cortex.
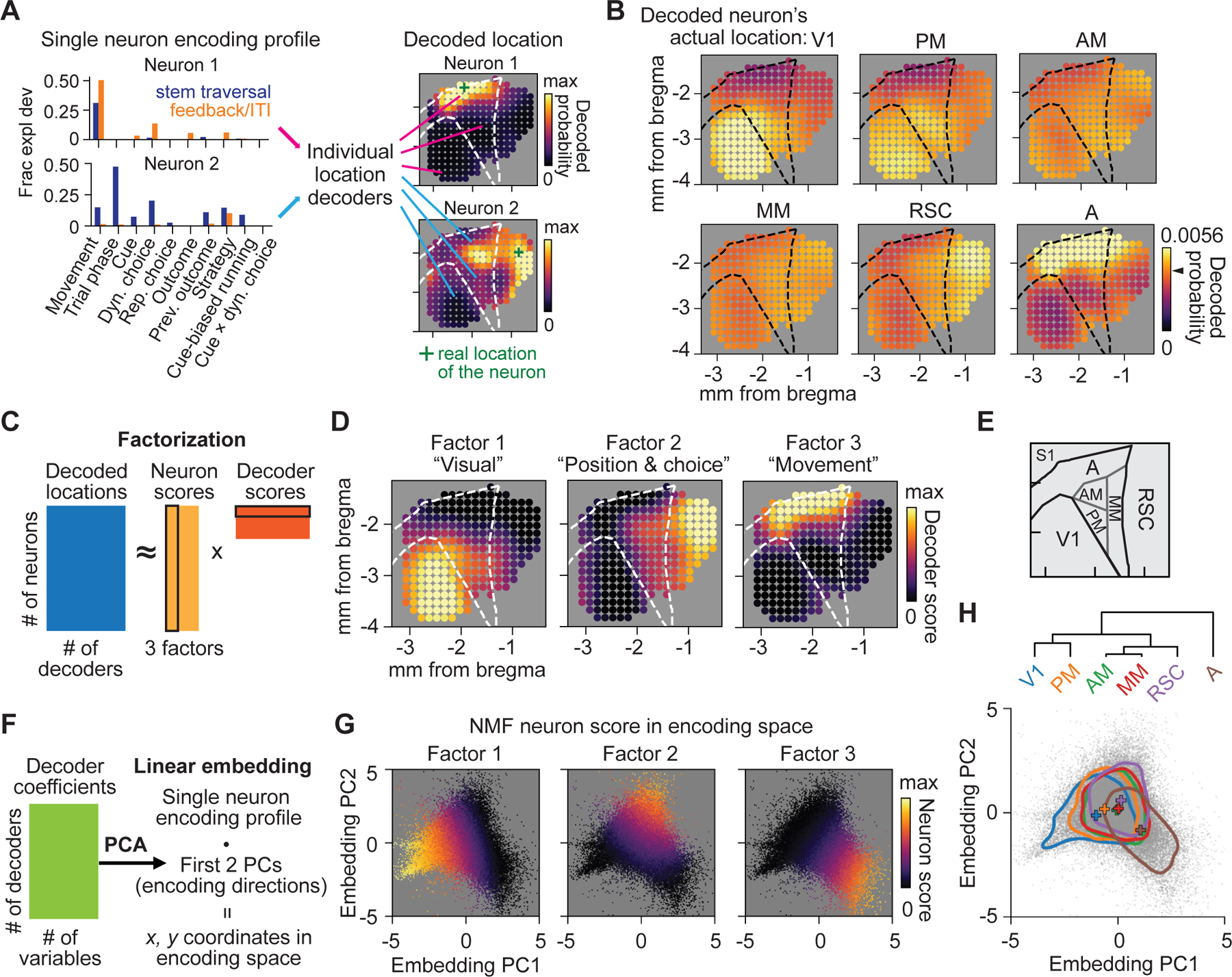
(A) Examples of decoding cortical locations from GLM-derived encoding profiles of single neurons.
(B) For all neurons in one of 6 areas, the average decoded probability distribution of a neuron’s location over posterior cortex. Chance level is 0.0041 (1/number of location decoders; black arrow on the color bar).
(C) Schematic of the non-negative factorization (NMF) of the decoded locations of all neurons.
(D) NMF decoder scores plotted spatially for each non-negative factor.
(E) Schematic of area parcellation.
(F) Schematic of embedding of single neuron encoding profiles.
(G) All neurons embedded in the encoding space, colored with the NMF neuron scores for each factor.
(H) Top: dendrogram showing hierarchical clustering of 6 areas by centroid locations. Bottom: Summary of distribution of neurons in 6 areas in the encoding space. Colored lines, contours at 25% of the peak density; plus signs, centroid locations.
See also Figure S6.
To identify the most significant spatial differences in encoding profiles across posterior cortex, we applied low-rank factorization to the predictions of these decoders – the probability that a neuron resided at each anatomical site based on its encoding profile (Figure 6C; STAR Methods – Non-negative matrix factorization of decoded locations). Three non-negative factors dominated the factorization (Figure S6I), each representing an encoding profile most typical to a set of distinct locations. Strikingly, these factors formed three distinct spatial gradients that dominated the anatomical organization of encoding with peaks in V1, RSC and A, respectively (Figure 6D). Although each factor’s encoding profile had contributions from diverse task and behavior variables, cue was greatest in factor 1, maze position and choice were greatest in factor 2, and movement was greatest in factor 3 (Figure S6G).
Although factorization revealed encoding profiles enriched in distinct areas, the actual locations of neurons exhibiting these encoding profiles were distributed throughout all areas (Figure S6H). To visualize the heterogeneity of encoding, we developed a linear embedding of each neuron’s encoding profile based on dimensionality reduction of the learned location decoder coefficients across all cortical locations (Figure 6F and S6J; STAR Methods – Linear embedding of single neuron encoding properties). This embedding positioned neurons nearby that, based on encoding profiles, were predicted to be in similar anatomical locations. The embedding mapped neurons onto a triangular manifold, corresponding closely to the representative encoding profiles of the three factors (Figure 6G and S6K). Neurons from individual cortical areas formed continuous, overlapping distributions in embedded space (Figure 6H and S6L). Although the centroids of the distributions (i.e. most typical encoding profiles) were offset from one another, many neurons were functionally closer to the centroid of a different area than to the centroid of the area where they resided. Our analyses showed how specialization and distributed representation coexist in posterior cortex: while V1, RSC, and A each contained neurons whose encoding profiles were mostly unique to each area, corresponding to the peaks of three spatial gradients, the majority of neurons in all areas had encoding profiles that could occur in any area.
Conjunctive structure of encoding in single neurons is similar across posterior cortex
The analyses of the encoding profiles of neurons revealed how different variables’ encoding strengths varied across cortical space, but they do not specify the higher-order principles by which variables are combined in single neurons, or conjunctive structure. Conjunctive structure may indicate computational functions that differ across posterior cortical space beyond that revealed in encoding strengths alone. For example, an area which integrates current movement with previous position to estimate present position should exhibit single neurons whose activity is modulated by both movement and position. In contrast, another area could encode these same variables with similar encoding strength, but with different variables preferentially encoded by separate neurons and relayed to distinct downstream targets. We therefore consider conjunctive structure a key component of cortical organization and examined whether such structures are similar or different across posterior cortical areas, which we refer to respectively as “generic” or “specialized” integration.
We first examined conjunctive coding in single neurons by visualizing joint histograms of the encoding strength rank for pairs of variables (Figure 7A–7C and S7A–S7C). We observed a wide distribution in how much individual cells encoded both variables, including cells that showed prominent conjunctive coding. Differences between joint histograms for each area were apparent, but mostly reflected the different marginal distributions of encoding strength in each area. To isolate conjunctive structure, we measured the correlation in encoding strength for both variables in single neurons within each area. A positive correlation indicates the variables are conjunctively encoded in single neurons, a correlation near zero reveals the encoding strength for one variable in a neuron is uninformative of encoding for other variables, and a negative correlation means the variables are encoded in distinct neurons. Strikingly, the correlations in encoding between pairs of cue, choice, and movement variables were similar across areas, despite major differences in the encoding strengths of these variables between areas (Figure 7D–7F and S7D–S7H). In addition, the correlation coefficients were close to zero, indicating near-random mixing of the variables within each area, which includes some neurons that conjunctively encode both variables.
Figure 7. Quantification of encoding correlations showed generic integration.
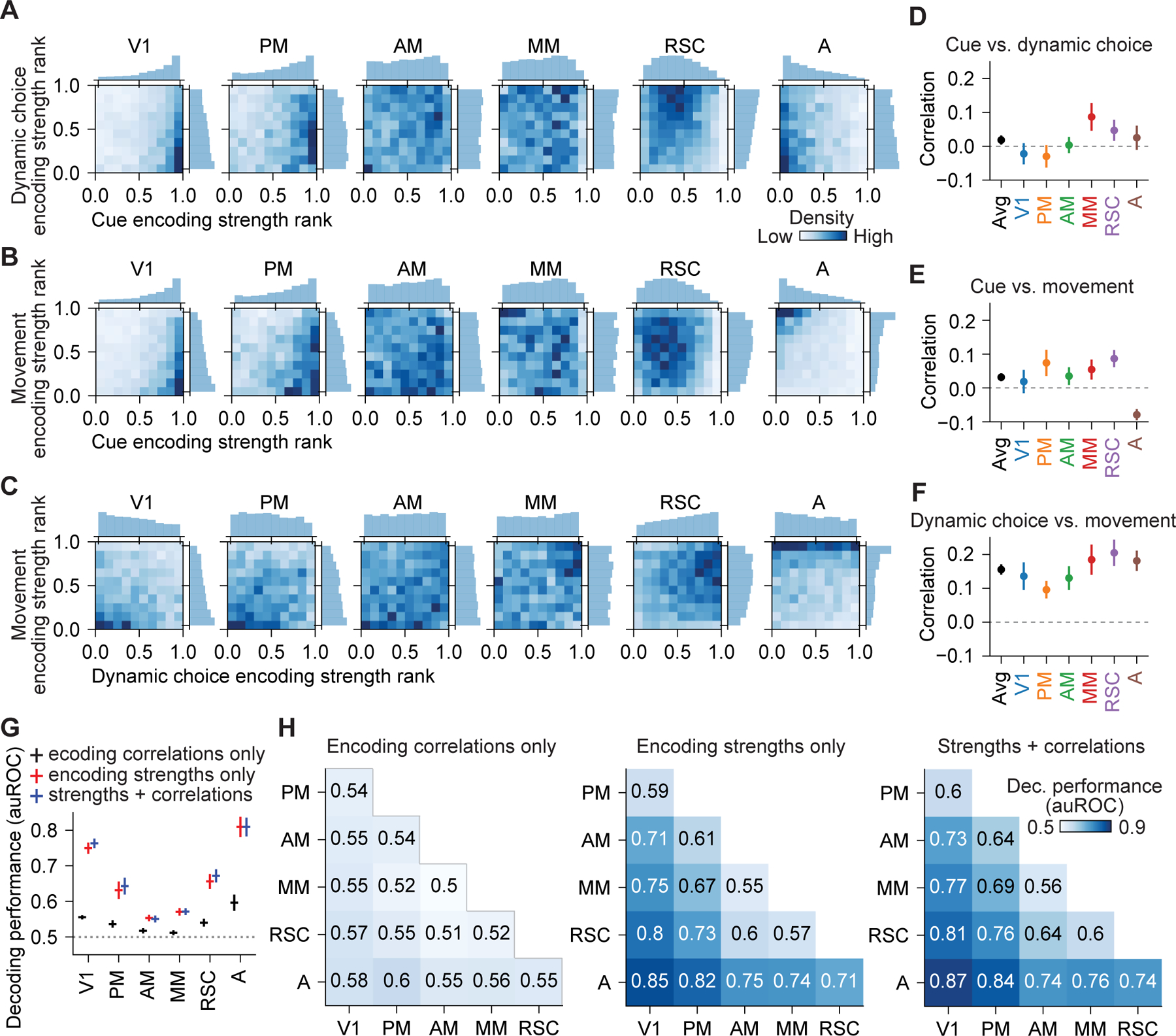
(A) Joint and marginal distributions for encoding strength rank of cue and dynamic choice during stem traversal in 6 areas.
(B) Same as (A), but for cue and movement.
(C) Same as (A), but for dynamic choice and movement.
(D) Pearson correlation between the encoding strength of cue and dynamic choice during stem traversal for neurons in 6 areas. Bootstrap mean ± SEM. Correlations in all areas were not significantly different from one another (p > 0.05).
(E) Same as (D), but for cue and movement. A vs. each other area, p < 0.013, whereas correlations in other 5 areas were not significantly different from each other (p > 0.05).
(F) Same as (D), but for dynamic choice and movement. Correlations in all areas were not significantly different from one another (p > 0.05).
(G) Decoding performance for one-vs.-others decoders that distinguished neurons in each of the 6 areas from neurons in all other areas based on encoding correlations only, encoding strengths only, and both, during stem traversal. Mean ± SEM with leave-one-mouse-out procedure. All decoding was above chance (p < 0.05), except encoding correlations only for PM and AM. Encoding strengths only vs. encoding correlations only: p < 0.05 in all areas except for AM. Encoding strengths only vs. strengths + correlations: p > 0.03 for all areas, not significant after multiple comparison correction. Wilcoxon signed-rank test.
(H) Decoding performance for pairwise decoders that distinguished neurons in a pair of areas during stem traversal.
See also Figure S7.
We then more thoroughly searched for differences in conjunctive structure by decoding the area a neuron resided in based on either the encoding strengths of variables or the encoding correlations between pairs of variables. The ability to decode a neuron’s location was dominated by the encoding of individual variables rather than the encoding correlations between variables (Figure 7G, 7H and S7H, S7I). Although decoding based on encoding correlations allowed above-chance performance, it was poor relative to decoding from encoding strengths alone. Further, decoding with both encoding correlations and encoding strengths was barely improved from decoding with encoding strengths alone. Therefore, differences in conjunctive structure between areas were not substantial, and posterior cortex exhibited generic integration across areas, rather than specialized integration in different areas.
Flexible, high-dimensional representations in posterior cortex
Having observed generic integration in the conjunctive structure of single-neuron encoding strengths, we next considered whether similar results would hold at the population level of representational geometry. Nonlinear mixing of variables in single neurons can create high-dimensional population representations, which provide downstream areas with flexibility and specificity in responding to task conditions (Fusi et al., 2016; Rigotti et al., 2013). As one example, we observed cue- and choice-selective sequences of activity during navigation (Harvey et al., 2012; Koay et al., 2021) (Figure 8A and 8B). These represent a mixing of tuning for position and cue or choice in individual neurons leading to a high dimensional representation, as decoders trained to predict cue or choice at one maze position degraded in accuracy when tested at other maze positions (Figure 8C and 8D). The high-dimensional representation for cue and choice with position would allow linear downstream readouts to trigger relevant actions at specific maze positions, dependent on a given cue or choice.
Figure 8. High dimensional representation of conjunctive variables across posterior cortex.
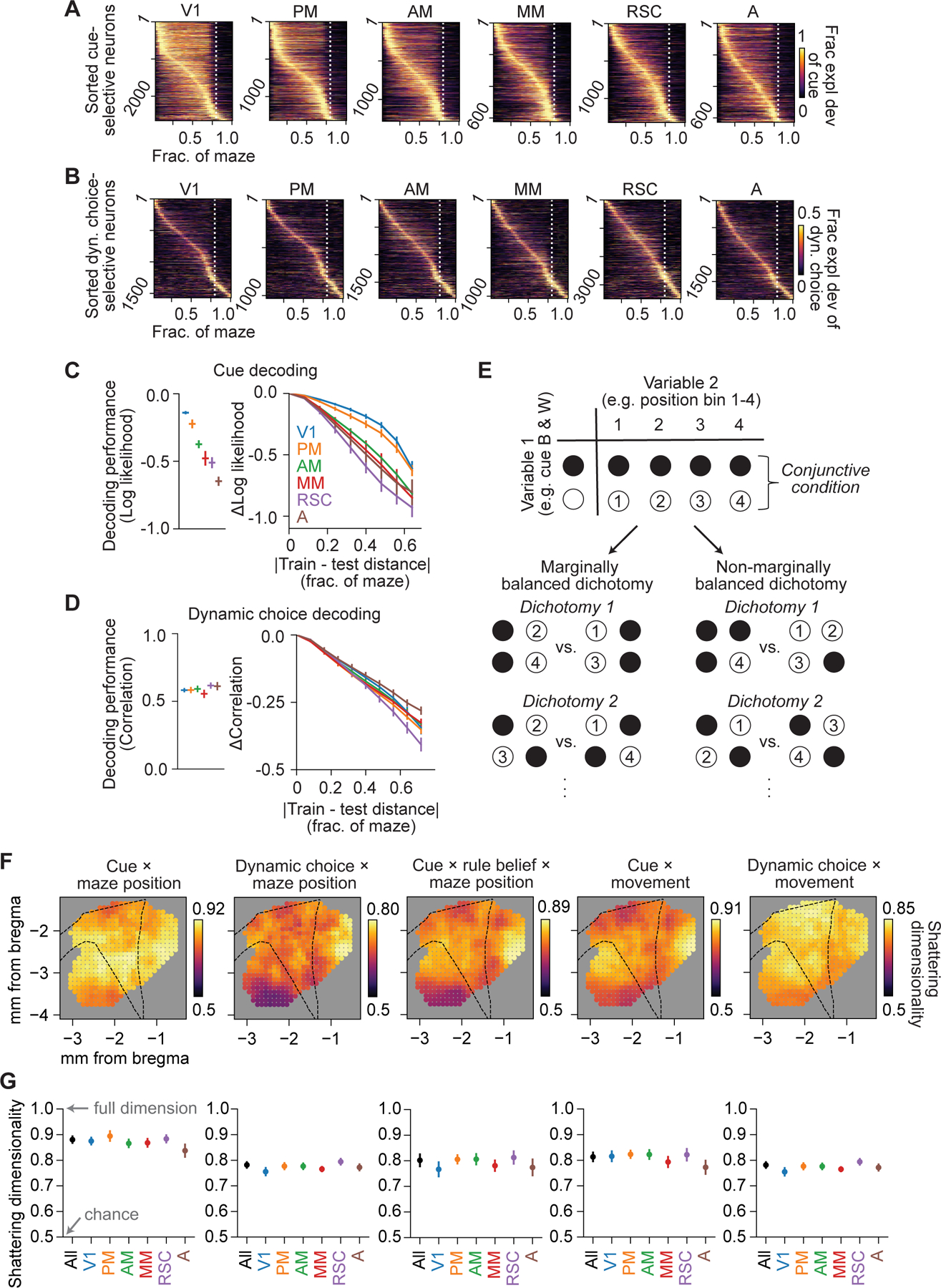
(A) Fraction explained deviance of cue for the top 25% cue-selective neurons across all cells, separated in 6 areas and sorted by peak location.
(B) Same as (A), except the top 25% of dynamic choice-selective neurons.
(C) Left: average decoding performance for cue based on populations of ~100 nearby neurons for 6 areas, quantified as log likelihood with log base 2. Right: change in decoding performance as a function of the distance between maze positions of the data that the decoders were trained on and tested on (restricted to positions where cue was present). n = 698 decoders.
(D) Same as (C), but for decoding performance of dynamic choice, quantified as the Spearman correlation between decoded and real values. n = 974 decoders.
(E) Schematic for identifying marginally balanced dichotomies over conjunctive conditions formed by a pair of variables.
(F) Spatial maps of shattering dimensionality (average decoding accuracy over all marginally balanced dichotomies) during stem traversal. Each dot indicates a population of 1000 nearby neurons centered on that cortical location.
(G) Shattering dimensionality based on populations of 1000 neurons subsampled from all neurons and each of the 6 areas. All datapoints were not significantly different from one another (p > 0.01, not significant after multiple comparison correction).
Data and statistics in (C), (D), (G) are presented as hierarchical bootstrap mean ± SEM.
See also Figure S8.
We compared the dimensionality of population representations across posterior cortex by adapting recent techniques to measure “shattering dimensionality” for a range of conjunctions including cue, choice, position, movement, and rule belief (Bernardi et al., 2020). Shattering dimensionality refers to the fraction of arbitrary groupings of task conditions that a linear decoder of population activity can discriminate between, which approaches one as the dimensionality of neural encoding approaches the dimensionality of task conditions. We generated conjunctive task conditions for a combination of variables by dividing each variable into discrete bins and averaged neural activity for each combination of bins across trials for pseudo-populations across posterior cortex. Dichotomies of conjunctive conditions with unbalanced marginal distributions were discarded, so that shattering dimensionality was quantified as decoding accuracy on only “marginally balanced” dichotomies, to strictly measure the nonlinear conjunctive coding rather than individual variable encoding strengths (Figure 8E; STAR Methods – Quantification of shattering dimensionality for conjunctive variables).
Shattering dimensionality for all conjunctions in all areas was well above chance, and interestingly, shattering dimensionality for each conjunction was similar across posterior cortex (Figure 8F, 8G and S8A–S8C). Almost all differences between areas were not statistically significant and fell within a range of < 10% classification accuracy for each conjunction (Figure 8G). Also, pseudo-populations including neurons from all areas exhibited nearly identical shattering dimensionality as when including only individual areas. Thus, for a range of conjunctions of variables, similar high-dimensional codes were present across posterior cortex, consistent with the generic integration scheme, and in contrast with significant differences in the encoding strength of individual variables. For example, cue and maze position conjunctions were decoded well by populations in V1, RSC, and A, despite cue and maze position encoding being strongest in V1 and RSC, respectively, and weak in A. Our results suggest that previously described neural sequences are examples of a more general function of posterior cortex, which may integrate diverse variables into a distributed, high-dimensional representation of task and behavioral state, while individual areas are specialized to handle inputs of different modalities.
Discussion
We observed that posterior cortical areas differed in the quantitative degree to which they encoded variables, not which variables they encoded, and surprisingly not the way variables are combined in single neurons or the resulting population geometry of conjunctive representation. This organization is poorly fit to the common notion of a “functional hierarchy”. Association areas (e.g. A, RSC) did not exhibit more complex representations than sensory areas (e.g. V1), and encoding of all variables was highly distributed, particularly for more abstract quantities like decision-making strategy variables. These results also argue against a “specialized integration” principle, in which areas generate distinct combinations of variables to subserve distinct computations. Instead, during flexible navigation decisions, our results point to a parallel organization of posterior cortex based on generic integration. While posterior cortical areas have differential enrichment in the modalities of information they process, all areas share a high-dimensional code for relevant task and behavioral variables. We caution that our analyses do not capture the conjunctions of behavior or task variables that were not measured in our task or modeled by the GLMs, and thus it is possible that posterior cortical specialization could be greater for different variables and tasks. However, in contrast to prevalent theories which conceive of cortical areas performing modular and hierarchically organized computations, the functional organization we observed suggests new hypotheses for the role of posterior cortex in navigation decisions.
In the task studied here, determining the next action to take at any moment depends on a combination of many variables, including visual cues, current position, goal location, internal rule estimate, and ongoing movement. We have shown that many parts of posterior cortex represent this high-dimensional state of variable conjunctions, which provides linear downstream readouts great flexibility and specificity in selecting appropriate actions, such as “run left at the Y-intersection when seeing the black cue during Rule A”. It is possible that identifying relevant combinations of variables and generating a corresponding representation of the behavioral and environmental state is a primary function of posterior cortex in guiding navigation decisions. In this case, areas may be specialized to integrate different signal modalities into a distributed, general high-dimensional state representation, which is then available to a range of circuits downstream of posterior cortex. This hypothesis has similarities to theories that cortex performs unsupervised learning on its inputs (Doya, 1999) and the machine learning concept of representation learning (Xie et al., 2020). In addition, results from the inactivation of PPC and RSC in this and previous studies are consistent with the notion that downstream areas use the posterior cortex’s state representation to guide navigation decisions, instead of PPC and RSC having a direct role in sensory perception or motor control, as inhibiting these areas eliminates associations between cue and choice without disrupting the mouse’s ability to locomote, or to perceive and respond to visual stimuli (Arlt et al., 2021; Harvey et al., 2012; Pinto et al., 2019). Furthermore, across studies, PPC and RSC have been shown to be necessary for a variety of decision tasks that lack common computational requirements (Akrami et al., 2018; Arlt et al., 2021; Hwang et al., 2017; Lyamzin and Benucci, 2019), consistent with these areas participating in a general-purpose state representation. It is likely this state representation coexists with localized and specialized computations that differ across posterior cortex. However, it is interesting to speculate that diverse cognitive functions proposed for posterior cortex across tasks, such as evidence accumulation or maintaining trial history of task variables, might be task-specific computations which contribute to the synthesis of a task-appropriate state representation.
The functional specializations we observed as encoding gradients, along with the great extent of conjunctive coding, is consistent with much prior work that investigated one or two areas at a time. The enrichment of visual signals in V1 and PM is consistent with studies mapping visual representations in posterior cortex, and the presence of spatial and motor information in these areas is in agreement with recent results showing a surprising degree of non-visual signals in V1 (Fiser et al., 2016; Keller et al., 2012; Parker et al., 2020; Saleem et al., 2018; Shuler and Bear, 2006; Stringer et al., 2019; Zmarz and Keller, 2016). The enrichment of choice and position information in RSC is consistent with its well characterized role in navigation, and the conjunctions of sensory, movement, position, and choice variables are in line with previous work (Alexander and Nitz, 2015; Bicanski and Burgess, 2016; Cho and Sharp, 2001; Fischer et al., 2020; Hinman et al., 2018; Keshavarzi et al., 2021; Mao et al., 2020). Our work highlights an important role of RSC in encoding dynamic choice, which is closely related to representation of navigation goals (Miller et al., 2019; Vale et al., 2020). The enrichment of encoding of navigation-relevant movement in area A relates to its identified roles in representing postures and self-motion in rodents (Mimica et al., 2018; Whitlock et al., 2012), and results in primates that suggest PPC contributes to movement intention and planning (Andersen and Cui, 2009; Desmurget et al., 2009; Hanks et al., 2006; Roitman and Shadlen, 2002; Thier and Andersen, 1998). However, this result is perhaps surprising given area A is sometimes considered to be a secondary visual area (Wang and Burkhalter, 2007; Wang et al., 2020). Our findings are also consistent with our previous study identifying distributed encoding of tens of task and behavior-related features in posterior cortex during a visually guided locomotion task (Minderer et al., 2019). As the number of distinct spatial gradients was not explicitly quantified in that study, here we showed that variability in tuning across cortical space was mostly captured by three functional modes (Figure 6D; see also STAR Methods – Analysis of dimensionality of encoding across neurons versus encoding across cortical space).
One critical feature of our approach was utilizing a model to extract a continuously evolving estimate of the animal’s decision from its running trajectory (dynamic choice). This was possible because navigation decisions were executed by continuous movement over many seconds, during which choice could evolve and influence the ongoing navigation trajectory of the mouse. Notably, similar embodiment of cognitive processes has been observed across diverse species and laboratory tasks (Kaufman et al., 2015; Lakshminarasimhan et al., 2020; Pinto et al., 2018; Redish, 2016; Resulaj et al., 2009; Song and Nakayama, 2009). Previous work has suggested that heading angle during navigation may predict neural activity better than (reported) choice (Krumin et al., 2018), and that it may reflect an accumulation of evidence (Pinto et al., 2018). Since heading angle was constant throughout maze traversals in our task by design, we believe these findings can be explained alternatively by neural representations for a continuously evolving choice signal that is tightly coupled to behavioral output. We note this relationship is sensitive to the incentives created by task design, as some studies have observed neural encoding of upcoming choice without substantial accompanying behavioral embodiment (Harvey et al., 2012). However, more generally, we anticipate that modeling behavioral outputs to infer cognitive processes will prove fruitful, especially in tasks with increasing complexity and unconstrained behaviors (Brunton et al., 2013; Havenith et al., 2018, 2019; Lakshminarasimhan et al., 2018; Rosenberg et al., 2021; Roy et al., 2021).
Our work uncovers an organizing principle for posterior cortex and proposes a functional role for it in flexible, goal-directed navigation. A major direction for future work will be to understand what aspects of the representations studied here arise within posterior cortex or are inherited from other regions. This important direction regarding the functional organization of representation versus computation can potentially be addressed with functional imaging at synaptic and dendritic levels, simultaneous recording of multiple brain areas, labeling neurons based on projection targets, and monitoring changes in neural activity during targeted perturbation of neural populations.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Christopher Harvey (harvey@hms.harvard.edu).
Material Availability
This study did not generate new unique reagents.
Data and Code Availability
Calcium imaging and mouse behavioral data reported in this paper will be shared by the lead contact upon request.
The original code for fitting generalized linear models has been deposited at Github and is publicly available as the date of publication. DOI is listed in the key resource table.
Other code to run all analyses and produce all figures in this paper will be shared by the lead contact upon request.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and virus strains | ||
| AAV2/1-synapsin-GCaMP6s-WPRE-SV40 | UPenn Vector Core | Catalog No: AV-1-PV2824 |
| Deposited data | ||
| Allen Mouse Common Coordinate Framework | Allen Institute for Brain Science | http://help.brain-map.org/display/mousebrain/Documentation |
| Retinotopic field sign maps | Allen Institute for Brain Science | https://portal.brain-map.org/ |
| Experimental models: Organisms/strains | ||
| C57BL/6J mouse | The Jackson Laboratory | RRID: IMSR_JAX:000064 |
| VGAT-ChR2-EYFP mouse | The Jackson Laboratory | RRID: IMSR_JAX:014548 |
| Software and algorithms | ||
| MATLAB | The MathWorks | https://www.mathworks.com/ |
| ViRMEn (Virtusl Reality Mouse Engine) | Aronov and Tank, 2014 | https://pni.princeton.edu/pni-software-tools/virmen |
| ScanImage 2016a | Vidrio Technologies | https://vidriotechnologies.com/scanimage/ |
| Image preprocessing and motion correction code | Chettih and Harvey, 2019 | https://github.com/HarveyLab/Acquisition2P_class |
| OASIS algorithm for calcium imaging deconvolution | Friedrich et al., 2017 | https://github.com/zhoupc/OASIS_matlab |
| CNMF algorithm for calcium imaging source extraction | Pnevmatikakis et al., 2016 | https://github.com/Selmaan/NMF-Source-Extraction |
| DataJoint 0.13 | DataJoint | https://datajoint.io/ |
| Python 3.6 | Python | https://www.python.org/ |
| Tensorflow v1 | Google Inc. | https://www.tensorflow.org/ |
| Code for fitting generalized linear models | This study | https://zenodo.org/badge/latestdoi/491659726 |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Animals
All experimental procedures were approved by the Harvard Medical School Institutional Animal Care and Use Committee and were performed in compliance with the Guide for Animal Care and Use of Laboratory Animals. Behavioral and imaging data were obtained from eight male C57BL/6J mice from Jackson Laboratory (stock no. 000664). Mice were 10–12 weeks old at the start of behavioral training, and 3–6 months old during imaging. For optogenetic inhibition experiments, seven male VGAT-ChR2-YFP mice from Jackson Laboratory (stock no. 014548) were used. These mice were 10 weeks to 1 year old during the photoinhibition experiments. All mice were kept on a reversed 12-hour dark/light cycle and housed in groups of 2–3 littermates per cage.
METHOD DETAILS
Behavioral task and training
Virtual reality system
For calcium imaging experiments, we used a virtual reality system that has been previously described (Harvey et al., 2009; Morcos and Harvey, 2016) for behavioral and imaging experiments. Mazes were constructed using ViRMEn (Virtual Reality Mouse Engine (Aronov and Tank, 2014)) in Matlab. Images were back-projected onto a half-cylindrical screen (24-inch diameter) using a PicoPro Projector (Celluon) at 60 Hz frame rate. For optogenetics experiments, a compact virtual reality system was used (https://github.com/HarveyLab/mouseVR). The compact system was assembled with laser-cut acrylic pieces and mirrors, with overall dimensions of 15 inches wide × 21 inches deep × 18 inches high. Images were projected onto a double-mirror system and a half-cylindrical screen (15-inch diameter) using a Laser Beam Pro projector. In both systems, head-restrained mice ran on an air-supported styrofoam spherical treadmill (8-inch diameter), and the ball movement was recorded using a pair of optical sensors (ADNS-9800, Avago Technologies) and converted into 3-dimensional rotation velocity signals with a microcontroller (Teensy 3.2, PJRC). The pitch velocity was used to translate forward/backward position throughout the maze, and the roll velocity controlled the lateral position. View angle was fixed along the forward direction.
Task description
The task took place in a virtual Y-maze (Figure 1B and S1A). For behavioral and imaging experiments, the full length of the maze was 250 cm with 200 cm for the stem and 50 cm for the arms. During behavioral training, the stem had a width of 60 cm, and the visual scene varied as the mouse made lateral movements in the stem. To control the visual stimulus during imaging experiments, stem width was reduced to 10 cm, starting a few sessions before imaging began, which prevented any lateral movement in the maze stem because the virtual agent could not approach closer than 5 cm to any wall. Therefore, during imaging experiments, the visual scene in the Y-stem was controlled entirely by the mouse’s position along the long axis of the Y-stem, with no lateral movement along the short axis and no angular rotation (view angle changes). While running down the stem of the Y-maze, mice were randomly presented with one of the two distinct cue patterns on the wall (black background with white dots or white background with black dots) and made lateral movement into one of the two arms after passing the Y-intersection. In the majority of sessions, the cue disappeared either 10 cm or 60 cm before the Y-intersection and was replaced by a gray wall pattern (“cue delay” sessions; fixed delay length per session). On other sessions, the cue was visible in the Y-intersection until the mice entered a maze arm (“no cue delay” sessions). We noticed that the task performance decayed as the mouse experienced multiple sessions with long cue delay. Thus, to keep the task performance stable over sessions, the presence and the length of the cue delay was manually adjusted based on the mouse’s performance in previous sessions. After the mice entered an arm, their lateral position was adjusted and locked to a central position such that every trial exhibited an identical view of a gray wall on all sides. After a one-second delay, a visual feedback (checkerboard pattern) replaced the gray wall for 2 seconds if the mouse made a correct choice, after which reward (3 μl 10x diluted condensed milk, Eagle Brand) was delivered through a lick sprout as the screen turned dark for 3 seconds before the onset of the next trial. On incorrect trials, the wall stayed gray during the feedback period for 2 seconds, followed by a 5 second timeout with dark screen. Some representative maze views are shown in Figure S1A. The associations between visual cues and rewarded arms were determined by one of the two rules (rule A: black cue-left arm/white cue-right arm; rule B: black cue-right arm/white cue-left arm; Figure 1A). The rule alternated in blocks with pre-determined length of 100–175 trials, without explicit signaling for the rule switches. Therefore, to maximize the reward, the mouse had to combine the visual cue with an estimate of the current rule (rule belief) to generate a choice, and update its rule belief by combining a memory of a trial’s cue and choice with the outcome. A typical session consisted of 350–450 trials with 2–3 switches. The mice consumed all rewards throughout the sessions with their licking behavior monitored with a lick sensor.
For photoinhibition experiments, a modified configuration of the virtual maze was used. The full length of the maze was 180 cm with 100 cm for the stem and 80 cm for the arms. The two cue patterns were vertical and horizontal bars, and these patterns extended into the walls in the maze arms.
For all experiments, we interleaved a small fraction (typically varying from 0 to 20%) of visually guided trials to assist behavioral performance. In these trials, the checkerboard pattern was present on the end wall of the rewarded arm and was visible to the mice before entering an arm. The inclusion of visually guided trials helped the mouse stay engaged and retain stable performance, and we manually determined the fraction based on the mouse’s task performance on previous sessions. These trials never appeared as the first trial after rule switches. We found that these visually guided trials did not have a larger impact than other trials on the update of the mouse’s rule belief (see the section Modeling of decision-making strategies), and we excluded them from all analyses unless mentioned otherwise.
Training procedure
Three to five days prior to behavioral training, mice were put on a water restriction schedule that limited their water consumption to 1 mL per day. Their body weight was monitored daily and kept above 80% of the pre-training weight with additional water supply when necessary. At the first stage of training, mice were head-restrained on top of the spherical treadmill and placed into a virtual linear track, in which the reward was available at the end of the track. Mice were randomly presented with one of the two cue patterns on the side walls on each trial, and the checkerboard pattern was always present on the wall at the end of the track prior to the reward delivery (to encourage association of reward with the checkerboard pattern). We gradually increased the length of the linear track from 15 cm to 300 cm as mice learned to run straight forward on the treadmill. This stage took 7–10 days, with one session per day. After the mice demonstrated proficient running skills, we moved them to the Y-maze. Visual cues were present throughout the maze (“no cue delay”). Both rules were introduced in alternating blocks within every session with at least 2 switches (3 blocks). At the early phase of this stage, all trials were visually guided, and the mice learned to follow the checkerboard pattern and move the ball laterally to enter the rewarded arms. As training progressed, we gradually decreased the fraction of visually guided trials, so the mice learned the rewarded cue-choice association imposed by both rules. At the late stage of training, we added a cue delay before the Y-intersection. Mice were considered well-trained when accuracy reached 70–75% with a low fraction of visually guided trials (0 to 20%). This training process took around 1–2 months and varied between individual mice.
Surgery
Cranial window
Prior to behavioral training, a cranial window implant surgery was performed. Mice were injected with dexamethasone (2 μg per g body weight) 4–12 hours before the surgery. For the surgery, mice were anesthetized with 1–2% isoflurane. A skin incision was created to expose the skull, and a titanium headplate was affixed to the skull with dental cement (Metabond, Parkell) mixed with India ink for light-proofing. A 3.5 mm-diameter craniotomy was created over the left hemisphere, centered at 2 mm lateral, 2.5 or 2.75 mm posterior to bregma, and the dura was removed. A glass plug constructed with two 3.5 mm-diameter inner coverslips and one 4.0 mm-diameter outer coverslip (#1 thickness, Warner Instruments) bonded together using optical adhesive (Norland Optics NOA 65) was inserted and sealed with dental cement. Mice were then put on behavioral training. After they learned to reliably perform the task, they were anesthetized again for injection of adeno-associated virus (AAV) after one day of free access to water. The dental cement around the window and the glass plug were removed, and 60–100 nL of AAV2/1-synapsin-GCaMP6s-WPRE-SV40 (U. Penn Vector Core, cat. no. AV-1-PV2824) diluted in phosphate-buffered saline (1/10 dilution with final titer ~4 × 1012 gc/ml) was injected into layer 2/3 and layer 5 (250 μm and 500 μm below the pia surface, respectively). Injections were targeted to 7–9 sites spaced evenly across areas of interest, including primary visual cortex (V1), posteromedial (PM), anteromedial (AM), mediomedial (MM), retrosplenial cortex (RSC), and anterior (A). Gradual and continuous injections were made using a glass pipette and a custom air-pressure system over 2–3 min per depth per site, and the pipette was left in place for an additional 3–5 min. A new glass plug was then inserted and sealed with dental cement.
Before the headplate implantation, mice were also injected with two retrogradely transported AAVs (AAV2retro-Syn-mTagBFP2 undiluted with concentration ~1.5 × 1013 gc/ml and AAV2retro-Syn-mScarlet 1/5 dilution in PBS with final concentration ~5 × 1011 gc/ml, both obtained from Boston Children’s Hospital Viral Core) in projection target areas of posterior cortex. Mice were injected with AAVretro-mTagBFP2 and mScarlet into one of the two sets of targets through craniotomies on the left hemisphere: (1) anterior ACC/M2 (3 sites: 1 mm anterior, 0.5 mm lateral, 0.3 and 1.0 mm in depth; 1 mm anterior, 0.8 mm lateral, 0.4 mm in depth; 300 nl AAVretro-mTagBFP2 per site) and dorsomedial striatum (3 sites: 1 mm anterior, 1.2 mm lateral, 2.1 mm in depth; 1 mm anterior, 1.5 mm lateral, 2.1 mm in depth; 0.2 mm posterior, 1.75 mm lateral, 2.1 mm in depth; 300 nl AAVretro-mScarlet per site), or (2) posterior ACC/M2 (4 sites: 0 mm anterior, 0.35 mm lateral, 0.4 and 0.8 mm in depth; 0 mm anterior, 0.7 mm lateral, 0.3 mm and 0.8 mm in depth; 300 nl AAVretro-mTagBFP2 per site) and orbital frontal areas (ORBvl: 2.45 mm anterior, 0.75 mm lateral, 1.8 mm in depth; ORBl: 2.45 mm anterior, 1.25 mm lateral, 1.8 mm in depth; 500 nl AAVretro-mScarlet per site). Craniotomies were sealed with dental cement before implantation of headplate. Note that the labeling resulting from AAVretro injections was not analyzed for this study.
In four of the mice used for imaging, only the headplate was implanted before behavioral training. AAVretro injections, cranial window creation and GCaMP injections were made at once after the mice achieved proficient performance for the task.
Clear skull cap
The surgical procedures for optogenetics experiments were described previously (Guo et al., 2014; Minderer et al., 2019). Mice were anesthetized with 1–2% isoflurane. The scalp was resected to expose the dorsal skull surface, and the periosteum was removed. A thin layer of cyanoacrylate glue (Insta-Cure, Bob Smith Industries) followed by several layers of transparent dental acrylic (Jet Repair Acrylic, Lang Dental, P/N 1223-clear) was applied to the skull to create the cap. A bar-shaped titanium headplate was affixed to the interparietal bone using dental cement for use during training. Prior to beginning photoinhibition, mice were anesthetized again, and the skull cap was polished with a polishing drill (Model 6100, Vogue Professional) using denture polishing bits (HP0412, AZDENT). A layer of clear nail polish (Electron Microscopy Sciences, 72180) was applied to the polished skull cap. An aluminum ring was then attached to the skull using dental cement mixed with India ink for light-proofing.
Photoinhibition experiments
We built the photostimulation system based on a previous design (Minderer et al., 2019). Light from a 470 nm collimated laser (LRD-0470-PFFD-00200, Laserglow Technologies) was coupled with a pair of galvanometric scan mirrors (6210H, Cambridge Technology) and focused onto the skull using an achromatic doublet lens (f = 300 mm, AC508–300-A-ML, Thorlabs). The analog power modulation along with the mirrors allowed rapid movement of the laser beam between multiple target sites for simultaneous stimulation. The focused laser beam had a diameter of approximately 200 µm.
Data from six out of seven mice for the photoinhibition experiments were included and analyzed differently as part of an independent study (Arlt et al., 2021). We started the photoinhibition after mice reached steady state performance within a rule block. Three cortical targets were selected: PPC (1 spot: 2 mm posterior, 1.75 mm lateral), RSC (3 spots: 1.5, 2.5, 3.5 mm posterior, 0.5 mm lateral), and S1 (1 spot: 0.5 mm posterior, 2.5 mm lateral) together with an out-of-cortex control site on the dental cement (1 spot: 2 mm anterior, 5 mm lateral) (Figure 1J). For the single spot targets (PPC, S1 and control), the laser power was sinusoidally modulated at 40 Hz and the time-average power was approximately 6.5 mW per spot. For RSC (3 spots), we used laser power modulated at 20 Hz with a mean of 5 mW per spot. The inhibition was performed bilaterally, with an estimated effect size of 1–2 mm radius on cortex (Guo et al., 2014; Pinto et al., 2019). Given this spatial resolution, the inhibition at the PPC coordinate would have effect on adjacent areas including A, AM, MM, and small portions of PM, lateral part of RSC and anterior part of V1 (the distance between PPC and anterior border of V1 is ~0.8 mm). The inhibition of RSC would have effect on MM and small portions of AM, PM and A. The majority of V1 would be less affected since its center is greater than 2 mm away from PPC and RSC coordinates.
In each session, inhibition blocks consisting of 50 trials started when the mouse’s performance reached 85% correct over the past 30 trials, followed by a rule switch right after the end of each inhibition block. The targets of the inhibition trials were randomly interleaved, with at least half of the trials targeting the control site. Within the trial, the inhibition started 0.5 s prior to the trial onset and lasted until the mouse reached the maze end. Overall, we collected data from 164 sessions from 7 mice. Each session consisted of 10.7 ± 4.3 trials per target and 34.0 ± 15.5 control trials (mean ± SD).
Two-photon calcium imaging
Microscope design
Imaging data were collected using a custom-built two-photon microscope. The scan path used a resonant-galvanometric mirror pair separated by a scan lens-based relay telescope to achieve fast scanning. The objective lens (Nikon 16 × 0.8 NA water immersion objective) was mounted on a piezo collar (nPFocus250 Piezo stage with LC 400 controller, nPoint) for slower axial scanning. An aluminum box housed the collection optics to prevent light contamination from the virtual reality display. Emitted fluorescence light was separated by a dichroic mirror (562 nm long-pass, Semrock) and bandpass filters (525/50 and 625/90 nm, Semrock) into green and red light before collected by GaAsP photomultiplier tubes (Hamamatsu). A Ti:sapphire laser (Coherent Chameleon Vision II) delivered excitation light at 920 nm. The microscope was operated with ScanImage (version 2016a, Vidrio Technologies). The spherical treadmill was mounted on an XYZ translation stage (Dover Motion) which positioned the mouse underneath the stationary objective.
Image acquisition
Volumetric images were acquired at 30 Hz in four axial planes covering a field-of-view of 512 × 512 pixels (675 μm × 750 μm), with planes spaced 20–30 μm apart. Acquisition was discarded during the fly-back period of the axial scanning. Therefore, the resultant frame rate for each plane was 6 Hz. The depth of the top plane was set at 100–130 μm below the pia surface for layer 2/3 imaging or 320–375 μm for layer 5 imaging. The analog signals of the ScanImage frame clock, together with the ball velocity signals and iteration signals from ViRMEn, were recorded at 2 kHz in WaveSurfer (version 0.9192, https://wavesurfer.janelia.org/releases/index.html). A reference image of the top plane was acquired at the beginning of the imaging and was used to correct translational shifts of the field-of-view at the middle of the sessions. At the end of each session, the overall shifts were measured, and used to estimate the XYZ-velocities added to stage movement that compensated the brain motion for the next session. In addition, an image of the vasculature pattern near the pia surface of the field-of-view was acquired, which was used for registration of the field-of-view into a window-centered coordinate frame.
Pre-processing of imaging data
Motion correction
Custom code was used to motion correct calcium imaging data: https://github.com/HarveyLab/Acquisition2P_class/tree/motionCorrection. Motion correction was implemented as a sum of shifts on three distinct temporal scales: sub-frame, full-frame, and minutes- to hour-long warping. First, sequential batches of 1000 frames were corrected for rigid translation using an efficient subpixel two-dimensional FFT method (Guizar-Sicairos et al., 2008). Then rigidly-corrected imaging frames were corrected for non-rigid image deformation on sub-frame timescales using a Lucas-Kanade method (Greenberg and Kerr, 2009). To correct for non-rigid deformation on long (minutes to hours) timescales, a reference image was computed as the average of each 1000-frame batch after correction, and one such average was selected as a global reference for the alignment of all other batches. This alignment was fit using a rigid two-dimensional translation as above, followed by an affine transform after the rigid shift (imregtform in Matlab), followed by a nonlinear warping (imregdemons in Matlab). We found that estimating alignment in this iterative way gave much more accurate and consistent results than attempting nonlinear alignment estimation in one step. Interpolating data multiple times can degrade quality, and so all image deformations (including sub- and full-frame shifts within batch) were converted to a pixel-displacement format and summed together to create a single composite shift for each pixel for each imaging frame. Raw data were then interpolated once using bi-cubic interpolation (interp2 in Matlab).
Source extraction
We used CNMF to identify sources and temporal activity traces in calcium imaging data (Pnevmatikakis et al., 2016). Minor modifications to the initialization algorithm were implemented as described previously (Chettih and Harvey, 2019) and available at https://github.com/Selmaan/NMF-Source-Extraction. Fluorescence traces of each source were then deconvolved using the constrained AR-1 OASIS method (Friedrich et al., 2017); decay constants were initialized at 1 s and then optimized for each source separately. ΔF/F traces were obtained by dividing CNMF traces by the average pixel intensity in the movie in the absence of neural activity (i.e., the sum of background components and the baseline fluorescence identified from deconvolution of a source’s CNMF trace). Deconvolved activity was also rescaled by this factor in order to have units of ΔF/F.
Classification of the sources
To separate CNMF sources into categories for cell bodies and other non-cell body sources, we trained a 3-layer convolutional neural network in Matlab to classify each source into one of the four classes: cell bodies, vertically oriented neural processes, horizontally extended neural processes, and unclassified sources or imaging artifacts. The spatial footprint of each source was centered and cropped into a 25 × 25 pixel image (~1.35 μm per pixel) as input to the network. The network was constructed with 3 convolutional layers (5 × 5 filters, stride 1, number of filters: 32, 16, 16 for each layer) followed by a 256-unit fully connected layer and a 4-unit softmax output layer. The network was trained on 35,771 manually classified sources with 12 folds augmentation with rotation, reflection, translation and rescaling using stochastic gradient descent with momentum, with the following hyperparameters: batch size = 1024, learning rate = 0.01, L2 regularization = 0.0001. Classification accuracy (agreement with manual labels) for cell body class on held-out data was above 90%, close to the variabilities of manual annotations.
The dataset consisted of 278,155 neurons collected in 300 sessions from 8 mice. Among those, only the neural data of 93,881 neurons from 141 sessions were recorded in layer 2/3 with task performance > 65% correct and are included in the subsequent analyses, whereas all behavioral data were used in this study. Data from layer 5 neurons were not analyzed for this study.
Widefield retinotopic mapping
Retinotopic mapping was performed in mice used for calcium imaging with a tandem-lens epifluorescence macroscope (Driscoll et al., 2017; Ratzlaff and Grinvald, 1991). Mice were anesthetized with 0.7–1.2% isoflurane. Excitation light (455 nm LED) was band-pass filtered (469 nm with 35 nm bandwidth, Thorlabs) and reflected onto the cranial window through a camera lens (NIKKOR AI-S FX 50 mm f/1.2, Nikon), focused at 400 μm below the brain surface. GCaMP6s emission was collected with the same lens, filtered (525 nm with 39 nm bandwidth, Thorlabs), and imaged with a CMOS camera (ace acA1920–155um, Basler; lens: SY85MAE-N 85 mm F1.4, Samyang) at 60 Hz. Visual stimuli were presented on a 27-inch IPS LCD monitor (MG279Q, Asus), centered in front of the right eye at a 30-degree angle from the mouse’s midline. The stimulus was a spherically corrected periodic black and white checkered moving bar (Marshel et al., 2011) with constant width (12.5 degrees), speed (10 deg/s) and alternating frequency of the checker pattern (3 Hz), presented in seven blocks consisting of 10 repeats along each of the two directions of cardinal axes. Retinotopic maps were constructed by computing the temporal Fourier transform at each pixel to extract phase at the stimulus frequency (Kalatsky and Stryker, 2003). The phase images were averaged across all trials for each direction. Field sign was calculated by taking the sine of the angle between the gradients of the averaged azimuth and altitude retinotopic maps (Sereno et al., 1994). An image of the vasculature pattern at the brain surface was taken under the same field-of-view, which was later used for aligning field sign to two-photon images.
Registration to the Allen Institute Mouse Common Coordinate Framework (CCF)
The aim of the registration was to assign a location in the Allen CCF for every neuron recorded in different sessions from different mice. The procedure was modified from our previous work (Minderer et al., 2019). For each mouse, we collected a high-resolution reference image of the vasculature patterns at the brain surface of the cranial window using two-photon microscope, by stitching together a tiled 4 × 4 grid of images acquired at typical field-of-view size (675 μm × 750 μm). The field sign was aligned to this reference image using a rigid transformation (translation, rotation, and scaling) identified with control point registration of the widefield vasculature image to the two-photon reference image (cpselect in Matlab). The aligned field sign was then registered to the Allen CCF by aligning the border between V1 and PM as well as the one between PM and AM to a CCF-aligned reference field sign map (available from Allen Institute: http://portal.brain-map.org/; Figure 3C, S3A and S3B), which gave us a window-to-CCF transformation function. To register individual neurons to CCF, the location of each neuron (center of mass of the spatial footprint) in the window-centered coordinate was first determined by aligning the vasculature pattern above each field-of-view to the two-photon reference image (using the imregtform in Matlab with rigid transformation), and then transformed to CCF using the window-to-CCF transformation function.
Area parcellation
In our imaging experiments, we tiled fields-of-view across posterior cortical space irrespective of area boundaries rather than targeting pre-specified cortical areas, because the definition of cortical areas in posterior cortex is ambiguous. For example, previous studies of PPC have recorded neurons near a stereotaxic coordinate (Driscoll et al., 2017; Harvey et al., 2012; Morcos and Harvey, 2016), but its borders are unclear. However, in some analyses, neurons or neural population decoders were grouped into six distinct areas: V1, PM, AM, MM, RSC, A (Figure 3D, 4I, 6E and S3C). To discretize the cortical space into non-overlapping areas, we adopted a combinatorial approach using anatomical and functional landmarks. Neurons in RSC and V1 were separated according to the medial border of RSC and contour of V1 provided by the Allen CCF v.3 (Wang et al., 2020), as these boundaries are generally agreed upon. Although the CCF provides area parcellations for the space in between V1, RSC, and the posterior border of S1, other researchers have suggested alternative and somewhat incompatible subdivisions of this region (Gămănuț et al., 2018; Paxinos and Franklin, 2013; Wang and Burkhalter, 2007; Zhuang et al., 2017). To promote identifiability and reproducibility of areas across experimenters, we subdivided this region into 4 areas using the following criteria. First, secondary visual areas AM and PM were identified by tracing their contours in average retinotopy field sign maps, which slightly deviates from CCF definitions of these areas, as is apparent in the Allen Institute CCF-aligned field sign maps. We then defined area A to mostly overlap with the Allen CCF definition for VisA, but excluding the region of retinotopic AM present in the CCF area VisA, and including a small fraction of neurons slightly posterior-lateral to VisA in CCF area VisRL. Finally, neurons medial to AM, PM, and A, but lateral to RSC, were assigned to area MM. MM is reliably identified in immunolabeling (Wang and Burkhalter, 2007) and cytoarchitecture (“V2MM”) (Paxinos and Franklin, 2013) but is not present in the Allen CCF. Note that a typical imaging field-of-view centered on coordinates previous used in studies of PPC (1.75 mm lateral, 2 mm posterior to bregma) (Harvey et al., 2012) would overlap with part of AM, MM and area A.
After parcellation, of the 93,881 neurons recorded from layer 2/3, we obtained 14,373 neurons in V1, 9,564 neurons in PM, 14,974 neurons in AM, 9,885 neurons in MM, 23,036 neurons in RSC, and 22,049 neurons in area A.
QUANTIFICATION AND STATISRICAL ANALYSIS
Software
All data from methods above were entered into a MySQL database and analyzed using custom-built pipelines in Datajoint for Matlab and Python (Yatsenko et al., 2015). Analyses were performed in Matlab and Python with following libraries: NumPy (Harris et al., 2020; Van Der Walt et al., 2011), SciPy (Virtanen et al., 2020), Matplotlib (Hunter, 2007), Scikit-learn (Pedregosa et al., 2011), and Tensorflow (Abadi et al., 2015).
Statistical procedures
The values of sample size n and what they represent for each analysis can be found in the figure legends and related sections in STAR Methods. Hierarchical bootstrapping was used to generate statistical estimates and significance throughout the analyses, unless indicated otherwise. The number of levels depended on different types of analyses. For analyses of quantities at the level of sessions, rule blocks, or switches, we generated resampled datasets by randomly sampling with replacement, first of the mice and then of the sessions, blocks, or switches. For strategy-binned trials, we resampled within individual strategy bins, first of the mice, then of the trials. For analyses of neurons or neural population decoders, resampled datasets were generated first of the mice and then of the neurons or neural population decoders. The number of bootstrap samples was 10,000 for analyses of behavior-related quantities and 1,000 for neural response-related quantities. The mean and standard error of the bootstrap sample were reported. For significance testing for paired quantities, we built the empirical distribution of the difference between the paired quantities and then computed the probability that the difference was greater or less than zero and took whichever was smaller. The two-tailed p value was reported as twice this probability. For comparing two non-paired bootstrapped samples, we computed the probability that one was greater or less than the other, used whichever was smaller, and multiplied it by two as the two-tailed p value. For one-tailed tests, we reported the p value as the probability that one is greater or less than the other, dependent on the direction of the null hypothesis. Most of the p values reported in this study are two-tailed, unless a one-tailed test is indicated. The Benjamini-Hochberg procedure was used when multiple statistical tests were conducted simultaneously, such as comparing a quantity between multiple areas, to control the false discovery rate at 0.05 (Benjamini and Hochberg, 1995).
Task performance analysis
These analyses refer to Figure S1B–S1F. For each behavioral session, the fraction of correct trials for the whole session and individual blocks were calculated. To further quantify the task performance across rule switches, a smoothed, time-varying function of reward rate of each block was estimated from the time series of trial outcome (correct: 1, incorrect: 0) by fitting to a sigmoid function,
where r(t) is the reward rate of a given trial t, t0 is the first trial of the fitted block. L, b, and k are the constrained parameters of the function. The fitting was performed by minimizing the cross-entropy loss of fitted and true values using the fminunc function in Matlab. Visually guided trials were excluded from the fitting.
To determine the initial and end performance of each block, we evaluated the fitted values at the first and last trial of the block. The recovery constant was identified as the trial number at which the fitted performance reached 63% increase of the difference between initial and end performance from the initial value for each block (Figure S1E and S1F). Blocks with end performance < 70% correct were viewed as unrecovered switches and excluded from the statistics for the recovery constant and subsequent switch-aligned metrics. Task performance for sessions with overall fraction correct > 0.5 was analyzed and shown in Figure 1D and S1B–S1F, but only sessions with overall fraction correct > 0.65 were included for subsequent behavioral and neural analyses.
Modeling of decision-making strategies
LSTM model
These analyses refer to Figure 1E and 1F. An LSTM for strategy modeling was trained for each mouse to predict its choice for each cue, at every trial in a session, based upon previous trials’ data (Figure 1F). The LSTM was constructed in Matlab with a 16-unit LSTM layer followed by a 2-unit sigmoid classification layer. Each input sequence consisted of the 4-channel time series of the cue of the current trial, the cue, choice, and outcome of the previous trial for all trials in each session, and an additional channel indicating the location of the visually guided checkerboard (1: left arm; −1: right arm; 0: not present). Note that visually guided trials were included in the modeling processes to retain continuation of the time series of trials, but model predictions and performance on these trials were excluded in all analyses. For photoinhibition experiments, we also included the presence of inhibition on the current trial as input (one dummy variable for each inhibition target). The training and testing were done with a leave-one-session-out procedure for all sessions recorded from individual mice. The network was trained on the complete input sequences for all sessions for that mouse except for the held-out session using Adam optimizer, with the following hyperparameters: batch size = 1, learning rate = 0.1, L2 regularization = 0.0123. To make predictions for the held-out session, we created two test sequences for every trial. For trial t, both sequences consisted of the real input sequence from the first trial to trial t-1, but the cue on trial t was set to either 0 or 1 to obtain choice predictions of the model for both possible cues. We thus predicted the probability of choosing left (PLeft) vs. the probability of choosing right (PRight), for both cues, for each trial given its trial history, as conditional probabilities: P(L|B), P(R|B), P(L|W) and P(R|W) (Figure 1E). The hyperparameters of network size and regularization strength were selected using a grid search with 60%/20%/20% division of each mouse’s data into training/validation/testing. Hyperparameters had small effects on prediction accuracy, and we selected the single set of hyperparameters with highest accuracy averaged across all mice, corresponding to test accuracy of 80.15%.
Decision-making strategy variables
These analyses refer to Figure 1G–1I and Figure S1I, S1J. Decision-making strategy variables were derived from the LSTM’s predicted conditional probabilities for each choice conditioned on each cue, using the full history of trials on that session. The probabilities shown below are thus all conditioned on the trial history with values varying across trials, which we omit for notational compactness. Our first set of strategy variables were direct transformations of these probabilities, to compute choice bias and rule belief. Choice bias captured the tendency of a mouse to make a left choice versus right choice on a given trial, independent of the cue identity. We computed the marginal probability for each choice and defined choice bias as the unsigned difference between marginal choice probabilities:
since both cues were equally likely. Alternatively, the signed version retained the directionality of the choice bias (positive for left bias and negative for right bias), as shown in Figure 1G.
The tendency of a mouse to use the given cue to make a choice based on either rule was described as the rule belief, quantified by comparing the average probability of the two cue-choice associations that matched each rule. It was defined as a signed value: positive for higher belief in rule B, negative for higher belief in rule A, or 0 for both random and fully biased choices.
Our second set of strategy variables compared our model predictions for a trial with the mouse’s actual choice. We considered the conditional probability of the mouse’s actual choice on each trial given that trial’s actual cue, and linearly subdivided this into contributions from the marginal probability of the choice and the additional contribution of the cue:
The −0.5 in bias-following centered its value at 0 when the marginal probability of the choice was 0.5, meaning that the mouse was equally likely to choose left versus right.
When the probability of actual choice was near 0.5, the mouse’s behavior was unbiased and unrelated to cues, and both bias-following and rule-following metrics were typically near 0, indicating “random guessing” (see Figure 1G and 1H, example trial 267). However, when the probability of actual choice was high, this could be due to a high bias-following, meaning the mouse made biased choices independent of the cue (example trial 114), or due to rule-following, meaning the animal made cue-dependent choices (example trial 164). Occasionally, when a mouse made an unlikely choice according to the model prediction (e.g. an “error” trial during a period of otherwise accurate rule-following behavior), the probability of actual choice can be below the chance level of 0.5. Because these choices were difficult to predict from previous trials, and this model inaccuracy appeared transiently, these choices likely reflected variability in the mouse’s decision-making strategy rather than a failure of our model. On these trials, either bias-following (example trial 117) or rule-following (example trial 208) could be negative, implying that the mouse’s behavior was counter to the local expectation of either biased or rule-guided choices. These metrics were capable of describing the wide range of behaviors exhibited during flexible decision-making. For example, positive/negative rule-following values are analogous to correct/incorrect trials during high-performance periods in tasks without rule switches.
To examine if visually guided trials and normal trials had distinct effects on updating the rule belief as modeled by the LSTMs, we compared the average amount of rule update per trial (Δrule belief, positive means increase of belief to current rule) between visually guided trials and normal trials for 30 trials after rule switches. The rule update per trial was 0.013 ± 0.0055 for visually guided trials and 0.0080 ± 0.0023 for normal trials (difference = 0.0052 ± 0.0057, p = 0.34, hierarchical bootstrap mean ± SEM, n = 265 switches). When we considered correct trials only, the rule update was 0.015 ± 0.0067 for visually guided trials and 0.017 ± 0.0093 for normal trials (difference = −0.0017 ± 0.0078, p = 0.89). Thus, no significant difference in the effect on rule updates between the two types of trials was observed in our modeling.
Reinforcement learning model
These analyses refer to Figure S1G–S1I. We built Q learning-based reinforcement learning models for decision-making strategy as an alternative to LSTM-based modeling. The Q function described the state-action value for each cue-choice pair and was updated using temporal difference learning rules after each trial:
For the trial type of the current trial (cue-choice pair):
For all other trial types:
α is the learning rate and δ is the decay rate bounded between 0 to 1. We set the initial Q-value Q0 to 0.
The likelihood of making a left turn for the given cue at trial t is:
βΔQ is the inverse temperature and β0 is the bias.
We further included a lapse term in order to compute the final likelihood, weighted by a factor λ.
We implemented several variants of models with various components included: choice perseverance, rule-coupling, and reward-dependent learning rates.
Choice perseverance can be modeled with additional parameters φ and τ, corresponding to the strength and timescale of choice perseverance, with modified likelihood as (Katahira, 2018):
I (‧) is the indicator function.
For models with rule-coupling, the Q value for the trial type of the same rule as the current trial type (e.g. the Q function for black-left following a white-right trial) is jointly updated with a coupling factor r.
For models with reward-dependent learning rates, we used separate learning rates αreward and αunreward to update Q values for trials with and without reward, respectively.
The parameters were tuned to minimize the negative log likelihood for all trials in all sessions for each mouse with the leave-one-session-out procedure for making predictions on held-out sessions using the fminunc function in Matlab. For model comparison, we selected the best model using log likelihood on held-out data (Figure S1G) and confirmed the results with AIC and BIC.
Running trajectory correlation analysis
These analyses refer to Figure 2C and Figure S2B. Movement signals (pitch, roll, and yaw velocities of the spherical treadmill) for single trials were first binned and averaged at a grid of maze positions. The running trajectory correlation between two trials was calculated as the Pearson correlation of the vectors of each position-binned signal and then averaged across three velocity types. Within a session, pairwise trajectory correlations between every given trial and all the other choice-matched trials were calculated and averaged. This value was compared to a baseline trajectory correlation as the average correlation of all choice-matched pairs. The difference (Δtrajectory correlation) was aligned to rule switches. To compare pre- and post-switch periods, we averaged Δtrajectory correlations 20 trials prior to and after the first trial of a switch.
Modeling of dynamic choice and cue-biased running
These analyses refer to Figure 2D–2G and Figure S2C–S2F. The LSTM neural network for dynamic choice and cue-biased running was constructed in Matlab with a 10-unit LSTM layer followed by a 2-unit sigmoid classification layer to predict the mouse’s reported choice or the cue identity at every timepoint within a trial, using the running trajectories from trial onset to that timepoint (Figure 2D). The input sequence consisted of the time series of the 3-channel running velocity signals and the forward positions in the maze for every trial. This sequence extended 5 seconds into feedback period/ITI, during which the time elapsed was linearly converted to a pseudo-position as an extended part of the virtual maze. We trained different models for individual behavioral sessions to account for variability in running across sessions. The training and testing procedure were done with both model-averaging and cross-validation. Specifically, we divided the data into 6 cross-validation folds and trained a different model for each group of 5 folds for prediction on the 6th, and then re-divided data into new cross-validation folds and repeated this procedure 6 times. Thus, each trial’s final prediction was the average prediction over 6 different cross-validated models. Training data were also sorted into batches by length and balanced by trial type within batches, by re-sampling additional trials as needed, and trials with abnormal length (length > 2 times average length) were excluded. The network was trained using Adam optimizer, with the following hyperparameters: batch size =100, learning rate = 0.1, L2 regularization = 0.1. The hyperparameters of the network architecture and training procedure were selected using a grid search in a small number of pilot sessions. For the reported choice decoder, the model output (Pleft) was named “dynamic choice”, and for the cue decoder, the output (Pblack) was termed “cue-biased running”. The decoder performance, or the decodability of reported choice or cue identity, was quantified as model log likelihood, equivalent to the negatively signed binary cross-entropy loss.
where y is the true binary value (reported choice or cue), and is the prediction (dynamic choice or cue-biased running). Log base 2 was used so that the log likelihood equals −1 for chance-level predictions and 0 for perfect prediction. When log likelihood was smaller than −1 (below chance model prediction), the dynamic choice or cue-biased running was more consistent with the opposite reported choice or cue. For reported choice decoding, we specifically referred to this log likelihood as “choice commitment”, measuring the consistency between the decoded choice from movement (until that timepoint) and the eventual reported choice. The latency for dynamic choice to cross a threshold was identified as the timepoint from trial onset at which dynamic choice reached 0.9 for left trials and 0.1 for right trials, normalized by the average trial duration of individual sessions.
We interpreted the dynamic choice as an approximation of the time-varying process of choice formation reflected in running trajectories, although such estimate should be regarded as a lower bound of the true choice formation process: when movements predict future choice one can conclude a decision is made, but it is possible for decisions to be made without becoming rapidly evident in motor behavior.
Logistic decoder for cue from movement
These analyses refer to Figure S2J and S2K. For a more easily interpretable analysis of cue-biased running, in addition to the LSTM network we fitted a logistic regression model to decode the cue identity using the movement at the first 25% of the maze stem, since the cue-biased running was most prominent early in the trial. Logistic decoders were trained on the average 3-channel running velocities over this period using the fitglm function in Matlab with 10-fold cross validation. The accuracy (fraction correct) of the model indicated the overall magnitude of cue-biased running, and the sign of the coefficient for roll velocity indicated the directionality of how cue identity was correlated with left-right movements (Figure S2K). The model trained for one session was also applied to other sessions from the same mouse, and the cross-session accuracy showed the consistency of this cue-lateral movement mapping across multiple sessions (Figure S2J).
Analysis of photoinhibition experiments
These analyses refer to Figure 1L–1M, Figure S1K–S1M and S2M. We assessed the impact of photoinhibition at each targeted area on the task performance (fraction correct) and the behavioral model-derived quantities (strategy variables, dynamic choice and cue-biased running) by comparing the values on target trials to the control trials within each session, using a modified hierarchical bootstrap procedure. For each target area, we generated 10,000 bootstrap datasets by sampling with replacement the mean values of interest on target trials and control trials for individual sessions, first of the mouse, then of the sessions. For each bootstrap dataset, we then averaged session-level data within each resampled mouse before averaging across mice. This procedure took into account the differences in number of trials and sessions collected from each mouse and weighted them equally.
Generalized Linear Models
To investigate the encoding properties of single neurons, we fitted Poisson generalized linear models to the deconvolved activity of each neuron. These analyses refer to the encoding maps as well as the comparison of encoding magnitude and time course between areas in Figure 3–7 and Figure S4–S8.
Design matrix
The schematic is shown in Figure 3H. Predictors of neural activity were grouped into two main categories: task variables and instantaneous movement. Task variables included trial phase (maze position during maze traversal and time elapsed in feedback period/ITI), binary-valued cue identity, reported choice, outcome (reward or no reward) of current and previous trials, as well as the continuous-valued strategy variables, dynamic choice, and cue-biased running. We also included pairwise interactions between strategy variables and cue/reported choice/outcome, as well as interactions between cue and dynamic choice. These interactions captured whether strategy variables changed the neural response to a cue or feedback of the outcome, and whether neurons were selective for a specific combination of cue and choice.
We assumed that neurons responded to these task variables in a trial phase-specific manner, given the transient activity of most of the neurons that were aligned to a specific epoch of the trial. We thus constructed a set of basis functions for trial phase, consisting of 20 equally spaced position bases during maze traversal and 16 temporal bases spanning 0–5 seconds in feedback period/ITI. These bases were parametrized as raised cosine bumps (Pillow et al., 2008):
where x is the maze position or time elapsed, ci is the center location of the ith kernel, and w is the width for the basis functions (4 times of the spacing between center locations). The mouse’s actual position during traversal and time elapsed in feedback period/ITI were first expanded with the trial phase basis functions. To load the task variables onto these basis functions, we took interactions between the time series of each task variable and the expanded position/temporal bases, resulting in 27 × (20 + 16) = 972 predictors for expanded task variables.
On the other hand, neurons encoding instantaneous movement should respond to movement variables consistently in a trial phase-invariant way. These variables included the 3-channel running velocity and acceleration signals as well as the pairwise interactions between velocities and between accelerations. To allow non-linear tuning for potentially complex movement features, we rank-transformed the velocity and acceleration signals within individual sessions and expanded with 7-degree-of-freedom b-splines using the patsy Python library (7 basis functions for each linear term and 49 basis functions for each pairwise interaction term). This resulted in 7 × 6 + 49 × 6 = 336 predictors for movement variables.
To account for slow changes in fluorescence signals caused by possible sample drift within a session, and our corrective manual realignment, we also included an offset term and a linearly increasing term for frames collected in every image acquisition block (see methods section Two-photon calcium imaging). These terms collectively represented a discontinuous piecewise function aligned to image acquisition blocks within a session, which would reflect sample drift in the brain relative to the microscope’s imaging plane. We then excluded neurons that had greater than 10% of null deviance explained by these terms from subsequent analyses, which we observed in a small subset of data to be indicative of failures to correct for sample drift. All the predictors were concatenated and z-scored independently to form the design matrix.
For the additional models shown in Figure S4D–S4E and S5M, we included temporally shifted movement kernels to investigate the encoding of past and upcoming movement. The velocity and acceleration signals were expanded with 5-degree-of-freedom b-splines and were shifted every 1/3 seconds for 2 seconds into the past and 2 seconds into the future. We did not include pairwise interaction terms for this model to avoid over-parameterization. For the other additional models shown in Figure S5N, we included a new variable “subjective lateral distance” which quantified the imaginary lateral displacement as if the mice were doing path integration based on their locomotor movement even without actual displacement in the stem of the virtual maze (as imposed by the experimental constraint). We calculated the accumulated sum of roll velocity at each timepoint for every trial as the numerical integration, z-scored the values across all trials in each session, and expanded with the position bases before including them into the design matrix.
Fitting procedure
The model was fit using custom-built code in Tensorflow 1.13.1 (Available at https://zenodo.org/badge/latestdoi/491659726). We used Adam optimizer (learning rate 0.001) for batch gradient descent to minimize Poisson loss (tf.nn.log_poisson_loss) with group lasso penalty (Yuan and Lin, 2006):
where λ is the regularization strength, gi and wi are the size and weight vector for variable group i, and is the Euclidean norm. Predictors of the same variables expanded with different basis functions were assigned to the same groups. The group lasso penalty encourages sparsity between tuning to different variables, but non-sparse L2 regularization on the within-variable kernels. All the trials within individual sessions were first split into 80% training trials and 20% test trials. On the 80% training data, we performed a 5-fold cross validation (split on trials) fitting procedure to select the optimal λ value (a series of 21 logarithmically spaced values between 10−5 to 10−1) for each neuron. In each fold, separate models were fitted on data points in 80% of the training trials with different λ values, and predictions were made on the 20% held-out training trials. Mean deviance on the predicted data across 5 CV folds was calculated and compared across all λ values to select the optimal one. All training data were then fitted with the optimal λ value to obtain the model coefficients. Model performance was evaluated as the fraction of Poisson deviance explained on the 20% test data (Figure 3I and S3D).
For analyses of the encoding magnitudes of single neurons (Figure 3–7; Figure S4–S8), we included well fit neurons (fraction deviance explained on test data > 0.2). 42,998 neurons were selected, including 7,775 neurons in V1, 4,934 neurons in PM, 6,878 neurons in AM, 3,991 neurons in MM, 10,329 neurons in RSC, and 9,091 neurons in area A. In Figure S8K–S8O, we included neurons with worse fits (fraction deviance explained on test data > 0.1), resulting in 68,532 neurons (11,240 neurons in V1, 7,190 neurons in PM, 10,790 neurons in AM, 6,788 neurons in MM, 17,074 neurons in RSC, and 15,450 neurons in area A).
Quantification of fraction explained deviance for individual variables (without re-fitting)
The schematic is shown in Figure S3G. To determine the contribution of individual variables (such as cue, dynamic choice, or roll velocity) or related groups of variables (such as all movement variables, all task variables, or all strategy variables) for predicting neural activity, we calculated the “fraction explained deviance” for target variable(s) in the GLM. For data points to be evaluated, we made two different predictions from a “full model” with all coefficients and an “ablated model” with coefficients zeroed for the target variable(s). The fraction explained deviance was then computed as the difference in Poisson deviance between “full” and “ablated” models, calculated independently for 36 trial phase bins evenly dividing the full trial, and normalized by the amount of deviance explained by the full model (averaged over all frames). For computational feasibility, and to minimize variability due to sub-selecting data, we evaluated the fraction explained deviance on CV held-out data (80% of full dataset) instead of test-data (20%). We confirmed that the difference in the fraction explained deviance evaluated on the CV held-out data and test data was sufficiently small (0.0010 ± 0.0006, mean ± SEM; Figure S3E), indicating that the model did not overfit due to the selection process of the single hyperparameter λ on CV-held out data. Results for example neurons were shown in Figure 3J.
To address the potential effect of different regularizations on the encoding magnitude of variables and the conjunctive structure between pairs of variables, we repeated this procedure with L2 regularization (ridge regression), rather than group lasso. The performance of the models on test data was worse on average than those with group lasso (difference in fraction of explained deviance: −0.0175 ± 0.0052, mean ± SEM; Figure S8D). The L2 regularization assigned weights more evenly to correlated variables, thus we observed a slight decrease of fraction explained deviance for variables with higher weights (e.g., cue) and an increase for variables with small weights (e.g., strategy), as well as an increase of correlations between encoding strength of pairs of variables. Nevertheless, the encoding gradients and comparison of encoding magnitude and conjunctive structure between individual areas remained consistent (Figure S8E–S8J).
Quantification of fraction null deviance for individual variables (with re-fitting)
The schematic is shown in Figure S3H. In addition to fraction explained deviance, we also performed a conservative procedure to quantify the contribution of individual variables. We fitted two separate models, one with all variables (“full model”) and the other with the target variables removed (“reduced model”), and computed the difference in deviance between the full and reduced models normalized by the null deviance (deviance of a model that only included an intercept) of each neuron’s deconvolved activity. New optimal regularization parameters (λ) were selected using 5-fold cross validation for the reduced models.
We report results without re-fitting in the main figures (Figure 3–7) and include re-fitting in extended data (Figure S4 and S5), since the advantages of each method are complementary. The procedure without re-fitting is similar to analysis of the magnitude of a model’s fitted coefficients in a linear model but adapted for a GLM where a nonlinear link function and Poisson observations can make interpreting model coefficients difficult. This procedure is in principle a less biased method to disentangle the relative contribution of correlated variables; however, this disentangling may be inaccurate if the model structure is a poor match for the actual data-generating process. The procedure with re-fitting is biased, in that it provides a lower bound on a variable’s contribution, rather than an accurate estimate of its true effect. The slack of this lower bound also depends on which other correlated variables are included besides the variable of interest. However, this method may be less susceptible to mismatch between model and data structure and so is a robust and conservative estimate of a variable’s contribution. Our results were qualitatively similar using both procedures.
Decoding analyses with population activity
Trial phase-specific logistic decoders
These analyses refer to Figure 3Q, 4D, 8C, 8D and Figure S5F, S5G, S5K, S5L. To decode the cue identity, reported choice, dynamic choice and cue-biased running from the neural population activity, we divided simultaneously imaged neurons from individual sessions into spatially adjacent, non-overlapping subpopulations of ~100 neurons. All recorded layer 2/3 neurons were included, without selection based on their GLM fit quality. To reduce over-parameterization of the model, we performed PCA on the deconvolved activity of the subpopulation and used the lowest number of principal components that accounted for >90% of variance for population decoding. We then fit a logistic regression to decode cue identity, reported choice, dynamic choice or cue-biased running on single imaging frames, using the lassoglm function in Matlab with a binomial distribution and elastic net regularization consisting of 10% L1 and 90% L2. We fit separate models for data in 11 equally spaced position bins spanning the maze length, to allow trial phase-specific decision boundaries arising from transient neural activity. The fitting was performed with 5-fold cross validation to generate predictions at each data point. The performance of the decoder was evaluated as the log likelihood (for binary variables) or Spearman correlation (for binary and continuous variables) between the true and predicted values on held-out data. The cortical location of each decoder was computed as the centroid of all neurons in that subpopulation. For Figure 8C, 8D and S5L, decoders were assigned into one of the 6 discrete areas according to their centroid locations. We obtained 698 decoders for Figure 8C (V1: 100, PM: 79, AM: 122, MM: 62, RSC: 157, A: 178) using only sessions with cue offset at 0.76 of maze length, 974 decoders in Figure 8D (V1: 151, PM: 106, AM: 149, MM: 108, RSC: 233, A: 227), and 998 decoders in Figure S5L (V1: 154, PM: 110, AM: 157, MM: 112, RSC: 236, A: 229).
Trial phase-invariant linear decoders for instantaneous movement
This analysis refers to Figure S4I. To decode instantaneous movement (pitch, roll, and yaw velocities and accelerations) from population activity, we first divided simultaneously imaged neurons into subpopulations of ~100 nearby neurons and reduced model overparameterization using PCA as described above, and then used linear regression to train and predict each of the movement variables from all timepoints of the denoised deconvolved activity with 10-fold cross-validation. Decoder performance was reported as the Spearman correlation between the true and predicted values on held-out data.
Analysis of dynamic choice and cue-biased running at matched positions
These analyses refer to Figure S5J–S5L. In these analyses, we wanted to compare the neural activity related to the dynamic choice and cue-biased running, given that these quantities were both derived from temporally integrated movement signals using the LSTM, but described different aspects of the mouse’s behavior during decision-making process. Since the time course and range of magnitude of dynamic choice was different from those of cue-biased running, and varied across individual sessions, we compared neural representations at timepoints around the maze positions at which the LSTM decoding performance of reported choice and cue were matched. For individual sessions, the trial-averaged decoding performance (log likelihood) of reported choice and cue was calculated as a function of maze position, and the positions at which the average log likelihood of both signals reached a threshold were identified over a range of threshold values (Figure S5J). Thresholds were spaced by 0.1 and spanned across of the range of decoding performance for that session. We then examined the GLM-derived encoding magnitude of single neurons as well as the population decoding performance for dynamic choice and cue-biased running at the matched positions for each threshold level. For single-neuron encoding, the fraction explained deviance of dynamic choice and cue-biased running at the matched positions were extracted and compared at different threshold levels. For population decoding, we trained logistic decoders on the three closest timepoints recorded around the matched maze positions for all trials using the same procedure described in the section Decoding analyses with population activity, and compared the model performance (Spearman correlation) for decoding of dynamic choice vs. cue-biased running at each threshold level. For comparison of both encoding magnitude and decoding performance, we averaged the values over all threshold levels and generated spatial maps or statistics for discrete areas, since results were similar for a wide range of individual thresholds.
Quantification of distributedness
Intuitive models
These analyses refer to Figure 5B–5D and Figure S6A–S6C. We developed two intuitive models to quantify the degree of distributedness for single-neuron encoding strengths across cortical areas. For both models, we first constructed a fully modular configuration with 1000 neurons for each of the 6 areas. We assigned a rank of encoding strength to all 6000 neurons and then assigned the area labels as contiguous, non-overlapping sets, i.e. neurons with rank 1–1000 belonged to area 1, rank 1001–2000 belonged to area 2, etc., as shown in first panel from the left in Figure 5D. Therefore, in the fully modular case, the encoding strength of a neuron is completely informative of its area label and vice versa. We quantified the mutual information between the rank of encoding strength and area label using the mutual_info_classif function from Scikit-learn.
For the random fraction model (Figure 5B), we initiated the fully distributed model by randomly assigning area labels to the neurons so that the encoding is completely dispersed across areas with zero mutual information. We then created different intermediate models by mixing neurons from the fully modular and the fully distributed models, parametrized by the fraction of the fully distributed model (“random fraction”), and computed the normalized mutual information. When the random fraction is closer to zero, the organization is more similar to fully modular, with larger distinctions between areas, whereas when this fraction is closer to one, the organization is more similar to fully distributed, with nearly no differences between areas. We repeated this process 100 times for 100 linearly spaced random fraction values from 0.01 to 1 to build the average normalized mutual information vs. random fraction curve in Figure S6B. For the “jitter” model (Figure 5C), we perturbed the distribution of the fully modular model by adding random Gaussian noise parametrized with “jitter”, i.e. the standard deviation of the noise, into the rank of encoding strength. The perturbed rank was then re-ranked, and the mutual information between the rank of encoding strength and area label was calculated. We then normalized the mutual information by that of the fully modular case. We repeated this process 100 times for 491 linearly spaced jitter values from 0.1 to 5 to build the average normalized mutual information vs. jitter curve in Figure S6C. These two intuitive models were complementary to each other. The random fraction model put the measurement of distributedness on a bounded range between zero to one and was easier to interpret, whereas the jitter model created simulated distributions that resembled the empirical distributions (Figure 5D).
Quantification on single variable encoding
These analyses refer to Figure 5E, 5F and Figure S6A. For each of the selected variables, we first determined the relevant epoch for encoding, e.g. stem period for cue, maze position and dynamic choice, feedback period for reported choice and outcome, and whole trial for movement, and identified active neurons in that epoch by selecting neurons with epoch-averaged null deviance in their deconvolved activity greater than their trial-averaged null deviance. We then subsampled 1000 active neurons in each area, rank-transformed their encoding strength (fraction explained deviance of that variable), and computed the mutual information between the rank of encoding strength and area label, normalized by that of the fully modular model. This process was repeated 1000 times to compute mean and standard error. To compute the “equivalent random fraction” or the “equivalent jitter” for the selected variable, we identified the random fraction or jitter value by searching the nearest neighbor of the mean normalized mutual information based on the normalized mutual information vs. random fraction or jitter curve. The selection procedure for epoch-specific active neurons resulted in 47% of neurons active during stem traversal (total 20,202 neurons; V1: 3641, PM: 2313, AM: 3350, MM: 1855, RSC: 5720, A: 3323) and 30% of neurons active in feedback period/ITI (total 12,719 neurons; V1: 2441, PM: 1208, AM: 1756, MM: 1040, RSC: 2341, A: 3933).
Besides the mutual information-based methods, we also performed a complementary approach to quantify the degree of distributedness based on decoding with discretized area labels. For each of the selected variables, we first identified the area with the highest average encoding strength, e.g. V1 for cue and area A for movement, and used logistic regression to decode neurons residing in this area from neurons in all other 5 areas based on the encoding strength of that variable, which we called “max vs. others” decoding (Figure S6D). Separately, we constructed 15 pairwise decoders that distinguished neurons from each pair of areas. Decoding was done using the LogisticRegression function from Scikit-learn with leave-one-mouse-out cross validation, and we reported the area under ROC on held-out data as an alternative measurement of the degree of distributedness. The auROC would equal 1 for the fully modular case and 0.5 for the fully distributed one. We subsampled 1000 neurons from each area for this analysis and repeated it 1000 times to compute mean and standard error.
Decoding anatomical locations from single-neuron encoding profiles
These analyses refer to Figure 6A, 6B and Figure S6E, S6F. To relate a neuron’s encoding properties to its anatomical location in the cortical space, we decoded each neuron’s cortical location from its GLM-derived encoding profile (Figure 6A). For each neuron, we computed the encoding profile as the mean fraction explained deviance of individual task and behavioral variables (trial phase, cue identity, reported choice, outcome of previous and current trials, decision-making strategy, dynamic choice, cue-biased running, interaction between cue and dynamic choice, and instantaneous movement and their pairwise interactions) over 6 different epochs of the trial (first and second half of maze stem, maze arm, delay between reported choice and feedback, feedback period, and reward consumption/ITI). To decode location continuously across posterior cortex, we used an array of logistic regressions with centers on a grid with 0.15 mm spacing (total 241 decoders). Each decoder was trained to predict the presence of a neuron nearby to that decoder’s center location, using its encoding profile. For each neuron, the target value for each decoder was a smooth function of distance from that decoder’s center location to the neuron’s actual location:
where yi, j is the target value of neuron i for decoder j, xi is the cortical location of neuron i, cj is the center location of decoder j, and σ is the standard deviation of the gaussian kernel (we used 0.15 mm).
The location decoders were fitted using logistic regression with our custom-built GLM code in Tensorflow to minimize cross-entropy loss with L2 regularization (Adam optimizer, learning rate: 0.01). We performed cross-validation in a leave-one-mouse-out manner: for every CV fold, the decoders were trained on neurons from 7 mice and tested on the 8th mouse. The predictions of each decoder were corrected by dividing by the sampling density of neurons at that location (to correct for a non-flat prior across space). Predictions for each neuron were then normalized across all decoders to a sum of 1 to generate a probability distribution over cortical space.
where is raw output for neuron i for decoder j, is the corrected output after adjusting the non-flat prior, is the final prediction after normalization across predictions from all decoders.
Non-negative matrix factorization of decoded locations
These analyses refer to Figure 6C, 6D, 6G and Figure S6G–S6I. Factorization of decoded neuron locations was performed using the NMF function from Scikit-learn to approximate the matrix of predictions for all neurons across all decoder locations (42,998 neurons × 241 decoded locations; Figure 6C). Separate factorizations were fit with a sequence of increasing numbers of factors (n_components, k = 1 to 10; Figure S6I). Factorization with k = 3 resulted in 34% of reconstruction error, with far less improvement by adding more factors. We thus presented the results with three factors. The characteristic encoding profile for each factor shown in Figure S6G was calculated as the average decoder coefficients of individual task and behavioral variables, weighted by the scores of each decoder/location on each factor:
where fi,k is the weighted encoding magnitude for variable i of factor j, sj,k is the decoder score for decoder j of factor k, and wi, j is the coefficient for variable i of factor j.
Linear embedding of single neuron encoding properties
These analyses refer to Figure 6F, 6G and Figure S6J–S6L. To investigate the heterogeneity of the single-neuron encoding within and across areas, we generated a linear embedding of each neuron’s encoding profile in a 2-dimensional encoding space (Figure 6F), using the coefficients of decoders trained to predict location from encoding profiles. Each location decoder was trained to predict the presence of a neuron near its center location, resulting in a vector of coefficients in encoding space which was most useful for differentiating a neuron’s proximity to the center location. We expected nearby location decoders to be similar to each other, and the total structure of variability across all locations to be much lower dimensional than the full number of location decoders. Thus, we performed principal component analysis on the full set of location decoder coefficients to identify the vectors in neural encoding space that were most relevant in differentiating the location of a neuron (Figure S6J). We then construct the encoding space using the first two principal components as the x and y axes. Each neuron’s coordinate in the 2-D encoding space was computed by projecting its encoding profile onto the embedding axes. We also used kernel smoothing (gaussian_kde from SciPy, bw_method = ‘scott’) to generate empirical densities of neurons from a single cortical area in the 2-D encoding space, from which we estimated the peak and 25% contour used for visualization (Figure 6H). The dendrogram, which captured the similarity of the averaged encoding between areas, was computed based on the Euclidean distances between the centroids of all neurons from 6 areas in the full-dimensional encoding space used for location decoders, using the linkage (method = ‘average’) and dendrogram function from SciPy.
Analyses of conjunctive structure
Correlation between encoding of pairs of variables
These analyses refer to Figure 7D–7F and Figure S7D–S7G. To compute the correlation between encoding strength of pairs of variables, we first removed spatial differences in average encoding strength by subtracting the local mean calculated in smoothed encoding maps (SD = 150 μm) as shown elsewhere in the paper. Without this subtraction, correlations in encoding strength might be biased by spatial gradients of encoding strength which do not perfectly align with area boundaries. We also identified active neurons for the relevant epoch for each correlation, to prevent possible biases in correlation contributed by neurons with little or no activity. Active neurons are defined as neurons with epoch-averaged null deviance in their deconvolved activity greater than their trial-averaged null deviance (See the section Quantification of distributedness, Quantification on single variable encoding). Computing correlations of fraction explained deviance between certain sets of variables (e.g. example movement and position) exhibited large negative correlations, as might be expected when the total explained deviance is similar to the sum of explained deviance. To avoid this bias, we instead computed all correlations using the fraction null deviance instead of fraction explained deviance. We then computed the Pearson correlation between the spatial-mean-subtracted encoding strength of selected pairs of variables for neurons in individual areas.
Decoding of area based on encoding correlations versus encoding strengths
These analyses refer to Figure 7G, 7H and Figure S7H, S7I. For decoding of area labels based on the encoding correlations between pairs of variables, we z-scored the spatial-mean-subtracted encoding strength for neurons within individual areas and took the pairwise interaction between these for 11 selected variables (trial phase, cue identity, reported choice, outcome of previous and current trials, decision-making strategy, dynamic choice, cue-biased running, interaction between cue and dynamic choice, and instantaneous movement and their pairwise interactions), for stem traversal or feedback period/ITI. Only active neurons for each of the relevant epoch were included. We then decoded the area labels using only these “interaction terms”, only linear terms of single variable encoding strengths, and a combination of both linear and interaction terms. We performed two types of decoding: 6 one-vs.-others decoders that distinguished neurons from each of the 6 areas versus all the other neurons not from this area, as well as 15 pairwise decoders that distinguished neurons from each pair of areas. Decoding was done using the LogisticRegression function from Scikit-learn, and the performance was quantified as the area under ROC on held-out data using leave-one-mouse-out cross validation.
We repeated these analyses with encoding strength estimated based on GLMs fitted using L2 regularization, which handled correlated variables differently than group lasso. The correlations between individual pairs of variables were higher than those with group lasso as expected from the effect of L2 regularization (Figure S8H); however, the results of decoding of area were consistent with those with group lasso (Figure S8I and S8J).
Quantification of shattering dimensionality for conjunctive variables
These analyses refer to Figure 8E–8G and Figure S8A–S8C. To quantify the dimensionality of population representations for conjunctive conditions formed by two or more variables, we modified the procedure described in Bernardi et al., 2020. The central idea is to construct dichotomies by partitioning these conjunctive conditions into two sets and use linear classifiers to decode these dichotomies from population activity. The higher the dimensionality is, the better the decoders can perform. For continuous variables such as maze position and movement, we discretized their values into several bins. In order to keep the total number of conditions similar for analyses of different conjunctions, we used 2 bins for cue or choice, 3 bins for rule belief, 10 linearly spaced position bins for cue- or choice-by-maze position, 6 position bins for cue-by-belief-by-position, 4 position bins for cue-by-choice-by-position, and 6 quantile bins for each axis of velocity. For example, the combination of cue and maze position would generate 2 cues × 10 position bins = 20 conjunctive conditions. For k conjunctive conditions, there are 2k possible dichotomies and balanced dichotomies (where the dichotomous sets are equally sized). We further restricted our analysis on “marginally balanced dichotomies” which contain the balanced number marginal conditions for each class (Figure 8E), because these dichotomies are only separable when encoding of the two variables exhibits nonlinear mixing. For the example of cue-by-position, each class in one of the marginally balanced dichotomies would contain 5 conjunctive conditions with black cue and 5 with white cue, as well as one conjunctive condition for each of the 10 positions. Populations with pure encoding of cue or position, or linear mixing of the two, would thus be uninformative for decoding regardless of the encoding strength.
Because we aimed to compute dimensionality formed by a large number of neurons, and potentially spread across large areas of posterior cortex, we focused our analysis on trial-averaged neural tuning rather than simultaneously recorded populations. We thus constructed pseudo-populations by pooling neurons across sessions and mice. We set up 481 center locations on a grid of 0.1 mm spacing across the cortical space in posterior cortex (Figure 8F and S8A). For each center location, we identified N nearest neurons from all neurons pooled across sessions and animals, where N was the population size. To generate training and test data for each neuron, we first identified all frames that occurred during each conjunctive condition within each trial during stem traversal, and took the average of the deconvolved activity to create a “trial sample” for that conjunctive condition. Next, we split all the trial samples for each conjunctive condition into training and test set with a 50–50 split, unless the number of test trials exceeded 30 trials in which case they were added to the training set. We then standardized the trial samples using the mean and standard deviation of the training set and took the average over all samples for both training and test sets. We concatenated data from each pseudo-population into training and test matrices of k conditions × N neurons and built linear SVMs to classify all marginally balanced dichotomies with the SVC function in Scikit-learn. We repeated the train-test split and decoding procedure 10 times. We reported the average classification accuracy on test data across all these dichotomies and all splits as the “shattering dimensionality” to measure the dimensionality of conjunctive neural representations.
In order to determine the statistical significance of differences in shattering dimensionality between areas, we repeated the analysis described above using pseudo-populations defined by area boundaries rather than proximity to centroid locations (Figure 8G, S8B and S8C). Specifically, we used a hierarchical bootstrap to resample N neurons from within a specific area, or randomly across all areas in our dataset. We then performed decoding as described above for each of the 1000 bootstrap samples to obtain distributions used to obtain mean and standard error within area, and statistical significance between each area’s dimensionality.
We repeated the analyses on different population sizes of 100, 250, 500, 1000, and 2000 neurons. All recorded layer 2/3 neurons were included, without selection based on their GLM fit quality. For each population size and each conjunction of variables, we selected the best hyperparameter C for the SVC function from a list of values: 0.01, 0.1, 1.0, and 10.0. The selected C for Figure 8F, 8G, S8A and S8B with population size = 1000 are C = 1.0 for cue and maze position, and C = 0.1 for all other conjunctions of variables.
Analysis of dimensionality of encoding across neurons versus encoding across cortical space
An interesting question one may have about the spatial structure of encoding is how the diverse encoding profiles across single neurons and the resulting seemingly complex encoding maps for individual variables give rise to the three functional gradients we observed. Here, we compare the dimensionality of encoding across single neurons versus encoding of cortical space to address this issue. The GLM extracted an encoding profile over a large number of task and behavioral predictors for every neuron, and collectively the encoding across neurons varied in a high dimensional encoding space given the diversity of encoding profiles. However, the dimensionality of encoding across neurons could be higher than the dimensionality of encoding across cortical space, or the number of distinct spatial gradients. This is because neurons that encode a set of variables could show no significant structure in their distribution across cortical space, or two distinct sets of variables could have similar encoding profiles across cortical space. Relatedly, in our previous work (Minderer et al., 2019), an artificial neural network was used to identify 64 distinct features related to optic flow, locomotion, and various task events that contributed to single neuron activity in posterior cortex during a visually-guided locomotion task. Although most of these features exhibited non-uniform encoding over cortical space, many of these spatial profiles were similar. This indicates a reduced dimensionality from encoding across neurons to encoding across cortical space, even though the number of distinct spatial gradients was not explicitly quantified in that study. In the present study, the distinct spatial gradients were identified based on the decoding of anatomical locations from single-neuron encoding profiles. In particular, the location decoders extract the part of the encoding profiles that is informative of a neuron’s cortical location, by assigning large weights to those spatially informative variables and converting single-neuron encoding profiles across variables to decoded probabilities across cortical locations.
To compare the dimensionality of encoding across neurons versus encoding across space, we considered the following three matrices: (1) the fitted GLM coefficients for individual task and behavioral variables (the matrix of neurons by coefficients for all variables), (2) the encoding strengths for individual task and behavioral variables (the matrix of neurons by fraction explained deviance for all variables), and (3) the outputs of the location decoders (the matrix of neurons by decoded location which we performed factorization on). Both matrices 1 and 2 describe encoding across neurons, but the entries in matrix 1 are signed, which captures both the directionality and magnitude of the tuning and is expected to have the highest dimensionality, whereas matrix 2 only represents the magnitude of the tuning with reduced dimensionality. Matrix 3 captures encoding across cortical space and is expected to show the lowest dimensionality. To confirm this, we performed principal component analysis to estimate the linear dimensionality of these three matrices. The number of principal components needed to explain 70% of the variance in the three matrices was 8, 6, and 3, respectively, and further, 35, 23, and 16 principal components were needed to explain 95% of the variance. These results thus justify how a small number of spatial gradients can describe the encoding across cortical space, even with the encoding profiles of individual neurons being diverse and relatively higher-dimensional.
Supplementary Material
Highlights.
Mice were trained on a flexible navigation decision task based on rule switches
Neural activity from 90,000 neurons was densely sampled across posterior cortex
Representations were highly distributed but organized in distinct spatial gradients
Conjunctive coding and dimensionality were similar between cortical areas
Acknowledgements
We thank Mark Andermann, Jan Drugowitsch, Matthias Minderer, and members of the Harvey lab for discussions; Deane Stryker, Annie Hunter, and Mary Gulino for assistance in developing the behavioral task and collecting pilot data; Noah Pettit for designing the compact virtual reality system; Pavel Gorelik and Ofer Mazor from the Research Instrumentation Core at Harvard Medical School; Tim LaFratta and John LeBlanc from the Department of Neurobiology Machine Shop (supported by grant P30 EY012196). This work was supported by an NIH Director’s Pioneer Award (DP1 MH125776), NIH grants from NINDS (R01 NS089521), the NIMH BRAINS program (R01 MH107620), and the BRAIN Initiative (R01 NS108410), an Armenise-Harvard Foundation Junior Faculty Grant (C.D.H.), a Stuart H.Q. & Victoria Quan Fellowship (S.-Y.T.), and an NSF Graduate Research Fellowship (S.N.C.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing interests.
References
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, et al. (2016). TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 10.48550/arXiv.1603.04467. [DOI] [Google Scholar]
- Akrami A, Kopec CD, Diamond ME, and Brody CD (2018). Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 554, 368–372. [DOI] [PubMed] [Google Scholar]
- Alexander AS, and Nitz DA (2015). Retrosplenial cortex maps the conjunction of internal and external spaces. Nat. Neurosci 18, 1143–1151. [DOI] [PubMed] [Google Scholar]
- Alexander AS, and Nitz DA (2017). Spatially Periodic Activation Patterns of Retrosplenial Cortex Encode Route Sub-spaces and Distance Traveled. Curr. Biol 27, 1551–1560. [DOI] [PubMed] [Google Scholar]
- Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen WE, Chen MZ, Pichamoorthy N, Tien RH, Pachitariu M, Luo L, and Deisseroth K (2019). Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science 364, eaav3932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andermann ML, Kerlin AM, Roumis DK, Glickfeld LL, and Reid RC (2011). Functional specialization of mouse higher visual cortical areas. Neuron 72, 1025–1039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen RA, and Cui H (2009). Intention, Action Planning, and Decision Making in Parietal-Frontal Circuits. Neuron 63, 568–583. [DOI] [PubMed] [Google Scholar]
- Arlt C, Barroso-Luque R, Kira S, Bruno CA, Xia N, Chettih SN, Soares S, Pettit NL, and Harvey CD (2021). Cognitive experience alters cortical involvement in navigation decisions. BioRxiv 10.1101/2021.12.10.472106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aronov D, and Tank DW (2014). Engagement of Neural Circuits Underlying 2D Spatial Navigation in a Rodent Virtual Reality System. Neuron 84, 442–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, and Hochberg Y (1995). Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B 57, 289–300. [Google Scholar]
- Bernardi S, Benna MK, Rigotti M, Munuera J, Fusi S, and Salzman CD (2020). The Geometry of Abstraction in the Hippocampus and Prefrontal Cortex. Cell 183, 954–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bicanski A, and Burgess N (2016). Environmental anchoring of head direction in a computational model of retrosplenial cortex. J. Neurosci 36, 11601–11618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunton BW, Botvinick MM, and Brody CD (2013). Rats and Humans Can Optimally Accumulate Evidence for Decision-Making. Science 340, 95–98. [DOI] [PubMed] [Google Scholar]
- Chettih SN, and Harvey CD (2019). Single-neuron perturbations reveal feature-specific competition in V1. Nature 567, 334–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho J, and Sharp PE (2001). Head direction, place, and movement correlates for cells in the rat retrosplenial cortex. Behav. Neurosci 115, 3–25. [DOI] [PubMed] [Google Scholar]
- Desmurget M, Reilly KT, Richard N, Szathmari A, Mottolese C, and Sirigu A (2009). Movement Intention After Parietal Cortex Stimulation in Humans. Science 324, 811–813. [DOI] [PubMed] [Google Scholar]
- Doya K (1999). What are the computations of the cerebellum, the basal ganglia and the cerebral cortex? Neural Networks 12, 961–974. [DOI] [PubMed] [Google Scholar]
- Driscoll LN, Pettit NL, Minderer M, Chettih SN, and Harvey CD (2017). Dynamic Reorganization of Neuronal Activity Patterns in Parietal Cortex. Cell 170, 986–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer LF, Mojica Soto-Albors R, Buck F, and Harnett MT (2020). Representation of visual landmarks in retrosplenial cortex. Elife 9, e51458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiser A, Mahringer D, Oyibo HK, Petersen AV, Leinweber M, and Keller GB (2016). Experience-dependent spatial expectations in mouse visual cortex. Nat. Neurosci 19, 1658–1664. [DOI] [PubMed] [Google Scholar]
- Friedrich J, Zhou P, and Paninski L (2017). Fast online deconvolution of calcium imaging data. PLoS Comput. Biol 13, e1005423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fusi S, Miller EK, and Rigotti M (2016). Why neurons mix: High dimensionality for higher cognition. Curr. Opin. Neurobiol 37, 66–74. [DOI] [PubMed] [Google Scholar]
- Gămănuț R, Kennedy H, Toroczkai Z, Essen D. Van, Knoblauch K, and Burkhalter A (2018). The Mouse Cortical Connectome Characterized by an Ultra Dense Cortical Graph Maintains Specificity by Distinct Connectivity Profiles. Neuron 97, 698–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glickfeld LL, and Olsen SR (2017). Higher-Order Areas of the Mouse Visual Cortex. Annu. Rev. Vis. Sci 3, 251–273. [DOI] [PubMed] [Google Scholar]
- Goard MJ, Pho GN, Woodson J, and Sur M (2016). Distinct roles of visual, parietal, and frontal motor cortices in memory-guided sensorimotor decisions. Elife 5, e1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg DS, and Kerr JND (2009). Automated correction of fast motion artifacts for two-photon imaging of awake animals. J. Neurosci. Methods 176, 1–15. [DOI] [PubMed] [Google Scholar]
- Guizar-Sicairos M, Thurman ST, and Fienup JR (2008). Efficient subpixel image registration algorithms. Opt. Lett 33, 156. [DOI] [PubMed] [Google Scholar]
- Guo ZV, Li N, Huber D, Ophir E, Gutnisky D, Ting JT, Feng G, and Svoboda K (2014). Flow of Cortical Activity Underlying a Tactile Decision in Mice. Neuron 81, 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, Ditterich J, and Shadlen MN (2006). Microstimulation of macaque area LIP affects decision-making in a motion discrimination task. Nat. Neurosci 9, 682–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, Kopec CD, Brunton BW, Duan CA, Erlich JC, and Brody CD (2015). Distinct relationships of parietal and prefrontal cortices to evidence accumulation. Nature 520, 220–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ, et al. (2020). Array programming with NumPy. Nature 585, 357–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Collman F, Dombeck DA, and Tank DW (2009). Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461, 941–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hattori R, Danskin B, Babic Z, Mlynaryk N, and Komiyama T (2019). Area-Specificity and Plasticity of History-Dependent Value Coding During Learning. Cell 177, 1858–1872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Havenith MN, Zijderveld PM, van Heukelum S, Abghari S, Glennon JC, and Tiesinga P (2018). The Virtual-Environment-Foraging Task enables rapid training and single-trial metrics of attention in head-fixed mice. Sci. Rep 8, 17371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Havenith MN, Zijderveld PM, van Heukelum S, Abghari S, Tiesinga P, and Glennon JC (2019). The Virtual-Environment-Foraging Task enables rapid training and single-trial metrics of rule acquisition and reversal in head-fixed mice. Sci. Rep 9, 4790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinman JR, Dannenberg H, Alexander AS, and Hasselmo ME (2018). Neural mechanisms of navigation involving interactions of cortical and subcortical structures. J. Neurophysiol 119, 2007–2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter JD (2007). Matplotlib: A 2D graphics environment. Comput. Sci. Eng 9, 99–104. [Google Scholar]
- Hwang EJ, Dahlen JE, Mukundan M, and Komiyama T (2017). History-based action selection bias in posterior parietal cortex. Nat. Commun 8, 1242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Link TD, Hu YY, Lu S, Wang EH, Lilascharoen V, Aronson S, O’Neil K, Lim BK, and Komiyama T (2019). Corticostriatal Flow of Action Selection Bias. Neuron 104, 1126–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob P, Casali G, Spieser L, Page H, Overington D, and Jeffery K (2017). An independent, landmark-dominated head-direction signal in dysgranular retrosplenial cortex. Nat. Neurosci 20, 173–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalatsky VA, and Stryker MP (2003). New Paradigm for Optical Imaging. Neuron 38, 529–545. [DOI] [PubMed] [Google Scholar]
- Katahira K (2018). The statistical structures of reinforcement learning with asymmetric value updates. J. Math. Psychol 87, 31–45. [Google Scholar]
- Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2015). Vacillation, indecision and hesitation in moment-by-moment decoding of monkey motor cortex. Elife 4, e04677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kauvar IV, Machado TA, Yuen E, Kochalka J, Choi M, Allen WE, Wetzstein G, and Deisseroth K (2020). Cortical Observation by Synchronous Multifocal Optical Sampling Reveals Widespread Population Encoding of Actions. Neuron 107, 351–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller GB, Bonhoeffer T, and Hübener M (2012). Sensorimotor Mismatch Signals in Primary Visual Cortex of the Behaving Mouse. Neuron 74, 809–815. [DOI] [PubMed] [Google Scholar]
- Keshavarzi S, Bracey EF, Faville RA, Campagner D, Tyson AL, Lenzi SC, Branco T, and Margrie TW (2022). Multisensory coding of angular head velocity in the retrosplenial cortex. Neuron 110, 532–543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koay SA, Charles AS, Thiberge SY, Brody CD, and Tank DW (2022). Sequential and efficient neural-population coding of complex task information. Neuron 110, 328–349. [DOI] [PubMed] [Google Scholar]
- Krumin M, Lee JJ, Harris KD, and Carandini M (2018). Decision and navigation in mouse parietal cortex. Elife 7, e42583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakshminarasimhan KJ, Petsalis M, Park H, DeAngelis GC, Pitkow X, and Angelaki DE (2018). A Dynamic Bayesian Observer Model Reveals Origins of Bias in Visual Path Integration. Neuron 99, 194–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakshminarasimhan KJ, Avila E, Neyhart E, DeAngelis GC, Pitkow X, and Angelaki DE (2020). Tracking the Mind’s Eye: Primate Gaze Behavior during Virtual Visuomotor Navigation Reflects Belief Dynamics. Neuron 106, 662–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, Chen S, Guo ZV, Chen H, Huo Y, Inagaki HK, Chen G, Davis C, Hansel D, Guo C, et al. (2019). Spatiotemporal constraints on optogenetic inactivation in cortical circuits. Elife 8, e48622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Licata AM, Kaufman MT, Raposo D, Ryan MB, Sheppard JP, and Churchland AK (2017). Posterior Parietal Cortex Guides Visual Decisions in Rats. J. Neurosci 37, 4954–4966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyamzin D, and Benucci A (2019). The mouse posterior parietal cortex: Anatomy and functions. Neurosci. Res 140, 14–22. [DOI] [PubMed] [Google Scholar]
- Mao D, Molina LA, Bonin V, and McNaughton BL (2020). Vision and Locomotion Combine to Drive Path Integration Sequences in Mouse Retrosplenial Cortex. Curr. Biol 30, 1680–1688. [DOI] [PubMed] [Google Scholar]
- Marshel JH, Garrett ME, Nauhaus I, and Callaway EM (2011). Functional Specialization of Seven Mouse Visual Cortical Areas. Neuron 72, 1040–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller AMP, Mau W, and Smith DM (2019). Retrosplenial Cortical Representations of Space and Future Goal Locations Develop with Learning. Curr. Biol 29, 2083–2090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mimica B, Dunn BA, Tombaz T, Bojja VPTNCS, and Whitlock JR (2018). Efficient cortical coding of 3D posture in freely behaving rats. Science 362, 584–589. [DOI] [PubMed] [Google Scholar]
- Minderer M, Brown KD, and Harvey CD (2019). The Spatial Structure of Neural Encoding in Mouse Posterior Cortex during Navigation. Neuron 102, 232–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morcos AS, and Harvey CD (2016). History-dependent variability in population dynamics during evidence accumulation in cortex. Nat. Neurosci 19, 1672–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nat. Neurosci 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nitz DA (2006). Tracking Route Progression in the Posterior Parietal Cortex. Neuron 49, 747–756. [DOI] [PubMed] [Google Scholar]
- Nitz DA (2012). Spaces within spaces: rat parietal cortex neurons register position across three reference frames. Nat. Neurosci 15, 1365–1367. [DOI] [PubMed] [Google Scholar]
- Parker PRL, Brown MA, Smear MC, and Niell CM (2020). Movement-Related Signals in Sensory Areas: Roles in Natural Behavior. Trends Neurosci 581–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, and Franklin KF (2013). The Mouse Brain in Stereotaxic Coordinates (Elsevier; ). [Google Scholar]
- Pedregosa F, Michel V, Grisel O, Blondel M, Prettenhofer P, Weiss R, Vanderplas J, Cournapeau D, Pedregosa F, Varoquaux G, et al. (2011). Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res 12, 2825–2830. [Google Scholar]
- Pho GN, Goard MJ, Woodson J, Crawford B, and Sur M (2018). Task-dependent representations of stimulus and choice in mouse parietal cortex. Nat. Commun 9, 2596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, and Simoncelli EP (2008). Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 454, 995–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinto L, Koay SA, Engelhard B, Yoon AM, Deverett B, Thiberge SY, Witten IB, Tank DW, and Brody CD (2018). An Accumulation-of-Evidence Task Using Visual Pulses for Mice Navigating in Virtual Reality. Front. Behav. Neurosci 12. Published online March 6, 2018. 10.3389/fnbeh.2018.00036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinto L, Rajan K, Depasquale B, Thiberge SY, Tank DW, Brody CD, Pinto L, Rajan K, Depasquale B, Thiberge SY, et al. (2019). Task-Dependent Changes in the Large-Scale Dynamics and Necessity of Cortical Regions. Neuron 104, 810–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W, et al. (2016). Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron 89, 285–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raposo D, Kaufman MT, and Churchland AK (2014). A category-free neural population supports evolving demands during decision-making. Nat. Neurosci 17, 1784–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratzlaff EH, and Grinvald A (1991). A tandem-lens epifluorescence macroscope: Hundred-fold brightness advantage for wide-field imaging. J. Neurosci. Methods 36, 127–137. [DOI] [PubMed] [Google Scholar]
- Redish AD (2016). Vicarious trial and error. Nat. Rev. Neurosci 17, 147–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Resulaj A, Kiani R, Wolpert DM, and Shadlen MN (2009). Changes of mind in decision-making. Nature 461, 263–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang XJ, Daw ND, Miller EK, and Fusi S (2013). The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roitman JD, and Shadlen MN (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci 22, 9475–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg M, Zhang T, Perona P, and Meister M (2021). Mice in a labyrinth: Rapid learning, sudden insight, and efficient exploration. Elife 10, e66175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy NA, Bak JH, Akrami A, Brody CD, and Pillow JW (2021). Extracting the dynamics of behavior in sensory decision-making experiments. Neuron 109, 597–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saleem AB, Diamanti EM, Fournier J, Harris KD, and Carandini M (2018). Coherent encoding of subjective spatial position in visual cortex and hippocampus. Nature 562, 124–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sereno MI, McDonald CT, and Allman JM (1994). Analysis of Retinotopic Maps in Extrastriate Cortex. Cereb. Cortex 4, 601–620. [DOI] [PubMed] [Google Scholar]
- Shuler MG, and Bear MF (2006). Reward timing in the primary visual cortex. Science (80-. ) 311, 1606–1609. [DOI] [PubMed] [Google Scholar]
- Siegle JH, Jia X, Durand S, Gale S, Bennett C, Graddis N, Heller G, Ramirez TK, Choi H, Luviano JA, et al. (2021). Survey of spiking in the mouse visual system reveals functional hierarchy. Nature 592, 86–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song J, and Nakayama K (2009). Hidden cognitive states revealed in choice reaching tasks. Trends Cogn. Sci 13, 360–366. [DOI] [PubMed] [Google Scholar]
- Steinmetz NA, Zatka-Haas P, Carandini M, and Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, eaav7893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thier P, and Andersen RA (1998). Electrical Microstimulation Distinguishes Distinct Saccade-Related Areas in the Posterior Parietal Cortex. J. Neurophysiol 80, 1713–1735. [DOI] [PubMed] [Google Scholar]
- Vale R, Campagner D, Iordanidou P, Arocas OP, Tan YL, Stempel AV, Keshavarzi SS, Petersen R, Margrie T, and Branco T (2020). A cortico-collicular circuit for accurate orientation to shelter during escape. BioRxiv 10.1101/2020.05.26.117598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. (2020). SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Der Walt S, Colbert SC, and Varoquaux G (2011). The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng 13, 22–30. [Google Scholar]
- Wang Q, and Burkhalter A (2007). Area map of mouse visual cortex. J. Comp. Neurol 502, 339–357. [DOI] [PubMed] [Google Scholar]
- Wang Q, Ding SL, Li Y, Royall J, Feng D, Lesnar P, Graddis N, Naeemi M, Facer B, Ho A, et al. (2020). The Allen Mouse Brain Common Coordinate Framework: A 3D Reference Atlas. Cell 181, 936–953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock JR, Pfuhl G, Dagslott N, Moser M-B, and Moser EI (2012). Functional Split between Parietal and Entorhinal Cortices in the Rat. Neuron 73, 789–802. [DOI] [PubMed] [Google Scholar]
- Wilber AA, Clark BJ, Forster TC, Tatsuno M, and McNaughton BL (2014). Interaction of Egocentric and World-Centered Reference Frames in the Rat Posterior Parietal Cortex. J. Neurosci 34, 5431–5446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie J, Gao R, Nijkamp E, Zhu SC, and Wu YN (2020). Representation learning: A statistical perspective. Annu. Rev. Stat. Its Appl 7, 303–335. [Google Scholar]
- Yatsenko D, Reimer J, Ecker AS, Walker EY, Sinz F, Berens P, Hoenselaar A, Cotton RJ, Siapas AS, and Tolias AS (2015). DataJoint: managing big scientific data using MATLAB or Python. BioRxiv 10.1101/031658. [DOI] [Google Scholar]
- Yuan M, and Lin Y (2006). Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B Stat. Methodol 68, 49–67. [Google Scholar]
- Zhuang J, Ng L, Williams D, Valley M, Li Y, Garrett M, and Waters J (2017). An extended retinotopic map of mouse cortex. Elife 6, e18372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zingg B, Hintiryan H, Gou L, Song MY, Bay M, Bienkowski MS, Foster NN, Yamashita S, Bowman I, Toga AW, et al. (2014). Neural networks of the mouse neocortex. Cell 156, 1096–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zmarz P, and Keller GB (2016). Mismatch Receptive Fields in Mouse Visual Cortex. Neuron 92, 766–772. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Calcium imaging and mouse behavioral data reported in this paper will be shared by the lead contact upon request.
The original code for fitting generalized linear models has been deposited at Github and is publicly available as the date of publication. DOI is listed in the key resource table.
Other code to run all analyses and produce all figures in this paper will be shared by the lead contact upon request.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and virus strains | ||
| AAV2/1-synapsin-GCaMP6s-WPRE-SV40 | UPenn Vector Core | Catalog No: AV-1-PV2824 |
| Deposited data | ||
| Allen Mouse Common Coordinate Framework | Allen Institute for Brain Science | http://help.brain-map.org/display/mousebrain/Documentation |
| Retinotopic field sign maps | Allen Institute for Brain Science | https://portal.brain-map.org/ |
| Experimental models: Organisms/strains | ||
| C57BL/6J mouse | The Jackson Laboratory | RRID: IMSR_JAX:000064 |
| VGAT-ChR2-EYFP mouse | The Jackson Laboratory | RRID: IMSR_JAX:014548 |
| Software and algorithms | ||
| MATLAB | The MathWorks | https://www.mathworks.com/ |
| ViRMEn (Virtusl Reality Mouse Engine) | Aronov and Tank, 2014 | https://pni.princeton.edu/pni-software-tools/virmen |
| ScanImage 2016a | Vidrio Technologies | https://vidriotechnologies.com/scanimage/ |
| Image preprocessing and motion correction code | Chettih and Harvey, 2019 | https://github.com/HarveyLab/Acquisition2P_class |
| OASIS algorithm for calcium imaging deconvolution | Friedrich et al., 2017 | https://github.com/zhoupc/OASIS_matlab |
| CNMF algorithm for calcium imaging source extraction | Pnevmatikakis et al., 2016 | https://github.com/Selmaan/NMF-Source-Extraction |
| DataJoint 0.13 | DataJoint | https://datajoint.io/ |
| Python 3.6 | Python | https://www.python.org/ |
| Tensorflow v1 | Google Inc. | https://www.tensorflow.org/ |
| Code for fitting generalized linear models | This study | https://zenodo.org/badge/latestdoi/491659726 |


