SUMMARY
Conformational changes are an essential component of functional cycles of many proteins but their characterization often requires an integrative structural biology approach. Here, we introduce and benchmark ConfChangeMover (CCM), a new method built into the widely used macromolecular modeling suite Rosetta that is tailored to model conformational changes in proteins using sparse experimental data. CCM can rotate and translate secondary structural elements and modify their backbone dihedral angles in regions of interest. We benchmarked CCM on soluble and membrane proteins with simulated Cα-Cα distance restraints and sparse experimental double electron-electron resonance (DEER) restraints, respectively. In both benchmarks, CCM outperformed state-of-the-art Rosetta methods showing that it can model a diverse array of conformational changes. In addition, the Rosetta framework allows a wide variety of experimental data to be integrated with CCM, thus extending its capability beyond DEER restraints. This method will contribute to the biophysical characterization of protein dynamics.
Graphical Abstract
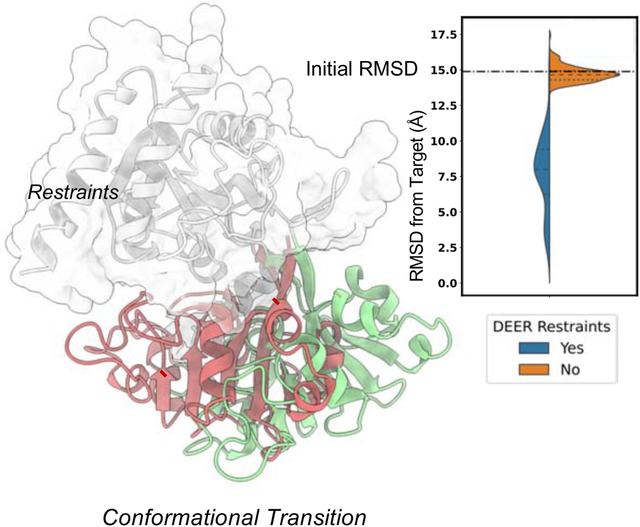
In Brief
Protein function relies on conformational changes of varying degrees. Computational and experimental methods alone have limited capacity of unveiling such transitions. Sala et al. have developed a method in the Rosetta modeling suite that allows to generate high-accuracy conformations consistent with sparse experimental data.
INTRODUCTION
Proteins exert a variety of functions that lead to fine-tuned control of biological processes. These functions rely on conformational changes of varying degrees, implying that a single static structure is insufficient to describe a molecular mechanism. While some proteins, such as certain enzymes, might require only small conformational changes for function, other proteins, and in particular membrane proteins such as transporters or receptors, need the motion of a number of structural elements to drive function. Despite great advances in experimental methods for protein structure determination (Nakane et al., 2020; Shimada et al., 2018; Yip et al., 2020), the complete characterization of multiple conformational states remains a challenge. Because membrane proteins function through shifts in ensembles of conformations, X-ray crystallography or electron microscopy provide only snapshots of selected conformations. Spectroscopic techniques such as Nuclear magnetic resonance (NMR) or electron paramagnetic resonance (EPR) are better suited to monitor shifts in ensembles of states but typically yield limited data that incompletely define the ensembles. Computational methods are challenged by the large space of conformations that are similar in energy and thus difficult to distinguish with imperfect energy functions. Although advances have recently been made in the prediction of proteins structure from sequence (Baek et al., 2021a; Jumper et al., 2021; Tunyasuvunakool et al., 2021), including those in multimeric complexes (Baek et al., 2021b; Green et al., 2021; Humphreys et al., 2021; Schaeffer et al., 2021), the prediction of conformational ensembles and protein dynamics remains a fundamental challenge (AlQuraishi, 2021).
Computational techniques such as molecular dynamics (MD) simulations have been extensively used to dissect mechanistically important aspects of protein motion (Maximova et al., 2016). Recent advances made it possible to reach large spatial and time scales that, in combination with atomic details, can provide insight into mechanisms of conformational changes (Bernardi et al., 2015). Nevertheless, large conformational transitions often occur at time scales beyond those achievable with MD, and consequently experimental measurements must be used to collect information on populations at equilibrium (Dastvan et al., 2016). Depending on the technique, these observables may represent Boltzmann-weighted averages of multiple sampled conformational states and may be limited by poor spatial/time representation (Bryn Fenwick et al., 2014; Greenleaf et al., 2007). In both cases, the obtained macroscopic measurements have the potential to unveil structural transitions between distinct conformations within the functional cycle.
Markov Chain Monte Carlo (MCMC) molecular modeling approaches can complement experimental techniques by determining meaningful three-dimensional structures consistent with limited experimental data (Bonomi et al., 2017; Palamini et al., 2016). Integrative structural biology combines structural information coming from multiple experimental sources, thus compensating for technique-specific shortcomings that result in data that is noisy, ambiguous, and/or unevenly distributed. Several molecular modeling programs have been developed that incorporate purpose-tailored modeling protocols in which experimental information is used as restraints to drive conformational sampling (Dominguez et al., 2003; Eswar et al., 2007; Leaver-Fay et al., 2011; Xia et al., 2018). Among them, the macromolecular modeling suite Rosetta has been widely adopted for this purpose, and a variety of applications have been developed addressing diverse modeling tasks (Leman et al., 2020). In a typical Rosetta pipeline, input poses alternate between stochastic modification using Movers and evaluation using one of several scoring functions. In contrast with MD, which relies on the application of Newtonian forces and is thus limited by the duration of femtosecond-level time steps, MCMC approaches rely on probabilistic sampling to collect models and have, in the case of Rosetta, no inherent timescale (Heilmann et al., 2020). Tailored sampling of input poses using MCMC can, as a result, overcome high-energy barriers in the energy landscape that might otherwise prevent physiologically relevant conformers from being sampled. In the past, assembly of secondary structure elements (SSEs) as rigid bodies have been widely used for de novo proteins determination of tertiary structures in Rosetta (Bradley et al., 2003, 2005; Rohl et al., 2004a) and other algorithms (Woetzel et al., 2012). On a similar principle, in proteins that use rigid-body movements to alternate between multiple states, such as enzymes, receptors and transporters, applying rigid-body rotations and translations to SSEs may allow alternative conformations of interest to be modeled. However, such motions are generally achieved by the ad hoc application of one of several other modeling methods, such as methods used for homology modeling or de novo structure prediction; a unified approach for conformational change modeling of proteins with diverse topologies using experimental data is still missing.
Here, we introduce ConfChangeMover (CCM), a new Rosetta Mover specifically developed to model conformational changes in proteins using limited experimental data. CCM combines rigid-body rotations and translations of SSEs with a “broken-chain kinematics” strategy previously used for high-accuracy homology modeling (Park et al., 2018; Song et al., 2013). We discuss several novel strategies designed to maximize structural similarity to the starting conformation in torsion space while exploring a diverse array of conformations in Cartesian space. CCM was benchmarked in two stages. First, conformational changes were evaluated in a panel of soluble proteins with multiple experimental structures using simulated Cα - Cα distance restraints. Then, experimental distance restraints collected using EPR double electron-electron resonance (DEER) were used to demonstrate how CCM can be applied to modeling of conformational change in large membrane proteins such as receptors and transporters. In both benchmarks, CCM outperformed state-of-the-art Rosetta methods to model conformational changes driven by sparse restraints, suggesting that it can be used to model proteins with a broad variety of topologies. Finally, we briefly demonstrate that CCM can be used for structural refinement of unfolded/misfolded proteins with both NMR and EPR data. Ultimately, the integration of this method in Rosetta allows a wide variety of experimental data to be used and enables users to customize their pipelines for a wide range of modelling tasks.
RESULTS
Modeling conformational changes of soluble proteins with simulated distance restraints
We first benchmarked ConfChangeMover (CCM) using simulated harmonic distance restraints on a dataset of seven soluble proteins with structures that have been experimentally determined in two or more conformations (Table 1). Proteins in the benchmark set were selected on the basis of their modes of conformational isomerization, wherein loops and secondary structure elements (SSEs) undergo structural changes that are unlikely to be sampled by rotation of backbone dihedral angles as shown by superimposing the two native conformations of each protein (Figure 1). CCM was compared to SingleFragmentMover (SFM) (Bystroff and Baker, 1998; Simons et al., 1997), a Monte Carlo-based approach that samples backbone torsions by fragment insertion. Additionally, CCM was further run without restraints to ascertain the effectiveness of the simulated distance restraints. To evaluate modeling accuracy, we calculated each model’s root mean squared deviation (RMSD) across Cα atoms relative to the target conformation. Overall, one hundred models were generated using each approach across each of 14 conformational transitions, with sampling and RMSD calculations focused on mobile regions of the protein structure.
Table 1.
Soluble proteins modeled with simulated Cα-Cα distance restraints.
| Protein (Organism) | Conformations (PDB ID) | No of Restraints | No of Modeled Residues | References |
|---|---|---|---|---|
| Adenosylcobinamide kinase (Salmonella enterica) | Apo (1CBU) - Holo (1C9K) | 18 | 33 | (Thompson et al., 1998, 1999) |
| Pol alpha DNA polymerase (Escherichia phage RB6) | Holo (1IG9) - Apo (1IH7) | 30 | 111 | (Franklin et al., 2001) |
| Glutamine-binding protein (Escherichia coli) | Holo (1WDN) - Apo (1GGG) | 21 | 248 (full length) | (Hsiao et al., 1996; Sun et al., 1998) |
| Leucine-binding protein (Escherichia coli) | Holo (1USI) - Apo (1USG) | 22 | 121 | (Magnusson et al., 2004) |
| DNA polymerase I (Thermophilus aquaticus) | Open (2KTQ) - Active (3KTQ) | 26 | 69 | (Li et al., 1998) |
| Aspartate aminotrasnferase (Gallus gallus) | Closed (1AMA) - Open (9AAT) | 28 | 167 | (McPhalen et al., 1992a, 1992b) |
| Lactoferrin (Homo sapiens) | Holo (1LFG) <-> Apo (1LFH) | 21 | 160 | (Haridas et al., 1995; Norris et al., 1991) |
Figure 1.
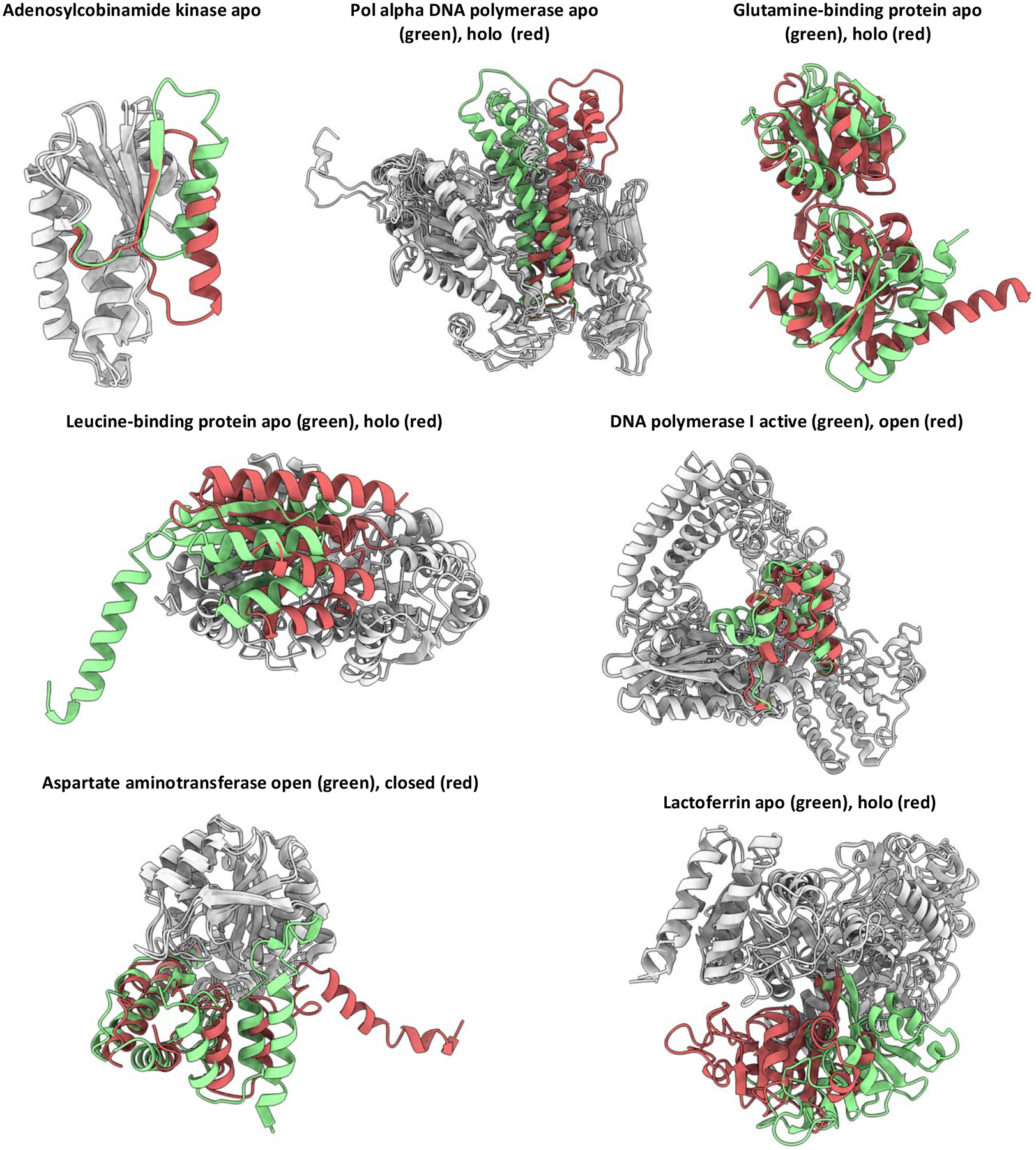
Conformational changes of soluble proteins in the benchmark. Regions modeled are in red or green. Regions not modeled are in gray.
The accuracy in modeling conformational changes of folded regions was assessed by calculating Cα RMSD of mobile residues forming helices or β-sheets (Figure 2). In the absence of restraints, the majority of models sampled using CCM were close to the starting conformation (dashed line in the plot) suggesting that starting structures occupied an energy minimum that may be difficult to escape. The inclusion of distance restraints generally led to models with lower RMSD values. By contrast, modeling conformational transitions using SFM with restraints led to models with a wide range of RMSD values; in many cases, these RMSD values increased compared to that of the starting conformation. Overall, CCM outperformed SFM in all the transitions with one exception, the modeling of DNA polymerase I from active to the more unfolded open conformation where SFM generated a slightly better ensemble than CCM. Even in that case, however, SFM generated far more outliers with high RMSD values than CCM. Only two transitions were modeled by CCM with an average RMSD > 7.5 Å: leucine-binding protein apo-to-holo and Pol alpha DNA polymerase holo-to-apo. The former requires the opening of the core helical bundle to host the apo detached helix, the latter requires dihedrals to change to bend the long helices. Both the transitions were hard to achieve without fine-tuning the protocol with either concerted motions of helices or more intensive fragments insertion, respectively.
Figure 2.
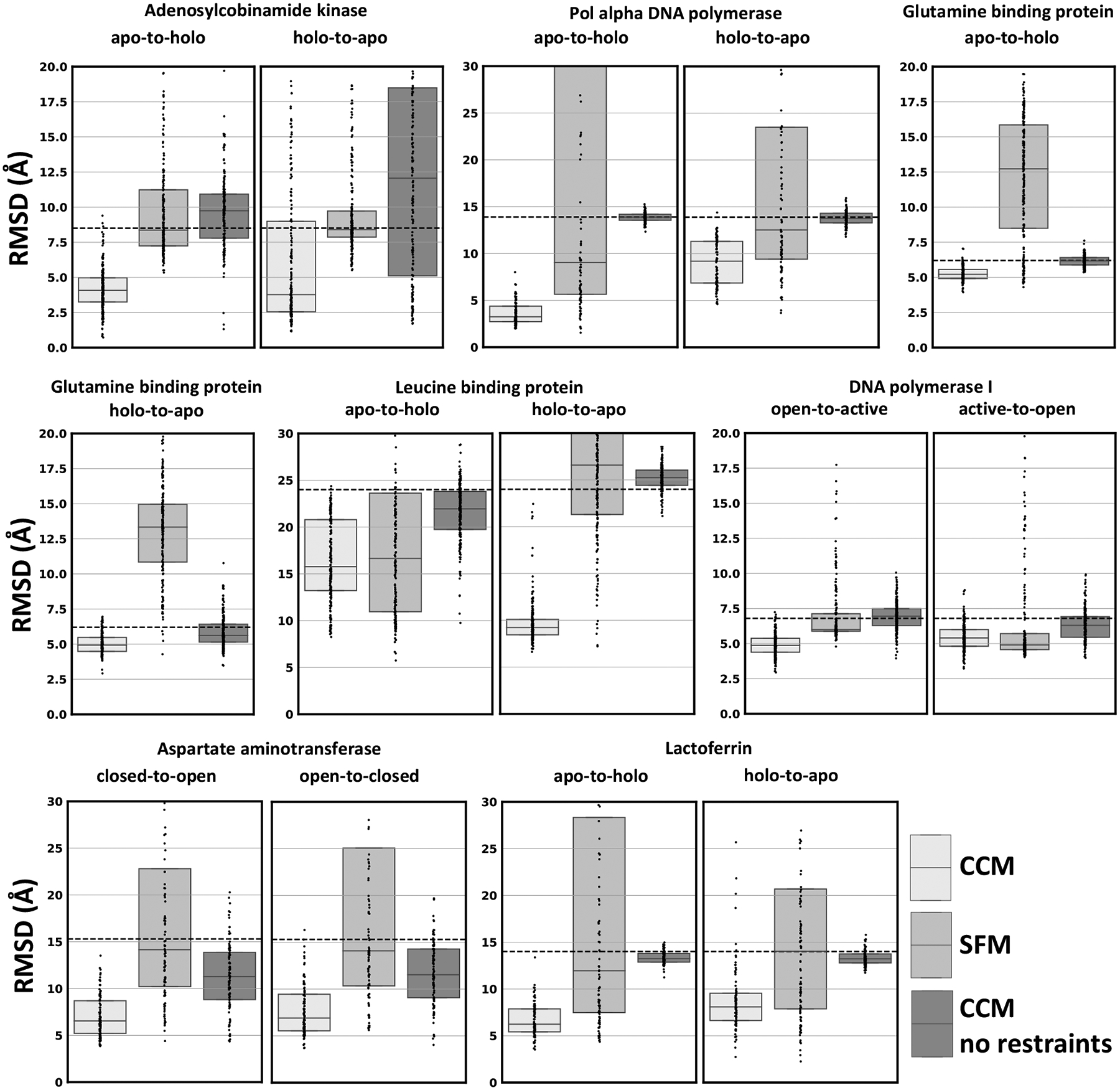
CCM modeled SSEs conformational changes of soluble proteins using simulated Cα-Cα distance restraints. Dots represent the real distribution of RMSD values from the target structure. RMSD between the two native conformations is shown as a dashed line.
Including loop regions in Cα RMSD measurements generally led to increases in median RMSD values (Figure S1), which was unsurprising given that loops are among the most conformationally flexible regions in proteins. In several cases, their inclusion during RMSD calculations yielded RMSD values that more closely approximated those of the starting models. For example, when modeling the apo-to-holo transition of Glutamine-binding protein, RMSD values improved on average by 0.9 Å when limiting RMSD calculations to residues on helices or sheets, but only 0.1 Å when loop regions were included in the calculation. Similarly, the RMSD values of models recapitulating the closed-to-open transition in DNA polymerase I were markedly similar to that of the starting structure only when loop regions were considered. We therefore suspected that CCM was generally more accurate in modeling SSEs rather than unfolded regions. To investigate this hypothesis, we computed the RMSD change of SSEs and loops with respect to the starting value observed between native conformations (Figure S2). Both CCM and SFM reduced RMSD improvements of models when loops are included in the measurements. However, models generated by CCM had a RMSD on average 1.2Å higher than SSEs only, a value that is double that of models generated by SFM. These results indicate that CCM was less effective at modeling disordered regions than at modeling structured regions. An illustrative example of this fact is the small DNA polymerase helix (residues range 638–647), which alternates between almost completely unfolded in the open conformation to fully folded in the active state (Figure S3). We found that CCM more accurately modeled the unfolded-to-folded transition than the folded-to-unfolded, whereas SFM left that region mostly unchanged in both cases.
Visual inspection of the models generated using CCM with the lowest RMSD values suggested that this method could more accurately model rigid-body rotations and translations of α-helices than either helical bending or manipulation of β-sheets (Figure 3). For example, models of the glutamine- and leucine-binding proteins, which have α/β topologies, were both more accurate on helices than on β-sheets. Similarly, whereas models of Adenosylcobinamide superimpose well with their target structures, their β-strands appear totally or partially unfolded in the apo and holo model, respectively. Similar observations were made in models of Lactoferrin, which may be due to the omission of full-atom refinement. The Pol alpha DNA polymerase holo conformation was modeled with an outstanding accuracy of 2 Å RMSD, whereas the apo conformation characterized by two long curved helices was less accurate. In agreement with previous considerations, DNA polymerase I models accurately recapitulated conserved SSEs but missed the dihedral changes needed to sample the small helix switching folding state.
Figure 3.
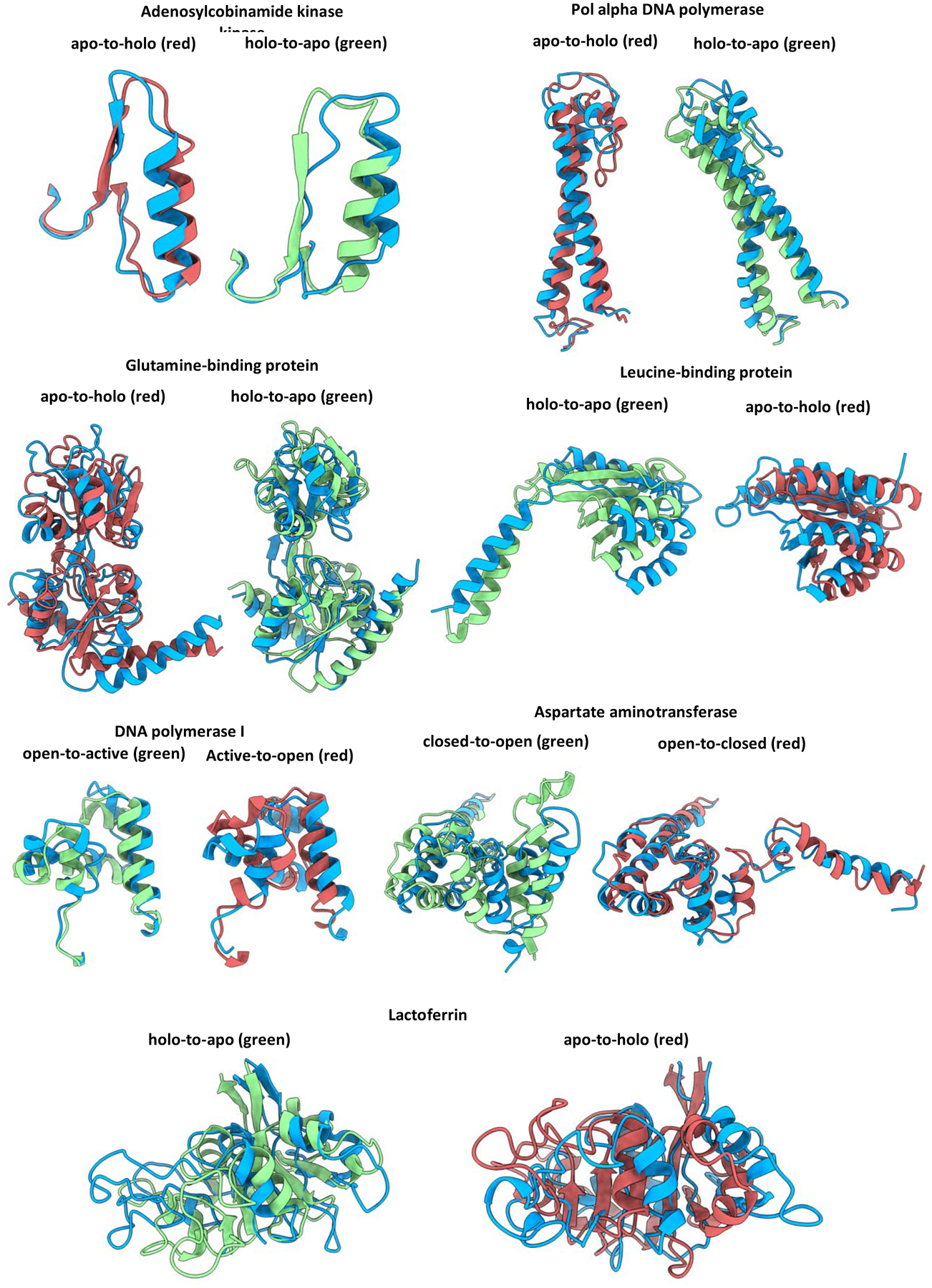
CCM with simulated Cα-Cα distances generated a high accuracy model for most of the benchmarked soluble proteins. The target conformation is in green or red, following the color code used in Fig 1. Models are in blue.
In summary, the data suggest that CCM is a robust and modular sampling method capable of accurately modeling conformational changes guided by simulated distance restraints. Its conservative sampling approach, which prioritizes rigid-body rotations and translations of SSEs, allows it to easily outperform SFM, which has previously been used to sample conformational changes in Rosetta (Rohl et al., 2004b). The primary drawback we observed was the modeling of new loops conformations, which was difficult mainly due to stage 2 parameters that erred toward conservative sampling. It should be noted that only 100 models were generated for each transition, and no attempt was made to fine-tune the sampler for each test case (see Discussion for modifications that can be introduced by the user). Indeed, protein-specific modifications to the protocol may ameliorate the slightly worse performance observed when modeling structural changes such as helical bending or unfolding events. We surmise this is likely due to the limited extent to which sequence fragments are used when modifying backbone dihedral angles. Similarly, more accurate loop conformations can be generated by simply using less conservative stage 2 parameters (e.g. decreasing the contribution of the appropriate score terms) while increasing the number of stage 2 models. Thus, while Cα RMSD values approached 2–6 Å in some cases of our benchmark, performance could almost certainly be improved across the board by either modifying the sampling parameters, increasing the duration or aggressiveness of sampling, or following CCM with full-atom minimization.
Modeling conformational changes of membrane proteins with experimental EPR DEER distance restraints
Having assessed the capacity of CCM on soluble proteins with simulated distance restraints, we evaluated its effectiveness at modeling membrane proteins using previously published experimental data (Table 2). The benchmarked proteins undergo divergent modes of conformational change to facilitate transmission of signals or translocation of substrates across the membrane (Figure 4). Here, we only allowed specific regions to move where experimental data are available. The only exception was Rhodopsin, for which only transmembrane (TM) helices 5, TM6 and TM7 responsible for mediating protein activation and deactivation were allowed to move. Experimental distance data was incorporated as restraints using the RosettaDEER module (del Alamo et al., 2020). RosettaDEER models the ensemble of nitroxide spin probe conformations using coarse-grained depictions (called pseudorotamers) designed to maximize computational efficiency. After removing pseudorotamers that clash with the protein, the average distance of the sampled distribution between pairs of ensembles was calculated and compared to the experimental average distance using two different scoring approaches. First, a direct comparison was carried out, and scores reflected the squared deviation between the sampled and experimental average distance values. Second, only deviations beyond 2.5 Å were penalized, permitting models to adopt conformations that may not be in full agreement with the data without penalty. Additionally, to ascertain the effect of these experimental restraints, we provided the median distance value simulated using the method MDDS (Islam and Roux, 2015; Islam et al., 2013) that generates distances with a strong correlation with those simulated using RosettaDEER (del Alamo et al., 2020). Finally, to directly compare the contribution of these probe-based measurements to Cα distance restraints, we provided simulated Cα distance restraints between the same residues used for experimental measurements.
Table 2.
Conformational transitions of membrane proteins modeled with experimental EPR DEER distance restraints.
| Protein (Organism) | Starting Conformation (PDB ID) | Target Conformation (PDB ID) | No of Restraints | No of helical Residues modeled | References |
|---|---|---|---|---|---|
| Rhodopsin (Bos taurus) | Active (2X72) | Inactive (1GZM) | 10 | 96 | (Li et al., 2004; Standfuss et al., 2011) |
| Rhodopsin | Inactive (1GZM) | Active (2X72) | 10 | 96 | |
| LeuT (Aquifex aeolicus) | Inward-facing (3TT3) | Outward-facing (2A65) | 11 | 167 | (Kazmier et al., 2014a; Krishnamurthy and Gouaux, 2012; Yamashita et al., 2005) |
| vSGLT (Vibrio parahaemolyticus) | Outward-opena (5NV9) | Substrate free (2XQ2) | 11 | 241 | (Paz et al., 2018; Wahlgren et al., 2018; Watanabe et al., 2010) |
| Mhp1 (Microbacterium liquefaciens) | Outward-facing (2JLN) | Inward-facing (2X79) | 14 | 209 | (Shimamura et al., 2010; Weyand et al., 2008) |
| Mhp1 | Inward-facing (2X79) | Outward-facing (2JLN) | 14 | 201 |
The vSGLT OF conformation was generated from the X-ray structure of the homolog SiaT.
Figure 4.
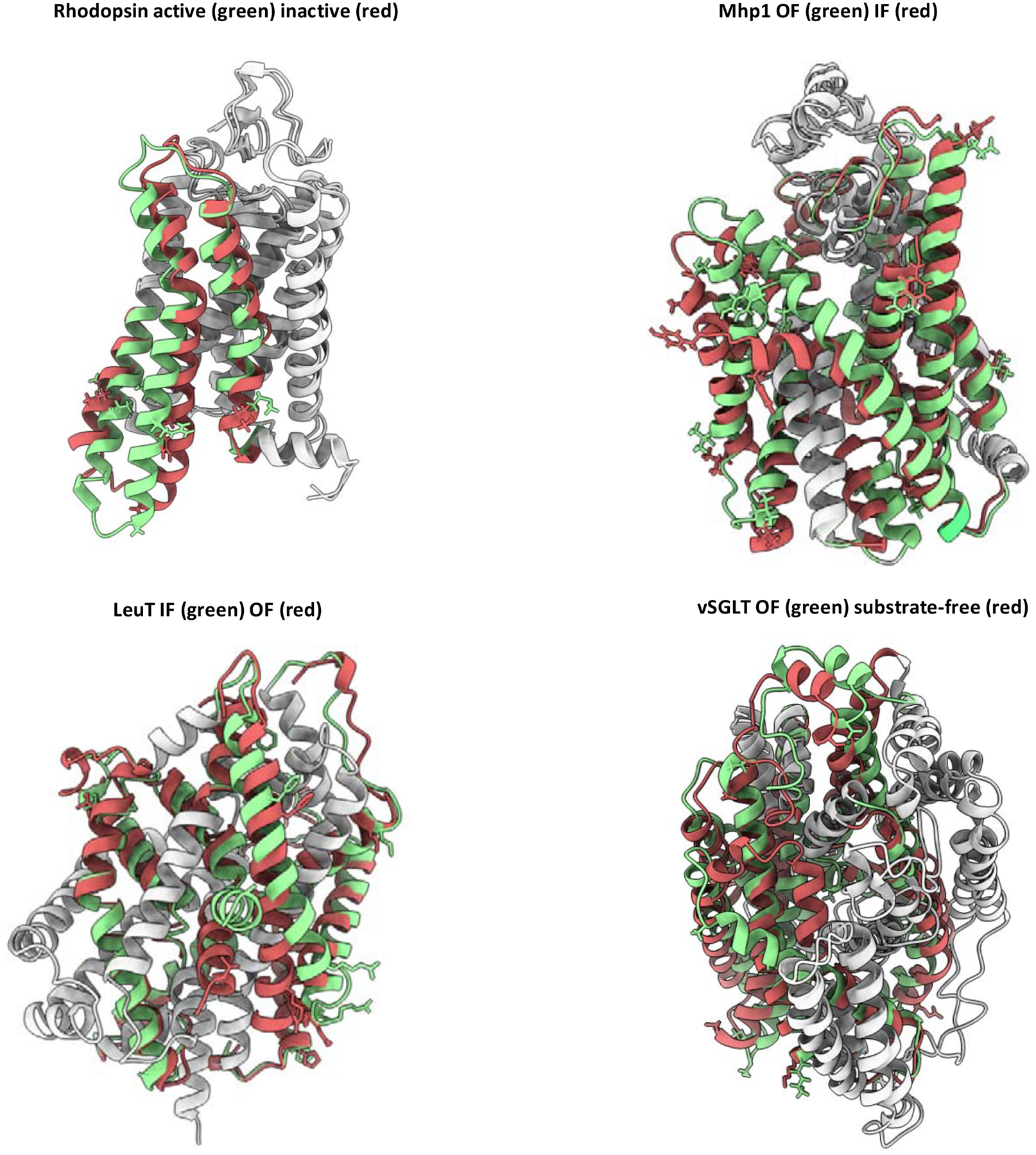
Benchmarked conformational changes of membrane proteins. Protein regions modeled are shown in red or green. Regions not modeled are in gray. Restrained residues are shown as sticks.
In this benchmark, CCM was compared to both SFM and the comparative modeling method RosettaCM (Song et al., 2013), which samples conformational movements in a superficially similar way and is also used to model conformational changes and refine protein structures (Hiranuma et al., 2021; Park et al., 2019). Each of these two methods exclusively used DEER restraints as experimental average distance values.
All approaches generated 1000 models, which were then compared to the target structures by RMSD (Figure 5). As with the soluble benchmark set discussed above, these data illustrate how CCM outperforms SFM in modeling each conformational change of interest. SFM generated models with a wide range of RMSD values, and visual inspection of these models indicated partial unfolding. By contrast, RosettaCM appeared to sample conformations that were structurally similar to the starting structure, which is likely due to its emphasis on sampling changes in torsion space and its inability to introduce the rigid-body rotations and translations of interest. In contrast, models generated using CCM showed a broader distribution of RMSD values, indicating that the method sampled SSEs more aggressively. As a result, in most cases this approach generated models with the lowest RMSD values among all methods considered. The two noteworthy exceptions are the outward-to-inward transition in Mhp1 and the inactive-to-active transition in Rhodopsin. However, distributions of models generated with simulated data suggest that this can be attributed to the quality of the restraints. Experimental restraints provided as median values or as ranges showed a similar performance with the exception of Rhodopsin transitions for which ranges allowed the sampling of alternative conformations closer to the target.
Figure 5.
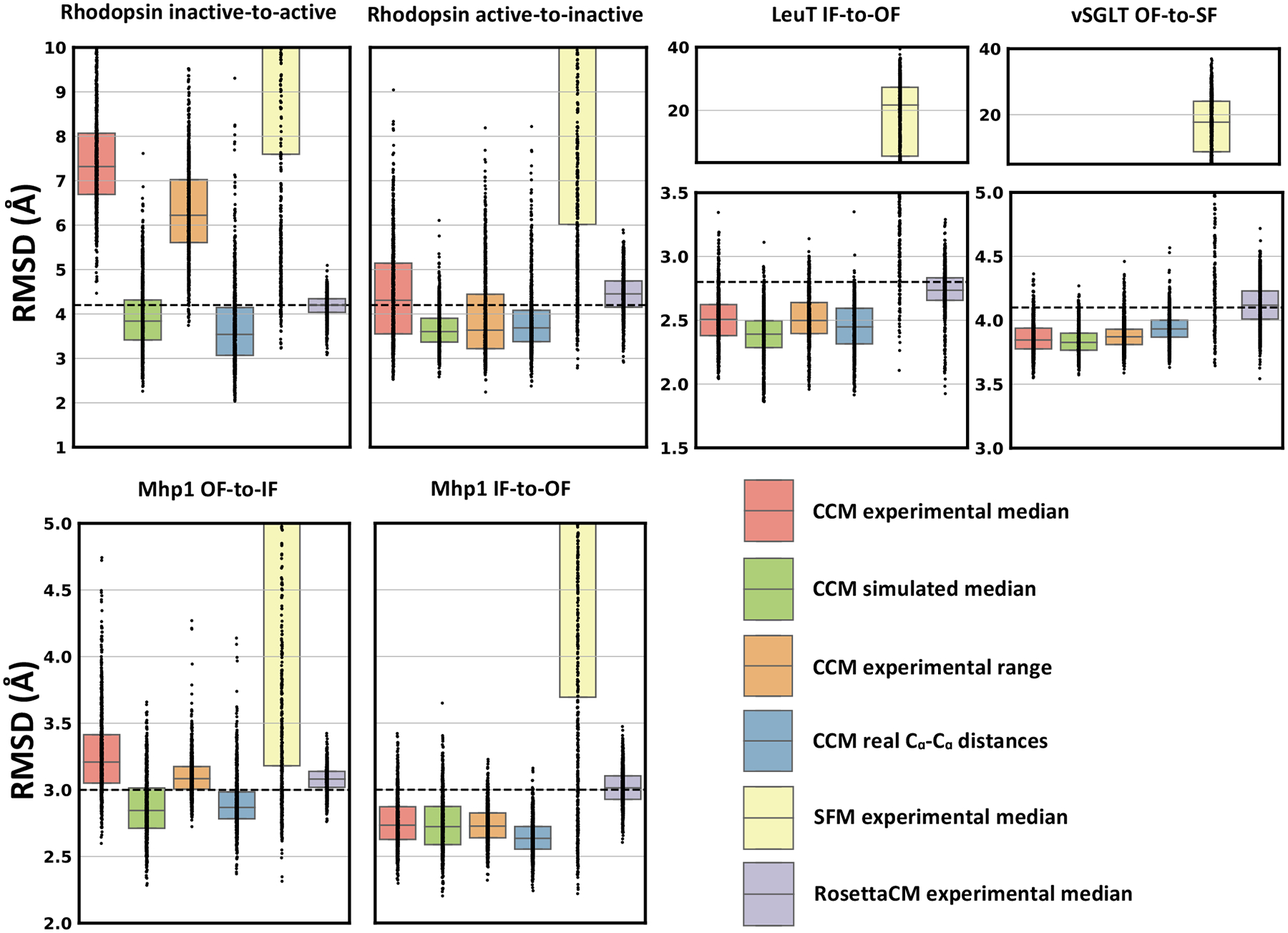
CCM outperformed other Rosetta methods in modeling conformational changes of membrane proteins. Restraints were provided as median values of the experimental distribution (experimental median) or as a range centered on the median value (experimental range). Dots represent the real distribution of RMSD values from the target conformation. RMSD between the two native conformations is shown as a dashed line.
The accuracy of each DEER dataset was evaluated by measuring its average RMSD from the simulated average (Figure S4). Substrate-free vSGLT and OF LeuT conformation featured the lowest and the highest RMSD of 2.7 Å and 4.6 Å, respectively. All the remaining datasets spanned a range between 3.5 Å and 4.0 Å. Active Rhodopsin and IF Mhp1, which were among the most difficult to model with experimental data, showed the broadest distributions of model accuracies. Thus, few highly inaccurate restraints may have been at least partially responsible of poor modeling. To identify the most inaccurate restraints, we computed the difference between experimental and simulated distance for each residue pair restraint (Figure S5). Restraints that stood out in the Rhodopsin active-state dataset included those involving residues 225 (TM5), and residues 241 and 252 (TM6). Analogously, Mhp1 residues 30 and 338 were involved in the most inaccurate restraints of the IF state. The contribution of these residues on the global RMSD of models was then assessed by computing their per-residue RMSD from the target conformation (Figure S6). As expected, all these residues have greater RMSD with respect to the median value of global RMSD of models (dashed line). Most of the Rhodopsin models have also per-residue RMSDs greater than in the starting conformation (red dots).
In addition to experimental restraints, accuracy of models is also affected by the complexity of the conformational change to be sampled. For each transition, we then superimposed the best model sampled with experimental restraints on the corresponding target structure (Figure 6). Not surprisingly, whereas TM6 of the active-state model of Rhodopsin superimposed poorly with the target structure, the Rhodopsin inactive state was modeled with high accuracy. Even the OF-state of Mhp1 was accurately modeled, especially the unbending of TM5, whereas the two small helices carrying the 278–362 restraint superimpose poorly onto the target structure. Further, in modeling the Mhp1 IF-state, the helix carrying residue 30 is significantly misplaced, and the bending of TM5 was not introduced using our approach. In LeuT, which underwent transitions defined by large-amplitude movements in the partially unwound helix TM1 and the fully continuous helix TM5, we found that CCM accurately modeled the former, but not the latter. In particular, the motions of the cytoplasmic end of TM5 were driven by the two poorly restrained residues 185 and 193, leading to partial unfolding in the model with the lowest RMSD. Interestingly, while helical bending was generally difficult to model, the vSGLT model correctly reproduced the challenging TM11 bending, which may be due to steric hindrance surrounding this helix. Thus, in general, the most inaccurate distance distributions in the restraints’ dataset appear to directly reduce the accuracy achieved in modeling the two SSEs containing the two spin-labeled residues.
Figure 6.
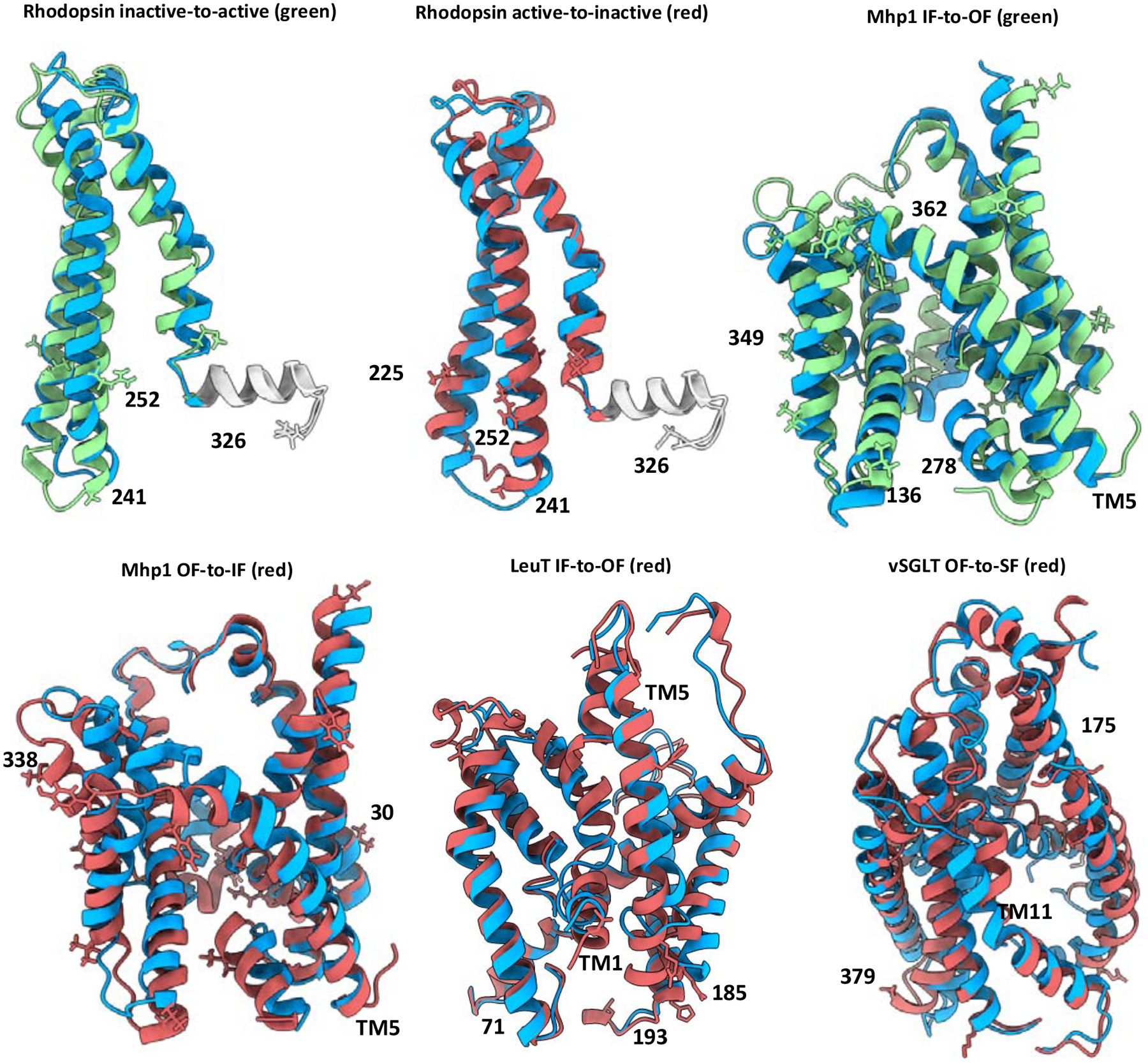
Complexity of conformational changes and accuracy of experimental restraints affect the accuracy achieved in modeling specific protein regions, see also Figures S5 and S6. The target conformation is in green or red, following the color code used in Fig 4. Rhodopsin helix 8 is in gray. The model is shown in blue. Restrained residues are represented as sticks. Residues involved in restraints featuring a relevant difference between experimental and simulated DEER distances are labeled and mapped on structures.
In summary, CCM outperformed RosettaCM and SFM in modeling conformational changes of membrane proteins driven by high-quality sparse DEER distances. Few highly inaccurate restraints hampered the sampling of accurate models in a couple of conformational transitions that however were successfully modeled with simulated restraints, proving the efficiency of the method. Of note, simulated restraints were applied on the same few residue-pairs of experimental data. As was observed in soluble proteins, conformational transitions involving partial and localized change in the folding state and change in backbone dihedral angles were difficult to sample without extensive fragments insertion. Ultimately, these results suggest that CCM is an effective protocol for conservative sampling of structural models, but that fine-tuning specific to each protein may be necessary to achieve the best results possible.
Protein refinement with EPR or NMR data
We note that although these results focus on the specific task of modeling conformational changes using DEER data, the functionality of CCM and its integration in Rosetta allows it to tackle a broader array of tasks. To demonstrate this, we attempted to refine a misfolded model of T4 lysozyme (15 Å from native structure) and a distorted ubiquitin conformation (5 Å from native structure) respectively using 45 experimental DEER distances (del Alamo et al., 2021a; Islam et al., 2013) and two experimental pseudo-contact shifts (PCS) datasets collected through NMR spectroscopy (Schmitz et al., 2012). The misfolded T4 lysozyme conformation had misplaced SSEs that split the protein in three structural domains, whereas the ubiquitin had the helix and its two connecting loops misplaced and partially unfolded. In both cases, we observed a RMSD drop only when experimental restraints were used (Figure 7). A number of models were found below 2 Å from the target structure, indicating that near-native models can be obtained from misfolded or partially distorted conformations. The superimposition of the best model and the starting conformation over the target structure highlights the complexity of the conformational changes modeled. Overall, these results indicate the broad applicability of this method and its ability to integrate a diverse array of experimental data.
Figure 7.
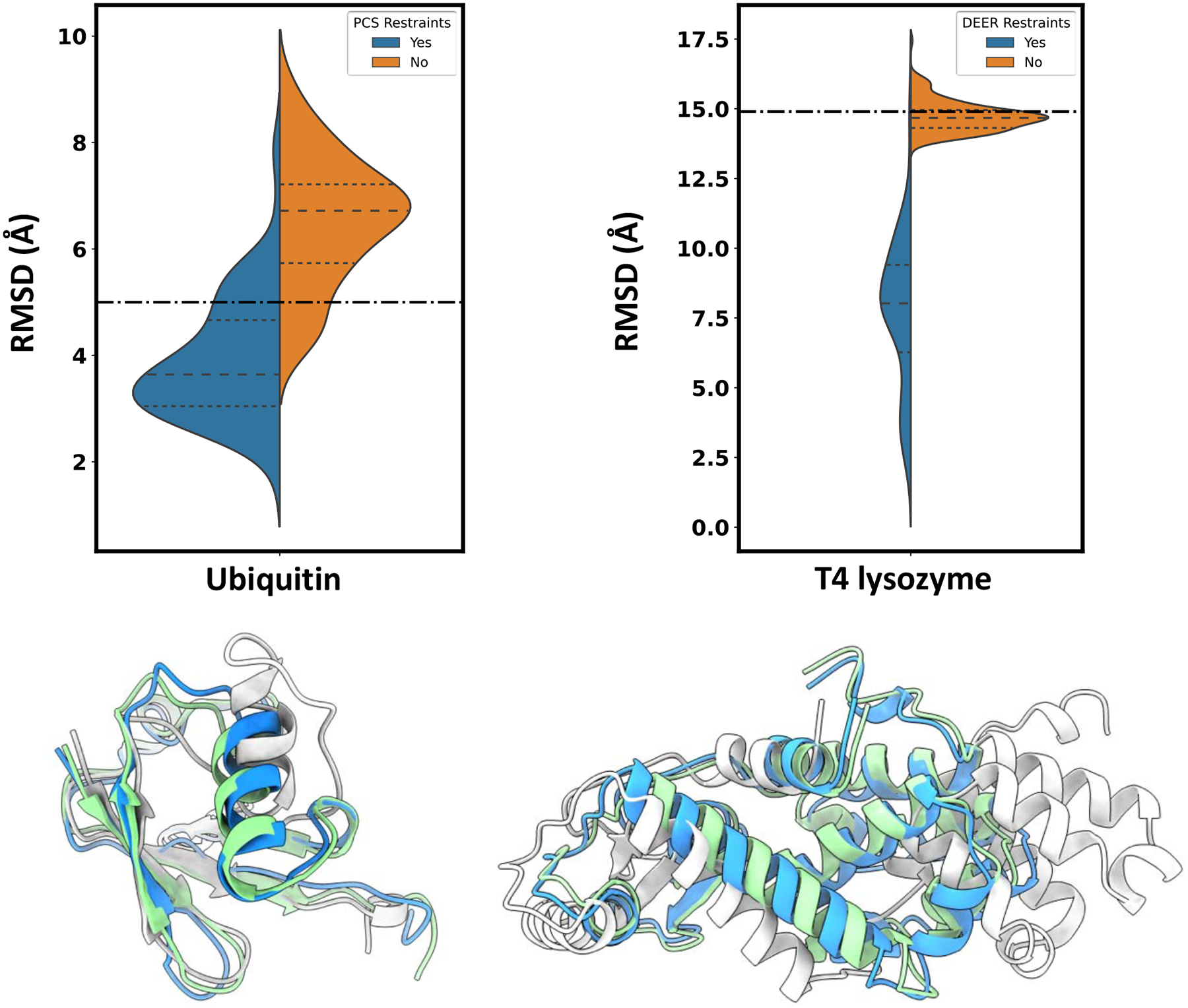
CCM in combination with NMR or EPR data can potentially be used to refine distorted or misfolded conformations. Dot dashed line indicates RMSD between starting and target structure. In colored cartoon are represented the initial conformation (light gray), the target structure (green) and the best model in the ensemble (blue).
DISCUSSION
Here, we described and benchmarked ConfChangeMover (CCM), a new modeling method in the software suite Rosetta that uses experimental restraints to model conformational changes in proteins. The performance of CCM was evaluated in both soluble and membrane proteins using simulated or experimental distance restraints, respectively. In both cases, CCM outperformed existing Rosetta methods that have been previously used to model conformational changes in proteins with a wide variety of topologies (Evans et al., 2020; Kuenze et al., 2019; Pilla et al., 2015; Rohl et al., 2004b), highlighting its versatility and robustness. We believe the main advantage of CCM over other methods stems from its ability to automatically identify, group, and move SSEs as rigid bodies, a task that has been absent from the Rosetta modeling suite. Notably, although CCM allows the user to define sets of SSEs that can only be moved as a group, this option was not used in our two benchmarks, potentially understating the extent to which this protocol can be used to accurately model conformational changes, as shown in the structural refinement of T4 lysozyme.
A secondary function of this protocol is fragment insertion to both diversify SSEs in dihedral space and close loops in Cartesian space following rigid-body manipulation of SSEs. Because CCM’s two-stage approach allows loop closure to be decoupled from structural diversification, multiple distinct loop conformations can be quickly generated following the more expensive structural diversification performed during the first stage. Throughout our benchmark, the accuracy achieved in modeling loop regions with simulated distances indicated that the sampling parameters may have been too conservative for accurate modeling. Besides increasing the intensity of sampling, loops can also be modeled afterwards with other Rosetta methods appositely developed for that purpose (del Alamo et al., 2021b; Canutescu and Dunbrack, 2003; Mandell et al., 2009; Stein and Kortemme, 2013), or refined using gradient minimization methods such as FastRelax, which can optimize backbone geometry following fragment insertion (Song et al., 2013). Full-atom refinement could further lead to the correction of small errors, such as the slight unfolding of beta structures observed in some models of soluble proteins.
An advantage of CCM that is not captured by these results is its potential flexibility and modularity. By interfacing with RosettaScripts, CCM provides many options to the user to adjust the protocol in accordance with expectations about the target conformation (see Data S1 for more details). In stage 1, the residues in each SSE can be manually defined using residue selectors, which can specify segments and/or change the extension of each segment. In addition, multiple SSEs can be treated as rigid bodies during stage 1. Finally, users can define the number, frequency, and magnitude of each move. During stage 2, the choice of which regions of the protein can be perturbed is also provided and can be expanded to include SSEs which are omitted by default. Additionally, since we found that stage 1 was far more computationally expensive than stage 2, we designed stage 2 to permit multiple output models to be generated from each pose sampled by stage 1. This would have the effect of generating topologically similar models with different loop conformations. However, the results discussed in this report do not use this feature.
It is important to note that despite the parametrization options available to the user, no modifications to the protocol were introduced that accounted for the varying topologies and sizes of protein targets in our benchmark set. Despite this handicap, CCM managed to extensively sample accurate models of soluble proteins using only one simulated distance restraint per twenty residues. Indeed, while the median RMSD improvements often exceeded 5 Å, specialized parametrization would almost certainly lead to further increases in accuracy. Models of membrane proteins generated with simulated restraints had less impressive RMSD improvements; however, the magnitude of their conformational changes were lower than those of soluble proteins, likely precluding comparable improvements in RMSD. We highlight that this benchmark does not account for the placement of experimental restraints in the membrane proteins modeled here, as these were guided by unique scientific questions specific to each protein (Hays et al., 2018). By contrast, the soluble protein benchmark used simulated restraints that were chosen using a well-validated algorithm, leading to well-distributed residue pairs covering most of the regions of interest. This methodological difference also explains why conformational changes were modeled in membrane proteins with fewer restraints per residue. Nevertheless, CCM consistently improved the RMSD of any conformational transition modeled, a record that was not shared by the other methods explored here.
While our benchmark was limited to distance restraints, the Rosetta framework allows a wide variety of types of experimental data, potentially from multiple sources, to be used for conformational change modeling tasks. In addition to EPR data, restraints may be obtained from data collected with NMR (Kuenze et al., 2019; Marzolf et al., 2021), mass spectrometry (Aprahamian et al., 2018; Biehn et al., 2021), and other sources of geometrical restraints such as FRET and cross-linking. Among them, we tested PCS in the structural refinement of a partially unfolded conformation. In addition to experimentally derived restraints, computational restrains can also be exploited in modeling conformational changes. Indeed, evolutionary couplings derived from multiple sequence alignments (MSA) can capture protein dynamics by exploring their use as reaction coordinates (Feng and Shukla, 2018).
In conclusion, CCM facilitates the effective sampling of protein dynamics. This method is well-positioned to deepen our understanding of proteins structural dynamics. Future directions may include structural refinement using residue-residue contacts predicted by machine-learning (ML) methods (Feng and Shukla, 2018), particularly by facilitating the detection of functional states in proteins spanning multiple heterogeneous conformational states. While the recent integration of ML methods in Rosetta (Hiranuma et al., 2021), a more promising strategy is to combine CCM with structure evaluation using deep learning algorithms such as AlphaFold2 (Jumper et al., 2021; Roney and Ovchinnikov, 2022). Combining MCMC sampling with ML structure evaluation methods could potentially bolster integrative modeling of conformational changes.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests should be directed to the lead contact, Jens Meiler (jens@meilerlab.org).
Materials availability
Information on the installation of Rosetta can be found at https://www.rosettacommons.org/software/academic. Instructions on using CCM can be found in the accompanying demos with Data S1 and within the deposited data at https://zenodo.org/record/6424150.
Data and code availability
Reported data have been deposited at Zenodo and are publicly available as of the date of publication. DOIs are listed in the key resources table.
All original code is part of Rosetta software suite and can be found at “path/to/Rosetta/main/source/src/protocols/rbsegment_relax/ConfChangeMover”. Rosetta is available to all non-commercial users for free.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key Resources Table
| RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Demos, protein models, scripts, input files. | This paper | https://zenodo.org/record/6424150 or https://doi.org/10.5281/zenodo.6424150 |
| Software and algorithms | ||
| Rosetta | RosettaCommons | https://www.rosettacommons.org/software/academic |
| ChimeraX | UCSF | https://www.cgl.ucsf.edu/chimerax/ |
| MatPlotLib | MatPlotLib | https://github.com/matplotlib/matplotlib |
| Seaborn | Seaborn | https://github.com/mwaskom/seaborn |
| Excel | Microsoft | https://www.microsoft.com/en-us/microsoft-365/excel |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
All data are generated from the datasets provided in the Key Resources Table.
METHOD DETAILS
Benchmark on soluble proteins
Seven topologically dissimilar proteins were selected from previous benchmarks on modeling conformational changes and used to determine the effectiveness of CCM (Jeschke, 2012; Sfriso et al., 2016) (Table 1). We first modeled all missing residues using RosettaCM (Song et al., 2013). Distance restraints between Cα atoms were chosen using a previously published restraint-picking algorithm implemented in the program MMM, which uses Normal Mode Analysis to predict mobile regions (Jeschke, 2012; Zheng and Brooks, 2005). The Rosetta scoring functions score3 and score4_smooth_cart were used for stages 1 and 2 of CCM, respectively. We compared CCM to SingleFragmentMover (SFM), which introduces fragment insertion into the backbone; 50,000 rounds of 3-mer fragments insertions were performed with GenericMonteCarlo mover and score3 scoring function. Fragments were collected using the Robetta web server as previously described (Kim et al., 2004). One hundred models were generated for each of the 14 conformational transitions in the benchmark. Cα root mean squared deviation (RMSD) calculations were limited to each target protein’s mobile regions.
Benchmark on membrane proteins
For this purpose, we used data collected using double electron-electron resonance (DEER) EPR spectroscopy, which measures distance distributions between nitroxide spin labels attached to the protein backbone. Proteins in the benchmark set were entirely alpha-helical in the transmembrane domain and include the G-protein coupled receptor (GPCR) Rhodopsin and the transporters LeuT (Kazmier et al., 2014a; Krishnamurthy and Gouaux, 2012; Yamashita et al., 2005), Mhp1 (Shimamura et al., 2010; Weyand et al., 2008), and vSGLT (Paz et al., 2018; Wahlgren et al., 2018; Watanabe et al., 2010) (Table 2). We note that unlike the soluble protein benchmark described above, we only sampled conformational changes when sufficient experimental data were available, which excluded both the outward-to-inward transition in LeuT (due to the small number of experimental measurements collected in the presence of the background mutations required to stabilize the target conformation) and the inward-to-outward transition of vSGLT (due to the lack of an experimental outward-facing structure). To serve as a starting point when modeling the outward-to-inward transition in vSGLT, we used a previously published outward-facing homology model generated from its homolog SiaT (Paz et al., 2018).
Simulated DEER distance restraints were computed with the MDDS method implemented in the charmm-gui webserver (Islam and Roux, 2015; Islam et al., 2013; Jo et al., 2008; Qi et al., 2020).The resulting simulated DEER distances as well as the simulated Cα – Cα distance restraints were applied only on the residue pairs of experimental restraints. Experimental DEER distances of LeuT-fold transporter proteins have previously been collected using EPR (Claxton et al., 2010; Kazmier et al., 2014b, 2014a; Paz et al., 2018). DEER restraints were provided to Rosetta through the RosettaDEER module either as quadratic functions centered on the median values of each distance distribution or as flat-bottom potentials centered on the median values, plus or minus 5 Å, of each distance distribution (del Alamo et al., 2020). The regions of the proteins spanning the membrane were predicted with OCTOPUS (Viklund and Elofsson, 2008). Rigid-body segments were modified to include all the residues involved in restraints. Fragments were collected as described above for soluble proteins. For CCM, we set stages 1 and 2 to consist of 30,000 rounds and 4,000 rounds, respectively. For SMF, 30,000 rounds of 3-mer fragments insertions were performed with GenericMonteCarlo mover. For all the runs, the Rosetta scoring function stage2_membrane was used (Yarov-Yarovoy et al., 2006). For RosettaCM, stage2_membrane was used in stage1 and stage2, whereas stage3_rlx_membrane was used in stage3.
ConfChangeMover Workflow
The ConfChangeMover (CCM) was developed in Rosetta and executed in RosettaScripts (Fleishman et al., 2011). It samples candidate structural models using a two-stage strategy that proceeds as follows:
Conversion of an input structure with a sequence identical to the input into coarse-grained model, with explicitly modeled side chains replaced by large immobile centroid pseudo-atoms.
Identification of rigid bodies, or SSEs, using backbone dihedral angles as specified by the Dictionary of Secondary Structure of Proteins (DSSP) (Kabsch and Sander, 1983)
Introduction of cutpoints on loops connecting pairs of SSEs to avoid the “lever-arm effect” (Tyka et al., 2012).
Introduction of backbone dihedral restraints (see below).
Sampling of rigid-body rotations and translations (Stage 1, see below)
Removal of cutpoints and loop closure using fragment insertion and Cartesian minimization (Stage 2, see below).
Final minimization using the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm (Byrd et al., 1995).
Introduction of backbone dihedral restraints
To account for the relative invariance of protein dihedral angles during conformational change modeling, circular sigmoidal restraints are added to the model’s ϕ and ψ angles based on either the starting conformation or a separate model provided by the user (Eq 1).
| (1) |
Here ϕsim/ψsim and ϕexp/ψexp are the ϕ and ψ angles observed in the model and starting conformation, respectively. These restraints penalize changes in backbone dihedral angles up to, but not beyond, a certain rotation angle. The use of sigmoid functions generally engenders restraint violations that are limited to relatively few degrees of freedom; in contrast, harmonic restraints instead typically distribute restraint violations throughout the features. Thus, these functions quantify the expectation that most, but not all, dihedral angles remain unchanged during isomerization; similar restraints have previously been applied when using ambiguous data such as residue coevolutionary couplings (Ovchinnikov et al., 2015). These restraints are added to residues belonging to SSEs in stage 1 and to loop regions in stage 2. The weight of the dihedral_constraint score term, which balances the contribution of these restraints relative to the other components in the scoring function, was set to 1.0 and 0.1 during the first and second stages, respectively.
Stage 1: Rigid-body structural perturbation
During the first stage, several types of perturbations are randomly introduced. First, SSEs can be moved in isolation, with rotation angles and translation vectors randomly drawn from normal distributions with user-defined standard deviations. In the soluble protein benchmark discussed below, these comprised 32% of all moves sampled in stage 1, and the standard deviation of rigid-body rotations and translations were 10° and 1.0 Å, respectively. Second, up to N − 1 SSEs close in space can be moved in tandem, where N is the number of SSEs in the model (accounting for 50% of moves). Third, helices may be twisted along their axis by a randomly chosen angle drawn from a normal distribution with a user-defined standard deviation (8% of moves). Finally, dihedral angles of three-residue stretches can be modified to match those of randomly chosen sequence fragments obtained from the PDB (10% of moves). In the soluble protein benchmark, stage 1 consisted of 50,000 total moves.
Throughout stage 1, loops are allowed to break and move independently at pre-specified cutpoints as described above. Nevertheless, plausible topologies are implicitly enforced throughout stage 1 with distance constraints between SSEs adjacent in sequence that prevent them from being separated by distances that cannot be bridged by the loops between them. The maximum allowable distance between the C-terminus of one SSE and the N-terminus of next SSE was set to (2.65*nres + 2.11) Å where nres is the number of residues in the loop, which has previously been used in de novo protein folding with implicit loops (Woetzel et al., 2012).
Stage 2: Loop closure and structural minimization
Between the first and second stages, coordinate constraints are applied to the Cα atoms of all residues in SSEs, thus preventing large-amplitude distance changes from being introduced during loop closure. During the second stage, loops are closed using an approach designed for multi-template homology modeling (Rohl et al., 2004b). Briefly, nine-residue sequence fragments obtained from the PDB are superimposed in Cartesian space on regions of the protein with chain breaks. During the final 25% of Stage 2, this superimposition is followed by Cartesian minimization using the L-BFGS minimization algorithm for five iterations, which further reduces the size of the gaps (Byrd et al., 1995; Conway et al., 2014). To increase model diversity, these superimpositions are periodically applied to regions of the protein that fail to have gaps (50% of moves in our soluble protein benchmark). Additionally, to maintain similarity to the starting structure, some of these nine-residue fragments are replaced by nine-to-fifteen residue fragments derived from the starting conformation (80% of moves in our soluble protein benchmark). In conjunction with the sigmoidal potentials described above, these moves minimize the magnitude of the changes undertaken by loop regions, which were otherwise observed to undergo dramatic movements inconsistent with experimental observations. We found that 5,000 moves were sufficient to close all loops. Finally, at the end of stage 2, the entire model is minimized using 2,000 iterations of the L-BFGS algorithm.
QUANTIFICATION AND STATISTICAL ANALYSIS
Median, second and third quartiles of Cα-atom RMSD distributions shown in Figure 2, 5, S1, S3 and S6 were carried out with Seaborn. Calculation of the difference between median Cα-atom RMSD values displayed in Figure S2 was carried out in Excel. The difference between simulated and experimental mean(±SD) of each DEER dataset shown in Figure S4 was computed in Python and plotted with Seaborn. Discrepancies between simulated and experimental DEER distances shown in Figure S5 were computed in Python and plotted with Seaborn.
Supplementary Material
Data S1. Demos on how to use CCM to model conformational changes of membrane and soluble proteins, related to STAR Methods.
Highlights.
A Rosetta method for modeling protein conformational changes is introduced
ConfChangeMover enables integrative structure modeling with multiple sources of data
High-accuracy models have been generated with simulated and experimental EPR data
Rosetta modularity allows ConfChangeMover to be used in a wide range of modeling tasks
Acknowledgments:
We would like to thank Drs. Jeff Abramson and Aviv Paz for providing us with the outward-facing model of vSGLT, Dr. Christian Altenbach for providing the experimental data for Rhodopsin, and Dr. Marion F. Sauer for fruitful discussions. Authors acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through SFB1423, project number 421152132 and the NIH R01 GM080403, R01 GM129261, R01 HL122010, and R01 DA046138.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests: The authors declare no competing interests.
References
- del Alamo D, Tessmer MH, Stein RA, Feix JB, Mchaourab HS, and Meiler J (2020). Rapid Simulation of Unprocessed DEER Decay Data for Protein Fold Prediction. Biophys. J 118, 366–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Alamo D, Jagessar KL, Meiler J, and McHaourab HS (2021a). Methodology for rigorous modeling of protein conformational changes by Rosetta using DEER distance restraints. PLoS Comput. Biol 17, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Alamo D, Fischer AW, Moretti R, Alexander NS, Mendenhall J, Hyman NJ, and Meiler J (2021b). Efficient Sampling of Protein Loop Regions Using Conformational Hashing Complemented with Random Coordinate Descent. J. Chem. Theory Comput 17, 560–570. [DOI] [PubMed] [Google Scholar]
- AlQuraishi M (2021). Machine learning in protein structure prediction. Curr. Opin. Chem. Biol 65, 1–8. [DOI] [PubMed] [Google Scholar]
- Aprahamian ML, Chea EE, Jones LM, and Lindert S (2018). Rosetta Protein Structure Prediction from Hydroxyl Radical Protein Footprinting Mass Spectrometry Data. Anal. Chem 90, 7721–7729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek M, DiMaio F, Anishchenko I, Dauparas J, Ovchinnikov S, Lee GR, Wang J, Cong Q, Kinch LN, Schaeffer RD, et al. (2021a). Accurate prediction of protein structures and interactions using a three-track neural network. Science (80-.) 373, 871–876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek M, Anishchenko I, Park H, Humphreys IR, and Baker D (2021b). Protein oligomer modeling guided by predicted interchain contacts in CASP14. Proteins Struct. Funct. Bioinforma [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardi RC, Melo MCR, and Schulten K (2015). Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta - Gen. Subj 1850, 872–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biehn SE, Limpikirati P, Vachet RW, and Lindert S (2021). Utilization of Hydrophobic Microenvironment Sensitivity in Diethylpyrocarbonate Labeling for Protein Structure Prediction. Anal. Chem 93, 8188–8195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonomi M, Heller GT, Camilloni C, and Vendruscolo M (2017). Principles of protein structural ensemble determination. Curr. Opin. Struct. Biol 42, 106–116. [DOI] [PubMed] [Google Scholar]
- Bradley P, Chivian D, Meiler J, Misura KMS, Rohl CA, Schief WR, Wedemeyer WJ, Schueler-Furman O, Murphy P, Schonbrun J, et al. (2003). Rosetta Predictions in CASP5: Successes, Failures, and Prospects for Complete Automation. In Proteins: Structure, Function and Genetics, pp. 457–468. [DOI] [PubMed] [Google Scholar]
- Bradley P, Malmström L, Qian B, Schonbrun J, Chivian D, Kim DE, Meiler J, Misura KMS, and Baker D (2005). Free modeling with Rosetta in CASP6. In Proteins: Structure, Function and Genetics, (John Wiley & Sons, Ltd; ), pp. 128–134. [DOI] [PubMed] [Google Scholar]
- Bryn Fenwick R, Van Den Bedem H, Fraser JS, and Wright PE (2014). Integrated description of protein dynamics from room-temperature X-ray crystallography and NMR. Proc. Natl. Acad. Sci. U. S. A 111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrd RH, Lu P, Nocedal J, and Zhu C (1995). A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput 16, 1190–1208. [Google Scholar]
- Bystroff C, and Baker D (1998). Prediction of local structure in proteins using a library of sequence-structure motifs. J. Mol. Biol 281, 565–577. [DOI] [PubMed] [Google Scholar]
- Canutescu AA, and Dunbrack RL (2003). Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Sci. 12, 963–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claxton DP, Quick M, Shi L, De Carvalho FD, Weinstein H, Javitch JA, and McHaourab HS (2010). Ion/substrate-dependent conformational dynamics of a bacterial homolog of neurotransmitter:sodium symporters. Nat. Struct. Mol. Biol 17, 822–829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conway P, Tyka MD, DiMaio F, Konerding DE, and Baker D (2014). Relaxation of backbone bond geometry improves protein energy landscape modeling. Protein Sci. 23, 47–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dastvan R, Fischer AW, Mishra S, Meiler J, and McHaourab HS (2016). Protonation-dependent conformational dynamics of the multidrug transporter EmrE. Proc. Natl. Acad. Sci. U. S. A 113, 1220–1225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dominguez C, Boelens R, and Bonvin AMJJ (2003). HADDOCK: A protein-protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc 125, 1731–1737. [DOI] [PubMed] [Google Scholar]
- Eswar N, Webb B, Marti-Renom MA, Madhusudhan MS, Eramian D, Shen M, Pieper U, and Sali A (2007). Comparative Protein Structure Modeling Using MODELLER. In Current Protocols in Protein Science, (Hoboken, NJ, USA: John Wiley & Sons, Inc.), pp. 2.9.1–2.9.31. [DOI] [PubMed] [Google Scholar]
- Evans EGB, Morgan JLW, DiMaio F, Zagotta WN, and Stoll S (2020). Allosteric conformational change of a cyclic nucleotide-gated ion channel revealed by DEER spectroscopy. Proc. Natl. Acad. Sci. U. S. A 117, 10839–10847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng J, and Shukla D (2018). Characterizing Conformational Dynamics of Proteins Using Evolutionary Couplings. J. Phys. Chem. B 122, 1017–1025. [DOI] [PubMed] [Google Scholar]
- Fleishman SJ, Leaver-Fay A, Corn JE, Strauch EM, Khare SD, Koga N, Ashworth J, Murphy P, Richter F, Lemmon G, et al. (2011). Rosettascripts: A scripting language interface to the Rosetta Macromolecular modeling suite. PLoS One 6, e20161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin MC, Wang J, and Steitz TA (2001). Structure of the replicating complex of a pol α family DNA polymerase. Cell 105, 657–667. [DOI] [PubMed] [Google Scholar]
- Green AG, Elhabashy H, Brock KP, Maddamsetti R, Kohlbacher O, and Marks DS (2021). Large-scale discovery of protein interactions at residue resolution using co-evolution calculated from genomic sequences. Nat. Commun 12, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenleaf WJ, Woodside MT, and Block SM (2007). High-resolution, single-molecule measurements of biomolecular motion. Annu. Rev. Biophys. Biomol. Struct 36, 171–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haridas M, Anderson BF, and Baker EN (1995). Structure of human diferrric lactoferrin refined at 2.2 Angstrom resolution. Acta Crystallogr. - Sect. D Biol. Crystallogr 51, 629–646. [DOI] [PubMed] [Google Scholar]
- Hays JM, Kieber MK, Li JZ, Han JI, Columbus L, and Kasson PM (2018). Refinement of Highly Flexible Protein Structures using Simulation-Guided Spectroscopy. Angew. Chemie - Int. Ed 57, 17110–17114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heilmann N, Wolf M, Kozlowska M, Sedghamiz E, Setzler J, Brieg M, and Wenzel W (2020). Sampling of the conformational landscape of small proteins with Monte Carlo methods. Sci. Rep 10, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hiranuma N, Park H, Baek M, Anishchenko I, Dauparas J, and Baker D (2021). Improved protein structure refinement guided by deep learning based accuracy estimation. Nat. Commun 12, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsiao CD, Sun YJ, Rose J, and Wang BC (1996). The crystal structure of glutamine-binding protein from Escherichia coli. J. Mol. Biol 262, 225–242. [DOI] [PubMed] [Google Scholar]
- Humphreys I, Pei J, Baek M, Krishnakumar A, Anishchenko I, Ovchinnikov S, Zhang J, Ness TJ, Banjade S, Bagde SR, et al. (2021). Computed structures of core eukaryotic protein complexes. Science (80-.) 374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Islam SM, and Roux B (2015). Simulating the distance distribution between spin-labels attached to proteins. J. Phys. Chem. B 119, 3901–3911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Islam SM, Stein RA, McHaourab HS, and Roux B (2013). Structural refinement from restrained-ensemble simulations based on EPR/DEER data: Application to T4 lysozyme. J. Phys. Chem. B 117, 4740–4754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeschke G (2012). Characterization of protein conformational changes with sparse spin-label distance constraints. J. Chem. Theory Comput 8, 3854–3863. [DOI] [PubMed] [Google Scholar]
- Jo S, Kim T, Iyer VG, and Im W (2008). CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem 29, 1859–1865. [DOI] [PubMed] [Google Scholar]
- Jumper J, Evans R, Pritzel A, Green T, Figurnov M, Ronneberger O, Tunyasuvunakool K, Bates R, Žídek A, Potapenko A, et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabsch W, and Sander C (1983). Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22, 2577–2637. [DOI] [PubMed] [Google Scholar]
- Kazmier K, Sharma S, Quick M, Islam SM, Roux B, Weinstein H, Javitch JA, and McHaourab HS (2014a). Conformational dynamics of ligand-dependent alternating access in LeuT. Nat. Struct. Mol. Biol 21, 472–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazmier K, Sharma S, Islam SM, Roux B, Mchaourab HS, and Wright EM (2014b). Conformational cycle and ion-coupling mechanism of the Na+/hydantoin transporter Mhp1. Proc. Natl. Acad. Sci. U. S. A 111, 14752–14757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim DE, Chivian D, and Baker D (2004). Protein structure prediction and analysis using the Robetta server. Nucleic Acids Res. 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnamurthy H, and Gouaux E (2012). X-ray structures of LeuT in substrate-free outward-open and apo inward-open states. Nature 481, 469–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuenze G, Bonneau R, Leman JK, and Meiler J (2019). Integrative Protein Modeling in RosettaNMR from Sparse Paramagnetic Restraints. Structure 27, 1721–1734.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leaver-Fay A, Tyka M, Lewis SM, Lange OF, Thompson J, Jacak R, Kaufman K, Renfrew PD, Smith CA, Sheffler W, et al. (2011). Rosetta3: An object-oriented software suite for the simulation and design of macromolecules. In Methods in Enzymology, (Methods Enzymol), pp. 545–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leman JK, Weitzner BD, Lewis SM, Adolf-Bryfogle J, Alam N, Alford RF, Aprahamian M, Baker D, Barlow KA, Barth P, et al. (2020). Macromolecular modeling and design in Rosetta: recent methods and frameworks. Nat. Methods [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Edwards PC, Burghammer M, Villa C, and Schertler GFX (2004). Structure of bovine rhodopsin in a trigonal crystal form. J. Mol. Biol 343, 1409–1438. [DOI] [PubMed] [Google Scholar]
- Li Y, Korolev S, and Waksman G (1998). Crystal structures of open and closed forms of binary and ternary complexes of the large fragment of Thermus aquaticus DNA polymerase I: Structural basis for nucleotide incorporation. EMBO J. 17, 7514–7525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnusson U, Salopek-Sondi B, Luck LA, and Mowbray SL (2004). X-ray Structures of the Leucine-binding Protein Illustrate Conformational Changes and the Basis of Ligand Specificity. J. Biol. Chem 279, 8747–8752. [DOI] [PubMed] [Google Scholar]
- Mandell DJ, Coutsias EA, and Kortemme T (2009). Sub-angstrom accuracy in protein loop reconstruction by robotics-inspired conformational sampling. Nat. Methods 6, 551–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marzolf DR, Seffernick JT, and Lindert S (2021). Protein Structure Prediction from NMR Hydrogen-Deuterium Exchange Data. J. Chem. Theory Comput 17, 2619–2629. [DOI] [PubMed] [Google Scholar]
- Maximova T, Moffatt R, Ma B, Nussinov R, and Shehu A (2016). Principles and Overview of Sampling Methods for Modeling Macromolecular Structure and Dynamics. PLoS Comput. Biol 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPhalen CA, Vincent MG, Picot D, Jansonius JN, Lesk AM, and Chothia C (1992a). Domain closure in mitochondrial aspartate aminotransferase. J. Mol. Biol 227, 197–213. [DOI] [PubMed] [Google Scholar]
- McPhalen CA, Vincent MG, and Jansonius JN (1992b). X-ray structure refinement and comparison of three forms of mitochondrial aspartate aminotransferase. J. Mol. Biol 225, 495–517. [DOI] [PubMed] [Google Scholar]
- Nakane T, Kotecha A, Sente A, McMullan G, Masiulis S, Brown PMGE, Grigoras IT, Malinauskaite L, Malinauskas T, Miehling J, et al. (2020). Single-particle cryo-EM at atomic resolution. Nature 587, 152–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norris GE, Anderson BF, and Baker EN (1991). Molecular replacement solution of the structure of apolactoferrin, a protein displaying large‐scale conformational change. Acta Crystallogr. Sect. B 47, 998–1004. [DOI] [PubMed] [Google Scholar]
- Ovchinnikov S, Kinch L, Park H, Liao Y, Pei J, Kim DE, Kamisetty H, Grishin NV, and Baker D (2015). Large-scale determination of previously unsolved protein structures using evolutionary information. Elife 4, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palamini M, Canciani A, and Forneris F (2016). Identifying and visualizing macromolecular flexibility in structural biology. Front. Mol. Biosci 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H, Ovchinnikov S, Kim DE, DiMaio F, and Baker D (2018). Protein homology model refinement by large-scale energy optimization. Proc. Natl. Acad. Sci. U. S. A 115, 3054–3059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H, Lee GR, Kim DE, Anishchenko I, Cong Q, and Baker D (2019). High-accuracy refinement using Rosetta in CASP13. Proteins Struct. Funct. Bioinforma 87, 1276–1282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz A, Claxton DP, Kumar JP, Kazmier K, Bisignano P, Sharma S, Nolte SA, Liwag TM, Nayak V, Wright EM, et al. (2018). Conformational transitions of the sodium-dependent sugar transporter, vSGLT. Proc. Natl. Acad. Sci. U. S. A 115, E2742–E2751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilla KB, Leman JK, Otting G, and Huber T (2015). Capturing conformational states in proteins using sparse paramagnetic NMR data. PLoS One 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi Y, Lee J, Cheng X, Shen R, Islam SM, Roux B, and Im W (2020). CHARMM-GUI DEER facilitator for spin-pair distance distribution calculations and preparation of restrained-ensemble molecular dynamics simulations. J. Comput. Chem 41, 415–420. [DOI] [PubMed] [Google Scholar]
- Rohl CA, Strauss CEM, Chivian D, and Baker D (2004a). Modeling Structurally Variable Regions in Homologous Proteins with Rosetta. Proteins Struct. Funct. Genet 55, 656–677. [DOI] [PubMed] [Google Scholar]
- Rohl CA, Strauss CEM, Chivian D, and Baker D (2004b). Modeling Structurally Variable Regions in Homologous Proteins with Rosetta. Proteins Struct. Funct. Genet 55, 656–677. [DOI] [PubMed] [Google Scholar]
- Roney JP, and Ovchinnikov S (2022). State-of-the-Art Estimation of Protein Model Accuracy using AlphaFold. BioRxiv 2022.03.11.484043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaeffer RD, Kinch L, Kryshtafovych A, and Grishin NV (2021). Assessment of domain interactions in CASP14. Proteins Struct. Funct. Bioinforma [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitz C, Vernon R, Otting G, Baker D, and Huber T (2012). Protein structure determination from pseudocontact shifts using ROSETTA. J. Mol. Biol 416, 668–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sfriso P, Duran-Frigola M, Mosca R, Emperador A, Aloy P, and Orozco M (2016). Residues Coevolution Guides the Systematic Identification of Alternative Functional Conformations in Proteins. Structure 24, 116–126. [DOI] [PubMed] [Google Scholar]
- Shimada I, Ueda T, Kofuku Y, Eddy MT, and Wüthrich K (2018). GPCR drug discovery: Integrating solution NMR data with crystal and cryo-EM structures. Nat. Rev. Drug Discov 18, 59–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimamura T, Weyand S, Beckstein O, Rutherford NG, Hadden JM, Sharpies D, Sansom MSP, Iwata S, Henderson PJF, and Cameron AD (2010). Molecular basis of alternating access membrane transport by the sodium-hydantoin transporter Mhp1. Science (80-.) 328, 470–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons KT, Kooperberg C, Huang E, and Baker D (1997). Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J. Mol. Biol 268, 209–225. [DOI] [PubMed] [Google Scholar]
- Song Y, Dimaio F, Wang RYR, Kim D, Miles C, Brunette T, Thompson J, and Baker D (2013). High-resolution comparative modeling with RosettaCM. Structure 21, 1735–1742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Standfuss J, Edwards PC, D’Antona A, Fransen M, Xie G, Oprian DD, and Schertler GFX (2011). The structural basis of agonist-induced activation in constitutively active rhodopsin. Nature 471, 656–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein A, and Kortemme T (2013). Improvements to Robotics-Inspired Conformational Sampling in Rosetta. PLoS One 8, e63090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun YJ, Rose J, Wang BC, and Hsiao CD (1998). The structure of glutamine-binding protein complexed with glutamine at 1.94 Å resolution: Comparisons with other amino acid binding proteins. J. Mol. Biol 278, 219–229. [DOI] [PubMed] [Google Scholar]
- Thompson TB, Thomas MG, Escalante-Semerena JC, and Rayment I (1998). Three-dimensional structure of adenosylcobinamide kinase/adenosylcobinamide phosphate guanylyltransferase from Salmonella typhimurium determined to 2.3 Å resolution. Biochemistry 37, 7686–7695. [DOI] [PubMed] [Google Scholar]
- Thompson TB, Thomas MG, Escalante-Semerena JC, and Rayment I (1999). Three-dimensional structure of adenosylcobinamide kinase/adenosylcobinamide phosphate guanylyltransferase (CobU) complexed with GMP: Evidence for a substrate-induced transferase active site. Biochemistry 38, 12995–13005. [DOI] [PubMed] [Google Scholar]
- Tunyasuvunakool K, Adler J, Wu Z, Green T, Zielinski M, Žídek A, Bridgland A, Cowie A, Meyer C, Laydon A, et al. (2021). Highly accurate protein structure prediction for the human proteome. Nature 596, 590–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyka MD, Jung K, and Baker D (2012). Efficient sampling of protein conformational space using fast loop building and batch minimization on highly parallel computers. J. Comput. Chem 33, 2483–2491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viklund H, and Elofsson A (2008). OCTOPUS: Improving topology prediction by two-track ANN-based preference scores and an extended topological grammar. Bioinformatics 24, 1662–1668. [DOI] [PubMed] [Google Scholar]
- Wahlgren WY, Dunevall E, North RA, Paz A, Scalise M, Bisignano P, Bengtsson-Palme J, Goyal P, Claesson E, Caing-Carlsson R, et al. (2018). Substrate-bound outward-open structure of a Na+-coupled sialic acid symporter reveals a new Na+ site. Nat. Commun 9, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe A, Choe S, Chaptal V, Rosenberg JM, Wright EM, Grabe M, and Abramson J (2010). The mechanism of sodium and substrate release from the binding pocket of vSGLT. Nature 468, 988–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weyand S, Shimamura T, Yajima S, Suzuki SNI, Mirza O, Krusong K, Carpenter EP, Rutherford NG, Hadden JM, O’Reilly J, et al. (2008). Structure and molecular mechanism of a nucleobase-cation-symport-1 family transporter. Science (80-.) 322, 709–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woetzel N, Karakaş M, Staritzbichler R, Müller R, Weiner BE, and Meiler J (2012). BCL::Score-Knowledge Based Energy Potentials for Ranking Protein Models Represented by Idealized Secondary Structure Elements. PLoS One 7, e49242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia Y, Fischer AW, Teixeira P, Weiner B, and Meiler J (2018). Integrated Structural Biology for α-Helical Membrane Protein Structure Determination. Structure 26, 657–666.e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita A, Singh SK, Kawate T, Jin Y, and Gouaux E (2005). Crystal structure of a bacterial homologue of Na+/Cl --dependent neurotransmitter transporters. Nature 437, 215–223. [DOI] [PubMed] [Google Scholar]
- Yarov-Yarovoy V, Schonbrun J, and Baker D (2006). Multipass membrane protein structure prediction using Rosetta. Proteins Struct. Funct. Genet 62, 1010–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yip KM, Fischer N, Paknia E, Chari A, and Stark H (2020). Atomic-resolution protein structure determination by cryo-EM. Nature 587, 157–161. [DOI] [PubMed] [Google Scholar]
- Zheng W, and Brooks BR (2005). Normal-modes-based prediction of protein conformational changes guided by distance constraints. Biophys. J 88, 3109–3117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Demos on how to use CCM to model conformational changes of membrane and soluble proteins, related to STAR Methods.
Data Availability Statement
Reported data have been deposited at Zenodo and are publicly available as of the date of publication. DOIs are listed in the key resources table.
All original code is part of Rosetta software suite and can be found at “path/to/Rosetta/main/source/src/protocols/rbsegment_relax/ConfChangeMover”. Rosetta is available to all non-commercial users for free.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key Resources Table
| RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Demos, protein models, scripts, input files. | This paper | https://zenodo.org/record/6424150 or https://doi.org/10.5281/zenodo.6424150 |
| Software and algorithms | ||
| Rosetta | RosettaCommons | https://www.rosettacommons.org/software/academic |
| ChimeraX | UCSF | https://www.cgl.ucsf.edu/chimerax/ |
| MatPlotLib | MatPlotLib | https://github.com/matplotlib/matplotlib |
| Seaborn | Seaborn | https://github.com/mwaskom/seaborn |
| Excel | Microsoft | https://www.microsoft.com/en-us/microsoft-365/excel |


