Deeply tailored adaptive interventions to reduce college student drinking: A real-world application of Q-learning for SMART studies

Abstract

M-bridge was a sequential multiple assignment randomized trial (SMART) that aimed to develop a resource-efficient adaptive preventive intervention (API) to reduce binge drinking in first-year college students. The main results of M-bridge suggested no difference, on average, in binge drinking between students randomized to APIs versus assessment-only control, but certain elements of the API were beneficial for at-risk subgroups. This paper extends the main results of M-bridge through an exploratory analysis using Q-learning, a novel algorithm from the computer science literature. Specifically, we sought to further tailor the two aspects of the M-bridge APIs to an individual and test whether deep tailoring offers a benefit over assessment-only control. Q-learning is a method to estimate decision rules that assign optimal treatment (i.e., to minimize binge drinking) based on student characteristics. For the first aspect of the M-bridge API (when to offer), we identified the optimal tailoring characteristic post-hoc from a set of 20 candidate variables. For the second (how to bridge), we used a known effect modifier from the trial. The results of our analysis are two rules that optimize 1) the timing of universal intervention for each student based on their motives for drinking and 2) the bridging strategy to indicated interventions (i.e., among those who continue to drink heavily mid-semester) based on mid-semester binge drinking frequency. We estimate that this newly tailored API, if offered to all first-year students, would reduce binge drinking by 1 occasion per 2.5 months (95% CI: decrease of 1.45 to 0.28 occasions, p<0.01) on average. Our analyses demonstrate a real-world implementation of Q-learning for a substantive purpose, and, if replicable in future trials, our results have practical implications for college campuses aiming to reduce student binge drinking.

Introduction

Binge drinking (defined as consuming 4+/5+ alcoholic drinks for females/males on an occasion; NIAAA, 2020) is a prevalent public health problem among first-year college students in the U.S. that can lead to harmful short- and long-term consequences (Fromme et al., 2008; Hingson et al., 2009; Patrick, Schulenberg, et al., 2011; Schulenberg et al., 2019). Empirically supported interventions to reduce college alcohol use include those that are intended for an entire student body (i.e., universal) and interventions specifically for students who show signs of problematic drinking (i.e., indicated). Adaptive preventive interventions (APIs), which alter the intensity, type, or delivery mode of an intervention over time based on changing student needs (Nahum-Shani et al., 2017), are a promising framework to transition students from universal to indicated interventions as needed.

The M-bridge study was a sequential multiple assignment randomized trial (SMART; a study design used to answer scientific questions about APIs). M-bridge was one of the first trials to examine APIs for reduction of binge drinking by applying a series of existing interventions in a “light-touch,” technology-based approach (Patrick et al., 2020, 2021). An example of an API embedded in the M-bridge study is: Have first-year college students begin a universal intervention before their first semester; then, bridge students identified as heavy drinkers to indicated interventions via a resource email. Main outcomes of M-bridge suggested no difference, on average, in binge drinking frequency between students randomized to APIs versus assessment-only control and no difference among the four APIs embedded in the SMART design. However, it is possible that, had the APIs been more personalized or deeply tailored to student needs, they might have led to greater reductions in binge drinking. The goal of the present study is to identify the optimal approach to personalizing the M-bridge APIs.

Indeed, moderator analyses from the M-bridge main outcomes analysis showed that APIs reduced binge drinking for students who were planning to pledge into fraternities and sororities, and mid-semester binge drinking modified the effect of a mid-semester intervention in heavy-drinking students, such that a resource email linking these students to indicated interventions was more beneficial than an online health coach. An example of an API that is more personalized or deeply tailored is: Have first-year college students who intend to pledge to a fraternity or sorority begin a universal intervention before their first semester, but offer the universal intervention to all other students after the semester begins; then, bridge students identified as heavy drinkers to indicated interventions via a resource email. This API is more deeply tailored because the timing of the universal intervention depends on student characteristics (i.e., intention to pledge Greek life). An open question that was not answered in the M-bridge main outcomes analysis is whether more personalization (i.e., deep tailoring) of the APIs would lead to lower binge drinking frequency on average across all students, relative to assessment-only control.

This paper is the follow-up in our series of papers on the M-bridge trial. In this paper, we conduct exploratory analyses that apply Q-learning to develop a new, deeply tailored API for binge drinking prevention in first-year college students using data from the M-bridge SMART. Q-learning is a backward induction algorithm from computer science literature that models the “quality” (hence, Q) of interventions over time to construct optimal (e.g., to minimize binge drinking), deeply tailored (e.g., dependent on student characteristics and behaviors) decision rules for intervention assignment at each stage of an API (Nahum-Shani et al., 2012, 2017; Watkins, 1989). In practice, Q-learning may be applied to data from a SMART to explore effect modification at multiple stages and build a more deeply tailored API for evaluation in subsequent confirmatory trials (Nahum-Shani et al., 2019).

In this exploratory analysis, we develop decision rules that would define a new, deeply tailored API to minimize past-month binge drinking frequency at the end of fall semester, using only one tailoring variable per stage so that the API may be practical to implement. Our paper builds on existing Q-learning tutorials (Nahum-Shani et al., 2012, 2017) by providing a substantive, real-world analysis with special considerations for variable selection, missing data, and comparison of average outcomes under an estimated API from Q-learning with outcomes under a non-adaptive control condition.

Methods

Study design and interventions

The current analysis builds on the main outcomes of the previously published M-bridge SMART study (Patrick et al., 2020, 2021), which was designed to answer key questions about 1) when a universal preventive intervention should be offered to incoming college students and 2) which strategy should be used to transition students to indicated interventions, if needed. The M-bridge trial randomly assigned 1/3 (n=300) of enrolled students to an assessment-only control condition, in which they did not receive an API but participated in study surveys in August (i.e., baseline) and December 2019. The remaining 2/3 (n=591) of students received a universal intervention that combined web-based personalized normative feedback (PNF) with biweekly self-monitoring, which facilitated self-reflection and ongoing data collection. To answer the study’s first question, students in the intervention group were randomized 1:1 in Stage 1 to receive PNF and start self-monitoring in August (before classes started; early) or September (after classes started; late).

If students reported heavy drinking in the past two weeks on the self-monitoring surveys, they flagged as “heavy drinkers” and were assigned a bridging strategy to indicated interventions. Heavy drinking was defined as 2+ occasions of binge drinking (4+/5+ drinks in for females/males) or 1+ occasion of high-intensity drinking (8+/10+ drinks for females/males) (Patrick et al., 2021). That is, the M-bridge study included an embedded tailoring variable (self-monitored heavy drinking), which triggered the attempt to bridge students to indicated interventions; this element is what makes the M-bridge intervention strategies adaptive. To answer the study’s second question, the students who flagged as heavy drinkers were re-randomized 1:1 in Stage 2 to receive an invitation to chat with an online health coach or a resource email. The two randomizations at Stage 1 and Stage 2 result in four embedded APIs: early/coach, early/email, late/coach, and late/email (Figure 1). As part of this design, only students who flagged as heavy drinkers received a bridging strategy.

Fig. 1.

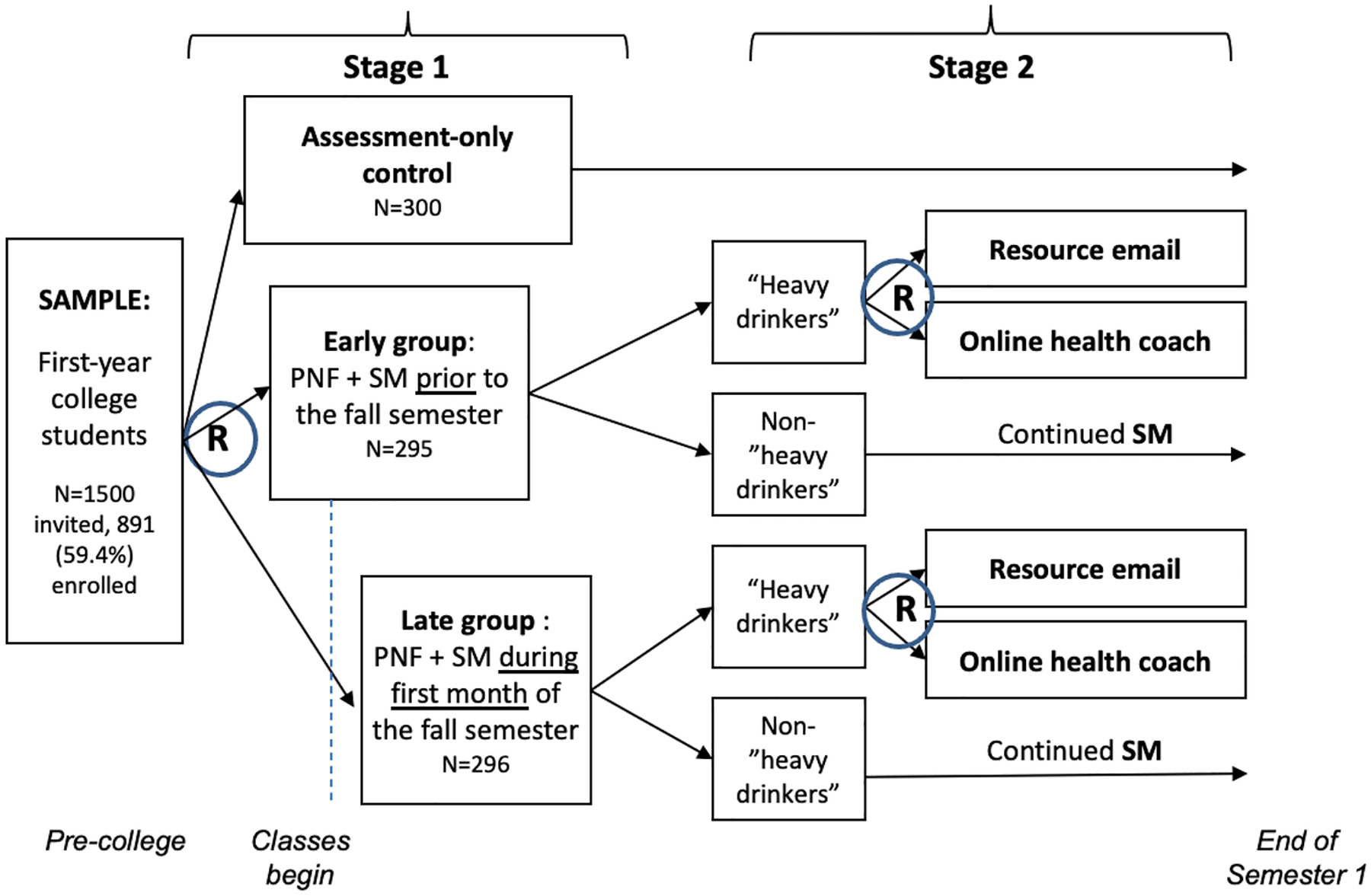
M-bridge study design

Measures

Outcome:

The outcome was frequency of binge drinking at the end of fall semester. On both the baseline (August) and December surveys, females/males reported the number of occasions they consumed 4+/5+ drinks within two hours in the past 30 days. Options were none, 1, 2, 3–5, 6–9, or 10+ times, recoded as 0, 1, 2, 4, 7, and 10, as in Patrick et al. (2021).

Stage 1 tailoring variable:

As described below, we present Q-learning results for the optimal Stage 1 tailoring variable of 20 that were considered (i.e., the variable that minimized average binge drinking frequency), which was the Drinking Motives Questionnaire (DMQ) (Cooper, 1994). The DMQ asks students to rate how often they drink for each of 20 reasons, from 1=“almost never/never” to 5=“almost always/always.” The reasons can be partitioned into four subscales with five items each: Conformity (α=0.82; e.g., “because your friends pressure you to drink”), social (α=0.89; e.g., “because it helps you enjoy a party”), enhancement (α=0.87; e.g., “because it’s fun”), and coping (α=0.81; e.g., “to forget your worries”). We dealt with missing values by imputing with the person-mean for the subscale if two or fewer items in the subscale were missing (Downey & King, 1998; Gilson et al., 2013); this affected six students. Scores are computed by summing the responses in each subscale. The M-bridge baseline survey included the DMQ for students who reported drinking alcohol before coming to college; students who reported not drinking before college were handled separately in the analysis.

Stage 2 tailoring variable:

A useful Stage 2 tailoring variable will qualitatively modify the effect of coach vs. email for heavy drinkers. Mid-semester binge drinking, measured as two-week binge drinking frequency from the student’s final self-monitoring survey, was proposed a priori and found to significantly modify the effect of coach vs. email in Patrick et al. (2021), with heavier drinkers benefitting more from the resource email compared to coach invitation. Therefore, we used this measure, recoded like the outcome variable, to tailor bridging strategy.

Q-learning algorithm for estimation of optimal decision rules

We ran the Q-learning algorithm for each of 20 proposed Stage 1 tailoring variables. Briefly, the steps of Q-learning were as follows: To first estimate the Stage 2 rule for assignment of optimal bridging strategy, we fit a model for December binge drinking frequency among heavy drinkers. Then, we used this model to determine the optimal bridging strategy for each heavy drinker and calculate their expected binge drinking frequency had they received that strategy. To estimate the Stage 1 rule for assignment of optimal timing, we fit a second model for December binge drinking frequency including non-heavy drinkers, which used the expected binge drinking frequency given optimal bridging strategy as the outcome for heavy drinkers. Decision rules were constructed using the estimated coefficients from these two models. In the next two sections, we describe this approach in greater statistical detail.

Step 1 - Estimate Stage 2 Q-function Using Standard Regression Methods:

Q-functions are conditional expectations that target the “quality” (hence, Q) of each intervention conditional on receiving the optimal intervention at all future stages (Barto & Sutton, 1992). Our Stage 2 Q-function was Q₂ (h₂, a₂) = E (Y|H₂ = h₂, A₂ = a₂), where Y is end-of-semester (December) binge drinking frequency, A₂ is bridging strategy (coded 1 for coach and −1 for email), and H₂ is covariate history prior to bridging strategy assignment (i.e., baseline binge drinking frequency, timing of universal intervention, Stage 1 tailoring variable, and mid-semester binge drinking). We posited the model $\text{log }{Q}_2\left(h_2,a_2;{\beta }_2,{\psi }_2\right)= {\beta }_2^T{h}_{20}+\left({\psi }_2^T{h}_{21}\right)a_2$, where h₂₁ includes an intercept and mid-semester binge drinking frequency. That is, we fit a log-linear model for December binge drinking frequency among heavy drinkers, conditional on baseline binge drinking frequency, timing (early vs. late), bridging strategy (coach vs. email), both tailoring variables, and their two-way interactions with timing and bridging strategy.

This model determined the optimal bridging strategy for all heavy drinkers in the data. Specifically, if ${\psi }_2^T{h}_{21}$ is positive, setting A₂ = −1 (email) will minimize expected binge drinking frequency; if ${\psi }_2^T{h}_{21}$ is negative, setting A₂ = 1 (coach) will. Thus, the optimal Stage 2 rule is $d_2\left(h_{21};{\psi }_2\right)=-\mathit{\text{sign}}\left({\psi }_2^T{h}_{21}\right)$, where sign (x) = 1 if x > 0 and −1 if x < 0. Let ${\widehat{\psi }}_2$ denote the maximum likelihood estimate of ψ₂.

Step 2 - Estimate Stage 1 Q-function Using Standard Regression Methods:

Our next step was to estimate $Q_1\left(h_1,a_1\right)=E({\text{min}}_{a_2}{Q}_2\left(h_2,a_2\right)|H_1=h_1,A_1=a_1)$, where H₁ is covariate history prior to Stage 1 intervention (i.e., baseline binge drinking frequency, Stage 1 tailoring variable) and A₁ is timing (coded 1 for early and −1 for late). Q₁ (h₁, a₁) is the average binge drinking frequency we would expect if the optimal bridging strategy were assigned to each heavy drinker in Stage 2. We posited the model $\text{log }{Q}_1\left(h_1,a_1;{\beta }_1,{\psi }_1\right)={\beta }_1^T{h}_{10}+\left({\psi }_1^T{h}_{11}\right)a_1$, where h₁₁ includes an intercept and the Stage 1 tailoring variable. That is, we fit a log-linear model for December binge drinking frequency conditional on baseline binge drinking frequency, timing, the Stage 1 tailoring variable, and the interaction of the Stage 1 tailoring variable with timing. To fit this model, we used $Q_2\left(h_2,d_2\left(h_{21};{\widehat{\psi }}_2\right);{\widehat{\beta }}_2,{\widehat{\psi }}_2\right)$ as the outcome variable for heavy drinkers and Y as the outcome variable for non-heavy drinkers, who did not receive a bridging strategy to optimize. The optimal Stage 1 rule is $d_1\left(h_{11};{\psi }_1\right)=-\mathit{\text{sign}}\left({\psi }_1^T{h}_{11}\right)$.

Variable selection:

A useful Stage 1 tailoring variable will qualitatively modify the effect of early vs. late universal intervention. Patrick et al. (2021) did not find any significant moderators of the effect of timing among a pre-specified list, so we considered 20 candidate variables for Stage 1 tailoring. The 20 variables included demographics (e.g., sex, race) and other factors that are theoretically and empirically associated with heavy alcohol use (e.g., motivations, perceived norms, plans to pledge Greek life; full list in Online Resource 1). We ran the Q-learning algorithm for each of the 20 different tailoring variables. We present Q-learning results for the optimal Stage 1 tailoring variable by value, which was the Drinking Motives Questionnaire (DMQ) (Cooper, 1994) (see Value of estimated APIs compared to control).

Missing Data:

To minimize bias due to missingness, we estimated the Q₂ and Q₁ functions in each of the 10 multiply imputed datasets that were generated for the M-bridge main outcomes paper (Patrick et al., 2021), and coefficients were averaged across imputed datasets. Let ${\widehat{\psi }}_{2,imp}$ and ${\widehat{\psi }}_{1,imp}$ denote the averaged coefficients; decision rules were estimated by $d_2\left(h_{21};{\widehat{\psi }}_{2,imp}\right)$ and $d_1\left(h_{11};{\widehat{\psi }}_{1,imp}\right)$. To perform inference on the averaged coefficients, we drew 1,000 bootstrap samples from each imputed dataset, ran Q-learning in each bootstrap sample, then pooled the resulting 10,000 estimates of the Q₁ and Q₂ coefficients to get percentile-based confidence intervals (Schomaker & Heumann, 2018).

Nonregularity:

Much has been written about nonregularity of the Q₁ coefficients (Chakraborty et al., 2010, 2013; Laber et al., 2014), which can cause the standard bootstrap to perform poorly. This nonregularity, however, exists only when there is a subset of students for whom the Stage 2 intervention has no effect (i.e., no difference between email and coach), which is unlikely when the Stage 2 tailoring variable is continuous (Laber et al., 2014). We, therefore, used standard n-out-of-n bootstrap methods to compute Q₁ coefficient confidence intervals.

Value of estimated APIs compared to control

The value of an intervention strategy is the expected outcome if the strategy were applied to the population from which data were drawn. In our analysis, the value is average binge drinking frequency; therefore, lower values are better. Let $V^{\widehat{d}}$ be the true value of estimated API $\widehat{d}$. Chakraborty et al. (2014) proposed an inverse-probability-weighted (IPW) estimator of $V^{\widehat{d}}$:

$${\widehat{V}}^{\widehat{d}}=\frac{1}{n}\sum _{i=1}^n\frac{Y_i\times I\left(A_{1i}={\widehat{d}}_1\left(H_{1i}\right),A_{2i}={\widehat{d}}_2\left(H_{2i}\right)\right)}{\text{Pr}(A_{1i}|H_{1i})\times \text{Pr}(A_{2i}|H_{2i})}$$

where n is the number of students who received an API and Pr(A_1i|H_1i) and Pr(A_2i|H_2i) are the probabilities of student i receiving their assigned interventions at Stage 1 and 2, respectively, conditional on their covariate history at the two time points. The indicator function $I\left(A_{1i}={\widehat{d}}_1\left(H_{1i}\right),A_{2i}={\widehat{d}}_2\left(H_{2i}\right)\right)$ equals 1 for so-called “lucky” students who, by chance, received the interventions they would have been assigned under the estimated API and 0 for students who did not receive their API-specified intervention for at least one of the stages. In our analysis, all non-heavy drinkers, who were not offered a bridging strategy, are lucky by default at Stage 2. Thus, ${\widehat{V}}^{\widehat{d}}$ is a weighted average of end-of-semester binge drinking frequency among the lucky students.

To absorb residual imbalances between randomized groups, we estimated intervention probabilities with two logistic regression models: 1) a model for timing conditional on baseline binge drinking frequency and maximum drinks consumed in 24 hours and 2) a model for bridging strategy conditional on timing and both baseline and mid-semester binge drinking frequency (Nahum-Shani et al., 2020). For non-heavy drinkers, Pr(A_2i|H_2i) = 1 and need not be estimated. The logistic regressions were re-fit in each imputed dataset to compute ${\widehat{V}}_j^{{\widehat{d}}_{imp}}$, the value of ${\widehat{d}}_{imp}=\left\{d_1\left(H_{11};{\widehat{\psi }}_{1,imp}\right),d_2\left(H_{21};{\widehat{\psi }}_{2,imp}\right)\right\}$ in the jth imputed dataset. The overall value was estimated by the average across imputed datasets, ${\widehat{V}}_{imp}^{{\widehat{d}}_{imp}}=\frac{1}{10}\sum _{j=1}^{10}{\widehat{V}}_j^{{\widehat{d}}_{imp}}$.

Inference on ${\widehat{V}}_{imp}^{{\widehat{d}}_{imp}}$ is complicated by the fact that $V^{{\widehat{d}}_{imp}}$ is a data-dependent parameter and standard methods to calculate confidence intervals, such as normal approximations or the n-out-of-n bootstrap, are inconsistent. This can result in confidence intervals that are too small and, for testing, overly optimistic p-values. Therefore, we used the m-out-of-n bootstrap proposed by Chakraborty et al. (2014), where m is a resample size smaller than n and is selected using a data-adaptive double bootstrap procedure detailed in the appendix of that manuscript. In brief, the double bootstrap procedure estimates coverage for each resample size across a grid of decreasing resample sizes, and when the nominal coverage is achieved, m is set to that resample size. Because the double bootstrap is computationally intensive, we conducted this search in one imputed dataset, then validated the choice of m in a second imputed dataset. Ultimately, we chose m to be 514 (out of n=591) and drew 1,000 samples of size m with replacement from each of the imputed datasets to compute percentile-based confidence intervals for both $V^{{\widehat{d}}_{imp}}$ and its contrast with the value of assessment-only control (details in Online Resource 2).

For comparison, we also estimated mean binge drinking frequency in the pooled API group and under each of the four embedded APIs. The pooled API mean can be viewed as the value of a stochastic intervention that assigns the four embedded APIs with the study probabilities; we combined averages across imputed datasets using Rubin’s rules (Rubin, 1987) and compared with the value of assessment-only control using an unequal-variance t-test. Unlike an estimated API, an embedded API has fixed rules (i.e., d₁ and d₂ instead of ${\widehat{d}}_1$ and ${\widehat{d}}_2$), so standard inferential methods can be used (Chakraborty et al., 2014). We estimated V^d for each embedded API by replacing ${\widehat{d}}_1$ and ${\widehat{d}}_2$ in the IPW estimator with the appropriate d₁ and d₂ and used the n-out-of-n bootstrap to compute percentile-based confidence intervals.

All confidence intervals were inverted to get two-sided p-values. All analyses were conducted in R version 3.6.2 (R Foundation for Statistical Computing, Vienna, Austria).

Results

After examining 20 candidate variables, we identified the Drinking Motives Questionnaire (DMQ) as the optimal Stage 1 tailoring variable because the DMQ minimized average binge drinking frequency (i.e., yielded the lowest value). Among the 357 students in the API group who drank at baseline, social and enhancement reasons to drink were greater motivators than conformity and coping reasons (Figure 2). Detailed Q-learning results for the DMQ follow, with a summary of all 20 possible tailoring variables in Online Resource 1.

Fig. 2.

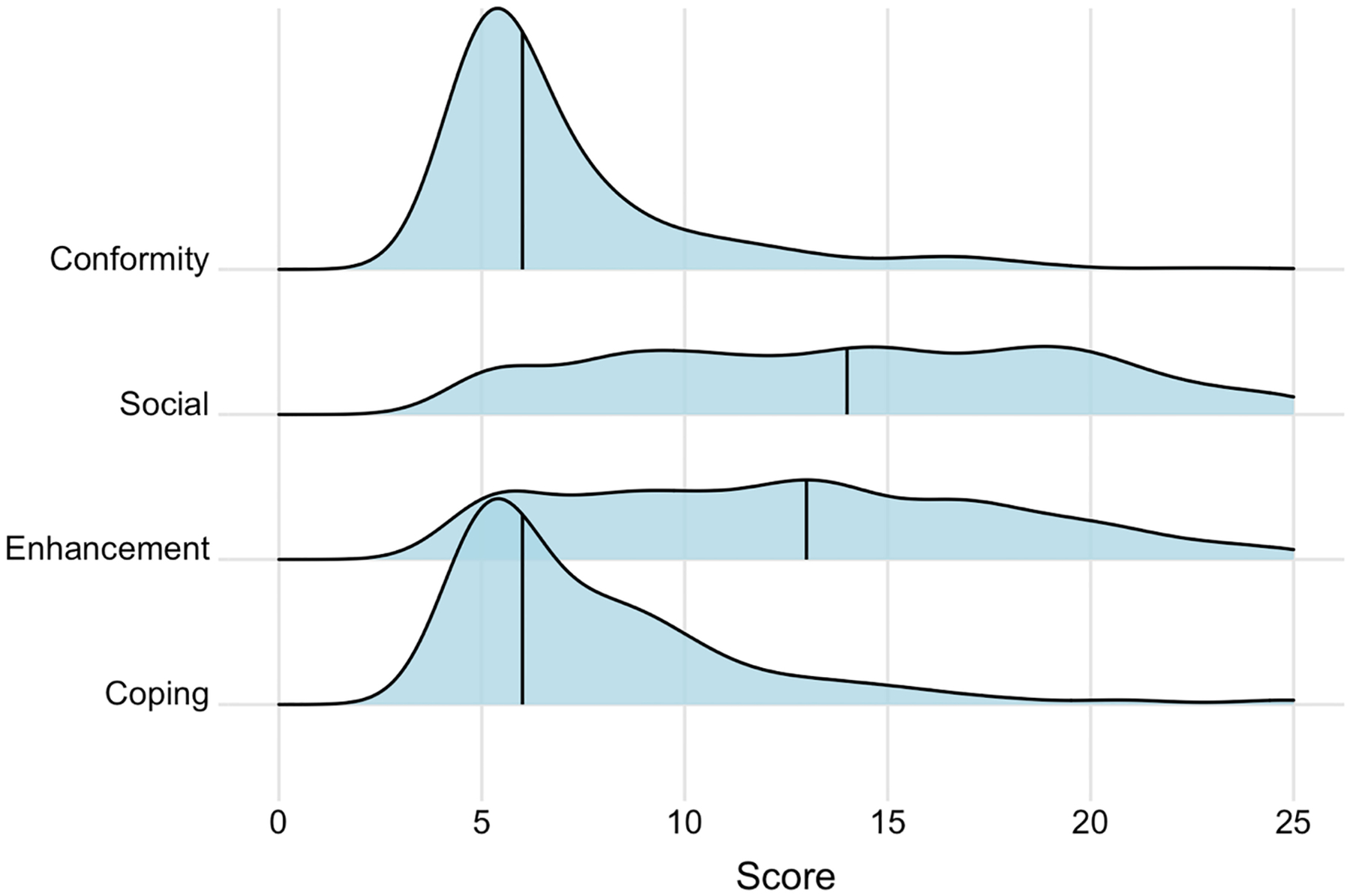
Density plots of Drinking Motives Questionnaire scores among students who drank at baseline and were randomized to an API (n=357)

Note: Vertical lines are drawn at the median (conformity: 6, social: 14, enhancement: 13, and coping: 6).

When the DMQ was the Stage 1 tailoring variable, we found the following: For participants who were not pre-college drinkers, the ratio of expected binge drinking occasions per month between the early and late intervention groups was essentially null (ratio [95% CI] = 1.00 [0.45, 2.20], p=0.98) (Table 1). For pre-college drinkers, early intervention was somewhat more effective for students with higher conformity and social scores, and somewhat less effective for students with higher enhancement and coping scores, given that heavy drinkers were assigned the optimal bridging strategy. For example, when conformity and social scores were set to their 25th percentile and other scores to their median, the ratio of expected December binge drinking occasions for early vs. late was 1.08 (0.68, 1.72; somewhat less binge drinking for late). When conformity and social scores were increased to their 75th percentile, this ratio decreased to 0.61 (0.35, 0.97; less binge drinking for early). In contrast, when enhancement and coping scores were increased from their 25th percentile to their 75th percentile, holding other scores at their median, the ratio of expected December binge drinking occasions for early vs. late increased from 0.65 (0.38, 1.02; less binge drinking for early) to 1.15 (0.79, 1.70; somewhat less binge drinking for late) (Figure 3). The overall test for the DMQ interactions with timing was not statistically significant (p=0.32).

Table 1.

Estimated coefficients and standard errors for the Stage 1 Q-function (n=591, pooled across 10 multiply imputed datasets with 1,000 bootstraps per imputed dataset)

Term	Coef.	Bootstrap SE	Percentile 95% CI - lower	Percentile 95% CI - upper	P-value
(Intercept)	−1.324	0.19	−1.78	−1.03	<0.001
Baseline binge drinking frequency (per 30 days)	0.161	0.04	0.11	0.25	<0.001
A1 (1=early, −1=late)	−0.002	0.20	−0.40	0.39	0.98
D (1=pre-college drinker, 0=non-drinker)	0.985	0.28	0.47	1.55	<0.001
D * conformity score	−0.015	0.02	−0.06	0.03	0.51
D * social score	0.019	0.02	−0.02	0.06	0.34
D * enhancement score	0.028	0.02	−0.01	0.06	0.12
D * coping score	−0.010	0.02	−0.05	0.02	0.48
A1 * D	−0.086	0.30	−0.68	0.51	0.76
A1 * D * conformity score	−0.016	0.02	−0.06	0.03	0.46
A1 * D * social score	−0.024	0.02	−0.07	0.01	0.20
A1 * D * enhancement score	0.017	0.02	−0.02	0.05	0.32
A1 * D * coping score	0.034	0.02	0.00	0.07	0.07

Fig. 3.

Ratio of expected number of December binge drinking occasions under early vs. late intervention for students who drank alcohol at baseline (n=357) with one-standard-error shading, by DMQ subscale scores

Note: The outcome is end-of-semester binge drinking frequency given that heavy drinkers receive their optimal bridging strategy. If the ratio of this outcome under early vs. late intervention is above 1, early leads to more binge drinking and late is better. If the ratio is below 1, early is better. To compute ratios across the range of one of the subscales, all other DMQ scores were set to their median (conformity: 6, social: 14, enhancement: 13, coping: 6).

In Stage 2, we estimated that the resource email was more effective for heavy drinkers with higher mid-semester binge drinking frequencies, though the Q-function interaction was also not statistically significant (p=0.10) (Table 2). For example, when heavy drinkers’ mid-semester binge drinking was increased from one time per week (25th percentile) to two times per week (75th percentile), the ratio of expected December binge drinking occasions for coach vs. email increased from 1.05 (0.70, 1.52) to 1.33 (1.04, 1.93) (Figure 4).

Table 2.

Estimated coefficients and standard errors for the Stage 2 Q-function in heavy drinkers (n=158, pooled across 10 multiply imputed datasets with 1,000 bootstraps per imputed dataset)

Term	Coef.	Bootstrap SE	Percentile 95% CI - lower	Percentile 95% CI - upper	P-value
(Intercept)	0.325	0.59	−0.35	0.80	0.30
Baseline binge drinking frequency (per 30 days)	0.099	0.05	0.03	0.23	0.01
A1 (1=early, −1=late)	0.193	0.59	−0.23	0.80	0.39
D (1= pre-college drinker, 0=non-drinker)	0.042	0.65	−0.66	0.87	0.86
D * conformity score	−0.021	0.03	−0.07	0.03	0.44
D * social score	0.021	0.02	−0.02	0.05	0.37
D * enhancement score	−0.016	0.02	−0.06	0.02	0.50
D * coping score	0.012	0.02	−0.03	0.05	0.70
A2 (1=coach, −1=email)	−0.094	0.18	−0.49	0.22	0.47
Mid-semester binge drinking frequency (per two weeks)	0.077	0.05	−0.03	0.16	0.12
A1 * D	−0.097	0.66	−0.92	0.64	0.83
A1 * D * conformity score	−0.044	0.03	−0.10	0.00	0.06
A1 * D * social score	−0.009	0.02	−0.05	0.03	0.55
A1 * D * enhancement score	0.004	0.02	−0.04	0.05	0.81
A1 * D * coping score	0.033	0.02	0.00	0.08	0.06
A2 * mid-semester binge drinking frequency	0.059	0.05	−0.01	0.18	0.10

Fig. 4.

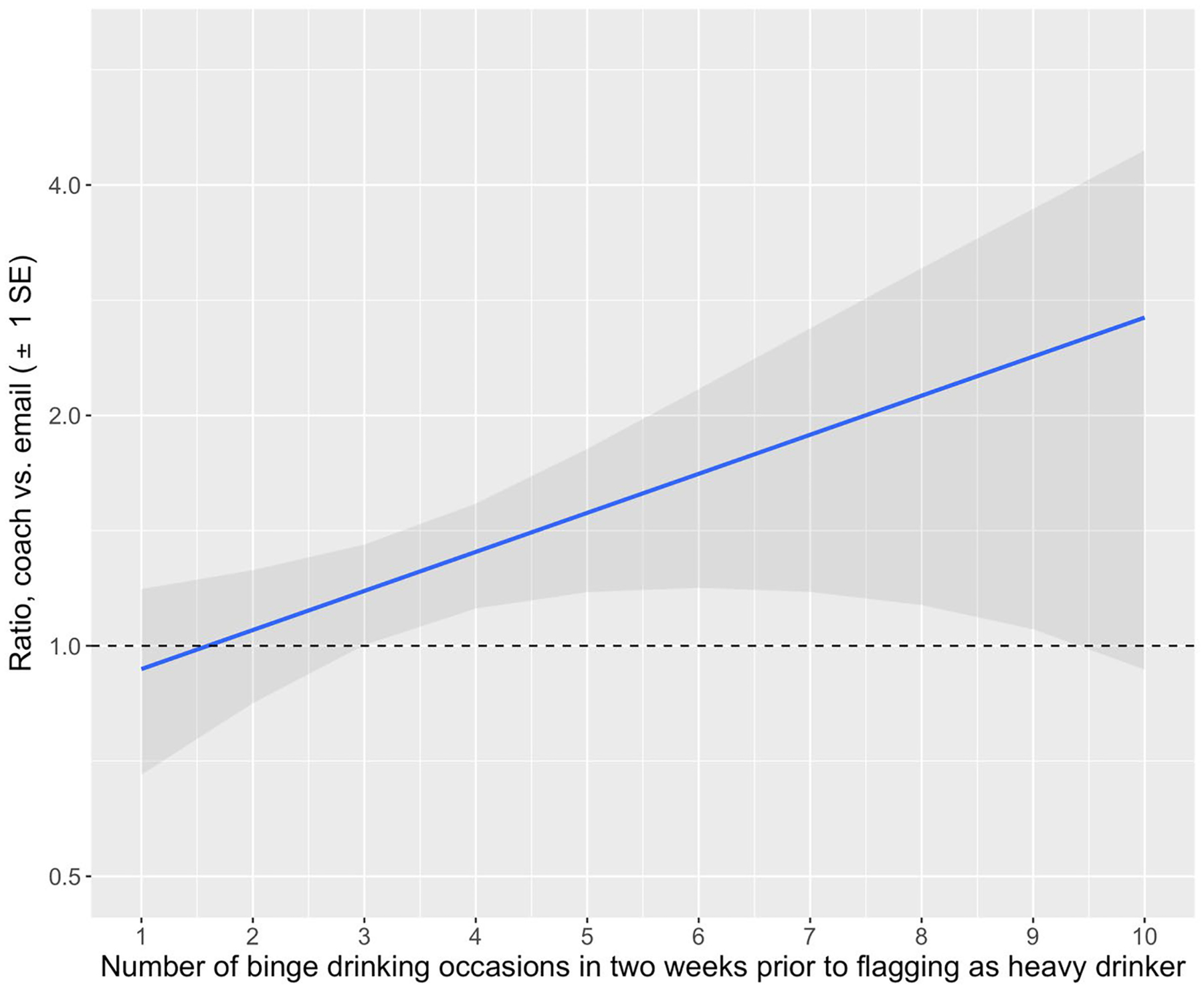
Ratio of expected number of December binge drinking occasions under coach vs. email among heavy drinkers (n=158) with one-standard-error shading

Note: If the ratio of binge drinking frequency under coach invitation vs. resource email is above 1, coach leads to more binge drinking and email is better. If the ratio is below 1, coach is better.

Using the estimated Q-function coefficients, we constructed two linear decision rules to assign the optimal intervention at each stage of the API. The estimated optimal Stage 1 rule was:

$$\begin{gathered} \text{If student does not drink alcohol at baseline:} \\ \text{Assign early intervention}. \\ \text{If student drinks alcohol at baseline:} \\ \text{AND if}-\left(160\times DM{Q}_{\mathit{\text{conformity}}}\right)-\left(240\times DM{Q}_{\mathit{\text{social}}}\right)+\left(168\times DM{Q}_{\mathit{\text{enhancement}}}\right)+ \left(339\times DM{Q}_{\mathit{\text{coping}}}\right)> 877: \\ \text{Assign late\hspace{0.17em}intervention}. \\ \text{\hspace{1em}Otherwise:} \\ \text{Assign early intervention}. \end{gathered}$$ (1)

In M-bridge, this rule would have assigned 503/591 (85.1%) students in the API group to early intervention and 88 (14.9%) to late intervention. For students who subsequently flagged as heavy drinkers, the estimated optimal Stage 2 rule was:

$$\begin{gathered} \text{If student binge drank 2+ times in the past two weeks:} \\ \text{Assign email}. \\ \text{Otherwise:} \\ \text{Assign coach}. \end{gathered}$$ (2)

To be flagged as a heavy drinker, a student must report at least one occasion of high-intensity drinking or at least two of binge drinking in the past two weeks, so this rule assigns coach only to those who flagged for one occasion of high-intensity drinking. In M-bridge, this rule would have assigned 7/158 (4.4%) heavy drinkers to coach and 151 (95.6%) to email.

Estimated values of APIs (i.e., the expected number of binge-drinking occasions per month if the API were offered to all students) are summarized and compared with assessment-only control in Table 3. Binge drinking frequency was not significantly different from control in the pooled API group (p=0.61), which is consistent with the main analysis of the M-bridge study (Patrick et al., 2021). Likewise, none of the embedded APIs had significantly better value than control. The deeply tailored API built from Q-learning, however, had a significantly lower estimated average binge drinking frequency (0.71 [0.54, 0.91] times per month) than control (difference=−0.41 (−0.69, −0.12), p=0.005). To isolate the effects of the Stage 1 and Stage 2 Q-learning rules, we also estimated the value of APIs that used only one of the deeply tailored rules from Q-learning and assigned the optimal intervention for most students at the other stage. We found that a deeply tailored API using only the Stage 1 rule (based on the DMQ) and assigning resource email to all heavy drinkers had an estimated value nearly identical to the API using both rules and was also significantly better than control (p=0.003). A deeply tailored API using only the Stage 2 rule (based on heavy drinkers’ mid-semester binge drinking frequency) and assigning early intervention to all students was no better than control (p=0.43).

Table 3.

Estimated average number of December binge drinking occasions (value) under embedded and deeply tailored APIs compared to assessment-only control

Intervention	Value (95% CI)	Difference from control (95% CI)	P-value for difference
Control	1.12 (0.91, 1.33)	—	—
Pooled APIs	1.05 (0.90, 1.20)	−0.07 (−0.33, 0.19)	0.61
Embedded APIs
Early/coach	1.01 (0.79, 1.25)	−0.11 (−0.42, 0.20)	0.47
Early/email	1.01 (0.78, 1.27)	−0.12 (−0.43, 0.22)	0.50
Late/coach	1.24 (0.99, 1.51)	0.12 (−0.20, 0.47)	0.47
Late/email	0.98 (0.75, 1.23)	−0.15 (−0.46, 0.18)	0.37
Deeply tailored APIs
Both rules –   Stage 1: Use DMQ to assign   Stage 2: Use mid-semester binge drinking frequency to assign	0.71 (0.54, 0.91)	−0.41 (−0.69, −0.12)	0.005
Stage 1 rule only –   Stage 1: Use DMQ to assign   Stage 2: Email	0.70 (0.52, 0.90)	−0.43 (−0.71, −0.14)	0.003
Stage 2 rule only –   Stage 1: Early   Stage 2: Use mid-semester binge drinking frequency to assign	0.99 (0.74, 1.27)	−0.13 (−0.47, 0.21)	0.43

Note: The two APIs (both deeply tailored) that resulted in significantly lower average binge drinking frequency compared to assessment-only control are shaded in gray.

Discussion

In this paper, we implement Q-learning to answer a substantive question motivated by the main outcomes of M-bridge (Patrick et al., 2021): Would deep tailoring of the M-bridge interventions reduce binge drinking more than assessment-only control? Our exploratory analysis builds on existing Q-learning tutorials, which typically assume that useful tailoring variables are known in advance and have not addressed how to compare an estimated API with a non-adaptive control group. To the best of our knowledge, this paper is one of the first to apply Q-learning, an innovative method from computer science, to a real-world trial in substance use research (Agniel et al., 2020; Nahum-Shani et al., 2017) and the first to compare the resulting estimated APIs with a non-adaptive control group from a randomized trial.

In this paper, we sought to develop a more deeply tailored API for binge drinking prevention for comparison with control. Given that no useful Stage 1 tailoring variable was known a priori, we identified the optimal tailoring variable by running Q-learning separately for 20 proposed tailoring variables and choosing the variable that minimized average binge drinking frequency (i.e., value). The resulting API is characterized by two rules, detailed in Equations 1 and 2, which depend on pre-college DMQ subscale scores and, for students flagged as heavy drinkers, their past two-week binge drinking frequency. We estimate that use of these rules would reduce binge drinking frequency by about 1 occasion per 2.5 months, on average, compared to assessment-only control (95% CI: decrease of 1.45 occasions to decrease of 0.28 occasions, p=0.005). This reduction was apparently driven by the Stage 1 rule, i.e., the rule that assigns when to intervene based on student drinking motives, because the API using both rules and the API using only the Stage 1 rule had nearly identical results (Table 3). In a population with a higher proportion of students who are flagged for one occasion of high-intensity drinking, the Stage 2 rule might offer more benefit. If our results can be replicated in future trials, these decision rules could be used by college campuses to more effectively deliver existing technology-based interventions for reduction of binge drinking.

We found that intervening early may benefit students motivated by conformity or social reasons to drink, while intervening later may be more effective for those motivated by enhancement and coping, with the strongest associations for social and coping reasons. This finding is novel and consistent with previous calls for targeting interventions based on drinking motives (Coffman et al., 2007; Patrick, Lee, et al., 2011). For students who are primarily trying to fit in (conformity) or be social (social motives), alcohol is a way to connect with friends and socialize. These students might have certain expectations or perceptions (i.e., overestimations) about how much their peers are drinking, and early intervention might be needed to correct these expectations or misperceptions to be more in line with reality before student behaviors are set in a new context. Prior research has shown stronger relations between perceived norms and alcohol consumption among college students with higher social motives to drink (Lee et al., 2007), as well as greater effectiveness of PNF for these students (Neighbors et al., 2004). If students with social drinking motives enter the college environment armed with the knowledge that most of their peers are drinking less than they thought, they might engage in healthier behaviors. On the other hand, students who drink to feel the intoxicating effects of alcohol (enhancement) or deal with life’s stressors (coping) might not plan their alcohol use before arriving at college. In fact, these students might have increased their alcohol use during the transition to college for problematic reasons. As a result, the normative information and self-reflection prompted by a monitoring intervention might be more salient once these students have experienced the onset of additional stressors during the first semester of college. We observed no difference between early vs. late intervention among the students who did not drink alcohol before college, which might reflect the lower risk level of these students, who were much less likely to binge drink at the end of fall semester. In practice, colleges might wish to offer the universal intervention to these students at whichever time point is most logistically straightforward for the campus.

Our paper also highlights the innovative design of the M-bridge study and offers several innovations from a statistical methods perspective. For one, we evaluated potential Stage 1 tailoring variables based on the value of resulting APIs (see Online Resource 1), rather than the significance of Q-function interactions (as in Nahum-Shani et al., 2012, 2017), and illustrated that a significant improvement over control is possible without statistically significant interactions. We demonstrated how to do inference on the value of an estimated API using the m-out-of-n bootstrap when standard inferential methods such as the n-out-of-n bootstrap could result in too-small p-values (Chakraborty et al., 2014). In terms of study design, non-adaptive control conditions in SMARTs are atypical, but the inclusion of a control group in M-bridge allowed us to compare binge drinking under our estimated deeply tailored API with binge drinking under assessment-only control. This is a novel method of evaluating an estimated API that has not been widely explored in the SMART literature. Researchers planning future SMARTs should consider including a control group in their original design to accelerate the pace of innovation and refinement of adaptive interventions.

Several limitations of this analysis are worth noting. Our findings might not generalize to other regions of the U.S. or other types of colleges and universities. In particular, the distribution of effect modifiers (i.e., proportion of students who drink before college, drinking motives, and binge drinking frequency among heavy drinkers) in other populations might affect the magnitude of the contrast between expected binge drinking frequency under our estimated deeply tailored API and binge drinking under assessment-only control. Another limitation is the possibility of inflated Type I error due to multiple testing, because we performed Q-learning separately for 20 proposed Stage 1 tailoring variables to identify the optimal variable. Thus, the significant contrast between our deeply tailored API and control could be due to chance. Relatedly, students were not randomized to our proposed API, although they were randomized to the component interventions. Future research should aim to replicate our findings, for example in a randomized confirmatory trial of our proposed API versus assessment-only control.

In conclusion, we applied novel reinforcement learning methods to create two rules that codify a deeply tailored API for reduction of binge drinking in first-year college students. Our Stage 1 rule dictates when a student should receive PNF and begin self-monitoring, as a function of whether the student drinks and, if so, their motives for drinking; and our Stage 2 rule dictates how to transition students who continue to drink heavily to indicated interventions, as a function of their mid-semester binge drinking frequency. If confirmed in future trials, our results could be used by college campuses that wish to tailor alcohol use interventions based on student characteristics. Furthermore, our analysis offers a real-world example template for other researchers who aim to develop deeply tailored APIs using SMART data, especially if the SMART includes a non-adaptive control group. In this exploratory analysis that extends the primary results of the M-bridge study, we observed that additional personalization through deep tailoring can lead to significant estimated reductions in binge drinking frequency relative to assessment-only control.

Data or code availability

Available from the corresponding author upon request.