Abstract
Extrinsic environmental factors influence the spatiotemporal dynamics of many organisms, including insects that transmit the pathogens responsible for vector‐borne diseases (VBDs). Temperature is an especially important constraint on the fitness of a wide variety of ectothermic insects. A mechanistic understanding of how temperature impacts traits of ectotherms, and thus the distribution of ectotherms and vector‐borne infections, is key to predicting the consequences of climate change on transmission of VBDs like malaria. However, the response of transmission to temperature and other drivers is complex, as thermal traits of ectotherms are typically nonlinear, and they interact to determine transmission constraints. In this study, we assess and compare the effect of temperature on the transmission of two malaria parasites, Plasmodium falciparum and Plasmodium vivax, by two malaria vector species, Anopheles gambiae and Anopheles stephensi. We model the nonlinear responses of temperature dependent mosquito and parasite traits (mosquito development rate, bite rate, fecundity, proportion of eggs surviving to adulthood, vector competence, mortality rate, and parasite development rate) and incorporate these traits into a suitability metric based on a model for the basic reproductive number across temperatures. Our model predicts that the optimum temperature for transmission suitability is similar for the four mosquito–parasite combinations assessed in this study, but may differ at the thermal limits. More specifically, we found significant differences in the upper thermal limit between parasites spread by the same mosquito (A. stephensi) and between mosquitoes carrying P. falciparum. In contrast, at the lower thermal limit the significant differences were primarily between the mosquito species that both carried the same pathogen (e.g., A. stephensi and A. gambiae both with P. falciparum). Using prevalence data, we show that the transmission suitability metric calculated from our mechanistic model is consistent with observed P. falciparum prevalence in Africa and Asia but is equivocal for P. vivax prevalence in Asia, and inconsistent with P. vivax prevalence in Africa. We mapped risk to illustrate the number of months various areas in Africa and Asia predicted to be suitable for malaria transmission based on this suitability metric. This mapping provides spatially explicit predictions for suitability and transmission risk.
Keywords: Africa, Asia, basic reproductive number, malaria, mosquito life history, Plasmodium falciparum, Plasmodium vivax, thermal performance curve, vector‐borne diseases
INTRODUCTION
Temperature is a prominent abiotic environmental factor that drives the physiological processes of organisms (e.g., microorganisms, insects, plants; Buckley & Huey, 2016; Clarke & Fraser, 2004). In the face of temperature changes, organisms must make necessary physiological adjustments to live in this environment (e.g., evolve, adapt) or move to a more suitable area permanently or temporarily (Berg et al., 2010). This requirement holds true for ectotherms whose physiological processes are highly constrained by ambient temperature and whose body temperatures fluctuate with ambient temperatures. In turn, the rates of most ectotherm biological and biochemical processes shift with temperature, impacting traits that impact fitness (e.g., development rate, survival; Abram et al., 2017; Kern et al., 2015). Thus temperature contributes to the observed dynamics and distributions of populations of ectotherms.
Predicting the impact of temperature on both the dynamics and distribution of ectotherms both now and in the future requires a detailed understanding of the relationship between temperature and performance traits (Cator et al., 2020). However, conducting experiments to explore these relationships can be challenging. Thus much of the best available ectotherm–temperature data are on insects, as they are small, relatively easy to handle, and have short generation times. Further, many insects, such as mosquitoes, are also of public health importance, and as such are well studied. Thus, mosquitoes are a convenient model to investigate the effects of temperature on ectotherms. Further, parasites transmitted by mosquitoes are also ectothermic, allowing the exploration of the impact of temperature on linked systems.
In this paper, we explore how temperature impacts the transmission of malaria by Anopheles mosquitoes. Malaria, a deadly mosquito‐borne disease, is present on five of the world's seven continents (excluding Australia and Antarctica; Sinka et al., 2010, 2011, 2012). The World Health Organization reported an estimated 229 million cases of malaria in 87 countries in 2019. Of these cases, 409,000 resulted in death (World Health Organization, 2020). The African region accounts for about 94% of malaria cases and mortality, followed by the Southeast Asian region with 3% of cases; the other 3% of cases occur in the Eastern Mediterranean Region and the Americas (World Health Organization, 2020). Despite intensive control efforts against malaria for more than a decade, malaria endemicity remains high in much of the world, with high morbidity and mortality, especially in children under 5 years of age (Tizifa et al., 2018).
The Plasmodium species that cause malaria are spread by Anopheles mosquitoes that differ in some important traits. Roughly 70 of the 462 known Anopheles species can transmit malaria (Hay et al., 2010). Anopheles gambiae is the main malaria vector in Africa (Geissbühler et al., 2007), while Anopheles stephensi is an important vector in southern and western Asia (Sinka et al., 2012). A variety of factors influence when and where malaria is transmitted by mosquitoes. For example, each species of mosquitoes exhibits particular habitat and host preferences, as well as resting and feeding behavior, all of which may impact the propensity of malaria transmitting mosquitoes to interact with humans. A. gambiae mosquitoes inhabit rural and peri‐urban areas and feed predominantly on humans and late at night. They lay eggs in sunlit, shallow, and temporary bodies of fresh water and rest in both indoors and outdoors environments (Sinka et al., 2010). In contrast, A. stephensi mosquitoes are well adapted to urban centers, though they are also found in rural areas, and they prefer to lay eggs in man‐made containers. A. stephensi prefer to feed on animals (e.g., bovids) but will also feed on humans. They also feed and inhabit/rest indoors (Sinka et al., 2011; Takken & Lindsay, 2019).
Only five of the more than 100 Plasmodium species cause malaria in humans: P. falciparum, P. vivax, P. malariae, P. ovale, and P. knowlesi. Of these P. falciparum and P. vivax are the most common Plasmodium species that cause malaria in humans (Snow et al., 2005). P. falciparum is responsible for approximately 93.5% of the recorded malaria cases worldwide, P. vivax is responsible for 3% of malaria cases worldwide, and the other three Plasmodium parasites are responsible for the other 3.5% of malaria cases worldwide (World Health Organization, 2020). In Africa, 99.7% of the malaria cases are caused by P. falciparum, and in contrast, Southeast Asia has a combination of types, with ~53% of cases caused by P. falciparum and ~46% by P. vivax (World Health Organization, 2020).
In this study, we use a mechanistic model to determine the impact of temperature on a suitability metric, , that is based on the reproductive number (). We aggregated available data from the literature on the thermal responses of mosquito and parasite traits (e.g., mosquito and parasite development rates) measured across multiple constant temperatures. We fit the thermal response of each component of independently to these data using a Bayesian approach (Johnson et al., 2015; Mordecai et al., 2013). We then incorporated the posterior distribution of each component trait into .
We also checked for the consistency of our models with field data on malaria prevalence from Africa and Asia. We then used the models that were most consistent with the case data to build suitability maps (i.e., where the probability of is at least 0.975) for the transmission of P. falciparum and P. vivax by A. stephensi and A. gambiae mosquitoes. The approach used here is relatively simple. It has been successfully used to estimate optimum temperature and the thermal limits in both related vector–pathogen transmission systems (e.g., other mosquito systems; Shocket et al., 2020) as well as non‐mosquito systems (e.g., psyllids and citrus greening; Taylor et al., 2019) in a similar way. This approach should be extensible to other vector–pathogen systems for which sufficient trait data of both vectors and pathogens exist. Further, if parasite trait data is not available, or if trait data for other insects (such as pests) exists, a similar approach could be used but could focus on the population rate of natural increase, , instead of the disease focused (Cator et al., 2020). Thus, the utility of the approach is much wider than the sort of mosquito system that is the focus here.
MATERIALS AND METHODS
Thermal trait data
We synthesized published data on the thermal responses of the following mosquito traits for nine mosquito species of the Anopheles genus that can transmit malaria: mosquito development rate, bite rate, proportion of eggs surviving to adulthood, fecundity measured in eggs per female per day, and mosquito mortality rate. We also synthesized data on the thermal response of the parasite development rate for four malaria parasites and on vector competence for all vector/parasite pairs that were available (Appendix S1: Table S2).
While malaria is one of the best studied vector‐borne diseases, the complete suite of temperature dependent mosquito, parasite, and compound traits for the mosquito–parasite system is only available for A. stephensi with P. falciparum. In other cases data are nearly complete. For example, A. stephensi with P. vivax is missing only vector competence (Appendix S1: Table S2). Others have moderate gaps. A. gambiae is missing data for bite rate, parasite development rate with P. vivax, and vector competence (with either P. falciparum or P. vivax). For other mosquito species, more than two thermal traits were absent. Thus we focus our analysis on A. stephensi and A. gambiae as these are the most complete (Appendix S1: Table S2). As even these sets have data gaps in thermal traits, where a gap exists, we use traits data available from the closest related species based on similar biologic and ecological characteristics (Appendix S1: Table S3).
Modeling the temperature dependence of suitability
Mathematical models of disease systems often use , the basic reproductive number, as a measure of disease transmissibility (Holme & Masuda, 2015). This basic reproductive number gives the average number of secondary cases that one infected individual generates during an infectious period in a susceptible population. The most common parameterizations of for vector‐borne infections are based on the Ross‐MacDonald model of malaria transmission (Dietz, 1993). Here we specifically use a formulation that incorporates multiple temperature‐dependent mosquito and parasite traits to approximate the mosquito population size (Johnson et al., 2015; Mordecai et al., 2013, 2017, 2019), that is we assume is given by
| (1) |
where: is the mosquito biting rate; is vector competence, which is the product of b, the probability of a person becoming infected by a bite of an infected mosquito, and c, the probability of a vector becoming infected by feeding on an infectious person; is the mosquito mortality rate; PDR is the parasite development rate; EFD is the mosquito fecundity expressed as the number of eggs per female per day; P EA is the proportion of eggs surviving to adulthood; MDR is the mosquito development rate; is the density of humans or hosts; and is the human recovery rate. Because we are interested in the shape of the thermal response only, we define a suitability metric, , that only incorporates the temperature‐dependent components, that is
| (2) |
Most thermal traits of ectotherms exhibit unimodal responses (Colinet et al., 2015; Mordecai et al., 2019). Although based exclusively on the (sometimes limited) data at hand, other options may seem reasonable (e.g., linear or asymptotic). We choose to incorporate this biological knowledge by constraining the functional forms and thus we assume that all of the components of are unimodal. More specifically, for each of these individual traits (e.g., bite rate) for each mosquito species, we fit one of three kinds of unimodal thermal response. For asymmetric responses like MDR, , and PDR we fit a Briére function (Briere et al., 1999)
| (3) |
where is the lower thermal limit (where the response becomes zero), is the upper thermal limit, and is a constant that determines the curvature at the optimum. Formally we assume a piecewise continuous function, so that the thermal trait is assumed to be zero if or . Symmetric responses come in two flavors: concave down or concave up (Amarasekare & Savage, 2012; Johnson et al., 2015). For concave‐down symmetric responses like , P EA, and EFD, we fit a quadratic function parameterized in terms of the temperature intercepts
| (4) |
where is the lower thermal limit, is the upper thermal limit, and is a constant that determines the curvature at the optimum. As with the Briére function, we assume the trait is piecewise zero above and below the thermal limits. For concave‐up symmetric responses like , we fit a concave‐up quadratic function (Johnson et al., 2015; Mordecai et al., 2019)
| (5) |
where , , and are the standard quadratic parameters. Note that, because all traits must be , we also truncate this function, creating a piecewise continuous function where is set to 0 if the quadratic evaluates to a negative value.
Bayesian fitting of thermal traits
We fit each unimodal thermal response for all traits for each mosquito species (A. stephensi and A. gambiae) or parasite species (P. falciparum and P. vivax) with a Bayesian approach using the JAGS/rjags package (Plummer, 2021) in R (R Development Core Team, 2017). We defined an appropriate likelihood for each trait (e.g., binomial likelihoods for proportion data, truncated normal for continuous numeric traits) with the mean defined by either a Briére function (for asymmetric relationships) or quadratic (symmetric relationships). For all traits, we chose relatively uninformative priors that limit each parameter to its biologically realistic range. More specifically, we assumed that temperatures below 0°C and above 45°C are lethal for both mosquitoes and malaria parasites (Lyons et al., 2012; Mordecai et al., 2019). Based on these assumptions, we set uniform priors for the minimum temperature () between 0° and 24°C and for the maximum temperature (), between 25° and 45°C (Johnson et al., 2015; Mordecai et al., 2017; Taylor et al., 2019). Priors for other parameters in the thermal responses were set, to ensure parameters were positive and not tightly constrained (Appendix S1: Table S4).
The rjags package uses a Metropolis algorithm within a Gibbs Markov Chain Monte Carlo sampling scheme to obtain samples from the joint posterior distribution of parameters. For each fitted trait, we obtained posterior samples from five Markov chains that were run for 20,000 iterations initiated with random starting values. These samples were obtained after using 10,000 iterations for adaptation and burning another 10,000 iterations. We visually assessed convergence of the Markov chains. To obtain the posterior summaries of each trait, we combined the 20,000 samples from each Markov chain from the posterior distribution, which resulted in a total of 100,000 posterior samples of the thermal response for each trait. Based on these samples, for each unimodal thermal response we calculated the posterior mean, the 95% highest posterior density (HPD) interval, and the 95% prediction interval around the mean of the thermal response and various summaries (e.g., the thermal minimum or maximum).
Once the posterior samples of parameters for all thermal traits across temperature for each species were obtained, these curves were combined to produce 100,000 posterior samples of (see Appendix S1: Table S5 for the traits used for each mosquito/parasite set). We used these samples of across temperature to calculate the posterior median and the 95% HPD of the overall thermal response of suitability, as well as for the critical thermal minimum, thermal maximum, and optimal temperature for transmission suitability for the four mosquito/parasite systems (A. stephensi and A. gambiae with P. falciparum and P. vivax).
We also used the posterior samples of the (lower thermal limit, upper thermal limit, and optimum) to assess the magnitude of the differences in these summaries between the four mosquito/parasite combinations. For all of the possible pairwise mosquito/parasite sets, we calculated the probability that the differences between each pair of samples of the posterior distributions for the mosquito/parasite combinations is greater than zero (Appendix S1: Section S8). We also performed an uncertainty analysis for to quantify the contribution of each trait to the overall uncertainty in mean suitability (Appendix S1: Section S9).
Consistency analysis
Consistency analysis is very important to determine whether the model accurately represents the behavior of the study system. We take two approaches to assess if our models are consistent with global malaria field data. Both approaches utilize open source data from the Malaria Atlas Project (MAP) on P. falciparum and P. vivax prevalence collected at the village level in 46 countries in Africa and 21 countries in Asia from 1990 to 2017 (Gething et al., 2011; Moyes et al., 2013; Pfeffer et al., 2018). The prevalence data were matched with environmental data (i.e., temperature) to the starting month of each study and to socio‐demographic data (i.e., population density, adjusted per capita gross domestic product [GDP]) using as merging points geographic coordinates and the year in which the prevalence study took place, respectively.
First, following existing methodology for spatial validation of suitability prediction models (Taylor et al., 2019; Tesla et al., 2018), we calculated the proportion of P. falciparum and P. vivax confirmed positive cases for Africa and Asia obtained from the MAP that falls into the months that are suitable for malaria transmission (0–12). The proportion of confirmed positive cases were calculated in areas that are suitable for either A. stephensi or A. gambiae in Africa and Asia (Appendix S1: Figures S20 and S21). This metric gives a rough check of consistency focusing on whether cases are within predicted thermal limits, that is to confirm that we do not observe many cases in areas that the model suggests are not suitable.
Our second approach uses logistic models to test whether is consistent with observed malaria prevalence in Africa and Asia. Instead of using the directly, we define STGZ, the posterior probability that is greater than zero, to again capture thermal limits, but to incorporate some of the inferred shape of . In addition to STGZ, we included two socioeconomic predictor variables in our analysis: adjusted per capita GDP and human population density (), which was available in periods of 5 years (e.g., 1990, 1995). These allow us to account for other potential sources of country to country or local variation in prevalence. Approximate human population density data at the village level where the prevalence studies took place were obtained from the Global Rural–Urban Mapping Project (GRUMP) project (Balk et al., 2006). GRUMP raster data containing human population density data were imported into ArcGIS software version 10.8.1 and human population density data at each location in our prevalence data set was extracted using the “extract values to points” tool from the spatial analysis tool set in ArcMap (Scott & Janikas, 2010). GDP data were obtained from the Institute for Health Metrics and Evaluation of the USA (James et al., 2012). Both human population density and GDP across countries exhibit clumpiness and variation across orders of magnitude, which can lead to high‐leverage data points having outsized influence on results. Logarithmic transformation of variables is a very common practice for addressing these issues with predictors (Sheather, 2009). Thus, for all of our analyses, we used the natural logarithm transformed versions of both human population density and GDP (Appendix S1: Section S10).
For each set of parasite prevalence data, we evaluated seven models including a combination of the logarithm of human population density, logarithm of GDP, and STGZ. This included three “null” models, which incorporated socioeconomic factors but not the suitability metric. We built null baseline models to represent the minimal factors that we expect should be correlated with observed cases. It is well known, for example, that you need more people to have more cases (Knudsen & Slooff, 1992) and that higher economic status countries tend to have lower disease burden per capita (Ricci, 2012). Thus, if we end up choosing a “null” model as the best model, this indicates that there is no signal of the environmental factors that we are exploring here. We ranked models based on the Bayesian Information Criterion (BIC), with the model with the lowest BIC/highest relative model probability being the best of the candidate models (Aho et al., 2014; Dunn & Smyth, 2018).
Mapping temperature suitability for malaria transmission
We focused on illustrating the number of months a year that locations are predicted to have suitable temperatures in Africa and Asia (where malaria is most prevalent). We define suitable areas as those with temperatures such that the probability of the is at least 0.975. We want to be more conservative than the common 0.95 threshold level to prevent including areas that are marginal at this 0.95 level. This corresponds to areas that we feel highly confident are within the thermal limits for malaria. For the curves based on A. gambiae traits, this is a very conservative approach, especially at the lower thermal limit, which is very uncertain. At each location in space, we calculated the number of months (0–12) that the pixel was within these bounds for each mosquito–parasite system (Ryan et al., 2015; Taylor et al., 2019). Monthly mean temperature rasters at a 30 s spatial resolution were downloaded from the WorldClim‐Global Climate Data project (Fick & Hijmans, 2017) using the raster package (Hijmans, 2021) in the R environment (R Development Core Team, 2017). We cropped the temperature raster maps to the Africa and Asia continents using the Crop function from the raster package in ArcMap 10.8.1 (Barik et al., 2017).
RESULTS
Posterior distributions of thermal traits
In Figure 1, we estimated the posterior mean and the 95% HPD around the mean for A. stephensi and A. gambiae mosquito thermal traits (see Appendix S1; Figures S2 and S4 for parasite and compound [mosquito + parasite] thermal traits). This visualization showed the extent of uncertainty around the mean thermal response. In general, we noticed that the uncertainty was greater in the thermal responses for traits of A. gambiae than A. stephensi, largely due to fewer data availability for estimating the responses to temperature for the former species (Figure 1; Appendix S1: Figures S1–S4). For example, A. gambiae development rate (MDR) and the number of EFD exhibited considerable uncertainty in the lower end of the thermal response because there are few or no data available below approximately 20°C (Figure 1f,i). Also, A. gambiae PDR and vector competence () with P. falciparum showed the greatest uncertainty, primarily due to lack of data (Appendix S1: Figure S4).
FIGURE 1.

Posterior mean (solid line) and 95% highest posterior density (HPD; dashed lines) of the thermal responses for mosquito traits for Anopheles stephensi (green) and Anopheles gambiae (blue). Traits modeled with a Brière thermal response are (a, f) mosquito development rate and (b, g) bite rate. Traits modeled with a concave down quadratic function are (c, h) proportion of eggs surviving to adulthood and (d, i) fecundity and (e, j) mortality rate, which is modeled with a concave‐up quadratic function. Data symbols correspond to the species of mosquitoes. Open circles, A. stephensi; solid circles, A. gambiae; crosses, A. arabiensis; stars, A. pseudopunctipennis. For parasites and compound traits (mosquitoes + parasites), see Appendix S1
In contrast, most A. stephensi traits exhibited considerably less uncertainty around the mean. Where uncertainty exists, for example in the thermal limits of bite rate (; Figure 1b), and mortality (; Figure 1e), this seems again to be due primarily to a lack of data near the thermal extremes. Parasite traits with A. stephensi mosquitoes typically have better data coverage than A. gambiae, and so have less uncertainty. However, vector competence, , for A. stephensi with P. falciparum is more uncertain at the minimum thermal limit because data were only available above 20°C (Appendix S1: Figure S2c). Similarly, PDR for P. falciparum is uncertain near the maximum thermal limit because there are only three data points above 31°C (Appendix S1: Figure S2a). In contrast, P. vivax‐related traits are better constrained.
Posterior distribution of
In Figure 2, we estimated the posterior median and 95% HPD of for each of the four mosquito–parasite combinations. To allow for more direct comparison, all curves were scaled to the maximum value of the posterior median curve, so the maximum value of the median for each individual curve is one. Overall, uncertainty (measured in the width of the HPD intervals after scaling) was greater for A. gambiae with P. falciparum and P. vivax compared to A. stephensi with P. falciparum and P. vivax (Figure 2). Based purely on posterior median values, A. stephensi mosquitoes had the greatest temperature range for transmission suitability, with a range of 15.3 to 37.2°C for P. falciparum (Figure 2e) and 15.7 to 32.5°C for P. vivax (Figure 2f). The median predicted temperature ranges for the suitability transmission of P. falciparum and P. vivax by A. gambiae mosquitoes are very similar with ranges from 19.1° to 30.1°C and 19.2° to 31.7°C, respectively (Figure 2g,h). However, these median ranges mask a great deal of uncertainty.
FIGURE 2.
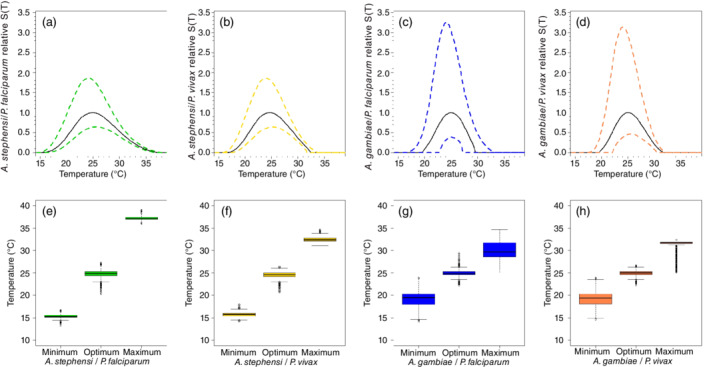
Top row: relative transmission suitability divided by the maximum value of the posterior median for (a) A. stephensi/Plasmodium falciparum, (b) A. stephensi/Plasmodium vivax, (c) A. gambiae/P. falciparum, and (d) A. gambiae/P. vivax. Bottom row: median, interquartile range, minimum, and maximum numbers from the posterior for the minimum temperature, optimum temperature, and maximum temperature for the of (e) A. stephensi/P. falciparum, (f) A. stephensi/P. vivax, (g) A. gambiae/P. falciparum, and (h) A. gambiae/P. vivax
The suitability metric for all four mosquito parasite pairs is predicted to peak (i.e., to have optimum) at approximately 25°C. Although there is some variability in this estimate, the posterior distributions of the optimum do not exhibit significant differences between them (Appendix S1: Figures S8 and S11). In contrast, there are indications that the upper and lower thermal limits may not be the same across the four pairs. In A. stephensi, there was strong evidence of a difference in the upper thermal transmission limit for these mosquitoes when they transmit P. falciparum (CI: 36.5°–38°C) versus P. vivax (CI: 31.7°–33.7°C) (Appendix S1: Table S8 and Figures S7a and S10a). Similarly, there was strong evidence for differences in the upper thermal limit for transmission of P. falciparum when comparing between A. stephensi and A. gambiae (Appendix S1: Table S8 and Figures S7c and S10c). The other comparisons at the maximum thermal limit are not significant (Appendix S1: Figures S7 and S10).
The predictions for the lower thermal limits were much more similar to each other. Our results showed that the only significant differences are between the transmission of P. falciparum by A. stephensi and by A. gambiae mosquitoes (Appendix S1: Figures S9c and S12c) and between the transmission of P. vivax by A. stephensi and by A. gambiae (Appendix S1: Figures S9d and S12d). The other comparisons at the minimum thermal limit were not significant (Appendix S1: Figures S9 and S12).
Sources of uncertainty in
Across all combinations of mosquitoes and parasites, the uncertainty in at intermediate temperatures was dominated by the uncertainty in the adult mosquito mortality rate, (Appendix S1: Figures S13 and S14). This is a common pattern as , so small changes in when is small (i.e., near optimal temperatures for mosquito longevity) will have an outsized impact on . This component is thus almost wholly responsible for the location and height of the peak of suitability.
In contrast, the traits that drive uncertainty in the temperatures around the thermal limits varies between each mosquito–parasite pair and is sensitive to the amount and quality of data available for each. For example, our suitability metric for P. falciparum in A. stephensi seems the most well resolved of all of the combinations. In this case, uncertainty in dominates across almost all temperatures, and it is only at the high temperature end, above ≈37°C, that most of the uncertainty was caused by another component, specifically the proportion of eggs surviving to adulthood (P EA). At temperatures between 32° and 37°C, vector competence () and PDR also contribute to the uncertainty, although they do not dominate over either or P EA. Similarly, near the lower temperature regime, PDR and P EA both contribute to the overall uncertainty, but do not dominate compared to (Appendix S1: Figure S13c). Because the mosquito traits are shared, the patterns seen in the P. vivax–A. stephensi pair are similar to those for P. falciparum–A. stephensi. Again, dominates at intermediate temperatures, but now near the upper thermal limit the uncertainty is almost entirely determined by uncertainty in vector competence (). At the lower limit, PDR contributed to the uncertainty but to a lesser extent than (Appendix S1: Figure S13d).
The patterns exhibited for suitability by A. gambiae are markedly different, reflecting the greater uncertainty across multiple traits. Although the uncertainty due to is the dominant source of uncertainty at intermediate temperatures, other parameters contributed to the uncertainty across much wider portions of the thermal response compared to A. stephensi (Appendix S1: Figure S14). For example, uncertainty for the P. falciparum–A. gambiae pair is dominated by PDR in the lower and upper limits while EFD and MDR influenced uncertainty in the mid to lower temperature ranges (Appendix S1: Figure S14c). For the P. vivax–A. gambiae pair, uncertainty near the lower and upper limits for transmission is dominated by EFD, MDR, and PDR, with each leading over slightly different ranges (Appendix S1: Figure S14d).
Consistency analysis
We first evaluated coarse consistency of the models with observed data by examining the histograms of the proportion of P. falciparum and P. vivax positive prevalence cases that falls within suitable areas for malaria transmission (0–12 months) by A. gambiae and A. stephensi mosquitoes in Africa and Asia (Appendix S1: Figures S20 and S21). If the observed data are consistent with the suitability metric, we could expect to see lower prevalence in areas that are suitable for few months of the year and high prevalence in areas that are suitable for many months. Based on this simple graphical metric, the models were broadly consistent with the data collected in Asia (i.e., the metric is not predicting that areas are not suitable where we see a lot of malaria), but were less consistent with data in Africa (Appendix S1: Figures S20 and S21). Further, the metrics based on A. stephensi traits seem more consistent with the data, likely due to significantly more uncertainty in the A. gambiae data, and a broader thermal envelope. Because of the combination of very poor consistency with the model (by this measure) and limited data, we conclude that our model cannot be assessed for P. vivax in Africa reliably, and we excluded this case from further analysis (Appendix S1: Figures S20 and S21).
Our quantitative approach, using logistic models, gives further evidence for a potential signal of temperature in observed prevalence data. The logistic models assessed the proportion of “successes” (i.e., infections) in each village instead of only examining the presence (prevalence ). For P. falciparum in Africa and Asia the best model included the linear combination of STGZ, log of human population density, and log of GDP interacted with location (i.e., different regression coefficients for GDP in Africa than in Asia; Appendix S1: Table S10). This indicates that including the suitability metric is significantly better at explaining patterns of malaria presence/absence than socioeconomic factors alone. In contrast, for P. vivax in Asia, the best model only included socioeconomic factors. The second best model included the linear combination of STGZ with the socioeconomic factors. However, this model has much lower model probability, based on BIC (0.02 compared to 0.98 for the top model; Appendix S1: Table S11). This indicates that the temperature metric does not substantially improve model fit for P. vivax, although the first consistency analysis does indicate consistency between cases and the suitability metric based exclusively on presences.
Mapping climate suitability for malaria transmission
Our maps illustrate the number of months of high suitability (months where the probability that is at least 0.975) for P. falciparum transmission by A. stephensi and A. gambiae in Africa (Figure 3a,b) and the number of months of high suitability for P. falciparum and P. vivax transmission by A. stephensi in Asia (Figure 3c,d). The maps predict the seasonality of temperature highly suitable for malaria transmission geographically, but they do not indicate malaria transmission magnitude. Our maps demonstrated that temperatures are highly suitable for the transmission of P. falciparum malaria by both mosquito species, A. gambiae and A. stephensi, in vast areas of Africa and the transmission of P. falciparum and P. vivax malaria by A. stephensi mosquitoes in vast areas of Asia.
FIGURE 3.

The number of months a year that locations fall within the predicted suitable range (probability of > 0 ) for the transmission of Plasmodium falciparum by (a) Anopheles stephensi and (b) Anopheles gambiae mosquitoes in Africa, and for the transmission of (c) P. falciparum and (d) Plasmodium vivax by A. stephensi mosquitoes in Asia
Our maps indicated that in Africa, approximately 15% of the continental land area has temperatures suitable year‐round for the transmission of P. falciparum malaria by A. stephensi mosquitoes, and 44% for at least 6 months of the year (Figure 3a). Countries in which most of the territory is suitable year‐round include Guinea, Liberia, Sierra Leone, Togo, Nigeria, Central African Republic, Democratic Republic of the Congo, Congo, Gabon, Cameroon, Cote d'Ivoire, Uganda, Kenya, Tanzania, Mozambique, Ethiopia, Madagascar, and Ghana. The area suitable year‐round for P. falciparum malaria transmission by A. gambiae in Africa is 8% and 30% of the area is suitable at least 6 months of the year (Figure 3b). Countries with most of their territory suitable year‐round include Sierra Leone, Liberia, Cote d'Ivoire, Cameroon, Gabon, Democratic Republic of Congo, Congo, Central African Republic, and Kenya. We also show the maps for P. vivax transmission by A. stephensi and A. gambiae in Africa in the supplementary material for completeness (Appendix S1: Figure S22), but we do not interpret these maps as the model needs refinement in this region.
In Asia, approximately 9% of the area is considered highly suitable for the transmission of P. falciparum malaria by A. stephensi mosquitoes year‐round, and 20% for six or more months of the year (Figure 3c). The area highly suitable for year‐round transmission of P. vivax by A. stephensi is approximately 7%, and for at least 6 months of the year is 16% (Figure 3d). Southeast Asia is the most vulnerable, with most of their territory suitable for malaria transmission year‐round. Some of the countries with suitable temperatures year‐round include Myanmar, Cambodia, Thailand, Vietnam, Indonesia, Malaysia, Singapore, Brunei, Timor‐Leste, and the Philippines (Figure 3c,d).
DISCUSSION
Determining the optimal, minimum, and maximum temperatures at which A. gambiae and A. stephensi mosquitoes are the most efficient vectors for the transmission of malaria parasites is important for assessing the potential for invasion and establishment in novel locations, and for assessing the potential impacts of climate change on the future geographical distribution of these two mosquito species and the malaria parasites they transmit. In this paper, we have updated predictions for thermal suitability of transmission of the two most common malaria parasites, P. falciparum and P. vivax, by two of the most common malaria vector species, A. gambiae and A. stephensi, using data from historical and newly published studies. We examined the extent to which predictions may vary between mosquito species and between parasite types and identified persistent data gaps that must be addressed to further improve these models and allow more precise comparisons between mosquito/parasite complexes.
Our results suggest that there is little difference in the optimal temperature for malaria transmission between A. gambiae and A. stephensi mosquitoes. Further we find optimal temperatures for malaria transmission suitability that are similar to other recent findings for the optimal temperature at the continental scales (e.g., Johnson et al., 2015; Lunde et al., 2013; Mordecai et al., 2013, 2019; Shapiro et al., 2017). Earlier studies had calculated higher optimal temperatures for malaria transmission (Craig et al., 1999; Mahmood, 1997; Parham & Michael, 2009). We attribute the difference to the use of linearly increasing/monotonic functions as a component of past models. The study of Shapiro et al. (2017) also reported an optimum temperature of 29°C using a temperature‐dependent model to estimate relative vectorial capacity based on thermal performance curves of bite rate, vector competence, daily mosquito mortality rate, and the length of the extrinsic incubation period. Empirical data usually violates several of the relative vectorial capacity model assumptions (Shapiro et al., 2017). In nature, biological and ecological mosquito and parasite traits usually show unimodal responses to temperature (Dell et al., 2011), in which traits increase exponentially from a minimum thermal limit to an optimal temperature, then decline to a zero at a maximum thermal limit (Dell et al., 2011).
However, we find that there are differences between the temperatures that could limit suitability for the two focal parasites to be spread by different mosquitoes. For example, we found evidence that there are differences in the upper thermal limit between P. vivax and P. falciparum when spread by A. stephensi, and between P. falciparum when spread by the two mosquitoes. There is also evidence that the lower suitability threshold differs by mosquito species when transmitting the same pathogen. However, there is a great deal of uncertainty in the estimates of these limits due to poor data availability, especially for traits of A. gambiae and P. falciparum. As a result of the observed difference in the upper and lower thermal limits across mosquito–parasite systems, we also observe differences in the predicted temperature ranges for suitability, with greater temperature ranges for pathogens transmitted by A. stephensi than A. gambiae (Figure 2). Based on available trait data and previous studies, A. stephensi mosquitoes seem to have greater range in thermal tolerance than A. gambiae mosquitoes (Kirby & Lindsay, 2004; Miazgowicz et al., 2020).
The larger thermal breadth for transmission of both P. falciparum and P. vivax by A. stephensi than A. gambiae has a knock‐on effect for the predicted spatial extent of suitability for transmission. Our maps show the areas that are potentially currently suitable, based on temperature, for the transmission of both P. falciparum and P. vivax by A. gambiae and A. stephensi mosquitoes. In Africa, vast regions between 22° N and 21° S latitude are highly suitable for A. gambiae and A. stephensi mosquitoes. A. gambiae is currently the dominant mosquito species that transmits malaria in Africa. Although A. stephensi is a native mosquito of Asia (Sinka et al., 2010), recent research has reported that An. stephensi mosquitoes are already present in Africa, for example, in Djibouti (Faulde et al., 2014), Ethiopia (Balkew et al., 2020; Carter et al., 2018; Tadesse et al., 2021), Sudan, and probably in neighboring countries (Takken & Lindsay, 2019). The current presence and the possible spread of An. stephensi to African countries poses a potential health risk since it is a malaria vector well adapted to urban centers that could cause malaria outbreaks of unprecedented sizes (Balkew et al., 2020; Sinka et al., 2020; Takken & Lindsay, 2019). Our model indicates that the breadth of temperature range for A. stephensi with P. falciparum (15.3°–37.2°C) is greater than the breadth for A. gambiae with P. falciparum (19.1°–30.1°C); and in a lesser degree, the breadth for A. stephensi with P. vivax (15.7°–32.5°C) is greater than the breadth for A. gambiae with P. vivax (19.2°–31.7°C; Appendix S1: Table S8). This indicates that a larger proportion of Africa may be suitable for transmission by A. stephensi than by A. gambiae, due to the larger thermal breadth. Thus, regions at the northern and southern limits of the area dominated by A. gambiae are suitable for A. stephensi. In these areas, malaria transmission could increase as A. stephensi becomes more established, which could also become a potential threat to malaria control in Africa.
The consistency analysis showed that for P. falciparum in Africa and Asia, the best logistic model to predict the probability of infection includes the linear combination of > 0, log of human population density, and log of GDP. However, for P. vivax in Asia, the best logistic model only includes socioeconomic factors despite the thermal suitability metric seeming to be more consistent with observed data than it is in Africa by our first consistency check (Appendix S1: Figure S20 vs. S21). We expect that there are three primary reasons why we may observe these contradictory results, given that we know that the biology of the vectors is temperature sensitive. First, in the parts of Asia where we have data the observed temperature range is small, and uncertainty in parameters increases as the range of the predictors decreases. In contrast, ranges in per capita GDP and population density are larger. This is the opposite of the pattern observed in Africa (Appendix S1: Figure S23). Second, in contrast to Africa where A. gambiae is the main malaria vector, in Asia, there are many other important malaria vectors (e.g., A. culicifacies, A. dirus; Bharati & Ganguly, 2013; Sinka et al., 2011) whose thermal performance curves could be different from A. stephensi. Furthermore, the overall amount of prevalence data is much smaller for P. vivax malaria than for P. falciparum, which could impact our ability to infer patterns. Once more P. vivax malaria prevalence data become available, our model predictions could be better compared with field data.
Previous research assessing the optimal temperature and temperature limits for malaria transmission using mechanistic trait‐based models has necessarily relied on data from a combination of mosquito and parasite species due to incomplete data availability for thermal traits of mosquitoes and parasites (Johnson et al., 2015; Mordecai et al., 2013). In this study, all mosquito traits used for the calculations were from the Anopheles genus. If data for a specific trait were not available for one of the studied species, we used data from the closest relative in the same genus (Appendix S1: Table S3). For example, for A. stephensi, all mosquito traits were from the same species, but for A. gambiae bite rate data are still not available so we used data from A. arabiensis and A. pseudopunctipennis mosquitoes instead. A similar approach was used for parasite traits. The amount of available data for each species has significant impact on the uncertainty in our model. To reduce uncertainty in these models, there is a need for more empirical data from the laboratory, especially for A. gambiae. For example, fecundity data for A. gambiae is lacking at low and high temperatures. There is also a need for vector competence and PDR data for A. stephensi with P. vivax, A. gambiae with P. vivax, and A. gambiae with P. falciparum and vector competence for A. stephensi with P. falciparum. These data would improve certainty in these models, especially at the thermal limits.
Our approach has some important limitations, some of which could be addressed by extending the mechanistic models. One limitation is that we use constant temperature data in our models, and did not incorporate daily and seasonal temperature variations, which occur in nature. However, nonlinearities make it difficult to measure mosquito and parasite traits even at constant temperatures, especially at the thermal limits (Johnson et al., 2015; Mordecai et al., 2019). Precipitation also influences malaria transmission, particularly via vector abundance, due to its role in mosquito life cycles, as does humidity (Bomblies, 2012). Incorporating the effect of different precipitation regimes on mosquito and parasites traits could also improve our mechanistic models, although capturing these dynamics is complicated (Caldwell et al., 2021).
Despite these limitations, there is consistency between these constant temperature mechanistic models with field data. For example, malaria prevalence data (our study), human case data (Mordecai et al., 2017), or entomological inoculation rate data (Mordecai et al., 2013) demonstrate that these simple temperature‐only models capture broad‐scale patterns of transmission of mosquito‐borne diseases. Due to the relative simplicity of the approach, similar studies combining empirical data and model fitting could estimate optimum temperature and the thermal limits for other vector–pathogen transmission systems in a similar way.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Supporting information
Appendix S1
ACKNOWLEDGMENTS
The authors want to thank Kerri Miazgowicz, Krijn Paaijmans, and Antoine Barreaux for kindly providing raw data used in our analyses. Leah R. Johnson, Oswaldo C. Villena, and Sadie J. Ryan were supported by NSF EEID no. 1518681. Leah R. Johnson was also supported by NSF DMS/DEB no. 1750113. Courtney C. Murdock was supported by NIAID R01 (1R01AI110793‐01A1).
Villena, Oswaldo C. , Ryan Sadie J., Murdock Courtney C., and Johnson Leah R.. 2022. “Temperature Impacts the Environmental Suitability for Malaria Transmission by Anopheles Gambiae and Anopheles Stephensi .” Ecology 103(8): e3685. 10.1002/ecy.3685
Handling Editor: Kathryn L. Cottingham
Funding information National Institute of Allergy and Infectious Diseases, Grant/Award Number: 1RO1AI110793‐01A1; NSF DMS/DEB, Grant/Award Number: 1750113; NSF EEID, Grant/Award Number: 1518681
DATA AVAILABILITY STATEMENT
Data and code (Villena, 2022) are available on Zenodo: https://doi.org/10.5281/zenodo.5874787.
REFERENCES
- Abram, P. K. , Boivin G., Moiroux J., and Brodeur J.. 2017. “Behavioural Effects of Temperature on Ectothermic Animals: Unifying Thermal Physiology and Behavioural Plasticity.” Biological Reviews 92: 1859–76. [DOI] [PubMed] [Google Scholar]
- Aho, K. , Derryberry D., and Peterson T.. 2014. “Model Selection for Ecologists: The Worldviews of AIC and BIC.” Ecology 95: 631–6. [DOI] [PubMed] [Google Scholar]
- Amarasekare, P. , and Savage V.. 2012. “A Framework for Elucidating the Temperature Dependence of Fitness.” The American Naturalist 179: 178–91. [DOI] [PubMed] [Google Scholar]
- Balk, D. L. , Deichmann U., Yetman G., Pozzi F., Hay S. I., and Nelson A.. 2006. “Determining Global Population Distribution: Methods, Applications and Data.” Advances in Parasitology 62: 119–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balkew, M. , Mumba P., Dengela D., Yohannes G., Getachew D., Yared S., Chibsa S., et al. 2020. “Geographical Distribution of Anopheles stephensi in Eastern Ethiopia.” Parasites & Vectors 13: 35. 10.1186/s13071-020-3904-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barik, R. K. , Lenka R. K., Ali S. M., Gupta N., Satpathy A., and Raj A.. 2017. “Investigation into the Efficacy of Geospatial Big Data Visualization Tools.” In Proceedings of the IEEE International Conference on Computing, Communication and Automation, Greater Noida, India, May 5‐6, 2017, edited by Astya P. N., Swaroop A., Sharma V., Singh M., and Gupta K., 88–93. New York, NY: Institute of Electrical and Electronics Engineers (IEEE). 10.1109/CCAA.2017.8229777 [DOI] [Google Scholar]
- Berg, M. P. , Kiers E. T., Driessen G., Van Der Heijden M., Kooi B. W., Kuenen F., Liefting M., Verhoef H. A., and Ellers J.. 2010. “Adapt or Disperse: Understanding Species Persistence in a Changing World.” Global Change Biology 16: 587–98. [Google Scholar]
- Bharati, K. , and Ganguly, N . 2013. “Tackling the Malaria Problem in the South‐East Asia Region: Need for a Change in Policy?” Indian Journal of Medical Research 137: 36–47. [PMC free article] [PubMed] [Google Scholar]
- Bomblies, A. 2012. “Modeling the Role of Rainfall Patterns in Seasonal Malaria Transmission.” Climatic Change 112: 673–85. [Google Scholar]
- Briere, J. F. , Pracros P., Le Roux A. Y., and Pierre J. S.. 1999. “A Novel Rate Model of Temperature‐Dependent Development for Arthropods.” Environmental Entomology 28: 22–9. [Google Scholar]
- Buckley, L. B. , and Huey R. B.. 2016. “How Extreme Temperatures Impact Organisms and the Evolution of their Thermal Tolerance.” Integrative and Comparative Biology 56: 98–109. [DOI] [PubMed] [Google Scholar]
- Caldwell, J. M. , LaBeaud A. D., Lambin E. F., Stewart‐Ibarra A. M., Ndenga B. A., Mutuku F. M., Krystosik A. R., et al. 2021. “Climate Predicts Geographic and Temporal Variation in Mosquito‐Borne Disease Dynamics on Two Continents.” Nature Communications 12: 1233. 10.1038/s41467-021-21496-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter, T. E. , Yared S., Gebresilassie A., Bonnell V., Damodaran L., Lopez K., Ibrahim M., Mohammed S., and Janies D.. 2018. “First Detection of Anopheles stephensi Liston, 1901 (Diptera: Culicidae) in Ethiopia Using Molecular and Morphological Approaches.” Acta Tropica 188: 180–6. [DOI] [PubMed] [Google Scholar]
- Cator, L. J. , Johnson L. R., Mordecai E. A., El Moustaid F., Smallwood T. R., LaDeau S. L., Johansson M. A., et al. 2020. “The Role of Vector Trait Variation in Vector‐Borne Disease Dynamics.” Frontiers in Ecology and Evolution 8: 189. 10.3389/fevo.2020.00189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke, A. , and Fraser K.. 2004. “Why Does Metabolism Scale with Temperature?” Functional Ecology 18: 243–51. [Google Scholar]
- Colinet, H. , Sinclair B. J., Vernon P., and Renault D.. 2015. “Insects in Fluctuating Thermal Environments.” Annual Review of Entomology 60: 123–40. [DOI] [PubMed] [Google Scholar]
- Craig, M. H. , Snow R., and le Sueur D.. 1999. “A Climate‐Based Distribution Model of Malaria Transmission in Sub‐Saharan Africa.” Parasitology Today 15: 105–11. [DOI] [PubMed] [Google Scholar]
- Dell, A. I. , Pawar S., and Savage V. M.. 2011. “Systematic Variation in the Temperature Dependence of Physiological and Ecological Traits.” Proceedings of the National Academy of Sciences USA 108: 10591–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietz, K. 1993. “The Estimation of the Basic Reproduction Number for Infectious Diseases.” Statistical Methods in Medical Research 2: 23–41. [DOI] [PubMed] [Google Scholar]
- Dunn, P. K. , and Smyth G. K.. 2018. Generalized Linear Models with Examples in R, First ed. New York, NY: Springer Texts in Statistics. 10.1007/978-1-4419-0118-7. [DOI] [Google Scholar]
- Faulde, M. K. , Rueda L. M., and Khaireh B. A.. 2014. “First Record of the Asian Malaria Vector Anopheles stephensi and its Possible Role in the Resurgence of Malaria in Djibouti, Horn of Africa.” Acta Tropica 139: 39–43. [DOI] [PubMed] [Google Scholar]
- Fick, S. E. , and Hijmans R. J.. 2017. “WorldClim 2: New 1‐km Spatial Resolution Climate Surfaces for Global Land Areas.” International Journal of Climatology 37: 4302–15. [Google Scholar]
- Geissbühler, Y. , Chaki P., Emidi B., Govella N. J., Shirima R., Mayagaya V., Mtasiwa D., et al. 2007. “Interdependence of Domestic Malaria Prevention Measures and Mosquito‐Human Interactions in Urban Dar es Salaam, Tanzania.” Malaria Journal 6: 126. 10.1186/1475-2875-6-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gething, P. W. , Patil A. P., Smith D. L., Guerra C. A., Elyazar I. R., Johnston G. L., Tatem A. J., and Hay S. I.. 2011. “A New World Malaria Map: Plasmodium falciparum Endemicity in 2010.” Malaria Journal 10: 378. 10.1186/1475-2875-10-378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay, S. I. , Sinka M. E., Okara R. M., Kabaria C. W., Mbithi P. M., Tago C. C., Benz D., et al. 2010. “Developing Global Maps of the Dominant Anopheles Vectors of Human Malaria.” PLoS Medicine 7(2): e1000209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hijmans, R. J. 2021. “Geographic data analysis and modeling [R package raster version 3.4‐10].” http://cran.stat.unipd.it/web/packages/raster/
- Holme, P. , and Masuda N.. 2015. “The Basic Reproduction Number as a Predictor for Epidemic Outbreaks in Temporal Networks.” PLoS One 10(3): e0120567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James, S. L. , Gubbins P., Murray C. J., and Gakidou E.. 2012. “Developing a Comprehensive Time Series of GDP Per Capita for 210 Countries from 1950 to 2015.” Population Health Metrics 10: 12. 10.1186/1478-7954-10-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, L. R. , Ben‐Horin T., Lafferty K. D., McNally A., Mordecai E., Paaijmans K. P., Pawar S., and Ryan S. J.. 2015. “Understanding Uncertainty in Temperature Effects on Vector‐Borne Disease: A Bayesian Approach.” Ecology 96: 203–13. [DOI] [PubMed] [Google Scholar]
- Kern, P. , Cramp R. L., and Franklin C. E.. 2015. “Physiological Responses of Ectotherms to Daily Temperature Variation.” Journal of Experimental Biology 218: 3068–76. [DOI] [PubMed] [Google Scholar]
- Kirby, M. , and Lindsay S.. 2004. “Responses of Adult Mosquitoes of Two Sibling Species, Anopheles arabiensis and A. gambiae s.s. (Diptera: Culicidae), to High Temperatures.” Bulletin of Entomological Research 94: 441–8. [DOI] [PubMed] [Google Scholar]
- Knudsen, A. B. , and Slooff R.. 1992. “Vector‐Borne Disease Problems in Rapid Urbanization: New Approaches to Vector Control.” Bulletin of the World Health Organization 70: 1–6. [PMC free article] [PubMed] [Google Scholar]
- Lunde, T. M. , Bayoh M. N., and Lindtjørn B.. 2013. “How Malaria Models Relate Temperature to Malaria Transmission.” Parasites & Vectors 6: 20. 10.1186/1756-3305-6-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons, C. L. , Coetzee M., Terblanche J. S., and Chown S. L.. 2012. “Thermal Limits of Wild and Laboratory Strains of Two African Malaria Vector Species, Anopheles arabiensis and Anopheles funestus .” Malaria Journal 11: 226. 10.1186/1475-2875-11-226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmood, F. 1997. “Life‐Table Attributes of Anopheles albimanus (Wiedemann) under Controlled Laboratory Conditions.” Journal of Vector Ecology 22: 103–8. [PubMed] [Google Scholar]
- Miazgowicz, K. , Shocket M., Ryan S., Villena O., Hall R., Owen J., Adanlawo T., et al. 2020. “Age Influences the Thermal Suitability of Plasmodium falciparum Transmission in the Asian Malaria Vector Anopheles stephensi .” Proceedings of the Royal Society B 287: 1931. 10.1098/rspb.2020.1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mordecai, E. A. , Caldwell J. M., Grossman M. K., Lippi C. A., Johnson L. R., Neira M., Rohr J. R., et al. 2019. “Thermal Biology of Mosquito‐Borne Disease.” Ecology Letters 22: 1690–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mordecai, E. A. , Cohen J. M., Evans M. V., Gudapati P., Johnson L. R., Lippi C. A., Miazgowicz K., et al. 2017. “Detecting the Impact of Temperature on Transmission of Zika, Dengue, and Chikungunya using Mechanistic Models.” PLoS Neglected Tropical Diseases 11(4): e0005568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mordecai, E. A. , Paaijmans K. P., Johnson L. R., Balzer C., Ben‐Horin T., de Moor E., McNally A., et al. 2013. “Optimal Temperature for Malaria Transmission Is Dramatically Lower Than Previously Predicted.” Ecology Letters 16: 22–30. [DOI] [PubMed] [Google Scholar]
- Moyes, C. L. , Temperley W. H., Henry A. J., Burgert C. R., and Hay S. I.. 2013. “Providing Open Access Data Online to Advance Malaria Research and Control.” Malaria Journal 12: 161. 10.1186/1475-2875-12-161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parham, P. E. , and Michael E.. 2009. “Modeling the Effects of Weather and Climate Change on Malaria Transmission.” Environmental Health Perspectives 118: 620–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeffer, D. A. , Lucas T. C., May D., Harris J., Rozier J., Twohig K. A., Dalrymple U., et al. 2018. “malariaAtlas: An R Interface to Global Malariometric Data Hosted by the Malaria Atlas Project.” Malaria Journal 17: 352. 10.1186/s12936-018-2500-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plummer, M. 2021. “rjags: Bayesian Graphical Models Using MCMC [R Package Rjags Version 4‐11].” https://https://cran.r-project.org/web/packages/rjags/index.html
- R Development Core Team . 2017. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. https://www.R-project.org/. [Google Scholar]
- Ricci, F. 2012. “Social Implications of Malaria and their Relationships with Poverty.” Mediterranean Journal of Hematology and Infectious Diseases 4(1): e2012048. 10.4084/MJHID.2012.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryan, S. J. , McNally A., Johnson L. R., Mordecai E. A., Ben‐Horin T., Paaijmans K., and Lafferty K. D.. 2015. “Mapping Physiological Suitability Limits for Malaria in Africa under Climate Change.” Vector‐Borne and Zoonotic Diseases 15: 718–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott, L. M. , and Janikas M. V.. 2010. “Spatial Statistics in ArcGIS.” In Handbook of Applied Spatial Analysis, edited by Fisher M. M. and Getis A., 27–41. New York, NY: Springer Publishing. [Google Scholar]
- Shapiro, L. L. , Whitehead S. A., and Thomas M. B.. 2017. “Quantifying the Effects of Temperature on Mosquito and Parasite Traits that Determine the Transmission Potential of Human Malaria.” PLoS Biology 15(10): e2003489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheather, S. 2009. A Modern Approach to Regression with R. New York, NY: Springer Texts in Statistics. 10.1007/978-0-387-09608-7. [DOI] [Google Scholar]
- Shocket, M. S. , Verwillow A. B., Numazu M. G., Slamani H., Cohen J. M., El Moustaid F., Rohr J., Johnson L. R., and Mordecai E. A.. 2020. “Transmission of West Nile and Five Other Temperate Mosquito‐Borne Viruses Peaks at Temperatures between 23 °C and 26 °C.” eLife 9: e58511. 10.7554/eLife.58511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinka, M. E. , Bangs M. J., Manguin S., Chareonviriyaphap T., Patil A. P., Temperley W. H., Gething P. W., et al. 2011. “The Dominant Anopheles Vectors of Human Malaria in the Asia‐Pacific Region: Occurrence Data, Distribution Maps and Bionomic précis.” Parasites & Vectors 4: 89. 10.1186/1756-3305-4-89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinka, M. E. , Bangs M. J., Manguin S., Coetzee M., Mbogo C. M., Hemingway J., Patil A. P., et al. 2010. “The Dominant Anopheles Vectors of Human Malaria in Africa, Europe and the Middle East: Occurrence Data, Distribution Maps and Bionomic Précis.” Parasites & Vectors 3: 117. 10.1186/1756-3305-3-117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinka, M. E. , Bangs M. J., Manguin S., Rubio‐Palis Y., Chareonviriyaphap T., Coetzee M., Mbogo C. M., et al. 2012. “A Global Map of Dominant Malaria Vectors.” Parasites & Vectors 5: 69. 10.1186/1756-3305-5-69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinka, M. , Pironon S., Massey N., Longbottom J., Hemingway J., Moyes C., and Willis K.. 2020. “A New Malaria Vector in Africa: Predicting the Expansion Range of Anopheles stephensi and Identifying the Urban Populations at Risk.” Proceedings of the National Academy of Sciences USA 117: 24900–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snow, R. W. , Guerra C. A., Noor A. M., Myint H. Y., and Hay S. I.. 2005. “The Global Distribution of Clinical Episodes of Plasmodium falciparum Malaria.” Nature 434: 214–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tadesse, F. G. , Ashine T., Teka H., Esayas E., Messenger L. A., Chali W., Meerstein‐Kessel L., et al. 2021. “ Anopheles stephensi Mosquitoes as Vectors of Plasmodium vivax and P. falciparum, Horn of Africa, 2019.” Emerging Infectious Diseases 27: 603–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takken, W. , and Lindsay S.. 2019. “Increased Threat of Urban Malaria from Anopheles stephensi Mosquitoes, Africa.” Emerging Infectious Diseases 25: 1431–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor, R. A. , Ryan S. J., Lippi C. A., Hall D. G., Narouei‐Khandan H. A., Rohr J. R., and Johnson L. R.. 2019. “Predicting the Fundamental Thermal Niche of Crop Pests and Diseases in a Changing World: A Case Study on Citrus Greening.” Journal of Applied Ecology 56: 2057–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tesla, B. , Demakovsky L. R., Mordecai E. A., Ryan S. J., Bonds M. H., Ngonghala C. N., Brindley M. A., and Murdock C. C.. 2018. “Temperature Drives Zika Virus Transmission: Evidence from Empirical and Mathematical Models.” Proceedings of the Royal Society B 285(1884): 20180795. 10.1098/rspb.2018.0795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tizifa, T. A. , Kabaghe A. N., McCann R. S., van den Berg H., Van Vugt M., and Phiri K. S.. 2018. “Prevention Efforts for Malaria.” Current Tropical Medicine Reports 5: 41–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villena, O. 2022. “oswaldov/Temperature impacts malaria transmission (v1.0.0).” Zenodo, software. 10.5281/zenodo.5874787. [DOI]
- World Health Organization . 2020. “World Malaria Report 2020: 20 Years of Global Progress and Challenges.” Technical Report. Geneva: WHO. https://who.int/publications/i/item/9789240015791
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1
Data Availability Statement
Data and code (Villena, 2022) are available on Zenodo: https://doi.org/10.5281/zenodo.5874787.


