Extracting Predictive Representations from Hundreds of Millions of Molecules

Abstract

The construction of appropriate representations remains essential for molecular predictions due to intricate molecular complexity. Additionally, it is often expensive and ethically constrained to generate labeled data for supervised learning in molecular sciences, leading to challenging small and diverse data sets. In this work, we develop a self-supervised learning approach to pretrain models from over 700 million unlabeled molecules in multiple databases. The intrinsic chemical logic learned from this approach enables the extraction of predictive representations from task-specific molecular sequences in a fine-tuned process. To understand the importance of self-supervised learning from unlabeled molecules, we assemble three models with different combinations of databases. Moreover, we propose a protocol based on data traits to automatically select the optimal model for a specific task. To validate the proposed method, we consider 10 benchmarks and 38 virtual screening data sets. Extensive validation indicates that the proposed method shows superb performance.

Graphical Abstract

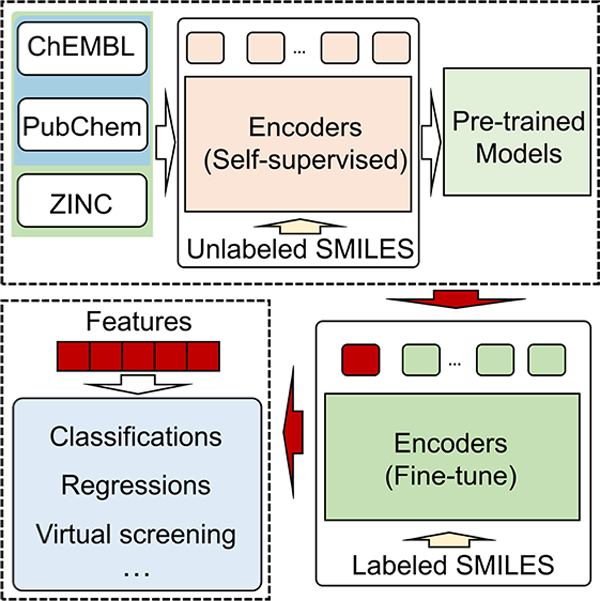
In the past few years, machine learning (ML) has profoundly changed the landscape of science, engineering, technology, finance, industry, defense, and society in general. It has become a new approach for scientific discovery, following traditional experiments, theories, and simulations. In image analysis, deep learning algorithms, such as convolutional neural networks (CCN), can automatically extract image features without resorting to hand-crafted descriptors. However, for molecular predictions, due to the internal complexity of molecules, generating molecular representations or descriptors is an essential issue that is as important as data and algorithm in determining ML performance.^1,2 It is a procedure that translates the chemical information in a molecule into a set of “machine” understandable features. Although many molecular descriptors of macroscopic physicochemical properties are obtained via experimental measurements, a wide variety of others has been extracted from molecular microscopic information, that is, atomic constitution, electron density, molecular structures, etc. Various fingerprints have been developed in the past few decades.^3,4 Two-dimensional (2D) fingerprints, such as ECFP, MACCS, Estate1, Daylight, etc.^3,5 are a class of commonly used molecular representations and can be extracted from molecular connection tables without three-dimensional (3D) structural information. Many popular software packages generate 2D fingerprints;^6,7 however, 2D fingerprints lack the 3D structural information on molecules, such as stereochemical information.

In recent years, molecular fingerprints based on 3D structures have been developed to capture the 3D spatial information on molecules.⁸ However, the complexity and elemental diversity of molecular structures are major obstacles to the design of 3D fingerprints.¹ A variety of advanced mathematics-based 3D molecular representations, including algebraic topology,⁹ differential geometry,¹⁰ and algebraic graph-based methods,¹¹⁻¹³ were devised to generate molecular fingerprints aimed at encoding 3D and elemental information on molecules by mathematical abstraction. These methods have been highly successful in the classification of proteins and ligands, as well as in the prediction of solubility, solubility free energy, protein−ligand binding affinity, protein folding stability changes after mutations, and mutation-induced protein−protein binding affinity changes.¹ However, these approaches rely on high-quality 3D molecular structures, which limits their applications.

Deep learning (DL) has been a successful and powerful tool in various fields, such as natural language processing,¹⁴ image classification,¹⁵ and bioinformatics.^16,17 Conventional deep learning methods are constructed based on deep neural networks (DNN). In molecular sciences, the input to these models is usually a pre-extracted molecular descriptor, for example, ECFP, MACCS. However, this type of input may not preserve certain molecular information and thus compromise the performance of downstream predictive tasks.^18,19 Additionally, DNN usually requires a large amount of data for training, which constrains the application of some supervised learning DL methods in molecular sciences. To address these issues, data-driven unsupervised learning methods have been developed in recent years, such as the recurrent neural network (RNN)-based autoencoder model²⁰ and the variational autoencoder model.²¹ These models are trained directly by a set of large and low-level molecular representations, that is, the simplified molecular input line entry specification (SMILES) representation.²² Some publicly available data sets, such as ChEMBL,²³ PubChem,²⁴ and ZINC,²⁵ provide a large amount of unlabeled SMILES data, which allows DNN autoencoder to be better trained. Typically, an autoencoder consists of two neural networks, encoder, and decoder. The encoder converts the input, for example, the SMILES of a molecule, into a continuous (latent space) representation of a fixed size. The decoder, on the other hand, takes the latent space representation as input and aims to convert it into the probability distribution of the design target of interest, which can be translated into a molecule, the next possible word, or some predicted event. The entire autoencoder network is trained to minimize the error of predicting the target of the interest. The latent representation in the model is often used as a molecular fingerprint for other tasks, such as molecular property prediction,²⁶ or virtual screening. In these tasks, the decoder is only used as a training device and does not contribute to the final prediction. The training of the decoder also takes up a large amount of computer time and memory.

In this work, we develop a self-supervised learning (SSL) platform to pretrain DL networks with over 700 million unlabeled SMILES data. With the data-mask pairs constructed from the unlabeled data, the SSL approach allows the model to be trained in a supervised learning fashion.²⁷ In particular, for SMILES data, we construct pairs of real SMILES and masked SMILES by hiding a certain percentage of symbols that have a specific physicochemical meaning.¹³ We use a transformer model based on an attention mechanism for SSL.²⁸ This model has higher parallelism capability and training efficiency compared to RNN-based models. Because of the advantage of SSL, we avoid the need to construct a complete encoder− decoder framework and achieve the encoding of SMILES using only the encoder, a bidirectional encoder transformer (BET). Similar to the cloze test practice in language learning, the model inferred the symbols of the masked part by learning the unprocessed symbols in SMILES during the pretraining process, so that the purpose of understanding SMILES language can be achieved. To investigate the benefit of excessively large training data sets, we constructed three models based on ChEMBL, the union of ChEMBL and PubChem, and the union of ChEMBL, PubChem, and ZINC, with data sizes ranging from over one million to over 700 million. We show that, for a given predictive task associated with a data set, the model trained on the largest data set is not necessarily the best one. To enable the automatic selection of the optimal model for a specific task, we construct a data set analysis module based on the Wasserstein distance to characterize the similarity between data set distributions. Using this module, the optimal pretrained model can be selected for any customized data set. Subsequently, the selected pretrained model is fine-tuned using the corresponding data set to obtain a task-specific molecular fingerprint. To investigate the accuracy, robustness, and usefulness of the proposed SSL platform, we consider a total of 48 data sets, including five regression data sets, five classification data sets, and two virtual screening tasks with 17 and 21 additional data sets. Extensive numerical experiments indicate the proposed platform is an accurate and robust strategy for generating molecular data representations and ML predictions in molecular sciences.

Data Processing for Self-Supervised Learning.

To enable the self-supervised learning, in this work, we preprocess the input SMILES. A total of 51 symbols, as listed in Supporting Information Table S1, are used to split these SMILES strings. ‘<s>‘ and ‘<\s>‘ two special symbols were added to the beginning and end of each input. The maximum length of the input data is limited to 256. Since the length of SMILES varies from molecule to molecule, the ‘<pad>‘ is used as a padding symbol to fill in short inputs to reach the preset length. In the masking process, 15% of the symbol of the SMILES will be operated. Among these 15% of symbols, 80% of symbols were masked, 10% of the symbols were unchanged, and the remaining 10% were randomly replaced. The strategy of dynamically changing the masking pattern was applied to the pretraining data.²⁹

Bidirectional Encoders of Transformer for Molecular Representation.

Unlike sequences learning models such as RNN-based models, transformer is based on an attention mechanism,²⁸ which is used to capture the importance of each symbol in the input sequence. The design of independent positional embedding allows the transformer to have better parallelism which dramatically reduces the training time for massive data. This feature also makes the training of Set CPZ (over 700 million data) possible. Inspired by the representation model for natural language processing called BERT introduced by Devlin et al.,³⁰ in the present work, only the encoder of the transformer is applied. The input to BET is a SMILES string. Unlike the sentences in a traditional BERT for natural language processing, the SMILES strings of different molecules are not logically linked. Therefore, we only keep the masked learning task in the prelearning process, which is to mask part of the input SMILES symbols during the training process and then recover the masked symbols by training.

The basic structure of our BET is the same as the encoders of traditional Transformers.²⁸ Specifically, our BET contains eight encoder layers, each encoder layer contains two sublayers, which are the self-attention layer and the fully connected feed-forward layer. The embedding dimension of each symbol is set to 512. For the self-attention layer, the number of the self-attention header is 8, while the embedding size of fully connected feed-forward layers is 1024. The maximum sequence length is set to 256, including the start and terminate symbols. The Adam optimizer is used in both pretraining and fine-tuning stages, the weight decay is set to 0.1. In addition, a warming-up strategy is applied for the first 5000 updates; the maximum learning rate is set to 0.0001. To ensure the model fully converges, each pretrained model is updated over 200 million times. The loss is defined by cross-entropy, which was applied to measure the difference between the predicted symbols and the real symbols at the masked position. The model is trained on six Tesla V100-SXM2 GPUs and the maximum sequence number in each GPU is set to 64. The structure of BET is shown in Figure S5.

For a specific downstream task, we use supervised learning to fine-tune the pretrained model if the data set is labeled. Otherwise, we still use the self-supervised learning method to fine-tune the model. There is no additional preprocessing for the input SMILES. The Adam optimizer is set as the same as that of pretraining. The warm-up strategy is used for the first 2 epochs, and a total of 50 epochs are trained for each data set. The mean square error and cross-entropy are used in the fine-tuning stage for the regression task and classification task, respectively. The process of fine-tuning is shown in Figure S5. The molecular representation was generated from the last encoder layer’s embedding vector of the first symbol, that is, ‘<s>’.

Wassertein Distance Analysis of Data Sets.

In this work, the Wasserstein distance is used to measure the correlation between two distributions. Mathematically, the Wasserstein distance is a distance function defined between probability distributions on a given metric space M. For p ≥ 1, the collection of all probability distribution on M with finite pth moment is denoted as P_p(M). And the pth Wasserstein distance between two probability distributions μ and v in P_p(M) is defined as

$$W_p\left(\mu ,\nu \right):={\left(\underset{\gamma \in \text{Γ}\left(\mu ,\nu \right)}{\inf }{\int }_{M\times M}\text{d}{\left(x,y\right)}^{p}d\gamma \left(x,y\right)\right)}^{1/p}$$ (1)

where Γ(μ, v) denotes the collection of all distributions on M × M with marginals μ and v on the first an second factors, respectively. Also, the Wasserstein metric is equivalently defined by

$$W_p\left(\mu ,\nu \right)={\left(\inf \mathbf{E}\left[d{\left(X,Y\right)}^p\right]\right)}^{1/p}$$ (2)

where E represents the expected value and the infimum is taken over all joint distributions of the random variables X and Y with marginals μ and ν, respectively.

For a downstream data set, a set of distributions, including the distributions of 61 symbols, SMILES length distribution, and the distribution of SMILES symbol types can be generated. Thus, the similarity of the customized data set to each pretraining set is determined by 63 Wasserstein distances. Since we have three pretraining data sets, a vector length of 189 features, denoted as X, will be used to determine the most appropriate pretraining model. Specifically, a ridge model was introduced to calculate the coefficient score for each pretraining data set. The ridge coefficients minimize a penalized residual sum of squares:

$$\underset{w}{\min }{‖X_w-y‖}_2^2+\alpha {‖w‖}_2^2$$ (3)

where α > 0 is the complexity parameter, and it controls the amount of shrinkage.³¹ Here y corresponds to the index of the three pretraining models, that is, 0, 1, and 2. Additionally, considering the influence of feature dimensionality on the accuracy of the least-squares, we use the principal component analysis (PCA) method to downscale the feature X. Figure S6 shows the accuracy of the model in selecting the best model as the feature dimension increases.

RESULTS AND DISCUSSION

We present the proposed self-supervised learning platform for molecular predictions. The combination of data sets, that is, ChEMBL,²³ PubChem,²⁴ and ZINC,²⁵ was used as the pretraining data sets, as listed in Table 1. For the evaluation of the proposed platform, we carried out five classification and five regression tasks, as listed in the Table 1. Two VS experiments were performed on overall 38 data sets, including 21 targets form the Directory of Useful Decoys (DUD) and 17 targets of the Maximum Unbiased Validation (MUV) data sets.^32,33

Table 1.

Three Pretraining Datasets and 10 Datsets Used for Benchmarking Our Platform

data sets	task type	compounds	split	metric
ChEMBL(C)23	pretrain	1 941 410		accuracy
ChEMBL and PubChem(CP)24	pretrain	103 395 400		accuracy
ChEMBL, PubChem, and ZINC(CPZ)25	pretrain	775 007 514		accuracy
Ames mutagenicity (Ames)34	classification	6 512	8:1:1	ROC-AUC
β-secretase 1 inhibition (bace)35	classification	1 513	8:1:1	ROC-AUC
blood−brain barrier penetration (bbbp)36	classification	2 039	8:1:1	ROC-AUC
toxicity in honeybees (beet)37	classification	254	8:1:1	ROC-AUC
ClinTox (Clinical trial results)38	classification	1 478	8:1:1	ROC-AUC
aqueous solubility (ESOL)39	regression	1 128	8:1:1	R 2
lipophilicity (Lipop)23	regression	4 200	8:1:1	R 2
free solvation database (FreeSolv)40	regression	642	8:1:1	R 2
LogS41	regression	4 801	8:1:1	R 2
DPP-4 inhibitors (DPP4)42	regression	3 933	8:1:1	R 2

Self-Supervised Learning Platform (SSLP).

As shown in Figure 1, there are four main modules involved in the platform, which are the pretraining data sets module (i.e., blue rectangle), data set analysis module (i.e., purple rectangle), pretrained model module (i.e., green rectangle), and fine-tune module (i.e., yellow rectangle). In the pretraining data sets module, the three pretraining data sets are obtained by combining three publicly available data sets, that is, ChEMBL,²³ PubChem,²⁴ and ZINC.²⁵ Set C represents only ChEMBL and was used as the pretraining data. Set CP represents the combination of data sets ChEMBL and PubChem. And Set CPZ represents the union of all three data sets. For all three pretraining data sets, duplicated compounds were removed after the combination of data sets. In the pretrained model module, we use a self-supervised learning strategy, especially the BET,^28,30 to obtain our pretrained models. In the pretraining stage, we mask the unlabeled data in the data set and then use the BET model to predict the masked parts of the SMILES for self-supervised learning. For the three pretraining data sets, that is, set C, set CP, and set CPZ, we can obtain three pretrained models corresponding to model C, model CP, and model CPZ. Each pretrained model can provide a self-supervised learning fingerprint (SSL-FP) for downstream tasks.

Figure 1.

Illustration of the self-supervised learning platform. (a) Three public data sets are involved in the pretraining data sets module (blue rectangle). Set C only contains the ChEMBL data set. Set CP consists of ChEMBL and PubChem data sets, and Set CPZ contains ChEMBL, PubChem, and ZINC data sets. (b) Based on those three data sets, three pretrained models (green rectangle) are obtained by self-supervised learning, which is Model C, Model CP, and Model CPZ, respectively. c The data set analysis module (purple rectangle) contains the Wasserstein distance analysis module and decision module. It will point to the best pretrained model for a specific data set. (d) The fine-tune module (yellow rectangle) fine-tunes the pretrained model using a specific data set. Finally, the fingerprints are generated from the fine-tuned model and used as input for the downstream machine learning tasks. (e) The correlations between pretraining data sets and downstream data sets, including five classifications (Classif.) and five regressions (Regre.) data sets, and pretrained data sets C, CP, and CPZ. (f) Normalized predicted results of the fingerprints from pretrained model C for DPP4, ESOL, FreeSolv, Lipophilicity (Lipop), and LogS five regression data sets.

For the data set analysis module, we use the Wasserstein distance analysis submodule and the decision submodule to decide the optimal model for the downstream task. First, we generated the distribution of the proportion of each symbol in each SMILES in the data set. The distribution of elemental symbols and the distribution of special symbols for the three pretraining data sets are shown in Figure 2a,b. It can be found that commonly occurred elements, including carbon, oxygen, and nitrogen, in the molecule, have an abundant ratio in SMILES strings. Since some special symbols always appear in pairs in SMILES, such as ‘(‘ and ‘)’, ‘[‘ and ‘]’, the distribution of these symbols is the same. All 61 symbols used in this work are listed in Table S1, and the distributions of complete symbols are shown in Figure S1. Additionally, we also counted the distribution of the number of symbol types contained in each SMILES, as shown in Figure 2c. To analyze a specific data set, we can also generate these distributions. In the second step, on the basis of the various distributions obtained (63 in total), we use the Wasserstein distance analysis submodule to analyze the correlation between different data sets in several ways. Finally, using the decision submodule, a ridge linear regression model is used to determine the most suitable SSLP for a specific small data set. Since the symbols in SMILES all have corresponding meanings, using the data set analysis module, we can make a comprehensive comparison of the data sets from these distributions. In the SSLP, the fine-tune module is used to generate the task-specific fingerprints for the specific data set. We can fine-tune the selected pretrained model by using the specific data set and generate the corresponding SSL-FPs for downstream machine learning tasks.

Figure 2.

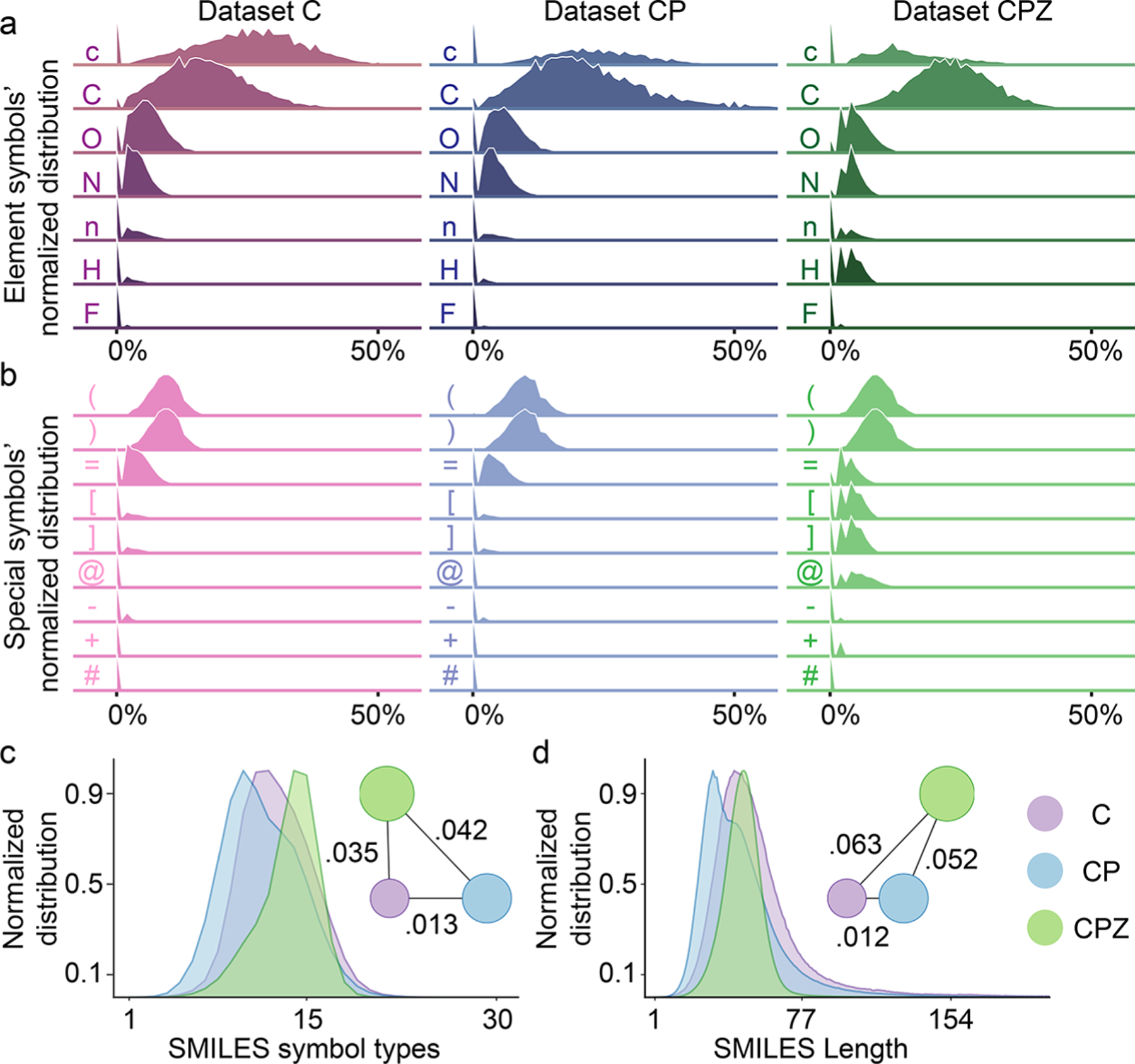
Data sets analysis for the pretraining data sets. (a and b) The normalized distributions of elements and special symbols within SMILES in data set ChEMBL (C), the concatenation of ChEMBL, and PubChem (CP), and the concatenation of ChEMBL, PubChem, and ZINC (CPZ), respectively. The x-axis represents the proportion of each symbol in a SMILES string, and the y-axis represents the proportion of SMILES in the data set. (c and d) The normalized distributions of SMILES symbol types within SMILES and SMILES length in data set C, CP, and CPZ. The x-axis represents the number of different symbols per SMILES. The circles represent three data sets, and the circle size corresponds to the data set size. The correlation of each pair of data sets is determined by the Wasserstein distance.

Evaluation on Regression and Classification Tasks.

To evaluate the proposed platform, we performed five classification and five regression tasks, and all these data sets are listed in Table 1. In addition, we compare three different fingerprints, namely, commonly used circular fingerprints³ (circular 2D, ECFP), autoencoder-based fingerprints (auto-FPs),²⁰ and the fingerprints generated from our platform (SSL-FPs). For the ECFP, three radii (1, 2, and 3) and three folding lengths (512, 1012, and 2048) are used in its generation, which results in nine different parameter settings. In the downstream tasks, we carry out our evaluation by using some standard machine learning algorithms from the scikit-learn library, namely, gradient boosted decision tree (GBDT), random forest (RF), and support vector machine (SVM).⁴³ To avoid overtuning the machine learning algorithm and to better compare the performance between fingerprints, we prefix a set of general machine learning parameters, as shown in Table S2. To reduce the systematic errors in the machine learning process, we applied for different random numbers and split all the data sets into training, validation, and test sets 10 times in the ratio of 8:1:1. For the split data sets, we repeated the computation five times for each machine learning model. The best-performing model of the three models was used for the final results. Three machine learning algorithms are used in this work, namely, GBDT, RF, and SVM.⁴³ To better compare the performance of molecular fingerprints, we did not oversearch for the best machine learning model hyperparameters. Therefore, for these three machine learning methods, we simply set universal parameters based on the amount of data in the training set for the downstream task, as shown in Table S2. The predictions from the model with the best performance were chosen as the final results. In this study, the squared Pearson correlation coefficient (R²) is used in regression tasks. The area under the receiver operating characteristic convex hull (AUC-ROC) is used to evaluate the performance of the model on classification tasks. All the definitions of related metrics are given in Supplementary Note 1.

Figure 3 panels a and b show the results of the three types of fingerprints on 10 tasks. The toxicity in the honey bees (beet) data set locates positive compounds above the threshold and negative below the selected threshold based on selected toxicity thresholds. In this work, 100 μ/bees were selected as the threshold. SSL-FPs, auto-FPs, and circular 2D FPs achieved the best results in 3, 4, and 3 tasks, respectively. For circular 2D fingerprints, in each task, we pick the best fingerprint from nine parameter settings for comparison. This means that 2D fingerprints, while still widely used, require a lot of experimentation to pick the best parameters, which limits their versatility. Although the SSL-FPs did not achieve the best performance on all tasks, they are still very competitive for most prediction tasks. SSL-FPs and auto-FPs are latent space vectors obtained from the deep learning of millions of compounds. As a result, they are robust for small data sets. For example, FreeSolv is a small data set with 642 samples. Both our SSL-FPs (R² = 0.755) and auto-FPs (R² = 0.713) perform better than 2D molecular fingerprints (best R² = 0.670). The complete results with multiple metrics are listed in Table S3. We also compared the fingerprints generated by different pretrained models, as shown in Figure 3c,d. It is interesting to see that model C achieved the best performance in 7 of the 10 tasks. For pretrained model C, we only applied about 1.9 million unlabeled data for pretraining, while models CP and CPZ were pretrained with over 103 million and 700 million data, respectively. This indicates that the performance of downstream molecular fingerprinting is not entirely determined by the size of the amount of pretrained data. In summary, for molecular property predictions with data sizes ranging from 254 to 6512, our SSL-FPs achieve comparable performance in most cases, indicating their robustness. We also found that the choice of a particular pretrained model is not absolutely correlated with the size of pretrained data. For all molecular property prediction tasks in this work, we performed 50 calculations, that is, 10 random splits of data, and 5 replicate machine learning experiments for each data split. Error bars are given in Figure 3.

Figure 3.

Results of the five classification and five regression tasks. (a and b) The comparison between our FPs (ours), autoencoder FPs (auto), and circular 2D FPs (ECFP, nine parameter settings). For circular 2D fingerprints, we choose the best fingerprint among the nine parameter settings for each task as the final result. These three fingerprints achieved the best results in 3, 4, and 3 tasks, respectively. (c,d) The comparison between the fingerprints from pretrained model C, model CP, and model CPZ. These three fingerprints produced the best performance on 7, 2, and 1 tasks of 10 tasks, respectively. All the results were generated by the best machine learning model among GBDT, RF, and SVM.

Ligand-Based Virtual Screening Experiments.

The basic idea of ligand-based virtual screening methods is to use existing information, for example, similarity, in known active ligands to rank a large set of compounds of their activity on certain targets. It is based on the assumption that similar compounds have similar biological activity. To estimate the performance of our SSL-FPs on VS experiments, we followed the benchmark protocol of Riniker et al.,⁴⁴ and 28 2D molecular fingerprints were used in the comparison as well as the auto-FPs. Since for VS experiments, there is no corresponding label for each compound, our SSL-FPs are directly derived from pretrained models. For each target in the DUD and MUV databases, five active compounds in the corresponding data set were randomly selected, and the remaining molecules in the data set were ranked by their average similarity to the selected active compounds. For the molecular fingerprints defined in the discrete spaces, that is, 28 molecular 2D fingerprints, the Tanimoto similarity was used as the metric. The cosine similarity is used for the molecular fingerprints defined in the continuous space, such as SSL-FPs and auto-FPs. To eliminate the effect of randomness on the VS experiments, we repeated the experiment 50 times for all fingerprints. The performance of VS experiments was evaluated by the mean ROC-AUC over 50 repetitions for each data set in DUD and MUV databases.

The results of the VS experiments for each target in the DUD database are shown in Figure 4a, and Figure 4b shows the results of the MUV database. The red diamond represents our SSL-FPs, specially generated from model C and the green circle represents the results of auto-FPs. The blue triangle is the 2D laval fingerprint, which is the best performing fingerprint among all 28 2D fingerprints. The color of the background in the figure is the same as the color of the best performing FPs in this target. The lightly colored scattered dots in the figure indicate 50 independent experiments. In the DUD data sets, our SSL-FPs have a smaller variance. Figure 4c shows the summary of all VS experiments, in which our SSL-FPs obtained the best results in 18 out of 38 data sets. The auto-FPs, on the other hand, obtained the best results in seven data sets, while laval obtained the best performance in only six tasks. The fingerprint ap obtained the best performance in seven tasks, of which six were in the MUV. Although our SSL-FPs do not achieve the best results on all data sets, it is easy to notice that our molecular fingerprinting can still show close performance on those tasks that fail to achieve the best result, such as the set ache and set ar data sets in DUD. To further measure the superiority of individual molecular fingerprints across all data sets, we calculated the average superiority, which is the average of the percentage of each molecular fingerprint outperforming the next best performing molecular fingerprint in the respective best performing data set. The average superiority aims to measure the superiority of molecular fingerprints across data sets. As listed in Table 2, our SSL-FPs showed the highest average superiority in both DUD and MUV, with 8.02% and 5.41%, respectively. Although fingerprint ap obtained the best performance in MUV across six data sets, its average superiority was only 3.76%, lower than that of the SSL-FPs and laval which indicates that other molecular fingerprints can also obtain very close performance in these data sets. It is worth noting that in the comparison, we selected the best 2D fingerprint from 28 2D fingerprints to compare with our molecular fingerprint, which means that our SSL-FPs showed stability, robustness, and superiority to these molecular fingerprints in VS experiments. The complete results for all fingerprints, including 28 types 2D fingerprints, auto-FPs, and our SSL-FPs, are listed in Table S4 and Table S5.

Figure 4.

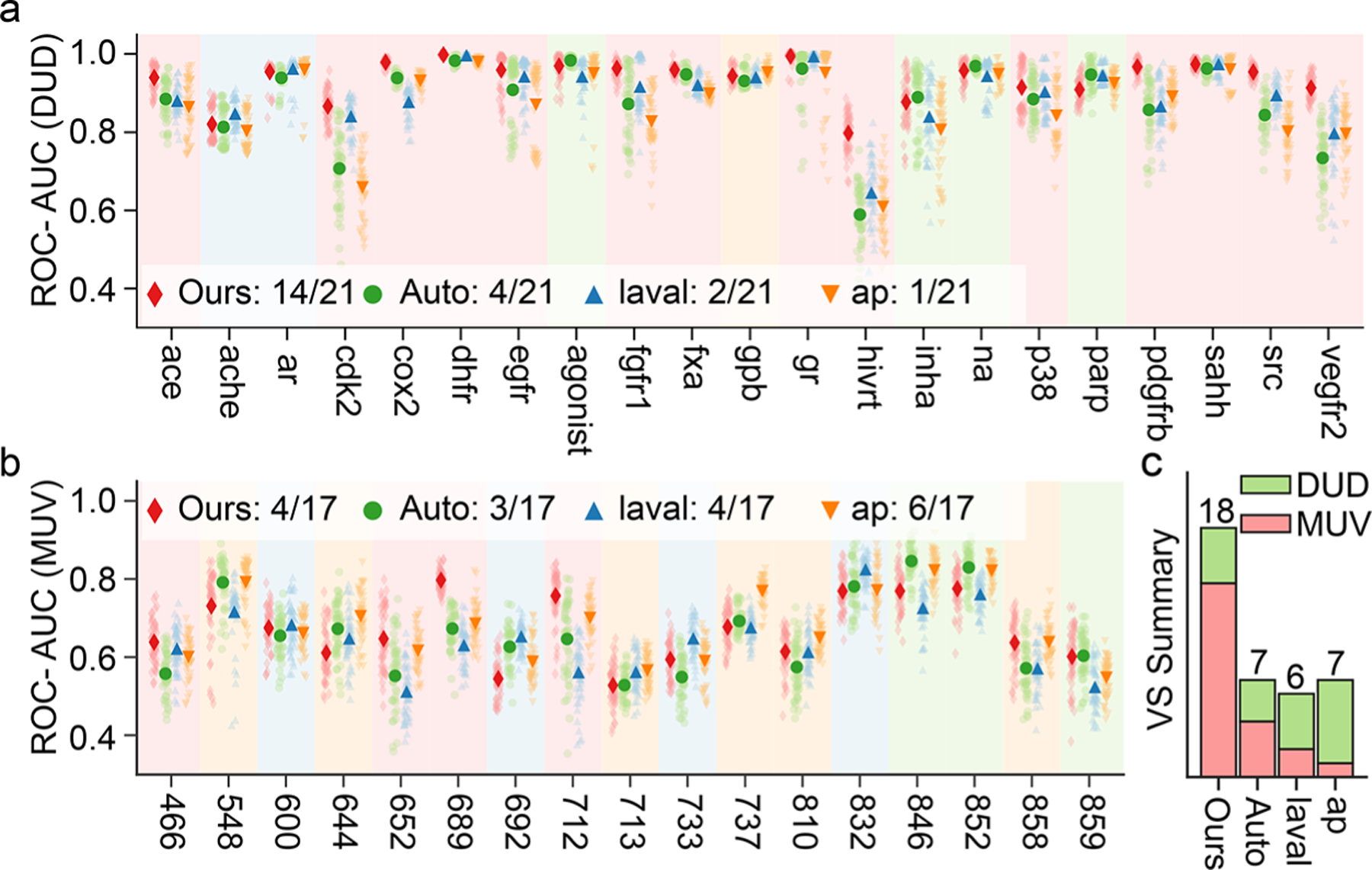
Results of the VS experiments for each target for the overall best fingerprints. (a,b) ROC-AUC of the VS experiments for DUD and MUV data sets for the fingerprint from model C (ours, red diamond), autoencoder fingerprint (auto, green circle), 2D fingerprint laval (laval, blue triangle), and 2D fingerprint ap (ap, orange triangle). The light-colored scattered dots indicate 50 independent experiments, while the highlighted data points indicate the average value. For each data set, the background color in the figure corresponds to the best performing fingerprint color. In the VS experiment, for the DUD database, fingerprint laval was the best performing fingerprint among 28 2D fingerprints, and in the MUV database, fingerprint ap was the best performing one among all the 2D fingerprints. (c) Summary of the VS experiments concluded that the four fingerprints, ours, auto, laval, and ap, obtained the best performance on 18, 7, 6, and 7 data sets, respectively.

Table 2.

Average Superiority of the Four Molecular Fingerprints, SSL-FPs, auto-FPs, laval, and ap, in the Two Databases DUD (21 Targets) and MUV (17 Targets)

	SSL-FPs	auto-FPs	laval	ap
MUV
avg superiority	8.02%	1.51%	5.01%	3.76%
DUD
avg superiority	5.41%	1.07%	1.80%	0.85%

Apply Self-Supervised Learning (SSL) in the Pretraining.

Self-supervised learning has been used in different fields, such as representation learning and natural language processing. It provides an efficient strategy to utilize large unlabeled data. In particular, this strategy learns from unlabeled data by constructing data-mask pairs, and this is called self-supervised learning. In molecular sciences, creating property labels through experiments or first-principle calculations can consume much time and resources. Therefore, it is often difficult to obtain a large number of property labels for deep neural network-based supervised learning. It is worth noting that the availability of large public chemical databases such asChEMBL, PubChem, and ZINC have provided massive unlabeled molecules. Additionally, the sequence-based representations of molecules such as SMILES strings have enabled the application of some techniques in the field of natural language processing to molecular sciences. Specifically, in the pretraining stage, we select a certain percentage of SMILES symbols and process them in three ways: masking, random replacement, or leaving them unchanged. The model is then trained to predict preselected symbols based on unprocessed SMILES information. This process is an unlabeled data-enabled supervised learning.

In this work, we applied the SSL strategy to train different BET-based models using three data sets, that is, Set C, Set CP, and Set CPZ (listed in Table 1). For a specific downstream task, such as a regression task, we simply use the task-specific data set as input data to fine-tune the model so that task-specific molecular fingerprints can be generated from the fine-tuned model. We carry out the fine-tuning process to adapt the model to a specific task, allowing the resulting molecular descriptors to focus on relevant task-based information, thereby improving the accuracy of downstream tasks. Figure 1f shows the comparison of normalized predicted values with true values obtained by the downstream machine learning algorithm using SSL-FPs generated from model C. The majority of experimental points are on the diagonal, and the average R² for the five regression tasks is 0.955, indicating that the predictions based on SSL-FPs are in high agreement with the experimental values. Figure S3 shows the comparison between true values and the predicted results obtained from SSL-FPs generated by model CP and model CPZ with an average R² of 0.953 and 0.952, respectively. On the other hand, the pretrained model itself is obtained based on the reconstructed molecular information from SMILES and thus can also be used directly to generate molecular descriptors. In the present work, all molecular fingerprints used in VS experiments are obtained directly from the pretrained model. As shown in Figure 4, the SSL-FPs from pretrained model C can also achieve 18 best results over 38 tasks.

In contrast to the encoder-decoder structure of traditional autoencoder models, in this work, our model is based on the self-supervised learning approach to pretrain the model. This approach allows the model to infer information on locations that have been ‘masked’ based on known information, that is, SMILES information on locations that have not been processed. Eventually, the model is allowed to learn the syntax of SMILES and understand the meaning of SMILES. This ‘comprehension capability’ gained by the model can put BT-FPs ahead of traditional auto-FPs on some data sets, such as the data set of hivrt and 689 in virtual screening. In addition, as shown in Table 2 in the text, our SSL-FPs are also more superior to others. Moreover, the parallel computing capability of the transformer was a crucial element for us to engage over 700 million molecules in our training.²⁸ The structure of the BET is shown in Figure S4.

Cross Data Set Analysis.

Three models, that is, model C, model CP, and model CPZ, are trained respectively from Set C with about 1.9 million data, Set CP with over 103 million data, and Set CPZ with over 775 million data. Interestingly, the performance of the molecular descriptors generated from these models did not improve proportionally with the size of pretrained data. On the contrary, the model with the smallest pretraining data set (model C) gives the best overall result as shown in Figure 3c,d. For the VS experiments, a similar observation can be drawn from Table S4 and Table S5, where model C can perform even better. However, on some data sets, such as the LogS data set in the regression tasks, the best performance is obtained by model CP. On the basis of this observation, we hypothesize that the performance of a model for a task depends on the correlation of the task-specific data set with the pretraining data set. To verify our hypothesis, we developed a data set analysis module in our self-supervised learning platform, which aims to identify pretrained models that can provide the best performance.

On the basis of the composition of symbols in SMILES strings, we counted 61 common symbols and all the symbols listed in Table S1. For each type of symbol, we calculated its percentage in each SMILES. Therefore, for each data set, we can obtain a distribution from 0% to 100% for each symbol, as shown in Figure 2. For the organic small molecule database, we can see that the distribution of carbon, oxygen, and nitrogen are the widest in each data set, which indicates high diversity of these essential elements. In addition, the symbol ‘c’ represents the carbon element in the ring structure. As shown in Figure 2, the ring structure of data set C has a higher diversity compared to the data set CP and data set CPZ. For the special symbols, it can be noted that data set CPZ has higher diversity for symbol ‘[‘, symbol ‘]’, and symbol ‘+’ which indicates that there is a more charged atom in the data set. In addition to the symbolic analysis, we also statisticize the distribution of SMILES lengths and the distribution of the number of element types contained in SMILES in each data set, as shown in Figure 2c,d.

After collecting the various distributions of the data set, the Wasserstein distance is employed to count the distance between the corresponding statistical distributions of the data set. As shown in Figure 2d, the circles represent the three pretraining data sets, the size of each circle corresponds to the number of SMILES in the data set, and the lines between the circles represent the Wasserstein distance between the SMILES length distributions of the corresponding data sets. For the SMILES length distribution, the distance between data set C and data set CP is the closest. Similarly, Wasserstein distance analysis can perform for the SMILES symbol type analysis. Then, on the basis of the 63 distributions, we can obtain 63 Wasserstein distances between every two data sets. In this work, we conducted experiments on a total of 48 downstream data sets, including five classification data sets, five regression data sets, 21 DUD virtual screening data sets, and 17 MUV virtual screening data sets. By analyzing the correlation of these data sets with three pretraining data sets, we constructed a 189-dimensional feature vector based on Wasserstein distance for each small data set pair of the pretraining data set. In this work, a total of 48 data points is considered. On the basis of these data points, we further constructed a linear classification model. With this model, a customized data set can be analyzed to point to the most suitable pretrained model. As shown in Figure 1e and Figure S2, with our decision module, each downstream data set can get its confidence score to the pretraining data set, and the value is indicated by colored line segments in the figure.

Data Availability.

The pretraining used in this work is the combination of ChEMBL27, PubChem, and ZINC13 3D data sets that are publicly available at https://ftp.ebi.ac.uk/pub/databases/chembl/ChEMBLdb/releases/chembl_27/,https://ftp.ncbi.nih.gov/pubchem/Compound/, and http://files.docking.org/3D/, respectively. To ensure the reproducibility of this work, the 10 data sets used in this work, including five classification data sets (Ames, bace, bbbp, beet, ClinTox), and five regression data sets (ESOL, Lipophilicity, FreeSolv, LogS, and DPP4) are available at https://weilab.math.msu.edu/DataLibrary/2D/. The overall models and related code have been released as an open-source code and is also available in the Github repository: https://github.com/WeilabMSU/PretrainModels.