Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jul 22;13(30):6905–6911. doi: 10.1021/acs.jpclett.2c01169

Polaritonic Chemistry from First Principles via Embedding Radiation Reaction

Christian Schäfer 1,*
PMCID: PMC9358701  PMID: 35866694

Abstract

graphic file with name jz2c01169_0005.jpg

The coherent interaction of a large collection of molecules with a common photonic mode results in strong light-matter coupling, a feature that has proven highly beneficial for chemistry and has introduced the research topics polaritonic and QED chemistry. Here, we demonstrate an embedding approach to capture the collective nature while retaining the full ab initio representation of single molecules—an approach ideal for polaritonic chemistry. The accuracy of the embedding radiation-reaction ansatz is demonstrated for time-dependent density-functional theory. Then, by virtue of a simple proton-tunneling model, we illustrate that the influence of collective strong coupling on chemical reactions features a nontrivial dependence on the number of emitters and can alternate between strong catalyzing and an inhibiting effect. Bridging classical electrodynamics, quantum optical descriptions, and the ab initio description of realistic molecules, this work can serve as a guiding light for future developments and investigations in the quickly growing fields of QED chemistry and QED material design.

The self-consistent interaction between light and matter developed over recent years into a viable and important tool to nonintrusively shape chemistry and materials on demand. Specific resonator geometries (cavities) support a limited set of eigenmodes which couple strongly to matter, resulting in new quasiparticles, so-called polaritons. Typical realizations of those resonators range between nanometer-sized plasmonic structures, that can couple to individual molecules, and Fabry-Pérot cavities, in which many molecules couple collectively.1−6 Such a hybridization between cavity mode(s) and matter exists also in the absence of driving, in contrast to Floquet physics, which is often limited by induced heating and decoherence7,8—the mere existence of the confined modes can alter materials. This includes the control of photochemical reactions by coupling to electronic excitations,9−18 ground-state chemical reactions via vibrational strong coupling,19−24 and energy and charge transfer over macroscopic dimensions.25−31 Furthermore, notable progress in the construction of cavities10,32−36 has led to a steadily rising number of applications outside chemistry, ranging from polariton-mediated lasing,37−39 over material design,40−43 to quantum information theory.44−46

However, most of the so far existing chemically relevant applications couple many molecules collectively to a common cavity mode. On one hand, a predictive theoretical study of chemical processes requires a thorough description of the electronic and vibrational structure from first principles. On the other hand, a direct evaluation of large ensembles is prohibited by the quickly increasing computational cost. The vast majority of theoretical studies are therefore based on simplified models that possess a limited applicability to complex systems and chemical reactions. Descriptions from first-principles have been restricted to small numbers of molecules.47−53 Notable representatives are quantum-electrodynamical density-functional theory (QEDFT)54−57 and cavity coupled-cluster theory.58,59

By embedding the majority of the molecular ensemble into a local potential, we will discover a path to open first-principles techniques toward collective strong-coupling with arbitrary numbers of ensemble molecules and species. This approach represents an extension of the radiation-reaction ansatz derived in reference (47) and inherits its computational and conceptual simplicity, allowing an almost effortless implementation into existing time-dependent density-functional theory (TDDFT) libraries.

Electronic and nuclear dynamics influenced by light are governed by the nonrelativistic Hamiltonian:

graphic file with name jz2c01169_m001.jpg

with fixed Coulomb gauge ∇·A = 0. The electromagnetic fields follow Maxwell’s equation; self-consistency emerges when light and matter are solved simultaneously. As demonstrated in reference (47), the classical interaction with light can be efficiently accounted for via the transverse component of the dyadic Green tensor G⊥ with Er,⊥(r,ω) = iμ0ω ∫V dr′G⊥(r,r′,ω)·(−ej(r′,ω)). The Green tensor is the formal solution of Helmholtz’s equation60

graphic file with name jz2c01169_m002.jpg

and characterizes the electromagnetic environment. The microscopic paramagnetic current j serves as driving inhomogeneity, i.e., oscillating charges emit light. In addition, we have the freedom to assume that parts of the system behave as a local and a potentially isotropic linear medium εr and μr which shape via the Helmholtz equation the electromagnetic environment, represented by G. In this way, G can subsume large fractions of a system while we free computational resources for the microscopic system described by j. The local radiation-reaction potential V̂rr(t) = −R̂·Er,⊥(t), with Er,⊥(t) = Ft–1(iμ0ωG⊥(ω))∗Ṙ(t) and recalling that Ṙ(t) = ∫ dr(−ej(rt)), is obtained from the derivative of the dipole moment provided by the real-time TDDFT propagation. It acts on the microscopic currents via the Schrödinger equation and manifests the self-consistent interaction with transverse fields within the long-wavelength approximation. This allows us to extend, for example, TDDFT with the self-consistent classical interaction between an electromagnetic environment and matter by simply adding vrr(rt) = er·Er,⊥(t) to the usual Kohn–Sham equations. We will focus in the following on polaritonic chemistry, i.e., electromagnetic environments that embody Fabry–Pérot-like eigenmodes and a large number of emitters. Clearly, G, and with it the presented embedding radiation-reaction ansatz, is generic and able to account for any kind of complex environment.47

In the collective strong-coupling regime between many molecules and a cavity, single photon processes dominate, and the individual effect of the cavity field acting on a single molecule is comparably weak. The electronic and vibrational excitation structure remains then largely unaffected; the combined light-matter system hybridizes based on those bare excitations (see SI for a detailed discussion). As long as this condition is satisfied, i.e., as long as light and matter do not couple ultra-strongly, it is safe to separate the matter ensemble into two parts. The first describes a single “impurity” molecule contributing the paramagnetic current j, which will be obtained as a solution to Schrödinger’s equation. The second accounts for all the remaining molecules as polarizable material εr(r,ω) = 1 + χE(r,ω). Surely this separation is also convenient to account for two different species, e.g., the reactive molecule and its solvent. In this sense, the problem of chemical reactions in collective light-matter coupling can be seen as an impurity problem; a single molecule undergoing a reaction is influenced by a large electromagnetic environment.

Knowing the bare Green tensor G0 (empty cavity), we can obtain the “ensemble-dressed” dyadic Green tensor with the help of the Dyson equation:

graphic file with name jz2c01169_m003.jpg

We assumed here (and earlier) that the generic susceptibility P(r,ω) = ε0 ∫ dr3χ(r,r′,ω)·E(r′,ω) is local χ(r,r′, ω) ≈ χ(r,ω)δ(r – r′). In many situations, the orientation of emitters within a gas or fluid will be random, and its average polarizability is consequentially isotropic.

For a dilute ensemble satisfying the long wavelength approximation, the widely believed regime of polaritonic chemistry, the response can be approximated as χE(r″,ω) ≈ χE(r0,ω)θ(r ∈ VE) ≈ χE(ω)VEδ(r – r0). Then,

graphic file with name jz2c01169_m004.jpg

is evaluated at the position of the explicit molecule and VE is the volume occupied by the ensemble of emitters. This simplifies further for the widely used one-dimensional Fabry–Pérot cavities

graphic file with name jz2c01169_m005.jpg

with G⊥(ω) ≈ ϵcϵcT/[G0–1(ω) – ω2/c2VEϵcT·χE(ω)·ϵc]. Cavity losses are accounted for by adding a weak cavity-decay rate η. The remaining task is now to identify χE(ω). The (dipolar) polarization can be conveniently obtained from the density–density response function61 as R(ω) = ∫ dr(−e)rδρ(rω) = α(ω)·δElocal(ω) = ∫ dr ∫ dr′(−e2)rχρρ(r,r′,ω)r′·δElocal(ω), a standard task for any TDDFT code. The induced dipole is related to the polarization density P(ω) used in Maxwell’s equation:

graphic file with name jz2c01169_m006.jpg

such that χE(ω) = NEVE–1ϵ0α(ω), if E ≈ δElocal. This approximation is reasonable if we focus on weak external fields. Alternatively, the Clausius–Mossotti relation62 provides a simple and reliable solution for isotropic systems

graphic file with name jz2c01169_m007.jpg

It might not always be possible or desirable to obtain the embedding kernel from first-principles, and instead simplified approaches such as the Drude-Lorentz model present easily accessible alternatives.

Equipped with the necessary framework, we are now able to describe the dynamic of single molecules in collective strong coupling relevant for polaritonic chemistry. We start by demonstrating the emergence of collective states for realistic systems from first-principles and validating the embedding radiation-reaction ansatz. We then shift our focus to chemistry and illustrate for a simple proton-tunneling model how chemical reactions are modified via collective vibrational strong-coupling.

The embedding radiation-reaction ansatz has been implemented into GPAW63—a simple task as the local potential is easily combined with the TDDFT framework. This allows us to validate the previous conceptions for a realistic system, here chosen to be a chain of sodium dimers in H-aggregate configuration oriented along the z direction. We follow the computational flow-chart illustrated in the table of contents (TOC) graphic with the simplification

graphic file with name jz2c01169_m008.jpg

First, we obtain the bare response of a single sodium dimer with a width given by the radiation-reaction potential47 with the cross-sectional area A = 102 Å2. Next, we obtain the polarizability αzz(ω) which defines G⊥(ω) and with it the corresponding embedding radiation-reaction potential. Finally, a linear-response calculation of a single sodium dimer that is affected by the ensemble-dressed cavity is performed.

Figure 1 sets the embedding approach (red) in relation with the direct response of N sodium dimers (black) coupled to the cavity mode. The spectra obtained from the embedding approach describe thus the response of a single molecule (e.g., the red molecule in the TOC graphic) and the spectral strength characterizes how strong this single molecule will contribute to the collective bright and dark polaritonic states. We expect therefore that the embedded response recovers the correct excitation poles of the collective states, but its spectral strength is that of the contribution of a single molecule to the collective state—precisely what Figure 1 demonstrates. The most notable difference is of course that the embedding approach describes the response of a single dimer, i.e., most of the spectral density is located in the dark state, which is not visible in the direct N-dimers + cavity calculations. The more molecules that couple collectively, the smaller (∝1/N, e.g., (2Na2)/(4Na2) ≈ 2) the contribution of a single molecule. Excitation energies and the asymmetry of the spectral weight are in excellent agreement. As expected, the embedding approach recovers the ‘with 1/N decreasing’ contribution of the single molecule to the collective state (see SI for an extended discussion). While the embedding approach sets its focus on the dynamic of single molecules, it allows recovery of the spectra of the full collective state (see SI for a detailed discussion). The direct calculations exhibit a weak blue-shift that can be removed by increasing the distance between dimers from 10 to 20 Å (magenta). Its origin lies in the Coulomb-mediated dipole–dipole interactions between the chain elements. Coulomb mediated couplings could be included in the longitudinal component of the embedding radiation-reaction ansatz or simply via commonly available techniques such as PCM or frozen-density embedding.64−66 This bright/dark state behavior represents the hallmark of collective strong coupling and is at the heart of polaritonic chemistry.1,67 However, if our single impurity molecule is detuned from the ensemble and cavity, the impurity will heavily out-weight all other molecules at the avoided crossing between impurity molecule and the polaritonic states (see SI and ref (68)).

Figure 1.

Figure 1

Open in a new tab

Photoabsorption of Na2 chains coupled to a single cavity mode with ℏωc = 2.98 eV and ℏηc = 10–2ℏωc. The response is calculated either directly using the TDDFT + radiation reaction for all N dimers (black) or using the embedding radiation-reaction approach (red) where only a single dimer is calculated explicitly. Different combinations of light-matter coupling strengths 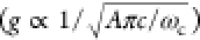Inline graphic and particle numbers N are illustrated. Vertical gray-dashed lines serve as a guide to the eye for specific polaritonic resonances. Please refer to the text for further explanations. The excitations have been artificially broadened; see the SI for numerical details.

Using the embedding radiation-reaction ansatz is substantially cheaper than calculating the full dimer chain explicitly. While the cost of the latter outgrows quickly all available computational resources, our embedding approach retains the cost of a single-dimer calculation. This computational advantage opens up the possibility to investigate far more complex systems and will allow us to consider polaritonic chemistry truly from first principles.

During a chemical reaction, structural changes of the molecule will alter its vibrational spectrum. In between the reactant and product state, the molecule will spend time in intermediate configurations which will likely feature different vibrational energies and oscillator strengths. The closer this detuned vibration is to the collective polaritonic states, the stronger its contribution will outweigh the individual contribution of an ensemble molecule (see, e.g., SI Figure 1). While the reactant configuration will therefore play a negligible role in the polaritonic state, during the reaction our individual molecule might play a dominant role. Even if the number of dark states might be large, the bright states can play a dominant role in this scenario.

Let us illustrate this concept for a simple proton-tunneling model that is designed to represent ground-state reactions. A tilted double well potential v(x, t) = x × 10−3 − x2 × 1.25 × 10−3 + x4 × (1 + 0.4/[1 + e−(t − 60fs)/10fs]) × 10−4 (in a.u.) shown in Figure 2 is slightly deformed over a time frame of approximately tp ≈ 0.1 ps. Such a deformation results in a weak excitation of the proton wave function and leads to a finite probability to overcome the barrier from the left to the right well. The amount of nuclear density that overcomes the barrier will be considered as an indication for the reactivity in our model. The role of the ensemble molecules is to modify the interaction between cavity mode and our impurity molecule; Figure 2b illustrates an exemplary Ft–1iωG(ω). Importantly, the collective coupling between cavity and ensemble has to be strong enough to induce beatings within the time frame of the reaction. This defines a minimal hybridization strength in G(ω) for a given reaction speed 1/ΩRabi ∼ TRabi < τreaction—a quick reaction demands a large hybridization. We consider the ensemble in the following as a generic second species which is represented by a Drude–Lorentz model

graphic file with name jz2c01169_m009.jpg

Figure 2.

Figure 2

Open in a new tab

(a) Potential energy surface before (black) and after (red) the deformation. Dashed horizontal lines indicate eigenvalues of the respective static single-proton Schrödinger equation. (b) Time-domain convolution-argument Ft–1iωG(ω) for g0/ℏωc = 0.0135, γe = 0.025ωc, η = 10–4ωc (see text for elaboration). Only for sizable hybridization strength can we observe the Rabi period on the time scale of the reaction time.

Figure 3 (top) shows the absolute influence of resonant collective light-matter coupling on the accumulated proton tunneling for various combinations of fundamental coupling and ensemble size. The influence of the ensemble on the reaction depends largely on the single-particle coupling strength to our impurity molecule and is, even for Nensemble = 0 (see top), already noticeably increased. Smaller coupling values (e.g., g0/ℏωc = 0.0027) show the tendency to decrease this effect when increasing the ensemble size, as one would intuitively expect. Increasing the fundamental light-matter coupling does not only shift the resulting curve to smaller Nensemble values but furthermore intensifies the overall trend. In the extreme case of g0/ℏωc = 0.0135, we observe initially an increase in catalysis followed by an inhibiting effect for larger Nensemble. However, Figure 3 (bottom) illustrates that the proton-tunneling dynamic features a complex, alternating dependence on Nensemble. The latter is fluctuating between a 100% increase and almost full inhibition of proton-tunneling. Particularly striking is that the magnitude of the cavity influence remains comparable between Nensemble = 0 and Nensemble = 104 or even increases in the case of g0/ℏωc = 0.00054 (yellow). Even for Nensemble > 108 can fading resonances be observed. Figure 3 (bottom) would suggest that, depending on cavity parameters; selected resonances; and the mixture of reactant, product and solvent, a chemical reaction can be selectively catalyzed or inhibited. Both catalyzing69 and inhibiting effects have been observed in experiments using either vibrational19,20 or electronic strong coupling.9,12

Figure 3.

Figure 3

Open in a new tab

(Top) Absolute cavity influence on reactivity CR = ∫0TdT/T[1 – (∫–∞dxn(x,t) – ∫0∞dxn(x,t))] – CRg0=0 for increasing the number of ensemble emitters. (Bottom) relative cavity influence CR/CRg0=0 in percent. The dependence of the cavity influence on the number of ensemble molecules Nensemble is nontrivial and far from a simple 1/Nensemble trend. Decoherences, for ensemble and cavity, are included but show no particularly striking effect as detailed in the SI. We use a Drude–Lorentz model with ℏωp = 6.387 × 10–4 eV. The first excitations are aligned at t = 0 ℏωc = 0.046721 eV = ℏωE = ℏω0–1; the cavity decay rate is fixed to η = 10–4ωc. For large ensembles and coupling values, the light-matter hybridization reaches significant values which calls the semi-classical description into question. We start to enter this domain around Nensemble = 104 for the largest coupling.

Figure 4 (top) illustrates that the influence of collective light-matter coupling is sensitive to the energetic alignment between the ensemble, cavity mode, and reacting system. The associated charge-transfer dynamic is shown in Figure 4 (bottom). Such a complex behavior for our simple model demonstrates that the influence of collective strong coupling on chemical reactivity can be highly situational—a strong argument for the importance of ab initio approaches.

Figure 4.

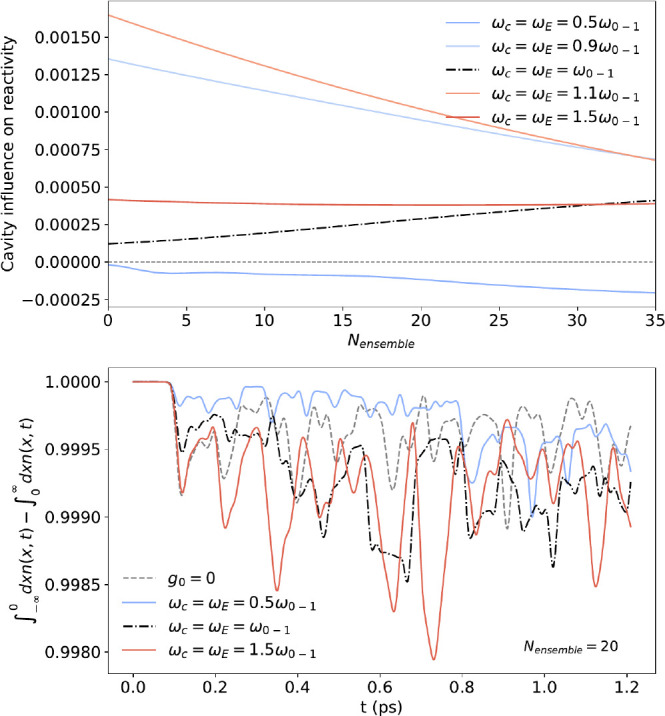
Figure 4

Open in a new tab

Top, absolute cavity influence on reactivity CR = ∫0TdT/T[1 − (∫–∞dxn(x,t) – ∫0∞dxn(x,t))] – CRg0=0 for an increasing number of ensemble emitters for different energetic alignments between cavity/ensemble frequency and bare excitation frequency of our impurity molecule. Bottom, proton-tunneling (∫–∞dxn(x,t) – ∫0∞dxn(x,t)) for Nensemble = 20. The complex excitation structure leads to a nontrivial influence on the proton tunneling. In contrast to the other parameters, the smallest frequency tends to inhibit the proton-tunneling process. We fixed the cavity volume V in all calculations to the value of the resonant alignment. It is apparent from the behavior with increasing ensemble number Nensemble that the specific effect of the cavity on the chemical reactivity is sensitive to the energetic alignment between cavity, ensemble, and reacting molecule as well as the hybridization between those systems.

Recall that the influence on the reactivity will depend not only on the energetic alignment between the reactant, product, solvent, and cavity but also its hybridization strength in relation to the reaction time. Identifying the specific influence of collective strong coupling on a chemical reaction remains an open and theoretically challenging problem. While the chosen proton-tunneling system is too simplistic to draw direct connections to the experiment, it demonstrates the feasibility of the introduced embedding radiation-reaction approach. Furthermore, it illustrates clearly that the cavity influence on chemical reactivity can persist even at a large Nensemble and that the catalyzing and inhibiting effect could be present for the same chemical reaction. Recent work22−24,70 showed promising progress, and yet much remains to be investigated. A conclusive understanding will likely demand a collaborative effort involving experimental work, ab initio theory, and simplified models.

To conclude, by embedding an ensemble of molecules into the recently proposed radiation-reaction potential,47 we have been able to tackle the conundrum of a first-principles description of the material structure combined with the collective light-matter interaction involving a large number of emitters. The embedding ansatz is trivial to implement into existing time-dependent density-functional theory libraries as it adds a simple local potential. This allowed us to treat collective strong coupling from first-principles featuring an arbitrarily large number of emitters with marginal additional computational cost compared to ordinary real-time TDDFT calculations. Last, by tuning the cavity in the infrared regime, we demonstrated that the modification of proton-tunneling reactions via collective strong coupling can possess a nontrivial dependence on the number of ensemble molecules, featuring domains of a 100% increase in reactivity but also near full inhibition. Cavity losses decrease the effect of collective strong coupling on the tunneling process but have an overall negligible influence (see SI).

This work paves the way to tackling new regimes of theoretical chemistry, accounting for the self-consistent interaction between light with macroscopic systems while focusing on the microscopic dynamic of single subsystems—entirely from first principles. This allows us to relax previous simplifications to only single or few molecules with artificially increased coupling strength.22,51,53,68 Already our here illustrated simple proton-tunneling model exhibited nontrivial behavior with the number of emitters. We can expect that complex multistep chemical reactions will further complicate this trend—a strong argument for the need of first-principles techniques. The seamless combination of embedding radiation-reaction and quantum-electrodynamical density-functional theory, especially the recently developed local-density approximation,56 ensures that quantum-corrections of the light-matter interaction can be properly accounted for if necessary. Possible extensions include a consistent treatment of near-field effects that are relevant for solvation, plasmonic environments, and J/H aggregates. Equipped with this toolset, describing consistently the seminal experimental work in polaritonic chemistry1−3 moves within reach.

Acknowledgments

I thank Göran Johansson for interesting discussions, Jakub Fojt for assistance with GPAW, and anonymous referee 1 for constructive comments that improved the publication. This work was supported by the Swedish Research Council (VR) through Grant No. 2016-06059 and the computational resources provided by the Swedish National Infrastructure for Computing at the Chalmers Centre for Computational Science and Engineering partially funded by the Swedish Research Council through grant agreement no. 2018-05973.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.2c01169.

  • Simulation details, influence of decoherence, detuning and integration-time for the proton-tunneling reaction, connection between single-molecule and collective spectra, additional explanations, and limitations of the embedding radiation-reaction approach (PDF)

  • Transparent Peer Review report available (PDF)

The author declares no competing financial interest.

This paper published ASAP on July 22, 2022 with a production error in the caption of Figure 3. The error was corrected and the revised paper reposted on July 25, 2022.

Supplementary Material

jz2c01169_si_001.pdf (1.9MB, pdf)
jz2c01169_si_002.pdf (474KB, pdf)

References

  1. Ebbesen T. W. Hybrid Light–Matter States in a Molecular and Material Science Perspective. Acc. Chem. Res. 2016, 49, 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
  2. Garcia-Vidal F. J.; Ciuti C.; Ebbesen T. W. Manipulating matter by strong coupling to vacuum fields. Science 2021, 373, eabd0336 10.1126/science.abd0336. [DOI] [PubMed] [Google Scholar]
  3. Simpkins B. S.; Dunkelberger A. D.; Owrutsky J. C. Mode-specific chemistry through vibrational strong coupling (or A wish come true). J. Phys. Chem. C 2021, 125, 19081–19087. 10.1021/acs.jpcc.1c05362. [DOI] [Google Scholar]
  4. Sidler D.; Ruggenthaler M.; Schäfer C.; Ronca E.; Rubio A. A perspective on ab initio modeling of polaritonic chemistry: The role of non-equilibrium effects and quantum collectivity. J. Chem. Phys 2022, 156, 230901. 10.1063/5.0094956. [DOI] [PubMed] [Google Scholar]
  5. Forn-Díaz P.; Lamata L.; Rico E.; Kono J.; Solano E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005. 10.1103/RevModPhys.91.025005. [DOI] [Google Scholar]
  6. Frisk Kockum A.; Miranowicz A.; De Liberato S.; Savasta S.; Nori F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19. 10.1038/s42254-018-0006-2. [DOI] [Google Scholar]
  7. Schäfer C.; Ruggenthaler M.; Rubio A. Ab initio nonrelativistic quantum electrodynamics: Bridging quantum chemistry and quantum optics from weak to strong coupling. Phys. Rev. A 2018, 98, 043801. 10.1103/PhysRevA.98.043801. [DOI] [Google Scholar]
  8. Sato S.; De Giovannini U.; Aeschlimann S.; Gierz I.; Hübener H.; Rubio A. Floquet states in dissipative open quantum systems. Journal of Physics B: Atomic, Molecular and Optical Physics 2020, 53, 225601. 10.1088/1361-6455/abb127. [DOI] [Google Scholar]
  9. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
  10. Chikkaraddy R.; de Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Galego J.; Garcia-Vidal F. J.; Feist J. Suppressing photochemical reactions with quantized light fields. Nat. Commun. 2016, 7, 13841. 10.1038/ncomms13841. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Munkhbat B.; Wersäll M.; Baranov D. G.; Antosiewicz T. J.; Shegai T. Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas. Sci. Adv. 2018, 4, eaas9552 10.1126/sciadv.aas9552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fregoni J.; Granucci G.; Coccia E.; Persico M.; Corni S. Manipulating azobenzene photoisomerization through strong light–molecule coupling. Nat. Commun. 2018, 9, 4688. 10.1038/s41467-018-06971-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Groenhof G.; Climent C.; Feist J.; Morozov D.; Toppari J. J. Tracking Polariton Relaxation with Multiscale Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2019, 10, 5476–5483. 10.1021/acs.jpclett.9b02192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kowalewski M.; Bennett K.; Mukamel S. Cavity femtochemistry: Manipulating nonadiabatic dynamics at avoided crossings. J. Phys. Chem. Lett. 2016, 7, 2050–2054. 10.1021/acs.jpclett.6b00864. [DOI] [PubMed] [Google Scholar]
  16. Vendrell O. Collective Jahn-Teller Interactions through Light-Matter Coupling in a Cavity. Phys. Rev. Lett. 2018, 121, 253001. 10.1103/PhysRevLett.121.253001. [DOI] [PubMed] [Google Scholar]
  17. Fábri C.; Halász G. J.; Vibók Á. Probing Light-Induced Conical Intersections by Monitoring Multidimensional Polaritonic Surfaces. J. Phys. Chem. Lett. 2022, 13, 1172–1179. 10.1021/acs.jpclett.1c03465. [DOI] [PubMed] [Google Scholar]
  18. Li T. E.; Tao Z.; Hammes-Schiffer S. Semiclassical Real-Time Nuclear-Electronic Orbital Dynamics for Molecular Polaritons: Unified Theory of Electronic and Vibrational Strong Couplings. arXiv Preprint 2022, arXiv:2203.04952. [DOI] [PubMed] [Google Scholar]
  19. Thomas A.; George J.; Shalabney A.; Dryzhakov M.; Varma S. J.; Moran J.; Chervy T.; Zhong X.; Devaux E.; Genet C.; et al. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angew. Chem., Int. Ed. 2016, 55, 11462–11466. 10.1002/anie.201605504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Thomas A.; Lethuillier-Karl L.; Nagarajan K.; Vergauwe R. M.; George J.; Chervy T.; Shalabney A.; Devaux E.; Genet C.; Moran J.; et al. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science 2019, 363, 615–619. 10.1126/science.aau7742. [DOI] [PubMed] [Google Scholar]
  21. Lather J.; Bhatt P.; Thomas A.; Ebbesen T. W.; George J. Cavity Catalysis by Cooperative Vibrational Strong Coupling of Reactant and Solvent Molecules. Angew. Chem., Int. Ed. 2019, 58, 10635–10638. 10.1002/anie.201905407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Schäfer C.; Flick J.; Ronca E.; Narang P.; Rubio A. Shining Light on the Microscopic Resonant Mechanism Responsible for Cavity-Mediated Chemical Reactivity. arXiv e-prints 2021, arXiv:2104.12429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Li T. E.; Nitzan A.; Subotnik J. E. Collective vibrational strong coupling effects on molecular vibrational relaxation and energy transfer: Numerical insights via cavity molecular dynamics simulations. Angew. Chem. 2021, 133, 15661–15668. 10.1002/ange.202103920. [DOI] [PubMed] [Google Scholar]
  24. Li X.; Mandal A.; Huo P. Cavity frequency-dependent theory for vibrational polariton chemistry. Nat. Commun. 2021, 12, 1315. 10.1038/s41467-021-21610-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Coles D. M.; Somaschi N.; Michetti P.; Clark C.; Lagoudakis P. G.; Savvidis P. G.; Lidzey D. G. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
  26. Feist J.; Garcia-Vidal F. J. Extraordinary Exciton Conductance Induced by Strong Coupling. Phys. Rev. Lett. 2015, 114, 196402. 10.1103/PhysRevLett.114.196402. [DOI] [PubMed] [Google Scholar]
  27. Orgiu E.; George J.; Hutchison J. A.; Devaux E.; Dayen J. F.; Doudin B.; Stellacci F.; Genet C.; Schachenmayer J.; Genes C.; et al. Conductivity in organic semiconductors hybridized with the vacuum field. Nat. Mater. 2015, 14, 1123–1129. 10.1038/nmat4392. [DOI] [PubMed] [Google Scholar]
  28. Zhong X.; Chervy T.; Zhang L.; Thomas A.; George J.; Genet C.; Hutchison J. A.; Ebbesen T. W. Energy Transfer between Spatially Separated Entangled Molecules. Angew. Chem., Int. Ed. 2017, 56, 9034–9038. 10.1002/anie.201703539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Schäfer C.; Ruggenthaler M.; Appel H.; Rubio A. Modification of excitation and charge transfer in cavity quantum-electrodynamical chemistry. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 4883–4892. 10.1073/pnas.1814178116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Du M.; Martínez-Martínez L. A.; Ribeiro R. F.; Hu Z.; Menon V. M.; Yuen-Zhou J. Theory for polariton-assisted remote energy transfer. Chem. Sci. 2018, 9, 6659–6669. 10.1039/C8SC00171E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hagenmüller D.; Schütz S.; Schachenmayer J.; Genes C.; Pupillo G. Cavity-assisted mesoscopic transport of fermions: Coherent and dissipative dynamics. Phys. Rev. B 2018, 97, 205303. 10.1103/PhysRevB.97.205303. [DOI] [Google Scholar]
  32. Wrigge G.; Gerhardt I.; Hwang J.; Zumofen G.; Sandoghdar V. Efficient coupling of photons to a single molecule and the observation of its resonance fluorescence. Nat. Phys. 2008, 4, 60–66. 10.1038/nphys812. [DOI] [Google Scholar]
  33. Bajoni D.; Senellart P.; Wertz E.; Sagnes I.; Miard A.; Lemaître A.; Bloch J. Polariton laser using single micropillar GaAs- GaAlAs semiconductor cavities. Physical review letters 2008, 100, 047401. 10.1103/PhysRevLett.100.047401. [DOI] [PubMed] [Google Scholar]
  34. Wang D.; Kelkar H.; Martin-Cano D.; Utikal T.; Götzinger S.; Sandoghdar V. Coherent Coupling of a Single Molecule to a Scanning Fabry-Perot Microcavity. Phys. Rev. X 2017, 7, 021014. [Google Scholar]
  35. Baranov D. G.; Munkhbat B.; Zhukova E.; Bisht A.; Canales A.; Rousseaux B.; Johansson G.; Antosiewicz T. J.; Shegai T. Ultrastrong coupling between nanoparticle plasmons and cavity photons at ambient conditions. Nat. Commun. 2020, 11, 2715. 10.1038/s41467-020-16524-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hübener H.; De Giovannini U.; Schäfer C.; Andberger J.; Ruggenthaler M.; Faist J.; Rubio A. Engineering quantum materials with chiral optical cavities. Nature materials 2021, 20, 438–442. 10.1038/s41563-020-00801-7. [DOI] [PubMed] [Google Scholar]
  37. Deng H.; Weihs G.; Snoke D.; Bloch J.; Yamamoto Y. Polariton lasing vs. photon lasing in a semiconductor microcavity. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 15318–15323. 10.1073/pnas.2634328100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Christopoulos S.; Von Högersthal G. B. H.; Grundy A.; Lagoudakis P.; Kavokin A.; Baumberg J.; Christmann G.; Butté R.; Feltin E.; Carlin J.-F.; et al. Room-temperature polariton lasing in semiconductor microcavities. Physical review letters 2007, 98, 126405. 10.1103/PhysRevLett.98.126405. [DOI] [PubMed] [Google Scholar]
  39. Kéna-Cohen S.; Forrest S. Room-temperature polariton lasing in an organic single-crystal microcavity. Nat. Photonics 2010, 4, 371–375. 10.1038/nphoton.2010.86. [DOI] [Google Scholar]
  40. Slootsky M.; Liu X.; Menon V. M.; Forrest S. R. Room temperature Frenkel-Wannier-Mott hybridization of degenerate excitons in a strongly coupled microcavity. Phys. Rev. Lett. 2014, 112, 076401. 10.1103/PhysRevLett.112.076401. [DOI] [PubMed] [Google Scholar]
  41. Graf A.; Held M.; Zakharko Y.; Tropf L.; Gather M. C.; Zaumseil J. Electrical pumping and tuning of exciton-polaritons in carbon nanotube microcavities. Nat. Mater. 2017, 16, 911. 10.1038/nmat4940. [DOI] [PubMed] [Google Scholar]
  42. Latini S.; Shin D.; Sato S. A.; Schäfer C.; De Giovannini U.; Hübener H.; Rubio A. The ferroelectric photo ground state of SrTiO3: Cavity materials engineering. Proc. Natl. Acad. Sci. U. S. A. 2021, 118, e2105618118. 10.1073/pnas.2105618118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Schlawin F.; Kennes D. M.; Sentef M. A. Cavity quantum materials. Applied Physics Reviews 2022, 9, 011312. 10.1063/5.0083825. [DOI] [Google Scholar]
  44. Ghosh S.; Liew T. C. Quantum computing with exciton-polariton condensates. npj Quantum Information 2020, 6, 1–6. 10.1038/s41534-020-0244-x. [DOI] [Google Scholar]
  45. Lüders C.; Pukrop M.; Rozas E.; Schneider C.; Höfling S.; Sperling J.; Schumacher S.; Aßmann M. Quantifying quantum coherence in polariton condensates. PRX Quantum 2021, 2, 030320. 10.1103/PRXQuantum.2.030320. [DOI] [PubMed] [Google Scholar]
  46. Wasielewski M. R.; Forbes M. D.; Frank N. L.; Kowalski K.; Scholes G. D.; Yuen-Zhou J.; Baldo M. A.; Freedman D. E.; Goldsmith R. H.; Goodson T.; et al. Exploiting chemistry and molecular systems for quantum information science. Nature Reviews Chemistry 2020, 4, 490–504. 10.1038/s41570-020-0200-5. [DOI] [PubMed] [Google Scholar]
  47. Schäfer C.; Johansson G. Shortcut to Self-Consistent Light-Matter Interaction and Realistic Spectra from First Principles. Phys. Rev. Lett. 2022, 128, 156402. 10.1103/PhysRevLett.128.156402. [DOI] [PubMed] [Google Scholar]
  48. Tancogne-Dejean N.; Oliveira M. J.; Andrade X.; Appel H.; Borca C. H.; Le Breton G.; Buchholz F.; Castro A.; Corni S.; Correa A. A.; et al. Octopus, a computational framework for exploring light-driven phenomena and quantum dynamics in extended and finite systems. J. Chem. Phys. 2020, 152, 124119. 10.1063/1.5142502. [DOI] [PubMed] [Google Scholar]
  49. Noda M.; Sato S. A.; Hirokawa Y.; Uemoto M.; Takeuchi T.; Yamada S.; Yamada A.; Shinohara Y.; Yamaguchi M.; Iida K.; et al. SALMON: Scalable ab-initio light–matter simulator for optics and nanoscience. Comput. Phys. Commun. 2019, 235, 356–365. 10.1016/j.cpc.2018.09.018. [DOI] [Google Scholar]
  50. Mennucci B.; Corni S. Multiscale modelling of photoinduced processes in composite systems. Nature Reviews Chemistry 2019, 3, 315–330. 10.1038/s41570-019-0092-4. [DOI] [Google Scholar]
  51. Luk H. L.; Feist J.; Toppari J. J.; Groenhof G. Multiscale Molecular Dynamics Simulations of Polaritonic Chemistry. J. Chem. Theory Comput. 2017, 13, 4324–4335. 10.1021/acs.jctc.7b00388. [DOI] [PubMed] [Google Scholar]
  52. Fregoni J.; Haugland T. S.; Pipolo S.; Giovannini T.; Koch H.; Corni S. Strong coupling between localized surface plasmons and molecules by coupled cluster theory. Nano Lett. 2021, 21, 6664–6670. 10.1021/acs.nanolett.1c02162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Bonini J.; Flick J. Ab initio linear-response approach to vibro-polaritons in the cavity Born-Oppenheimer approximation. arXiv preprint 2021, arXiv:2108.11564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Tokatly I. V. Time-Dependent Density Functional Theory for Many-Electron Systems Interacting with Cavity Photons. Phys. Rev. Lett. 2013, 110, 233001. 10.1103/PhysRevLett.110.233001. [DOI] [PubMed] [Google Scholar]
  55. Ruggenthaler M.; Flick J.; Pellegrini C.; Appel H.; Tokatly I. V.; Rubio A. Quantum-electrodynamical density-functional theory: Bridging quantum optics and electronic-structure theory. Phys. Rev. A 2014, 90, 012508. 10.1103/PhysRevA.90.012508. [DOI] [Google Scholar]
  56. Schäfer C.; Buchholz F.; Penz M.; Ruggenthaler M.; Rubio A. Making ab initio QED functional(s): Nonperturbative and photon-free effective frameworks for strong light–matter coupling. Proc. Natl. Acad. Sci. U. S. A. 2021, 118, e2110464118. 10.1073/pnas.2110464118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Flick J.; Narang P. Cavity-Correlated Electron-Nuclear Dynamics from First Principles. Phys. Rev. Lett. 2018, 121, 113002. 10.1103/PhysRevLett.121.113002. [DOI] [PubMed] [Google Scholar]
  58. Haugland T. S.; Ronca E.; Kjønstad E. F.; Rubio A.; Koch H. Coupled cluster theory for molecular polaritons: Changing ground and excited states. Phys. Rev. X 2020, 10, 041043. [Google Scholar]
  59. Haugland T. S.; Schäfer C.; Ronca E.; Rubio A.; Koch H. Intermolecular interactions in optical cavities: An ab initio QED study. J. Chem. Phys. 2021, 154, 094113. 10.1063/5.0039256. [DOI] [PubMed] [Google Scholar]
  60. Buhmann S.Dispersion Forces I: Macroscopic Quantum Electrodynamics and Ground-State Casimir, Casimir–Polder and van der Waals Forces; Springer, 2013; Vol. 247. [Google Scholar]
  61. Ullrich C. A.Time-Dependent Density-Functional Theory: Concepts and Applications; OUP Oxford, 2011. [Google Scholar]
  62. Kittel C.; Holcomb D. F. Introduction to solid state physics. American Journal of Physics 1967, 35, 547–548. 10.1119/1.1974177. [DOI] [Google Scholar]
  63. Enkovaara J.; Rostgaard C.; Mortensen J. J.; Chen J.; Dułak M.; Ferrighi L.; Gavnholt J.; Glinsvad C.; Haikola V.; Hansen H.; et al. Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method. J. Phys.: Condens. Matter 2010, 22, 253202. 10.1088/0953-8984/22/25/253202. [DOI] [PubMed] [Google Scholar]
  64. Tomasi J.; Mennucci B.; Cammi R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  65. Gao Y.; Neuhauser D. Communication: Dynamical embedding: Correct quantum response from coupling TDDFT for a small cluster with classical near-field electrodynamics for an extended region. J. Chem. Phys. 2013, 138, 181105. 10.1063/1.4804544. [DOI] [PubMed] [Google Scholar]
  66. De Santis M.; Belpassi L.; Jacob C. R.; Severo Pereira Gomes A.; Tarantelli F.; Visscher L.; Storchi L. Environmental Effects with Frozen-Density Embedding in Real-Time Time-Dependent Density Functional Theory Using Localized Basis Functions. J. Chem. Theory Comput. 2020, 16, 5695–5711. 10.1021/acs.jctc.0c00603. [DOI] [PMC free article] [PubMed] [Google Scholar]; PMID: 32786918.
  67. Yuen-Zhou J.; Menon V. M. Polariton chemistry: Thinking inside the (photon) box. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 5214–5216. 10.1073/pnas.1900795116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Sidler D.; Schäfer C.; Ruggenthaler M.; Rubio A. Polaritonic chemistry: Collective strong coupling implies strong local modification of chemical properties. J. Phys. Chem. Lett. 2021, 12, 508–516. 10.1021/acs.jpclett.0c03436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Lather J.; Bhatt P.; Thomas A.; Ebbesen T. W.; George J. Cavity catalysis by cooperative vibrational strong coupling of reactant and solvent molecules. Angew. Chem. 2019, 131, 10745–10748. 10.1002/ange.201905407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Sun J.; Vendrell O. Suppression and Enhancement of Thermal Chemical Rates in a Cavity. J. Phys. Chem. Lett. 2022, 13, 4441–4446. 10.1021/acs.jpclett.2c00974. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz2c01169_si_001.pdf (1.9MB, pdf)
jz2c01169_si_002.pdf (474KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES