Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jul 28;13(30):7072–7080. doi: 10.1021/acs.jpclett.2c01694

A Plausible Mechanism of Uracil Photohydration Involves an Unusual Intermediate

Woojin Park †, Michael Filatov (Gulak) †,*, Saima Sadiq †, Igor Gerasimov †, Seunghoon Lee ‡, Taiha Joo §,*, Cheol Ho Choi †,*
PMCID: PMC9358713  PMID: 35900137

Abstract

graphic file with name jz2c01694_0005.jpg

It is well-known that photolysis of pyrimidine nucleobases, such as uracil, in an aqueous environment results in the formation of hydrate as one of the main products. Although several hypotheses regarding photohydration have been proposed in the past, e.g., the zwitterionic and “hot” ground-state mechanisms, its detailed mechanism remains elusive. Here, theoretical nonadiabatic simulations of the uracil photodynamics reveal the formation of a highly energetic but kinetically stable intermediate that features a half-chair puckered pyrimidine ring and a strongly twisted intracyclic double bond. The existence and the kinetic stability of the intermediate are confirmed by a variety of computational chemistry methods. According to the simulations, the unusual intermediate is mainly formed almost immediately (∼50–200 fs) upon photoabsorption and survives long enough to engage in a hydration reaction with a neighboring water. A plausible mechanism of uracil photohydration is proposed on the basis of the modeling of nucleophilic insertion of water into the twisted double bond of the intermediate.

For several decades, photolysis of pyrimidine nucleobases (i.e., uracil, thymine, and cytosine) and their derivatives in an aqueous environment has been known to result in the formation of two main photoproducts:1−6 a hydrate and a dimer (shown in Chart 1 for uracil). The early experimental measurements evidenced that dimer formation occurs presumably with the involvement of a triplet state of the pyrimidine base,7−10 e.g., uracil (1), while hydrate is formed from the singlet excited state exclusively.3−5,7,11−13 It has been hypothesized that hydrate formation proceeds through a zwitterionic excited state4,5,12 (see Chart 1); however, the involvement of a “hot” ground-state intermediate has not been completely ruled out.3,11

Chart 1. Uracil (1), Its Photohydrate (2), and Photohydration Mechanism Hypothesized in ref (5)a.

Chart 1

Open in a new tab

a The inset shows the uracil cyclobutene dimer (3).

In spite of the significance of nucleobase photoreactions,14−17 a detailed understanding of the mechanism of their photolysis is still lacking.18,19 Thus, Chakraborty et al.19 have performed multireference ab initio computations and obtained a much too high (∼1.8 eV or ∼42 kcal/mol) barrier for the insertion of water into the photoexcited uracil. Franzen et al.,18 in their single-reference ab initio computations, obtained barriers of ∼2.0–2.5 eV for the insertion of water into the ground-state pyrimidine bases. In both cases, the theoretically stipulated mechanisms contradicted the experimentally observed characteristics of the photohydration reaction. The experiment strongly indicates that water insertion is closely related with the excited state and not the ground state and that the reaction should occur on a time scale incompatible with the barriers that are several electronvolts high.12

Here, we report on a computational discovery of an unusual intermediate that offers a unified explanation of the mechanism of the photohydration and, possibly, photodimerization reactions of pyrimidines, carried out with the help of the newly developed MRSF-TDDFT methodology.20,21 The new intermediate (4) (see Chart 2) features a half-chair conformation of the pyrimidine ring with a pronounced torsion about the C5–C6 bond (see Chart 1 for the numbering). Intermediate 4  has been discovered during routine nonadiabatic molecular dynamics (NAMD) simulations of photoexcited uracil decay and appears to be sufficiently kinetically stable to survive long enough for a bimolecular reaction with water to occur. Although 4  is in a singlet electronic state, a metastable triplet-state conformation similar to 4 occurs within a narrow energy range (∼11 kcal/mol) and intersystem crossing (ISC) with the triplet manifold seems plausible.

Chart 2. A Reactive Intermediate Proposed in This Worka.

Chart 2

Open in a new tab

a The HC5C6H dihedral angle is shown.

The appearance of a strongly puckered pyrimidine ring in 4  is not unusual. For example, the experimental observation of puckered radical-anion species of uracil with the ∠C4C5C6H angle reaching ≲30° has been reported.22−24 By contrast, 4 features more pronounced puckering with a ∠C4C5C6H of ≈65°, which implies a substantially torsionally strained C5=C6 bond. Because of this, 4  should be a highly reactive species capable of easily engaging in, e.g., nucleophilic reaction with water. Because 4  is formed as a result of the passage through a specific S1/S0 conical intersection (CI), also termed the ethylenic CI in the literature,25,26 which has a very similar geometry, the possibility that the water molecule attacks the photoexcited uracil at geometries close to the CI cannot be entirely excluded. This may remain an open question, which path (via the ethylenic CI, via ground state 4 , or both) the photohydration reaction can take, but the very existence of 4  and its survival on a sufficiently long time scale offer a unified mechanistic explanation of the most iconic photoreactions of pyrimidine bases.

As mentioned above, intermediate 4 has been observed during NAMD simulations of uracil photodynamics. Theoretical modeling of the excited-state decay of nucleobases has attracted considerable attention (see refs (25) and (27) and references cited therein) due to the need to understand their photostability. Typically, nucleobases are capable of dissipating the excitation energy on an ultrafast time scale;28−34 however, in the gas phase, some display rather long excited-state lifetimes, on the order of several picoseconds.35,36 For example, thymine displays, perhaps, the longest excited-state lifetime in the gas phase, ∼6–7 ps.37 Because uracil lacks the exocyclic methyl group of thymine, it can be expected that it might display an excited-state decay faster than that of thymine. However, in addition to the expected faster decay rate, the NAMD simulations of photoexcited uracil revealed a minor photoproduct, which could not be seen in thymine due to the limited duration of the NAMD simulations.37 The discovery of the latter product is perhaps the most interesting finding of this work and is believed to have significant implications for the mechanism of photolysis of uracil and other pyrimidine nucleobases.

A detailed description of NAMD simulations is provided in the Supporting Information, and here only a general discussion is given. NAMD simulations of uracil were carried out using the trajectory surface hopping (TSH) formalism38 in connection with the MRSF-TDDFT/BH&HLYP/6-31G* level of theory20,21 to obtain the adiabatic-state energies, forces on the nuclei, and nonadiabatic couplings39,40 (see the Supporting Information for abbreviations and details of the methodology). The fundamental difference between the MRSF method and the traditional DFT/TDDFT approach is that the former can correctly describe the double-cone topology of the conical intersections between the ground and excited states,41 whereas the latter yields an incorrect linear topology of the crossing.42 This difference is crucial for the correct description of nonadiabatic population transfer to the ground electronic state.43 The ability of the MRSF method to produce the correct excited-state dynamics is illustrated in Figure S6, which shows that the MRSF population dynamics of uracil is virtually identical with the dynamics obtained in the much more expensive XMS-CASPT2 NAMD simulations,26 where the latter simulations could afford a propagation time of only 300 fs. For a more complete description of the MRSF method, see the Supporting Information and references therein.

One hundred trajectories have been started from the initial conditions prepared by sampling the Wigner distribution44,45 of the ground-state uracil, of which 88 trajectories have been completed successfully and have been used in the analysis described below. In the obtained sampling geometries, excited states S1–S3 were calculated and the optically brightest states were populated at 0 fs. This gave ∼11% of the initial structures in the S1 adiabatic state and 89% in the S2 adiabatic state.

In the ground-state equilibrium geometry, the S1 state corresponds to the 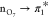Inline graphic one-electron transition (see Figure S1 for the frontier orbitals of the uracil) and is a dark state with an oscillator strength of only 0.0012. The S2 state is optically bright (oscillator strength of 0.64) and corresponds to the 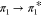Inline graphic, i.e., HOMO (the highest occupied molecular orbital) → LUMO (the lowest unoccupied molecular orbital), one-electron transition. Although the S2–S1 energy gap in the Franck–Condon (FC) geometry is 0.4 eV, in good agreement with the value of 0.45 eV obtained previously by the completely renormalized EOM-CCSD(T) [CR-EOM-CCSD(T)] formalism46 (see Table S2), the state ordering changes at some of the sampled geometries (vibrationally distorted), and the optically bright state is the lowest.

The NAMD simulations covered four adiabatic electronic states, S0–S3, and were propagated for ≤5000 fs (5 ps). Figure 1a [see also Figure S9a (100 fs)] shows the time evolution of the populations of these states. At first, the S2 population is rapidly transferred (τ1 = 37.0 ± 1.2 fs) to S1 through a (nearly) planar S2/S1 CI, CI21,BLA, which is located near the FC geometry. CI21,BLA is reached by a rapid bond-length-alternation (BLA) distortion, which involves lengthening of the C5=C6 and C4=O8 bonds and shortening of the C4–C5 bond (see Figure S7b). Figure S7b (see also Figure S7a,c) shows that a substantial fraction of these population transfers (red circles) occur within the first ≲50 fs in geometries with a near-zero HC5C6H dihedral angle (denoted as φ in the figure), which is typical for CI21,BLA (see Figure S2 for the geometry).

Figure 1.

Figure 1

Open in a new tab

(a) Evolution of the population of the adiabatic S0–S3 states during the NAMD simulations. The time constants of the monoexponential fit of the S2 population and the biexponential fit of S0 are also shown. The margins of error were determined by bootstrapping.47 (b) Evolution of the HC5C6H dihedral angle (φ) during the NAMD simulations. The red circles show the S2 → S1 nonadiabatic transitions (surface hops), and the blue circles the S1 → S0 nonadiabatic transitions. The dashed horizontal lines show the dihedral angle values in the structures given to the right of the plot (see the text for more details). (c) MEPs on the S2 (blue), S1 (red), and S0 (black) PESs of uracil obtained using the nudged elastic band (NEB) optimization48,49 in connection with the MRSF-TDDFT/BH&HLYP/6-31G* method. The MEPs are described in terms of the HC5C6H dihedral angle (denoted as φ) and the BLA distortion. The relative energies (in electronvolts) are given with respect to the S0 equilibrium geometry of uracil. The (BLA (Å), φ (deg), ΔE (eV)) values of the critical structures are (0, 0, 6.09) for FC, (0.13, 0.36, 5.58) for CI21,BLA, (0.19, 48.0, 5.27) for CI21,+ , (0.21, 2.00, 4.23) for S1,min, (0.02, 118.21, 4.35) for CI10,+, and (−0.04, 176.33, 3.54) for S0,min+. The green arrows show the relaxation paths characterized by distinct decay constants, τ1–τ3. The S1,min → CI10,+ path merges with the CI21,+ → CI10,+ MEP (at BLA = 0.013 Å, φ = 152.4°, and ΔE = 4.32 eV). (d) Structure and frontier orbitals of intermediate 4.

In addition to planar CI21,BLA, the S2 → S1 transfers occur at the S2/S1 CIs, CI21,+ and CI21,–, featuring hydrogen out of plane (HOOP) torsion about the C5=C6 bond (see Figure S2 for their geometries). These CIs have φ values of ≈±48°, and their position is shown in Figure 1b by the red dashed lines. As the HOOP motion is nearly as rapid as the BLA displacement, the nonplanar CI21,+ and CI21,– become active in the S2 → S1 population transfer at approximately the same time as the planar CI21,BLA and this deactivation channel competes with the BLA channel (see the red circles in Figure 1b and Figure S7c). By ∼100 fs, nearly all of the S2 population is transferred to S1; however, a small number of trajectories remain in S2 for a longer period.

The early S1 → S0 transitions begin at ∼40 fs from the start, and a majority of these transitions are due to a very rapid (τ2 = 107.8 ± 0.4 fs) S2 → CI21,± → S1 → CI10,± → S0 cascade of population transfers. The S1 → S0 transfers (see the blue circles in Figure 1b and Figure S7c) are mediated by nonplanar CI10,+ and CI10,– featuring pronounced HOOP distortion with a ∠HC5C6H of ±118.2° (see Figure S2 for the geometry). These CIs are accessed almost immediately after passage through CI21,± due to continued motion in the HOOP direction. However, ∼50% of the S1 population is diverted toward a local minimum, S1,min, on the S1 potential energy surface (PES), which has a planar geometry and a greater BLA deviation from the FC geometry than CI21,BLA (see Figure S2). This fraction of the S1 population remains in the vicinity of S1,min for a long time and slowly (τ3 = 1.919 ± 0.015 ps) decays to S0 through CI10,±, which lies ∼0.12 eV (2.8 kcal/mol) above the minimum.

Therefore, the S1 → S0 population transfer is divided into two channels: a slow channel and a rapid channel. In the slow S1 → S0 decay channel, the S1 population initially settles in the vicinity of the planar S1,min geometry, reaches the nonplanar CI10,± funnel, and decays in S0 with a decay constant τ3 of 1.919 ± 0.015 ps (see Figure 1a). This is the major decay channel and leads to the re-formation of uracil in its S0 equilibrium geometry, i.e., the internal conversion. In the rapid channel, the population arriving in S1 through CI21,± almost immediately decays to S0 via CI10,±; both CIs, CI21,± and CI10,±, have very similar nonplanar geometries (shown in Figure S2). The rapid channel has a decay constant τ2 of 107.8 ± 0.4 fs, which is more than an order of magnitude faster than the decay constant of the slow channel. The main product in this channel is ground-state uracil in a highly distorted geometry S0,min±, which is formed with a quite small yield of ∼0.08 (see also Figure S8c), which shows the time evolution of the populations of different ground-state species. Ground-state structure S0,min± survives until the end of the simulations, i.e., 5 ps. Therefore, S0,min± is a metastable ground-state species (see also the discussion below).

The results of our NAMD simulations generally agree with the experimental measurements and the results of the recent XMS-CASPT2 simulations by Chakraborty et al.26 It is noteworthy that the XMS-CASPT2 simulations described above were limited to 300 fs, so that only the shortest decay constant τ1 of 12.5 fs was obtained by Chakraborty et al.26 with statistical certainty. This constant is in reasonable agreement with the τ1 of 37.0 fs obtained here. Most of the experimental measurements display two time constants, a short ≲200 fs constant and a long ∼2–3 ps constant29−31,34,50−52 (see Table S4 for a compilation of the experimental and theoretical results). The latter two decay constants are in very good agreement with the constants obtained in our NAMD simulations (τ1 + τ2 ∼ 144 fs, and τ3 ∼ 1.92 ps).

The theoretically obtained mechanism for uracil photodynamics is summarized in Figure 1c (see also Figure S5), which shows the minimum energy paths (MEPs) connecting the critical geometries on the S2, S1, and S0 PESs (see Figure S2). The solid and dashed green arrows show the relaxation channels observed during the NAMD simulations. The main characteristics of the uracil photodecay dynamics are similar to those of the thymine gas phase photodynamics recently reported by Park et al.37 The main features are a rapid S2 → S1 internal conversion (IC) through a nearly planar CI and a slow S1 → S0 IC through a CI involving torsion about the C5=C6 bond.37 However, a marked difference between the thymine and uracil photodynamics is that the latter displays a very rapid S2 → S1 → S0 decay channel through a cascade of CIs, CI21,± and CI10,±, featuring an HOOP distortion, also known as the ethylenic CIs.25,26 Such a channel was not observed in the thymine dynamics, most likely due to the involvement of a heavier exocyclic Me group; this resulted in a slower C5=C6 torsional motion, which could not compete with a much faster BLA deactivation channel.37 It is this rapid channel that leads to the formation of a ground-state product that has not been detected previously for thymine, 4, denoted as S0,min± and seen on the right-hand side of Figure 1c at a ΔE of 3.54 eV (0.81 eV below CI10,±).

Although the formation of 4  is observed in only a small percentage of NAMD trajectories (∼8%), the fact that it survives for 5 ps implies that this is a kinetically stable species. According to the gas phase MRSF-TDDFT/BH&HLYP/6-31G* calculations, 4  lies 3.54 eV (81.6 kcal/mol) above the S0 stable (planar) minimum 1  [see Figure 1c (see also Figure S5)]. Analysis of its vibrational normal modes at the MRSF-TDDFT/BH&HLYP/6-31G* level yields no imaginary frequencies; hence, 4  is a local minimum on the S0 PES. The geometry of 4  has also been optimized using other computational methods. In these calculations, a larger cc-pVTZ basis set53 was used to mitigate the basis set incompleteness. Therefore, the standard spin-restricted Kohn–Sham (RKS) method of DFT in connection with the BH&HLYP density functional, BH&HLYP/cc-pVTZ, yielded a geometry and relative energy of 4, 3.64 eV (84.0 kcal/mol), very similar to those of MRSF (see Figure 1d). A very similar result was obtained using the CCSD/cc-pVTZ geometry optimization of 1  and 4 , which produced a relative energy of 76.4 kcal/mol. At the CCSD(T)/aug-cc-pVTZ level, the relative energy was slightly reduced to 73.0 kcal/mol. As 4  is the ground-state species, in the following, its structure and reactivity are studied using the BH&HLYP/cc-pVTZ computations, which reasonably agree with the CCSD/CCSD(T) results.

According to BH&HLYP/cc-pVTZ (as well as the other methods), 4 features a twisted C5=C6 bond and a puckered pyrimidine ring (see Figure 1d). The Cremer–Pople54 puckering parameters (Q, θ, φ) of the isomers of 4 , S0,min+ and S0,min– in Figure 1b, are (0.6 Å, 125°, 80°) and (0.6 Å, 55°, 260°), respectively. Therefore, 4  is a half-chair conformation with the 5H4 and 4H5 pucker.55 Because both are mirror images of each other, only the 5H4 conformation of 4  (S0,min+) is explicitly considered below.

Because atoms C5 and C6 are pyramidalized, the ∠HC5C6H and ∠C4C5C6N1 angles, 176.3° and 82.9°, respectively, do not adequately reflect the degree of twist of the double bond. A dihedral angle θ between the CR2 groups defined in Figure 1d is 59.5° (CCSD, 57.7°), indicating an intermediately twisted and strained double bond. However, the π component of the bond remains intact, as seen in the HOMO and LUMO of 4  in Figure 1d. The C5=C6 bond is only slightly elongated compared to the S0 equilibrium geometry, from 1.339 to 1.372 Å (CCSD, 1.367 Å). The C4–C5 bond undergoes the strongest variation, from 1.450 Å in 1  to 1.496 Å (CCSD, 1.504 Å) in 4. The lengths of the other bonds vary by only approximately ±0.02 Å (see Figure 1d). Contrary to expectation, 4  is not a zwitterionic species, as an only slight variation of the charges occurs between 1  and 4  (see Figure S3 for Mulliken charges on individual atoms). It is not a biradicaloid species either, because the (fractional) occupation numbers of the natural orbitals from the MRSF-TDDFT/BH&HLYP/6-31G* density matrix of 4 remain close to 2 and 0, which is typical for closed-shell species. 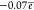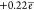Hence, the C5=C6 bond in 4 is torsionally strained and slightly polarized due to the presence of polar groups (the carbonyl group and amino nitrogen) in the pyrimidine ring: The C5 atom is slightly negatively charged (the overall charge on the C5H group is Inline graphic), and the C6 atom is positively charged (the charge on the C6H group is Inline graphic).

Despite its torsionally strained structure, 4 is separated from the global S0 minimum 1 by a barrier of 8.1 kcal/mol (BH&HLYP/cc-pVTZ) (see the Supporting Information for the geometry of the transition state). The other computational methods yield barriers of 10.8 kcal/mol (MRSF-TDDFT/BH&HLYP/6-31G*) and 14.0 kcal/mol [CCSD(T)/aug-cc-pVTZ]. Therefore, at ambient temperature, 4 can survive for approximately 0.1–1 ns, which seems sufficient for reaction with molecules in the environment. Furthermore, a torsionally strained double bond displays a greater reactivity,56−58 which renders 4 a highly reactive species capable of undergoing a nucleophilic attack by water molecules in its immediate environment. Therefore, the formation of 4 in the course of uracil photodeactivation offers a simple explanation for its photohydration mechanism. In addition to uracil, the possibility of the existence of intermediates similar to 4  has been confirmed by optimizations of the geometry of cytosine and thymine, as described in the Supporting Information. However, the probability of formation of these intermediates during the photodynamics can be very different from that of uracil.

To demonstrate the feasibility of the reaction between 4 and the surrounding water molecules, the transition states, intermediates, and end products of a simple uracil + H2O reaction have been identified by the BH&HLYP/cc-pVTZ geometry optimizations. The effect of the environment (water) is taken into account implicitly through the polarizable continuum model (PCM).

As shown in Chart 3a, the most stable product of the 4 + H2O reaction is (R)-6-hydroxydihydropyrimidine-2,4(1H,3H)-dione, denoted R-2 below. The S-2  conformer has a very close energy, and for the 5H4 ring pucker, it seems to be the most likely product of the hydration reaction (cf. the conformation of 4 in Chart 2). In both R-2  and S-2, the hydration occurs at the C6 atom, which is the preferred site for a nucleophilic attack due to a positive total charge on the C6H group. The C5 atom is a disfavored site of a nucleophilic attack (it is almost electrically neutral), and the respective R-5 and S-5 products are noticeably less stable than the C6 hydration products, especially when the solvent effects are included through the PCM.

Chart 3. (a) Conformations of Hydroxo-uracila and (b) Relative Energies (kilocalories per mole) of the Intermediate Species in the Mechanism of Uracil 1 Hydration Obtained Using the BH&HLYP/cc-pVTZ Method on the PES of the Electronic Ground Stateb.

Chart 3

Open in a new tab

a Only the conformations with the 5H4 pucker are shown. The relative energies (kilocalories per mole) are given beside each conformation. In parentheses are the values obtained using the PCM implicit solvent (water) computations.

b In parentheses, the values obtained using the PCM implicit solvent (water) computations are given. The CCSD(T)/aug-cc-pVTZ relative energies of some species are shown in italics. The excited-state energies of 1* and CI10+ with one water molecule included from the MRSF-TDDFT/BH&HLYP/6-31G* calculations are also given. The inset shows the interpolation paths connecting the critical geometries on the excited-state PESs calculated using the MRSF-TDDFT/BH&HLYP/6-31G* method.

Chart 3b shows the relative energies (with respect to 1 + H2O with and without PCM) of the intermediate species in the hydration of 4. For the excited-state species, the MRSF-TDDFT/BH&HLYP/6-31G* relative energies are shown with respect to the gas phase 1 + H2O energy. The geometries of the ground-state species (see the Supporting Information) were optimized in the gas phase and in a PCM (water) environment; the latter energies are given parenthetically in Chart 3b.

Transition state TS42 for the insertion of water into 4  occurs ∼7.8 kcal/mol above the energy level of 4 + H2O. As the hydration reaction occurs immediately after the S1 → S0 nonadiabatic relaxation, the molecule remains in a vibrationally “hot” state, where, judging by the nuclear kinetic energy in the NAMD simulations, the local vibrational temperature may reach nearly 1000 K. At such a temperature, the TS42 barrier can be crossed within a characteristic time of ∼8 ps, which falls within a time range, ∼5–20 ps, typical for the cooling of a vibrationally “hot” state.59

The barrier to ring planarization, TS41, is considerably lower (1.3 vs 7.8 kcal/mol) than the water insertion barrier TS42. Note that the barriers produced in our DFT calculations are likely to be the lower bounds of the actual barrier heights, and the more accurate computational methods [e.g., CCSD(T)] can produce barriers a few kilocalories per mole higher. For example, the gas phase barrier to the ring planarization of 4 is 14.0 kcal/mol from CCSD(T) and 8.1 kcal/mol from DFT. Assuming that the local vibrational temperature is ∼1000 K, we find the relationship between the two barriers results in a rather low yield, ∼3 × 10–2, of hydration product S-2. From NAMD simulations, the quantum yield of formation of 4 is ∼8 × 10–2, resulting in a total quantum yield of the hydration product of ∼2.4 × 10–3. The estimated quantum yield of hydrated uracil appears to be consistent with the experimental value measured in the dimethyluracil photohydration reaction, 3.75–4.63 × 10–3.60,61 A direct hydration of uracil in its ground-state equilibrium conformation 1 seems highly unlikely, as this involves a barrier, TS12, as high as ∼62 kcal/mol (see Chart 3b). Hence, the energies of the intermediate species reported in Chart 3b demonstrate that the most probable mechanism of uracil photohydration involves the formation of a highly energetic intermediate, 4, which undergoes a nucleophilic attack by water at the C6 atom.

In addition to the 4 + H2O reaction on the S0 PES, the formation of uracil hydrate S-2 can occur as a result of the insertion of water in the vicinity of the S1/S0 conical intersection, CI10,+. Indeed, CI10,+ is the funnel of the S1 → S0 nonadiabatic relaxation of the excited state and can be reached on the excited-state PES nearly barrierlessly (see the inset of Chart 3b). As the geometry of CI10,+ is quite similar to the geometry of 4 (see Figure S2), it seems likely that this structure can also undergo a nucleophilic attack by a nearby water molecule. In a realistic situation, with water molecules in the vicinity of the uracil, such an attack by water can even reduce the probability of re-formation of ground-state uracil 1 through the CI10,+ structure and result in hydration bypassing the formation of 4.

However, a more accurate evaluation of the probability of such a reaction would require the NAMD simulations with an explicit account of the water molecules at the quantum mechanical (i.e., not a QM/MM) level. Furthermore, due to a very low quantum yield of the hydration reaction and its relatively slow rate, obtaining a statistically significant description would require a very large number of trajectory simulations (∼104) with a duration of up to 20–50 ps to be run, which currently is not practically affordable. However, on the basis of the results of the MRSF-TDDFT/BH&HLYP/6-31G* optimization of the geometry of the critical species on the excited-state PESs in the presence of a water molecule, there exists a barrierless path from the FC geometry to the S1/S0 CI (see the inset of Chart 3b). Therefore, such a reaction pathway cannot be excluded.

From the results in Chart 3b, 4 is the central species in the proposed uracil photohydration mechanism. For its experimental detection, ultrafast time-resolved infrared (TRIR) spectroscopy can be proposed. In fact, a comparison of the IR spectra of 1 and 4, calculated with the use of the BH&HLYP/cc-pVTZ method and shown in Figure S11, shows that 4 has a sufficiently strong IR absorption band near ∼1050 cm–1, which is absent in 1 (see Figure S11). The 1050 cm–1 IR band is formed by two closely spaced vibrational normal modes, ν16 and ν17 (see Figure S11), which are characteristic of the puckered ring of 4. Because the calculated IR spectrum of the uracil compares favorably with the experimental spectrum obtained in inert matrices,62 the prediction of the IR band near 1050 cm–1 seems to be sufficiently reliable to be used for the detection of 4. In a water environment, the proposed IR absorption band can be obscured by the broad IR absorption bands of water. Therefore, it can be suggested to carry out the TRIR identification of 4 in a different environment or in the gas phase, where only the low quantum yield of 4 (∼0.08) will limit the possibility of its observation.

In summary, on the basis of the results of the NAMD simulations and the quantum chemical calculation of the stationary points on the adiabatic PESs of the uracil + H2O system, we propose that the uracil photohydration mechanism proceeds (see Chart 4) through the formation of an intermediate (4) that has not been previously identified. 4 features a half-chair conformation of the pyrimidine ring with 5H4 and 4H5 pucker and with a strongly (∼60°) twisted C5=C6 bond. Although 4  is a highly energetic species ∼80 kcal/mol above the ground-state equilibrium conformation 1, it is a kinetically stable species and is separated from 1 by a barrier of ∼10 kcal/mol. The existence and kinetic stability of 4 have been confirmed by several computational methods used in this work, including the CCSD/CCSD(T) theory.

Chart 4. Mechanism of Uracil Photohydration Suggested in This Worka.

Chart 4

Open in a new tab

a IC stands for internal conversion, and CI stands for conical intersection.

Intermediate 4 is formed as a transient species immediately upon S1 → S0 nonadiabatic relaxation and, according to the NAMD simulations and investigation of the static structures, is capable of surviving for a sufficiently long time to engage in reactions with the molecules in its vicinity. In particular, 4 can undergo a nucleophilic attack by a neighboring water molecule to produce uracil hydrate 2, more specifically, (S)-6-hydroxydihydropyrimidine-2,4(1H,3H)-dione shown in Chart 3a as S-2. Although 4 engages in a nucleophilic addition of water, it is not a zwitterionic species and there is no charge transfer from C6 to O4. Instead, 4 has a torsionally strained C5=C6 bond, which renders it a highly reactive species.

In addition to hydration through 4, which occurs on the S0 PES, uracil can possibly undergo hydration through the CI10,± funnel, which may occur during the S1 → S0 internal conversion. At present, the exact computational modeling of this reaction channel does not seem affordable and its participation in the uracil photohydration reaction remains hypothetical. It is also noteworthy that a T1 local minimum, which features a half-chair geometry, occurs only 11 kcal/mol below 4. This fact can potentially offer a unified mechanism of uracil photolysis, of both hydration and dimerization reactions, where the latter reaction proceeds through intersystem crossing between the singlet and a nearby triplet state of 4. The investigation of this possibility is currently underway. However, the existence of intermediate 4, identified here for the first time, can potentially stimulate research on the photochemistry of pyrimidine nucleobases and the search for experimental evidence of the existence of highly unusual species such as 4.

Acknowledgments

The support by Samsung Science and Technology Foundations Grant SSTF-BA1701-12 and Grants 2020R1A2C2008246 and 2020R1A5A1019141 funded by the Ministry of Science and ICT is acknowledged. This work was also supported by the Korea Polar Research Institute (KOPRI, PE21120).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.2c01694.

  • Detailed description of the computational settings, results of the NAMD simulations and static computations, and geometries of all species identified in this work (PDF)

  • Animation of one of the trajectories that end in the formation of intermediate 4 (MP4)

The authors declare no competing financial interest.

Supplementary Material

jz2c01694_si_001.pdf (52.6MB, pdf)
jz2c01694_si_002.mp4 (4.8MB, mp4)

References

  1. Sinsheimer R. L.; Hastings R. A reversible photochemical alteration of uracil and uridine. Science 1949, 110, 525–526. 10.1126/science.110.2864.525. [DOI] [PubMed] [Google Scholar]
  2. Moore A. M. Ultraviolet irradiation of pyrimidine derivatives: II. Note on the synthesis of the product of reversible photolysis of uracil. Can. J. Chem. 1958, 36, 281–283. 10.1139/v58-038. [DOI] [Google Scholar]
  3. Burr J. G.; Gordon B. R.; Park E. H. The mechanism of photohydration of uracil and N-substituted uracils. Photochem. Photobiol. 1968, 8, 73–78. 10.1111/j.1751-1097.1968.tb05847.x. [DOI] [Google Scholar]
  4. Burr J. G.; Gordon B. R.; Park E. H. In Radiation Chemistry; Hart E. J., Ed.; Advances in Chemistry; American Chemical Society: Washington, DC, 1968; Vol. 81, Chapter 29, pp 418–434. [Google Scholar]
  5. Burr J. G. In Advances in the photochemistry of nucleic acid derivatives; Noyes W. A. Jr., Hammond G. S., Pitts J. N. Jr., Eds.; Advances in Photochemistry; John Wiley & Sons, Ltd., 1968; Vol. 6, Chapter 3, pp 193–299. [Google Scholar]
  6. Wechter W. J.; Smith K. C. Nucleic acids. IX. Structure and chemistry of uridine photohydrate. Biochemistry 1968, 7, 4064–4069. 10.1021/bi00851a039. [DOI] [PubMed] [Google Scholar]
  7. Lamola A. A.; Mittal J. P. Solution photochemistry of thymine and uracil. Science 1966, 154, 1560–1561. 10.1126/science.154.3756.1560. [DOI] [PubMed] [Google Scholar]
  8. Greenstock C.; Brown I.; Hunt J.; Johns H. Photodimerization of pyrimidine nucleic acid derivatives in aqueous solution and the effect of oxygen. Biochem. Biophys. Res. Commun. 1967, 27, 431–436. 10.1016/S0006-291X(67)80002-0. [DOI] [PubMed] [Google Scholar]
  9. Brown I. H.; Johns H. E. Photochemistry of uracil. Intersystem crossing and dimerization in aqueous solution. J. Photochem. Photobiol. 1968, 8, 273–286. 10.1111/j.1751-1097.1968.tb05871.x. [DOI] [Google Scholar]
  10. Inaki Y. In CRC Handbook of Organic Photochemistry and Photobiology; Horspool W. M., Lenci F., Eds.; CRC Press: Boca Raton, FL, 2003; Vols. 1 and 2, Chapter 104. [Google Scholar]
  11. Wang S. Y.; Nnadi J. C. Mechanism for the photohydration of pyrimidines. Chem. Commun. (London) 1968, 1160–1162. 10.1039/c19680001160. [DOI] [Google Scholar]
  12. Burr J. G.; Park E. H.; Chan A. Nature of the reactive species in the photohydration of uracil and cytosine derivatives. J. Am. Chem. Soc. 1972, 94, 5866–5872. 10.1021/ja00771a054. [DOI] [PubMed] [Google Scholar]
  13. Wang S. Y. In Excited States in Organic Chemistry and Biochemistry; Pullman B., Goldblum N., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1977; pp 39–52. [Google Scholar]
  14. Cerutti P.; Remsen J. F.; Mattern M.; Miller N. Photohydration of uridine in the ribonucleic acid of coliphage R17. Lethality of uridine photohydrates and nonlethality of cyclobutane-type photodimers. Biochemistry 1971, 10, 524–529. 10.1021/bi00779a027. [DOI] [PubMed] [Google Scholar]
  15. Boorstein R. J.; Hilbert T. P.; Cunningham R. P.; Teebor G. W. Formation and stability of repairable pyrimidine photohydrates in DNA. Biochemistry 1990, 29, 10455–10460. 10.1021/bi00498a004. [DOI] [PubMed] [Google Scholar]
  16. Ganguly T.; Duker N. J. Stability of DNA thymine hydrates. Nucleic Acids Res. 1991, 19, 3319–3323. 10.1093/nar/19.12.3319. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Ganguly T.; Duker N. J. Inhibition of DNA polymerase activity by thymine hydrates. Mutat. Res./DNA Repair 1992, 293, 71–77. 10.1016/0921-8777(92)90010-Z. [DOI] [PubMed] [Google Scholar]
  18. Franzen S.; Skalski B.; Bartolotti L.; Delley B. The coupling of tautomerization to hydration in the transition state on the pyrimidine photohydration reaction path. Phys. Chem. Chem. Phys. 2014, 16, 20164–20174. 10.1039/C4CP02160F. [DOI] [PubMed] [Google Scholar]
  19. Chakraborty P.; Karsili T. N.; Marchetti B.; Matsika S. Mechanistic insights into photoinduced damage of DNA and RNA nucleobases in the gas phase and in bulk solution. Faraday discuss 2018, 207, 329–350. 10.1039/C7FD00188F. [DOI] [PubMed] [Google Scholar]
  20. Lee S.; Filatov M.; Lee S.; Choi C. H. Eliminating spin-contamination of spin-flip time dependent density functional theory within linear response formalism by the use of zeroth-order mixed-reference (MR) reduced density matrix. J. Chem. Phys. 2018, 149, 104101. 10.1063/1.5044202. [DOI] [PubMed] [Google Scholar]
  21. Lee S.; Kim E. E.; Nakata H.; Lee S.; Choi C. H. Efficient implementations of analytic energy gradient for mixed-reference spin-flip time-dependent density functional theory (MRSF-TDDFT). J. Chem. Phys. 2019, 150, 184111. 10.1063/1.5086895. [DOI] [PubMed] [Google Scholar]
  22. Wetmore S. D.; Boyd R. J.; Eriksson L. A. Radiation products of thymine, 1-methylthymine, and uracil investigated by density functional theory. J. Phys. Chem. B 1998, 102, 5369–5377. 10.1021/jp9809078. [DOI] [Google Scholar]
  23. Lü J. M.; Geimer J.; Naumov S.; Beckert D. A Fourier transform EPR study of uracil and thymine radical anions in aqueous solution. Phys. Chem. Chem. Phys. 2001, 3, 952–956. 10.1039/b008892g. [DOI] [Google Scholar]
  24. Naumov S.; Beckert D. Reply to the ‘Comment on “A Fourier transform EPR study of uracil and thymine radical anions in aqueous solution”’ by D. M. Close. Phys. Chem. Chem. Phys. 2002, 4, 45. 10.1039/b109230h. [DOI] [Google Scholar]
  25. Barbatti M.; Aquino A. J.; Szymczak J. J.; Nachtigallová D.; Hobza P.; Lischka H. Relaxation mechanisms of UV-photoexcited DNA and RNA nucleobases. Proc. Natl. Acad. Sci. U.S.A 2010, 107, 21453–21458. 10.1073/pnas.1014982107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Chakraborty P.; Liu Y.; Weinacht T.; Matsika S. Effect of dynamic correlation on the ultrafast relaxation of uracil in the gas phase. Faraday Discuss. 2021, 228, 266–285. 10.1039/D0FD00110D. [DOI] [PubMed] [Google Scholar]
  27. Improta R.; Santoro F.; Blancafort L. Quantum mechanical studies on the photophysics and the photochemistry of nucleic acids and nucleobases. Chem. Rev. 2016, 116, 3540–3593. 10.1021/acs.chemrev.5b00444. [DOI] [PubMed] [Google Scholar]
  28. Pecourt J.-M. L.; Peon J.; Kohler B. Ultrafast Internal Conversion of Electronically Excited RNA and DNA Nucleosides in Water. J. Am. Chem. Soc. 2000, 122, 9348–9349. 10.1021/ja0021520. [DOI] [Google Scholar]
  29. Kang H.; Lee K. T.; Jung B.; Ko Y. J.; Kim S. K. Intrinsic lifetimes of the excited state of DNA and RNA bases. J. Am. Chem. Soc. 2002, 124, 12958–12959. 10.1021/ja027627x. [DOI] [PubMed] [Google Scholar]
  30. Ullrich S.; Schultz T.; Zgierski M. Z.; Stolow A. Electronic relaxation dynamics in DNA and RNA bases studied by time-resolved photoelectron spectroscopy. Phys. Chem. Chem. Phys. 2004, 6, 2796–2801. 10.1039/b316324e. [DOI] [PubMed] [Google Scholar]
  31. Canuel C.; Mons M.; Piuzzi F.; Tardivel B.; Dimicoli I.; Elhanine M. Excited states dynamics of DNA and RNA bases: Characterization of a stepwise deactivation pathway in the gas phase. J. Chem. Phys. 2005, 122, 074316. 10.1063/1.1850469. [DOI] [PubMed] [Google Scholar]
  32. Samoylova E.; Lippert H.; Ullrich S.; Hertel I. V.; Radloff W.; Schultz T. Dynamics of photoinduced processes in adenine and thymine base pairs. J. Am. Chem. Soc. 2005, 127, 1782–1786. 10.1021/ja044369q. [DOI] [PubMed] [Google Scholar]
  33. McFarland B. K.; Farrell J. P.; Miyabe S.; Tarantelli F.; Aguilar A.; Berrah N.; Bostedt C.; Bozek J. D.; Bucksbaum P. H.; Castagna J. C.; et al. Ultrafast X-ray Auger probing of photoexcited molecular dynamics. Nat. Commun. 2014, 5, 4235. 10.1038/ncomms5235. [DOI] [PubMed] [Google Scholar]
  34. Yu H.; Sanchez-Rodriguez J. A.; Pollum M.; Crespo-Hernández C. E.; Mai S.; Marquetand P.; González L.; Ullrich S. Internal conversion and intersystem crossing pathways in UV excited, isolated uracils and their implications in prebiotic chemistry. Phys. Chem. Chem. Phys. 2016, 18, 20168–20176. 10.1039/C6CP01790H. [DOI] [PubMed] [Google Scholar]
  35. He Y.; Wu C.; Kong W. Photophysics of methyl-substituted uracils and thymines and their water complexes in the gas phase. J. Phys. Chem. A 2004, 108, 943–949. 10.1021/jp036553o. [DOI] [Google Scholar]
  36. Hudock H. R.; Levine B. G.; Thompson A. L.; Satzger H.; Townsend D.; Gador N.; Ullrich S.; Stolow A.; Martinez T. J. Ab initio molecular dynamics and time-resolved photoelectron spectroscopy of electronically excited uracil and thymine. J. Phys. Chem. A 2007, 111, 8500–8508. 10.1021/jp0723665. [DOI] [PubMed] [Google Scholar]
  37. Park W.; Lee S.; Huix-Rotllant M.; Filatov M.; Choi C. H. Impact of the dynamic electron correlation on the unusually long excited-state lifetime of thymine. J. Phys. Chem. Lett. 2021, 12, 4339–4346. 10.1021/acs.jpclett.1c00712. [DOI] [PubMed] [Google Scholar]
  38. Tully J. C. Molecular dynamics with electronic transitions. J. Chem. Phys. 1990, 93, 1061. 10.1063/1.459170. [DOI] [Google Scholar]
  39. Lee S.; Kim E.; Lee S.; Choi C. H. Fast overlap evaluations for nonadiabatic molecular dynamics simulations: applications to SF-TDDFT and TDDFT. J. Chem. Theory Comput. 2019, 15, 882. 10.1021/acs.jctc.8b01049. [DOI] [PubMed] [Google Scholar]
  40. Lee S.; Horbatenko Y.; Filatov M.; Choi C. H. Fast and accurate computation of nonadiabatic coupling matrix elements using the truncated leibniz formula and mixed-reference spin-flip time-dependent density functional theory. J. Phys. Chem. Lett. 2021, 12, 4722–4728. 10.1021/acs.jpclett.1c00932. [DOI] [PubMed] [Google Scholar]
  41. Lee S.; Shostak S.; Filatov M.; Choi C. H. Conical intersections in organic molecules: Benchmarking mixed-reference spin–flip time-dependent DFT (MRSF-TD-DFT) vs spin–flip TD-DFT. J. Phys. Chem. A 2019, 123, 6455–6462. 10.1021/acs.jpca.9b06142. [DOI] [PubMed] [Google Scholar]
  42. Nikiforov A.; Gamez J. A.; Thiel W.; Huix-Rotllant M.; Filatov M. Assessment of approximate computational methods for conical intersections and branching plane vectors in organic molecules. J. Chem. Phys. 2014, 141, 124122. 10.1063/1.4896372. [DOI] [PubMed] [Google Scholar]
  43. Zhang X.; Herbert J. M. Nonadiabatic dynamics with spin-flip vs linear-response time-dependent density functional theory: A case study for the protonated Schiff base C5H6NH2+. J. Chem. Phys. 2021, 155, 124111. 10.1063/5.0062757. [DOI] [PubMed] [Google Scholar]
  44. Oppenheim I.; Ross J. Temperature dependence of distribution functions in quantum statistical mechanics. Phys. Rev. 1957, 107, 28–32. 10.1103/PhysRev.107.28. [DOI] [Google Scholar]
  45. Davies R. W.; Davies K. T. R. On the Wigner distribution function for an oscillator. Ann. Phys. 1975, 89, 261–273. 10.1016/0003-4916(75)90182-7. [DOI] [Google Scholar]
  46. Epifanovsky E.; Kowalski K.; Fan P.-D.; Valiev M.; Matsika S.; Krylov A. I. On the electronically excited states of uracil. J. Phys. Chem. A 2008, 112, 9983–9992. 10.1021/jp803758q. [DOI] [PubMed] [Google Scholar]
  47. Nangia S.; Jasper A. W.; Miller T. F.; Truhlar D. G. Army ants algorithm for rare event sampling of delocalized nonadiabatic transitions by trajectory surface hopping and the estimation of sampling errors by the bootstrap method. J. Chem. Phys. 2004, 120, 3586–3597. 10.1063/1.1641019. [DOI] [PubMed] [Google Scholar]
  48. Jónsson H.; Mills G.; Jacobsen K. W. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne B. J., Ciccotti G., Coker D. F., Eds.; World Scientific: Singapore, 1998; Chapter 16, pp 385–404. [Google Scholar]
  49. Kästner J.; Carr J. M.; Keal T. W.; Thiel W.; Wander A.; Sherwood P. DL-FIND: an open-source geometry optimizer for atomistic simulations. J. Phys. Chem. A 2009, 113, 11856–11865. 10.1021/jp9028968. [DOI] [PubMed] [Google Scholar]
  50. Kotur M.; Weinacht T. C.; Zhou C.; Matsika S. Following ultrafast radiationless relaxation dynamics with strong field dissociative ionization: a comparison between adenine, uracil, and cytosine. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 187–194. 10.1109/JSTQE.2011.2107892. [DOI] [Google Scholar]
  51. Horton S. L.; Liu Y.; Chakraborty P.; Marquetand P.; Rozgonyi T.; Matsika S.; Weinacht T. Strong-field-versus weak-field-ionization pump-probe spectroscopy. Phys. Rev. A 2018, 98, 053416. 10.1103/PhysRevA.98.053416. [DOI] [Google Scholar]
  52. Ghafur O.; Crane S. W.; Ryszka M.; Bockova J.; Rebelo A.; Saalbach L.; De Camillis S.; Greenwood J. B.; Eden S.; Townsend D. Ultraviolet relaxation dynamics in uracil: Time-resolved photoion yield studies using a laser-based thermal desorption source. J. Chem. Phys. 2018, 149, 034301. 10.1063/1.5034419. [DOI] [PubMed] [Google Scholar]
  53. Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  54. Cremer D.; Pople J. A. General definition of ring puckering coordinates. J. Am. Chem. Soc. 1975, 97, 1354–1358. 10.1021/ja00839a011. [DOI] [Google Scholar]
  55. Hill A. D.; Reilly P. J. Puckering coordinates of monocyclic rings by triangular decomposition. J. Chem. Inf. Model. 2007, 47, 1031–1035. 10.1021/ci600492e. [DOI] [PubMed] [Google Scholar]
  56. Wiberg K. B. The concept of strain in organic chemistry. Angew. Chem., Int. Ed. Engl. 1986, 25, 312–322. 10.1002/anie.198603121. [DOI] [Google Scholar]
  57. Shea K. J.; Kim J. S. Influence of strain on chemical reactivity. Relative reactivity of torsionally strained double bonds in 1,3-dipolar cycloadditions. J. Am. Chem. Soc. 1992, 114, 4846–4855. 10.1021/ja00038a059. [DOI] [Google Scholar]
  58. Sella A.; Basch H.; Hoz S. Reactivity of strained compounds: Is ground state destabilization the major cause for rate enhancement?. J. Am. Chem. Soc. 1996, 118, 416–420. 10.1021/ja951408c. [DOI] [Google Scholar]
  59. Park S.-M.; Nguyen P. H.; Stock G. Molecular dynamics simulation of cooling: Heat transfer from a photoexcited peptide to the solvent. J. Chem. Phys. 2009, 131, 184503. 10.1063/1.3259971. [DOI] [PubMed] [Google Scholar]
  60. Burr J. G.; Park E. H.; Chan A. Nature of the reactive species in the photohydration of uracil and cytosine derivatives. J. Am. Chem. Soc. 1972, 94, 5866–5872. 10.1021/ja00771a054. [DOI] [PubMed] [Google Scholar]
  61. Wang S. Y. Analysis of the rate of the ultraviolet irradiation and reconstitution reactions of 1,3-dimethyluracil and uridine. Photochem. Photobiol. 1962, 1, 135–145. 10.1111/j.1751-1097.1962.tb08086.x. [DOI] [Google Scholar]
  62. Puzzarini C.; Biczysko M.; Barone V. Accurate anharmonic vibrational frequencies for uracil: the performance of composite schemes and hybrid CC/DFT model. J. Chem. Theory Comput. 2011, 7, 3702–3710. 10.1021/ct200552m. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz2c01694_si_001.pdf (52.6MB, pdf)
jz2c01694_si_002.mp4 (4.8MB, mp4)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES