A new vaccine supply chain network under COVID-19 conditions considering system dynamic: Artificial intelligence algorithms

Abstract

With the discovery of the COVID-19 vaccine, what has always been worrying the decision-makers is related to the distribution management, the vaccination centers' location, and the inventory control of all types of vaccines. As the COVID-19 vaccine is highly demanded, planning for its fair distribution is a must. University is one of the most densely populated areas in a city, so it is critical to vaccinate university students so that the spread of this virus is curbed. As a result, in the present study, a new stochastic multi-objective, multi-period, and multi-commodity simulation-optimization model has been developed for the COVID-19 vaccine's production, distribution, location, allocation, and inventory control decisions. In this study, the proposed supply chain network includes four echelons of manufacturers, hospitals, vaccination centers, and volunteer vaccine students. Vaccine manufacturers send the vaccines to the vaccination centers and hospitals after production. The students with a history of special diseases such as heart disease, corticosteroids, blood clots, etc. are vaccinated in hospitals because of accessing more medical care, and the rest of the students are vaccinated in the vaccination centers. Then, a system dynamic structure of the prevalence of COVID -19 in universities is developed and the vaccine demand is estimated using simulation, in which the demand enters the mathematical model as a given stochastic parameter. Thus, the model pursues some goals, namely, to minimize supply chain costs, maximize student desirability for vaccination, and maximize justice in vaccine distribution. To solve the proposed model, Variable Neighborhood Search (VNS) and Whale Optimization Algorithm (WOA) algorithms are used. In terms of novelties, the most important novelties in the simulation model are considering the virtual education and exerted quarantine effect on estimating the number of the vaccines. In terms of the mathematical model, one of the remarkable contributions is paying attention to social distancing while receiving the injection and the possibility of the injection during working and non-working hours, and regarding the novelties in the solution methodology, a new heuristic method based on a meta-heuristic algorithm called Modified WOA with VNS (MVWOA) is developed. In terms of the performance metrics and the CPU time, the MOWOA is discovered with a superior performance than other given algorithms. Moreover, regarding the data, a case study related to the COVID-19 pandemic period in Tehran/Iran is provided to validate the proposed algorithm. The outcomes indicate that with the demand increase, the costs increase sharply while the vaccination desirability for students decreases with a slight slope.

1. Introduction

Vaccination is a simple, safe, and effective way to protect the body against dangerous diseases [1]. In fact, vaccines train the body's immune system to produce and shield antibodies against potential infections and viruses [2]. Antibodies fight germs that enter our bodies. The weakened samples of viruses or bacteria are usually employed to make vaccines and then, injected into the body [3]. So far, the weak or inactivated viruses have been used to make most vaccines, such as the flu and triple vaccines (vaccines for diphtheria, tetanus, and pertussis). But the COVID-19 specially designed vaccine was made with the new MRNA technology and is the first vaccine produced with this technology [4]. Since the COVID-19 virus epidemic broke out, the efforts to discover its vaccine have been made parallel with the medication [5]. Various COVID-19 specialized vaccines are currently being produced worldwide, but there are still lots of doubts surrounding them [6]. The important point is that with the high vaccine demand volume in countries around the world, an efficient approach is required to predict the vaccine demand so that to minimize vaccine shortages [7]. Some of these vaccines have been approved by COVID-19 vaccine monitoring organizations in various countries, while others are still awaiting approval for public use [8,9]. Thus, 11 countries' vaccination trend is reported in Table 1 .

Table 1.

Vaccination trend in 11 countries (2.14.2022).

Region	COVID-19 vaccination % to total population	Total doses
China	85.05	3,036,707,000
USA	64.25	547,154,250
India	54.51	1,729,559,610
Brazil	71.30	337,626,315
UK	71.51	138,942,048
Germany	74.21	167,885,429
France	77.19	139,804,600
Italy	77.87	132,064,916
Turkey	61.92	144,007,120
Mexico	60.26	172,480,864

Human has the right to access vaccines and the government is obligated to exercise this right at the earliest opportunity using all potential. The COVID-19 virus has incurred huge human, financial, economic, and social losses imposed on the countries so far [10]. Therefore, to control the epidemic and its harms, it's highly imperative to effectively perform vaccination and run efficient logistic planning against it [11]. Due to an uncertain vaccine demand quantity worldwide and not all people being able to simultaneously access the vaccine, the population groups are prioritized to receive the COVID-19 vaccine [12]. Prioritizing the population groups to receive the vaccines pursues the goal to reduce the COVID-19 induced severe maladies and death rate and mitigating the epidemic born negative effects on various aspects of people's lives and society economically, socially, and culturally [13]. For example, now that September is approaching and universities get opening in most countries, they are considering running the students' vaccination plan. Vaccinating the students both activates the higher education cycle and helps to lower the transmission cycle in the community [14]. Thus, planning for fairly vaccinating the students along with decreasing the vaccine distribution cost is one of the concerns for the governments.

One of the reasons behind the lack of public vaccine acceptance is the accumulation at the vaccination site and the possibility of contacting COVID-19 in the vaccination centers (Ehde et al., 2021). Accordingly, it is critical to maintaining social distance in the vaccination centers. One way to prevent crowds at the vaccination centers is to consider non-working shifts as reserved for injection candidates. This can to some extent guarantee the candidates’ satisfaction and desirability. Also in many countries, the due facilities are supplied for people with a history of taking certain diseases/medications such as corticosteroids or the diseases such as blood clots [15]. Instead of going to the vaccination centers, such individuals can go to the hospitals to have a medical examination before the vaccine injection and get vaccinated if the conditions are favorable.

Hence, in this research, student-oriented vaccination planning is discussed. First of all, the required vaccine quantity for the students is estimated using a simulation approach. In the proposed simulation model, the effects of virtual education, quarantine, wearing a mask, etc. on the calculated vaccine amount are considered. After calculating the required vaccine dose, this output enters as an input parameter (i.e., random variable) to a multi-objective, multi-echelon, and multi-period stochastic mathematical model developed to manage the production, distribution, location, allocation, and inventory planning of COVID-19 vaccines. In this study, the proposed supply chain network includes four echelons of manufacturers, hospitals, vaccination centers, and volunteer vaccine students. Vaccine manufacturers send the vaccines to the vaccination centers and hospitals after production. The proposed model targets minimizing the logistic costs of vaccine distribution, maximizing justice in the COVID-19 vaccines’ distribution, and maximizing vaccination desirability for students. Designing working and non-working hours and a reserving scheme to maintain the social distancing while receiving the injection are two contributions of the proposed mathematical model. To solve the model, Variable Neighborhood Search (VNS) and Whale Optimization Algorithm (WOA) algorithms are utilized and a new meta-heuristic algorithm-based heuristic method called Modified WOA with VNS (MVWOA) is developed for the first time. The most important novelties in the simulation model are considering the virtual education and exerted quarantine effect on estimating the number of the vaccines. In terms of the mathematical model, of the remarkable contributions is paying attention to social distancing when injecting the vaccine and the possibility of the injection during working and non-working hours.

The rest of the proposed research is organized into six sections. The second section presents the literature review. In the third section, the problem description, the simulation approach, the assumptions, and the mathematical modeling are given. The fourth section presents the solution methods for the proposed model. The fifth section illustrates the case study, the results of the proposed model and the simulation approach, and the sensitivity analysis, respectively. The sixth section deals with the conclusions and future works.

2. Literature review

The literature review section is presented in two parts. The first part deals with forecasting approaches for the COVID-19 cases number. The second part examines the production-distribution-location-allocation-inventory planning in the COVID-19 epidemic.

2.1. Forecasting approaches for COVID-19 cases number

Melin et al. [16] represented a hybrid intelligent fuzzy fractal approach according to the combination of the fuzzy logic mathematical constructs and the fractal theoretical concepts to classify the countries based on the prevalence rate of COVID-19. Their proposed hybrid approach is composed of a fuzzy system using fuzzy rules. They used the fractal dimensions as the inputs and generated the classification of the countries as the final output. As the COVID-19 data confirmed death cases suggest, the hybrid approach was calculated. Hence, they employed 11 countries' data as the base to create the fuzzy system and considered 15 various countries to validate their classification method. [17] in Bangladesh the Long Short-Term Memory network (LSTM) and ANFIS approaches to analyze and forecast the newly COVID-19 infected cases. The main goal they pursued was to achieve the proper machine learning algorithm able to forecast the new daily COVID-19 infected cases with higher accuracy. Finally, the results indicated that the LSTM outperformed the ANFIS. [18] suggested a prediction model for forecasting the confirmed COVID-19 cases' number in Vietnam according to the Particle Swarm Optimization (PSO) and Fuzzy Time Series (FTS). The PSO was employed to adjust and find the suitable number and length of the intervals in order to acquire the predicting accuracy. Moreover, the fuzzy relationship groups were applied to overcome the drawbacks of the fuzzy relationship matrix when developing the fuzzy predicting model. Hence, the numerical examples were used to validate the model's efficiency. [19] presented a short-term predicting model utilizing the Adaptive Neuro-Fuzzy Inference System (ANFIS). They developed a new method called the Chaotic Marine Predators (CMP) algorithm and in order to increase the ANFIS, they used an improved the CMP algorithm and the PSO algorithm. After that, they compared the predicting models' accuracy utilizing various statistical evaluation metrics. [20] proposed a procedure to classify and analyze the resulted forecasting model from Coronavirus symptoms. They applied the ANFIS for determining those features assisting in the early detection of Coronavirus illness. Therefore, through the ANFIS, the best classifier was selected to detect COVID-19 disease based on the comparative analysis, and also various machine learning classifier's accuracy was calculated. [21] suggested a new forecasting model that revealed a hybrid method among the ANFIS, the Improved Beetle Antennae Search (IBAS) meta-heuristic algorithm, and machine learning. The IBAS was employed to identify the ANFIS parameters and to improve the forecasting model's efficiency. Moreover, their hybrid approach was evaluated utilizing the WHO's data to forecast the COVID-19 cases in China. [22] forecasted the total number of COVID-19 cases in the upcoming days in Bangladesh using Autoregressive Integrated Moving Average (ARIMA) and ANFIS approaches. Finally, based on the root mean squared relative error and the mean absolute percentage error, both models' extracted results were compared. Additionally, in order to forecast the COVID-19-time series with type-2 fuzzy logic in a weighted average integration approach, the firefly algorithm was presented by Ref. [23] for the ensemble neural network optimization. They used the number of the required artificial neural networks to create an ensemble neural network and employed their architecture utilizing a type-2 fuzzy inference system to mix the answers of the individual artificial neural networks to apply the final forecasting. Finally, they investigated the latest global COVID-19 epidemic forecasting model. [24] provided the Learner's Academic Performance (LAP) based system using the ANFIS. They considered the ANFIS model to forecast the Cumulative Grade Point Average (CGPA) of learners. Accordingly, the accuracy of the ANFIS model's outcome was indicated according to the root-mean-square-errors values. To validate their model, T-test significance was used. Finally, the results displayed that the ANFIS model was a reliable technique to forecast the LAP. Yogachi et al. [25] designed and developed a fuzzy logic application (Mamdani approach) to forecast the number of COVID-19 cases. Then, the entered variables were divided into three categories including the ODP, PDP, and COVID-19 positive along with 3 sets of the low, medium, and high, respectively. Then, the output variable was positive forecasting 14 days later.

2.2. Production-distribution-location-allocation-inventory planning in the COVID-19 epidemic

[26] explained the challenges of fair vaccine distribution during the COVID-19 epidemic, while dividing the challenges into four categories including ($i)$ health outcomes, ($ii$) user-centric impact, ($iii$) communication, and ($iv$) logistics. They analyzed their examined challenges according to the data privacy, economy, individual behavior, society, and disease spread. [27] examined the multi-value ethics framework on how to fairly allocate the vaccines during the COVID-19 pandemic outbreak. They addressed several challenges for the COVID-19 vaccines' allocation, including distributive justice, ability to implement, ability to develop or purchase, and reciprocity for developing an allocation model. [28] investigated the challenges related to the COVID-19 vaccine being accepted during the COVID-19 epidemic in China. [29] developed a new method called the COVID-19 Optimizer Algorithm (CVA) to solve the optimization problems. Plus, they suggested a simulation approach for the COVID-19 distribution process across the world. They mainly targeted to decrease the pandemic spread speed and the number of the COVID-19 infected countries. Volcano Eruption Algorithm (VEA), Gray Wolf Optimizer (GWO), Particle Swarm Optimization (PSO), and Genetic Algorithm (GA) were used to solve their model, and finally, they were compared with the CVA. As the results indicated, the CVA had a high quality over the proposed algorithms. Then, according to the susceptibility rate, the operational constraints with the transshipment capacity, the capacity of the medical centers, the vaccine stocks, and the exposure risk, [30] developed a vaccine allocation model during the COVID-19 epidemic. They especially pursued the goals to integrate a vaccine distribution system, a centralized booking system, risk profiling, and prioritization in their conceptual model. To test various scenarios of vaccine distribution and allocation, they examined a real case study in Australia. [31] developed an integrated sustainable medical supply chain network for the COVID-19 pandemic associated production, distribution, inventory, allocation, location problems. Moreover, they formulated a multi-objective, multi-echelon, multi-product, and multi-period mixed-integer linear programming model. To solve their model, they developed three new hybrid meta-heuristic algorithms called ant fish swarm algorithm, firefly algorithm, and colony optimization with variable neighborhood search. At last, to validate their algorithms and the model, they provided a real case study, sensitivity analysis, assessment metrics, and simulation approach. [32] discussed the challenges and opportunities for the COVID-19 vaccine distribution. Besides, Thul and Powell [33] proposed the stochastic optimization for the COVID-19 vaccine and the test kit allocation for this pandemic outbreak. Following that, they addressed the construct beliefs' data related to the states and decisions about the resources' allocation. According to the vaccine allocation relevant decisions, they presented a new simulation model with optimization-based considering an adjustable forecast policy. Rastegar et al. [8,9] designed an inventory-location mixed-integer linear programming model for the COVID-19 epidemic in terms of fair vaccine distribution. They predominantly focused on the COVID-19 vaccine distribution for the elderly, those requiring healthcare and the first individuals who demand the vaccine, those with underlying health conditions, and pregnant women. Eventually, they provided a real case study in a developing country to demonstrate their model's performance. [34] employed game-theoretic and optimization methods for modeling the COVID-19 U.S. vaccine pricing problem. They considered a duopoly situation, i.e., Moderna and Pfizer-BioNTech in their model. Their model-derived results indicated that their model suggested prices were consistent with those forecasted in the media. [35] presented a multi-period mathematical model for vaccine supply chain management in India. Their main novelty is to calculate the amount of savings and the level of service to the vaccinated. Their main goal is to manage the inventory of vaccines and minimize perished vaccines. Their proposed model is solved using a heuristic approach and the results indicated the proper performance of their proposed solution approach. [36] presented a multi-objective nonlinear mathematical model for vaccine supply chain management. The main purpose of their study is to minimize supply chain costs along with maximizing the number of fully open vaccination stations. Their proposed model was solved using the Epsilon constraint approach. Their study is conducted in the Shenzhen Nanshan region and the results showed that transportation costs increase exponentially as demand increases.

Based on the examined papers in the literature review, some extracted research gaps are as follows:

• •Ignoring the dynamic structure of the COVID-19 pandemic outbreak. Designing the dynamic structure of the COVID-19 pandemic outbreak can help realize the strengths and weaknesses of this disease outbreak control,
• •Overlooking the quarantine and e-learning impact on estimating and distributing the COVID-19 vaccines,
• •Not paying attention to the social distancing rule and limiting the vaccination centers' capacity in the context of the outbreak of COVID-19,
• •Overlooking the vaccines' distribution justice among the vaccination centers,
• •Ignoring the candidates' desirability for the vaccination against COVID-19,
• •Ignoring the novel structure of the supply chain for a real case study during the COVID-19 pandemic,
• •Not paying attention to new and hybrid solution methods to solve the problems.

The considered contributions are divided into two general categories: 1) Contributions related to demand estimation; 2) Contributions related to the mathematical model. They are investigated as follows:

• ✓
  Demand Estimation Related Contributions:

  • •
    Estimating the amount of COVID-19 vaccine required for the students using the simulation approach,
  • •
    Considering the virtual education and quarantine-induced effect on the estimated number of vaccines.
• ✓
  Mathematical Model Related Contributions:

  • •
    Observing the social distancing and planning to inject the COVID-19 vaccine during working and non-working hours,
  • •
    Maximizing justice in the COVID-19 vaccines' distribution while minimizing the supply chain costs,
  • •
    Maximizing the vaccination desirability for students in the most profitable and effective way possible,
  • •
    Employing two VNS and WOA meta-heuristics and developing a new heuristic method called MVWOA algorithms based on the considered local search approach of the VNS.
  • •
    Customizing a real case study to check the accuracy of the suggested model and the effectiveness of the developed solution approaches.

3. Problem statement

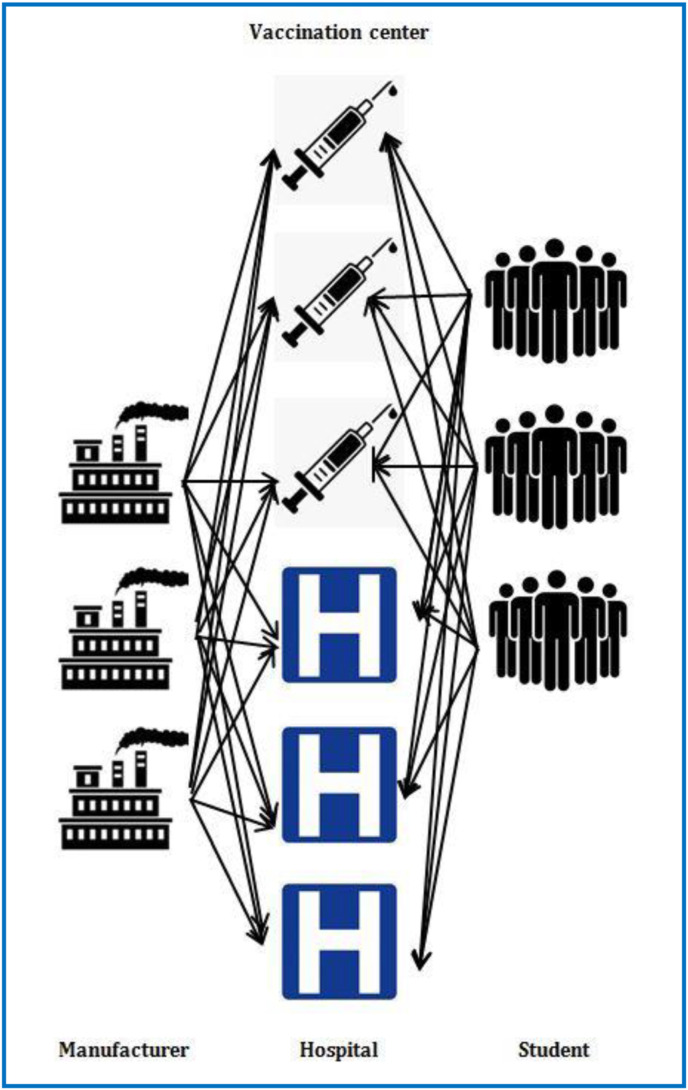
In this study, the proposed Supply Chain Network (SCN) includes four echelons of manufacturers, hospitals, vaccination centers, and volunteer students. Fig. 1 depicts the proposed SCN structure. Vaccine manufacturers send the produced vaccines to the vaccination centers and hospitals after their production. Students refer to the vaccination centers to get vaccinated. It should be noted that the students with a history of special diseases like heart disease, corticosteroids, blood clots, etc. should go to a hospital for vaccination, the reason behind this is the access to more medical care and facilities in hospitals and also the students would be under various care and tests. It is noteworthy that not only waiting in the queues to receive the injection, but also immediately after receiving the injection, immunity against the virus is not guaranteed, so it is still necessary to observe the due social distancing. To model this concern, we assumed that the vaccination centers are operating with a limited capacity. Also, we assumed a reserving scheme where the student can go to the vaccination centers based on a reserved date and time if they wish.

Fig. 1.

Configuration of the considered COVID-19 vaccine supply chain network.

Since the COVID-19 vaccines are perishable, cases being efficiently distributed can increase social satisfaction and its effectiveness. In this study, the vaccines inventory management in the vaccination centers and hospitals is addressed. Moreover, the way to allocate the manufacturers to the hospitals and the vaccination centers and control the vaccines' flow is investigated for the first time to the best of our knowledge. In addition, locating the vaccination centers minimizes the supply chain costs and provides better coverage and faster services to the students. Therefore, deciding on the location-allocation of the vaccination centers is considered in the proposed model. It's worth mentioning that only a few countries have the knowledge of producing vaccines and therefore, the whole world is suffering from a vaccine shortage. As a solution to this serious concern, most countries have vaccination plans based on various types of vaccines (e.g., Pfizer, Moderna, Sputnik, AstraZeneca, Sinopharm) Therefore, the suggested model in this research is viewed as a multi-product one.

The major goal of the proposed mathematical model is to minimize the vaccine supply chain costs including those of the set-up, shortages, transportation, and production. The second goal is to maximize the satisfaction of vaccine candidates, which can be realized in the form of incentives and cash payments to the students. The third goal of the study is to maximize the justice in distributing the vaccines. Paying attention to justice prevents prioritizing one center over other centers and this way, all centers are served equally. It should be noted that the vaccine demand is estimated by simulation and a system dynamic approach. The estimated demand plugs into the mathematical model as a given stochastic parameter. Therefore, the proposed model is stochastic. To tackle the stochasticity of the proposed mathematical model, the chance constraint method is used in this study (See Appendix A).

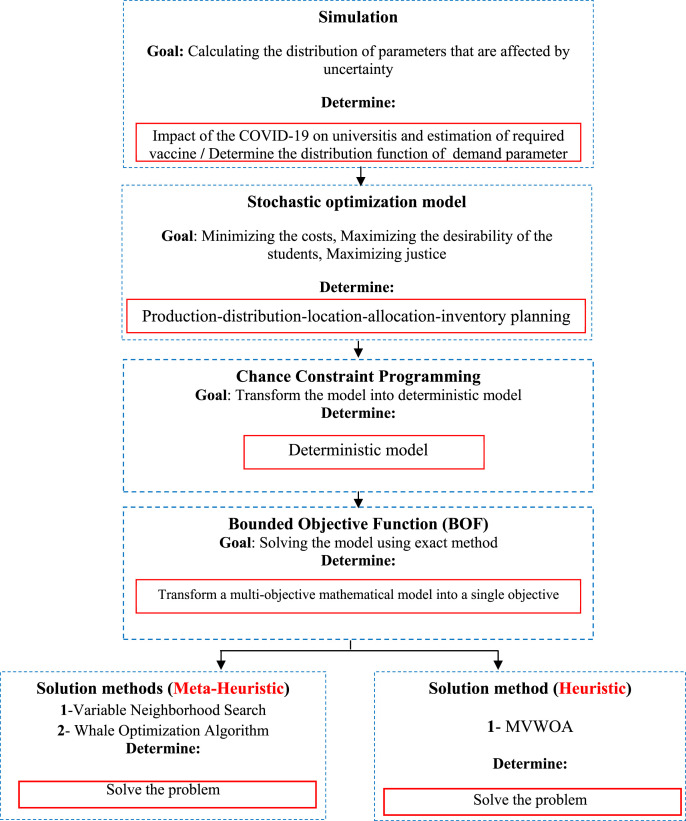
In Fig. 2 the research framework is depicted. In the first step, the model of the dynamic system of COVID-19 transmission in universities is designed to estimate the amount of vaccine demand. In the second step, a new stochastic multi-objective, multi-period, and multi-commodity simulation-based optimization model is presented. In the third step, the stochastic mathematical model is transformed into its deterministic counterpart by using the stochastic chance constraint approach. Then, the proposed model is converted into a single objective model using the Bounded Objective Function (BOF) technique in the fourth step. Finally, as the model can only be solved in small sizes by the BOF technique, two meta-heuristic methods (VNS and WOA) and one heuristic method (Modified WOA with VNS) are developed to efficiently solve the medium- and large-sized instances.

Fig. 2.

Research framework.

3.1. Simulation approach

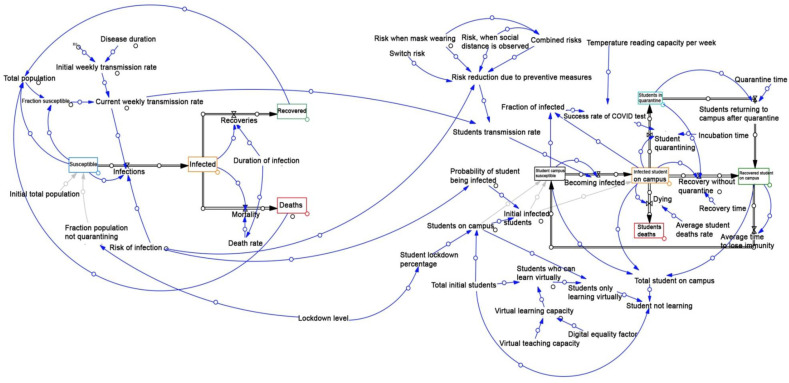
In Fig. 3 , the interaction structure of the COVID-19 prevalence in universities is modeled. Analyzing this structure can help determine the number of the affected, the deceased, and the healthy students. The structure consists of four main sections. The first section, on the left of the figure, shows the initial population, the deaths number, and the patients' number. The second one illustrates the virtual education's impact on the number of the infected and the deceased students. The third one demonstrates the quarantine and lockdown-induced effect on the number of the infected and the dead students. Finally, the fourth one indicates the effect of mask-wearing, constant body temperature checking, observing social distance, and so on.

Fig. 3.

Interaction structure of COVID-19 prevalence in universities.

As known, by increasing “the weekly transmission rate”, the mortality rate increases. The “infected” should perform the “recovery” operation which will be based on “the duration of the infection”. Virtual learning also depends on the “virtual learning capacity” and “digital equity factors”. Virtual learning can reduce the transmission rate due to the traffic getting lower, therefore, it exerts an effect on “the probability of a student being infected” and also lowers the “risk of infection”.

“Risk reduction due to the preventive measures” is divided into some sections such as the risk at the time of “wearing a mask”, “the risk when social distancing is observed”, and “combined risk”. The combined risk refers to the time when social distance is not observed, and no mask is worn. The mentioned factors together with the week-based temperature-reading factor can reduce the student transmission rate, where the “the student transmission rate” reduces the “risk of infection”.

The students suffering from being infected with COVID-19 should be quarantined. The quarantine period depends on the incubation time and the recovery time. The students can return to the campus after the due quarantine period. It is also possible to spend the recovery period out of quarantine. To boost the students’ physical immunity and shorten the recovery period, some complementary medicine and vitamins can be taken. All these parameters can affect the student transmission rate.

As seen in Fig. 3, the values of the initial population, disease duration, transmission rate, average death rate, the total students on campus, etc. are entered into the system dynamic simulation model as the parameters. The system output is made up of the number of healthy students, the number of infected students, the number of deaths, the number of those requiring quarantine, the number of individuals requiring virtual learning, and the number of recovered students. Therefore, the deceased, the susceptible, the recovered, the quarantined students, etc. are regarded as the stock variables. Also, virtual learning capacity, etc. are taken as the auxiliary variables.

Having drawn the COVID-19 expansion interaction structure on campus, this structure is simulated using the Enterprise Dynamic (ED) software. The ED is a discrete event simulation software that is object-oriented, and the desired objects can be easily dragged from this software's library to the modeling environment. Hence, this software can simulate a variety of optimization problems using 4D Script codes such as the supply chain networks, production planning, scheduling problems, etc. The proposed simulation model consists of 37 atoms in the simulation structure with 35 server atoms, 1 source atom, and 1 sink atom. The servers are responsible for interacting with the expansion factor of COVID-19 and calculating the number of the infected, the deceased, the quarantined, the recovered, and so on. The source atom also displays how the entities enter the simulation system. COVID-19 synapses are entered into the system with a negative exponential distribution function with an average of 20, and the source capacity is considered unlimited. Besides, the first input occurs after 10 s when the system starts.

Two performance measures are involved in the present study's simulation model, the first one is $AvgContent$ ($cs$), indicating the average of existing entities in each atom and the second measure, the output ($cs$), indicates the value of the exiting entities from the system. The output of the simulation system is a function of the probability distribution of the vaccine demand. The considered simulation observation period is 5,000,000 h. The current study warm-up period is considered 500,000 h. It is worth noting that the warm-up period is the time that the simulation will run before starting to collect results [37]. This allows the system to get into a steady state where normal running conditions are in place (e.g., queues) [38]. Also, in this study, simulation model is run in 5 separate replications. Several 4D scripts are written for the proposed simulation model. So, for calculating the number of vaccines, the 4D Script code is as stated in Equation (1).

$$Vaccinenumber:Triggeronentry=\left(AvgContent\left(AtomByName(2\ast \left[\left[Totalstudent\right]-\left[infected\right]-\left[Deaths\right]\right],Model)\right)\right)$$ (1)

Equation (1) calculates the number of vaccine doses required. Therefore, in this equation, the number of required vaccines is equal to the total number of students minus the number of infected and deaths (who cannot be vaccinated). A factor of 2 also indicates two doses of vaccine.

3.2. Assumptions

In this section, the assumptions, notations, and the developed mathematical model is presented. The assumptions of the proposed model are discussed in the following:

• •According to the due social distancing and limited capacity of hospitals and vaccination centers, it is possible to receive the injection during non-working hours.
• •The safety stock is considered to minimize vaccine shortages in hospitals.
• •The vaccine is a perishable commodity and can expire in the proposed SCN.
• •The amount of vaccine demand is estimated by the system dynamic simulation approach and plugs into the mathematical model as a stochastic parameter.
• •The demolishing cost of the perished vaccine is based on the age of the vaccine where the higher the age of the vaccine, the higher the cost of demolishment.
• •Most students prefer to go to the vaccination centers on time and based on a reserved date and time. Also, the students can refer to the vaccination centers without reservation. Without reservation, one can receive the vaccine only during working hours but with reservation, both working and non-working hours can be applied.
• •Hospital and vaccination center beds are available to be reserved for both reserved and unreserved students.
• •The effectiveness of a vaccination center depends on the accessibility level of and the applicants' admission capacity.

The notations and the developed mathematical formulation are as follows:

Index
$h$	Set of the hospitals ($h=1,\dots ,H)$
$m$	Set of the manufacturers ($m=1,\dots ,M)$
$o$	Set of the vaccine age ($o=1,\dots ,O)$
$v$	Set of the vaccination centers ($v=1,\dots ,V)$
$i$	Types of the vaccines $(i=1,\dots ,I)$
$t$	Set of the time periods $(t=1,\dots ,T)$
Parameters
$M$	A big number
${\tilde{d}}_{ivt}$	Vaccine $i$ demand at vaccination center $v$ in period $t$
${\widetilde{d^{\prime }}}_{iht}$	Vaccine $i$ demand in hospital $h$ in period $t$
$Cos{t}_{oh}$	The priority cost of vaccines with age $o$ in the hospital $h$
$Cost{\prime }_{ov}$	The priority cost of vaccines with age $o$ in the vaccination center $v$
$c{o}_{vt}$	The cost of establishing vaccination center $v$ in period $t$
$c{t}_{mht}$	The cost of transporting a dose of vaccine from manufacturer $m$ to hospital $h$ in period $t$
$e{c}_{iht}$	The demolishing cost of perished vaccine $i$ in hospital $h$ in period $t$
$ec{\prime }_{imt}$	The demolishing cost of perished vaccine $i$ in the manufacturer $m$ in period $t$
$f{c}_{imvt}$	The cost of purchasing and transporting a dose of vaccine $i$ from the manufacturer $m$ to the vaccination center $v$ in period $t$ for the unreserved student
$fc{\prime }_{imvt}$	The cost of purchasing and transporting a dose of vaccine $i$ from the manufacturer $m$ to the vaccination center $v$ in period $t$ for the reserved student
$v{c}_{imt}$	The cost of producing a dose of vaccine $i$ by the manufacturer $m$ in period $t$
$m{c}_{iht}$	The cost of holding a dose of vaccine $i$ by the hospital $h$ in period $t$
$mc{\prime }_{imt}$	The cost of holding a dose of vaccine $i$ by the manufacturer $m$ in period $t$
$m{c}^{\prime }{\prime }_{ivt}$	The cost of holding a dose of vaccine $i$ by the vaccination center $v$ in period $t$
$z{c}_{mt}$	The cost of setting up manufacturer $m$ in period $t$
$w{c}_{vt}$	The cost of overtime at vaccination center $v$ in period $t$
$k{c}_{iht}$	The cost of vaccine $i$ shortage in hospital $h$ in period $t$
$kc{\prime }_{ivt}$	The cost of vaccine $i$ shortage in vaccination center $v$ in period $t$
$k{c}^{\prime }{\prime }_{imt}$	The cost of vaccine $i$ shortage in manufacturer $m$ in period $t$
$b{d}_{ht}$	Number of vacant beds in hospital $h$ in period $t$
$bd{\prime }_{vt}$	Number of vacant beds in vaccination center $v$ for students in period $t$
$n{i}_t$	The initial number of reserved students in period $t$
$ca{p}_{iht}$	The storage capacity of hospital $h$ for vaccine $i$ in period $t$
$cap{\prime }_{ivt}$	The storage capacity of vaccination center $v$ for vaccine $i$ in period $t$
$ca{p}^{\prime }{\prime }_{imt}$	The production capacity of manufacturer $m$ for vaccine $i$ in period $t$
$s{s}_{ioht}$	The amount of vaccine $i$ safety stock with age $o$ stored in hospital $h$ in period $t$
$ss{\prime }_{iovt}$	The amount of vaccine $i$ safety stock with age $o$ stored in vaccination center $v$ in period $t$
${\pi }_t$	The desire of the students to receive money for vaccinations in period t,${\pi }_t>0$
${\beta }_{vt}$	The level of the effectiveness of vaccination center $\text{v}$ in period $t,{\beta }_{vt}\in \left[\mathrm{0,1}\right]$
Decision variables
$s{h}_{iht}$	The shortage amount of vaccine $i$ in hospital $h$ in period $t$
$sh{\prime }_{ivt}$	The shortage amount of vaccine $i$ in vaccination center $v$ in period $t$
$s{h}_{imt}^{\prime }$	The shortage amount of vaccine $i$ shortage in manufacturer $m$ in period $t$
$n{s}_{vt}$	Number of reserved students at the vaccination center $v$ in period $t$
$ns{\prime }_{vt}$	Number of unreserved students at the vaccination center $v$ during working hours in period $t$
$n{h}_{ht}$	Number of reserved students at hospital $h$ in period $t$
$nh{\prime }_{ht}$	Number of unreserved students at hospital $h$ during working hours in period $t$
$f_{iomht}$	The amount of vaccine $i$ with age $o$ transferred from manufacturer $m$ to hospital $h$ in period $t$
$p_{iomvt}$	The amount of vaccine $i$ with age $o$ transferred from manufacturer $m$ to vaccination center $v$ in period $t$
$v{p}_{imt}$	The amount of vaccine $i$ produced by manufacturer $m$ in period $t$
$q_{iomt}$	The amount of vaccine $i$ inventory with age $o$ in manufacturer $m$ in period $t$
$q{\prime }_{ioht}$	The amount of vaccine $i$ inventory with age $o$ in hospital $h$ in period $t$
$q^{\prime }{\prime }_{iovt}$	The amount of vaccine $i$ inventory with age $o$ in vaccination center $v$ in period $t$
$y_{imt}$	1 If vaccine $i$ is produced in manufacturer $m$ in period $t$, otherwise 0
$l_{ihot}$	1 If hospital $h$ uses vaccine $i$ safety stock with age $o$ in period $t$, otherwise 0
$l{\prime }_{ivot}$	1 If vaccination center $v$ uses vaccine $i$ safety stock with age $o$ in period $t$, otherwise 0
$r_{vt}$	1 If unreserved students are referred to vaccination center $v$ in period $t$, otherwise 0
$r{\prime }_{ht}$	1 If unreserved students are referred to hospital $h$ in period $t$, otherwise 0
$lo{c}_{vt}$	1 If vaccination center $v$ is established at period $t$, otherwise 0

3.3. Mathematical model

$$\begin{array}{l}\text{Min}\mathit{Z}1={\sum }_m{\sum }_i{\sum }_t{y}_{imt}.z{c}_{mt}+{\sum }_m{\sum }_v{\sum }_i{\sum }_{t}n{s}_{vt}.f{c}_{imvt}^{\prime }+{\sum }_m{\sum }_v{\sum }_i{\sum }_{t}n{s^{\prime }}_{vt}.f{c}_{imvt}+\\ {\sum }_i{\sum }_m{\sum }_h{\sum }_0{\sum }_t{\widetilde{d^{\prime }}}_{iht}.c{t}_{mht}.y_{imt}+{\sum }_i{\sum }_m{\sum }_o{\sum }_t{q}_{iomt}.m{c}_{imt}^{\prime }+{\sum }_i{\sum }_h{\sum }_o{\sum }_t{q}_{ioht}^{\prime }\cdot m{c}_{iht}+\\ {\sum }_i{\sum }_v{\sum }_o{\sum }_t{q^{″}}_{iovt}.m{c}_{ivt}^{″}+{\sum }_i{\sum }_h{\sum }_o{\sum }_{t}s{s}_{ioht}.\left(1-l_{ihot}\right)m{c}_{iht}+\\ {\sum }_i{\sum }_v{\sum }_o{\sum }_{t}s{s}_{iovt}^{\prime }.\left(1-{l^{\prime }}_{ivot}\right)m{c}_{ivt}^{″}+{\sum }_h{\sum }_i{\sum }_{t}s{h}_{iht}.k{c}_{iht}+{\sum }_v{\sum }_i{\sum }_{t}s{h^{\prime }}_{ivt}.k{c}_{ivt}^{\prime }+\\ {\sum }_m{\sum }_i{\sum }_{t}s{h^{″}}_{imt}.k{c}_{imt}^{″}+{\sum }_i{\sum }_m{\sum }_{t}v{p}_{imt}.v{c}_{imt}+{\sum }_v{\sum }_{t}c{o}_{vt}lo{c}_{vt}+\\ {\sum }_v{\sum }_t{\sum }_i{\sum }_{o}Cos{t}_{ov}^{\prime }.{q^{″}}_{iovt}+{\sum }_h{\sum }_t{\sum }_i{\sum }_{o}Cos{t}_{Oh}.{q^{\prime }}_{ioht}\end{array}$$ (2)

$$\text{Max}\mathit{Z}2=\sum _i\sum _o\sum _m\sum _v\sum _t{\beta }_{vt}.p_{iomvt}-\sum _i\sum _o\sum _m\sum _v\sum _t{\pi }_t{p}_{iomvt}$$ (3)

$$\text{Max}\mathit{Z}3=\text{Min}\left\{\sum _i\sum _m\sum _h\sum _o\sum _t\frac{f_{iomht}}{{\widetilde{d^{\prime }}}_{iht}}+\sum _i\sum _o\sum _m\sum _v\sum _t\frac{p_{iomvt}}{{\tilde{d}}_{ivt}}\right\}$$ (4)

Constraints

$${\widetilde{d^{\prime }}}_{iht}\ge \sum _m\sum _o{f}_{iomht}\forall t,i,h$$ (5)

$${\tilde{d}}_{ivt}\ge \sum _m\sum _o{p}_{iomvt}\forall i,v,t$$ (6)

$$s{h}_{iht}=\text{Max}\{0,{\widetilde{d^{\prime }}}_{iht}-(\sum _o{q}_{ioht-1}^{{}^{\prime }}+\sum _{o}s{s}_{ioht}+\sum _o\sum _m{f}_{iomht})\}\forall i,h,t$$ (7)

$$s{h}_{ivt}^{\prime }=\text{Max}\{0,{\tilde{d}}_{ivt}-\left(\sum _o\sum _m{p}_{iomvt-1}+\sum _o{q^{″}}_{iovt}+\sum _{o}s{s}_{iovt}^{\prime }\right)\}\forall i,v,t$$ (8)

$$s{h}_{imt}^{\prime }=\text{Max}\{0,\sum _o\sum _v{f}_{iomht}+\sum _o\sum _h{p}_{iomvt}-(v{p}_{imt}+\sum _o{q}_{iomt-1})\}\forall i,m,t$$ (9)

$$s{h}_{iht}\le M.(1-l_{ihot})\forall o,i,h,t$$ (10)

$$s{h}_{ivt}^{\prime }\le M.(1-l{\prime }_{ivot})\forall o,i,v,t$$ (11)

$$\sum _{o}q{\prime }_{ioht}\le ca{p}_{iht}\forall i,h,t$$ (12)

$$\sum _o{p}_{iomvt}\le ca{p}_{ivt}^{\prime }.y_{imt}\forall i,v,m,t$$ (13)

$$v{p}_{imt}\le ca{p}^{\prime }{\prime }_{imt}.y_{imt}\forall i,m,t$$ (14)

$${\tilde{d}}_{ivt}=n{s}_{vt}+ns{\prime }_{vt}\forall i,v,t$$ (15)

$$\widetilde{d{\prime }_{iht}}=n{h}_{ht}+nh{\prime }_{ht}\forall i,h,t$$ (16)

$$ns{\prime }_{vt}\le r_{vt}.M\forall v,t$$ (17)

$$nh{\prime }_{ht}\le r{\prime }_{ht}.M\forall h,t\forall h,t$$ (18)

$$\sum _o\sum _v{p}_{iomvt}\le v{p}_{imt}\forall i,m,t$$ (19)

$$\sum _o\sum _h{f}_{iomht}\le v{p}_{imt}\forall i,m,t$$ (20)

$$n{s}_{vt}\le M.lo{c}_{vt}\forall v,t$$ (21)

$$ns{\prime }_{vt}\le M.lo{c}_{vt}\forall v,t$$ (22)

$$r_{vt}\le lo{c}_{vt}\forall v,t$$ (23)

$$p_{iomvt}\le M.lo{c}_{vt}\forall i,o,m,v,t$$ (24)

$$n{h}_{ht}+nh{\prime }_{ht}\le b{d}_{ht}\forall h,t$$ (25)

$$n{s}_{vt}+ns{\prime }_{vt}\le bd{\prime }_{vt}\forall v,t$$ (26)

$$lo{c}_{vt+1}\ge lo{c}_{vt}\forall v,t$$ (27)

$$y_{imt+1}\ge y_{imt}\forall i,m,t$$ (28)

$$y_{imt},l_{ihot},l{\prime }_{ivot},r_{vt},r{\prime }_{ht},lo{c}_{vt}\in \left\{\mathrm{0,1}\right\}\forall i,m,v,h,o,t$$ (29)

$$s{h}_{iht},s{h^{\prime }}_{ivt},n{s}_{vt},n{s^{\prime }}_{vt},n{h}_{ht},n{h^{\prime }}_{ht},f_{iomht},p_{iomvt},v{p}_{imt},q_{iomt},{q^{\prime }}_{ioht},q^{\prime }{\prime }_{iovt}\ge 0\forall i,m,s,v,h,o,t$$ (30)

The objective function (2) minimizes the total vaccine distribution costs of the SCN including the costs of manufacturers set up, purchasing and transporting cost of vaccines from manufacturers to vaccination centers for reserved and unreserved students, transporting cost of vaccines from manufacturers to hospitals, the inventory cost of vaccine stock in manufacturers, hospitals, and vaccination centers, the safety stock cost of holding in hospitals and vaccination centers, the shortage costs in hospitals, vaccination centers, and manufacturers, the vaccines producing cost by the manufacturers, the establishment cost of vaccination centers and the costs of demolishing the perished vaccine in hospitals and vaccination centers. The point is that the older the vaccine, the higher the demolishing cost. The priority cost of vaccines is the cost of vaccines that are close to their expiration date. Therefore, the older the vaccine, the higher the priority, and the older the vaccine, the lower the priority cost, $Cos{t}_{oh}$ and $Cost{\text{′}}_{ov}$. In another word, the mathematical model tries to increase the flow of older vaccines and the model aims to minimize the number of perishable vaccines.

The objective function (3) represents maximizing the desirability of the students willing to be vaccinated. Thus, the students seek better vaccination centers in terms of money payments and other incentives and in terms of effectively performing the vaccination steps. Trivially, the objective function tries to minimize the cost of incentives (i.e., the amount of money paid to the students) from the SCN point of view by considering it as a negative argument in the objective function. ${\pi }_t$ parameter is for people who accept to be vaccinated only if they receive some incentives/money. These people express their desire in a survey. ${\pi }_t$ is a normalized parameter between 0 and 1 and the higher the desire, the closer the value to 1. The level of effectiveness of the vaccination center is determined based on a survey carried out on vaccinated people in vaccination centers. In the survey, criteria such as the facilities of vaccination centers, the congestion of the centers, the attitude of the staff, etc. have been considered. The level of effectiveness, ${\beta }_{vt}$, is considered as a normalized parameter between 0 and 1 in the model. The objective function (3) known as the humanitarian utility function has been used in many humanitarian studies, such as [39,40]; Fathalikhani et al. (2018), Fathalikhani et al. (2020) has been used.

The objective function (4) maximizes the minimum ratio of vaccine delivery to vaccine demand. Equation (4) calculates the mathematical expectation of the minimum ratio of vaccine flow to hospitals to their demand and the ratio of vaccine flow to vaccination centers to their demand. This equation indicates that the priority is to send more vaccines to the centers that received lower inflows regarding their demands. So, this objective function ensures justice in the vaccine distribution in each node.

Constraints (5) and (6) state that the number of vaccines sent by manufacturers must be less than the amount of demand. Constraints (7) and (8) indicate the vaccine availability balance in hospitals and vaccination centers. As perceived from the two constraints, the total inventory and safety stock of the centers minus the amount of the shortage is equal to the number of vaccines sent to the center minus the demand of that center. Constraint (9) indicates the vaccine availability balance in the manufacturers. The total number of vaccines sent to hospitals and vaccination centers minus the amount of the shortage is equal to the amount of vaccine produced by manufacturers and the amount of vaccine inventory in the previous period. Constraints (10) and (11) guarantee that the safety stock is used if there is a shortage in hospitals and vaccination centers. Constraints (12), (13), and (14) indicate the vaccine storage capacity in hospitals, vaccination centers, and manufacturers, respectively. Constraints (15) and (16) state that the number of vaccines sent from manufacturers to vaccination centers and hospitals has to be equal to the total number of reserved and unreserved students in those centers. Constraints (17) and (18) denote the relationship between the number of unreserved students in hospitals and vaccination centers and their corresponding binary variables. As indicated by Constraints (19) and (20), the number of vaccines sent from manufacturers to hospitals and vaccination centers has to be less than vaccines produced by manufacturers. Constraints (21), (22), (23), and (24) are related to the location. Constraints (21) and (22) ensure that vaccination centers have to be established first and then the reserved students can be referred to those centers. Constraint (23) displays the relationship between the number of unreserved and the referred students to vaccination centers with the location variable. Constraint (24) indicates that for manufacturers to be able to send the vaccine to a center, the vaccination center has to be built first. Constraints (25) and (26) indicate hospitals' and vaccination centers’ bed capacities for the reserved and unreserved students. Based on Constraint (27), each vaccination center can be established only once per period. As grasped by Constraint (28), if the vaccine is produced in one period by a manufacturer, it will be produced by the same manufacturer in the subsequent periods. Constraints (29) and (30) determine the type of the decision variables.

3.4. Linearization

According to the non-linearity of the third objective function, Equation (4), the variable $\mu$ and Equations (31), (32) are introduced for linearization purposes.

$$\mu =\text{Min}\left\{\sum _i\sum _m\sum _h\sum _o\sum _t\frac{f_{iomht}}{{\widetilde{d^{\prime }}}_{iht}}+\sum _i\sum _o\sum _m\sum _v\sum _t\frac{p_{iomvt}}{{\tilde{d}}_{ivt}}\right\}\forall i,o,m,h,v,t$$ (31)

$$\mu \le \sum _i\sum _m\sum _h\sum _o\sum _t\frac{f_{iomht}}{{\widetilde{d^{\prime }}}_{iht}}+\sum _i\sum _o\sum _m\sum _v\sum _t\frac{p_{iomvt}}{{\tilde{d}}_{ivt}}\forall i,o,m,h,v,t$$ (32)

Also, the linearization of Constraints (7)–(9) is performed by introducing Constraints (33)–(41) where $w_{iht}$, $w{\prime }_{ivt}$ and $w{\prime }_{imt}^{\prime }$ are the auxiliary binary variables and $z_{iht}$, $z{\prime }_{ivt}$ and $z^{\prime }{\prime }_{imt}$ are the positive variables.

$$s{h}_{iht}\le M.w_{iht}\forall i,h,t$$ (33)

$$z_{iht}\le M.(1-w_{iht})\forall i,h,t$$ (34)

$$sh{\prime }_{ivt}\le M.w{\prime }_{ivt}\forall i,v,t$$ (35)

$$z{\prime }_{ivt}\le M.(1-w{\prime }_{ivt})\forall i,v,t$$ (36)

$$s{h}_{imt}^{\prime }\le M.w^{\prime }{\prime }_{imt}\forall i,m,t$$ (37)

$$z^{\prime }{\prime }_{imt}\le M.(1-w{\prime }_{imt}^{\prime })\forall i,m,t$$ (38)

$${\widetilde{d^{\prime }}}_{iht}-(\sum _o{q^{\prime }}_{ioht-1}+\sum _{o}s{s}_{ioht}+\sum _o\sum _m{f}_{iomht})=s{h}_{iht}-z_{iht}\forall i,h,t$$ (39)

$${\tilde{d}}_{ivt}-\left(\sum _o\sum _m{p}_{iomvt-1}+\sum _o{q^{″}}_{iovt}+\sum _{o}s{s}_{iovt}^{\prime }\right)=s{h^{\prime }}_{ivt}-z{\prime }_{ivt}\forall i,v,t$$ (40)

$$\sum _o\sum _v{f}_{iomht}+\sum _o\sum _h{p}_{iomvt}-(v{p}_{imt}+\sum _o{q}_{iomt-1})=s{h}_{imt}^{\prime }-z^{\prime }{\prime }_{imt}\forall i,m,t$$ (41)

Therefore, the linearized mathematical model is modified as follows (It should be noted that $\mu$ is a positive variable):

Objective functions (2) and (3)

$$\text{Max}z=\mu$$ (42)

$S.t.$

$$\mu \le \sum _i\sum _m\sum _h\sum _o\sum _t\frac{f_{iomht}}{{\widetilde{d^{\prime }}}_{iht}}+\sum _i\sum _o\sum _m\sum _v\sum _t\frac{p_{iomvt}}{{\tilde{d}}_{ivt}}\forall i,o,m,h,v,t$$ (43)

Constraints (5)–(6), (10)–(30) and (33)–(41).

4. Solution methodology

As mentioned earlier, the proposed mathematical model is a multi-objective function model, therefore, to be able to solve the model via commercial solvers (e.g., GAMS), a technique called Bounded Objective Function (BOF) is used to transform the model into a single objective one. Then, in order to efficiently solve the real-sized problems, two meta-heuristic algorithms called VNS and WOA, and one hybrid meta-heuristic algorithm called modified WOA with VNS (MVWOA) are developed. In the next subsections, the BOF approach, solution representation, and the structures of the presented VNS, WOA, and MVWOA algorithms are explained.

4.1. BOF approach

Multiple objective programming is a part of mathematical programming where multi-objective functions require to be simultaneously optimized over a feasible set of decisions. This type of mathematical programming is prevalent in human activities including management, healthcare, and engineering [41].

The present study employs the Bounded Objective Function (BOF) approach to transform a multiple objective mathematical model into a single objective one. The BOF approach can help the proposed model attain a compromise among the presented three different objective functions. In this approach, one of the objective functions remains as an objective function, and the others are transformed into constraints while an upper and a lower bound is determined for them [41]. The BOF approach is mathematically illustrated in Model (44).

$\text{Minimize}{Z}_i\left(x\right)$

Subject to:

$$\begin{array}{l}L{B}_k\le Z_k\left(x\right)\le U{B}_{k}k=1,\dots ,mk\ne i\\ x\in N\end{array}$$ (44)

where $N$ represents the feasible space, $m$ and $Z_k\left(x\right)$ shows the number of objective functions and objective function $k$, respectively, and $U{B}_k$ and $L{B}_k$ represent the bounds of the $k$ th objective function. In this study, the first objective function is kept as the objective function, and the two other objective functions are transformed into the constraints.

4.2. Solution representation

In this research, the Random-Key (RK) method is applied as the encoding process to analyze the original solution [31]. This method transforms an unfeasible solution into a feasible one by a set of processes in two steps [42]. Then, the presented problem's sub-solutions are explained as the following:

To determine if a vaccine center is established, a sub-solution is employed. Accordingly, firstly, a matrix with $\left|V\right|$ elements is created with uniform distribution $U\left(\mathrm{0,1}\right)$. Next, the first $V_{Max}$ units with the biggest values are chosen as the built vaccine center. For instance, the encoded solution {0.42, 0.68, 0.22, 0.52, 0.81, 0.11} with Max $V_{Max}$ = 5 illustrates the decoded solution {0, 1, 0, 1, 1, 0}. In addition, the production of the vaccines by the manufacturer is used as the previous sub-section solution.

To specify if a hospital uses vaccine safety stock with age o in the period, a sub-solution is employed. Therefore, first of all, a matrix with |M| elements is provided with uniform distribution U (0,1). Secondly, the first $M_{Max}$ units with the biggest values are selected as the hospital using the vaccine safety stock. For example, the encoded solution {0.13, 0.45, 0.62, 0.32, 0.71, 0.31} with Max $M_{Max}$ = 2 shows the decoded solution {0, 0, 1, 0, 1, 0}. Additionally, to refer unreserved students to the vaccination center and hospital, the same sub-section solutions are used.

The sub-solution of the transportation of the amount of vaccine from manufacturer to hospital is employed to determine transportation for each vaccine. Hence, a vector max (1* $M_{Max}$) with uniform distribution in the range (1, $\left|transportationoftheamountofvaccine\right|$) is generated. Accordingly, RK rounds the numbers to obtain the selected transportation of the amount of vaccine. For example, the encoded solution {3.16, 1.23, 2.19, 3.78, 1.56} indicates the parsed solution {3, 1, 2, 4, 2} that shows one dose of vaccine type 1 is transported from the second manufacturer to the second hospital and the 4 doses of vaccines type 1 are transported from the second manufacturer to the second hospital, and so on. The encoding structure of the shortage number of vaccines in hospitals and vaccination centers and the number of reserved and unreserved students at the vaccination center and hospital are conducted the same in this process.

4.3. Variable neighborhood search

Variable neighborhood search is a well-known local search approach due to its convenience and performance in solving different problems [43]. A complete study of this algorithm is accessible in Refs. [43,44]. The VNS algorithm was first introduced by Mladenović and Hansen, [43].

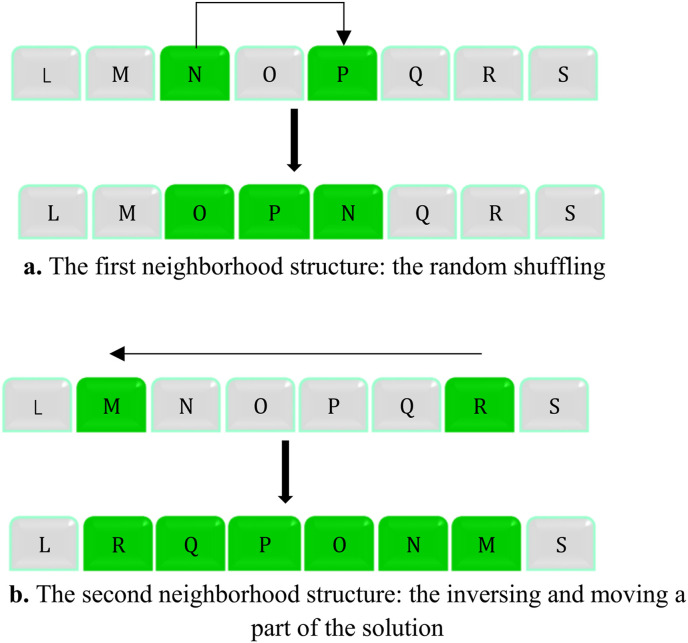
As Fig. 4 depicts the pseudo-code of the VNS algorithm, this algorithm starts with an initialization process. After that, a set of neighborhood structures symbolized by $N_{ns}(ns=\mathrm{1,2},\dots ,n{s}_{max})$ is utilized to achieve the near-optimal solution, where $n{s}_{max}$ indicates the maximum number of the neighborhood structures with the specified sequence. The quality of the achieved answers in this method directly depends on the performance of the neighborhood structures. Hence, to produce a new solution, various types of neighborhood structures are used in various sectors of a solution independently. Neighborhood structures are divided into some parts including random shuffling, swap, intelligent swap, inversing and moving a part of the solution, exchange of two neighbors, reversion, max/min swap, slide, and moving a part of the solution [45]. Accordingly, the inversing and moving of a part of the solution and random shuffling of neighborhood structures are used in this paper (shown in Fig. 5 ). In each iteration, two neighborhood search structures are used in the best solution. In a random shuffling structure, two elements are selected randomly and then they shuffle their values as shown in Fig. 5a. In the other neighborhood structure as shown in Fig. 5b, the values are inverted between two randomly selected elements. Each neighborhood search structure obtains the value of the fitness function according to the quality of its solution. A number of neighborhood search structures either shuffling or selecting are randomly selected. A separate selection is performed for each of the solution variables. Therefore, the neighborhood search structures improve the current solution, replace the current solution with new solutions, and start the same neighborhood search structure again. Otherwise, if neighborhood search structures do not improve the current solution, the current solutions selection mechanism is used, and the next neighborhood search structure is selected.

Fig. 4.

VNS pseudo-code [43].

Fig. 5.

The neighborhood structures.

4.4. Whale Optimization Algorithm

In this subsection, we take advantage of the WOA algorithm first developed by Ref. [46]. In this regard, the interesting point about whale's life, as the source of inspiration for the WOA algorithm, is the feeding and hunting method of humpback whales, which is known as bubble-net. For more information, the interested reader can be referred to the mentioned reference [46]. The WOA algorithm's pseudo-code is given in Fig. 6 .

Fig. 6.

WOA pseudo-code [46].

The WOA algorithm begins with a set of random solutions. In each iteration, the search agents update their position consistent with a random search agent or the best solution ever. Parameter $a$ is reduced from 2 to 0 to enable exploration and exploitation, respectively. When $\left|\overrightarrow{A}\right|>1$, a search agent is randomly selected, and when $\left|\overrightarrow{A}\right|<1$, the best solution is selected to update the search agents' position. Depending on the value of p, this algorithm is able to change between the spiral and circular motion. Finally, the WOA algorithm is completed by satisfying the constraint related to the end of the algorithm [46].

The reason behind using the WOA algorithm is being considered as a global optimization algorithm equipped with the search/exploration capability. Moreover, the super cube mechanism defines the search space in the best solution area and allows other search agents to explore the current best case in that area. Then, changing the search vector, $A$, allows this algorithm to easily switch between search and exploration. By reducing $A$, some iterations search and others explore. It's worth mentioning that the WOA contains only two main internal parameters ($A$ and $C$) required to be set.

4.5. Modified WOA algorithm (MVWOA)

The modified algorithms provide an opportunity to create an intelligent method by taking two or more algorithms and benefitting from them. In the MVWOA, we modify the WOA exploitation features using the VNS algorithm as a local search. This algorithm considers the VNS rules in search and acceptance of the response to update the search agents in the main loop of the WOA algorithm. This modified algorithm is to improve the WOA's searching performance. Finally, in the developed MVWOA algorithms, the VNS is viewed as a local search approach fulfilled on the best solution gained from the main loop in each iteration (see Fig. 7 ).

Fig. 7.

MVWOA pseudo-code.

4.6. Constraint handling strategy

In the proposed model, Constraints (5)–(11) and (15)–(30) are satisfied by the proposed solution algorithms, but the rest of the constraints are satisfied by the penalty strategy. For example, the penalty strategy for constraints (12), (13), and (14) is defined as follows. It should be noted that the index $p$ represents the number of objective functions. For more information on the performance of constraint handling strategy, see Khalili et al. [47]. The $A_p,B_{p}and{C}_p$ are auxiliary variables that indicate the value of the violation of the $p$ th constraint.

$$A_p={\text{Max}}_{\forall i,h,t}\{\sum _o{q^{\prime }}_{ioht}-ca{p}_{iht}\}\forall p=\mathrm{1,2,3}$$ (45)

$$B_p={\text{Max}}_{\forall i,v,m,t}\{\sum _o{p}_{iomvt}-ca{p}_{ivt}^{\prime }.y_{imt}\}\forall p=\mathrm{1,2,3}$$ (46)

$$C_p=v{p}_{imt}-ca{p}^{\prime }{\prime }_{imt}.y_{imt}\forall p=\mathrm{1,2,3}$$ (47)

The total value of the penalty in the proposed model is equal to the sum of the penalties of the violated constraints. It should be noted that the amount of violation is dynamic and varies based on the number of iterations. Therefore, according to Equation (48), the higher the number of iterations, the greater the amount of violation.

$$Violatio{n}_p=\left(A_p+B_p+C_p\right)\ast iteration$$ (48)

Finally, the value of the objective function based on the violation is calculated by Equation (49). It is obvious that the objective function does not get worse.

$$f_p=f_p+Penalty\ast Violatio{n}_p\forall p=\mathrm{1,2,3}$$ (49)

5. Experimental evaluation

In this section, first of all, the experimental problems are provided for the proposed model. Based on the three objective functions, four assessment metrics, namely, (a) the number of Pareto solutions (NPS), (b) the Mean ideal distance (MID), (c) the Percentage of Domination (POD), and (e) the Maximum Spread (MS) are employed to assess the effectiveness of the proposed algorithms' non-dominant solutions. Additionally, to tune the algorithm's parameters, the Taguchi approach is used. Then, the proposed solution methods are compared with each other, and the case study is solved via the best-resulted method. Finally, to validate the proposed mathematical model, a set of sensitivity analyses is applied. Enterprise Dynamic 8 software is employed for computer-based simulation and the Cplex solver of GAMS 24.1 software is used to solve the problems. Also, the metaheuristics are run using MATLAB R2020b software. All tests are run on a computer with an Intel Core™ i7-4200 M CPU 1.60 GHz CPU and 6 GB RAM.

5.1. Data generation

Due to the novelty of the proposed problem, there is no similar study in the literature review. Thus, the existing benchmarks in the literature review are not at hand for the model. As a result, an approach is required to design the test problems. Ten experimental problems in two sizes, i.e., small: S1 to S5 and medium: M1 to M5 are provided. In this regard, a real case study is suggested for large-sized problems. Table 2 gives a numerical experiment of problems in the proposed sizes, including the hospitals ($h$), the manufacturers ($m$), the vaccine age ($o$), the vaccination centers ($v$), the types of vaccines ($i$), and the periods ($t$). In addition, the range of the proposed parameters is reported in Table 3 . It should be noted that parameters ${\tilde{d}}_{ivt}$ and ${\widetilde{d^{\prime }}}_{iht}$ in small and medium problems are considered as a Uniform function and for a case study based on simulation estimates follow the Normal distribution.

Table 2.

Numerical experiment of problems in different sizes.

Classification	Example	$\mathit{h}$	$\mathit{m}$	$\mathit{o}$	$\mathit{v}$	$\mathit{i}$	$\mathit{t}$
Small	S1	2	1	1	2	1	1
	S2	3	1	1	3	1	1
	S3	4	1	2	4	1	1
	S4	4	2	2	5	1	2
	S5	5	2	2	6	1	2
Medium	M1	8	3	3	8	2	3
	M2	10	3	3	14	2	4
	M3	12	4	4	18	2	4
	M4	14	4	5	24	2	5
	M5	18	6	5	28	2	6

Table 3.

Presented parameters ($u$ =uniform).

Parameter	Value	Parameter	Value
$\mathit{M}$	1,000,000,000,000	$z{c}_{mt}$	$u\sim$ (15, 45)$
${\tilde{\mathit{d}}}_{\mathit{ivt}}$	$u\sim$ (50, 1000)	$w{c}_{vt}$	$u\sim$ (20, 65)$
${\widetilde{{\mathit{d}}^{\prime }}}_{\mathit{iht}}$	$u\sim$ (100, 500)	$k{c}_{iht}$	$u\sim$ (5, 25)$
$\mathit{Cos}{\mathit{t}}_{\mathit{h}}$	$u\sim$ (5, 10)$	$kc{\prime }_{ivt}$	$u\sim$ (15, 45)$
$\mathit{Cost}{\prime }_{\mathit{v}}$	$u\sim$ (6, 12)$	$k{c}^{\prime }{\prime }_{imt}$	$u\sim$ (10, 25)$
$\mathit{c}{\mathit{o}}_{\mathit{vt}}$	$u\sim$ (100, 700)$	$b{d}_{ht}$	$u\sim$ (10, 35)
$\mathit{c}{\mathit{t}}_{\mathit{mht}}$	$u\sim$ (5, 60)$	$bd{\prime }_{vt}$	$u\sim$ (15, 25)
$\mathit{e}{\mathit{c}}_{\mathit{iht}}$	$u\sim$ (5, 15)$	$n{i}_t$	$u\sim$ (20, 250)
$\mathit{ec}{\prime }_{\mathit{imt}}$	$u\sim$ (10, 20)$	$ca{p}_{iht}$	$u\sim$ (15, 100)
$\mathit{f}{\mathit{c}}_{\mathit{imvt}}$	$u\sim$ (15, 45)$	$cap{\prime }_{ivt}$	$u\sim$ (10, 150)
$\mathit{fc}{\prime }_{\mathit{imvt}}$	$u\sim$ (20, 65)$	$ca{p}^{\prime }{\prime }_{imt}$	$u\sim$ (50, 1000)
$\mathit{v}{\mathit{c}}_{\mathit{imt}}$	$u\sim$ (25, 45)$	$s{s}_{ioht}$	$u\sim$ (15, 100)
$\mathit{m}{\mathit{c}}_{\mathit{iht}}$	$u\sim$ (15, 45)$	$ss{\prime }_{iovt}$	$u\sim$ (10, 100)
$\mathit{mc}{\prime }_{\mathit{imt}}$	$u\sim$ (10, 25)$	${\pi }_t$	$u\sim$ (5, 10)
${\mathit{mc}}^{\prime }{\prime }_{\mathit{ivt}}$	$u\sim$ (20, 35)$	${\beta }_{vt}$	$u\sim$ (0.15, 0.86)

5.2. Assessment metrics

This sub-section explains different efficiency assessment metrics so that to compare the quality of the yielded non-dominant solutions based on the proposed methods. In this research, four assessment metrics are used, namely, (a) the number of Pareto solutions (NPS), (b) the Mean ideal distance (MID), (c) the Percentage of Domination (POD), and (e) the Maximum Spread (MS). As perceived, the suggested assessment metrics were utilized in the recent papers (see Ref. [48]).

5.3. Tuning Algorithm's parameters

In order to tune and control the proposed algorithm's parameters, the Taguchi approach is employed [49]. The approach comparison findings are divided into two categories including noise and control factors. The proposed approach mainly computes the Signal-to-Noise (S/N) ratio-based response change value to achieve the goal as to tune the algorithm's parameters. Therefore, the mechanism of this approach depends on the response type, which means the small the better, the large the better form, and the nominal is the best type. Vaccination desirability for student values is specified by considering S/N ratios, whereas the presented response of the current paper is a minimization type, “the smaller the better” is utilized to tune the proposed algorithm's parameters. In Equation (50), the question S/N value is formulated for this paper:

$$S/N=-10\times log\left(\sum _{i=1}^n{Y}_i^2/n\right)$$ (50)

where $Y_i$ illustrates the response value for $i$ th orthogonal array and $n$ shows the number of the orthogonal arrays.

Since the scale of the objective functions in each example is various, they could not be utilized directly. So, the Relative Percent Deviation (RPD) is employed for each example to solve this problem. The RPD value for the data is gained using Equation (51).

$$RPD=\frac{Al{g}_{sol}-Mi{n}_{sol}}{Mi{n}_{sol}}\times 100$$ (51)

where $Mi{n}_{sol}$ and $Al{g}_{sol}$ stand for the best acquired solution and the resulted values of the objective for each iteration of the experiment in a given example, respectively. Thus, the mean RPD is computed for each experiment after the objective values being converted into the RPDs.

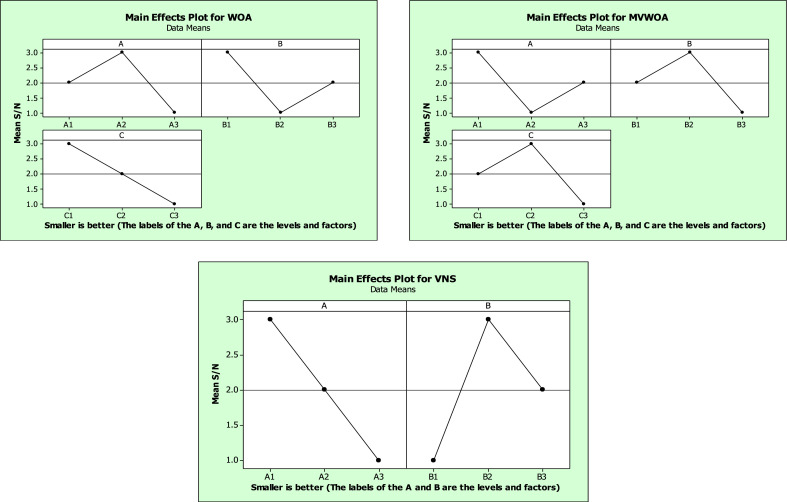
The presented levels and factors of the proposed algorithms are illustrated in Table 4 , in which the algorithms' parameters are the terminology of the factors for each algorithm. Hence, a maximum value out of the three levels is reported for the algorithms' factors. So, to decrease the total number of experiments, the Taguchi approach is used to provide a set of orthogonal arrays to control the algorithm's parameters in a reasonable time. This approach presents L9 for the WOA, the MVWOA, and the VNS algorithms. Table 5, Table 6 give the mentioned orthogonal arrays' details. The mean RPDs are converted into Taguchi approach-based S/N ratios, seen in Fig. 8 , to come up with the best levels of each algorithm.

Table 4.

Presented levels and factors for the proposed algorithms.

Algorithm	Factor	Level
		1 2 3
WOA, MVWOA	A. Maximum iteration ($Maxit$) B. Population size ($nPop$) C. Coefficient vectors	A1:500 A2:1500 A3: 2000 B1:100 B2:200 B3: 300 C1:0.15C2:0.35C3: 0.75
VNS	A. Maximum iteration ($Maxit$) B. Population size ($nPop$)	A1:500 A2:1500 A3:2000 B1:100 B2:200 B3:300

Table 5.

Orthogonal array L9 for WOA and MVWOA.

L9	A	B	C
1	1	1	1
2	1	2	2
3	1	3	3
4	2	1	2
5	2	2	3
6	2	3	1
7	3	1	3
8	3	2	1
9	3	3	2

Table 6.

Orthogonal array L9 for VNS.

L9	A	B
1	1	1
2	1	2
3	1	3
4	2	1
5	2	2
6	2	3
7	3	1
8	3	2
9	3	3

Fig. 8.

Mean S/N ratio plot for each level of the factors.

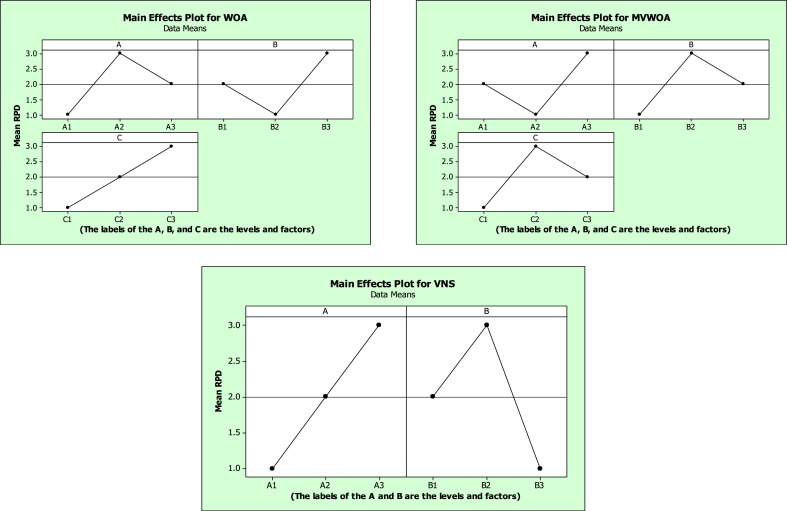
Also, the RPD is utilized for confirming the best-selected factors based on the S/N ratios. Fig. 9 demonstrates the RPD outcomes for each parameter level. As seen in Fig. 9, the RPD shows the best factors confirming the same outcomes as the S/N ratios.

Fig. 9.

Mean RPD plot for each level of the factors.

5.4. Comparison of results

The present study employed the NPS, the MID, the POD, and the MS metrics for comparing the efficiency of suggested algorithms. For all the problems, the assessment metrics are used to evaluate the effectiveness of each meta-heuristic, as given in Table 7 . Here, to boost the proposed algorithms' reliability, the mean of the outcomes for thirty run times is reported in this sub-section. The multi-objective algorithms’ outcomes are investigated by an exact single objective approach. It should be noted that the meta-heuristic algorithms are stochastic optimization types in nature. To validate the outcomes, an exact method, i.e., the BOF approach is used to make this goal realized in this paper.

Table 7.

Assessment metrics derived results for the effectiveness of each meta-heuristic.

Example	NPS WOA VNS MVWOA	MID WOA VNS MVWOA	POD WOA VNS MVWOA	MS WOA VNS MVWOA
S1	4 3 7	2.34 3.56 1.45	21% 15% 28%	12,045 9765 13,422
S2	3 2 5	2.56 3.78 1.78	23% 17% 31%	11,034 9653 12,098
S3	5 3 6	3.02 3.89 2.02	27% 19% 35%	13,981 10,234 14,567
S4	6 4 8	3.22 4.67 2.12	17% 15% 22%	10,342 9543 11,234
S5	4 2 6	2.81 3.49 1.23	19% 16% 25%	9654 8765 10,221
M1	7 5 9	4.23 5.65 3.05	15% 13% 19%	8761 6754 9876
M2	4 2 6	4.56 5.34 3.12	21% 19% 26%	11,298 10,451 13,411
M3	8 6 10	3.72 4.92 2.76	28% 25% 34%	9213 8766 9876
M4	5 3 9	4.13 5.12 3.34	27% 20% 31%	12,098 10,221 14,533
M5	7 6 8	5.18 6.22 4.55	20% 18% 24%	11,302 10,332 13,209

As depicted in Table 7, in terms of the NPS, POD, and MS metrics, the MVWOA algorithm has more reliability and quality than the WOA and the VNS. As understood, the higher the values of these three assessment metrics, the better and the more favorable they are and vice versa. That is, the lower the value of the MID metric, the higher it's quality and efficiency is.

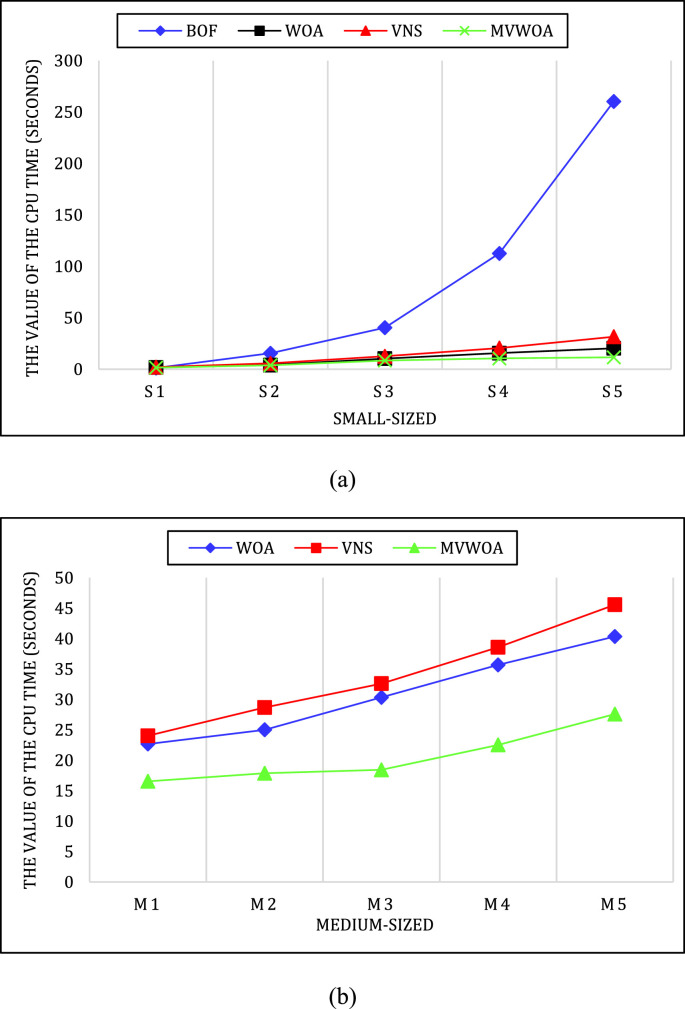
Regarding the computational time (CPU time), the trend of the proposed methods in solving the model with different sizes is displayed in Fig. 10 . As spotted in Fig. 10, the BOF method cannot solve the proposed model in a reasonable time with the problems’ size increase. Because of this, the meta-heuristic algorithms are used in large-sized problems, in which the MVWOA algorithm has lower CPU time than other proposed algorithms.

Fig. 10.

CPU time trend.

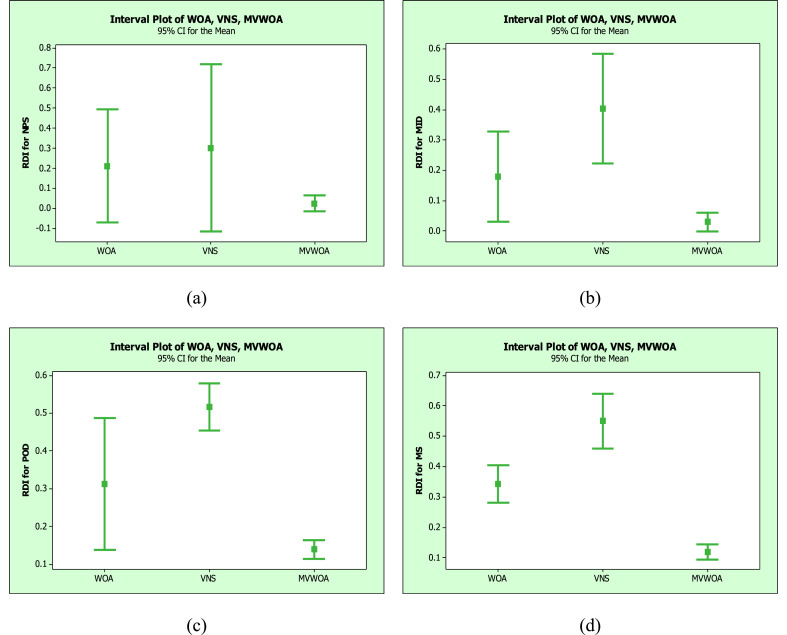
Plus, to come up with a better algorithm with higher quality, the proposed meta-heuristics are statistically compared based on the presented assessment metrics. Thus, the yielded outcomes of the problems are transformed into the Relative Deviation Index (RDI) computed in Equation (52).

$$RDI=\frac{\left|Al{g}_{sol}-Bes{t}_{sol}\right|}{Ma{x}_{sol}-Mi{n}_{sol}}\times 100$$ (52)

where $Mi{n}_{sol}$ and $Ma{x}_{sol}$ depict the min and max values of each of the assessment metrics, respectively. $Bes{t}_{sol}$ is the best solution out of the meta-heuristics, and $Al{g}_{sol}$ indicates the objective value. It's worth pointing out that the lower RDI value indicates better quality and efficiency. Moreover, for the assessment metrics in the proposed meta-heuristics, a confidence interval of 95% is utilized to statistically analyze the meta-heuristics performance. Fig. 11 demonstrates the means plot and the Least Significant Difference (LSD) intervals for the suggested meta-heuristics.

Fig. 11.

The means plot and LSD intervals for the suggested meta-heuristics.

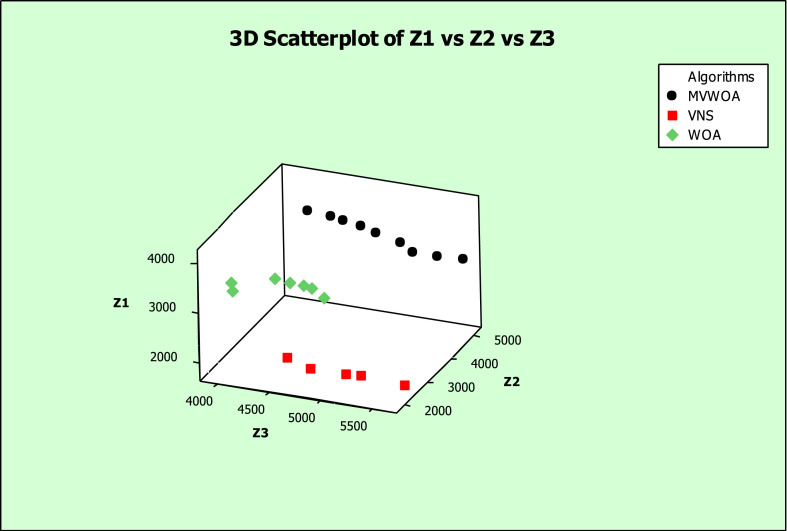
As vividly observed in Fig. 11(a) and (b), there are some overlaps between the proposed meta-heuristics based on the NPS and MID metrics induced results, where the MVWOA is revealed with higher quality than the WOA and the VNS. As shown in Fig. 11(c) and (d), based on the proposed assessment metrics’ outcomes, there is a statistically significant difference between the proposed meta-heuristics in the MS and the POD metrics. Compared with the MS and POD, the MVWOA statistically exceeds other meta-heuristics. In addition, an instance of the non-dominant solutions for the proposed algorithms is demonstrated in Fig. 13 as an experimental problem (e.g., M1). As seen in Fig. 12 , the VNS shows the worst efficiency; however, the MVWOA algorithm demonstrates the best performance.

Fig. 13.

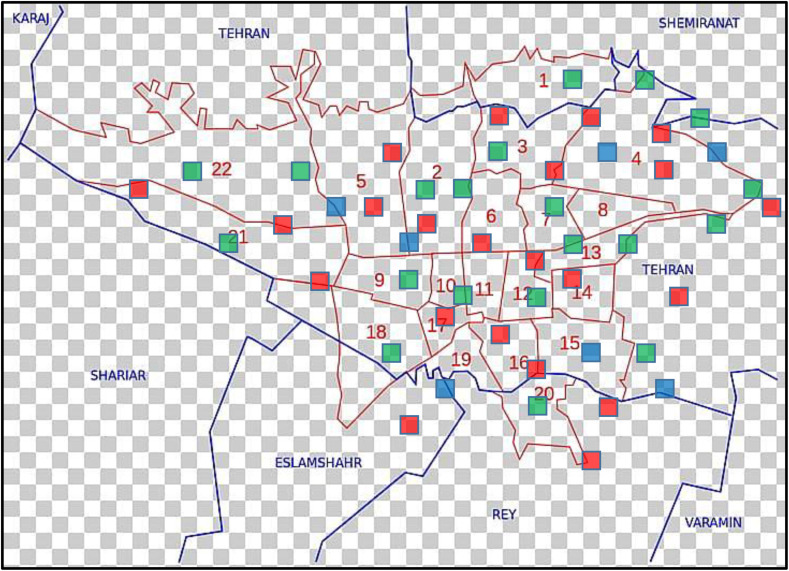
The case study map in Tehran/Iran.

Fig. 12.

The derived non-dominant solutions' dispersion behavior by the proposed meta-heuristics in problem M1.

5.5. Case study

In this section, a case study related to the COVID-19 pandemic period in Tehran/Iran is provided to validate the proposed algorithm. Tehran is the largest city and the capital of Iran. Tehran houses 8,693,706 population and it covers 730 km². It is the 25th most populous city and the 27th largest city in the world, which is divided into 22 districts and 122 urban areas [50]. As reported, 2021.03.07, 3,270,843 people have got infected with COVID-19 and 84,949 died [51]. The main purpose of this case study is to manage the production, distribution, location, allocation, and inventory of the COVID-19 vaccine in Tehran. The case study map is given in Fig. 13. The hospitals, the vaccination centers, and the manufacturers are colored in green, red and blue, respectively. Therefore, 20 hospitals, 22 vaccination centers, and 7 manufacturers are taken into account. In these centers, two types of vaccines, i.e., $Barekat$ and $Sputnik$ are planned to be used. The case study has considered two 1-month-length periods when the students in Tehran get vaccinated.

Table 8 shows the parameters related to the vaccination centers. As seen, the establishment costs, the overtime cost, the number of beds, and the effectiveness level of the vaccination centers are given in this table. All the costs are in dollars. In Table 9 , the storage capacity of the hospitals’ vaccines is provided in dose. For example, the storage capacity of the $Barekat$ vaccine in the hospital 2 is 6000 doses and the storage capacity of the $Sputnik$ vaccine in the hospital 3 is 3000 doses. Table 10 illustrates the transportation cost of a dose of the vaccine from the manufacturers to the hospitals. For instance, it costs $ 0.7 to ship one round of vaccines from manufacturer 2 to hospital 7.

Table 8.

Vaccination centers related parameters.

Center	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11
Cost of establishing ($)	150,000	200,000	150,000	100,000	200,000	300,000	100,000	300,000	150,000	150,000	150,000
Center	V12	V13	V14	V15	V16	V17	V18	V19	V20	V21	V22
Cost of establishing ($)	200,000	200,000	300,000	150,000	400,000	200,000	130,000	180,000	250,000	200,000	350,000
Center	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11
Cost of overtime ($)	2	1	2	2	2	1	1	2	1	1.5	1
Center	V12	V13	V14	V15	V16	V17	V18	V19	V20	V21	V22
Cost of overtime	1	2	2	2	1	1	2	1.5	2	1.5	2
Center	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11
Number of beds	2000	3000	3000	4000	3000	2500	1000	4000	1500	4000	3000
Center	V12	V13	V14	V15	V16	V17	V18	V19	V20	V21	V22
Number of beds	3000	1000	3500	2000	3000	1500	3000	5000	4000	3000	3000
Center	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11
Effectiveness level	0.5	0.7	0.4	0.5	0.4	0.3	0.8	0.5	0.7	0.4	0.4
Center	V12	V13	V14	V15	V16	V17	V18	V19	V20	V21	V22
Effectiveness level	0.5	0.5	0.6	0.5	0.7	0.3	0.5	0.7	0.6	0.6	0.7

Table 9.

Storage capacity of vaccines in hospitals.

Vaccine	Barekat
Hospitals	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10
Storage capacity	6000	6000	5000	6000	4000	6000	5000	7000	5000	3500
Hospitals	H11	H12	H13	H14	H15	H16	H17	H18	H19	H20
Storage capacity	5000	4000	5500	4000	8000	4000	5000	7000	8000	6000
Vaccine	Sputnik
Hospitals	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10
Storage capacity	4000	3000	3000	5000	7000	4000	5000	3000	7000	5000
Hospitals	H11	H12	H13	H14	H15	H16	H17	H18	H19	H20
Storage capacity	4000	5000	6000	7000	8000	7000	7000	5000	6000	8000

Table 10.

Transportation cost of a dose of vaccine from manufacturers to hospitals in dollar.

Transportation cost	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10
M1	1	0.5	2	0.7	2	1	1	1	0.5	0.7
M2	1.5	2	0.5	0.8	2	1.5	0.7	1.1	0.8	2.5
M3	0.5	1.8	2	2.3	2.9	0.8	1	1.5	1.5	2.8
M4	3	1	1.1	0.3	0.3	1	0.4	0.5	0.7	0.7
M5	0.6	0.3	1	1.1	0.9	0.2	1	0.4	0.1	0.1
M6	0.4	0.5	1	0.5	1	0.8	0.5	0.4	0.6	0.9
Transportation cost	H11	H12	H13	H14	H15	H16	H17	H18	H19	H20
M1	1	0.5	1.5	0.8	1.5	1.2	1.2	1.1	0.6	0.8
M2	1.5	2	0.4	0.8	1.5	1.2	0.6	1.5	1	1
M3	1	2	2	2.3	2.5	0.8	0.8	1	2	2
M4	2.5	1	1.1	0.3	0.5	1	0.4	0.5	0.6	0.6
M5	0.6	0.5	1	1	0.9	0.5	0.8	0.4	0.1	0.5
M6	0.4	0.4	1.2	0.5	1	1	0.5	0.4	0.7	0.8

5.6. Computational results

The simulation model inputs are reported in Table 11 , based on which the values of the Incubation Time, Disease Duration, Quarantine Length, and Transmission Rate are 6 days, 14 days, 15 days, and 60 contacts/person, respectively.

Table 11.

Simulation model parameters’ values.

Parameters	Value	References
First COVID-19 case date reported	13th March 2020	Assumed
Susceptible population	3000	Assumed
Incubation time	6 days	[31]
Disease duration	14 days	[41]
Number of cases reported at the start	42	Assumed
Quarantine length	15 days	[53]
Fraction of the infected	2%	[41]
Average time to lose immunity	5 days	[53]
Number of available tests per day	1000 per day	Assumed
Total students on campus	8856	Assumed
Average deaths rate	3%	World Health Organization. (2021).
Transmission rate	60 contacts/person	[25]

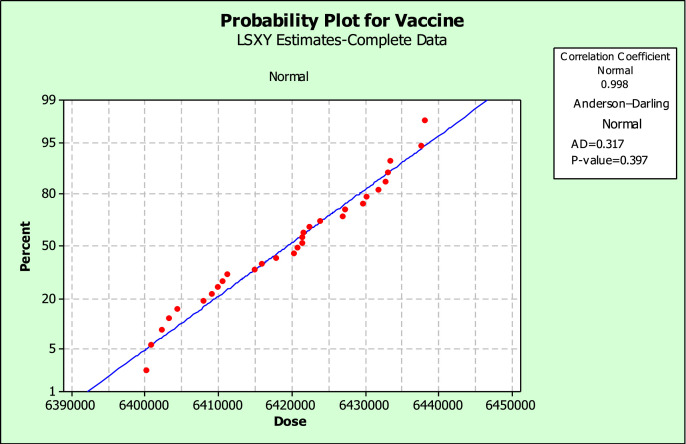
In Fig. 14 , the distribution function of the estimated required vaccine doses by the simulation is illustrated. As observed, the amount of the required vaccine follows the Normal distribution function with a correlation coefficient of 0.998. The Anderson-Darling test is used to validate the estimated distribution function. The Anderson–Darling test is a statistical test of whether a given sample of data is drawn from a given probability distribution. The Anderson-Darling test is defined as: $H_0$: The data follow a specified distribution. $H_1$: The data do not follow the specified distribution. Thus, the test statistics value is 0.317. According to the $p-value$ > 0.05, there is no sufficient evidence to reject zero hypotheses.

Fig. 14.

Distribution function of the estimated vaccine dose value.

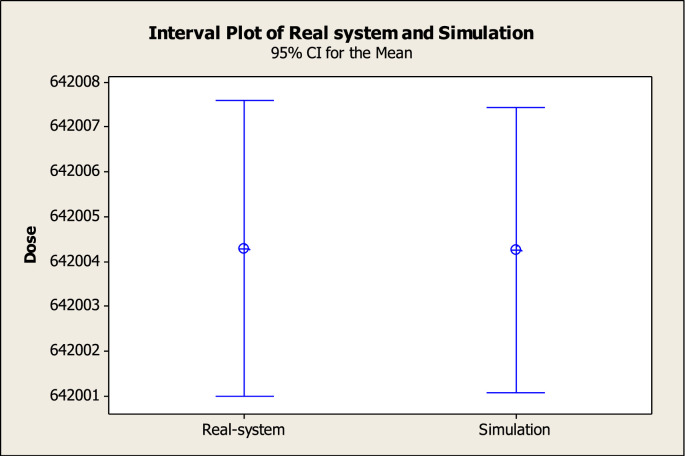
The simulation method has been validated by applying the test on the equality of the means at the confidence interval of 95%. Therefore, the simulation model has been run 100 times for 5 million hours and the average dose of the required vaccine has been reported. The real system data are also acquired from the Ministry of Health of Iran. It can be stated that with 95% reliability, the simulation model can have a proper estimate of the real system (see Fig. 15 ). The Mann-Whitney nonparametric test has also been utilized to determine whether the two populations are equal ($H0$) or not ($H1$). Thus, the test statistics value is 0.365. According to the $p-value$ > 0.05, there is no sufficient evidence to reject zero hypotheses.

Fig. 15.

Comparison of simulation results with real system.

Moreover, the number of transported vaccines from the manufacturer to the vaccination centers by dose in the first period is given in Table 12 . For example, 810 doses of $Barekat$ vaccine from manufacturer 1 are sent to vaccination center 7 and 1155 doses of $Sputnik$ vaccine from manufacturer 2 are transported to vaccination center 20. In addition, the amount of the stored vaccines in the hospitals by dose in the first period is given in Table 13 . For instance, as known, 1678 doses of $Sputnik$ vaccine are stored in hospital 10 and 1762 doses of $Baraket$ vaccine are stored in hospital 15. Based on the results from solving the presented model, the vaccination centers 4, 8, 13, and 21 are not established in the first period.

Table 12.

Total amount of transferred vaccines from manufacturers to vaccination centers.

			Barekat
Center	V1	V2	V3	V5	V6	V7	V9	V10	V11
M1	1580	–	–	2330	1240	810	–	2051	–
M2	540	2710	3125	–	1127	–	–	–	–
M3	–	3906	3892	1977	–	3843	2047	–	–
M4	2878	1616	–	3948	–	–	–	1324	2398
M5	1809	–	–	1490	2157	3154	1060	2644	2811
M6	–	–	–	–	–	–	–	–	–
M7	–	–	–	2932	960	3270	817	3145	1828
Center	V12	V14	V15	V16	V17	V18	V19	V20	V22
M1	2370		–	1410	814	518	3040	–	–
M2	–	2242	–	3912	2379	–	3796	3554	3269
M3	2822	1093	–	1296	–	1125	–	–	1713
M4	–	–	3878	–	1228	1250	1658	–	834
M5	2692	3855	–	3422	2013	–	–	–	–
M6	–	–	–	–	–	–	–	–	–
M7	2242	–	–	3205	–	1873	–	3509	1204
Sputnik
Center	V1	V2	V3	V5	V6	V7	V9	V10	V11
M1	3588	4682	–	4686	2471	–	2060	–	–
M2	1202	2336	2358	3830	3235	2103	3793	2850	1250
M3	–	4561	3154	823	–	877	801	4643	–
M4	–	–	2969	–	2458	3413	–	–	–
M5	1390	1513	1149	1278	1559	2666	822	3558	3719
M6	–	3393	1959	3747	–	1115	–	3603	–
M7	–	–	–	–	–	–	–	–	–
Center	V12	V14	V15	V16	V17	V18	V19	V20	V22
M1	–	3660	–	3708	–	1078	3972	–	1021
M2	2776	–	2718	3628	950	3343	3895	1155	2703
M3	3441	853	–	3756	–	–	3217	–	–
M4	–	3556	–	2335	–	–	3837	–	–
M5	–	3526	3793	–	2957	–	1672	1507	–
M6	3388	–	3931	840	3357	–	1196	3994	–
M7	–	–	–	–	–	–	–	–	–

Table 13.

Vaccines inventory in hospitals.

					Sputnik
Hospital	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10
Inventory	1120	718	1516	550	2110	1325	1405	827	918	1678
Hospital	H11	H12	H13	H14	H15	H16	H17	H18	H19	H20
Inventory	1008	649	2164	686	2410	556	728	1076	1100	887
Barekat
Hospital	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10
Inventory	516	1060	1970	1564	1410	2175	918	615	1884	716
Hospital	H11	H12	H13	H14	H15	H16	H17	H18	H19	H20
Inventory	2015	614	2466	1469	1762	819	2126	1736	910	1022

5.7. Sensitivity analysis

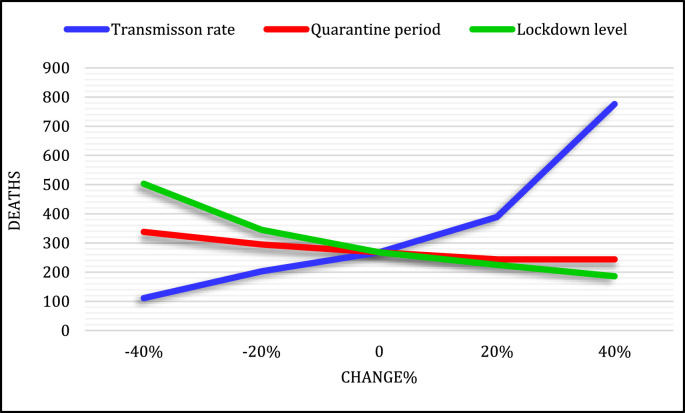
Fig. 16 illustrates the sensitivity analysis of the simulation model. As it is known, as the transmission rate increase, the number of deaths rises exponentially. Besides, under normal circumstances and assuming the transfer rate equal to 60 contacts/person, the number of deaths equals 268 people. With the transmission rate increasing by 20 and 40%, the number of deaths increases to 389 and 776, respectively. Also, with the transmission rate decline by 20 and 40%, the deaths number reduces to 203 and 111, respectively. After that, with the infected students’ quarantine time reduced by 20 and 40%, the number of deaths increases to 295 and 338, respectively. The reason is the standard quarantine period is not completed by the affected students and they are still virus carriers, therefore, they can infect more students. Increasing the quarantine period of the infected students by 20 and 40% does not affect the number of deaths as it remains constant at 244. Finally, increasing the lockdown level by 40% reduces the number of deaths to 186, and decreasing it by 40%, increases the number of deaths to 503. Therefore, the lockdown level can have a very impressive effect on the number of deaths.

Fig. 16.

Simulation model's sensitivity analysis.

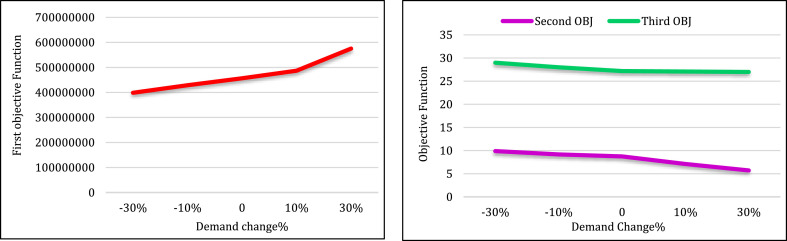
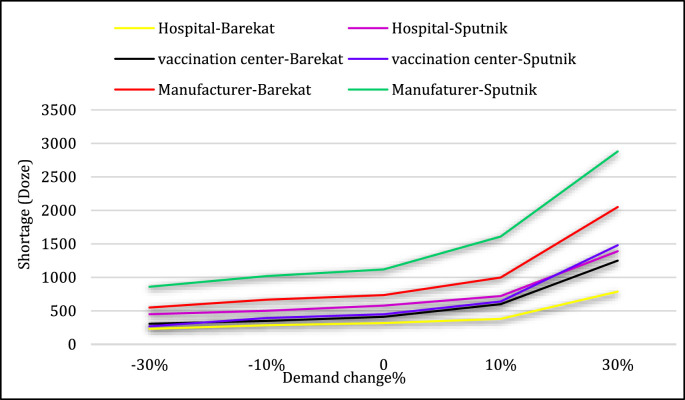
Fig. 17 demonstrates the effect of demand change on the objective functions. As perceived, by the demand increase, the costs (the first objective function) sharply increase. In this regard, with a 30% demand increase, the costs increase to 575230819.1 units (20%), and with a 30% demand decrease, the costs drop to 398,618,116 units (12%).

Fig. 17.

Demand change behavior's effect on three objective functions.

Increase in demand would require establishing more vaccination centers and more transportations, which results in increasing the SC cost. Also, as the demand increases, the vaccination desirability for students (the second objective function) declines with a slight slope. Finally, as the demand increases, the third objective function remains almost constant. A 60% increase in demand leads to a 6% decrease in the third objective function. As demand increases, the amount of flow initially remains constant, so the value of the function is initially reduced. The amount of current then increases so that the objective function (from 10 to 30%) remains constant. This suggests that the proposed model has the due flexibility in justice for the vaccine distribution.

Fig. 18 displays the demand change-induced effect on the amount of the vaccine shortage in terms of dose. It is clear that as demand increases, the vaccine shortage increase in the manufacturers, the vaccination centers, and the hospitals. For example, $Barekat$ vaccine demand raised by 30% in the hospitals, increases the shortage to 788 doses, and $Sputnik$ vaccine demand increased by 30% in the manufacturers, increases the shortage to 2880 doses.

Fig. 18.

The trend of demand changes' effect on vaccine shortage amount by dose.

6. Conclusion and future works

In the present study, a stochastic simulation-optimization model is developed for the COVID-19 vaccine supply chain network. Statistical sample of the study is drawn from the students’ population in Tehran/Iran. First, the COVID-19 outbreak in universities is investigated via the system dynamics-based simulation model. The parameters considered in the simulation approach encompass the Disease Duration, Quarantine Length, Average Deaths Rate, Transmission Rate, and Lockdown Level.

A new stochastic multi-objective, multi-period, and multi-commodity simulation-optimization model has been developed for the COVID-19 vaccine's production, distribution, location, allocation, and inventory control decisions. To solve the proposed model in small-sized problems, the BOF approach is utilized. The proposed model is solved using the VNS and WOA algorithms. In terms of the solution methods' novelties, a new heuristic method known as the MVWOA is developed based on the VNS and the WOA to solve the presented problem in various sized problems. To control and tune the algorithm's parameters, the Taguchi method is suggested. In terms of the assessment metrics and the CPU time, the MOWOA is equipped with higher performance and efficiency than other given algorithms.

The number of the estimated required vaccines follows the Normal distribution with a correlation coefficient of 0.998. According to the simulation results, with 95% reliability, the simulation results are accurate estimates of the real world. Also, the Anderson-Darling test and Mann-Whitney non-parametric test are applied to check the simulation results’ accuracy, verifying the simulation results as an accurate estimate of the real world. According to the sensitivity analysis results, as the transmission rate increases, the number of deaths increases. Also, as the quarantine period decreases, the mortality rate increases with a slight slope. Then, by the quarantine period drop of 20%, the mortality rate increases by 10%.

6.1. Research contributions

The most distinguished contribution in the simulation approach is considering the virtual education and quarantine-induced effect on estimating the number of vaccines. Next, the estimated vaccine demand is entered into the mathematical model as a parameter. The proposed mathematical model's major goals are to minimize the vaccine distribution supply chain's costs, to maximize the vaccination desirability for students, and to maximize justice in distrusting the vaccines. Meanwhile, the social distancing and the injection plan during the working and non-working hours are other contributions of the proposed model. In addition, the production, distribution, location, allocation, and inventory problems of the vaccines are dealt with in the presented model.

6.2. Limitations and future remarks

As there was no official database for some parts of cost elements, the driver's estimations were asked to help. The questions about the transportation costs for each route have been categorized and the estimated costs have been entered into the mathematical model. Despite the existence of several ways of COVID-19 transmission, in the system dynamic structure of the simulation model, only two ways of physical contact and transmission through sneezing and coughing are considered.

The following issues are recommended for the would-be studies:

• •Considering other goals such as maximizing the level of demand coverage and minimizing service time
• •Examining the COVID-19 pandemic's impact on the vaccine supply chain with the support of a discrete-event simulation
• •Enhancing vaccine supply chain resilience in a post-pandemic environment
• •Developing digital vaccine SC twin using real-time data to support the decision-making during the COVID-19 outbreak by simulating disruption impacts on the alternative SC designs

Author statement

Mehdi A. Kamran: Conceptualization; Formal analysis; Investigation; Methodology; Project administration; Supervision; Validation; Writing - review & editing, Reza Kia: Conceptualization; Formal analysis; Investigation; Methodology; Project administration; Supervision; Validation; Writing - review & editing, Fariba Goodarzian: Data curation; Formal analysis; Investigation; Methodology; Resources; Software; Validation; Visualization, Peiman Ghasemi: Data curation; Formal analysis; Investigation; Methodology; Software; Validation; Visualization; Writing - review & editing.

Appendix A.

Stochastic chance constraint programming

Stochastic chance constraint programming is one of the most common methods for solving stochastic mathematical models. This method was first introduced by Charnes and Copper [52] to convert a stochastic mathematical model to a deterministic counterpart. To solve a stochastic model in this method, a degree of confidence such as $\alpha$ is defined by the modeler to have a suitable confidence margin. The way it works is that all constraints including the uncertainty parameter must be at least as reliable as $\alpha$ percent. Consider the following minimization mathematical model with parameters ${\tilde{q}}_{ij}$, ${\tilde{c}}_{rj}$ and ${\tilde{s}}_i$ which $\sim$ represents the uncertainty and $w_j$ of the decision variable. Also, r represents the number of objective functions, m shows the total number of constraints, and $i$ indicates the constraint of $i$. The general form of stochastic chance constraint programming is as follows:

$$\begin{array}{l}\min f_r=E\left(\sum _{j=1}^n{\tilde{c}}_{rj}{w}_j\ge {\tilde{s}}_i\right)r=1,\dots ,R\\ i=\mathrm{1,2},\dots ,m\end{array}$$ (a1)

$$p\left(\sum _{j=1}^n{\tilde{q}}_{ij}{w}_j\ge {\tilde{s}}_i\right)\ge {\alpha }_{i}i=\mathrm{1,2},\dots ,m$$ (a2)

$$w=\left(w_1,\dots ,w_n\right)$$ (a3)

$$w\ge 0$$ (a4)

A summary of the results of chance constrained programming for minimization and maximization problems is as follows.

$$E\left(\sum _{j=1}^n{\tilde{c}}_{rj}{w}_j-f_r^{-}\right)+{\phi }^{-1}(1-{\alpha }_r)\sqrt{Var(\sum _{j=1}^n{\tilde{c}}_{rj}{w}_j-f_r^{-})}\ge 0r=1,\dots ,R$$ (a5)

So that $f_r^{-}=\min \sum _{j=1}^n{c}_{rj}^{\ast }{w}_j$.

$$E\left(\sum _{j=1}^n{\tilde{c}}_{rj}{w}_j-f_k^{+}\right)+{\phi }^{-1}\left({\alpha }_r\right)\sqrt{Var(\sum _{j=1}^n{\tilde{c}}_{rj}{w}_j-f_r^{+})}\le 0r=1,\dots ,R$$ (a6)

So that $f_r^{+}=\max c_{rj}^{\ast }{w}_j$

$$E\left(\sum _{j=1}^n{\tilde{q}}_{ij}{w}_j-{\tilde{s}}_i\right)+{\phi }^{-1}\left({\alpha }_i\right)\sqrt{Var(\sum _{j=1}^n{\tilde{q}}_{ij}{w}_j-{\tilde{s}}_i)}\ge 0i=\mathrm{1,2},\dots ,m$$ (a7)

For more information on this algorithm, see Ref. [53]. Based on the constraints of (a5)-(a7), the chance constraint model at the α% level for the constraints (5)–(6), (15)–(16) and third objective function is defined as follows:

$$E\left({\widetilde{d^{\prime }}}_{iht}\right)+{\phi }^{-1}(1-{\alpha }_i)\sqrt{var\left({\tilde{d}}_{ivt}\right)}-\sum _m\sum _o{f}_{iomht}\ge 0\forall t,i,h$$ (a8)

$$E\left({\tilde{d}}_{ivt}\right)+{\phi }^{-1}\left(1-{\alpha }_i\right)\sqrt{var\left({\tilde{d}}_{ivt}\right)}-\sum _m\sum _o{p}_{iomvt}\ge 0\forall i,v,t$$ (a9)

$$E\left({\tilde{d}}_{ivt}\right)+{\phi }^{-1}(1-{\alpha }_i)\sqrt{var\left({\tilde{d}}_{ivt}\right)}=n{s}_{vt}+ns{\prime }_{vt}\forall i,v,t$$ (a10)

$$E\left({\widetilde{d^{\prime }}}_{iht}\right)+{\phi }^{-1}(1-{\alpha }_i)\sqrt{var\left({\tilde{d}}_{ivt}\right)}=n{h}_{ht}+nh{\prime }_{ht}\forall i,h,t$$ (a11)

$$\mu \le \sum _i\sum _m\sum _h\sum _o\sum _t\frac{f_{iomht}}{E\left({\widetilde{d^{\prime }}}_{iht}\right)+{\phi }^{-1}(1-{\alpha }_i)\sqrt{var\left({\tilde{d}}_{ivt}\right)}}+\sum _i\sum _o\sum _m\sum _v\sum _t\frac{p_{iomvt}}{E\left({\widetilde{d^{\prime }}}_{iht}\right)+{\phi }^{-1}(1-{\alpha }_i)\sqrt{var\left({\tilde{d}}_{ivt}\right)}}\forall i,o,m,h,v,t$$ (a12)