PPI-Affinity: A Web Tool for the Prediction and Optimization of Protein–Peptide and Protein–Protein Binding Affinity

Abstract

Virtual screening of protein–protein and protein–peptide interactions is a challenging task that directly impacts the processes of hit identification and hit-to-lead optimization in drug design projects involving peptide-based pharmaceuticals. Although several screening tools designed to predict the binding affinity of protein–protein complexes have been proposed, methods specifically developed to predict protein–peptide binding affinity are comparatively scarce. Frequently, predictors trained to score the affinity of small molecules are used for peptides indistinctively, despite the larger complexity and heterogeneity of interactions rendered by peptide binders. To address this issue, we introduce PPI-Affinity, a tool that leverages support vector machine (SVM) predictors of binding affinity to screen datasets of protein–protein and protein–peptide complexes, as well as to generate and rank mutants of a given structure. The performance of the SVM models was assessed on four benchmark datasets, which include protein–protein and protein–peptide binding affinity data. In addition, we evaluated our model on a set of mutants of EPI-X4, an endogenous peptide inhibitor of the chemokine receptor CXCR4, and on complexes of the serine proteases HTRA1 and HTRA3 with peptides. PPI-Affinity is freely accessible at https://protdcal.zmb.uni-due.de/PPIAffinity.

Introduction

Protein–protein interactions (PPIs) are fundamental to most biological processes.¹ Prominent disorders, such as cancer and degenerative diseases, are related to aberrant PPIs.² In therapy, optimized PPIs are also critical for the strong binding of antibodies to their protein antigens.³ Therefore, the characterization of PPIs in terms of their binding affinity (BA) is highly relevant to the design of new biologics and therapeutic compounds.⁴ Notably, peptides are a promising class of bioactive compounds, which often have higher specificity and reduced side effects compared to small-molecule pharmaceuticals.⁵ Currently, there are more than 60 approved peptide drugs, and hundreds of peptidic compounds undergo clinical or preclinical trials.⁶ However, the design of peptide drugs remains a challenging task due to their flexible structures and diversity of binding sites.⁷

Virtual screening approaches, based on BA predictions, reduce the time of the drug development pipelines.³ Thus, over the past decades, several screening tools based on the BA of protein–protein complexes have been introduced.⁸⁻²⁶ Relevant examples of these methods are DFIRE,⁹ CP_PIE,¹⁶ ISLAND,²⁴ and the web server PRODIGY,^21,27 (which tailored and improved the original model introduced by Kastritis et al.).²⁰ Protein–peptide complexes are usually scored with functions derived from binding affinity data of small molecules. Examples of such scoring methods are RF-Score²⁸ and Kdeep,²⁹ which used a random forest algorithm³⁰ and a convolutional neural network,^31,32 respectively, to train their models. Supporting Information Table SI-1 summarizes the above-mentioned BA predictors, as well as other state-of-the-art methods that contribute to the broad field of PPI prediction tools.

Noteworthy, to the best of our knowledge, there is no publicly available web tool specifically designed to predict and optimize the BA of diverse protein–peptide complexes, by considering as a peptide an amino acid sequence with less than 30 residues. Several works have approached this aim specifically for the identification of binders of the major histocompatibility complexes MHC-I, II.^33,34 However, given that their training is restricted to MHC data, these models are not applicable to predict the binding free energy of other protein–peptide complexes. Besides, the available tools typically do not leverage the possibility of optimizing the primary structure of the peptide to improve the affinity of the complex.

We evaluated the performance of the above-mentioned screening tools for estimating the BA of protein–peptide complexes by testing 100 randomly selected protein–peptide complexes from the Biolip³⁵ database. This test set contained complexes with peptides ranging from 4 to 29 amino acids, coupled to receptors with sizes between 51 and 496 amino acids. The binding free energy of the complexes covered the range between −12.6 and −4.6 kcal/mol. The highest correlation was delivered by Kdeep (R = 0.32), while the correlation with all of the other methods was in the range R = [0.13, 0.24] (Supporting Information Table SI-2). This comparison evidences the rather low dependability of state-of-the-art screening tools for the prediction of the BA of protein–peptide complexes.

Given the remarkable scaffold that peptides represent for drug development, we addressed this issue by developing machine-learning-based predictors of BA that are specific for protein–peptide complexes. In addition, we present a predictor of protein–protein BA that rivals the performance of the state-of-the-art screening tools built for such systems. Both predictors are integrated into a novel tool named PPI-Affinity, which is a web server designed to score protein–protein and protein–peptide complexes based on their predicted BA, as well as to optimize the affinity of a complex by mutating and screening selected residues. With such functionalities, PPI-Affinity can be employed at early steps of drug design processes, which are focused on the screening and optimization of protein/peptide binders for a given protein target.

Materials and Methods

In this section, we describe the dataset and the modeling procedure used to develop both predictors. In both scenarios, protein–protein and protein–peptide systems, the performance of the models is evaluated with cross-validation and hold-out test sets.

Data Collection: Protein–Protein Complexes

We initially retrieved 2 852 protein–protein complexes with known BA data deposited in the PDBbind (v.2020)³⁶ database. Subsequently, we curated these data by extracting only dimeric complexes and removed those in common with the benchmark used by Vangone and Bonvin²¹ to assess their model. We excluded those cases in which the binding affinity values were reported with measures other than K_d, K_i, or ΔG_bind. Likewise, those instances with imprecise BA values (i.e., reporting ranges of K_d values instead of precise values) were removed. Cases with binding free energy values outside the range [−18.1, −3.1] kcal/mol were also excluded, as these instances are sparingly represented and the difference between their BA value and the rest of the distribution was ΔG ≥ 0.5. The application of such filters rendered a dataset of 833 protein–protein complexes (Supporting Information Figure SI-1 depicts the distribution of binding free energy values for this dataset). All of the structures were preprocessed by adding hydrogens and other missing atoms with MODELLER v9.23³⁷⁻⁴⁰ and PDB2PQR.⁴¹

Features Generation

We employed the 3D-structure descriptors implemented in the protein codification package ProtDCal.⁴² This program is accessible via the web server ProtDCal-Suite,⁴³ which also provides access to other models developed by us using this codification approach. ProtDCal has a workflow of four automated steps, which are: (i) residue-wise codification, (ii) modification based on the vicinity, (iii) residue grouping based on amino acid types, and (iv) numerical aggregation using descriptive statistics. The options selected at each step are used in a combinatorial scheme to generate an array of numerical descriptors that characterize the input structure. Each descriptor in the array is the result of the combination of one residue property (e.g., reside-wise contact order, RWCO),⁴⁴ a vicinity operator (e.g., autocorrelation, AC), a grouping criterion (e.g., nonpolar residues, NPR), and an aggregation operator (e.g., variance, V); thus, every element in the array is identified by a unique label (e.g., RWCO_AC_NPR_V). In the Supporting Information Section SI-1, we provide the configuration file used to compute the descriptors employed in this study. This configuration generates 23 040 descriptors for each protein–protein complex. In ProtDCal, interchain residue contacts are determined by a maximum spatial distance (d) measured between the α carbons of the residues. We set up the calculation of such contacts with a spatial cutoff d = 10 Å. ProtDCal has been successfully applied by us and other authors to model post-translational modifications,^42,45,46 protein–protein interaction,⁴⁷ enzyme-like amino acid sequences,⁴⁸ critical residues for protein function,⁴⁹ and antibacterial peptides.^50,51

Modeling Protocol for Protein–Protein Affinity Data

The learning process was carried out with Weka 3.8.4.⁵² Support Vector Machine (SVM) was selected as the learning algorithm after performing a preliminary study that showed that it is the simplest and best-performing solution for developing the models (Supporting Information Section SI-2). SVM is a successful approach widely validated in drug discovery.^53,54 This technique has delivered a worthy performance on small and mid-sized datasets,⁵⁵ where deeper machine learning (ML) approaches, such as various neural network architectures, tend to overfit.^56,57 The implementation of SVM for regression in the package SMOreg⁵⁸ was employed to develop the models. We randomly split the collected data into three datasets: a training set with 653 complexes, a development set with 90 complexes, and a test set with 90 complexes (Script SI-1). The purpose of the development set was to monitor the generalization of multiple configurations of the hyperparameters during the training process. The hold-out test set was exclusively used to compare the final model with external predictors.

Initially, every instance in the training set was represented as a vector of 23 040 molecular descriptors generated with ProtDCal. The steps of feature selection included the removal of invariant descriptors and those carrying missing values. Next, an optimal subset of attributes was searched with a supervised exploration guided by the error in the prediction of the binding affinity for cases in the training set. The resulting optimal subset comprised 26 descriptors, which were used to train the final models (Supporting Information Section SI-3). Supporting Information File SI-1 provides a configuration file for ProtDCal to compute this specific list of descriptors.

We adopted an ensemble learning approach by creating four partially overlapping subsets of the training data with a distribution of the output variable flatter than the complete training set (Supporting Information Figure SI-2). Thus, we trained independent models with each subset and combined their outcomes using the Vote method implemented in Weka 3.8.4,^52,59,60 with combination schemes based on the average, maximum, and minimum predicted values among selected models.

With each training subset, the hyperparameters of the SVM were adjusted using a grid search.⁶¹ The search space was defined by the following range of hyperparameter values:

• Complexity (C): 2^–5, 2^–4.5, 2^–4, 2^–3.5, 2^–3,..., 2¹, 2^1.5, 2², 2^2.5, 2³, 2^3.5 and 2⁴

• Degree (D) of the polynomial function kernel: 1, 2, and 3

The models generated during the search were assessed using the Pearson’s correlation coefficient (R) (eq 1) of the estimations in the training data via resubstitution and 10-fold cross-validation (10-fold CV), as well as in the development set.

1

The terms y_i and y̅ are the actual affinity values and their mean in the datasets. Analogously, the terms y_i^pred and y̅^pred correspond to the same type of values but as predicted by the model.

To identify the optimum values of the hyperparameters, we formulated an ad hoc fitness-robustness score (FRS) (eq 2) as a function of the correlation coefficient, which combines in a single measure the performance of a model in terms of goodness of fit and robustness. The FRS function has an optimum maximum value at FRS = 1; thus, we selected the configuration that maximized the FRS function.

2

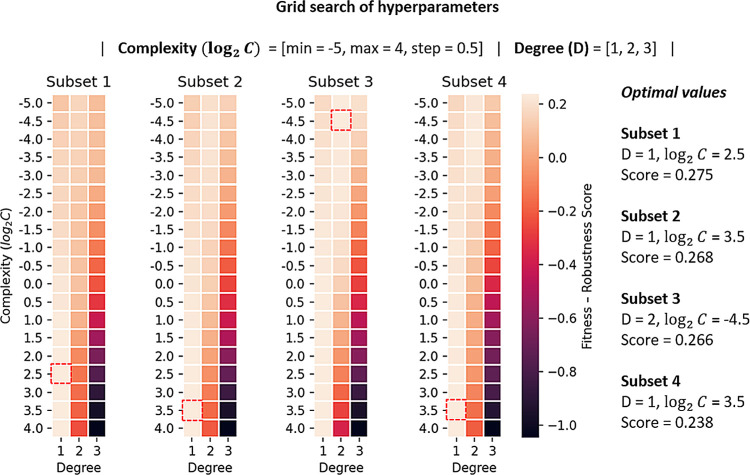
The terms R_TS, R_CV, and R_DEV are the correlation coefficients obtained on the training set, in 10-fold CV, and development set, respectively. R̅ is the arithmetic mean of the performance on these three tests. The first term of the function aims to combine the performance on the training set (goodness of fit), with the performance in cross-validation and development set (generalization). The next two terms reduce the deviations between the performance on the training set and the performance when evaluating in cross-validation and development set. These weighting terms improve the robustness of the selected model by considering the generalization power of the predictor in addition to the goodness of fit. Overall, such a unified quantity is a highly informative measure to guide the optimization of hyperparameters during the modeling. We intend to continue challenging this formulation in further studies and applications. Figure 1 summarizes the results of the optimization of the hyperparameter values in each training subset. A complete list of all of the intermediate models and performance measures is provided in Supporting Information Table SI-3.

Figure 1.

Results of the optimization of hyperparameters. The selected model per training subset is marked with a red square and corresponds to the combination of degree (D) and complexity (log₂ C) values that maximized the fitness-robustness score defined in eq 2.

All possible combinations with at least two models were evaluated in the development set to determine the best ensemble model. We summarized all of the performance measures for the independent models and the distinct ensembles in Supporting Information Table SI-4.

Data Collection: Protein–Peptide Complexes

The model was developed with data extracted from the Biolip database, which also incorporates data from the PDBbind Protein-Ligand³⁶ database. We downloaded the nonredundant dataset of Biolip, containing 105 152 entries. Only protein–peptide complexes with less than 90% of identity between the binding site′s residues and the full receptor sequence are included in these data. We extracted the complexes containing single-chain receptor only and a peptide formed by standard residues with a minimum length of three residues. Instances reported with post-translational modifications or fusion constructs (peptide/nonpeptide) were discarded. Subsequently, we selected the cases for which their BA values are reported in terms of the dissociation (K_d) or inhibition (K_i) constants only. We excluded the complexes with ambiguous K_d or K_i values (i.e., reporting a range of values), and those with binding free energies outside the range from −14.4 to −3.6 kcal/mol, as these instances were poorly represented and the difference between their BA value and the rest of the distribution was ΔG ≥ 0.5. The curated dataset contained 1149 complexes, with peptides of length ranging between 3 and 29 amino acids and receptors of sizes between 31 and 957 amino acids (Supporting Information Figure SI-3). Hydrogen atoms and other missing atoms were added to the structures using MODELLER v9.23³⁷⁻⁴⁰ and PDB2PQR.⁴¹

Modeling Protocol for the Protein–Peptide BA Data

We used SVM, implemented in the package SMOreg⁵⁸ in Weka 3.8.4, following a protocol equivalent to that employed for the protein-protein model described above. In summary, we randomly divided the dataset into three subsets: training dataset (949 instances), development dataset (100 instances), and test dataset (100 instances) (Script SI-1). Subsequently, we extracted numerical descriptors from the complexes’ structure using ProtDCal^42,43 with the configuration file summarized in Supporting Information Section SI-1. This step generated 23 040 molecular descriptors for each instance in the dataset. Next, we reduced this large multidimensional space to 37 descriptors through a features selection process (Supporting Information Section SI-4; a list of the extracted set of descriptors can be found in the file SI-2).

The training scheme used to develop the final predictor followed an ensemble approach. Four individual models were built with partially overlapping subsets of the training set. The subsets are random samples of the training data with a flatter distribution of the BA values (Supporting Information Figure SI-4) compared to the entire training set. This is achieved by undersampling the region next to the mode value of the distribution, while keeping the tails. Such transformation in the distribution of the data allows a balanced error weight along the entire range of the response variable. Subsequently, we optimized the hyperparameters of each model independently and combined their predictions with the Vote method implemented in Weka 3.8.4, according to the average, maximum, and minimum ensemble rules.

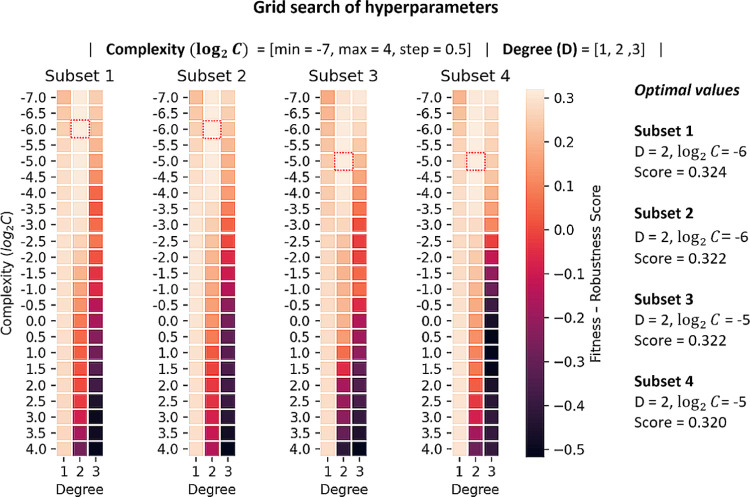
To create the models, the hyperparameters of the estimator were adjusted in a grid search following the same methodology as for the protein–protein model. During the optimization of the hyperparameters, the performance of the models was monitored in the training data, in 10-fold CV, and the development set. The optimum set of hyperparameter values for each training dataset was selected according to the FRS defined in eq 2. Figure 2 shows the results of the hyperparameters tuning process for each training subset. A complete list of all of the intermediate models and performance measures can be found in Supporting Information Table SI-5.

Figure 2.

Results of the optimization of hyperparameters. The selected model per training subset is marked with a red square and corresponds to the combination of degree (D) and complexity (log₂ C) values that maximized the FRS.

Next, the best ensemble model was selected by evaluating all possible combinations of models on the development set (Supporting Information Table SI-6). The selected ensemble model was evaluated on the hold-out test set of 100 complexes and compared with other available state-of-the-art protein–protein and protein–ligand BA predictors. Finally, the ranking power of the model was assessed on a set of mutants of the peptide EPI-X4, an endogenous inhibitor of CXCR4 whose activity was experimentally determined and on a set of complexes between peptides and the serine proteases HTRA1 or HTRA3.

Results and Discussion

In this section, we analyze the performance of the developed models and compare them with other state-of-the-art predictors.

Performance of the Protein–Protein Model

The best ensemble model contains two out of the four training subsets, whose individual correlations are R₂ = R₃ = 0.50. The ensemble model improved the individual ones achieving a correlation of R = 0.53 on the development set. The rule of minimum predicted value was used to build the ensemble predictor.

Recently, Vangone and Bonvin²¹ developed a model that predicts the BA based on two structural descriptors: the network of inter-residue contacts (ICs) and the noninteracting surface (NIS). The model, named ICs/NIS-based predictor was implemented in the web server PRODIGY.²⁷ This tool delivered a much better performance (R = 0.74 and MAE = 1.4) than other state-of-the-art methods on a benchmark set of 79 protein–protein complexes. Thus, we employed this benchmark set to evaluate our method (Table 1, Test set 1) against the ICs/NIS-based model, the other two top-ranked and currently available tools in that assessment, and the ISLAND method. We estimated the performance of our ensemble model on this benchmark set and obtained a correlation coefficient R = 0.62 and MAE = 1.8 kcal/mol (Test set 1) that ranks our method second, after PRODIGY.

Table 1. Summary of the Evaluation of PPI-Affinity and State-of-the-Art BA Predictors on Two Sets of Protein–Protein Affinity Data^a.

	test set 1		test set 2
method	R	MAE (kcal/mol)	R	MAE (kcal/mol)
PRODIGY	0.74	1.4	0.31	2.5
DFIRE	0.60	4.6	0.10	25.4
CP_PIE	–0.52	8.8	–0.10	11.0
ISLAND	0.38	2.1	0.27	2.2
PPI-Affinity	0.62	1.8	0.50	1.8

^aThe performance is expressed as the Pearson’s correlation coefficient (R) between experimental and predicted BA. The test set 1 corresponds to the benchmark employed by Vangone and Bonvin,²¹ while the test set 2 corresponds to the hold-out set of 90 data points taken from PDBbind (v.2020). The performance for the other methods on test set 1 was reported by Vangone and Bonvin.²¹ The negative values of the correlation coefficients indicate that the corresponding method predicts unbinding free energy.

Next, we challenged the predictors with a larger hold-out test set of 90 complexes, which was initially extracted from the data collected from the PDBbind (v.2020) protein–protein dataset (Table 1, test set 2). In this test, our model renders a correlation coefficient of R = 0.50, with an error MAE = 1.8 kcal/mol (Test set 2), performance which is only marginally inferior to that obtained in the benchmark set of Vangone and Bonvin²¹ (R = 0.62; MAE = 1.8 kcal/mol). The performance of ISLAND was diminished with respect to our method. Nevertheless, ISLAND delivered consistent results, in general superior to those delivered by other methods, in both test sets. The other predictors (PRODIGY, DFIRE, CP_PIE) show a large decrease in their performance with respect to their results in the test set 1 (Table 1, test set 1), with PRODIGY being the second best with a correlation coefficient R = 0.31 and MAE = 2.5 kcal/mol. Such a dramatic decay in the predictions suggests the presence of overfitting toward the previous benchmark set, specifically in the case of PRODIGY. Nonetheless, the analysis of the performance of the other predictors is hindered by the lack of applicability domain (AD) definition for using the methods. The absence of a defined AD limits the analysis of the errors of the predictions, as it is not possible to examine whether test samples are simply outside the scope of these predictors or there is a specific structural issue that affects the quality of the prediction.

In short, the data evidence the generalization achieved by our predictor, which performs consistently well in different external test sets. Supporting Information Figure SI-5 displays plots of experimental versus predicted BA values for PPI-Affinity in both test sets.

Next, we evaluated the performance of PPI-Affinity on a set of mutants taken from the SKEMPI v2.0⁶² dataset (Figure 3). This database reports the binding affinity changes of 7085 mutations of 345 protein–protein interactions for which the structure of the complex has been resolved. We selected a subset from this dataset by applying the following filtering steps: (I) we extracted the dimeric complexes having at least 30 amino acids in each protein sequence; (II) we removed the complexes overlapping between the selected data, the PDBbind (v.2020) dataset, and the benchmark set of Vangone and Bonvin;²¹ and (III) we removed the wild-type systems with more than one binding affinity value reported, as well as all mutants with ambiguous or unreported binding affinities. The output of the filtering steps reduced the dataset to 34 wild-type complexes and 182 mutants. We fed the conformed test set to PPI-Affinity. Eight wild-type complexes and their related mutants were found outside the applicability domain of the model. Thus, the final test set contained 26 wild-type structures and 151 mutants. The assessed mutants featured between one and six mutations per protein sequence, with 80% of the structures accounting for only one mutation. The binding free energy of all of the complexes was in the range of −16.3 to −5.5 kcal/mol.

Figure 3.

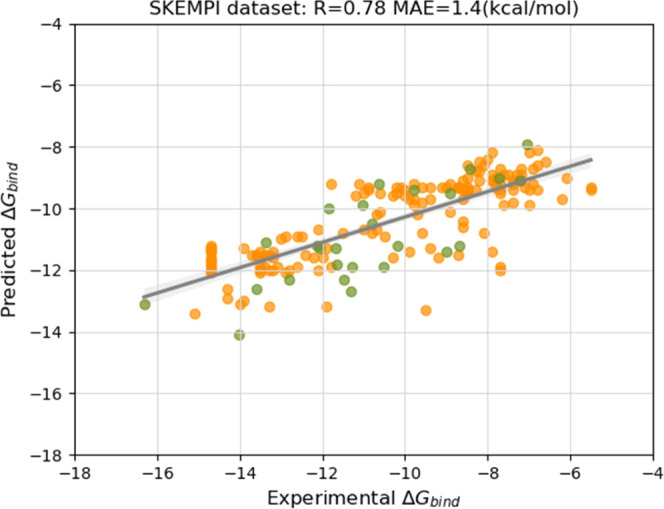
Performance of PPI-Affinity on the test set of 26 wild-type complexes and 151 mutants of protein–protein affinity data points taken from the SKEMPI dataset. The performance is reported as the Pearson’s correlation coefficient (R) between experimental and predicted BA. The green points correspond to BA values of the wild-type complexes, and the orange points correspond to the BA values of the mutants.

The performance of PPI-Affinity (R = 0.78 and MAE = 1.4 kcal/mol) on the SKEMPI dataset is superior to that obtained in the Vangone and Bonvin benchmark²¹ (Table 1, Test set 1) and in the 90 protein–protein complexes taken from the PDBbind (v.2020) database (Table 1, Test set 2). When considering only the wild-type complexes, PPI-Affinity delivered a performance of R = 0.77 and MAE = 1.1 kcal/mol. These results evidence the robustness of our protein–protein model in a third external dataset, at the time that show the ability of PPI-Affinity to characterize the changes upon mutations of protein–protein complexes.

Additionally, we assessed the performance of PPI-Affinity against the LUPIA²⁶ classifier. LUPIA uses a threshold value to classify as “high” or “low” the binding affinity of protein–protein complexes. This evaluation (Supporting Information Section SI-5) evidenced the shortcomings of discretizing the BA values to train classifiers rather than regressors models. Taken together, the performance of our protein–protein model on several tests ranks our ensemble model on the top of state-of-the-art fast protein–protein BA predictors.

Performance of the Protein–Peptide Model

The best ensemble model was obtained by two out of the four training subsets, improving their performances (R₁ = 0.53, R₃ = 0.54) to R = 0.56 on the development set. The rule of maximum value was used to build the ensemble model. The model was assessed on the test set of 100 protein–peptide complexes initially hold-out from the data extracted from the Biolip database (Supporting Information Figure SI-6). Here, we compared the results of our method with state-of-the-art protein–protein and protein–ligand BA predictors. The considered tools include Kdeep and RF-Score for protein–ligand complexes, as well as the above-presented PRODIGY, DFIRE, and CP_PIE methods. ISLAND requires a minimum size of 20 amino acids for each protein sequence. For this reason, the tool was applied to the assessment of only the protein–protein model.

Our protein–peptide affinity model outperformed all the other tools, showing a correlation coefficient of R = 0.55 with MAE = 1.1 kcal/mol (Table 2). The low correlations values delivered by other state-of-the-art tools can be related to the fact that the functions of Kdeep and RF-Score are fitted primarily using small organic ligands.^63,64 This suggests that fitting with mostly small ligand data cannot capture the differences imposed by the larger size of the peptides, as well as the diversity of peptide interactions with the target and the solvent.

Table 2. Correlation Coefficient (R) of Protein–Protein and Protein–Ligand BA Predictors on the Test Set of 100 Protein–Peptide Complexes^a.

method	R	MAE (kcal/mol)
PRODIGY	0.13	1.9
DFIRE	0.29	8.7
CP_PIE	–0.28	9.0
Kdeep*	0.32	10.7
RF-Score*	0.23	1.8
PPI-Affinity	0.55	1.1

^aProtein–ligand methods are marked with a star. The negative values of the correlation coefficients indicate that the corresponding method predicts unbinding free energy.

Case Study I: Ranking the Affinity of Mutants of EPI-X4

EPI-X4 (Endogenous Peptide Inhibitor of CXCR4) is a fragment of albumin identified as an endogenous antagonist of the CXC chemokine receptor 4 (CXCR4) by Zirafi et al.⁶⁵ Given the implication of CXCR4 in viral (HIV) infection, inflammation and cancer,^66,67 this peptide represents a highly promising scaffold to develop therapeutic drugs targeting the CXCR4 receptor.

Recently, mutants of EPI-X4 have been screened to identify derivatives with enhanced stability and affinity. For this, the affinity values (in terms of IC₅₀ nanomolar, nM) of EPI-X4 and 56 derivatives to CXCR4 were estimated using an antibody competition assay.⁶⁷ The scheme of this assay is based on the competitive binding of a fluorescently labeled anti-CXCR4 antibody (clone 12G5) with CXCR4 ligands (Supporting Information Section SI-6).⁶⁷ These derivatives are peptides with size in the range of 6–16 amino acids. From the experiments, 26 mutants out of 30 active (IC₅₀ < 10 000nM) derivatives were found to be more active compared to EPI-X4. Here, we employed these data to evaluate the ranking power of our protein–peptide affinity model. For doing this, we use the enrichment factor (EF_I),⁶⁸ defined as (eq 3):

3

where I represents a fixed number of top-ranked instances based on predicted values; N_active^top_i is the number of active peptides, within the top I instances of the dataset; N_active is the number of active peptides; and N_total is the total number of peptides in the whole dataset. Peptides with IC₅₀ < 10 000 nM were defined as active for an initial test. In a second and more stringent evaluation, the active peptides were considered as those more active than EPI-X4.

The structures of the complexes, formed by CXCR4 and each peptide mutant, were generated via homology modeling using as a template the structural model of the complex CXCR4/EPI-X4, reported by Sokkar et al.^69,70 We estimated the BA of each complex with different predictors, as well as the associated enrichment factors.

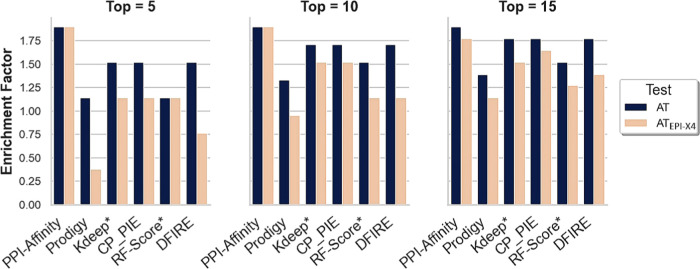
Figure 4 shows the results of the tests corresponding to (1) the conventional activity test using the activity threshold determined by the competition assay (IC₅₀ = 10 000 nM) and (2) the peptides with an affinity higher than EPI-X4. PPI-Affinity achieved the maximum enrichment EF₅ = EF₁₀ = EF₁₅ = 1.9 for this test, i.e., the 15 top-ranked instances according to the PPI-Affinity estimation are active. In the case of the stringent test, taking only those with higher affinity than EPI-X4 as active, the maximum EF was obtained within the top 10 peptides, i.e., EF₅ = EF₁₀ = 1.9, while the enrichment within the top 15 derivatives also reached a high value EF₁₅ = 1.8. The high enrichment factor within the top 5, 10, and 15 peptides, representing more than 25% of the dataset, evidenced the remarkable ranking capabilities of PPI-Affinity. The other tools show moderate to high enrichment values although below the level reached by PPI-Affinity (Figure 4). Noteworthy are CP_PIE and Kdeep, which deliver a steady high performance in the different tests.

Figure 4.

Performance of protein–protein and protein–ligand BA predictors on the set of 56 derivatives of EPI-X4. The performance of the methods is based on the enrichment factor (EF) obtained among the top 5, 10, and 15 ranked candidates. Two results are shown per tool, one corresponding to the activity test (AT), and the second corresponding to the peptides with an affinity higher than EPI-X4 (AT_EPI-X4).

Case Study II: Ranking the Affinity of Peptides for the PDZ Domains of HtrAs

High-temperature requirement serine proteases (HtrAs) are involved in many physiological processes and neurodegenerative diseases such as Alzheimer’s disease and CARASIL.⁷¹ These proteases are largely regulated by an allosteric mechanism whose initial step is the interaction of polypeptide chains with the peripheric PDZ domain. Here, we challenged PPI-Affinity with a series of peptides bound to PDZ domains of two human HtrAs: HTRA1 and HTRA3.

For these sets of protein–peptide interactions, we compared the relative ranking based on the binding affinity predicted by PPI-Affinity to the ranking based on the experimentally determined IC₅₀ values⁷² (Tables 3 and 4).

Table 3. Ranking of BA of Protein–Peptide Interactions in HTRA1 as Predicted by PPI-Affinity and Based on the Experimental IC₅₀ Values^c.

PPI-Affinity		experimental
ranking	ΔG (kcal/mol)	ranking	(IC50 (μM))a
(1) DSAIWWV	–8.8	(1) DSRIWWV	0.9 ± 0.1
(2) GWKTWIL	–8.5	(2) DARIWWV	1.3 ± 0.1
(3) WDKIWHV	–8.2	(3) DSAIWWV	2.5 ± 0.4
(4) DSRIWWV	–8.1	(4) WDKIWHV	2.8 ± 0.3
(5) DARIWWV	–8.0	(5) ASRIWWV	2.8 ± 0.3
(6) ASRIWWV	–8.0	(6) DSRIWWA	3.5 ± 0.9
(7) DIETWLL	–7.8	(7) DSRIWAV	6 ± 1
(8) DSRIWWA	–7.3	(8) GWKTWIL	7.7 ± 0.6
(9) DSRAWWV	–7.3	(9) DSRAWWV	13 ± 1
(10) DSRIWAV	–7.2	(10) DIGPVCFL	16 ± 3
(11) DIGPVCFLb	–7.1	(11) DIETWLL	23 ± 3
(12) EVKIMVVb	–7.0	(12) EVKIMVV	24 ± 8
(13) DSRIAWV	–6.9	(13) DSRIAWV	40 ± 5

^aValues taken from ref (72).

^bProtein–peptide structures that are at the border of the applicability domain of PPI-Affinity.

^cNo protein–peptide structure is outside the applicability domain.

Table 4. Ranking of BA of Protein–Peptide Interactions in HTRA3 as Predicted by PPI-Affinity and Based on the Experimental IC₅₀ Values.

PPI-Affinity		experimental
ranking	ΔG (kcal/mol)	ranking	(IC50 (μM))a
(1) FGAWVc	–7.7	(1) FGRWV	0.6 ± 0.1
(2) FGRWVb	–7.5	(2) RSWWV	0.6 ± 0.1
(3) FGRWIc	–7.5	(3) FGAWVb	0.9 ± 0.1
(4) RSWWV	–7.4	(4) FGRWIb	1.0 ± 0.1
(5) FGRWFc	–7.3	(5) GRWV	1.0 ± 0.1
(6) GRWVb	–7.2	(6) FARWVb	1.1 ± 0.2
(7) FGRWAb	–7.1	(7) RWV	1.3 ± 0.1
(8) FGRAVb	–6.9	(8) FGRWL	2.9 ± 0.3
(9) FGRWLb	–6.6	(9) FGRWA	3.5 ± 0.3
(10) WVc	–6.6	(10) WVb	4.7 ± 0.4
(11) WAc	–6.5	(11) FGRWFb	7.7 ± 0.8
(12) FARWVc	–6.4	(12) WAb	14 ± 1
(13) WGc	–6.2	(13) WGb	22 ± 3
(14) RWVb	–5.2	(14) FGRAV	270 ± 110

^aValues from ref (72).

^bProtein–peptide structures are at the border of the applicability domain of PPI-Affinity.

^cProtein–peptide structures that are outside the applicability domain of PPI-Affinity.

The prediction of PPI-Affinity suggests that three of the peptides have more affinity for the PDZ domain of HTRA1 than the experimentally determined best binder DSRIWWV (in bold, Table 3). However, the calculated binding affinities of those peptides differ from that of DSRIWWV by only 0.1, 0.4, and 0.7 kcal/mol (for WDKIWHV, GWKTWIL, and DSAIWWV, respectively). These differences are very small and within the MAE of PPI-Affinity (Table 2).

The rest of the peptides are correctly predicted by the method as weaker binders than DSRIWWV to the PDZ domain of HTRA1. We note, however, that the binding energy differences for most of these peptides also fall within the MAE reported for our method based on the test set of protein–peptide affinity (Table 3).

Interestingly, even the two peptides (DIGPVCFL and EVKIMVV) at the border of the applicability domain of our method are correctly predicted as weaker binders to the PDZ domain of HTRA1 compared to DSRIWWV. Nevertheless, the predicted values for peptides that are outside the applicability domain of PPI-Affinity should be considered with care. The K_d of the complex between HTRA1 and DSRIWWV is experimentally reported as 1.3 ± 0.2 μM, which corresponds to ΔG = −8.2 ± 0.1 kcal/mol at the experimental temperature of 301.15 K. This value is in excellent agreement with the value of −8.1 kcal/mol predicted by PPI-Affinity (Table 3).

We also tested our method on peptides binding to the PDZ domain of HTRA3 (Table 4). In this set of protein–peptide complexes, eight systems are outside the applicability domain of PPI-Affinity.

As shown in Table 4, only one peptide (FGAWV) is incorrectly predicted to have better BA for HTRA3 than the best experimental binder FGRWV. We note that FGRWV lies outside the applicability domain of the model, and this prediction should be taken with caution.

In addition, we measured the overall ranking power of PPI-Affinity by calculating Kendall’s correlation coefficient⁷³ on both test sets, HTRA1 and HTRA3 protein–peptide complexes (Table 5). The results obtained with PRODIGY, Kdeep, RF-Score, DFIRE, and CP_PIE are also shown for comparison. The binding affinity values delivered by each tool are listed in Supporting Information Section SI-7.

Table 5. Correlation of IC₅₀ Values with the Estimations from PPI-Affinity and Other State-of-the-Art BA Predictors on the Sets of HTRA1’s and HTRA3’s PDZ Binders.

	R		τ
method	HTRA1	HTRA3	HTRA1	HTRA3
PRODIGY	0.25	0.29	0.18	0.01
DFIRE	0.59	0.24	0.38	0.15
CP_PIE	–0.11	–0.03	–0.25	–0.08
Kdeep*	0.38	0.11	0.16	0.41
RF-Score*	0.56	0.13	0.56	0.27
PPI-Affinity	0.63	0.02	0.59	0.42

Kendall’s tau coefficient is a robust nonparametric measure highly suitable to discriminate correlated from uncorrelated variables. This measure involves two main magnitudes: the number of concordant and discordant pairs. Two observations (x_i, y_i) and (x_j, y_j) are classified as a concordant pair if x_i > x_j, and y_i > y_j, or vice versa x_i < x_j and y_i < y_j. If none of these conditions are true, the pair is known as discordant.

The Kendall’s tau correlation coefficient (τ) is defined as (eq 4)

4

where N_c and N_d are the number of concordant and discordant pairs, respectively; N_t is the number of ties in the order of the binding affinity determined by PPI-Affinity; and N_u is the number of ties in the experimental binding affinity. The Kendall’s correlation coefficient is equal to 1 if the calculated ranking of the peptides completely agrees with the ranking determined experimentally.

Importantly, here we correlate IC₅₀ values with predicted binding free energy changes; these magnitudes are expected to be linked by a nonlinear relation, which then violates the linearity requirement for the proper interpretation of Pearson’s correlation coefficient. Besides, the small size of the data induces violations of the bivariate normality requisite of this coefficient. Consequently, the use of a robust nonparametric measure such as Kendall’s tau coefficient is a requirement to achieve a correct interpretation of the correlation tests.

The Pearson’s correlation coefficient obtained by PPI-Affinity (R = 0.02) in the HTRA3 test set evidences the lack of correlation with the experimentally measured IC₅₀ values. Beyond the previously noted shortcomings of Pearson’s coefficient to assess these data, this result can be also a consequence of half of the peptides in the test set being outside the applicability domain of PPI-Affinity. For HTRA1 binders, where all cases are within the applicability domain, PPI-Affinity delivers the highest correlation coefficient value (R = 0.63).

In terms of Kendall’s tau coefficient, PPI-Affinity produces the highest values for both targets (τ = 0.59 and τ = 0.42 for HTRA1 and HTRA3, respectively), evidencing its better ranking power compared to other state-of-the-art predictors. Interestingly, RF-Score gives the second-best performance on the HTRA1 test set with τ = 0.56, which is diminished by about half on the HTRA3 test set (τ = 0.27). Conversely, Kdeep’s performance is close to PPI-Affinity’s on the HTRA3 test set (τ = 0.41), but Kdeep delivers the lowest positive Kendall’s tau value on the HTRA1 test set (τ = 0.16). The weak performance of PRODIGY on both test sets might be related to the limitations of its protein–protein affinity predictor to evaluate smaller protein–peptide complexes. An important advantage of PPI-Affinity is that, thanks to two tailored models for protein–protein and protein–peptide complexes, PPI-Affinity can deliver comparable performance levels for both types of biomolecular systems.

In short, the evaluation of BA predictors on different tests and test sets evidenced that state-of-the-art BA predictors, either intended for protein–protein or protein–ligand complexes, deliver low accuracy in the prediction of the BA of protein–peptide complexes. Although it improves the accuracy of the state-of-the-art approaches only slightly, PPI-Affinity is a solution to that issue since it delivers a significantly better and robust performance among different tests. This fact tackles the inherent issues in generalization and overfitting that apparently affect other predictors. The shortcomings in the accuracy of predictions of absolute binding free energy values are to a large extent a consequence of the inherent deviations in the experimental data available for training, which arise from uneven standards under the experimental conditions and measurement procedures. Nonetheless, within such a noisy scenario, the support vector machine models developed by us allow making predictions that improve to some extent the state of the art at the same time of showing steady performance in both absolute binding affinity prediction and ranking assessments.

Web Server Implementation

We implemented PPI-Affinity as a web server to facilitate the use of our models. PPI-Affinity is a suite organized in three modules, which are summarized below by order of increasing complexity of their functionality.

Binding Affinity Predictor

This method is the direct application of the prediction models in a set of PDB files with protein–protein and protein–peptide complexes that should be provided by the users. The module has the functionality to characterize diverse complexes, whose structures were obtained from external sources, based on their binding affinity.

Build & Predict

This module follows the same purpose as the previous one. However, instead of receiving coordinate files with the complexes of interest, it only requires a template file (in PDB format) and a list of amino acid sequences (in FASTA format). Then, the server builds five structural homology models for each sequence in the list, using MODELLER, and selects the structure with the lowest DOPE as the best candidate to represent the complex. Subsequently, it scores all the complexes using the predictor of binding affinity. The Build & Predict module is particularly suitable for screening structurally similar complexes for which no structure has been elucidated.

Protein Engineering

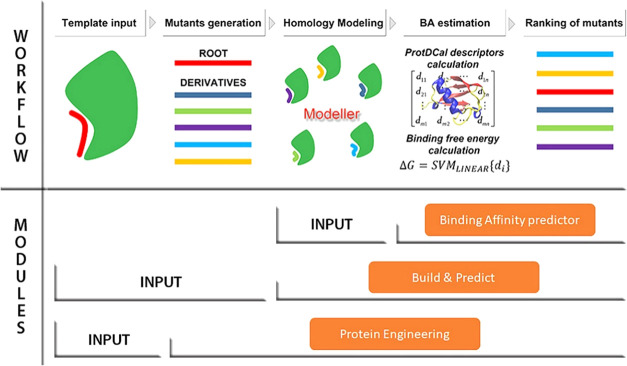
This third and most comprehensive module allows for the automatic generation and scoring of mutations at the interface of the complexes, which aims to optimize the affinity of these complexes. Figure 5 depicts the workflow of the module, which encompasses the next steps:

Figure 5.

Workflow of the three modules included in PPI-Affinity. For each module, the required input data and associated steps are indicated. The main difference among them lies in the input data: the Binding Affinity predictor module receives as input a set of protein–protein/peptide complexes (in PDB format); the Build & Predict module generates the complexes from a template file and a list of amino acid sequences (in FASTA format) provided by the user; and the Protein Engineering module receives as input only a template model, generates a list of derivatives for one of the protein/peptide contained in the PDB file, and calculates homology models for all created mutants. Regardless of the module, once the PDB files have been prepared, PPI-Affinity computes the structural descriptors with ProtDCal, estimates the BA values with the machine learning models, and returns the list of derivatives ranked by their BA values.

Step 1: Template Input

The user provides an input structure of the complex (in PDB format) and optionally the amino acid sequences of the chains in FASTA format. In addition, the user must specify which chain will be optimized.

Step 2: Mutants Generation

Next, a maximum of 10 000 derivatives is constructed for the specified chain. The generation of mutants is controlled by the following parameters: the maximum number of modifications to the reference sequence, deletion and mutation probabilities, maximum molecular weight, type of mutations, and a mutability vector whose elements take value 0 for residues that remain unmodified and a value between 0 and 1 representing the probability of modifying each position. The types of mutations are defined by groups of amino acids; the types are “Conservative” formed by the groups Polar (NCQHSTG), Acid (DE), Basic (KR), Non-polar (AILMPV), and Aromatic (WYF) residues; “Conservative extended” for Polar extended (NCQHSTGDEKR) and Non-polar extended (AILMPVWYF) residues; and “Unrestrained” allows the residues to be changed by any other type of residue.

Step 3: Homology Modeling

In this step, five structural models per derivative are generated with MODELLER. Among them, the structure with the lowest DOPE value is selected as the best model for the corresponding mutant.

Step 4: BA Estimation

The binding free energy is calculated using either the protein–protein or the protein–peptide affinity predictor. The selection of the estimator depends on the lengths of the chains in the structure; if a chain contains less than 30 residues, the protein–peptide predictor is used, otherwise the protein–protein estimator is applied.

Step 5: Ranking of Mutants

Finally, the mutants will be arranged in decreasing or increasing order of affinity, and either all or a selection of top candidates are returned to the user. The two sorting schemes allow the use of this module not only as an optimizer of the complex but also to spot mutations that can largely destabilize the complex of interest.

Applicability Domain

Defining the applicability domain (AD) of a model is an important step before the deployment of a predictor as it allows to provide insights into the reliability of the estimations in new systems.⁷⁴ Here, the AD is the subspace defined by the value range of the variables of the models (structural descriptors) in our training dataset (Supporting Information Tables SI-7 and SI-8). Thus, the descriptors’ value of a new complex is checked to determine whether this structure is within the AD of the model. The result of this analysis is provided to the users alongside the predicted binding affinity value. Estimations associated with instances outside the AD should be interpreted with special care and probably corroborated by other methods. Additionally, Supporting Information Table SI-9 summarizes the sizes of the peptides and receptors used to train and test the protein–peptide model. Supporting Information Tables SI-10 and SI-11 present the descriptive statistics of the training, development, and test sets used in the modeling.

Implementation Details

The frontend of PPI-Affinity was implemented with the Python Framework Django v3.1.1 for uploading and validating the user data. The backend, which constitutes the core of the program, was programmed in Python 3. Internally, PPI-Affinity uses MODELLER³⁷⁻⁴⁰ to create the new homology structures. ProtDCal⁴² is used to calculate the structural descriptors required by the SVM models, and Weka 3.8.4⁵² is the interpreter of these predictors to predict the binding free energy of the generated structures. Finally, a queuing system is employed for the management of the jobs sent by the users.

Conclusions

We developed PPI-Affinity, a binding free energy predictor targeting protein–protein and protein–peptide complexes specifically. This fast-screening tool moderately outperformed the predictions and ranking power of similar empirical predictors. The performance of the models was evaluated on various test sets, which include a largely used benchmark set for empirical binding free energy predictors and scoring functions, as well as new augmented datasets gathered in this work from BioLip and PDBbind. We also evaluated the ranking power of the protein–peptide model on a set of EPI-X4 derivatives and HtrAs peptide binders. Altogether, these tests highlight PPI-Affinity, not only as a top-ranked predictor but also as the most robust tool with respect to performance in different tests.

Furthermore, we implemented our models in a freely available web server that incorporates diverse functionalities that allow the screening of protein complexes as well as the engineering of the amino acid composition at the interface of the complex, to enhance the binding affinity or to spotlight critical mutants that may destabilize the interaction. The PPI-Affinity web server is thus a versatile tool with a direct impact on the design of peptide binders as well as in protein engineering and design.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jproteome.2c00020.

• Setup of parameters used for the calculation of the structural descriptors (Supporting Information Section SI-1); preliminary study of Machine Learning (ML) techniques (Supporting Information Section SI-2); feature selection process for the protein–protein BA modeling (Supporting Information Section SI-3); feature selection process for the protein–peptide BA modeling (Supporting Information Section SI-4); evaluation of PPI-Affinity and a state-of-the-art classifier (Supporting Information Section SI-5); assays used to determine the BA of EPI-X4 derivatives against the CRCX4 receptor (Supporting Information Section SI-6); generation and ranking of peptide binders to the PDZ domains of HTRA1 and HTRA3 (Supporting Information Section SI-7); tabular description of PPI-Affinity and other state-of-the-art PPI prediction tools (Supporting Information Table SI-1); correlation coefficient (R) of BA predictors on the test set of 100 protein–peptide complexes (Supporting Information Table SI-2); performance of intermediate models for the protein–protein BA modeling during the hyperparameters tuning process (Supporting Information Table SI-3); performance of individual and ensemble models for the protein–protein complexes (Supporting Information Table SI-4); performance of the intermediate models for the protein–peptide modeling during the hyperparameters tuning process (Supporting Information Table SI-5); performance of individual and ensemble models for the protein–peptide complexes (Supporting Information Table SI-6); applicability domain of the protein–protein model (Supporting Information Table SI-7); applicability domain of the protein–peptide model (Supporting Information Table SI-8); minimum and maximum values of the sequences’ length of peptides and proteins (Supporting Information Table SI-9); descriptive statistics of the protein–protein data sets (Supporting Information Table SI-10); descriptive statistics of the protein–peptide data sets (Supporting Information Table SI-11); distribution of ΔG bind values in the dataset of protein–protein complexes (Supporting Information Figure SI-1); distribution of ΔG bind values in the datasets of the protein–protein ensemble model (Supporting Information Figure SI-2); characterization of the dataset of protein–peptide complexes (Supporting Information Figure SI-3); distribution of ΔG bind values in the datasets of the protein–peptide ensemble model (Supporting Information Figure SI-4); plots of experimental vs predicted on the test sets of protein–protein BA data (Supporting Information Figure SI-5); plot of experimental vs predicted on the test set of protein–peptide BA data (Supporting Information Figure SI-6) (PDF)

• Python script used to randomly split the datasets into training, development, and test subsets (Script SI-1); configuration file for ProtDCal to compute the descriptors of the protein–protein model (File SI-1); configuration file for ProtDCal to compute the descriptors of the protein–peptide model (File SI-2); binding affinity predictions of PPI-Affinity and state-of-the-art tools on the benchmark of 79 protein–protein complexes employed by Vangone and Bonvin²¹ (File SI-3); binding affinity predictions of PPI-Affinity and state-of-the-art tools on the hold-out set of 90 protein–protein complexes taken from PDBbind (v.2020) (File SI-4); binding affinity predictions of PPI-Affinity and state-of-the-art tools on the hold-out set of 177 (26 wild-type and 151 mutants) protein–protein complexes taken from the SKEMPI v2.0 dataset (File SI-5); binding affinity predictions of PPI-Affinity and state-of-the-art tools on the hold-out set of 100 protein–peptide complexes taken from the Biolip database (File SI-6); binding affinity predictions of PPI-Affinity and other state-of-the-art tools on the test set of protein–peptide complexes containing EPI-X4 and 56 derivatives coupled to the CXCR4 receptor (File SI-7); and summary of the protein–protein and protein–peptide complexes used in the training, validation, and test of the PPI-Affinity models (File SI-8) (ZIP)

Author Contributions

S.R.-M., Y.B.R.-B., and E.S.-G. designed the project. S.R.-M. implemented the codes, performed the machine learning analyses and part of the validation tests, and built the webserver. J.M.-P. carried out the HtrAs validation tests. Y.B.R.-B. and E.S.-G. supervised the modeling and implementation of the method. S.R.-M., J.M.-P., Y.B.R.-B., and E.S.-G. wrote the manuscript. M.H. carried out the antibody competition assays. J.M. supervised the experiments and the synthesis of the peptides, and both, J.M. and M.H., contributed to the analysis of the experimental data. M.E. contributed HtrAs expertise. All authors contributed to revising and editing the manuscript. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.