Characterization of wax valving and μPIV analysis of microscale flow in paper-fluidic devices for improved modeling and design

Abstract

Paper-fluidic devices are a popular platform for point-of-care diagnostics due to their low cost, ease of use, and equipment-free detection of target molecules. They are limited, however, by their lack of sensitivity and inability to incorporate more complex processes, such as nucleic acid amplification or enzymatic signal enhancement. To address these limitations, various valves have previously been implemented in paper-fluidic devices to control fluid obstruction and release. However, incorporation of valves into new devices is a highly iterative, time-intensive process due to limited experimental data describing the microscale flow that drives the biophysical reactions in the assay. In this paper, we tested and modeled different geometries of thermally actuated valves to investigate how they can be more easily implemented in an LFIA with precise control of actuation time, flow rate, and flow pattern. We demonstrate that bulk flow measurements alone cannot estimate the highly variable microscale properties and effects on LFIA signal development. To further quantify the microfluidic properties of paper-fluidic devices, micro-particle image velocimetry was used to quantify fluorescent nanoparticle flow through the membranes and demonstrated divergent properties from bulk flow that may explain additional variability in LFIA signal generation. Altogether, we demonstrate that a more robust characterization of paper-fluidic devices can permit fine-tuning of parameters for precise automation of multi-step assays and inform analytical models for more efficient design.

INTRODUCTION

Paper-fluidic assays are an extensively used platform for point-of-care diagnostics due to their straightforward and low-cost implementation in remote and resource-limited settings.¹ Capillary action through fibrous and porous membranes draws a deposited sample through the matrix for colorimetric analysis, circumventing the pumps typically required for small-molecule detection.² In some lateral flow immunoassays (LFIAs), for example, analytes in the sample bind to nanoparticles via detection antibodies, flow along the membrane channel, and are captured at test and control regions downstream, resulting in colorimetric signal generation. This equipment-free analysis makes paper-fluidic devices an ideal platform for the rapid screening of a broad spectrum of environmental and biological analytes.³

Sensitive detection in a porous membrane requires sufficient reaction time between the analyte in the sample and reagents, which is difficult to achieve as timing is dictated by capillary flow rate.⁴ LFIAs and other paper-fluidic devices are painstakingly engineered and optimized through a lengthy trial-and-error process for each analyte of interest.⁵ Furthermore, many forms of biomolecule detection require more complex processes that cannot be integrated in a simple LFIA, such as nucleic acid amplification or chemical signal enhancement. Emerging assays have successfully incorporated such processes into paper-fluidic platforms, including enzymatic and catalytic signal amplification^6-8, polymerization-based signal amplification^9-11, isothermal nucleic acid amplification systems^12-16, and CRISPR/Cas systems for nucleic acid detection^17-19; however, most require multiple precisely timed user steps, complicating their implementation at the point of care.

There is great potential for paper-fluidic devices to be significantly improved through designs that permit the incorporation of more complex reactions while minimizing additional user steps. LFIAs have been re-engineered to include sample flow redirections and delay elements generated by elaborate geometries^20,21, additional materials such as absorbent pads²², stacked films with different reagents²³, sugar, surfactant, or protein surface modifications^24-27, and wax²⁸. These additions have improved sensitivity, specificity, and breadth of analyte targets over original LFIA designs. Previously, thermally-actuated wax valves were demonstrated to offer complete, timed-control of fluid obstruction and release in an LFIA, permitting multiple reactions within self-contained devices^29,30. However, there can be high variability in the mean flow downstream of the wax, requiring iterative optimization based on assay conditions.

Developing and optimizing any paper-fluidic device, especially with more complex delay components as described above, is a complicated and highly-iterative process comprising many experiments to identify the best conditions for each sample and assay type.³¹ Mathematical modeling can minimize time-intensive experimentation by using fundamental transport principles to inform LFIA design.³² One such model by Berli et al. simulates analyte dynamics by defining dimensionless numbers describing relative flow rate and analyte concentration.³³ Other models validate mathematical predictions with experimental data. For example, Liang and colleagues experimentally investigated pre-mixed and sequentially-added reagents on an LFIA for malaria detection, using those results to validate a COMSOL model to explain how different binding kinetics yielded different results.³⁴ Notably, Gasperino and colleagues combined mathematical descriptions of fluid behavior in porous membranes, including the Lucas-Washburn Equation, Darcy’s Law, and the Richards Equation, to model the detection of a malaria antigen in an LFIA. This model was validated against physical LFIAs with different antigen concentrations and used to develop a software basing LFIA design decisions on fifteen reaction scheme hypotheses.⁴

Despite these advances, the models described previously are limited by their exclusive treatment of bulk behavior and neglect of experimental data analyzing sample flow through the porous membrane at the micro/nanoscale. Micro-particle image velocimetry (μPIV)³⁵ can visualize and quantify particle transport within paper membranes, in turn improving existing models and validating assumptions of membrane homogeneity, laminar flow and binding kinetics. In fields outside biomedical diagnostics, μPIV has been used to provide parameters for modeling solute transport in porous media and expand existing particle transport models^36-40; in work directly relevant to paper-fluidic diagnostics, μPIV was used to demonstrate the reduced speed of magnetic particles flowing in modeled LFIAs.⁴¹ Further implementation of μPIV could provide unique insight into the microscale flow in paper-fluidic devices to validate fluid delay mechanisms and elucidate in-flow binding properties.

Here, we demonstrate robust experimental and computational analyses to determine the optimal thermally-actuated wax valve geometries for precise fluid delay and rapid delivery upon actuation. We investigate the factors contributing to unusual parabolic flow profiles past heated valves using scanning electron microscopy and computational modeling. We examine mathematical explanations of these flow profiles using basic fluid flow assumptions and equations fit to experimental data in MATLAB. We also use a COMSOL model to investigate the hypothesis that flow velocities past the valves vary due to temperature heterogeneity across the wax. Further, we develop a novel method for imaging and evaluating microscopic particle flow in paper membranes using μPIV to investigate the relationship between macroscopic and microscopic flow. Finally, we discuss how these analytical and mathematical data can be combined to inform efficient design of future paper-fluidic devices.

MATERIALS AND METHODS

Test strip construction

Test strips were constructed by adhering a SelfSeal laminating sheet (3M) to one face of AE99 unbacked nitrocellulose membrane (GE Healthcare). The laminated nitrocellulose was then cut with a razor blade into 35 mm x 5 mm strips.

Macroscopic imaging and analysis

Test strips were placed laminate side down on a piece of double-sided tape (3M) next to a ruler with 0.5 mm increments. A 5 mm x 10 mm glass fiber pad was placed at one end of the test strip. To evaluate flow behavior, 40 μL deionized (DI) water was added to the glass fiber pad and subsequently flowed into the nitrocellulose membrane. While unblocked nitrocellulose and DI water may not be representative of flow rates from a real sample and its biological and chemical components, these conditions were used in these experimental models to control variation between macroscopic and microscopic evaluations. A Samsung S7 phone was placed on top of a 150 mm container and used to record video beginning when water was added to the glass fiber pad and ending when the water reached the opposite end of the nitrocellulose strip.

Videos were converted into a sequence of images with one image for each second of video. These image sequences were loaded into ImageJ, processed to enhance contrast between the water and the paper, and fit with a grid dividing the membrane into five equal areas 1 mm across at the middle and edges of its surface. The location of the fluid front, measured with respect to the ruler adjacent to each test strip, was recorded for each section.

Wax valve analysis

Wax valves were designed in Adobe Illustrator to have straight, concave, and convex geometries, as shown in ESI Scheme S1A. Valves of different geometries were compared across three different equal printed surface areas (2.5 mm², 5 mm², and 10 mm²) to ensure wax volume was a controlled variable. As described in previous work²⁹, valves were printed with solid wax ink onto AE99 nitrocellulose membrane using a Xerox ColorQube 8570. After printing, the membranes were heated for 60 seconds at 80°C in a tabletop oven (VWR) to permit penetration of the ink through the depth of the membrane, closing the valve. Once the valves were closed, the nitrocellulose was cut with a razor blade into 35 mm x 50 mm strips with one complete valve on each strip.

To analyze flow past opening valves in real time, strips with fully closed valves were placed on a 164.3 Ω polyamide thin film heater (Cole-Parmer) and sealed with a laminating sheet to limit fluid evaporation from wetted strips, as shown in ESI Scheme S1B. Forty (40) μL of DI water was manually deposited onto one end of the strip, then the entire strip was heated by applying 2.1A of current to the resistive heater to melt the wax, opening the valves and permitting fluid passage through them. Other work from our group describes how this heating step can be automated through the use of preprogrammed timers and resistive heating incorporated in the device.¹²

The behavior of flow through the valves was evaluated by first characterizing the amount of time for fluid to travel through the valves and then calculating its flow rate through the nitrocellulose past the opened valve. The latter was accomplished by recording and processing videos using the same method described in “Macroscopic Imaging and Analysis”.

Signal intensity improvement with alternative wax valve geometries

A model LFIA of 4 test spots, two each at 10 mm and 15 mm upstream of the valve (ESI Scheme S1C), was fabricated to model a four-segment LFIA with test spots for three different analytes of interest and a control spot. These LFIAs were tested with straight, concave, and convex valves, all of with an area of 5 mm², and a control without a wax valve. Biotinylated goat anti-mouse antibody (Sigma-Aldrich) was prepared as previously described⁴²and deposited at the test zones with a sciFLEXARRAYER S3 (Scienion). Forty (40) μL of streptavidin-coated 150 nm gold nanoshells (nanoComposix) diluted 1:1 in 5% BSA (Sigma-Aldrich) in 1XPBST was added to the sample pad. The valves were actuated by placing the strips on a 70°C heat block. After 10 minutes, the strips were removed from the heat and after 30 minutes, they were scanned on an Epson Perfection V550 scanner. The valves were heated for 10 minutes here to allow the wax to stay in a liquid for long enough that the large 150 nm gold nanoshells can travel through the valves. The strips are left for 30 minutes before scanning because this allows sufficient time for the gold nanoshells to travel down the length of the membrane and form signal. The resulting signal-to-background ratio of the visible signal at the antibody test spots was analyzed using MATLAB (Mathworks).

COMSOL simulation of wax ink valve heating

To characterize the heating of valves, a Multiphysics-based model of valves in porous media partially saturated with liquid water and water vapor was created, as shown in ESI Scheme S2. Evaluations of heated valves were produced using COMSOL Multiphysics 5.4 with the Heat Transfer, CFD, Microfluidics, and Subsurface Flow Modules. The 3D geometry was built in COMSOL; valves domains were created by importing the shapes from Adobe Illustrator. A membrane test strip was modeled as a porous block with a layer (straight valve) or extruded geometry (concave and convex valves) surrounded by a block of dry air. A boundary heat source on the bottom face of the geometry simulated heating from a thin film heater. The sources of heat loss were 1) a convective heat flux with ambient air in laminar flow simplified to only flow in the x-direction and 2) evaporative heat loss based on the model “Evaporation in Porous Media with Large Evaporation Rates”.⁴³ Radiation effects were evaluated but were not included in the final model because they were determined to be negligible compared to convective and evaporative effects (details in ESI). Model parameters are listed in ESI Table S1.

Microscopic imaging

To visualize the microscopic properties of fluid flow within the test strips, 400 nm and 100 nm green fluorescent nanoparticles (ThermoFisher) were imaged as they travelled through a nitrocellulose membrane. To assemble the test strips for microscopic imaging, double-sided tape (3M) was adhered to a glass microscope slide, overlapping the slide by 1 mm on one end and 14 mm on the other end. A 5 mm x 10 mm glass fiber pad (Millipore) was adhered to the 1 mm overhang of the laminating sheet. Next, the paper test strip was placed paper side down with one end overlapping the glass fiber pad by 1 mm and the remaining portion of the strip adhered firmly to the laminate sheet. The arrangement of the sample pad and membrane, particle-containing fluid sample, and microscope field of view is diagrammed in ESI Scheme S3.

To image particle motion within the paper test strip, the glass slide assembly was placed paper side down on the stage of an inverted fluorescent microscope (Zeiss Axio Observer Inverted Microscope) and illuminated with an AlexFluor 488 light. A 40X objective (Plan-Apochromat 40X/0.95 Korr M27-Air, Zeiss) was used to focus on the membrane surface at a region of interest in a 116.22 by 116.22 μm field of view. Forty (40) μL of 0.02% w/v green fluorescent nanoparticles were added to the glass fiber sample pad and then flowed into the nitrocellulose membrane. When the nanoparticles became visible in the selected field of view, a ten second video was captured at 40 frames per second with 2-by-2-pixel binning. To analyze discrepancies in particle velocity along the length of the test strip, videos were taken 5, 10, 15, 20, and 25 mm from the sample pad end of the membrane (n = 3 repetitions of videos for each field of view).

Microscopic Analysis

Micro-particle image velocimetry (μPIV) was used to assess the velocity of particles flowing within the nitrocellulose membrane. Microscope videos were translated from the microscope software format (.czi) to a sequence of bitmap (.bmp) images, with one image per video frame using a MATLAB code. The μPIV software EDPIV (developed by Dr. Lichuan Gui) was used to convert the sequence of .bmp images to a .lis file, which was then loaded into EDPIV as an image group.

Prior to running the μPIV analysis, an “Overlapping –" boundary mask was created over the sequence of images to subtract regions of obstructed flow from the evaluation. This mask removes the background from the image sequence, so background signal is not included in the velocity calculation. After this boundary mask was applied, an EDPIV evaluation was run with a 126 by 128-pixel window size, a 64-by-64-pixel grid size, a 63-pixel searching radius, central difference interrogation, central window shifting, and 4-pixel image correction. The resulting vector field was evaluated as an average function of the entire image set, and each evaluation was run for three iterations. Following completion of this evaluation, the resulting velocity data was interpolated onto a 32-by-32-pixel grid and the evaluation was run again using this data as a starting point to estimate the velocity change more precisely in each window. This process was used to analyze each video. The vector fields from the EDPIV analyses were saved as .dat files for processing in MATLAB, where the vector fields were scaled, plotted, and overlaid with a composite image of all the video frames to visualize the flow described by the vectors.

Statistical Analysis

Statistical analysis was performed with GraphPad Prism. ANOVA was used to determine the statistical significance of valve opening times, flow rates, and LFIA signal intensity data.

RESULTS AND DISCUSSION

We used computational and experimental methods to determine how valve geometry influences fluid traveling through a nitrocellulose membrane with multiple stages separated by wax valves. These methods are underpinned by assumptions that liquid and particles would flow freely through nitrocellulose membrane and would be completely obstructed upon reaching a wax valve (as confirmed in ESI Figure S1), These analyses showed that both valve actuation, the amount of time between when the resistive heater is turned on and when fluid first begins to flow through the valve, and the rate of fluid flow past actuated valves were significantly affected by valve surface area and geometry.

Valve actuation

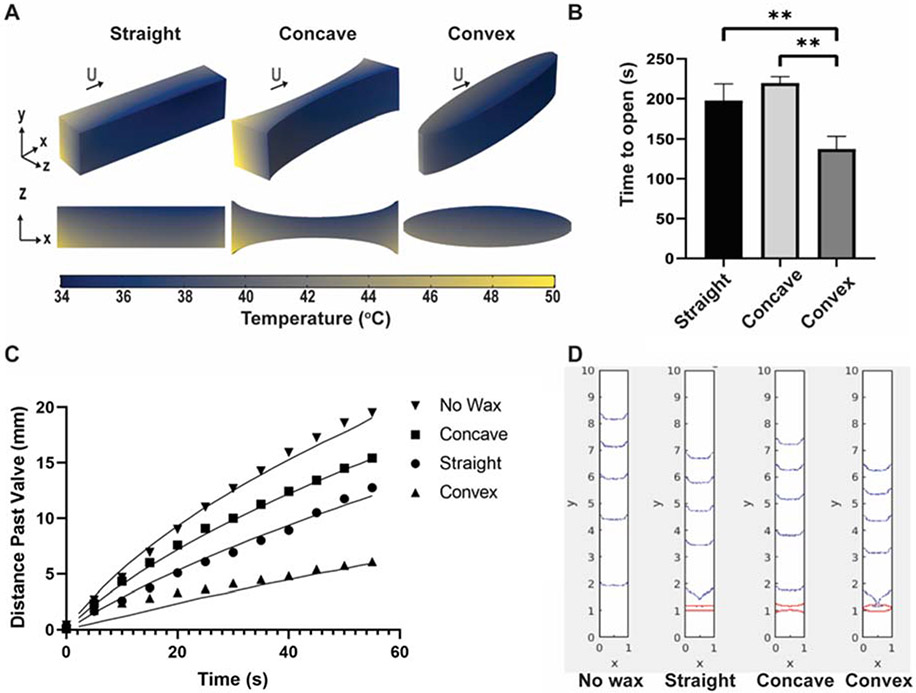
As illustrated in Figure 1A, the temperature is several degrees warmer on the bottom face of the valve than on the top face of the valve. This temperature difference is consistent with previous experimental results in which liquid tended to flow through and past the valves faster along the bottom face of the membrane rather than along the top face of the membrane.²⁹ The lower density of wax along the bottom face of the valve (ESI Figure S2) likely provides less resistance to fluid passage. If the temperature is also higher at the bottom face, as the COMSOL results indicate, then more wax on the bottom face would be melted and similarly permit fluid passage. These effects combined can explain the greater flow along the bottom face of the membrane.

Figure 1:

(A) Computational model of heat distribution with varying valve geometries of constant volume (0.005 cm³). After 120 seconds of simulated heating of the model, there is a several-degree temperature gradient through the depth and length of linear, convex, and concave shaped valves when convective and evaporative heat losses are included in the COMSOL model. (B) Experimental actuation time of valves with surface area = 5 mm² of different geometries (n = 3 and error bars represent standard deviation. ** indicate p < 0.01 determined by ANOVA. (C) Experimental rate of fluid flow past 5 mm² valves of different geometries and flow in unobstructed nitrocellulose (data points) compared to computational model data (solid lines). An extended version of the experimental data only with error bars is available in Figure S5B. D. Visualization of computational model of flow pattern along nitrocellulose membrane at equally spaced time points past valves of different geometries.

ESI Figure S3 investigates the effects of convective heat transfer and evaporative heat loss on temperature at the middle and edges of different valve geometries of equal surface area. As the time to open a valve is influenced by the width of that valve (ESI Figure S4), the temperature was plotted at the thinnest upstream region of the simulated valves (i.e. the edge of a linear and a convex valve and the middle of the concave valve). Previous work has demonstrated that in straight valves, fluid is observed to flow through the edges of the valve first.²⁹ Therefore, it follows that convex valves, which are thinner at the edges of the test strip than straight or concave valves, would actuate fastest and a concave valve would take the longest to open. Indeed, experimental data in Figure 1B confirm this model. Comparing valves of equal surface area (5 mm²), convex valves result in the shortest average actuation time when compared to straight and concave valves of the same surface area.

Macroscopic flow analysis

In addition to actuation time, we hypothesized that the flow rate of fluid past the valve will have a large effect on reactions downstream. We performed macroscopic experimental analyses to evaluate the relationship between valve geometry and fluid flow rate past actuated valves. Figure 1C compares the distance traveled by fluid past straight, concave, and convex valves with equal two-dimensional printed surface areas of 5 mm². With all valves, fluid traveled slower than it would through unobstructed nitrocellulose, but concave valves clearly resulted in the fastest fluid flow of all the valves, straight valves resulted in intermediate fluid flow, and convex valves resulted in the slowest fluid flow. The tunable range in flow rate varies with distance; at 5 mm upstream of the valve is between approximately 0.12 and 0.47 mm/s, as shown in Figure 1C. Extended flow data, along with error bars indicating the precision in terms of the standard error of the mean, is shown in ESI Figure S5.

In many preliminary experiments investigating macroscopic fluid flow, the shape of the fluid front was observed to vary greatly across the width of the test strip. For example, the fluid at the edges of the strip would advance faster than the fluid in the middle of the test strip. This pattern, observed with fluid traveling through unobstructed nitrocellulose and sometimes with fluid traveling past a valve, contradicts the expectations of traditional laminar pipe flow which follows a parabolic profile fastest in the middle of the test strip.⁴⁴ Experimental data showing variation in flow rate across the width of the test strip following different valve geometries of equal surface area can be found in the supplemental data (ESI Figure S6). With straight valves, there was no statistically significant difference in the distance traveled by the fluid front across the width of the test strip, but a large amount of variation was present between the trials, likely due to different and uneven fluid fronts in each individual trial. Concave valves resulted in both the most even fluid front and the smallest standard error in fluid front distance at each time point. Finally, within the first minute of flow past convex valves, a largely uneven flow front was observed; however, flow rates converge as the front fully develops with more time (after 90 seconds, data not shown). Our COMSOL model incorporating both evaporative and convective sources of heat loss also demonstrated that the difference between the edge and middle of a concave valve is approximately half that of a convex valve (2°C and 4°C, respectively). The lower variability in the model would indicate a more even flow front in the concave valve upon actuation than the flow front of a convex valve.

Due to the variation in the shape of the fluid front observed during experimental analysis, a MATLAB model was developed to further characterize macroscopic fluid flow in the nitrocellulose membrane and the effect of valve geometry on fluid front shape, and to compare our theoretical characterization to experimental observations.

To create a mathematical model describing the observed differences in fluid front flow rates and patterns, the Richards equation was applied to the porous membrane system to describe partially saturated flow:

$$\frac{\partial \theta }{\partial t}=\frac{\partial }{\partial x}\left(D(\theta )\frac{\partial \theta }{\partial x}\right)+\frac{\partial }{\partial y}\left(D(\theta )\frac{\partial \theta }{\partial y}\right),$$

where ϑ is the volumetric content of liquid in the membrane, D(ϑ) is the equivalent diffusivity, and x and y are two dimensions of the nitrocellulose membrane. Further details describing the mathematical model of fluid flow are described in the ESI.

In systems that included wax valves, the presence of wax changed both the porosity and permeability of the nitrocellulose membrane. When wax is heated, the phase changes gradually, and it flows through the membrane like a viscous liquid, as can be described by the Lucas-Washburn equation. Due to the boundary effect of heat conduction, different wax valve geometries resulted in a different melting ratio at each point of the valve. Experimental observations suggested that the wax may only need to fully melt across a small portion of the valve to permit fluid flow in certain regions such as the edge of the membrane or the narrow region in the center of the concave valve. Considering these observations, the diffusivity was modified for each geometry with respect to the measured data:

$$D_i=D^{\prime }(\theta )+F_i(x),$$

where F_i(x) is dependent on the change of permeability in the wax valve regions and the geometry of the wax valves, with different properties for each i valve. These diffusivity equations were substituted into the Richards equation and solved to produce the results for fluid flow velocity past each different valve.

From these mathematical models, Figure 1D shows the fluid front profile at equally spaced time points for fluid flowing through unobstructed nitrocellulose and past straight, convex, and concave valves. This figure’s visualization of fluid front patterns agrees with experimental observations, where an inverted parabolic profile is observed with fluid progressing faster along the edges of the paper. The model also demonstrates fluid traveling fastest through unobstructed nitrocellulose, followed by fluid traveling past concave valves, then straight valves, and finally traveling the slowest past convex valves.

Considering both the experimental and mathematical modeling results, it is apparent that the location where fluid first travels through the valve affects the overall flow rate of that fluid downstream. This macroscopic analysis demonstrated a counterintuitive relationship between actuation time and flow rate within the curved valves. The convex valves had the fastest actuation time and yet the slowest flow rate following actuation. Conversely, concave valves took the longest to actuate but resulted in the fastest flow rate. The main difference between actuation of these two different valves was the location across the strip where flow was first observed. With convex valves, flow was always first observed at the edges of the membrane, similar to straight valves. In contrast, concave valves most often resulted in fluid flow through the middle of the valve first. Due to these divergent behaviors, concave valves quickly resulted in a continuous fluid front as soon as the flow reached both edges of the paper, while flow after convex and straight valves took longer to fully develop into a continuous fluid front. One possible explanation for the slower fluid front development observed in convex and straight valves could be backfilling at the valves, where liquid that initially travels downstream through the edges of the valve is pulled back upstream into the empty membrane in front of the center of the valve. This hypothesis could be investigated in future work using μPIV to quantify particle motion across the width of a membrane downstream of a valve as the valve melts and fluid passes through.

Another notable aspect of the macroscopic data was the large amount of variation present in the flow rate of fluid past the straight valves compared to the convex and concave valves. Figure S7 visualizes the standard error of the mean (SEM) over time for flow past different valves, and Table S2 displays the results of a one-way ANOVA and Tukey’s multiple comparisons test calculating the variation in the SEMs between the different valves. As shown in Figure 1A, a possible explanation for this phenomenon is the uneven conductivity of heat across the valve given the greater wax-air interface at the edges of the membrane and the downstream edge of the valve as compared to the wax-liquid interface at the upstream edge of the valve. For this reason, the valves likely opened in inconsistent locations depending on the heat distribution rather than the geometry of the printed wax.

Mathematical modeling of macroscopic fluid flow is a valuable tool for visualizing and explaining expected patterns based on known phenomena of transport within porous media. Although this preliminary model used experimental data to obtain diffusivity, additional investigations will allow refinement of the model to estimate diffusivity more precisely for the particular membrane(s) of interest. This can be done using experimental methods, such as predicting this value from the measured water retention curve^45,46, or by fitting an exponential function to many more sets of experimental data to ensure a more reliable fit. With more certainty about the physical membrane properties driving flow in paper-fluidic assays, a more robust model can be developed that can make accurate predictions about flow behavior based on input parameters and assay design. Quantitative data describing microscale flow in membranes, for example, would greatly improve the accuracy of these models and help overcome limitations caused by assumptions, oversimplifications, and equation-fitting. Despite the limitations in our current model, it offers a preliminary explanation as to how counterintuitive flow results, such as the deviance in flow rate and actuation time observed with different valve geometries, can be described mathematically.

In addition to flow rate, understanding how to manipulate the shape of the fluid front is especially helpful in multi-step assays. For example, in a two-dimensional paper network, fluid that travels faster to one inlet than it does to another could be problematic for assay efficacy; or a sample that interacts unevenly with capture reagents dried across the width of the membrane might be ineffective at producing a readable signal. On the other hand, an uneven fluid front could also be exploited for more effective multi-step assays (an example design is shown in ESI Figure S9). In one such instance, it might be helpful for a sample to separately reach outlets on opposite sides of a two-dimensional paper network before proceeding further down the main channel, drastically slowing fluid flow. With the need to develop more complex and self-contained assays, an empirical understanding of ways to manipulate fluid flow simply and effectively will be invaluable for efficient device design.

Understanding how flow rate can be controlled by altering valve types and geometry is essential for rational development of multi-step assays that employ wax valves. This data facilitates troubleshooting of common issues with paper-fluidic assays, specifically more complex ones that require sustained incubation times and multiple steps as facilitated by the valves investigated here. For example, an assay with low signal intensity could be improved by using a convex valve that results in decreased flow rate of the sample across the signal line and allows more time for analyte binding.

Valve geometry effect on signal formation

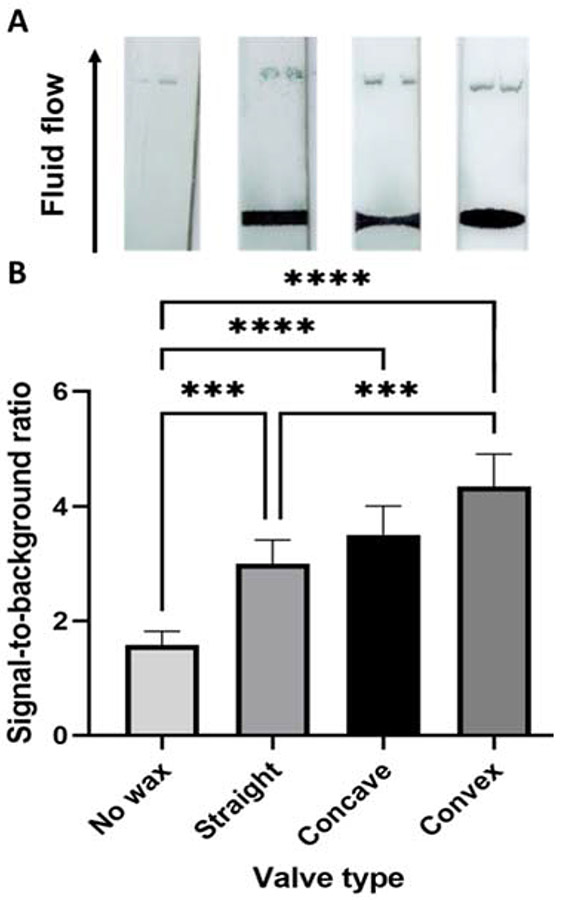
To demonstrate the effect of different wax valve geometries on signal formation in a multiplexed LFIA, a model 4-segment sandwich assay was created using biotinylated antibody spots and streptavidin-coated gold nanoshells. This design was implemented to model a system in which one reporter, such as nanoparticles or an enzymatic signal, is capable of detecting several different targets^16,47. Wax valves of straight, concave, and convex geometries were printed on nitrocellulose membranes and signal intensities of antibody spots printed at 10 mm past the valves were compared to those of the sandwich assay with no wax valve.

Representative images of the multiplex LFIA flowing through no valve, straight, convex, and concave valves are demonstrated in Figure 2A. As shown in Figure 2B, in the absence of a wax valve, signal was weak at the binding sites 10 mm past the valve. When a valve was added to the system, all three valve types resulted in a significantly (p < 0.01) increased signal for the spots.

Figure 2:

A. Representative images of LFIAs without a wax valve and with straight, concave, and convex valves. B. Signal-to-background ratio for test spot signal 1 cm past the valve location. Error bars represent standard deviation. A one-way ANOVA was performed on this dataset. ***=p< 0.01, **** indicates p<0.001

When wax valves of different geometries are added to this model assay, the resulting flow rates and patterns can be quickly and easily tuned to improve assay performance. Here, a slower flow rate induced by the addition of all valve types corresponded to improved signal at the first detection region. Notably, convex valves resulted in a strong signal despite their more variable flow profiles in our models. This is likely due to the slowest flow rate, and therefore the highest time for potential antigen capture, at the binding site. Conversely, in a situation where a faster flow rate is desired, a concave valve could be implemented. Surprisingly, straight valves, which had the most variable flow rates in our previous experiments in Figure 2, resulted in the most consistent signal across the detection region.

To model a 4-segment LFIA, two spots were also printed 15 mm past the valves, as shown in ESI Scheme S1C. Multiplex LFIAs that employ digital readouts are an efficient way to detect many different targets on a single test strip, but can struggle with signal formation at downstream detection spots when flow is interrupted by upstream detection spots.⁴⁷ As shown in ESI Figure S8, without a wax valve, the spots at 15 mm are below the visible signal-to-background threshold. When concave, straight, and convex wax valves are added, the spots at 15 mm become visible; however, concave and convex valves result in 15 mm spots that have much lower signal than the spots at 10 mm. One possible hypothesis is that in these strips, the flow interrupted by the 10 mm spots is not fully developed by the time it reaches the 10 mm spots.

Further experimentation at the macro and microscale are needed to investigate this hypothesis and formulate a strategy for overcoming this limitation. The wax valves characterized above require no additional user steps for actuation, and allow precisely tunable fluid release flow rate, and pattern of fluid front based on the needs of individual assays. There are, however, a few key limitations that might limit their ability to be widely adopted in point-of-care diagnostic technologies. First, the requirement of a heat source adds extra material instrumentation components to the manufacturing and use of the device, potentially making them more expensive and sensitive to environmental conditions than room-temperature paper-only assays. Although these types of multi-step assays require user manipulation (for example, rotational valves²⁰), their low cost and lack of instrumentation requirements is a major advantage over wax valves. Finally, while the improvement of assay sensitivity as described in Figure 2 is a helpful benefit of wax valves, it is only one signal enhancement strategy that relies on slowing fluid flow within the assay; other strategies like using a membrane with smaller pore sizes, paper shunts²², wax barriers²⁸, and others can also delay fluid flow to the same effect. Nevertheless, valves like the ones described here can be incorporated into different kinds of multi-step assays, including silver signal enhancement and isothermal amplification reactions that already require heaters, such as loop-mediated isothermal nucleic acid amplification (LAMP) coupled with lateral flow assay detection.^12,29 Furthermore, adjusting the geometry of the valves to modulate fluid flow is a quick and easy way to improve sensitivity in a device that already incorporates wax valves, while other methods such as changing the membrane pore size or adding extra components often involve tedious trial-and-error experiments to find the optimal parameters for any given system.⁴

Given the somewhat surprising differences in the effects of valve types on LFIA signal production compared to bulk flow rates, we further explored particle flow at the microscopic level. While the flow of the gold nanoshell suspension buffer is comparable to the flow rate analyzed previously, the gold nanoshells through the porous membrane likely travelled much slower due to their larger size than the molecules comprising the resuspension buffer. The following section explains a novel implementation of μPIV that enables measurement and characterization of this difference to reduce trial-and error.

Microscopic flow analysis

Because of the discrepancies between the hypothesized detection line intensities and the experimental results demonstrating non-uniform and unexpected particle binding interactions, we investigated whether local microscopic particle flow in porous membranes actually followed the bulk flow rates. Interestingly, we found that transport patterns at the particle level do not, in fact, conform to those observed at the bulk flow scale. Previous models of flow in nitrocellulose membranes rely primarily on bulk flow when analyzing fluid motion, however, inclusion of microscale flow is essential to build more thorough and accurate models.⁴ For this reason, our μPIV experiments aimed to investigate how particles travel through the membrane’s pores to elucidate how nanoparticle flow in paper-fluidic assays can be more precisely tuned with microscale transport considerations.

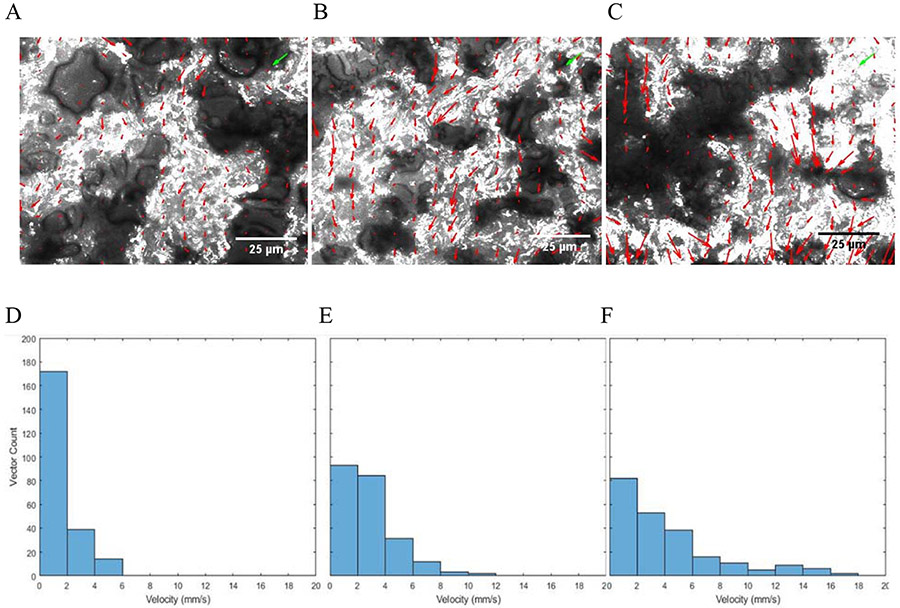
To visualize and quantify microscopic flow properties within the nitrocellulose membrane, fluorescent nanoparticles were imaged at different distances along the middle of the membrane test strips and quantified with μPIV using the EDPIV software. A video of particle flow 5 mm downstream of the sample pad can be found in the ESI. As shown in Figure 3 (A-C), the distribution and length of velocity vectors agrees relatively well with the flow of particles throughout the video and demonstrates that particle motion can be accurately measured and quantified using fluorescent microscopy and μPIV. The histogram of the corresponding vector velocities in Figure 3D-E, shows that velocities are skewed right, with many very low velocity particles (0 to 4 mm/s) and some higher velocity particles (8-18 mm/s) downstream of the flow initiation at 10, 15, and 20 mm from the sample pad. This lower apparent velocity is likely due to areas of the membrane in which either particle flow itself or visualization of particle flow is obstructed, seen as dark patches in the images. This pattern of right-skewed histograms was observed for every video taken, though areas had differing degrees of obstruction in each field of view.

Figure 3:

μPIV analyses of flow through nitrocellulose. A-C. Composites of 400 images from a 10 second time series taken 10 (A), 15 (B), and 20 (C) mm from the sample pad in the center of the membrane combined into a single image to display locations of visible particles, with an overlaying vector field from EDPIV analysis (red arrows; green arrow represents the length of a 1 mm/s velocity vector in both the x and y directions). D-F. Histogram reflecting the velocity distribution of all 225 vectors of each above analysis.

Compared to bulk flow rate of 0.345 mm/s (10mm) and 0.263 mm/s (15 mm) in non-wax valves (Figure 2), the migration of particles flowing more quickly than this, has wide reaching ramifications in LFIA and interactions within porous media. In the 10 mm and 15 mm channels analyzed via PIV, 76% and 93% of particles were flowing faster than the bulk flow rate. This calculation is available in the “MATLAB Model of Fluid Flow” section of the ESI. Thus, most nanoparticle binding reactions have significantly less time to interact than previously considered. This would result in significantly less intense signal generation than bulk flow rates would suggest.

While the 400 nm particles are easily visible in the fluorescent microscopic setup, 400 nm is just outside the particle size range that can accurately model flow in a porous nitrocelllose membrane according to Peclet and Darmholer numbers.⁴ Therefore, we also repeated the expieriment with 100 nm particles which are well within the range of LFIA nanoparticle conjugates, such as the 150 nm gold nanoshells demonstrated in our valve experiments. These particles are difficult to visualize by eye with fluorescent miscroscopy, however, μPIV relies on image cross-correlation instead of visualization and tracking of individual particles; thus flow of 100 nm particles was able to be analyzed using μPIV (data in ESI Figure S10).

The microscopic analysis of particle flow within the nitrocellulose membrane and resulting quantitative description with PIV-generated vectors is an entirely novel development in the realm of investigating paper-fluidic transport properties. This particle-scale velocity analysis within a porous membrane promises to serve as a valuable tool in more precise analyses of the biophysical phenomena driving paper-based diagnostics. These results are also in agreement with measurements from similar analyses simulating nanoparticle flow in LFIAs, supporting the conclusion that our measurements are accurate and valid.⁴¹

A few modifications to the analysis techniques used here can permit more robust future quantitative analyses using μPIV in paper membranes. Here, there was a wide distribution of calculated velocities in each video, and that distribution varied greatly between videos. There was also large amount of local variation in membrane structure. For this reason, it was not possible to discern statistically significant differences in flow patterns and velocities between videos taken in triplicate at the same location across different membranes. Future work may be able to remedy this limitation with improved test strip fabrication methods. Specifically, here, laminate was manually applied to unbacked nitrocellulose due to particle visualization limitations through white backing on pre-backed nitrocellulose. This may have resulted in local membrane deformities such as small bubbles of air or even crushing of the membrane and may have yielded obstruction observed in each video. Additionally, while we used 400 nm and 100 nm fluorescent polystyrene particles for visualization, often smaller particles, such as 40 nm gold particles are common in LFIAs. These particles would be expected to travel through the nitrocellulose pores with even greater ease than our imaged particles, possibly resulting in differing flow patterns and particle velocities. Furthermore, the charge of the unconjugated polystyrene particles in water within an unblocked nitrocellulose membranes rather than protein-conjugated particles in buffer on blocked membranes here may affect the electrostatic interactions between the particles and membrane, potentially slowing particles further. Nevertheless, visualization of the particle flow dynamics has the potential to provide important new insights into paper- and membrane-based device designs.

These microPIV experiments demonstrate the importance of local particle velocity when interacting with a small reaction zone such as a 100 μm striped LFA detection zone. The μPIV field of view was only 1/50^th of the width of the channel but represented 1/6^th of the detection zone length. Thus, while the μPIV does not well-represent the width of the channel, it does provide a strong indication of the particle speed the reaction zone. The reality that not all particles are moving at the same bulk speed has profound impacts on LFIA development and has the potential to be used to optimize reaction kinetics at the detection zone more precisely and efficiently than is possible using current LFIA prototyping methods.

CONCLUSION

Computational and experimental analyses of multi-step paper-fluidic assays can inform more precise and efficient development of next-generation point-of-care diagnostic technologies. We demonstrated that changing the geometric properties of wax valves significantly influences their actuation time and resulting flow patterns, indicating that while convex valves open quickest the flow downstream is much slower than concave or straight valves. Conversely, concave valves result in the most rapid fluid flow downstream of the valve and most even and consistent fluid front. Our bulk flow models indicate that concave valves would permit the most rapid, reliable, and uniform delivery of reagents following actuation. However, this was not replicated in actual valve experiments. Instead, all valves performed better than the No Valve controls but convex valves yielded the strongest signal. Microscale analyses demonstrated that local flow is highly variable and that many particles travel more much more rapidly than bulk flow alone. These can have a profound effect on the resulting signal intensities even when the variability of bulk flow is well controlled.

Tunable valve parameters can be incorporated into a variety of different and more complex paper-fluidic devices to increase signal and flow uniformity. We designed computational models based on fundamental equations governing fluid flow and the structural properties of nitrocellulose membrane validated using SEM and showed that the information gleaned from these models agreed with empirical data and observations. This agreement demonstrates the validity of these models for designing and predicting sample behavior in multi-step paper-fluidic assays. Finally, we described and demonstrated a novel method for experimentally observing and quantifying particle flow in porous membranes using fluorescent nanoparticles and μPIV. This method can be employed to interrogate many different microscale properties of paper-based assays. Examples of possible uses include quantifying flow in various assay stages and materials, comparing the velocities of different sized particles representative of different sample components (such as gold or latex nanoparticles commonly used in LFIAs or chemical substrates used in signal amplification), or understanding how fluid travels between different functional steps in a variety of multi-step assays.

In this work, instantaneous flow velocities at each location were derived from fitting macroscopic data to relevant fluid flow models. This novel experimental contribution to the literature will help researchers to understand how macroscopic flow compares to microscopic particle-scale flow within porous membranes, a relationship that has previously been relegated to theoretical calculations alone. The robust combination of experimental and computational analyses describing heat transfer, wax phase transition, and nanoparticle flow herein build a detailed framework for designing and evaluating flow in paper and support rational design of increasingly complex paper-fluidic devices.