Improved prediction of immune checkpoint blockade efficacy across multiple cancer types

Abstract

Only a fraction of patients with cancer respond to immune checkpoint blockade (ICB) treatment, but current decision-making procedures have limited accuracy. In this study, we developed a machine learning model to predict ICB response by integrating genomic, molecular, demographic and clinical data from a comprehensively curated cohort (MSK-IMPACT) with 1,479 patients treated with ICB across 16 different cancer types. In a retrospective analysis, the model achieved high sensitivity and specificity in predicting clinical response to immunotherapy and predicted both overall survival and progression-free survival in the test data across different cancer types. Our model significantly outperformed predictions based on tumor mutational burden, which was recently approved by the U.S. Food and Drug Administration for this purpose¹. Additionally, the model provides quantitative assessments of the model features that are most salient for the predictions. We anticipate that this approach will substantially improve clinical decision-making in immunotherapy and inform future interventions.

Cancer immunotherapies, such as ICB, are capable of inducing the immune system to effectively recognize and attack tumors². The primary approved agents include antibodies that target CTLA-4 or PD-1/PD-L1, which can induce durable responses in patients with advanced-stage cancers. However, most patients do not derive clinical benefit². Some large phase 3 clinical trials have reported negative results in unselected patients^3–6, highlighting the need to identify who will respond to immunotherapy. Recent studies have described different biological factors that affect ICB efficacy^2,7–9. However, none of these factors acts in isolation and, thus, cannot alone optimally identify patients who benefit from ICB across different cancer types⁷.

Machine learning approaches have been shown to successfully overcome limitations of predictors that rely on a single feature by combining different types of features in a non-linear fashion^10,11. These models have already improved prediction and prognostication in healthcare and biomedicine and hold considerable promise to further improve healthcare delivery and clinical medicine¹¹ The aim of this study was to develop a machine learning algorithm to generate an accurate prediction of a patient’s probability of immunotherapy response by comprehensively integrating multiple biological features associated with immunotherapy efficacy and to assess their individual contribution to response when combined in a single predictive framework.

We acquired complete clinical, tumor and normal sequencing data of 1,479 patients across 16 different cancer types from Memorial Sloan Kettering Cancer Center (MSKCC) (Fig. 1a and Supplementary Fig. 1). Approximately 37% of the patients had non-small cell lung cancer (NSCLC), 13% had melanoma and the remaining 50% had other cancer types (hereafter referred to as ‘others’), including renal cell carcinoma and bladder, head and neck and colorectal cancer (Fig. 1a and Table 1). These patients were treated with PD-1/PD-L1 inhibitors, CTLA-4 blockade or a combination of both immunotherapy agents (Table 1). In total, there are 409 patients whose tumors responded to immunotherapy and 1,070 patients whose tumors did not respond across the different cancers (Fig. 1a and Table 1). Response was based on Response Evaluation Criteria in Solid Tumors (RECIST) v1.1 (ref. ¹²) or best overall response on imaging (Methods). Patients who experienced complete response (CR) or partial response (PR) were classified as responders (R); patients who experienced stable disease (SD) or progressive disease (PD) were classified as non-responders (NR). Patients’ tumors were profiled using the U.S. Food and Drug Administration (FDA)-cleared MSK-IMPACT next-generation sequencing platform¹³ (Methods).

Fig. 1|. Overview of development of the model for integrated clinical-genetic prediction of ICB response.

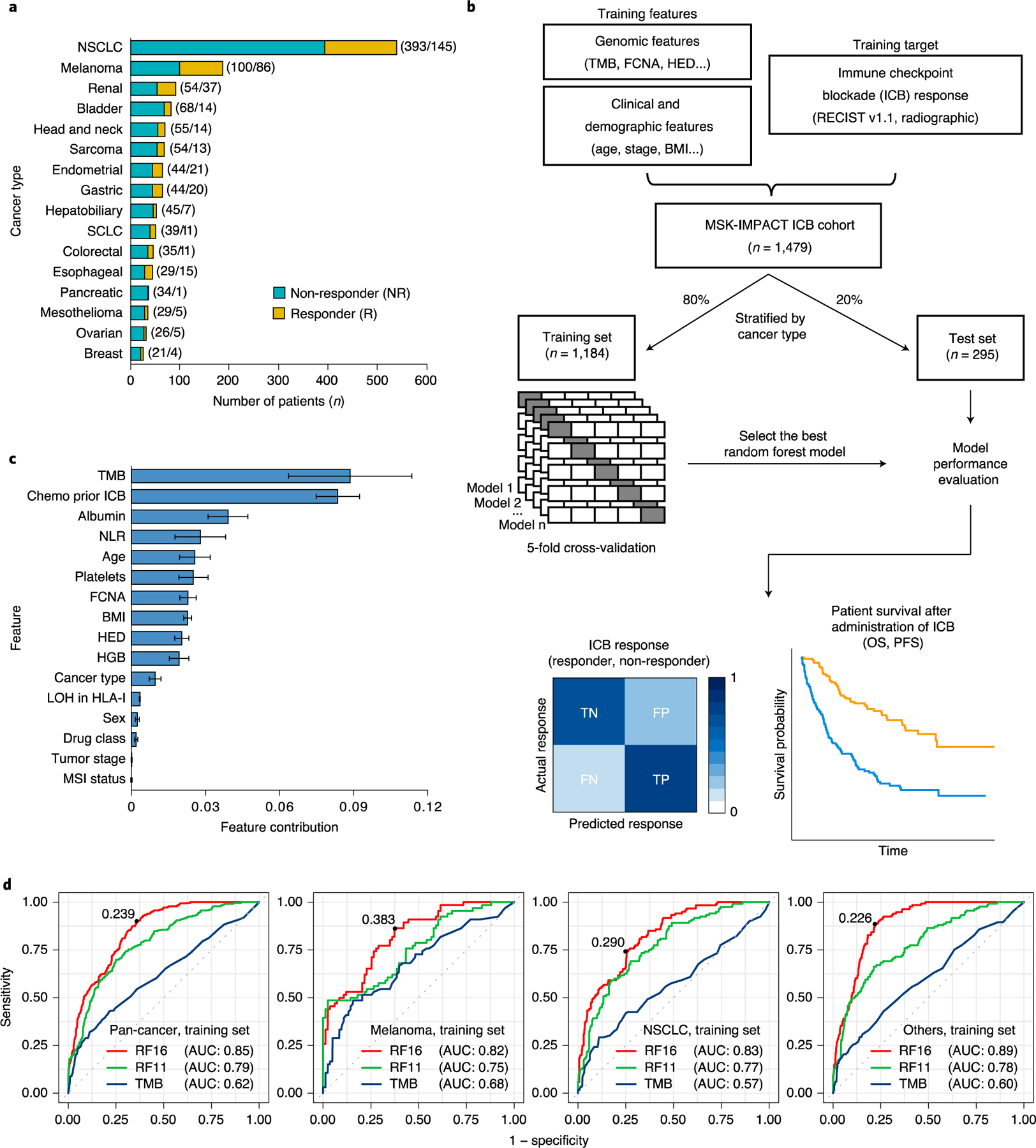
a, Bar chart showing the number of patients in each of the 16 cancer types. We categorized response based on RECIST vl.1 (ref.¹²) or best radiographic response. CR and PR were classified as R; SD and PD were classified as NR. Numbers in parentheses denote the number of patients in NR and R groups, respectively. b, General overview of the random forest model training and testing procedure. Sixteen cancer types were divided into training (80%) and testing (20%) subsets individually. A random forest model was trained on multiple genomic, molecular, demographic and clinical features on the training data using five-fold cross-validation to predict ICB response (NR and R). The resulting trained model with the best hyperparameters was evaluated using various performance metrics using the test set. c, Feature contribution of the 16 model features calculated in the training set (n = 1,184) to predict ICB response. The error bars denote standard deviation of feature contribution. d, ROC curves and the corresponding AUC values of RF16, RF11 and TMB alone in the training set across multiple cancer types. The numbers on the ROC curves denote the corresponding optimal cutpoints for RF16, which maximize the sensitivity and specificity of the response prediction. SCLC, small cell lung cancer.

Table 1|.

Characteristics of patients in the study

Characteristic	Total patients (n = 1,479)	Training set (n = 1,184)	Test set (n = 295)
Sex, n (%)
Female	668 (45.17)	529 (44.68)	139 (47.12)
Male	811 (54.83)	655 (55.32)	156 (52.88)
Age, median, years (IQR)	64 (55–71)	64 (55–71)	64 (55–72)
Cancer type, n (%)
NSCLC	538 (36.38)	430 (36.32)	108 (36.61)
Melanoma	186 (12.58)	149 (12.58)	37 (12.54)
Renal	91 (6.15)	73 (6.17)	18 (6.10)
Bladder	82 (5.54)	66 (5.57)	16 (5.42)
Head and neck	69 (4.67)	55 (4.65)	14 (4.75)
Sarcoma	67 (4.53)	54 (4.56)	13 (4.41)
Endometrial	65 (4.39)	52 (4.39)	13 (4.41)
Gastric	64 (4.33)	51 (4.31)	13 (4.41)
Hepatobiliary	52 (3.52)	42 (3.55)	10 (3.39)
SCLC	50 (3.38)	40 (3.38)	10 (3.39)
Colorectal	46 (3.11)	37 (3.13)	9 (3.05)
Esophageal	44 (2.97)	35 (2.96)	9 (3.05)
Pancreatic	35 (2.37)	28 (2.36)	7 (2.37)
Mesothelioma	34 (2.30)	27 (2.28)	7 (2.37)
Ovarian	31 (2.1)	25 (2.11)	6 (2.03)
Breast	25 (1.69)	20 (1.69)	5 (1.69)
Drug class, n (%)
PD-1/PD-L1	1,221 (82.56)	969 (81.84)	252 (85.42)
CTLA-4	5 (0.33)	5 (0.42)	0 (0.00)
Combo	253 (17.11)	210 (17.74)	43 (14.58)
ICB response, n (%)
Responder	409 (27.65)	319 (26.94)	90 (30.51)
Non-responder	1,070 (72.35)	865 (73.06)	205 (69.49)
Chemotherapy prior ICB, n (%)
No	463 (31.30)	370 (31.25)	93 (31.53)
Yes	1,016 (68.70)	814 (68.75)	202 (68.47)
Stage, n (%)
I-III	97 (6.56)	78 (6.59)	19 (6.56)
IV	1,382 (93.44)	1,106 (93.41)	276 (93.44)

Combo, PD-1/PD-L1 plus CTLA-4; IQR, interquartile range; SCLC, small cell lung cancer.

To calculate the probability of response to immunotherapy, we developed an ensemble learning random forest¹⁴ classifier with 16 input features (hereafter called RF16). We incorporated genomic, molecular, clinical and demographic variables in the model, some previously reported to be associated with ICB response. The variables incorporated included tumor mutational burden (TMB)^15–22, fraction of copy number alteration (FCNA)²³, HLA-I evolutionary divergence (HED)²⁴, loss of heterozygosity (LOH) status in HLA-I²⁵, microsatellite instability (MSI) status^26,27, body mass index (BMI)^28,29, sex³⁰, blood neutrophil-to-lymphocyte ratio (NLR)^31–33, tumor stage³⁴, immunotherapy drug agent²⁰ and age³⁵ (Methods). Additionally, we included cancer type, whether the patient received chemotherapy before immunotherapy and blood levels of albumin, platelets and hemoglobin (HGB)^36–38 (Fig. 1b).

We randomized our dataset by cancer type into a training subsample (80%, n = 1,184) (Fig. 1b and Table 1), for which we developed the prediction algorithm, and a test subsample (20%, n = 295), on which we evaluated the trained classifier (Fig. 1b and Table 1). We used five-fold cross-validation on the training data to derive the ICB response predictive model based on binary classification (responder and non-responder) (Fig. 1b).

The resulting trained model aggregates the predictive effects across the selected clinical, molecular, demographic and genomic features to derive a cancer type-specific probability of immunotherapy response. By using this type of model, we can quantify how much the various features contribute to explaining patient-to-patient variation in response (Fig. 1c). These estimates represent the contributions of the various categories of predictors to response outcomes at the population level. At the individual level, we can score each patient based on their response probability (higher values indicate higher probability of ICB response) (Supplementary Fig. 2a,b).

When comparing single feature contributions of response prediction, TMB was the predictor exerting the greatest effect (Fig. 1c), which is consistent with many independent studies showing its association with response^15–20. Additionally, the effect of chemotherapy history on ICB response was similar to that of TMB. Notably, MSI status was not selected by the model as one of the top predictors, likely owing to its strong association with TMB (Supplementary Fig. 3). In addition, we quantified the relative contribution of levels of albumin, HGB and platelets to ICB response (Fig. 1c). These blood markers are known to provide information about the extent of systemic and potentially tumor-promoting inflammation, which has emerged as an important component of the tumor microenvironment because it has the potential to promote angiogenesis, metastasis and immunosuppression^31,39–41. Although some of the markers have been associated with overall prognosis of patients with cancer^36–38, it is intriguing that, here, they contributed to radiographic response to ICB treatment itself.

We sought to evaluate the performance of the integrated clinical-genetic model using multiple metrics^42,43. To assess the predictive power of integrating the cancer type, whether the patient received chemotherapy before immunotherapy and the blood markers (albumin, HGB and platelets), with the other variables that influence ICB response, we developed a second random forest model (hereafter called RF11), including only the variables FCNA, TMB, HED, NLR, BMI, LOH in HLA-I, sex, age, MSI status, tumor stage and drug class. We used the RF11 model as a reference for the RF16 model to determine the added value of including additional variables that have not been used widely before to predict ICB response (Fig. 1c). Because TMB has been approved by the FDA as a biomarker to predict ICB efficacy in solid tumors¹, we also compared the performance of the integrated RF16 and RF11 models with predictions based on TMB alone.

We first calculated the area under the receiver operating characteristic (ROC) curves and precision-recall curves by using the response probabilities computed by the respective RF16 and RF11 models and the continuous values of TMB. The integrated RF16 model achieved superior performance as indicated by the area under the curve (AUC) in predicting responders and non-responders across cancer types compared to TMB alone and the RF11 model in both the training set (Fig. 1d; pan-cancer AUC 0.85 for RF16 versus 0.79 for RF11 versus 0.62 for TMB) and the test set (Fig. 2a; pan-cancer AUC 0.79 for RF16 versus 0.71 for RF11 versus 0.63 for TMB). We also confirmed higher area under the precision-recall curve (AUPRC) achieved by the RF16 model than TMB alone and RF11 in both the training set (Supplementary Fig. 4) and the test set (Supplementary Fig. 5). None of RF16’s features alone could achieve the level of performance achieved by RF16, suggesting that a non-linear combination of multiple features contributed with various degrees to the overall prediction performance (Fig. 1c and Supplementary Fig. 6a,b). Additionally, the continuous probabilities calculated by the integrated RF16 model were significantly associated with response across tumors in the test set (Fig. 2b). The differences in response probability between responders and non-responders were significantly higher compared to differences in TMB between responder and non-responder groups across the various cancers (Fig. 2b,c; pan-cancer P < 0.0001 and P = 0.0005 for RF16 and TMB, respectively).

Fig. 2|. Model performance across multiple cancer types in the test set.

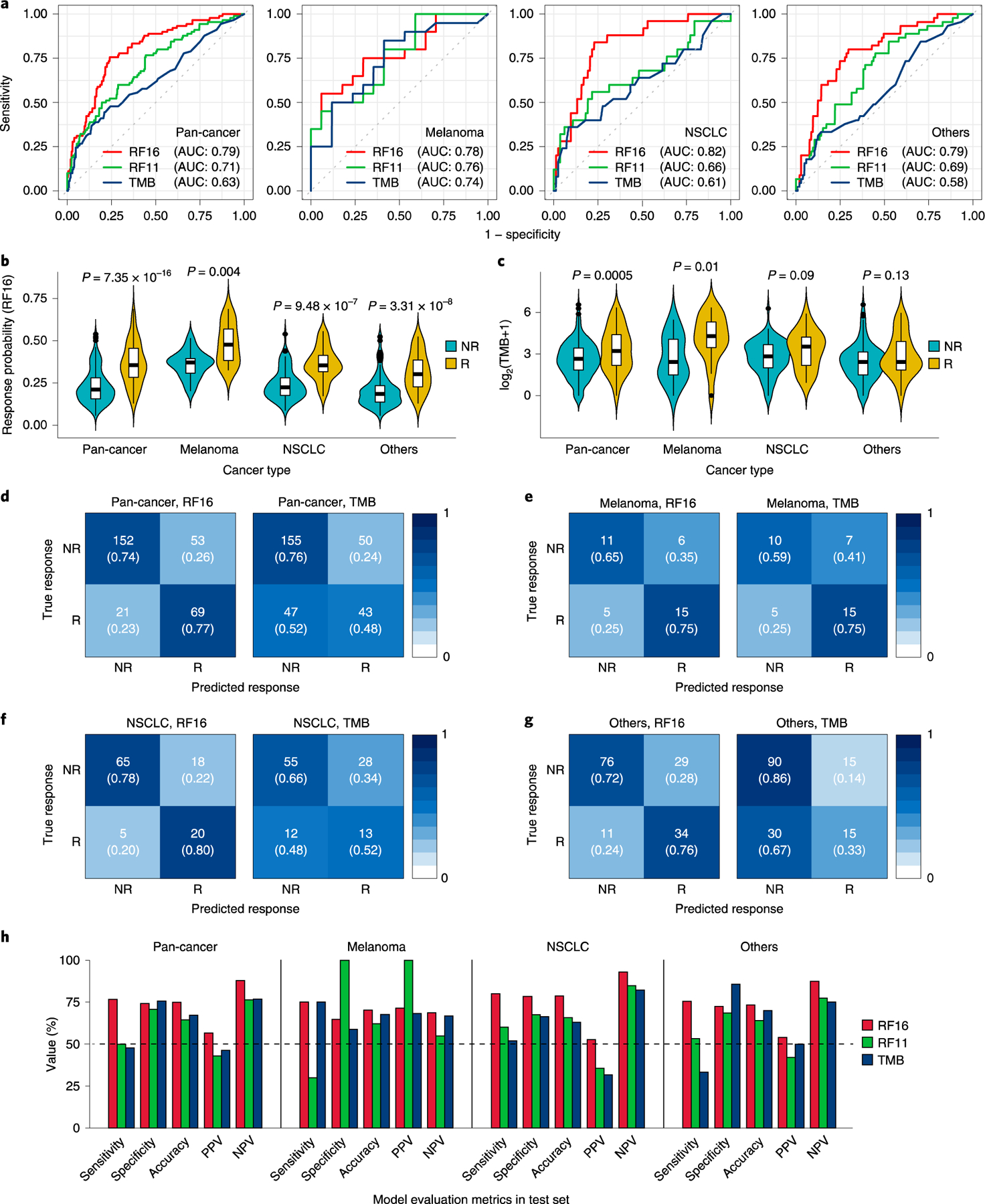
a, ROC curves and corresponding AUC values of RF16, RF11 and TMB alone. b, Comparison of response probability distributions calculated by RF16 between NR and R groups. Two-sided P values were calculated using the Mann-Whitney U test. Center bar, median; box, interquartile range; whiskers, first and third quartiles ±1.5x interquartile range. c, Comparison of TMB between NR and R groups. Two-sided P values were calculated using the Mann-Whitney U test. Center bar, median; box, interquartile range; whiskers, first and third quartiles ±1.5x interquartile range. d-g, Confusion matrices showing predicted outcomes generated by RF16 and TMB, as indicated, in pan-cancer (d), in melanoma (e), in NSCLC (f) and in others (not melanoma/NSCLC) (g), respectively. To define high TMB tumors, we applied the threshold of ≥10 mut/Mb, which was approved by the FDA to predict ICB efficacy of solid tumors with pembrolizumab¹. h, Performance measurements of RF16, RF11 and TMB illustrated by sensitivity, specificity, accuracy, PPV and NPV.

To stratify the continuous probabilities generated by RF16 into predicted responder and non-responder groups, we found the probability that optimizes the sensitivity and specificity of the ROC curves in the training set (Fig. 1d). When the probability value exceeds the optimal operating point threshold, the patient would be considered a ‘predicted responder’. We observed that the probability distributions significantly varied across tumor types in the training set (Supplementary Fig. 2a). Therefore, the default cutoff of 0.5 used during cross-validation (Methods) or a single optimal pan-cancer cutpoint to discriminate responders and non-responders would result in low true-positive rate or high false-positive rate, respectively, in the training set (Supplementary Fig. 7a,b). We, thus, dichotomized the probabilities into predicted responder and non-responder groups by optimizing the sensitivity and specificity in the training set for each cancer group (melanoma, NSCLC and others) separately (Fig. 1d and Supplementary Fig. 2a), which resolved both the low sensitivity or specificity significantly (Supplementary Fig. 7c). To test the discriminatory power of these optimal cancer-specific cutpoints, we applied them to each cancer group of the test set (Fig. 2d–g). To compare the performance of predicting responders and non-responders by RF16 with TMB alone, we used ≥10 mutations per megabase (mut/Mb) as the cutpoint for TMB, which was approved by the FDA for pembrolizumab¹. We found that the RF16 model consistently achieved higher predictive performance as measured by sensitivity, specificity, accuracy, positive predictive value (PPV) and negative predictive value (NPV) compared to TMB alone (Fig. 2h and Supplementary Fig. 7d,e). In particular, the RF16 model achieved significantly higher sensitivity than TMB in NSCLC (80.00% for RF16 versus 52.00% for TMB) and other cancer types (75.56% for RF16 versus 33.33% for TMB) in the test set (Fig. 2h). In a pan-cancer analysis, the RF16 model achieved 76.67% sensitivity and 74.15% specificity compared to 47.78% sensitivity and 75.61% specificity achieved by TMB alone in the test set (Fig. 2h). Taken together, our integrated RF16 model predicts response to ICB therapy with high accuracy, as shown by various common performance metrics across different cancer types.

Additionally, the distributions of response probabilities generated from the RF16 model trained on pan-cancer data were compared with those from separate models trained on cancer-specific data. These response probability distributions were statistically similar in both the training and test sets (Supplementary Fig. 8a,b). The RF16 model trained on the pan-cancer data achieved higher predictive performance compared to the RF16 model trained on cancer-specific data in the test set (Supplementary Fig. 9a–e and Supplementary Table 1). Thus, these results suggest that RF16 trained on the large pan-cancer data was able to both learn cancer-specific relationships and generalize relationships that could be relevant across cancers, leading to higher predictive performance in the test set.

We further compared the performance of RF16 with that of a logistic regression using the same training data and same model features for model calibration (Supplementary Table 2). The RF16 model consistently achieved higher predictive performance compared to the logistic regression in pan-cancer, melanoma, NSCLC and others, in both the training and test sets (Supplementary Fig. 10a–f). This result might be partly explained because RF16 does not assume that the relationships between the model variables and the log odds of immunotherapy response are linear, which logistic regression does assume.

To test whether our model could also predict overall survival (OS) before administration of immunotherapy, we used the Brier score⁴², which quantifies the accuracy of a set of predictions by calculating the error between observed and predicted OS probabilities. Predictions from RF16 resulted in a smaller error than predictions based on reference (random) model, TMB alone, or RF11; both in training and test data (Supplementary Figs. 11a and 12). We further calculated the concordance index (C-index)⁴² for OS, which ranges between 0 and 1 (0.5 being random performance). We found that the C-indices of the RF16 predictions were significantly higher than those generated by TMB or RF11 across tumor types, both in the training set (Supplementary Fig. 11b; pan-cancer C-index 0.71 for RF16 versus 0.66 for RF11 versus 0.54 for TMB, P < 0.0001) and the test set (Fig. 3a,c,e,g; pan-cancer C-index 0.68 for RF16 versus 0.62 for RF11 versus 0.55 for TMB, P < 0.0001). Additionally, we found that responders predicted by our RF16 model were significantly associated with longer OS compared to patients classified as non-responders in the training set (Supplementary Fig. 13a,c,e,g; pan-cancer P < 0.0001, hazard ratio (HR) = 0.31, 95% confidence interval (CI) = 0.26–0.36) and the test set (Fig. 3b,d,f,h; pan-cancer P < 0.0001, HR=0.29, 95% CI = 0.21–0.41). Furthermore, the differences in OS between responders and non-responders predicted by RF16 were significantly higher compared to differences between responder and non-responder groups predicted by TMB alone across the various cancer types (Fig. 3b,d,f,h and Supplementary Fig. 13,14). Additionally, the predictions of progression-free survival (PFS) produced by RF16 were significantly more accurate than both TMB alone and based on RF11 in the training set (Supplementary Fig. 15; pan-cancer C-index 0.68 for RF16 versus 0.66 for RF11 versus 0.56 for TMB, P < 0.0001) and the test set (Fig. 3i,k,m,o; pan-cancer C-index 0.67 for RF16 versus 0.62 for RF11 versus 0.56 for TMB, P = 0.0007 and P < 0.0001, respectively). Consistent with these results, responders predicted by the RF16 model also had significantly better PFS than predicted non-responders in the training data (Supplementary Fig. 16a,c,e,g; pan-cancer P < 0.0001, HR=0.31, 95% CI = 0.27–0.36) and the test data (Fig. 3j,l,n,p; pan-cancer P < 0.0001, HR=0.34, 95% CI = 0.25–0.44), with larger PFS differences between responders and non-responders predicted by RF16 than TMB alone across the various cancer types (Fig. 3j,l,n,p and Supplementary Fig. 16,17).

Fig. 3|. Model predicts OS and PFS across multiple cancer types in the test set.

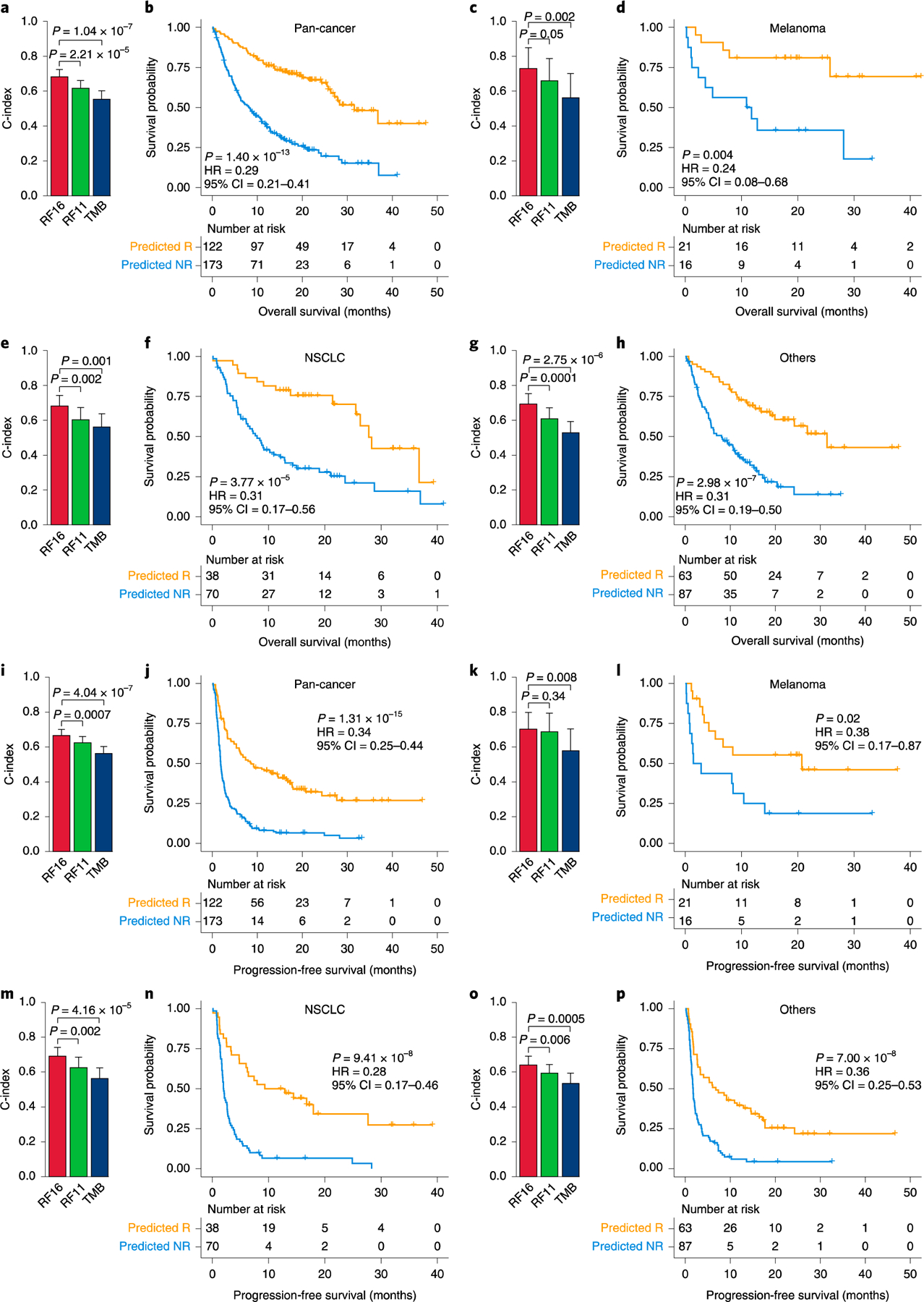
a, Comparison of C-index and 95% Cl for predicting OS among RF16, RF11 and TMB in the pan-cancer cohort (n = 295). b, Pan-cancer association between ICB response predicted by RF16 and OS. c, Comparison of C-index and 95% Cl for predicting OS among RF16, RF11 and TMB in melanoma (n = 37). d, Association between ICB response predicted by RF16 and OS in melanoma, e, Comparison of C-index and 95% Cl for predicting OS among RF16, RF11 and TMB in NSCLC (n=108). f, Association between ICB response predicted by RF16 and OS in NSCLC. g, Comparison of C-index and 95% Cl for predicting OS among RF16, RF11 and TMB in others (not melanoma/NSCLC) (n = 150). h, Association between ICB response predicted by RF16 and OS in others. i, Comparison of C-index and 95% Cl for predicting PFS among RF16, RF11 and TMB in the pan-cancer cohort (n = 295). j, Pan-cancer association between ICB response predicted by RF16 and PFS. k, Comparison of C-index and 95% Cl for predicting PFS among RF16, RF11 and TMB in melanoma (n = 37). l, Association between ICB response predicted by RF16 and PFS in melanoma. m, Comparison of C-index and 95% Cl for predicting PFS among RF16, RF11 and TMB in NSCLC (n = 108). n, Association between ICB response predicted by RF16 and PFS in NSCLC. o, Comparison of C-index and 95% Cl for predicting PFS among RF16, RF11 and TMB in others (n = 150). p, Association between ICB response predicted by RF16 and PFS in others. Two-sided P values for comparison of C-indices and survival times were computed using the paired Student’s t-test and log-rank test, respectively.

Altogether, these data demonstrate that our machine learning approach can forecast response, OS and PFS before administration of immunotherapy at high accuracy. In addition, our results demonstrate that accurate prediction of ICB response required an integrated model incorporating genetic (both germline and somatic), clinical and demographic factors and blood markers suggestive of the overall health of the patient. Each of the model features can be easily measured from blood and from tumor tissue DNA sequencing. Additionally, the values of the peripheral blood markers used in the model, such as NLR, albumin, platelets and HGB, are routinely performed in almost all blood tests in the clinic. In contrast to what has been suggested⁴⁴, the association of TMB with immunotherapy response was not confounded by melanoma subtype (Supplementary Fig 18). One limitation of our model is that we did not have transcriptomic data available or tumor PD-L1 staining, which are important information to assess the tumor microenvironment. Our analyses provide finer granularity for understanding and quantifying the heterogeneity in response to immunotherapy. Additionally, our analyses revealed that a non-linear combination of multiple biological factors contributed, with various degrees of contribution, to response.

In this study, we developed and tested our model on a large, clinically representative database of patients with different cancer types. However, this patient population is limited in size and not necessarily representative of the global target population and requires further testing on additional large patient cohorts within the context of a clinical trial, which will provide a more accurate estimate of model performance. We anticipate that forthcoming prospective trials will use similar machine learning approaches to improve existing state-of-the-art classifiers as we advance in both understanding and availability of molecular data. Specifically, molecular features of the tumor immune microenvironment^45–49; microbiome composition⁵⁰; diversity of the T cell receptor repertoire⁵¹; specific tumor genomic alterations^52–56, such as mutations of DNA damage response and repair-related genes^57,58 or mutations associated with resistance to ICB; and transcriptomic data might further help improve predictive performance. We think that such quantitative models will have important implications in the area of precision immuno-oncology for improving patient outcomes.

Methods

Patient data description.

The use of the patient data was approved by the MSKCC Institutional Review Board (IRB). All patients provided informed consent to a Memorial Sloan Kettering IRB-approved protocol. The main study question (whether our integrated model could predict response to immunotherapy, OS and PFS) was specified before data collection began. We addressed potential immortal time bias due to left truncation by limiting the cohort to patients followed after receiving a cancer diagnosis during the period when tumor sequencing at our center was routinely performed. Patients initially selected for this study were those with solid tumors diagnosed from 2015 through 2018 who received at least one dose of ICB at our center (n = 2,827). All tumors, along with DNA from peripheral blood, were genomically profiled using the MSK-IMPACT next-generation sequencing platform (CLIA-approved hybridization capture-based assay)¹³. We excluded patients with a history of more than one cancer, patients without a complete blood count within 30 d before the first dose of ICB, patients enrolled in blinded trials and cancer types with fewer than 25 cases. The clinical records of the remaining 1,854 patients were manually reviewed to evaluate response to therapy, OS and PFS. The process was blinded to patients’ genomic, molecular and clinical data. We excluded patients who received ICB in a neoadjuvant or adjuvant setting and patients with unevaluable response (lost to follow-up without imaging after ICB start). Patients without HLA data due to consent for germline testing or poor HLA genotyping quality were also excluded. We further excluded patients without stage and BMI information. The final set consisted of 1,479 patients from 16 cancer types (Supplementary Fig. 1).

Response, OS and PFS.

The primary study outcomes were response to ICB, OS and PFS. We categorized response based on RECIST vl.l (ref.¹²). If formal RECIST reads were not available, we manually reviewed physician notes and imaging studies to categorize overall best response for each patient using the same criteria based on change in the sum of diameters of target lesions. CR and PR were classified as responders; SD and PD were classified as non-responders. PFS was calculated from ICB first infusion to disease progression or death from any cause; patients without progression were censored at last attended appointment at MSKCC with any clinician. OS was calculated from ICB first infusion to death from any cause; patients alive at the time of review were censored at last contact. For patients who received multiple lines of ICB, the first line was used for analysis.

Genomic, demographic, molecular and clinical data.

NLR was calculated as the absolute count of neutrophils (per nanoliter) divided by the absolute count of lymphocytes (per nanoliter). The units for albumin and HGB were g dl⁻¹ and platelets per nanoliter. All peripheral blood values were gathered from the closest blood test before the first ICB infusion (all within 1 month before ICB start). BMI was calculated by dividing patients’ body weight (kg) over the square of height (m²) assessed before ICB treatment. TMB was defined as the total number of somatic tumor non-synonymous mutations normalized to the exonic coverage of the respective MSK-IMPACT panel in mut/Mb²⁰. The MSK-IMPACT panel identifies non-synonymous mutations in 468 genes (earlier versions included 341 or 410 genes). For tumor-derived genomic data, the MSK-IMPACT performed from the earliest retrieved sample was used if a patient had more than one MSK-IMPACT test. Clinical and demographic variables incorporated in the model were age at ICB first infusion, sex, cancer type, ICB drug class, tumor stage at ICB first infusion and history of chemotherapy before ICB treatment start. Cancers were staged according to the American Joint Committee on Cancer, 8th edition⁵⁹ FCNA was calculated as the length of FACETS^60,61 segments with | cnlr.median.clust | ≥0.2 (that is, segments with log₂ CNA value >0.2) divided by the total length of all segments. FACETS segments were classified as LOH if they had total copy number (tcn) ≥2 and minor allele copy number (lcn) = 0. HLA-I loci were classified as LOH if they overlapped (by any amount) an LOH segment. Segments with tcn = 1 and lcn = 0 were considered hemizygous, not LOH. MSI status of each tumor was determined by MSIsensor⁶² with the following criteria: stable (0 ≤ MSI score < 3), indeterminate (3 ≤ MSI score < 10) and unstable (10 ≤ MSI score). In the machine learning model, we used two groups for MSI status: MSI unstable versus MSI stable/indeterminate.

We performed high-resolution HLA-I genotyping from germline normal DNA sequencing data. For each patient, the most recent MSK-IMPACT targeted gene panel was obtained, and Polysolver was used to identify HLA-I alleles with default parameter settings⁶³. For quality assurance of HLA-I genotyping using MSK-IMPACT, we compared HLA-I typing by Polysolver between 37 samples that we sequenced with MSK-IMPACT and whole exome. The MSK-IMPACT panel successfully captured HLA-A, HLA-B and HLA-C reads, and validation was previously performed²⁵. The overall concordance of HLA-I typing between the MSK-IMPACT samples and their matched whole exome sequencing samples was 96%. To ensure that HLA-I genes had adequate coverage in MSK-IMPACT BAM files, we also applied bedtools multicov tool⁶⁴, which reports the count of alignments from multiple position-sorted and indexed BAM files that overlap with target intervals in a BED format. Only high-quality reads were counted, and only samples with sufficient coverage were used.

HED was calculated as previously described in Pierini and Lenz⁶⁵ and Chowell el al.²⁴. Briefly, we first extracted the protein sequence of exons 2 and 3 of each allele of each patients HLA-I genotype, which correspond to the peptide-binding domains. Protein sequences were obtained from the IMGT/HLA database⁶⁶, and exons coding for the variable peptide-binding domains were selected following the annotation obtained from the Ensembl database⁶⁷. Divergence values between allele sequences were calculated using the Grantham distance metric⁶⁸, as implemented in Pierini and Lenz⁶⁵. The Grantham distance is a quantitative pairwise distance in which the physiochemical properties of amino acids, and, hence, the functional similarity between sequences, are considered⁶⁸. Given a particular HLA-I locus with two alleles, the sequences of the peptide-binding domains of each allele are aligned⁶⁹, and the Grantham distance is calculated as the sum of amino acid differences (taking into account the biochemical composition, polarity and volume of each amino acid) along the sequences of the peptide-binding domains, following the formula by Grantham⁶⁸

$$\text{Grantham}\hspace{0.17em}\text{Distance}=\sum D_{ij}=\sum {\left[\alpha {\left(c_i-c_j\right)}^2+\beta {\left(p_i-p_j\right)}^2+\gamma {\left(v_i-v_j\right)}^2\right]}^{1/2}$$ (1)

where i and j are the two homologous amino acids at a given position in the alignment; c, p and v represent composition, polarity and volume of the amino acids, respectively; and α, β and γ are constants; all values are taken from the original study⁶⁸. The final Grantham distance is calculated by normalizing the value from (1) by the length of the alignment between the peptide-binding domains of a particular HLA-I genotype’s two alleles. In our model, we refer to HED as mean HED, which was calculated as the mean of divergences at HLA-A, HLA-B and HLA-C.

Model description.

We implemented a random forest classifier using the scikit-learn package⁷⁰ in Python 3.83 programming language (https://www.python.org/). To generate the training (80%) and test (20%) datasets, we split the dataset using the train_test_split function, which randomly partitions a dataset into training and test subsets with test_size=0.2 parameter. We applied this function to each cancer type individually. To build a random forest classifier with the best hyperparameters, we implemented the exhaustive grid search approach using the GridSearchCV function to the training dataset with five-fold cross-validation. Model features were used as discrete values (chemotherapy prior ICB, cancer type, LOH in HLA-I, drug class, MSI status and tumor stage) or continuous values (TMB, albumin, NLR, age, HGB, platelets, FCNA, BMI and HED). A total of 10.000 random forest classifier models were evaluated with different combinations of hyperparameters: max_features=“auto”; n_estimators ranging from 100 to 1.000 with an interval of 100; max_depth ranging from 2 to 20 with an interval of 2; min_samples_leaf ranging from 2 to 20 with an interval of 2; and min_ samples_split ranging from 2 to 20 with an interval of 2. As a result, we selected a model with n_estimators= 1,000, max_depth=8, min_samples_leaf=20 and min samples_split=2 hyperparameters, which showed the highest average accuracy at 0.7559. Also, the RF11 model was built with n_estimators=300, max_depth=4, min_samples_leaf=12 and min_samples_split=2 hyperparameters, which showed the highest average accuracy at 0.7576. The default cutoff of 0.5 was used when using GridSearchCV. To compute the feature importance for the RF16 model, we used the permutation-based importance (function Permutationlmportance) from the ELI5 Python package (https://eli5.readthedocs.io/).

Logistic regression analysis.

We used the glm function for the logistic regression model. The stepAIC function from the MASS package was applied to model selection, and we used the predict function to get the response probability of samples in the test set. To compute standardized coefficients, the beta function from the reghelper package was used. All the analyses were performed using R programming language (https://www.r-project.org/).

ROC and precision-recall curve analyses.

We generated AUC and AUPRC values for random forest and logistic regression models using the precrec package⁷¹. The prediction power of individual variable was measured by the same approach. For continuous variables, we used the actual values of each of the variables to generate the AUC and AUPRC values; for categorical variables, such as chemotherapy prior ICB (yes or no), drug class (combo or monotherapy), LOH in HLA-I (yes or no), MSI (unstable or stable/indeterminate), sex (male or female) and stage (IV or others), binary values were used. The optimal thresholds of the probabilities of response computed by the random forest and the logistic regression models, which discriminate responder and non-responder, were determined in the training set by using the Youden’s index method from the ROC curve using the pROC package⁷². We also determined the optimal threshold with the highest F-score, and there was no significant difference in the predictive power of the thresholds using Youden’s index or F-score.

Statistical analyses.

To compare the distributions of response probability generated by the integrated model and TMB among response groups, the two-sided Mann-Whitney U test was used. The correlation coefficients between the response probabilities from the pan-cancer and cancer-specific models were calculated by Spearman’s rank test using the cor_test function from the correlation package. We calculated the C-index of our model predictions and TMB alone by the concordance.index function and compared them using the cindex.comp function, which implements a paired Student’s t-test from the survcomp package⁷³. Brier score was calculated using the pec package⁷⁴. We visualized ROC and precision-recall curves and calculated the AUC using the precrec package⁷¹. The Kaplan-Meier plot, log-rank P values and Cox proportional HRs were generated by the survminer package. All the aforementioned packages and functions are included in R programming language (https://www.r-project.org/).

Data availability

All de-identified data needed to replicate all analyses are in Supplementary Table 3 and are available online at https://www.ioexplorer.org.