DOUBLY DEBIASED LASSO: HIGH-DIMENSIONAL INFERENCE UNDER HIDDEN CONFOUNDING

Abstract

Inferring causal relationships or related associations from observational data can be invalidated by the existence of hidden confounding. We focus on a high-dimensional linear regression setting, where the measured covariates are affected by hidden confounding and propose the Doubly Debiased Lasso estimator for individual components of the regression coefficient vector. Our advocated method simultaneously corrects both the bias due to estimation of high-dimensional parameters as well as the bias caused by the hidden confounding. We establish its asymptotic normality and also prove that it is efficient in the Gauss-Markov sense. The validity of our methodology relies on a dense confounding assumption, i.e. that every confounding variable affects many covariates. The finite sample performance is illustrated with an extensive simulation study and a genomic application.

1. Introduction.

Observational studies are often used to infer causal relationship in fields such as genetics, medicine, economics or finance. A major concern for confirmatory conclusions is the existence of hidden confounding [27, 42]. In this case, standard statistical methods can be severely biased, particularly for large-scale observational studies, where many measured covariates are possibly confounded.

To better address this problem, let us consider first the following linear Structural Equation Model (SEM) with a response Y_i, high-dimensional measured covariates $X_{i,\cdot }\in {ℝ}^p$ and hidden confounders $H_{i,\cdot }\in {ℝ}^q$:

$$Y_i\leftarrow {\beta }^{\top }{X}_{i,\cdot }+{\varphi }^{\top }{H}_{i,\cdot }+e_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{X}_{i,\cdot }\leftarrow {\mathrm{\Psi }}^{\top }{H}_{i,\cdot }+E_{i,\cdot }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.33em}\text{1}\le i\le n,$$ (1)

where the random error $e_i\in ℝ$ is independent of $X_{i,\cdot }\in {ℝ}^p$, $H_{i,\cdot }\in {ℝ}^q$ and $E_{i,\cdot }\in {ℝ}^p$ and the components of $E_{i,\cdot }\in {ℝ}^p$ are uncorrelated with the components of $H_{i,\cdot }\in {ℝ}^q$ The focus on a SEM as in (1) is not necessary and we relax this restriction in model (2) below. Such kind of models are used for e.g. biological studies to explore the effects of measured genetic variants on the disease risk factor, and the hidden confounders can be geographic information [46], data sources in mental analysis [48] or general population stratification in GWAS [43].

Our aim is to perform statistical inference for individual components β_j, 1≤ j ≤ p, of the coefficient vector, where p can be large, in terms of obtaining confidence intervals or statistical tests. This inference problem is challenging due to high dimensionality of the model and the existence of hidden confounders. As a side remark, we mention that our proposed methodology can also be used for certain measurement error models, an important general topic in statistics and economics [11, 62].

1.1. Our Results and Contributions.

We focus on a dense confounding model, where the hidden confounders H_i,· in (1) are associated with many measured covariates X_i,.. Such dense confounding model seems reasonable in quite many practical applications, e.g. for addressing the problem of batch effects in biological studies [29, 33, 38].

We propose a two-step estimator for the regression coefficient β_j for 1 ≤ j ≤ p in the high-dimensional dense confounding setting, where a large number of covariates have possibly been affected by hidden confounding. In the first step, we construct a penalized spectral deconfounding estimator ${\widehat{\beta }}^{init}$ as in [12], where the standard squared error loss is replaced by a squared error loss after applying a certain spectral transformation to the design matrix X and the response Y. In the second step, for the regression coefficient of interest β_j, we estimate the high-dimensional nuisance parameters β_−j = {β_l; l ≠ j} by ${\widehat{\beta }}_{-j}^{init}$ and construct an approximately unbiased estimator ${\widehat{\beta }}_j$.

The main idea of the second step is to correct the bias from two sources, one from estimating the high-dimensional nuisance vector β_−j by ${\widehat{\beta }}_{-j}^{init}$ and the other arising from hidden confounding. In the standard high-dimensional regression setting with no hidden confounding, debiasing, desparsifying or Neyman’s Orthogonalization were proposed for inference for β_j [65, 56, 32, 4, 15, 21, 14]. However, these methods, or some of its direct extensions, do not account for the bias arising from hidden confounding. In order to address this issue, we introduce a Doubly Debiased Lasso estimator which corrects both biases simultaneously. Specifically, we construct a spectral transformation ${𝓟}^{\left(j\right)}\in {ℝ}^{n\times n}$, which is applied to the nuisance design matrix X_−j when the parameter of interest is β_j. This spectral transformation is crucial to simultaneously correcting the two sources of bias.

We establish the asymptotic normality of the proposed Doubly Debiased Lasso estimator in Theorem 1. An efficiency result is also provided in Theorem 2 of Section 4.2.1, showing that the Doubly Debiased Lasso estimator retains the same Gauss-Markov efficiency bound as in standard high-dimensional linear regression with no hidden confounding [56, 31]. Our result is in sharp contrast to Instrumental Variables (IV) based methods, see Section 1.2, whose inflated variance is often of concern, especially with a limited amount of data [62, 6]. This remarkable efficiency result is possible by assuming denseness of confounding. Various intermediary results of independent interest are also derived in Section A of the supplementary material. Finally, the performance of the proposed estimator is illustrated on simulated and real genomic data in Section 5.

To summarize, our main contribution is two-fold:

1. We propose a novel Doubly Debiased Lasso estimator for individual coefficients β_j and estimation of the corresponding standard error in a high-dimensional linear SEM with hidden confounding.

2. We show that the proposed estimator is asymptotically Gaussian and efficient in the Gauss-Markov sense. This implies the construction of asymptotically optimal confidence intervals for individual coefficients β_j.

The code for using the Doubly Debiased Lasso estimator is available at https://github.com/zijguo/Doubly-Debiased-Lasso.

1.2. Related Work.

In econometrics, hidden confounding and measurement errors are unified under the framework of endogenous variables. Inference for treatment effects or corresponding regression parameters in presence of hidden confounders or measurement errors has been extensively studied in the literature with Instrumental Variables (IV) regression. The construction of IVs typically requires a lot of domain knowledge, and obtained IVs are often suspected of violating the main underlying assumptions [30, 62, 34, 8, 28, 61]. In high dimensions, the construction of IVs is even more challenging, since for identification of the causal effect, one has to construct as many IVs as the number of confounded covariates, which is the so-called “rank condition" [62]. Some recent work on the high-dimensional hidden confounding problem relying on the construction of IVs includes [23, 18, 40, 3, 67, 45, 25]. Another approach builds on directly estimating and adjusting with respect to latent factors [60].

A major distinction of the current work from the contributions above is that we consider a confounding model with a denseness assumption [13, 12, 53]. [12] consider point estimation of β in the high-dimensional hidden confounding model (1), whereas [53] deal with point estimation of the precision and covariance matrix of high-dimensional covariates, which are possibly confounded. The current paper is different in that it considers the challenging problem of confidence interval construction, which requires novel ideas for both methodology and theory.

The dense confounding model is also connected to the high-dimensional factor models [17, 37, 36, 20, 59]. The main difference is that the factor model literature focuses on accurately extracting the factors, while our method is essentially filtering them out in order to provide consistent estimators of regression coefficients, under much weaker requirements than for the identification of factors.

Another line of research [22, 55, 58] studies the latent confounder adjustment models but focuses on a different setting where many outcome variables can be possibly associated with a small number of observed covariates and several hidden confounders.

Notation.

We use $X_j\in {ℝ}^n$ and $X_{-j}\in {ℝ}^{n\times \left(p-1\right)}$ to denote the j—th column of the matrix X and the sub-matrix of X excluding the j—th column, respectively; $X_{i,\cdot }\in {ℝ}^p$ is used to denote the i—th row of the matrix X (as a column vector); X_i,−j and X_i,−j denote respectively the (i, j) entry of the matrix X and the sub-row of X_i,· excluding the j-th entry. Let [p]= {1, 2,... , p}. For a subset $J\subseteq \left[p\right]$ and a vector $x\in {ℝ}^p$, x_J is the sub-vector of x with indices in J and x_−J is the sub-vector with indices in J^c. For a set S, |S| denotes the cardinality of S. For a vector $x\in {ℝ}^p$, the ℓ_q norm of x is defined as ${‖x‖}_q={\left({\sum }_{l=1}^p{\left|x_l\right|}^q\right)}^{\frac{1}{q}}$ for q ≥ 0 with ${‖x‖}_0=\left|\left\{1\le l\le p:x_l\ne 0\right\}\right|$ and ${‖x‖}_{\infty }={\max }_{1\le l\le p}\left|x_l\right|$. We use e_i to denote the i-th standard basis vector in ${ℝ}^p$ and I_p to denote the identity matrix of size p × p. We use c and C to denote generic positive constants that may vary from place to place. For a sub-Gaussian random variable X, we use ${‖X‖}_{{\psi }_2}$ to denote its sub-Gaussian norm; see definitions 5.7 and 5.22 in [57]. For a sequence of random variables X_n indexed by n, we use $X_n\stackrel{p}{\to }X$ and $X_n\stackrel{d}{\to }X$ to represent that X_n converges to X in probability and in distribution, respectively. For a sequence of random variables X_n and numbers a_n, we define X_n = o_p(a_n) if X_n/a_n converges to zero in probability. For two positive sequences a_n and b_n, $a_n\lesssim b_n$ means that $\exists C>0$ such that a_n ≤ Cb_n for all n; $a_n\asymp b_n$ if $a_n\lesssim b_n$ and $b_n\lesssim a_n$, and a_n ≪ b_n if $\lim {\sup }_{n\to \infty }{a}_n/b_n=0$. For a matrix M, we use ‖ M ‖_F, ‖ M ‖ ₂ and ‖ M ‖₂ and ‖ M ‖_ꚙ to denote its Frobenius norm, spectral norm and element-wise maximum norm, respectively. We use λ_j(M) to denote the j-th largest singular value of some matrix M, that is, λ₁(M) ≥ λ₂(M) ≥ … ≥ λ_q (M) ≥ 0. For a symmetric matrix A, we use λ_max(A) and λ_min(A) to denote its maximum and minimum eigenvalues, respectively.

2. Hidden Confounding Model.

We consider the Hidden Confounding Model for i.i.d. data {X_i,·, Y_i}_1≤i≤n and unobserved i.i.d. confounders {H_i,·}_1≤i≤n, given by:

$$Y_i={\beta }^{\top }{X}_{i,\cdot }+{\varphi }^{\top }{H}_{i,\cdot }+e_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{X}_{i,\cdot }={\mathrm{\Psi }}^{\top }{H}_{i,\cdot }+E_{i,\cdot },$$ (2)

where $Y_i\in ℝ$ and $X_{i,\cdot }\in {ℝ}^p$ respectively denote the response and the measured covariates and $H_{i,\cdot }\in {ℝ}^q$ represents the hidden confounders. We assume that the random error $e_i\in ℝ$ is independent of $X_{i,\cdot }\in {ℝ}^p$, $H_{i,\cdot }\in {ℝ}^q$ and $E_{i,\cdot }\in {ℝ}^p$ and the components of $E_{i,\cdot }\in {ℝ}^p$ are uncorrelated with the components of $H_{i,\cdot }\in {ℝ}^q$.

The coefficient matrices $\mathrm{\Psi }\in {ℝ}^{q\times p}$ and $\varphi \in {ℝ}^{q\times 1}$ encode the linear effect of the hidden confounders H_i,· on the measured covariates X_i, and the response Y_i, respectively. We consider the high-dimensional setting where p might be much larger than n. Throughout the paper it is assumed that the regression vector $\beta \in {ℝ}^p$ is sparse, with a small number k of nonzero components, and that the number q of confounding variables is a small positive integer. However, both k and q are allowed to grow with n and p. We write ${\sum }_E$ or ${\sum }_X$ for the covariance matrices of E_i, or X_i,., respectively. Without loss of generality, it is assumed that $\mathbb{E}{X}_{i,\cdot }=0$, $\mathbb{E}{H}_{i,\cdot }=0$, Cov(H_i,.)= I_q and hence ${\sum }_X={\mathrm{\Psi }}^{\top }\mathrm{\Psi }+{\sum }_E$.

The probability model (2) is more general than the Structural Equation Model in (1). It only describes the observational distribution of the latent variable H_i,· and the observed data (X_i,., Y_i), which possibly may be generated from the hidden confounding SEM (1).

Our goal is to construct confidence intervals for the components of β, which in the model (1) describes the causal effect of X on the response Y. The problem is challenging due to the presence of unobserved confounding. In fact, the regression parameter β can not even be identified without additional assumptions. Our main condition addressing this issue is a denseness assumption that the rows ${\mathrm{\Psi }}_{j,\cdot }\in {ℝ}^p$ are dense in a certain sense (see Condition (A2) in Section 4), i.e., many covariates of $X_{i,\cdot }\in {ℝ}^p$ are simultaneously affected by hidden confounders $H_{i,\cdot }\in {ℝ}^q$.

2.1. Representation as a Linear Model.

The Hidden Confounding Model (2) can be represented as a linear model for the observed data {X_i,., Y_i}_1≤i≤n:

$$Y_i={\left(\beta +b\right)}^{\top }{X}_{i,\cdot }+{ϵ}_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{X}_{i,\cdot }={\mathrm{\Psi }}^{\top }{H}_{i,\cdot }+E_{i,\cdot },$$ (3)

by writing

$${ϵ}_i=e_i+{\varphi }^{\top }{H}_{i,\cdot }-b^{\top }{X}_{i,\cdot \hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{b=}{\sum }_X^{-1}{\mathrm{\Psi }}^{\top }\varphi .$$

As in (2) we assume that E_i,·· is uncorrelated with H_i,· and, by construction of b, ϵ_i is uncorrelated w ith X_i,·. With ${\sigma }_e^2$ denoting the variance of e_i, the variance of the error ϵ_i equals ${\sigma }_{ϵ}^2={\sigma }_e^2+{\varphi }^{\top }\left({\text{I}}_q-\mathrm{\Psi }{\sum }_X^{-1}{\mathrm{\Psi }}^{\top }\right)\varphi$. In model (3) the response is generated from a linear model where the sparse coefficient vector β has been perturbed by some perturbation vector $b\in {ℝ}^p$. This representation reveals how the parameter of interest β is not in general identifiable from observational data, where one can not easily differentiate it from the perturbed coefficient vector β +b, with the perturbation vector b induced by hidden confounding. However, as shown in Lemma 2 in the supplement, b is dense and ‖ b ‖₂ is small for large p under the assumption of dense confounding, which enables us to identify β asymptotically. It is important to note that the term b^⊤X_i,. induced by hidden confounders H_i, is not necessarily small and hence cannot be simply ignored in model (3), but requires novel methodological approach.

Connection to measurement errors.

We briefly relate certain measurement error models to the Hidden Confounding Model (2). Consider a linear model for the outcome Y_i and covariates $X_{i\cdot }^0\in {ℝ}^p$, where we only observe $X_{i,\cdot }\in {ℝ}^p$ with measurement error $W_{i,\cdot }\in {ℝ}^p$:

$$Y_i={\beta }^{\top }{X}_{i\cdot }^0+e_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{X}_{i,\cdot }=X_{i,\cdot }^0+W_{i,\cdot \hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for1}\le i\le n.$$ (4)

Here, e_i is a random error independent of $X_{i,\cdot }^0$ and W_i,. and W_i,· is the measurement error independent of $X_i^0$. We can then express a linear dependence of Y_i on the observed Xi,.,

$$Y_i={\beta }^{\top }{X}_{i,\cdot }+\left(e_i-{\beta }^{\top }{W}_{i,\cdot }\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{X}_{i,\cdot }=W_{i,\cdot }+X_{i,\cdot }^0$$

We further assume the following structure of the measurement error:

$$W_{i,\cdot }={\mathrm{\Psi }}^{\top }{H}_{i,\cdot },$$

i.e. there exist certain latent variables $H_{i,\cdot }\in {ℝ}^q$ that contribute independently and linearly to the measurement error, a conceivable assumption in some practical applications. Combining this with the equation above we get

$$Y_i={\beta }^{\top }{X}_{i,\cdot }+\left(e_i-{\varphi }^{\top }{H}_{i,\cdot }\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{X}_{i,\cdot }={\mathrm{\Psi }}^{\top }{H}_{i,\cdot }+X_{i\cdot }^0,$$ (5)

where $\varphi =\mathrm{\Psi }\beta \in {ℝ}^q$. Therefore, the model (5) can be seen as a special case of the model (2), by identifying $X_{i\cdot }^0$ in (5) with E_i,· in (2).

3. Doubly Debiased Lasso Estimator.

In this section, for a fixed index j ϵ{1,..., p}, we propose an inference method for the regression coefficient β_j of the Hidden Confounding Model (2). The validity of the method is demonstrated by considering the equivalent model (3).

3.1. Double Debiasing.

We denote by ${\widehat{\beta }}^{init}$ an initial estimator of β. We will use the spectral deconfounding estimator proposed in [12], described in detail in Section 3.4. We start from the following decomposition:

$$Y-X_{-j}{\widehat{\beta }}_{-j}^{init}=X_j\left({\beta }_j+b_j\right)+X_{-j}\left({\beta }_{-j}-{\widehat{\beta }}_{-j}^{init}\right)+X_{-j}{b}_{-j}+ϵ\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j\in \left\{1,\mathrm{...},p\right\}.$$ (6)

The above decomposition reveals two sources of bias: the bias $X_{-j}\left({\beta }_{-j}-{\widehat{\beta }}_{-j}^{init}\right)$ due to the error of the initial estimator ${\widehat{\beta }}^{init}$ and the bias X_−jb_−j induced by the perturbation vector b in the model (3), arising by marginalizing out the hidden confounding in (2). Note that the bias b_j is negligible in the dense confounding setting, see Lemma 2 in the supplement. The first bias, due to penalization, appears in the standard high-dimensional linear regression as well, and can be corrected with the debiasing methods proposed in [65, 56, 32] when assuming no hidden confounding. However, in presence of hidden confounders, methodological innovation is required for correcting both bias terms and conducting the resulting statistical inference. We propose a novel Doubly Debiased Lasso estimator for correcting both sources of bias simultaneously.

Denote by ${𝓟}^{\left(j\right)}\in {ℝ}^{n\times n}$ a symmetric spectral transformation matrix, which shrinks the singular values of the sub-design $X_{-j}\in {ℝ}^{n\times \left(p-1\right)}$. The detailed construction, together with some examples, is given in Section 3.3. We shall point out that the construction of the transformation matrix ${𝓟}^{\left(j\right)}$ depends on which coefficient β_j is our target and hence refer to ${𝓟}^{\left(j\right)}$ as the nuisance spectral transformation with respect to the coefficient β_j. Multiplying both sides of the decomposition (6) with the transformation ${𝓟}^{\left(j\right)}$ gives:

$${𝓟}^{\left(j\right)}\left(Y-X_{-j}{\widehat{\beta }}_{-j}^{init}\right)={𝓟}^{\left(j\right)}{X}_j\left({\beta }_j+b_j\right)+{𝓟}^{\left(j\right)}{X}_{-j}\left({\beta }_{-j}-{\widehat{\beta }}_{-j}^{init}\right)+{𝓟}^{\left(j\right)}{X}_{-j}{b}_{-j}+{𝓟}^{\left(j\right)}ϵ.$$ (7)

The quantity of interest β_j appears on the RHS of the equation (7) next to the vector ${𝓟}^{\left(j\right)}{X}_j$, whereas the additional bias lies in the span of the columns of ${𝓟}^{\left(j\right)}{X}_{-j}$. For this reason, we construct a projection direction vector ${𝓟}^{\left(j\right)}{Z}_j\in {ℝ}^n$ as the transformed residuals of regressing X_j on X_−j:

$$Z_j=X_j-X_{-j}\widehat{\gamma },$$ (8)

where the coefficients $\widehat{\gamma }$ are estimated with the Lasso for the transformed covariates using ${𝓟}^{\left(j\right)}$:

$$\widehat{\gamma }=\underset{\gamma \in {ℝ}^{p-1}}{\arg \min }\left\{\frac{1}{2n}{‖{𝓟}^{\left(j\right)}{X}_j-{𝓟}^{\left(j\right)}{X}_{-j}\gamma ‖}_2^2+{\lambda }_j\sum _{l\ne j}\frac{{‖{𝓟}^{\left(j\right)}{X}_l‖}_2}{\sqrt{n}}\left|{\gamma }_l\right|\right\},$$ (9)

with ${\lambda }_j=A{\sigma }_j\sqrt{\log p/n}$ for some positive constant $A>\sqrt{2}$ (for σ_j, see Section 4.1).

Finally, motivated by the equation (7), we propose the following estimator for β_j:

$${\widehat{\beta }}_j=\frac{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}\left(Y-X_{-j}{\widehat{\beta }}_{-j}^{init}\right)}{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_j}.$$ (10)

We refer to this estimator as the Doubly Debiased Lasso estimator as it simultaneously corrects the bias induced by ${\widehat{\beta }}^{init}$ and the confounding bias X_−jb_−j by using the spectral transformation ${𝓟}^{\left(j\right)}$.

In the following, we briefly explain why the proposed estimator estimates β_j well. We start with the following error decomposition of ${\widehat{\beta }}_j$, derived from (7)

$${\widehat{\beta }}_j-{\beta }_j=\underset{\text{Variance}}{\underbrace{\frac{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}ϵ}{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_j}}}+\underset{\text{Remaining Bias}}{\underbrace{\frac{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_{-j}\left({\beta }_{-j}-{\widehat{\beta }}_{-j}^{init}\right)}{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_j}+\frac{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_{-j}{b}_{-j}}{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_j}+b_j}}.$$ (11)

In the above equation, the bias after correction consists of two components: the remaining bias due to the estimation error of ${\widehat{\beta }}_{-j}^{init}$ and the remaining confounding bias due to X_−jb_−j. and b_j. These two components can be shown to be negligible in comparison to the variance component under certain model assumptions, see Theorem 1 and its proof for details. Intuitively, the construction of the spectral transformation matrix ${𝓟}^{\left(j\right)}$ is essential for reducing the bias due to the hidden confounding. The term $\frac{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_{-j}{b}_{-j}}{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_j}$ in equation (11) is of a small order because ${𝓟}^{\left(j\right)}$ shrinks the leading singular values of X_−j and hence ${𝓟}^{\left(j\right)}{X}_{-j}{b}_{-j}$ is significantly smaller than X_−jb_−j. The induced bias X_−jb_−j is not negligible since b_−j points in the direction of leading right singular vectors of X_−j, thus leading to ${‖\frac{1}{\sqrt{n}}{X}_{-j}{b}_{-j}‖}_2$ being of constant order. By applying a spectral transformation to shrink the leading singular values, one can show that ${‖\frac{1}{\sqrt{n}}{𝓟}^{\left(j\right)}{X}_{-j}{b}_{-j}‖}_2=O_p\left(1/\sqrt{\min \left\{n,p\right\}}\right).$.

Furthermore, the other remaining bias term $\frac{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_{-j}\left({\beta }_{-j}-{\widehat{\beta }}_{-j}^{init}\right)}{{\left({𝓟}^{\left(j\right)}{Z}_j\right)}^{\top }{𝓟}^{\left(j\right)}{X}_j}$ in (11) is small since the initial estimator ${\widehat{\beta }}^{init}$ is close to β in ℓ₁ norm and ${𝓟}^{\left(j\right)}{Z}_j$ and ${𝓟}^{\left(j\right)}{X}_{-j}$ are nearly orthogonal due to the construction of $\widehat{\gamma }$ in (9). This bias correction idea is analogous to the Debiased Lasso estimator introduced in [65] for the standard high-dimensional linear regression:

$${\widehat{\beta }}_j^{DB}=\frac{{\left(Z_j^{DB}\right)}^{\top }\left(Y-X_{-j}{\widehat{\beta }}_{-j}^{init}\right)}{{\left(Z_j^{DB}\right)}^{\top }{X}_j}$$ (12)

where $Z_j^{DB}$ is constructed similarly as in (8) and (9) with setting ${𝓟}^{\left(j\right)}$ as the identity matrix. Therefore, the main difference between the estimator in (12) and our proposed estimator (10) is that we additionally apply the nuisance spectral transformation ${𝓟}^{\left(j\right)}$.

We emphasize that the additional spectral transformation ${𝓟}^{\left(j\right)}$ is necessary even for just correcting the bias of ${\widehat{\beta }}_{-j}^{init}$ in presence of confounding (i.e., it is also needed for the first besides the second bias term in (11)). To see this, we define the best linear projection of X_1,j to all other variables $X_{1,-j}\in {ℝ}^{p-1}$ with the coefficient vector $\gamma ={\left[\mathbb{E}\left(X_{i,-j}{X}_{i,-j}^{\top }\right)\right]}^{-1}\mathbb{E}\left(X_{i,-j}{X}_{i,j}\right)\in {ℝ}^{p-1}$ (which is then estimated by the Lasso in the standard construction of $Z_j^{DB}$). We notice that γ need not be sparse due to the fact that all covariates are affected by a common set of hidden confounders yielding spurious associations. Hence, the standard construction of $Z_j^{DB}$ in (12) is not favorable in the current setting. In contrast, the proposed method with ${𝓟}^{\left(j\right)}$ works for two reasons: first, the application of ${𝓟}^{\left(j\right)}$ in (9) leads to a consistent estimator of the sparse component of γ, denoted as γγ^E (see the expression of γ^E in Lemma 1); second, the application of ${𝓟}^{\left(j\right)}$ leads to a small prediction error ${𝓟}^{\left(j\right)}{X}_{-j}\left(\widehat{\gamma }-{\gamma }^E\right)$. We illustrate in Section 5 how the application of ^{${𝓟}^{\left(j\right)}$} corrects the bias due to ${\widehat{\beta }}_{-j}^{init}$ and observe a better empirical coverage after applying ${𝓟}^{\left(j\right)}$ in comparison to the standard debiased Lasso in (12); see Figure 7.

FIG 7.

(No confounding bias) Dependence of the (scaled) absolute bias terms |B_β| and |B_b| (left), standard deviation V^1/2 (middle) and the coverage of the 95% confidence interval (right) on the number of covariates p, while keeping n = 500 fixed. In the plots on the left, |B_β| and |B_b| are denoted by a dashed and a solid line, respectively, but B_b =0 since we have enforced b = 0. Top row corresponds to the spiked covariance case ${\Sigma }_X={\mathrm{\Psi }}^T\mathrm{\Psi }+I$, whereas for the bottom row we set ${\Sigma }_X=I$. Blue color corresponds to the Doubly Debiased Lasso, red color represents the standard Debiased Lasso and green color corresponds also to the Debiased Lasso estimator, but with the same ${\widehat{\beta }}^{init}$ as our proposed method. Note that the last two methods have almost indistinguishable V.

3.2. Confidence Interval Construction.

In Section 4, we establish the asymptotic normal limiting distribution of the proposed estimator ${\widehat{\beta }}_j$ under certain regularity conditions. Its standard deviation can be estimated by $\sqrt{\frac{{\widehat{\sigma }}_e^2\cdot Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^4{Z}_j}{{\left[Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_j\right]}^2}}$ with ${\widehat{\sigma }}_e$ denoting a consistent estimator of σ_e. The detailed construction of ${\widehat{\sigma }}_e$ is described in Section 3.5. Therefore, a confidence interval (CI) with asymptotic coverage 1 – α can be obtained as

$$\text{CI}\left({\beta }_j\right)=\left({\widehat{\beta }}_j-z_{1-\frac{\alpha }{2}}\sqrt{\frac{{\widehat{\sigma }}_e^2\cdot Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^4{Z}_j}{{\left[Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_j\right]}^2}},{\widehat{\beta }}_j-z_{1-\frac{\alpha }{2}}\sqrt{\frac{{\widehat{\sigma }}_e^2\cdot Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^4{Z}_j}{{\left[Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_j\right]}^2}}\right),$$ (13)

where $z_{1-\frac{\alpha }{2}}$ is the $1-\frac{\alpha }{2}$ quantile of a standard normal random variable.

3.3. Construction of Spectral Transformations.

Construction of the spectral transformation ${𝓟}^{\left(j\right)}\in {ℝ}^{n\times n}$ is an essential step for the Doubly Debiased Lasso estimator (10). The transformation ${𝓟}^{\left(j\right)}\in {ℝ}^{n\times n}$ is a symmetric matrix shrinking the leading singular values of the design matrix $X_{-j}\in {ℝ}^{n\times \left(p-1\right)}$. Denote by m = min{n, p— 1} and the SVD of the matrix X_−j by X_−j = U(X_−j) Λ (X_−j)[V (X_−j)]^⸆, where $U\left(X_{-j}\right)\in {ℝ}^{n\times m}$ and $V\left(X_{-j}\right)\in {ℝ}^{\left(p-1\right)\times m}$ have orthonormal columns and $\mathrm{\Lambda }\left(X_{-j}\right)\in {ℝ}^{m\times m}$ is a diagonal matrix of singular values which are sorted in a decreasing order. We then define the spectral transformation ${𝓟}^{\left(j\right)}$ for X_−j as ${𝓟}^{\left(j\right)}=U\left(X_{-j}\right)S\left(X_{-j}\right){\left[U\left(X_{-j}\right)\right]}^{\top }$, where $S\left(X_{-j}\right)\in {ℝ}^{m\times m}$ is a diagonal shrinkage matrix with 0 ≤ S_l,l(X_−j) ≤ 1 for 1 ≤ 1≤ m. The SVD for the complete design matrix X is defined analogously. We highlight the dependence of the SVD decomposition on X_−j, but for simplicity it will be omitted when there is no confusion. Note that ${𝓟}^{\left(j\right)}{X}_{-j}=U\left(S\mathrm{\Lambda }\right)V^{\top }$, so the spectral transformation shrinks the singular values ${\left\{{\mathrm{\Lambda }}_{l,l}\right\}}_{1\le l\le m}$ to ${\left\{S_{l,l}{\mathrm{\Lambda }}_{l,l}\right\}}_{1\le l\le m}$, where ${\mathrm{\Lambda }}_{l,l}={\mathrm{\Lambda }}_{l,l}\left(X_{-j}\right)$.

Trim transform.

For the rest of this paper, the spectral transformation that is used is the Trim transform [12]. It limits any singular value to be at most some threshold τ. This means that the shrinkage matrix S is given as: for 1 ≤ l ≤ m,

$$S_{l,l}=\left\{\begin{array}{l}\tau /{\mathrm{\Lambda }}_{l,l}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{\Lambda }}_{l,l}>\tau \\ 1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{otherwise}\end{array}\right.\hspace{0.17em}\hspace{0.17em}.$$

A good default choice for the threshold τ is the median singular value ${\mathrm{\Lambda }}_{⌊m/2⌋,⌊m/2⌋}$, so only the top half of the singular values is shrunk to the bulk value ${\mathrm{\Lambda }}_{⌊m/2⌋,⌊m/2⌋}$ and the bottom half is left intact. More generally, one can use any percentile ρ_j ϵ (0, 1) to shrink the top (100ρ_j)% singular values to the corresponding ρ_j-quantile ${\mathrm{\Lambda }}_{⌊{\rho }_{j}m⌋,⌊{\rho }_{j}m⌋}$. We define the ρ_j-Trim transform ${𝓟}^{\left(j\right)}$ as

$${𝓟}^{\left(j\right)}=U\left(X_{-j}\right)S\left(X_{-j}\right){\left[U\left(X_{-j}\right)\right]}^{\top }\text{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_{l,l}\left(X_{-j}\right)=\left\{\begin{array}{ll}\frac{{\mathrm{\Lambda }}_{⌊{\rho }_{j}m⌋,⌊{\rho }_{j}m⌋}\hspace{0.17em}\left(X_{-j}\right)}{{\mathrm{\Lambda }}_{l,l}\left(X_{-j}\right)}\hfill & \text{if}\hspace{0.17em}l\le ⌊{\rho }_{j}m⌋\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}\right..$$ (14)

In Section 4 we investigate the dependence of the asymptotic efficiency of the resulting Doubly Debiased Lasso ${\widehat{\beta }}_j$ on the percentile choice ${\rho }_j={\rho }_j\left(n\right)$. There is a certain trade-off in choosing ρ_j: a smaller value of ρ_j leads to a more efficient estimator, but one needs to be careful to keep ρ_j m sufficiently large compared to the number of hidden confounders q, in order to ensure reduction of the confounding bias. In Section A.1 of the supplementary material, we describe the general conditions that the used spectral transformations need to satisfy to ensure good performance of the resulting estimator.

3.4. Initial Estimator ${\widehat{\beta }}^{init}$.

For the Doubly Debiased Lasso (10), we use the spectral deconfounding estimator proposed in [12] as our initial estimator ${\widehat{\beta }}^{init}$. It uses a spectral transformation $𝓠=𝓠\left(X\right)$, constructed similarly as the transformation ${𝓟}^{\left(j\right)}$ described in Section 3.3, with the difference that instead of shrinking the singular values of X_−j, $𝓠$ shrinks the leading singular values of the whole design matrix $X\in {ℝ}^{n\times p}$. Specifically, for any percentile ρ ϵ (0, 1), the ρ-Trim transform $𝓠$ is given by

$$𝓠=U\left(X\right)S\left(X\right){\left[U\left(X\right)\right]}^{\top }\text{with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{S}_{l,l}\left(X\right)=\left\{\begin{array}{ll}\frac{{\mathrm{\Lambda }}_{⌊\rho m⌋,⌊\rho m⌋}\hspace{0.17em}\left(X\right)}{{\mathrm{\Lambda }}_{l,l}\left(X\right)}\hfill & \text{if}\hspace{0.17em}l\le ⌊\rho m⌋\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}\right..$$ (15)

The estimator ${\widehat{\beta }}^{init}$ is computed by applying the Lasso to the transformed data $𝓠X$ and $𝓠Y$:

$${\widehat{\beta }}^{init}=\arg \underset{\beta \in {ℝ}^p}{\min }\frac{1}{2n}{‖𝓠\left(y-X\beta \right)‖}_2^2+\lambda \sum _{j=1}^p\frac{{‖𝓠X_{\cdot j}‖}_2}{\sqrt{n}}\left|{\beta }_j\right|,$$ (16)

where $\lambda =A{\sigma }_e\sqrt{\log p/n}$ is a tuning parameter with $A>\sqrt{2}$.

The transformation $𝓠$ reduces the effect of the confounding and thus helps for estimation of β. In Section A.3, the ℓ₁ and ℓ₂-error rates of ${\widehat{\beta }}^{init}$ are given, thereby extending the results of [12].

3.5. Noise Level Estimator.

In addition to an initial estimator of β, we also require a consistent estimator ${\widehat{\sigma }}_e^2$ of the error variance ${\widehat{\sigma }}_e^2=\mathbb{E}\left(e_i^2\right)$ for construction of confidence intervals. Choosing a noise level estimator which performs well for a wide range of settings is not easy to do in practice [50]. We propose using the following estimator:

$${\widehat{\sigma }}_e^2=\frac{1}{\text{Tr}\left({𝓠}^2\right)}{‖𝓠y-𝓠X{\widehat{\beta }}^{init}‖}_2^2,$$ (17)

where $𝓠$ is the same spectral transformation as in (16).

The motivation for this estimator is based on the expression

$$𝓠y-𝓠X{\widehat{\beta }}^{init}=𝓠ϵ+𝓠X\left(\beta -{\widehat{\beta }}^{init}\right)+𝓠Xb,$$ (18)

which follows from the model (3). The consistency of the proposed noise level estimator, formally shown in Proposition 2, follows from the following observations: the initial spectral deconfounding estimator ${\widehat{\beta }}^{init}$ has a good rate of convergence for estimating β; the spectral transformation $𝓠$ significantly reduces the additional error Xb induced by the hidden confounders; ${‖𝓠ϵ‖}_2^2/\text{Tr}\left({𝓠}^2\right)$ consistently estimates ${\sigma }_{ϵ}^2$. Additionally, the dense confounding model is shown to lead to a small difference between the noise levels ${\sigma }_{ϵ}^2$ and ${\sigma }_e^2$, see Lemma 2 in the supplement. In Section 4 we show that variance estimator ${\widehat{\sigma }}_e^2$ defined in (17) is a consistent estimator of ${\sigma }_e^2$.

3.6. Method Overview and Choice of the Tuning Parameters.

The Doubly Debiased Lasso needs specification of various tuning parameters. A good and theoretically justified rule of thumb is to use the Trim transform with ρ = ρ_{j =} 1/2, which shrinks the large singular values to the median singular value, see (14). Furthermore, similarly to the standard Debiased Lasso [65], our proposed method involves the regularization parameters λ in the Lasso regression for the initial estimator ${\widehat{\beta }}^{init}$ (see equation (16)) and λ_j in the Lasso regression for the projection direction ${𝓠}^{\left(j\right)}{Z}_j$ (see equation (9)). For choosing λ we use 10-fold cross-validation, whereas for λ_j, we increase slightly the penalty chosen by the 10-fold cross-validation, so that the variance of our estimator, which can be determined from the data up to a proportionality factor ${\sigma }_e^2$, increases by 25%, as proposed in [16].

The proposed Doubly Debiased Lasso method is summarized in Algorithm 1, which

$$\overline{\underset{¯}{\begin{array}{l}\mathbf{A}\mathbf{l}\mathbf{g}\mathbf{o}\mathbf{r}\mathbf{i}\mathbf{t}\mathbf{h}\mathbf{m} 1\text{ Doubly Debiased Lasso}\\ \overline{\begin{array}{l}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\mathbf{I}\mathbf{n}\mathbf{p}\mathbf{u}\mathbf{t}:\text{ Data}\hspace{0.33em}X\in {ℝ}^{n\times p},Y\in {ℝ}^n;\hspace{0.33em}\text{index}\hspace{0.33em}j,\hspace{0.33em}\text{tuning}\hspace{0.33em}\text{parameters}\hspace{0.33em}\rho ,{\rho }_j\in \left(0,1\right)\hspace{0.33em}\text{and}\hspace{0.33em}\lambda >0,{\lambda }_j>0\\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}\mathbf{O}\mathbf{u}\mathbf{t}\mathbf{p}\mathbf{u}\mathbf{t}:\hspace{0.33em}\text{Point}\hspace{0.33em}\text{estimator}\hspace{0.33em}{\widehat{\beta }}_j,\hspace{0.33em}\text{standard error estimate}\hspace{0.33em}{\widehat{\sigma }}_e^2\hspace{0.33em}\text{and confidence interval CI}\left({\beta }_j\right)\\ 1:\hspace{0.33em}𝓠\leftarrow \hspace{0.33em}\text{TRIMTRANSFORM}\left(X,\rho \right)\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}⊳\hspace{0.33em}\text{construct}\hspace{0.33em}\rho \text{-trim}\hspace{0.33em}\text{as}\hspace{0.33em}\text{in}\hspace{0.33em}\left(15\right)\\ 2:{\widehat{\beta }}^{init}\leftarrow \hspace{0.33em}\text{LASSO}\left(𝓠X,𝓠Y,\lambda \right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}⊳\text{Lasso regression with transformed data, see}\left(16\right)\\ 3:{𝓟}^{\left(j\right)}\leftarrow \text{TRIMTRANSFORM}\left(X_{-j},{\rho }_j\right)\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}⊳\text{construct}\hspace{0.33em}{\rho }_j\text{-trim}\hspace{0.33em}\text{as}\hspace{0.33em}\text{in}\left(14\right)\\ 4:\widehat{\gamma }\leftarrow \hspace{0.33em}\text{LASSO}\left({𝓟}^{\left(j\right)}{X}_{-j},{𝓟}^{\left(j\right)}{X}_j,{\lambda }_j\right)\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⊳\text{Lasso regression with transformed data, see}\left(9\right)\\ 5:{𝓟}^{\left(j\right)}{Z}_j\leftarrow {𝓟}^{\left(j\right)}{X}_j-{𝓟}^{\left(j\right)}{X}_{-j}\widehat{\gamma }\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.17em}⊳\text{take the residuals as the projection direction}\\ 6:\widehat{\beta }\leftarrow \text{DEBIASEDLASSO}\left({\widehat{\beta }}^{init},{𝓟}^{\left(j\right)}{X}_{-j},{𝓟}^{\left(j\right)}{X}_j,{𝓟}^{\left(j\right)}{Z}_j\right)\hspace{0.33em}\hspace{0.33em}\hspace{0.17em}⊳\text{compute Doubly Debiased Lasso as in}\hspace{0.33em}\left(12\right)\\ 7:\hspace{0.33em}{\widehat{\sigma }}_e^2\leftarrow \hspace{0.33em}\text{NOISELEVEL}\left(X,Y,{\widehat{\beta }}^{init},𝓠\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.33em}⊳\text{compute noise level as in}\hspace{0.33em}\left(17\right)\\ 8:\hspace{0.33em}\text{CI}\left({\beta }_j\right)\leftarrow \hspace{0.33em}\text{CONFIDENCEINTERVAL}\left({\widehat{\beta }}_j,{𝓟}^{\left(j\right)}{X}_j,{𝓟}^{\left(j\right)}{Z}_j,{\widehat{\sigma }}_e^2,\alpha \right)\hspace{0.33em}⊳\text{compute the }\left(1-\alpha \right)\text{-CI}\hspace{0.33em}\text{as}\hspace{0.33em}\text{in}\hspace{0.33em}\left(13\right)\end{array}}\end{array}}}$$

4. Theoretical Justification.

This section provides theoretical justifications of the proposed method for the Hidden Confounding Model (2). The proofs of the main results are presented in Sections A and B of the supplementary material together with several other technical results of independent interest.

4.1. Model assumptions.

In the following, we fix the index 1 ≤ j ≤ p and introduce the model assumptions for establishing the asymptotic normality of our proposed estimator ${\widehat{\beta }}_j$ defined in (10). For the coefficient matrix $\mathrm{\Psi }\in {ℝ}^{q\times p}$ in (3), we use ${\mathrm{\Psi }}_j\in {ℝ}^q$ to denote the j-th column and ${\mathrm{\Psi }}_{-j}\in {ℝ}^{q\times \left(p-1\right)}$ denotes the sub-matrix with the remaining p – 1 columns. Furthermore, we write γ for the best linear approximation of $X_{1,j}\in ℝ$ by $X_{1,-j}\in {ℝ}^{p-1}$, that is $\gamma =\arg {\min }_{{\gamma }^{\prime }\in {ℝ}^{p-1}}\mathbb{E}{\left(X_{1,j}-X_{1,-j}{\gamma }^{\prime }\right)}^2$, whose explicit expression is:

$$\gamma ={\left[\mathbb{E}\left(X_{1,-j}{X}_{1,-j}^{\top }\right)\right]}^{-1}\mathbb{E}\left(X_{1,-j}{X}_{1,j}\right).$$

For ease of notation, we do not explicitly express the dependence of γ on j. Similarly, define

$${\gamma }^E={\left[\mathbb{E}\left(E_{1,-j}{E}_{1,-j}^{\top }\right)\right]}^{-1}\mathbb{E}\left(E_{1,-j}{E}_{1,j}\right).$$

We denote the corresponding residuals by ${\eta }_{i,j}=X_{i,j}-X_{i,-j}^{\top }\gamma$ and ${\nu }_{i,j}=E_{i,j}-E_{i,-j}^{\top }{\gamma }^E$ for 1 ≤ i ≤ n. We use σ_j to denote the standard deviation of v_i,j.

The first assumption is on the precision matrix of $E_{i,\cdot }\in {ℝ}^p$ in (2):

(A1) The precision matrix ${\mathrm{\Omega }}_E={\left[\mathbb{E}\left(E_{i,\cdot }{E}_{i,\cdot }^{\top }\right)\right]}^{-1}$ satisfies $c_0\le {\lambda }_{\min }\left({\mathrm{\Omega }}_E\right)\le {\lambda }_{\max }\left({\mathrm{\Omega }}_E\right)\le C_0$ and ${‖{\left({\mathrm{\Omega }}_E\right)}_{\cdot ,j}‖}_0\le s$ where C₀ > 0 and c₀ > 0 are some positive constants and s denotes the sparsity level which can grow with n and p.

Such assumptions on well-posedness and sparsity are commonly required for estimation of the precision matrix [44, 35, 64, 9] and are also used for confidence interval construction in the standard high-dimensional regression model without unmeasured confounding [56]. Here, the conditions are not directly imposed on the covariates X_i,.·, but rather on their unconfounded part E_i,.. In the high-dimensional linear model without hidden confounders, the sparse precision matrix assumption can be relaxed using the technique in [32]. However, it is unclear whether the method in [32] can be generalized to our model due to the additional hidden confounding bias as in (11).

The second assumption is about the coefficient matrix $\mathrm{\Psi }$ in (3), which describes the effect of the hidden confounding variables $H_{i,\cdot }\in {ℝ}^q$ on the measured variables $X_{i,\cdot }\in {ℝ}^p$:

(A2) The q-th singular value of the coefficient matrix ${\mathrm{\Psi }}_{-j}\in {ℝ}^{q\times \left(p-1\right)}$ satisfies

$${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)\gg l\left(n,p,q\right):=\max \left\{M\sqrt{\frac{qp}{n}}{\left(\log p\right)}^{3/4},\sqrt{Mq}{p}^{1/4}{\left(\log p\right)}^{3/8},\sqrt{qn\log p}\right\}$$ (19)

where M is the sub-Gaussian norm for components of X_i,., as defined in Assumption (A3). Furthermore, we have

$$\max \left\{{‖\mathrm{\Psi }{\left({\mathrm{\Omega }}_E\right)}_{\cdot ,j}‖}_2,{‖{\mathrm{\Psi }}_j‖}_2,{‖{\mathrm{\Psi }}_{-j}{\left({\mathrm{\Omega }}_E\right)}_{-j,j}‖}_2,{‖\varphi ‖}_2\right\}\lesssim \sqrt{q}{\left(\log p\right)}^c,$$ (20)

where $\mathrm{\Psi }$ and ϕ are defined in (2) and 0 < c ≤ 1/4 is some positive constant.

The condition (A2) is crucial for identifying the coefficient β_j in the high-dimensional Hidden Confounding Model (2). Condition (A2) is referred to as the dense confounding assumption. A few remarks are in order regarding when this identifiability condition holds.

Since all vectors $\mathrm{\Psi }{\left({\mathrm{\Omega }}_E\right)}_{\cdot ,j}$, ${\mathrm{\Psi }}_j$, ${\mathrm{\Psi }}_{-j}{\left({\mathrm{\Omega }}_E\right)}_{-j,j}$ and ϕ are q-dimensional, the upper bound condition (20) on their ℓ₂ norms is mild. If the vector $\varphi \in {ℝ}^q$ has bounded entries and the vectors ${\left\{{\mathrm{\Psi }}_{\cdot ,l}\right\}}_{1\le l\le p}\in {ℝ}^q$ are independently generated with zero mean and bounded second moments, then the condition (20) holds with probability larger than 1 – (log p)^−2c, where c is defined in (20). A larger value c > 1/4 is possible: the condition then holds with even higher probability, but makes the upper bounds for (32) in Lemma 1 and (35) in Lemma 2 slightly worse, which then requires more stringent conditions on ${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)$ in Theorem 1, up to polynomial order of log p.

In the factor model literature [19, 59] the spiked singular value condition ${\lambda }_q\left(\mathrm{\Psi }\right)\asymp \sqrt{p}$ is quite common and holds under mild conditions. The Hidden Confounding Model is closely related to the factor model, where the hidden confounders H_i,· are the factors and the matrix $\mathrm{\Psi }$ describes how these factors affect the observed variables X_i,.. However, for our analysis, our assumption on ${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)$ in (19) can be much weaker than the classical factor assumption ${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)\asymp \sqrt{p}$, especially for a range of dimensionality where p ≫ n. In certain dense confounding settings, we can show that condition (19) holds with high probability. Consider first the special case with a single hidden confounder, that is, q = 1 and the effect matrix is reduced to a vector $\mathrm{\Psi }\in {ℝ}^p$. In this case, ${\lambda }_1\left({\mathrm{\Psi }}_{-j}\right)={‖{\mathrm{\Psi }}_{-j}‖}_2$ and the denseness of the effect vector ${\mathrm{\Psi }}_{-j}$ leads to a large ${\lambda }_1\left({\mathrm{\Psi }}_{-j}\right)$. The condition (19) can be satisfied even if only a certain proportion of covariates is affected by hidden confounding. When q = 1, if we assume that there exists a set $A\subseteq \left\{1,2,\dots ,p\right\}$ such that ${\left\{{\mathrm{\Psi }}_l\right\}}_{l\in A}$ are i.i.d. and $\left|A\right|\gg l{\left(n,p,q\right)}^2$, where l(n,p,q) is defined in (19), then with high probability ${\lambda }_q\left(\mathrm{\Psi }\right)\gtrsim \sqrt{\left|A\right|}\gg l\left(n,p,q\right)$. In the multiple hidden confounders setting, if the vectors ${\left\{{\mathrm{\Psi }}_l\right\}}_{l\in A}$ are generated as i.i.d. sub-Gaussian random vectors, which has an interpretation that all covariates are analogously affected by the confounders, then the spiked singular value condition (19) is satisfied with high probability as well. See Lemmas 4 and 5 in Section A.5 of the supplementary material for the exact statement. In Section 5.1, we also explore the numerical performance of the method when different proportions of the covariates are affected and observe that the proposed method works well even if the hidden confounders only affect a small percentage of the covariates, say 5%.

Under the model (2), if the entries of $\mathrm{\Psi }$ are assumed to be i.i.d. sub-Gaussian with zero mean and variance ${\sigma }_{\mathrm{\Psi }}^2$, then we have ${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)\asymp \sqrt{p}{\sigma }_{\mathrm{\Psi }}$ with high probability. Together with (19) this requires

$${\sigma }_{\mathrm{\Psi }}\gg \max \left\{M\sqrt{\frac{q}{n}}{\left(\log p\right)}^{3/4},\sqrt{\frac{qn\log p}{p}},\frac{\sqrt{qM{\left(\log p\right)}^{3/4}}}{p^{1/4}}\right\}.$$

So if p ≫ qn log p and $\min \left\{n,p\right\}\gg q^3{\left(\log p\right)}^{3/2}{M}^2$, then the required effect size ${\sigma }_{\mathrm{\Psi }}$ of the hidden confounder H_i,· on an individual covariate X_i,j can diminish to zero fairly quickly.

The condition (19) can in fact be empirically checked using the sample covariance matrix ${\widehat{\Sigma }}_X$. Since ${\Sigma }_X={\mathrm{\Psi }}^{\top }\mathrm{\Psi }+{\Sigma }_E$, then the condition (19) implies that ${\Sigma }_X$ has at least q spiked eigenvalues. If the population covariance matrix ${\Sigma }_X$ has a few spikes, the corresponding sample covariance matrix will also have spiked eigenvalue structure with a high probability [59]. Hence, we can inspect the spectrum of the sample covariance matrix ${\widehat{\Sigma }}_X$ and informally check whether it has spiked singular values. See the left panel of Figure 2 for an illustration.

FIG 2.

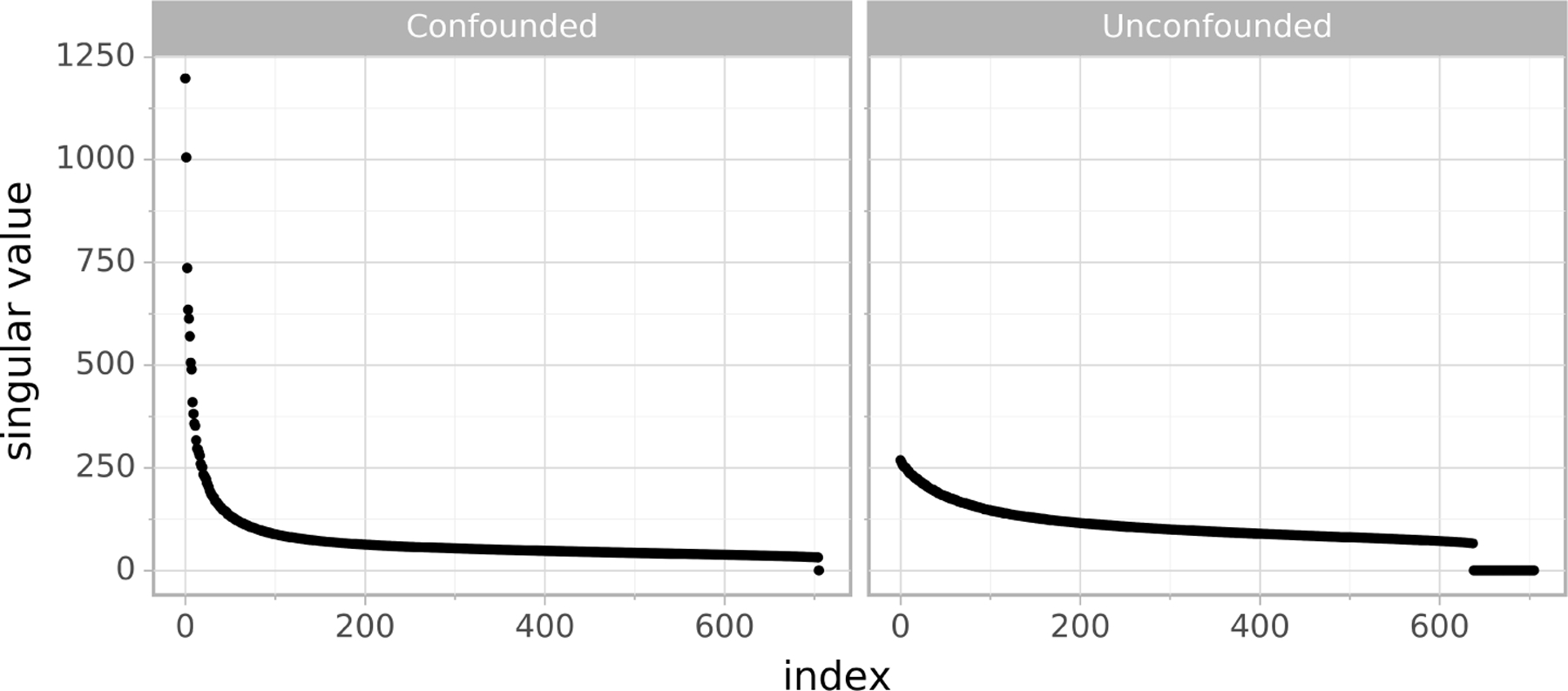
Left: Spiked singular values of the standardized gene expression matrix (see Section 5.2) indicate possible confounding. Right: Singular values after regressing out the q = 65 confounding proxies given in the data set (thus labeled as “unconfounded”). The singular values in both plots are sorted decreasingly.

The third assumption is imposed on the distribution of various terms:

(A3) The random error e_i in (2) is assumed to be independent of ${\left(X_{i,\cdot }^{\top },H_{i,\cdot }^{\top }\right)}^{\top }$, the error vector E_i, is assumed to be independent of the hidden confounder H_i,., and the noise term ${\nu }_{i,j}=E_{i,j}-E_{i,-j}^{\top }{\gamma }^E$ is assumed to be independent of E_i,−j. Furthermore, E_i,· is a sub-Gaussian random vector and e_i and v_i,j are sub-Gaussian random variables, whose sub-Gaussian norms satisfy $\max \left\{{‖E_{i,\cdot }‖}_{{\psi }_2},{‖e_i‖}_{{\psi }_2},{\max }_{1\le l\le p}{‖{\nu }_{i,l}‖}_2\right\}\le C$, where C> 0 is a positive constant independent of n and p. For 1 ≤ l≤ p, X_i,l are sub-Gaussian random variables whose sub-Gaussian norms satisfy ${\max }_{1\le l\le p}{‖X_{i,l}‖}_{{\psi }_2}\le M$, where $1\lesssim M\lesssim \sqrt{q\log p}$.

The independence assumption between the random error e_i and ${\left(X_{i,\cdot }^{\top },H_{i,\cdot }^{\top }\right)}^{\top }$ is commonly assumed for the SEM (1) and thus it holds in the induced Hidden Confounding Model (2) as well, see for example [47]. Analogously, when modelling X_i,· as a SEM where the hidden variables H_i,.· are directly influencing X_i,. that is, they are parents of the X_i,.·’s, the independence of E_i,· from H_i,· is a standard assumption. The independence assumption between v_i,j and E_i,−j holds automatically if E_i,.· has a multivariate Gaussian distribution (but X_i,· is still allowed to be non-Gaussian, e.g. due to non-Gaussian confounders). Additionally, the independence assumption between v_i,j and E_i,−j holds if all elements of E_i,· are independent, but not necessarily Gaussian. In Appendix D, we explore the robustness of our proposed Doubly Debiased Lasso estimator to the violation of this independence assumption; see Figure A2 for details.

We emphasize that the individual components X_i,j are assumed to be sub-Gaussian, instead of the whole vector $X_{i,\cdot }\in {ℝ}^p$. The sub-Gaussian norm M is allowed to grow with q and p. Particularly, if we assume H_i,· to be a sub-Gaussian vector, then condition (20) implies that $M\lesssim \sqrt{q}{\left(\log p\right)}^c{‖H_{i,\cdot }‖}_{{\psi }_2}$. Furthermore, our theoretical analysis also covers the case when the sub-Gaussian norm M is of constant order. This happens, for example, when the entries of $\mathrm{\Psi }$ are of order $1/\sqrt{q}$, since $M\asymp {\max }_{l=1,\dots ,p}{‖{\mathrm{\Psi }}_l‖}_2$.

The final assumption is that the restricted eigenvalue condition [5] for the transformed design matrices $𝓟X$ and ${𝓟}^{\left(j\right)}{X}_{-j}$ is satisfied with high probability.

(A4) With probability at least 1 – exp(−cn), we have

$$\text{RE}\left(\frac{1}{n}{X}^{\top }{𝓠}^{2}X\right)=\underset{\begin{array}{l}𝓣\subseteq \left[p\right]\\ \hspace{0.17em}\left|𝓣\right|\le k\end{array}}{\inf }\underset{\begin{array}{c}\omega \in {ℝ}^p\\ {‖{\omega }_{{𝓣}^c}‖}_1\le CM{‖{\omega }_{𝓣}‖}_1\end{array}}{\min }\frac{{\omega }^{\top }\left(\frac{1}{n}{X}^{\top }{𝓠}^{2}X\right)\omega }{{‖\omega ‖}_2^2}\ge {\tau }_{\ast };$$ (21)

$$\text{RE}\left(\frac{1}{n}{X}_{-j}^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_{-j}\right)=\underset{\begin{array}{c}𝓣\subseteq \left[p\right]\backslash \left\{j\right\}\\ \left|𝓣\right|\le s\end{array}}{\inf }\underset{\begin{array}{c}\omega \in {ℝ}^{p-1}\\ {‖{\omega }_{{𝓣}^c}‖}_1\le CM{‖{\omega }_{𝓣}‖}_1\end{array}}{\min }\frac{{\omega }^{\top }\left(\frac{1}{n}{X}_{-j}^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_{-j}\right)\omega }{{‖\omega ‖}_2^2}\ge {\tau }_{\ast }$$ (22)

where c, C, τ* > 0 are positive constants independent of n and p and M is the sub-Gaussian norm for components of X_i,., as defined in Assumption (A3). For ease of notation, the same constants τ* and C are used in (21) and (22).

Such assumptions are common in the high-dimensional statistics literature, see [7]. The restricted eigenvalue condition (A4) is similar, but more complicated than the standard restricted eigenvalue condition introduced in [5]. The main complexity is that, rather than for the original design matrix, the restricted eigenvalue condition is imposed on the transformed design matrices ${𝓟}^{\left(j\right)}{X}_{-j}$ and $𝓟X$, after applying the Trim transforms ${𝓟}^{\left(j\right)}$ and $𝓟$, described in detail in Sections 3.3 and 3.4, respectively. In the following, we verify the restricted eigenvalue condition (A4) for $\frac{1}{n}{X}^{\top }{𝓟}^{2}X$ and the argument can be extended to $\frac{1}{n}{X}_{-j}^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_{-j}$.

PROPOSITION 1. Suppose that assumptions (A1) and (A3) hold, H_i is a sub-Gaussian random vector, $q+\log p\lesssim \sqrt{n}$ and $k={‖\beta ‖}_0$ satisfies M²kq² log p log n/n → 0. Assume further that the loading martrix $\mathrm{\Psi }\in {ℝ}^{q\times p}$ satisfies ${‖\mathrm{\Psi }‖}_{\infty }\lesssim \sqrt{\log \left(qp\right)}$, ${\lambda }_1\left(\mathrm{\Psi }\right)/{\lambda }_q\left(\mathrm{\Psi }\right)\lesssim 1$ and that

$${\lambda }_q\left(\mathrm{\Psi }\right)\gg \frac{\sqrt{Mp}\max \left\{k^{1/4}{q}^{5/4},1\right\}\log \left(np\right)}{\min {\left\{n,p\right\}}^{1/4}}$$ (23)

If ${\lambda }_{\left[\rho m\right]}\left(\frac{1}{n}X{X}^{\top }\right)\ge c\max \left\{1,p/n\right\}$ for ρ defined in(15) and some positive constant c> 0 independent of n and p, then there exist positive constants c₁, c₂ > 0 such that, with probability larger than $1-p^{-c_2}-\exp \left(-c_{2}n\right)$, we have $\text{RE}\left(\frac{1}{n}{X}^{\top }{𝓠}^{2}X\right)\ge c_1{\lambda }_{\min }\left({\Sigma }_X\right)$.

An important condition for establishing Proposition 1 is the condition (23). Under the commonly assumed spiked singular value condition ${\lambda }_q\left(\mathrm{\Psi }\right)\asymp \sqrt{p}$ [19, 59, 1, 2], the condition (23) is reduced to k ≪ min {n, p} / (M ²q⁵ log(np)⁴). As a comparison, for the standard high-dimensional regression model with no hidden confounders, [66, 49] verified the restricted eigenvalue condition under the sparsity condition k ≪n/log p. That is, if ${\lambda }_q\left(\mathrm{\Psi }\right)\asymp \sqrt{p}$, then the sparsity requirement in Proposition 1 is the same as that for the high-dimensional regression model with no hidden confounders, up to a polynomial order of q and log(np),

In comparison to the condition (19) in (A2), (23) can be slightly stronger for a range of dimensionality where p ≫ n^3/2. However, Proposition 1 does not require the strong spiked singular value condition ${\lambda }_q\left(\mathrm{\Psi }\right)\asymp \sqrt{p}$. The proof of Proposition 1 is presented in Appendix B in the supplement. The condition ${\lambda }_{⌊\rho m⌋}\left(\frac{1}{n}X{X}^{\top }\right)\ge c\max \left\{1,p/n\right\}$ can be empirically verified from the data. In Appendix B.1, further theoretical justification for this condition is provided, under mild assumptions.

4.2. Main Results.

In this section we present the most important properties of the proposed estimator (10). We always consider asymptotic expressions in the limit where both n, p →∞1 and focus on the high-dimensional regime with c* = lim p/n ϵ (0, ∞]. We mention here that we also give some new results on point estimation of the initial estimator ${\widehat{\beta }}^{init}$ defined in (16) in Appendix A.3, as they are established under more general conditions than in [12].

4.2.1. Asymptotic normality.

We first present the limiting distribution of the proposed Doubly Debiased Lasso estimator. The proof of Theorem 1 and important intermediary results for establishing Theorem 1 are presented in Appendix A in the supplement.

THEOREM 1. Consider the Hidden Confounding Model (2). Suppose that conditions (A1)-(A4) hold and further assume that $c^{\ast }=\lim p/n\in \left(0,\infty \right]$, $k:={‖\beta ‖}_0\ll \sqrt{n}/\left(M^3\log p\right)$, $s:={‖{\left({\mathrm{\Omega }}_E\right)}_{\cdot ,j}‖}_0\ll n/\left(M^2\log p\right)$ and $e_i~N\left(0,{\sigma }_e^2\right)$. Let the tuning parameters for ${\widehat{\beta }}^{init}$ in (16) and $\widehat{\gamma }$ in (9) respectively be $\lambda \asymp {\sigma }_e\sqrt{\log p/n}+\sqrt{q\log p/{\lambda }_q^2\left(\mathrm{\Psi }\right)}$ and ${\lambda }_j\asymp {\sigma }_j\sqrt{\log p/n}+\sqrt{q\log p/{\lambda }_q^2\left({\mathrm{\Psi }}_{-j}\right)}$.Furthermore, let $𝓟$ and ${𝓟}^{\left(j\right)}$ be the Trim transform (14) with min{ρ, ρ_j} ≥ (q + 1)/min {n, p – 1} and max {ρ, ρ_j} < 1. Then the Doubly Debiased Lasso estimator (10) satisfies

$$\frac{1}{\sqrt{V}}\left({\widehat{\beta }}_j-{\beta }_j\right)\stackrel{d}{\to }N\left(0,1\right).$$ (24)

where

$$\text{V}=\frac{{\sigma }_e^2{Z}_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^4{Z}_j}{{\left[Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_j\right]}^2}\hspace{1em}and\hspace{1em}{V}^{-1}\frac{{\sigma }_e^2\text{Tr}\left[{\left({𝓟}^{\left(j\right)}\right)}^4\right]}{{\sigma }_j^2{\text{Tr}}^2\left[{\left({𝓟}^{\left(j\right)}\right)}^2\right]}\stackrel{p}{\to }1.$$ (25)

REMARK 1. The Gaussianity of the random error e_i is mainly imposed to simplify the proof of asymptotic normality. We believe that this assumption is a technical condition and can be removed by applying more refined probability arguments as in [26], where the asymptotic normality of quadratic forms ${\left({𝓟}^{\left(j\right)}e\right)}^{\top }{𝓟}^{\left(j\right)}e$ is established for the general sub-Gaussian case. The argument could be extended to obtain the asymptotic normality for ${\left({𝓟}^{\left(j\right)}{\eta }_j\right)}^{\top }{𝓟}^{\left(j\right)}e$, which is essentially needed for the current result.

REMARK 2. For constructing $𝓟$ and ${𝓟}^{\left(j\right)}$, the main requirement is to trim the singular values enough in both cases, that is, min{ρ, ρ_j} ≥ (q + 1)/min{n, p – 1}. This condition is mild in the high-dimensional setting with a small number of hidden confounders. Our results are not limited to the proposed estimator which uses the Trim transform ${𝓟}^{\left(j\right)}$ in (14) and the penalized estimators $\widehat{\gamma }$ and ${\widehat{\beta }}^{init}$ in (9) and (16), but hold for any transformation satisfying the conditions given in Section A.1 of the supplementary material and any initial estimator satisfying the error rates presented in Section A.3 of the supplementary material.

REMARK 3. If we further assume the error ϵ_i in the model (3) to be independent of X_i,., then the requirement (19) of the condition (A2) can be relaxed to

$${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)\gg \max \left\{M\sqrt{\frac{qp}{n}}{\left(\log p\right)}^{3/4},\sqrt{qM}{p}^{1/4}{\left(\log p\right)}^{3/8},\sqrt{\left(s{M}^2+k\sqrt{n}{M}^3\right)q\log p}\right\}.$$

Note that the factor model implies the upper bound ${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)\lesssim \sqrt{p}$. Even if n ≥ p, the above condition on ${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)$ can still hold if $p\gg kq{M}^3\log p\sqrt{n}$. On the other hand, the condition (19) together with ${\lambda }_q\left({\mathrm{\Psi }}_{-j}\right)\lesssim \sqrt{p}$ imply that p ≫ qn log p, which excludes the setting n ≥ p.

There are three conditions on the parameters s, q, k imposed in the Theorem 1 above. The most stringent one is the sparsity assumption $k\ll \sqrt{n}/\left[M^3\log p\right]$. In standard high-dimensional sparse linear regression, a related sparsity assumption $k\ll \sqrt{n}/\log p$ has also been used for confidence interval construction [65, 56, 32] and has been established in [10] as a necessary condition for constructing adaptive confidence intervals. In the high-dimensional Hidden Confounding Model with $M\asymp 1$, the condition on the sparsity of β is then of the same asymptotic order as in the standard high-dimensional regression with no hidden confounding. The condition on the sparsity of the precision matrix, $s={‖{\left({\mathrm{\Omega }}_E\right)}_{\cdot ,j}‖}_0\ll n/\left(M^2\log p\right)$, is mild in the sense that, for $M\asymp 1$, it is the maximal sparsity level for identifying (Ω_E).,_j. Implied by (19), the condition that the number of hidden confounders q is small is fundamental for all reasonable factor or confounding models.

4.2.2. Efficiency.

We investigate now the dependence of the asymptotic variance V in (25) on the choice of the spectral transformation ${𝓟}^{\left(j\right)}$. We further show that the proposed Doubly Debiased Lasso estimator (10) is efficient in the Gauss-Markov sense, with a careful construction of the transformation ${𝓟}^{\left(j\right)}$.

The Gauss-Markov theorem states that the smallest variance of any unbiased linear estimator of β_j in the standard low-dimensional regression setting (with no hidden confounding) is ${\sigma }_e^2/\left(n{\sigma }_j^2\right)$, which we use as a benchmark. The corresponding discussion on efficiency of the standard high-dimensional regression can be found in Section 2.3.3 of [56]. The expression for the asymptotic variance V of our proposed estimator (10) is given by $\frac{{\sigma }_e^2\text{Tr}\left[{\left({𝓟}^{\left(j\right)}\right)}^4\right]}{{\sigma }_j^2{\text{Tr}}^2\left[{\left({𝓟}^{\left(j\right)}\right)}^2\right]}$ (see Theorem 1). For the Trim transform defined in (14), which trims top (100 ρ_j)% of the singular values, we have that

$$\frac{{\sigma }_e^2\text{Tr}\left[{\left({𝓟}^{\left(j\right)}\right)}^4\right]}{{\sigma }_j^2{\text{Tr}}^2\left[{\left({𝓟}^{\left(j\right)}\right)}^2\right]}=\frac{{\sigma }_e^2}{{\sigma }_j^2}\cdot \frac{{\sum }_{l=1}^m{S}_{l,l}^4}{{\left({\sum }_{l=1}^m{S}_{l,l}^2\right)}^2},$$

where we write m = min{n, p – 1} and S_l,l = S_l,l(X_−j) ϵ [0, 1]. Since $S_{l,l}^4\le S_{l,l}^2$ for every l, ${\sum }_{l=1}^m{S}_{l,l}^2\ge \left(1-{\rho }_j\right)m$ and ${\left({\sum }_{l=1}^m{S}_{l,l}^2\right)}^2\le m\cdot {\sum }_{l=1}^m{S}_{l,l}^4$, we obtain

$$\frac{{\sigma }_e^2}{{\sigma }_j^{2}m}\le \frac{{\sigma }_e^2\text{Tr}\left[{\left({𝓟}^{\left(j\right)}\right)}^4\right]}{{\sigma }_j^2{\text{Tr}}^2\left[{\left({𝓟}^{\left(j\right)}\right)}^2\right]}\le \frac{1}{1-{\rho }_j}\cdot \frac{{\sigma }_e^2}{{\sigma }_j^{2}m}.$$

In the high-dimensional setting where p – 1 ≥ n, we have m = n and then

$$\frac{{\sigma }_e^2}{{\sigma }_j^{2}n}\le \frac{{\sigma }_e^2\text{Tr}\left[{\left({𝓟}^{\left(j\right)}\right)}^4\right]}{{\sigma }_j^2{\text{Tr}}^2\left[{\left({𝓟}^{\left(j\right)}\right)}^2\right]}\le \frac{1}{1-{\rho }_j}\cdot \frac{{\sigma }_e^2}{{\sigma }_j^{2}n}.$$ (26)

THEOREM 2. Suppose that the assumptions of Theorem 1 hold. If p ≥ n +1 and ρ_j = ρ_j(n) → 0, then the Doubly Debiased Lasso estimator in (10) has asymptotic variance $\frac{{\sigma }_e^2}{{\sigma }_j^{2}n}$, that is, it achieves the Gauss-Markov efficiency bound.

The above theorem shows that in the q ≪ n regime, the Doubly Debiased Lasso achieves the Gauss-Markov efficiency bound if ρ_j = ρ_j (n) → 0 and min {ρ, ρ_j} ≥ (q + 1)/n (which is also a condition of Theorem 1). When using the median Trim transform, i.e. ρ_j = 1/2, the bound in (26) implies that the variance of the resulting estimator is at most twice the size of the Gauss-Markov bound. In Section 5, we illustrate the finite-sample performance of the Doubly Debiased Lasso estimator for different values of ρ_j; see Figure 6.

FIG 6.

(Trimming level) Dependence of the (scaled) absolyte bias terms |B_β| and |B_b| (left), standard deviation V_1/2 (middle) and the coverage of the 95% confidence interval (right) on the trimming level ρ_j of the Trim transform (see Equation (14)). The sample size is fixed at n = 300 and the dimension at p = 1, 000. On the leftmost plot, |B_β| and |B_b| are denoted by a dashed and a solid line, respectively. The case ρ_j =0 corresponds to Debiased Lasso with the spectral deconfounding initial estimator ${\widehat{\beta }}^{init}$, described in (16).

In general for the high-dimensional setting p/n → c* ∈ (0, ∞], the Asymptotic Relative Efficiency (ARE) of the proposed Doubly Debiased Lasso estimator with respect to the Gauss-Markov efficiency bound satisfies the following:

$$\text{ARE}\in \left(\frac{1}{\min \left\{c^{\ast },1\right\}},\frac{1}{\left(1-{\rho }^{\ast }\right)\min \left\{c^{\ast },1\right\}}\right),$$ (27)

where ${\rho }^{\ast }={\lim }_{n\to \infty }{\rho }_j\left(n\right)\in \left[0,1\right)$. The equation (27) reveals how the efficiency of the Doubly Debiased Lasso is affected by the choice of the percentile ρ_j = ρ_j(n) in transformation ${𝓟}^{\left(j\right)}$ and the dimensionality of the problem. Smaller ρ_j leads to a more efficient estimator, as long as the top few singular values are properly shrunk. Intuitively, a smaller percentile ρ_j means that less information in X_−j is trimmed out and hence the proposed estimator is more efficient. In addition, for the case ρ* = 0, we have ARE = {max 1/c*, 1}. With ρ* = 0, a plot of ARE with respect to the ratio c* = lim p/n is given in Figure 1. We see that for c* < 1 (that is p< n), the relative efficiency of the proposed estimator increases as the dimension p increases and when c* ≥ 1 (that is p ≥ n), we have that ARE = 1, saying that the Doubly Debiased Lasso achieves the efficiency bound in the Gauss-Markov sense.

FIG 1.

The plot of ARE versus c* = lim p/n, for the setting of ρ* =0.

The phenomenon that the efficiency is retained even in presence of hidden confounding is quite remarkable. For comparison, even in the classical low-dimensional setting, the most commonly used approach assumes availability of sufficiently many instrumental variables (IV) satisfying certain stringent conditions under which one can consistently estimate the effects in presence of hidden confounding. In Theorem 5.2 of [62], the popular IV estimator, two-stage-least-squares (2SLS), is shown to have variance strictly larger than the efficiency bound in the Gauss-Markov setting (with no unmeasured confounding). It has been also shown in Theorem 5.3 of [62] that the 2SLS estimator is efficient in the class of all linear instrumental variable estimators and thus, all linear instrumental variable estimators are strictly less efficient than our Doubly Debiased Lasso. On the other hand, our proposed method not only avoids the difficult step of coming up with a large number of valid instrumental variables, but also achieves the efficiency bound with a careful construction of the spectral transformation ${𝓟}^{\left(j\right)}$. This occurs due to a blessing of dimensionality and the assumption of dense confounding, where a large number of covariates are assumed to be affected by a small number of hidden confounders.

4.2.3. Asymptotic validity of confidence intervals.

The asymptotic normal limiting distribution in Theorem 1 can be used for construction of confidence intervals for β_j. Consistently estimating the variance V of our estimator, defined in (25), requires a consistent estimator of the error variance ${\sigma }_e^2$. The following proposition establishes the rate of convergence of the estimator ${\widehat{\sigma }}_e^2$ proposed in (17):

PROPOSITION 2. Consider the Hidden Confounding Model (2). Suppose that conditions (A1)-(A4) hold. Suppose further that c* = lim p/n ∈ (0, ∞],k ≾ n/log p and q ≪ min{n, p/log p}. Then with probability larger $1-\exp \left(-c{t}^2\right)-\frac{1}{t^2}-c\left(\log p\right)-n^{-c}$ for some positive constant c > 0 and for any $0<t\le \sqrt{n}$, we have

$$\left|{\widehat{\sigma }}_e^2-{\sigma }_e^2\right|\lesssim \frac{t}{\sqrt{n}}+M^{2}k\frac{\log p}{n}+\frac{q\log p}{p}+\frac{pq\sqrt{\log p}/n+M^{2}kq\log p}{{\lambda }_q^2\left(\mathrm{\Psi }\right)},$$

where M is the sub-Gaussian norm for components of $X_{i,\cdot }$ defined in Assumption (A3).

Together with (19) of the condition (A2), we apply the above proposition and establish ${\widehat{\sigma }}_e^2-{\sigma }_e^2\stackrel{p}{\to }0$. As a remark, the estimation error $\left|{\widehat{\sigma }}_e^2-{\sigma }_{ϵ}^2\right|$ is of the same order of magnitude as $\left|{\widehat{\sigma }}_e^2-{\sigma }_e^2\right|$ since the difference ${\sigma }_{ϵ}^2-{\sigma }_e^2$ is small in the dense confounding model, see Lemma 2 in the supplement.

Proposition 2, together with Theorem 1, imply the asymptotic coverage and precision properties of the proposed confidence interval CI(β_j), described in (13):

COROLLARY 1. Suppose that the conditions of Theorem 1 hold, then the confidence interval defined in (13) satisfies the following properties:

$$\underset{n,p\to \infty }{\lim \inf }\mathbb{P}\left({\beta }_j\in \text{CI}\left({\beta }_j\right)\right)\ge 1-\alpha ,$$ (28)

$$\underset{n,p\to \infty }{\lim \sup }\mathbb{P}\left(\text{L}\left(\text{CI}\left({\beta }_j\right)\right)\ge \left(2+c\right)z_{1-\frac{\alpha }{2}}\sqrt{\frac{{\sigma }_e^2\text{Tr}\left[{\left({𝓟}^{\left(j\right)}\right)}^4\right]}{{\sigma }_j^2\text{Tr}\left[{\left({𝓟}^{\left(j\right)}\right)}^2\right]}}\right)=0,$$ (29)

for any positive constant c> 0, where L (CI(β_j)) denotes the length of the proposed confidence interval.

Similarly to the efficiency results in Section 4.2.2, the exact length depends on the construction of the spectral transformation ${𝓟}^{\left(j\right)}$. Together with (26), the above proposition shows that the length of constructed confidence interval is shrinking at the rate of n^−1/2 for the Trim transform in the high-dimensional setting. Specifically, for the setting p ≥ n + 1, if we choose ρ_j = ρ_j(n) (q + 1)/n and ρ_j(n) → 0, the constructed confidence interval has asymptotically optimal length.

5. Empirical results.

In this section we consider the practical aspects of Doubly Debiased Lasso methodology and illustrate its empirical performance on both real and simulated data. The overview of the method and the tuning parameters selection can be found in Section 3.6.

In order to investigate whether the given data set is potentially confounded, one can inspect the principal components of the design matrix X, or equivalently consider its SVD. Spiked singular value structure (see Figure 2) indicates the existence of hidden confounding, as much of the variance of our data can be explained by a small number of latent factors. This also serves as an informal check of the spiked singular value condition in the assumption (A2).

The scree plot can also be used for choosing the trimming thresholds, if one wants to depart from the default median rule (see Section 3.6). We have seen from the theoretical considerations in Section 4 that we can reduce the estimator variance by decreasing the trimming thresholds for the spectral transformation ${𝓟}^{\left(j\right)}$. On the other hand, it is crucial to choose them so that the number of shrunk singular values is still sufficiently large compared to the number of confounders. However, exactly estimating the number of confounders, e.g. by detecting the elbow in the scree plot [59], is not necessary with our method, since the efficiency of our estimator decreases relatively slowly as we decrease the trimming threshold.

In what follows, we illustrate the empirical performance of the Doubly Debiased Lasso in practice. We compare the performance with the standard Debiased Lasso [65], even though it is not really a competitor for dealing with hidden confounding. Our goal is to illustrate and quantify the error and bias when using the naive and popular approach which ignores potential hidden confounding. We first investigate the performance of our method on simulated data for a range of data generating mechanisms and then investigate its behaviour on a gene expression data set from the GTEx project [41].

5.1. Simulations.

In this section, we compare the Doubly Debiased Lasso with the standard Debiased Lasso in several different simulation settings for estimation of β_j and construction of the corresponding confidence intervals.

In order to make comparisons with the standard Debiased Lasso as fair as possible, we use the same procedure for constructing the standard Debiased Lasso, but with $𝓠={\text{I}}_p$, ${𝓟}^{\left(j\right)}={\text{I}}_{p-1}$, whereas for the Doubly Debiased Lasso, ${𝓟}^{\left(j\right)}$, $𝓠$, are taken to be median Trim transform matrices, unless specified otherwise. Finally, to investigate the usefulness of double debiasing, we additionally include the standard Debiased Lasso estimator with the same initial estimator ${\widehat{\beta }}^{init}$ as our proposed method, see Section 3.4. Therefore, this corresponds to the case where $𝓟$ is the median Trim transform, whereas ${𝓟}^{\left(j\right)}={\text{I}}_{p-1}$.

We will compare the (scaled) bias and variance of the corresponding estimators. For a fixed index j, from the equation (11) we have

$$V^{-1/2}\left({\widehat{\beta }}_j-{\beta }_j\right)=N\left(0,1\right)+B_{\beta }+B_b,$$

where the estimator variance V is defined in (25) and the bias terms B_β and B_b are given by

$$B_{\beta }=V^{-1/2}\frac{Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_{-j}\left({\widehat{\beta }}_{-j}^{init}-{\beta }_{-j}\right)}{Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_j},\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{B}_b=V^{-1/2}\frac{Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^{2}Xb}{Z_j^{\top }{\left({𝓟}^{\left(j\right)}\right)}^2{X}_j}.$$

Larger estimator variance makes the confidence intervals wider. However, large bias makes the confidence intervals inaccurate. We quantify this with the scaled bias terms B_β, which is due to the error in estimation of β, and B_b, which is due to the perturbation b arising from the hidden confounding. Having small |B_β| and |B_b| is essential for having a correct coverage, since the construction of confidence intervals is based on the approximation $V^{-1/2}\left({\widehat{\beta }}_j-{\beta }_j\right)\approx N\left(0,1\right)$.

We investigate the validity of the confidence interval construction by measuring the coverage of the nominal 95% confidence interval. We present here a wide range of simulations settings and further simulations can be found in the Appendix D.

Simulation parameters.

Unless specified otherwise, in all simulations we fix q = 3, s =5 and β = (1, 1, 1, 1, 1, 0,... 0)^T and we target the coefficient β₁ = 1. The rows of the unconfounded design matrix E are generated from $N\left(0,{\Sigma }_E\right)$ distribution, where ${\Sigma }_E={\text{I}}_p$, as a default. The matrix of confounding variables H, the additive error e and the coefficient matrices $\mathrm{\Psi }$ and ϕ all have i.i.d. N(0, 1) entries, unless stated otherwise. Each simulation is averaged over 5, 000 independent repetitions.

Varying dimensions n and p.

In this simulation setting we investigate how the performance of our estimator depends on the dimensionality of the problem. The results can be seen in Figure 3. In the first scenario, shown in the top row, we have p = 500 and n varying from 50 to 2, 000, thus covering both low-dimensional and high-dimensional cases. In the second scenario, shown in the bottom row, the sample size is fixed at n = 500 and the number of covariates p varies from 100 to 2, 000. We provide analogous simulations in Appendix D, where both the random variables and the model parameters are generated from non-Gaussian distributions.

FIG 3.

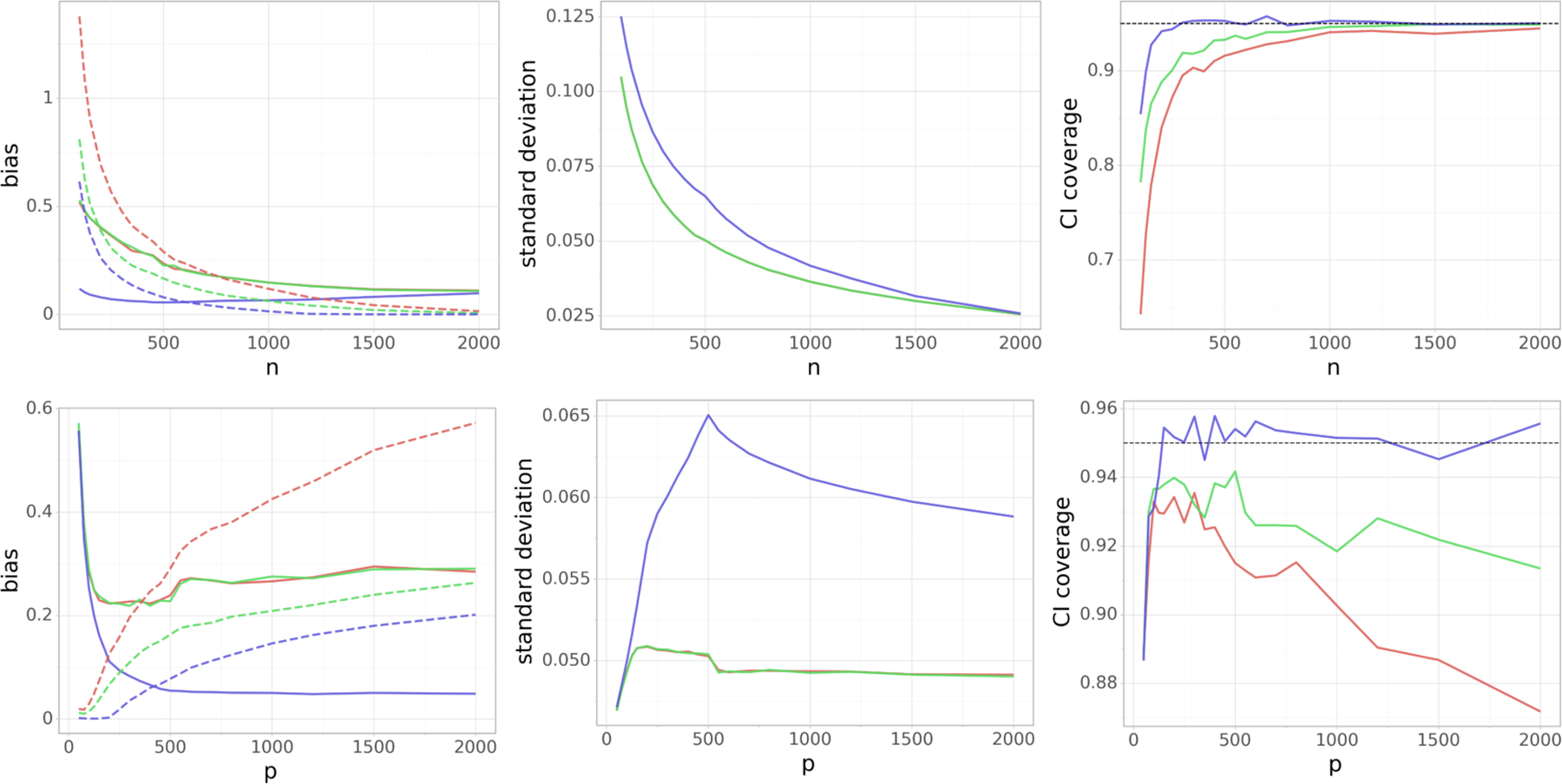
(Varying dimensions) Dependence of the (scaled) absolute bias terms |Bβ| and |Bb| (left), standard deviation V^1/2 (middle) and the coverage of the 95% confidence interval (right) on the number of data points n (top row) and the number of covariates p (bottom row). On the left side, |Bβ| and |Bb| are denoted by a dashed and a solid line, respectively. In the top row we fix p = 500, whereas in the bottom row we have n = 500. Blue color corresponds to the Doubly Debiased Lasso, red color represents the standard Debiased Lasso and green color corresponds also to the Debiased Lasso estimator, but with the same ${\widehat{\beta }}^{init}$ as our proposed method. Note that the last two methods have almost indistinguishable |B_b| and V.

We see that the absolute bias term |B_b| due to confounding is substantially smaller for Doubly Debiased Lasso compared to the standard Debiased Lasso, regardless of which initial estimator is used. This is because ${𝓟}^{\left(j\right)}$ additionally removes bias by shrinking large principal components of X_−j. This spectral transformation helps also to make the absolute bias term |B_β| smaller for the Doubly Debiased Lasso compared to the Debiased Lasso, even when using the same initial estimator ${\widehat{\beta }}^{init}$. This comes however at the expense of slightly larger variance, but we can see that the decrease in bias reflects positively on the validity of the constructed confidence intervals. Their coverage is significantly more accurate for Doubly Debiased Lasso, over a large range of n and p.

There are two challenging regimes for estimation under confounding. Firstly, when the dimension p is much larger than the sample size n, the coverage can be lower than 95%, since in this regime it is difficult to estimate β accurately and thus the term |B_β| is fairly large, even after the bias correction step. We see that the absolute bias |B_β| grows with p, but it is much smaller for the Doubly Debiased Lasso which positively impacts the coverage. Secondly, in the regime where p is relatively small compared to n, |B_β| begins to dominate and leads to undercoverage of confidence intervals. B_b is caused by the hidden confounding and does not disappear when n →∞, while keeping p constant. The simulation results agree with the asymptotic analysis of the bias term in (52) in the Supplementary material, where the term |B_b| vanishes as ${\lambda }_q\left(\mathrm{\Psi }\right)$ increases, in addition to increasing the sample size n. In the regime considered in this simulation, |B_b| can even grow, since the bias becomes increasingly large compared to the estimator’s variance. However, it is important to note that even in these difficult regimes, Doubly Debiased Lasso performs significantly better than the standard Debiased Lasso (irrespective of the initial estimator) as it manages to additionally decrease the estimator’s bias.

Toeplitz covariance structure for ${\Sigma }_E$.

Now we fix n = 300,p = 1, 000, but we generate the covariance matrix ${\Sigma }_E$ of the unconfounded part of the design matrix X to have Toeplitz covariance structure:${\left({\Sigma }_E\right)}_{i,j}={\kappa }^{\left|i-j\right|}$, where we vary κ across the interval [0, 0.97]. As we increase κ, the covariates X₁,..., X₅ in the active set get more correlated, so it gets harder to distinguish their effects on the response and therefore to estimate β. Similarly, it gets as well harder to estimate γ in the regression of X_j on X_−j, since X_j can be explained well by many linear combinations of the other covariates that are correlated with X_j. In Figure 4 we can see that Doubly Debiased Lasso is much less affected by correlated covariates. The (scaled) absolute bias terms |B_b| and |B_β| are much larger for standard Debiased Lasso, which causes the coverage to worsen significantly for values of κ that are closer to 1.

FIG 4.

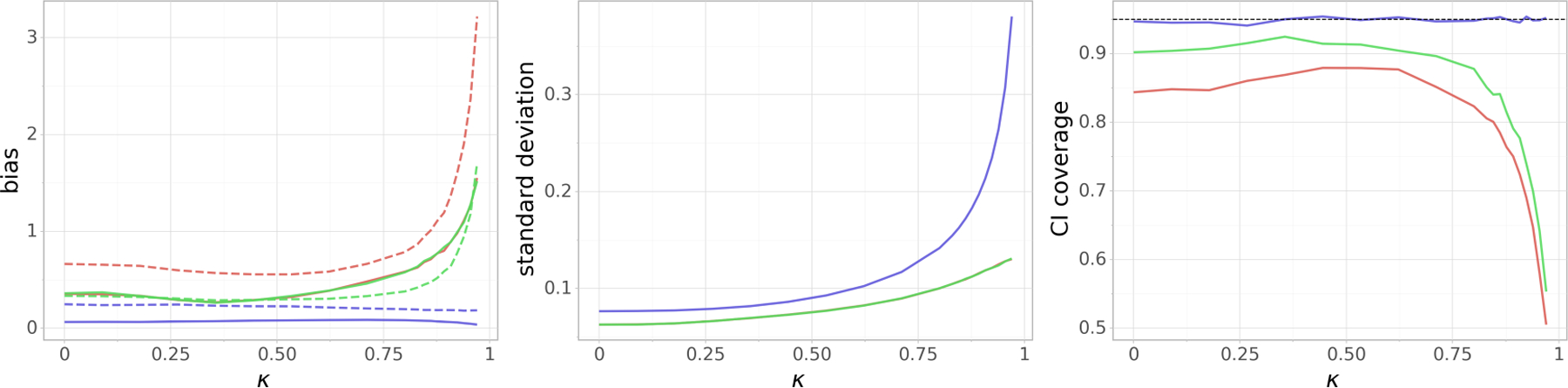
(Toeplitz covariance for ${\Sigma }_E$) Dependence of the (scaled) absolute bias terms |B_β| and |B_b| (left), standard deviation V^1/2 (middle) and the coverage of the 95% confidence interval (right) on the parameter κ of the Toeplitz covariance structure. n = 300 and p = 1, 000 are fixed. On the leftmost plot, |B_β| and |Bb| are denoted by a dashed and a solid line, respectively. Blue color corresponds to the Doubly Debiased Lasso, red color represents the standard Debiased Lasso and green color corresponds also to the Debiased Lasso estimator, but with the same ${\widehat{\beta }}^{init}$ as our proposed method. Note that the last two methods have almost indistinguishable |B_b| and V.

Proportion of confounded covariates.

In order to investigate how the confounding denseness affects the performance of our method, we now again fix n = 300 and p = 1, 000, but we change the proportion of covariates X_i that are affected by each confounding variable. We do this by setting to zero a desired proportion of entries in each row of the matrix $\mathrm{\Psi }\in {ℝ}^{q\times p}$, which describes the effect of the confounding variables on each predictor. Its non-zero entries are still generated as N(0, 1). We set once again ${\Sigma }_E={\text{I}}_p$ and we vary the proportion of nonzero entries of $\mathrm{\Psi }$ from 5% to 100%. The results can be seen in Figure 5. We can see that Doubly Debiased Lasso performs well even when only a very small number (5%) of the covariates are affected by the confounding variables, which agrees with our theoretical discussion for assumption (A2). We can also see that the coverage of the standard Debiased Lasso is poor even for a small number of affected variables and it worsens as the confounding variables affect more and more covariates. The coverage improves to some extent when we use a better initial estimator, but is still worse than our proposed method.

FIG 5.

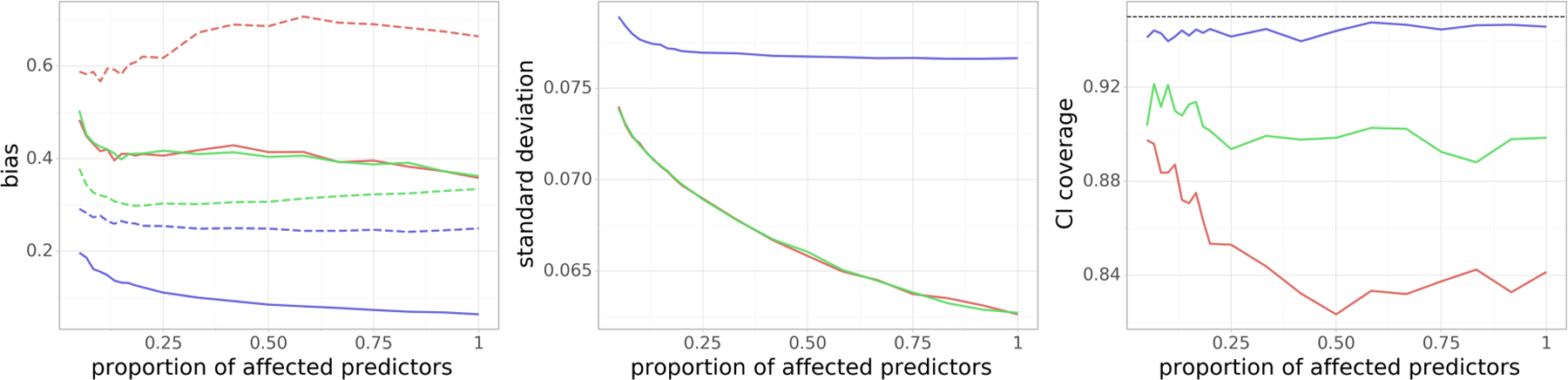
(Proportion confounded) Dependence of the (scaled) absolute bias terms |B_β| and |B_b| (left), standard deviation V_1/2 (middle) and the coverage of the 95% confidence interval (right) on proportion of confounded covariates. n = 300 and p = 1, 000 are fixed. On the leftmost plot, |B_β| and |B_b| are denoted by a dashed and a solid line, respectively. Blue color corresponds to the Doubly Debiased Lasso, red color represents the standard Debiased Lasso and green color corresponds also to the Debiased Lasso estimator, but with the same ${\widehat{\beta }}^{init}$ as our proposed method. Note that the last two methods have almost indistinguishable |B_b| and V.

In Appendix D we also show how the performance changes with the strength of confounding, by gradually decreasing the size of the entries of the loading matrix $\mathrm{\Psi }$.

Trimming level.

We investigate here the dependence of the performance on the choice of the trimming threshold for the Trim transform (14), parametrized by the proportion of singular values ρ_j which we shrink. The spectral transformation $𝓟$ used for the initial estimator ${\widehat{\beta }}^{init}$ is fixed to be the default choice of Trim transform with median rule. We fix n = 300 and p = 1, 000 and consider the same setup as in Figure 3. We take $\tau ={\mathrm{\Lambda }}_{⌊{\rho }_{j}m⌋,⌊{\rho }_{j}m⌋}$ to be the ρ_j-quantile of the set of singular values of the design matrix X, where we vary ρ_j across the interval [0, 0.9]. When ρ_j = 0, τ is the maximal singular value, so there is no shrinkage and our estimator reduces to the standard Debiased Lasso (with the initial estimator ${\widehat{\beta }}^{init}$). The results are displayed in Figure 6. We can see that Doubly Debiased Lasso is quite insensitive to the trimming level, as long as the number of shrunken singular values is large enough compared to the number of confounding variables q. In the simulation q =3 and the (scaled) absolute bias terms |B_b| and |B_β| are still small when ρ_j ≈0.02, corresponding to shrinking 6 largest singular values. We see that the standard deviation decreases as ρ_j decreases, i.e. as the trimming level τ increases, which matches our efficiency analysis in Section 4.2.1. However, we see that the default choice $\tau ={\mathrm{\Lambda }}_{⌊m/2⌋,⌊m/2⌋}$ has decent performance as well. In Appendix D we also explore whether the choice of spectral transformation significantly affects the performance, with a focus on the PCA adjustment, which maps first several singular values to 0, while keeping the others intact.

No confounding bias.

We consider now the same simulation setting as in Figure 3, where we fix n = 500 and vary p, but where in addition we remove the effect of the perturbation b that arises due to the confounding. We generate from the model (2), but then adjust for the confounding bias: Y ← (Y – Xb), where b is the induced coefficient perturbation, as in Equation (3). In this way we still have a perturbed linear model, but where we have enforced b = 0 while keeping the same spiked covariance structure of $X:{\Sigma }_X={\Sigma }_E+{\mathrm{\Psi }}^{\top }\mathrm{\Psi }$ as in (2). The results can be seen in the top row of Figure 7. We see that Doubly Debiased Lasso still has smaller absolute bias |B_β|, slightly higher variance and better coverage than the standard Debiased Lasso, even in absence of confounding. The bias term B_b equals 0, since we have put b = 0. We can even observe a decrease in estimation bias for large p, and thus an improvement in the confidence interval coverage. This is due to the fact that X has a spiked covariance structure and trimming the large singular values reduces the correlations between the predictors. This phenomenon is also illustrated in the additional simulations in the Appendix D, where we set q = 0 and put E to have either Toeplitz or equicorrelation covariance structure with varying degree of spikiness (by varying the correlation parameters).

In the bottom row of Figure 7 we repeat the same simulation, but where we set q =0 and take ${\Sigma }_X={\Sigma }_E=I$ in order to investigate the performance of the method in the setting without confounding, but where the covariance matrix of the predictors is not spiked. We see that there is not much difference in the bias and only a slight increase in the variance of our estimator and thus also there is not much difference in the coverage of the confidence intervals. We conclude that our method can provide certain robustness against dense confounding: if there is such confounding, our proposed method is able to significantly reduce the bias caused by it; on the other hand, if there is no confounding, in comparison to the standard Debiased Lasso, our proposed method still has essentially as good performance, with a small increase in variance.

Measurement error.

We now generate from the measurement error model (4), which can be viewed as a special case of our model (2). The measurement error $W={\mathrm{\Psi }}^{\top }H$ is generated by q =3 latent variables $H_{i,\cdot }\in {ℝ}^q$ for 1 ≤ i ≤ n. We fix the number of data points to be n = 500 and vary the number of covariates p from 50 to 1, 000, as in Figure 3. The results are displayed in Figure 8, where we can see a similar pattern as before: Doubly Debiased Lasso decreases the bias at the expense of a slightly inflated variance, which in turn makes the inference much more accurate and the confidence intervals have significantly better coverage.

FIG 8.

(Measurement error) Dependence of the (scaled) absolute bias terms |B_β| and |B_b| (left), standard deviation V_1/2 (middle) and the coverage of the 95% confidence interval (right) on the number of covariates p in the measurement error model (4). The sample size is fixed at n = 500. On the leftmost plot, |B_β| and |B_b| are denoted by a dashed and a solid line, respectively. Blue color corresponds to the Doubly Debiased Lasso, red color represents the standard Debiased Lasso and green color corresponds also to the Debiased Lasso estimator, but with the same ${\widehat{\beta }}^{init}$ as our proposed method. Note that the last two methods have almost indistinguishable |B_b| and V.

5.2. Real data.

We investigate here the performance of Doubly Debiased Lasso (with a default trimming level of 50%) on a genomic data set. The data are obtained from the GTEx project [41], where the gene expression has been measured postmortem on samples coming from various tissue types. For our purposes, we use fully processed and normalized gene expression data for the skeletal muscle tissue. The gene expression matrix X consists of measurements of expressions of p = 12, 646 protein-coding genes for n = 706 individuals. Genomic data sets are particularly prone to confounding [39, 22, 24], and for our analysis we are provided with q = 65 proxies for hidden confounding, computed with genotyping principal components and PEER factors.

We investigate the associations between the expressions of different genes by regressing one target gene expression X_i on the expression of other genes X_−i Since the expression of many genes is very correlated, researchers often use just ~ 1, 000 carefully chosen landmark genes as representatives of the whole gene expression [54]. We will use several such landmark genes as the responses in our analysis.

In Figure 9 we can see a comparison of 95%-confidence intervals that are obtained from Doubly Debiased Lasso and standard Debiased Lasso. For a fixed response landmark gene X_i, we choose 25 predictor genes X_j where j ≠ i such that their corresponding coefficients of the Lasso estimator for regressing X_i on X_−i are non-zero. The covariates are ordered according to decreasing absolute values of their estimated Lasso coefficients. We notice that the confidence intervals follow a similar pattern, but that the Doubly Debiased Lasso, besides removing bias due to confounding, is more conservative as the resulting confidence intervals are wider.

FIG 9.

Comparison of 95% confidence intervals obtained by Doubly Debiased Lasso (blue) and Doubly Debiased Lasso (red) for regression of the expression of one target landmark gene on the other gene expressions.

This behavior becomes even more apparent in Figure 10, where we compare all p-values for a fixed response landmark gene. We see that Doubly Debiased Lasso is more conservative and it declares significantly less covariates significant than the standard Debiased Lasso. Even though the p-values of the two methods are correlated (see also Figure 12), we see that it can happen that one method declares a predictor significant, whereas the other does not.

FIG 10.

Comparison of p-values for two-sided test of the hypothesis β_j = 0, obtained by Doubly Debiased Lasso (red) and Doubly Debiased Lasso (blue) for regression of the expression of one target gene on the other gene expressions. The covariates are ordered by decreasing significance, either estimated by the Debiased Lasso (left) or by the Doubly Debiased Lasso (right). Black dotted line indicates the 5% significance level.

FIG 12.

Comparison of p-values for two-sided test of the hypothesis β_j = 0, obtained by Doubly Debiased Lasso and standard Debiased Lasso for regression of the expression of one target gene on the other gene expressions. The points are aggregated over 10 landmark response genes. The p-values are either determined using the original gene expression matrix (left) or the matrix where we have regressed out the given q = 65 confounding proxies (right). Horizontal and vertical black dashed lines indicate the 5% significance level.

Robustness against hidden confounding.

We now adjust the data matrix X by regressing out the q = 65 provided hidden confounding proxies. By regressing out these covariates, we obtain an estimate of the unconfounded gene expression matrix $\tilde{X}$. We compare the estimates for the original gene expression matrix with the estimates obtained from the adjusted matrix.

For a fixed response landmark gene expression X_i, we can determine significance of the predictor genes by considering the p-values. One can perform variable screening by considering the set of most significant genes. For Doubly Debiased Lasso and the standard Lasso we compare the sets of most significant variables determined from the gene expression matrix X and the deconfounded matrix $\tilde{X}$. The difference of the chosen sets is measured by the Jaccard distance. A larger Jaccard distance indicates a larger difference between the chosen sets. The results can be seen in Figure 11. The results are averaged over 10 different response landmark genes. We see that the Doubly Debiased Lasso gives more similar sets for the large model size, indicating that the analysis conclusions obtained by using Doubly Debiased Lasso are more robust in presence of confounding variables. However, for small model size we do not see large gains. In this case the sets produced by any method are quite different, i.e. the Jaccard distance is very large. This indicates that the problem of determining the most significant covariates is quite difficult, since X and $\tilde{X}$ differ a lot.

FIG 11.

Comparison of the sets of the most significant covariates chosen based on the original expression matrix X and the deconfounded gene expression matrix $\tilde{X}$, for different cardinalities of the sets (model size). The set differences are measured by Jaccard distance. Red line represents the standard Debiased Lasso method, whereas the blue and green lines denote the Doubly Debiased Lasso that uses ρ = 0.5 and ρ = 0.1 for obtaining the trimming threshold, respectively; see Equation (14).

In Figure 12 we can see the relationship between the p-values obtained by Doubly Debiased Lasso and the standard Debiased Lasso for the original gene expression matrix X and the deconfounded matrix $\tilde{X}$. The p-values are aggregated over 10 response landmark genes and are computed for all possible predictor genes. We can see from the left plot that the Doubly Debiased Lasso is much more conservative for the confounded data. The cloud of points is skewed upwards showing that the standard Debiased Lasso declares many more covariates significant in presence of the hidden confounding. On the other hand, in the right plot we can see that the p-values obtained by the two methods are much more similar for the unconfounded data and the point cloud is significantly less skewed upwards. The remaining deviation from the y = x line might be due to the remaining confounding, not accounted for by regressing out the given confounder proxies.

6. Discussion.

We propose the Doubly Debiased Lasso estimator for hypothesis testing and confidence interval construction for single regression coefficients in high-dimensional settings with “dense” confounding. We present theoretical and empirical justifications and argue that our double debiasing leads to robustness against hidden confounding. In case of no confounding, the price to be paid is (typically) small, with a small increase in variance but even a decrease in estimation bias, in comparison to the standard Debiased Lasso [65]; but there can be substantial gain when “dense" confounding is present.

It is ambitious to claim significance based on observational data. One always needs to make additional assumptions to guard against confounding. We believe that our robust Doubly Debiased Lasso is a clear improvement over the use of standard inferential high-dimensional techniques, yet it is simple and easy to implement, requiring two additional SVDs only, with no additional tuning parameters when using our default choice of trimming ρ = ρ_j = 50% of the singular values in Equations (14) and (15).