Abstract
We consider nonparametric estimation of probability measures for parameters in problems where only aggregate (population level) data are available. We summarize an existing computational method for the estimation problem which has been developed over the past several decades [24, 5, 12, 28, 16]. Theoretical results are presented which establish the existence and consistency of very general (ordinary, generalized and other) least squares estimates and estimators for the measure estimation problem with specific application to random PDEs.
Keywords: 62G07, 34A55, 46S50, 93E24, inverse problems, aggregate data, individual data, existence and approximation of estimators
1. INTRODUCTION
Our ideas of using distributions for parameters in inverse problems grew out of work in [7] and use of Sinko-Streifer models for mosquitofish growth rates where only aggregate data were available due to periodic sampling of different subsets of the population. The first theoretical results in the context of inverse problems was in [12]. There were numerous subsequent uses including shrimp population size models in [4, 11] and carboxyfluorescein succinimidyl ester (CFSE) labeling models [13]. In our presentation here we consider approximation methods in estimation or inverse problems but the quantity of interest is a probability distribution. Assume we have a parameterized system (q ∈ Ω) with state model responses x(t; q) describing the population of interest. For data or observations, we are given a set of values {yl ≈ Cx(tl; q)} for the expected values
for observations yl(q) = Cx(tl, q) with respect to the unknown probability distribution P describing the distribution of parameters q over the population.
We use data to choose from a given family of distributions the distribution P∗ that gives the best fit of the underlying model to data. This is accomplished by formulating an ordinary least squares (OLS) problem; however we note that we could equally well use a weighted least squares (WLS) or maximum likelihood estimation (MLE) framework. Specifically we seek to minimize
over . Even for simple dynamics for yl(q) this yields an infinite dimensional optimization problem. Therefore one needs approximations that lead to computationally tractable schemes. That is, it is useful to formulate methods to yield finite dimensional sets over which to minimize J(P). Of course, we wish to choose these methods so that in some sense. In our case we shall use the Prohorov Metric [5, 24] of weak star convergence of measures to assure the desired approximation convergences as well as consistency of the estimators.
The data {yl} available (which, in general, will involve longitudinal or time evolution data) determines the nature of the problem. In gerneral there are three classes of problems:
Type I: The most classical problem (which we shall refer to as a Type I problem) is one in which individual longitudinal data is available for each member in the population. In this case there is a wide statistical literature (in the context of hierarchical modeling, mixing distributions, mixed or random effects, mixture models, etc.) [29, 33, 34, 35, 36, 50, 49, 51, 53, 65, 64, 63] which provides theory and methodology for estimating not only individual parameters but also population level parameters and allows one to investigate both intra-individual and inter-individual variability in the population and data.
Type II: In what we shall refer to as Type II problems one has only aggregate or population level longitudinal data available. This is common in marine, insect, etc., catch and release experiments [17] where one samples at different times from the same population but cannot be guaranteed of observing the same subset of individuals at each sample time under constant environmental, etc., conditions. This type of data is also typical in experiments where the organism or population member being studied is sacrificed in the process of making a single observation (e.g., certain physiologically based pharmacokinetic (PBPK) modeling [1, 21, 66, 57] and whole organism transport models [17]). In this case one may still have dynamic (i.e., time course) models for individuals, but no individual data are available.
Type III: Finally, the third class of problems which we shall refer to as Type III problems involves dynamics which depend explicitly on the probability distribution P itself. In this case one only has dynamics (aggregate dynamics) for the expected value
of the state variable. No dynamics are available for individual trajectories x(t, q) for a given q ∈ Q. Such problems arise in viscoelasticity and electromagnetics as well as biology (the HIV cellular models of [6]) see also [5, 15, 14, 20, 44].
While the approximations we discuss below are applicable to all three types of problems, our primary interest here is problems of Type II and Type III. In particular we shall illustrate and provide theoretical underpinnings for our earlier computational results in the context of Transdermal Alcohol Concentration (TAC) and Glioblastoma Multiforme (GBM) cancer where the inverse problems are of Type II. Finally, we note that in the problems considered here, one can not sample directly from the probability distribution being estimated and this again is somewhat different from the usual case treated in some of the statistical literature, e.g., see [81, 82] and the references cited therein.
We first describe two relevant examples currently under investigation: the first is a linear partial differential equation with unknown diffusion; the second is a nonlinear diffusion-growth system for tumors.
2. EXAMPLE 1: ESTIMATING BLOOD/BREATH ALCOHOL CONCENTRATION FROM TRANSDERMAL ALCOHOL CONCENTRATION(TAC)
The measurement of the alcohol level in the human body for the purpose of medical research, clinical therapy, and law enforcement (e.g. DUI, etc.), typically takes the form of blood alcohol concentration (BAC). However, in the absence of a blood sample, which is almost always the case, a surrogate, breath alcohol concentration (BrAC) as measured by an instrument known as a breath analyzer, is used. The underlying chemistry of the breath analyzer (based on Henry’s Law [48]) has been shown to be reasonably robust and consistent across individuals and ambient conditions, thus allowing for the relatively straight forward conversion of breath alcohol concentration (BrAC) to blood alcohol concentration (BAC). Unfortunately, however, there are two significant drawbacks to collecting data using a breath analyzer: properly blowing into a breath analyzer so as to obtain accurate measurements can be challenging, and the collection of breath data that is near-continuous in time and in a naturalistic setting is all but impossible.
Recently, technology has been developed to allow for the measurement of transdermal alcohol, or alcohol that diffuses from the skin’s dermal layer which has an active blood supply, through the epidermal layer of the skin. These devices use a variety of technologies (electro-chemical, enzymatic, optical, etc.) to count the number of ethanol molecules evaporating from the surface of the skin through normal perspiration. The current generation of transdermal alcohol biosensors are reasonably compact and relatively unobtrusive, and generally resemble a digital watch, ankle bracelet, or activity tracker. Two such devices are the WrisTAS™7 alcohol biosensor designed and manufactured by Giner, Inc. of Waltham, MA and the Secure Continuous Alcohol Monitoring System (SCRAM) device manufactured by Alcohol Monitoring Systems in Littleton, Colorado (see Figure 1). These devices offer the possibility of passively collecting drinking and intoxication data both in the lab or clinic and out in the field, that is essentially continuous in time over extended periods such as hours, days, or even weeks. It is also conceivable that they could be further miniaturized and included as a feature in the next generation of wearable health monitoring technology. At present, however, with the exception of one company that monitors abstinence of DUI offenders under contract to the courts, these devices are primarily only being used in the research community, with the devices themselves (their utility, practicality, accuracy, dependability, etc.) the central focus of the research project. This is because while it has been known for a long time that the alcohol level in perspiration correlates well with the alcohol concentration in the blood or breath [77, 78, 79, 80], there are significant variations (1) from sensor to sensor and (2) in the rate at which alcohol diffuses through the skin both across individuals and across distinct drinking episodes within individuals under differing environmental conditions. Consequently the meaningful quantitative interpretation of transdermal alcohol levels poses a significant challenge. More to the point, there is currently no known direct and generally accepted method for converting what these devices measure, transdermal alcohol concentration or TAC, to the quantities that researchers, clinicians, law enforcement and the public at large are all most familiar with and that are well understood measures of intoxication, BAC and/or BrAC.
Figure 1:

Alcohol Biosensor Devices: The WrisTAS (left) and the SCRAM (right).
Some of the difficulties involved in converting TAC to BAC or BrAC are illustrated in the following two example data sets. A WrisTAS™7 was worn by a participant for 18 days. During each drinking episode, the participant collected BrAC data (i.e., blew into a breath analyzer) approximately every 30 minutes. The first drinking episode was conducted in the laboratory and BrAC was measured every 15 minutes until it returned to 0.000. The participant then wore the device for the following 17 days and consumed alcohol ad libitum. During those days, BrAC was measured every 30 minutes starting from the beginning of the drinking session until its value returned to 0.000. The WrisTAS™7 measured and recorded ethanol level at the skin surface every 5-minutes. During those 17 days, the data were collected in a naturalistic setting. The plot in Figure 2 shows the measured BrAC and TAC over 11 drinking episodes. Note that in drinking episodes 1, 2, 4, 6, 7, 8, and 11 the peak BrAC value was higher than the bench calibrated peak TAC value, while in drinking episodes 3, 5, 9, and 10 the peak TAC value was higher than the peak BrAC value.
Figure 2:
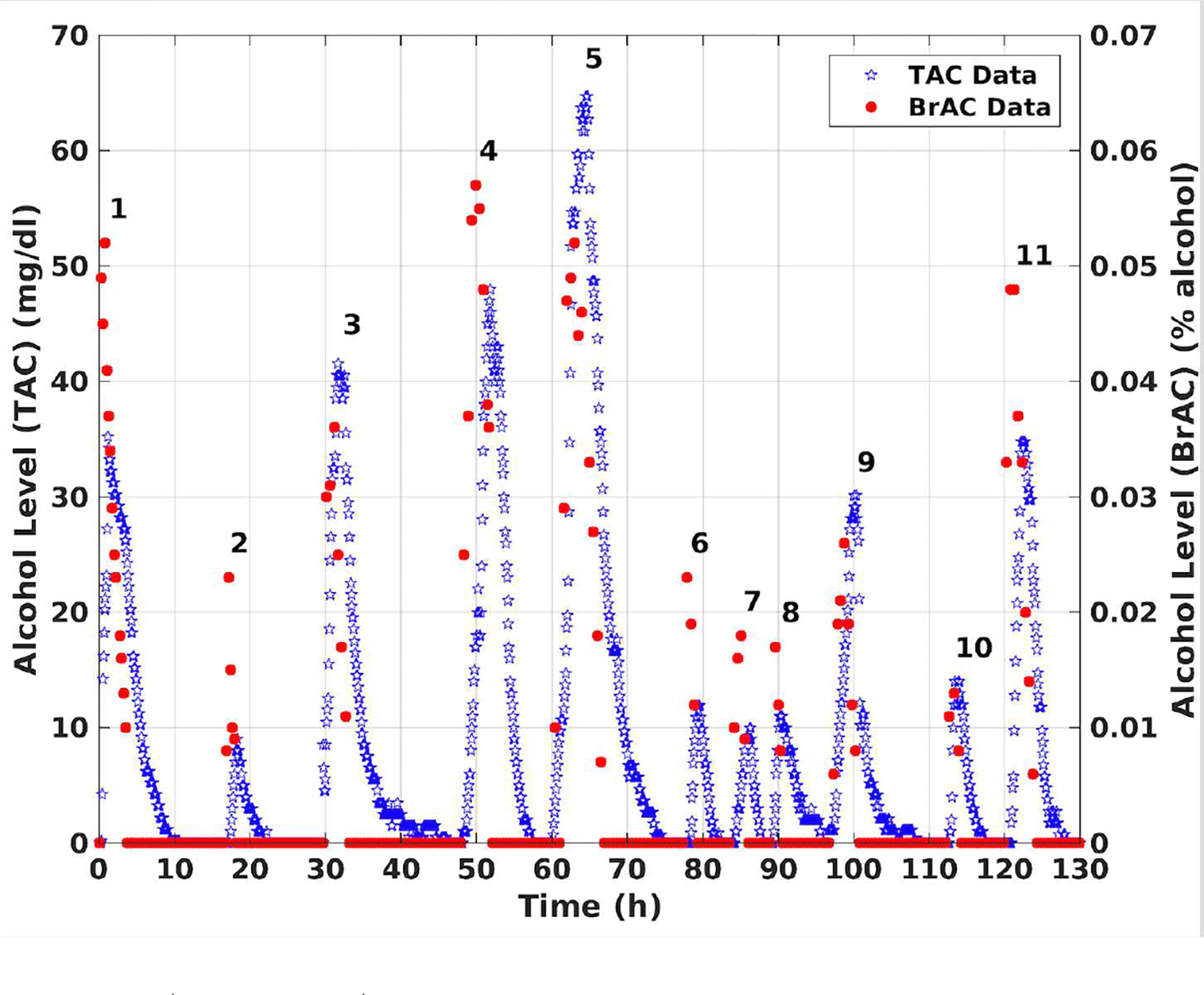
BrAC and TAC measurements for multiple drinking episodes by a single subject.
In a second example, data were collected from multiple subjects at the University of Illinois at Urbana-Champaign using the AMS SCRAM alcohol biosensor. In this study 60 participants were given a gender and weight adjusted dose of alcohol calculated to yield a peak BrAC of approximately .08%. The participants were then asked to provide breath analyzer readings at 30 minute intervals. The SCRAM sensor was worn and provided transdermal readings also at a rate of one every 30 minutes. We then fit the two parameters in the first principles physics based forward model to be described below to 18 of the 60 data sets collected. While for each participant’s data, the resulting models produced estimated BrAC that closely fit the observed BrAC (obtained by inverting the forward model) and estimated TAC (obtained by putting the estimated BrAC back through the forward model) that essentially reproduced the measured or observed TAC, as the scatter plot below clearly shows, there was nevertheless a wide variance in the values of the fit parameters.
A number of researchers have looked at the TAC to BAC/BrAC conversion problem (see, for example, [37, 38, 39]) with the goal being to produce reliable quantitative estimates of BrAC/BAC (eBrAC/eBAC) from TAC data. In a series of papers [32, 40, 59, 68] one of the co-authors of this paper (IGR) together with other members of his research group devised a two-step protocol that used individual calibration data (i.e., simultaneously-collected breath analyzer BrAC measurements and biosensor TAC measurements) to first fit a first principles physics/physiological-based forward model to capture the transport of ethanol from the blood, through the skin, and its eventual processing and measurement by the TAC sensor. They then used the fit forward model together with deconvolution techniques to estimate the eBrAC/eBAC input to the model from the TAC output for other drinking episodes not included in the training set. Such an approach has the obvious drawback of requiring that the forward model be tuned to each individual and device and the ambient environmental conditions (e.g., temperature, humidity, etc.). Indeed, our algorithms have been used in alcohol related consumption and behavioral studies [52] in which drinking patterns in individuals with and without alcohol metabolizing genetic variants were investigated, and in [41] to investigate the relationship between social familiarity and alcohol reward in naturalistic drinking settings and compared this to alcohol reward observed in laboratory drinking settings. The results of these studies clearly indicated that at least a portion of the dynamics of the system are not being captured by the models. In addition, the requisite calibration procedure is a significant burden to researchers, clinicians and participants. They may also pose a number of ethical concerns (e.g., requiring the offering of alcoholic beverages to participants known to be pregnant or suffering from alcohol use disorder).
In a more recent series of papers [69, 67, 70], this same research group has proposed eliminating the need to calibrate the forward models, by developing population models based on their physics based models. The parameters in the model are assumed to be random and instead of using their actual values as a basis for fitting the model, the training data is used to estimate the distribution of these random parameters. In those studies, however, the arguments used to demonstrate the convergence of their method required the assumption that the distributions were described by appropriately constrained parameterized families of probability density functions. The theory we describe here demonstrates how this restrictive assumption can be eliminated.
By essentially converting all quantities in our first principles physics based model to dimensionless variables, we are able to eliminate some non-identifiable (i.e., dependent) parameters and obtain the initial-boundary value problem given by
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where the partial differential equation (1) describes the one dimensional transport of ethanol through the epidermal layer of the skin, and the boundary conditions (2) and (3) describe respectively the evaporation of ethanol at the skin surface (η = 0) and the flux of ethanol across the boundary between the epidermal and dermal layers of the skin (η = 1; note that the dermal layer has a blood supply whereas the epidermal layer does not). The initial conditions are given in (4) (typically we will have ϕ0 = 0 since we will assume that at the start of any drinking episode there is no alcohol in the body) and the output equation, (5) says that TAC is measured by the biosensor at the skin surface. The state of the system, ϕ(t, η) essentially denotes the concentration of ethanol at depth η, 0 ≤ η ≤ 1 in the epidermal layer at time t ≥ 0, while u(t) and y(t) denote, respectively, the BAC/BrAC and TAC at time t. The parameters q1 (normalized “diffusion”) and q2 (normalized flux control input coefficient) are assumed to lie in a compact subset, Q, of endowed with the metric dQ.
While our ultimate goal is to deconvolve the BAC/BrAC input u from the biosensor measured TAC output y, our concern in this study is dealing with the uncertainty in the model parameters. Indeed, since the parameters q which are unknown and dependent on 1) the individual wearing the sensor, 2) the ambient environmental conditions at the time the TAC measurements or observations were made, and 3) the particular sensor being worn, the problem of estimating BAC/BrAC from observations of TAC is in fact a blind deconvolution problem involving aggregate data. Our approach involves replacing the q-dependent model with a population model which captures and quantifies the variability and uncertainty that exists across all the individual members of the population (we use the term individual to mean not just different subjects, but also unmodelled different environmental conditions and different hardware, and for that matter any other un-modeled dynamics present in the system). Thus we view our problem as the class of Type II described in the Introduction. The details involved in deconvolving the BAC/BrAC from the TAC once the population model has been estimated along with associated error bars can be found in [68].
We define the population model to be the system (1)-(5) with the parameters q ∈ Q defined to be a random vector together with the distribution for the parameters in the form of a probability measure P0 or joint distribution function F0. We assume (1) that ν data sets have been collected, and (2) the statistical model given by
| (6) |
Where in (6) Yj (q, ui) is the random variable corresponding to (1)-(5) and , j = 0, …,νi, i = 1, …,ν, represent measurement noise and are assumed to be independent and identically distributed with mean 0 and common variance σ2. Then for P a probability measure defined on the σ-algebra of events in the probability space associated with the random vector q, and F its corresponding cumulative distribution function, define for an observation operator the the mean behavior at time j, j = 0, …,νi,
| (7) |
where q ~ F and yj is a realization for Yj.
The estimation problem is then to estimate the measure P0, using a least squares approach
| (8) |
where the vi(j; P) are as given in (7).
3. EXAMPLE 2: GLIOBLASTOMA MULTIFORME (GBM)
Glioblastoma Multiforme (GBM) is a deadly primary brain tumor. Due to it’s highly infiltrative nature, GBM remains difficult to treat: although resection surgery may remove the primary tumor, many tumor cells can remain throughout the brain, resulting in nearly all tumors recurring [83]. It has been shown that tumors that exhibit nodular growth patterns (i.e., low diffusivity) result in better patient prognosis [2]. Thus, it is increasingly important to be able to accurately ascertain the growth and diffusion phenotypes present in individual tumors.
GBM is often modeled in vivo using partial differential equations. The simplest models of GBM growth only consider the reaction-diffusion equation [55, 75, 61], given by:
| (9) |
where c(t, x) represents the cell density at time t and spatial location x, D is the diffusion coefficient, and ρ is the intrinsic growth rate. However, this simplistic model assumes diffusion is isotropic, which does not accurately describe resulting in vivo tumor shapes.
There are multiple methods to incorporate anisotropic diffusion in order to make glioma models more physiologically accurate. These methods introduce heterogeneity into the diffusion coefficients. For example, one can incorporate a spatially-dependent piece-wise diffusion coefficient to explain diffusion of cells in grey matter versus white matter [76]. In a similar vein, diffusion weighted imaging (DWI), which contains information about water diffusion, has been used to infer cellular diffusion through the brain [30, 31, 46, 47, 56]. Other approaches to incorporating cellular heterogeneity include density-dependent diffusion functions [73].
A landmark study discovered that, even in vitro, a reaction-diffusion equation was insufficient to describe the cellular dynamics [71]. In the work, the authors performed cell line experiments on most common mutation of Epidermal Growth Factor Receptor gene (U87ΔEGFR) and wild-type EGFR (U87WT). This showed there are distinct behavioral differences between ‘migrating’ cells and ‘proliferating cells’ and thus concluded that migrating and proliferating cells should be modeled separately. This observation resulted in the modeling of cellular heterogeneity as a collection of two phenotypic subpopulations, one of which mainly migrated and one that mainly proliferated. This “go or grow” hypothesis [45] remains widely used in mathematical models of glioma growth today [72, 43]. For a recent review on the status of mathematical modeling in GBM see [54].
We proposed in [60] to perform an inverse problem to estimate the diffusion D, and growth rate ρ in the reaction-diffusion equation as distributions of a random differential equation rather than as point estimates for a deterministic differential equation. In this case any spatiotemporal data involves a growing/decreasing population of different individual cells and even if one has frequent measurements of the changing populations, one expects (because of a continuum of growth/death of the individual cells) this to represent (as in the case of many biological cell data counts [13]) aggregates of different populations at different times of data collections.
In [60], we proposed a model of GBM growth with the option of phenotypic heterogeneity by using parameter distributions for the parameters ρ and D. The random differential equation for GBM growth and diffusion is given by:
| (10) |
where D and ρ are random variables defined on a compact set Ω = ΩD ×Ωρ. In order to obtain the aggregate observable, we take the expectation over all subpopulations:
| (11) |
The given random differential equation has the option of phenotypic heterogeneity because we can easily recover the basic reaction-diffusion equation (Eq. 9) when D and ρ are point distributions. Moreover, we are able to model a “go or grow” system by considering bigaussian distributions of the parameters. Most importantly, we are able to model these distributions (and more) without making any assumptions on the underlying distributions.
Several different methods for approximating the probability measures P(D,ρ) include using either discrete approximations based on delta functions or continuous approximations based on spline basis functions. Although using higher order spline functions are known [3, 9, 10, 20] to yield more accurate convergence in the case of smooth probability density functions (PDF) and cumulative distribution functions (CDF), delta functions are able to better approximate CDFs that have discontinuous derivatives. Therefore, in [60] we discussed the use of both approximations since we did not wish to make any assumptions about, or restrictions on, the CDF.
Suppose that the aggregate spatiotemporal data we want to model is given by vji, representing the data at time j and spatial location i, where j = 1, …, Nt and i = 1,…,Nx. Then, we estimate using N = Nt × Nx data points
(This, of course, is an idealized version of available data sets but we will use this notation when discussing consistency. We assume in our subsequent discussions involving N → ∞ statements it is understood both Nt,Nx → ∞.)
This becomes
| (12) |
where c is the solution of the random differential equation (10).
4. PROHOROV ESTIMATES AND THEIR APPROXIMATIONS
Convergence in the Prohorov metric is equivalent to the weak* convergence of measures when the space of probability measures is imbedded in the dual C∗(Ω) of the space of bounded continuous functions on Ω. We discuss briefly existence, convergence, and consistency theory, assuming here we are only estimating D of the GBM example above as a distribution. We note the theory readily extends to two parameters (diffusion and growth rates) for the GBM example and to the vector parameters in the case of the TAC example discussed above.
In the following discussions we adopt the following notation : N = (Nt, Nx) = Nt × Nx are the number of data points or observations; are the state approximations to v(t, x; ω), so is the index for state approximations; M will be the parameter approximation index
We assume a family of permissible probability functions for our diffusion rates. We attempt to perform the estimation in a least-squares framework
| (13) |
where N observations are used to obtain a best fit for a nominal or “true” parameter P0. In order to approximate this minimizer, we replace the infinite dimensional optimization problem by a sequence of finite-dimensional optimization problems with, for example, Dirac or spline-based distributions. Thus, if we use the Dirac approximating families, we set , where M represents the number of nodes, or elements, used in the approximation. Our family of approximating probability functions becomes
where represents the Dirac delta function at the point Dk and wk are the weights and/or probabilities. It has been previously proven [23, 28] that there exists a minimizer for the discrete approximation problem
| (14) |
A further approximation arises when we appproximate the state variable v by numerical approximation , e.g., by finite elements for example, and seek to solve
| (15) |
There are a number of questions that arise immediately in the class of problems we have defined. Perhaps the most obvious are questions of convergence (what happens as M → ∞ in the Dirac or spline approximations?) and consistency (what happens as N = (Nt, Nx) → ∞?) These questions have been successfully investigated both theoretically ([28, 20, 22] and the references therein) and computationally ([10, 9] and the references therein) for certain classes of problems. A further issue involves the partial differential equation approximations (e.g., finite element approximations of the realizations of the the random PDE (10)) to the solution c. Again, elements of the necessary convergence issues have been addressed in [28, 17]. In summary we wish to establish for the problems discussed here that the approximations converge to a “true” distribution P0 as the number of elements used in the approximations increases (i.e., M, N, ).
Significantly, the Prohorov Metric Framework is computationally constructive. That is, in practice, one does not construct a sequence of estimates for increasing values of M and ; rather, one fixes the values of M and to be sufficiently large to attain a desired level of accuracy. To do this we need only to have some enumeration of the elements of in order to compute an approximate estimate . Practically, this is accomplished by selecting M nodes in Ω, . The optimization problem (15) is then reduced to a standard constrained estimation problem over Euclidean M-space in which one determines the values of the weights corresponding to each node. Thus,
| (16) |
| (17) |
| (18) |
where in the final line we seek the weights . These are sufficient to characterize the approximating discrete estimate since the nodes are assumed to be fixed in advance. Moreover, define
Then one can equivalently compute [10]
| (19) |
From this reformulation, it is clear that the approximate problem (16) has a unique solution if H is positive definite and the minimum occurs in the interior of the space. If the individual mathematical model is independent of P (See [23, Sec. 14.1.2] for a complete discussion) then the matrices H and f can be precomputed in advance. Then one can rapidly (and exactly) compute the gradient and Hessian of the objective function in a numerical optimization routine. As M grows large, the quadratic optimization problem (19) becomes poorly conditioned [10, 9] and there exists a trade-off: M must be chosen sufficiently large so that the computational approximation is accurate, but not so large that ill-conditioning leads to large numerical errors. The efficient choice of M as well as the choice of the nodes are open research problem-dependent questions.
It should be acknowledged that the uniqueness of the computational problem (i.e., when H is positive definite) is not sufficient to ensure the uniqueness of the limiting estimate in Theorem 5.4 below (as there could be multiple convergent subsequences). However, if of (13) is uniquely minimized, then every subsequence of which converges must converge to that unique minimizer. Moreover, under assumptions (A1)–(A7) detailed below, it can be shown that (as N grows large) with probability one, and the function J0(P) is assumed to be uniquely minimized by P0.
To illustrate the ideas, we continue our discussions with Ω = ΩD taken as the continuum of values in [0, Dmax]. Hence the family of probability functions is a compact metric space in the Prohorov metric. The minimizer function is continuous in P; and there exists a (not necessarily unique) minimizer .
5. RESULTS FOR RANDOM PDE MODELS
We first note that the results of [22] are given in terms of estimators PN and estimates for nonlinear random ordinary differential equations
| (20) |
| (21) |
We claim that the results of [22] hold immediately if we replace the random DEs with the random partial differential equations (10) or (1)-(5). This can be readily established by a careful reading of all the details of [22]. We summarize and discuss the resulting RDE details.
5.1. Existence of the Estimator
For RDE models one can then prove the existence [22, Thm 3.1] of PN and as measurable functions mapping a subset of (that is, the data where N = (Nt, Nx) in the case of our GBM example) into the space of probability measures on Ω. We remark that the statement of the existence theorem concerns the estimate obtained from the data realizations of the random vector . This is sufficient to establish the existence of the estimator PN as a measurable function as well, since the random vector is by definition a measurable function from a probability triple into , and the composition of measurable functions is measurable. We note that the nonlinearities such as those in the GBM example discussed above or the vector nature of the parameters in the TAC example above play no role in the proofs given in [22]. We therefore restate the existence results here without proof, referring the reader to [22] for further details.
Theorem 5.1.
Define the function according to Equation (13). Assume (Ω, d) is separable and compact and take the space of probability measures with the Prohorov metric ρ. Assume further that JN(·, P) is a measurable function from for each , and that is continuous for each . Then there exists a measurable function such that
5.2. Consistency of the Estimator
We can next establish consistency for estimators in the case of random partial differential equation problems. The assumptions are essentially the same as those in the case of ordinary differential equation estimators.
(A1) For any fixed N = Nt × Nx, the error random variables are independent and identically distributed, defined on some probability triple (Θ, ΣΘ, PΘ).
(A2) For , and where IN is the N × N identity matrix.
(A3) (Ω, d) is a separable, compact metric space; the space is taken with the Prohorov metric ρ.
(A4) For all j, 1 ≤ j ≤ Nt, i, 1 ≤ i ≤ Nx, for some compact space .
(A5) The model function .
(A6) There exists a measure μ on such that for all
(A7) The functional is uniquely minimized at .
Under the assumptions one can prove consistency.
Theorem 5.2.
Under assumptions (A1)-(A7), there exists a set A ∈ ΣΘ with PΘ(A) = 1 such that for all θ ∈ A,
as N → ∞ and for each . Moreover, the convergence is uniform on .
Theorem 5.3.
Under assumptions (A1)-(A7), the estimators as N → ∞ with probability 1. That is,
Complete proofs of these two theorems are given in [22].
Theorem 5.3 establishes the consistency of the estimator (12). Given a set of data , it follows that the estimate corresponding to the estimator PN will converge to the true distribution P0 under the stated assumptions. We remark that these assumptions are not overly restrictive (compare [12, 28, 42]) though some of the assumptions may be difficult to verify in practice. Assumptions (A3)–(A5) are mathematical in nature and may be verified directly for each specific problem. Assumptions (A1) and (A2) describe the error process which is assumed to generate the collected data. While it may be possible to ascertain a priori that the error process satisfies these assumptions (see [8]), one may also use posterior analysis such as residual plots [27, Ch. 3] to investigate the appropriateness of the assumptions of the statistical model. Assumption (A6) reflects the manner in which data is sampled and, together with Assumption (A7), constitutes an identifiability condition for the model. The limiting sampling distribution function μ may be known if the experimenter has complete control over the values tj, xi of the independent variables (e.g., if the tj, xi are measurement times and locations) but this may not always be the case.
The novel results in [22] establishes the desirable property of consistency of the estimator PN as a measurable function mapping the data observation process to the space of probability measures. However, it is generally not possible to directly solve the optimization problems (13) for as a function of . As a result, approximate (generally numerical) methods must be used in order to solve (15) and obtain an approximate estimate . We must ascertain, then, how the approximate estimate relates to the exact estimate (for any fixed value of N.)
The following result establishes the computational convergence of the Prohorov Metric framework for fixed N. These results establish a comprehensive body of theory for the least squares estimation of the measure P0 that is assumed to have generated the observed data. It is given in [22, Theorem 5.1]:
Theorem 5.4.
(Convergence) Let (Ω, d) be a compact, separable metric space and consider the space of probability measures on Ω with the Prohorov metric, as before. Let be as defined as above (e.g., using Dirac or spline approximates for elements of Ω). Assume
The map is continuous for all , N;
For any sequence of probability measures Pk → P in , as , k → ∞;
The function v(t, x; P) is uniformly bounded for all t, x, P.
Then there exists minimizers satisfying (15). Moreover, for fixed N, there exists a subsequence (as M,) of the approximate estimates which converges to some which satisfies (13).
This theorem provides a set of conditions under which a sequence of approximate estimates converges to the estimate of interest. This estimate is itself a realization (for a particular data set) of the estimator PN which has been shown to exist and to be consistent, so that PN → P0 with probability one. Thus we are assured that a computed measure is an accurate estimate of the true distribution P0. The assumptions of Theorem 5.4 are not restrictive. In typical problems (and, indeed, in the assumptions of other theorems appearing in this document) it is assumed that the parameter space Ω as well as the independent variable space T × X are compact. In such a case, Assumptions 1 and 3 above are satisfied if the individual model solutions c(t, x; D, ρ) are continuous on T × X × Ω. Assumption 2 is then simply a condition on the convergence of the numerical procedures used in obtaining model solutions which we turn to discuss now! This result is, in essence, a verification of an analogue for our problems of hypothesis (iv) of Theorem 3.1 of [12].
6. ESTIMATION AND APPROXIMATION ARGUMENTS
Recall that we are interested in minimizing for fixed N the least squares cost functional (22):
| (22) |
We first argue the following:
Theorem 6.1.
Suppose for each t, x, uniformly in ω in Ω, and that, for each t, x, the mapping ω → v(t, x; ω) is continuous on Ω. Suppose Pk → P in . Then for each t, x as , k → ∞ we have
Proof. For each fixed t, x we have
| (23) |
For the first term, we find
Suppose ϵ > 0. Choose N0 so that implies
Then for every k we have
Thus I → 0 as uniformly in k.
Considering the second term, we have
But for each t, x, v(t, x; ·) is in C(Ω) and by definition of the Prohorov metric (actually, one of it’s equivalent characterizations!), we have immediately that II → 0 and the theorem is proved.
It remains to verify that for each t, x, uniformly in ω in Ω”. But this is simply a finite element type approximation for the systems (1)-(5) or (9) [62, 74, 58]. These arguments have been given for Sinko-Streifer types hyperbolic systems [26] as well the nonlinear parabolic models of interest here [25, 17, 18, 3]. Indeed, combining the nonlinear approximation arguments of [19, p. 585; take qn ≡ q throughout] with the linear system arguments for in [18, 3] yields the desired approximation results. (Here is the orthogonal projection on to the finite element approximation subspaces.)
7. CONCLUDING REMARKS
Inter-individual or intra-individual heterogeneity is often ignored in mathematical models. In the above discussions we model heterogeneity using random differential equation models. That is, we formulate (partial) differential equations in which some parameters are random variables. In particular, we are concerned with the ability to recover the parameter distributions without making any assumptions about the probability distributions.
We have illustrated and validated the computational results in the context of Transdermal Alcohol Concentration (TAC) models and Glioblastoma Multiforme (GBM) cancer where the inverse problems are of the aggregate data/individual model type. We have established existence of estimators in classes of probability distributions, convergence of approximations and consistency of the estimators.
ACKNOWLEDGEMENT
This research was supported in part by the National Institute on Alcohol Abuse and Alcoholism (HTB) under grant number 1R01AA022714-01A1, in part by the Air Force Office of Scientific Research (HTB) under grant number AFOSR FA9550-15-1-0298, in part by the National Science Foundation (KBF,EMR) under NSF grant number DMS-1514929, in part by the National Institute on Alcohol Abuse and Alcoholism (IGR,MS) under grant number NIAAA R21AA17711. We would also like to acknowledge Professor Susan Luczak of the Department of Psychology at USC (Figure 2) and Professor Catharine E. Fairbairn of the Department of Psychology at UIUC (Figure 3) for allowing us to use the data (collected under grant under grant number NIAAA R01AA025969) described in the two examples in Section 2.
Figure 3:
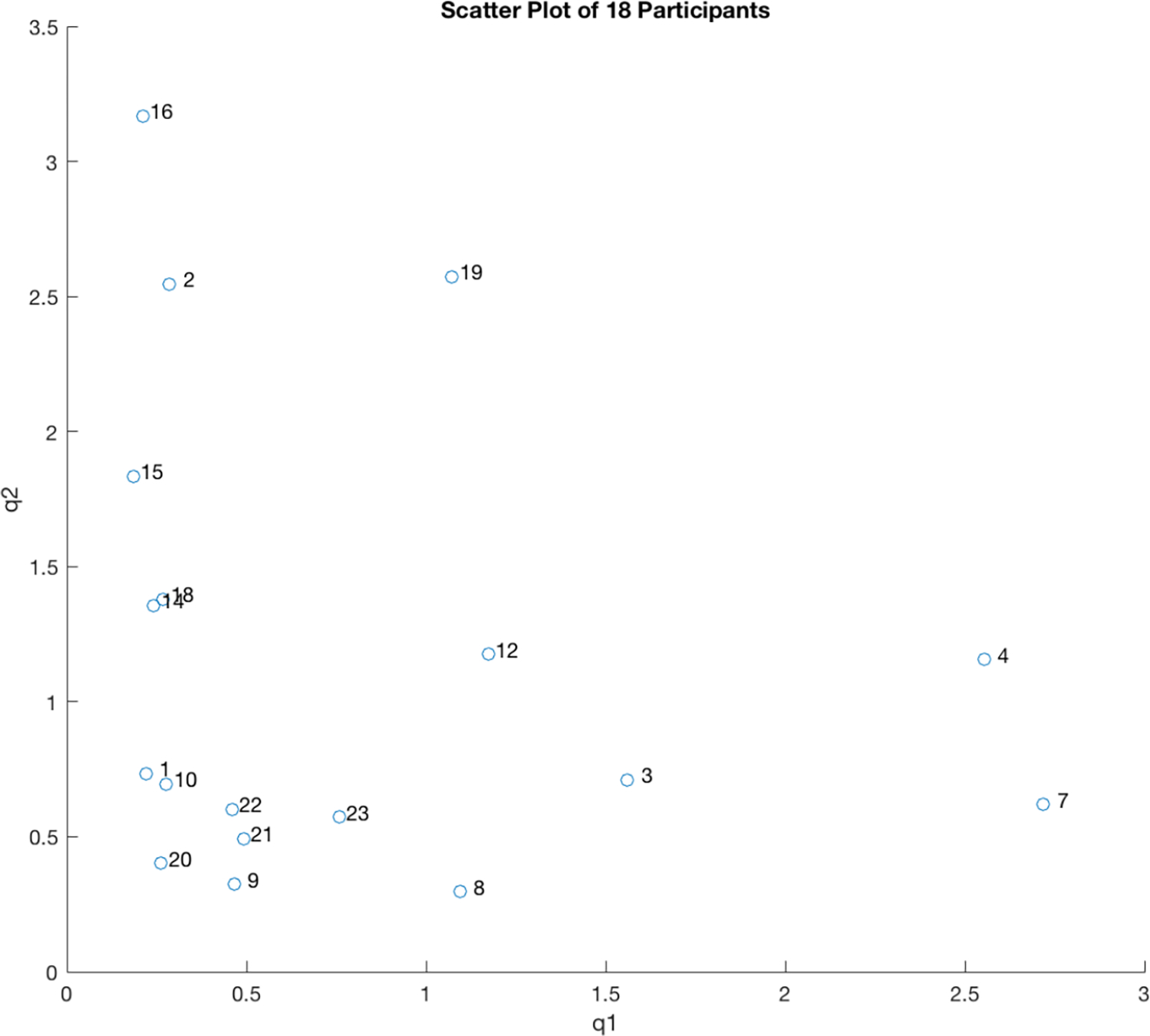
Scatter plot of deterministically obtained parameter estimates for BrAC and TAC measurements from a single drinking episode from each of 18 subjects.
REFERENCES
- [1].Albanese RA, Banks HT, Evans MV, and Potter LK, Physiologically based pharmacokinetic models for the transport of trichloroethylene in adipose tissue, Bulletin of Mathematical Biology 64 (2002), no. 1, 97. [DOI] [PubMed] [Google Scholar]
- [2].Baldock AL, Ahn S, Rockne R, Johnston S, Neal M, Corwin D, Clark-Swanson K, Sterin G, Trister AD, Malone H, et al. , Patient-specific metrics of invasiveness reveal significant prognostic benefit of resection in a predictable subset of gliomas, PloS One 9 (2014), no. 10, e99057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Banks HT, Crowley J, and Kunisch K, Cubic spline approximation techniques for parameter estimation in distributed systems, IEEE Transactions on Automatic Control 28 (1983), no. 7, 773–786. [Google Scholar]
- [4].Banks HT, Bokil V, Hu S, Dhar AK, Bullis R, Browdy C, and Allmutt F, Modeling shrimp biomass and viral infection for production of biological countermeasures, Mathematical Biosciences and Engineering 3 (2006), no. 4, 635–660. [DOI] [PubMed] [Google Scholar]
- [5].Banks HT, Bortz D, Pinter G, and Potter L, Modeling and imaging techniques with potential for application in bioterrorism, Bioterrorism: Mathematical Modeling Applications in Homeland Security, SIAM, 2003, pp. 129–154. [Google Scholar]
- [6].Banks HT, Bortz D, and Holte S, Incorporation of variability into the modeling of viral delays in hiv infection dynamics, Mathematical Biosciences 183 (2003), no. 1, 63–91. [DOI] [PubMed] [Google Scholar]
- [7].Banks HT, Botsford LW, Kappel F, and Wang C, Modeling and estimation in size structured population models, LCDS-CCS Report 87–13, Brown University; Proc. 2nd Course on Mathematical Ecology, (Trieste, December 8–12, 1986) (1988), 521–541. [Google Scholar]
- [8].Banks HT, Catenacci J and Hu S, Use of difference-based methods to explore statistical and mathematical model discrepancy in inverse problems, CRSC-TR15-05, May, 2015; J. Inverse Ill-Posed Problems, 24 (2016), 413–433. [Google Scholar]
- [9].Banks HT and Davis JL, Quantifying uncertainty in the estimation of probability distributions with confidence bands, CRSC-TR07-21, December, 2007; Mathematical Biosciences and Engineering 5 (2008), 647–667. [DOI] [PubMed] [Google Scholar]
- [10].Banks HT and Davis JL, A comparison of approximation methods for the estimation of probability distributions on parameters, Applied Numerical Mathematics 57 (2007), no. 5–7, 753–777. [Google Scholar]
- [11].Banks HT, Davis JL, Ernstberger SL, Hu S, Artimovich E, and Dhar AK, Experimental design and estimation of growth rate distributions in size-structured shrimp populations, Inverse Problems 25 (2009), no. 9, 095003. [Google Scholar]
- [12].Banks HT and Fitzpatrick BG, Estimation of growth rate distributions in size structured population models, Quarterly of Applied Mathematics 49 (1991), no. 2, 215–235. [Google Scholar]
- [13].Banks HT, Flores KB, Langlois CR, Serio TR, and Sindi SS, Estimating the rate of prion aggregate amplification in yeast with a generation and structured population model, Inverse Problems in Science and Engineering (2017), 1–23. [Google Scholar]
- [14].Banks HT and Gibson NL, Electromagnetic inverse problems involving distributions of dielectric mechanisms and parameters, CRSC-TR05-29, August, 2005; Quarterly of Applied Mathematics 64 (2006), 749–795. [Google Scholar]
- [15].Banks HT and Gibson NL, Well-posedness in maxwell systems with distributions of polarization relaxation parameters, Applied Mathematics Letters 18 (2005), no. 4, 423–430. [Google Scholar]
- [16].Banks HT, Kenz ZR, and Thompson WC, A review of selected techniques in inverse problem nonparametric probability distribution estimation, CRSC-TR12-13, May 2012; J. Inverse and Ill-Posed Problems (2012), 429–460. [Google Scholar]
- [17].Banks HT and Kunisch K, Estimation Techniques for Distributed Parameter Systems, Birkhausen, Boston, 1989. [Google Scholar]
- [18].Banks HT and Lamm P, Estimation of variable coefficients in parabolic distributed systems, IEEE Transactions on Automatic Control 30 (1985), no. 4, 386–398. [Google Scholar]
- [19].Banks HT and Murphy K, Estimation of nonlinearities in parabolic models for growth, predation, and dispersal of populations, Journal of Mathematical Analysis and Applications 141 (1989), no. 2, 580–602. [Google Scholar]
- [20].Banks HT and Pinter GA, A probabilistic multiscale approach to hysteresis in shear wave propagation in biotissue, Multiscale Modeling & Simulation 3 (2005), no. 2, 395–412. [Google Scholar]
- [21].Banks HT and Potter LK, Probabilistic methods for addressing uncertainty and variability in biological models: Application to a toxicokinetic model, CRSC-TR02-27, September, 2002; Mathematical Biosciences 192 (2004), 193–22. [DOI] [PubMed] [Google Scholar]
- [22].Banks HT and Thompson WC, Existence and consistency of a nonparametric estimator of probability measures in the Prohorov Metric Framework, International Journal of Pure and Applied Mathematics 103 (2015), no. 4, 819–843. [Google Scholar]
- [23].Banks HT, A functional analysis framework for modeling, estimation and control in science and engineering, CRC Press, 2012. [Google Scholar]
- [24].Banks HT and Bihari KL, Modelling and estimating uncertainty in parameter estimation, Inverse Problems 17 (2001), no. 1, 95. [Google Scholar]
- [25].Banks HT, Kareiva PM, and Murphy KA, Parameter estimation techniques for interaction and redistribution models: a predator-prey example, Oecologia 74 (1987), no. 3, 356–362. [DOI] [PubMed] [Google Scholar]
- [26].Banks HT and Murphy KA, Quantitative modeling of growth and dispersal in population models, Mathematical topics in population biology, morphogenesis and neurosciences, Springer, 1987, pp. 98–109. [Google Scholar]
- [27].Banks HT and Tran HT, Mathematical and experimental modeling of physical and biological processes, CRC Press, 2009. [Google Scholar]
- [28].Banks HT, Hu S, and Thompson WC, Modeling and inverse problems in the presence of uncertainty, CRC Press, 2014. [Google Scholar]
- [29].Beal SL and Sheiner LB, Estimating population kinetics., Critical Reviews in Biomedical Engineering 8 (1982), no. 3, 195–222. [PubMed] [Google Scholar]
- [30].Bondiau P-Y, Clatz O, Sermesant M, Marcy P-Y, Delingette H, Frenay M, and Ayache N, Biocomputing: numerical simulation of glioblastoma growth using diffusion tensor imaging, Physics in Medicine and Biology 53 (2008), no. 4, 879. [DOI] [PubMed] [Google Scholar]
- [31].Clatz O, Sermesant M, Bondiau P-Y, Delingette H, Warfield SK, Malandain G, and Ayache N, Realistic simulation of the 3-d growth of brain tumors in mr images coupling diffusion with biomechanical deformation, IEEE Transactions on Medical Imaging 24 (2005), no. 10, 1334–1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Dai Z, Rosen I, Wang C, Barnett N, and Luczak SE, Using drinking data and pharmacokinetic modeling to calibrate transport model and blind deconvolution based data analysis software for transdermal alcohol biosensors., Mathematical Biosciences and Engineering 13 (2016), no. 5, 911–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Davidian M and Gallant AR, Smooth nonparametric maximum likelihood estimation for population pharmacokinetics, with application to quinidine, Journal of Pharmacokinetics and Biopharmaceutics 20 (1992), no. 5, 529–556. [DOI] [PubMed] [Google Scholar]
- [34].Davidian M and Gallant AR, The nonlinear mixed effects model with a smooth random effects density, Biometrika 80 (1993), no. 3, 475–488. [Google Scholar]
- [35].Davidian M and Giltinan DM, Nonlinear models for repeated measurement data, Chapman & Hall, 1995. [Google Scholar]
- [36].Davidian M and Giltinan DM, Nonlinear models for repeated measurement data: an overview and update, Journal of Agricultural, Biological, and Environmental Statistics 8 (2003), no. 4, 387. [Google Scholar]
- [37].Dougherty DM, Charles NE, Acheson A, John S, Furr RM, and Hill-Kapturczak N, Comparing the detection of transdermal and breath alcohol concentrations during periods of alcohol consumption ranging from moderate drinking to binge drinking., Experimental and Clinical Psychopharmacology 20 (2012), no. 5, 373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Dougherty DM, Hill-Kapturczak N, Liang Y, Karns TE, Cates SE, Lake SL, Mullen J, and Roache JD, Use of continuous transdermal alcohol monitoring during a contingency management procedure to reduce excessive alcohol use, Drug & Alcohol Dependence 142 (2014), 301–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Dougherty DM, Karns TE, Mullen J, Liang Y, Lake SL, Roache JD, and Hill-Kapturczak N, Transdermal alcohol concentration data collected during a contingency management program to reduce at-risk drinking, Drug & Alcohol Dependence 148 (2015), 77–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Dumett MA, Rosen I, Sabat J, Shaman A, Tempelman L, Wang C, and Swift R, Deconvolving an estimate of breath measured blood alcohol concentration from biosensor collected transdermal ethanol data, Applied Mathematics and Computation 196 (2008), no. 2, 724–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Fairbairn CE, Bresin K, Kang D, Rosen IG, Ariss T, Luczak SE, Barnett NP, and Eckland NS, A multimodal investigation of contextual effects on alcohol’s emotional rewards., Journal of Abnormal Psychology 127 (2018), no. 4, 359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Gallant AR, Nonlinear statistical models, John Wiley & Sons, 1987. [Google Scholar]
- [43].Gerlee P and Nelander S, Travelling wave analysis of a mathematical model of glioblastoma growth, Mathematical Biosciences and Engineering 276 (2016), 75–81. [DOI] [PubMed] [Google Scholar]
- [44].Gibson NL, Terahertz-based electromagnetic interrogation techniques for damage detection, Ph.D. thesis, North Carolina State University, August 2004. [Google Scholar]
- [45].Hatzikirou H, Basanta D, Simon M, Schaller K, and Deutsch A, ‘Go or grow’: the key to the emergence of invasion in tumour progression?, Mathematical Medicine and Biology 29 (2012), no. 1, 49–65. [DOI] [PubMed] [Google Scholar]
- [46].Jbabdi S, Mandonnet E, Duffau H, Capelle L, Swanson KR, Pélégrini-Issac M, Guillevin R, and Benali H, Simulation of anisotropic growth of low-grade gliomas using diffusion tensor imaging, Magnetic Resonance in Medicine 54 (2005), no. 3, 616–624. [DOI] [PubMed] [Google Scholar]
- [47].Konukoglu E, Clatz O, Bondiau P-Y, Sermesant M, Delingette H, and Ayache N, Towards an identification of tumor growth parameters from time series of images, Medical Image Computing and Computer-Assisted Intervention–MICCAI 2007, Springer, 2007, pp. 549–556. [DOI] [PubMed] [Google Scholar]
- [48].Labianca DA, The chemical basis of the breathalyzer: A critical analysis, Journal of Chemical Education 67 (1990), no. 3, 259. [Google Scholar]
- [49].Lindsay BG, Mixture models: theory, geometry and applications, NSF-CBMS regional conference series in probability and statistics, JSTOR, 1995, pp. i–163. [Google Scholar]
- [50].Lindsay BG et al. , The geometry of mixture likelihoods: a general theory, The Annals of Statistics 11 (1983), no. 1, 86–94. [Google Scholar]
- [51].Lindsay BG and Lesperance ML, A review of semiparametric mixture models, Journal of Statistical Planning and Inference 47 (1995), no. 1–2, 29–39. [Google Scholar]
- [52].Luczak SE, Rosen IG, and Wall TL, Development of a real-time repeated-measures assessment protocol to capture change over the course of a drinking episode, Alcohol and Alcoholism 50 (2015), no. 2, 180–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Mallet A, A maximum likelihood estimation method for random coefficient regression models, Biometrika 73 (1986), no. 3, 645–656. [Google Scholar]
- [54].Martirosyan NL, Rutter EM, Ramey WL, Kostelich EJ, Kuang Y, and Preul MC, Mathematically modeling the biological properties of gliomas: A review, Mathematical Biosciences and Engineering 12 (2015), no. 4, 879–905. [DOI] [PubMed] [Google Scholar]
- [55].Murray JD, Mathematical biology ii: Spatial models and biomedical applications, 3 ed., Springer-Verlag New York Incorporated, 2003. [Google Scholar]
- [56].Painter K and Hillen T, Mathematical modelling of glioma growth: the use of diffusion tensor imaging (dti) data to predict the anisotropic pathways of cancer invasion, Journal of Theoretical Biology 323 (2013), 25–39. [DOI] [PubMed] [Google Scholar]
- [57].Potter LK, Physiologically based pharmacokinetic models for the systemic transport of trichloroethylene, Ph.D. thesis, North Carolina State Univeristy, August 2001. [Google Scholar]
- [58].Prenter PM, Splines and variational methods, John Wiley & Sons, 1975. [Google Scholar]
- [59].Rosen IG, Luczak SE, and Weiss J, Blind deconvolution for distributed parameter systems with unbounded input and output and determining blood alcohol concentration from transdermal biosensor data, Applied Mathematics and Computation 231 (2014), 357–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Rutter EM, Banks HT, and Flores KB, Estimating intratumoral heterogeneity from spatiotemporal data, Journal of Mathematical Biology (2018). [DOI] [PubMed] [Google Scholar]
- [61].Rutter EM, Stepien TL, Anderies BJ, Plasencia JD, Woolf EC, Scheck AC, Turner GH, Liu Q, Frakes D, Kodibagkar V, Kuang Y, Preul MC, and Kostelich EJ, Mathematical analysis of glioma growth in a murine model, Scientific Reports 7 (2017), 2508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Schultz MH, Spline analysis, Prentice-Hall, 1973. [Google Scholar]
- [63].Schumitzky A, The nonparametric maximum likelihood approach to pharmacokinetic population analysis, Proceedings of the 1993 Western Simulation Multiconference: Simulation for Health Care. San Diego Society for Computer Simulation, 1993, pp. 95–100. [Google Scholar]
- [64].Schumitzky A, Nonparametric em algorithms for estimating prior distributions, Applied Mathematics and Computation 45 (1991), no. 2, 143–157. [Google Scholar]
- [65].Sheiner LB, Rosenberg B, and Melmon KL, Modelling of individual pharmacokinetics for computer-aided drug dosage, Computers and Biomedical Research 5 (1972), no. 5, 441–459. [DOI] [PubMed] [Google Scholar]
- [66].Simmons J, Boyes W, Bushnell P, Raymer J, Limsakun T, McDonald A, Sey Y, and Evans M, A physiologically based pharmacokinetic model for trichloroethylene in the male long-evans rat, Toxicological Sciences 69 (2002), no. 1, 3–15. [DOI] [PubMed] [Google Scholar]
- [67].Sirlanci M, Luczak S, and Rosen I, Approximation and convergence in the estimation of random parameters in linear holomorphic semigroups generated by regularly dissipative operators, American Control Conference (ACC), 2017, IEEE, 2017, pp. 3171–3176. [Google Scholar]
- [68].Sirlanci M, Luczak SE, Fairbairn CE, Bresin K, Kang D, and Rosen I, Deconvolving the input to random abstract parabolic systems: a population model-based approach to estimating blood/breath alcohol concentration from transdermal alcohol biosensor data, Submitted for publication (2018). [DOI] [PMC free article] [PubMed]
- [69].Sirlanci M, Luczak SE, Fairbairn CE, Kang D, Pan R, Yu X, and Rosen I, Estimation of the distribution of random parameters in a diffusion equation forward model for a transdermal alcohol biosensor, Submitted for publication (2017). [DOI] [PMC free article] [PubMed]
- [70].Sirlanci M and Rosen I, Estimation of the distribution of random parameters in discrete time abstract parabolic systems with unbounded input and output: Approximation and convergence, Submitted for publication (2017). [DOI] [PMC free article] [PubMed]
- [71].Stein AM, Demuth T, Mobley D, Berens M, and Sander LM, A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment, Biophysical Journal 92 (2007), no. 1, 356–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Stepien TL, Rutter EM, and Kuang Y, Traveling waves of a go-or-grow model of glioma growth, SIAM Journal of Applied Mathematics (2018). [Google Scholar]
- [73].Stepien TL, Rutter EM, and Kuang Y, A data-motivated density-dependent diffusion model of in vitro glioblastoma growth, Mathematical Biosciences and Engineering 12 (2015), no. 6, 1157–1172. [DOI] [PubMed] [Google Scholar]
- [74].Strang G and Fix GJ, An analysis of the finite element method, vol. 212, Prentice-hall; Englewood Cliffs, NJ, 1973. [Google Scholar]
- [75].Swanson K, Alvord E, and Murray J, A quantitative model for differential motility of gliomas in grey and white matter, Cell Proliferation 33 (2000), no. 5, 317–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Swanson KR, Bridge C, Murray J, and Alvord EC, Virtual and real brain tumors: using mathematical modeling to quantify glioma growth and invasion, Journal of the Neurological Sciences 216 (2003), no. 1, 1–10. [DOI] [PubMed] [Google Scholar]
- [77].Swift RM, Transdermal alcohol measurement for estimation of blood alcohol concentration, Alcoholism: Clinical and Experimental Research 24 (2000), no. 4, 422–423. [PubMed] [Google Scholar]
- [78].Swift RM, Direct measurement of alcohol and its metabolites, Addiction 98 (2003), no. s2, 73–80. [DOI] [PubMed] [Google Scholar]
- [79].Swift RM, Transdermal measurement of alcohol consumption, Addiction 88 (1993), no. 8, 1037–1039. [DOI] [PubMed] [Google Scholar]
- [80].Swift RM, Martin CS, Swette L, Laconti A, and Kackley N, Studies on a wearable, electronic, transdermal alcohol sensor, Alcoholism: Clinical and Experimental Research 16 (1992), no. 4, 721–725. [DOI] [PubMed] [Google Scholar]
- [81].Wahba G, Bayesian” confidence intervals” for the cross-validated smoothing spline, Journal of the Royal Statistical Society. Series B (Methodological) (1983), 133–150. [Google Scholar]
- [82].Wahba G, Splines in nonparametric regression, Wiley Online Library, 2000. [Google Scholar]
- [83].Wen PY and Kesari S, Malignant gliomas in adults, New England Journal of Medicine 359 (2008), no. 5, 492–507. [DOI] [PubMed] [Google Scholar]


