Electronic landscape of the f-electron intermetallics with the ThCr₂Si₂ structure

Abstract

Although strongly correlated f-electron systems are well known as reservoirs for quantum phenomena, a persistent challenge is to design specific states. What is often missing are simple ways to determine whether a given compound can be expected to exhibit certain behaviors and what tuning vector(s) would be useful to select the ground state. In this review, we address this question by aggregating information about Ce, Eu, Yb, and U compounds with the ThCr₂Si₂ structure. We construct electronic/magnetic state maps that are parameterized in terms of unit cell volumes and d-shell filling, which reveals useful trends including that (i) the magnetic and nonmagnetic examples are well separated, and (ii) the crossover regions harbor the examples with exotic states. These insights are used to propose structural/chemical regions of interest in these and related materials, with the goal of accelerating discovery of the next generation of f-electron quantum materials.

Chemical/structural maps provide guidance for discovery of exotic quantum states in f-electron intermetallics.

INTRODUCTION

Interest in strongly correlated f-electron intermetallics is periodically renewed by discoveries of exemplary materials with remarkable behaviors [e.g., hidden order and superconductivity in URu₂Si₂ (1), anomalously high temperature superconductivity in PuCoGa₅ (2), topological insulating behavior in SmB₆ (3), strongly correlated Weyl-Kondo semimetallic behavior in Ce-based compounds (4), and heavy fermion superconductivity in many Ce- and U-based systems (5, 6)]. The vitality of this cycle was recently seen in the emergence of unconventional spin triplet superconductivity in UTe₂ (7, 8), which features anomalously large upper critical fields and magnetic field–driven reentrant superconductivity. Even among the heavily studied variants of the ThCr₂Si₂ structure, this trend toward serendipitous discovery is alive and well. For example, CeRh₂As₂ (CaBe₂Ge₂-type structure) was recently shown to exhibit unconventional superconductivity, anomalously large upper critical fields, and evidence for several superconducting order parameters (9, 10). Both of these materials may even feature nontrivial electronic topologies.

These types of discoveries clearly invite continued efforts to develop f-electron intermetallics, but the field is hampered by a lack of clarity regarding where to look for examples with enhanced properties. This is largely because (i) the relative strengths of interactions (e.g., Kondo, RKKY, valence instability, spin orbit, crystal electric field splitting, etc.) vary widely between different materials, (ii) unusual states often emerge as a result of finely balanced or cumulative interactions, and (iii) calculations to quantify the relative importance of different interactions often have limited success. Historically, this has necessitated systematic experimental surveys of the chemical/structural phase space to uncover materials with novel electronic and magnetic states (11). However, it is also widely held that these resource-intensive surveys are not optimal—at least in the sense that the discovery of examples with remarkable physics requires sifting through a large number of related examples.

What is often missing in this process is a simple way to determine whether a given compound can reasonably be expected to exhibit novel behavior (either intrinsically or under modest tuning) and what tuning vector(s) would be useful. Here, we address this challenge by reexamining the families of materials with the AT₂X₂ composition (12, 13), where we show that for the A = Ce-, Eu-, Yb-, and U-based subsets with the ThCr₂Si₂-type structure, (i) the magnetic and nonmagnetic examples are well separated, (ii) the crossover region that separates them follows a simple but nontrivial trajectory, and (iii) the crossover region hosts the examples that exhibit attractive behavior such as unconventional superconductivity and non–Fermi liquid behavior. These observations are consistent with earlier organizing principles [e.g., the Doniach phase diagram (14), the Hill plot (15), and surveys of Ce- and U-based 122 compounds (16–18) that emphasize electronic hybridization strength] but have the benefit that they (i) clarify chemical strategies to search for new examples with novel behavior and (ii) provide a concise summary of behaviors in this structural family. We also suggest that this approach is well suited to elementary data mining of electronic databases that can be used to investigate many other structural families.

STRUCTURE, CHEMISTRY, AND GENERIC PHASE DIAGRAMS

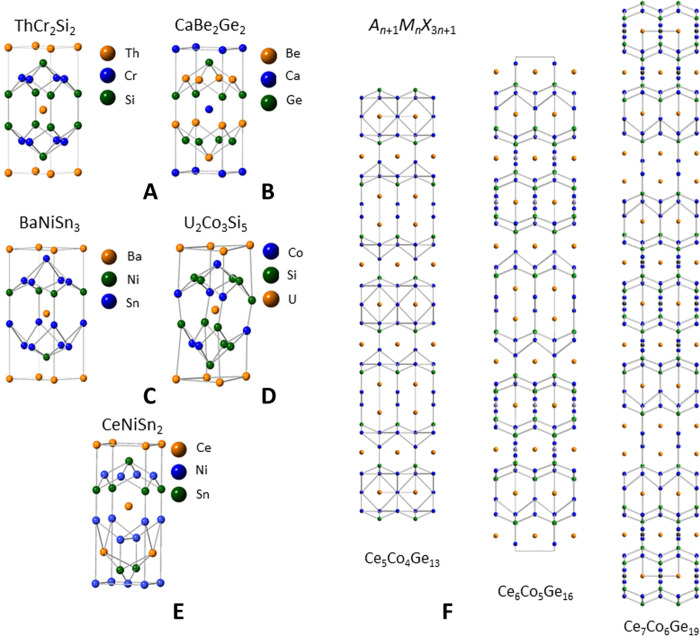
The ThCr₂Si₂ structure (Fig. 1A) was first reported by Ban and Sikirica in (12), and since then, it has proven to be one of the most ubiquitous structural arrangements for ternary combinations of elements. There are many detailed reviews that address trends in this family, and several are listed in (13). To summarize, it is a ternary variant of the BaAl₄ prototype (space group I4/mmm) and is generically expressed as AT₂X₂, where the A, T, and X atoms are located on the Wyckoff sites 2a (0,0,0), 4d (0,0.5,0.25), and 4e (0,0,z), respectively. This provides distinct high-symmetry environments around the A, T, and X atoms that influence the physical properties of the chemical variants. This structure also exhibits pronounced chemical flexibility, where the A site can be populated by alkali metal, alkaline earth, rare earths, first column transition metals, lanthanide, and actinide elements; the T site can be occupied by transition metal, light alkali metals and alkaline earths, and p-block elements; and the X site can be occupied by p-block elements and some transition metals. There are many other closely related structures [e.g., CaBe₂Ge₂, CeNiSi₂, BaNiSn₃, and U₂Co₃Si₅ types (19–22)], and there are even hybrid examples that combine this family and other prototypes (Fig. 1, B to F) (23–25), which opens the prospect of developing design principles that span families of materials.

Fig. 1. Summary of crystalline structures that relate to the ThCr₂Si₂ prototype.

(A to E) The ThCr₂Si₂, CaBe₂Ge₂, BaNiSn₃, U₂Co₃Si₅, and CeNiSi₂ structures taken from (12, 13, 19–22). (F) The structure for the A_n+1M_nX_3n+1 (A = lanthanide, M = transition metal, X = tetrels), n = 4 to 6 compounds, composed of complex layering of subunits. Ce, Co, and Ge are represented as orange, green, and blue spheres, respectively. Structural details obtained from (23–25).

A multitude of behaviors emerge from these simple crystal structures when f-elements are introduced into them, including local moment and complex magnetism (26), charge instabilities (27), structural instabilities (28), unconventional superconductivity (29, 30), hidden order (1), multipolar order (31), and topologically protected electronic states (9, 10). For the Ce-, Yb-, and U-based systems, the behavior is especially rich and is often understood in terms of the Ruderman-Kittel-Kasuya-Yosida (RKKY) and Kondo interactions (14, 32–35), where (i) the RKKY interaction provides an indirect magnetic exchange between localized f-spins through the conduction electrons and favors magnetic ordering while (ii) the Kondo interaction drives hybridization between the conduction electron and f-states that results in screening of the f-spin and strongly reduces the effective magnetic moment. The connection between these parameters has been discussed extensively in terms of the Doniach model and is summarized in (5, 6). The resulting generic phase diagrams are shown schematically in Fig. 2 (A and B) for Ce and Yb, where a tuning parameter δ (e.g., pressure or chemical substitution) varies the ground state. For the case of Ce, at small δ, the valence is close to 3+, hybridization between the f- and conduction electrons is weak, and there typically is a magnetically ordered ground state at T_N,C. As δ increases, T_N,C may initially increase as the RKKY interaction strengthens, but eventually, it tends to be suppressed toward zero temperature at δ_c. Under some conditions, this results in a quantum critical point that is surrounded by a fan-like region of non–Fermi liquid behavior. For many CeT₂X₂ compounds, the quantum critical point is also surrounded by a dome of unconventional superconductivity. At larger δ, the hybridization strength increases further, Fermi liquid behavior is observed below a crossover temperature T_FL, and eventually intermediate valence or a tetravalent state emerges. The Ce and Yb phase diagrams are related but are inverted with respect to each other owing to how Hund’s rules determine the total angular momentum J: for Ce³⁺ (J = 5/2) and Ce⁴⁺ (J = 0), and for Yb 2+ (J = 0) and Yb 3+ (J = 7/2).

Fig. 2. Schematic phase diagrams for strongly correlated f-electron intermetallics.

Temperature T versus control parameter δ phase diagram for the compounds (A) CeT₂X₂ (5, 6), (B) YbT₂X₂ (5, 6), and (C) EuT₂X₂ (36, 37), where T = transition metal and X = p-block element. Here, δ is the chemical composition x or pressure P. The trends for the magnetic ordering temperatures T_N,C, superconducting transition temperatures T_c, valence change transition temperatures T_V, and Fermi liquid crossovers T_FL that are observed in these phase diagrams are described in the text. The solid lines represent phase boundaries, whereas the dotted lines represent crossover regions: e.g., temperature ranges over which a system enters a Fermi liquid or intermediate valence (IV) ground state. The f-electron valences are also indicated (3+ or 4+ for cerium, 2+ or 3+ for ytterbium, and 2+ or 3+ for europium). Note that these diagrams focus on the critical regions near δ_c, but the more general Doniach phase diagram includes a region where the ordering temperatures increase with δ as the RKKY interaction strengthens, before collapsing toward T = 0 at δ_c (14). This trend is seen in the ordering temperatures presented in Fig. 3.

Some lanthanide- and actinide-based materials with multiple f-orbitals exhibit related phase diagrams, but additional complexities are involved. For example, a semi-universal phase diagram has been proposed for Eu-based intermetallics (36, 37), which resembles the Doniach picture but also includes distinct features relating to the valence transition between the Eu²⁺ (J = 7/2) and Eu³⁺ (J = 0) states (Fig. 2C). There is also an ongoing debate about the importance of valence instabilities in Ce- and Yb-based materials, their role in determining classes of quantum criticality, and impact on superconductivity (38–40). We point out that related behavior might even be expected in families containing Pr, Sm, and Tm where multiple valence states are available (41, 42). Among actinide-based materials, the situation is even more complicated due to the greater tendency toward f-state itinerancy, the potential impact of relativistic effects, and the presence of multiple f-electron orbitals that could experience differing degrees of hybridization (43). Nonetheless, phase diagrams that resemble those shown in Fig. 2 (A to C) are sometimes observed (44, 45). Last, all of these behaviors should be contrasted with those of the remaining lanthanides, where (i) the valence is rigidly fixed to be trivalent and (ii) hybridization between the conduction electron and f-states is weak.

On the basis of these observations, it is appealing to suggest that although there are wide-ranging behaviors in this family of materials, the QCP scenario provides a powerful design principle for producing examples with attractive behaviors. However, even with these insights, it remains unclear (i) which ones are best suited to further investigations because they are near a magnetic or valence instability and (ii) for a given material (or family of materials) what is the best tuning strategy to access regions of interest. To address this, we assemble maps in the chemical-structural phase space for the compounds (Ce,Yb,Eu,U)T₂X₂ with the ThCr₂Si₂ structure and identify regions of interest. We also comment on related structures and prospects for uncovering novel phenomena in them.

ELECTRONIC-MAGNETIC MAPS FOR (Ce,Yb,Eu,U)T₂X₂ WITH THE ThCr₂Si₂ STRUCTURE

Figure 3A presents the phase map for the compounds CeT₂X₂ (T = transition metal and X = Si, Ge) by providing the lattice constants and f-state as reported in literature (16–18, 29, 40, 46–77). By organizing these compounds based on their transition metal column and unit cell volume, it is seen that (i) there is a clear separation between those with trivalent Ce and tetravalent or intermediate valence Ce; (ii) the crossover region includes all of the examples that exhibit Kondo lattice heavy fermion, quantum criticality, non–Fermi liquid, and superconducting behavior; and (iii) the crossover region depends on a nearly linear relationship between shell filling and unit cell volume. Points (i) and (ii) are illustrated by the evolution from a strongly hybridized Kondo lattice (CeCu₂Si₂) toward weakened hybridization and strengthened magnetism as the unit cell volume increases (29). This is also noticeable for the other isovalent transition metal series, which all go from tetravalent examples [e.g., CeNi₂Si₂ (61)] through strongly hybridized Kondo lattices [e.g., CeNi₂Ge₂ (60, 61)] to trivalent cerium magnetism [CePd₂Ge₂ (59, 60)]. Supporting evidence for this evolution is seen by examining the unit cell volume lanthanide contractions for each family of materials, where reductions from the trivalent lanthanide contraction are seen for tetravalent or intermediate valence examples. Related behavior is observed for many other cerium-based intermetallics and is generally understood in the context of the Doniach picture or in terms of empirical frameworks such as Hill plots (Fig. 2A) (6, 14, 15).

Fig. 3. Phase map for the valence and ground state behavior of the compounds CeT₂X₂ (T = transition metal and X = Si/Ge and P/As) that crystallize in the ThCr₂Si₂-type structure (16–18, 29, 40, 46–77).

The axes that control the ground state are the unit cell volume (V) and the d-shell filling going from the Cu column to the Fe column. The white band that traverses the center of the phase diagram is a guide to the eye that approximately separates the examples with tetravalent or intermediate valence cerium [lower left-hand side (blue background)] from those with trivalent cerium [upper right-hand side (red background)]. Ordering temperatures are labeled (Neel temperature T_N and Curie temperature T_C). Also shown in some cases are the critical pressures where magnetism collapses (P_c) and the associated superconducting transition temperature (T_c). These values and their associated references are summarized in table S1.

The effect of non-isoelectronic tuning is less easily anticipated but is clarified by earlier studies showing that the hybridization strength between the f-electron and conduction electron states tends to decrease going from the iron column toward the copper column (16–18). Within the Ce-map, the importance of this is seen for the group of materials with unit cell volumes near 170 ų, where there is a progression from intermediate valence or tetravalent behavior [CeOs₂Si₂ (51)] to heavy fermion Kondo lattice behavior [CeIr₂Si₂ (56)], to quantum-critical non–Fermi liquid behavior and superconductivity [CeNi₂Ge₂ (60, 61)], and lastly trivalent magnetic ordering [CeCu₂(Si_1−xGe_x)₂ at x ≈ 0.2 (66)]. This illustrates that weakening hybridization causes the boundary between magnetic (Ce³⁺) and nonmagnetic (Ce⁴⁺ or intermediate valence) behavior to shift toward smaller unit cell volumes with increasing d-shell filling. Outside of this crossover region, horizontal lines always traverse either intermediate valence or tetravalent cerium states (small volumes) or trivalent cerium states with magnetic ordering (large volumes).

The examples that exhibit heavy Fermi liquid Kondo lattice behavior, superconductivity, or non–Fermi liquid behavior [e.g., CeRu₂Si₂ (50), CeCu₂Si₂ (29), and CeNi₂Ge₂ (60, 61)] appear at the boundary between the two regions and are readily tuned through it by changing either the unit cell volume or the d-shell filling. For example, in the cases of CeCu₂Si₂ and CeNi₂Ge₂, applied pressure drives the ambient pressure superconducting transition through a dome-like region (29, 60). Fermi liquid behavior that is consistent with the system entering either an intermediate valence or tetravalent cerium state emerges at large pressures, where a second dome of superconductivity is observed. In contrast, isoelectronic chemical substitution that expands the lattice drives these compounds into magnetic ground states where the hybridization strength is reduced. It is also seen that the examples with magnetically ordered ground states that are near the boundary [e.g., CePd₂Si₂ (60) and CeRh₂Si₂ (54)] are readily moved into it using applied pressure, while larger pressures are needed to move more distant examples [e.g., CeAu₂Si₂ (40) and CeCu₂Ge₂ (67)] into the crossover region. Non-isoelectronic chemical substitution series reveal related trends: e.g., when antiferromagnetic Ce(Cu_1−xT_x)₂Ge₂ (x = 0) is chemically substituted by T = Ni or Co, the boundary region is crossed and critical behavior is observed over a limited x-range (47, 69).

Thus, it is clear that for the entire CeT₂(Si,Ge)₂ series, the region that separates the magnetic and nonmagnetic members varies systematically with both the unit cell volume and the electronic shell filling, each tuning the hybridization strength in a distinct way. This perspective is reinforced by considering the related maps for the compounds CeT₂X₂ (T = transition metal and X = P, As; Fig. 3B) (70–77). Although it is less clear in this case, we infer from these data and the trends that are seen for the Si/Ge analogs that there is a similar nontrivial vector separating the magnetic and nonmagnetic regions. As before, the examples that exhibit strongly correlated electron physics [e.g., CeRu₂P₂ (71)] are on the boundary.

Given the success of this simple scheme in describing the Ce-based ThCr₂Si₂ compounds, we next examine the maps for the Yb examples (Fig. 4) (30, 31, 78–97). Note that few pnictide analogs have been reported, so a map is not included. For the Si/Ge series, there is a strong resemblance between the Yb and Ce maps, but the magnetic and nonmagnetic regions are inverted. This is due to Hund’s rules producing J = 7/2 for trivalent ytterbium (4f¹³), while divalent Yb has a full f-shell (4f¹⁴ and J = 0). In the intermediate volume region, there are several nearly critical Kondo lattice systems, as well as the well-known quantum critical material YbRh₂Si₂ (30, 84). Chemical substitution studies have been performed for many of these examples: e.g., (i) Rh → Co substitution in YbRh₂Si₂ stabilizes magnetism, weakens the hybridization strength, and leads to magnetic ordering (97); (ii) applied pressure drives YbFe₂Ge₂ from being a heavy fermion Kondo lattice through a quantum critical point with non–Fermi liquid behavior, into an antiferromagnetically ordered ground state (80); and (iii) applied pressure drives divalent YbCu₂Ge₂ toward intermediate valence behavior (94). Similar behavior is seen for tuning studies of other examples such as YbIr₂Si₂ (83), YbCu₂Si₂ (95), and YbPd₂Si₂ (96). These observations suggest that the hybridization strength for the Yb compounds is strongly controlled by a combination of lattice contraction and d-shell filling in a manner that resembles what is seen for the Ce analogs.

Fig. 4. Phase map for the valence and ground state behavior of the compounds YbT₂X₂ (T = transition metal and X = Si/Ge) that crystallize in the ThCr₂Si₂-type structure (30, 31, 78–97).

The white band that traverses the center of the phase diagram is a guide to the eye that approximately separates the examples with trivalent [bottom (red background)] from those with divalent ytterbium [upper right-hand side (blue background)]. Ordering temperatures are labeled (Neel temperature T_N and Curie temperature T_C). Critical pressures P_c are labeled. These values and their associated references are summarized in table S2.

It is also of interest to examine other Pr-, Sm-, Eu-, and Tm-based compounds that potentially could exhibit valence instabilities (41, 42). Among this group, those with Pr, Sm, and Tm so far show no evidence in their bulk properties for crossover regions. This is supported by inspection of the evolution of their unit cell volumes, where all examples conform to the trivalent lanthanide contraction. This leads us to expect that although these families might, in principle, include interface regions, they are not within the chemical phase space of the naturally occurring examples in this structure.

In contrast, the Eu compounds show trends that are related to the Ce and Yb analogs (Fig. 5) (36, 37, 98–131). The compressed volume examples all exhibit either trivalent (4f⁶, J = 0) or intermediate valence behavior while the expanded volume examples exhibit divalent (4f⁷, J = 7/2) behavior. Examples close to the crossover region are readily tuned through it: e.g., the Eu valence and unit cell volume of EuCu₂Si₂ vary between 2+ and 3+ depending on synthesis method (115, 116) while EuIr₂Si₂ exhibits behavior that is similar to what is seen in Kondo lattice systems with modest hybridization strength (104). When the antiferromagnets EuNi₂Ge₂ (108) and EuRh₂Si₂ (102) are compressed using hydrostatic pressure, they evolve toward Kondo lattice–like behavior similar to that of EuIr₂Si₂. Remarkable behavior is seen for EuPd₂Si₂, which is nearly divalent at room temperature but its temperature-dependent volume contraction is sufficient to drive a phase transition into the trivalent state (36, 107). Among the pnictides, it is noteworthy that although most of them exhibit a divalent state, the heavy fermion Kondo lattice EuNi₂P₂ appears to be in a crossover region where the critical unit cell volume is substantially smaller than that of the Si/Ge analogs (130, 131). These maps also reveal an important distinction from the Ce and Yb analogs, since here the electronic shell filling has a negligible impact on the location of the crossover region.

Fig. 5. Phase map for the valence and ground state behavior of the compounds EuT₂X₂ (T = transition metal and X = Si/Ge and P/As) that crystallize in the ThCr₂Si₂-type structure (36, 37, 98–131).

The white band that traverses the center of the phase diagram is a guide to the eye that separates the examples with trivalent or intermediate valence europium [lower half (blue background)] from those with divalent europium [upper half (red background)]. Ordering temperatures are labeled (Neel temperature T_N and Curie temperature T_C). Critical pressures P_c are labeled. These values and their associated references are summarized in table S3.

Last, Fig. 6 summarizes results for the compounds UT₂X₂ (1, 79, 132–146). There are a limited number of pnictide examples, so we focus on the Si/Ge group. Again, there is a separation between the magnetic and nonmagnetic examples, but in this case, the latter group is clustered around the Fe/Ru/Os transition metal group. Most of these compounds are Pauli paramagnets [e.g., UFe₂Si₂ (134), UFe₂Ge₂ (133), and UOs₂Si₂ (132)] where strong hybridization between the f- and conduction electron states causes the f-state to become delocalized. It is interesting to note that the hidden order compound, URu₂Si₂, is located in close vicinity to these examples, which is consistent with the view that strong hybridization plays an important role in this material (1). Similar to what is seen for the lanthanides, the hybridization strength weakens going toward the Cu/Ag/Au column (16, 17). The result is that the remainder of the compounds all exhibit magnetic ground states with large ordering temperatures. Some of these examples host complex magnetism [e.g., spin glass behavior in URh₂Ge₂ (135) and multiple phase transitions in many others] and are susceptible to disorder effects, but these behaviors do not appear to be associated with the crossover region. Decreases in the unit cell volume tend to slowly suppress the ordering temperature, but in contrast to the Ce, Yb, and Eu analogs, there is no volume-driven crossover region for this family. Instead, large pressures are needed to access it, as demonstrated for UCo₂Si₂ that has a critical pressure near 8 GPa (140). For UNi₂Si₂ and UCu₂Si₂, even larger pressures would be needed, as experiments have so far been unsuccessful in fully suppressing the magnetism (141, 146). Thus, it is clear that the U series is distinct from the Ce, Yb, and Eu analogs in terms of the conditions that would be useful for driving critical behavior. This has been remarked upon previously (146) and likely reflects differences between the 5f and 4f states. Such information is of high importance in developing tuning strategies to access the critical region.

Fig. 6. Phase map for the valence and ground state behavior of the compounds UT₂X₂ (T = transition metal and X = Si/Ge) that crystallize in the ThCr₂Si₂-type structure (1, 79, 132–146).

The white band separates the examples with Pauli paramagnetism [left-hand side (blue background)] from those with magnetically ordered ground states [right-hand side (red background)] is a guide to the eye. Ordering temperatures are labeled (Neel temperature T_N, Curie temperature T_C, hidden order temperature T_HO, spin glass temperature T_sg, and superconducting transition temperature T_c). Critical pressures P_c are labeled. These values and their associated references are summarized in table S4.

OUTLOOK FOR FUTURE EFFORTS

These insights are immediately useful for focusing investigations of materials with the ThCr₂Si₂ structure. For example, although the Ce-series has already been extensively studied, there remain some attractive examples that have not received close attention. CeCo₂As₂ (73) is of interest because it is simultaneously near the crossover region and may also exhibit strong d-electron magnetism similar to what is seen for CeCo₂P₂ (74). Preliminary results reveal ferromagnetic ordering at T_C ≈ 40 K (73), and we speculate that the ordered state would be readily suppressed using applied pressure, As → P substitution, or Co → Fe or Ni substitution. Examination of the Eu and Yb families reveals other opportunities. Both EuFe₂Ge₂ and EuRu₂Si₂ have not been reported, although the related compounds RFe₂Ge₂ (R = Y, Pr, Nd, Sm, Gd-Tm, and Lu) and EuT₂Ge₂ (T = transition metal) are described in (147, 148). Here, it was inferred that EuFe₂Ge₂ is not a stable phase under conventional growth conditions. This leads us to propose that this phase, and others that are “missing” from the maps, might be accessible as metastable phases where modest amounts of applied or chemical pressure might be sufficient to stabilize them. If they can be formed, they might exhibit complex phase diagrams involving valence instability physics similar to what is seen in EuPd₂Si₂ (36, 107), EuRh₂Si₂ (102), or EuCo₂Ge₂ (103), where modest lattice contractions are sufficient to access the valence change region. The heavy fermion Kondo lattice EuNi₂P₂ appears to be within the crossover region and exhibits Kondo lattice–like behavior (130, 131). This invites efforts to traverse the crossover region using chemical substitution. Last, for the Yb-based examples, we note that there have already been substantial efforts, where the focus has been on the prototypical quantum critical point material YbRh₂Si₂ (30, 84). Nonetheless, there are several other remarkable materials in this family including YbRu₂Ge₂ (31), which exhibits quadrupolar order and strongly correlated electron behavior. This is unique among all other lanthanide-based materials with the ThCr₂Si₂ structure and motivates chemical substitution studies that span the crossover region.

The U-based examples show distinct trends that draw attention toward d-shell filling as being the only viable route for entering the crossover region. This perspective has already been explored for URu₂Si₂ (149, 150), where electronic shell filling produces a semi-universal T-x phase diagram with three main regions: (i) The hidden order state is rapidly suppressed toward zero temperature for x ≲ x_cr,1, (ii) paramagnetism with a heavy–Fermi liquid ground state is seen for x_cr,1 ≲ x ≲ x_cr,2, and (iii) complex antiferromagnetic order appears for x_cr,2 ≲ x. Unexpectedly, this behavior is induced regardless of the type of chemical substitution (e.g., Ru → Rh, Ir, and Si → P), as long as it effectively adds electrons. This motivates further studies of the nearby Pauli paramagnetic analogs, where non-isoelectronic chemical substitution can be used to tune toward the magnetic region [e.g., U(Fe_1−xT_x)₂Ge₂, where T = Co, Rh, and Ir].

Last, it will be valuable to use these insights to cast a wider net into the structural variants with the CaBe₂Ge₂, CeNiSi₂, BaNiSn₃, and U₂Co₃Si₅ structure types, where a preliminary survey indicates that they exhibit maps that are similar to those presented here. Recent work has also shown that there are complex hybrid structures that combine standard building blocks with other structural elements. An example of this is seen for the homologous series A_n+1M_nX_3n+1 (A = lanthanide, M = transition metal, X = tetrels, and n = 1 to 6), which are constructed from basic structural subunits such as AlB₂, AuCu₃, and BaNiSn₃ (Fig. 1F). Examples spanning n = 1 to 6 for the A = Ce series have already been uncovered (23–25), where complex magnetism and Kondo lattice physics is observed. For example, Ce₇Co_6+xGe_19−ySn_y (n = 6), with four crystallographically unique lanthanide sites, was recently shown to have five magnetic transitions of 5, 6, 7.2, 12.4, and 16.5 K. It was also shown that three of the n = 6 magnetic transitions are also found in the n = 5 member (24). This opens the possibility that magnetic/electronic behaviors can be controlled using varied stacking arrangements. The diversity of this behavior invites further investigations, where we expect (i) additional n variation and (ii) chemical flexibility on all of the crystallographic sites. It is easy to look forward to (i) the Eu, Yb, and U analogs being hosts for many different novel electronic/magnetic behaviors and (ii) the transition metal and tetrel sites accomodating isoelectronic replacement and possibly even nonisoelectronic substitution. While a brute force examination of the chemical phase space is not feasible, our maps offer a route forward. For example, all of the Ce-based examples that have been uncovered so far exhibit local f-moment magnetism. Taking inspiration from the maps for the ThCr₂Si₂ Ce-based materials, this implies that efforts should be made to increase the hybridization strength by compressing the unit cell volume (e.g., using applied pressure or Ge → Si substitution) and undertaking chemical substitution studies that point toward the iron column.

SUMMARY AND CONCLUSION

In this review, we have constructed structural/chemical maps for intermetallics with the ThCr₂Si₂ structure, which reveal distinct regions where classes of f-state behaviors emerge. In particular, among the Ce, Eu, Yb, and U families, the cases with magnetic f-states are separated from those with strongly hybridized nonmagnetic f-states by a well-contained crossover region that depends on both unit cell volume and electron shell filling. The examples that exhibit emergent behavior that is associated with quantum criticality are found in the crossover region. This agrees with earlier perspectives (e.g., Doniach and Hill) but clarifies the role of chemical composition without resorting to computational methods. These insights will be useful to pinpoint regions of interest in families of materials related to the ThCr₂Si₂ prototype and have the potential to accelerate discoveries of intriguing phenomena. This approach may even be applicable to other structural families, where mining of electronic databases could be used to accelerate progress.

Supplementary Materials

This PDF file includes:

Tables S1 to S4