Use of Confidence Intervals in Interpreting Nonstatistically Significant Results

The goal of much of medical research is to determine which of 2 or more therapeutic approaches is most effective in a given situation. The power of a study is the probability of detecting a true treatment effect of a given magnitude and is highly dependent on the number of patients studied. When a retrospective observational study design is used, researchers have little or no control over the sample size, and thus little control over the power to detect a particular treatment effect. When such a study yields nonstatistically significant results (referred to as nonsignificant results in this article), an important question is whether the lack of statistical significance was likely due to a true absence of difference between the approaches or due to insufficient power. To address this issue, some researchers may consider conducting a power calculation for the completed study. However, power calculations—even for randomized clinical trials—are irrelevant once a study has been completed.^1,2 Careful use of confidence intervals (CIs), however, can aid in the interpretation of nonsignificant findings across all study designs.

In a 2018 article in JAMA Surgery, Hung et al³ examined the association between treatment with reoperation and receipt of radioactive iodine (RAI) vs reoperation without receipt of RAI and time to structural recurrence (defined by recurrence of “malignant tissue confirmed by fine-needle aspiration biopsy or histopathologic findings”) for patients with persistent or recurrent papillary thyroid cancer. In this retrospective cohort study that included 102 patients, a statistically significant difference between the 2 approaches was not observed. The authors performed a power analysis to determine the effect size that could be detected with 80% power in a sample like theirs and ultimately concluded that “reoperation with receipt of RAI is not associated with a significant prolongation of recurrence-free survival,” noting that “[the] study may not be adequately powered to detect a modest effect of treatment with RAI after reoperation.”³ The authors reported a 95% CI for the outcome of interest, the hazard ratio for structural recurrence.

Explanation of the Concept

What Is a CI?

In statistical analyses comparing 2 treatments, with the threshold for statistical significance set at .05, or 5%, a 95% CI contains all values for the treatment effect that, if proposed as null hypotheses, would not be rejected using the current data.⁴ The CI can be considered a “compatibility interval,” containing the effect sizes most compatible with the data as judged by yielding nonsignificant P values when comparing the observed data with a range of hypothetical effect sizes.⁵ For any CI, the corresponding significance threshold is 100 minus the confidence level (the number before the percentage sign). Thus, a 90% CI gives the values most compatible with the data if a 10% (.10) significance threshold were used.

Why Are CIs Useful When Interpreting Nonsignificant Findings?

Use of CIs can allow for a richer interpretation of findings that fail to find a statistically significant difference between treatment groups (ie, a negative result) compared with a binary interpretation based on whether a finding reached statistical significance. For many comparisons in medical research, a range of treatment effects would be considered clinically meaningless. For example, a decrease or increase in blood pressure of 3 mm Hg is not relevant to a clinician, even if statistically significant. By first identifying the minimal clinically important difference (MCID),⁶ researchers can explicitly identify the range of clinically irrelevant values, generally centered around 0 for continuous measures and around 1 for odds ratios or hazard ratios. If specified based on previous findings before analysis begins, the MCID can greatly enhance the interpretation of CIs.

The Figure shows the 3 possibilities for a CI summarizing the results from a study with a prespecified MCID and nonsignificant results. In this example, the MCID for treatment benefit and the MCID for treatment harm are equal in absolute value, but this does not have to be the case. All 3 CIs contain 0; thus, all 3 cases are compatible with the lack of an effect or association, and the study would be interpreted as having negative or neutral results. Yet, because of the specification of the MCID, each interval has a distinct interpretation. Interval A contains only values that lie between the MCID for harm and the MCID for benefit. An interpretation of this result would be that all the treatment effects most compatible with the data are not clinically relevant. Interval B spans values including those in interval A, as well as values greater than the MCID for benefit of the treatment. An interpretation of this result would be that the treatment effects most compatible with the data are inconsistent with meaningful harm, and include both no important effect and meaningful benefit. Interval C spans the entire region spanned by interval B as well as values greater (in absolute value) than the MCID for harm. An interpretation of this result would be that the treatment effects most compatible with the data include clinically irrelevant values, as well as both meaningful benefit and harm.⁵ In cases in which it is not possible to specify the MCID in advance, it is still possible to enhance the presentation of nonsignificant results by describing the range of the values included in the CI.

Figure.

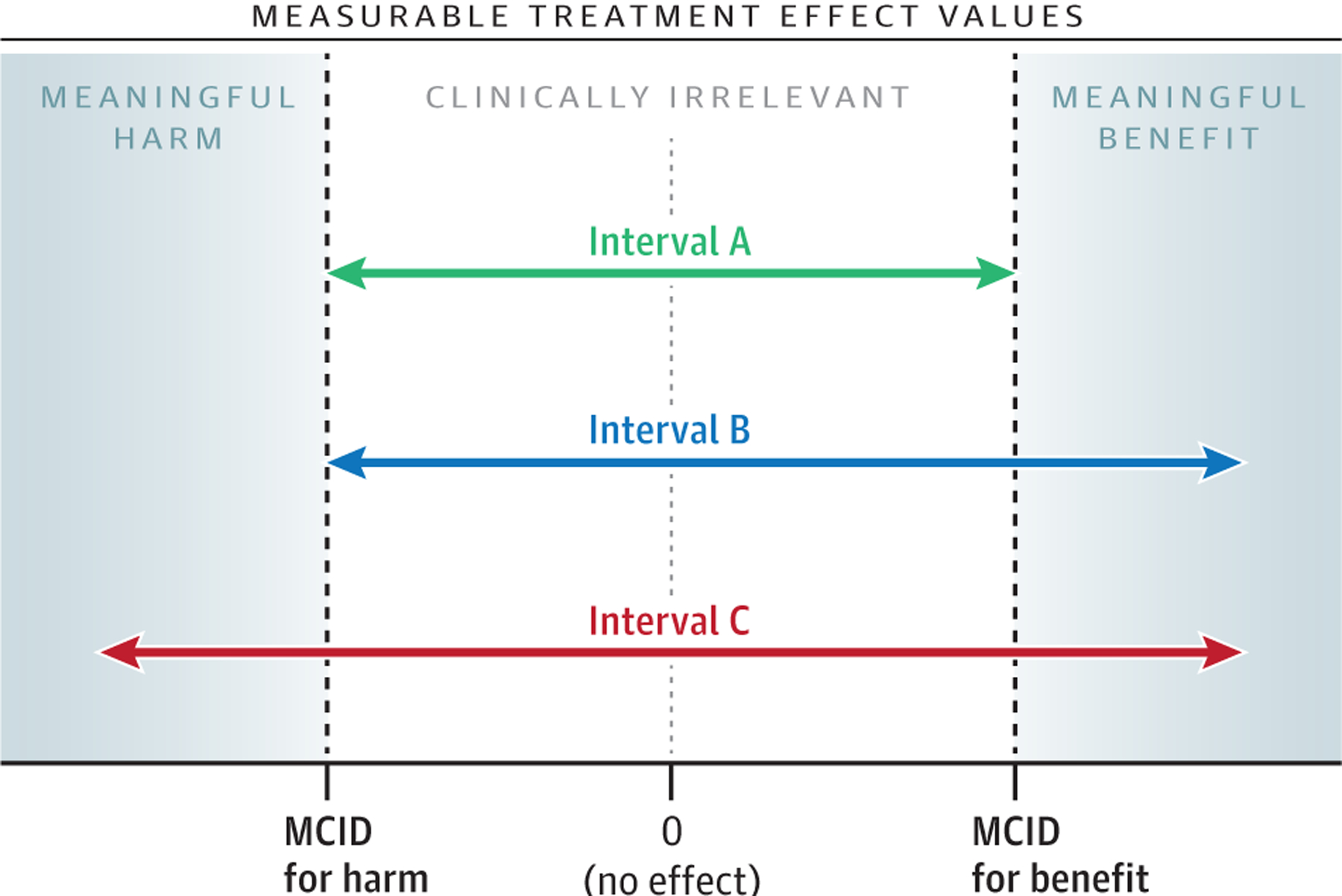
Three Possible Confidence Intervals From a Study With Statistically Nonsignificant Results

MCID indicates minimal clinically important difference.

Limitations of CIs

Although CIs can be used to enhance the interpretation of a study, they have a number of limitations.⁷ For example, a 95% CI does not have a 95% probability of containing the true value of interest (eg, the true treatment effect), even though it is commonly described that way. Creating an interval that does have a specified probability of containing the true value—termed a probability interval—requires a bayesian analysis.⁸ In addition, the values within a 95% CI are not the only values that could possibly lead to the current data and model results; they are simply the values that are most compatible.

How Was a CI Applied in the Study by Hung et al?

In describing their statistical analysis, Hung et al³ wrote, “Finally, we performed a power analysis with regard to our ability to detect a difference in second recurrences between patients who underwent reoperation with RAI vs patients who underwent reoperation without RAI; we determined that we had 80% power to detect a 22% difference in second recurrences.” It appears that the calculation was an attempt to determine the minimum effect size that could be detected with 80% power in a sample with 50 patients in one group and 52 in the other. In an adjusted Cox proportional hazards regression, Hung et al³ found a hazard ratio of 1.12 with a 95% CI of 0.43 to 2.98 (P = .81). Citing their post hoc power calculation, they conclude, “reoperation with receipt of RAI is not associated with a significant prolongation of recurrence-free survival. A difference of less than 22% remains possible.”³

For the reasons cited above,^1,2 another presentation of the data from Hung et al³ would be to replace the post hoc power calculation with an interpretation of the CI, eg, “The outcomes of patients undergoing reoperation with receipt of RAI were consistent with hazard ratios ranging from 0.43 (lower risk of recurrence) to 2.98 (higher risk of recurrence) compared with reoperation without RAI.” With the addition of MCID values based on previous studies, further information could be offered as to whether the range of the CIs contain meaningful clinical values. This approach could provide a conclusion centered around an understanding of the parameter values that are best supported by the data.