Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jul 26;7(31):27755–27768. doi: 10.1021/acsomega.2c03942

Exploring Conformational Preferences of Leu-enkephalin Using the Conformational Search and Double-Hybrid DFT Energy Calculations

Hae Sook Park †, Byung Jin Byun ‡, Young Kee Kang §,*
PMCID: PMC9366962  PMID: 35967045

Abstract

graphic file with name ao2c03942_0008.jpg

The conformational preferences of Leu-enkephalin (Leu-Enk) were explored by the conformational search and density functional theory (DFT) calculations. By a combination of low-energy conformers of each residue, the initial structures of the neutral Leu-Enk were generated and optimized using the ECEPP3 force field in the gas phase. These structures were reoptimized at the HF/3-21G(d) and M06-2X levels of theory with 6-31G(d) and 6-31+G(d) basis functions. We finally located the 139 structures with the relative energy <10 kcal mol–1 in the gas phase, from which the structures of the corresponding zwitterionic Leu-Enk were generated and reoptimized at the M06-2X/6-31+G(d) level of theory using the implicit solvation model based on density (SMD) in water. The conformational preferences of Leu-Enk were analyzed using Gibbs free energies corrected by single-point energies calculated at the double-hybrid DSD-PBEP86-D3BJ/def2-TZVP level of theory in the gas phase and in water. The neutral Leu-Enk dominantly adopted a folded structure in the gas phase stabilized by three H-bonds with a βII′-bend-like motif at the Gly3–Phe4 sequence and a close contact between the side chains of Phe4 and Leu5. The zwitterionic Leu-Enk exhibited a folded structure in water stabilized by three H-bonds with double β-bends such as a βII′ bend at the Gly2–Gly3 sequence and a βI bend at the Gly3–Phe4 sequence. The calculated ensemble-averaged distance between CGly2α and CLeu5α of the zwitterionic Leu-Enk in water is consistent with the value estimated from the simulated annealing using the distance constraints derived from nuclear Overhauser effect spectroscopy (NOESY) spectra in water. Interestingly, the preferred conformations of the neutral and zwitterionic Leu-Enk are new folded structures not predicted by earlier computational studies. According to the refined model of the zwitterionic Leu-Enk bound to δ-opioid receptor (δOR), there were favorable interactions of the terminal charged groups of Leu-Enk with the side chains of charged residues of δOR as well as a favorable CAryl···H interaction of the Phe4 residue of Leu-Enk with Trp284 of δOR. Hence, these favorable interactions would induce the folded structure of the zwitterionic Leu-Enk with double β-bends isolated in water into the “bioactive conformation” like an extended structure when binding to δOR.

Introduction

Enkephalins are endogenous opioid pentapeptides that are generated from the precursor proenkephalin (proEnk) in central and peripheral nervous systems and multiple organ systems.1−5 The proEnk is proteolytically cleavaged to produce Met-enkephalin (Met-Enk, H-Tyr-Gly-Gly-Phe-Met-OH) and Leu-enkephalin (Leu-Enk, H-Tyr-Gly-Gly-Phe-Leu-OH). Both enkephalins have a higher binding affinity for the δ-opioid receptor (δOR), followed by the μ-opioid receptor and the ability to elicit signaling through G proteins and β-arrestin.2,3

Leu-Enk adopted three different conformations, namely, single β-bend,6,7 double β-bend,8,9 and extended10−12 structures in the crystalline state. On the other hand, the peptide chain of Met-Enk was fully extended in the crystal.12 For four decades, considerable NMR13−26 and laser Raman/IR15,27−31 spectroscopic measurements have been performed to investigate the preferred conformations of Leu-Enk in solution and in the solid state. It was known that Leu-Enk exists as a mixture of uncharged and zwitterionic species in dimethyl sulfoxide (DMSO), whereas it is a zwitterionic form in water.15,21,30,31 According to the results from laser Raman/IR spectroscopic measurements,27−29,31 Leu-Enk exists in different conformations in different solvents; i.e., it adopts folded β-bend structures in DMSO, whereas it exists as an ensemble of different conformations in water. In particular, it was suggested that the dominant conformation of Leu-Enk is a folded structure with a type I or II′ β-bend at the Gly3–Phe4 sequence with a C10 H-bond between the C=O of the Gly2 residue and the H–N of the Leu5 residue in DMSO by NMR experiments.13,14,16,18 Furthermore, the side chains of Phe4 and Leu5 residues were predominantly populated in the gauche– (g–) configuration in DMSO.14,16 It was suggested that this preferred conformation of the Leu5 residue brings the hydrophobic leucyl side chain toward the backbone far from the Tyr1 residue and hence plays a crucial role in the selective interaction of Leu-Enk with δOR.16 In particular, the MD simulations using distance restraints obtained from the combination of nuclear Overhauser effect spectroscopy (NOESY) and rotating-frame nuclear Overhauser effect spectroscopy (ROESY) experiments supported that Leu-Enk exists as an ensemble of single-bent, double-bent, and extended structures in water, where the bent structures are β-bend-like structures without any H-bonds.24 In addition, there have been several experimental works focused on the conformational preference of Leu-Enk in micelles and bicelles as membrane-mimicking environment in the absence and/or presence of ganglioside GM1.23,24,32−38 The structures with single β-bend or double β-bend were found to be predominantly populated in phospholipid micelles and bicelles.

There have been many computational studies performed to identify the most preferred (or lowest-energy) conformation of Leu-Enk based on the conformational search and energy minimization39−51 as well as the molecular dynamics (MD) simulations23,36,51−57 using molecular force fields. Based on the conformational search and energy minimization with the ECEPP358 force field, three hairpin structures with a βII′ bend centered at the Gly3–Phe4 or Gly2–Gly3 sequences were suggested as the most preferred conformation of Leu-Enk in the absence of solvent.40,43,48,50 In DMSO, MD simulations indicated that the zwitterionic Leu-Enk forms a clear close contact between N- and C-terminal ends, but there is no preferred conformation for the neutral form.52 However, the simulations of the zwitterionic Leu-Enk in water suggested that the peptide backbone exists as a mixture of folded and unfolded forms52−54 and the folded form possesses a N–H(Gly2) → O=C(Leu5) H-bond and a close head-to-tail separation.53,54 In addition, the water molecules were suggested to play as bridges in the formation of β-turns at the Gly2–Gly3 and Gly3–Phe4 sequences of the folded structure in water.55

Limited studies have been focused on the structures, vibrational frequencies, vibrational absorption (VA), vibrational circular dichroism (VCD), and Raman intensities of the neutral Leu-Enk using density functional theory (DFT) methods.59−62 From starting structures generated from three conformational motifs such as the extended, single β-bend, and double β-bend structures taken from X-ray data,6,9,11,12 three probable structures with a single β-bend were located at the B3LYP/6-31G(d) level of theory, of which VA and VCD spectra are consistent with those of experiments in DMSO.60,61 It was suggested that one (i.e., the conformer s4 in refs (59−61)) with a βI′ turn at the Gly2–Gly3 sequence of the three single β-bend structures is the most probable in DMSO.61 Watson and Hirst identified 23 local minima of Leu-Enk at the EDF1/6-31+G(d) level of theory, of which initial structures were generated from the conformational search and energy minimizations using the CHARMM force field and from three X-ray structures.62 They found that the lowest-energy structure is a kinked-extended structure with a γ-turn at the Gly2 residue, for which the amide I vibrational frequencies were calculated at the same level of theory. Recently, Frau et al. optimized the extended structure of the neutral Leu-Enk at eight DFT levels of theory with the def2-SVP basis set and the implicit solvation model in water and calculated the chemical descriptors.63

There are two crystal structures of δOR complexed with enkephalin-like ligands. The first one is the crystal structure of the human δ-opioid 7TM receptor complexed with the subtype-selective ligand naltrindole at 1.8 Å resolution (PDB ID 4N6H).64 The second one is the active δOR crystal structure with the potent opioid agonist peptide KGCHM07 at 2.8 Å resolution (PDB ID 6PT2).65 Sanfelice and Temussi66 performed the molecular docking of δOR complexed with Leu-Enk using the crystal structure of PDB 4N6H, in which two conformations of Leu-Enk derived from NOE data in a DMSO/H2O mixture (ref (33)) were used starting structures for docking. Recently, Sharma et al. reported the molecular docking of δOR complexed with the Leu-Enk derivative bearing the Tyr1-ψ[(Z)CF=CH]-Gly2 substitution using the crystal structure of PDB 6PT2.67 However, the “bioactive conformations” of Leu-Enk bound to δOR were different from each other and will be discussed in the Results and Discussion section.

As described above, considerable computational studies have been performed to investigate the conformational preferences of Leu-Enk in the absence and presence of solvent but no consensus conformation has been obtained, though all suggested conformations have similar structural features to those deduced from experiments. In particular, there was not any progress in high-resolution X-ray diffraction studies and quantum-mechanical computational studies at the high level of theory for Leu-Enk even in the 2000s to date. In the present work, we explored the conformational preferences of the neutral form of Leu-Enk in the absence of solvent (i.e., in the gas phase) and the zwitterionic form of Leu-Enk in water using DFT methods. In particular, the energies of preferred conformers of Leu-Enk for both forms were calculated at the double-hybrid DSD-PBEP86 level of theory with dispersion corrections,68 which is one of the fifth-rung functionals. The conformational preferences were analyzed by conformational Gibbs free energies in the gas phase and in water.

Computational Methods

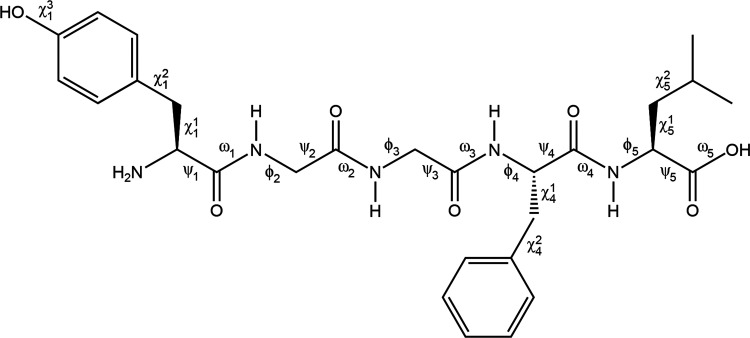
Chemical structures and torsion angles for the neutral and zwitterionic forms of Leu-Enk are defined in Figure 1. At the DFT level of theory, all geometry optimizations were performed using the M06-2X69 functional and the implicit solvation model based on density (SMD)70 implemented in the Gaussian 09 program.71 Although the M06-2X functional is a hybrid-meta-generalized gradient approximation (GGA) functional with the improved medium-range correlation energy, it performs well in predicting noncovalent interactions of small molecules and relative stabilities of biological compounds.72

Figure 1.

Figure 1

Open in a new tab

Chemical structure and torsion angles of the neutral Leu-Enk. The same definition of torsion angles was applied to the zwitterionic Leu-Enk.

As pointed out by Scheraga,73,74 a large number of local minima are expected to exist on the multidimensional conformational energy surface of the flexible oligopeptide like Leu-Enk. However, the energy minimization procedure usually leads only to the local minimum closest to the starting structure, rather than to the global (or lowest-energy) minimum.73,74 It is, therefore, necessary to have efficient methods for searching conformational space to locate the lowest-energy minimum.73,74 As one of the methods for conformational search, the Scheraga group developed the buildup procedure and applied it to the conformational search of Met-Enk.75 The buildup procedure starts with low-energy conformations of single residues and uses the combinations of these to build up feasible structures of dipeptides, tripeptides, and so on, carrying out energy minimization at each stage. However, some strategies were applied to eliminate the high-energy conformations due to the huge storage required for many low-energy conformations as longer peptides are built up.

In the present work, first, we performed the conformational search of the neutral form of Leu-Enk in the gas phase, in which initial structures were generated by the combinations of low-energy conformers of each terminally blocked residue without any eliminations. For Ac-X-NHMe, there were 31, 7, 18, and 27 local minima for X = Tyr, Gly, Phe, and Leu, respectively, with the relative energy (ΔEECEPP3) optimized by the ECEPP3 force field less than 5 kcal mol–1.76 Hence, we generated 738,234 (31 × 7 × 7 × 18 × 27) initial structures for the neutral Leu-Enk by all combinations of these single-residue minima, which were followed by optimizations using the ECEPP3 force field and we obtained 2,633 local minima with ΔEECEPP3 < 5 kcal mol–1. Then, these 2,633 structures were reoptimized at the HF/3-21G(d) level of theory, which resulted in 984 local minima with the relative energy (ΔE) < 20 kcal mol–1. At the M06-2X/6-31G(d) level of theory, we reoptimized these 984 structures and identified 883 local minima with ΔE < 10 kcal mol–1. Then, it was followed by optimizations at the M06-2X/6-31+G(d) level of theory, which finally resulted in 139 structures with ΔE < 10 kcal mol–1.

From the 883 local minima of the neutral Leu-Enk with ΔE < 10 kcal mol–1 at the M06-2X/6-31G(d) level of theory, the corresponding initial structures of the zwitterionic Leu-Enk were built by the transfer of a proton from the C-terminal −COOH to the N-terminal −NH2 using GaussView.77 For these initial structures of the zwitterionic Leu-Enk, we calculated the single-point energies at the SMD M06-2X/6-31G(d) level of theory in water and we obtained the 114 structures with ΔE < 10 kcal mol–1 in water. Then, these 114 structures were reoptimized at the SMD M06-2X/6-31+G(d) level of theory in water, which finally resulted in the 98 local minima with ΔE < 10 kcal mol–1 in water.

For all local minima of Leu-Enk with ΔE < 10 kcal mol–1 in the gas phase and in water, vibrational frequencies were calculated at the M06-2X/6-31+G(d) level of theory in the gas phase and the SMD M06-2X/6-31+G(d) level of theory in water at 25 °C and 1 atm. The scale factor used is 0.9440 that was chosen to reproduce the experimental frequency of 1707 cm–1 for the amide I band of N-methylacetamide in Ar and N2 matrixes.78 The zero-point energy correction and the thermal energy corrections were employed in calculating the Gibbs free energy of each conformation. Here, the ideal gas, rigid rotor, and harmonic oscillator approximations were used for the translational, rotational, and vibrational contributions to the Gibbs free energy, respectively.79

In addition, single-point energies were calculated at the M06-2X/def2-TZVP level of theory for all local minima with ΔE < 10 kcal mol–1 in the gas phase and in water. We identified the 37 structures of the neutral Leu-Enk with the relative Gibbs free energy (ΔG) < 5 kcal mol–1 at the M06-2X/def2-TZVP//M06-2X/6-31+G(d) level of theory in the gas phase and the 46 structures of the zwitterionic Leu-Enk with ΔG < 5 kcal mol–1 at the M06-2X/def2-TZVP//SMD M06-2X/6-31+G(d) level of theory in water. Then, it was followed by the additional single-point energy calculations at the double-hybrid DSD-PBEP86 functional68 with D3BJ dispersion corrections80 and the def2-TZVP basis set for these low-free-energy structures in the gas phase and in water. The DSD-PBEP86-D3BJ level of theory is one of the highest fifth-rung functionals on the Jacob’s Ladder.81 The DSD-PBEP86-D3BJ/def2-TZVP//M06-2X/6-31+G(d) and M06-2X/def2-TZVP//M06-2X/6-31+G(d) levels of theory are abbreviated as DSD-dTZ and M062X-dTZ hereafter in the present work.

Recently, the DSD-dTZ level of theory exhibited good performance for relative energies of the 24 representative conformations of the alanine tetrapeptide in the gas phase82 and the 45 local minima for the cationic nylon-3 dipeptide in water83 with RMSD = 0.31 and 0.19 kcal mol–1, respectively, against the corresponding CCSD(T)/CBS-limit energies. In particular, the DSD-dTZ level of theory reproduced well relative conformational energies of six conformers of Ac-Ala-NHMe and seven conformers of Ac-Pro-NHMe with RMSD = 0.05 kcal mol–1 against the corresponding CCSD(T)/CBS-limit energies.84 All three-dimensional (3D) graphics of optimized structures of Leu-Enk were prepared using PyMOL.85

Results and Discussion

Neutral Leu-Enk in the Gas Phase

There were the 29 local minima for the neutral Leu-Enk with the relative Gibbs free energy (ΔG) < 5 kcal mol–1 at the DSD-PBEP86-D3BJ/def2-TZVP//M06-2X/6-31+G(d) (abbreviated as DSD-dTZ hereafter) level of theory in the gas phase. The torsion angles of these 29 local minima optimized at the M06-2X/6-31+G(d) level of theory are listed in Table S1 in the Supporting Information. The types of H-bond, β-bend, thermodynamic properties, and population of the corresponding structures calculated at the DSD-dTZ level of theory are shown in Table S2 in the Supporting Information, in which the thermodynamic properties and population at the M06-2X/def2-TZVP//M06-2X/6-31+G(d) (abbreviated as M062X-dTZ hereafter) level of theory are also included. The corresponding absolute electronic energies, enthalpies, Gibbs free energies, and single-point energies are listed in Table S3 in the Supporting Information.

Conformational Preferences of Neutral Leu-Enk

We identified the 11 structures for the neutral Leu-Enk with ΔG < 3 kcal mol–1 at the DSD-dTZ level of theory in the gas phase, whose torsion angles optimized at the M06-2X/6-31+G(d) level of theory are listed in Table 1. The types of H-bond and thermodynamic properties of the corresponding structures are shown in Table 2. The 3D structures of the first six preferred conformers with ΔG < 2 kcal mol–1 are depicted in Figure 2, whose Cartesian coordinates are also listed in the Supporting Information.

Table 1. Torsion Angles of 11 Local Minima for the Neutral Leu-EnK Optimized at the M06-2X/6-31+G(d) Level of Theory in the Gas Phasea.
  Tyr1
 Gly2
 Gly3
 Phe4
 Leu5
conf. ψ1 χ11 ϕ2 ψ2 ϕ3 ψ3 ϕ4 ψ4 χ41 ϕ5 ψ5 χ51
n01 –3 64 115 –18 84 –73 –74 –15 66 –161 –42 177
n02 –2 66 110 –4 77 –90 –84 –13 61 –154 65 –175
n03 –1 66 113 –15 81 –76 –66 –33 –59 –143 –36 –64
n04 –3 65 115 –16 82 –74 –68 –23 –56 –158 –40 177
n05 –1 64 113 –15 82 –71 –97 –2 –58 –172 8 43
n06 –2 64 112 –13 82 –76 –106 10 61 –151 –20 63
n07 –2 64 112 –13 84 –71 –107 5 70 –166 6 46
n08 –2 64 114 –14 83 –70 –109 14 –57 –166 –20 61
n09 –2 65 114 –15 81 –76 –59 –37 176 –151 –31 –179
n10 –2 64 115 –17 84 –73 –76 –13 67 –160 –45 178
n11 2 67 114 –24 81 –75 –82 101 178 56 34 –49
Open in a new tab
a

Torsion angles (°) are defined in Figure 1. Only 11 local minima with the relative Gibbs free energy (ΔG) < 3 kcal mol–1 are listed.

Table 2. Type of H-bond, β-Bend, Thermodynamic Properties, and Population of 11 Local Minima for the Neutral Leu-EnK Calculated at the DSD-PBEP86-D3BJ/def2-TZVP//M06-2X/6-31+G(d) Level of Theory in the Gas Phasea.
conf. H-bond typeb β-bendc ΔEd ΔHe ΔGf wg
n01 OH1 → 3, 4 → 2, OH5 → 1   0.00 0.00 0.00 63.6
n02 OH1 → 3, 4 → 2, 5 → 2, OH5 → 1 βII′34 2.48 2.55 1.18 8.6
n03 OH1 → 3, 4 → 2, OH5 → 1   1.95 2.07 1.23 7.9
n04 OH1 → 3, 4 → 2, OH5 → 1   2.06 2.09 1.25 7.7
n05 OH1 → 3, 4 → 2, OH5 → 1   2.79 3.03 1.83 2.9
n06 OH1 → 3, 4 → 2, OH5 → 1   1.86 1.97 1.85 2.8
n07 OH1 → 3, 4 → 2, OH5 → 1   0.47 0.70 2.19 1.6
n08 OH1 → 3, 4 → 2, OH5 → 1   3.74 3.93 2.25 1.4
n09 OH1 → 3, 4 → 2, OH5 → 1   4.20 3.95 2.44 1.0
n10 OH1 → 3, 4 → 2, OH5 → 1   1.47 1.80 2.74 0.6
n11 OH1 → 3, 4 → 2, OH5 → 1   2.96 3.02 2.90 0.5
Open in a new tab
a

Torsion angles (°) are listed in Table 1. Only 11 local minima with the relative Gibbs free energy (ΔG) < 3 kcal mol–1 are listed.

b

Each H-bond type n → m stands for the H-bond between the H donor (e.g., the amide H atom for backbone) of the residue n and the H acceptor (e.g., the carbonyl O atom for backbone) of the residue m. In addition, OH1 and OH5 represent the hydroxyl H atom of the side chain of the Tyr1 residue and the carboxylic H atom of the Leu5 residue, respectively. 5OH represents the O atom of the carboxylic OH group of the Leu5 residue.

c

βII′34 stands for the type II′ β-bend at the Gly3–Phe4 sequence, which is stabilized by the 5 → 2 H-bond.

d

Relative electronic energies in kcal mol–1.

e

Relative enthalpies in kcal mol–1 at 25 °C.

f

Relative Gibbs free energies in kcal mol–1 at 25 °C and 1 atm.

g

The population of each conformer was calculated by its ΔG at 25 °C.

Figure 2.

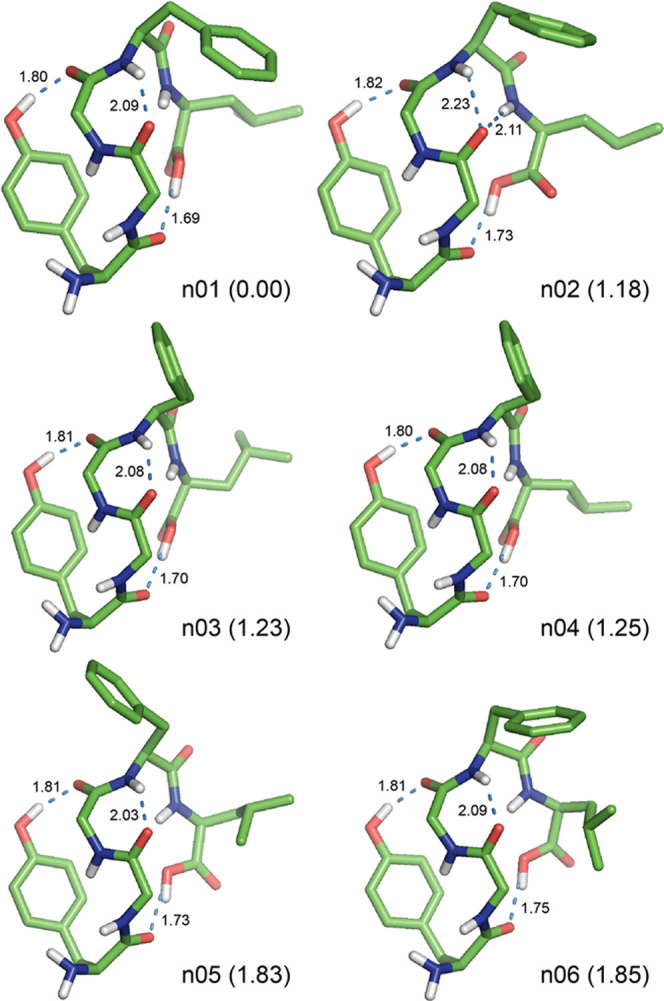
Figure 2

Open in a new tab

Preferred structures of the neutral Leu-EnK optimized at the M06-2X/6-31+G(d) level of theory in the gas phase. The relative Gibbs free energy (ΔG in kcal mol–1) at the DSD-PBEP86-D3BJ/def2-TZVP//M06-2X/6-31+G(d) level of theory is shown in parentheses behind each conformation name. For clarity, all nonpolar hydrogen atoms are omitted. All H-bonds are represented by dotted lines with distances in Å.

In the gas phase, the most preferred conformer n01 with ΔE = 0.00 and ΔG = 0.00 kcal mol–1 (populated at 63.6%) adopted a folded structure with three H-bonds such as an OH1 → 3 type of the 16-membered (i.e., C16) side chain-to-backbone H-bond between O–H(Tyr1) and C=O(Gly3) with the distance of 1.80 Å; a 4 → 2 type of the C7 backbone-to-backbone H-bond between N–H(Phe4) and C=O(Gly2) with the distance of 2.09 Å; and an OH5 → 1 type of the C16 backbone-to-backbone H-bond between O–H(Leu5) and C=O(Tyr1) with the distance of 1.69 Å (Figure 2). In particular, the formation of the second C7 4 → 2 H-bond seems to affect the torsion angle ψ3 of Gly3 moved to the less negative value of −73° (cf. the standard value of −120° reported in the literature86) and to prevent the formation of a type II′ β-bend (i.e., βII′34) at the Gly3–Phe4 sequence (therefore, it is a βII′34-like motif without a 5 → 2 H-bond). In addition, there was a close contact with a distance of about 3.5 Å between the phenyl ring of the side chain of Phe4 and the Hβ proton of the side chain of Leu5.

The second preferred conformer n02 with ΔG = 1.18 kcal mol–1 (populated at 8.6%) exhibited a folded structure with four H-bonds such as OH1 → 3, 4 → 2, 5 → 2, and OH5 → 1 types of H-bonds with the distances of 1.82, 2.23, 2.11, and 1.73 Å, respectively (Figure 2). The structure of conformer n02 is quite similar to that of the most preferred conformer n01, except for the formation of a bifurcated H-bond with 4 → 2 and 5 → 2 types of H-bond and a βII′34 bend at the Gly3–Phe4 sequence (Table 2). However, conformer n02 was 2.48 kcal mol–1 less stable in conformational energy (ΔE) than conformer n01.

The third-to-eleventh preferred conformer n03-to-n11 adopted a similar folded structure to that of the most preferred conformer n01 with three H-bonds such as OH1 → 3, 4 → 2, and OH5 → 1 types of H-bond with the distances of 1.80–1.84, 2.01–2.09, and 1.69–1.80 Å, respectively (Figure 2). However, there were somewhat greater differences in torsion angles of the backbone and side chains of Phe4 and Leu5, which would result in the increase of ΔE values as 0.47 to 4.20 kcal mol–1 and ΔG values as 1.23 to 2.90 kcal mol–1 (populated at 7.9 to 0.5%, respectively) compared with that of the most preferred conformer n01 (Table 2). In particular, the seventh conformer n07 exhibited a folded structure quite similar to conformer n06 but it had the second lowest energy of 0.47 kcal mol–1.

Hence, the neutral Leu-Enk dominantly adopted a folded structure stabilized by a side chain-to-backbone (OH1 → 3) H-bond and two backbone-to-backbone (4 → 2 and OH5 → 1) H-bonds with a βII′-like motif at the Gly3–Phe4 sequence and a close contact between the side chains of Phe4 and Leu5 in the gas phase.

Comparison with Earlier Works

There have been several computational studies performed to identify the lowest-energy conformation of the neutral Leu-Enk using the conformational search and energy minimization with the ECEPP3 force field43,50 and DFT methods.59,62 Using the initials of author’s last names, the conformers suggested by the ECEPP3 force field were denoted as MM1–MM443 and VG;50 and those by DFT methods as J1–J359 and WH1–WH362 at B3LYP/6-31G(d) and EDF1/6-31+G(d) levels of theory, respectively. Conformer J1, J2, and J3 correspond to s10ndp, s4ndp, and s7ndp in ref (59), respectively; and conformer WH1, WH2, and WH3 correspond to qm-1-ke, qm-2-ebt, and qm-3-e in ref (62), respectively. In addition, the first nine preferred conformers predicted by the ECEPP3 force field in the present work were denoted as ECEPP3-1 to ECEPP3-9. All of these structures were reoptimized at the M06-2X/6-31+G(d) level of theory.

The torsion angles of optimized structures that were initially generated by ECEPP3 force field and DFT methods are listed in Table 3. The types of H-bond and thermodynamic properties of the corresponding structures calculated at the DSD-dTZ level of theory are shown in Table 4. The corresponding data calculated at the M062X-dTZ level of theory are shown in Table S4 in the Supporting Information. The corresponding absolute electronic energies, enthalpies, Gibbs free energies, and single-point energies are listed in Table S5 in the Supporting Information. The corresponding optimized structures are shown in Figures S1–S3 in the Supporting Information.

Table 3. Torsion Angles of Local Minima of the Neutral Leu-EnK Optimized at the M06-2X/6-31+G(d) Level of Theory from the Structures Obtained by the ECEPP Force Field and DFT Methods in the Gas Phasea.
    Tyr1
 Gly2
 Gly3
 Phe4
 Leu5
conf.   ψ1 χ11 ϕ2 ψ2 ϕ3 ψ3 ϕ4 ψ4 χ41 ϕ5 ψ5 χ51
ECEPP3-1 present work –38 165 113 0 88 –76 –83 –58 –179 –122 157 –179
ECEPP3-2 present work –38 164 116 7 86 –84 –83 –41 –61 –144 148 –180
ECEPP3-3 present work –36 161 112 5 83 –75 –90 –47 174 –120 –16 –176
ECEPP3-4 present work 133 –171 –84 63 70 –110 –62 –40 177 –171 –61 172
ECEPP3-5 present work –25 173 58 –124 –109 1 –176 147 40 –57 150 –180
ECEPP3-6 present work 146 –171 –81 54 75 –97 –96 –13 64 –117 148 –179
ECEPP3-7 present work –38 164 115 10 86 –88 –87 –32 65 –146 141 178
ECEPP3-8 present work –21 –165 51 –137 –107 33 –169 137 23 –56 144 –178
ECEPP3-9 present work 122 180 –91 34 87 –48 –117 –6 66 –167 145 180
MM1b ref (43) 132 176 –119 29 77 –95 –85 –10 62 –119 143 176
MM2b ref (43) –25 173 58 –124 –109 1 –176 147 40 –57 150 –180
MM3b ref (43) –140 –167 –87 64 86 7 –164 169 64 –151 –33 –175
MM4b ref (43) –169 58 –75 94 107 –15 –163 –174 –151 –138 162 –66
VGc ref (50) –31 –65 169 148 57 –137 –97 16 55 –123 15 –60
J1d ref (59) 92 –59 63 14 103 –19 –84 84 –64 –81 58 –53
J2d ref (59) 85 –64 63 13 103 –16 –72 102 –69 –145 162 –70
J3d ref (59) –26 –66 63 24 103 –23 –88 76 –65 –80 58 –51
WH1e ref (62) –39 170 74 2 109 –31 –165 127 –178 –161 156 –174
WH2e ref (62) –29 –178 57 –133 –108 35 –55 144 177 –150 156 –177
WH3e ref (62) 137 170 –151 153 158 149 –163 169 –162 –54 148 179
Open in a new tab
a

Torsion angles (°) are defined in Figure 1.

b

Optimized from the ECEPP2 structures of Meirovitch and Meirovitch.

c

Optimized from the ECEPP3 structures of Vengadesan and Gautham using the MOLS technique.

d

Optimized from the structures of Jalkanen obtained at the B3LYP/6-31G(d) level of theory.

e

Optimized from the structures of Watson and Hirst obtained at the EDF1/6-31+G(d) level of theory.

Table 4. Type of H-Bond, β-Bend, and Thermodynamic Properties of Local Minima for the Neutral Leu-EnK Optimized from the Structures Obtained by the ECEPP Force Field and DFT Methods at the DSD-PBEP86-D3BJ/def2-TZVP//M06-2X/6-31+G(d) Level of Theory in the Gas Phaseah.
conf.b H-bond typec β-bendd ΔEe ΔHf ΔGg
ECEPP3-1 OH1 → 4, 4 → 3, OH5 → 1   10.64 10.61 9.46
ECEPP3-2 OH1 → 4, 4 → 3, OH5 → 1   10.50 10.93 8.85
ECEPP3-3 OH1 → 4, 4 → 3, OH5 → 1   11.94 11.86 11.31
ECEPP3-4 OH1 → 4, 2 → 5, 3 → 1, 5 → 2 βII′34 10.32 10.72 11.25
ECEPP3-5 OH1 → 3, 4 → 1 βII′23 17.75 17.47 15.62
ECEPP3-6 OH1 → 4, 2 → 5, 3 → 1, 4 → 2, 5 → 2 βII′34 4.22 4.57 4.76
ECEPP3-7 OH1 → 4, 4 → 2, OH5 → 1   8.89 8.85 6.60
ECEPP3-8 4 → 1 βII′23 20.59 19.97 17.65
ECEPP3-9 OH1 → 3, 2 → 5, 4 → 3   6.90 6.92 5.88
MM1 OH1 → 3, 2 → 5, 4 → 2, 5 → 2 βII′34 7.24 7.44 5.11
MM2 OH1 → 3, 4 → 1 βII′23 17.75 17.47 15.62
MM3 1 → 4, 3 → 1   17.69 17.45 13.78
MM4 1 → 4, 3 → 1   17.08 16.72 14.30
VG 2 → OH5, 5 → 2 βII′34 11.50 11.32 7.42
J1 1 → 4, 4 → 1, 5 → 3, OH5 → 4 βI′23 13.99 14.18 12.16
J2 1 → 4, 4 → 1, 5 → 3 βI′23 13.70 13.62 10.73
J3 4 → 1, 5 → 3, OH5 → 4 βI′23 11.59 11.22 9.39
WH1 OH1 → 3, 4 → 1 βI′23 12.23 12.31 10.61
WH2 OH1 → 4, 4 → 1 βII′23 11.60 11.41 9.26
WH3 OH1 → 3   18.08 17.58 13.52
Open in a new tab
a

Torsion angles (°) are listed in Table 3.

b

The definition of conformations is noted in footnotes b–e of Table 3.

c

Each H-bond type n → m stands for the H-bond between the H donor (e.g., the amide H atom for backbone) of the residue n and the H acceptor (e.g., the carbonyl O atom for backbone) of the residue m. In addition, OH1 and OH5 represent the hydroxyl H atom of the side chain of the Tyr1 residue and the carboxylic H atom of the Leu5 residue, respectively. 5OH represents the O atom of the carboxylic OH group of the Leu5 residue.

d

βII′23 and βI′23 stand for the type II′ and I′ β-bend at the Gly2–Gly3 sequence, which are stabilized by the 4 → 1 H-bond. βII′34 stands for the type II′ β-bend at the Gly3–Phe4 sequence, which is stabilized by the 5 → 2 H-bond.

e

Relative electronic energies in kcal mol–1.

f

Relative enthalpies in kcal mol–1 at 25 °C.

g

Relative Gibbs free energies in kcal mol–1 at 25 °C and 1 atm.

h

The population of each conformer was calculated by its ΔG at 25 °C.

The most preferred conformer was ECEPP3-6, MM1, VG, J3, and WH2 for each group of computations with ΔG = 4.76, 5.11, 7.42, 9.39, and 9.26 kcal mol–1, respectively, which are shown in Figure 3. Conformer ECEPP3-6, MM1, and VG adopted different folded structures with different types of H-bond (i.e., five H-bonds such as OH1 → 4, 2 → 5, 3 → 1, 4 → 2, and 5 → 2 types of H-bond for ECEPP3-6; four H-bonds such as OH1 → 3, 2 → 5, 4 → 2, and 5 → 2 types of H-bond for MM1; and two H-bonds such as 2 → OH5 and 5 → 2 types of H-bond for VG), despite the same βII′34 bend at the Gly3–Phe4 sequence stabilized by the 5 → 2 H-bond. However, conformer J3 and WH2 exhibited a folded structure with βI′23 and βII′23 bends at the Gly2–Gly3 sequence, respectively, stabilized by the 4 → 1 H-bond. The former had three H-bonds such as 4 → 1, 5 → 3, and OH5 → 4 types of H-bond, whereas the latter had two H-bonds such as OH1 → 4 and 4 → 1 types of H-bond.

Figure 3.

Figure 3

Open in a new tab

Structures of the neutral Leu-EnK obtained by (i) the search methods with the ECEPP force field (ECEPP3-6 in the present work, MM1 from ref (43), and VG from ref (50)) and (ii) the DFT calculations (J3 from ref (59) and WH2 from ref (62)), which were optimized at the M06-2X/6-31+G(d) level of theory in the gas phase. The relative Gibbs free energy (ΔG in kcal mol–1) at the DSD-PBEP86-D3BJ/def2-TZVP//M06-2X/6-31+G(d) level of theory is shown in parentheses behind each conformation name. For clarity, all nonpolar hydrogen atoms are omitted. All H-bonds are represented by dotted lines with distances in Å.

In particular, all of these five structures possessed different types of H-bonds despite the formation of the common β-bend motifs, which are also quite different from that of the most preferred conformer n01, as described above (see Figures 2 and 3). Hence, the most preferred conformer n01 is a new folded structure for the neutral Leu-Enk in the gas phase, not predicted in earlier works.

Zwitterionic Leu-Enk in Water

There were the 43 local minima for the zwitterionic Leu-Enk with the relative Gibbs free energy (ΔGw) < 5 kcal mol–1 at the DSD-PBEP86-D3BJ/def2-TZVP//SMD M06-2X/6-31+G(d) (abbreviated as DSD-dTZ/SMD hereafter) level of theory in water. The torsion angles of these 43 local minima optimized at the SMD M06-2X/6-31+G(d) level of theory are listed in Table S6 in the Supporting Information. The types of H-bond, β-bend, thermodynamic properties, and population of the corresponding structures calculated at the DSD-dTZ/SMD level of theory are shown in Table S7 in the Supporting Information, in which the thermodynamic properties and population at the M06-2X/def2-TZVP//SMD M06-2X/6-31+G(d) (abbreviated as M062X-dTZ/SMD hereafter) level of theory are also included. The corresponding absolute electronic energies, enthalpies, Gibbs free energies, and single-point energies are listed in Table S8 in the Supporting Information.

Conformational Preferences of Zwitterionic Leu-Enk

We found the 16 structures for the zwitterionic Leu-Enk with ΔGw < 3 kcal mol–1 at the DSD-dTZ/SMD level of theory in water, whose torsion angles optimized at the SMD M06-2X/6-31+G(d) level of theory in water are listed in Table 5. The types of H-bond and thermodynamic properties of the corresponding structures are shown in Table 6. The 3D structures of the first eight preferred conformers with ΔGw < 2 kcal mol–1 in water are depicted in Figure 4, whose Cartesian coordinates are also listed in the Supporting Information.

Table 5. Torsion Angles of 16 Local Minima for the Zwitterionic Leu-EnK Optimized at the SMD M06-2X/6-31+G(d) Level of Theory in Watera.
  Tyr1
 Gly2
 Gly3
 Phe4
 Leu5
conf. ψ1 χ11 ϕ2 ψ2 ϕ3 ψ3 ϕ4 ψ4 χ41 ϕ5 ψ5 χ51
zw01 159 63 55 –141 –68 –13 –76 –10 –50 69 23 –40
zw02 164 64 68 –122 –78 7 –152 170 52 –58 134 180
zw03 163 61 72 –118 –80 6 –155 167 51 –59 140 –61
zw04 145 175 63 –134 –63 –19 –84 –3 –61 72 15 –41
zw05 143 178 –80 93 –66 –14 –69 –12 68 –133 –179 56
zw06 142 –175 –79 104 –69 –10 –66 –13 59 –89 38 –57
zw07 –54 –69 169 144 57 –136 –68 –22 67 –82 –43 –174
zw08 141 179 –98 19 88 –46 –115 –12 63 –162 148 –178
zw09 129 176 –125 32 89 –70 –95 2 64 –161 170 76
zw10 142 180 –99 22 87 –45 –118 –11 63 –160 144 179
zw11 173 –167 165 –175 –69 –10 –69 –6 59 –151 1 –168
zw12 131 173 –110 17 85 –71 –68 –20 66 –162 144 –179
zw13 –180 –160 84 –69 –59 –37 –99 140 173 –125 –35 –61
zw14 131 174 –107 14 83 –70 –56 –39 175 –157 150 –177
zw15 142 –180 –101 18 86 –60 –79 –40 –63 –152 165 –64
zw16 149 –166 –150 172 –70 –9 –71 –11 68 –141 13 55
Open in a new tab
a

Torsion angles (°) are defined in Figure 1. Only 16 local minima with the relative Gibbs free energy (ΔGw) < 3 kcal mol–1 are listed.

Table 6. Type of H-bond, β-Bend, Thermodynamic Properties, and Population of 16 Local Minima for the Zwitterionic Leu-EnK Calculated at the DSD-PBEP86-D3BJ/def2-TZVP//SMD M06-2X/6-31+G(d) Level of Theory in Watera.
conf. H-bond typeb β-bendc ΔEwd ΔHwe ΔGwf wg
zw01 1 → 5, 4 → 1, 5 → 2 βII′23, βI34 0.84 0.61 0.00 48.1
zw02 1 → 4, 1 → 5, 4 → 1 βII′23 1.15 1.39 0.69 15.0
zw03 1 → 4, 1 → 5, 4 → 1 βII′23 1.78 1.74 0.69 15.0
zw04 1 → 5, 4 → 1, 5 → 2 βII′23, βI34 3.66 3.50 1.54 3.6
zw05 OH1 → 5, 5 → 2 βI34 0.00 0.00 1.70 2.8
zw06 OH1 → 5, 5 → 2 βI34 1.16 1.46 1.77 2.4
zw07 1 → 5, 2 → 5, 5 → 2 βII′34 3.49 3.38 1.94 1.8
zw08 OH1 → 3, 2 → 5, 4 → 2   1.65 1.69 1.96 1.8
zw09 OH1 → 3, 2 → 5, 4 → 2   1.71 1.67 2.12 1.4
zw10 OH1 → 3, 2 → 5, 4 → 2   3.34 3.26 2.15 1.3
zw11 OH1 → 5, 5 → 2 βI34 1.25 1.44 2.27 1.1
zw12 OH1 → 3, 2 → 5, 4 → 2   1.75 2.02 2.27 1.0
zw13 OH1 → 5, 2 → 4, 3 → 1   1.55 1.52 2.50 0.7
zw14 OH1 → 3, 2 → 5, 4 → 2   3.05 3.20 2.77 0.5
zw15 OH1 → 3, 2 → 5, 4 → 2   3.35 3.70 2.97 0.3
zw16 OH1 → 5, 5 → 2 βI34 2.37 2.15 2.98 0.3
Open in a new tab
a

Torsion angles (°) are listed in Table 5. Only 16 local minima with the relative Gibbs free energy (ΔGw) < 3 kcal mol–1 are listed.

b

Each H-bond type n → m stands for the H-bond between the H donor (e.g., the amide H atom for backbone) of the residue n and the H acceptor (e.g., the carbonyl O atom for backbone) of the residue m. In addition, OH1 represents the hydroxyl H atom of the side chain of the Tyr1 residue.

c

βII′23 stands for the type II′ β-bend at the Gly2–Gly3 sequence, which are stabilized by the 4 → 1 H-bond. βI34 and βII′34 stand for the type I and II′ β-bend at the Gly3–Phe4 sequence, respectively, which are stabilized by the 5 → 2 H-bond.

d

Relative electronic energies in kcal mol–1.

e

Relative enthalpies in kcal mol–1 at 25 °C.

f

Relative Gibbs free energies in kcal mol–1 at 25 °C and 1 atm.

g

The population of each conformer was calculated by its ΔGw at 25 °C.

Figure 4.

Figure 4

Open in a new tab

Preferred structures of the zwitterionic Leu-EnK optimized at the SMD M06-2X/6-31+G(d) level of theory in water. The relative Gibbs free energy (ΔG in kcal mol–1) at the DSD-PBEP86-D3BJ/def2-TZVP//SMD M06-2X/6-31+G(d) level of theory is shown in parentheses behind each conformation name. For clarity, all nonpolar hydrogen atoms are omitted. All H-bonds are represented by dotted lines with distances in Å.

In water, the most preferred conformer zw01 with ΔGw = 0.00 kcal mol–1 (populated at 48.1%) exhibited a folded structure with three H-bonds such as a 1 → 5 type of the C17 head-to-tail H-bond between zwitterionic N–H+(Tyr1) and C=O–(Leu5) species with a short distance of 1.72 Å; 4 → 1 and 5 → 2 types of the C10 backbone-to-backbone H-bond between N–H(Phe4) and C=O(Tyr1) and between N–H(Leu5) and C=O(Gly2) with the same distance of 2.04 Å, respectively. In particular, the two H-bonds of the latter induced the formation of double β-bends such as a βII′23 bend at the Gly2–Gly3 sequence and a βI34 bend at the Gly3–Phe4 sequence, respectively (Figure 4).

The second and third preferred conformers zw02 and zw03 were iso-Gibbs free energy structures with ΔGw = 0.69 kcal mol–1 (populated at 15.0%). Both conformers adopted a folded structure with three H-bonds such as a 1 → 4 type of the C14 backbone-to-backbone H-bond between N–H+(Tyr1) and C=O(Phe4); a 1 → 5 type of the C17 head-to-tail H-bond between N–H+(Tyr1) and C=O–(Leu5); and a 4 → 1 type of the C10 backbone-to-backbone H-bond between N–H(Phe4) and C=O(Tyr1). The distances of 1 → 4, 1 → 5, and 4 → 1 types of H-bond were calculated as 1.82, 2.29, and 2.20 Å for conformer zw02, respectively; and 1.82, 2.33, and 2.25 Å for conformer zw03, respectively (Figure 4). In particular, two conformer zw02 and zw03 possessed in common a βII′23 bend at the Gly2–Gly3 sequence stabilized by the 1 → 4 H-bond but different orientations of Phe4 and Leu5 residues.

The fourth preferred conformer zw04 adopted a folded structure quire similar to the most preferred conformer zw01 stabilized by three H-bonds such as 1 → 5, 4 → 1, and 5 → 2 types of H-bond with the distances of 1.69, 2.05, and 1.97 Å, respectively, but having the different orientation of the Tyr1 residue (Figure 2). However, conformer zw04 was 1.54 kcal mol–1 less stable in ΔGw (populated at 3.6%) than conformer zw01, although both conformers had the same types of βII′23 and βI34 bends.

Conformer zw05 and zw06 were nearly iso-Gibbs free energy structures with ΔGw = 1.70 and 1.77 kcal mol–1, respectively (populated at 2.8 and 2.4%, respectively). Both conformers adopted a folded structure stabilized by OH1 → 5 and 5 → 2 types of H-bond, the latter of which induced the formation of a βI34 bend at the Gly3–Phe4 sequence (Figure 4). The distances of OH1 → 5 and 5 → 2 types of H-bond were calculated as 1.71 and 2.03 Å for conformer zw05, respectively; 1.70 and 1.94 Å for conformer zw06, respectively. In particular, it should be noted that conformer zw05 was 0.84 kcal mol–1 more stable in ΔEw than the most preferred conformer zw01 (Table 6).

The seventh preferred conformer zw07 with a βII′34 bend at the Gly3–Phe4 sequence was stabilized by three H-bonds such as 1 → 5, 2 → 5, and 5 → 2 types of backbone-to-backbone H-bond with the distances of 1.70, 1.90, and 2.07 Å, respectively, but it was 1.94 kcal mol–1 less stable in ΔGw (populated at 1.8%) than conformer zw01. The eighth preferred conformer zw08 was stabilized by three H-bonds such as OH1 → 3, 2 → 5, and 4 → 2 types of H-bond with the distances of 1.97, 1.85, and 2.22 Å, respectively. However, this conformer did not have any β-bend and it was 1.96 kcal mol–1 less stable in ΔGw (populated at 1.8%) than conformer zw01.

Hence, the zwitterionic Leu-Enk predominantly adopted a folded structure stabilized by three 1 → 5, 4 → 1, and 5 → 2 types of H-bond in water, of which the second and third H-bonds induced the formation of double β-bends such as a βII′23 bend at the Gly2–Gly3 sequence and a βI34 bend at the Gly3–Phe4 sequence, respectively. This most preferred conformer of the zwitterionic Leu-Enk in water was quite different from that of the neutral Leu-Enk in the gas, as described above. It was suggested that the dominant conformation of Leu-Enk is a folded structure with a type βI34 or βII′34 bend stabilized by the 5 → 2 H-bond in DMSO by NMR experiments.13,14,16,18 Furthermore, the side chains of Phe4 and Leu5 residues were predominantly populated in the gauche– (g–) configuration in DMSO.14,16 In addition, the distance restraints obtained from the combination of NOESY and ROESY experiments supported that Leu-Enk exists as an ensemble of single β-bend, double β-bend, and extended structures in water.24 These conformational preferences deduced by NMR experiments in DMSO and water are reasonably consistent with those of the preferred conformer zw01, zw02, and zw03 (populated at 48.1, 15.0, and 15.0%, respectively) in water in the present work (see Table 6).

Comparison with Earlier Works

Several studies have focused on the preferred conformation of the zwitterionic Leu-Enk in the crystalline state and in water. Leu-Enk adopted three different conformations, namely, single β-bend (CSD ID LENKPH117), double β-bend (CSD ID GEWWAG8), and extended (CSD ID BIXNIF1011 and FABJEX12) structures in the crystalline state. The three representative conformations (denoted by MD-AA1, MD-AA2, and MD-AA3 in the present work) were suggested from the MD simulations of the zwitterionic Leu-Enk in water.53 All of these seven structures were reoptimized at the SMD M06-2X/6-31+G(d) level of theory in water, whose torsion angles are listed in Table 7. The types of H-bond and thermodynamic properties of the corresponding structures calculated at the DSD-dTZ/SMD level of theory are shown in Table 8. The corresponding data calculated at the M062X-dTZ/SMD level of theory are shown in Table S9 in the Supporting Information. The corresponding absolute electronic energies, enthalpies, Gibbs free energies, and single-point energies are listed in Table S10 in the Supporting Information. The corresponding optimized structures are shown in Figures S4 and S5 in the Supporting Information.

Table 7. Torsion Angles of Local Minima of the Zwitterionic Leu-EnK Optimized at the SMD M06-2X/6-31+G(d) Level of Theory from the Structures Obtained by X-ray Diffraction, MD Simulation, and Molecular Docking in Watera.
    Tyr1
 Gly2
 Gly3
 Phe4
 Leu5
conf.   ψ1 χ11 ϕ2 ψ2 ϕ3 ψ3 ϕ4 ψ4 χ41 ϕ5 ψ5 χ51
LENKPH11b ref (7) 114 –56 62 21 99 7 –139 128 –62 –141 –20 –67
GEWWAGb ref (8) 124 170 –67 –22 –66 –15 –87 –10 –58 –60 141 –177
BIXNIF10b ref (11) 160 62 170 –169 –178 –177 –151 151 –58 –58 159 –61
FABJEXb ref (12) 164 60 –173 –177 –177 –179 –150 138 –58 –167 170 73
MD-AA1c ref (53) 142 –177 –161 137 80 –111 –104 –5 62 –161 –9 –118
MD-AA2c ref (53) 151 –170 –145 169 71 –179 –63 138 –64 –87 118 –174
MD-AA3c ref (53) 142 –162 –90 –129 –86 –102 –57 –40 174 –133 –28 –68
Docking1d ref (66) 178 –151 105 –14 –91 4 –85 85 –69 59 20 –118
Docking2e ref (67) 139 175 63 –148 –159 175 –152 147 –54 –53 142 179
Docking2-ce ref (67) 144 177 115 160 138 –167 –111 135 –62 –76 167 –84
Open in a new tab
a

Torsion angles (°) are defined in Figure 1.

b

Optimized from X-ray structures with CSD IDs.

c

Optimized from the structures obtained by MD simulations in water.

d

Optimized from the structure of Leu-Enk bound to the human δ-opioid receptor 7TM (PDB ID 4N6H, ref (64)) by molecular docking.

e

Optimized from the structure of Leu-Enk bound to the active δ-opioid receptor crystal structure with the potent opioid agonist peptide KGCHM07 (PDB ID 6PT2, ref (65)) by molecular docking. The structure obtained by optimization with a constraint of four torsion angles (ϕ2, ϕ3, ϕ4, and ϕ5) fixed at X-ray values is denoted by “Docking2-c”, whereas the structure obtained by the fully relaxed optimization is represented by “Docking2”.

Table 8. Type of H-bond, β-Bend, and Thermodynamic Properties of Local Minima for the Zwitterionic Leu-EnK Optimized from the Structures Obtained by X-ray Diffraction, MD Simulation, and Molecular Docking at the DSD-PBEP86-D3BJ/def2-TZVP//M06-2X/6-31+G(d) Level of Theory in Watera.
conf.b H-bond typec β-bendd ΔEwe ΔHwf ΔGwg
LENKPH11 1 → 4, 4 → 1 βI′23 5.75 5.22 4.55
GEWWAG 4 → 1, 5 → 2 βI23, βI34 4.61 4.25 4.57
BIXNIF10 ext   14.07 13.95 8.05
FABJEX ext   14.67 14.25 8.75
MD-AA1 OH1 → 3, 2 → 5   4.58 5.11 5.91
MD-AA2 OH1 → 4   7.71 7.79 3.90
MD-AA3 OH1 → 4, 2 → 5, 3 → 5   3.47 4.08 3.60
Docking1 5 → 3   16.59 16.92 16.14
Docking2 ext   12.66 12.12 8.39
Docking2-c ext   18.93 15.70 13.22
Open in a new tab
a

Torsion angles (°) are listed in Table 3.

b

The definition of conformations are noted in footnotes b–e of Table 7.

c

Each H-bond type n → m stands for the H-bond between the H donor (e.g., the amide H atom for backbone) of the residue n and the H acceptor (e.g., the carbonyl O atom for backbone) of the residue m. In addition, OH1 represents the hydroxyl H atom of the side chain of the Tyr1 residue.

d

βI23 and βI′23 stand for the type I and I′ β-bend at the Gly2–Gly3 sequence, which are stabilized by the 4 → 1 H-bond. βI34 stands for the type I β-bend at the Gly3–Phe4 sequence, which is stabilized by the 5 → 2 H-bond.

e

Relative electronic energies in kcal mol–1.

f

Relative enthalpies in kcal mol–1 at 25 °C.

g

Relative Gibbs free energies in kcal mol–1 at 25 °C and 1 atm.

Two conformers of LENKPH11 with a single βI′23 bend and GEWWAG with double βI23 and βI34 bends were nearly iso-Gibbs free energy structures with ΔGw = 4.55 and 4.57 kcal mol–1 in water, respectively (Table 8). However, two conformers adopted different folded structures stabilized by 1 → 4 and 4 → 1 types of H-bond with the distances of 1.78 and 2.06 Å, respectively, for conformer LENKPH11; 4 → 1 and 5 → 2 types of H-bond with the distances of 2.17 and 2.10 Å, respectively, for conformer GEWWAG (Figure 5). Two conformers BIXNIF10 and FABJEX adopted extended structures with ΔGw = 8.05 and 8.75 kcal mol–1 in water, respectively (Table 8 and Figure S4 in the Supporting Information).

Figure 5.

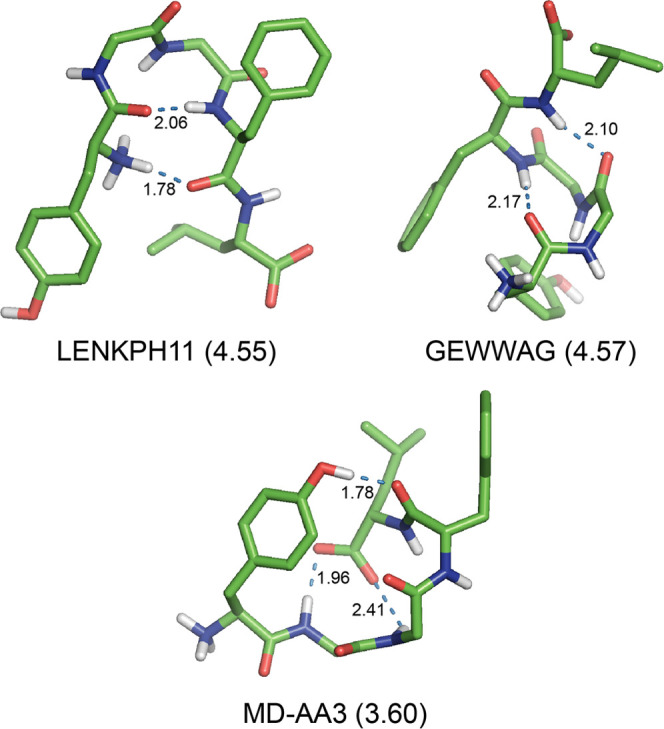
Figure 5

Open in a new tab

Structures of the zwitterionic Leu-EnK obtained by (i) the X-ray diffractions (LENKPH11 from ref (7) and GEWWAG from ref (8)) and (ii) the MD simulations (MD-AA3 from ref (53)), which were optimized at the SMD M06-2X/6-31+G(d) level of theory in water. The relative Gibbs free energy (ΔG in kcal mol–1) at the DSD-PBEP86-D3BJ/def2-TZVP//SMD M06-2X/6-31+G(d) level of theory is shown in parentheses behind each conformation name. For clarity, all nonpolar hydrogen atoms are omitted. All H-bonds are represented by dotted lines with distances in Å.

The conformer MD-AA3 adopted a folded structure with ΔGw = 3.60 kcal mol–1 in water (Table 8) stabilized by three H-bonds such as OH1 → 4, 2 → 5, and 3 → 5 types of H-bond with the distances of 1.78, 1.96, and 2.41 Å, respectively, without any β-bends (Figure 5). The conformer MD-AA2 exhibited a folded structure with ΔGw = 3.90 kcal mol–1 in water stabilized by a single OH1 → 4 H-bond with the distance of 1.76 Å without any β-bends (Figure S5 in the Supporting Information). The conformer MD-AA1 adopted a folded structure with ΔGw = 5.91 kcal mol–1 in water (Table 8) stabilized by two H-bonds such as OH1 → 3 and 2 → 5 types of H-bond with the distances of 1.81 and 1.83 Å, respectively. In particular, it had a βII′34-like motif at the Gly3–Phe4 sequence with a longer distance of 2.80 Å for the 5 → 2 contact due to the more positive shift of torsion angle ϕ3 from the standard value of 60° (Figure S5 in the Supporting Information).

Hence, none of these seven structures optimized in water from X-ray diffractions and MD simulations is consistent with the most preferred conformer zw01 in water. The most preferred conformer zw01 with double β-bends such as βII′23 and βI34 bends is a new folded structure for the zwitterionic Leu-Enk in water, not predicted in earlier works.

To check whether the conformational preference of the zwitterionic Leu-Enk in water is consistent with the structure deduced from NMR experiments, we calculated the ensemble-averaged distances of d(CTyr1α···CPhe4α) and d(CGly2α···CLeu5α) from 43 conformers with ΔGw < 5 kcal mol–1 in Table S6 in the Supporting Information, which can be useful to monitor the formation of β-bend at Gly2–Gly3 and Gly3–Phe4 sequences, respectively. The calculated ensemble-averaged values were 5.74 and 6.13 Å for d(CTyr1α···CPhe4α) and d(CGly2α···CLeu5α), respectively. The latter is consistent with the value of 6.0 Å estimated from the simulated annealing using the 44 distance constraints derived from NOESY spectra.36 MD simulations starting from this NMR model structure indicated that the zwitterionic Leu-Enk exists as an ensemble of the structures with β-bends at the Gly2 and Phe4 residues and a β-bend at the Gly3 residue in water.36 This may imply the formation of a double β-bend at Gly2–Gly3 and Gly3–Phe4 sequences and a single β-bend at the Gly2–Gly3 sequence, of which the former is consistent with conformer zw01 and the latter with conformers zw02 and zw03 in the present work.

Structures of Leu-Enk Bound to δOR

There were two studies for the molecular docking of δOR complexed with Leu-Enk using the crystal structures. Sanfelice and Temussi66 performed the molecular docking of δOR complexed with Leu-Enk using the crystal structure of PDB 4N6H. Recently, Sharma et al. reported the molecular docking of δOR complexed with the Leu-Enk derivative bearing the Tyr1-ψ[(Z)CF=CH]-Gly2 substitution using the crystal structure of PDB 6PT2.67 These two structures of the zwitterionic Leu-Enk bound to δOR were denoted as Docking1 and Docking2 in the present work, respectively, which were reoptimized at the SMD M06-2X/6-31+G(d) level of theory in water. In addition, Docking2 was reoptimized with the constraint of torsion angles ϕ2, ϕ3, ϕ4, and ϕ5 fixed at the values of the corresponding structure of Leu-Enk bound to δOR at the same level of theory in water, which was denoted as Docking2-c. The optimized torsion angles of these three conformers are listed in Table 7. The types of H-bond and thermodynamic properties of the corresponding structures calculated at the DSD-dTZ/SMD level of theory in water are shown in Table 8. The corresponding data calculated at the M062X-dTZ/SMD level of theory are shown in Table S9 in the Supporting Information. The corresponding absolute electronic energies, enthalpies, Gibbs free energies, and single-point energies are listed in Table S10 in the Supporting Information. The three optimized structures are depicted in Figure 6.

Figure 6.

Figure 6

Open in a new tab

Structures of the zwitterionic Leu-EnK from those bound to δOR optimized at the SMD M06-2X/6-31+G(d) level of theory in water. The relative Gibbs free energy (ΔG in kcal mol–1) at the DSD-PBEP86-D3BJ/def2-TZVP//SMD M06-2X/6-31+G(d) level of theory is shown in parentheses behind each conformation name. For clarity, all nonpolar hydrogen atoms are omitted. H-bond is represented by the dotted line with the distance in Å.

Conformer Docking1 adopted a partially folded structure with ΔGw = 16.14 kcal mol–1 in water (Table 8) stabilized by a single 5 → 3 type of H-bond with the distance of 2.28 Å (Figure 6). In particular, there was a close contact (about 3.4 Å) between two phenyl rings of Tyr1 and Phe4 residues for conformer Docking1, of which the aromatic ring of the Tyr1 residue was suggested to be essentially stacked with the aromatic ring of the Trp274 in the binding pocket of δOR.66

On the other hand, conformer Docking2 exhibited a nearly extended structure in water that did not possess any types of H-bond nor close contacts (Table 8 and Figure 6), but it was 3.93 and 7.75 kcal mol–1 more stable in ΔEw and ΔGw, respectively, than conformer Docking1. However, the orientations of the side chain of the Phe4 residue and the carboxylate group of the Leu5 of the fully optimized conformer Docking2 were quite different from those of conformer Docking2 bound to δOR.67 So, we located another conformer Docking2-c by the constrained optimization with four torsion angles ϕ2–ϕ5 fixed at the values of conformer Docking2 bound to δOR. The values of ΔEw and ΔGw for conformer Docking2-c were 6.27 and 4.83 kcal mol–1 higher than those of the fully optimized conformer Docking2, respectively.

According to the refined model of the zwitterionic Leu-Enk bound to δOR (PDB ID 5C1M),67 there were favorable interactions of the charged groups NH3+(Tyr1), C=O(Leu5), and C–O–(Leu5) of Leu-Enk with the side chains of Asp128, Lys108, and Arg291 residues of δOR, respectively, as well as a favorable CAryl···H interaction of the Phe4 residue of Leu-Enk with Trp284 of δOR instead of the π···π interaction. Hence, these favorable interactions would induce the conformation of the zwitterionic Leu-Enk (i.e., the folded structure of conformer zw01 with a βII′23 bend at the Gly2–Gly3 sequence and a βI34 bend at the Gly3–Phe4 sequence) isolated in water into the “bioactive conformation” like as conformer Docking2-c when binding to δOR.

Conclusions

The conformational preferences of Leu-Enk were explored by the conformational search and DFT calculations. First, the 738,234 initial structures of the neutral Leu-Enk were generated by a combination of low-energy conformers of each residue and optimized using the ECEPP3 force field in the gas phase, resulting in 2,633 feasible conformations with the relative energy <5 kcal mol–1. Then, these structures were reoptimized at the HF/3-21G(d) level of theory and followed by the optimizations at the M06-2X level of theory with 6-31G(d) and 6-31+G(d) basis functions. We finally identified the 139 structures with the relative energy <10 kcal mol–1 in the gas phase, from which the structures of the corresponding zwitterionic Leu-Enk were generated and reoptimized at the SMD M06-2X/6-31+G(d) level of theory in water. The conformational preferences of the neutral and zwitterionic Leu-Enk were analyzed using Gibbs free energies corrected by single-point energies calculated at the double-hybrid DSD-PBEP86-D3BJ/def2-TZVP level of theory in the gas phase and in water.

In the gas phase, the neutral Leu-Enk dominantly adopted a folded structure stabilized by a side chain-to-backbone (OH1 → 3) H-bond and two backbone-to-backbone (4 → 2 and OH5 → 1) H-bonds with a βII′-bend-like motif at the Gly3–Phe4 sequence and a close contact between the side chains of Phe4 and Leu5. On the other hand, the zwitterionic Leu-Enk exhibited a folded structure in water with a head-to-tail (1 → 5) H-bond between zwitterionic N–H+(Tyr1) and C=O–(Leu5) species and two backbone-to-backbone (4 → 1 and 5 → 2) H-bonds between N–H(Phe4) and C=O(Tyr1) and between N–H(Leu5) and C=O(Gly2). In particular, the two H-bonds of the latter induced the formation of double β-bends such as a βII′ bend at the Gly2–Gly3 sequence and a βI bend at the Gly3–Phe4 sequence, respectively. Hence, the preferred conformations of the neutral and zwitterionic Leu-Enk are new folded structures not predicted by earlier computational studies. However, the calculated ensemble-averaged distance between CGly2α and CLeu5α of the zwitterionic Leu-Enk in water is consistent with the value estimated from the simulated annealing using the distance constraints derived from NOESY spectra in water.

According to the refined model of the zwitterionic Leu-Enk bound to δOR, there were favorable interactions of the charged groups NH3+(Tyr1), C=O(Leu5), and C–O–(Leu5) of Leu-Enk with the side chains of Asp128, Lys108, and Arg291 residues of δOR, respectively, as well as a favorable CAryl···H interaction of the Phe4 residue of Leu-Enk with Trp284 of δOR. Hence, these favorable interactions would induce the structure of the zwitterionic Leu-Enk with double β-bends isolated in water into the “bioactive conformation” like an extended structure when binding to δOR.

Acknowledgments

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1I1A3053400).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c03942.

  • Torsion angles, thermodynamic properties, absolute energies, and optimized structures of preferred conformers for the neutral and zwitterionic Leu-Enk and their Cartesian coordinates (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c03942_si_001.pdf (573.1KB, pdf)

References

  1. Stein C. Opioid Receptors. Annu. Rev. Med. 2016, 67, 433–451. 10.1146/annurev-med-062613-093100. [DOI] [PubMed] [Google Scholar]
  2. Henry M. S.; Gendron L.; Tremblay M.-E.; Frolet G. Enkephalins: Endogenous Analgesics with an Emerging Role in Stress Resilience. Neural Plast. 2017, 1546125 10.1155/2017/1546125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Fricker L. D.; Margolis E. B.; Gomes I.; Devi L. A. Five Decades of Research on Opioid Peptides: Current Knowledge and Unanswered Questions. Mol. Pharmacol. 2020, 98, 96–108. 10.1124/mol.120.119388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Takahashi A.Enkephalin. In Handbook of Hormones, 2nd ed.; Ando H.; Ukena K.; Nagata S., Eds.; Academic Press: London, U.K., 2021; Vol. 1, pp 91–94. [Google Scholar]
  5. Cullen J. M.; Cascella M.. Physiology, Enkephalin. In StatPearls; StatPearls Publishing LLC: Treasure Island, Fl, 2021. [Google Scholar]
  6. Smith G. D.; Griffin J. F. Conformation of [Leu5]Enkephalin from X-ray Diffraction: Features Important for Recognition at Opiate Receptor. Science 1978, 199, 1214–1216. 10.1126/science.204006. [DOI] [PubMed] [Google Scholar]
  7. Blundell T. L.; Hearn L.; Tickle I. J.; Palmer R. A.; Morgab B. A.; Smith G. D.; Griffin J. F. Crystal Structure of [Leu5]Enkephalin. Science 1979, 205, 220. 10.1126/science.451597. [DOI] [PubMed] [Google Scholar]
  8. Aubry A.; Birlirakis N.; Sakarellos-Daitsiotis M.; Sakarellos C.; Marraud M. Relationship of the Crystal and Molecular Structure of Leucine-enkephalin Trihydrate to that of Morphine. J. Chem. Soc., Chem. Commun. 1988, 963–964. 10.1039/c39880000963. [DOI] [Google Scholar]
  9. Aubry A.; Birlirakis N.; Sakarellos-Daitsiotis M.; Sakarellos C.; Marraud M. A Crystal Molecular Conformation of Leucine-Enkephalin Related to the Morphine Molecule. Biopolymers 1989, 28, 27–40. 10.1002/bip.360280106. [DOI] [PubMed] [Google Scholar]
  10. Camerman A.; Mastropaolo D.; Karle I.; Karle J.; Camerman N. Crystal Structure of Leucine-Enkephalin. Nature 1983, 306, 447–450. 10.1038/306447a0. [DOI] [PubMed] [Google Scholar]
  11. Karle I. L.; Karle J.; Mastropaolo D.; Camerman A.; Camerman N. [Leu5]encephalin: Four Cocrystallizing Conformers with Extended Backbones that Form an Antiparallel β-Sheet. Acta Crystallogr., Sect. B: Struct. Sci. 1983, 39, 625–637. [Google Scholar]
  12. Griffin J. F.; Langs D. A.; Smith G. D.; Blundell T. L.; Tickle I. J.; Bedarkar S. The Crystal Structures of [Met5]enkephalin and a Third Form of [Leu5]encephalin: Observations of a Novel Pleated β-Sheet. Proc. Natl. Acad. Sci. U.S.A. 1986, 83, 3272–3276. 10.1073/pnas.83.10.3272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Garbay-Jaureguiberry C.; Roques B. P.; Oberlin R.; Anteunis M.; Combrisson S.; Lallemand J. Y. 1H and 13C NMR Studies of Conformational Behaviour of Leu-Enkephalin. FEBS Lett. 1977, 76, 93–98. 10.1016/0014-5793(77)80128-2. [DOI] [PubMed] [Google Scholar]
  14. Stimson E. R.; Meinwald Y. C.; Scheraga H. A. Solution Conformation of Enkephalin. A Nuclear Magnetic Resonance Study of 13C-Enriched Carbonyl Carbons in [Leu5]-Enkephalin. Biochemistry 1979, 18, 1661–1671. 10.1021/bi00576a005. [DOI] [PubMed] [Google Scholar]
  15. Han S. L.; Stimson E. R.; Maxfield F. R.; Leach S. J.; Scheraga H. A. Study of the State of Ionization of [Leu5]-Enkephalin in the Crystal and in Solution. Int. J. Pept. Protein Res. 1980, 16, 183–190. 10.1111/j.1399-3011.1980.tb02951.x. [DOI] [PubMed] [Google Scholar]
  16. Garbay-Jaureguiberry C.; Marion D.; Fellion E.; Roques B. P. Refinement of Conformational Preferences of Leu Enkephalin and Tyr-Gly-Gly-Phe by 15N N.M.R. Chemical Shifts and Vicinal Coupling Constants. Int. J. Pept. Protein Res. 1982, 20, 443–450. 10.1111/j.1399-3011.1982.tb03066.x. [DOI] [PubMed] [Google Scholar]
  17. Gerothanassis I. P.; Karayannis T.; Sakarellos-Daitsiotis M.; Sakarellos C.; Marraud M. Nitrogen-14 Nuclear Magnetic Resonance of the Amino Terminal Group of Leu-Enkephalin in Aqueous Solution. J. Magn. Reson. 1987, 75, 513–516. 10.1016/0022-2364(87)90107-7. [DOI] [Google Scholar]
  18. Vesterman B.; Saulitis J.; Betins J.; Liepins E.; Nikiforovich G. V. Dynamic Space Structure of the Leu-Enkephalin Molecule in DMSO Solution. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 1989, 998, 204–209. 10.1016/0167-4838(89)90274-4. [DOI] [PubMed] [Google Scholar]
  19. Sakarellos C.; Gerothanassis I. P.; Birlirakis N.; Karayannis T.; Sakarellos-Daitsiotis M.; Marraud M. 17O-NMR Studies of the Conformational and Dynamic Properties of Enkephalins in Aqueous and Organic Solutions Using Selectively Labeled Analogues. Biopolymers 1989, 28, 15–26. 10.1002/bip.360280105. [DOI] [PubMed] [Google Scholar]
  20. Karayannis T.; Gerothanassis I. P.; Sakarellos-Daitsiotis M.; Sakarellos C.; Marraud M. 17O- and 14N-NMR Studies of Leu-Enkephalin and Enkephalin-Related Fragments in Aqueous Solution. Biopolymers 1990, 29, 423–439. 10.1002/bip.360290213. [DOI] [PubMed] [Google Scholar]
  21. Gerothanassis I. P.; Birlirakis N.; Karayannis T.; Tsikaris V.; Sakarellos-Daitsiotis M.; Sakarellos C.; Vitoux B.; Marraud M. 17O NMR and FT-IR Study of the Ionization State of Peptides in Aprotic Solvents. Application to Leu-Enkephalin. FEBS Lett. 1992, 298, 188–190. 10.1016/0014-5793(92)80053-J. [DOI] [PubMed] [Google Scholar]
  22. Amodeo P.; Naider F.; Picone D.; Tancredi T.; Temussi P. A. Conformational Sampling of Bioactive Conformers: A Low-Temperature NMR Study of 15N-Leu-Enkephalin. J. Pept. Sci. 1998, 4, 253–265. . [DOI] [PubMed] [Google Scholar]
  23. Chatterjee C.; Mukhopadhyay C. Structural Alterations of Enkephalins in the Presence of GM1 Ganglioside Micelles. Biopolymers 2003, 70, 512–521. 10.1002/bip.10509. [DOI] [PubMed] [Google Scholar]
  24. Gayen A.; Mukhopadhyay C. Evidence for Effect of GM1 on Opioid Peptide Conformation: NMR Study on Leucine Enkephalin in Ganglioside-Containing Isotropic Phospholipid Bicelles. Langmuir 2008, 24, 5422–5432. 10.1021/la704056d. [DOI] [PubMed] [Google Scholar]
  25. Nishimura K.; Naito A.; Tuzi S.; Saitô H.; Hashimoto C.; Aida M. Determination of the Three-Dimensional Structure of Crystalline Leu-Enkephalin Dihydrate Based on Six Sets of Accurately Determined Interatomic Distances from 13C-REDOR NMR and the Conformation-Dependent 13C Chemical Shifts. J. Phys. Chem. B 1998, 102, 7476–7483. 10.1021/jp981683w. [DOI] [Google Scholar]
  26. Pawlak T.; Potrzebowski M. J. Fine Refinement of Solid-State Molecular Structures of Leu- and Met-Enkephalins by NMR Crystallography. J. Phys. Chem. B 2014, 118, 3298–3309. 10.1021/jp500379e. [DOI] [PubMed] [Google Scholar]
  27. Han S. L.; Stimson E. R.; Maxfield F. R.; Scheraga H. A. Conformational Study of [Leu5]-Enkephalin by Laser Raman Spectroscopy. Int. J. Pept. Protein Res. 1980, 16, 173–182. 10.1111/j.1399-3011.1980.tb02950.x. [DOI] [PubMed] [Google Scholar]
  28. Renugopalakrishnan V.; Rapaka R. S.; Collette T. W.; Carreira L. A.; Bhatnagar R. S. Conformational States of Leu5- and Met5-Enkephalins in Solution. Biochem. Biophys. Res. Commun. 1985, 126, 1029–1035. 10.1016/0006-291X(85)90288-8. [DOI] [PubMed] [Google Scholar]
  29. Surewicz W. K.; Mantsch H. H. Solution and Membrane Structure of Enkephalins as Studied by Infrared Spectroscopy. Biochem. Biophys. Res. Commun. 1988, 150, 245–251. 10.1016/0006-291X(88)90512-8. [DOI] [PubMed] [Google Scholar]
  30. Abdali S.; Refstrup P.; Nielsen O. F.; Bohr H. Enkephalins: Raman Spectral Analysis and Comparison as Function of pH 1–13. Biopolymers 2003, 72, 318–328. 10.1002/bip.10404. [DOI] [PubMed] [Google Scholar]
  31. Takekiyo T.; Kato M.; Taniguchi Y. FT-IR Spectroscopic Study on Conformational Equilibria of [Leu]5-Enkephalin in DMSO and 2H2O Solutions. J. Mol. Liq. 2005, 119, 147–152. 10.1016/j.molliq.2004.10.021. [DOI] [Google Scholar]
  32. Deber C. M.; Behnam B. A. Role of Membrane Lipids in Peptide Hormone Function: Binding of Enkephalins to Micelles. Proc. Natl. Acad. Sci. U.S.A. 1984, 81, 61–65. 10.1073/pnas.81.1.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Picone D.; D’Ursi A.; Motta A.; Tancredi T.; Temussi P. A. Conformational Preferences of [Leu5]Enkephalin in Biomimetic Media. Investigation by 1H NMR. Eur. J. Biochem. 1990, 192, 433–439. 10.1111/j.1432-1033.1990.tb19245.x. [DOI] [PubMed] [Google Scholar]
  34. Schwyzer R.; Moutevelis-Minakakis P.; Kimura S.; Gremlich H.-U. Lipid-Induced Secondary Structures and Orientations of [Leu5]-Enkephalin: Helical and Crystallographic Double-Bend Conformers Revealed by IRATR and Molecular Modelling. J. Pept. Sci. 1997, 3, 65–81. . [DOI] [PubMed] [Google Scholar]
  35. Rudolph-Böhner S.; Quarzago D.; Czisch M.; Ragnarsson U.; Moroder L. Conformational Preferences of Leu-Enkephalin in Reverse Micelles as Membrane-Mimicking Environment. Biopolymers 1997, 41, 591–606. . [DOI] [Google Scholar]
  36. Chandrasekhar I.; van Gunsteren W. F.; Zandomeneghi G.; Williamson P. T. F.; Meier B. H. Orientation and Conformational Preference of Leucine-Enkephalin at the Surface of a Hydrated Dimyristoylphosphatidylcholine Bilayer: NMR and MD Simulation. J. Am. Chem. Soc. 2006, 128, 159–170. 10.1021/ja054785q. [DOI] [PubMed] [Google Scholar]
  37. Begotka B. A.; Hunsader J. L.; Oparaeche C.; Vincent J. K.; Morris K. F. A Pulsed Field Gradient NMR Diffusion Investigation of Enkephalin Peptide-Sodium Dodecyl Sulfate Micelle Association. Magn. Reson. Chem. 2006, 44, 586–593. 10.1002/mrc.1793. [DOI] [PubMed] [Google Scholar]
  38. Laird D. J.; Mulvihill M. M.; Lillig J. A. W. Membrane-Induced Peptide Structural Changes Monitored by Infrared and Circular Dichroism Spectroscopy. Biophys. Chem. 2009, 145, 72–78. 10.1016/j.bpc.2009.09.002. [DOI] [PubMed] [Google Scholar]
  39. Isogai Y.; Némethy G.; Scheraga H. A. Enkephalin: Conformational Analysis by Means of Empirical Energy Calulations. Proc. Natl. Acad. Sci. U.S.A. 1977, 74, 414–418. 10.1073/pnas.74.2.414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Glasser L.; Scheraga H. A. Calculations on Crystal Packing of a Flexible Molecule, Leu-enkephalin. J. Mol. Biol. 1988, 199, 513–524. 10.1016/0022-2836(88)90622-5. [DOI] [PubMed] [Google Scholar]
  41. Meirovitch H.; Meirovitch E.; Michel A. G.; Vásquez M. A Simple and Effective Procedure for Conformational Search of Macromolecules: Application to Met- and Leu-Enkephalin. J. Phys. Chem. A 1994, 98, 6241–6243. 10.1021/j100076a002. [DOI] [Google Scholar]
  42. Meirovitch H.; Meirovitch E.; Lee J. New Theoretical Methodology for Elucidating the Solution Structure of Peptides from NMR Data. 1. The Relative Contribution of Low-Energy Microstates to the Partition Function. J. Phys. Chem. B 1995, 99, 4847–4854. 10.1021/j100013a065. [DOI] [Google Scholar]
  43. Meirovitch E.; Meirovitch H. New Theoretical Methodology for Elucidating the Solution Structure of Peptides from NMR data. II. Free Energy of Dominant Microstates of Leu-Enkephalin and Population-Weighted Average Nuclear Overhauser Effects Intensities. Biopolymers 1996, 38, 69–88. . [DOI] [PubMed] [Google Scholar]
  44. Meirovitch E.; Meirovitch H. New Theoretical Methodology for Elucidating the Solution Structure of Peptides from NMR Data. 3. Solvation Effects. J. Phys. Chem. 1996, 100, 5123–5133. 10.1021/jp953016y. [DOI] [PubMed] [Google Scholar]
  45. Meirovitch H.; Vásquez M. Efficiency of Simulated Annealing and the Monte Carlo Minimization Method for Generating a Set of Low Energy Structures of Peptides. J. Mol. Struct.: THEOCHEM 1997, 398–399, 517–522. 10.1016/S0166-1280(97)00041-9. [DOI] [Google Scholar]
  46. Kříž Z.; Carlsen P. H. J.; Koča J. Conformational Features of Linear and Cyclic Enkephalins. A Computational Study. J. Mol. Struct.: THEOCHEM 2001, 540, 231–250. 10.1016/S0166-1280(00)00728-4. [DOI] [Google Scholar]
  47. Ozkan S. B.; Meirovitch H. Efficient Conformational Search Method for Peptides and Proteins: Monte Carlo Minimization with an Adaptive Bias. J. Phys. Chem. B 2003, 107, 9128–9131. 10.1021/jp0346615. [DOI] [PubMed] [Google Scholar]
  48. Klepeis J. L.; Floudas C. A. Comparative Study of Global Minimum Energy Conformations of Hydrated Peptides. J. Comput. Chem. 1999, 20, 636–654. . [DOI] [Google Scholar]
  49. Garduño-Juárez R.; Morales L. B. A Genetic Algorithm with Conformational Memories for Structure Prediction of Polypeptides. J. Biomol. Struct. Dyn. 2003, 21, 65–87. 10.1080/07391102.2003.10506906. [DOI] [PubMed] [Google Scholar]
  50. Vengadesan K.; Gautham N. Conformational Studies on Enkephalins Using the MOLS Technique. Biopolymers 2004, 74, 476–494. 10.1002/bip.20021. [DOI] [PubMed] [Google Scholar]
  51. Ramya L.; Gautham N. Conformational Space Exploration of Met- and Leu-Enkephalin Using the MOLS Method, Molecular Dynamics, and Monte Carlo Simulation - A Comparative Study. Biopolymers 2012, 97, 165–176. 10.1002/bip.21721. [DOI] [PubMed] [Google Scholar]
  52. van der Spoel D.; Berendsen H. J. C. Molecular Dynamics Simulations of Leu-Enkephalin in Water and DMSO. Biophys. J. 1997, 72, 2032–2041. 10.1016/S0006-3495(97)78847-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Aburi M.; Smith P. E. A Conformational Analysis of Leucine Enkephalin as a Function of pH. Biopolymers 2002, 64, 177–188. 10.1002/bip.10158. [DOI] [PubMed] [Google Scholar]
  54. Aburi M.; Smith P. E. A Combined Simulation and Kirkwood-Buff Approach to Quantify Cosolvent Effects on the Conformational Preferences of Peptides in Solution. J. Phys. Chem. B 2004, 108, 7382–7388. 10.1021/jp036582z. [DOI] [Google Scholar]
  55. Karvounis G.; Nerukh D.; Glen R. C. Water Network Dynamics at the Critical Moment of a Peptide’s β-Turn Formation: A Molecular Dynamics Study. J. Chem. Phys. 2004, 121, 4925–4935. 10.1063/1.1780152. [DOI] [PubMed] [Google Scholar]
  56. Unruh J. R.; Kuczera K.; Johnson C. K. Conformational Heterogeneity of a Leucine Enkephalin Analogue in Aqueous Solution and Sodium Dodecyl Sulfate Micelles: Comparison of Time-Resolved FRET and Molecular Dynamics Simulations. J. Phys. Chem. B 2009, 113, 14381–14392. 10.1021/jp903302k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Sul S.; Feng Y.; Le U.; Tobias D. J.; Ge N.-H. Interactions of Tyrosine in Leu-Enkephalin at a Membrane-Water Interface: An Ultrafast Two-Dimensional Infrared Study Combined with Density Functional Calculations and Molecular Dynamics Simulations. J. Phys. Chem. B 2010, 114, 1180–1190. 10.1021/jp9105844. [DOI] [PubMed] [Google Scholar]
  58. Nemethy G.; Gibson K. D.; Palmer K. A.; Yoon C. N.; Paterlini G.; Zagari A.; Rumsey S.; Scheraga H. A. Energy Parameters in Polypeptldes. 10. Improved Geometrical Parameters and Nonbonded Interactions for Use in the ECEPP/3 Algorithm, with Appllcatlon to Proline-Containing Peptides. J. Phys. Chem. 1992, 96, 6472–6484. 10.1021/j100194a068. [DOI] [Google Scholar]
  59. Jalkanen K. J. Energetics, Structures, Vibrational Frequencies, Vibrational Absorption, Vibrational Circular Dichroism and Raman Intensities of Leu-enkephalin. J. Phys.: Condens. Matter 2003, 15, S1823–S1851. 10.1088/0953-8984/15/18/315. [DOI] [Google Scholar]
  60. Abdali S.; Niehaus T. A.; Jalkanen K. J.; Cao X.; Nafie L. A.; Frauenheim Th.; Suhai S.; Bohr H. Vibrational Absorption Spectra, DFT and SCC-DFTB Conformational Study and Analysis of [Leu]enkephalin. Phys. Chem. Chem. Phys. 2003, 5, 1295–1300. 10.1039/b210893c. [DOI] [Google Scholar]
  61. Abdali S.; Jalkanen K. J.; Cao X.; Nafie L. A.; Bohr H. Conformational Determination of [Leu]enkephalin Based on Theoretical and Experimental VA and VCD Spectral Analyses. Phys. Chem. Chem. Phys. 2004, 6, 2434–2439. 10.1039/b314433j. [DOI] [Google Scholar]
  62. Watson T. M.; Hirst J. D. Theoretical Studies of the Amide I Vibrational Frequencies of [Leu]-Enkephalin. Mol. Phys. 2005, 103, 1531–1546. 10.1080/00268970500052387. [DOI] [Google Scholar]
  63. Frau J.; Flores-Holguín N.; Glossman-Mitnik D. Conceptual Density Functional Theory Study of the Chemical Reactivity Properties and Bioactivity Scores of the Leu-Enkephalin Opioid Peptide Neurotransmitter. Comput. Mol. Biosci. 2019, 9, 13–26. 10.4236/cmb.2019.91002. [DOI] [Google Scholar]
  64. Fenalti G.; Giguere P. M.; Katritch V.; Huang X.-P.; Thompson A. A.; Cherezov V.; Roth B. L.; Stevens R. C. Molecular Control of δ-Opioid Receptor Signalling. Nature 2014, 506, 191–196. 10.1038/nature12944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Claff T.; Yu J.; Blais V.; Patel N.; Martin C.; Wu L.; Han G. W.; Holleran B. J.; Van der Poorten O.; White K. L.; Hanson M. A.; Sarret P.; Gendron L.; Cherezov V.; Katritch V.; Ballet S.; Liu Z. J.; Müller C. E.; Stevens R. C. Elucidating the Active δ-Opioid Receptor Crystal Structure with Peptide and Small-Molecule Agonists. Sci. Adv. 2019, 5, eaax9115 10.1126/sciadv.aax9115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Sanfelice D.; Temussi P. A. The Conformation of Encephalin Bound to Its Rceptor: An “Elusive Goal” Becoming Reality. Front. Mol. Biosci. 2014, 1, 14 10.3389/fmolb.2014.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Sharma K. K.; Cassell R. J.; Meqbil Y. J.; Su H.; Blaine A. T.; Cummins B. R.; Mores K. L.; Johnson D. K.; van Rijn R. M.; Altman R. A. Modulating β-Arrestin 2 Recruitment at the δ- and μ-Opioid Receptors using Peptidomimetic Ligands. RSC Med. Chem. 2021, 12, 1958–1967. 10.1039/D1MD00025J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Kozuch S.; Martin J. M. L. DSD-PBEP86: In Search of the Best Double-Hybrid DFT with Spin-Component Scaled MP2 and Dispersion Corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104–20107. 10.1039/c1cp22592h. [DOI] [PubMed] [Google Scholar]
  69. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  70. Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  71. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Rev. D01; Gaussian, Inc.: Wallingford, CT, 2013.
  72. Zhao Y.; Truhlar D. G. Applications and Validations of the Minnesota Density Functionals. Chem. Phys. Lett. 2011, 502, 1–13. 10.1016/j.cplett.2010.11.060. [DOI] [Google Scholar]
  73. Scheraga H. A.Predicting Three-Dimensional Structures of Oligopeptides. In Reviews in Computational Chemistry, John Wiley & Sons, Ltd., 1992, Vol 3; pp 73–142. [Google Scholar]
  74. Scheraga H. A. Recent Developments in the Theory of Protein Folding: Searching for the Global Energy Minimum. Biophys. Chem. 1996, 59, 329–339. 10.1016/0301-4622(95)00126-3. [DOI] [PubMed] [Google Scholar]
  75. Vásquez M.; Scheraga H. A. Use of Buildup and Energy-Minimization Procedures to Compute Low-Energy Structures of the Backbone of Enkephalin. Biopolymers 1985, 24, 1437–1447. 10.1002/bip.360240803. [DOI] [PubMed] [Google Scholar]
  76. Vásquez M.; Némethy G.; Scheraga H. A. Computed Conformational States of the 20 Naturally Occurring Amino Acid Residues and of the Prototype Residue α-Aminobutyric Acid. Macromolecules 1983, 16, 1043–1049. 10.1021/ma00241a004. [DOI] [Google Scholar]
  77. Dennington R. D. II; Keith T. A.; Millam J.. GaussView, Version 6.0; Gaussian: Wallingford, CT, 2016.
  78. Kang Y. K. Ab Initio MO and Density Functional Studies on Trans and Cis Conformers of N-Methylacetamide. J. Mol. Struct.: THEOCHEM 2001, 546, 183–193. 10.1016/S0166-1280(01)00445-6. [DOI] [Google Scholar]
  79. Hehre W. J.; Radom L.; Schleyer P. v. R.; Pople J. A.. Ab Initio Molecular Orbital Theory; John Wiley & Sons: New York, 1986; Chapter 6. [Google Scholar]
  80. Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  81. Martin J. M. L.; Santra G. Empirical Double-Hybrid Density Functional Theory: A ‘Third Way’ in Between WFT and DFT. Isr. J. Chem. 2020, 60, 787–804. 10.1002/ijch.201900114. [DOI] [Google Scholar]
  82. Kang Y. K.; Park H. S. Exploring Conformational Preferences of Alanine Tetrapeptide by CCSD(T), MP2, and Dispersion-Corrected DFT Methods. Chem. Phys. Lett. 2018, 702, 69–75. 10.1016/j.cplett.2018.05.006. [DOI] [Google Scholar]
  83. Kang Y. K.; Park H. S. Conformational Preferences of Cationic β-Peptide in Water Studied by CCSD(T), MP2, and DFT Methods. Heliyon 2020, 6, e04721 10.1016/j.heliyon.2020.e04721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  84. Kang Y. K.; Park H. S. Assessment of CCSD(T), MP2, DFT-D, CBS-QB3, and G4(MP2) Methods for Conformational Study of Alanine and Proline Dipeptides. Chem. Phys. Lett. 2014, 600, 112–117. 10.1016/j.cplett.2014.03.067. [DOI] [Google Scholar]
  85. The PyMOL Molecular Graphics System, Version 2.6; Schrödinger, LLC.
  86. Zimmerman S. S.; Scheraga H. A. Influence of Local Interactions on Protein Structure. I. Conformational Energy Studies of N-Acetyl-N′-Methylamides of Pro-X and X-Pro Dipeptides. Biopolymers 1977, 16, 811–843. 10.1002/bip.1977.360160408. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c03942_si_001.pdf (573.1KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES