Solubility of Organic Salts in Solvent–Antisolvent Mixtures: A Combined Experimental and Molecular Dynamics Simulations Approach

Abstract

We combine molecular dynamics simulations with experiments to estimate solubilities of an organic salt in complex growth environments. We predict the solubility by simulations of the growth and dissolution of ions at the crystal surface kink sites at different solution concentrations. Thereby, the solubility is identified as the solution’s salt concentration, where the energy of the ion pair dissolved in solution equals the energy of the ion pair crystallized at the kink sites. The simulation methodology is demonstrated for the case of anhydrous sodium acetate crystallized from various solvent–antisolvent mixtures. To validate the predicted solubilities, we have measured the solubilities of sodium acetate in-house, using an experimental setup and measurement protocol that guarantees moisture-free conditions, which is key for a hygroscopic compound like sodium acetate. We observe excellent agreement between the experimental and the computationally evaluated solubilities for sodium acetate in different solvent–antisolvent mixtures. Given the agreement and the rich data the simulations produce, we can use them to complement experimental tasks, which in turn will reduce time and capital in the design of complicated industrial crystallization processes of organic salts.

Introduction

Solubilities of organic salts play an important role in the pharmaceutical industry. Salt formation is a common way of tailoring the solubility of an active pharmaceutical ingredient (API), thus modifying its dissolution rate.^1,2 Typically, in the design and development of the drug’s crystallization process, the API’s solubility is the first property that is quantified via experimental measurements. However, with the improving capabilities of computational methods, and in particular molecular dynamics (MD) simulations, future measurements and high throughput studies both in academia and in the industry will benefit tremendously from an experimentally validated computational approach. Here, we demonstrate that this is possible by combining a dedicated experimental setup together with a recently introduced MD method.³ We find that such a framework yields an accurate estimation of key properties like solubility, thus paving the way for a combined methodology, which has the potential of significantly reducing time and the cost of such an endeavor.

Most often, to measure the solubility of a given compound in crystallization processes, one employs gravimetric, spectroscopic, and chromatographic experiments, or a combination thereof.⁴⁻¹⁰ Despite their widespread use, these methods suffer from several technical challenges, which are subject of active research.¹¹ In hygroscopic or thermally unstable compounds, all these methods fail if adopted in the absence of careful consideration of the experimental environment. For example, to maintain a moisture-free environment one might have to perform experiments in an inert atmosphere, e.g., in a glovebox or in a Schlenk line. For compounds with low solubility, low spectral peak sensitivity, or low absolute changes in concentration, spectroscopic methods do not yield accurate concentration estimates. Even though some of these issues can be resolved through chromatography, they usually require a tedious and time-consuming sample preparation step. It must be kept in mind that even despite being the norm, the experimental approach to measure solubility is not efficient in terms of resources and time required as it will be evident from the experimental study presented hereafter.

MD simulations have become an effective tool to gain insights into crystallization phenomena and to resolve them at the atomistic level.¹²⁻¹⁶ In the case of organic salts, MD simulations can be used to predict solubility and to understand the mechanism of ion attachment and detachment during crystal growth and dissolution, respectively. As such, MD simulations help reducing empiricism, and guiding and accelerating the experimental campaign for crystallization process development. Recently, we have introduced an MD simulation setup that allows the prediction of solubility of organic molecules in various solvents.³ This approach concentrates on the growth and dissolution process at kink sites, which constitute the end points of unfinished molecular (or ionic) rows on the edges of a crystal surface,¹⁷⁻¹⁹ as kink sites are the most relevant growth and dissolution sites for solutions at concentrations close to the solubility limit.²⁰ It is important to note that with this method, the crystal structure needs to be known a priori.

In this work, we intend to show by direct comparison with experiments that this MD simulation approach, once properly tailored, can be used to predict reliably the solubility of organic salts. For the first time, we present a methodology to estimate the solubility of organic salts, by extending our previous work on kink growth and dissolution.³ Note that the extension of this approach from organic crystals (one species involved in the growth and dissolution events) to organic salts where at least two ions must be considered is challenging per se. In addition, because we consider different solvent–antisolvent mixtures, one has to deal with a ternary system. In this work, we have selected anhydrous sodium acetate (NaOAc) and its polymorph I²¹ as the organic salt on which to apply the new approach. We have used methanol (MeOH) as the solvent and either propan-1-ol (PrOH) or acetonitrile (MeCN) as the antisolvent; in either case, mixtures with different solvent–antisolvent ratios were considered.

NaOAc’s properties are well documented in the literature,²²⁻²⁴ and sodium is frequently used as a counterion in salt formulations of acidic APIs.² NaOAc is not only a suitable model compound to study organic salts but also an important substance with a wide range of uses. Most notably, its trihydrate form is an important phase-change material,²⁵ which can absorb and release heat through solid state changes. In the design of phase-change materials, it is important to understand the properties of all of its solid state forms, including the anhydrous ones.²⁶ NaOAc’s solubility is weakly dependent on temperature, which is common for salts, and therefore the use of antisolvents is necessary to induce and control crystallization. Despite having a simple form for an organic salt, NaOAc is a challenging system, both in experiments and in simulations.

Anhydrous NaOAc rapidly changes into its hydrated form upon adsorption of moisture as it inevitably does when it comes into contact with ambient atmosphere.²⁷ Therefore, carrying out experimental measurements with NaOAc suffer from challenges that are related to the adsorption of moisture. Thus, we undertook a laborious but successful experimental campaign, in which we took care of avoiding exposure to moisture. First, we handled the anhydrous NaOAc in a glovebox. Second, we performed all the solubility measurements in a Schlenk line. Finally, we used chromatography instead of a gravimetric method. We overcame the challenge and obtained the solubility curves for NaOAc in different solvent–antisolvent mixtures, which could be used as a reference to gauge the predictive capabilities of the MD simulations.

MD simulations have the advantage to provide more control over the crystal–solution system, but simulations of NaOAc crystal growth in solvent–antisolvent mixtures pose considerable hurdles as well, which manifest in size and time-scale limitations. In regular MD simulations, as the crystal grows, the solution is quickly depleted because of system size limitations. Such depletion can be prevented with the constant chemical potential molecular dynamics (CμMD) algorithm, developed by Perego et al.²⁸ The NaOAc simulations require the control of the chemical potential of a complex solution composed of two dissociated ions, a solvent, and an antisolvent. With the right choice of system parameters, the CμMD algorithm allowed us to keep the solution concentration constant in the proximity of the crystal surface. Furthermore, salt compounds have large activation energy barriers both for growth and dissolution.^12,14,15 Thus, it is impossible to run an ordinary MD simulation for a time long enough to observe a number of growth and dissolution events sufficient to calculate solubility with any accuracy. To overcome this limitation, we use well-tempered Metadynamics²⁹ (WTMetaD) together with a set of collective variables³ (CVs), which capture the slow degrees of freedom for the kink growth and dissolution for sodium (Na⁺) and acetate (AcO^–) ions.

Methodology

Experiments

We measure the solubility of NaOAc, χ_exp^*, in different solvent–antisolvent mixtures using the equilibrium concentration method. In this method, we add excess salt to a given solvent–antisolvent mixture and let the solution equilibrate for a given period of time; we assume the concentration measured at the end of the equilibration time to be the solubility of the salt at that specific condition.

The experimental protocol consists of two steps, namely, a sample preparation step and a concentration estimation step. In the sample preparation step, we add excess anhydrous sodium acetate (NaOAc, anhydrous ≥99%, Sigma-Aldrich, Buchs, Switzerland) to a given mixture of solvent–antisolvent. We use methanol (MeOH, gradient grade, Merck KGaA, Darmstadt, Germany) as the solvent for all the experiments and we use propan-1-ol (PrOH, ≥99.5%, Fisher Scientific, Reinach, Switzerland) or acetonitrile (MeCN, ≥99.5%, Sigma-Aldrich, Buchs, Switzerland) as the antisolvent. We prepare the pure solvent (100% MeOH) as well as solvent–antisolvent mixtures (on a weight basis) by mixing predetermined quantities of MeOH–PrOH (80–20%, 60–40%, 40–60%) or MeOH–MeCN (75–25%, 50–50%). To avoid atmospheric moisture exposure, we handle the NaOAc crystals in a glovebox under an argon environment. We add excess NaOAc crystals to a three neck 500 mL round-bottomed flask with a magnetic stirrer, we seal it and move it from the glovebox to a Schlenk line. We flush the Schlenk line and saturate it with argon, before opening the flask to add the solvent–antisolvent mixture prepared in advance. Note that we perform this addition using a syringe, with the flask attached to the Schlenk line and under a constant flow of argon. Upon the complete addition of the solvent–antisolvent mixture, we seal the flask and move it to a thermal bath, which is kept at a constant temperature of 25 °C. We stir this suspension at constant temperature for 20 h. On the basis of preliminary experiments to estimate the solubility, where the suspension was saturated for 20, 48, and 72 h, we concluded that 20 h was sufficient to guarantee equilibrium between the crystals of the solute and its solution in the solvent–antisolvent mixture.

For the concentration measurement, we use high performance liquid chromatography (HPLC), i.e. by measuring the amount of acetate present in a given sample. To this aim, we first obtain a solid-free saturated solution from the previous step. To obtain this solution, we reattach the flask with the suspension to the Schlenk line under an argon environment. We use a second three neck 500 mL round-bottomed flask to collect the solids-free saturated solution. These two flasks are connected using a Teflon tube with a filter element to remove the solids. We pull a vacuum through the second flask attached to the Schlenk line and we exploit the pressure gradient between the two flasks to facilitate the transfer of suspension from the first flask through the filter to the second flask. Finally, we switch from a vacuum environment to an argon environment. Subsequently, we take samples of the filtered saturated solution and dilute it using deionized and filtered (filter size of 0.22 μm) water obtained from a Milli-QAdvantage A10 system (Millipore, Zug, Switzerland). We perform this step as the HPLC is typically employed to detect concentrations under dilute conditions. To convert the HPLC chromatogram to a concentration estimate, we performed a thorough calibration using acetic acid as the reference (i.e., a calibration curve that relates area under the curve for the acetic acid peak in the chromatogram to the acetic acid concentration). In our actual experiments, upon dilution of the saturated solution in water, the sodium acetate dissociates into sodium and acetate ions. We use sulfuric acid (pH = 2) as the mobile phase, hence, the acetate ion is converted into acetic acid. The retention of acetic acid in the column, enables us to integrate the area of the peak at a given retention time to obtain the acetic acid concentration and thereby the NaOAc concentration.

A typical experiment to obtain a single solubility point (i.e., one concentration estimate at a given temperature and at a given solvent–antisolvent mixture composition) can take around 2 days, which makes the whole procedure rather cumbersome and tedious; such experimental complexity is unavoidable considering the absolute need to avoid exposure of the samples to ambient moisture.

Simulations

As discussed in the introduction, our simulation was made possible by the use of the WTMetaD²⁹ enhanced sampling method that extends the time-scale limit and the use of the constant chemical potential method²⁸ that much reduces finite-size effects. Details on the setup of the simulations can be found in the Supporting Information (SI) in Sections S2, S3, and S4.

With these methods, we study the growth and dissolution of NaOAc ions at the kink sites (kink in short) of a crystal surface. After a new kink is grown, the surface free energy does not change because the addition of a new kink only moves the kink by one step, but otherwise the kink structure remains chemically identical. For this reason, kink growth and kink dissolution enable us to extract the free energy difference between the state of a growth unit dissolved in solution and that of a growth unit integrated within the crystal.³⁰ However, NaOAc is composed of two growth units, not just one as organic crystals. For NaOAc, both Na⁺ and AcO^– need to attach and detach during the simulation of growth and dissolution to enable the estimation of solubility. Two kink growth events, one for each ion, have to take place to return to the initial surface free energy.

We expose the {200} face of anhydrous NaOAc polymorph I²¹ (see SI Section S2) to the solution, because it is the only monatomic face of the polymorph, which has a zero electrostatic dipole moment perpendicular to the face, and therefore it is also the only stable monatomic face. Ionic crystal faces with a nonzero dipole moment perpendicular to the surface are not stable.³¹ We consider the kinks along the edge in crystal lattice direction [010]. The Na⁺ and AcO^– ions alternate in the row along the [010] direction (see also SI Section S2).

Unbiased MD simulations indicate that at concentrations close to the solubility limit, the molecules in solution are fully dissociated and enter the kink sites individually, not as a dimer. We infer that in such a scenario the attachment of Na⁺ and AcO^– as a pair to the specific kink site is less likely because it requires a very rare process of simultaneous desolvation of both the ions and the kink sites, followed by their crystallization as a dimer. At concentrations around solubility, the dimeric unit grows invariably according to the sequence of events illustrated in Figure 1. We shall call the site that incorporates the kink sites of both ions the dimeric unit.³²

Figure 1.

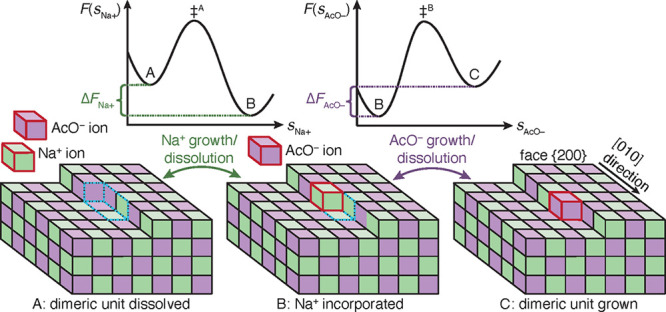
Schematic of the kink growth and dissolution process of an ion dimer for NaOAc polymorph I at surface {200} along edge [010]. Na⁺ and AcO^– growth units are shown as green and purple cubes. State A shows a dissociated Na⁺ and AcO^– (red frames) in solution and a crystal surface with a kink site; the dimeric unit, which is about to grow, is framed with dashed blue lines. In state B, the Na⁺ has grown at its kink site, while the AcO^– ion’s kink site is still dissolved. In state C, both ions are incorporated into the fully crystalline dimeric unit. The growth process takes place as a sequence A → B → C, and the reverse sequence occurs for dissolution. Over each double sided arrow in the figure, indicating the growth and dissolution process of the ions, the corresponding schemes of the free energy surfaces, F, are shown. The F’s are functions of the crystallinity CVs of Na⁺ and AcO^–, i.e. s_Na+ and s_AcO–, which describe the states A and B, as well as B and C. The transition states, ‡^A and ‡^B, indicate the ion’s growth and dissolution are activated processes. Because of the sequential growth and dissolution, the F’s are sampled in separate simulations for each ion at a given mole fraction, χ. The free energy difference of the dimeric unit is the sum ΔF = ΔF_Na+ + ΔF_AcO–. χ, where ΔF = 0, equates to the solubility.

In state A, the site of the dimeric unit is fully solvated. For the crystal to grow, first a Na⁺ ion enters its kink site position leading to state B, which has one Na⁺ ion incorporated into the dimeric unit but no AcO^– ion. The scheme for the free energy surface (FES) of the Na⁺ growth is shown in Figure 1 above the illustrations of state A and B. The quantity s_Na+ is a CV, which defines the solvated and crystalline Na⁺ kink site, A and B, in the dimeric unit. The transition state is labeled by the symbol ‡^A, and its higher position between states A and B in the FES indicates that the Na⁺ growth as well as its dissolution are activated processes. The energy difference for the grown and dissolved Na⁺ kink site is given by ΔF_Na+ = F_B – F_A.

Only once the Na⁺ ion is adsorbed, can the AcO^– ion get attached to its kink site. The incorporation of the AcO^– ion transforms the system from state B to state C along the crystallinity CV, s_AcO–. The free energy profile associated with this step is shown in the schematic. Similar to the Na⁺ case, here also the AcO^– attachment involves overcoming a free energy barrier (with transition state ‡^B) and thus it is an activated process. The free energy difference between the crystalline and dissolved AcO^– kink site is computed as ΔF_AcO– = F_C – F_B. During the dissolution process, the detachment of the ions follow the opposite sequence, i.e. the AcO^– ion first, followed by the Na⁺ ion.

The surface energy remains unaltered going from state A to C because of the conservation of the total number and type of ions residing at kink sites and edges on the surface. The free energy difference solely originates from the attachment of a new dimeric unit of NaOAc to the crystal, and the free energy difference between the crystallized and the dissolved states is given by, ΔF = ΔF_Na+ + ΔF_AcO–. Therefore, this particular kink growth process allows predicting solubility, χ_sim^* as the mole fraction, χ, at which ΔF = 0.

To overcome the time-scale limitations encountered in kink growth and dissolution, we apply enhanced sampling via WTMetaD. In the WTMetaD method, a bias potential is constructed as a function of a few selected slow degrees of freedom, i.e. the biased CVs, and once applied, during the simulation it discourages the system from visiting the already sampled states and thereby allows the system to come out of a free energy well, here in our context, the solvated- or the crystallized kink site state, in reasonable simulation times.

In the specific case of NaOAc, each ion undergoes the following steps during growth. The ion diffuses to the kink site, then the kink site and the ion undergo desolvation, so that the ion can adsorb onto the kink site. Diffusion and desolvation are slow processes.^15,30,33 To describe the diffusion and adsorption of each ion, we define the biased CV as a function³⁴⁻³⁷ of the local densities of solute, as well as solvent and antisolvent, at the kink site. In WTMetaD simulations, the solute density part of the biased CV enhances the ion’s diffusion toward- as well as its adsorption at the kink site, while the solvent–antisolvent density part enhances the desolvation of the kink site so that the ion can adsorb, and vice versa in the dissolution process. The functional form of the biased CV is discussed in the SI (Section S4.3) and in our previous work.³ To compute the energy differences, ΔF_Na+ and ΔF_AcO–, the trajectories of the biased CV for each ion have to be reweighed³⁸ with a set of CVs that capture the crystallinity of the specific ion’s kink site (see SI Sections S4.4 and S5 for details).

The depletion of sodium acetate from the bulk solution during the kink growth is prevented by the use of the CμMD algorithm,²⁸ which keeps the solution’s chemical potential constant in the proximity of the crystal surface. The algorithm was originally developed for a binary solution, consisting of a molecular solute and water, and it was later extended to three-component system, consisting of a dissociated salt aqueous solution.¹⁶ In this work, we have to keep the chemical potential constant for a four-component system, consisting of Na⁺, AcO^–, solvent, and antisolvent, which is achieved by properly choosing the simulation parameters (see also SI Section S3).

Because the NaOAc crystal with a kink site is in a metastable state, it is likely that during the simulation crystalline molecules of the unfinished surface layer dissolve. This would alter the biased kink site’s environment and would lead to difficulties in the sampling. We prevent this undesired effect by the introduction of a harmonic potential, which prevents the ions from dissolution while at the same time not interfering with the natural vibrations of the ions in their lattice positions.

For all investigated molecules,³⁹ the General AMBER force fields (GAFF)⁴⁰⁻⁴⁵ were used with full atomistic description. Force field parameters of NaOAc were taken from Kashefolgheta et al.^24,46,47 The NaOAc force fields with full point charges produce a considerably larger melting temperature⁴⁸ of the NaOAc crystal compared to experiments.²² This would drastically lower the solubility and thus deviate dramatically from experiments.³ This is not unexpected, as in reality, there should be considerable polarization as well as charge transfer between the two oppositely charged ions. To incorporate such polarization and charge transfer effects, albeit approximately, we have scaled down the charges with a scaling factor of 0.807 (see other studies involving ions in references (49), (50), and (51)). The scaling factor was fitted to reproduce the experimental melting temperature. Now the Na⁺ and AcO^– force fields have charges +0.807 and −0.807, respectively. We provide further discussion on the impact of charges on the estimated melting point and solubility in Sections S1.2 and S7 of the SI.

A representative visualization of the simulation setup is shown in Figure 2 for the case of Na⁺ grown in a pure MeOH solution at a solute mole fraction of χ = 0.0138. For all simulations, face {200} of anhydrous NaOAc polymorph I²¹ was exposed to the solution. The unfinished surface layer was cut along the [010] direction. The growth units along this specific edge are composed of one Na⁺ and one AcO^–. As previously discussed, growth along these edges consists of the integration of the Na⁺ ion first and then of the AcO^– ion, and vice versa for dissolution. This decoupled growth allows simulating the growth and dissolution of each ion separately. For the AcO^– growth and dissolution simulations, the Na⁺ ion of the biased dimeric unit was considered as part of the unfinished surface layer.

Figure 2.

Visualization⁶³ of the kink growth simulation setup for Na⁺ grown in pure MeOH solution. The biased kink site is positioned in the center of the upper surface layer. AcO^– and Na⁺ of the unfinished layer are colored in gray and orange, respectively. Atoms of all other ions and molecules are colored in black for carbon, red for oxygen, and green for sodium. MeOHs are shown in faded colors and hydrogens are omitted for clarity.

All simulations were performed with Gromacs 2016.5⁵²⁻⁵⁶ patched with a custom version of Plumed 2.5.0.⁵⁷ Simulations were run at a time integration step of 0.002 ps, whereas the covalent bonds involving hydrogen atoms were constrained with the LINCS algorithm.^55,58 For long-range electrostatics, the particle mesh Ewald algorithm^59,60 was used, and the nonbonded interactions (electrostatic and van der Waals) cutoff was set to 1 nm. The simulations were run at a temperature of T = 298.15 K using the stochastic velocity rescale thermostat⁶¹ in the NVT ensemble. The simulation box lengths were fixed at their average values which were obtained from NPT simulations run at 1 bar pressure using the Parrinello–Rahman barostat.⁶² A simulation time of at least 1.0 μs was necessary to obtain sufficient growth and dissolution events for each ion and to obtain a converged ΔF.

Results

We have measured through experiments and estimated through MD simulations the solubility of sodium acetate in six different solvent–antisolvent mixtures, using the approaches described in the Methodology section.

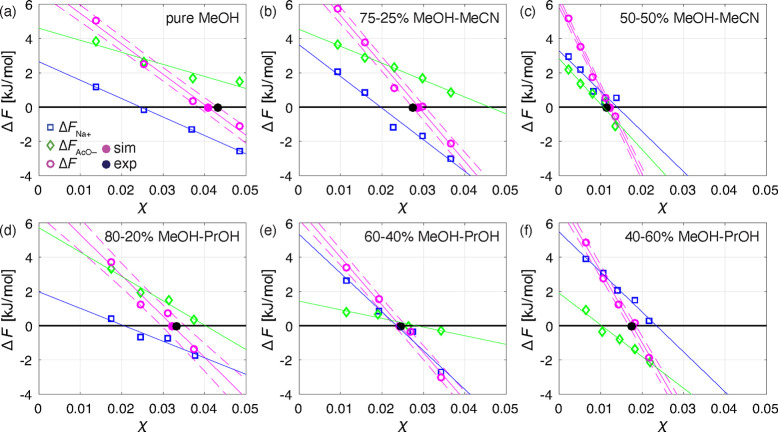
Figure 3 shows the results for all the solution compositions investigated: pure MeOH (panel a), 75–25% MeOH–MeCN (panel b), 50–50% MeOH–MeCN (panel c), 80–20% MeOH–PrOH (panel d), 60–40% MeOH–PrOH (panel e), and 40–60% MeOH–PrOH (panel f). In this figure, ΔF_Na+ corresponds to blue boxes, ΔF_AcO– to green diamonds, and ΔF to purple circles. The blue and green lines are linear regressions of ΔF_Na+ and ΔF_AcO– as functions of χ respectively. We obtain χ_sim^* through linear regression of ΔF as a function of χ, plotted as a purple line, with the corresponding lower and upper bounds of the standard deviation plotted as dashed purple lines (which contain the 68% confidence interval). The estimated solubility, χ_sim, is the intersection point of the regression line with the horizontal axis (the corresponding point is the purple filled circle). The experimental solubilities, χ_exp^*, are plotted as black filled circles. The values obtained through experiments and MD simulations are also listed in Table 1.

Figure 3.

Sampled energy differences between grown and solvated kink sites of Na⁺, ΔF_Na+ (blue boxes), and AcO^–, ΔF_AcO– (green diamonds), as well as the dimeric unit, ΔF = ΔF_Na+ + ΔF_AcO– (purple circles), as a function of NaOAc mole fraction, χ, and compared to the experimental solubility values (black filled circles). Straight purple lines represent the linear regression of ΔF and the dashed lines are the corresponding standard deviations. The blue and green straight lines are the linear regressions of ΔF_Na+ and ΔF_AcO–, respectively. The predicted solubilities (purple filled circles) correspond to the mole fraction at ΔF = 0 obtained through a linear regression of ΔF as a function of χ. The results are shown for the systems of crystalline NaOAc exposed to following solutions: (a) pure MeOH; (b) 75–25% MeOH–MeCN; (c) 50–50% MeOH–MeCN; (d) 80–20% MeOH–PrOH; (e) 60–40% MeOH–PrOH; (f) 40–60% MeOH–PrOH. It is important to note that some of the presented ΔF_Na+ and ΔF_AcO– points are the averages of simulation repetitions (see SI Section S6).

Table 1. Values of the Experimental Solubilities, χ_exp^*, Measured at a Temperature of T = 298.15 K, and the Respective Predicted Solubilities, χ_sim, with the Standard Errors in Parentheses.

		MeOH–MeCN		MeOH–PrOH
	pure MeOH 100%	75–25%	50–50%	80–20%	60–40%	40–60%
χexp* [−]	0.0440	0.0275	0.0113	0.0333	0.0246	0.0175
χsim* [−]	0.0407(24)	0.0288(16)	0.0122(5)	0.0321(26)	0.0244(14)	0.0176(9)

There are a few remarks worth making.

First, in all cases linear regression of the predicted values of ΔF_Na+, ΔF_AcO–, and of their sum, i.e. ΔF, exhibits a satisfactory goodness-of-fit. Therefore, the quantitative and qualitative behaviors of the corresponding trend lines are worth analyzing.

Second, when considering the intersection of the free energy change upon growth of one dimeric unit at the kink site, i.e. ΔF = 0 at the solute solubility concentration, χ_sim^*, one observes that as expected solubility is the highest in pure MeOH, and it decreases with increasing levels of antisolvent in the solution, in the case of both propan-1-ol and acetonitrile.

Third, when comparing the trend lines exhibited by each individual free energy difference in the six different cases illustrated in Figure 3, one can make the following observations: (i) the ΔF trend lines intersect the horizontal axis from right to left obviously in the same sequence as the decreasing values of solubility, χ_sim^*, the steeper the line the lower the solubility; (ii) the ΔF_Na+ values are much less affected by the change in solvent system, with their intersection with the horizontal line ΔF_Na+ = 0 between χ ≈ 0.015 and χ ≈ 0.025; the ΔF_AcO– values are strongly affected by the presence of the antisolvent, with their intersection with the horizontal line ΔF_AcO– = 0 between χ ≈ 0.01 and χ ≈ 0.065 (the high values being those of the systems with MeOH only or with a lot of it, and the low values being associated with the systems with a lot of antisolvent).

Fourth, the last observation can be given a mechanistic interpretation, which is supported by unbiased simulations not reported here for brevity. The adsorption and inclusion of the acetate ion, AcO^–, onto the kink site is strongly affected by the local environment, which is obviously dependent on the solution composition and on the concentration of the antisolvent. In this study, the two antisolvents are bulkier and less polar than methanol, the solvent. As a consequence, the latter tends to occupy the kink site with stronger bonds than the former, thus making it more difficult for the acetate ion to adsorb and to be incorporated in the crystal lattice. The ensuing lower energy difference ΔF_AcO– in the case of higher antisolvent concentrations leads to lower solubility. This is indeed the case, because , as we have observed, adsorption and inclusion of the sodium ion, Na⁺, onto the kink site is rather weakly affected by the presence of the antisolvent and by its concentration, which is possibly because of its tiny size as compared to the acetate ion and to the solvent and antisolvent molecules.

The fifth observation is that, as it is apparent, both in the table and in the figure, the predicted and the measured solubility values are in excellent agreement, the maximum relative difference being 8% for the case 50–50% MeOH–MeCN. The values of solubility predicted by the MD simulations and those measured experimentally match so well despite they have been obtained using two completely different methods, each of which representing a significant novelty in modeling and in experimental characterization.

Finally, it is worth noting that thanks to the NaOAc force fields²⁴ used for the simulations, with proper charge scaling, we are able to accurately predict the experimental melting temperature and thereby the experimental solubility under all conditions explored in this work. This is consistent with our previous observations on estimating the solubility of organic molecules using MD simulations.³

Conclusions

In this work, we present a MD simulation method for the prediction of the solubility of organic salts and validate the predicted solubilities with the experiment outcome. The simulation method focuses on the growth and dissolution of ions at kink sites and identifies the solubility, where the energy difference between the ion-pair crystallized at the kink sites and dissolved in solution equals zero. We showcase the method’s potential by applying it to estimate the solubility of anhydrous sodium acetate in a variety of solvent–antisolvent mixtures. In parallel, we measure the salt’s solubility with an in-house experimental setup, which, coping with the difficulties due to the salt’s strong hygroscopicity, allows us to estimate the solubility under moisture-free conditions. We obtain an excellent agreement between experiments and simulations.

The presented simulation setup is general and can be used to predict solubilities of organic salts in complex growth environments. The method becomes particularly interesting for growth environments, which are very difficult to attain and control experimentally, such as for substances, which are sensitive to air humidity, as in the studied case of anhydrous sodium acetate. Computing solubility using our method can allow significant acceleration and cost-reduction in the estimation of solubility in compounds of interest under varying conditions. These advantages become especially compelling when high throughput endeavors are considered, in particular if nonstandard experimental equipment, such as the one presented here, needs to be utilized. Moreover, with the rapid improvement in accuracy and efficiency of MD simulations because of utilization of GPUs and machine learning based force fields,^64,65 the advantages of using the approach introduced here is bound to increase further substantially.

An interesting application of the simulation method can be in the field of counterion screening. Counterions of organic salt APIs are often screened to tailor the substance’s solubility.² Through simulations, a much clearer picture can be gained on how the particular counterion behaves in the solution and at the kink sites. This in turn can guide and speed up the counterion selection procedure to attain the desired solubility properties of the specific substance in the solution of interest.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c00304.

• Further simulation details (PDF)

The authors declare no competing financial interest.