Abstract
We develop a second-order correction to commonly used density functional approximations (DFAs) to eliminate the systematic delocalization error. The method, based on the previously developed global scaling correction (GSC), is an exact quadratic correction to the DFA for the fractional charge behavior and uses the analytical second derivatives of the total energy with respect to fractional occupation numbers of the canonical molecular orbitals. For small and medium-size molecules, this correction leads to ground-state orbital energies that are a highly accurate approximation to the corresponding quasiparticle energies. It provides excellent predictions of ionization potentials, electron affinities, photoemission spectrum, and photoexcitation energies beyond previous approximate second-order approaches, thus showing potential for broad applications in computational spectroscopy.
Graphical Abstract

The Kohn–Sham density functional theory (DFT)1–3 has experienced much success in modern chemistry, materials science, and physics. Most density functional approximations (DFAs) to the exchange–correlation energy Exc usually produce reasonable total energies for small and medium-size molecules; however, they have major deficiencies in orbital energies. As has been known for a long time, for finite systems, the eigenvalue of the highest occupied molecular orbital (HOMO) for the exact Kohn–Sham potential is equal to the negative of the first ionization potential (IP) for finite systems, based on the asymptotic decay behavior of the exact electron density and the requirement that the Kohn–Sham effective potential be zero at infinity.3 However, in a Kohn–Sham calculation, the local Kohn–Sham potential can have any additive constant and still have the same total energy and density, but different orbital energies. Thus, the argument based on the long-range behavior of density and potential hinges on a particular choice of the additive constant of the potential.
The general physical meaning of orbital energies, for both the HOMO and the lowest unoccupied molecular orbital (LUMO), has been established through three key results. It is based on the property of the total energy functional (approximate or exact). First, the Janak theorem links Kohn–Sham orbital energies to the derivatives of the total energy with respect to the orbital occupation numbers, which were not related to any physical observables.4 Second, the derivatives of the total energy with respect to the total electron number, which are the chemical potentials, are respectively the negative of the first ionization potential (IP) and the first electron affinity (EA) for the exact functional based on the linear condition on the behavior of energy for fractional number of electrons.5 Finally, the chemical potentials were established to be equal to the derivatives of the total energy with respect to the HOMO/LUMO orbital occupation numbers in the Kohn–Sham calculation with exchange–correlation energy being functionals of the density, or the generalized Kohn–Sham calculation with exchange–correlation energy being functionals of the noninteracting one-electron density matrix.6 Combining these theoretical results, the HOMO and LUMO energies are the negative of the first IP and the first EA for electron removal and addition, respectively, as approximated by the corresponding DFA used.6 This physical interpretation of the HOMO and LUMO energies holds true for general molecules and bulk systems with commonly used DFAs. Exceptions occur in some strongly correlated systems when the DFA used has the desired explicit derivative discontinuity.7
Thus, the HOMO and LUMO energies are fully established for the theoretical prediction of the IP and the EA in a DFA calculation. However, conventional DFAs have the systematic error in significantly underestimating the IP and overestimating the EA, and thus the fundamental gap.6,8–10
To describe the systematic error of DFAs, the concept of the delocalization error6,8–10 has been developed, and it can be understood from the perspective of fractional charges.6,8 For systems of small or moderate physical sizes, conventional DFAs usually have good accuracy in total energies when there are integer number of electrons. When there are fractional number of electrons, conventional DFAs, however, violate the Perdew–Parr–Levy–Balduz (PPLB) linearity condition,5,11,12 which states the exact ground-state energy Egs(N) is a linear function of the fractional electron numbers connecting adjacent integer points. Inconsistent with the requirement of the PPLB linearity condition, Egs(N) curves from conventional DFAs are usually convex, with drastic underestimation to the ground-state energies of fractional systems. The convex deviation of conventional DFAs decreases when the systems are larger and vanishes at the bulk limit.8 However, the delocalization error is exhibited in another way, in which the error manifests as too low relative ground-state energies of ionized systems and incorrect linear Egs(N) curves with wrong slopes at the bulk limit.
To reduce the error, enormous efforts have been devoted to the development of new exchange–correlation functionals during last decades. These developments, including global hybrid,13,14 local hybrid,15,16 double-hybrid,17–19 and range-separated functionals,20–25 mainly incorporate a certain amount of Hartree–Fock (HF) exchange in the Exc. The HF exchange exhibits a concave deviation to the linear condition, which is opposite to conventional DFAs and called the localization error.6,8 Some hybrid and range-separated functionals mostly rely on system-dependent tuned parameters.26
There are many other efforts to eliminate the systematical error of DFAs, from the perspective of the delocalization error or from different understandings. Self-interaction error (SIE)27,28 was the first concept to describe the systematic error of DFAs. SIE associates the error to the incomplete cancellation between the electron self-Coulomb and self-exchange energies, which is a different interpretation of the error source compared to the concept of delocalization error. Many approaches have been designed on the basis of correcting SIE,27–34 including the latest development with Fermi localized orbitals.32,34 Beside SIE, there are other approaches developed with the focus on specific properties, such as the Koopmans-compliant functionals,35,36 the generalized transition state,37 and related methods38 extending the straight line condition with Wannier functions for band gap predictions of solid.
Following the understanding of the delocalization error, researchers at the Yang laboratory developed a set of correction methods to conventional DFAs to systematically reduce the delocalization error,39–43 in which the PPLB linearity condition is imposed by applying explicit treatments to systems of fractional charges to restore the correct behavior of Egs(N). Specifically, the global scaling correction (GSC)39 method imposes the PPLB linearity condition globally on the (delocalized) canonical molecular orbital occupation numbers. On the basis of the accurate description of ground-state energies from conventional DFAs for small integer systems, the GSC was designed to preserve the energy of integer systems and correct the convex Egs(N) curve to be linear for fractional systems. It should be noted that the GSC is applicable only for small and moderate-size systems, because the convex deviation of conventional DFAs from the linear line for fractional charges decreases with increasing system size, and the delocalization error manifests as underestimated ground-state energies for integer systems and incorrect linear Egs(N) curves with wrong slopes at the bulk limits.6,8,10 To reduce the delocalization error for large systems, the local scaling correction (LSC) method40 was developed with a focus on the local regions of molecular systems to apply the energy correction locally. Combining the ideas of the GSC and the LSC, the Yang laboratory recently developed the localized orbital scaling correction (LOSC)41–43 to achieve size-consistent and systematic improvement, in which orbitalets, orbitals localized in space and in energy and linearly combining both occupied and virtual orbitals, were developed to apply the global or local corrections adaptively. All these scaling correction methods have shown major improvements in describing challenging properties for conventional DFAs, including IPs, EAs, photoemission spectra, and polarizabilities.41–46
Though the GSC method has its limitations for large and bulk systems, the method is very useful for spectrum properties and excitation energies of small and moderate-size molecules. Therefore, improving the accuracy of GSC can have a significant impact for large areas of DFT applications. In addition, because the GSC and the LOSC become the same for small and moderate-size molecules when the orbital localization does not take place, insight on the GSC can lead to improvements for the LOSC, which is applicable to general systems. To improve the accuracy of the GSC method, Xiao and co-workers developed a correction form that utilizes higher-order density expansions to go beyond the frozen orbital approximation in the original GSC work.47,48 Up to third-order orbital derivatives were calculated, and remarkable improvements were achieved. However, the exchange–correlation component was still treated approximately as the LDA exchange energy, regardless of the DFA used. All contributions39,47,48 to date are approximate second-order corrections to the DFA total energy for fractional-electron systems.
In this work, we present an exact formula for the second-order correction to DFA energies with respect to occupation numbers of canonical molecular orbitals. This constitutes an exact global scaling correction if the convex deviation is quadratic. We will also show that, to be accurate to the second order in the density expansion, only the first-order orbital derivatives are required. The result of this work is an energy correction to DFAs under the framework of GSC but with the exact second-order expansions and much improved accuracy.
To start, we briefly review the methodology of the GSC method.39 The aim of GSC is to correct originally nonstraight E(N) curves produced by DFAs to straight lines, as required by the PPLB linearity condition:
| (1) |
where n is a fraction, 0 ≤ n ≤ 1. Therefore, the GSC energy correction can be easily seen as
| (2) |
According to eqs 1 and 2, the GSC preserves the total energy of integer systems, while it produces corrections to total energies of fractional systems. In the original work of the GSC,39 ΔGSC is evaluated based on the expansion of the density matrix for (N + n) electrons:
| (3) |
To the first order in n, and with the frozen orbital approximation in the Fukui function,49 it can be shown that
| (4) |
where ψf represents the frontier orbital that has fractional occupation nf = n. By inserting the density matrix expansion (eq 4) into eq 2, and keeping terms up to the second order in n, the GSC corrected total energy reads
| (5) |
The approximate expression of the coefficients κ that was derived based the LDA is
| (6) |
in which ρf(r) = |ψf(r)|2 and .39 The first term corresponds to the Coulomb part, and the second term corresponds to the exchange part; the parameter τ is used to balance the contribution of two parts, which is set to 1 in the original work.
The outcome of recovering a linear E(N) curve is the correction to the orbital energies for integer systems with the GSC method. Based on the GSC energy expression (eq 5), the chemical potential associated with the frontier orbital is
| (7) |
where is the frontier orbital energy from the parent DFA, according to the Janak theorem.4 Although κ is dependent on ψf, which further depends on the density matrix and the set of occupation numbers, the contribution from the derivative of vanishes for integer systems, as (nf − nf2) = 0 when nf is either 1 or 0. Thus, eq 7 leads to simple corrections for HOMO/LUMO energies of integer systems with and , which are equal to the negative of IP and EA, respectively, as predicted by the GSC, based on the theoretical developments.5,6
One limitation in the original GSC work is, because the PPLB linearity condition holds only for ground states, the orbital energy correction applies to the HOMO and the LUMO only. In most cases, the HOMO and the LUMO energies are of particular interest, because they are related to IPs, EAs, and thus the fundamental gaps. However, precise descriptions of orbitals other than HOMO/LUMO can also play important roles in certain cases, for example, in calculations of the photoemission spectra and excitation energies from orbital energies.45,50 Therefore, a natural extension to excited states is necessary, and similar constructions for the correction to all orbitals have already been established in LOSC41 and recent work from Xiao and co-workers on GSC.48 To facilitate the discussion of orbitals above LUMO and under the HOMO, we need to extend the ground-state energy E(N), as a function of N, the total number of electrons, to E({npσ}), the total energy as a function of the canonical orbital occupation numbers {npσ}, which can correspond to some excited states. This energy function is what was used in Janak’s work,3,4 and it is given by the following minimum:
| (8) |
where the canonical orbitals {ψpσ} are constrained to be orthogonormal and the density matrix is . Following the same procedure for the cases of HOMO/LUMO and generalizing to all orbitals, the extended definition of the GSC energy correction becomes
| (9) |
The second-order correction term depends on the corresponding orbital density ρpσ = |ψpσ|2, and the coefficients κpσ has the exact same expression as shown in eq 6, except with the ρpσ instead of ρf(r). As a result, the orbital energy corrections are for occupied orbitals and for virtual orbitals.
Although the original GSC has shown great improvements to conventional DFAs for the description of many challenging properties, it is still possible to achieve better accuracy within the GSC framework. Recently, it has been reported that involving higher-order terms to evaluate the response of electron density to the electron number (eq 3) can provide more accurate GSC orbital energies, giving excellent performance for IPs, EAs, and other quasihole energetics.47,48 However, the correlation energy contribution is still missing in the existing approximate expression of κpσ. Furthermore, the exchange part was derived from the LDA only, and directly applying it to GGAs and hybrid functionals may not produce ideal results. It is therefore the goal of this Letter to develop a more accurate form for the GSC, namely, the exact functional expression for {κpσ}.
In this work, instead of considering the density relaxation as in ref 47, we directly deal with the function E({nmτ}) and find the correction to the second order. Consider E({nmτ + δmτ}), where 0 ≤ nmτ + δmτ ≤ 1, and expand the energy function in a Taylor series to the second order in {δmτ}. We have the following relation:
| (10) |
where the partial derivatives are evaluated at δpσ = 0, and contains all terms with order or higher.
In eq 10, we omit the cross terms in the second order, which are discussed in the Supporting Information. The reason for the omission here is that we only need to consider changing one specific occupation number at a time. Particularly, consider only one specific orbital, ψpσ, with a fractional occupation at a time, while the rest of orbitals are fully occupied with {niτ = 1}, i ≠ p or unoccupied with {naτ = 0}, a ≠ p. Denote this set of occupations as [npτ] and its energy as E([npτ]). We now apply eq 10 to the system with an integer number of electrons, with npτ + δpτ = 1 for the N + 1-electron system and with npτ + δpτ = 0 for the N-electron system, and we obtain the total energies of the two integer systems up to the second order with the error in . Substituting the resulting energies of integer systems with the truncation at the second order into eq 2, we obtain the energy correction from the GSC associated with the orbital ψpσ as
| (11) |
which is equally valid for the entire range of occupation, 0 ≤ npτ ≤ 1, with the partial derivative evaluated locally at the corresponding occupation number npτ. The detailed derivation is given in the Supporting Information.
Summing up contributions from all the orbitals, we have
| (12) |
Equation 12 gives the exact second-order correction for the GSC method with the coefficients evaluated as the second-order derivative of the energy with respect to occupation numbers.
Compared to the original GSC, the new formalism in this work, eq 12, naturally involves both the exchange and correlation contribution in Exc in the corrections, applicable to all commonly used DFAs, which was not achieved in previous works. Another difference is that the energy function expansion in this work is directly expanded on occupation numbers, while the original GSC indirectly uses the relaxation of the density matrix. As shown in the Supporting Information, both approaches produce identical results as long as everything is dealt precisely up to the second order. Using the occupation numbers as the direct variables has the advantage of clearer definition and cleaner equations obtained. Using the density matrix as the variable will require the second-order density matrix relaxation, which is also shown to require first-order orbital derivatives only (in contrast to requiring second-order orbital derivatives in previous developments47,48). The reason is that the second-order density matrix relaxation part cancels with other parts to give zero net contributions (see the Supporting Information for details).
In addition, we emphasize that the only approximation for the new formalism shown in eq 12 is the truncation of the energy function at the second order. Because the energy function E({npσ}) has been known to be very close to quadratic,39–42,51–53 such a treatment is clean and reasonable, which is a great advantage compared to the approximate correction derived previously. This new correction from eq 12 also surpasses the previous approximate ones for the case in which the energy function from a DFA is exactly quadratic. Under this condition, the coefficient , from the exact second-order correction, shows the correct behavior, that is being a constant in [N, N + 1]. However, the approximate one varies when the electron number changes, because it is evaluated from canonical orbitals that are from each (N + n)-electron systems. In summary, the GSC with the exact second-order correction shown in eq 12 is capable of restoring the correct linear behavior exactly when the DFA produces a quadratic error in fractional charge and approximately when the error deviates from a quadratic behavior.
Note that the second-order derivatives of the energy with respect to frontier orbital occupation numbers have already been well-established.54 They are recognized as the chemical hardness generated from DFAs,54 and an extension to fractional occupation numbers was also made.55 By using the energy function as defined in eq 8, with similar procedures through the Maxwell relationship and linear response theory, we show that the general second-order derivative of the energy with respect to any occupation number is
| (13) |
| (14) |
where χτυ is the generalized linear response function,54,55 Kστ represents Hartree-exchange–correlation kernels, defined as the functional derivative of , the (generalized) Kohn–Sham Hamiltonian for spin σ with respect to , the Kohn–Sham density matrix for spin τ:
| (15) |
| (16) |
in which Exc is the exchange–correlation energy. Kppσ,qqτ represents the corresponding kernel matrix56
| (17) |
| (18) |
and the matrix element Miaτ,jbυ is defined as
| (19) |
The detailed derivation for the second-order derivative of total energy with respect to occupation number can be found in the Supporting Information. In connection to the chemical hardness, we here call the orbital hardness. It is noteworthy that solving coupled perturbed Kohn–Sham equations can give the same answer, which is also shown in the Supporting Information.
We now examine the physical meaning of the orbital hardness (shown in the Supporting Information with details). The associated 4-point generalized dielectric function εστ can be defined as
| (20) |
where vτ(r3, r4) is the generalized external potential, which is nonlocal and spin-dependent, as an extension from the physical potential, v(r), which is local and spin-independent, first introduced in ref 55. Then, the expression of eq 13 for the orbital hardness leads to its interpretation as the interaction of orbitals through the 4-point generalized screened interaction
| (21) |
The 4-point generalized functions, χτυ, (ε−1)συ, and Wσζ are the natural extensions of the corresponding spinless two-point functions commonly used in many-body perturbation theory.57
Note that the matrix Miaτ,jbυ in eq 14 involves all the pairs of occupied and virtual orbitals, which gives the dimension of , with being the number of occupied orbitals and being the number of virtual orbitals for τ spin. Therefore, directly evaluating eq 14 has the computational complexity of 𝒪((NoccNvir)3). If only a few orbital energies, like the frontier orbitals, are of interest in practice, one can evaluate the second-order derivative numerically to bypass the analytical expression, which is a shortcut to reduce the computation to be several times of SCF calculations, or one can use efficient iterative solution to linear equations of the coupled perturbed Kohn–Sham approach, instead of matrix inversion for the associated orbitals, which has lower computational complexity of 𝒪((NoccNvir)2).
In the following, we present the results to show the performance of the new expression for the GSC with the analytical and exact second-order corrections (denoted as GSC2). The original GSC39 with the approximate coefficients κpσ is denoted as GSC1. Because the effective Hamiltonian from the GSC method for integer systems is a projection operator consisting of canonical orbitals from the associated DFA, the GSC method does not change the canonical orbitals, the eigenstates for the associated DFA Hamiltonian, and applying the GSC method with a post-SCF or SCF manner produces identical results. Therefore, all the calculations of GSC1 and GSC2 are performed with the post-SCF calculation for the purpose of efficiency. Details for the calculations, numerical results, and more clarification to the SCF calculations of the GSC method are documented in the Supporting Information.
The E(N) curve comes to our attention first because the goal of the GSC method is to make it linear. Figure 1 shows the E(N) curve of the F atom with BLYP as the parent DFA for the calculations of GSC1 and GSC2. The BLYP functional shows great delocalization errors, while the GSC1-BLYP with the approximate correction overcorrected and showed the localization errors. With the exact second-order correction, GSC2-BLYP is capable of producing mostly linear behavior for the E(N) curve with much smaller errors.
Figure 1.

Total energies of F atom from BLYP, GSC1-BLYP, and GSC2-BLYP: (a) total energy versus electron number; (b) total energy difference versus electron number, ΔE(N) = EDFA(N) − Elinear. aug-cc-pVTZ is used as the basis set.
The first IPs and EAs are part of the main outcome from the GSC method, because for integer systems only orbital energies get corrected. The quality of IPs and EAs can reflect the performance of the correction, and thus, they are worthwhile to be examined. The first IP and EA of an N-electron system can be evaluated with the negative HOMO and LUMO energies of the N-electron system, which are associated with one-electron removal and one-electron addition processes, respectively.6 For the purpose of comparison, the Δ-SCF method is conducted as well to evaluate the first IPs and EAs, in which the energy differences are calculated, i.e., EIP = E(N − 1) − E(N) for IPs and EEA = E(N) − E(N + 1) for EAs. The test sets for the first IPs and EAs are taken from ref 43. Experimental data are used as the reference to evaluate the mean absolute error (MAE).
According to Figure 2, both GSC1 and GSC2 greatly improve the quality of the first IPs and EAs upon associated parent DFAs, and the GSC2 apparently outperforms the approximate GSC1. Taking B3LYP as an example, the MAE of the first IPs/EAs predicted from the calculations of N-electron systems is 0.20/0.17 eV for GSC2 and 0.41/0.38 eV for GSC1, where the errors get nearly halved in the new approach GSC2. In addition, the GSC2 produces results that are close to those from the Δ-SCF method, while this is not the case for the approximate GSC1 approach. This indicates that the GSC method with exact second-order derivatives has a more systematic and accurate correction to the DFA E(N) curve, producing mostly linear curves for all these systems and thus good IPs/EAs.
Figure 2.
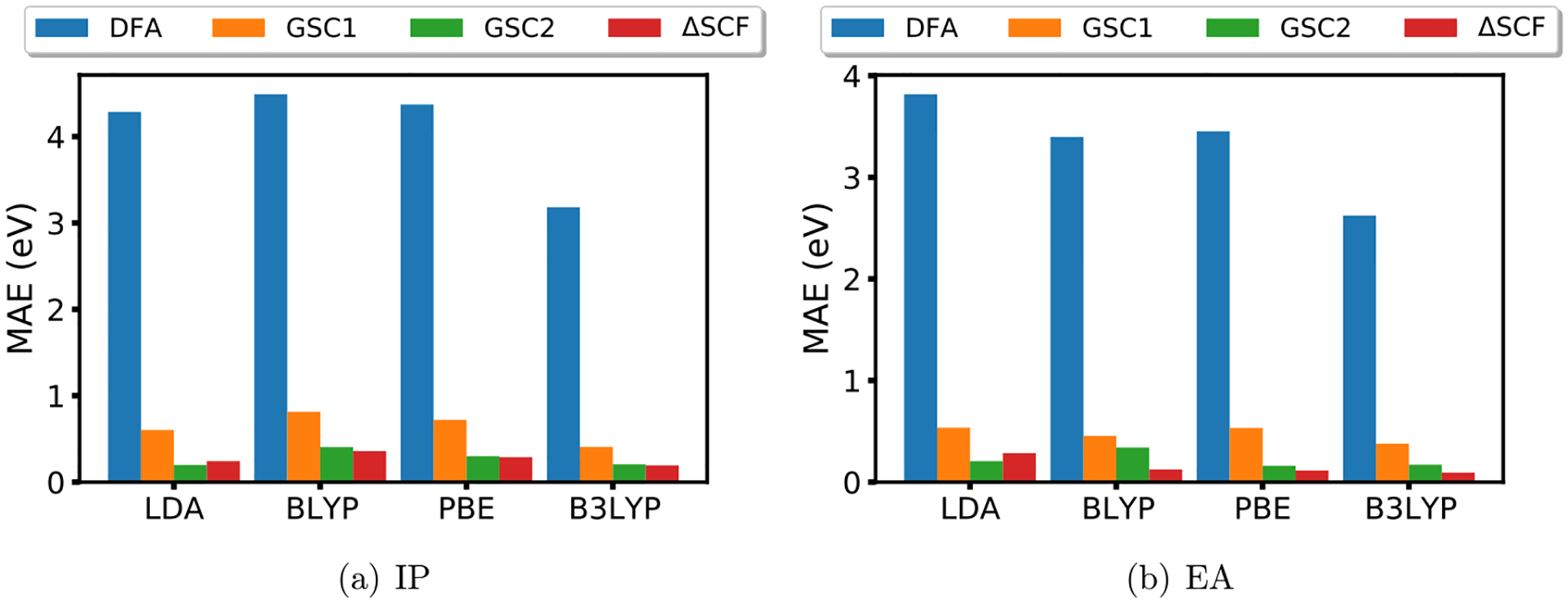
Mean absolute error in eV for the first (a) IPs (64 cases) and (b) EAs (39 cases) obtained from different methods.
Besides evaluating the first IP and EA of an N-electron system from the negative HOMO and LUMO energy of an N-electron system, one can also approximate the first IP with the negative LUMO energy of the (N − 1)-electron system (associated with a one-electron addition process), and the first EA with the negative HOMO energy of the (N + 1)-electron system (associated with a one-electron removal process). Similar results are observed from these two approaches, and the detailed results are shown in the Supporting Information.
Next, we examine the prediction of other quasiparticle energies besides the first IPs and EAs. The PPLB linearity condition defines for the first IPs and EAs only; it is still worthy to investigate quasihole or quasiparticle energies other than the HOMO or LUMO. A parallel extension to quasihole/quasiparticle energies with orbital energies other than the HOMO or LUMO has been assumed and applied with numerical success.45 These quasihole energies are predicted by the negative orbital energies of the corresponding occupied orbitals of the N-electron systems from DFT calculations. We use the same set of molecules as in ref 48 to test the performance of the GSC method. Experimental data are used as references. As shown in Figure 3, conventional DFAs produce significant errors, while the GSC method corrects the orbital energies to have an MAE that is below 1 eV. In addition, GSC2 outperforms GSC1 as expected. For example, the MAE from GSC1 is 0.63 eV, while GSC2 gives 0.32 eV.
Figure 3.

Quasihole energies (52 cases from 11 small molecules) of the N-electron systems evaluated by the corresponding negative occupied orbital energies (−ϵi) from different DFAs: (a) the MAEs for different DFAs, GSC1-DFAs, and GSC2-DFAs. (b) Experimental quasihole energies versus the negative orbital energies from B3LYP, GSC1-B3LYP, and GSC2-B3LYP.
The photoemission spectra is another good source to evaluate the quality of orbital energies. We select 10 organic molecules with small or moderate sizes from ref 45 to test. Experimental spectra are used as the reference. Besides the DFT calculations, we also conduct GW (G0W0) and eigenvalue self-consistent GW (evGW) calculations to obtain the quasiparticle energies. The calculated spectra are obtained from the Gaussian expansion of calculated quasiparticle energies with a standard deviation of 0.2 eV. Figure 4 shows the results for two representative molecules, maleic anhydride and benzonitrile. It can be seen that GSC2 consistently outperforms the approximate GSC1, as the peaks align better to experimental references and have good agreement with those from GW calculations. The spectra of additional molecules tested can be found in the Supporting Information.
Figure 4.

Photoemission spectrum for (a) maleic anhydride and (b) benzonitrile. Experimental spectrum was obtained from ref 58 for panel a and ref 59 for panel b. Calculations for GSC1, GSC2, and GW were associated with PBE60 functional.
The benchmark for low-lying excitation energies from the QE-DFT method45,50 is also carried out. The excitation energy in QE-DFT is computed as the difference between two corresponding (generalized) Kohn–Sham orbital energies. We use the test set provided by ref 45 to calculate the first and second singlet and triplet excitation energies. The results from the Δ-SCF method and time-dependent DFT with B3LYP functional are taken from ref 45 for comparison. As shown in Figure 5, the QE-GSC2 produces improved excitation energies compared to QE-GSC1. In particular, the results from QE-GSC2 are comparable to those from Δ-SCF-B3LYP. In addition, GSC2-B3LYP shows comparable performance to TD-B3LYP. This shows a potential application for the original GSC and the GSC2 form developed in this work, as multiple excited states are immediately accessible after only one calculation.
Figure 5.

Mean absolute error (in eV) for the low-lying excitation energies from various QE-DFAs, Δ-B3LYP, and TD-B3LYP. The excitation includes 19 cases of triplet states and 25 cases of singlet states. The reference data were calculated from high-level wave function methods, and results for Δ-B3LYP and TD-B3LYP were taken from ref 45.
Although there are great improvements from the GSC method to the associated DFAs, it should be noted that the GSC method has its intrinsic limitations. The delocalization error cannot be corrected effectively under the framework of the GSC method for systems with large size, and there is no GSC correction at all for bulk systems, which are clearly demonstrated with calculations for the hydrogen chain and the helium cluster.8,41 For these scenarios, the LOSC method is designed by using the orbitalets that can dynamically switch between the canonical orbitals and localized orbitals to systematically reduce the delocalization error.41,42 Note that the formalism of LOSC is generalized based on the original GSC work with the approximate corrections.41,42 Therefore, if there is no localization and the orbitalets are just the canonical orbitals, the LOSC method would become the same as the original GSC approach.41,42
To investigate the size dependence for the application of the GSC method, we selected many real molecules with the equilibrium structures and various sizes ranging from small systems, like water (H2O), to large systems, like fullerene (C60). Then we calculated the first IPs of these molecules from GSC1, GSC2, and the latest version of LOSC42 for comparison. The error distribution over the number of atoms is plotted in Figure 6. According to Figure 6, we see GSC2 outperforms GSC1 regardless of the molecular size, because of the exact second-order correction instead of the approximated one. In addition, the comparison between GSC2 and LOSC clearly shows the size dependence of the GSC method. For systems with less than about 20 atoms, GSC2 shows better accuracy than LOSC. This is because the orbitalets used in LOSC are more like canonical orbitals, and the LOSC at these scenarios is close to the original GSC with approximate second-order corrections. For systems larger than about 20 atoms, we observe the opposite behavior that LOSC shows better accuracy. This is because the LOSC at these scenarios characterizes the delocalization error more effectively than the GSC method, in which the orbitalets used in LOSC are more localized than the canonical orbitals. This observation also suggests that developing more accurate correction in the scheme of LOSC, like the exact second-order correction in GSC2, would further improve the performance of the LOSC for large and complex systems.
Figure 6.

Error distribution of first IPs obtained from GSC1, GSC2, and LOSC for molecules with different sizes.
In conclusion, we have developed further the global scaling correction method with analytical and exact second-order energy corrections to better deal with delocalization errors existing in conventional DFAs. With the application of the exact second-order correction in the GSC method, we demonstrated the excellent performance of the GSC2 approach to describe the first IPs, EAs, other quasihole/quasiparticle energies, and low-lying excitation energies, which are all obtained from accurate (generalized) KS orbital energies in ground-state calculations.
Supplementary Material
ACKNOWLEDGMENTS
Y.M. and Z.C. acknowledge the support from the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R01-GM061870. W.Y. acknowledges the support from the National Science Foundation (Grant No. CHE-1900338). Y.M. was also supported by the Shaffer-Hunnicutt Fellowship, and Z.C. was supported by the Kathleen Zielik Fellowship from Duke University.
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c01962.
Mathematical derivations for the coupled perturbed equations, alternative derivations for energy second-order derivative, comparison between using density matrix as the direct variable and using occupation numbers as the direct variable, computational details, and numerical results (PDF)
Complete contact information is available at: https://pubs.acs.org/10.1021/acs.jpclett.1c01962
The authors declare no competing financial interest.
Contributor Information
Yuncai Mei, Department of Chemistry, Duke University, Durham, North Carolina 27708, United States.
Zehua Chen, Department of Chemistry, Duke University, Durham, North Carolina 27708, United States.
Weitao Yang, Department of Chemistry and Department of Physics, Duke University, Durham, North Carolina 27708, United States.
REFERENCES
- (1).Hohenberg P; Kohn W Inhomogeneous Electron Gas. Phys. Rev 1964, 136, B864–B871. [Google Scholar]
- (2).Kohn W; Sham LJ Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev 1965, 140, A1133–A1138. [Google Scholar]
- (3).Parr RG; Yang W Density-Functional Theory of Atoms and Molecules; International Series of Monographs on Chemistry; Oxford University Press: Oxford, NY, 1989. [Google Scholar]
- (4).Janak JF Proof That δE/δNi = ε in Density-Functional Theory. Phys. Rev. B: Condens. Matter Mater. Phys 1978, 18, 7165–7168. [Google Scholar]
- (5).Perdew JP; Parr RG; Levy M; Balduz JL Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy. Phys. Rev. Lett 1982, 49, 1691–1694. [Google Scholar]
- (6).Cohen AJ; Mori-Sánchez P; Yang W Fractional Charge Perspective on the Band Gap in Density-Functional Theory. Phys. Rev. B: Condens. Matter Mater. Phys 2008, 77, 115123. [Google Scholar]
- (7).Mori-Sánchez P; Cohen AJ; Yang W Discontinuous Nature of the Exchange-Correlation Functional in Strongly Correlated Systems. Phys. Rev. Lett 2009, 102, 066403. [DOI] [PubMed] [Google Scholar]
- (8).Mori-Sánchez P; Cohen AJ; Yang W Localization and Delocalization Errors in Density Functional Theory and Implications for Band-Gap Prediction. Phys. Rev. Lett 2008, 100, 146401. [DOI] [PubMed] [Google Scholar]
- (9).Cohen AJ; Mori-Sánchez P; Yang W Insights into Current Limitations of Density Functional Theory. Science 2008, 321, 792–794. [DOI] [PubMed] [Google Scholar]
- (10).Cohen AJ; Mori-Sánchez P; Yang W Challenges for Density Functional Theory. Chem. Rev 2012, 112, 289–320. [DOI] [PubMed] [Google Scholar]
- (11).Yang W; Zhang Y; Ayers PW Degenerate Ground States and a Fractional Number of Electrons in Density and Reduced Density Matrix Functional Theory. Phys. Rev. Lett 2000, 84, 5172–5175. [DOI] [PubMed] [Google Scholar]
- (12).Zhang Y; Yang W In Theoretical Chemistry Accounts: New Century Issue; Cramer CJ, Truhlar DG, Eds.; Springer: Berlin, 2001; pp 346–348. [Google Scholar]
- (13).Adamo C; Barone V Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0Model. J. Chem. Phys 1999, 110, 6158–6170. [Google Scholar]
- (14).Lee C; Yang W; Parr RG Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
- (15).Jaramillo J; Scuseria GE; Ernzerhof M Local Hybrid Functionals. J. Chem. Phys 2003, 118, 1068–1073. [Google Scholar]
- (16).Arbuznikov AV; Kaupp M Local Hybrid Exchange-Correlation Functionals Based on the Dimensionless Density Gradient. Chem. Phys. Lett 2007, 440, 160–168. [Google Scholar]
- (17).Grimme S Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys 2006, 124, 034108. [DOI] [PubMed] [Google Scholar]
- (18).Zhang Y; Xu X; Goddard WA Doubly Hybrid Density Functional for Accurate Descriptions of Nonbond Interactions, Thermochemistry, and Thermochemical Kinetics. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 4963–4968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Su NQ; Yang W; Mori-Sánchez P; Xu X Fractional Charge Behavior and Band Gap Predictions with the XYG3 Type of Doubly Hybrid Density Functionals. J. Phys. Chem. A 2014, 118, 9201–9211. [DOI] [PubMed] [Google Scholar]
- (20).Savin A; Flad H-J Density Functionals for the Yukawa Electron-Electron Interaction. Int. J. Quantum Chem 1995, 56, 327–332. [Google Scholar]
- (21).Savin A In Recent Developments and Applications of Modern Density Functional Theory; Theoretical and Computational Chemistry; Seminario JM, Ed.; Elsevier, 1996; Vol. 4, pp 327–357. [Google Scholar]
- (22).Iikura H; Tsuneda T; Yanai T; Hirao K A Long-Range Correction Scheme for Generalized-Gradient-Approximation Exchange Functionals. J. Chem. Phys 2001, 115, 3540–3544. [Google Scholar]
- (23).Yanai T; Tew DP; Handy NC A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett 2004, 393, 51–57. [Google Scholar]
- (24).Vydrov OA; Scuseria GE Assessment of a Long-Range Corrected Hybrid Functional. J. Chem. Phys 2006, 125, 234109. [DOI] [PubMed] [Google Scholar]
- (25).Chai J-D; Head-Gordon M Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys 2008, 10, 6615–6620. [DOI] [PubMed] [Google Scholar]
- (26).Baer R; Livshits E; Salzner U Tuned Range-Separated Hybrids in Density Functional Theory. Annu. Rev. Phys. Chem 2010, 61, 85–109. [DOI] [PubMed] [Google Scholar]
- (27).Perdew JP; Zunger A Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B: Condens. Matter Mater. Phys 1981, 23, 5048–5079. [Google Scholar]
- (28).Mori-Sánchez P; Cohen AJ; Yang W Many-Electron Self-Interaction Error in Approximate Density Functionals. J. Chem. Phys 2006, 125, 201102. [DOI] [PubMed] [Google Scholar]
- (29).Mori-Sánchez P; Cohen AJ; Yang W Self-Interaction-Free Exchange-Correlation Functional for Thermochemistry and Kinetics. J. Chem. Phys 2006, 124, 091102. [DOI] [PubMed] [Google Scholar]
- (30).Perdew JP; Staroverov VN; Tao J; Scuseria GE Density Functional with Full Exact Exchange, Balanced Nonlocality of Correlation, and Constraint Satisfaction. Phys. Rev. A: At., Mol., Opt. Phys 2008, 78, 052513. [Google Scholar]
- (31).Schmidt T; Kraisler E; Kronik L; Kümmel S One-Electron Self-Interaction and the Asymptotics of the Kohn–Sham Potential: An Impaired Relation. Phys. Chem. Chem. Phys 2014, 16, 14357–14367. [DOI] [PubMed] [Google Scholar]
- (32).Pederson MR; Ruzsinszky A; Perdew JP Communication: Self-Interaction Correction with Unitary Invariance in Density Functional Theory. J. Chem. Phys 2014, 140, 121103. [DOI] [PubMed] [Google Scholar]
- (33).Schmidt T; Kümmel S One- and Many-Electron Self-Interaction Error in Local and Global Hybrid Functionals. Phys. Rev. B: Condens. Matter Mater. Phys 2016, 93, 165120. [Google Scholar]
- (34).Yang Z.-h.; Pederson MR; Perdew JP Full Self-Consistency in the Fermi-Orbital Self-Interaction Correction. Phys. Rev. A: At., Mol., Opt. Phys 2017, 95, 052505. [Google Scholar]
- (35).Borghi G; Ferretti A; Nguyen NL; Dabo I; Marzari N Koopmans-Compliant Functionals and Their Performance against Reference Molecular Data. Phys. Rev. B: Condens. Matter Mater. Phys 2014, 90, 075135. [Google Scholar]
- (36).Colonna N; Nguyen NL; Ferretti A; Marzari N Koopmans-Compliant Functionals and Potentials and Their Application to the GW100 Test Set. J. Chem. Theory Comput 2019, 15, 1905–1914. [DOI] [PubMed] [Google Scholar]
- (37).Anisimov VI; Kozhevnikov AV Transition State Method and Wannier Functions. Phys. Rev. B: Condens. Matter Mater. Phys 2005, 72, 075125. [Google Scholar]
- (38).Ma J; Wang L-W Using Wannier Functions to Improve Solid Band Gap Predictions in Density Functional Theory. Sci. Rep 2016, 6, 24924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Zheng X; Cohen AJ; Mori-Sánchez P; Hu X; Yang W Improving Band Gap Prediction in Density Functional Theory from Molecules to Solids. Phys. Rev. Lett 2011, 107, 026403. [DOI] [PubMed] [Google Scholar]
- (40).Li C; Zheng X; Cohen AJ; Mori-Sánchez P; Yang W Local Scaling Correction for Reducing Delocalization Error in Density Functional Approximations. Phys. Rev. Lett 2015, 114, 053001. [DOI] [PubMed] [Google Scholar]
- (41).Li C; Zheng X; Su NQ; Yang W Localized Orbital Scaling Correction for Systematic Elimination of Delocalization Error in Density Functional Approximations. Natl. Sci. Rev 2018, 5, 203–215. [Google Scholar]
- (42).Su NQ; Mahler A; Yang W Preserving Symmetry and Degeneracy in the Localized Orbital Scaling Correction Approach. J. Phys. Chem. Lett 2020, 11, 1528–1535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Mei Y; Chen Z; Yang W Self-Consistent Calculation of the Localized Orbital Scaling Correction for Correct Electron Densities and Energy-Level Alignments in Density Functional Theory. J. Phys. Chem. Lett 2020, 11, 10269–10277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Mei Y; Li C; Su NQ; Yang W Approximating Quasiparticle and Excitation Energies from Ground State Generalized Kohn-Sham Calculations. arXiv [physics.chem-ph] 2019, 1810.09906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Mei Y; Li C; Su NQ; Yang W Approximating Quasiparticle and Excitation Energies from Ground State Generalized Kohn–Sham Calculations. J. Phys. Chem. A 2019, 123, 666–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Mei Y; Yang N; Yang W Describing Polymer Polarizability with Localized Orbital Scaling Correction in Density Functional Theory. J. Chem. Phys 2021, 154, 054302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Zhang D; Zheng X; Li C; Yang W Orbital Relaxation Effects on Kohn–Sham Frontier Orbital Energies in Density Functional Theory. J. Chem. Phys 2015, 142, 154113. [DOI] [PubMed] [Google Scholar]
- (48).Yang X; Zheng X; Yang W Density Functional Prediction of Quasiparticle, Excitation, and Resonance Energies of Molecules With a Global Scaling Correction Approach. Front. Chem 2020, 8, 979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Parr RG; Yang W Density Functional Approach to the Frontier-Electron Theory of Chemical Reactivity. J. Am. Chem. Soc 1984, 106, 4049–4050. [Google Scholar]
- (50).Mei Y; Yang W Excited-State Potential Energy Surfaces, Conical Intersections, and Analytical Gradients from Ground-State Density Functional Theory. J. Phys. Chem. Lett 2019, 10, 2538–2545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Cococcioni M; de Gironcoli S Linear Response Approach to the Calculation of the Effective Interaction Parameters in the LDA + U Method. Phys. Rev. B: Condens. Matter Mater. Phys 2005, 71, 035105. [Google Scholar]
- (52).Bajaj A; Janet JP; Kulik HJ Communication: Recovering the Flat-Plane Condition in Electronic Structure Theory at Semi-Local DFT Cost. J. Chem. Phys 2017, 147, 191101. [DOI] [PubMed] [Google Scholar]
- (53).Hait D; Head-Gordon M Delocalization Errors in Density Functional Theory Are Essentially Quadratic in Fractional Occupation Number. J. Phys. Chem. Lett 2018, 9, 6280–6288. [DOI] [PubMed] [Google Scholar]
- (54).Yang W; Cohen AJ; De Proft F; Geerlings P Analytical Evaluation of Fukui Functions and Real-Space Linear Response Function. J. Chem. Phys 2012, 136, 144110. [DOI] [PubMed] [Google Scholar]
- (55).Peng D; Yang W Fukui Function and Response Function for Nonlocal and Fractional Systems. J. Chem. Phys 2013, 138, 184108. [DOI] [PubMed] [Google Scholar]
- (56).Hirata S; Head-Gordon M Time-Dependent Density Functional Theory for Radicals: An Improved Description of Excited States with Substantial Double Excitation Character. Chem. Phys. Lett 1999, 302, 375–382. [Google Scholar]
- (57).Martin RM; Reining L; Ceperley DM Interacting Electrons; Cambridge University Press, 2016. [Google Scholar]
- (58).Knight JW; Wang X; Gallandi L; Dolgounitcheva O; Ren X; Ortiz JV; Rinke P; Körzdörfer T; Marom N Accurate Ionization Potentials and Electron Affinities of Acceptor Molecules III: A Benchmark of GW Methods. J. Chem. Theory Comput 2016, 12, 615–626. [DOI] [PubMed] [Google Scholar]
- (59).Kimura KK Handbook of HeI Photoelectron Spectra of Fundamental Organic Molecules; Halsted Press, 1981. [Google Scholar]
- (60).Perdew JP; Burke K; Ernzerhof M Generalized Gradient Approximation Made Simple. Phys. Rev. Lett 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


