Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Aug 1;34(15):6883–6893. doi: 10.1021/acs.chemmater.2c01282

High-Throughput Selection and Experimental Realization of Two New Ce-Based Nitride Perovskites: CeMoN3 and CeWN3

Rachel Sherbondy †,‡,*, Rebecca W Smaha †, Christopher J Bartel , Megan E Holtz ‡, Kevin R Talley †, Ben Levy-Wendt §,∥, Craig L Perkins †, Serena Eley ⊥, Andriy Zakutayev †,*, Geoff L Brennecka ‡,*
PMCID: PMC9367680  PMID: 35965892

Abstract

graphic file with name cm2c01282_0008.jpg

Nitride perovskites have only been experimentally realized in very few cases despite the widespread existence and commercial importance of perovskite materials. From oxide perovskites used in ultrasonics to halide perovskites that have revolutionized the photovoltaics industry, the discovery of new perovskite materials has historically impacted a wide number of fields. Here, we add two new perovskites, CeWN3 and CeMoN3, to the list of experimentally realized perovskite nitrides using high-throughput computational screening and subsequent high-throughput thin film growth techniques. Candidate compositions are first down-selected using a tolerance factor and then thermochemical stability. A novel competing fluorite-family phase is identified for both material systems, which we hypothesize is a transient intermediate phase that crystallizes during the evolution from an amorphous material to a stable perovskite. Different processing routes to overcome the competing fluorite phase and obtain phase-pure nitride perovskites are demonstrated for the CeMoN3–x and CeWN3–x material systems, which provide a starting point for the development of future nitride perovskites. Additionally, we find that these new perovskite phases have interesting low-temperature magnetic behavior: CeMoN3–x orders antiferromagnetically below TN ≈ 8 K with indications of strong magnetic frustration, while CeWN3–x exhibits no long-range order down to T = 2 K but has strong antiferromagnetic correlations. This work demonstrates the importance and effectiveness of using high-throughput techniques, both computational and experimental: they are integral to optimize the process of realizing two entirely novel nitride perovskites.

Introduction

As chemists and materials scientists expand the palette of available materials, interest in new nitrides continues to grow.1,2 The perovskite structure, with the basic formula ABX3, underlies the properties and function of materials crucial to fields including solar research, ultrasonics, fuel cells, and many more, but there is a notable lack of reported nitrides with the perovskite structure. A few recent computational studies have predicted the stability of rare earth transition metal nitride perovskites3−6 and interesting ferroic properties such as ferroelectricity in LaWN3 and ferromagnetism in a broad range of REMN3 (RE = rare earth; M = W, Re) compounds.7,8 Experimental reports are quite limited and frequently resulted instead in oxynitrides, though these too have been shown to exhibit a variety of interesting properties, from electrochemical activity to colossal magnetoresistance.9−15 In contrast, a number of nitrogen-containing antiperovskites have been successfully synthesized.16

The paucity of nitride perovskites reflects the difficulty of synthesizing oxygen-free phases in these systems. However, recent work from our team,17 realizing thin film perovskite LaWN3, and from Kloß et al.,18 synthesizing bulk perovskite LaReN3, has paved the way for additional investigations into nitride perovskites. LaWN3 was grown in thin film form as an oxygen-free, polar rhombohedral perovskite phase that exhibited a strong piezoelectric response;17 the use of an activated nitrogen plasma increased the chemical potential of nitrogen, which has been shown to aid the stabilization of nitrides.19 LaReN3, which exhibits metallic conductivity and Pauli paramagnetism, was synthesized via high pressure–high temperature methods and crystallized in triclinic symmetry because of orbital ordering distortions, despite a Goldschmidt tolerance factor of 0.99, which would normally suggest cubic symmetry.18 These recent studies provide motivation and potential approaches to expand the phase space of nitride perovskites.

The present work focuses on experimental realization of new nitride perovskites in thin film form following a high-throughput materials investigation scheme, which has been successful in uncovering many new ternary nitride compounds.1,2,15,20−30 We first identify likely candidates via a computational screening process using a recent radii-based method developed by a portion of our team31 to predict the likelihood of each candidate forming in a perovskite structure—improving upon the Goldschmidt tolerance factor32—followed by density functional theory (DFT) calculations to predict their stability.

Six pairs of A- and B-site cations computationally identified as likely to form stable nitride perovskites are experimentally explored in initial combinatorial thin film libraries with intentional chemical gradients to ensure the presence of a 1:1 cation ratio without the need for multiple synthesis experiments for each chemistry. Throughout this manuscript, ABN3 refers to the ideal perovskite phase of that composition. In experimentally realized films, we use ABN3–x to designate the perovskite phase with unknown anion versus cation stoichiometry. We use (A,B)N3–x to refer to the overall compositionally graded films.

Two compositions, CeMoN3 and CeWN3, are selected for further study. Initial growths of these two compounds exhibit a mixture of phases, fluorite family and perovskite family, and we posit that the fluorite phase is an intermediate stabilized by defects and/or cation disorder. We investigate different synthetic routes for achieving phase-pure perovskite by overcoming this competing fluorite phase. This joint computational and experimental study results in the growth of two new nitride perovskites CeMoN3–x and CeWN3–x in thin film form, and we characterize their structure and composition as well as their low-temperature magnetic properties.

Methods Section

Computational Methods

To generate a theoretical library of potential ABN3 perovskites, we considered 39 A/B cations—Li, Na, K, Rb, Cs, Mg, Ca, Sr, Ba, Sc, Y, Ti, Zr, Hf, La, Ce, V, Nb, Ta, Cr, Mo, W, Mn, Fe, Co, Ni, Pd, Pt, Cu, Ag, Au, Zn, Al, Ga, In, C, Si, Ge, and Sn. These cations were applied combinatorically to generate 741 ABN3 formulas. Oxidation states for each formula were assigned automatically using the approach described in ref (31). Ionic radii were then assigned for each ion using the table provided by Shannon,33 allowing for the application of radii-based descriptors (Goldschmidt’s tolerance factor, the octahedral factor, and the recently introduced tolerance factor τ31). In the perovskite structure, the anion is 6-fold coordinated, but Shannon’s table of effective ionic radii does not provide an ionic radius for N3– in a 6-fold coordination. We therefore increased the provided 4-fold coordination radius of 1.46 Å to 1.54 Å to account for the 6-fold coordination environment using the following relation from ref (34):

graphic file with name cm2c01282_m001.jpg 1

where x = 4 has a known radius of 1.46 Å for N3–, allowing the calculation of the radius of 1.54 Å for x = 6 for N3–. The descriptor values are provided in Table S1 in the Supporting Information for all 189 charge-balanced ABN3 compositions.

For all 9 of the ABN3 compounds predicted to be stable as perovskites on the basis of the radii-based descriptors that are listed in Table 1, we used density functional theory (DFT) to support their stabilities in the perovskite structure and calculate some basic electronic properties. All DFT calculations were performed using the projector augmented wave method35,36 as implemented in the Vienna ab initio simulation package (VASP).37 For initial calculations on these 9 compounds, we used the generalized gradient approximation (GGA) as implemented by Perdew, Burke, and Ernzerhof (PBE).38 We calculated the thermodynamic stability of each phase relative to all stable compounds in each A-B-N chemical space available in the Materials Project.39 Formation enthalpies, ΔHf, were calculated using elemental reference energies computed in ref (40). Decomposition enthalpies, ΔHd, were computed using the convex hull formalism.41 Each ABN3 composition was initialized in 2 × 2 × 2 supercells of the cubic perovskite structure with random perturbations of 0.2 Å applied to each ion to break symmetry.42 Geometry optimizations were performed using spin-polarized calculations with an initial high-spin ferromagnetic configuration, a plane wave energy cutoff of 520 eV, and a Γ-centered Monkhorst–Pack k-point grid with 25|bi| discretizations along each reciprocal lattice vector. Additional antiferromagnetic (AFM) configurations were also sampled for orthorhombic CeMoN3 and CeWN3. For all calculations, electronic iterations were converged to 10–6 eV and ionic iterations were converged to 0.02 eV/Å.

Table 1. Summary of Stability and Predicted Properties for 9 Compositions Evaluated for Viability as Nitride Perovskitesa.

formula P(τ) t μ ΔHf (eV/atom) ΔHd (eV/atom) Eg (eV) Egd (eV)
CeNbN3 1.00 0.87 0.42 –1.132 –0.086 0.63 0.63
CeTaN3 1.00 0.87 0.42 –1.314 –0.115 0.65 0.65
CeMoN3 0.98 0.96 0.38 –0.887 –0.133 metal metal
CeWN3 0.98 0.95 0.39 –1.021 –0.249 metal metal
LaMoN3 0.98 0.96 0.38 –0.867 –0.182 0.55 0.55
LaWN3 0.98 0.96 0.39 –1.011 –0.309 1.11 1.11
YMoN3 0.94 0.87 0.38 –0.870 –0.023 1.18 1.30
YWN3 0.94 0.86 0.39 –0.998 –0.135 1.07 1.18
InMoN3 0.55 0.82 0.38 0.212 0.368 1.00 1.02
Open in a new tab
a

P(τ) is the probability of forming the perovskite on the basis of the recently introduced tolerance factor, τ (values > 0.5 indicate perovskite). t is Goldschmidt’s tolerance factor, with values between 0.8 and 1.1 usually indicating perovskite is plausible. μ is the octahedral factor, where values > 0.38 indicate the B cation can likely be coordinated by at least six anions. ΔHf is the formation enthalpy, ΔHd is the decomposition enthalpy, Eg is the band gap, and Egd the direct band gap, all computed with PBE.38.

For detailed investigations into CeMoN3 and CeWN3, the r2SCAN meta-GGA density functional43 was used with an increased plane wave energy cutoff of 680 eV. These compounds were calculated in the cubic, orthorhombic, tetragonal, and rhombohedral perovskite symmetries, with the orthorhombic symmetry being identified as the lowest energy distortion for both chemistries. To further validate the thermodynamic stability of these two compounds, a number of binary competing phases in the Ce–N, W–N, and Mo–N chemical spaces were also calculated. In the Ce–N space, we considered cubic CeN, bixbyite Ce2N3, pyrochlore Ce4N7, and fluorite CeN2–x (x = 1/4, 1/2, 3/4, 1). In the M–N (M = Mo, W) chemical spaces, we considered anatase M2N, WC-structured MN, pernitride MN2, and hexagonal MN1–x (x = 0, 1/8, 1/4, 3/8, 1/2).

Synthesis Methods

Based upon these calculations, compositions of LaWN3 (confirming earlier work),17 LaMoN3, CeWN3, CeMoN3, YWN3, and YMoN3 were targeted for experimental screening. The initial sample libraries were synthesized using RF magnetron cosputtering from elemental metallic targets of Ce (QS Advanced Materials, 99.9%), W (Kurt J. Lesker, 99.95%), and Mo (Kurt J. Lesker, 99.95%) in a reactive nitrogen atmosphere. For each material ABN3, a gradient of the A–B cations was intentionally grown in a nitriding environment to observe correlations between the stoichiometry and the phases present. Deposition parameters and resulting composition gradient ranges are shown in the Supporting Information, Table S2. These screening films were capped with ∼50 nm of sputtered AlN without breaking vacuum to protect against oxidation. All initial films were grown using a nitrogen plasma with RF power of 450 W, and all were grown using a liquid nitrogen cryoshroud to minimize water vapor near the substrate. The base pressure in the chamber was between 1.8 × 10–7 and 4.5 × 10–7 Torr. All initial screening samples were annealed at 1173 K for 1 min in a ULVAC MILA-3000 rapid thermal anneal (RTA) furnace under flowing N2. Subsequent semiautomated, highly parallelized measurement and characterization, as described elsewhere,2,15,22,44−46 were performed to analyze the initial growth results.

Initial screening prioritized CeWN3 and CeMoN3 for further study, as discussed in the High-Throughput Computational and Experimental Screening section below. Additional CeWN3 sample libraries were grown with an approximate substrate temperature of 900 K, 40 W on the W target (13 W/in2), 60 W on the Ce target (19 W/in2), a deposition time of 120 min after 70 min of presputtering (using the same powers and gas flows listed but with the sample shutter closed), a RF nitrogen plasma power of 450 W, a total chamber pressure of 4 mTorr, 8 sccm of flowing N2, and 4 sccm of flowing Ar. A RF substrate bias of 50 W was used in this case. This film was grown on a substrate of 100 nm LCPVD-grown SiNx on miscut Si (University Wafers).

Additional CeMoN3 films were grown after screening on p-doped Si at an approximate substrate temperature of 900 K, 35 W on the Mo target (11 W/in2), 65 W on the Ce target (21 W/in2), a deposition time of 360 min after 60 min of presputtering, no applied substrate bias, a total chamber pressure of 4 mTorr, 8 sccm of flowing N2, and 4 sccm of flowing Ar. CeMoN3 films were treated with a RTA after growth under flowing N2. Heating profiles always started with a 3 min hold at 373 K followed by a 2 min ramp to 1173 K with hold times of 5 min, with successive rounds of this same treatment as listed below. The total time given is in terms of the cumulative hold times only.

Characterization Methods

Combinatorial data (lab XRD and XRF) were analyzed using the COMBIgor software package.44 X-ray diffraction (XRD) patterns were collected using a Bruker D8 Discover with Cu Kα radiation. LeBail fits were performed with GSAS-II.47 Bright field transmission electron microscopy (BF TEM) images and scanning transmission electron microscopy (STEM) images were acquired on a ThermoFisher FEI Talos F200X. Cross-sectional specimens for TEM analysis were prepared using focused ion beam liftout on a ThermoFisher FEI Helios NanoLab 600i (CeWN) and a TESCAN S8000G Raman FIB-SEM (CeMoN) with a final ion-beam cleaning at 2 kV to minimize surface amorphization.

X-ray fluorescence (XRF) measurements were carried out using a Fischer XDD XRF to map compositions across sample libraries, with a particular emphasis on cation ratio and to estimate the thickness of the films. Light elements (N and O) were analyzed using Auger emission spectroscopy (AES) on a PHI electronics AES 680 nanoprobe with a 5 kV/20 nA defocused electron beam such that a circular area 50 μm in diameter was probed. Between measurement cycles, ion milling was performed using a 3 kV atomic argon beam. Compositions of samples imaged with transmission electron microsopy (TEM) were also confirmed via EDS.

Magnetic properties were measured via superconducting quantum interference device (SQUID) magnetometry in a Quantum Design Magnetic Properties Measurement System (MPMS3). The films were measured from 1.8 to 300 K under applied fields from −7 to +7 T. To isolate the signal of the films, bare substrates were also measured and subtracted. The substrates used were p-doped Si for CeWN3 and p-doped Si with a thin film of metallic Mo on the back for CeMoN3. The measured CeWN3 film was ∼150–200 nm thick, and the measured CeMoN3 film was ∼800–1000 nm thick.

Results and Discussion

High-Throughput Computational and Experimental Screening

Potential ABN3 perovskite nitrides were identified using a tiered screening approach. In the first step, we specified 39 cations that could sit on the A or B sites, yielding 741 candidate ABN3 compositions. For each of these formulas, we applied three descriptors to assess their viability in the perovskite crystal structure—Goldschmidt’s tolerance factor, t, the octahedral factor, μ, and a recently introduced tolerance factor, τ.31,32 Using these descriptors, we identified 9 ABN3 compositions that are likely to crystallize in perovskite structures on the basis of the following criteria: charge-balanced, 0.8 < t < 1, μ > 0.38, and P(τ) > 0.5, where P(τ) is the calibrated probability of forming perovskite given τ.31 We applied a series of descriptors primarily because τ has not been thoroughly benchmarked on nitrides. The 9 compositions predicted to be stable as perovskites using these criteria are listed in Table 1 along with thermodynamic and electronic properties as calculated with PBE.38 Eight out of 9 of the descriptor-predicted perovskites are also calculated to be thermodynamically stable with respect to competing phases (ΔHd < 0), supporting the use of these descriptors for nitride perovskites. The one exception, InMoN3, notably has the lowest P(τ) of the 9 compounds. LaWN3, which is predicted and calculated to be thermodynamically stable in this work, was successfully synthesized in a recent report.17 A recent computational study also reports the stabilities of CeTaN3, CeNbN3, CeWN3, and CeMoN3 in perovskite structures.6

From this evaluation, the compounds LaWN3, LaMoN3, CeWN3, CeMoN3, YWN3, and YMoN3 were prioritized for experimental testing because of their calculated stabilities (ΔHd < 0) and to provide variety across both A- and B-site cations; it should be noted that perovskite LaWN3 has already been successfully synthesized17 and was included here for validation purposes.

We attempted to synthesize these six compositions via combinatorial RF cosputtering of metallic targets with the substrate at ambient chamber temperature. The depositions were carried out in ultrahigh vacuum to minimize oxygen contamination. Figure S1 in the Supporting Information shows the diffraction patterns from these initial screening studies. Diffraction from the (Y,Mo)N and (Y,W)N sample libraries showed clear diffraction peaks only from the AlN capping layer. Despite the AlN capping layer, (La,Mo)N sample libraries oxidized and visibly degraded in a matter of 24–48 h of air exposure, greatly complicating detailed investigation. (Ce,Mo)N and (Ce,W)N sample libraries exhibited clear diffraction peaks and showed no visible evidence of degradation after growth; therefore, these compositions were prioritized for further investigation.

Closer examination of the diffraction patterns from Ce-containing compositions showed two distinct phases with lattice parameters close to those predicted for the perovskite phase (Figure 1). One phase matches diffraction peaks predicted for a perovskite, though the peaks are far too broad to confidently refine the exact symmetry of this phase and therefore are labeled according to pseudocubic axes. The other phase coexisting at the 1:1 A:B cation stoichiometry and Ce-rich compositions for both systems can be matched to a fluorite structure.

Figure 1.

Figure 1

Open in a new tab

Lab XRD of different stoichiometries in the (Ce,Mo)N system (A) and the (Ce,W)N system (B) showing the coexisting fluorite family near the perovskite 1:1 cation ratio. The white boxes highlight the coexistence of the highest intensity perovskite and highest intensity fluorite diffraction peaks. Reference peaks are based off of the cubic prototype of the perovskite structure.

To investigate the relative stabilities of phases in the Ce–Mo–N and Ce–W–N phase spaces and to complement the promising experimental results for synthesizing Ce-based perovskites, we expanded our computational analysis of CeMoN3 and CeWN3. We recomputed the ternary Ce–Mo–N and Ce–W–N phase diagrams using the r2SCAN meta-GGA density functional43 with additional sampling of potential crystal structures for CeMoN3 and CeWN3 and potential competing phases in the Ce–N, Mo–N, and W–N chemical spaces. The computed ternary phase diagrams for these systems are shown in Figure 2 and further support the thermodynamic stability of CeMoN3 (ΔHd = −178 meV/atom) and CeWN3 (ΔHd = −284 meV/atom) in the orthorhombic perovskite structure (Pmc21). No fluorite or fluorite-related phase was represented in either phase diagram, although several fluorite-structured CeN2–x phases were considered. Ce4N7 was shown to be stable in the fluorite structure, and Ce2N3 was shown to be very nearly stable (ΔHd = +2 meV/atom). It is possible that ternary fluorites could be stable or nearly stable (similar to those identified in refs (48 and 49)), but these were not considered as it is difficult to resolve the stoichiometry in the fluorite phase. This strongly suggests that the fluorite-family phase observed experimentally here is not the thermodynamic equilibrium phase for stoichiometric CeWN3 or CeMoN3.

Figure 2.

Figure 2

Open in a new tab

Computed ternary phase diagrams for CeMoN3 (A) and CeWN3 (B) showing possible competing phases for each chemistry studied. ΔHd is shown for the stability-defining reaction for each perovskite phase: (1/4)Ce4N7 + (3/4)MoN + (1/4)MoN2 → CeMoN3 and CeN + WN2 → CeWN3. Blue circles indicate thermodynamically stable phases, and red triangles indicate thermodynamically unstable phases.

Fluorite phases are famously tolerant to large concentrations of point defects and cation disorder, and they are often encountered as competing phases with Pb-based perovskites such as lead zirconate titanate (PZT) and lead magnesium niobate (PMN)-based piezoelectrics.50 Both Pb-rich PZT and Pb-deficient PZT—and even kinetically limited cation-disordered stoichiometric PZT—derived from chemical solutions have been shown to favor crystallization in a fluorite (or pyrochlore, in this case simply an ordered derivative of the fluorite) phase at modest temperatures en route to the stable perovskite phase.51,52 It has also been shown that it is possible to convert fluorite phases to perovskite phases with adequate heating in such systems, provided that the stoichiometry is preserved or corrected.52,53 Following the successful navigation of the fluorite–perovskite landscape in PZT and the computational guidance that the perovskite phase is lower energy for these targeted stoichiometric chemistries, it should be possible to fabricate single phase nitride perovskites by either immediately accessing the thermodynamically stable phase (e.g., at high temperature) or by adding energy (annealing) and progressively monitoring the phase evolution from mixed fluorite+perovskite to single phase perovskite.

Crystallization Dynamics of CeMoN3–x

Initial (Ce,Mo)N3–x XRD patterns (Figure 1A) showed two phases present. Postdeposition annealing was performed to encourage crystallization of the thermodynamically stable phase. Extended anneals at 1173 K in flowing N2 of the initially mixed-phase (perovskite + fluorite) (Ce,Mo)N3–x film grown at 900 K gradually increased the phase fraction of the perovskite phase at the expense of the fluorite (Figure 3A).

Figure 3.

Figure 3

Open in a new tab

(A) Lab XRD of a single point on a (Ce,Mo)N3–x film with nominal composition Ce0.66Mo0.34N3–x by XRF annealed at 1173 K for progressive holds in a flowing N2 atmosphere. A vertical offset is applied to separate the data. (B) LeBail fit in space group Pm3̅m of lab XRD data of the same (Ce,Mo)N3–x film with nominal composition Ce0.61Mo0.39N3–x annealed at 1173 K for 10 min. wR = 8.68%, and goodness of fit (GOF) = 10.32.

To investigate whether this structural evolution may be due to oxidation during annealing, Auger emission spectroscopy (AES) was performed. Shown in Figure 4B, it indicates very low oxygen content through the thickness of the annealed film, confirming the synthesis of an oxygen-free nitride perovskite phase. This goal has proven to be a significant synthetic challenge. Prior to the current work, only two oxygen-free nitride perovskites have been reported, one via high pressure–high temperature methods to synthesize LaReN3 in bulk18 and our prior work that used activated nitrogen via a RF plasma to form LaWN3.17 The low oxygen content confirms that the 1173 K anneal in flowing N2 did not cause this fluorite-to-perovskite transition through the inadvertent introduction of oxygen. We therefore conclude that the phenomenon observed in CeMoN3–x films is similar to that previously documented for the PZT system. While the ground state structure is perovskite (Table 1), significant disorder favors crystallization first into a defect- and disorder-tolerant fluorite phase, which can then transform into the stable perovskite after annealing. As shown previously for PZT, the gradual nature of this transition is enabled by the similarity of the perovskite (101) and fluorite (pyrochlore) (222) planes;53 we presume an analogous scenario here.

Figure 4.

Figure 4

Open in a new tab

(A) BF STEM cross section showing a very fine grain size and (B) AES depth profile of light element signals of a CeMoN3–x film with nominal composition Ce0.54Mo0.46N3–x by XRF after annealing for 10 min in flowing N2. Only the surface layer of the sample contains significant oxygen; the majority of the sample has very low oxygen signal, indicating that the change during annealing is not due to incorporation of oxygen but to crystallization kinetics.

A LeBail fit of the lab XRD data of a spot with composition Ce0.61Mo0.39N3–x to a pseudocubic perovskite structure with Pm3̅m symmetry is shown in Figure 3B. The extracted lattice parameter was a = 4.0668(7) Å. It is likely that the true symmetry is lower given the presence of several peaks unaccounted for by this cubic space group and given the theoretical calculations that predicted orthorhombic Pmc21 symmetry with lattice parameters a = 5.50528 Å, b = 5.59140 Å, and c = 7.85589 Å (see Table S3 in the Supporting Information). Determination of the precise space group from the experimental data was hindered by the weak nature of the additional peaks and the broad nature of thin film diffraction peaks.

Direct Growth of Perovskite CeWN3–x

Initial results in the (Ce,W)N family (Figure 1B)—deposited at ambient temperature followed by 1 min of annealing in N2 at 1173 K—also revealed an initial mixture of perovskite and fluorite phases near and above the 1:1 cation ratio, but annealing CeWN3–x films with a 1:1 Ce:W ratio at 1173 K in N2—analogous to the conditions that produced the perovskite phase in CeMoN3–x—yielded W metal or film delamination. Increasing the substrate temperature to ∼900 K (the maximum capability of the chamber) during growth yielded perovskite films without evidence of a coexisting fluorite phase, as shown in Figure 5A. There appears to be some effect of texturing for the highest Ce-containing compositions, as the most Ce-rich composition detected showed only a very strong perovskite pseudocubic (110) peak. Comparison of lab X-ray, synchrotron X-ray diffraction (SXRD), and electron diffraction (TEM SAED) data confirms that assignment of a perovskite structure to this phase is appropriate across both long-range (X-ray) and short-range (electron) diffraction lengths (see Figure S2 in the Supporting Information). However, determination of a specific space group is hindered by the small number of peaks present in the phase-pure films. We therefore performed a Le Bail fit to the pseudocubic perovskite structure in space group Pm3̅m, shown in Figure 5B for the composition Ce0.5W0.5N3–x. The extracted lattice parameter is a = 4.020(4) Å. We note that the pseudocubic symmetry used in the LeBail refinement is different from the theoretically predicted cell in orthorhombic Pmc21 symmetry with lattice parameters a = 5.5370 Å, b = 5.60061 Å, and c = 7.88645 Å.

Figure 5.

Figure 5

Open in a new tab

(A) Lab XRD of (Ce,W)N films grown at 900 K showing a phase-pure perovskite near and slightly above the 1:1 Ce:W ratio. At compositions with lower Ce content, W-rich phases formed. A peak associated with the substrate has been removed by removing a range of χ from the integration after it did not appear in electron diffraction in Figure S2 in the Supporting Information. (B) LeBail fit in space group Pm3̅m of the lab XRD pattern of the composition Ce0.5W0.5N3–x in panel A. The 2θ region around a peak associated with the Si substrate has been removed. wR = 9.38%, and goodness of fit (GOF) = 9.85.

In bright field (BF) TEM images, the CeWN3–x films show columnar grains and a dense microstructure (Figure 6A). The columnar grains indicate that crystallization occurred early in the growth, and the established crystals continued to grow, unlike in the above CeMoN3–x microstructure that was amorphous during growth and crystallized during postgrowth annealing steps, leading to the lack of columns in the TEM in Figure 4A. AES results (Figure 6B) show much higher oxygen content for these films than for their CeMoN3–x counterparts (Figure 4B). This sample experienced significant air exposure between growth and the AES measurement, so it is unknown what fraction of the oxygen content was incorporated during growth. The fact that the oxygen to nitrogen ratio measured by AES decreases through the film toward the substrate suggests that some or all of this oxidation occurred after growth. We therefore consider the 2.5:1 nitrogen:oxygen ratio closest to the substrate to be a ceiling on the amount of oxygen incorporated during growth, though it is likely that the as-grown films had much less oxygen.

Figure 6.

Figure 6

Open in a new tab

(A) BF STEM cross section of a CeWN3–x film with nominal composition Ce0.51W0.49N3–x by XRF showing columnar microstructure within the film. The dark layer at the top is Pt from sample preparation. (B) AES of the same CeWN3–x film showing increasing oxygen content near the surface of the film, presumably because of prolonged exposure to oxygen in the atmosphere. Two scans were performed as the first did not penetrate the full film depth, which caused a spike in oxygen measured at the newly created surface.

Growth Summary

The above crystallization pathways of (1) postdeposition annealing and (2) high substrate temperature during deposition demonstrate the challenges and flexibility of fabricating new nitride perovskites. In CeMoN3–x, the direct growth of the single-phase perovskite was not achieved because the fluorite structure appears to be more kinetically accessible than the perovskite for stoichiometries with a 1:1 Ce:Mo ratio. However, it was possible to access the thermodynamically stable perovskite after annealing. In CeWN3–x, the direct growth of perovskite was achieved using the hottest substrate temperature possible in the chamber (∼900 K) to access the thermodynamically stable perovskite, but postprocessing annealing in a flowing nitrogen chamber induced reduction to W metal. For comparison, the recently reported nitride perovskite LaWN317 was achieved both with a high substrate temperature during initial sputtering and by postdeposition annealing. These growth pathways can serve as blueprints for accessing more nitride perovskite compounds in the yet-unexplored chemical space.

Magnetic Ground State Calculations

As a result of the presence of unpaired electrons (either f1 Ce3+ or d1 W5+/Mo5+) in stoichiometric CeMN3–x, there is the possibility for long-range magnetic order in these systems. We calculated the magnetic ground states of CeMoN3 and CeWN3, as shown in Table 2, using the r2SCAN functional and orthorhombic Pmc21 unit cells (see Table S3 in the Supporting Information for atomic positions and lattice parameters). Three initial configurations were considered for each compound: a ferromagnetic configuration (“FM”) in which moments of +5 μB were placed on all Ce and M, and two different antiferromagnetic configurations (“AFM-1” and “AFM-2”) in which each Ce or M had a moment of either +5 μB or −5 μB; these two are different in terms of how the up and down spins are distributed. The optimized net moments for the Ce and M sublattices and the optimized overall net moments resulting from each initial configuration are shown in Table 2. The calculated magnetic moments for each Ce and M site are shown in Table S4 in the Supporting Information.

Table 2. Magnetic Ground-State Calculations for Orthorhombic CeMoN3 and CeWN3 Performed with r2SCANa.

formula initial configuration total energy (eV/atom) net Ce moment (μB) net M moment (μB) net moment (μB) ΔEgs (meV/atom)
CeMoN3 FM –18.0105 –0.25 –0.136 –0.386 0
AFM-1 –18.0104 –0.001 0 –0.001 0.0945
AFM-2 –18.0105 0.006 0.004 0.01 0.0505
CeWN3 FM –23.1576 0.456 0.02 0.476 2.3705
AFM-1 –23.1590 –0.004 –0.002 –0.006 0.9115
AFM-2 –23.1600 0.201 –0.022 0.179 0
Open in a new tab
a

ΔEgs is the energy of that magnetic configuration above the lowest energy magnetic configuration considered. FM = initial high-spin ferromagnetic ordering. AFM = initial high-spin anti-ferromagnetic ordering. AFM-1 and AFM-2 differ in the arrangement of positive and negative spins. M refers to either Mo or W.

The ground states and optimized magnetic moments (Table S4 in the Supporting Information) suggest FM ordering for CeMoN3 with a small net moment of ∼0.4 μB. The presence of net moments on both Ce and Mo sublattices implies that the existence of potentially mixed oxidation states for both metals (Ce3+/Ce4+, Mo6+/Mo5+). However, both AFM configurations are very close in energy to the FM ground state. For CeWN3, the calculated ground state (“AFM-2”) contains ferrimagnetic ordering of the Ce sites (see Table S4 in the Supporting Information) and no significant moment on any W, yielding a very small net moment of ∼0.2 μB. The other configurations are quite close in energy. Flores-Livas et al. calculated CeWN3 in Pnma symmetry to be weakly FM8 using a lower level of theory (LDA), considering only Ce, but also accounting for spin–orbit coupling. Our higher level r2SCAN calculations performed on a larger unit cell are not necessarily inconsistent with these prior results, as both calculations yielded a net moment, and we show the energy difference between different magnetic configurations is quite small.

Magnetic Susceptibility Measurements

To compare with the calculated magnetic ground states, we performed magnetic susceptibility measurements on perovskite CeWN3–x and CeMoN3–x. Bare substrates were also measured and subtracted in order to isolate the signal from the perovskite phases. As the mass of the perovskite thin film cannot be quantified precisely, we show the data either as magnetization (M, in μB) or as susceptibility (χ, in emu/Oe) calculated with an assumed sample mass of 0.0001 g; these values are thus approximate and therefore cannot be accurately compared across samples or used to extract meaningful effective moments (μeff, in μB) or Curie constant (C, in K emu/mol) values from the Curie–Weiss fits. We also note that both films may have some amorphous/nanocrystalline phase fraction in addition to the crystalline perovskite phase; this is not easily separable in the susceptibility data and could complicate the extraction of quantitative susceptibility and effective moment values.

Low-field (μ0H = 0.005 T) zero field cooled (ZFC) and field cooled (FC) DC susceptibility measurements were performed on a phase-pure perovskite CeWN3–x film with approximate composition Ce0.51W0.49N3–x measured by XRF (Figure 7A). No indications of long-range magnetic ordering or bifurcation beyond error between the ZFC and the FC scans are observed, indicating overall paramagnetism. Magnetization as a function of applied field (Figure 7B) confirms this behavior: no hysteresis loop or net moment is visible at either T = 2 K or T = 10 K. However, the change in slope between these two temperatures suggests the presence of short-range correlations. To probe this, a Curie–Weiss fit was performed on high temperature (T = 150–300 K) inverse susceptibility data collected at μ0H = 5 T (Figure 7A, inset). The negative extracted Weiss temperature θ = −95(4) K indicates the presence of strong antiferromagnetic (AFM) interactions. This suggests the presence of geometric magnetic frustration, an intriguing possibility in this new material, and one that is relatively common in (double) perovskite oxides and oxynitrides.54−56

Figure 7.

Figure 7

Open in a new tab

Magnetic properties of CeWN3–x and CeMoN3–x. (A) Low-field zero field cooled (ZFC) and field cooled (FC) susceptibility of CeWN3–x measured in an applied field of μ0H = 0.005 T. Inset: Inverse susceptibility measured in an applied field of μ0H = 5 T with a diamagnetic correction of χ0 = −3.91 × 10–4 emu/Oe. Data in the range T = 237–256 K are masked out because of instrumental artifacts. The line is a Curie–Weiss fit from T = 150 to T = 300 K. (B) Magnetization of CeWN3–x as a function of applied field at T = 2 K and T = 10 K. (C) Low-field ZFC and FC susceptibility of CeMoN3–x measured in applied fields of μ0H = 0.005–0.5 T. Inset: Inverse susceptibility measured in an applied field of μ0H = 5 T with a diamagnetic correction of χ0 = −4.33 × 10–4 emu/Oe. Data in the range T = 238–263 K are masked out because of instrumental artifacts. The line is a Curie–Weiss fit from T = 150 to T = 300 K. (D) Magnetization of CeMoN3–x as a function of applied field at T = 2 K and T = 10 K.

Analogous low-field ZFC and FC measurements collected on a CeMoN3–x film with approximate composition Ce0.61Mo0.39N3–x, chosen for strong perovskite diffraction peaks, display bifurcation below T ∼ 10 K and a peak at TN ∼ 8 K, which we assign as a transition to long-range AFM order (Figure 7C). This splitting closes as the applied field is increased, and no splitting is observed above μ0H ∼ 0.2 T. The magnetization as a function of applied field (Figure 7D) at T = 2 K is consistent with AFM order. At T = 10 K, the magnetization is linear, as expected in the paramagnetic state. A Curie–Weiss fit performed on high temperature (T = 150–300 K) inverse susceptibility data collected at μ0H = 5 T (Figure 7C, inset) yields a negative Weiss temperature θ = −106(3) K, confirming the dominance of AFM correlations in this material. The frustration index f, which quantifies the magnetic frustration as the ratio between the Weiss temperature and the Néel transition temperature 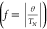Inline graphic, is approximately 13, indicating a very high degree of frustration.57 The upturn below TN may be attributed to the highly frustrated nature of this compound and/or to a possibly paramagnetic amorphous phase fraction.

While both CeWN3–x and CeMoN3–x show signs of strong short-range AFM correlations as evidenced by their large, negative Weiss temperatures, CeWN3–x remains paramagnetic down to the lowest temperature measured while CeMoN3–x has a transition to long-range AFM order at TN ∼ 8 K. This suggests the energy scale of the magnetic interactions is different in these two compounds, most likely because of the difference in spin–orbit coupling between W and Mo. However, subtle differences in structure, stoichiometry, and coupling between the A- and B-site sublattices—or a combination of several effects—may also have a large influence upon the magnetism and must be studied further.

The optimized magnetic moments from our calculations of the orthorhombic perovskites at the r2SCAN level of theory suggest AFM Ce3+ and d0 W6+ for CeWN3—consistent with the short-range AFM correlations we extract from the Curie–Weiss fits, although we observe a paramagnetic ground state—but FM ordering and potentially mixed oxidation states (Ce3+/Ce4+, Mo6+/Mo5+) for CeMoN3. However, the calculated AFM configurations for CeMoN3 are very close in energy to the FM ground state, and therefore the observed AFM behavior may easily be stabilized.

The origin of the observed magnetic behavior will be the focus of further detailed study, as the background subtraction of substrates and the uncertainty in film mass complicate the accurate extraction of magnetization and μeff values, which are ideally able to distinguish between S = 1/2 W5+/Mo5+ (μeff = 1.73 μB) and J = 5/2 Ce3+ (μeff = 2.54 μB). Both simple pictures—f1 Ce3+ or d1 W5+/Mo5+—are possible because AFM correlations are common in both. While most rare earth elements often display ferromagnetic (FM) correlations, Ce3+ cations are affected by two competing interactions: indirect exchange mediated by conduction electrons (i.e., the RKKY interaction),58,59 which generally stabilizes the AFM order,60−63 and Kondo screening, which leads to a nonmagnetic ground state.64,65 Only occasionally is a FM ground state observed, either via an itinerant mechanism or arising at very low temperatures in fierce competition with AFM order.66,67 However, the possibility of Ce in a mixed +3/+4 valence state, which typically carries no stable magnetic moment, must also be considered; this is reported to be the ground state of CeN.68 Future work incorporating other magnetic transition metals (TMs)—such as 3d TMs (e.g., Fe, Co, Mn, ...) or 4d/5d TMs (e.g., Re, Ir, Ru, ...) that often cause useful or exotic magnetism in oxide perovskites—would be intriguing but may be difficult given charge balance requirements for nitride perovskites. Several of these TMs were probed computationally in this study (Nb, Ta, Cr, Mn, Fe, Co, Ni), but the cutoffs for P(τ), t, or μ were not met in the screening section (see the High-Throughput Computational and Experimental Screening section above and Table S1 in the Supporting Information).

Conclusions

In this study, two new compositions of nitride perovskites have been experimentally realized. Candidate compositions were first filtered using radii-based descriptors and DFT calculations of thermodynamic stability, then through high-throughput experimental growths before efforts were focused on CeMoN3 and CeWN3 for further study. Initial films of compositions both grown at ambient temperature and annealed at elevated temperature exhibited a perovskite and a coexisting phase that is hypothesized to be in the fluorite family. Similar to what is seen in the PZT system, the fluorite phase appears to be a transient intermediate phase that is present during crystallization from amorphous material to a more stable perovskite phase. For CeMoN3–x films, growth at the maximum substrate temperature achievable in our chamber produced films with a mix of fluorite and perovskite phases, and extended annealing promoted conversion of the fluorite to perovskite. This compound was shown to be oxygen-free, representing only the third known oxygen-free nitride perovskite. With progressive annealing, this phase showed a deviation from the pseudocubic pattern: peak splitting suggested a transition to a lower symmetry, such as the predicted orthorhombic phase. CeWN3–x films grown at this maximum substrate temperature (∼900 K) were single-phase perovskite as grown. Magnetic susceptibility measurements of these perovskite samples indicate that CeWN3–x is paramagnetic down to T = 2 K with strong short-range antiferromagnetic correlations, while CeMoN3–x orders antiferromagnetically at TN ≈ 8 K. Both materials show indications of a high degree of magnetic frustration. These observations differ from the previously predicted ferromagnetic behavior,8 as well as our current calculations of ferrimagnetic and ferromagnetic ground states for orthorhombic CeWN3 and CeMoN3, respectively. This work clearly demonstrates the value of coupled high-throughput computation and experiment for the discovery and successful realization of new materials and a promising outlook for synthesis of new nitride perovskites.

Acknowledgments

This work was authored in part at the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding was provided by the Office of Science (SC), Basic Energy Sciences (BES), Materials Chemistry program, as a part of the Early Career Award “Kinetic Synthesis of Metastable Nitrides” (synthesis) and by the National Science Foundation (NSF) through Grants No. DMR-1555015 and DMREF-1534503 (characterization). The TESCAN S800G FIB-SEM used in this work was acquired through the support of the National Science Foundation (DMR-1828454). The MPMS3 measurement system used was acquired through NSF MRI Grant No. 1917860. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-76SF00515. This work also used computational resources sponsored by the Department of Energy’s Office of Energy Efficiency and Renewable Energy, located at NREL. R.S. was supported by the NSF Graduate Research Fellowship Program under Grant No. 1646713. R.W.S. acknowledges support from the Director’s Fellowship within NREL’s Laboratory Directed Research and Development program. The authors thank A.M. Holder for useful discussions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.2c01282.

  • Tolerance factor data for all charge-balanced nitride compositions, deposition parameters for experimental screening films, X-ray diffraction of the screening experimental films, additional TEM data, calculated CIFs, and calculations of magnetic ground states (PDF)

  • Crystallographic information file for CeMoN3 (CIF)

  • Crystallographic information file for CeWN3 (CIF)

Author Present Address

# Qorvo Inc., Bend, Oregon 97701, United States

The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government.

The authors declare no competing financial interest.

Supplementary Material

cm2c01282_si_001.pdf (1,014.8KB, pdf)
cm2c01282_si_002.cif (1.5KB, cif)
cm2c01282_si_003.cif (1.5KB, cif)

References

  1. Sun W.; Bartel C. J.; Arca E.; Bauers S. R.; Matthews B.; Orvañanos B.; Chen B. R.; Toney M. F.; Schelhas L. T.; Tumas W.; Tate J.; Zakutayev A.; Lany S.; Holder A. M.; Ceder G. A map of the inorganic ternary metal nitrides. Nat. Mater. 2019, 18, 732–739. 10.1038/s41563-019-0396-2. [DOI] [PubMed] [Google Scholar]
  2. Zakutayev A.; Bauers S. R.; Lany S. Experimental Synthesis of Theoretically Predicted Multivalent Ternary Nitride Materials. Chem. Mater. 2022, 34, 1418–1438. 10.1021/acs.chemmater.1c03014. [DOI] [Google Scholar]
  3. Matar S. F.; Demazeau G. Potential existence of post-perovskite nitrides; DFT studies of ThTaN3. J. Solid State Chem. 2010, 183, 994–999. 10.1016/j.jssc.2010.03.002. [DOI] [Google Scholar]
  4. Sarmiento-Pérez R.; Cerqueira T. F. T.; Körbel S.; Botti S.; Marques M. A. L. Prediction of Stable Nitride Perovskites. Chem. Mater. 2015, 27, 5957–5963. 10.1021/acs.chemmater.5b02026. [DOI] [Google Scholar]
  5. Jung M.-C.; Lee K.-W.; Pickett W. E. Perovskite ThTaN3: A large-thermopower topological crystalline insulator. Phys. Rev. B 2018, 97, 121104. 10.1103/PhysRevB.97.121104. [DOI] [Google Scholar]
  6. Ha V.-a.; Lee H.; Giustino F. CeTaN3 and CeNbN3: Prospective Nitride Perovskites with Optimal Photovoltaic Band Gaps. Chem. Mater. 2022, 34, 2107–2122. 10.1021/acs.chemmater.1c03503. [DOI] [Google Scholar]
  7. Fang Y.-W.; Fisher C. A. J.; Kuwabara A.; Shen X.-W.; Ogawa T.; Moriwake H.; Huang R.; Duan C.-G. Lattice dynamics and ferroelectric properties of the nitride perovskite LaWN3. Phys. Rev. B 2017, 95, 014111. 10.1103/PhysRevB.95.014111. [DOI] [Google Scholar]
  8. Flores-Livas J. A.; Sarmiento-Pérez R.; Botti S.; Goedecker S.; Marques M. A. L. Rare-earth magnetic nitride perovskites. Journal of Physics: Materials 2019, 2, 025003. 10.1088/2515-7639/ab083e. [DOI] [Google Scholar]
  9. Bacher P.; Antoine P.; Marchand R.; L’Haridon P.; Laurent Y.; Roult G. Time-of-flight neutron diffraction study of the structure of the perovskite-type oxynitride LaWO0.6N2.4. J. Solid State Chem. 1988, 77, 67–71. 10.1016/0022-4596(88)90091-6. [DOI] [Google Scholar]
  10. Brese N. E.; DiSalvo F. Synthesis of the First Thorium-Containing Nitride Perovskite, TaThN3. J. Solid State Chem. 1995, 120, 378–380. 10.1006/jssc.1995.1423. [DOI] [Google Scholar]
  11. Clarke S. J.; Guinot B. P.; Michie C. W.; Calmont M. J.; Rosseinsky M. J. Oxynitride perovskites: Synthesis and structures of LaZrO2N, NdTiO2N, and LaTiO2N and comparison with oxide perovskites. Chem. Mater. 2002, 14, 288–294. 10.1021/cm010577v. [DOI] [Google Scholar]
  12. Yang M.; Oró-Solé J.; Kusmartseva A.; Fuertes A.; Attfield J. P. Electronic tuning of two metals and colossal magnetoresistances in EuWO1+xN2–x perovskites. J. Am. Chem. Soc. 2010, 132, 4822–4829. 10.1021/ja910745b. [DOI] [PubMed] [Google Scholar]
  13. Fuertes A. Chemistry and applications of oxynitride perovskites. J. Mater. Chem. 2012, 22, 3293–3299. 10.1039/c2jm13182j. [DOI] [Google Scholar]
  14. Black A. P.; Johnston H. E.; Oró-Solé J.; Bozzo B.; Ritter C.; Frontera C.; Attfield J. P.; Fuertes A. Nitride tuning of lanthanide chromites. Chem. Commun. 2016, 52, 4317–4320. 10.1039/C6CC00744A. [DOI] [PubMed] [Google Scholar]
  15. Talley K. R.; Mangum J.; Perkins C. L.; Woods-Robinson R.; Mehta A.; Gorman B. P.; Brennecka G. L.; Zakutayev A. Synthesis of Lanthanum Tungsten Oxynitride Perovskite Thin Films. Adv. Electron. Mater. 2019, 5, 1900214. 10.1002/aelm.201900214. [DOI] [Google Scholar]
  16. Niewa R. Metal-Rich Ternary Perovskite Nitrides. Eur. J. Inorg. Chem. 2019, 2019, 3647–3660. 10.1002/ejic.201900756. [DOI] [Google Scholar]
  17. Talley K. R.; Perkins C. L.; Diercks D. R.; Brennecka G. L.; Zakutayev A. Synthesis of LaWN3 nitride perovskite with polar symmetry. Science 2021, 374, 1488–1491. 10.1126/science.abm3466. [DOI] [PubMed] [Google Scholar]
  18. Kloß S. D.; Weidemann M. L.; Attfield J. P. Preparation of Bulk-Phase Nitride Perovskite LaReN3 and Topotactic Reduction to LaNiO2-Type LaReN2. Angew. Chem., Int. Ed. 2021, 60, 22260–22264. 10.1002/anie.202108759. [DOI] [PubMed] [Google Scholar]
  19. Caskey C. M.; Richards R. M.; Ginley D. S.; Zakutayev A. Thin film synthesis and properties of copper nitride, a metastable semiconductor. Mater. Horiz. 2014, 1, 424–430. 10.1039/C4MH00049H. [DOI] [Google Scholar]
  20. Bauers S. R.; Holder A.; Sun W.; Melamed C. L.; Woods-Robinson R.; Mangum J.; Perkins J.; Tumas W.; Gorman B.; Tamboli A.; Ceder G.; Lany S.; Zakutayev A. Ternary nitride semiconductors in the rocksalt crystal structure. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 14829–14834. 10.1073/pnas.1904926116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Heinselman K. N.; Lany S.; Perkins J. D.; Talley K. R.; Zakutayev A. Thin Film Synthesis of Semiconductors in the Mg–Sb–N Materials System. Chem. Mater. 2019, 31, 8717–8724. 10.1021/acs.chemmater.9b02380. [DOI] [Google Scholar]
  22. Greenaway A. L.; Loutris A. L.; Heinselman K. N.; Melamed C. L.; Schnepf R. R.; Tellekamp M. B.; Woods-Robinson R.; Sherbondy R.; Bardgett D.; Bauers S.; Zakutayev A.; Christensen S. T.; Lany S.; Tamboli A. C. Combinatorial Synthesis of Magnesium Tin Nitride Semiconductors. J. Am. Chem. Soc. 2020, 142, 8421–8430. 10.1021/jacs.0c02092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Fioretti A. N.; Zakutayev A.; Moutinho H.; Melamed C.; Perkins J. D.; Norman A. G.; Al-Jassim M.; Toberer E. S.; Tamboli A. C. Combinatorial insights into doping control and transport properties of zinc tin nitride. J. Mater. Chem. C 2015, 3, 11017–11028. 10.1039/C5TC02663F. [DOI] [Google Scholar]
  24. Manna S.; Talley K. R.; Gorai P.; Mangum J.; Zakutayev A.; Brennecka G. L.; Stevanović V.; Ciobanu C. V. Enhanced Piezoelectric Response of AlN via CrN Alloying. Phys. Rev. Appl. 2018, 9, 034026. 10.1103/PhysRevApplied.9.034026. [DOI] [Google Scholar]
  25. Bikowski A.; Siol S.; Gu J.; Holder A.; Mangum J. S.; Gorman B.; Tumas W.; Lany S.; Zakutayev A. Design of Metastable Tin Titanium Nitride Semiconductor Alloys. Chem. Mater. 2017, 29, 6511–6517. 10.1021/acs.chemmater.7b02122. [DOI] [Google Scholar]
  26. Nguyen H. H.; Oguchi H.; Van Minh L.; Kuwano H. High-throughput investigation of a lead-free AlN-Based piezoelectric material, (Mg,Hf)xAl1–xN. ACS Comb. Sci. 2017, 19, 365–369. 10.1021/acscombsci.6b00193. [DOI] [PubMed] [Google Scholar]
  27. Riedl A.; Daniel R.; Todt J.; Stefenelli M.; Holec D.; Sartory B.; Krywka C.; Müller M.; Mitterer C.; Keckes J. A combinatorial X-ray sub-micron diffraction study of microstructure, residual stress and phase stability in TiAlN coatings. Surf. Coat. Technol. 2014, 257, 108–113. 10.1016/j.surfcoat.2014.03.045. [DOI] [Google Scholar]
  28. Reeswinkel T.; Sangiovanni D. G.; Chirita V.; Hultman L.; Schneider J. M. Structure and mechanical properties of TiAlN-WNx thin films. Surf. Coat. Technol. 2011, 205, 4821–4827. 10.1016/j.surfcoat.2011.04.066. [DOI] [Google Scholar]
  29. Tholander C.; Tasnádi F.; Abrikosov I. A.; Hultman L.; Birch J.; Alling B. Large piezoelectric response of quarternary wurtzite nitride alloys and its physical origin from first principles. Phys. Rev. B 2015, 92, 174119. 10.1103/PhysRevB.92.174119. [DOI] [Google Scholar]
  30. Bauers S. R.; Mangum J.; Harvey S. P.; Perkins J. D.; Gorman B.; Zakutayev A. Epitaxial growth of rock salt MgZrN2 semiconductors on MgO and GaN. Appl. Phys. Lett. 2020, 116, 102102. 10.1063/1.5140469. [DOI] [Google Scholar]
  31. Bartel C. J.; Sutton C.; Goldsmith B. R.; Ouyang R.; Musgrave C. B.; Ghiringhelli L. M.; Scheffler M. New tolerance factor to predict the stability of perovskite oxides and halides. Sci. Adv. 2019, 5, eaav0693. 10.1126/sciadv.aav0693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Goldschmidt V. M. Die Gesetze der Krystallochemie. Naturwissenschaften 1926, 14, 477–485. 10.1007/BF01507527. [DOI] [Google Scholar]
  33. Shannon R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr., Sect. A 1976, 32, 751–767. 10.1107/S0567739476001551. [DOI] [Google Scholar]
  34. Dronskowski R.Computational Chemistry of Solid State Materials: A Guide for Materials Scientists, Chemists, Physicists and others; Wiley-VCH Verlag GmbH: 2005. [Google Scholar]
  35. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  36. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  37. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  38. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  39. Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; Persson K. A. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. Appl. Phys. Lett. Mater. 2013, 1, 011002. 10.1063/1.4812323. [DOI] [Google Scholar]
  40. Bartel C. J.; Weimer A. W.; Lany S.; Musgrave C. B.; Holder A. M. The role of decomposition reactions in assessing first-principles predictions of solid stability. npj Comput. Mater. 2019, 5, 4. 10.1038/s41524-018-0143-2. [DOI] [Google Scholar]
  41. Bartel C. J. Review of computational approaches to predict the thermodynamic stability of inorganic solids. J. Mater. Sci. 2022, 57, 10475. 10.1007/s10853-022-06915-4. [DOI] [Google Scholar]
  42. Bartel C. J.; Clary J. M.; Sutton C.; Vigil-Fowler D.; Goldsmith B. R.; Holder A. M.; Musgrave C. B. Inorganic Halide Double Perovskites with Optoelectronic Properties Modulated by Sublattice Mixing. J. Am. Chem. Soc. 2020, 142, 5135–5145. 10.1021/jacs.9b12440. [DOI] [PubMed] [Google Scholar]
  43. Furness J. W.; Kaplan A. D.; Ning J.; Perdew J. P.; Sun J. Accurate and Numerically Efficient r2SCAN Meta-Generalized Gradient Approximation. J. Phys. Chem. Lett. 2020, 11, 8208–8215. 10.1021/acs.jpclett.0c02405. [DOI] [PubMed] [Google Scholar]
  44. Talley K. R.; Bauers S. R.; Melamed C. L.; Papac M. C.; Heinselman K. N.; Khan I.; Roberts D. M.; Jacobson V.; Mis A.; Brennecka G. L.; Perkins J. D.; Zakutayev A. COMBIgor: Data-analysis package for combinatorial materials science. ACS Comb. Sci. 2019, 21, 537–547. 10.1021/acscombsci.9b00077. [DOI] [PubMed] [Google Scholar]
  45. Zakutayev A.; Wunder N.; Schwarting M.; Perkins J. D.; White R.; Munch K.; Tumas W.; Phillips C. An open experimental database for exploring inorganic materials. Sci. Data 2018, 5, 180053. 10.1038/sdata.2018.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Talley K. R.; White R.; Wunder N.; Eash M.; Schwarting M.; Evenson D.; Perkins J. D.; Tumas W.; Munch K.; Phillips C.; Zakutayev A. Research data infrastructure for high-throughput experimental materials science. Patterns 2021, 2, 100373. 10.1016/j.patter.2021.100373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Toby B. H.; Von Dreele R. B. GSAS-II: the genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 2013, 46, 544–549. 10.1107/S0021889813003531. [DOI] [Google Scholar]
  48. Jacobs H.; Hellmann B. Synthesis and structure of a caesium niobium(V) nitride, CsNbN2. J. Alloys Compd. 1993, 191, 277–278. 10.1016/0925-8388(93)90077-Z. [DOI] [Google Scholar]
  49. Jacobs H.; von Pinkowski E. Synthese ternärer nitride von alkalimetallen: Verbindungen MIT tantal, MTaN2MIT M ≡ Na, K, Rb und Cs. J. Less-Common Met. 1989, 146, 147–160. 10.1016/0022-5088(89)90371-8. [DOI] [Google Scholar]
  50. Swartz S. L.; Shrout T. R. Fabrication of perovskite lead magnesium niobate. Mater. Res. Bull. 1982, 17, 1245–1250. 10.1016/0025-5408(82)90159-3. [DOI] [Google Scholar]
  51. Polli A. D.; Lange F. F.; Levi C. G. Metastability of the Fluorite, Pyrochlore, and Perovskite Structures in the PbO—ZrO2—TiO2 System. J. Am. Ceram. Soc. 2000, 83, 873–881. 10.1111/j.1151-2916.2000.tb01288.x. [DOI] [Google Scholar]
  52. Brennecka G. L.; Parish C. M.; Tuttle B. A.; Brewer L. N.; Rodriguez M. A. Reversibility of the Perovskite-to-Fluorite Phase Transformation in Lead-Based Thin and Ultrathin Films. Adv. Mater. 2008, 20, 1407–1411. 10.1002/adma.200702442. [DOI] [Google Scholar]
  53. Voigt J. A.; Tuttle B. A.; Headley T. J.; Lamppa D. L. The Pyrochlore-to-Perovskite Transformation in Solution-Derived Lead Zirconate Titanate Thin Films. MRS Online Proc. Library 1995, 395–402. 10.1557/PROC-361-395. [DOI] [Google Scholar]
  54. Vasala S.; Karppinen M. A2B’B”O6 perovskites: A review. Prog. Solid State Chem. 2015, 43, 1–36. 10.1016/j.progsolidstchem.2014.08.001. [DOI] [Google Scholar]
  55. Fuertes A. Metal oxynitrides as emerging materials with photocatalytic and electronic properties. Mater. Horiz. 2015, 2, 453–461. 10.1039/C5MH00046G. [DOI] [Google Scholar]
  56. Ishida K.; Tassel C.; Watabe D.; Takatsu H.; Brown C. M.; Nilsen G. J.; Kageyama H. Spin Frustration in Double Perovskite Oxides and Oxynitrides: Enhanced Frustration in La2MnTaO5N with a Large Octahedral Rotation. Inorg. Chem. 2021, 60, 8252–8258. 10.1021/acs.inorgchem.1c00927. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Ramirez A. P. Strongly Geometrically Frustrated Magnets. Annu. Rev. Mater. Sci. 1994, 24, 453–480. 10.1146/annurev.ms.24.080194.002321. [DOI] [Google Scholar]
  58. Ruderman M. A.; Kittel C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. 10.1103/PhysRev.96.99. [DOI] [Google Scholar]
  59. Kasuya T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. 10.1143/PTP.16.45. [DOI] [Google Scholar]
  60. Rossat-Mignod J.; Burlet P.; Quezel S.; Effantin J.; Delacôte D.; Bartholin H.; Vogt O.; Ravot D. Magnetic properties of cerium monopnictides. J. Magn. Magn. Mater. 1983, 31–34, 398–404. 10.1016/0304-8853(83)90295-0. [DOI] [Google Scholar]
  61. Fikáček J.; Prokleška J.; Prchal J.; Custers J.; Sechovský V. Nature of the magnetic ground state in the mixed valence compound CeRuSn: a single-crystal study. J. Phys.: Condens. Matter 2013, 25, 416006. 10.1088/0953-8984/25/41/416006. [DOI] [PubMed] [Google Scholar]
  62. Pöttgen R.; Chevalier B. Cerium intermetallics with ZrNiAl-type structure – a review. Z. Naturforsch., B 2015, 70, 289–304. 10.1515/znb-2015-0018. [DOI] [Google Scholar]
  63. Porter S. H.; Huang Z.; Cheng Z.; Avdeev M.; Chen Z.; Dou S.; Woodward P. M. Structural and magnetic properties of RTiNO2 (R = Ce, Pr, Nd) perovskite nitride oxides. J. Solid State Chem. 2015, 226, 279–285. 10.1016/j.jssc.2015.01.023. [DOI] [Google Scholar]
  64. Kondo J. Resistance Minimum in Dilute Magnetic Alloys. Prog. Theor. Phys. 1964, 32, 37–49. 10.1143/PTP.32.37. [DOI] [Google Scholar]
  65. Galler A.; Ener S.; Maccari F.; Dirba I.; Skokov K. P.; Gutfleisch O.; Biermann S.; Pourovskii L. V. Intrinsically weak magnetic anisotropy of cerium in potential hard-magnetic intermetallics. npj Quantum Mater. 2021, 6, 2. 10.1038/s41535-020-00301-6. [DOI] [Google Scholar]
  66. Kishimoto Y.; Kawasaki Y.; Ohno T. 11B NMR Study of Magnetism in RRh3B2 (R = La, Ce, Nd, Sm, Eu and Gd). J. Phys. Soc. Jpn. 2004, 73, 1970–1981. 10.1143/JPSJ.73.1970. [DOI] [Google Scholar]
  67. Prakash O.; Thamizhavel A.; Ramakrishnan S. Ferromagnetic ordering of minority Ce3+ spins in a quasi-skutterudite Ce3Os4Ge13 single crystal. Phys. Rev. B 2016, 93, 064427. 10.1103/PhysRevB.93.064427. [DOI] [Google Scholar]
  68. Schumacher D. P.; Wallace W. E. Magnetic Characteristics of Some Lanthanide Nitrides. Inorg. Chem. 1966, 5, 1563–1567. 10.1021/ic50043a021. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cm2c01282_si_001.pdf (1,014.8KB, pdf)
cm2c01282_si_002.cif (1.5KB, cif)
cm2c01282_si_003.cif (1.5KB, cif)

Articles from Chemistry of Materials are provided here courtesy of American Chemical Society

RESOURCES