Abstract
Long-time dynamical processes, such as those involving protein unfolding and ligand interactions, can be accelerated and realized through steered molecular dynamics (SMD). The challenge has been the extraction of information from such simulations that generalize for complex nonequilibrium processes. The use of Jarzynski’s equality opened the possibility of determining the free energy along the steered coordinate, but sampling over the nonequilibrium trajectories is slow to converge. Adaptive steered molecular dynamics (ASMD) and other related techniques have been introduced to overcome this challenge through the use of stages. Here, we take advantage of these stages to address the numerical cost that arises from the required use of very large solvent boxes. We introduce telescoping box schemes within adaptive steered molecular dynamics (ASMD) in which we adjust the solvent box between stages and thereby vary (and optimize) the required number of solvent molecules. We have benchmarked the method on a relatively long α-helical peptide, Ala30, with respect to the potential of mean force and hydrogen bonds. We show that the use of telescoping boxes introduces little numerical error while significantly reducing the computational cost.
1. Introduction
Molecular dynamics (MD) simulations provide an exquisite level of detail about the movements of molecules at atomic resolution not always readily available to experiments.1 Consequently, they have been widely used to, for example, complement experiments in uncovering the underlying mechanism of chemical reactions,2−4 refine protein structures,5 or guide experiments in the discovery of promising compounds or materials.6−8 However, the accuracy of MD is often limited by approximations in the underlying force fields and the accuracy of the numerical integrator, while its predictions may be limited by the convergence of the sampling trajectories.9−13 Meanwhile, due to the millions of interatomic interactions involved, the accessible time scale of all-atom simulation is often too short to observe many “interesting” water-involved biological processes that take place at longer times—from microseconds or milliseconds—and that involve important processes such as protein folding.14−16 The size of these simulations is also much larger than that of the selected process because the solvent must be included and must be large enough to limit boundary effects. Moreover, while water is a ubiquitous solvent, it is also particularly difficult to model because of its important quantum mechanical and associative properties. It is also relatively expensive to simulate at the explicit—viz. all-atom—level, and several models are available17−20 and continue to be developed. This computational challenge can be side-stepped—albeit it with the sacrifice of some accuracy (see refs (21 and 22))—through the use of an implicit solvent which significantly reduces the number of degrees of freedom of the modern system. Coarse-grained modeling can also further reduce the computational cost—though at the price of additional approximation— for even larger systems.23−29 It scales up particle sizes and smoothens the energy landscape to escape energy “traps” that limit sampling. However, they may be limited by the determination of enthalpy and entropy balance and loss of essential details.30 The objective of this work is to demonstrate that, in those systems which require an all-atom description of the solvent box, we can use a staged approach to vary the size of the box during the simulation so as to limit the associated computational cost.
The need for longer times in MD trajectories is driven not only by the determination of time-dependent variables but also that of equilibrium observables that are obtained by averaging over trajectories. The latter requires algorithm developments to accelerate the trajectories—which for example emerge ipso facto from coarse-graining techniques—and to increase sampling efficiency.31−37 SMD,38 for example, has been used to reveal structural changes in proteins39,40 and unbinding potentials41 as candidate drugs are pulled away from them. In tandem with nonequilibrium work theorems, Schulten and Park,42,43 used SMD to reveal the mechanism or underlying unbinding potentials efficiently by applying an external force on the system. Unfortunately, sampling of the nonequilibrium trajectories in SMD can also be plagued by convergence. The use of the Jarzynski equality (JE) to average across the nonequilibrium trajectories makes it possible to obtain the free energy difference across the pulling direction. However, as the deviation along the pulling coordinate increases, so does the spread of the work functions, thereby limiting the accuracy of the Jarzynski average (JA). Indeed, in some cases, a single trajectory remains the one with the lowest work function and dominates the JA arbitrarily. These numerical errors are exacerbated by larger systems which effect larger fluctuations and require even longer pulling distances to fully unravel. The speed of the pulling of the nonequilibrium trajectories has also been seen to affect convergence, as, for example, Li et al.44 found that fast pulling can affect the PMF results when a limited number of realizations are performed. Specifically, as the pulling speed V is increased, the nonequilibrium work values used to determine the JA increase in concert as a quadratic function of ln(V).44 Thus, a low pulling speed and a reasonably large number of trajectories are often needed to obtain accurate results through SMD, which in turn requires significant to inaccessibly large computational resources.
ASMD45−47 was developed to address the convergence challenges in SMD by dividing the process of interest into a series of stages that ipso facto converge readily. Staged approaches have been used to obtain free energies in several contexts,48−54 and it is not surprising that they are useful in the context of SMD. Within each stage of ASMD, standard SMD simulations are carried out. At the end of each stage, a contraction of the trajectories is performed to reduce the sample space of the nonequilibrium system to be within a neighborhood of the equilibrium distribution. The implementation of ASMD is contingent on the choice of the contraction criterion which in turn leads to various versions of the method—e.g., naïve adaptive steered molecular dynamics (naïve ASMD),45−47 multibranched adaptive steered molecular dynamics (MB-ASMD),55 and full-relaxation adaptive steered molecular dynamics (FR-ASMD).56 Note that no matter which contraction is used, the relative cost of the calculation depends on the size of the solvent box. As many applications57−59 of the external force involve the restructuring of the target system, the solvent box is often large and exacerbates the cost of the sampling. Beyond our group, ASMD has been used successfully to obtain the energetics of several challenging systems, including the characterization of a host–guest interaction,60,61 mechanism of the complex dynamics,62 mutagenesis,63 binding affinity,64 protein–ligand interactions,65−70 and protonation effects.71
There has been much debate in the literature about the need for an explicit—viz. all-atom—description of solvent particles and the size requirements for the solvent box to provide converged and accurate results.72−78 Notably, Gapsys and de Groot recently concluded that the box size shows no significant impact on the system, both thermodynamically and kinetically79 in agreement with conclusions from prior work by several groups,80−82 presumably as long as the box is big enough. Moreover, an explicit solvent model is necessary to accurately capture solvent-mediated interactions when they play an important role in the dynamics. For example, water is known to play a structural role in biological systems,58,83−86 and this sometimes necessitates the use of explicit water in the solvent.
Molecular dynamics (MD) simulations scale at best at 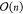 with the size of the system—viz. n atoms.87,88 For large systems,
a high pulling speed and reduced number of trajectories are generally
needed to complete SMD and ASMD simulations within reasonable wall
clock times. In turn, this tends to sacrifice accuracy. In deference
to this limitation, the number of atoms in the simulation is often
kept to the minimum necessary to still capture the dynamics of the
system of interest. As most of the atoms in the simulation are often
found in the solvent, it should therefore not be surprising that limiting
the size of the solvent box is common practice as long as it is large
enough per the previous discussion. In principle, as the system changes
in size, the solvent box can also be adjusted in the process of carrying
out the simulation to maintain this optimally efficient condition.
Indeed, there are literature precedents for adjusting the size of
the periodic box and resolvating the system as the simulation progresses.59,81,82,89,90 However, none of these approaches, to our
knowledge, have been applied to staged steering such as implemented
in ASMD, which is the approach we take here in designing the so-called
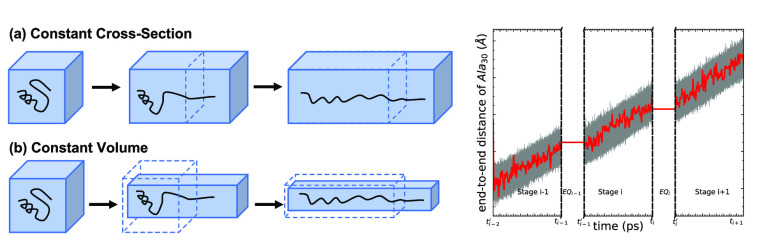
telescoping boxes illustrated in Figure 1.
with the size of the system—viz. n atoms.87,88 For large systems,
a high pulling speed and reduced number of trajectories are generally
needed to complete SMD and ASMD simulations within reasonable wall
clock times. In turn, this tends to sacrifice accuracy. In deference
to this limitation, the number of atoms in the simulation is often
kept to the minimum necessary to still capture the dynamics of the
system of interest. As most of the atoms in the simulation are often
found in the solvent, it should therefore not be surprising that limiting
the size of the solvent box is common practice as long as it is large
enough per the previous discussion. In principle, as the system changes
in size, the solvent box can also be adjusted in the process of carrying
out the simulation to maintain this optimally efficient condition.
Indeed, there are literature precedents for adjusting the size of
the periodic box and resolvating the system as the simulation progresses.59,81,82,89,90 However, none of these approaches, to our
knowledge, have been applied to staged steering such as implemented
in ASMD, which is the approach we take here in designing the so-called
telescoping boxes illustrated in Figure 1.
Figure 1.
Two possible schemes for the implementation
of telescoping boxes
in ASMD: (a) constant cross section in which one adjusts—viz. increases or pulls—only the length between the
end points of the protein which defines an axis labeled as z or (b) constant volume in which one adjusts all three
widths to preserve the volume by increasing along z by a factor of f and along x and y each by a factor of 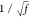 .
.
The challenge to address the growing footprint of proteins as they are pulled apart manifests itself in several cases. While the examples benchmarked here involve a linear stretch, ASMD and other steered approaches have been implemented along nonlinear paths, e.g., the circular opening of NPY addressed via ASMD.45,91 As we consider larger proteins with a large number of secondary structural components and identify more complex unfolding paths along which they are pulled apart, the resulting structures will likely grow in one or more directions.
Thus, we introduce here the scheme of telescoping boxes within ASMD by way of modifying the periodic box in between stages to maintain an optimal size of solvent particles. Compared to prior work in which successive boxes are larger from stage to stage,81,89 the telescoping box scheme also allows for the reduction along one or more dimensions of the periodic box. A special case considered here involves a constant volume deformation of the telescoping box as one of the dimensions is increased and the others are concomitantly decreased. We report here the use of this scheme on the Ala30 peptide to benchmark and validate it by performing the potential of mean force (PMF) profile calculation and other observables, such as hydrogen bonds.
2. Models and Methods
2.1. Steered Molecular Dynamics
Steered molecular dynamics (SMD) provides a controlled deformation of a molecule within an MD simulation in analogy to that which can be realized experimentally in atomic force microscopy (AFM) or optical tweezers experiments, though at much faster speeds.92,93 Schulten and Park42,43 introduced the use of the JE to average over an ensemble of nonequilibrium SMD trajectories to obtain the PMF and other equilibrium observables.
In a typical implementation of SMD, an auxiliary particle is attached to a system variable—e.g., a selected atom or some collective coordinates associated with a region of interest—through a harmonic potential. The motion of the auxiliary particle is predicated on following a particular path under a prescribed condition such as constant force or constant velocity. Through the auxiliary particle’s coupling to a system variable—e.g., an atom or residue at the terminus of a protein—while another variable is fixed—e.g., an atom or residue at the other terminus of a protein—it steers the protein along the selected path—e.g., the unfolding of the protein as the termini are pulled apart.
For each nonequilibrium
trajectory integrated using SMD, the change
in the position of the selected system variable ξ relative to
the auxiliary particle is tracked to obtain the instantaneous applied
force, and its accumulation is the work 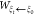 along the path from ξ0 to ξt. An average over the trajectories
is performed using the JE94−97 to obtain the PMF, G(ξt), along the selected path—or reaction
coordinate—ξt,
along the path from ξ0 to ξt. An average over the trajectories
is performed using the JE94−97 to obtain the PMF, G(ξt), along the selected path—or reaction
coordinate—ξt,
| 1 |
where β is 1/kBT with kB as the Boltzmann constant and T as the absolute temperature.
While all of the nonequilibrium trajectories in the average of eq 1 formally contribute, in practice those with the lowest work values near the resulting average are dominant. The nonequilibrium trajectories tend to wander ever farther from the dominant pathways as they are extended. This leads to a number of trajectories with work functions characteristic of the correct average to decrease dramatically along the steered path. To overcome this sampling challenge, one could simply calculate more trajectories. Unfortunately, this becomes prohibitively expensive very quickly and has limited the use of SMD with the JA.
2.2. Adaptive Steered Molecular Dynamics
To overcome the limitation of SMD and improve the efficiency of sampling, ASMD was developed earlier.45,46 In ASMD, the steering along the whole reaction coordinate is completed sequentially in several stages. A standard SMD simulation is performed within each stage to obtain the corresponding piece of the PMF. At the end of each stage, a contraction is performed, without adding additional work to the system, to obtain a set of representative structures of the equilibrium ensemble which can be used to initiate the next stage. Since no work is added to the system during contraction, the PMF calculation is not affected across the various variants of ASMD as long as the contraction does not somehow reduce the ensemble that is being averaged over. Naïve ASMD provides the strongest reduction, and the other variants become necessary for systems that sample complex pathways in the ensemble.
In the implementations of ASMD, we have generally used constant velocity vp pulls along a linear segment between the initial and final points of a given stage. This allows a simplification in parametrizing the path in time t and designates the segments with respect to the time intervals (tj–1, tj) of the jth stage for j from 1 to N total stages. As the PMF accumulates along the pulling path, its value can be written relative to that at the beginning of the stage. For example, if the reaction coordinate is selected as the end-to-end distance ree and the path is taken from its value ree(t0) for the initial compact structure to that of ree(tN) for an extended chain, then the accumulated free energy—viz. the PMF—at a time t ∈ (tj–1, tj) is
| 2 |
where Wj is the nonequilibrium work from tj–1 to t evaluated for each
of the N trajectories 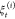 in the jth stage.97 The time increment of the stages is selected
to be short so as to avoid the spreading of the nonequilibrium trajectories
that plague SMD.
in the jth stage.97 The time increment of the stages is selected
to be short so as to avoid the spreading of the nonequilibrium trajectories
that plague SMD.
2.3. ASMD with a Telescoping Box
We have reported that ASMD can reduce the number of trajectories needed to converge the PMF relative to a standard SMD calculation by as much as a factor of 100.98 Nevertheless, the solvent box must be large enough to fully solvate the protein through the entire extension, and this can be quite expensive because the number of solvent molecules is consequently large. Using the schematic structures shown in Figure 1, such a simulation corresponds to using the large box shown at the end of case (a) for the entire simulation. In order to enhance the efficiency of nonequilibrium sampling without affecting the accuracy of the various ASMD methods, we introduce here the telescoping box schemes shown in Figure 1: (a) constant cross-section telescoping boxes in which the length of the box is extended along the direction parallel to the pulling direction while maintaining the sides orthogonal to the pulling direction constant and (b) constant volume telescoping boxes in which the length of the box along the parallel direction is extended while the orthogonal directions are reduced so as to maintain a constant volume. In case (b), the number of solvent molecules remains approximately constant, and thus, the constant-volume telescoping box offers the greatest possible savings in simulation time.
The existence of transitions between the ASMD stages during which the contraction takes place offers an opportunity to restructure the solvation box as long as it is performed without doing work to the system. As indicated in the two panels of Figure 1, the strategy involves using solvent boxes within each stage whose size is matched to the amount of solvent required to properly solvate the protein structures along the path of the given stage. The resizing of the box can be performed in at least two different ways: (i) the entire solvent is eliminated, and the remaining protein is resolvated in the new periodic box while protein ends are held fixed, or (ii) only those waters outside of the new periodic box are eliminated, and the remaining protein plus water system is immersed and resolvated into the periodic box. After this resolvation, the system is equilibrated while the end-to-end distance, ree, remains fixed at the value of the previous stage. Since the system is constrained during equilibration, no additional work is performed and added to the system. Therefore, there is no nontrivial contribution to the JA from the resizing of the box. The results reported below explicitly employed approach (i) though we also found that approach (ii) led to similar results.
2.4. Simulation Methods
To demonstrate and validate the ASMD schemes employing telescoping boxes, we use a midsized peptide, Ala30, whose PMF was benchmarked earlier.98 All of the simulations are initiated with the same starting structure of the protein and solvent. Specifically, Ala30 was built using the VMD plugin molefacture99 and capped with an acetylated N-terminus and amidated C-terminus (309 atoms) and can be seen to exhibit a single helical domain. It was immersed in an explicit TIP3P water solvent box of sides along x × y × z equal to 40 Å × 40 Å × 75 Å which required ∼11,000 atoms.
In all SMD simulations, the system is propagated using NAMD.100 Interactions are described by the CHARMM36 force field101 in consideration of the CMAP correction terms for the peptide’s helical structure. All simulations were performed at 300 K. A 1 ns NPT equilibration step is first performed on the system with the Cα ends constrained and the damping coefficient set to 5 ps–1. A Nosé–Hoover Langevin piston is used to regulate pressure with a decay period of 100 fs and a damping time constant of 50 fs. Thereafter, the system is equilibrated under NVT conditions in three successive 200 ps propagations in which the backbone is constrained using a harmonic spring that is released gradually taking on the values 10.0, 5.0, and 1.0 kcal/(mol Å2), in turn. The peptide is then once again fully relaxed without constraint for 1 ns. This results in a deviation in its primary axis from the z-axis, and so the entire system—that is, protein and solvent—is rotated to place the proteins back along the z-axis. This structure is then relaxed for an additional 1 ns under NPT conditions with the protein ends constrained at their positions on the z-axis. The initial structure (or structures) for the ASMD simulations is randomly selected from the equilibrated structures near the end of this last constrained trajectory. The final structure is verified through the root mean square deviation (RMSD) analysis of the backbone using the corresponding NAMD plug-in.
In the ASMD simulation, the peptide is stretched by 60 Å along the z-axis in 25 stages—each 2.4 Å in length—at a 1 Å/ns pulling speed for 100 trajectories per stage (tps). This is sufficient to fully break the intrapeptide interactions. During the ASMD stages, the Cα of the first residue was held fixed, and the Cα at the other end is attached to the auxiliary atom which is steered along the pulling path. We introduce the telescoping box schemes described above at the end of each stage. First, based on the selection criterion of ASMD, one or more structures with work values near the JA are selected to represent the equilibrium ensemble. In the case of naïve ASMD, for example, only one structure is selected, and it is the one whose work value is closest to the JA. Second, after completing the contraction, the periodic bounding box is resized according to the selected protocol. For simplicity, we extend the box along the z-axis—viz. the direction parallel to the direction that the protein is pulled—in equal increments—viz. 2.4 Å in length—concomitant to the number of stages being pulled. The lengths of the boxes in the x and y directions are either held fixed for constant cross-section telescoping boxes or reduced proportionally to ensure constant volume telescoping boxes. The selected configuration(s) are then resolvated and equilibrated in the new bounding box. The equilibration of the newly solvated system is again propagated at 300 K and fixed NPT conditions with the ends of the protein fixed for the short but additional time needed to reach an equilibrated structure confirmed according to the equilibration of the RMSD.
3. Results and Discussion
The main advantage for the use of telescoping boxes in ASMD is the reduction in the number of solvent molecules required at each stage and the associated savings in the numerical propagation of the resulting smaller solvent configurations. For example, naïve ASMD simulations of an all-atom Ala30 solvated in water are typically propagated in a 40 Å × 40 Å × 130 Å periodic bounding box and require configurations of ∼19,500 atoms throughout. In comparison, in a telescoping box scheme at a constant cross section which takes the periodic bounding box from 40 Å × 40 Å × 75 Å to 40 Å × 40 Å × 130 Å, the initial structure needs roughly half of the number of atoms and averages about 75% of the atoms over the simulation. Meanwhile, the constant cross-section scheme ends with a box of dimensions, 29.8 Å × 29.8 Å × 135 Å, requiring only approximately half the number of atoms throughout the pull. In terms of computing performance, naïve ASMD using a constant (but large) box of sufficient size to fully solvate all of the structures of the protein from its initial compact to final extended coil structures requires ∼2,100 s on a single K80 GPU node for one trajectory per stage. Meanwhile, through the introduction of telescoping boxes, the simulation time for each trajectory decreases to ∼1,500 s for the first stage and ∼1,700 s (in the constant volume scheme) or ∼2,250 s (in the constant cross-section scheme) for the last stage. For the constant volume scheme, since the number of atoms remains approximately constant during the simulations, the computational time for each stage is approximately the same. On the other hand, in the constant cross-section scheme, the number of atoms increases from ∼11,000 to ∼20,000 over the simulation, and thus, the simulation time increases over the stage. Furthermore, for the constant volume scheme, 3000–3500 s are required for a 5 ns equilibration simulation, while for the constant cross-section scheme, the largest system (in the last stage) would take ∼4,000 s for a 5 ns equilibration simulation. In summary, even though the telescoping box in ASMD requires an additional equilibration of the solvent in the resized box at the end of each stage, the impact of system size on the computational efficiency is still significant. Moreover, as more trajectories are generated to increase accuracy, the reduction in the required computation time resulting from the use of the telescoping boxes for each trajectory adds up, making this a useful approach.
Since the contraction criterion for the naïve
ASMD selects
one representative structure whose work is closest to the JA at the
end of each stage, only one structure with the ends fixed is resolvated
and equilibrated during the equilibration step at the end of the contraction
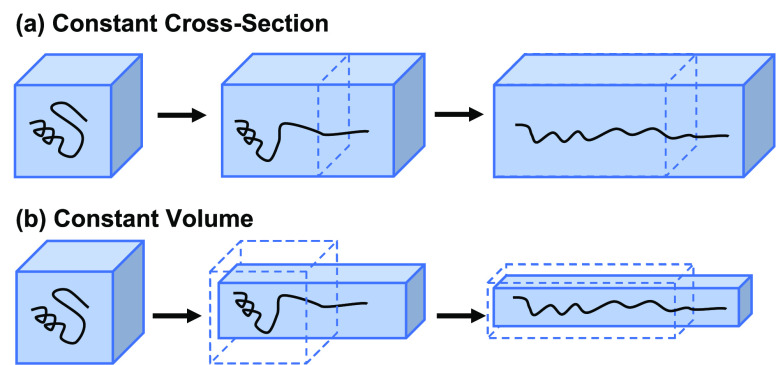
as shown in Figure 2. The gray curves represent the trace of the end-to-end distance
for all trajectories, while the red curve refers to the selected trajectory
based on the naïve ASMD criterion. During the production phase
of the (i – 1)th stage from time 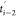 to ti–1, the protein is stretched at a constant pulling speed
by the auxiliary atom, and thus, the end-to-end distance increases
linearly with fluctuations. At the end of the (i–1)th stage, the protein is resolvated and equilibrated with a
bigger solvent box in the auxiliary stage, EQi–1, either under constant cross section or constant
volume. The time ti–1 to
to ti–1, the protein is stretched at a constant pulling speed
by the auxiliary atom, and thus, the end-to-end distance increases
linearly with fluctuations. At the end of the (i–1)th stage, the protein is resolvated and equilibrated with a
bigger solvent box in the auxiliary stage, EQi–1, either under constant cross section or constant
volume. The time ti–1 to 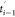 for equilibration can vary and depends
on the system and solvent. In the case of naïve ASMD, only
one structure is retained after contraction, and the ends are fixed
during the auxiliary equilibration stage, EQi–1. Consequently, the end-to-end distance does not change
and is shown as a line in Figure 2. In other variants of ASMD, each of the structures
available after the contraction is separately equilibrated while holding
the ends fixed. Consequently, the average of their end-to-end distances
also does not change during the equilibration step, also leading to
a line in this step. Once the structure (or structures) is reconverged
in the larger box, it serves as the initial structure for the SMD
pulling of the protein in the ith stage.
for equilibration can vary and depends
on the system and solvent. In the case of naïve ASMD, only
one structure is retained after contraction, and the ends are fixed
during the auxiliary equilibration stage, EQi–1. Consequently, the end-to-end distance does not change
and is shown as a line in Figure 2. In other variants of ASMD, each of the structures
available after the contraction is separately equilibrated while holding
the ends fixed. Consequently, the average of their end-to-end distances
also does not change during the equilibration step, also leading to
a line in this step. Once the structure (or structures) is reconverged
in the larger box, it serves as the initial structure for the SMD
pulling of the protein in the ith stage.
Figure 2.
An illustration of the progression of end-to-end distances of the ensemble of Ala30 structures along the stretching in and between two characteristic stages. The average end-to-end distance ree is shown in red, and the ensemble of trajectories is overlapped in gray. For specificity, the data shown here comes from the pulling of Ala30 for the three stages starting from the initial pull—viz. i = 2 in the notation of the x-axis labels.
3.1. Energetics
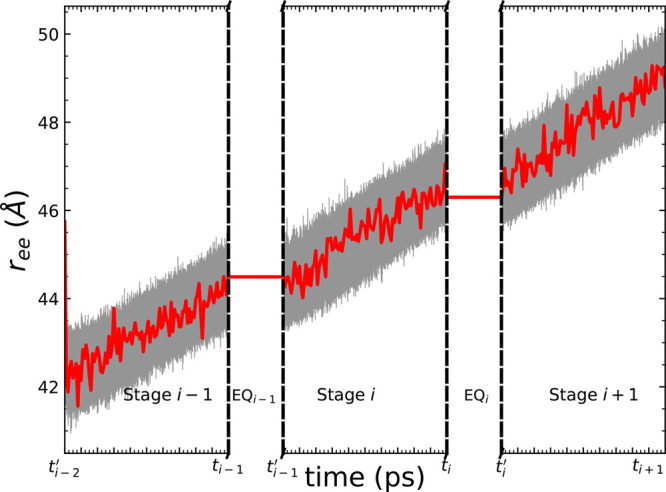
The use of telescoping boxes in naïve ASMD does not affect the PMF profiles of the overall process as shown in Figures 3 and 4 for the test case of the unfolding of Ala30. As detailed in the Methods section, the ASMD simulations are divided across 25 stages so that each stage is small enough that the spreading of the distribution of work values does not lead to many effectively noncontributing trajectories. In Figure 3, the curves for the work across all of the nonequilibrium trajectories (100 tps) are overlaid in each stage. As the trajectories sampled for each of the ASMD implementations are different, the fans of the work trajectories in each stage are necessarily different across the schemes. However, the JA over the work trajectories results in the same PMFs within their error bars as indicated in Figure 4 and Figure 5. We do not benchmark these results relative to those from an equilibrium free energy method, because the PMFs obtained from SMD and umbrella sampling have been seen to be in agreement when both are sufficiently converged,102 and we have earlier benchmarked ASMD relative to SMD in our past work.46,97 Meanwhile, it is also notable that the auxiliary equilibration stage (after resolvation) performs no work on the system, and hence there is no additional energy bump in between stages with the use of the telescoping boxes. ASMD could get the converged PMF results from a reasonable number of nonequilibrium trajectories.
Figure 3.
Work values of the ensemble of trajectories in naïve ASMD along the unfolding direction of Ala30 employing three different schemes: (a) constant (and large) solvation box, (b) telescoping boxes with constant volume scheme, and (c) telescoping boxes with constant cross section. The black curves represent the work values for all generated trajectories, while the red dashed curves are the PMF. All PMF profiles have been obtained using 100 tps at 1 Å/ns. The naïve ASMD results for case (a) are the same as reported and benchmarked in ref (98).
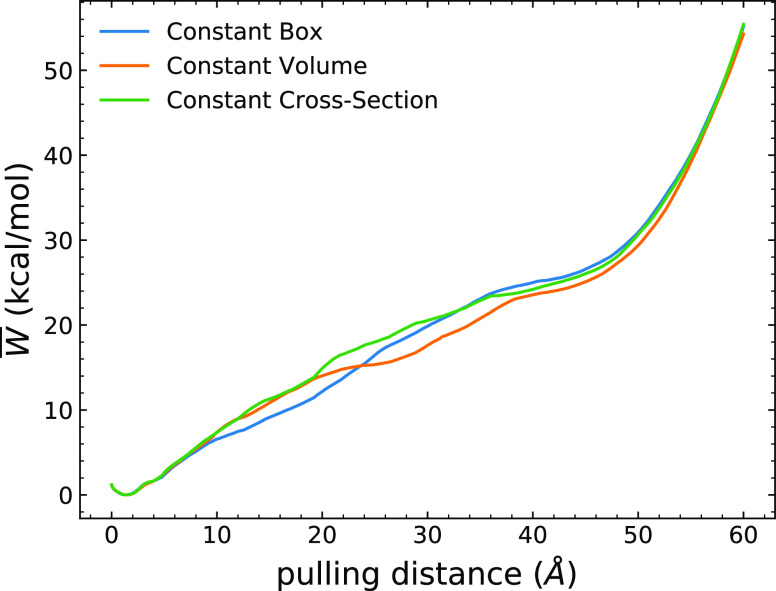
Figure 4.
Comparison of the energetics of Ala30 among different ASMD variants. The blue curve corresponds to naïve ASMD with a constant solvent box from ref (98), while the orange and green curves correspond to ASMD with the telescoping box schemes noted in the legend. The PMFs have been obtained using 100 tps at 1 Å/ns.
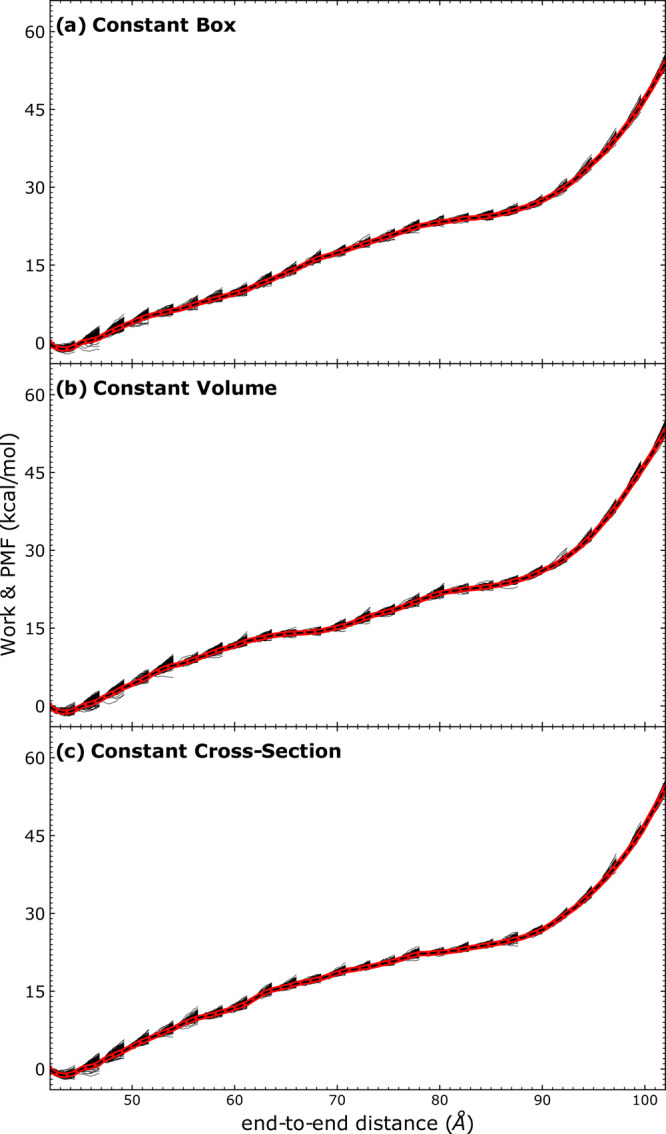
Figure 5.
RMSE analysis for two types of telescoping box schemes compared to naïve ASMD with a constant box (dashed black curve) from ref (98).
The PMF overlaid with the RMSE profiles resulting from the use of two kinds of telescoping box schemes in naïve ASMD are also shown in Figure 5 in comparison to the PMF reported earlier using naïve ASMD with a constant box. The error is determined as the sum of the accumulations from the previous stages and the current stage as97
| 3 |
where δEi is the error for stage i, and ti refers to the time at the end of stage i. Both PMF profiles of the telescoping box schemes show comparable results with the one from naïve ASMD. Furthermore, compared with the scale of PMF results, the error bar shown as the shaded area is relatively small, indicating the robustness of the result from these methods. These results also suggest the negligible impact of solvent box size as has been reported by others for related systems.79,80,89
3.2. Hydrogen Bonding Profiles
Other observables,
such as the hydrogen bonds, can also be determined based on the Jarzynski
weights of each nonequilibrium trajectory, which are again not affected
by the addition of equilibration in the implementation of the telescoping
box schemes. The hydrogen bond counts for each trajectory were determined
using the recent update of MDAnalysis (2.0).103−106 It provides an improved detection of hydrogens bonded to heavy atoms
and for consideration of capping atoms which resulted in small changes
in the hydrogen-bonding profiles we report here in comparison to our
earlier work. The donor(D)–acceptor(A) distance cutoff is set
as 4.0 Å, and the D–H–A angle is set as 140°.
The MDAnalysis code provides the instantaneous number of hydrogen
bonds 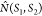 between two selected sets of molecular
units—e.g., all of the water molecules, the whole protein,
or some subset of the protein. We use the hat in
between two selected sets of molecular
units—e.g., all of the water molecules, the whole protein,
or some subset of the protein. We use the hat in 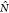 to distinguish the value for a given configuration
and drop it when we refer to the corresponding observable over many
trajectories. Specifically, it is97
to distinguish the value for a given configuration
and drop it when we refer to the corresponding observable over many
trajectories. Specifically, it is97
| 4 |
where 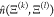 is the number of hydrogen bonds between
the two specified relative components Ξ(k) in S1 and Ξ(l) in S2, respectively.
Consequently, the weighted observable(s) for the number of hydrogen
bonds across the distribution of N nonequilibrium
trajectories is(are)97
is the number of hydrogen bonds between
the two specified relative components Ξ(k) in S1 and Ξ(l) in S2, respectively.
Consequently, the weighted observable(s) for the number of hydrogen
bonds across the distribution of N nonequilibrium
trajectories is(are)97
| 5 |
following the notation used earlier in eq 2.
As in the PMF profiles, the hydrogen bond profiles along the end-to-end distance shown in Figure 6 exhibit the same trends regardless of which scheme—fixed box or telescoping boxes—is implemented within naïve ASMD. The intrapeptide hydrogen bonds are lost almost linearly along the process, from ca. 20 to 0. Moreover, the intrapeptide hydrogen bonds (Figure 6 (top)) are also replaced with the protein–water hydrogen bonds (Figure 6 (bottom)) as previously reported.98 The protein–water hydrogen bonds were determined for water molecules around 10 Å of the peptide. However, abrupt changes in hydrogen bond values were also observed during the stretch, which is caused by the contraction between stages. That is, at the end of each stage, only one configuration is selected (in the case of naïve ASMD), and the observed value for that one specific selected structure fluctuates from the average.
Figure 6.
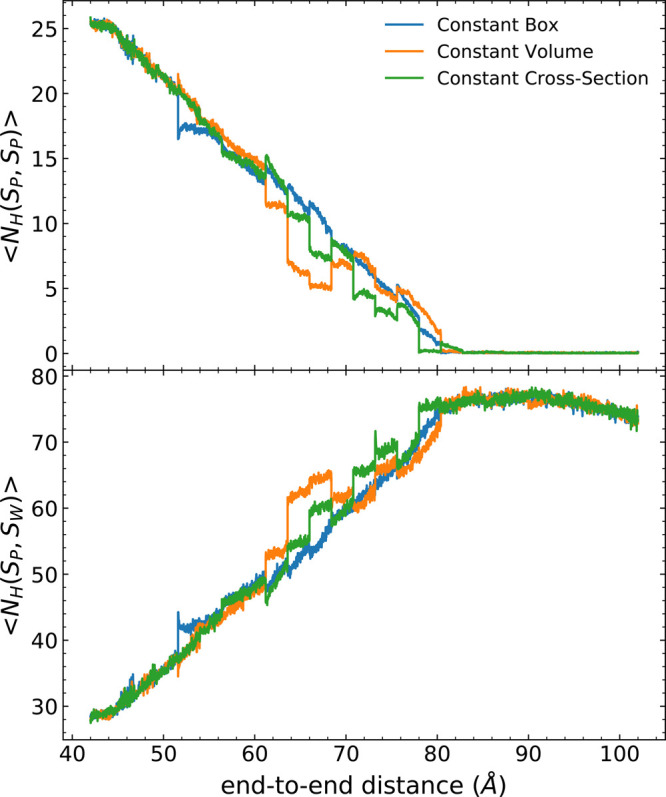
Hydrogen bond profiles for different schemes of ASMD: constant box (blue), constant volume (orange), and constant cross section (green). The top panel corresponds to the intrapeptide hydrogen bond interaction, while the bottom panel corresponds to the number of the peptide-water hydrogen bonds for the water molecules within 10 Å of the peptide. The results98 for naïve ASMD with a constant box was reanalyzed with MDAnalysis 2.0 version in consideration of the capped atoms of the peptide, resulting in slightly different but improved estimates of the hydrogen bonding.
Furthermore, from ca. 62 Å to 76 Å of the end-to-end distance (ca. 20 Å to 34 Å of ree), the intrapeptide hydrogen bond values of both telescoping boxes schemes were lower than the one gained from naïve ASMD. Coupled with the telescoping box schemes, the extra resolvation stage also allows the partially unfolded protein to re-equilibrate itself and reform hydrogen bonds at a given pulling distance. Consequently, the conformation of the hydrogen bond structure through the stage is not a trivial test. Based on Figure 6, the general trend is that intrapeptide bonds are lost linearly over time for all three method schemes. There are fluctuations between the stages primarily because of the over-reliance of the contraction to a single structure in naïve ASMD but that appear to be averaged out through the sampling. The partially unfolded Ala30 intermediates have previously been reported to form the polyProline II (pPII) conformation.107,108 Indeed, we found in our previous work (Figure S2 of ref (98)) that the proportion of the pPII structure keeps increasing as the pulling proceeds, and we found the same trends in all three box schemes (not shown).
Intrapeptide hydrogen bonds can be classified according to the number of residues in the chain between the contact pair: i → i + 3 (310-helix), i → i + 4 (α-helix), and i → i + 5 (π-helix). As seen in Figure 7, most of the intrapeptide hydrogen bonds are α-helical contacts (shown in the bottom panel) which are successively broken as the protein is unfolded. The π-helical contacts are not reported in the figure because there were essentially zero such contacts when averaged across the ensemble of nonequilibrium trajectories. The 310-helical contacts at the end-caps are broken in the first 15 Å of the stretch of the protein. The continued stretch of the protein also leads to an apparent steady-state number of 310-helical contacts (shown in the top panel) in which the most recently created contacts are broken as new ones emerge from the sites that recently lost α-helical contacts. At ca. 65 Å, there are deviations in the number of hydrogen bonds observed in (i → i + 4) contacts from the telescoping box schemes (orange and green curves) in Figure 7 in comparison to those from the constant box scheme. This may arise from a reorganization of the structure—such as from a premature formation of pPII helix configurations—that is not quite relaxed during the application of telescoping boxes under the current pulling conditions with respect to this observable. However, the error is small and can be minimized with additional sampling, if need be.
Figure 7.
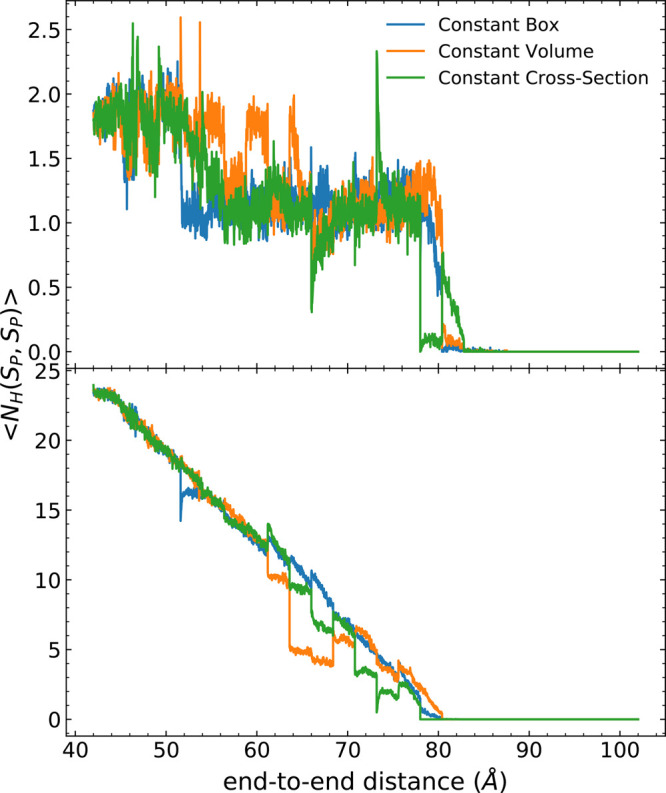
Classification of hydrogen bonds, including 310- (top) and α-helical (bottom) for each ASMD method for the three schemes of constraining the box size as labeled in Figure 6. The π-helical contacts are not shown because they were essentially zero along the process.
We noted earlier that de Groot’s analysis79 of an alanine dipeptide suggested that the discrepancy among various sizes of solvent boxes can be eliminated by increasing the number of trajectories sufficiently. The general agreement for both the PMF and hydrogen bond profiles between the different choices of schemes with and without telescoping boxes suggests that the solvent box can even be changed throughout the course of the simulation.
4. Conclusion
The combination of the SMD method and JE provides a way to sample rare events within the time accessible to MD simulations and thereby also provides insight on possible mechanisms. However, it is hampered by the lack of convergence in the average of the exponential of work over the nonequilibrium trajectories as the extension of the external pull grows larger and larger. ASMD was developed to enhance the sampling by limiting the spread of work for the overall process so that all generated trajectories can sample the most significant events. It has been previously reported that ASMD can produce similar or even better results than SMD methods.46,47,56 Nevertheless, SMD and ASMD are both hampered by the fact that one must use a constant solvent box that is large enough to solvate the compact and coil structures of the protein and every structure in between.
In this work, we found that we can avoid the limitations caused by the constant box in ASMD by adjusting the size of the solvent boxes between stages. The introduction of telescoping boxes in this way improves the efficiency of the simulations as fewer solvent molecules must be included in most of the stages. In addition to the fewer atoms involved in the simulations, the extra equilibration between stages required to relax the solvent and the protein with its ends fixed provides a narrowing of the nonequilibrium distribution similar to that seen in FR-ASMD, leading to the possibility of improved convergence of the method. One concern about the use of ASMD is that the contraction can lead to abrupt changes in observables between stages, and this error appeared to worsen slightly in the naïve implementation of telescoping boxes. However, it can be mitigated through the application of a resolvation approach in which only some of the solvent is inserted (in the region not previously occupied by the solvent box) and addressed through less strict contractions such as that implemented in MB-ASMD. Furthermore, though not shown here, the telescoping box scheme can also be implemented with other variants of ASMD as needed when the unfolding of the protein is more complex,97 that is, for those proteins whose unfolding traverses multiple attractive basins as they unfold, or when more than one configuration needs to be sampled. Examples that can benefit from this new scheme include the resolution of the effect on the energetics of proteins upon mutation such as Trpzip1.91,109 While that class of protein was accessible without telescoping boxes, larger proteins such as actophorin (with its 138 amino acids) are much more expensive110,111 and will be pursued in future work.
In the telescoping scheme, there are at least two possible ways to adjust the size of boxes: (a) elongating the length of the solvent box with a constant cross-section area or (b) adjusting the dimension of the solvent box but keeping the volume unchanged. We found that both schemes provide similar results as ASMD with a constant solvent box. Although additional equilibration integration time is needed for the telescoping box scheme, the payoff of adjustable box size from the stretch process is still significant. The impact of the telescoping box scheme on systems with ions or arbitrary proteins has not been confirmed here and is the subject of future research.
Acknowledgments
This work has been partially supported by the National Science Foundation (NSF) through Grant No. CHE 2102455. The computing resources necessary for this work were provided in part by the Extreme Science and Engineering Discovery Environment (XSEDE) supported by the National Science Foundation (NSF) grant number ACI-1548562 through allocation CTS090079 and in part by the Advanced Research Computing at Hopkins (ARCH) high-performance computing (HPC) facilities supported by NSF grant number OAC-1920103.
The authors declare no competing financial interest.
References
- Frenkel D. Simulations: The Dark Side. Eur. Phys. J. Plus 2013, 128, 1–10. 10.1140/epjp/i2013-13010-8. [DOI] [Google Scholar]
- Herce H. D.; Garcia A. E. Molecular Dynamics Simulations Suggest a Mechanism for Translocation of the HIV-1 TAT Peptide Across Lipid Membranes. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 20805–20810. 10.1073/pnas.0706574105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vettoretti G.; Moroni E.; Sattin S.; Tao J.; Agard D. A.; Bernardi A.; Colombo G. Molecular Dynamics Simulations Reveal the Mechanisms of Allosteric Activation of Hsp90 by Designed Ligands. Sci. Rep. 2016, 6, 23830. 10.1038/srep23830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardi R. C.; Durner E.; Schoeler C.; Malinowska K. H.; Carvalho B. G.; Bayer E. A.; Luthey-Schulten Z.; Gaub H. E.; Nash M. A. Mechanisms of Nanonewton Mechanostability in a Protein Complex Revealed by Molecular Dynamics Simulations and Single-Molecule Force Spectroscopy. J. Am. Chem. Soc. 2019, 141, 14752–14763. 10.1021/jacs.9b06776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heo L.; Feig M. Experimental Accuracy in Protein Structure Refinement via Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, 13276–13281. 10.1073/pnas.1811364115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Ma C.; Fiorin G.; Carnevale V.; Wang T.; Hu F.; Lamb R. A.; Pinto L. H.; Hong M.; Klein M. L.; DeGrado W. F. Molecular Dynamics Simulation Directed Rational Design of Inhibitors Targeting Drug-Resistant Mutants of Influenza A Virus M2. J. Am. Chem. Soc. 2011, 133, 12834–12841. 10.1021/ja204969m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wassman C. D.; Baronio R.; Demir Ö.; Wallentine B. D.; Chen C.-K.; Hall L. V.; Salehi F.; Lin D.-W.; Chung B. P.; Hatfield G. W.; Chamberlin A. R.; Luecke H.; Lathrop R. H.; Kaiser P.; Amaro R. E. Computational Identification of a Transiently Open L1/S3 Pocket for Reactivation of Mutant p53. Nat. Commun. 2013, 4, 1407. 10.1038/ncomms2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun L.; Zhou Y.-X.; Wang X.-D.; Chen Y.-H.; Deringer V. L.; Mazzarello R.; Zhang W. Ab Initio Molecular Dynamics and Materials Design for Embedded Phase-Change Memory. npj Comput. Mater. 2021, 7, 29. 10.1038/s41524-021-00496-7. [DOI] [Google Scholar]
- Serafeim A.-P.; Salamanos G.; Patapati K. K.; Glykos N. M. Sensitivity of Folding Molecular Dynamics Simulations to Even Minor Force Field Changes. J. Chem. Inf. Model. 2016, 56, 2035–2041. 10.1021/acs.jcim.6b00493. [DOI] [PubMed] [Google Scholar]
- Robustelli P.; Piana S.; Shaw D. E. Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, E4758–E4766. 10.1073/pnas.1800690115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp B.; Ospina L.; Deane C. M. Avoiding False Positive Conclusions in Molecular Simulation: The Importance of Replicas. J. Chem. Theory Comput. 2018, 14, 6127–6138. 10.1021/acs.jctc.8b00391. [DOI] [PubMed] [Google Scholar]
- Jorge M.; Garrido N. M.; Queimada A. J.; Economou I. G.; Macedo E. A. Effect of the Integration Method on the Accuracy and Computational Efficiency of Free Energy Calculations Using Thermodynamic Integration. J. Chem. Theory Comput. 2010, 6, 1018–1027. 10.1021/ct900661c.20467461 [DOI] [Google Scholar]
- van Gunsteren W. F.; Daura X.; Hansen N.; Mark A. E.; Oostenbrink C.; Riniker S.; Smith L. J. Validation of Molecular Simulation: An Overview of Issues. Angew. Chem., Int. Ed. 2018, 57, 884–902. 10.1002/anie.201702945. [DOI] [PubMed] [Google Scholar]
- Voelz V. A.; Bowman G. R.; Beauchamp K.; Pande V. S. Molecular Simulation of ab Initio Protein Folding for a Millisecond Folder NTL9(1–39). J. Am. Chem. Soc. 2010, 132, 1526–1528. 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freddolino P. L.; Harrison C. B.; Liu Y.; Schulten K. Challenges in Protein Folding Simulations: Timescale, Representation, and Analysis. Nat. Phys. 2010, 6, 751–758. 10.1038/nphys1713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piana S.; Lindorff-Larsen K.; Shaw D. Atomic-Level Description of Ubiquitin Folding. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 5915–5920. 10.1073/pnas.1218321110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mark P.; Nilsson L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. 10.1021/jp003020w. [DOI] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J. In Intermolecular Forces: Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry Held in Jerusalem, Israel, April 13–16, 1981; Pullman B., Ed.; Springer Netherlands: Dordrecht, 2001; Vol. 14, pp 331–342, 10.1007/978-94-015-7658-1_21. [DOI]
- Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
- Kadaoluwa Pathirannahalage S. P.; Meftahi N.; Elbourne A.; Weiss A. C. G.; McConville C. F.; Padua A.; Winkler D. A.; Gomes M. C.; Greaves T. L.; Le T. C.; Besford Q. A.; Christofferson A. J. Systematic Comparison of the Structural and Dynamic Properties of Commonly Used Water Models for Molecular Dynamics Simulations. J. Chem. Inf. Model. 2021, 61, 4521–4536. 10.1021/acs.jcim.1c00794. [DOI] [PubMed] [Google Scholar]
- Salari R.; Chong L. T. Desolvation Costs of Salt Bridges Across Protein Binding Interfaces: Similarities and Differences Between Implicit and Explicit Solvent Models. J. Phys. Chem. Lett. 2010, 1, 2844–2848. 10.1021/jz1010863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou R. Free Energy Landscape of Protein Folding in Water: Explicit vs. Implicit Solvent. Proteins: Struct., Funct., Bioinf. 2003, 53, 148–161. 10.1002/prot.10483. [DOI] [PubMed] [Google Scholar]
- Levitt M.; Warshel A. Computer Simulation of Protein Folding. Nature 1975, 253, 694–698. 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
- Monticelli L.; Kandasamy S. K.; Periole X.; Larson R. G.; Tieleman D. P.; Marrink S.-J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008, 4, 819–834. 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
- Yesylevskyy S. O.; Schäfer L. V.; Sengupta D.; Marrink S. J. Polarizable Water Model for the Coarse-Grained MARTINI Force Field. PLoS Comp. Biol. 2010, 6, e1000810 10.1371/journal.pcbi.1000810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Jong D. H.; Singh G.; Bennett W. F. D.; Arnarez C.; Wassenaar T. A.; Schäfer L. V.; Periole X.; Tieleman D. P.; Marrink S. J. Improved Parameters for the MARTINI Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697. 10.1021/ct300646g. [DOI] [PubMed] [Google Scholar]
- Wan C.-K.; Han W.; Wu Y.-D. Parameterization of PACE Force Field for Membrane Environment and Simulation of Helical Peptides and Helix–Helix Association. J. Chem. Theory Comput. 2012, 8, 300–313. 10.1021/ct2004275. [DOI] [PubMed] [Google Scholar]
- Peter E. K.; Pivkin I. V. A Polarizable Coarse-Grained Water Model for Dissipative Particle Dynamics. J. Chem. Phys. 2014, 141, 164506. 10.1063/1.4899317. [DOI] [PubMed] [Google Scholar]
- Bereau T.; Deserno M. Generic Coarse-Grained Model for Protein Folding and Aggregation. J. Chem. Phys. 2009, 130, 235106. 10.1063/1.3152842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kmiecik S.; Gront D.; Kolinski M.; Wieteska L.; Dawid A. E.; Kolinski A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. 10.1021/acs.chemrev.6b00163. [DOI] [PubMed] [Google Scholar]
- Torrie G. M.; Valleau J. P. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
- Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13, 1011–1021. 10.1002/jcc.540130812. [DOI] [Google Scholar]
- Hamelberg D.; Mongan J.; McCammon J. A. Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules. J. Chem. Phys. 2004, 120, 11919–29. 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem. Phys. Lett. 1999, 314, 141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Becker O. M.; Karplus M. The Topology of Multidimensional Potential Energy Surfaces: Theory and Application to Peptide Structure and Kinetics. J. Chem. Phys. 1997, 106, 1495–1517. 10.1063/1.473299. [DOI] [Google Scholar]
- Laio A.; Rodriguez-Fortea A.; Gervasio F. L.; Ceccarelli M.; Parrinello M. Assessing the Accuracy of Metadynamics. J. Phys. Chem. B 2005, 109, 6714–21. 10.1021/jp045424k. [DOI] [PubMed] [Google Scholar]
- Wang X.; Tu X.; Deng B.; Zhang J. Z. H.; Sun Z. Bar-based Optimum Adaptive Steered MD for Configurational Sampling. J. Chem. Theory Comput. 2019, 40, 1270–1289. 10.1002/jcc.25784. [DOI] [PubMed] [Google Scholar]
- Grubmüller H.; Heymann B.; Tavan P. Ligand Binding: Molecular Mechanics Calculation of the Streptavidin-Biotin Rupture Force. Science 1996, 271, 997–999. 10.1126/science.271.5251.997. [DOI] [PubMed] [Google Scholar]
- Mai B. K.; Viet M. H.; Li M. S. Top Leads for Swine Influenza A/H1N1 Virus Revealed by Steered Molecular Dynamics Approach. J. Chem. Inf. Model. 2010, 50, 2236–2247. 10.1021/ci100346s. [DOI] [PubMed] [Google Scholar]
- Schmidtke P.; Luque F. J.; Murray J. B.; Barril X. Shielded Hydrogen Bonds as Structural Determinants of Binding Kinetics: Application in Drug Design. J. Am. Chem. Soc. 2011, 133, 18903–18910. 10.1021/ja207494u. [DOI] [PubMed] [Google Scholar]
- Colizzi F.; Perozzo R.; Scapozza L.; Recanatini M.; Cavalli A. Single-Molecule Pulling Simulations Can Discern Active from Inactive Enzyme Inhibitors. J. Am. Chem. Soc. 2010, 132, 7361–7371. 10.1021/ja100259r. [DOI] [PubMed] [Google Scholar]
- Park S.; Khalili-Araghi F.; Tajkhorshid E.; Schulten K. Free Energy Calculation from Steered Molecular Dynamics Simulations Using Jarzynski’s Equality. J. Chem. Phys. 2003, 119, 3559–3566. 10.1063/1.1590311. [DOI] [Google Scholar]
- Park S.; Schulten K. Calculating Potentials of Mean Force from Steered Molecular Dynamics Simulations. J. Chem. Phys. 2004, 120, 5946–5961. 10.1063/1.1651473. [DOI] [PubMed] [Google Scholar]
- Pham H. A.; Truong D. T.; Li M. S. Dependence of Work on the Pulling Speed in Mechanical Ligand Unbinding. J. Phys. Chem. B 2021, 125, 8325–8330. 10.1021/acs.jpcb.1c01818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozer G.; Valeev E.; Quirk S.; Hernandez R. Adaptive Steered Molecular Dynamics of the Long-Distance Unfolding of Neuropeptide Y. J. Chem. Theory Comput. 2010, 6, 3026–3038. 10.1021/ct100320g. [DOI] [PubMed] [Google Scholar]
- Ozer G.; Quirk S.; Hernandez R. Adaptive Steered Molecular Dynamics: Validiation of the Selection Criterion and Benchmarking Energetics in Vacuum. J. Chem. Phys. 2012, 136, 215104. 10.1063/1.4725183. [DOI] [PubMed] [Google Scholar]
- Ozer G.; Quirk S.; Hernandez R. Thermodynamics of Decaalanine Stretching in Water Obtained by Adaptive Steered Molecular Dynamics Simulations. J. Chem. Theory Comput. 2012, 8, 4837–4844. 10.1021/ct300709u. [DOI] [PubMed] [Google Scholar]
- Lu N.; Kofke D. A. Optimal Intermediates in Staged Free Energy Calculations. J. Chem. Phys. 1999, 111, 4414–4423. 10.1063/1.479206. [DOI] [Google Scholar]
- Wu D.; Kofke D. A. Phase-Space Overlap Measures. II. Design and Implementation of Staging Methods for Free-Energy Calculations. J. Chem. Phys. 2005, 123, 084109. 10.1063/1.2011391. [DOI] [PubMed] [Google Scholar]
- Echeverria I.; Amzel L. M. Helix Propensities Calculations for Amino Acids in Alanine Based Peptides Using Jarzynski’s Equality. Proteins: Struct., Funct., Bioinf. 2010, 78, 1302–1310. 10.1002/prot.22649. [DOI] [PubMed] [Google Scholar]
- Echeverria I.; Amzel L. M. Estimation of Free-Energy Differences from Computed Work Distributions: An Application of Jarzynski’s Equality. J. Phys. Chem. B 2012, 116, 10986–10995. 10.1021/jp300527q. [DOI] [PubMed] [Google Scholar]
- MacFadyen J.; Andricioaei I. A Skewed-Momenta Method to Efficiently Generate Conformational-Transition Trajectories. J. Chem. Phys. 2005, 123 (7), 074107. 10.1063/1.2000242. [DOI] [PubMed] [Google Scholar]
- Oberhofer H.; Dellago C.; Boresch S. Single Molecule Pulling with Large Time Steps. Phys. Rev. E 2007, 75, 061106. 10.1103/PhysRevE.75.061106. [DOI] [PubMed] [Google Scholar]
- Do T. N.; Carloni P.; Varani G.; Bussi G. RNA/Peptide Binding Driven by Electrostatics—Insight from Bidirectional Pulling Simulations. J. Chem. Theory Comput. 2013, 9, 1720–1730. 10.1021/ct3009914. [DOI] [PubMed] [Google Scholar]
- Ozer G.; Keyes T.; Quirk S.; Hernandez R. Multiple Branched Adaptive Steered Molecular Dynamics. J. Chem. Phys. 2014, 141, 064101. 10.1063/1.4891807. [DOI] [PubMed] [Google Scholar]
- Bureau H. R.; Merz D. Jr.; Hershkovits E.; Quirk S.; Hernandez R. Constrained Unfolding of a Helical Peptide: Implicit Versus Explicit Solvents. PLoS One 2015, 10, e0127034 10.1371/journal.pone.0127034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heymann B.; Grubmüller H. Molecular Dynamics Force Probe Simulations of Antibody/Antigen Unbinding: Entropic Control and Nonadditivity of Unbinding Forces. Biophys. J. 2001, 81, 1295–1313. 10.1016/S0006-3495(01)75787-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J.; Fernandez J. M.; Berne B. J. Water’s Role in the Force-Induced Unfolding of Ubiquitin. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 19284–19289. 10.1073/pnas.1013159107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang P.; Wang D.; Yang W.; Marszalek P. E. Piecewise All-Atom SMD Simulations Reveal Key Secondary Structures in Luciferase Unfolding Pathway. Biophys. J. 2020, 119, 2251–2261. 10.1016/j.bpj.2020.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie H.; Gunawardana V. W. L.; Finnegan T. J.; Xie W.; Badjić J. D. Picking on Carbonate: Kinetic Selectivity in the Encapsulation of Anions. Angew. Chem., Int. Ed. 2022, 61, e202116518 10.1002/anie.202116518. [DOI] [PubMed] [Google Scholar]
- Jiang Y.; Zhang H.; Cui Z.; Tan T. Modeling Coordination-Directed Self-Assembly of M2l4 Nanocapsule Featuring Competitive Guest Encapsulation. J. Phys. Chem. Lett. 2017, 8, 2082–2086. 10.1021/acs.jpclett.7b00773. [DOI] [PubMed] [Google Scholar]
- Ning S.; Zeng C.; Zeng C.; Zhao Y. The TAR Binding Dynamics and Its Implication in Tat Degradation Mechanism. Biophys. J. 2021, 120, 5158–5168. 10.1016/j.bpj.2021.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hantz E. R.; Lindert S. Adaptative Steered Molecular Dynamics Study of Mutagenesis Effects on Calcium Affinity in the Regulatory Domain of Cardiac Troponin C. J. Chem. Inf. Model. 2021, 61, 3052–3057. 10.1021/acs.jcim.1c00419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng C.; Zhu Z.; Shi Y.; Wang X.; Mu K.; Yang Y.; Zhang X.; Xu Z.; Zhu W. Computational Insights into the Conformational Accessibility and Binding Strength of SARS-CoV-2 Spike Protein to Human Angiotensin-Converting Enzyme 2. J. Phys. Chem. Lett. 2020, 11, 10482–10488. 10.1021/acs.jpclett.0c02958. [DOI] [PubMed] [Google Scholar]
- Wang Y.; Cai W.-S.; Chen L.; Wang G. Molecular Dynamics Simulation Reveals How Phosphorylation of Tyrosine 26 of Phosphoglycerate Mutase 1 Upregulates Glycolysis and Promotes Tumor Growth. Oncotarget 2017, 8, 12093. 10.18632/oncotarget.14517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J.-R.; Li H.; Zhang H.-X.; Zheng Q.-C. Exploring the Structure Characteristics and Major Channels of Cytochrome P450 2a6, 2a13, and 2e1 with Pilocarpine. Biopolymers 2018, 109, e23108 10.1002/bip.23108. [DOI] [PubMed] [Google Scholar]
- Sun D.-R.; Zheng Q.-C.; Zhang H.-X. Molecular Dynamics Investigation of Stereoselective Inhibition Mechanism of HIF-2α/ARNT Heterodimer. J. Mol. Recognit 2018, 31, e2675 10.1002/jmr.2675. [DOI] [PubMed] [Google Scholar]
- Wang X.; Bie L.; Fei J.; Gao J. Insights into the Loop at the E-Selectin Binding Site: From Open to Close Conformation. J. Chem. Inf. Model. 2020, 60, 5153–5161. 10.1021/acs.jcim.0c00939. [DOI] [PubMed] [Google Scholar]
- Moesgaard L.; Reinholdt P.; Wüstner D.; Kongsted J. Modeling the Sterol-Binding Domain of Aster-A Provides Insight into Its Multiligand Specificity. J. Chem. Inf. Model. 2020, 60, 2268–2281. 10.1021/acs.jcim.0c00086. [DOI] [PubMed] [Google Scholar]
- Hu Z.; Bie L.; Gao J.; Wang X. Insights into Selectin Inhibitor Design from Endogenous Isomeric Ligands of SLea and SLex. J. Chem. Inf. Model. 2021, 61, 6085–6093. 10.1021/acs.jcim.1c01356. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Zheng Q.-C. What Are the Effects of the Serine Triad on Proton Conduction of an Influenza B M2 Channel? An Investigation by Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2019, 21, 8820–8826. 10.1039/C9CP00612E. [DOI] [PubMed] [Google Scholar]
- El Hage K.; Hédin F.; Gupta P. K.; Meuwly M.; Karplus M. Valid Molecular Dynamics Simulations of Human Hemoglobin Require a Surprisingly Large Box Size. eLife 2018, 7, e35560 10.7554/eLife.35560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Hage K.; Hédin F.; Gupta P. K.; Meuwly M.; Karplus M. Response to Comment on “Valid Molecular Dynamics Simulations of Human Hemoglobin Require a Surprisingly Large Box Size”. eLife 2019, 8, e45318. 10.7554/eLife.45318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asthagiri D.; Tomar D. S. System Size Dependence of Hydration-Shell Occupancy and Its Implications for Assessing the Hydrophobic and Hydrophilic Contributions to Hydration. J. Phys. Chem. B 2020, 124, 798–806. 10.1021/acs.jpcb.9b11200. [DOI] [PubMed] [Google Scholar]
- Gapsys V.; de Groot B. L. Comment on “Valid Molecular Dynamics Simulations of Human Hemoglobin Require a Surprisingly Large Box Size”. eLife 2019, 8, e44718 10.7554/eLife.44718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehra R.; Kepp K. P. Cell Size Effects in the Molecular Dynamics of the Intrinsically Disordered Aβ Peptide. J. Chem. Phys. 2019, 151, 085101. 10.1063/1.5115085. [DOI] [PubMed] [Google Scholar]
- Ogawa K.; Oga H.; Kusudo H.; Yamaguchi Y.; Omori T.; Merabia S.; Joly L. Large Effect of Lateral Box Size in Molecular Dynamics Simulations of Liquid-Solid Friction. Phys. Rev. E 2019, 100, 023101. 10.1103/PhysRevE.100.023101. [DOI] [PubMed] [Google Scholar]
- Yeh I.-C.; Hummer G. System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873–15879. 10.1021/jp0477147. [DOI] [Google Scholar]
- Gapsys V.; de Groot B. L. On the Importance of Statistics in Molecular Simulations for Thermodynamics, Kinetics and Simulation Box Size. eLife 2020, 9, e57589 10.7554/eLife.57589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parameswaran S.; Mobley D. L. Box Size Effects Are Negligible for Solvation Free Energies of Neutral Solutes. J. Comput. Aided Mol. Des. 2014, 28, 825–829. 10.1007/s10822-014-9766-7. [DOI] [PubMed] [Google Scholar]
- Gilquin B.; Guilbert C.; Perahia D. Unfolding of Hen Egg Lysozyme by Molecular Dynamics Simulations at 300K: Insight into the Role of the Interdomain Interface. Proteins: Struct., Funct., Bioinf. 2000, 41, 58–74. . [DOI] [PubMed] [Google Scholar]
- Ma B.; Nussinov R. Molecular Dynamics Simulations of the Unfolding of 2-Microglobulin and Its Variants. Protein Eng. Des. Sel. 2003, 16, 561–575. 10.1093/protein/gzg079. [DOI] [PubMed] [Google Scholar]
- Levy Y.; Onuchic J. N. Water Mediation in Protein Folding and Molecular Recognition. Annu. Rev. Biophys. Biomol. Struct. 2006, 35, 389–415. 10.1146/annurev.biophys.35.040405.102134. [DOI] [PubMed] [Google Scholar]
- Meister K.; Ebbinghaus S.; Xu Y.; Duman J. G.; DeVries A.; Gruebele M.; Leitner D. M.; Havenith M. Long-Range Protein–Water Dynamics in Hyperactiveinsect Antifreeze Proteins. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 1617–1622. 10.1073/pnas.1214911110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noel J. K.; Onuchic J. N.; Sulkowska J. I. Knotting a Protein in Explicit Solvent. J. Phys. Chem. Lett. 2013, 4, 3570–3573. 10.1021/jz401842f. [DOI] [Google Scholar]
- Jungwirth P. Biological Water or Rather Water in Biology?. J. Phys. Chem. Lett. 2015, 6, 2449–2451. 10.1021/acs.jpclett.5b01143. [DOI] [PubMed] [Google Scholar]
- Shan Y.; Klepeis J. L.; Eastwood M. P.; Dror R. O.; Shaw D. E. Gaussian Split Ewald: A Fast Ewald Mesh Method for Molecular Simulation. J. Chem. Phys. 2005, 122, 054101. 10.1063/1.1839571. [DOI] [PubMed] [Google Scholar]
- Schneider R.; Sharma A. R.; Rai A.. Introduction to Molecular Dynamics. In Computational Many-Particle Physics; Springer: Berlin, Heidelberg, 2008; Vol. 739, 10.1007/978-3-540-74686-7_1. [DOI] [Google Scholar]
- Best R. B.; Li B.; Steward A.; Daggett V.; Clarke J. Can Non-Mechanical Proteins Withstand Force? Stretching Barnase by Atomic Force Microscopy and Molecular Dynamics Simulation. Biophys. J. 2001, 81, 2344–2356. 10.1016/S0006-3495(01)75881-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryer A. J.; Reddy T.; Lyman E.; Perilla J. R. Full Scale Structural, Mechanical and Dynamical Properties of HIV-1 Liposomes. PLoS Comp. Biol. 2022, 18, e1009781 10.1371/journal.pcbi.1009781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quirk S.; Hopkins M.; Bureau H.; Lusk R.; Hernandez R.; Bain D. Mutational Analysis of Neuropeptide Y Reveals Unusual Thermal Stability Linked to Higher-Order Self-Association. ACS Omega 2018, 3, 2141–2154. 10.1021/acsomega.7b01949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheridan S.; Gräter F.; Daday C. How Fast Is Too Fast in Force-Probe Molecular Dynamics Simulations?. J. Phys. Chem. B 2019, 123, 3658–3664. 10.1021/acs.jpcb.9b01251. [DOI] [PubMed] [Google Scholar]
- Han Z.; Hilburg S. L.; Alexander-Katz A. Forced Unfolding of Protein-Inspired Single-Chain Random Heteropolymers. Macromolecules 2022, 55, 1295–1309. 10.1021/acs.macromol.1c02411. [DOI] [Google Scholar]
- Jarzynski C. Equilibrium Free-Energy Differences from Nonequilibrium Measurements: A Master-Equation Approach. Phys. Rev. E 1997, 56, 5018–5035. 10.1103/PhysRevE.56.5018. [DOI] [Google Scholar]
- Jarzynski C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. 10.1103/PhysRevLett.78.2690. [DOI] [Google Scholar]
- Crooks G. E. Nonequilibrium Measurements of Free Energy Differences for Microscopically Reversible Markovian Systems. J. Stat. Phys. 1998, 90, 1481–1487. 10.1023/A:1023208217925. [DOI] [Google Scholar]
- Zhuang Y.; Bureau H.; Quirk S.; Hernandez R. Adaptive Steered Molecular Dynamics of Biomolecules. Mol. Sim. 2021, 47, 408–419. 10.1080/08927022.2020.1807542. [DOI] [Google Scholar]
- Zhuang Y.; Bureau H. R.; Lopez C.; Bucher R.; Quirk S.; Hernandez R. Energetics and Structure of Alanine-Rich α-Helices via Adaptive Steered Molecular Dynamics (ASMD). Biophys. J. 2021, 120, 2009–2018. 10.1016/j.bpj.2021.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD - Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Kalé L.; Skeel R.; Bhandarkar M.; Brunner R.; Gursoy A.; Krawetz N.; Phillips J.; Shinozaki A.; Varadarajan K.; Schulten K. NAMD2: Greater Scalability for Parallel Molecular Dynamics. J. Comput. Phys. 1999, 151, 283–312. 10.1006/jcph.1999.6201. [DOI] [Google Scholar]
- Best R. B.; Zhu X.; Shim J.; Lopes P. E. M.; Mittal J.; Feig M.; Mackerell A. D. Jr Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone Phi, Psi and Side-Chain Chi1 and Chi2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noh S. Y.; Notman R. Comparison of Umbrella Sampling and Steered Molecular Dynamics Methods for Computing Free Energy Profiles of Aromatic Substrates Through Phospholipid Bilayers. J. Chem. Phys. 2020, 153, 034115. 10.1063/5.0016114. [DOI] [PubMed] [Google Scholar]
- Michaud-Agrawal N.; Denning E. J.; Woolf T. B.; Beckstein O. MDAnalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations. J. Comput. Chem. 2011, 32, 2319–2327. 10.1002/jcc.21787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowers R.; Linke M.; Barnoud J.; Reddy T.; Melo M.; Seyler S.; Domański J.; Dotson D.; Buchoux S.; Kenney I.; Beckstein O.. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. In Proceedings of the Python in Science Conference; Benthall S., Rostrup S., Eds.; SciPy: 2016; pp 98–105, 10.25080/majora-629e541a-00e. [DOI]
- Gowers R. J.; Carbone P. A Multiscale Approach to Model Hydrogen Bonding: The Case of Polyamide. J. Chem. Phys. 2015, 142, 224907. 10.1063/1.4922445. [DOI] [PubMed] [Google Scholar]
- Smith P.; Ziolek R. M.; Gazzarrini E.; Owen D. M.; Lorenz C. D. On the Interaction of Hyaluronic Acid with Synovial Fluid Lipid Membranes. Phys. Chem. Chem. Phys. 2019, 21, 9845–9857. 10.1039/C9CP01532A. [DOI] [PubMed] [Google Scholar]
- Mezei M.; Fleming P. J.; Srinivasan R.; Rose G. D. Polyproline II Helix Is the Preferred Conformation for Unfolded Polyalanine in Water. Proteins: Struct., Funct., Bioinf. 2004, 55, 502–507. 10.1002/prot.20050. [DOI] [PubMed] [Google Scholar]
- Rose G. D.; Fleming P. J.; Banavar J. R.; Maritan A. A Backbone-Based Theory of Protein Folding. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 16623–16633. 10.1073/pnas.0606843103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bureau H.; Quirk S.; Hernandez R. The Relative Stability of Trpzip1 and Its Mutants Determined by Computation and Experiment. RSC Adv. 2020, 10, 6520. 10.1039/D0RA00920B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quirk S.; Lieberman R. L. Improved Resolution Crystal Structure of Acanthamoeba Actophorin Reveals Structural Plasticity Not Induced by Microgravity. Acta. Cryst. F 2021, 77 (12), 452–458. 10.1107/S2053230X21011419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quirk S.; Lieberman R. L. Structure and Activity of a Thermally Stable Mutant of Acanthamoeba Actophorin. Acta. Crsyt. F 2022, 78, 150–160. 10.1107/S2053230X22002448. [DOI] [PMC free article] [PubMed] [Google Scholar]