Random encounters and amoeba locomotion drive the predation of Listeria monocytogenes by Acanthamoeba castellanii

Significance

Acanthamoeba are considered among the most predominant and efficient microscale predators in environments such as soil and natural water systems. While it is known that Acanthamoeba castellanii employ a “backpacking” strategy to trap and aggregate bacterial prey prior to phagocytosis, a mechanistic understanding of this fascinating predation strategy has been lacking. By integrating microfluidics, high-resolution microscopy, and state-of-the-art image-analysis methods, we discovered that capture dynamics of Listeria monocytogenes by A. castellanii are mediated purely by random encounters, further enhanced by bacterial motility. Furthermore, tracking of captured L. monocytogenes on the outer surface of A. castellanii indicates a crucial role of the amoeba locomotion in the assembly of trapped cells into backpacks.

Abstract

Predatory protozoa play an essential role in shaping microbial populations. Among these protozoa, Acanthamoeba are ubiquitous in the soil and aqueous environments inhabited by Listeria monocytogenes. Observations of predator–prey interactions between these two microorganisms revealed a predation strategy in which Acanthamoeba castellanii assemble L. monocytogenes in aggregates, termed backpacks, on their posterior. The rapid formation and specific location of backpacks led to the assumption that A. castellanii may recruit L. monocytogenes by releasing an attractant. However, this hypothesis has not been validated, and the mechanisms driving this process remained unknown. Here, we combined video microscopy, microfluidics, single-cell image analyses, and theoretical modeling to characterize predator–prey interactions of A. castellanii and L. monocytogenes and determined whether bacterial chemotaxis contributes to the backpack formation. Our results indicate that L. monocytogenes captures are not driven by chemotaxis. Instead, random encounters of bacteria with amoebae initialize bacterial capture and aggregation. This is supported by the strong correlation between experimentally derived capture rates and theoretical encounter models at the single-cell level. Observations of the spatial rearrangement of L. monocytogenes trapped by A. castellanii revealed that bacterial aggregation into backpacks is mainly driven by amoeboid locomotion. Overall, we show that two nonspecific, independent mechanisms, namely random encounters enhanced by bacterial motility and predator surface-bound locomotion, drive backpack formation, resulting in a bacterial aggregate on the amoeba ready for phagocytosis. Due to the prevalence of these two processes in the environment, we expect this strategy to be widespread among amoebae, contributing to their effectiveness as predators.

Predators play a crucial role in maintaining the balance of ecosystems through the top-down regulation of prey populations (1). Numerous studies on predator–prey interactions at the macroscale have yielded a deep understanding of the role of predators in food webs and have shown that predators often use sophisticated strategies to attract prey for capture. In the Amazon rainforest, neotropical cats attract their prey by imitating the prey species’ vocalizations (2). New Zealand glow worms produce bioluminescence to attract flying insects then trap them with their prehung vertical threads (3). Bolas spiders can mimic the chemical odor of a female moth to attract male moth prey (4). At the microscale, our knowledge of the role of predators and their strategies to catch prey is rather limited (5). One of these microscale predators, the protozoan Acanthamoeba castellanii, hunts its bacterial prey using a strategy that involves a bacterial aggregation phenomenon called backpack formation (Fig. 1 A–E) prior to phagocytosis and digestion (6). Although it has been hypothesized that A. castellanii, in a microscopic equivalent of the macroscale strategies described above, exploit bacterial chemotaxis to attract their prey through the release of an attractant (6), this hypothesis has remained untested and the mechanism underlying this predation strategy has remained unknown.

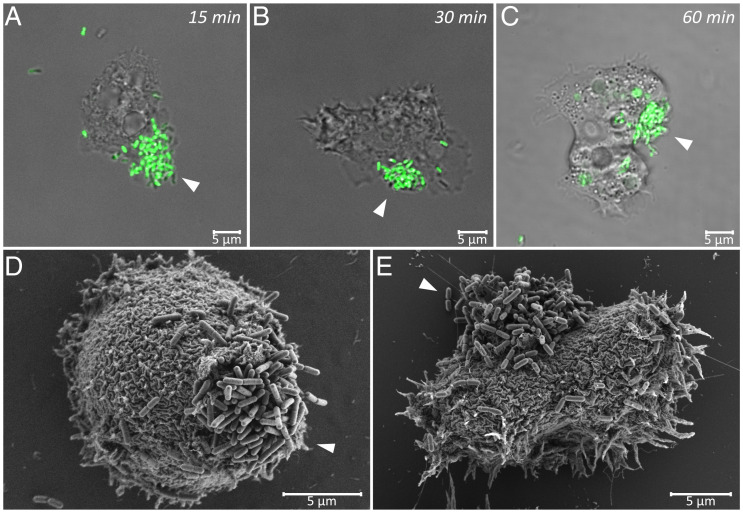
Fig. 1.

Captured L. monocytogenes cells form backpack structures on the surface of A. castellanii trophozoites (SI Appendix, Visualization of Backpacks). (A–C) Confocal laser scanning microscopy images of GFP-expressing L. monocytogenes (strain Scott A::pPL2P_hyp gfp) in coculture with A. castellanii. Backpacks consisting of trapped L. monocytogenes cells are marked with white arrowheads. Images were taken 15 min (A), 30 min (B), or 1 h (C) after the start of coincubation. (D and E) SEM images of L. monocytogenes (strain Scott A wild type) backpacks, marked with white arrowheads, on the surface of A. castellanii trophozoites after 1 h of coincubation.

Acanthamoeba are ubiquitous in soil and aquatic systems and are also widely found in human-related environments, including drinking water treatment plants and food-processing facilities (7–9). They have two life stages: an active trophozoite stage that feeds and reproduces (10) and a dormant cyst stage that can overcome unfavorable conditions (11). In aqueous environments, Acanthamoeba trophozoites are usually not able to access the bulk water column. They are mainly found on solid substrates and at the water–air interface where they employ surface-bound motility, achieving a maximum speed of 0.8 µm/s (12), driven by the reversible change of cytoplasm from sol to gel state (13). As well as feeding on organic particles, Acanthamoeba trophozoites prey on bacteria, fungi, algae, and other small protozoa (14). As such, they play an essential role in influencing the composition and ecology of microbial communities (15–17) and contribute to processes such as nutrient remineralization (18, 19). Simultaneously, Acanthamoeba can also act as protective shelters for many pathogenic bacteria (20–22).

During predation, Acanthamoeba assemble bacteria on their outer surface into aggregates known as backpacks, because they form on the back of the trophozoites. Although this process was first described during a study on the interaction between A. castellanii and the bacterium Listeria monocytogenes, other bacterial strains are also susceptible to being trapped in backpacks (6). L. monocytogenes is an opportunistic foodborne pathogen that can cause severe infection in susceptible individuals with a mortality rate of up to 30% (23, 24) after switching from an environmental saprophyte to an intracellular pathogen (25). Listeria are ubiquitous in the environment, sharing similar aquatic habitats with predatory protozoa such as Acanthamoeba (26). Formation of backpacks by A. castellanii was observed in coculture with L. monocytogenes (6). Backpacks form within minutes near the uroid (6), an excretory organ located on the posterior of the Acanthamoeba trophozoite. Due to the highly specific localization and short timeframe of backpack formation, it was hypothesized that A. castellanii actively attract and recruit L. monocytogenes cells by inducing chemotaxis of the bacteria to its uroid region through the excretion of a chemoattractant (6). Chemotaxis allows bacteria to sense chemical gradients and change the direction of their motility accordingly. Yet, this hypothesis has remained untested, leaving the mechanism of backpack formation unexplained to date.

Here, we present experiments to characterize the backpack formation strategy that A. castellanii uses to catch its prey L. monocytogenes to determine its underlying mechanisms and gain insights into its ecological and evolutionary origins. To challenge the hypothesis that A. castellanii attracts its prey L. monocytogenes by chemotaxis through the release of a chemical cue, we used a combination of microfluidics and high-resolution microscopy to observe the response of L. monocytogenes to potential chemical gradients derived from A. castellanii. Additionally, we tracked single swimming L. monocytogenes cells during their interaction with individual A. castellanii, as well as the spatial rearrangement of bacterial cells on the surface of A. castellanii after capture. Our results show that capture of L. monocytogenes by A. castellanii is actually a result of random encounters, not chemotaxis, and that backpack formation is driven after capture by the surface-bound locomotion of A. castellanii.

Results

L. monocytogenes Are Not Chemoattracted to A. castellanii.

To test the hypothesis that A. castellanii releases a chemical attractant to capture L. monocytogenes, we developed a linear gradient generator (LGG) microfluidic device (Fig. 2 A and B) in which we could expose L. monocytogenes cells (1 × 10⁷ colony-forming units [CFU]/mL) to a steady, linear concentration profile of a putative chemoattractant. Hydrogel walls within the LGG allowed diffusion between solutions flowing in the two side channels (a source channel containing a test solution and a sink channel containing buffer) to create a chemical gradient across the central observation channel while providing a physical barrier preventing bacterial movement out of the observation channel. The response of L. monocytogenes in the observation channel (Fig. 2C) toward gradients created with different solutions was recorded by phase-contrast microscopy over a 20-min period. This is a typical time window within which the redistribution of bacterial populations through chemotaxis occurs (27) and during which backpack formation occurs when A. castellanii and L. monocytogenes are cocultured (6). Image analysis was used to quantify the cell concentration across the observation channel, which was used to assess the occurrence of chemotaxis, a uniform cell concentration being indicative of the absence of chemotaxis (Fig. 2 D and F).

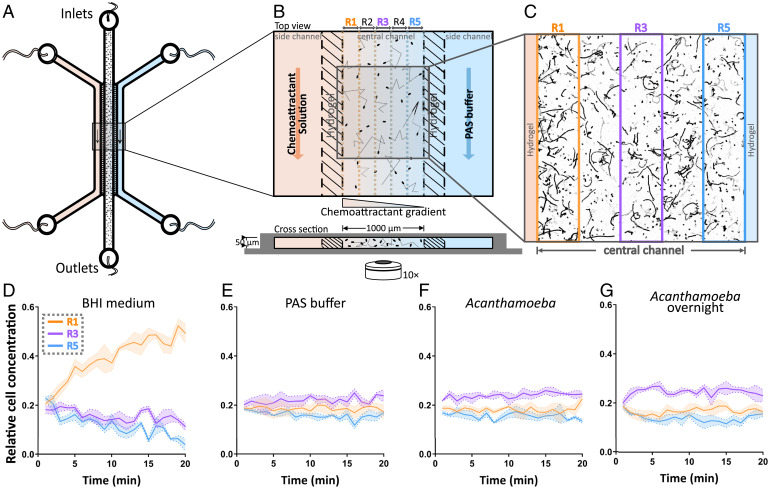
Fig. 2.

L. monocytogenes is not attracted by A. castellanii secretions. (A and B) Schematic representation of the LGG used for the chemotaxis assays (Materials and Methods). Outer channels allow the flow of a potential chemoattractant solution and PAS buffer, generating a gradient across the hydrogel walls and the central channel. The central channel, which has no flow, contains a suspension of L. monocytogenes. By quantifying the spatial distribution of Listeria cells across the width of the central channel (subdivided into five 200-µm-wide regions, R1 to R5, for analysis), the chemotactic response of the cells to the potential chemoattractant can be quantified. (C) Example image showing accumulation of L. monocytogenes cells close to the left hydrogel wall, saturated with 10% brain heart infusion (BHI) broth as the positive control, 5 min after cells were introduced into the central channel. (D–G) Relative cell concentrations of L. monocytogenes as a function of time for three regions within the central channel: R1 closest to the source channel containing the potential chemoattractant (orange), R3 along the middle of the central channel (purple), and R5 closest to the sink channel (blue). Solid colored lines show the average probability distributions over three replicate experiments, and shaded areas represent the SD. Relative cell concentrations over time are shown for experiments in which the chemoattractant channel contained (D) 10% BHI medium, (E) PAS buffer, (F) A. castellanii cells used directly after washing (Acanthamoeba), and (G) A. castellanii cells incubated overnight in PAS buffer after washing (Acanthamoeba overnight). Accumulation of L. monocytogenes toward the source channel was only observed in response to BHI broth used as a positive control.

Experiments in which cells were exposed to a gradient of the culture medium, 10% brain heart infusion (BHI) broth, demonstrated that L. monocytogenes is capable of chemotaxis. After 20 min, approximately half of the bacterial population (i.e., a relative cell concentration of 0.5) had migrated to the region closest to the gradient source (R1, Fig. 2D). Correspondingly, a depletion of cell concentrations over time could be observed in the regions further away from the source (e.g., R3 and R5, Fig. 2D). In contrast, a gradient created using nonnutrient Page’s amoeba saline (PAS) buffer as a negative control resulted in a uniform distribution profile at all times, with no accumulation, denoting the absence of chemotaxis (Fig. 2E). Taken together, these control experiments demonstrate that L. monocytogenes is in general capable of chemotaxis and that the LGG enables the observations of such behavior.

To test the ability of A. castellanii to attract L. monocytogenes, experiments with the LGG were performed in which an A. castellanii culture was continuously flowed through one side channel. Initial experiments were performed using freshly washed A. castellanii cultures, which did not elicit a chemotactic response in L. monocytogenes (Fig. 2F). To ensure that enough time was provided for A. castellanii to secrete potential chemoattractants, an additional 24-h incubation step was introduced, after washing, in follow-up experiments. This 24-h starvation step was included to account for the possibility that a higher concentration of A. castellanii secretions would accumulate in the medium during this time. Starved A. castellanii cells are still able to trap, assemble, and ingest backpacks of L. monocytogenes (SI Appendix, Fig. S8 E–G). This additional incubation also did not elicit a chemotactic response (Fig. 2G). These experiments therefore provide support against the original hypothesis that L. monocytogenes is chemotactic toward the secretion products of A. castellanii, especially since the experimental conditions (i.e., cell concentrations for Listeria and Acanthamoeba) are similar to experiments in which the backpack formation could be clearly observed, such as the backpack visualization (Fig. 1) and capture dynamics (Fig. 3) experiments described here and in earlier reports (6). This finding prompted us to investigate whether the capture of L. monocytogenes by A. castellanii can be explained by random encounters of the motile bacteria with the amoebae, instead of directional chemotactic motion of the bacteria.

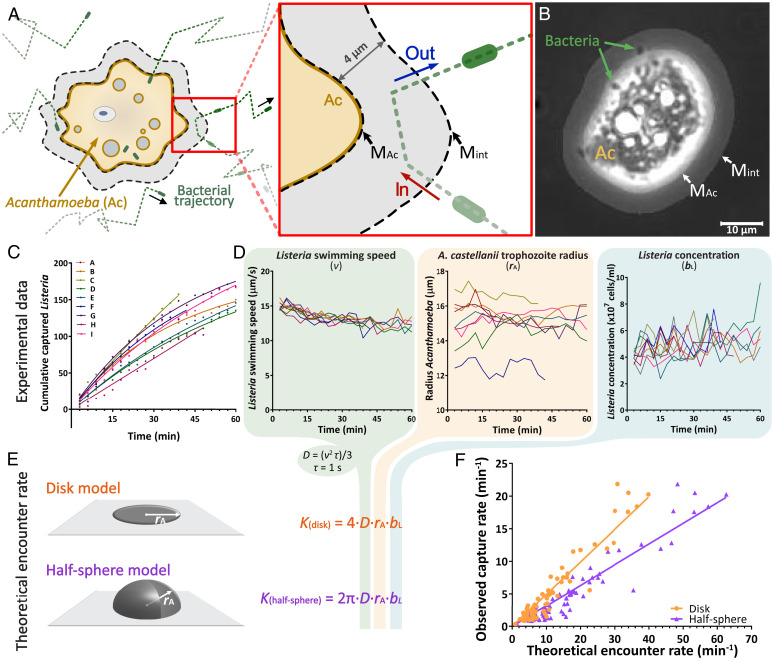
Fig. 3.

Random encounters enhanced by bacterial motility govern the capture of L. monocytogenes by A. castellanii. (A) Schematic representation of the region of interest around an A. castellanii trophozoite, illustrating the image analysis masks used to quantify L. monocytogenes capture rates in a microfluidic arena (Movie S1). For each A. castellanii trophozoite, two masks were created: an Acanthamoeba mask (M_Ac), covering the cell and an interaction mask (M_int), which extended 4 µm out from the boundary of the Acanthamoeba mask. The number of captured bacteria over time was quantified by tracking individual L. monocytogenes cells and calculating the number of bacteria entering the interaction mask (red “In” arrow) minus the number of cells exiting from the interaction mask (blue “Out” arrow). (B) Example image showing an A. castellanii trophozoite overlaid with the two masks. The mask boundaries are indicated by white arrows. (C) Cumulative number of captured L. monocytogenes cells for each of nine monitored A. castellanii trophozoites (color-coded, from A to I), for one experiment at an initial concentration of 1.0 × 10⁷ CFU/mL L. monocytogenes. Colored lines represent the fitted exponential saturation function for each A. castellanii trophozoite (see Materials and Methods). Plots for each experiment are provided in SI Appendix, Fig. S1. (D) Mean L. monocytogenes swimming speed (v), mean A. castellanii trophozoite radius (r_A), and mean L. monocytogenes concentration (b_L), each as a function of time, estimated within the region of interest centered on each of the nine A. castellanii trophozoites shown in C (color-coded, from A to I). The time-averaged values of these parameters for each individual A. castellanii trophozoite were used to estimate their theoretical encounter rates using the equations in E. (E) Schematic representations and equations of the theoretical encounter rate models for a flux of particles that encounters a perfectly absorbing disk (orange) or halfsphere (purple) with radius (r_A). (F) Observed capture rates, γ (Eq. 2), of individual A. castellanii trophozoites plotted as a function of the theoretical encounter rates calculated using the model for a disk (orange circles) or for a half-sphere (purple triangles) that assume random bacterial encounter and perfect absorption (see Results). The two models were parameterized for each A. castellanii trophozoite using values for Listeria concentration, Listeria swimming speed, and A. castellanii radius quantified from individual experiments. Solid lines represent linear regressions for each model in the respective color (R² = 0.90 in both cases).

Capture Dynamics of L. monocytogenes by A. castellanii Are Compatible with Capture by Random Encounters.

To quantify the capture dynamics of L. monocytogenes by A. castellanii, we incubated A. castellanii cultures together with three different concentrations of bacteria (0.5 × 10⁷, 1 × 10⁷, and 2 × 10⁷ CFU/mL, based on OD₆₀₀ [optical density at 600 nm] measurements) in a single-channel microfluidic chip (without flow). Predator–prey interactions were recorded by acquiring 2-min videos (20 frames per second [fps]) in phase-contrast microscopy (10× objective) during 1 h, with 1-min intervals between videos. To count the number of L. monocytogenes cells captured in each 2-min time interval by each individual A. castellanii trophozoite, we developed an image analysis pipeline that calculates the difference between the number of L. monocytogenes cells that enter and those that exit the boundary of a region surrounding each A. castellanii trophozoite (this region is a dynamic interaction mask which extends 4 μm from the physical boundary of the amoeba) (Fig. 3 A and B and Movie S1). Application to control regions containing no A. castellanii trophozoite, from the same experimental videos, showed equal rates of cell entry and exit (SI Appendix, Fig. S1), providing a benchmark for the analysis method. These experiments thus enabled us to quantify the number of L. monocytogenes cells captured by A. castellanii over time. Using this information, we derived an individual capture rate per amoebal cell, which we then compared with theoretical encounter rate estimates.

The capture dynamics showed a characteristic pattern, with the cumulative number of captured L. monocytogenes cells for each A. castellanii trophozoite increasing approximately linearly with time at the beginning of each experiment (Fig. 3C and SI Appendix, Fig. S1). Saturation of the cumulative capture curves was observed across a wide range of bacterial concentrations (0.5 × 10⁷, 1 × 10⁷, and 2 × 10⁷ CFU/mL) after 15 to 20 min (Fig. 3C and SI Appendix, Fig. S1 B, C, and F–H). For each amoeba, the cumulative capture curve was fitted (SI Appendix, Fig. S1) with a saturating exponential function of time (Materials and Methods, Eq. 1). The saturated exponential function captured the observed dynamics well, with an average R² value across all amoebae of 0.93 (SD = 0.07) (SI Appendix, Fig. S1). Using the saturated exponential function, the capture rate per amoeba before saturation, $\gamma$ (Materials and Methods, Eq. 2), was derived. The capture rate ranged between 0.3 and 21.9 (global average = 5.1; SD = 5.2) L. monocytogenes cells per minute per amoeba. Note that the capture rate scales with the concentration of prey bacteria, which varied greatly between experiments and contributes to the wide range of observed capture rates (SI Appendix, Fig. S6).

To understand the mechanism underlying capture, we compared the capture rate for each A. castellanii trophozoite to a theoretical encounter, $K_{\text{disk}}$ (Materials and Methods, Eq. 3), quantifying the encounter of an amoeba, represented by a perfectly absorbing flat disk attached to a surface, by bacteria that are motile but not chemotactic, i.e., through “random motility,” represented by Listeria’s diffusivity, $D$ (Materials and Methods, Eq. 4) (28). The predicted encounter rate is based on experimentally observed organism characteristics, i.e., Listeria swimming speed $v$ and concentration $b_{\text{L}}$ and Acanthamoeba radius $r_{\text{A}}$ (Fig. 3D). The average radius, $r_{\text{A}}$, of tracked A. castellanii trophozoites (SI Appendix, Fig. S4), calculated for each time point (n = 1,294), ranged between 10.6 and 20.7 μm, with a global average of 15.3 μm (SD = 1.5 μm). L. monocytogenes average swimming speed, $v$, calculated around each individual A. castellanii trophozoite for each time point (n = 1,281), ranged from a minimum of 1.5 μm/s to a maximum of 20.8 μm/s, with a global average of 12.5 μm/s (SD = 2.5 μm/s) (SI Appendix, Fig. S3). Concentrations of L. monocytogenes, $b_{\text{L}}$, calculated for each time point (n = 1,293), ranged from 0 to 2.2 × 10⁸ cells/mL, somewhat higher than the estimated inoculum concentrations (0.5 × 10⁷, 1 × 10⁷, and 2 × 10⁷ CFU/mL) (SI Appendix, Fig. S2). This discrepancy was to be expected since experimental observations were performed directly above a solid surface, a region in which motile bacteria are known to accumulate (29). Notably, no differences in bacterial concentrations were observed between regions of interest surrounding individual A. castellanii trophozoites and digital control regions lacking A. castellanii (SI Appendix, Fig S2). This provides additional evidence that bacterial chemotaxis does not play a role in the interaction between these two microorganisms. L. monocytogenes swimming speeds ($v$) and concentrations ($b_{\text{L}}$) decreased during the course of certain experiments (SI Appendix, Figs. S2 B, F, G, and I and S3 B, F, and G), which coincided with the strongest cases of saturation in the cumulative capture curves (SI Appendix, Fig. S1 B, F, G, and I).

If the capture dynamics between L. monocytogenes and A. castellanii stem from a random encounter mechanism, we expect the capture rates $\gamma$ for the individual A. castellanii trophozoites to scale linearly with the theoretical encounter rate ($K_{\text{disk}}$), with a slope between 0 and 1 corresponding to the capture efficiency, assuming a disk-like shape of the trophozoite. Indeed, a linear regression between theoretical encounter rates $K_{\text{disk}}$ and capture rates $\gamma$ showed that captures of L. monocytogenes by A. castellanii were well-predicted (Fig. 3F, orange line; $\gamma$ = 0.50 × $K_{\text{disk}}$, R² = 0.90), resulting in a capture efficiency, corresponding to the slope of the linear regression, of 50%. A. castellanii, while being rather flat in shape, actually has a surface area larger than the idealized disk due to some variation in thickness. Inherently, a larger surface would result in larger theoretical encounter rates and thus lower capture efficiencies. To quantify the sensitivity to the specific geometry and to get a lower bound for capture efficiency, we additionally derived theoretical encounter rates for a half-sphere, $K_{\text{hs}}$ (Materials and Methods, Eq. 5), based on the same assumptions as the disk model $K_{\text{disk}}$. In this scenario, the linear regression for the half-sphere model $K_{\text{hs}}$ (Fig. 3F, purple line; $\gamma$ = 0.32 × $K_{\text{hs}}$, R² = 0.90) resulted in a capture efficiency of 32%, which is lower compared to the disk model $K_{\text{disk}}$. As the shape of an Acanthamoeba trophozoite lies between a disk and a half-sphere, the actual capture efficiency sits in the range of these two limit values, i.e., 32% and 50%. To ensure the proper working of our analysis pipeline, the comparison of capture rates and theoretical encounter rates was also determined for an interaction mask that is 50% smaller (i.e., a mask which extends 2 μm from the physical boundary of the amoeba) (SI Appendix, Fig. S5). This resulted in capture efficiencies of 29% for the disk model $K_{\text{disk}}$ and 45% for the half-sphere model $K_{\text{hs}}$.

Ultimately, we conclude that captures of L. monocytogenes by its predator, A. castellanii, originate from random encounters and not chemotaxis. As random encounters result in uniform prey capture over the predator’s surface, our next question was what mechanism translates a uniform prey distribution on the predator’s surface into the tight backpacks observed experimentally in the posterior uroid region of the A. castellanii trophozoites (6).

A. castellanii Locomotion Drives the Aggregation of Trapped L. monocytogenes into Backpacks.

Since the interaction between L. monocytogenes and A. castellanii is fully compatible with random encounter models, we can assume that A. castellanii has an equal chance to capture L. monocytogenes on its exposed surface. This suggests that the aggregation of trapped L. monocytogenes cells into a backpack is the result of a postcapture rearrangement of trapped cells on the A. castellanii outer surface. To test this hypothesis, confocal laser scanning fluorescence microscopy was used to image and track individual A. castellanii trophozoites in the process of forming backpacks when incubated with green fluorescent protein (GFP)-expressing L. monocytogenes (in a 1:4 ratio with wild-type L. monocytogenes; total bacterial concentration 2 × 10⁷ CFU/mL).

Microscopic monitoring of L. monocytogenes trapped on the surface of A. castellanii revealed that the locomotion of A. castellanii is responsible for the rearrangement of L. monocytogenes into backpacks (Movies S2 and S3). Our data showed that during locomotion of A. castellanii trophozoites, each trapped L. monocytogenes cell remained stationary relative to the substratum until it reached the posterior of the A. castellanii trophozoite, at which point it was assembled into a growing backpack (Fig. 4 A and B and Movie S2). The role of A. castellanii’s locomotion in backpack formation is further supported by the observed lack of backpack formation by nonmoving A. castellanii trophozoites (Fig. 4A and Movie S3).

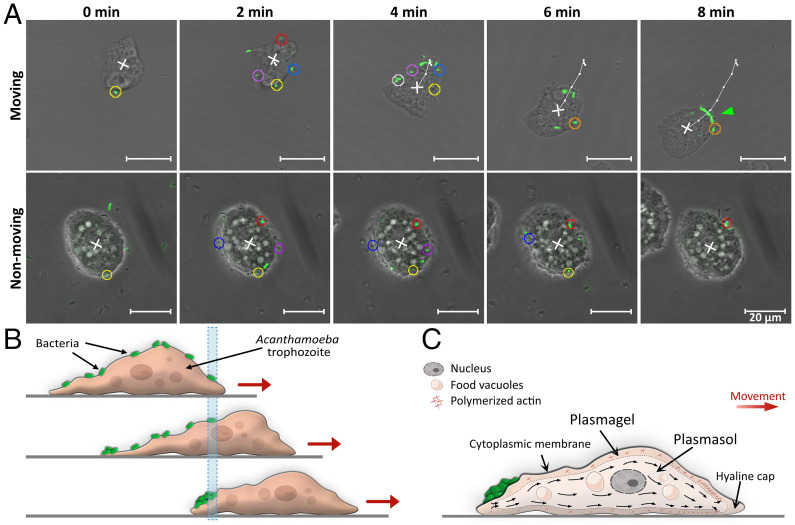
Fig. 4.

Captured bacteria are incorporated into a backpack upon reaching the rear of the A. castellanii trophozoite as the amoeba moves forward. (A) Time series monitoring the capture and relocation of fluorescent L. monocytogenes on the surface of a moving and a nonmoving A. castellanii trophozoite. Motile L. monocytogenes from all directions (green rods, marked with circles of color according to their time of arrival, in the order yellow, red, blue, purple, white, orange) were trapped on the surface of an A. castellanii trophozoite. A backpack, marked with a green arrowhead, was observed 8 min after the first capture by the moving Acanthamoeba trophozoite. In contrast, L. monocytogenes cells trapped on nonmoving Acanthamoeba trophozoites did not assemble into a backpack. The white cross indicates the position of the geometric center of the A. castellanii trophozoite, and the white line and dots indicate its trajectory as the trophozoite moves (Movies S2 and S3). (B) Schematic representation of our proposed model for backpack formation. The initial location of the anteriormost bacterium is marked with a blue bar. As the A. castellanii trophozoite moves on a surface, the bacteria (in green) remain stationary relative to the substratum until they reach the posterior of the trophozoite, where the bacteria are accumulated into a backpack. (C) Hypothetic model for backpack formation associated with the sol–gel–sol theory for the movement of amoebae on surfaces. Actin filaments are polymerized at the front of the trophozoite to form plasmagel and are subsequently depolymerized at the rear to form plasmasol that contains a pool of unpolymerized monomers. Bacteria (in green) captured on the surface of the trophozoite are deposited in a backpack at the region where plasmagel becomes plasmasol.

The mechanism of backpack formation can be explained by the reversible change of cytoplasm from sol to gel state that drives the locomotion of Acanthamoeba trophozoites (13). The cytoplasm, enveloped by the cytoplasmic membrane, consists of a central fluid plasmasol surrounded by a more viscous plasmagel. The plasmasol streams toward the front of the cell to form projecting pseudopodia, which propel the cell forward. As it reaches the front of the cell, the plasmasol converts into plasmagel, which remains stationary relative to the substrate. Meanwhile, at the rear of the cell, plasmagel is reconverted into plasmasol (30). We thus propose that this continuous conversion between gel and sol and the associated movement of trapped bacterial cells rearwards relative to A. castellanii’s absolute position drive the aggregation of trapped bacteria into backpacks (Fig. 4C). In summary, backpack formation results from a combination of two sequential processes, both related to motility: The capture of L. monocytogenes cells is a result of random encounters, enhanced by the bacteria’s motility, while the rearward transport and aggregation of captured bacteria into a backpack is the result of the amoeboid motility of A. castellanii.

Discussion

We provided a detailed understanding of the mechanisms that drive a peculiar predation strategy used by A. castellanii, namely backpack formation, in which motile L. monocytogenes are trapped and aggregated prior to phagocytosis and digestion. Our results demonstrate that the capture dynamics of L. monocytogenes by A. castellanii can be explained by theoretical models of random encounter rates, and contrary to what had been previously hypothesized there is no evidence of chemotactic attraction of the bacteria toward chemicals released by the amoebae (6). Backpack formation, i.e., the aggregation of trapped L. monocytogenes cells at the rear of the amoeba, is driven by the locomotion of A. castellanii trophozoites through the reversible change of cytoplasm from gel to sol.

Backpacks of L. monocytogenes are assembled by A. castellanii trophozoites very rapidly (5 to 10 min) and in close proximity to the A. castellanii uroid, an excretory organ at the rear of the trophozoite. This led to the initial hypothesis that A. castellanii recruits L. monocytogenes by secreting chemoattractants (6). Our microfluidic chemotaxis assays demonstrated that L. monocytogenes are capable of chemotaxis toward a gradient of BHI broth, which is frequently used as a growth medium for Listeria. However, L. monocytogenes showed no accumulation toward the secretions of a dense culture of A. castellanii, despite such cultures readily giving rise to backpack formation once mixed with L. monocytogenes. Some studies suggest that bacteria-derived volatile organic compounds may serve as signals for protists to sense bacterial prey (31, 32). We cannot entirely rule out that A. castellanii produces a highly volatile compound that could act as a signal to attract Listeria. However, we would expect such a compound to attract a higher number of Listeria cells nearby A. castellanii compared to regions without acanthamoeba, something we did not observe during our experiments to quantify the capture dynamics (SI Appendix, Fig. S2), even during saturated phases when the capture of L. monocytogenes had ceased (SI Appendix, Fig. S1). Thus, results from the capture dynamics experiments indicate that chemoattractants do not play a role in backpack formation, which is consistent with the observations from the chemotaxis assays. One could argue that the production of a chemoattractant by A. castellanii might be delayed if it requires induction by initial contact with prey bacteria. However, this possibility is not supported by the observed capture dynamics. If production of chemoattractants required induction, we would expect that the slope of the cumulative capture curves would be low initially and would increase over time as the production of chemoattractants ramped up. In contrast, we observed the opposite, with saturation of the cumulative capture curves over time. Therefore, our results suggest that chemotaxis does not play a role in the encounter and backpack formation of L. monocytogenes cells by A. castellanii. We note that L. monocytogenes has only two known chemoreceptor genes, a lot less than other bacteria that are known for strong chemotaxis, such as Escherichia coli (5 genes) or Pseudomonas aeruginosa (24 to 26 genes) (33). The possibility that other chemotactic bacteria may sense specific signal molecules secreted from A. castellanii trophozoites cannot be excluded. Nevertheless, our results show that bacterial chemotaxis is not a requirement for backpack formation, since this aggregation phenomenon can be observed with L. monocytogenes which are not chemotactic toward A. castellanii.

The lack of evidence for bacterial chemotaxis in the interaction between L. monocytogenes and A. castellanii led us to microscopically investigate the time-resolved capture dynamics associated with this predator–prey interaction to better understand the backpack formation strategy. The linear relationship between experimentally derived capture rates and theoretically calculated encounter rates strongly supports the hypothesis that random encounters govern the capture dynamics (Fig. 3F). This comparison between theory and observations also yielded an estimate of the capture efficiency (i.e., the percentage of encountered L. monocytogenes cells that are captured), which falls in the range 32 to 50%. These capture efficiencies should be interpreted with care, because the estimates of both the observed capture rates and the theoretical encounter rates involve a number of approximations that may lead to underestimation. First, the experimentally derived capture rates are limited by the depth of field of the recorded images and subsequently of our particle-tracking script, which effectively results in a two-dimensional system, while actual captures occur from the fluid in three dimensions. Therefore, we expect actual capture rates to be higher than reported. Second, theoretical estimates of encounter rates were computed with an estimated diffusivity based on observed near-surface speeds, which can be lower than bulk speeds, thus resulting in lower estimates of diffusivity and therefore encounter rates. Third, we assumed in our estimated diffusivity complete randomness between reorientations, whereas a bias toward previous swimming direction, as observed for example in E. coli (34), can also increase diffusivity and therefore encounter rates. Fourth, we assumed the average run time of L. monocytogenes between orientations to be equal to 1 s, as a typical value for bacteria (28, 35, 36), in our estimation of Listeria diffusivities. A reduction or increase in the average run time would proportionally reduce or increase the theoretical encounter rates, respectively. However, the linear fit between theoretical encounter rates and experimentally derived capture rates would be preserved, validating a random encounter process at play. Nevertheless, our estimates of the capture efficiency are comparable with values published for other aquatic predatory microorganisms, such as the dinoflagellate Oblea rotunda, which captures the raphidophyte Fibrocapsa japonica with a capture efficiency of 45% (37).

An important bacterial phenotype that strongly increases encounter rates is motility (38). Using the equation for an absorbing disk (Materials and Methods, Eq. 1), an A. castellanii trophozoite with radius $r_a$ = 15.5 μm would encounter two motile L. monocytogenes cells per minute for bacteria with mean swimming speed $v$ = 12.5 μm/s (the mean observed in our experiments) and cell concentration $b_L$ = 10⁷ cells/mL. In contrast, if L. monocytogenes cells were nonmotile, an A. castellanii cell of the same radius and exposed to the same L. monocytogenes concentration would encounter only 0.008 L. monocytogenes cells per minute, a 250-fold decrease (assuming a Brownian motion regime for which the diffusivity [D_B] is calculated using the Stokes–Einstein equation at temperature 25 °C and L. monocytogenes radius of 1 μm). On the other hand, swimming motility can also be an effective escape mechanism against protozoan predators, allowing bacteria to wiggle free and thus escape capture. For instance, motility helps 83% of F. japonica cells to escape when captured by dinoflagellate predators (37). Furthermore, experimental observations of bacteria incubated with predatory flagellates suggest that 95% of bacteria with an average swimming speed higher than 55 µm/s were able to escape capture after cell contact, whereas only 57% of nonmotile bacteria survived contact with a predator (39). Given these two contrasting effects of motility in enhancing encounters but also enhancing escape, bacteria with moderate swimming speeds (10 to 20 µm/s) have been shown to have the highest probability of being predated by flagellates, compared to slower or faster species (39). While these results were obtained for predation mechanisms differing significantly from the one studied here, they highlight the nontrivial variations of predatory success rate in relation to bacterial prey swimming speed, due to the contrasting effects of increasing swimming speed on encounter rate and capture efficiency. Moreover, the quadratic increase of encounter rates with bacterial swimming speed leads us to speculate that for the mechanism of capture documented here, higher swimming speeds might mostly result in higher capture rate, putting an effective cap on the maximum speed of this species in presence of predators.

In addition to motility, encounter and capture rates were influenced by A. castellanii’s size and the concentration of L. monocytogenes cells. Our results demonstrate that higher encounter rates, resulting in higher capture rates, occur at higher bacterial concentrations (SI Appendix, Fig. S6). A saturation phase was observed in the capture dynamics of L. monocytogenes, especially at higher cell concentrations. This observation suggests that A. castellanii may require a handling time after accumulating a certain number of bacteria in a backpack, during which capture rates may be reduced. The change in amoebae culture conditions, from an axenic rich medium to saline buffer containing bacteria, might provide an explanation for the observed delay in the phagocytosis of already assembled backpacks at high concentrations of L. monocytogenes. However, the assembly and digestion of backpacks of trapped L. monocytogenes cells was also observed during coculture in nutrient-rich peptone–yeast–glucose (PYG) broth (SI Appendix, Fig. S8 A–D), demonstrating that A. castellanii feeds on bacteria even in an environment with readily available nutrients. Alternatively, there might be a limit to the capacity of A. castellanii to trap and carry a large number of bacterial cells on their surface (40). This could be due to a physical limit on the space available on the amoeba’s surface or to the regulation of the structures responsible for maintaining the bacteria attached to its surface. Due to the highly dynamic nature of capture, aggregation, and phagocytosis of L. monocytogenes cells, we were not able to quantify handling times or backpack size limitations in this study.

Over the course of an experiment, decreasing swimming speeds and/or cell densities of L. monocytogenes would result in a lower encounter rate and therefore would contribute to the saturation of cumulative captures. However, only in one experiment, encounter rates based on the disk model $K_{\text{disk}}$ (Materials and Methods, Eq. 3) get close to zero (SI Appendix, Fig. S7G), which explains the saturation phase of the corresponding cumulative capture curves (SI Appendix, Fig. S1G). For all other experiments with a noticeable saturation phase, the encounter rate stays well above one cell per min (SI Appendix, Fig. S7 B, C, F, and I), which should result in a net increase in the cumulative L. monocytogenes captures. Thus, the observed saturation of the cumulative capture curves suggests that there is a limit on the capacity of the A. castellanii trophozoite for bacterial capture (40).

While encounters are strongly driven by the motility of the bacterium, our observations show that the backpack formation process itself is driven by the motility of the amoeba. Backpacks are only observed in the posterior region of A. castellanii (6), whereas L. monocytogenes cells are initially trapped over the entire trophozoite surface upon encounter. During A. castellanii locomotion, trapped L. monocytogenes remained stationary relative to the substratum until they reached the posterior of the A. castellanii trophozoite and were integrated into the backpack. The locomotion of Acanthamoeba trophozoites is driven by the continuous conversion of cytoplasm from sol to gel at the anterior and reconversion to sol at the posterior (30). An actin-rich network provides rigidity of the plasmagel layer and may explain why trapped Listeria cells remain stationary relative to the substratum until reaching the uroid. Similar observations have been made using beads attached to the dorsal surface of migrating Dictyostelium discoideum, and this behavior has been attributed to stationary cortical actin filaments on Dictyostelium cells during migration (41). The movement of beads to the rear of the cell was also recorded in studies on mouse macrophages (42).

The mechanism responsible for keeping L. monocytogenes trapped on the surface of A. castellanii trophozoites remains unknown. In a previous study, filamentous structures of unknown origin have been observed within backpack aggregations (6). These filaments are generally considered crucial in the assembly of food particles by A. castellanii. Beside these thin filaments, acanthopodia, spike-like structures 1 to 2 µm in diameter and up to 8 µm in length (43), may be used to capture bacterial cells. The surface receptors of A. castellanii trophozoites, such as mannose-binding receptors, might also contribute to keeping captured bacteria in place (44, 45). Further studies to determine the functioning and composition of these capture structures would be of value for their potential to inspire bacterial immobilizing methods in biomimicry applications.

Overall, our findings show that backpack formation occurs as a result of two nonspecific, motility-related processes: random encounters enhanced by bacterial motility and rearward transport and accumulation of captured bacteria driven by the amoeba’s locomotion. These two behaviors are fundamental to bacteria and amoebae, respectively; this induces us to expect the strategy of backpack formation to be more widespread among amoebae-like eukaryotes, a hypothesis that will require broader screening. Hitherto, observations of backpack formation with trapped L. monocytogenes or other bacterial species have only been reported for cocultures performed in the laboratory. Additionally, we propose that this capture strategy is energetically efficient for A. castellanii, as encounters are driven by the prey’s movement and backpack formation occurs based on the amoeba’s own movement. The ability of A. castellanii to exploit bacterial motility to enhance its predation rate, a surprising strategy in view of the role of motility as an escape mechanism of some bacteria from protozoan predators (46), allows A. castellanii to achieve a high predation rate and to consume bacteria from the bulk while being confined to surfaces. Therefore, even though attraction of prey by their chemotaxis does not seem to play a role in the predation strategy of A. castellanii, motility of its prey organism is still relevant for determining the capture rate, as it drives the rate of random encounters with the predator. In contrast, the predator’s movement, which is known to enhance prey encounters in other micropredators (47), provides here the mechanism to assimilate captured bacteria into backpacks ready to be consumed by phagocytosis.

Materials and Methods

Culture Conditions.

All experiments were performed using L. monocytogenes Scott A wild type or a strain that expresses GFP, L. monocytogenes Scott A::pPL2P_hypgfp (48, 49). Before each experiment, a clonal population was inoculated in half-strength BHI broth (1/2 BHI; Biolife) and grown overnight in an orbital shaker (Innova 42; New Brunswick) at 200 rpm and 30 °C. The overnight culture was resuspended and diluted (1:100) in fresh 1/2 BHI and incubated in an orbital shaker (Innova 42; New Brunswick) at 200 rpm and 30 °C until midexponential phase (OD_600nm = 0.7 to 0.8), because our preliminary experiments revealed that L. monocytogenes Scott A shows highest motility during this growth phase. Listeria cultures were washed once by centrifugation in 1.5-mL Eppendorf tubes (10 min at 1,000 rpm, equivalent to 94 rcf; room temperature; Eppendorf 5425R centrifuge) and resuspended at the required concentration in nonnutrient PAS buffer (0.12 g/L NaCl, 3.94 mg/L MgSO₄·7H₂O, 3.02 mg/L CaCl₂, 0.358 g/L Na₂PO₄·12H₂O, and 0.136 g/L KH₂PO₄). Only one washing step was performed because strong or long-term centrifugation during multiple washing steps causes damage to the flagella and drastically reduces Listeria’s motility. All bacterial optical density measurements were performed at a wavelength of 600 nm using a spectrophotometer (WPA Biowave CO8000 Cell Density Meter; Biochrom). A. castellanii Neff strain (6) was used in all experiments. Acanthamoeba trophozoites were axenically cultured to exponential phase (approximately 5 × 10⁵ cells per mL) as a monolayer in 75-cm² cell culture flasks (Bioswisstec) at room temperature in 10 mL PYG broth [20 g/L peptone (LLG Labware), 18 g/L glucose (Roth), 2 g/L yeast extract (LLG Labware), 1 g/L trisodium citrate·2H₂O (Merck Group), 980 mg/L MgSO₄·7H₂O, 52 mg/L Na₂PO₄·12H₂O, 340 mg/L KH₂PO₄, and 20 mg/L Fe(NH₄)₂(SO₄)₂·6H₂O]. Further preparations with amoebae are specified for each individual experiment below. A. castellanii concentrations were determined using a Brand counter chamber (Brandblau Neubauer pattern, 0.100 mm depth; Merck). Attached A. castellanii cells were gently scraped from the bottom of the flask with one-directional movement using a cell scraper (Bioswisstec). All chemicals used to make PAS buffer and PYG broth were obtained from Sigma-Aldrich, unless stated otherwise.

Visualization of Backpacks.

Backpacks (Fig. 1 and SI Appendix, Fig. S8) were visualized using confocal laser scanning microscopy and scanning electron microscopy (SEM) (SI Appendix, Visualization of Backpacks).

Microfluidic Fabrication for Chemotaxis Assays.

Chemotaxis assays were performed to investigate whether L. monocytogenes Scott A wild-type strain were attracted to substances secreted by A. castellanii trophozoites. To expose L. monocytogenes to potential chemoattractants and quantify cell behavior, a microfluidic LGG was developed, consisting of three straight channels separated by polyacrylamide hydrogel walls (Fig. 2A) (SI Appendix, Microfabrication of Chemotaxis Assay). All channels within the LGG were 50 µm in height and 1.5 cm in length; the central channel was 1,000 µm in width, while the two side channels and the hydrogel walls were 500 µm in width. A mold for the LGG was fabricated from an Su-8 resin template on a silicon wafer. Microfluidic channels were then created by casting polydimethylsiloxane (PDMS; Sylgard 184) onto the mold. Hydrogel walls were then precisely and locally cured within the microfluidic chip on a microscope stage (50) while simultaneously chemically bonding the walls to the top and bottom PDMS layers (51).

Experimental Setup of Chemotaxis Assays.

Prior to performing chemotaxis assays, the LGG microfluidic chip was rinsed with PAS buffer for 12 h, at a flow rate of 5 µL/min, to remove all remaining unpolymerized acrylamide monomers, to guarantee biocompatibility (52). The LGG chip was then preloaded with the respective samples (see below). This was achieved by connecting each of the inlets of the chip to a syringe (10 mL, BD Luer-Lok Sterile syringes with 23-gauge 1/2 5FVJ3 syringe tips) with tubing (Cole-Parmer Tygon Tubing PG-06419-01) (SI Appendix, Fig. S9). The three syringes were mounted on a syringe pump (PHD2000; Harvard Apparatus); one syringe was loaded with the respective sample and connected to one side channel, and the other two syringes were loaded with PAS buffer and connected to the other side channel and to the central channel (Fig. 2A). Outlets were connected via tubing (as above) to an empty 50-mL Falcon tube to collect waste liquid. Unless specified otherwise, flow rate of 15 µL/min was applied for the experiment. In order to accelerate the establishment of the gradient across the central channel, the source hydrogel wall was presoaked for 30 min with the potential chemoattractants contained by the respective sample. Next, without stopping the flow in the two side channels, the syringe connected to the central channel was replaced by a 5-mL syringe filled with a washed Listeria culture (see Culture Conditions), diluted to concentration of 1 × 10⁷ CFU/mL. The cell suspension was injected into the central channel by gently pushing on the syringe plunger manually until continuous drops were seen to emerge from the outlet tubing. The inlet and outlet tubes of the central channel were then blocked with scissor clamps to prevent residual flow in the channel, which would impair accurate visualization of the behavioral response of the bacteria. Immediately afterward, a video acquisition routine was initiated, consisting of recording 5-s videos (50 fps) at 1-min intervals, focused at midplane depth in the central channel, using a Nikon Ti2 microscope with a 10× objective (Nikon CFI Plan Fluor 10×) in phase contrast. The field of view was placed at a randomly chosen location along the length of the central channel and spanned the full width of the channel including a portion of both hydrogel walls. A total of 20 videos were recorded per experiment.

The chemotaxis assays were conducted with different samples to determine whether motile L. monocytogenes Scott A wild type perform chemotaxis and whether A. castellanii secretions are among the cues that attract L. monocytogenes. Two samples consisted of 10% BHI broth as a positive control and PAS buffer as a negative control. The two other samples represented suspensions of A. castellanii cells (see Culture Conditions) that were washed with PAS buffer, 10 times in total, to ensure complete removal of the PYG broth used to culture A. castellanii, to avoid it acting as a potential chemoattractant. For the first suspension (Acanthamoeba), the amoebae were scraped from the bottom of the culture flask and diluted in PAS buffer to a final concentration of ∼5 × 10⁵ cells per mL. Next, the suspension was transferred to a syringe and, after a 30-min waiting period, injected into the source channel. For the second suspension (Acanthamoeba overnight), A. castellanii trophozoites were first starved for 24 h in PAS buffer. Next, attached cells were scraped from the bottom of the culture flask and diluted in PAS buffer to a final concentration of ∼5 × 10⁵ cells per mL. The suspension was transferred to a syringe and injected into the source channel with a flow rate of 15 µL/min. This high flow rate was chosen for two reasons. First, it ensures that the concentration of potential chemoattractant in the source channel (which serves as the boundary condition for the gradient in the central channel) is maintained constant, since the source channel’s contents are refreshed 40 times per minute. Second, a high flow rate removes the effect of any potential patchiness in the distribution of A. castellanii on the gradient in the central channel, since the latter is determined by a rapidly refreshed boundary condition in the source channel.

Image processing and analysis were performed using ImageJ (NIH) and in-house Python scripts (SI Appendix, Python Scripts). Raw 16-bit video files (.ND2) were converted to 16-bit tiff-files using ImageJ. Videos were cropped so that the resulting frames (∼1,000 × 1,000 µm) contained the full width of the central channel but no regions of the hydrogel walls. To reduce background noise, the median value for each pixel over all frames was subtracted from that pixel for each frame. This resulted in a pixel-value distribution centered around zero. A custom 8-bit conversion was then performed by adding 125 to all pixel values and setting the resulting pixel values that were smaller than 0 to 0 and those that were greater than 255 to 255. This resulted in videos with reduced file size while maintaining a broad dynamic range of pixel values. A 2- × 2-pixel Gaussian blur was performed (to reduce pixel noise) prior to thresholding all pixel values above 118 to 255 to remove nonbacterial features. In the resulting videos, bacteria appear as dark objects on a white background.

Bacterial cells were segmented and tracked from frame to frame using TrackPy (53). Nonmotile cells were then excluded as motility is crucial to perform chemotaxis. To achieve this, mean squared displacements were calculated with a maximum delay time of 1 s (or 25 frames, which is the minimum timeframe for a trajectory to be considered for analysis). The slope of the mean squared displacement, known as the translational component, can be used to categorize bacteria on the basis of their movement into adherers (cells that stick to the surface), diffusers (cells that are nonmotile and randomly diffuse), and superdiffusers (cells that are motile and randomly diffuse) (54). Here, we set the threshold for the translational component to 1.2, above which all bacterial trajectories were considered to fall within the superdiffuser or motile regime. In order to obtain a single point position for each bacterial trajectory, the average position of each trajectory was calculated. These positions were then used to calculate the relative cell concentration over the width of the central channel in five bins of 200 µm (Fig. 2B, regions R1 to R5). The presence or absence of chemotaxis was then determined by evaluating the change in relative number of bacteria over time for the different regions of the central channel. If L. monocytogenes were not attracted to the generated chemical gradient, the relative cell numbers within each region would be expected to remain stable over the course of the experiment. In contrast, a significant increase of relative cell numbers in the region closest to the chemoattractant containing source channel (R1) combined with a decrease in the region furthest away (R5) would indicate the presence of bacterial accumulation, and hence chemotaxis.

Capture Rate Experiments.

To quantify capture rates, we observed the interactions between L. monocytogenes Scott A and A. castellanii within a microfluidic channel (Fig. 3A). A. castellanii trophozoites (see Culture Conditions) were washed, 10 times in total, with PAS buffer. Attached cells were scraped from the bottom of the culture flask and diluted in PAS buffer to a final concentration of ∼5 × 10⁴ cells per mL. A volume of 200 µL A. castellanii suspension was transferred into a single-channel microfluidic chip (µ-Slide I 0.6 Luer ibiTreat chip; Ibidi), where they were left for 20 to 30 min to allow cells to attach to the surface. The buffer was then gently replaced with a washed and diluted L. monocytogenes suspension (200 µL), at one of three bacterial concentrations: 2 × 10⁷, 1 × 10⁷, or 0.5 × 10⁷ CFU/mL (based on OD₆₀₀ measurements). The microfluidic chip was then immediately transferred to an inverted microscope (Nikon Ti2) for image acquisition using a 20× objective (numerical aperture = 0.45). A region of interest encompassing at least five A. castellanii cells was selected and the focal plane was set to 5 µm above the bottom surface of the microfluidic channel. For a period of 1 h, 2-min time-lapse videos were recorded at 20 fps, with 1-min intervals between videos, resulting in 20 time points for each experiment. Triplicate experiments were performed for each bacterial concentration.

Image processing and analysis were performed using ImageJ (NIH) and in-house Python scripts (SI Appendix, Python Scripts). Raw video files were converted from 16-bit ND2-files to 16-bit TIFF-files using ImageJ (NIH). Around each unobstructed A. castellanii trophozoite (i.e., located more than 20 µm from the edge of the field of view and from any other A. castellanii trophozoite), a region of interest (350 × 350 pixels or 113.75 × 113.75 μm) was cropped and saved as a separate video. Using Python, pixel values within each video were rescaled and converted to 8 bit to reduce file size, without compromising dynamic pixel value range. This was achieved by dividing the 16-bit pixel values by 2.5, then centering all pixel values around 125 by subtracting the global median value of all pixels over all frames from all pixels in each frame and adding 125. Pixel values above 255 and below 0 were set to 255 and 0, respectively.

Prior to tracking of the Listeria cells with Trackpy (53), two dynamic masks (an Acanthamoeba mask and an interaction mask for each individual frame) were created for each region of interest using mathematical operations from the OpenCV (55) and SciPy (56) modules (Fig. 3A and Movie S1). The Acanthamoeba mask covered the area of the A. castellanii cell and was used to remove particles detected in this area over all frames of the recording prior to trajectory building. Without this mask, trajectory building of free-swimming L. monocytogenes was severely impaired. The interaction mask was a larger version of the Acanthamoeba mask, extending 4 μm (approximately twice the length of a Listeria cell) beyond the Acanthamoeba mask, all around its boundary (Fig. 3B). The interaction mask allowed us to count the captured Listeria for each time point by taking the difference between the numbers of bacterial cells that entered and left this mask.

For each experiment, digital controls were performed by selecting a region of interest where no A. castellanii cells were present. Within this region, we counted “captured” L. monocytogenes cells using a randomly chosen and randomly positioned interaction mask from the same experiment. Since there was no A. castellanii present in these control regions, the expected number of captured L. monocytogenes cells is zero (as bacteria have an equal chance of entering and exiting this control mask), thereby providing a way to validate the imaging analysis method used to quantify the capture rate. Because we imaged for 2 out of every 3 minutes, we estimated the number of captured L. monocytogenes between two time points by increasing the observed number of captured L. monocytogenes by a factor of 1.5. Using the same approach as described for the chemotaxis assays, nonmotile L. monocytogenes were identified by the translational component of their mean squared displacement, with values lower than 1.2 being excluded (54). For each region of interest (those around A. castellanii and those used as controls), we also computed the concentration of motile Listeria, the mean swimming speed of motile Listeria, and the projected area of the A. castellanii cell (equal to the area of the Acanthamoeba mask).

The capture rate experiments were performed three times for each of the three initial Listeria concentrations, with three digital controls in each replicate. As a result, we analyzed the capture rate in a total of 76 A. castellanii time series and 27 control time series (each time series lasting 1 h) (SI Appendix, Fig. S1).

Comparison of Experimentally Derived Capture Rates and Theoretical Encounter Rates.

To investigate the mechanisms driving the capture dynamics of L. monocytogenes by A. castellanii, we quantified capture rates from the cumulative capture curves derived from our video analyses and compared them to theoretical encounter rates expected from random bacterial swimming motility, which we estimated for each A. castellanii trophozoite based on parameters estimated individually. Based on the shape of the experimental cumulative capture curves and after testing several regression methods, we selected a saturating exponential function of time for the cumulative captured number of L. monocytogenes cells per A. castellanii cell based on fit performance. Regressions were performed in Graphpad Prism version 9.0.1 for Windows (GraphPad Software). For each amoeba, the cumulative capture curve was fitted (SI Appendix, Fig. S1) with a saturating exponential function of time t,

$$C=\alpha \left(1-e^{\frac{-t}{\beta }}\right),$$ [1]

from which the maximum number of captured Listeria cells for that amoeba, α, and the saturation time, $\beta$, were obtained. α is equal to the y-value of the horizontal asymptote that forms the upper limit of the saturating function, and $\beta$ represents the typical time at which the function starts significantly saturating. The capture rate $\gamma$ (cells per minute) per amoeba was then computed as

$$\gamma =\frac{\alpha }{\beta },$$ [2]

which is equal to the slope of the initial, near linear phase of the cumulative capture curve.

In order to determine the number of L. monocytogenes cells that each A. castellanii cell would be expected to encounter, we selected two known analytical expressions for a flux of randomly diffusing particles that encounter a perfectly absorbing geometry (28), in which A. castellanii trophozoites are modeled as a disk or as a half-sphere attached to a surface, with bacterial encounters happening only on the surface of the trophozoite not in contact with substrate. We considered these two equations because the shape of the A. castellanii trophozoite lies between these two geometries. For the disk scenario $K_{\text{disk}}$, bacteria were encountered at a rate (cells per unit time)

$$K_{\text{disk}}=4D{r}_{\text{A}}{b}_{\text{L}},$$ [3]

where $D$ is the diffusivity, $b_{\text{L}}$ is the concentration of motile Listeria cells, and $r_{\text{A}}$ is the radius of the A. castellanii trophozoite. In Eq. 3, all encountered cells are considered to be captured. The diffusivity of motile L. monocytogenes was quantified from the classical approximation (28) as

$$D=\frac{v^2\tau }{3},$$ [4]

where $v$ is the average swimming speed obtained from tracking motile Listeria cells and $\tau$ is the average duration of a run between reorientations. This run duration is here taken to be 1 s, as is typical for Listeria (36) and other species such as E. coli (28) and Bacillus subtilis (35). The linear dependency of encounter rates with this parameter makes our conclusions robust to variation in its precise value (see Discussion). For the scenario with a half-sphere geometry $K_{\text{hs}}$, bacteria were encountered at a rate (cells per unit time)

$$K_{\text{hs}}=2\mathrm{\text{π}}D{r}_{\text{A}}{b}_{\text{L}}.$$ [5]

Also here, the model considers all encountered cells to be captured.

To compute the theoretical encounter rates based on the experimentally observed organism characteristics, we focused on the initial phase of the cumulative capture curves (SI Appendix, Fig. S1), corresponding to the capture rates prior to saturation $\gamma$, Eq. 2. Specifically, in quantifying $K_{\text{disk}}$ and $K_{\text{hs}}$ (Eqs. 3 and 5, respectively) for each individual A. castellanii trophozoite, we used values of $v$, $r_{\text{A}}$, and $b_{\text{L}}$ obtained by averaging experimental values up to time t = $\beta$ from the start of an experiment, in a (113.75 × 113.75 μm, i.e., 350 × 350 pixels) region of interest surrounding the trophozoite (Fig. 3D). Experimentally derived capture rates ($\gamma$) were plotted as a function of the two theoretically derived random encounter rates (K_disk and K_hs) and linear regressions performed to assess the goodness of fit. The slope of these linear regressions represents the capture efficiency.

Tracking Captured L. monocytogenes Cells on the Surface of A. castellanii Trophozoites.

To visualize the rearrangement of L. monocytogenes cells trapped on the surface of A. castellanii trophozoites into backpacks, we imaged the bacteria and the amoebae in an eight-well IbiTreat µ-Slide (Ibidi). A. castellanii trophozoites (see Culture Conditions) were scraped from the bottom of the culture flask and diluted with PYG broth to a final concentration of ∼5 × 10⁴ cells per mL. A volume of 200 µL of A. castellanii suspension was added into a well and the cells were allowed to settle on the bottom surface for 20 to 30 min before the well was gently washed three times with 200 µL PAS buffer. L. monocytogenes cells were then added, consisting of a 1:4 ratio of prewashed L. monocytogenes Scott A::pPL2P_hypgfp and Scott A wild-type cells in PAS buffer, at a total concentration of 2 × 10⁷ CFU/mL. Thus, only 20% of the L. monocytogenes population was fluorescently labeled to ensure that tracking of individual cells was possible. The µ-Slide was immediately transferred to a confocal laser scanning microscope (TCS-SPE; Leica Microsystems). An A. castellanii trophozoite was rapidly and randomly selected from the field of view, and a time-lapse video (0.75 fps) was recorded using a 100× objective (Leica HCX PL FLUOTAR Oil 100×) with an excitation wavelength of 488 nm and an emission wavelength range of 500 to 565 nm. The focal plane varied slightly between and during observations to ensure trapped L. monocytogenes cells stayed in focus. The time-lapse recording lasted until a clear backpack of bacterial cells was observed on the surface of the A. castellanii, which typically took between 4 and 7 min. A total of eight A. castellanii trophozoites from three biological replicate cultures were recorded in eight separate experiments. Movement of the A. castellanii trophozoite and relocation of captured GFP-expressing L. monocytogenes cells were tracked manually using ImageJ (SI Appendix, Manual Tracking of Individual GFP-Expressing L. monocytogenes Trapped on the Outer Surface of A. castellanii). Upon capture by A. castellanii, each GFP-expressing L. monocytogenes cell was marked with a colored circle and tracked until the bacterium was added into the backpack. To represent the instantaneous location of the A. castellanii, a white cross was placed at the mass center of the cell, calculated by ImageJ. The trajectory of the A. castellanii trophozoite was obtained by connecting these mass centers in consecutive images.

Data Availability

The Python scripts used for the analyses and all resulting data(57) are available via a public GitHub repository at (https://github.com/FdeSchae/Acanthamoeba-Listeria. The raw microscopy data generated in this project have a volume of ∼2.5 terabyte and can be shared in the form of an external hard drive upon request.