Significance
The cortex is particularly vulnerable to perturbations during sensitive periods, such as the critical period when manipulating sensory experience can induce long-lasting changes in brain structure. Depriving rodents of vision in one eye (known as monocular deprivation [MD]) reduces network activity over two days, whereby inhibitory neurons decrease their firing rates one day after MD, while excitatory neurons are delayed by an additional day. We use spiking networks to mechanistically dissect the requirements for this independent firing-rate regulation after sensory deprivation. We find that in networks stabilized by recurrent inhibition, at least two interneuron subtypes (parvalbumin-expressing and somatostatin-expressing interneurons) are necessary to dynamically alter the circuit response after deprivation and generalize the result across sensory cortices.
Keywords: interneurons, cortical circuits, sensory deprivation, synaptic plasticity, network model
Abstract
Diverse interneuron subtypes shape sensory processing in mature cortical circuits. During development, sensory deprivation evokes powerful synaptic plasticity that alters circuitry, but how different inhibitory subtypes modulate circuit dynamics in response to this plasticity remains unclear. We investigate how deprivation-induced synaptic changes affect excitatory and inhibitory firing rates in a microcircuit model of the sensory cortex with multiple interneuron subtypes. We find that with a single interneuron subtype (parvalbumin-expressing [PV]), excitatory and inhibitory firing rates can only be comodulated—increased or decreased together. To explain the experimentally observed independent modulation, whereby one firing rate increases and the other decreases, requires strong feedback from a second interneuron subtype (somatostatin-expressing [SST]). Our model applies to the visual and somatosensory cortex, suggesting a general mechanism across sensory cortices. Therefore, we provide a mechanistic explanation for the differential role of interneuron subtypes in regulating firing rates, contributing to the already diverse roles they serve in the cortex.
Diverse interneurons serve multiple cell-type-specific functions in the cortex (1, 2). The connectivity among excitatory pyramidal neurons and different subtypes of interneurons plays a key role in establishing these functions. In mature cortical circuits, interneurons are involved in disinhibition during locomotion and learning (3, 4), response reversal during top-down modulation (3, 5–7), surround suppression (8, 9), and affect excitatory tuning (10, 11). Inhibitory synapses are plastic (12, 13) and drive plasticity in excitatory circuits (14); however, we still do not understand how the plasticity of connections among the different interneuron subtypes and excitatory neurons shapes circuit dynamics and computations.
Cortical circuits are particularly sensitive to perturbations in development and young adulthood during so-called critical periods, when manipulating sensory experience can induce long-lasting changes in circuit connectivity (15–17). Depriving rodents of vision in one eye (known as monocular deprivation, or MD) causes a biphasic response in the monocular region of the primary visual cortex (V1m), driven exclusively by the contralateral eye, that first reduces and then restores excitability (18–20). The plasticity of inhibitory synapses contributes to these processes (21–25). However, it primarily pertains to fast-spiking interneurons, which most likely correspond to parvalbumin-expressing (PV) interneurons, the most abundant and best-studied interneuron subtype in the cortex (2).
Previous work has found that the plasticity of recurrent connectivity, and especially the potentiation of intracortical inhibition, dominates over the depression of feedforward connectivity to explain the initial decrease of excitatory and inhibitory activity after MD (24). However, recent experiments show that the network behavior might be more complex with fast-spiking, putative PV inhibitory neurons decreasing their firing rates 1 d after MD (MD1), while excitatory neurons are delayed by an additional day (19, 26). What mechanism lies behind this independent modulation of excitatory and inhibitory firing rates remains unclear.
We used a spiking recurrent network with balanced excitation and inhibition to study this process in a microcircuit model of the sensory cortex. Theoretical work has shown that the dynamics of these networks depend on the operating regime, which is determined by the strength of recurrent coupling (27–31). Strong excitatory recurrent coupling needs to be stabilized by sufficiently strong inhibition, giving rise to “inhibition-stabilized networks” (ISNs) (8, 32). A signature of inhibition stabilization is the “paradoxical effect,” which refers to the decrease of inhibitory firing rate following direct excitatory drive to inhibitory interneurons (32). Recent experiments have confirmed the paradoxical effect in cortical circuits, suggesting that they operate in the ISN regime (33, 34). This raises the important question of whether ISNs can explain the independent modulation of excitatory and inhibitory firing rates after brief MD.
We found that ISNs cannot capture the independent modulation of excitatory and inhibitory firing rates after brief MD. Even in the presence of heterogeneous connectivity, recurrently driven inhibitory neurons cannot independently modulate their firing rates relative to excitatory neurons. Considering the diversity of interneuron subtypes in the sensory cortex and their role in modulating cortical dynamics, we also modeled somatostatin-expressing (SST) interneurons, the second-most-abundant subtype of interneurons in the cortex (2). Our results demonstrate that the addition of SST interneurons inverts the firing-rate response of PV interneurons relative to excitatory neurons in response to MD-induced plasticity by reversing the paradoxical effect. In contrast to previous work that focused on the paradoxical effect in response to externally injected currents (6, 35, 36), we find that recurrent interactions are the main drivers, specifically, the strength of the feedback from SST interneurons to PV interneurons and excitatory neurons. Importantly, we implement synaptic changes observed experimentally both along the feedforward [from the thalamus (24, 37)] and recurrent [within the cortex (21, 23, 38)] pathways that significantly expand the possibilities for modulating cortical firing rates beyond external drive to the inhibitory population. Hence, our results explain the independent modulation of excitatory and inhibitory firing rates, consistent with their sequential suppression during early MD with inhibitory preceding excitatory firing rates (19, 20). We also applied our model to whisker deprivation (WD) in the somatosensory cortex, which affects interneuron intrinsic excitability rather than synaptic strength onto interneurons (39). Our model predicts similar modulations of the firing rates when changing the intrinsic excitability, suggesting that similar principles might be at work in different sensory cortices. Therefore, our work provides a mechanistic explanation for the experimentally observed temporally offset modulation of excitatory and inhibitory activity after sensory deprivation. It also establishes a more general framework to study how the interaction of three factors—cortical operating regime, interneuron diversity, and plasticity in feedforward and recurrent pathways—shapes circuit dynamics and computations.
Results
Changes in Network Firing Rates from MD-Induced Plasticity in an ISN.
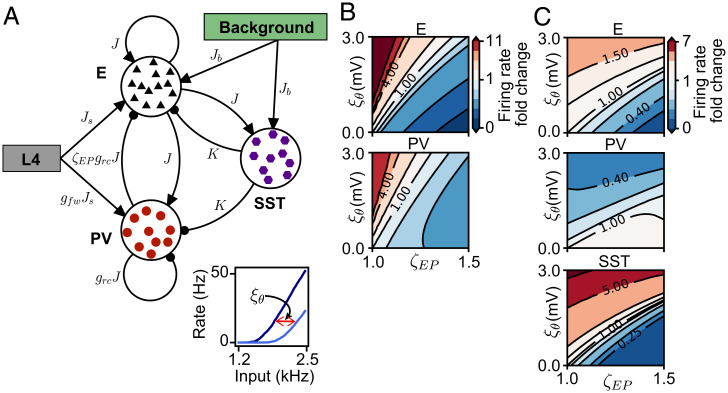
To investigate excitatory and inhibitory activity changes in response to synaptic plasticity after brief MD, we built a network model of the primary visual cortex (V1) consisting of excitatory and inhibitory spiking neurons (Fig. 1A and Materials and Methods). Following previous theoretical work, we first only modeled a single class of interneurons, which we equated with parvalbumin-positive (PV), the largest class of interneurons in the mammalian neocortex (2, 40). The networks have strong recurrent coupling, denoted by the overall coupling scale J. The coupling scale describes the operating state of the network (8, 33, 41) and determines the networks’ dynamical and computational properties (27–31). This strong recurrent coupling needs to be stabilized by sufficiently strong inhibition denoted by the parameter (Fig. 1A) (8, 32). Such a network produces sparse, asynchronous, and irregular spiking activity (27, 28).
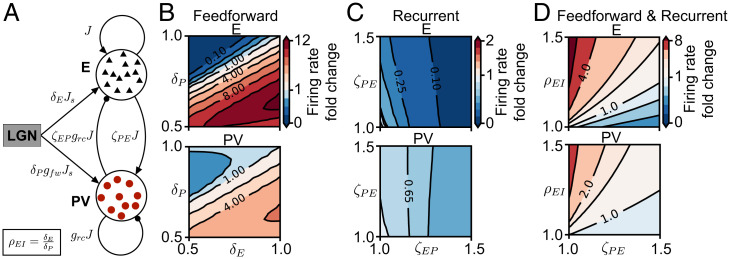
Fig. 1.
Spiking network response to synaptic changes induced by brief MD. (A) Network schematic of synaptic connections among neurons with J denoting the overall coupling scale, as the dominance of recurrent inhibition, and as the dominance of feedforward inhibition. The parameters to model MD-induced synaptic plasticity are: depression of feedforward drive to excitatory neurons () and to PV interneurons () and potentiation of recurrent excitation to PV interneurons () and of recurrent inhibition from PV to excitatory neurons () (see Materials and Methods). (B) Network firing rate in the () plane as fold change of baseline firing rate (top right corner, ) for excitatory neurons (Upper) and PV interneurons (Lower). (C) Network firing rate in the () plane as fold change of baseline firing rate (bottom left corner, ). (D) Combined feedforward (through the E/I ratio of feedforward synaptic changes, ) and recurrent plasticity (through the potentiation of recurrent excitation to PV interneurons, ). Network firing rate in the () plane as fold change of baseline firing rate (bottom left corner, ).
We first modeled synaptic changes measured experimentally in the cortical circuits during brief (1 to 2 d of) MD, both along the feedforward pathway from the lateral geniculate nucleus (LGN) to the cortex and in the recurrent cortical circuit. In particular, feedforward excitatory synaptic inputs from the LGN to both excitatory and inhibitory neurons in the cortex depress during MD (42, 43), while recurrent intracortical inhibition potentiates (refs. 21–25; but see ref. 44). To investigate the relative contribution of these two factors—decrease in feedforward excitation vs. increase in recurrent inhibition—on the modulation of firing rates, we introduced four model parameters to represent the synaptic changes (Fig. 1A): 1) depression of feedforward synapses onto excitatory neurons (); 2) depression of feedforward synapses onto PV interneurons (); 3) potentiation of recurrent synapses from excitatory neurons to PV interneurons (); and 4) potentiation of recurrent synapses from PV to excitatory neurons (). These synaptic changes have been measured experimentally in the visual cortex after 2 d of MD (MD2), in contrast to other synaptic changes, including those between excitatory neurons and between PV interneurons (21), and are therefore the most likely to change activity as measured during the first 2 d of MD (19). Specifically, we asked if the independent modulation of excitatory and PV rates can be captured by specific combinations of the four synaptic changes.
We investigated the effect of these feedforward and recurrent synaptic changes on excitatory and inhibitory activity separately to quantify the extent of comodulation. For both feedforward () and recurrent () synaptic changes, we generated a plane of firing-rate changes in the excitatory and PV populations relative to their respective baseline firing rates before plasticity (Fig. 1 B and C). We used synaptic change ranges (Materials and Methods), which are consistent with experimental results (23, 24). We found that depression of feedforward synaptic strengths, which reduces the feedforward drive to the network, can have either facilitating or suppressive effects on the activity of excitatory neurons and PV interneurons (Fig. 1B). A linear relationship between and separates the facilitation and suppression areas of excitatory and PV firing rates. The slope of this line is determined by the relatively stronger feedforward drive onto PV interneurons compared to excitatory neurons (; Fig. 1A and Materials and Methods), determined experimentally (40, 45). To capture the relationship between the relative excitatory and inhibitory feedforward drive, we introduced the excitation/inhibition (E/I) ratio of feedforward synaptic changes, . This ratio has been measured to be bigger than unity after brief MD from the thalamus to layer 4 (L4) (24) and also from L4 to layer 2/3 (L2/3), in the visual cortex (46). Therefore, we found that synaptic changes exclusively in the feedforward pathway from the thalamus to cortex, which increase the E/I ratio, increase both excitatory and inhibitory firing rates (Fig. 1B). In contrast, purely recurrent synaptic changes measured in L4 of V1 after 2 d of MD (21, 24), which potentiate synaptic strengths from excitatory neurons to PV interneurons () and from PV interneurons to excitatory neurons (), have a purely suppressive effect on the excitatory and inhibitory firing rates (Fig. 1C). Combining feedforward and recurrent plasticity can either increase or decrease excitatory and inhibitory firing rates, depending on whether feedforward or recurrent synaptic changes dominate (Fig. 1D).
Intriguingly, modeling feedforward and recurrent plasticity separately reveals that firing-rate changes of excitatory and PV neurons tightly follow each other in the entire parameter space of feedforward and recurrent synaptic changes (Fig. 1 B–D).
This implies that if inhibitory firing rates decrease at MD1, so should excitatory firing rates (when, in fact, experimentally, they stay at baseline), and if excitatory firing rates decrease at MD2, so should inhibitory firing rates (when, in fact, experimentally, they recover back to baseline). Hence, this result is inconsistent with the independent modulation of excitatory and PV firing rates following brief MD observed in vivo (19), suggesting that other factors might be at play.
The Network Response to MD-Induced Synaptic Changes Depends on Coupling Scale.
We next sought to identify a plausible mechanism behind the lack of independent modulation of firing-rate changes in the excitatory and PV populations. Of the two parameters that determine recurrent synaptic strengths in the model network, the overall coupling scale, J, is more important than the relative scale of the inhibitory synaptic strength, , in determining the network response to MD-induced plasticity (Fig. 1A). The parameter J has been extensively studied as a determinant of the operating regime of the network (27–31). A network with a strong coupling scale J operates in a regime where the excitatory dynamics are stabilized by recurrent inhibition (ISN). In contrast, a network with weak J operates in a regime where the excitatory dynamics are stable without recurrent inhibition (non-ISN) (32). We found two very different behaviors in the network at the opposite ends of the coupling scale J. While at high coupling, excitatory and PV responses show a tight alignment (Fig. 1 with J = 0.1 nS), for weak to intermediate coupling, when the network is in the non-ISN regime, excitatory and PV firing rates can be independently modulated for all feedforward and recurrent synaptic changes (SI Appendix, Fig. S1 with J = 0.01 nS). Hence, the transition from independent to tight modulation of excitatory and inhibitory firing rates matches the transition from non-ISN to ISN with increasing coupling scale J.
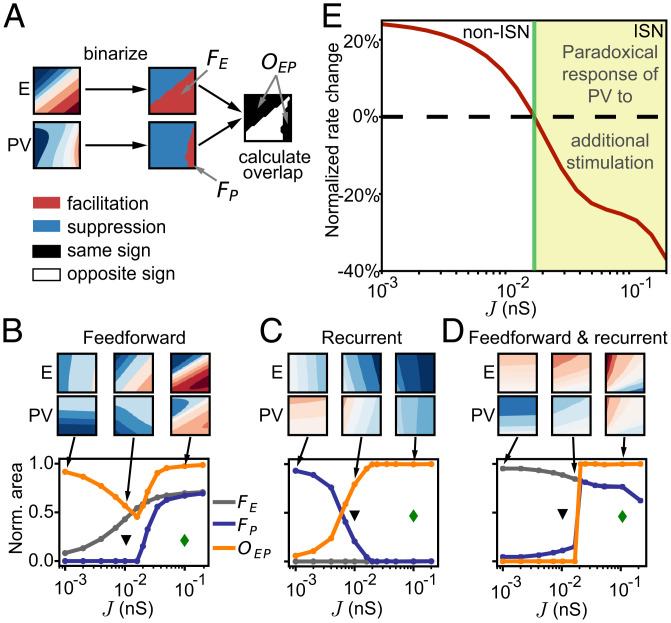
To quantify how closely the firing rates of excitatory and inhibitory neurons follow each other in the entire parameter space of feedforward and recurrent synaptic changes, we computed the fractional response area of facilitation for excitatory neurons () and for PV interneurons () and the overlap between excitatory and PV response areas as a function of J (; Fig. 2A). We first computed these measures for feedforward () synaptic changes (Fig. 2B). We found that the facilitation area for PV interneurons, and consequently the overlap between excitatory and PV response areas, abruptly changes at a critical value of coupling ( nS). In particular, PV facilitation emerges at nS (; Fig. 2B), the same value of J where the overlap switches from decreasing to increasing (; Fig. 2B). These measures do not depend on the range of synaptic changes (SI Appendix, Fig. S2A).
Fig. 2.
Firing-rate changes in response to MD depend on the network coupling scale J. (A) Schematic to determine the overlap of facilitating and suppressive response areas of excitatory and PV neurons. The thresholded plane of responses (Fig. 1) for both neuron types is used to compute the total facilitating area and quantify how closely excitatory and PV firing rates follow each other through the overlap of facilitation and suppression. (B) Network with feedforward depression only (Fig. 1B). Fractional area of facilitation for excitatory neurons (; gray), PV interneurons (; blue), and the overlap between excitatory and PV response areas (; orange) as a function of the overall coupling scale J. The green diamond shows the value of J used in Fig. 1 (ISN), and the black triangle shows the value of J used in SI Appendix, Fig. S1 (non-ISN). (C) Same as B for recurrent potentiation only (Fig. 1C). (D) Same as B for combined feedforward and recurrent plasticity (Fig. 1D). (E) Normalized rate change of PV interneurons in response to additional input to them as a function of coupling scale J. Additional input is given as increase in (from 1 to 1.1). Norm., normalized.
Using a reduced linear population-rate model (SI Appendix, Figs. S3 and S4 and Materials and Methods) (32, 47), we found that a key network property related to the transition from non-ISN to ISN is the emergence of facilitation in PV interneurons at the critical coupling J following feedforward plasticity (Materials and Methods and Fig. 2B; note that in the linear model, the parameter representing the coupling scale is w). This transition is related to the emergence of the paradoxical effect at the critical J (w), where in response to external excitatory drive, the inhibitory population paradoxically decreases its rate together with the excitatory population (Fig. 2E and Eq. 28) (32). Beyond applying an external excitatory drive to the inhibitory population, we applied synaptic changes, which affect the external drive to both the excitatory and inhibitory populations simultaneously, allowing us to extend the paradoxical effect to multiple dimensions (Fig. 2B).
Existing work on the paradoxical effect does not tell us how changes in recurrent drive might affect firing rates (6, 35, 36). Consequently, we computed the fractional response area of facilitation for excitatory neurons and for PV interneurons and the overlap between excitatory and PV response areas also in the parameter space for recurrent synaptic changes () (Fig. 2C and SI Appendix, Fig. S2B). Here, we found that at the same critical value of coupling ( nS), the facilitation area for PV interneurons decreases to zero (; Fig. 2C), suggesting a dominance of recurrent inhibition in ISNs triggered by the potentiation of recurrent inhibition after MD (21, 24). Combining feedforward and recurrent plasticity demonstrated a similar transition of the PV facilitation area at the critical value of J (Fig. 2D and SI Appendix, Fig. S2C).
These results argue that only the non-ISN supports the experimentally observed independent modulation of excitatory and inhibitory firing rates in response to synaptic changes after brief MD (SI Appendix, Fig. S1). However, cortical circuits seem to operate in the ISN regime (8, 33, 41), which cannot explain the independent modulation of excitatory and inhibitory firing rates due to concurrent feedforward and recurrent synaptic changes after brief MD. Moreover, in the non-ISN, the magnitude of this modulation to this plasticity is much weaker, suggesting that experimentally measurable changes in firing rates might require synaptic changes larger than what seems biologically plausible.
To quantify the difference of susceptibility of the firing rates to synaptic changes in the two regimes (ISN in Fig. 1 and non-ISN in SI Appendix, Fig. S1), we computed the gradient of excitatory and PV responses in the different parameter spaces (Materials and Methods and SI Appendix, Fig. S5 B–D). For feedforward and combined plasticity, the small gradient lengths in the non-ISN suggest weak susceptibility (SI Appendix, Fig. S5 B–D, black triangle). The lengths steeply increase with J, leading to strong susceptibility in the ISN (SI Appendix, Fig. S5 B–D, green diamond). The small angle between the gradients for large J confirmed the coordinated firing-rate changes of excitatory and PV interneurons in the ISN regime in contrast to the non-ISN (SI Appendix, Fig. S5 E–G).
A Network Model with Two Subtypes of Interneurons.
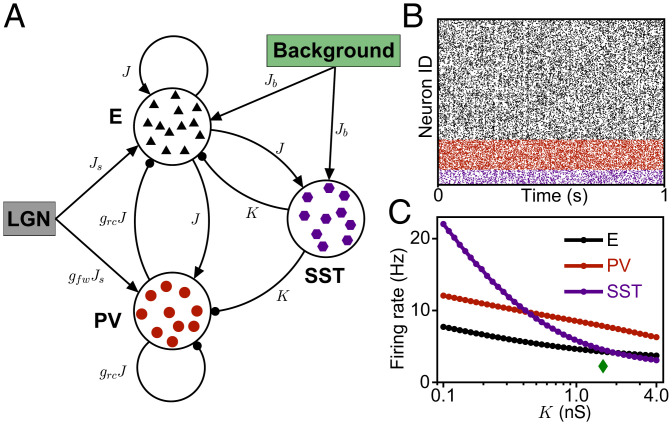
Given the role of interneuron diversity in a range of cortical functions, including disinhibition, response reversal, and surround suppression, we next added the second-largest class of cortical interneurons, SST interneurons, to the ISN (2, 48). We modeled SST interneurons, which project to excitatory neurons and PV interneurons via the coupling parameter K, but which do not receive inhibition from PV interneurons or inhibit each other (Fig. 3A), following previous work (40, 49). SST interneurons receive almost no thalamic feedforward input (45), but receive feedback from higher-order cortical centers and integrate inputs over large areas in the visual cortex (2, 9, 50, 51). We modeled these inputs from outside the local patch of cortex represented by the network as a background that provides input to both SST and excitatory neurons (Fig. 3A). Upon introducing SST interneurons, the ISN remained in an asynchronous and irregular firing state, independent of the SST feedback K (Fig. 3B). We found that the effect of K on the mean rate is suppressive (Fig. 3C), although SST feedback is symmetric, providing direct inhibition to excitatory neurons and indirect disinhibition to excitatory neurons via PV interneurons. We next studied whether the ISN with two subtypes of inhibitory interneurons can explain the independent modulation of excitatory and inhibitory firing rates.
Fig. 3.
Network structure and spiking activity in the model with two subtypes of interneurons. (A) Schematic connectivity in the network with two subtypes of interneurons. (B) Spike raster of activity in the network with K = 1.6 nS. (C) Firing rates as a function of K. The green diamond shows the value of K used in B.
SST Interneuron Feedback Can Invert PV Interneuron Responses.
Implementing feedforward synaptic changes in this ISN with two inhibitory subtypes, we found that the excitatory response is qualitatively similar as in the network without SST feedback (Fig. 4A vs. Fig. 1B). Strikingly, the presence of strong SST feedback K inverts the response of PV interneurons in the entire () plane of feedforward synaptic changes (Fig. 4A vs. Fig. 1B). To explain the mechanism behind the inversion of PV responses in the ISN with two inhibitory subtypes, we considered a generalization of the paradoxical effect studied in previous work (35). In this generalized paradoxical effect, when multiple interneurons are present, it is the total inhibitory current received by excitatory neurons, rather than the inhibitory firing rate, that responds paradoxically to external drive to an inhibitory population (35). This enables the firing rates of the different inhibitory populations to respond either paradoxically or nonparadoxically. Therefore, indeed, in the presence of strong SST feedback, the PV population can respond nonparadoxically in response to changes in feedforward drive. This generalized notion also holds when multiple subtypes of excitatory neurons are present, in addition to multiple subtypes of inhibitory interneurons (36).
Fig. 4.
SST feedback selectively inverts PV responses. (A) Network firing rate in the () plane as fold change of baseline firing rate (baseline in top right corner) for excitatory (Top), PV (Middle), and SST (Bottom) neurons in the network with strong SST feedback (K = 1.6 nS). (B) Network firing rate in the () plane as fold change of baseline firing rate (baseline in bottom left corner). (C) Network firing rate in the () plane as fold change of baseline firing rate (baseline in bottom left corner). (D) Network with feedforward depression only. Fractional area of facilitation for excitatory neurons (; gray), PV interneurons (; blue), and the overlap between excitatory and PV response areas (; orange). (E) Same as D for recurrent potentiation only. (F) Same as D for combined feedforward and recurrent plasticity. The green diamond in D–F shows the value of K used in A–C. Norm., normalized.
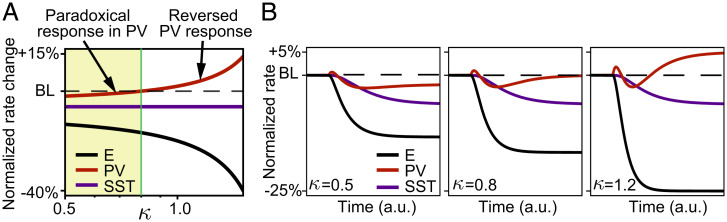
Since strong SST feedback was needed to invert PV firing rates, we studied their inversion in the linear population model as a function of the strength of output synapses of the SST population, described by the parameter κ (Eq. 11). Increasing the strength of this SST feedback reverses the paradoxical effect in PV interneurons (Eq. 30 and Fig. 5A). For any value of κ, the PV population activity initially transiently increases, leading to a decrease of excitatory population activity (Fig. 5B). For small κ, the decrease of excitatory activity suppresses the steady-state PV activity below baseline, leading to the classical paradoxical effect (Fig. 5 B, Left). As κ increases, the steady-state PV activity is not only dictated by the dwindling of recurrent excitation, as in the case of the paradoxical effect. Rather, PV activity becomes dominated by the release from inhibition mediated through SST. Hence, the paradoxical decrease of PV activity is only transient, followed by a recovery of PV activity back to baseline at an intermediate value of κ (Fig. 5 B, Center). For large κ, the steady-state PV activity increases above baseline (Fig. 5 B, Right). Assuming an intrinsic timescale in our linear rate model of 20 ms generates PV transients that last 10 to 20 ms, and a steady state is reached after ∼50 ms. This has been observed following optogenetic activation of PV interneurons to induce the paradoxical effect in adult animals (33).
Fig. 5.
The inversion of responses of PV interneurons emerges as a function of the SST feedback. (A) Relative change of steady-state rate induced by current injection to PV interneurons as a function of SST feedback κ. The rate of each population is normalized to its baseline firing rate (BL) before additional current injection. (B) Dynamics of the linear population rate model following onset of step current to PV interneurons for (Left), (Center), and (Right). Colors are the same as in A. a.u., arbitrary units.
Similar to the network with a single interneuron type, we simultaneously varied feedforward synaptic changes to the excitatory and PV populations (Fig. 4 A and D). To quantify the joint modulation of excitatory and PV firing rates, we computed the fractional response area of facilitation for excitatory neurons (), for PV interneurons (), and for the overlap between excitatory and PV response areas (), now as a function of K (Fig. 4D). The weak dependence of these measures on the range of studied plasticity did not affect the conclusions about the joint modulation of excitatory and PV firing rates to MD-induced plasticity (SI Appendix, Fig. S6A). As predicted by the linear rate model, at a critical value of the SST feedback ( nS), we found that the facilitation area of PV responses achieves a minimum (; Fig. 4D). Using the rate model, we proved that the area of PV facilitation vanishes and reemerges at the value of SST feedback that also inverts the PV responses (Materials and Methods and SI Appendix, Fig. S7).
Recurrent plasticity continues to have a strong suppressive effect on the excitatory firing rates, accompanied by a similar response in the SST interneurons (Fig. 4B vs. Fig. 1C). As the SST feedback K increases, PV interneurons invert their response, exhibiting pure facilitation for large values of K (Fig. 4B vs. Fig. 1C). Hence, the overlap between the excitatory and PV responses decays to zero (; Fig. 4E and SI Appendix, Fig. S6B). Combining feedforward and recurrent synaptic changes further corroborates the inversion of PV responses with increasing SST feedback K (Fig. 4 C and F and SI Appendix, Fig. S6C). The inversion for recurrent and combined synaptic changes is smoother in the spiking network than in the linear model, possibly due to changes of the effective gain through changes of recurrent synapses (Fig. 4 E and F vs. SI Appendix, Fig. S7 E and F and Materials and Methods).
In contrast to the non-ISN, the lengths of the gradients for excitatory and PV populations as a function of K revealed that the ISN retains high susceptibility of the firing rates to all types of synaptic change throughout values of K (SI Appendix, Fig. S8 A–C). The angle between the gradients further underscores the inversion of PV responses in the presence of strong SST feedback (SI Appendix, Fig. S8 D–F).
We conclude that, in ISNs typical of the sensory cortex, sufficiently strong feedback from SST interneurons can invert the responses of PV interneurons. While some of this inversion can be explained by the generalized paradoxical effect, our analysis achieves this for simultaneous feedforward and recurrent synaptic changes to both the excitatory and PV populations. We propose that the inversion of PV responses in an ISN with strong SST feedback provides a natural substrate for the independent modulation of excitatory and inhibitory firing rates as observed in vivo during MD (19), while ensuring high firing-rate susceptibility to synaptic changes.
PV Responses in Networks with Heterogeneous Connectivity.
Besides the diversity of interneuron subtypes in cortical circuits, neurons within a subtype are also highly variable (52). We investigated the response to MD-induced plasticity with heterogeneous connectivity to excitatory and inhibitory neurons (53, 54), which is observed in cortical circuits (55, 56) (SI Appendix, SI Text). We found that heterogeneity does not impact the average responses of the entire neuronal populations in a non-ISN, an ISN with a single subtype of interneurons (PV) or an ISN with two (PV and SST) subtypes of interneurons (SI Appendix, Figs. S9–S11). Next, we dissected the responses of PV by the level of recurrent inputs they receive. We found that in heterogeneous networks with a single subtype of interneurons, PV interneurons dominated by feedforward input can be modulated independently from excitatory neurons, but PV interneurons densely innervated by recurrent input closely follow excitatory neurons (SI Appendix, Fig. S12). In contrast, in heterogeneous networks with SST feedback, also highly recurrent PV interneurons can be modulated independently from excitatory neurons (SI Appendix, Fig. S13). Recurrently dominated PV interneurons are prevalent in the cortex and play important functional roles (57). Our results imply that PV interneurons with such dense recurrent innervation cannot be independently modulated in a model network with heterogeneous connectivity, unless strong feedback from SST is included. Hence, feedback from SST interneurons appears to be an important factor to explain the MD-induced firing-rate changes also for recurrently dominated PV interneurons.
Sensory Perturbation Induces Similar Activity Changes in Somatosensory Cortex via Different Plasticity Mechanisms.
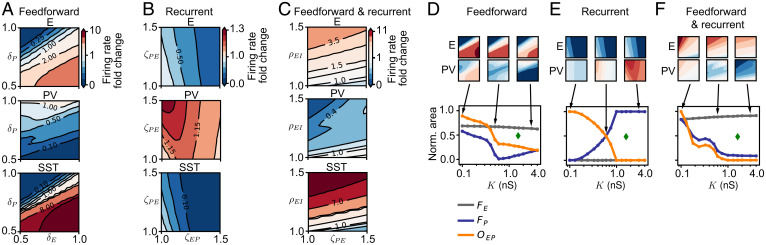
Similar to MD, WD is a sensory deprivation, where plucking a subset of the whiskers on one cheek of the animal affects the barrel cortex of the rodent primary somatosensory cortex (S1). However, it is not clear that these two paradigms should yield similar modifications of the circuitry in the respective sensory cortices. Indeed, experimentally measured plasticity in S1 induced by brief WD seems to be different from the plasticity in V1 after brief MD (39, 58, 59). Rather than the depression of feedforward synapses to PV interneurons in V1 found after brief MD (24), a reduction of feedforward inhibition emerges from a decrease in the intrinsic excitability of PV interneurons through an increase of their firing threshold (39). Our modeling approach allowed us to investigate whether these different types of plasticity in V1 and S1 during sensory deprivation change the modulation of excitatory and inhibitory firing rates in a corresponding microcircuit model of S1 (Fig. 6A).
Fig. 6.
Combining feedforward and recurrent plasticity in S1. (A) Schematic for combined recurrent and feedforward plasticity in S1: shift in recurrent E/I ratio through , shift in feedforward E/I ratio through increasing firing threshold of PV interneurons (). (A, Inset) The f–I curve of a single LIF neuron for baseline firing threshold (dark blue) and with increased firing threshold (light blue). The excitability of PV interneurons is decreased via the parameter . (B) Network firing rate as fold change of baseline firing rate (baseline in bottom left corner) in the () plane in the network with only one type of interneurons (PV). (C) Network firing rate as fold change of baseline firing rate in () plane in the network with two subtypes of interneurons (PV and SST), with strong SST feedback K = 1.6 nS.
As before, we first considered a network with a single interneuron type by setting the SST feedback, K, to zero. We modeled the decrease of the intrinsic excitability of PV interneurons by increasing their firing threshold by (Fig. 6 A, Inset). In an ISN model of S1 with only PV interneurons, increasing the firing threshold of PV interneurons facilitates their firing rates, just like the depression of the feedforward synaptic strength from the LGN onto excitatory and inhibitory neurons in the model V1 network. This decrease of intrinsic excitability of PV interneurons in S1 was proposed as a homeostatic mechanism that counteracts the lack of stimulation after deprivation and enhances firing rates (see also refs. 58 and 59).
We further implemented potentiation of recurrent inhibition as in V1 by . Experimentally, brief (1 d of) WD in S1 has shown a tendency, but no statistical significance, for the potentiation of recurrent inhibitory synapses from PV to excitatory neurons (39). In contrast, prolonged (6 to 12 d of) WD has shown a pronounced increase in this connection strength (58). Hence, the potentiation of recurrent inhibition by seems to counteract the facilitation of activity by , giving rise to the same antagonistic regulation we found for early MD-induced plasticity in V1 (Fig. 6B; compare to Fig. 1D). Similar to MD-induced plasticity, excitatory and PV activity changes in this network with WD-induced plasticity were tightly coordinated in the ISN. Importantly, after introducing strong feedback from SST interneurons, the response of PV interneurons again inverts relative to the excitatory responses due to the reversal of the paradoxical effect (Fig. 6C).
Therefore, our modeling demonstrates that the dissimilar circuit changes induced by sensory deprivation (WD or MD) in two different sensory cortices, which decrease intrinsic excitability of PV interneurons or depress feedforward drive to PV interneurons, respectively, lead to similar regulation of overall activity as they interact with potentiation of recurrent inhibition. This could point to a shared principle of firing-rate regulation invoked by sensory perturbation that is implemented by different means in these two sensory cortices.
Discussion
We investigated how synaptic changes induced by sensory deprivation affect the firing rates of excitatory and inhibitory neurons in a microcircuit model of the sensory cortex. Specifically, we modeled two pathways: 1) the reduction of feedforward excitability manifested as a depression of feedforward, thalamocortical synapses onto excitatory and inhibitory neurons observed following MD in visual cortex (or as a decrease of intrinsic excitability in inhibitory neurons following WD in somatosensory cortex); and 2) the potentiation of recurrent synapses between excitatory and inhibitory neurons. Crucially, we found that strong feedback from a second interneuron subtype, SST, in addition to PV interneurons, is needed to explain the independent modulation of excitatory and inhibitory activity observed experimentally in V1 during the critical period of plasticity.
Previous studies have investigated MD-induced plasticity in V1, but with a focus on ocular dominance plasticity in binocular cortex governed by winner-take-all competition, where the open eye outcompetes the closed eye (46, 60–63). Since most brain regions do not exhibit such strong competition, we focused on plasticity in the V1m, where synaptic and activity changes during MD have recently been measured (19, 20, 24). Some models have begun to incorporate these experiments by implementing a careful orchestration of biologically inspired synaptic and homeostatic plasticity rules to explain the recovery of diverse aspects of network dynamics after MD (26, 64, 65). As our approach is agnostic about the plasticity rules underlying deprivation-induced synaptic changes, it offers the advantage to turn individual synaptic changes “on” or “off” in different network regimes. This gives us full control to study the effect of the timing of individual plasticity mechanisms in the network.
Although anatomical and functional experimental studies have highlighted the role that diverse interneuron subtypes play for multiple functions in the cortex (1, 2), theoretical network models of the cortex have only recently started to incorporate these diverse subtypes and model their influence on network dynamics (6, 14, 34, 35, 66). In rodent cortex, three major interneuron subtypes, PV, SST, and vasointestinal peptide-expressing (VIP) interneurons, comprise 80 to 90% of all inhibitory interneurons (2, 48). In our model, we included only the two largest interneuron populations, PV and SST, in L4 of V1. This minimized the computational complexity of the model by reducing the number of free parameters. We do not expect that our results will change if we also add VIP interneurons, given recent modeling work showing that mutual inhibition between SST and VIP can switch SST feedback on or off (67). Hence, VIP can be considered to provide modulatory input to SST (66).
We found that the operating regime of the network, determined by the overall coupling scale, has a major impact on how deprivation-induced plasticity shapes firing-rate changes. ISNs with a single inhibitory subtype and strong coupling, commonly used to describe the cortex (33), cannot capture the independent modulation of excitatory and inhibitory firing rates after brief MD, even when including heterogeneous connectivity. We showed that this can be partially explained by the presence of the paradoxical effect, but generalized it to changes in the drive to both excitatory and inhibitory neurons and along both the feedforward and recurrent pathways. We proposed that feedback from SST interneurons can achieve the independent modulation of excitatory and inhibitory firing rates in response to MD-induced synaptic changes by reversing the response of PV interneurons for many combinations of synaptic changes. This is consistent with previous theoretical results for a network with multiple subtypes of interneurons, where a specific inhibitory population can behave nonparadoxically in response to an external input, even if the whole network operates as an ISN (6, 35). Rather than relying on an external current, we found that strength of the feedback from SST interneurons to PV interneurons and excitatory neurons is the key driver behind the inverted PV responses. The reversed responses persist for many combinations of synaptic changes, including experimentally measured ones, suggesting that the independent modulation of excitatory and inhibitory firing rates is not sensitive to the exact timing and strength of plastic changes.
Our model suggests that a nonparadoxical response of PV interneurons upon stimulation is behind the independent modulation of excitatory and PV firing rates, yet recent experiments find that PV interneurons in L2/3, upper L4, and deep layers of V1 show a paradoxical response following optogenetic stimulation (33). The type of response (paradoxical or not) could depend on the anatomical region or the cortical layer (10, 34, 68–70). More intriguingly, however, it is possible that the nonparadoxical response of PV interneurons is a transient property of the developing cortex during the critical period that disappears with maturation. PV can respond nonparadoxically either in a non-ISN or in an ISN with strong SST feedback. Thus, there are two possible developmental processes that could resolve the tension between the independent firing-rate modulations during the critical period and the paradoxical effect in the adult. First, the cortical circuit during the critical period could operate as a non-ISN with weak recurrent excitation, which strengthens as the animal matures together with recurrent inhibition, turning into an ISN. Second, the circuit could operate as an ISN both during the critical period and in the adult with a reversal of the paradoxical effect in PV through strong SST feedback as a transient property. This could emerge, for example, through a developmental decrease of initially strong coupling from SST onto PV interneurons (71). Although we favor an ISN with strong SST feedback to explain the independent modulation of excitatory and inhibitory firing rates during MD, direct evidence of the operating regime of cortical circuits during the critical period is lacking. Several pieces of evidence indirectly suggest that inhibition is needed to stabilize network dynamics already before eye opening and before the onset of the critical period. First, perturbing GABAergic signaling at these early ages when the sensory cortex experiences spontaneous activity seems to elicit very high levels of activity (72, 73). Additionally, the reversal potential of GABA decreases, leading to the hyperpolarizing action of GABA during the same developmental period (72, 74, 75). However, this requirement for inhibition to stabilize network dynamics is not a definite proof that the cortex operate as an ISN before the critical period because inhibition reduces overall network activity also in a non-ISN. To determine the cortical operating regime at these early ages would require similar perturbations as recently performed in the adult (33, 34).
An alternative to changing the operating regime by changing the overall coupling scale is to change the response gain of single neurons in the network, as is the case in the stabilized supralinear network (SSN). The SSN has recently gained attention as a circuit model of V1 with powerful computational capabilities, including contrast-gain control and nonlinear response amplification (76). Our systematic analysis over a wide range of coupling scales could be interpreted as the local linear approximation of the SSN in response to MD-induced synaptic changes. Hence, we expect all results to hold also in the SSN.
Our results make concrete predictions that can be tested with further experiments that characterize population activity by affecting individual circuit elements at different stages during development and in different layers. First, we predict that SST interneurons in L4 during the critical period should decrease their activity in response to additional stimulation of PV interneurons (e.g., through optogenetic activation). This decrease would be the result of a withdrawal of recurrent excitation, rather than direct inhibition from PV to SST interneurons, and could specifically be investigated by experimentally measuring the respective conductances in individual SST interneurons. A second, related prediction is that the firing rates of SST interneurons during the first 2 d of MD should be tightly coordinated with excitatory firing rates.
A further unknown is the plasticity of recurrent connections involving SST interneurons in L4 during MD (48). Although the plasticity of synapses involving electrophysiologically identified regular spiking nonpyramidal units has been measured (77), these cells were not genetically labeled as SST, and the measurements were performed before the onset of the critical period, where plasticity acts differently than in the critical period (38). We modeled the potentiation of intracortical inhibition during brief MD as a change in the excitatory drive from excitatory neurons to PV interneurons to be consistent with known plasticity mechanisms (21, 24). However, it is possible that the additional sources of inhibition from SST interneurons contribute to this increase in inhibition. For instance, potentiation of synaptic strength from SST onto excitatory neurons and/or depression of synaptic strength from SST onto PV interneurons could also underlie the increase in intracortical inhibition. We found that implementing these changes in our recurrent network generates comparable results to the firing-rate modulation of excitatory and PV interneurons (SI Appendix, Fig. S14). Therefore, a third prediction is the existence of a parallel, possibly redundant, pathway to generate the same firing-rate changes.
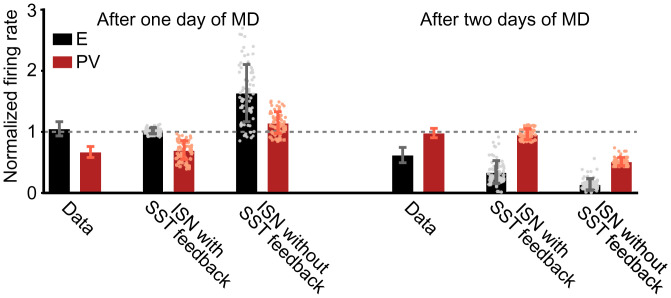
In summary, our mechanistic modeling suggests the following sequence as the most parsimonious explanation for the independent modulation of excitatory and inhibitory firing rates after sensory deprivation observed experimentally (Fig. 7). First, during the first day of deprivation, depression of the feedforward synaptic weights from LGN to excitatory neurons and PV interneurons in the visual cortex (or reduction of PV excitability in the somatosensory cortex) can give rise to strong suppression of PV firing rates, while excitatory rates remain at baseline, only in the ISN with strong SST feedback (Fig. 7, Left). Instead, in the ISN without SST feedback, the firing rates of both excitatory and PV populations facilitate or suppress together. Second, during the second day of deprivation, potentiation of recurrent inhibition in the cortex can strongly suppress excitatory firing rates and recover PV firing rates to baseline through potentiation of activity from the earlier suppressed state (Fig. 7, Right). Again, this is only possible in the ISN with strong SST feedback. More generally, our work provides a critical link between changes on the single-synapse level and activity modulation on the circuit level during perturbation of normal development as a function of cortical operating regime and interneuron diversity.
Fig. 7.
An ISN with strong SST feedback can capture the independent modulation of excitatory and inhibitory firing rates observed during brief MD. Firing rates of excitatory (black) and PV (red) neurons at MD1 (Left) and at MD2 (Right), normalized by the firing rates before MD induction, are shown. Data are extracted from ref. 19 and reproduced in the spiking network in the ISN regime that includes strong feedback from SST and in an ISN without SST feedback (Materials and Methods). Experimental data are mean ± SEM; simulation data are mean ± SD.
Materials and Methods
Spiking Network Model.
We studied recurrent networks of leaky integrate-and-fire (LIF) neurons, consisting of excitatory neurons, PV interneurons, and SST interneurons (Table 1). The membrane potential V(t) of a single neuron follows the dynamics:
| [1] |
Table 1.
Neuron and network model parameters
| Symbol | Value | Description |
|---|---|---|
| 200 pF | Membrane capacitance | |
| 10 nS | Leak conductance | |
| –70 mV | Leak-reversal potential | |
| –50 mV | Threshold potential | |
| –58 mV | Postspike reset potential | |
| 0 mV | Excitatory reversal potential | |
| –85 mV | Inhibitory reversal potential from PV and SST | |
| 5 ms | Synaptic conductance time constant | |
| 4,000 | Number of excitatory neurons | |
| 1,000 | Number of PV interneurons | |
| 500 | Number of SST interneurons | |
| p | 0.1 | Connection probability between any two neurons |
| J | 0.1 nS | EPSG amplitude E →E, E →PV and E →SST |
| 0.8 nS | IPSG amplitude PV →E and PV →PV | |
| K | 1.6 nS | IPSG amplitude SST →E and SST →PV |
| 0.5 nS | EPSG amplitude LGN →E, and scale of EPSG amplitude LGN →PV | |
| 2 | Multiplicative factor for EPSG amplitude LGN →PV | |
| 0.5 nS | EPSG ampltiude BKG →E and BKG →SST | |
| 1,000 Hz | Rate of input spike trains LGN →E, LGN →PV, BKG →E, and BKG →SST | |
| [0.5,1.0] | Depression of feedforward synapses LGN →E | |
| [0.5,1.0] | Depression of feedforward synapses LGN →PV | |
| [1.0,1.5] | Potentiation of recurrent synapses E →PV | |
| [1.0,1.5] | Potentiation of recurrent synapses PV →E | |
| [1.0,1.5] | E/I ratio of feedforward synaptic changes (for V1 model) | |
| [0,3] mV | Firing threshold of PV interneurons (for S1 model) |
EPSG, excitatory postsynaptic conductance; IPSG, inhibitory postsynaptic conductance.
where is the membrane capacitance, is the conductance of the leak-current, is the leak-reversal potential, and I(t) is the total input current. When the membrane potential reaches a firing threshold , a spike is emitted, and the potential is reset to . The neurons are randomly and sparsely connected with connection probability p with fixed in-degree by conductance-based synapses, or weights. Thus, all values for synaptic weights are positive, and the excitatory or inhibitory action of a presynaptic neuron is determined by the respective reversal potential (Table 1). All excitatory synapses have weight J, regardless of the postsynaptic target (28); this parameter describes the coupling scale and determines the operating regime of the network (32). Synapses from PV interneurons are scaled by the factor (28). Synapses from SST interneurons have weight K. Hence, the population connectivity matrix is given by:
| [2] |
where WAB denotes the connection from population B to population A, for excitatory neurons (E), PV interneurons (P), and SST interneurons (S). The case with only two populations, excitatory and PV, corresponds to K = 0.
External inputs to the model network come from two different sources: feedforward input from the LGN and background (BKG) inputs from the surrounding cortical tissue or higher-order cortical centers (9, 50). Each excitatory neuron receives two individual spike trains with Poisson statistics from the two different sources that are uncorrelated to each other, as well as to all spike trains received by other neurons. We denote the weight of the inputs from LGN to the excitatory neurons by and from BKG by ; PV interneurons only receive feedforward input from LGN that is considerably stronger than the input to excitatory neurons by the factor ; this is consistent with experimentally measured inputs from the LGN to L4 (45), as well as from L4 to L2/3 (40). SST interneurons only receive inputs from BKG with weight . The input spike trains from the LGN to the excitatory and PV neurons are modulated by the plasticity of the feedforward synaptic connections, while the input spike trains from the BKG to the excitatory and SST neurons are not modulated since the corresponding synapses do not experience plasticity. To minimize the number of parameters, we made the weights of LGN and BKG inputs the same (Table 1). We can write the feedforward population connectivity vector as:
| [3] |
where denotes LGN and denotes BKG.
The total input current to neuron i from population , is the sum of synaptic input current from neurons in all populations B coupled to A, , and the external input current, :
| [4] |
Denoting the spike train of neuron j in population B by and the feedforward input spike train to neuron i by , we write:
| [5] |
where is an exponentially decaying synaptic kernel with a synaptic time constant , and * denotes a convolution. Note that here, is the excitatory reversal potential, while EB could be either the excitatory, , or the inhibitory reversal potential, . To extract firing rates, we simulated the network with NEST (78) for 30 s and calculated the time-averaged population rate.
Implementation of Deprivation-Induced Circuit Changes.
We introduced the parameters and to model the depression of feedforward synapses and and to model the potentiation of recurrent synapses (Table 1). MD-induced synaptic changes were applied multiplicatively, with a new population-connectivity matrix (Table 1):
| [6] |
This is consistent with experimental measurements where the synaptic strength from excitatory to excitatory neurons and from fast-spiking to fast-spiking interneurons is unaffected, but other synapses potentiate (21, 24). There is no experimental evidence of plasticity in synapses of SST interneurons during MD. The new feedforward population-connectivity vector after MD is:
| [7] |
Note that we did not change the rate of the feedforward input, consistent with experimental findings (79).
To map firing-rate changes in response to brief MD, we separately simulated networks with feedforward and recurrent plasticity. For each type of synaptic change, the networks were simulated with parameters on a grid in the respective two-dimensional planes (Figs. 1 B and C and 4 A and B). To study the interaction of feedforward and recurrent plasticity, we combined and into the E/I ratio of feedforward synaptic changes . To simulate networks with varying E/I ratio, we fixed and varied (Figs. 1D and 4C).
Feedforward plasticity in S1 was driven by a decrease of intrinsic excitability of PV interneurons through an increase of their firing threshold (39). In the simulations, we thus changed the firing threshold of PV interneurons by adding , without changing any feedforward inputs. For recurrent plasticity, we modeled the potentiation from PV to excitatory neurons () (39). We simulated the S1 network with combined feedforward and recurrent plasticity as described above to extract the plane of firing-rate changes (Fig. 6 B and C).
Quantification of the Activity Changes Induced by Deprivation.
For each pair (x, y) of synaptic changes in the two-dimensional parameter space, for feedforward plasticity, for recurrent plasticity, and for combined plasticity, we obtained a matrix of rate fold changes of population at MD, , relative to baseline, :
| [8] |
To quantify the responses, we first studied the fractional area of facilitation. Elements of were thresholded at one, which denotes the border between suppression () and facilitation (). All matrix elements corresponding to facilitation were then set to 1, while those for suppression to –1. Summing up all the positive entries in this thresholded matrix and dividing by the total number of matrix elements produced the fractional area of facilitation ( in Figs. 2 and 4). We calculated the overlap of the response areas in excitatory neurons and PV interneurons by multiplying the thresholded matrices of excitatory and PV responses element-wise. After this multiplication, matrix elements corresponding to pairs of synaptic changes that resulted in the simultaneous suppression or facilitation of excitatory and PV responses were + 1, while elements corresponding to opposite responses of excitatory and PV neurons were –1. We summed all positive values and divided this sum by the total number of matrix elements to calculate the fractional area of overlap for facilitation and suppression in the two populations ( in Figs. 2 and 4).
We calculated these measures within biologically realistic ranges of synaptic changes ( of the baseline weight; Figs. 2 and 4) based on experiments (23, 24). This range includes suppression of feedforward synapses with parameters , potentiation of recurrent synapses , and increase of the feedforward E/I ratio . To ensure that the simulated range does not alter our results, we simulated our networks with a decreased () and increased range () (SI Appendix, Figs. S2 and S6).
To quantify response strengths, we calculated the gradient numerically from the matrix of fold changes . The two components of the gradient at each point (x, y) in the parameter space are:
| [9] |
where Δ is the grid spacing of the matrix of fold changes . From this, we computed the lengths of and the angle between gradients for excitatory and PV neurons at all points in the respective parameter spaces (feedforward, recurrent, and combined). We then averaged these lengths for the entire population A to obtain the average gradient lengths ( in SI Appendix, Figs. S5 B–D and S8 A–C) and the average angle between the gradients ( in SI Appendix, Figs. S5 E–G and S8 D–F). An angle close to 0 in the ISN without SST feedback confirms the tight coordination in excitatory and PV neurons (SI Appendix, Fig. S5). In the non-ISN and the ISN with strong SST feedback, the angles are ∼90 or 180, uncovering independent or opposite modulation of firing rates, respectively (SI Appendix, Figs. S5 and S8).
Capturing the Sequence of Firing-Rate Suppression and Recovery.
We extracted the experimental data for firing-rate fold changes of excitatory and fast-spiking interneurons during the first 2 d of MD from figure 3D in ref. 19 using open-source software (80). We hypothesized that MD should affect feedforward connections immediately. Therefore, to capture excitatory and PV firing rates on the first day of MD, we assumed that only feedforward synapses change (Fig. 7, Left). We simulated ISNs with strong SST feedback for 70 randomly drawn ()-pairs chosen from a range in which excitatory neurons have normalized firing rates close to baseline ( in Fig. 4A). This set of parameters produces suppressed PV firing rates. To capture excitatory and PV firing rates on the second day of MD, we assumed that recurrent connections change in addition to feedforward connections (Fig. 7, Right). For each ()-pair, we found a ()-pair that can recover the firing rates of PV interneurons close to baseline (0.98 ±0.15 in Fig. 4B). We also simulated the ISN without SST feedback with the same synaptic changes to test how the firing-rate changes in this network compare with the experimentally measured.
Linear Population-Rate Model.
To analytically study firing-rate changes during MD, we used a linear population model with population dynamics (32, 47):
| [10] |
where r is the vector of rates, s is the vector of external inputs, and W is the population-connectivity matrix of the rate-based model:
| [11] |
where w denotes the coupling scale, γ is the scaling factor of PV feedback, and κ is the weight of SST output synapses, which we refer to as the SST feedback. As in the simulated network, input to the network comes from two sources, LGN and BKG. As before, we set the input rates from both sources to be the same, , in which we also absorb the input weights:
| [12] |
We used a rectified-linear population input–output function:
| [13] |
where Γ is the input–output gain, chosen to be the same for all populations. With steady inputs and assuming that the network operates in the linear regime away from rectification, the steady state of the rates is:
| [14] |
From this steady state, we can calculate the fold change of the network rate after MD relative to baseline for each combination of synaptic changes. Synaptic changes induced by MD were applied multiplicatively as before, with and affecting W and s, similarly to Eqs. 6 and 7:
| [15] |
and
| [16] |
We solve the steady state in Eq. 14 for MD by inverting . Without loss of generality, we absorbed the response gain factor Γ into the interaction parameters (w and κ, respectively), as well as into the feedforward input (), by rescaling them with a common factor and find:
| [17] |
with
| [18] |
To generate the planes of firing-rate change in response to MD-induced plasticity, we solved the rate model in Eq. 10 numerically, taking into account rectification. We found that the rate model could capture firing-rates changes in the spiking networks both for the network with a single subtype of interneuron (compare SI Appendix, Fig. S3 A–C vs. Fig. 1 B–D and SI Appendix, Fig. S3 D–F vs. Fig. 2 B–D) and for the network with two subtypes of interneurons (compare SI Appendix, Fig. S7 vs. Fig. 4). We observed a largely linear input–output function of the spiking network when firing is well above threshold, which corroborates this overall match of the linear model with the spiking network. However, the linear model showed sharp transitions for recurrent and combined (feedforward and recurrent) plasticity when we increased κ (SI Appendix, Fig. S7 E and F), in contrast to the spiking network, where the effects of SST feedback changed more gradually when we increased K (Fig. 4 E and F). This discrepancy could be due to a changing gain in the spiking network when recurrent synapses change, in contrast to the fixed gain in the linear model.
Analysis of the Reversal of PV Responses.
In the linear model, setting the coupling scale w = 1 marks the transition between the non-ISN (w < 1) and the ISN (w > 1) regimes (32). A hallmark of the ISN regime is the paradoxical effect, whereby an excitatory input to the inhibitory population decreases its firing rate.
We first considered the network with a single subtype of interneuron, by setting κ = 0. In this case, the firing-rate change in response to additional drive to the PV population becomes:
| [19] |
where the scalar term is always positive when the network is stable. Each population responds to this additional drive to the PV population as:
| [20] |
Hence, the response of the excitatory neurons is always in the opposite direction to ξ for any network parameters ( and w > 0). However, the response of the PV population depends on the value of w. When w < 1 and the network is in the non-ISN regime, PV population activity changes in the same direction as ξ. When w > 1 and the network is in the ISN regime, PV population activity changes in the opposite direction to ξ, as the excitatory population. Since the depression of synapses to PV interneurons in early MD is equivalent to providing an inhibitory input to the PV population in the linear model—i.e., —the operating regime of the network and the presence of the paradoxical effect in the ISN regime can be related to the observed firing-rate changes in response to MD. Therefore, in the non-ISN, the excitatory and PV populations respond to MD by changing their firing rates in the opposite direction, while in the ISN regime, the excitatory and PV firing-rate changes closely follow each other (SI Appendix, Fig. S3). We confirmed through simulation that the value of J where the same change in PV responses to MD-induced plasticity occurs in the spiking network is indeed the point where the spiking network goes from non-ISN to ISN and is related to the paradoxical effect (Fig. 2).
We extended this result in the network with two types of interneurons. The firing-rate change in response to additional drive to the PV population is:
| [21] |
where , which is always positive when the network is stable. The responses of the excitatory and the PV population to this additional drive to the PV population are:
| [22] |
As for the network with a single type of interneurons, the response of the excitatory neurons is always in the opposite direction to ξ for any network parameters, independent of the strength of SST feedback κ. The response of the PV population is proportional to . Thus, the direction of rate changes in the PV population no longer depends only on w, but also on the strength of SST feedback κ. In the non-ISN, the PV population responds with a change of activity in the same direction as ξ since w < 1 and , independent of κ. In the ISN, where w > 1, the PV population responds with a change of activity in the opposite direction to ξ when the following condition is satisfied:
| [23] |
This implies that for any w > 1, there exists a sufficiently large κ that leads to a reversal of the paradoxical effect and thus a nonparadoxical response of the PV population, even in a network operating as ISN (Fig. 5).
Relating Facilitation of PV Firing Rate to the Paradoxical Effect.
Next, we related the above conditions (Eq. 23 and w > 1) for the presence of the paradoxical effect in networks with one or two types of interneurons to the presence of facilitatory responses for PV interneurons in the parameter spaces of MD-induced plasticity. In particular, in the network with a single type of interneuron, PV interneurons start showing a facilitatory response in response to feedforward plasticity at a specific value of coupling (SI Appendix, Fig. S3D). In the network with two subtypes of interneurons operating in the ISN regime, the facilitatory response of PV interneurons vanishes for a specific strength of SST feedback κ and reemerges at a higher value of κ (SI Appendix, Fig. S7D).
From Eq. 17, the PV population rate after induction of MD plasticity is:
| [24] |
We focus on feedforward plasticity only, since recurrent plasticity affects (Eq. 18). In the case of feedforward plasticity, the rate for the PV population after induction of MD-plasticity reduces to:
| [25] |
Setting all MD-related parameters to one, the baseline rate is:
| [26] |
Therefore, the condition for the emergence a facilitatory area of PV responses after MD is:
| [27] |
We first considered the network with a single type of interneuron by setting κ = 0. Then, the condition for the emergence a facilitatory area of PV responses after MD becomes:
| [28] |
Because feedforward plasticity in response to MD depresses synaptic inputs to excitatory and PV neurons, , this condition can never be satisfied in the non-ISN regime, where w < 1. Thus, PV responses to feedforward depression in the non-ISN never increase above baseline (SI Appendix, Fig. S3D).
In the ISN regime, w > 1, the condition can be fulfilled, giving a specific linear relationship between and that is the boundary between suppression and facilitation (SI Appendix, Fig. S3A and Fig. 1B). Thus, the position of the boundary between facilitation and suppression depends on w and . Well in the ISN regime, for ; thus, the slope and offset of this linear relationship depend mainly on .
In the ISN with SST interneurons, where w > 1, we studied the condition for the emergence of a facilitatory area of PV responses for increasing κ. Assuming that , the condition yields again a linear relation between and that separates facilitatory and suppressive areas of the parameter space:
| [29] |
As long as
| [30] |
the condition Eq. 29 can be satisfied with depression of feedforward synapses. Note that this is exactly the condition Eq. 23 for which the PV population switches to nonparadoxical behavior due to SST feedback. As κ increases, the condition Eq. 29 becomes harder to satisfy because grows monotonically. Thus, the facilitation area of the PV population in the parameter space of feedforward plasticity decreases (SI Appendix, Fig. S7D). As κ increases, the condition Eq. 29 can no longer be satisfied, and PV responses no longer show facilitation (SI Appendix, Fig. S7D; at for the chosen parameters; see also switch of paradoxical response in Fig. 5).
As κ approaches one, the condition in Eq. 29 would go through a singularity. Because goes to zero and becomes negative for . Here, division by in Eq. 27 switches the inequality. Therefore, the condition for the emergence of facilitation of PV responses after MD in Eq. 29 switches sign:
| [31] |
PV interneurons can again show facilitation during MD-induced plasticity for , but on the opposite side of the linear boundary (SI Appendix, Fig. S7A). This switch of the inequality is the inversion of the PV response to MD-induced plasticity.
For networks well in the ISN regime, where , the conditions for the disappearance of the facilitatory area and the reemergence on the opposite side of the linear boundary become the same because . Here, the condition for reversal of the paradoxical effect in PV interneurons through SST feedback and for the opposite firing-rate changes of excitatory neurons and PV interneurons through SST feedback become the same.
Supplementary Material
Acknowledgments
We thank all members of the “Computation in Neural Circuits” group for discussions; Gina Turrigiano for fruitful discussions throughout the project and critical feedback on the manuscript; and Matthias Kaschube and Hiroshi Ito for additional comments on the manuscript. This work was supported by the Max Planck Society and has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 804824 to J.G.) and from the Deutsche Forschungsgemeinschaft in the Collaborative Research Centre 1080 (to J.G.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2116895119/-/DCSupplemental.
Data Availability
All data can be generated with our code available on GitHub (81).
References
- 1.Wood K. C., Blackwell J. M., Geffen M. N., Cortical inhibitory interneurons control sensory processing. Curr. Opin. Neurobiol. 46, 200–207 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tremblay R., Lee S., Rudy B., GABAergic interneurons in the neocortex: From cellular properties to circuits. Neuron 91, 260–292 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fu Y., et al., A cortical circuit for gain control by behavioral state. Cell 156, 1139–1152 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Letzkus J. J., et al., A disinhibitory microcircuit for associative fear learning in the auditory cortex. Nature 480, 331–335 (2011). [DOI] [PubMed] [Google Scholar]
- 5.Pakan J. M. P., et al., Behavioral-state modulation of inhibition is context-dependent and cell type specific in mouse visual cortex. eLife 5, e14985 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Garcia Del Molino L. C., Yang G. R., Mejias J. F., Wang X. J., Paradoxical response reversal of top-down modulation in cortical circuits with three interneuron types. eLife 6, e29742 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dipoppa M., et al., Vision and locomotion shape the interactions between neuron types in mouse visual cortex. Neuron 98, 602–615.e8 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ozeki H., Finn I. M., Schaffer E. S., Miller K. D., Ferster D., Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron 62, 578–592 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Adesnik H., Bruns W., Taniguchi H., Huang Z. J., Scanziani M., A neural circuit for spatial summation in visual cortex. Nature 490, 226–231 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Atallah B. V., Bruns W., Carandini M., Scanziani M., Parvalbumin-expressing interneurons linearly transform cortical responses to visual stimuli. Neuron 73, 159–170 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee S. H., et al., Activation of specific interneurons improves V1 feature selectivity and visual perception. Nature 488, 379–383 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.D’amour J. A., Froemke R. C., Inhibitory and excitatory spike-timing-dependent plasticity in the auditory cortex. Neuron 86, 514–528 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Field R. E., et al., Heterosynaptic plasticity determines the set point for cortical excitatory-inhibitory balance. Neuron 106, 842–854.e4 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wilmes K. A., Clopath C., Inhibitory microcircuits for top-down plasticity of sensory representations. Nat. Commun. 10, 5055 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hensch T. K., Critical period plasticity in local cortical circuits. Nat. Rev. Neurosci. 6, 877–888 (2005). [DOI] [PubMed] [Google Scholar]
- 16.Turrigiano G., Too many cooks? Intrinsic and synaptic homeostatic mechanisms in cortical circuit refinement. Annu. Rev. Neurosci. 34, 89–103 (2011). [DOI] [PubMed] [Google Scholar]
- 17.Gainey M. A., Feldman D. E., Multiple shared mechanisms for homeostatic plasticity in rodent somatosensory and visual cortex. Philos. Trans. R. Soc. Lond. B Biol. Sci. 372, 20160157 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kaneko M., Stellwagen D., Malenka R. C., Stryker M. P., Tumor necrosis factor-alpha mediates one component of competitive, experience-dependent plasticity in developing visual cortex. Neuron 58, 673–680 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hengen K. B., Lambo M. E., Van Hooser S. D., Katz D. B., Turrigiano G. G., Firing rate homeostasis in visual cortex of freely behaving rodents. Neuron 80, 335–342 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hengen K. B., Torrado Pacheco A., McGregor J. N., Van Hooser S. D., Turrigiano G. G., Neuronal firing rate homeostasis is inhibited by sleep and promoted by wake. Cell 165, 180–191 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Maffei A., Nataraj K., Nelson S. B., Turrigiano G. G., Potentiation of cortical inhibition by visual deprivation. Nature 443, 81–84 (2006). [DOI] [PubMed] [Google Scholar]
- 22.Maffei A., Lambo M. E., Turrigiano G. G., Critical period for inhibitory plasticity in rodent binocular V1. J. Neurosci. 30, 3304–3309 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nahmani M., Turrigiano G. G., Deprivation-induced strengthening of presynaptic and postsynaptic inhibitory transmission in layer 4 of visual cortex during the critical period. J. Neurosci. 34, 2571–2582 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Miska N. J., Richter L. M. A., Cary B. A., Gjorgjieva J., Turrigiano G. G., Sensory experience inversely regulates feedforward and feedback excitation-inhibition ratio in rodent visual cortex. eLife 7, e38846 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kannan M., Gross G. G., Arnold D. B., Higley M. J., Visual deprivation during the critical period enhances layer 2/3 GABAergic inhibition in mouse V1. J. Neurosci. 36, 5914–5919 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ma Z., Turrigiano G. G., Wessel R., Hengen K. B., Cortical circuit dynamics are homeostatically tuned to criticality in vivo. Neuron 104, 655–664.e4 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.van Vreeswijk C., Sompolinsky H., Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726 (1996). [DOI] [PubMed] [Google Scholar]
- 28.Brunel N., Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8, 183–208 (2000). [DOI] [PubMed] [Google Scholar]
- 29.Renart A., et al., The asynchronous state in cortical circuits. Science 327, 587–590 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Murphy B. K., Miller K. D., Balanced amplification: A new mechanism of selective amplification of neural activity patterns. Neuron 61, 635–648 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hennequin G., Ahmadian Y., Rubin D. B., Lengyel M., Miller K. D., The dynamical regime of sensory cortex: Stable dynamics around a single stimulus-tuned attractor account for patterns of noise variability. Neuron 98, 846–860.e5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tsodyks M. V., Skaggs W. E., Sejnowski T. J., McNaughton B. L., Paradoxical effects of external modulation of inhibitory interneurons. J. Neurosci. 17, 4382–4388 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sanzeni A., et al., Inhibition stabilization is a widespread property of cortical networks. eLife 9, e54875 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mahrach A., Chen G., Li N., van Vreeswijk C., Hansel D., Mechanisms underlying the response of mouse cortical networks to optogenetic manipulation. eLife 9, e49967 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Litwin-Kumar A., Rosenbaum R., Doiron B., Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes. J. Neurophysiol. 115, 1399–1409 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Miller K. D., Palmigiano A., Generalized paradoxical effects in excitatory/inhibitory networks. bioRxiv [Preprint] (2020). https://www.biorxiv.org/content/10.1101/2020.10.13.336727v1. Accessed 14 July 2022.
- 37.Wang L., Kloc M., Gu Y., Ge S., Maffei A., Layer-specific experience-dependent rewiring of thalamocortical circuits. J. Neurosci. 33, 4181–4191 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lefort S., Gray A. C., Turrigiano G. G., Long-term inhibitory plasticity in visual cortical layer 4 switches sign at the opening of the critical period. Proc. Natl. Acad. Sci. U.S.A. 110, E4540–E4547 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gainey M. A., Aman J. W., Feldman D. E., Rapid disinhibition by adjustment of PV intrinsic excitability during whisker map plasticity in mouse S1. J. Neurosci. 38, 4749–4761 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pfeffer C. K., Xue M., He M., Huang Z. J., Scanziani M., Inhibition of inhibition in visual cortex: The logic of connections between molecularly distinct interneurons. Nat. Neurosci. 16, 1068–1076 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lien A. D., Scanziani M., Tuned thalamic excitation is amplified by visual cortical circuits. Nat. Neurosci. 16, 1315–1323 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Smith G. B., Heynen A. J., Bear M. F., Bidirectional synaptic mechanisms of ocular dominance plasticity in visual cortex. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 357–367 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lambo M. E., Turrigiano G. G., Synaptic and intrinsic homeostatic mechanisms cooperate to increase L2/3 pyramidal neuron excitability during a late phase of critical period plasticity. J. Neurosci. 33, 8810–8819 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Khibnik L. A., Cho K. K. A., Bear M. F., Relative contribution of feedforward excitatory connections to expression of ocular dominance plasticity in layer 4 of visual cortex. Neuron 66, 493–500 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ji X. Y., et al., Thalamocortical innervation pattern in mouse auditory and visual cortex: Laminar and cell-type specificity. Cereb. Cortex 26, 2612–2625 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kuhlman S. J., et al., A disinhibitory microcircuit initiates critical-period plasticity in the visual cortex. Nature 501, 543–546 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wilson H. R., Cowan J. D., Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Urban-Ciecko J., Barth A. L., Somatostatin-expressing neurons in cortical networks. Nat. Rev. Neurosci. 17, 401–409 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Xu H., Jeong H. Y., Tremblay R., Rudy B., Neocortical somatostatin-expressing GABAergic interneurons disinhibit the thalamorecipient layer 4. Neuron 77, 155–167 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang S., et al., Selective attention. Long-range and local circuits for top-down modulation of visual cortex processing. Science 345, 660–665 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Batista-Brito R., Zagha E., Ratliff J. M., Vinck M., Modulation of cortical circuits by top-down processing and arousal state in health and disease. Curr. Opin. Neurobiol. 52, 172–181 (2018). [DOI] [PubMed] [Google Scholar]
- 52.Cembrowski M. S., Spruston N., Heterogeneity within classical cell types is the rule: Lessons from hippocampal pyramidal neurons. Nat. Rev. Neurosci. 20, 193–204 (2019). [DOI] [PubMed] [Google Scholar]
- 53.Landau I. D., Egger R., Dercksen V. J., Oberlaender M., Sompolinsky H., The impact of structural heterogeneity on excitation-inhibition balance in cortical networks. Neuron 92, 1106–1121 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Vegué M., Roxin A., Firing rate distributions in spiking networks with heterogeneous connectivity. Phys. Rev. E 100, 022208 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Xue M., Atallah B. V., Scanziani M., Equalizing excitation-inhibition ratios across visual cortical neurons. Nature 511, 596–600 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Okun M., et al., Diverse coupling of neurons to populations in sensory cortex. Nature 521, 511–515 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hofer S. B., et al., Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex. Nat. Neurosci. 14, 1045–1052 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.House D. R. C., Elstrott J., Koh E., Chung J., Feldman D. E., Parallel regulation of feedforward inhibition and excitation during whisker map plasticity. Neuron 72, 819–831 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Li L., Gainey M. A., Goldbeck J. E., Feldman D. E., Rapid homeostasis by disinhibition during whisker map plasticity. Proc. Natl. Acad. Sci. U.S.A. 111, 1616–1621 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Miller K. D., Keller J. B., Stryker M. P., Ocular dominance column development: Analysis and simulation. Science 245, 605–615 (1989). [DOI] [PubMed] [Google Scholar]
- 61.Blais B. S., Cooper L. N., Shouval H. Z., Effect of correlated lateral geniculate nucleus firing rates on predictions for monocular eye closure versus monocular retinal inactivation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80, 061915 (2009). [DOI] [PubMed] [Google Scholar]
- 62.Toyoizumi T., et al., A theory of the transition to critical period plasticity: Inhibition selectively suppresses spontaneous activity. Neuron 80, 51–63 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Toyoizumi T., Miller K. D., Equalization of ocular dominance columns induced by an activity-dependent learning rule and the maturation of inhibition. J. Neurosci. 29, 6514–6525 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wu Y. K., Hengen K. B., Turrigiano G. G., Gjorgjieva J., Homeostatic mechanisms regulate distinct aspects of cortical circuit dynamics. Proc. Natl. Acad. Sci. U.S.A. 117, 24514–24525 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sweeney Y., Barnes S. J., Clopath C., (2018) Diverse homeostatic responses to visual deprivation by uncovering recurrent subnetworks. bioRxiv [Preprint] (2018). https://www.biorxiv.org/content/10.1101/312926v1. Accessed 14 July 2022.
- 66.Bos H., Oswald A. M., Doiron B., (2020) Untangling stability and gain modulation in cortical circuits with multiple interneuron classes. bioRxiv [Preprint] (2020). https://www.biorxiv.org/content/10.1101/2020.06.15.148114v2. Accessed 14 July 2022.
- 67.Hertäg L., Sprekeler H., Amplifying the redistribution of somato-dendritic inhibition by the interplay of three interneuron types. PLOS Comput. Biol. 15, e1006999 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sadeh S., Silver R. A., Mrsic-Flogel T. D., Muir D. R., Assessing the role of inhibition in stabilizing neocortical networks requires large-scale perturbation of the inhibitory population. J. Neurosci. 37, 12050–12067 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Adesnik H., Synaptic mechanisms of feature coding in the visual cortex of awake mice. Neuron 95, 1147–1159.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kato H. K., Asinof S. K., Isaacson J. S., Network-level control of frequency tuning in auditory cortex. Neuron 95, 412–423.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Tuncdemir S. N., et al., Early somatostatin interneuron connectivity mediates the maturation of deep layer cortical circuits. Neuron 89, 521–535 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kirmse K., et al., GABA depolarizes immature neurons and inhibits network activity in the neonatal neocortex in vivo. Nat. Commun. 6, 7750 (2015). [DOI] [PubMed] [Google Scholar]
- 73.Leighton A. H., et al., Somatostatin interneurons restrict cell recruitment to retinally driven spontaneous activity in the developing cortex. Cell Rep. 36, 109316 (2021). [DOI] [PubMed] [Google Scholar]
- 74.Owens D. F., Boyce L. H., Davis M. B. E., Kriegstein A. R., Excitatory GABA responses in embryonic and neonatal cortical slices demonstrated by gramicidin perforated-patch recordings and calcium imaging. J. Neurosci. 16, 6414–6423 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ben-Ari Y., Cherubini E., Corradetti R., Gaiarsa J. L., Giant synaptic potentials in immature rat CA3 hippocampal neurones. J. Physiol. 416, 303–325 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Rubin D. B., Van Hooser S. D., Miller K. D., The stabilized supralinear network: A unifying circuit motif underlying multi-input integration in sensory cortex. Neuron 85, 402–417 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Maffei A., Nelson S. B., Turrigiano G. G., Selective reconfiguration of layer 4 visual cortical circuitry by visual deprivation. Nat. Neurosci. 7, 1353–1359 (2004). [DOI] [PubMed] [Google Scholar]
- 78.Linssen C., et al., Nest 2.16.0. Zenodo. https://zenodo.org/record/1400175#.Ys_HW99CQ2w. Accessed 14 July 2022.
- 79.Linden M. L., Heynen A. J., Haslinger R. H., Bear M. F., Thalamic activity that drives visual cortical plasticity. Nat. Neurosci. 12, 390–392 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Rohatgi A., Webplotdigitizer. https://automeris.io/WebPlotDigitizer/. Accessed 14 July 2022.
- 81.Richter L. M. A., Gjorgjieva J., Code for “A circuit mechanism for independent modulation of excitatory and inhibitory firing rates after sensory deprivation.” GitHub. https://github.com/comp-neural-circuits/MD-dynamics. Deposited 25 May 2021. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data can be generated with our code available on GitHub (81).