A permeability‐ and perfusion‐based PBPK model for improved prediction of concentration‐time profiles

Abstract

To improve predictions of concentration‐time (C‐t) profiles of drugs, a new physiologically based pharmacokinetic modeling framework (termed ‘PermQ’) has been developed. This model includes permeability into and out of capillaries, cell membranes, and intracellular lipids. New modeling components include (i) lumping of tissues into compartments based on both blood flow and capillary permeability, and (ii) parameterizing clearances in and out of membranes with apparent permeability and membrane partitioning values. Novel observations include the need for a shallow distribution compartment particularly for bases. C‐t profiles were modeled for 24 drugs (7 acidic, 5 neutral, and 12 basic) using the same experimental inputs for three different models: Rodgers and Rowland (RR), a perfusion‐limited membrane‐based model (K_p,mem), and PermQ. K_p,mem and PermQ can be directly compared since both models have identical tissue partition coefficient parameters. For the 24 molecules used for model development, errors in V_ss and t _1/2 were reduced by 37% and 43%, respectively, with the PermQ model. Errors in C‐t profiles were reduced (increased EOC) by 43%. The improvement was generally greater for bases than for acids and neutrals. Predictions were improved for all 3 models with the use of parameters optimized for the PermQ model. For five drugs in a test set, similar results were observed. These results suggest that prediction of C‐t profiles can be improved by including capillary and cellular permeability components for all tissues.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Compared to compartmental models, concentration‐time profiles of drugs are often not well‐predicted by perfusion‐limited PBPK models.

• WHAT QUESTION DID THIS STUDY ADDRESS?

Can C‐t profiles be better predicted by including capillary, cellular and membrane permeability in a new PBPK framework?

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

This study suggests that variable capillary permeability for different tissues is an important anatomical component for drug distribution. Apparent permeability and membrane partitioning can be used to model clearances in and out of membranes. Early distribution kinetics observed in the C‐t profile of basic drugs indicates that an additional shallow distribution compartment is necessary. Parameters optimized for input into the new PermQ framework also decrease the prediction errors in perfusion‐limited PBPK models.

• HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

Improved prediction of drug concentration‐time profiles with new modeling frameworks such as the PermQ model can result in improved therapeutic outcomes for healthy and special populations.

INTRODUCTION

Pharmacokinetic models are generally categorized as simple compartmental or physiologically‐based. Compartmental models with one to three compartments will usually reproduce most C‐t profiles. However, the compartments have little physiological meaning besides providing a description of global distribution processes. Physiologically‐based pharmacokinetic (PBPK) models have become widely used in pharmaceutical development. ¹ Since they are constructed using some physiological parameters, the models can be extrapolated to special populations. ² , ³ , ⁴ , ⁵ However, since most PBPK models are perfusion limited, distribution processes that include transporters or are diffusion‐limited are not reproduced with these models. Some PBPK models have included diffusion limiting components for all organs, ³ , ⁶ , ⁷ , ⁸ but most recent studies describe models in which specific organs (e.g., brain, ⁴ , ⁹ liver, ¹⁰ , ¹¹ kidney, ¹² etc.) or tumors ¹³ are modeled with both perfusion and diffusion/transport processes included. These models are not necessarily designed to better reproduce C‐t profiles but are intended to better reproduce drug concentrations in important tissues.

Drug diffusion into and across cells includes partitioning into and diffusion across membranes. Our recently described models use membrane partitioning to predict volume of distribution at steady‐state (V_ss), ¹⁴ and a PBPK model that uses membrane partitioning as the major component of tissue‐plasma partition coefficients (K_p,mem). ¹⁵ Although the K_p,mem model performed similar to the method described by Rodgers and Rowland (RR) ¹⁶ , ¹⁷ , ¹⁸ for predicting K_p and V_ss, neither model could reproduce complex C‐t profiles for some drugs. These models were perfusion‐limited, and we hypothesized that inclusion of permeability limitation would improve C‐t profile predictions. In the present work, we present a new framework (PermQ) that used both membrane permeability and partitioning to predict the rate and extent of tissue distribution. All tissues and lumped compartments include perfusion and permeability components and contain capillaries, extracellular fluid, plasma membranes, neutral lipids, and phospholipids. Details of the development and refinement of the PermQ model are presented here.

METHODS

A full permeability‐ and perfusion‐limited PBPK model (PermQ) was developed using the following basic framework: (1) Reversible diffusion of drug between capillaries and interstitial fluid (ISF) can occur by diffusion through fenestra or discontinuities in capillaries, or by transcellular diffusion through endothelial cells. (2) Reversible drug diffusion between ISF and cytosol occurs by either passive membrane permeability or is transporter mediated. (3) In addition to aqueous volumes, drugs can partition into intracellular phospholipids and neutral lipids. All models were constructed and evaluated using Mathematica version 12.3 (Wolfram Research Inc.).

Anatomical framework

Tissue blood flow and capillary ‘leakiness’ are well understood to impact drug disposition. Since different tissues have different blood flows ¹⁹ and capillary physiology, ²⁰ tissue compartments can be classified as: low perfusion, low capillary permeability (lplcp); low perfusion, high capillary permeability (lphcp); high perfusion, low capillary permeability (hplcp); and high perfusion, high capillary permeability (hphcp). In this model, tissues were combined into four compartments (C1: lplcp, C2: lphcp, C3: hplcp, and C4: hphcp). C1 includes muscle, skin and ¼ rest‐of‐body (RB), C2 includes bone and ¼ RB, C3 includes heart and ¼ RB, and C4 includes kidney and ¼ RB. The gut was segregated into mesentery/gut serosa and mucosa (Segregated Flow Model) as described by Pang ²¹ , ²² This is particularly important when considering gut clearance. Also, capillaries of the gut mucosa are fenestrated whereas other capillaries of the gut are not. Tissues with unique properties or blood flows were treated explicitly: lung, liver, spleen, gut mucosa, mesentery/gut serosa, and brain. The resulting model is shown in Figure 1. Derivations for Equations 1,3 and 4 are provided in Supplementary Materials.

FIGURE 1.

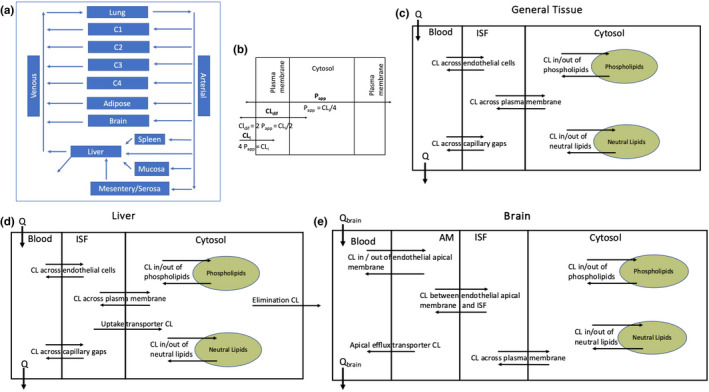
The PermQ model. (a) Physiological representation of the model. (b) Relationship between membrane permeability and apparent permeability (P_app) and partitioning. (c) Representation of a general non‐eliminating tissue compartment. (d) Representation of the liver. (e) Representation of the brain.

Model assumptions

Compartments for most tissues include blood, interstitial fluid (ISF), cytosol, intracellular phospholipids (pl), and intracellular neutral lipids (nl). Bidirectional distribution barriers for these tissues include passive trans‐endothelial‐cell diffusion between blood and ISF, bidirectional diffusion between blood and ISF through fenestra and capillary discontinuities, and passive membrane diffusion between ISF and cytosol (Figure 1c). The liver has an additional uptake transporter pathway from ISF to cytosol and an unbound intrinsic clearance pathway (CL_int’) from the cytosol (Figure 1d). Due to the blood–brain‐barrier (BBB), the brain has no diffusion between blood and ISF through fenestra or discontinuities. To model efflux transporters at the BBB, an explicit apical membrane compartment is added between blood and ISF (Figure 1e). As necessary, concentrations are corrected for fraction unbound in blood (f_ub), fraction unbound in plasma (f_up), and fraction unbound in ISF (f_ui). For ionizable compounds, only the neutral fraction crosses membranes by passive diffusion, and can partition into neutral lipids (not shown in Figure 1 for clarity).

Correcting experimental permeability values

Beyond the documented interlaboratory variability in apparent permeabilities (P_app), ²³ monolayer permeability experiments suffer from compression at the high and low end of observed values. At the high end, crossing the aqueous boundry layer can be rate limiting in vitro, limiting the measurable values of cellular permeability. ²⁴ , ²⁵ , ²⁶ At the low end, any opening in the tight junctions can limit the low end of experimental permeabilities. ²⁵ , ²⁷ We correct experimental P_app values with the following equation:

$${\mathrm{P}}_{\mathrm{app},\mathrm{cor}}=\frac{{\mathrm{P}}_{\mathrm{aq}}{\mathrm{P}}_{\mathrm{app}}-{\mathrm{P}}_{\mathrm{aq}}{\mathrm{P}}_{\text{para}}}{{\mathrm{P}}_{\mathrm{aq}}+{\mathrm{P}}_{\text{para}}-{\mathrm{P}}_{\mathrm{app}}}$$ (1)

where P_aq is aqueous boundry layer permeability and P_para is paracellular permeability. This equation expands the upper end as P_app approaches P_aq and expands the lower end as P_app approaches P_para. P_aq and P_para were emperically set to 100 × 10⁻⁶ and 0.2 × 10⁻⁶ cm/s, respectively. These limits were based on the highest and lowest reported experimental P_app values across all drugs in this work. These corrected Papp values were used in all calculations.

Capillary permeability

Capillarity permeability is modeled by the combination of two processes: passive trans‐endothelial‐cell diffusion (P_app) between blood and ISF, and diffusion between blood and ISF through fenestra and capillary discontinuities (P_gap). Low capillary permeability tissues are those without fenestra and a single low P_gap value is divided by MW⁻³ to yield a drug‐specific low P_gap. For high capillary permeability tissues with fenestra, a single high P_gap value is used. For trans‐endothelial‐cell diffusion, Caco‐2 or MDCK cell P_app is multiplied by capillary surface area of the tissue (SA_b) to obtain the trans‐endothelial cell clearance. Use of a monolayer P_app is valid if (a) active transport is insignificant in the monolayer experiment, (b) Equation 1 corrects for the unstirred boundary layer and is no longer rate limiting, and (c) steady state is reached and a molecule entering the cell from the donor compartment corresponds to a molecule leaving the cell into the receiving compartment. Experimental surface areas for brain, kidney, liver, lung, and muscle are from Crone, ²⁸ adipose from Belcik, ²⁹ and lung from Buchacker et al. ³⁰ For other tissues, capillary surface areas were calculated from tissue blood flows using the empirical relationship in Equation 2 (see model in Supplementary Material):

$${\mathrm{SA}}_{\mathrm{B}}=293{\text{flow}}^{0.5}$$ (2)

where SA_B is the capillary surface area (cm²/g), flow is tissue blood flow (L/min, L). It should be noted that the SA per tissue weight values from Crone are canine values, the value from Buchacker is for mouse lung and are assumed to be the same for humans.

Compartments C1, C3, adipose, mesentery/gut serosa, and lung are modeled as low permeability tissues, and compartments C2, C4, and gut mucosa as high permeability tissues. Since proteins cannot readily leave capillaries, all tissues above are restricted by plasma protein binding. ³¹ Diffusion through fenestra and paracellular permeability (P_gap) was fit to experimental data using the complete model. The P_gap value for low capillary permeability tissues was divided by MW^1/3 since passive diffusion is anticipated to be proportional the molecule's radius. For the drugs in this study, MW^1/3 varied between 6.1and 7.9, and the resulting permeabilities ranging from 7.6 × 10⁻⁵ to 5.9 × 10⁻⁵ dm/min (note: To obtain transfer clearances, P_gap values are multiplied by the entire capillary surface area and not the area of the discontinuities.

Diffusion into and across membranes and cells (Figure 1 b)

We have shown previously ³² and in the accompanying net clearances tutorial that clearance across a lipid bilayer is one‐half the clearance into the membrane (CL_i/2), and that clearance across a monolayer of cells (P_app) where two membranes must be crossed is CL_i/4. Therefore, diffusion into membranes is modeled as 4 P_app for (1) partitioning into phospholipids and lipid droplets and (2) diffusion into the apical membrane of endothelial cells at the BBB. Diffusion across membranes is modeled as 2 P_app for the ISF‐cytosol barrier. Diffusion across cells is modeled as P_app for the transcellular blood‐ISF barrier.

Modeling an additional shallow compartment (C0)

Preliminary studies revealed that concentrations of many drugs were greatly over‐predicted at very early time points after IV bolus or infusion, particularly for hydrophobic bases with high BP. Based on a working hypothesis that drugs interact with endothelial cells, several models were developed. Since erythrocytes have membranes and a glycocalyx similar to endothelial cells, erythrocyte partitioning along with the fraction unbound in microsomes (f_um) and LogP were evaluated as descriptors to predict partitioning into a shallow compartment (C0). The BP due to external association with erythrocytes (BP_C0) is calculated by subtracting drug inside the erythrocyte (f_up Hct) from experimental BP values:

$${\mathrm{BP}}_{\mathrm{C}0}=\mathrm{BP}-{\mathrm{f}}_{\mathrm{up}}\mathrm{Hct}$$ (3)

Equation 3 was derived in the same manner as the BP equation provided in, ³³ starting with a mass balance:

Total amount in RBC = amount inside RBC cytosol + amount externally associated with RBC, and Amount in blood = amount in plasma + (total amount in RBC – amount inside RBC cytosol). Thus, Equation 3 can also be written as BP_C0 = 1 + Hct[fu K_pBC – fu – 1], where K_pBC is the RBC partition coefficient.

To keep K_ery,C0 > 0 in Equation 4, if BP_C0 was calculated to be $\le$0.55, it was set to 0.55001. The associated partition coefficient for external association with erythrocytes (K_ery,C0) is calculated as:

$${\mathrm{K}}_{\mathrm{ery},\mathrm{C}0}=\frac{{\mathrm{BP}}_{\mathrm{C}0}-\left(1-\mathrm{Hct}\right)}{{\mathrm{f}}_{\mathrm{up}}\mathrm{Hct}}$$ (4)

The partition coefficient K_ery,C0 can also be derived as being equal to the term K_pBC‐1. The partition coefficients K_ery,C0, (1‐f_um)/f_um, and LogP were tested, individually and in combination, for their ability to predict the partition coefficient (K_C0) that best simulates the observed early time point concentrations for 14 weak bases. The compartment C0 was modeled as a non‐saturable binding compartment in contact with venous blood with an assumed fast k_on = 1000 μM⁻¹ min⁻¹, and a 1 μM binding site nominal concentration. The k_off value that gave the best fit to early time points was used to calculate the K_C0. Using K_ery,C0 alone resulted in the best model as determined by AICc values and the resulting equations below were used (see also Figure 2a):

$${\mathrm{K}}_{\mathrm{C}0}={\mathrm{c}}_1{{\mathrm{K}}_{\mathrm{ery},\mathrm{C}0}}^{{\mathrm{c}}_2}$$ (5)

$${\mathrm{k}}_{\mathrm{off}}=\frac{{\mathrm{k}}_{\mathrm{on}}}{{\mathrm{K}}_{\mathrm{C}0}}$$ (6)

where c₁ and c₂ were constants optimized to 19.0 and 0.69, respectively.

FIGURE 2.

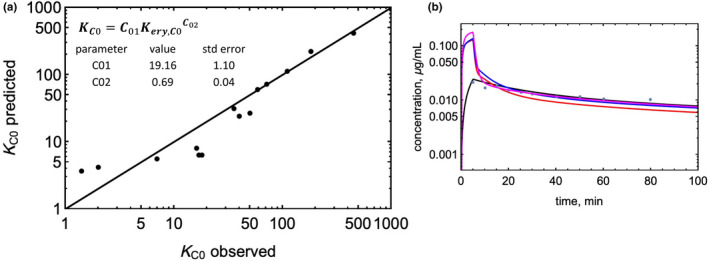
Modeling a shallow distribution compartment. (a) Observed versus predicted partition coefficient (K_C0) for the shallow compartment. (b) Impact of adding a shallow compartment on the predicted C‐t profile of metoprolol. Model‐predicted profiles are as follows: blue: RR model; red: K_p,mem model; magenta: PermQ model without a shallow compartment, black: PermQ model with a shallow compartment.

PermQ model

The physiological parameters for tissues are listed in Table 1. For the entire model, P_app,cor (Equation 1) was used with experimental inputs for P_app from Table 2. For the following equations, net clearance from compartment x to compartment y is denoted as CL_xy. Equations for the clearances from blood to ISF for the tissues in Figure 1c and d are:

$${\mathrm{CL}}_{\mathrm{bi}}=\frac{{\mathrm{f}}_{\mathrm{up}}{\mathrm{P}}_{\mathrm{gap}}{\mathrm{SA}}_{\mathrm{b}}}{\mathrm{BP}}+\frac{{\mathrm{f}}_{\mathrm{up}}{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{b}}}{\mathrm{BP}}$$ (7)

Likewise, the clearance from ISF to blood is:

$${\mathrm{CL}}_{\mathrm{ib}}={\mathrm{f}}_{\mathrm{ui}}{\mathrm{P}}_{\mathrm{gap}}{\mathrm{SA}}_{\mathrm{b}}+{\mathrm{f}}_{\mathrm{ui}}{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{b}}$$ (8)

where f_ui is the unbound fraction in ISF, calculated by:

$${\mathrm{f}}_{\mathrm{ui}}=1/\left(1+\frac{\mathrm{Re}\left(1-{\mathrm{f}}_{\mathrm{up}}\right)}{{\mathrm{f}}_{\mathrm{up}}}\right)$$ (9)

where Re is the tissue: plasma albumin ratio for acids and neutrals and 0.448 × tissue: plasma albumin ratio for bases. ¹⁵ , ¹⁷ , ¹⁸ , ³³

TABLE 1.

PermQ model physiological inputs. Blood flows, volumes, and surface areas used as inputs for the PermQ model

	Low perfusion low capillary permeability		Low perfusion high capillary permeability	High perfusion low capillary permeability			High perfusion high capillary permeability				Brain
Parameter	C1	Adipose	C2	C3	Lung	Mesentery	C4	Mucosa	Spleen	Liver	Brain a
Q (L/min)	1.359	0.284	0.391	0.335	5.691	0.972	1.188	0.108	0.171	1.451	0.683
Re1	0.780	0.363	1.000	0.491	0.631	0.560	0.476	0.560	0.469	0.534	0.296
Re2	0.350	0.163	0.448	0.220	0.283	0.251	0.213	0.251	0.210	0.239	0.133
Vb (L)	0.405	0.18	0.104	0.094	0.023	0.05	0.084	0.002	0.009	0.079	0.058
Ve (L)	3.55	1.682	1.175	0.506	0.178	0.305	0.426	0.034	0.035	0.293	0.227
Vc (L)	19.30	0.212	4.28	0.72	0.236	0.513	0.753	0.057	0.098	1.043	0.868
Vnl (L)	0.79	10.62	0.201	0.018	0.01	0.038	0.011	0.004	0.001	0.016	0.054
Vpl (L)	0.193	0.016	0.015	0.013	0.005	0.011	0.030	0.0012	0.0015	0.035	0.002
SAb (103 dm2)	21.6	9.58	5.54	5.0	4.42	2.64	4.48	0.098	0.46	4.21	3.11
SAISF (103 dm2)	324	144	83.0	75.0	18.4	39.6	67.2	1.47	6.94	500	46.7
SAnl (103 dm2)	948	2125	241	21.6	12.1	45.4	13.7	5.04	1.01	19.1	65.2
SApl (103 dm2)	6040	498	470	419	163	335	936	37.2	45.5	1083	52.5

Abbreviations: Q, blood flow; re1, ratio of albumin in ISF outside plasma to total plasma protein; re2, ratio of alpha acid glycoprotein in ISF outside plasma to total plasma protein; SA_b, surface area of blood capillaries; SA_isf, surface area of cells facing the ISF; SA_nl, surface area of neutral lipid membranes; SA_pl, surface area of phospholipid membranes; V_am, volume of the apical membrane; V_b, volume of blood capillaries; V_i, volume of ISF; V_nl, volume of neutral lipids; V_pl, volume of phospholipids.

^a For brain, V_am (L) = 6.533 × 10⁻⁵ was used.

TABLE 2.

PermQ model drug inputs. Physicochemical and in vitro ADME inputs for neutral, acid, and base drugs

Drug	MW	logP	pKa,a	pKa,b	fup	fum	BP	Papp	fe	CL
Training set
Acid
Cefazolin	454.5	0.58	3.5	1	0.15	0.83 a	0.55	0.24	0.99	0.071
Diclofenac	296.1	4.51	4.15	1	0.0044	0.87	0.55	53.9	0.0	0.27
Furosemide	330.7	2.03	4.72	1	0.019	0.94	0.56 b	0.42	0.9	0.19
Glyburide	494.0	4.29	5.38	1	0.0013	0.81	0.59	19.0	0.0	0.083
Ketoprofen	254.3	3.01	4.45	1	0.0235	0.93	0.55 b	20.4	0.0	0.086
Nafcillin c	414.5	3.31	3.3	1	0.141	0.940	0.55	0.67	0.39	0.49
Warfarin	308.3	2.7	5.05	1	0.0127	0.953	0.55 b	44.0	0.0	0.002
Neutral
Caffeine	194.2	−0.07	14	1	0.72	0.99 b	0.8 b	32.0	0.0	0.088
Diazepam	284.7	3.1	14	3.4	0.03 b	0.48 b	0.62	42.2	0.0	0.022
Fluconazole	306.3	0.8	14	1.77	0.93	0.96	0.75 (1.06) d	22.4	0.8	0.023
Midazolam	325.8	3.15	14	6.01	0.0345	0.68	0.71	42.4	0.0	0.29
Phenytoin	252.3	2.21	8.32	1	0.13 b	0.83 b	0.61	24.7	0.3	0.029
Base
Atenolol c	266.3	0.16	14	9.6	0.9	0.93	1.08	0.35	0.9	0.79
Betaxolol	307.4	2.81	14	9.4	0.5	0.66	1.09	43.5	0.15	0.17
Carvedilol	406.5	3.8	14	8.7	0.03	0.28 b	0.78	6.9 b	0	0.68
Diltiazem	414.5	2.8	14	8.9	0.26	0.55	1	38.3	0.4	1.63
Diphenhydramine	255.3	3.27	14	8.98	0.4	0.60 b	1.1 (0.65) d	46.0	0.0	0.88
Imipramine	280.4	4.8	14	9.4	0.19 b	0.2	1.2	50 b	0.0	0.59
Metoprolol	267.4	1.88	14	9.7	0.86	0.83	1.1	28.0	0.0	1.00
Mibefradil	495.6	3.07	14	9.8	0.012	0.05 b	0.85 (0.64) d	25.7 b	0.0	0.27
Quinidine	324.4	3.52	14	8.94	0.2244	0.61	0.934	23.7	0.0	0.44
Ranitidine	314.4	0.2	14	8.2	0.9	0.97	1.02	0.62	0.7	0.66
Terbutaline	225.3	0.9	14	9.6	0.76	0.97	0.9 (0.95–1.58) d	2.50 b	0.55	0.22
Verapamil	455.6	3.79	14	8.92	0.07 b	0.37	0.81	72.0 b	0.0	0.85
Test set
Aprepitant	534.4	4.8	9.15	2.45	0.02	0.137	0.667	13.0	0.0	0.072
Bumetanide	364.4	2.6	4.69	1	0.05	0.92	0.56	1.70	0.45	0.13
Buprenorphine	467.6	4.82	14	8.31	0.04	0.1	0.6	66.7	0	0.63
Ciprofloxacin	331.3	0.28	6.09	8.62	0.75	0.84	0.73	2.50	0.5	0.59
Zidovudine	357.8	0.05	9.95	1	0.8	0.89	0.98	6.1	0.29	1.30

Abbreviations: Values for f_up, f_um, BP, and P_app (×10⁻⁶ cm/s) are means of the experimental values reported in the references listed in Supplementary Material, unless specified otherwise. Values of fe were from DrugBank (www.drugbank.com) or Goodman and Gilman 10th ed. CL (L/min) calculated as D/AUC from compartmental modeling of literature data, see references in Supplementary Materials.

^a Value was calculated as reported previously.

^b Values are within the range reported in the references listed in Supplementary Material.

^c Hepatic uptake transporter activity was included upon optimization, with atenolol CL_up = 35 L/min and nafcillin CL_up = 0.2 L/min.

^d Value is outside the range reported in the references listed in Supplementary Material (with reported value or range in parentheses).

ISF to Cytosol – From the ISF, drug can either diffuse back into the capillary or diffuse through the plasma membrane into the epithelial cell cytosol (Figure 1c and d). Fractional ISF volumes for tissues are taken from Rodgers and Rowland. ¹⁷ , ¹⁸ Clearance into the cell is calculated by membrane permeability (2 P_app) × ISF surface area (SA_isf), multiplied by the unbound fraction in the ISF (f_ui). Currently, the SA_isf for all tissues except liver is empirically set to 15 times capillary surface area. This was an estimate based on 10⁻⁴ cm² per cell, 150 × 10⁶ cells per gram tissue, a capillary surface area of 250 cm²/g and a fractional accessible surface area of 0.25. For the liver, the fraction of cell surface available to the space of Disse is 0.85 and the basolateral membrane contains microvilli. ³⁴ Therefore, liver ISF surface area was increased by ~8 fold (Table 1). The resulting net clearances from ISF to cytosol and cytosol to ISF are:

$${\mathrm{CL}}_{\mathrm{ic}}={\mathrm{f}}_{\mathrm{ui}}2{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{isf}}$$ (10)

$${\mathrm{CL}}_{\mathrm{ci}}=\frac{\mathrm{Y}}{\mathrm{X}}2{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{isf}}$$ (11)

where 1/X and 1/Y are the neutral fractions of ionizable compounds in the cytosol and ISF, respectively, calculated by:

$$\mathrm{X}=1+{10}^{\left(\mathrm{p}{\mathrm{Ka}}_{\mathrm{b}}-{\mathrm{pH}}_{\mathrm{iw}}\right)}+{10}^{\left({\mathrm{pH}}_{\mathrm{iw}}-\mathrm{p}{\mathrm{Ka}}_{\mathrm{a}}\right)}$$ (12)

$$\mathrm{Y}=1+{10}^{\left({\mathrm{pH}}_{\mathrm{isf}}-\mathrm{p}{\mathrm{Ka}}_{\mathrm{b}}\right)}+{10}^{\left({\mathrm{pH}}_{\mathrm{isf}}-\mathrm{p}{\mathrm{Ka}}_{\mathrm{a}}\right)}$$ (13)

In Equations 12 and 13, pKa_b is the pKa of the base and pKa_a is set to 14, and pKa_a is the pKa of the acid and pKa_b is set to 1. The tissue pH values used were: pH_iw = 7.0, and pH_isf = 7.4.

Distribution into Lipids – From the cytosol, a compound can partition into phospholipids or neutral lipids. Fractional cytosol, phospholipid, and neutral lipid volumes for tissues are from Rodgers and Rowland. ¹⁷ , ¹⁸ The rate of partitioning into phospholipid membranes is modeled as 4 P_app SA_pl, where SA_pl is the surface area of the phospholipids in the tissue using a 3.2 nm membrane depth. The rate out of a phospholipid membrane is 4 P_app SA_pl/K_pl where K_pl is the partition coefficient calculated from f_um by K_pl = [L](1‐f_um)/f_um. [L], the in vitro lipid concentration, has been determined empirically from our PBPK based volume prediction method ¹⁵ and is consistent with the lipid content in microsomes. Drug ionization is not considered since experimental f_um values are used. The net clearances in and out of phospholipids from the cytosol are:

$${\mathrm{CL}}_{\mathrm{cp}}=4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{pl}}$$ (14)

$${\mathrm{CL}}_{\mathrm{pc}}=\frac{4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{pl}}}{{\mathrm{K}}_{\mathrm{pl}}}$$ (15)

The rate of partitioning into neutral lipids from cytosol is modeled as 4 P_app SA_nl, where SA_nl is the surface area of neutral lipid droplets in tissue assuming a 500 nm droplet diameter. ³⁵ For adipose tissue, 1500 nm droplets were assumed based on preliminary sensitivity analysis (no change in EOCs for a range of 50–10,000 nm diameter). The rate out of a lipid droplet is 4 P_app SA_nl /K_nl where K_nl is proportional to the octanol/water partition coefficient. The proportionality constant was been determined empirically. ¹⁵ Drug ionization is considered since only the neutral fraction is expected to partition into neutral lipids.

$${\mathrm{CL}}_{\mathrm{cn}}=4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{nl}}$$ (16)

$${\mathrm{CL}}_{\mathrm{nc}}=\frac{4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{nl}}}{\mathrm{X}{\mathrm{K}}_{\mathrm{nl}}}$$ (17)

Brain Model – The model for brain (Figure 1e) has tight junctions (P_gap = 0) and includes an explicit apical membrane compartment. This compartment is necessary since the transporters P‐gp and BCRP (CL_eff in Figure 1e) efflux drugs from the membrane and modeling efflux from the cytosol will over‐predict tissue concentrations. ³⁶ Rather than include an endothelial cell cytosol compartment, a calculated net clearance includes the necessary diffusion across the basolateral membrane. The resulting net clearance is 4 P_app SA_b/3 K_pL, as derived in the accompanying net clearance tutorial. Net clearance equations unique to the brain model are:

$${\mathrm{CL}}_{\mathrm{ba}}=\frac{{\mathrm{f}}_{\mathrm{up}}4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{b}}}{\mathrm{BP}}$$ (18)

$${\mathrm{CL}}_{\mathrm{ab}}=\frac{4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{b}}}{{\mathrm{K}}_{\mathrm{pl}}}+{\mathrm{CL}}_{\mathrm{eff}}$$ (19)

$${\mathrm{CL}}_{\mathrm{ai}}=\frac{4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{b}}}{3{\mathrm{K}}_{\mathrm{pl}}}$$ (20)

$${\mathrm{CL}}_{\mathrm{ia}}=\frac{{\mathrm{f}}_{\mathrm{ue}}4{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{b}}}{3}$$ (21)

Liver Model – For the liver (Figure 1d), an uptake transporter clearance (CL_up) is included when the drug is an OATP substrate. This transport process can be modeled as either first order or saturable and is presumed to transport unbound drug from the ISF to the cytosol. For first order uptake:

$${\mathrm{CL}}_{\mathrm{ic},\text{liver}}={\mathrm{f}}_{\mathrm{ui}}2{\mathrm{P}}_{\mathrm{app}}{\mathrm{SA}}_{\mathrm{isf}}+{\mathrm{f}}_{\mathrm{ui}}{\mathrm{CL}}_{\mathrm{up}}$$ (22)

CL (Table 2) was determined from the experimental IV data. All metabolism was assumed to take place in the liver and CL_h is calculated as CL(1‐fe), where fe is the fraction of non‐hepatic clearance and CL is the observed systemic clearance. Hepatic elimination is modeled by an unbound intrinsic clearance term CL_int. In this report, experimental clearances (derived from the compartmental model) are used, and the CL_int value required to obtain the hepatic clearance (CL_h) can be calculated from the net clearance equations from blood to elimination as follows:

$${\mathrm{CL}}_{\mathrm{i}-\text{elim}}=\frac{{\mathrm{CL}}_{\mathrm{ic}}{\mathrm{CL}}_{\mathrm{int}}}{{\mathrm{CL}}_{\mathrm{ci}}+{\mathrm{CL}}_{\mathrm{int}}}$$ (23)

$${\mathrm{CL}}_{\mathrm{b}-\text{elim}}=\frac{{\mathrm{CL}}_{\mathrm{bi}}{\mathrm{CL}}_{\mathrm{i}-\text{elim}}}{{\mathrm{CL}}_{\mathrm{ib}}+{\mathrm{CL}}_{\mathrm{i}-\text{elim}}}$$ (24)

$$\frac{{\mathrm{CL}}_{\mathrm{h}}}{\mathrm{BP}}=\frac{{\mathrm{Q}}_{\text{liver}}{\mathrm{CL}}_{\mathrm{b}-\text{elim}}}{{\mathrm{Q}}_{\text{liver}}+{\mathrm{CL}}_{\mathrm{b}-\text{elim}}}$$ (25)

where CL_i‐elim and CL_b‐elim are the net clearances for elimination from the ISF and blood, respectively, Q_liver is liver blood flow, and CL_h is the experimental hepatic clearance. Solving Equations (23), (24), (25) for CL_int results in a PBPK model with the correct experimental value for CL_h. All net clearances can be derived using Figure 1d and the accompanying tutorial on net clearances. All model derived clearances (dose/AUC) were compared with experimental clearances and the ratio was always 1.000.

The PermQ model can be constructed from net clearances. For each general tissue:

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{b},\mathrm{tis}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{b},\mathrm{tis}}={\mathrm{Q}}_{\mathrm{tis}}\left({\mathrm{C}}_{\mathrm{ab}}\left[\mathrm{t}\right]-{\mathrm{C}}_{\mathrm{b},\mathrm{tis}}\left[\mathrm{t}\right]\right)\hfill \\ -{\mathrm{C}}_{\mathrm{b},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{bi},\mathrm{tis}}+{\mathrm{C}}_{\mathrm{i},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ib},\mathrm{tis}}\hfill \end{array}$$ (26)

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{i},\mathrm{tis}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{i},\mathrm{tis}}={\mathrm{C}}_{\mathrm{b},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{bi},\mathrm{tis}}-{\mathrm{C}}_{\mathrm{i},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ib},\mathrm{tis}}\hfill \\ -{\mathrm{C}}_{\mathrm{i},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ic},\mathrm{tis}}+{\mathrm{C}}_{\mathrm{c},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ci},\mathrm{tis}}\hfill \end{array}$$ (27)

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{c},\mathrm{tis}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{c},\mathrm{tis}}={\mathrm{C}}_{\mathrm{i},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ec},\mathrm{tis}}-{\mathrm{C}}_{\mathrm{c},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ci},\mathrm{tis}}\hfill \\ -{\mathrm{C}}_{\mathrm{c},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{cp},\mathrm{tis}}+{\mathrm{C}}_{\mathrm{p},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{pc},\mathrm{tis}}\hfill \\ -{\mathrm{C}}_{\mathrm{c},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{cn},\mathrm{tis}}+{\mathrm{C}}_{\mathrm{n},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{nc},\mathrm{tis}}\hfill \end{array}$$ (28)

$${\mathrm{C}}_{\mathrm{p},\mathrm{tis}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{p},\mathrm{tis}}={\mathrm{C}}_{\mathrm{c},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{cp},\mathrm{tis}}-{\mathrm{C}}_{\mathrm{p},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{pc},\mathrm{tis}}$$ (29)

$${\mathrm{C}}_{\mathrm{n},\mathrm{tis}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{n},\mathrm{tis}}={\mathrm{C}}_{\mathrm{c},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{cn},\mathrm{tis}}-{\mathrm{C}}_{\mathrm{n},\mathrm{tis}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{nc},\mathrm{tis}}$$ (30)

where C_ab is drug concentration in arterial blood, C_b,tis, C_i,tis, C_c,tis, C_p,tis, and C_n,tis are concentrations in tissue blood, ISF, cytosol, phospholipid, and neutral lipid, respectively, and V_x,tis are the respective volumes.

For the lung, input to the tissue is venous blood (C_vb):

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{b},\mathrm{lun}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{b},\mathrm{lun}}={\mathrm{Q}}_{\text{lung}}\left({\mathrm{C}}_{\mathrm{vb}}\left[\mathrm{t}\right]-{\mathrm{C}}_{\mathrm{b},\mathrm{lun}}\left[\mathrm{t}\right]\right)-{\mathrm{C}}_{\mathrm{b},\mathrm{lun}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{bi},\mathrm{lun}}\hfill \\ +{\mathrm{C}}_{\mathrm{i},\mathrm{lun}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ib},\mathrm{lun}}\hfill \end{array}$$ (31)

Liver and brain the following equations that are different from the general equations above are listed below:

For the liver:

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{b},\mathrm{liv}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{b},\mathrm{liv}}={\mathrm{C}}_{\mathrm{ab}}\left[\mathrm{t}\right]\left({\mathrm{Q}}_{\mathrm{liv}}-{\mathrm{Q}}_{\mathrm{mes}}-{\mathrm{Q}}_{\mathrm{muc}}-{\mathrm{Q}}_{\mathrm{spl}}\right)+{\mathrm{C}}_{\mathrm{b},\mathrm{mes}}\left[\mathrm{t}\right]{\mathrm{Q}}_{\mathrm{mes}}\hfill \\ +{\mathrm{C}}_{\mathrm{b},\mathrm{muc}}\left[\mathrm{t}\right]{\mathrm{Q}}_{\mathrm{muc}}+{\mathrm{C}}_{\mathrm{b},\mathrm{spl}}\left[\mathrm{t}\right]{\mathrm{Q}}_{\mathrm{spl}}-{\mathrm{C}}_{\mathrm{b},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{Q}}_{\mathrm{liv}}\hfill \\ -{\mathrm{C}}_{\mathrm{b},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{bi},\mathrm{liv}}+{\mathrm{C}}_{\mathrm{i},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ib},\mathrm{liv}}\hfill \end{array}$$ (32)

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{c},\mathrm{liv}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{c},\mathrm{liv}}={\mathrm{C}}_{\mathrm{i},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ic},\mathrm{liv}}-{\mathrm{C}}_{\mathrm{c},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ci},\mathrm{liv}}\hfill \\ -{\mathrm{C}}_{\mathrm{c},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{cp},\mathrm{liv}}+{\mathrm{C}}_{\mathrm{p},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{pc},\mathrm{liv}}\hfill \\ -{\mathrm{C}}_{\mathrm{c},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{cn},\mathrm{liv}}+{\mathrm{C}}_{\mathrm{n},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{nc},\mathrm{liv}}\hfill \\ -{\mathrm{C}}_{\mathrm{c},\mathrm{liv}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{int}}\hfill \end{array}$$ (33)

For the brain:

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{b},\mathrm{brn}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{b},\mathrm{brn}}={\mathrm{Q}}_{\mathrm{brn}}\left({\mathrm{C}}_{\mathrm{ab}}\left[\mathrm{t}\right]-{\mathrm{C}}_{\mathrm{b},\mathrm{brn}}\left[\mathrm{t}\right]\right)-{\mathrm{C}}_{\mathrm{b},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ba},\mathrm{brn}}\hfill \\ +{\mathrm{C}}_{\mathrm{a},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ab},\mathrm{brn}}\hfill \end{array}$$ (34)

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{a},\mathrm{brn}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{a},\mathrm{brn}}={\mathrm{C}}_{\mathrm{b},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ba},\mathrm{brn}}-{\mathrm{C}}_{\mathrm{a},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ab},\mathrm{brn}}\hfill \\ -{\mathrm{C}}_{\mathrm{a},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ai},\mathrm{brn}}+{\mathrm{C}}_{\mathrm{i},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ia},\mathrm{brn}}\hfill \end{array}$$ (35)

$$\begin{array}{c}{\mathrm{C}}_{\mathrm{i},\mathrm{brn}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{i},\mathrm{tis}}={\mathrm{C}}_{\mathrm{a},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ai},\mathrm{brn}}-{\mathrm{C}}_{\mathrm{i},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ia},\mathrm{brn}}\hfill \\ -{\mathrm{C}}_{\mathrm{i},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ic},\mathrm{brn}}+{\mathrm{C}}_{\mathrm{c},\mathrm{brn}}\left[\mathrm{t}\right]{\mathrm{CL}}_{\mathrm{ci},\mathrm{brn}}\hfill \end{array}$$ (36)

For arterial blood:

$${\mathrm{C}}_{\mathrm{ab}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{ab}}={\mathrm{Q}}_{\mathrm{c}}\left({\mathrm{C}}_{\mathrm{b},\mathrm{lun}}\left[\mathrm{t}\right]-{\mathrm{C}}_{\mathrm{ab}}\left[\mathrm{t}\right]\right)$$ (37)

where Q_c is cardiac output.

For venous blood, we include an additional non‐hepatic clearance pathway, fe x CL. We also introduce the shallow compartment binding, C0 described above, as follows:

$$\begin{array}{c}\begin{array}{c}{\mathrm{C}}_{\mathrm{vb}}^{\prime }\left[\mathrm{t}\right]{\mathrm{V}}_{\mathrm{vb}}={\mathrm{Q}}_{\mathrm{C}1}{\mathrm{C}}_{\mathrm{b},\mathrm{C}1}\left[\mathrm{t}\right]+{\mathrm{Q}}_{\mathrm{adp}}{\mathrm{C}}_{\mathrm{b},\mathrm{adp}}\left[\mathrm{t}\right]+{\mathrm{Q}}_{\mathrm{C}2}{\mathrm{C}}_{\mathrm{b},\mathrm{C}2}\left[\mathrm{t}\right]\hfill \\ +{\mathrm{Q}}_{\mathrm{C}3}{\mathrm{C}}_{\mathrm{b},\mathrm{C}3}\left[\mathrm{t}\right]+{\mathrm{Q}}_{\mathrm{C}4}{\mathrm{C}}_{\mathrm{b},\mathrm{C}4}\left[\mathrm{t}\right]+{\mathrm{Q}}_{\mathrm{liv}}{\mathrm{C}}_{\mathrm{b},\mathrm{liv}}\left[\mathrm{t}\right]\hfill \\ \hfill \\ +{\mathrm{Q}}_{\mathrm{brn}}{\mathrm{C}}_{\mathrm{b},\mathrm{brn}}\left[\mathrm{t}\right]-\frac{{\mathrm{C}}_{\mathrm{vb}}\left[\mathrm{t}\right]\mathrm{fe}\mathrm{CL}}{\mathrm{BP}}-{\mathrm{Q}}_{\mathrm{c}}{\mathrm{C}}_{\mathrm{vb}}\left[\mathrm{t}\right]+{\mathrm{K}}_{\inf }\left[\mathrm{t}\right]\hfill \\ \hfill \\ -\left(\frac{{\mathrm{k}}_{\mathrm{on}}{\mathrm{f}}_{\mathrm{up}}{\mathrm{C}}_{\mathrm{vb}}\left[\mathrm{t}\right]\left[\mathrm{C}0\right]1000}{\mathrm{MW}\mathrm{BP}}-\left[\mathrm{C}0\mathrm{D}\right]\left[\mathrm{t}\right]{\mathrm{k}}_{\mathrm{off}}\right){\mathrm{V}}_{\mathrm{vb}}\hfill \end{array}\hfill \end{array}$$ (38)

$$\begin{array}{c}{\left[\mathrm{C}0\mathrm{D}\right]}^{\prime }\left[\mathrm{t}\right]=\frac{{\mathrm{k}}_{\mathrm{on}}{\mathrm{f}}_{\mathrm{up}}{\mathrm{C}}_{\mathrm{vb}}\left[\mathrm{t}\right]\left[\mathrm{C}0\right]1000}{\mathrm{MW}\mathrm{BP}}-\mathrm{C}0\mathrm{D}\left[\mathrm{t}\right]{\mathrm{k}}_{\mathrm{off}}\hfill \end{array}$$ (39)

where tissue subscripts correspond to tissues and lumped compartments in Figure 1a. K_inf is the infusion rate, with the IV bolus administration ‘infusion’ time set to 1 min. The C0 compartment is modeled as non‐saturable binding to a nominal C0 concentration, [C0], of 1 μM binding sites, with k_on = 1000 μM⁻¹ min⁻¹ and [C0D] is the concentration of bound drug.

The clearance calculated by dose/AUC is an average clearance (CL_av), since elimination does not occur from the sampling compartment, but the value will reproduce the experimental clearance used to calculate CL_int. Simulations showing CL vs. time are provided in Supplementary Materials. Also, since clearance is not constant, the mean residence time (MRT) should be calculated by Equation 40. However, we use the apparent MRT (Equation 41) times CL_av to estimate the steady state volume of distribution (Vss), since this is the value which can be calculated from the experimental C‐t profile. Differences in MRT values calculated by Equations 40 and 41, ³⁷ are <10% for the drugs modeled.

$$\mathrm{MRT}=\frac{{\int }_0^{\infty }\mathrm{t}\mathrm{CL}\left[\mathrm{t}\right]\mathrm{C}\left[\mathrm{t}\right]\mathrm{dt}}{{\int }_0^{\infty }\mathrm{CL}\left[\mathrm{t}\right]\mathrm{C}\left[\mathrm{t}\right]\mathrm{dt}}-\frac{\text{inftime}}{2}$$ (40)

$${\mathrm{MRT}}_{\mathrm{app}}=\frac{{\int }_0^{\infty }\mathrm{t}\mathrm{C}\left[\mathrm{t}\right]\mathrm{dt}}{{\int }_0^{\infty }\mathrm{C}\left[\mathrm{t}\right]\mathrm{dt}}-\frac{\text{inftime}}{2}$$ (41)

$${\mathrm{V}}_{\mathrm{ss}}={\mathrm{MRT}}_{\mathrm{app}}{\mathrm{CL}}_{\mathrm{av}}$$ (42)

To determine the accuracy of the C‐t profiles, we calculate the exposure overlap coefficient (EOC) from Equation 43. This is a slight modification from the previously reported method, ¹⁵ , ³⁸ since the integrals are evaluated from 0 to 20 t_last (to approximate from 0 to infinity).

$$\mathrm{EOC}=\frac{{\int }_0^{20\mathrm{t}}\mathrm{Min}\left[{\mathrm{C}}_{\mathrm{vb},\text{expt}}\left[\mathrm{t}\right],{\mathrm{C}}_{\mathrm{vb},\text{pred}}\left[\mathrm{t}\right]\right]}{{\int }_0^{20\mathrm{t}}{\mathrm{C}}_{\mathrm{vb},\text{expt}}\left[\mathrm{t}\right]}$$ (43)

Other Model Parameters – Tissue volumes and blood flows, ³⁹ , ⁴⁰ , ⁴¹ ISF and cytosolic volumes, neutral and phospholipid fractions ¹⁷ , ¹⁸ were obtained from the literature. Rest‐of‐the‐body volumes were divided equally between the four lumped compartments (C1‐C4), and properties were weighted averages of tissues in the compartment. Tissue blood volumes were calculated from capillary surface area, assuming a 10 mm capillary diameter. Tissue capillary blood volumes were proportionally subtracted from standard arterial and venous blood volumes. The resulting parameters are given in Table 1.

Drug specific parameters

Parameters for the 24 drugs in this study are listed in Table 2. LogP, pKa, and fe were taken from literature or from DrugBank. Values for f_up, f_um, BP, and P_app were obtained from literature from the references provided in Supplementary Material. Extreme values were excluded, resulting in a range that was not greater than 5‐fold above and below the mean. Values used in the model were either the mean value, a value within the range of published values or values outside the range of published values (Table 2). Drug clearances were determined by fitting 2‐ or 3‐compartment models to IV data.

PermQ modeling

Twenty‐four drugs were used for model development. PK profiles for these drugs were simulated using three PBPK models. The first model uses methods published by Rodgers and Rowland (RR) to calculate tissue K_p values. ¹⁷ , ¹⁸ This method uses different equations to parameterize acids and bases. The second model used a recently published method utilizing microsomal partitioning and LogP to calculate tissue K_p values (K_p,mem). ¹⁵ Both methods include only perfusion limited tissue distribution, whereas the third (PermQ) model includes both perfusion and permeability distribution components for all tissues. All clearances were generated from fitting a 2‐ or 3‐compartment model for each drug to IV data. Therefore, AUC values for all three models are identical to the AUC generated with the compartmental model.

When developing PermQ, initial values for f_up, f_um, BP, and P_app were the means of literature parameters. However, for some drugs, using parameters within the range of the literature values (instead of the mean) provided better results for all three models. For four drugs (fluconazole, diphenhydramine, mibefradil, and terbutaline), we used optimized BP values outside the range of the literature values. For three of these drugs, only one value was reported. In addition, there is one reported f_um value for cefazolin, and an optimized value was used for this as well. For these five drugs, simulations were run using both the mean value and the optimized value. Parameters ultimately used in the simulations (Table 2) consisted of 72 mean values, 19 values within the reported range, and five values outside the range of reported values.

After model development, a test set was used to evaluate the model. A review of PBPK models by Thompson et al. ⁴² was used to select the test set. From this review, PBPK models published between 2018 and 2021 provided five drugs for which IV data and the required in vitro parameters were available. The input parameters are listed in Table 2. None of the input parameters were optimized. Instead, parameters were selected from the modeling publications or from other publications when experimental values were not available.

RESULTS

The shallow compartment (C0) was optimized using the early time points of C‐t profiles. The best fit to Equation 5 gave c₁ and c₂ constants of 19.0 and 0.69, respectively. The fit to Equation 5 is shown in Figure 2a, and the impact of including the shallow compartment on all three models for a representative base (metoprolol) is in Figure 2b.

When parameter values different from the mean were used, they were optimized for the PermQ model. Therefore, the V_ss errors and EOC values reported do not reflect an accurate comparison between the three models. However, the comparison between the K_p,mem and PermQ models are more relevant since they use identical partition coefficients for partitioning into neutral lipids and phospholipids. The resulting C‐t profile simulations for the three models, using the drug parameters in Table 2 are shown in Figures 3, 4, and 5a. Table 3 gives the experimental and predicted V_ss and t_1/2 values and the absolute average fold errors as well as the EOC values using the drug parameters in Table 2. For the training set of 24 drugs, the AAFEs for V_ss prediction were 1.31 (RR), 1.30 (K_p,mem), and 1.19 (PermQ). The AAFEs for t_1/2 prediction were 1.59 (RR), 1.58 (K_p,mem), and 1.33 (PermQ). The mean EOCs were 0.86 (RR), 0.86 (K_p,mem), and 0.92 (PermQ).

FIGURE 3.

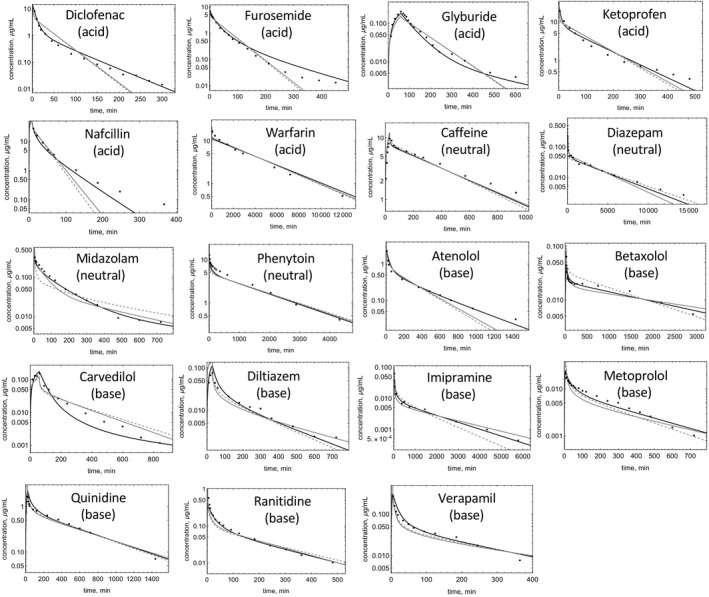
Observed and predicted C‐t profiles of drugs in the training set. Model‐predicted C‐t profiles for RR (dashed), K_p,mem (gray solid), and PermQ (black solid) for training drugs modeled using parameters within the literature‐reported range.

FIGURE 4.

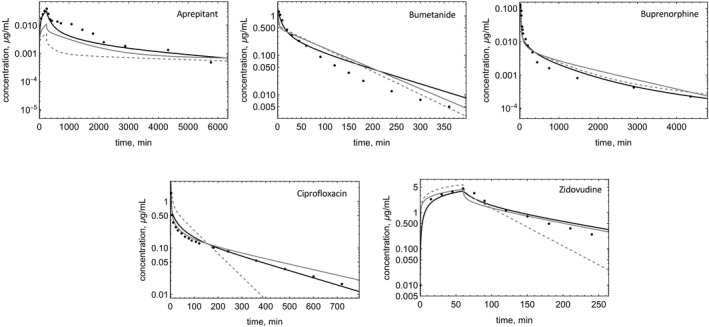
Observed and predicted C‐t profiles of drugs in the test set. Model‐predicted C‐t profiles for RR (dashed), K_p,mem (gray solid), and PermQ (black solid) for test drugs modeled using literature parameters.

FIGURE 5.

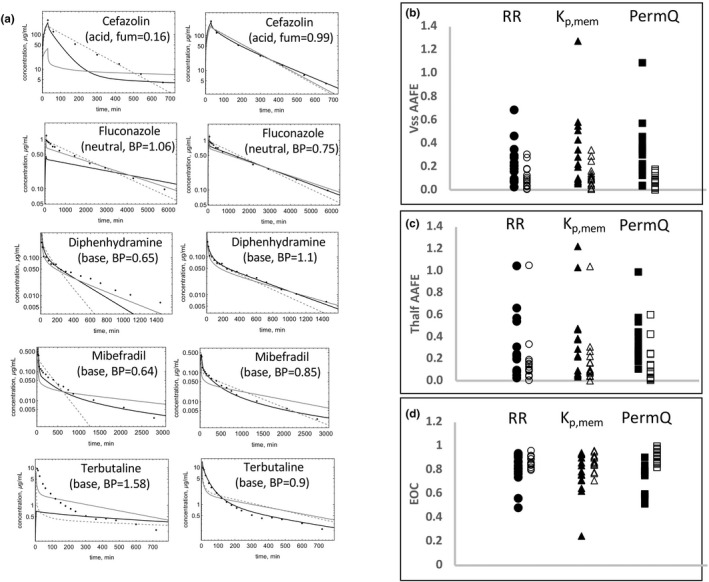
Observed and predicted C‐t profiles of selected drugs in the training set. (a) Model‐predicted C‐t profiles for RR (dashed), K_p,mem (gray solid), and PermQ (black solid) for drugs modeled using parameters outside the literature‐reported range. The left column depicts modeling with the reported mean parameter value, and the right column depicts modeling with an optimized value of the parameter. (b) AAFE in Vss estimates, (c) AAFE in t_1/2 estimates, and (d) EOC values are shown for n = 15 drugs where one parameter used was different from the reported mean (see Table 1) with RR (circles), K_p,mem (triangles), and PermQ (squares). Closed symbols depict AAFE values with mean parameters used, and open symbols depict AAFE values with optimized parameters used.

TABLE 3.

Model predictions. Model predicted Vss (L) and elimination half‐life (t_1/2, min), absolute average fold error (AAFE) in V_ss (L) and t_1/2 (min) versus experimental (exp) values, and individual and mean exposure overlap coefficients (EOC) in experimental versus predicted C‐t profiles with the RR, K_p,mem and PermQ models

Drug	Vss exp	Vss RR	Vss Kp,mem	Vss PermQ	t1/2 exp	t1/2 RR	t1/2 Kp,mem	t1/2 PermQ	EOC RR	EOC Kp,mem	EOC PermQ
Training set
Acid
Cefazolin	11.0	11.3	10.6	11.4	128	103	106	137	0.92	0.92	0.98
Diclofenac	7.91	8.53	8.63	8.77	61	24	25	45	0.79	0.79	0.97
Furosemide	17.8	8.84	9.07	12.2	393	35	36	98	0.91	0.90	0.97
Glyburide	11.6	11.7	9.33	12.1	223	80	81	244	0.83	0.83	0.89
Ketoprofen	11.7	8.76	9.19	9.58	157	73	77	90	0.84	0.84	0.87
Nafcillin	18.5	11.8	11.2	12.9	44	17	20	48	0.89	0.90	0.85
Warfarin	8.07	8.64	8.82	9.26	2747	2708	2765	2908	0.96	0.96	0.94
Neutral
Caffeine	42.8	34.8	37.7	36.3	345	275	309	298	0.86	0.87	0.86
Diazepam	102	101	74.1	86.8	3605	3280	2438	2942	0.89	0.84	0.89
Fluconazole	63.0	50.9	71.0	63.2	1965	1529	2158	1922	0.92	0.95	0.98
Midazolam	55.8	123	71.4	99.3	214	383	297	407	0.71	0.85	0.91
Phenytoin	42.3	53.9	51.9	49.6	1035	1306	1273	1242	0.84	0.85	0.86
Base
Atenololc	268	176	189	275	309	200	217	327	0.83	0.84	0.90
Betaxolol	359	257	468	395	1509	1105	2381	1672	0.88	0.93	0.96
Carvedilol	88.2	167	128	107	162	201	179	432	0.81	0.84	0.82
Diltiazem	322	248	341	267	169	165	260	183	0.87	0.84	0.94
Diphenhydramine	440	291	446	412	407	303	481	380	0.86	0.86	0.97
Imipramine	1012	1203	1266	952	1409	1000	1790	1355	0.85	0.91	0.95
Metoprolol	280	243	348	344	201	228	335	277	0.82	0.77	0.91
Mibefradil	170	185	375	256	750	523	1091	1335	0.86	0.71	0.92
Quinidine	227	235	253	246	376	430	477	447	0.95	0.93	0.97
Ranitidine	91.3	134	115	120	132	177	153	169	0.79	0.82	0.86
Terbutaline	79.9	86.5	105	80.0	440	291	356	410	0.80	0.78	1.00
Verapamil	108	163	192	152	121	190	226	171	0.89	0.85	0.85
Mean AAFE or mean EOC		1.31	1.30	1.19		1.59	1.58	1.33	0.86	0.86	0.92
Test set
Aprepitant	89.1	2868	1437	846	1087	10,445	13,793	3313	0.21	0.41	0.72
Bumetanide	7.70	9.19	10.3	10.7	122	52	59	81	0.84	0.82	0.92
Buprenorphine	406	882	646	620	1468	2262	1123	1898	0.71	0.69	0.80
Ciprofloxacin	116	39.4	164	107	204	60	258	196	0.68	0.88	0.94
Zidovudine	75.7	74.3	94.0	115	59	29	80	87	0.80	0.88	0.88
Mean AAFE or mean EOC		3.02	2.27	2.02		3.00	2.26	1.56	0.65	0.74	0.85

Abbreviations: AAFE, absolute average fold error; C‐t, concentration‐time; EOC, exposure overlap coefficients; K_p,mem, perfusion‐limited membrane‐based model; PermQ, new physiologically‐based pharmacokinetic modeling framework; RR, Rodgers and Rowland; t_½, terminal half‐life.

Model predicted V_ss (L) and t_½, min, AAFE in V_ss (L) and t_1/2 (min) versus experimental (exp) values, and individual and mean EOC in experimental versus predicted C‐t profiles with the RR, K_p,mem, and PermQ models.

Comparing the training set EOC values for the K_p,mem and PermQ models (Table 2) for the seven acids in the training set (Table 3), five C‐t profile predictions (EOC values) were improved using the PermQ model, one (warfarin) was slightly decreased (2%), and one (nafcillin) was decreased (5%). For the five neutrals in the training set, EOCs were improved for two and were similar for three drugs. For the 12 bases in the training set, seven EOCs were improved while two (carvedilol and verapamil) were similar. Four of the drugs (glyburide, diclofenac, nafcillin, and atenolol) are reported to be OATP transporter substrates. ⁴³ , ⁴⁴ , ⁴⁵ , ⁴⁶ Including first order hepatic uptake for nafcillin (CL_up = 330 ml/min) and atenolol (CL_up = 170 ml/min) improved the EOCs, but hepatic uptake had no effect on glyburide and diclofenac EOCs.

Figure 5a shows simulations using both the reported and optimal value in Table 2 for the five drugs for which one parameter was outside the reported range. For all five drugs, much better C‐t profiles were obtained for all models using the optimized values (Figure 5a). For PermQ, EOCs improved by 0.39 (cefazolin), 0.23 (fluconazole), 0.22 (diphenhydramine), 0.13 (mibefradil), and 0.49 (terbutaline). Figure 5b‐d shows the AAFE for the V_ss and t_1/2 estimates and EOC for all 15 drugs where one or more mean value was not used (within and outside of the range, Table 2). Almost all drugs showed improvement in V_ss and t_1/2 predictions and EOC values (Figure 5) for all three models.

For the five drugs in the test set (Figure 4), predictions were made without optimization of input parameters. The AAFEs for V_ss prediction were 3.02 (RR), 2.27 (K_p,mem), and 2.02 (PermQ). The AAFEs for t_1/2 prediction were 3.00 (RR), 2.26 (K_p,mem), and 1.56 (PermQ). The mean EOCs were 0.65 (RR), 0.74 (K_p,mem), and 0.85 (PermQ).

The optimized low P_gap × MW value was 4.5 × 10⁻⁴ dm Da^1/3/min, which is divided by MW^1/3 to yield drug‐specific low P_gap. The high permeability P_gap value optimized to 7.2 × 10⁻⁴ dm/min. For the liver and spleen, P_gap a value of 1.02 × 10⁻³ dm/min was used. Sensitivity analyses on high and low P_gap were performed for 12 representative drugs. Increasing or decreasing low and high capillary permeability through discontinuities (P_gap) values by five‐fold resulted in changes in EOC values of 0 to 8 percent, with an average absolute change of 1.8 percent. Increasing or decreasing high capillary permeability through discontinuities (P_gap) values by five‐fold resulted in changes in EOC values of 0 to 2 percent, with an average absolute change of 0.35 percent. For these drugs, EOCs were not sensitive to neutral lipid droplet size for adipose and other tissues. Sensitivity analysis of p_para (decreasing p_para by 100‐fold) for the six lowest permeability compounds showed decreases in EOC values of 11% (terbutaline), 4% (atenolol), 1% (cefazolin), 0.8% (nafcillin), 0.2% (furosemide), and 0.1% (ranitidine). Sensitivity analysis of p_aq (Increasing p_aq by 100‐fold) for the six highest permeability compounds showed decreases in EOC values of 4% (verapamil), 2% (imipramine), 0.7% (diphenhydramine), 0.6% (diclofenac), and 0% (warfarin, betaxolol).

The test set of compounds was used to evaluate the impact of including the shallow compartment, C0. Removal of C0 resulted in decreased EOCs for buprenorphine (3%), and zidovudine (3%), aprepitant (2%), with minimal changes for bumetanide and ciprofloxacin.

DISCUSSION

For the 24 molecules used for model development, errors in V_ss and t_1/2 were reduced by 37% and 43%, respectively, with the PermQ model. Errors in C‐t profiles were reduced (increased EOC) by 43%. The improvement was generally greater for bases than for acids and neutrals. For the five drugs in the test set, similar results were seen, even though the errors were generally higher for all models. This is expected since some of the experimental values for model development were optimized, and the optimized values improved all three models.

Therefore, it appears that the PermQ model framework has the potential to improve prediction of drug C‐t profiles from in vitro data. This model combines components similar to those described previously by us and others. Permeability in and out of capillaries can occur by transcellular endothelial cell diffusion, or paracellularly either through fenestra or other discontinuities between cells. Similar models have been developed for large molecule disposition. ⁷ , ³¹ , ⁴⁷ Liu and Jusko have used four different cellular permeabilities to construct a full permeability‐limited PBPK model. ⁸ We have previously described membrane permeability as CL_i/2 ³² and partitioning as CL_i/CL_o. Phospholipid and neutral lipid components for tissue distribution were used to predict V_ss, ¹⁵ K_p values, ¹⁴ and partitioning into enterocytes. ⁴⁸ The separation of intestinal blood flow into mucosal and serosal components was described previously by Pang et al. ²¹

The PermQ model has some unique features. First, the model uses experimental cellular permeability (P_app) and membrane partitioning (f_um) to define the clearance in (CL_i) and out (CL_o) of membranes. Other models included “lumped” tissues based on blood flow while PermQ considers both similar blood flow and capillary permeability parameters. The necessity for considering tissue compartments in this specific manner has not been tested in the present work, but it provides a mechanistic framework to evaluate processes where capillary leakiness may be critical. This model also includes a shallow compartment based on erythrocyte partitioning. To our knowledge, all of these components have never been combined into a single PBPK framework. While not components of the PermQ framework, (1) the ability to use net clearances (see companion tutorial and Supplementary Material) to rapidly develop model components and (2) use of EOCs to compare model predicted C‐t profiles has been invaluable in this effort.

Our goal was to investigate if inclusion of permeability dependent processes could improve the prediction of C‐t profiles. In the PermQ model, these processes include diffusion in and out of capillaries, across the plasma membrane, into and out of phospholipids and neutral lipids. This method and all other PBPK methods rely heavily on experimental data. Specifically, the PermQ experimental inputs, f_up, f_um, BP and P_app, all suffer from interlaboratory experimental variability (e.g., f_up values include those determined by ultracentrifugation or without pH control).

The K_p,mem and PermQ models use f_um as a major determinant to predict tissue K_p values. Whereas most current PBPK methods assume a correlation between acidic phospholipid content and K_p for bases, previous analyses suggest that hydrophobic bases bind to all phospholipid membranes. ¹⁴ , ¹⁵ , ³⁸ , ⁴⁹ , ⁵⁰ Current methods use erythrocyte partitioning to determine affinity to acidic phospholipids. However, it is likely that the ability to reproduce tissue K_p values for bases results from the strong correlation between unbound V_ss and erythrocyte partitioning. ⁵¹

During model development, it was observed that early time points were not well predicted for permeable hydrophobic bases. The addition of a shallow (rapidly equilibrating) compartment improved the prediction of early timepoint concentrations, particularly for bases (Figure 2b). This led to the hypothesis that drugs interact rapidly with endothelial cell membranes. The endothelial cell surface area of capillaries (Table 1) is similar to the surface area of erythrocytes ⁵² and similar to erythrocytes, contains a large number of negative charges. ⁵³ To model the hypothesized partitioning into endothelial cells, a shallow compartment was parameterized using early time points and erythrocyte partitioning calculated with the corrected BP and f_up values. Although the fit of K_C0 to K_ery,C0 is good (Figure 2a), this approach is not ideal without good experimental data and an accurate estimate of the hematocrit. Equations 3 and 4 are very sensitive to all parameters at low f_up and BP values. Hematocrit values are often not available in clinical datasets and errors in BP and f_up may be too large for an accurate estimation of K_C0.

An alternate explanation for over‐predicting early concentrations has been provided by Levitt, ⁵⁴ Musther et al. ⁵⁵ and Huang and Isoherranen. ⁵⁶ It has been proposed that addition of a forearm compartment for sampling could result in lower initial peripheral venous concentrations relative to central venous sampling. This would be observed if the partition coefficient of the forearm was greater than, or the shunted blood was less than the average for the rest of the body. ⁵⁴ , ⁵⁵ , ⁵⁶ While this possibility has not been evaluated within the PermQ framework, similar results may be expected. The shallow compartment hypothesized in this paper is parameterized with erythrocyte partitioning. Since partition coefficients for bases are highly correlated with erythrocyte partitioning, ⁵¹ lower peripheral plasma levels due to forearm partitioning might be expected to correlate with drug partition coefficients, particularly for bases. One or both of these proposed mechanisms may be involved, and further research in this area is necessary.

In the PermQ model, diffusion through a cell can be appropriately parameterized as P_app x surface area (SA). Diffusion through a single membrane can be modeled as CL_i/2 as described previously ³² and in the accompanying tutorial. At a minimum, transcellular permeability requires that a drug cross two membranes (i.e. apical and basolateral plasma membranes). PermQ assumes that cellular permeability includes the passage of drugs through two membranes. Therefore, entering a membrane has a clearance of 4 P_app SA, crossing a membrane is 2 P_app SA, and crossing a cell is P_app SA (Figure 1b). However, it is conceivable that the average path across a cell at steady state may involve crossing more than two membranes. As described in the tutorial, the equation for crossing multiple mandatory membranes is CL_i = 2n P_app SA, where n is the number of mandatory membranes crossed for transcellular permeability. Two factors prevent determining the optimum number of mandatory membranes to use in the PermQ model. First, the variability of our experimental dataset required that some in vitro parameters be optimized, including five of the 24 P_app values (Table 2). Second, the ISF surface area was set to 15 times the capillary surface area. This scaling factor is covariant with permeability since clearance is permeability times surface area.

The primary goal of this effort was to evaluate if a PBPK model with specific permeability components can better predict C‐t profiles. Although variability of in vitro experimental data precludes direct model comparison of the different models, PermQ was able to produce much improved C‐t profiles for many drugs. Jeong et al. ⁵⁷ developed rat PBPK models using either measured tissue concentrations or P_eff SA parameterized using artificial membrane (PAMPA) permeabilities. These results cannot be compared directly since the species are different, but the predicted C‐t profiles were improved for poorly permeable compounds (furosemide and cefazolin) to a similar degree to poorly permeable compounds in this study (furosemide, cefazolin, nafcillin, and ciprofloxacin). In general, the permeability and perfusion ‐limited models reproduced C‐t profiles as well or better than perfusion‐only limited models.

For this approach to be generally applicable, several improvements in in vitro data may be needed. First, transcellular permeability measurements should be improved, particularly for poorly permeable compounds. Reporting paracellular permeability measurements (often characterized using lucifer yellow) would allow determination of true transcellular values. Second, if endothelial cell interactions are experimentally shown to be responsible for the observed shallow compartment, direct measurement and detailed characterization of erythrocyte partitioning could be incorporated. Third, experiments characterizing the relationship between permeability across a single membrane and P_app are needed. Several of these experiments are ongoing in our laboratories. Other improvements can be envisioned throughout the model. For example, better physiological constants (e.g. capillary surface areas and permeabilities) for individual tissues could result in more accurate predictions. The PermQ model assumes either high or low paracellular capillary permeabilities for tissues and parameterizing individual tissues to reproduce experimental perfusion data may be necessary, particularly if concentration data for that tissue is needed.

The reported PermQ model should be considered a preliminary framework for adding permeability limited characteristics to PBPK models using experimental P_app and f_um values to model transmembrane permeabilities and a two‐pore size model for capillary permeabilities. The code for the PermQ model has been provided and we encourage others to improve this modeling framework. In summary, PermQ model simulations identified potential improvements in PBPK modeling. Improved prediction of C‐t profiles may be possible by including capillary and cellular permeability components for all tissues.

AUTHOR CONTRIBUTIONS

Wrote Manuscript: Ken Korzekwa and Swati Nagar. Designed Research: Ken Korzekwa. Performed Research: Ken Korzekwa and Swati Nagar. Analyzed Data: Ken Korzekwa, Casey Radice, and Swati Nagar.

CONFLICT OF INTEREST

All authors declared no competing interests for this work.

Supporting information

Appendix S1

Korzekwa K, Radice C, Nagar S. A permeability‐ and perfusion‐based PBPK model for improved prediction of concentration‐time profiles. Clin Transl Sci. 2022;15:2035‐2052. doi: 10.1111/cts.13314