Evolutionary Genomics of a Subdivided Species

Abstract

The ways in which genetic variation is distributed within and among populations is a key determinant of the evolutionary features of a species. However, most comprehensive studies of these features have been restricted to studies of subdivision in settings known to have been driven by local adaptation, leaving our understanding of the natural dispersion of allelic variation less than ideal. Here, we present a geographic population-genomic analysis of 10 populations of the freshwater microcrustacean Daphnia pulex, an emerging model system in evolutionary genomics. These populations exhibit a pattern of moderate isolation-by-distance, with an average migration rate of 0.6 individuals per generation, and average effective population sizes of ∼650,000 individuals. Most populations contain numerous private alleles, and genomic scans highlight the presence of islands of excessively high population subdivision for more common alleles. A large fraction of such islands of population divergence likely reflect historical neutral changes, including rare stochastic migration and hybridization events. The data do point to local adaptive divergence, although the precise nature of the relevant variation is diffuse and cannot be associated with particular loci, despite the very large sample sizes involved in this study. In contrast, an analysis of between-species divergence highlights positive selection operating on a large set of genes with functions nearly nonoverlapping with those involved in local adaptation, in particular ribosome structure, mitochondrial bioenergetics, light reception and response, detoxification, and gene regulation. These results set the stage for using D. pulex as a model for understanding the relationship between molecular and cellular evolution in the context of natural environments.

Introduction

Species consisting of metapopulations of demes connected by moderate gene flow offer opportunities for understanding the genetic basis of local adaptation, as individual populations may experience different ecologies driving genomic differentiation, whereas the relative magnitudes of migration and selection dictate the evolutionary capacity to respond to such differences (Luikart et al. 2003; Ellegren 2014). Molecular surveys of subdivided populations have been profitably applied in the genetic dissection of traits known in advance to have diverged among populations (e.g., Barreiro et al. 2008; Hohenlohe et al. 2010; Aeschbacher et al. 2017; Pfeifer et al. 2018; Yeaman et al. 2018), but the underlying ascertainment bias leaves uncertain many general issues concerning natural levels of spatial population structure and the underlying determinants. In addition, species with continuous distributions impose technical challenges for such study, as sampling schemes often cannot be confidently aligned with demic structure.

North American pond populations of the freshwater microcrustacean Daphnia pulex have well-defined boundaries, providing excellent prospects for such work. Previous studies of population subdivision based on allozymes, microsatellites, and mitochondrial DNA (Crease et al. 1990; Lynch and Crease 1990; Innes 1991; Lynch and Spitze 1994; Morgan et al. 2001; Allen et al. 2010) have mostly led to the conclusion that genetic differentiation among populations is moderate. One limitation of this prior work is its reliance on very small numbers of marker loci, in most cases of uncertain functional significance. The recent establishment of genomic reference sequences for D. pulex (Ye et al. 2017) and population-level applications of high-throughput sequencing technologies (Lynch et al. 2017) now enable expansion to genome-wide population-genetic analysis of single-nucleotide polymorphisms (SNPs), the finest scale of molecular analysis.

For most of the growing season, Daphnia reproduce by ameiotic parthenogenesis. However, many Daphnia populations switch to sexual reproduction on an annual basis, which yields resting eggs (ephippia) surrounded by protective membranes (Hebert 1978). These egg capsules are resistant to desiccation and digestion, and have spines along the dorsal margin that facilitate attachment to terrestrial animals, the primary mode of migration, although in some cases passive dispersal can occur by wind or flowing water (Brendonck and De Meester 2003; Havel and Shurin 2004; Figuerola et al. 2005).

As an entrée into the evolutionary forces shaping among-population genetic differentiation in this model species, here we report on the complete genomes of >800 diploid individuals distributed over 10 D. pulex populations, in one of the largest studies of geographic subdivision ever performed. The study populations are widely distributed across the midwestern United States and Canada, and are sampled agnostically with respect to ecological differentiation, thereby minimizing issues with respect to ascertainment bias, although not ruling out the opportunity for adaptive divergence. Each population inhabits a temporary pond that typically contains water only during the months of March through June. Thus, annual bouts of sexual reproduction and resting-egg production are enforced, typically after no more than five clonal generations, with genotype frequencies remaining in near Hardy–Weinberg equilibrium throughout such periods (Lynch 1984a, 1984b). Despite the periodic clonal nature, the average per-generation recombination rate is higher than that in another popular model system, Drosophila melanogaster, owing to the small number of chromosomes and lack of male recombination in the latter (Lynch et al. 2017).

With an average of 82 genotypes characterized for each population, this study allows an unbiased evaluation of genetic variation within and among populations and the associated causal factors. D. pulex is already one of the best-characterized invertebrate species with respect to the rate and molecular spectrum of mutations (Keith et al. 2016), recombination (Lynch et al. 2014; Xu, Ackerman et al. 2015; Urban 2018), and the power of random genetic drift (Lynch et al. 2020), and the results from this study provide robust estimates of average migration rates. With this background information on the power of the nonadaptive forces of evolution, the stage is set for quantifying the form and intensity of selection operating on various functional genomic sites across the genome, and for identifying genetic loci that are under particularly strong diversifying selection associated with ecological factors.

Results

Within-population Genetic Variation

In total, this study encompassed the genomic sequences of 824 clones from 10 populations, with the range of sequenced individuals being 71–93 among populations (supplementary table S1, Supplementary Material online). On average, $\sim {10}^8$ nucleotide sites were assayed per population (table 1), >95% of which were monomorphic for the same allele across all populations (supplementary table S2, Supplementary Material online). Among polymorphic sites, >97% contain just two nucleotides per site, that is, tri- and tetra-allelic sites are rare.

Table 1.

Summary of Within-Population Genetic Variation.

Population	${\pi }_T$	No. of Sites	$F_{IS}$	SE ($F_{IS}$)	No. of SNPs	$N_e$
BUS	0.0079	104,644,342	−0.0929	0.0002	2,379,001	617,000
CHQ	0.0052	84,417,136	−0.0238	0.0001	1,716,628	427,000
EB	0.0093	102,029,955	−0.0297	0.0001	4,045,041	754,000
KAP	0.0087	98,571,437	−0.0020	0.0001	4,635,427	744,000
LPA	0.0082	96,791,394	0.0144	0.0001	4,103,982	689,000
LPB	0.0070	86,819,534	0.0082	0.0001	2,777,315	573,000
NFL	0.0084	93,093,572	0.0170	0.0001	3,605,326	718,000
PA	0.0075	101,931,067	−0.0285	0.0001	2,629,288	605,000
POV	0.0077	100,315,688	−0.0124	0.0001	3,806,203	652,000
TEX	0.0076	97,237,517	−0.0480	0.0001	3,520,170	618,000
Mean	0.0078		−0.0198			640,000
SE	0.0004		0.0100			31,000

Note:—${\pi }_T$ is the mean nucleotide diversity over all sites; the standard errors of the population estimates are all $\simeq$0.000005. The average inbreeding coefficients, $F_{IS}$, are based on polymorphisms with maximum-likelihood MAF estimates >0.02 significant at the 5% level. Effective population size estimates, $N_e$, were obtained from diversity at silent sites and restricted intron positions (internally, 8–34 from both ends; Lynch et al. 2017), using the mutation rate estimate from Keith et al. (2016).

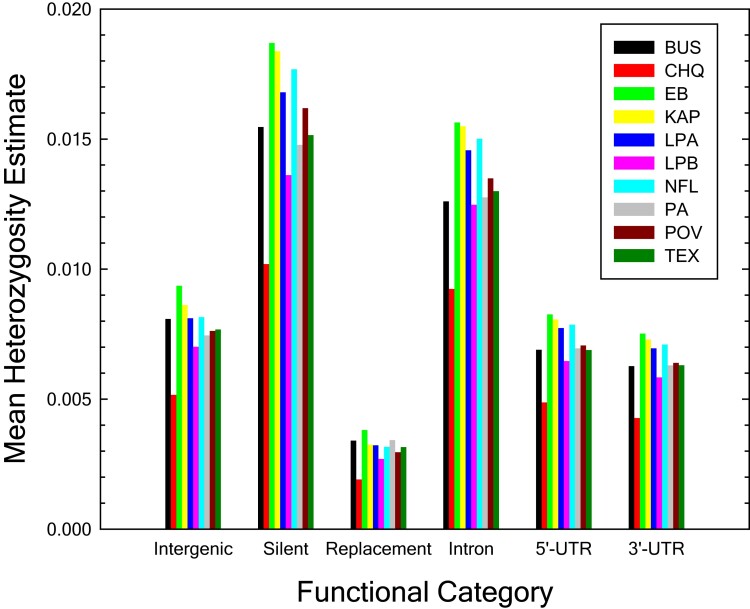
Average nucleotide diversity (estimated as heterozygosity under the assumption of Hardy–Weinberg equilibrium) across genomic sites is similar among the populations, with an overall within-population mean of 0.0078, and standard error (SE) of 0.0004. The CHQ population has the lowest estimate, suggesting a lower effective population size than in other populations, as reported elsewhere in a more elaborate study of historical demography (Lynch et al. 2020) (table 1). Consistent differences in nucleotide diversity exist among functionally different genomic sites (fig. 1). Heterozygosity is the highest at silent sites followed by restricted intron sites (internal positions 8–34 bp from both ends (Lynch et al. 2017), and hereafter referred to as intron sites), and lowest at amino-acid replacement sites, with intergenic and UTR sites having similar intermediate levels. These observations are consistent with a predominant role for purifying selection in decreasing heterozygosity estimates at functionally more important sites (Kimura 1983).

Fig. 1.

Genome-wide heterozygosity estimates at sites in different functional categories. Intergenic sites are outside of untranslated regions (UTR), exons, and introns. Silent, replacement, and intron sites are, respectively, 4-fold redundant, 0-fold redundant and restricted intron (internal positions 8 to 34 from both ends; Lynch et al. 2017) sites. Tri- and tetra-allelic sites are excluded from the calculations, but make trivial contributions. The standard errors of the individual estimates are too small to visualize on the graph ($6\times {10}^{-6}$ to $5\times {10}^{-5}$).

Using the base-substitution mutation rate estimate of $u=5.69\times {10}^{-9}$ per site per generation from Keith et al. (2016) and the means of the heterozygosity estimates at silent and restricted intron sites (${\pi }_s$), previously found to be evolving in a nearly neutral fashion (Lynch et al. 2017), we estimated the long-term average effective size $N_e$ of each population by equating ${\pi }_s$ with the neutral equilibrium expectation $4N_{e}u$ (table 1). With the exception of the CHQ population, all $N_e$ estimates fall in the range of 570,000–750,000, with a mean of 640,000 ($\mathrm{SE}=31,000$).

Population Structure

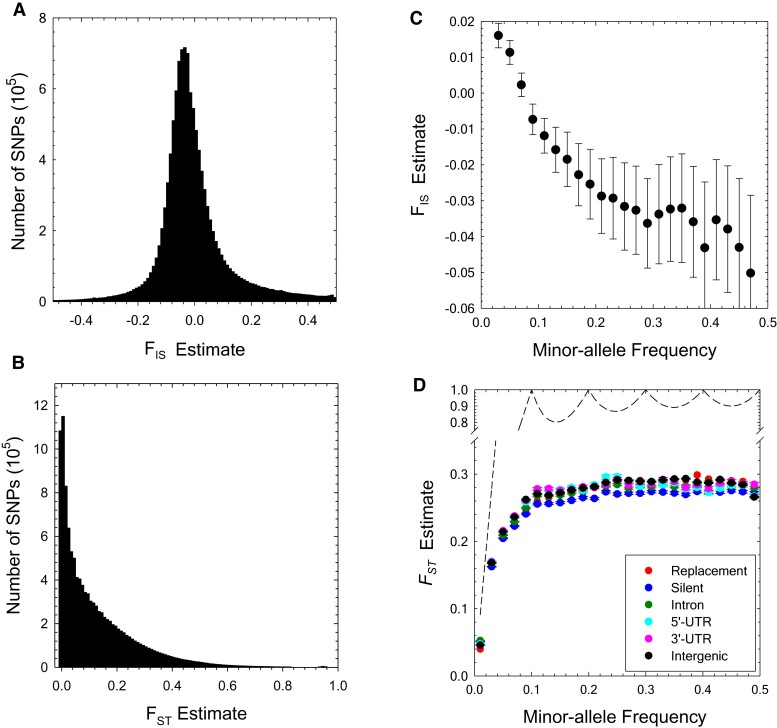
To ascertain the genetic structure of the study populations, we estimated Wright’s (1951) fixation indices (fig. 2). With one exception, the mean inbreeding-coefficient estimates of the individual populations, $F_{IS}$, have absolute values <0.05 (table 1). Although there is a gradient in the behavior of $F_{IS}$ with the minor-allele frequency (MAF) (fig. 2C), average estimates in all frequency classes are very small, falling in the range of −0.050 to 0.016. The overall mean, −0.020 ($\mathrm{SE}=0.010$), is just slightly less than zero, with slightly positive values at low-frequency sites being balanced by slightly negative values at high-frequency sites. As noted earlier (Lynch et al. 2017), these estimates of $F_{IS}$ are closer to zero than those obtained in studies of other purely sexual species such as Drosophila. Thus, at the times of sampling, genotypic frequencies in the study populations are in close accord with Hardy–Weinberg equilibrium (HWE) expectations across the genome, in agreement with earlier allozyme studies (Lynch 1983; Lynch and Spitze 1994). The negative mean inbreeding-coefficient estimate in BUS (−0.09) is consistent with, although not as extreme, as a prior estimate of −0.18 for microsatellite loci in this population (Allen et al. 2010).

Fig. 2.

(A,B) Genome-wide distributions of the $F_{IS}$ and $F_{ST}$ estimates, shown using bins of width 0.01. The results are based on 11,731,566 SNP sites with significant polymorphisms (determined by the ML allele-frequency estimator, using a 95% confidence cutoff level). The medians of the $F_{IS}$ and $F_{ST}$ estimates are −0.01 and 0.08, respectively. (C) The profile of average $F_{IS}$ with respect to minor-allele frequency (MAF) class (standard errors denoted by the vertical bars), based on polymorphisms with maximum-likelihood MAF estimates significant at the 5% level. (D) The profile of average $F_{ST}$ with respect to minor-allele frequency class (standard errors denoted by the vertical bars); dashed line is the statistical upper bound for $F_{ST}$ obtained using equation (5) of Alcala and Rosenberg (2017).

The mode of the genome-wide distribution of site-specific $F_{ST}$ estimates is near zero (fig. 2B), but the mean $F_{ST}$ is 0.126 ($\mathrm{SE}=0.00004$), indicating moderate differentiation among populations. The average level of population subdivision differs just slightly among functional categories of sites (fig. 2D, table 2), being highest at intron and silent sites, lowest at replacement sites, and intermediate at intergenic and UTR sites. These observations are consistent with previous studies reporting lower average $F_{ST}$ at sites under stronger functional constraints (Barreiro et al. 2008; Maruki et al. 2012; Jackson et al. 2015). However, such comparisons can be clouded by the dependence of the statistical upper bounds of $F_{ST}$ estimates on allele frequencies (Alcala and Rosenberg 2017), a problem that is compounded when functional categories of SNPs have different site-frequency spectra.

Table 2.

Mean $F_{ST}$ Estimates at Sites in Different Functional Categories, Along with Average Nucleotide Diversities at the Among-Population ($\varphi$) and Total Metapopulation ($\mathrm{\Pi }$) Levels.

Category	Mean (SE)	$\varphi$	$\mathrm{\Pi }$
Silent	0.1458 (0.0002)	0.0054	0.0215
Replacement	0.1082 (0.0002)	0.0010	0.0040
Intron	0.1473 (0.0002)	0.0048	0.0182
$5^{\mathrm{\prime }}$ -UTR	0.1305 (0.0003)	0.0024	0.0095
$3^{\mathrm{\prime }}$ -UTR	0.1270 (0.0002)	0.0022	0.0086
Intergenic	0.1213 (0.0001)	0.0026	0.0101

Note:—The means for $F_{ST}$ are calculated using sites with significant polymorphisms at the 5% level in at least one of the populations (SEs are in parentheses). Intergenic sites are those outside of untranslated regions (UTR), exons, and introns. Silent, replacement, and intron sites are, respectively, 4-fold redundant, 0-fold redundant and restricted intron sites. Standard errors for all mean estimates of nucleotide diversity are <0.0001.

The latter issue is made clear in figure 2D, where it can be seen that average $F_{ST}$ increases with the MAF until the latter exceeds 0.1, in accordance with the strong downward bias on the upper limit below this point. Focusing just on silent sites, above $\mathrm{MAF}=0.1$, the mean $F_{ST}$ is 0.269 (0.002), and if the individual estimates are scaled by dividing by their upper bounds, this increases slightly to 0.297 (0.003). In addition, contrary to the analysis based on the full set of sites (table 2), for $\mathrm{MAF}\ge 0.1$, there is consistently ∼5% more population divergence for all functional categories of sites than for silent sites. Thus, the excess divergence for silent sites with the full analysis in this study, and likely in many prior studies, is due to the fact that the site-frequency spectrum (SFS) is dominated by the lowest frequency classes, which are even more enriched for functional sites (below) and hence have the most constrained upper bounds for $F_{ST}$.

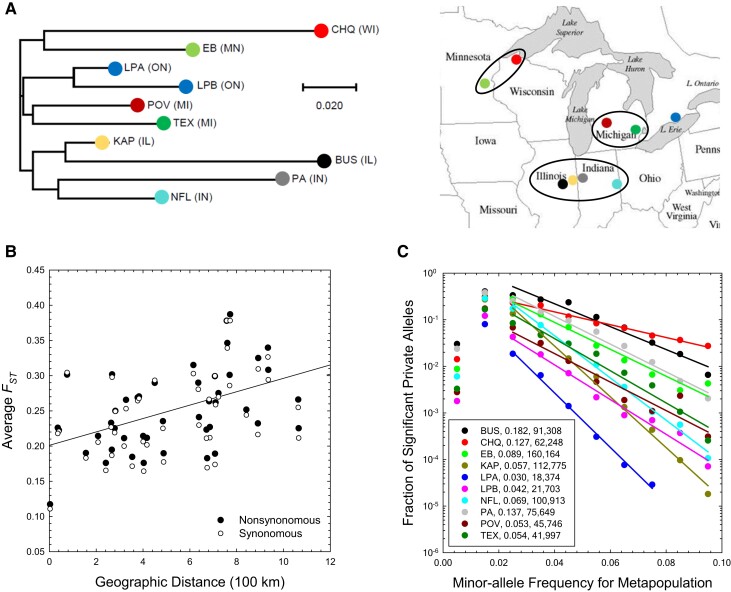
To examine the relationship between sampling locations and genetic differentiation, we constructed a neighbor-joining tree (Saitou and Nei 1987) based on mean pairwise $F_{ST}$ estimates (fig. 3A). Geographically close populations cluster together in the tree, consistent with gene flow among populations being limited by geographic distance. A significant positive regression between mean pairwise $F_{ST}$ estimates and geographic distance, for both silent ($t=3.55$ and $P<0.005$) and replacement ($t=3.11$ and $P<0.005$) sites in protein-coding sequences, further supports this inference (fig. 3B), as does an alternative statistical analysis of isolation-by-distance using a distance-based Moran’s eigenvector map analysis ($F=1.85$ and $P<0.05$ at silent sites, and $F=1.91$ and $P<0.01$ at replacement sites). However, the scale of geographic divergence is quite weak. Nearly adjacent populations have an average $F_{ST}\simeq 0.20$, and this increases to just $\simeq$0.29 at a distance of ${10}^3$ km, with geographic distance accounting for only $20\text{\%}$ of the variation in average pairwise $F_{ST}$.

Fig. 3.

Pairwise $F_{ST}$ estimates and private-allele statistics. (A) Neighbor-joining tree based on pairwise $F_{ST}$. The letters in parentheses denote the US state/Canadian province abbreviation, with specific locations shown to the right; the scale bar is for the $F_{ST}$ estimates. (B) The relationship of population-pairwise $F_{ST}$ (for sites with $\mathrm{MAF}\ge 0.1$) with geographic distance (results for amino-acid replacement and silent sites are given by the solid points/solid line and open points/dashed line, respectively). The results for both types of sites are very similar (SEs in parentheses): silent sites – intercept = 0.20 (0.02), slope = 0.0088 (0.0028), $r^2=0.429$, $P=0.0033$; replacement sites – intercept = 0.20 (0.02), slope = 0.0095 (0.0027), $r^2=0.475$, $P=0.0010$. (C) Conditional on the minor-allele frequency (MAF) in the entire metapopulation, the proportion of SNPs in each population that are private to the population and significantly more abundant than expected based on random sampling of a panmictic metapopulation. The plotted lines are the least-squares regressions for MAFs in the range of 0.02–0.10; the inset numbers denote the average frequencies of private alleles per population, and the total numbers of private alleles in each population that are significantly more frequent than expected by chance under a model of no subdivision.

Given the approximate constancy of $N_e$ estimates across populations (table 1) and over time (Lynch et al. 2020), the near neutral behavior of silent sites, and the near invariance of $F_{ST}$ for $\mathrm{MAF}\ge 0.1$, an estimate of the average migration rate using equilibrium theory appears justified. As the level of subdivision is only weakly associated with geographic distance, we used Wright’s (1951) island model in which a metapopulation consists of a large number of demes of size $N_e$, with each deme experiencing an equivalent migration rate of m (randomly distributed among demes), which yields an expected equilibrium value of $F_{ST}$ for neutral markers of $(1+4N_{e}m{)}^{-1}$. Using 0.297 for the estimated $F_{ST}$, the mean number of migrants per deme per generation is estimated to be $N_{e}m=0.59$, which with the average $N_e$ in table 1 implies a migration rate of $m\simeq 9.2\times {10}^{-7}$. Thus, ${10}^{-6}$ provides a useful benchmark for understanding the limits to local adaptation in this D. pulex metapopulation—for an allele to be promoted via positive population-specific effects, a local selective advantage $>{10}^{-6}$ is required to offset the swamping effects of gene flow (Felsenstein 1976).

Finally, an analysis of subdivision using the complete sequences of mitochondrial genomes of the study populations yields an estimate of $F_{ST}$ for $\mathrm{MAF}\ge 0.1$ virtually identical to that for the nuclear genome, 0.243 (0.009) (Ye et al. 2022), suggesting similar migration rates for nuclear and mitochondrial genes, as expected given that gene flow is restricted to resting-egg transport. We tested for cyto-nuclear disequilibrium for within-population variants, comparing the two most common mitochondrial haplotypes within each population with the full set of nuclear SNPs with $\mathrm{MAF}\ge 0.05$. Using the ${\chi }^2$-test for nonindependence advocated by Hill (1975) and Hedrick (1987), followed by Bonferroni correction, we found no evidence for within-population cytonuclear disequilibria, with just 1–4% of sites exhibiting significant disequilibria (at the $P=0.05$ test level), even before sample-size correction.

Private Alleles Within Populations

Further insight into the nature of population subdivision derives from observations on the distribution of private alleles, that is, alleles confined to samples from just a single population. Owing to finite sample sizes, such alleles will almost always be present in genome-wide samples, but private alleles whose local frequencies exceed the expectations based on random sampling from an otherwise nonsubdivided population are of special interest. In this study, alleles with metapopulation-wide $\mathrm{MAFs}<0.02$ will be represented by <4 copies across the whole metapopulation sample, rendering a high likelihood of inferring a private allele by chance alone. In addition, assuming equal sample sizes, with just 10 populations involved in the analysis, a metapopulation MAF cannot exceed $1/10$ if an allele is to be present within just a single deme. Focusing just on alleles with metapopulation MAFs in the range of $0.02$–$0.10$, all of the populations exhibit a near exponential decline in the fraction of private alleles per MAF class with increasing frequency (fig. 3C). On the order of 5–10% of alleles with metapopulation MAFs in the range of 0.02–0.04 are private to a particular population, whereas <1% of alleles with $\mathrm{MAF}>0.09$ are private.

Using the method of Slatkin (1985), an estimate of the migration rate can be obtained from information on the mean frequency of all private alleles in a population, $p(1)$. These frequencies are given in the inset of figure 3C, and then converted to estimates of $N_{e}m$ using equation (3) of Slatkin (1985) and correcting for sample size as described on his page 57. Applying this method to each population yields an average estimate of $N_{e}m=0.73$ ($\mathrm{SE}=0.23$), fully consistent with the estimate based on $F_{ST}$ analysis. Although this method was developed for the ideal island model in which all populations experience identical rates of migration from all others, Slatkin (1985) showed that similar results are obtained for two-dimensional stepping-stone structures.

Further insight into the biological significance of private alleles requires gene-specific analyses. Using the genome-wide estimate of the frequency of private alleles per site as the null hypothesis, for each protein-coding gene in each population, assuming a Poisson distribution for the number of private alleles over entire genic regions (from the start of the $5^{\mathrm{\prime }}$ UTR to the termination of the $3^{\mathrm{\prime }}$ UTR), we determined the subset of genes containing significantly more private alleles than expected by chance in each population. After Bonferroni correction, this analysis revealed that 11–102 genes (<1%) in each population ($\mathrm{mean}=33$, $\mathrm{SD}=31$) were enriched for private alleles beyond the background expectation (supplementary table S3, Supplementary Material online). In total, 284 genes were significantly enriched in private alleles in at least one population, with 12 of these being enriched for different sets of private alleles in two populations. On average, these enriched genes had 30.2 ($\mathrm{SE}=2.1$) private SNPs, with mean within-population private-allele frequency 0.244 (0.006).

The source of such alleles remains unclear, but some sort of introgression seems likely, as there are a number of cases where stretches of linked genes are enriched with private alleles. For example, for the BUS population, there is a 0.55 Mb region (scaffold 10, chromosome 12) containing 18 private-enriched genes, and a 0.44 Mb region (scaffold 19, chromosome 12) containing 16 such genes. Taken together, these two blocks account for 34 of the 78 private-enriched genes in this population. Likewise, for the TEX population, there is a 1.0 Mb (scaffold 6, chromosome 7) region containing 10 genes enriched with private SNPs.

One potential source of introgression is a close sister taxon, the predominantly lake-dwelling D. pulicaria, which can hybridize with D. pulex (Heier and Dudycha 2009; Vergilino et al. 2011; Xu, Spitze et al. (2015); Moy et al. 2021). Introgression from D. pulicaria is known to be associated with the origin of obligately asexual lineages of D. pulex (not included in this study) (Tucker et al. 2013); and a ∼1.2-Mb region at the tip of chromosome 1 conferring an inability to produce males is thought to be derived from D. pulicaria and segregates at low frequencies in some of the study populations Ye et al. (2019).

To evaluate the potential broader incidence of D. pulicaria introgression events, we screened the set of private-enriched genes against the reference genome of D. pulicaria. Although the majority (54%) of private-enriched genes contain no private alleles (SNPs) matching D. pulicaria reference nucleotides, the overall average fraction of private alleles/gene matching unique variants in D. pulicaria (which are, by definition, absent from other D. pulex) is 0.112 ($\mathrm{SE}=0.010$). For 56 of the 284 private-enriched genes, >30% of the private alleles were attributable to D. pulicaria, and 22 of these genes had between 50 and $92\text{\%}$D. pulicaria variants. For the two blocks of BUS private-allele genes noted above, the average fraction of D. pulicaria-like private alleles is 0.33 (0.04) and 0.25 (0.05). Thus, there is little question that some gene-sharing occurs between these two species, although the number of genes involved is a small fraction of the overall genome (<1%), implying that introgression from D. pulicaria is unlikely to be the main cause of the private alleles.

As there is an old report of a D. pulex-obtusa hybrid (Agar 1920), and the two species can coexist in the same pond, we also searched for potential evidence of introgression from D. obtusa, which is more phylogenetically distant from D. pulex than D. pulicaria. The average fraction of private alleles per enriched gene matching D. obtusa reference nucleotides was just 0.068 (0.005), although 13 enriched genes had levels between 0.30 and 0.50. Extending the matching criterion to a private allele being present in both the D. pulicaria and D. obtusa genomes, the mean frequency is reduced further to 0.025 (0.003), with 75% of the private-enriched genes having no alleles matching both species, and only three exceeding $30\text{\%}$ matching. Taken together, given that there are few large blocks of private alleles in any population, these results suggest that a small fraction of private alleles are remnants of rare and old hybridization events, likely involving one or both of these outgroup species, D. pulicaria much more so than D. obtusa.

Site-frequency Spectra

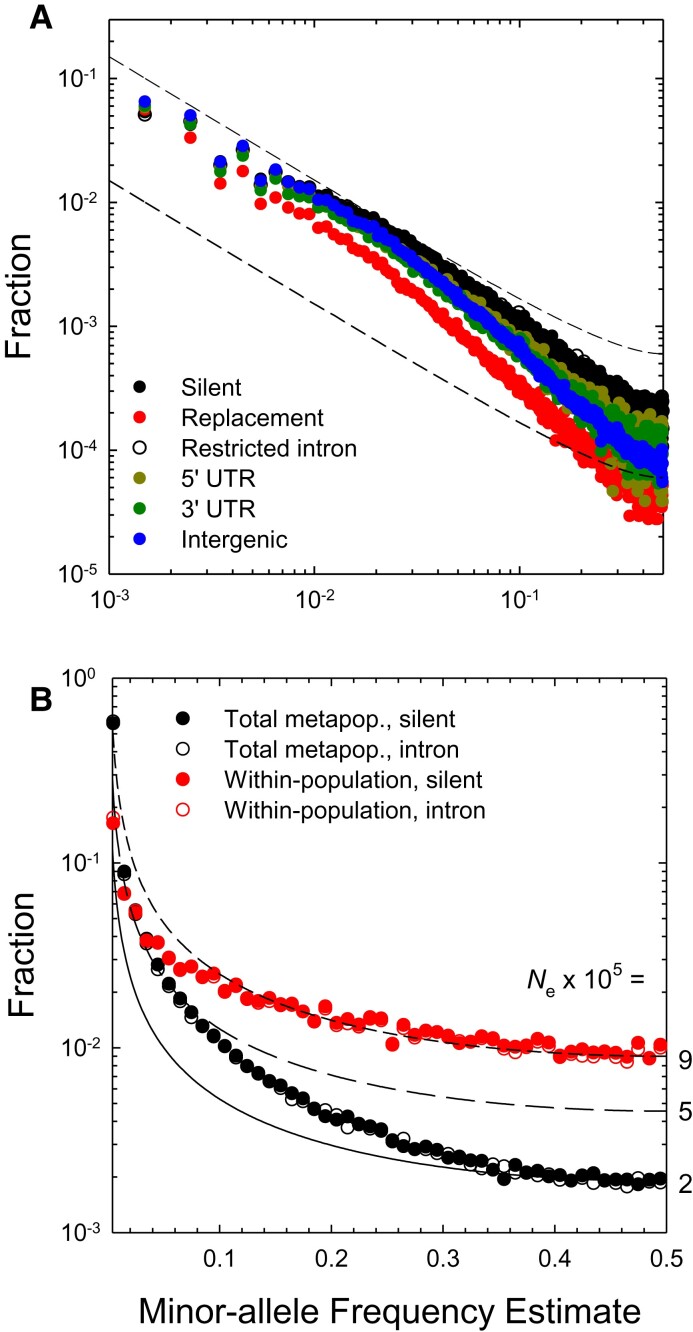
An SFS describes the genome-wide distribution of SNP frequencies. Here, we describe the folded SFS based on MAFs, as we are not yet able to confidently assign ancestral states. Under neutral evolution in a single panmictic population of constant size, the folded SFS is expected to scale as $1/[x(1-x)]$, where x is the minor-allele-class frequency, with the elevation of the SFS being defined by the composite parameter $4N_{e}u$ (Wright 1938; Messer 2009).

With a diploid sample size >800, highly refined SFSs (with frequency class width 0.001) are obtained for the total metapopulation. The SFSs for silent and intron sites are indistinguishable, as expected if they are subject to the same selective forces (or lack thereof) (fig. 4A). All other classes of sites show a more rapid decline of the SFS with increasing MAF, with that for amino-acid replacement sites being most extreme. Notably, even for the putatively neutral sites, the metapopulation SFS does not conform with the expected scaling noted above. Rather, as anticipated from the results in the preceding section, relative to the high-frequency classes ($\mathrm{MAF}>0.1$), there is an excess of low-frequency alleles.

Fig. 4.

(A) Site-frequency spectra at the metapopulation level, obtained by pooling samples from all populations, for various functional categories of genomic sites. The dashed lines denote the expected scaling of the SFS under neutrality for a single panmictic population. The heights of these curves are arbitrarily placed for visual comparison against the observed SFSs, showing that alleles with low to moderate frequencies are in excess of expectations relative to high-frequency alleles. (B) A comparison of silent- and intron-site SFSs at the metapopulation level with the average of the 10 within-population SFSs. Again, lines denote the neutral expectations, in this case for three effective population sizes (given the D. pulex mutation rate) under the assumption of single panmictic populations. The SFS at the metapopulation level is much more strongly bowed than that at the within-population level, which itself is less bowed than expected under the null model.

This contrast becomes most striking when one compares the metapopulation SFS for neutral sites with the average of the within-population SFSs, which necessarily have to be based on wider allele-frequency bin sizes of 0.01 (fig. 4B). Although the scaling of the latter is close to the neutral expectation for $\mathrm{MAFs}>0.1$, there is in this case a deficit of low-frequency alleles. This type of distortion of the SFS is expected in single demes sampled from a subdivided population, as the lowest frequency alleles have typically not had time to spread through the entire metapopulation (e.g., singletons) and hence transiently experience a reduced effective population size (De and Durrett 2007; Städler et al. 2009). However, neutral theory also predicts that depending on the sampling scheme and the migration rate, the SFS for neutral sites in a pooled metapopulation sample should still either scale as $1/[x(1-x)]$, or exhibit a deficit of low-frequency alleles, provided the population is in demographic equilibrium. The strong excess of low- to moderate-frequency alleles at the metapopulation level is inconsistent with this expectation, and may arise because rather than being in demographic equilibrium, D. pulex is still in a phase of metapopulation expansion following the last glaciation (Lynch et al. 2020).

Genomic Regions Exhibiting Excess Population Subdivision

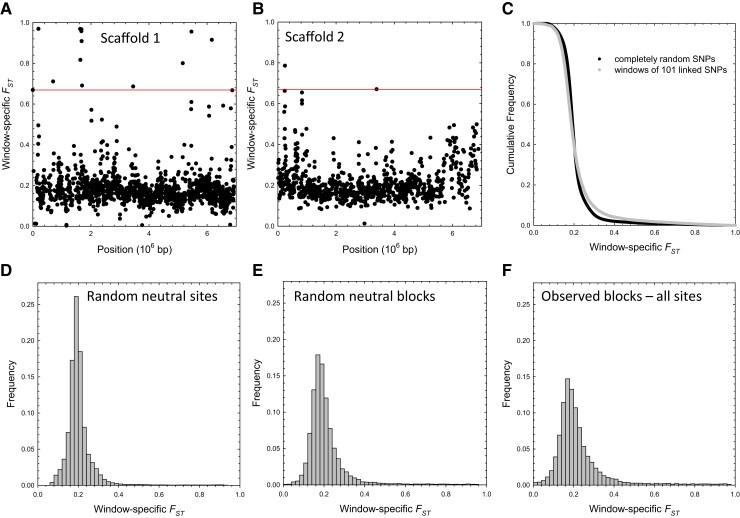
It has been thought that $F_{ST}$ and related statistics are useful for finding signatures of natural selection (Charlesworth et al. 1997; Black et al. 2001; Günther and Coop 2013). However, $F_{ST}$ estimates at individual SNP sites are highly sensitive to sampling error (Weir and Hill 2002), and as noted above, are intrinsically biased downwardly when allele frequencies are low. To minimize both problems in searching for genes with excess among-population divergence, we performed sliding-window analyses of the spatial patterns of $F_{ST}$ along scaffolds, using only sites with metapopulation-wide $\mathrm{MAFs}\ge 0.1$. Calculation of average indices over spatial spans of 101 SNPs allowed the analysis of 19,425 windows. Owing to variation in locations of polymorphic sites, these windows vary in physical length, but still remain quite small, averaging 7.5 ($\mathrm{SD}=9.7$) kb, and containing 0.84 ($\mathrm{SD}=0.75$) genes each. This means that the span lengths employed are sufficiently narrow that windows with outlier $F_{ST}$ estimates almost never encompass more than one or two protein-coding genes. As shown in figure 5A, 5B for the two largest scaffolds, most window-specific $F_{ST}$ estimates are in the range of 0.1–0.3, but there are occasional clusters with much higher values. Only ∼4% of the window-specific $F_{ST}$ estimates exceed 0.50.

Fig. 5.

Window-specific genomic scans of $F_{ST}$, using sites with $\mathrm{MAF}\ge 0.1$. (A,B) Example results for the two largest scaffolds; horizontal red lines denote Bonferroni-corrected cutoffs for the 0.05 probability level for upper outliers. (C) Cumulative frequency distribution of the window-specific estimates compared with the expectations based on random SNPs; the difference is a result of linkage disequilibrium (LD). (D) The genome-wide expected distribution for windows based on neutral (silent and intron) sites alone, under the assumption of global linkage equilibrium. (E) The empirical distribution obtained when only silent sites are used with linkage relationships retained. (F) The empirical distribution based on full sets of SNPs.

As there has been some concern that heterogeneity in background genetic differentiation among different population pairs can confound the identification of outlier genes showing high $F_{ST}$, we carried out similar analyses with the $X^{T}X$ statistic, an $F_{ST}$ analog advocated by Günther and Coop (2013). The $F_{ST}$ and $X^{T}X$ estimates were highly correlated ($r^2=0.80$). As both measures identified similar outlier regions, we conclude that the heterogeneity in genetic differentiation among populations is not a significant problem in this particular study, and confine the following discussion to $F_{ST}$.

In exploratory analyses such as this, there are numerous ways to identify windows with excess among-population divergence relative to null-model expectations (Lotterhos and Whitlock 2015). In obtaining a minimal list of candidate chromosomal regions and genes with excess divergence, here referred to as $F_{ST}$ outliers, simple ranking of estimates is undesirable, as the level of sampling variance is not the same in all windows. Thus, to identify genomic spans with excess $F_{ST}$ relative to the population average, we utilized the empirical distribution of window-specific $F_{ST}$, thereby retaining natural levels of spatial variation in linkage-disequilibrium (LD) and SNP density, while also accounting for the sampling variance of each $F_{ST}$ estimate (Methods).

The approach taken here is conservative for two reasons. First, as the empirical null distribution includes contributions from any outliers, the distance between the global mean $F_{ST}$ and that of any outlier is somewhat downwardly biased. Second, alternative null distributions based on just neutral (silent and restricted-intron) sites expand the physical width of windows relative to the actual distribution based on all sites, and have lower means and variances relative to the actual distribution (figs. 5C–5F), which would expand the list of candidate outliers beyond what we report here. The mean and standard deviation (SD) of the actual distribution of window-specific $F_{ST}$ estimates are 0.224 and 0.131, respectively. Exploration of the distribution of window-specific values based only on neutral (silent and restricted-intron) sites, yields a $\mathrm{mean}=0.210$ and $\mathrm{SD}=0.104$, whereas bootstrapping of random neutral sites across the genome, which eliminates LD, yields a $\mathrm{mean}=0.205$ and $\mathrm{SD}=0.077$. The means of these two neutral distributions differ slightly owing to the weighting scheme used to obtain the window-specific estimates; the difference in SDs between the two neutral distributions indicates that ∼46% of the variance in window-specific values is a simple consequence of LD.

In total, 471 windows (2.4% of the total evaluated) were identified by this method as having significantly elevated $F_{ST}$ (supplementary table S4, Supplementary Material online), with all windows with $F_{ST}>0.672$ meeting the criterion of 5% significance after Bonferroni correction for multiple comparisons (far out on the right tail of the asymmetric empirical distribution; fig. 5F). Of this select group of windows, with average $F_{ST}=0.817$ ($\mathrm{SE}=0.004$), 224 (47.6%) were devoid of protein-coding genes, 192 (40.8%) contained one, 54 (11.5%) contained two, and one (0.2%) contained three, for a total of 224 genes (after accounting for overlap between adjacent windows). This distribution is slightly enriched for gene-free regions, as for the full set of 19,425 windows, the proportions containing 0, 1, 2, and 3 protein-coding genes are 36.6%, 44.1%, 18.4%, and 0.8%, respectively.

Remarkably, of the 439 outlier windows that could be assigned to specific chromosomes, 263 ($59\text{\%}$) reside on chromosome 2. With a length of ∼150 cM (13.4 Mb), chromosome 2 is the third largest of the 12 D. pulex chromosomes, but it is not abnormally large, as the remaining 11 range from 82 to 141 cM (8.3–16.3 Mb) with mean 119 cM (11.1 Mb) (Xu, Spitze et al. (2015)). On this chromosome, long blocks of elevated $F_{ST}$ are present. For example, within positions ∼0.78 to 3.43 Mb on scaffold 8, there are 147 windows with elevated $F_{ST}$, containing a total of 104 annotated genes; and on scaffold 50, positions 0.17–0.96 Mb, there are 59 outlier windows, containing a total of 23 genes. This being said, the average $F_{ST}$ for sites with $\mathrm{MAF}\ge 0.1$ on chromosome 2, 0.3255 (0.0005), is not extraordinarily high, as the highest is 0.3352 (0.0004) for chromosome 6, and the lowest is 0.2440 (0.0004) for chromosome 11 (supplementary table S4, Supplementary Material online). The chromosome-wide estimate of $\pi$ for chromosome 2, 0.0065, is significantly smaller than the average chromosomal value of 0.0077, but its average among-population diversity, 0.0027, is almost identical to the average chromosomal mean of 0.0026 (SEs all $\ll$0.0001). Thus, there is no compelling evidence that chromosome 2 is strongly driving its way through the metapopulation.

Of the 224 protein-coding genes residing in these $F_{ST}$-outlier windows (supplementary table S4, Supplementary Material online), only 2 overlap with the pool of genes significantly enriched with private SNPs. Gene-ontology (GO) analysis provides no compelling evidence of this subset of genes being enriched with any particular set of functions.

Local Adaptation Associated with Protein-coding Genes

To obtain additional insight into the hierarchical pattern of selection influencing functional amino-acid divergence, we calculated ratios of genetic changes per replacement and silent sites for genes at three levels: ${\pi }_N/{\pi }_S$ within populations, ${\varphi }_N/{\varphi }_S$ among populations, and interspecific divergence $d_N/d_S$ between D. pulex and its close congener D. obtusa (supplementary table S5, Supplementary Material online).

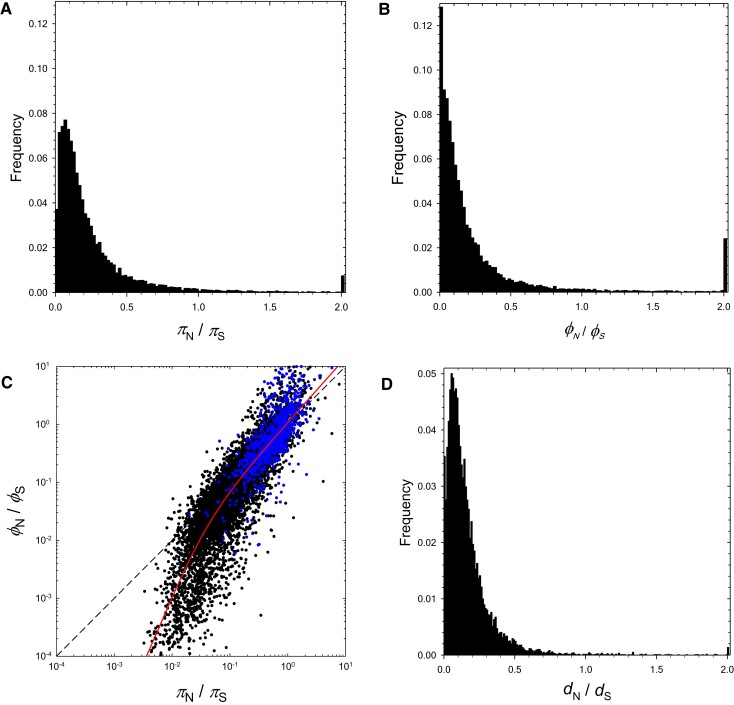
At the within-population level, there is little evidence of balancing selection maintaining variation at the amino-acid level. To reduce sampling-variance problems associated with the generation of extreme values with ratios, we have opted to compute gene-specific ${\pi }_N/{\pi }_S$ using the mean estimates of ${\pi }_N$ and ${\pi }_S$ across populations to determine the ratios, as opposed to taking the mean ${\pi }_N/{\pi }_S$ across populations. (Estimates using both approaches were highly correlated, and the same overall conclusions were reached.) Confining analyses to the 12,898 genes for which there were adequate coverage data for at least four of the populations, the average gene-specific ${\overline{\pi }}_N/{\overline{\pi }}_S$ is 0.267 (0.005), with the distribution having a long tail to the right, a mode of just 0.07, and a median of 0.15 (fig. 6A). Of the total pool of genes with ${\overline{\pi }}_N/{\overline{\pi }}_S$ estimates, 3.3% (422) have values >1.0, but just 119 of these have ${\overline{\pi }}_N$ estimates that exceed ${\overline{\pi }}_S$ by more than two standard errors. Using a one-tailed Z-test followed by Bonferroni correction for multiple comparisons, just 28 of these are deemed to be significant at the 0.05 level, 15 of which are without orthologs in the outgroup D. obtusa, and only 5 of these 15 having apparent orthologs in other metazoans.

Fig. 6.

Distributions of the within- and among-population ratios ${\pi }_N/{\pi }_S$ and ${\varphi }_N/{\varphi }_S$, and the between-species ratio over all protein-coding genes. In (A), (B), and (D), the final peaks to the right are the sums of all ratios exceeding 2.0. In (C), the black and blue points denote, respectively, genes with and without apparent orthologs in the outgroup D. obtusa, and the diagonal dashed line denotes points of equality. The red line is a least-squares fitted function: $\log (y)=0.028+[\log (x)/(0.014+x)]\cdot (0.025+1.12x)$; under this model, $y={\varphi }_N/{\varphi }_S$ scales with the 1.79 power of $x={\pi }_N/{\pi }_S$ when the latter is small, but with the 1.12 power when the latter is large, with the inflection point between the two scalings falling at ${\pi }_N/{\pi }_S=0.014$.

The 1,064 D. pulex genes with no uniquely identifiable orthologs in D. obtusa have an average ${\overline{\pi }}_N/{\overline{\pi }}_S$ of 0.755 ($\mathrm{SE}=0.030$), with a median of 0.56, contrasting dramatically with the remaining genes with outgroup orthologs, which have an average ${\overline{\pi }}_N/{\overline{\pi }}_S=0.223$ (0.004) and a median of 0.14. Most of the genes in the former set have been annotated based on some form of mRNA support (Ye et al. 2017), but this does not rule out the possibility that an absence of significant function is responsible for $46\text{\%}$ of such genes having ${\overline{\pi }}_N/{\overline{\pi }}_S$ within two SEs of the neutral expectation of 1.0. In contrast, only $5\text{\%}$ of genes with D. obtusa orthologs have ${\overline{\pi }}_N/{\overline{\pi }}_S$ estimates consistent with neutrality.

The among-population analyses lead to a very similar conclusion with respect to balancing selection at the metapopulation level. After removing 85 outliers (∼1% of all genes) with ratios >10.0 (likely due to spuriously low estimates of ${\varphi }_S$), the mean estimate of ${\varphi }_N/{\varphi }_S$ is 0.272 (0.006), very similar to the mean ${\overline{\pi }}_N/{\overline{\pi }}_S$ estimate of 0.267. For only 55 ($0.4\text{\%}$ of the total) genes did ${\varphi }_N$ exceed ${\varphi }_S$ by more than two SEs, and none of these (including the outliers) were significant after Bonferroni correction with a one-tailed Z-test. The mean ${\varphi }_N/{\varphi }_S$ for genes with D. obtusa orthologs, excluding those with ratios >10.0, is just 0.220 ($\mathrm{SE}=0.004$), whereas that without such orthologs is 1.035 ($\mathrm{SE}=0.052$), again suggesting that many of the latter genes may be evolving neutrally. The bulk of the distribution of ${\varphi }_N/{\varphi }_S$ is more skewed than that of ${\overline{\pi }}_N/{\overline{\pi }}_S$, with mode $\simeq$0.01, median $\simeq$0.12, and a larger secondary peak to the right (fig. 6B).

Local adaptation is suggested if ${\varphi }_N/{\varphi }_S$ exceeds ${\overline{\pi }}_N/{\overline{\pi }}_S$, as this implies that, relative to synonymous mutations, nonsynonymous changes rise to higher frequencies at the among-population level. Overall, $28\text{\%}$ of genes have ${\varphi }_N/{\varphi }_S>{\overline{\pi }}_N/{\overline{\pi }}_S$, although there is a strong asymmetry. Almost all genes with low ${\overline{\pi }}_N/{\overline{\pi }}_S$ exhibit still lower values of ${\varphi }_N/{\varphi }_S$, consistent with persistent purifying selection, but genes with high ${\overline{\pi }}_N/{\overline{\pi }}_S$ tend to exhibit still higher values of ${\varphi }_N/{\varphi }_S$, consistent with local adaptation (fig. 6C). This suggests that a subset of genes with high levels of ${\overline{\pi }}_N/{\overline{\pi }}_S$, even if below or not significantly different from 1.0, are under some form of local positive selection at the amino-acid sequence level.

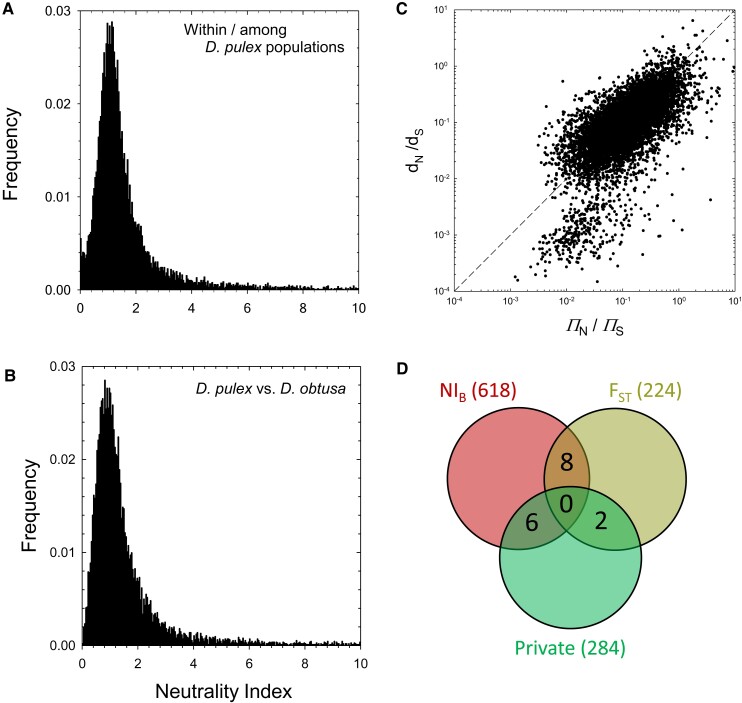
A within-species neutrality index, NI${}_W$, which is the ratio of ${\pi }_N/{\pi }_S$ to ${\varphi }_N/{\varphi }_S$, summarizes this information further (fig. 7A). For the full set of genes in the analysis, mean ${\mathrm{NI}}_W=3.37$ ($\mathrm{SE}=0.13$, $\mathrm{mode}=1.06$, $\mathrm{median}=1.29$), and even after removal of 596 genes with ${\mathrm{NI}}_W>10.0$, the mean is still 1.61 (0.01), again implying that purifying selection is the primary mode of selection at the among-population level. Only seven genes have a ${\pi }_N/{\pi }_S$ estimate that is significantly smaller than ${\varphi }_N/{\varphi }_S$, and none of these are significant after Bonferroni correction in one-tailed Z-tests. Thus, despite the general genome-wide pattern outlined in figure 6C, this very large data set is unable to assign a compelling signal of local adaptation to any individual gene.

Fig. 7.

(A) The distribution of the metapopulation neutrality index, NI${}_W$, for the set of 11,623 protein-coding genes with sufficient coverage data from at least four D. pulex populations; not included in the graph are $5.1\text{\%}$ of all genes with ${\mathrm{NI}}_W\ge 10$ (i.e., under strong purifying selection). (B) The distribution of the between-species neutrality index, NI${}_B$, for the set of 11,652 protein-coding genes with identifiable orthologs in D. obtusa; $3.0\text{\%}$ of all genes have ${\mathrm{NI}}_B\ge 10$. (C) The relationship between $d_N/d_S$ and ${\mathrm{\Pi }}_N/{\mathrm{\Pi }}_S$. (D) A Venn diagram of the outlier genes identified by three different methods.

Protein-coding Genes under Elevated Metapopulation-wide Positive Selection

Daphnia obtusa provides an excellent outgroup for the analysis of the fates of nucleotide variants over longer time scales, as the mean silent-site divergence from D. pulex, 0.1183 ($\mathrm{SE}=0.0004$), is small enough to avoid issues with multiple substitutions per site, while exceeding average ${\pi }_S=0.0148$ in the study populations by a factor of nearly eight (ample time for fixation of nearly all ancestral polymorphisms plus the fixation of de novo mutations). As for the within- and among-population ratios, the distribution of $d_N/d_S$ is highly skewed towards low values (fig. 6D), with a mean value of 0.167 ($\mathrm{SE}=0.003$, excluding 2 estimates >10.0; median 0.118; and mode 0.055). Just 57 genes have $d_N/d_S$ estimates exceeding the neutral expectation of 1.0, with 34 of these exceeding this benchmark at the $P=0.05$ level using a one-tailed Z-test after Bonferroni correction, and 13 of the 34 having no apparent orthologs outside of Daphnia (supplementary table S5, Supplementary Material online).

Although a $d_N/d_S$ ratio significantly greater than 1.0 provides a strong indication of positive selection at the amino-acid level, this is an extremely conservative test, as it ignores the fact that the majority of amino-acid altering mutations are deleterious. A more powerful approach involves a neutrality index comparing within- and between-species diversity, ${\mathrm{NI}}_B=({\mathrm{\Pi }}_N/{\mathrm{\Pi }}_S)/(d_N/d_S)$, where ${\mathrm{\Pi }}_x={\pi }_x+{\varphi }_x$ is the total metapopulation diversity (with $x=N$ or S). This index is expected to take on values <1.0 when there is substantial positive selection for protein-sequence divergence at the between—relative to the within-species level, and values >1.0 when selection is primarily purifying in nature.

The overall distribution of NI${}_B$ (fig. 7B) is fairly similar to that for NI${}_W$, with a mean over all protein-coding genes of 2.61 ($\mathrm{SE}=0.15$; $\mathrm{mode}=0.86$, $\mathrm{median}=1.13$), which declines to 1.32 (0.01) if 348 genes with ${\mathrm{NI}}_B\ge 10$ (under very strong purifying selection) are ignored. Again, the implication is that the preponderance of selection operating on amino-acid altering mutations is purifying in nature. However, of the 11,652 genes in this analysis, 42% have ${\mathrm{NI}}_B<1.0$, 619 of which are significant at the $P=0.05$ level in the one-tailed Z-test after Bonferroni correction, making them candidates for positive selection in one or both species. As with the within-species analysis, genes with low ${\mathrm{\Pi }}_N/{\mathrm{\Pi }}_S$ ratios tend to have still lower $d_N/d_S$ ratios, although the pattern is weaker (fig. 7C).

A GO enrichment analysis of the 619 NI${}_B$-outlier genes provides further insight into the functional categories under the strongest positive, species-wide selection. Here, we focused on GO categories with at least 10 classified genes in the overall genome and with ${\chi }^2$-test significance levels of $P<0.01$ reduced 64-fold to account for the number of independent GO categories that could be evaluated. The end result was 24 partially overlapping categories with functions at various hierarchical GO levels (supplementary table S6, Supplementary Material online). The primary enriched gene categories are associated with: (1) ribosomes, with all but 5 of the highlighted genes encoding for ribosomal proteins, and 15 of the 20 of these being associated with mitochondrial ribosomes; (2) light reception and response (including 5 opsin genes); (3) sterol transport; (4) proteolysis; and (5) transcription initiation. There is almost no overlap of these genes with those highlighted in the $F_{ST}$ and private-allele analyses (fig. 7D).

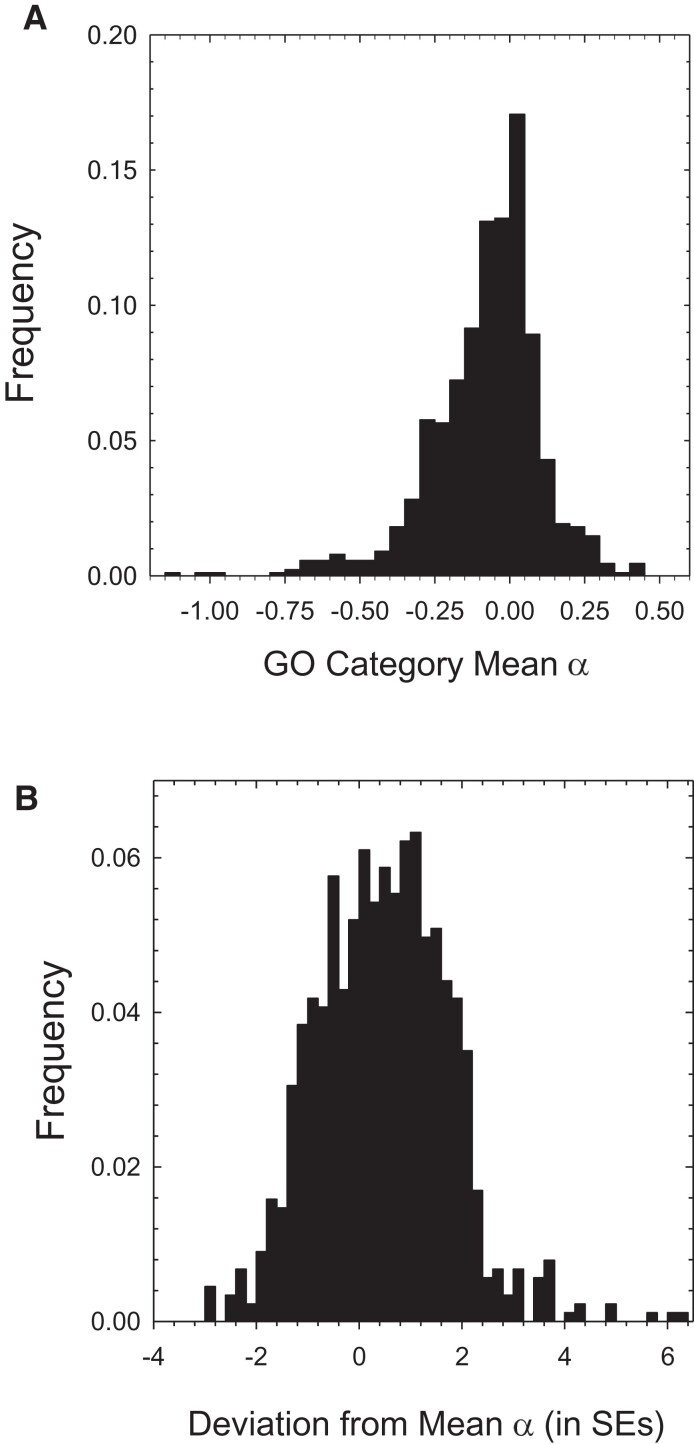
To gain further insight into the functional categories of genes under the most extensive overall positive selection (regardless of the degree of gene enrichment), we estimated the fraction of substitutions at nonsynonymous sites that have been adaptive, α, within GO categories. To this end, we used Stoletzki and Eyre-Walker’s (2011; their eq. 3) modification of the group-specific NI estimator, given as equation (10.9c) in Walsh and Lynch (2018), as this reduces a number of biases that result from single-gene estimators. As the focus here is on metapopulation-wide selection, we used the silent- and replacement-site heterozygosities at the metapopulation level ($\mathrm{\Pi }$) as the reference. Based on 885 groupings of GO-ontology categories, regardless of the ontology level, the mean estimated α is −0.13 (0.01) (fig. 8A; supplementary table S7, Supplementary Material online). Given that α is approximately equal to $1-{\mathrm{NI}}_B$, this negative average is consistent with mean estimates of NI${}_B$ exceeding 1.0 resulting from the presence of segregating deleterious alleles within populations.

Fig. 8.

(A) Distribution of the mean adaptive-evolution index (α) for 885 GO classes of genes. (B) Distribution of the 885 group-specific α estimates measured as a deviation from the mean of the overall distribution in A, each normalized by its sampling standard error.

To focus further on the gene classifications most strongly associated with positive selection, we considered the magnitudes by which the group-specific estimates exceed −0.13 in units of sampling standard errors of α obtained by bootstrapping. Just 56 of the 885 ontology classes (6.3% of the total) exceeded −0.13 by more than two SEs (fig. 8B). Obtaining corrected cutoff values for multiple comparisons is not straight-forward here, as there can be considerable overlap among various GO categories within and among ontogeny levels, that is, the tests are not independent. Given the sample sizes, the critical values for one-tailed Z tests $\simeq$3.6 at all levels, and in this exploratory analysis, we focus on categories for which the group-specific α exceeded the mean by three SEs, which is far to the right of the overall probability mass. This resulted in 21 significant GO terms (2.4%), which after accounting for nesting, yielded seven major categories focused on below, with pooled average α ranging from 0.04 to 0.24 (table 3).

Table 3.

Mean α Estimates for Gene-ontology Categories that are 3.0 SEs in Excess of the Genome-wide Average Across all Categories ($-0.13$).

GO Term	Level	Description	Count	α	SE	Deviation
98,869	4	Cellular oxidant detoxification	72	0.24	0.05	6.87
97,237	5	Cellular response to toxic substance	76	0.23	0.06	6.04
9,636	4	Response to toxic substance	91	0.21	0.06	5.84
16,684	4	Oxidoreductase activity, acting on peroxide acceptor	59	0.16	0.05	5.49
5,840	6	Ribosome	152	0.21	0.07	4.76
6,979	4	Response to oxidative stress	76	0.19	0.07	4.70
44,391	4	Ribosomal subunit	108	0.26	0.09	4.16
37,00	4	DNA-binding transcription factor activity	206	0.12	0.06	4.06
10,035	4	Response to inorganic substance	25	0.38	0.13	3.87
46,906	4	Tetrapyrrole binding	127	0.05	0.05	3.59
5,739	6	Mitochondrion	360	0.04	0.04	3.58
313	7	Organellar ribosome	40	0.34	0.14	3.46
15,934	5	Large ribosomal subunit	66	0.23	0.11	3.46
71,478	5	Cellular response to radiation	25	0.24	0.11	3.45
104,004	4	Cellular response to environmental stimulus	28	0.23	0.11	3.43
40,008	4	Regulation of growth	28	0.19	0.09	3.42
50,909	7	Sensory perception of taste	24	0.20	0.10	3.39
22,626	7	Cytosolic ribosome	74	0.24	0.11	3.39
71,214	4	Cellular response to abiotic stimulus	28	0.23	0.11	3.38
20,037	5	Heme binding	122	0.04	0.05	3.35
19,220	5	Regulation of phosphate metabolic process	90	0.14	0.08	3.23

Note:—There is overlap between some categories owing to the hierarchical nature of the analysis. Level refers to the level in the GO-term hierarchy; count is the number of genes in the category.

The highlighted groupings reveal a fairly cohesive picture. The eight primary clusters of ontology classes (gene members are contained in supplementary table S7, Supplementary Material online) under the strongest apparent levels of positive selection can be summarized as follows: (1) Responses to environmental stimuli, including toxins, stress, and taste. The genes associated with sensory perception and response fall into several classes, among the more prominent being: taste (including glucosyl glucuronosyl transferases, and gustatory receptors); photoreception (G protein-coupled receptors in the rhodopsin family, including uv-sensitive opsins); detoxification (superoxide dismutases, phospholipid-hydroperoxide glutathione peroxidases, and catalases); and neurotransmission (acetylcholine receptors). Also included in this cluster are 20 genes encoding chorion peroxidases. (2) Ribosomes. Consisting primarily of ribosomal proteins, 43% of which are associated with mitochondrial ribosomes. (3) Transcription factors covering a wide range of cellular and developmental functions, including CCAAT-enhancer binding, cyclic AMP response element-binding, forkhead box, homeobox, and steroid hormone-receptor protein components. (4) Heme/tetrapyrrole binding. These include the peroxidases noted above, as well as peroxinectin, and multiple genes for cytochrome P450 (33), globins (12), and methyl farnesoate epoxidase (6). (5) Mitochondria. In addition to the ribosomal proteins noted above, the list here includes genes associated with energy production (e.g., subunits for ATP synthase, cytochrome oxidases, ubiquinones, and NADH deydrogenases), membrane translocation (TIM and TOM complex members), and superoxide dismutase. (6) Growth regulation. This is a relatively small group of 29 genes, but includes plexins and semaphorins used in the guidance of axon growth. (7) Phosphate metabolic processes. These include cAMP-dependent, cyclin-dependent, and numerous other kinases.

Discussion

In terms of within- and among-population sampling, this is one of the largest population-genomic studies ever performed in any organism. By revealing the metapopulation properties for D. pulex at a genome-wide level, the results establish this species as a model for the study of evolutionary and ecological genetic issues in natural populations, expanding our understanding of the system far beyond what was possible a few decades ago (Lynch 1983; Lynch and Spitze 1994). As D. pulex is already one of the favored targets of study by zooplankton ecologists (Kerfoot 1980; Ebert 2008; Lampert 2011), the future goal will be to integrate the molecular-genomic data with quantitative-genetic studies and, ideally, with functional studies at the cellular and developmental levels.

As variation at 4-fold redundant sites in protein-coding genes and restricted intron sites appears to behave in a nearly neutral fashion (Lynch et al. 2017), such genomic positions provide a compelling basis for inferring aspects of population demography and spatial structure. In addition, the relatively large and historically stable effective sizes (Lynch et al. 2020) of the study populations and their moderate level of subdivision minimize the many confounding effects that can thwart the identification of signatures of positive selection. Finally, unlike inbred lines used in downstream analyses involving population-genomic studies of species such as Drosophila, Daphnia isolates can be extracted from natural populations and then maintained clonally in the lab for indefinite periods, thereby minimizing potential issues with recessive deleterious genes in phenotypic studies. Along with the substantial body of baseline data contained herein, these features establish D. pulex as an excellent system for evaluating the molecular basis of evolutionary change and investigating genotype–phenotype relationships in natural contexts.

The Population-genetic Environment

Individual Daphnia populations occupy habitats with discrete boundaries, and in principle experience distinct ecological conditions. In addition, the temporary-pond populations in this study are exposed to brief enough periods of clonal selection that the genotype frequencies at most molecular markers adhere as closely to Hardy–Weinberg expectations (if not more) as most obligately sexual species. Indeed, prior work with temporary-pond D. pulex has shown that such genetic composition is generally maintained throughout the growing season even in the face of substantial selection on quantitative traits (Lynch 1984a, 1984b). On average, the study populations have long-term genetic effective sizes of $N_e\simeq 6\times {10}^5$, with little variation in $N_e$ among them. Although a fine-scale analysis of historical demography suggested an expansion to $N_e\simeq {10}^7$ over the past 2,000–4,000 years (Lynch et al. 2020), such inferred inflation may be partly an artifact of metapopulation subdivision, which increases the incidence of rare SNPs in isolated populations (fig. 4A). As a caveat for future studies of this sort in other species, it is worth noting that this kind of distortion of the SFS would not be visible with sample sizes on the order of 100 or smaller (fig. 4B).

Although the study populations undergo dramatic population-size expansions and contractions during each growing season, they commonly have densities in excess of ${10}^4$ individuals per square-meter (Lynch 1983). With a typical pond being on the order of ${10}^3$ square-meters or more in surface area at peak filling, this means that absolute population sizes, and hence the numbers of targets for mutation, are commonly $>10\times$ greater than $N_e$.

Over a geographic sampling area of $\sim {10}^6$ km${}^2$, the study populations exhibit moderate levels of subdivision, with average $F_{ST}$ across the genome being ∼0.27 if downwardly biased estimates from low-frequency alleles are excluded (and $\simeq$0.13 if included). These estimates are comparable to those obtained with this and other Daphnia species using smaller numbers of markers (including allozymes), all of which fall in the range of 0.12–0.31 (Lynch and Spitze 1994; Morgan et al. 2001; Orsini et al. 2013; Fields et al. 2015). The degree of isolation by distance is weak, with $F_{ST}$ ranging from an average of ∼0.1 to 0.2 between nearly adjacent populations to an average of ∼0.3 for populations separated by 1,000 km, again consistent with prior studies (Lynch and Spitze 1994; Fields et al. 2015). The $F_{ST}$ results, along with an analysis based on private-allele frequencies, imply an average of ∼0.6 migrants per generation/population, equivalent to a migration rate per generation of ${10}^{-6}$. Although these gene-flow estimates assume an equilibrium situation, theoretical work shows that equilibrium $F_{ST}$ is achieved in a relatively small number of generations even if the within- and among-population levels of variation have not yet equilibrated (Crow and Aoki 1984).

By comparison, $F_{ST}$ for the well-studied dipteran Drosophila melanogaster is on the order of 0.01–0.06 among samples within continents, expanding to 0.20–0.30 for intercontinental comparisons (Pool et al. 2012; Lack et al. 2016). Global estimates of $F_{ST}$ for humans are on the order of 0.05 to 0.15 (Akey et al. 2002; Thousand Genomes Project Consortium 2010; Alcala and Rosenberg 2017), depending on the geographic breadth of samples. However, as the fly and human estimates include alleles of all frequencies, which causes downward bias in $F_{ST}$ estimates by a factor of at least 2.0, it appears that the Daphnia study populations are about half as subdivided as the global fly population, while approximating that for the global human population. Of course, the physical distributions of terrestrial species are much more continuous than those for organisms inhabiting lakes and ponds.

These results establish a baseline understanding of what natural selection can accomplish in D. pulex. As a first-order approximation, with the migration rate and the power of drift both being $\sim {10}^{-6}$, mutations with selection coefficients with absolute values $<{10}^{-6}$ will be largely immune to the eyes of natural selection. Given that average values of ${\pi }_N/{\pi }_S,$${\varphi }_N/{\varphi }_S$, and $d_N/d_S$ are all $\ll$1.0, it is clear that the predominant mode of selection operating on amino-acid sequences is purifying in nature, as seen in essentially all studies of other organisms, and implying in this case a substantial fraction of replacement-site mutations with selection coefficients opposing substitution $>{10}^{-6}$. This conclusion is also supported by the differences in forms of the site-frequency spectra for amino-acid replacement vs. silent sites. Nonetheless, a large fraction of genes have $({\pi }_N/{\pi }_S)<({\varphi }_N/{\varphi }_S)$ and/or $({\mathrm{\Phi }}_N/{\mathrm{\Phi }}_S)<(d_N/d_S)$, suggesting that significant numbers of amino-acid altering mutations are promoted at the among-population and/or between-species levels by positive selection.

Targets of Local Adaptation

One of the goals of evolutionary genomics is to identify molecular signatures of various forms of selection, and in particular to identify genes likely to be under strong selection, in hopes of revealing important underlying evolutionary features at the cellular, developmental, and/or ecological levels. With respect to potential local adaptation in individual D. pulex populations, the evidence is quite subtle. On the one hand, there is ∼5% elevation in population subdivision at amino-acid replacement and UTR sites relative to that at silent sites. However, although 224 protein-coding genes were found to reside in windows with $F_{ST}$ significantly elevated above background levels, only 23% of these have ${\mathrm{NI}}_W<1.0$, the overall average NI${}_W$ estimate of 4.6 ($\mathrm{SE}=1.2$) is higher than that for the full genome (3.4), and no $F_{ST}$-outlier gene is an NI${}_W$ outlier (supplementary table S4, Supplementary Material online). Thus, there is no compelling evidence that the genetic loci showing the most substantial overall population subdivision are particular targets of local adaptation. In addition, none of 284 genes deemed to be significantly enriched with private SNPs can be inferred to be under strong local adaptation, given the lack of significant gene-specific NI${}_W$, so the distribution of private SNPs also appears to be uninformative with respect to local adaptation.

This is not to say that D. pulex is not commonly under selection at the proteome level. Substantial evidence based on quantitative-genetic analysis supports the idea that D. pulex populations are under strong selection at the level of body-size and life-history traits, both among populations and across temporal periods within populations (Lynch and Spitze 1994; Lynch et al. 1999). However, it has also been noted that substantial phenotypic shifts often proceed in the absence of significant changes in allele frequencies at the molecular level (Lynch 1984a, 1984b; Pfrender et al. 2000; Pfrender and Lynch 2000). Such decoupling of molecular and phenotypic evolution is consistent with the targets of selection for life-history traits being distributed over large numbers of loci with individually small allelic effects, as often postulated in models of quantitative genetics (Walsh and Lynch 2018).

For traits with this kind of genetic architecture, deciphering the molecular basis of phenotypic change with genome-wide molecular-marker data will be extremely difficult unless sample sizes are far beyond those in this already very large study. The general tendency for genes with high ${\pi }_N/{\pi }_S$ to exhibit still higher values of ${\varphi }_N/{\varphi }_S$ (fig. 6C) provides support for local adaptation. However, the failure to find an enrichment of $F_{ST}$-outlier genes in any particular GO category, combined with the failure to identify any specific positively selected genes with the among-population neutrality index NI${}_W$ again highlights the subtle nature of adaptation. This raises the concern that many prior studies in search of adaptive mutations with sample sizes far below those here may commonly be plagued with issues of false positives, as noted by Bierne et al. (2013) and Flanagan and Jones (2017).

Only one prior Daphnia study (Muñoz et al. 2016) has pursued a genome-wide analysis for outlier gene categories in interpopulation divergence, a study of D. pulicaria populations known in advance to occupy environments with a wide range of nutrient conditions. Although this study invoked among-population divergence enriched for genes associated with metabolism of nucleotides, amino acids, and lipids, the entire study was based on a small fraction of the genome (∼1%) and just 53 individuals. As the conclusions were also drawn from the differential distribution of a small number of SNPs without reference to their coding-sequence context, it is difficult to say if any of the outliers in this study were actually experiencing local adaptation. A geographic survey of genome-wide variation in Daphnia magna is silent on the matter of local adaptation, as only a single individual was surveyed per population (Fields et al. 2022).

Finally, we note that $59\text{\%}$ of windows with elevated $F_{ST}$ in this study reside on chromosome 2, which comprises only $10\text{\%}$ of the genome. The extreme behavior for this chromosome is not caused by private alleles, as just two of the 224 $F_{ST}$ outlier genes are significantly enriched in private alleles. Nor is it associated with genes with unusually high among-population amino-acid sequence divergence, as there are no significant NI${}_W$ outliers. As there is no evidence that chromosome 2 is subject to an unusual degree of introgression or recombination, the unusual behavior of this particular chromosome remains unresolved.

Targets of Species-wide Positive Selection

This study has also provided a basis for ascertaining patterns of gene-sequence divergence on a longer time scale by drawing comparisons to the outgroup D. obtusa The latter species occupies temporary ponds in the same geographic region as D. pulex, often coexisting with it. Here, the GO enrichment analysis on NI${}_B$ outliers highlights a rather different set of genes than the among-population analyses, and in a much more convincing manner. Most notably, the pool of outlier genes associated with positive selection at the between-species level are enriched in categories associated with ribosome structure, mitochondrial bioenergetics, light perception, gustatory reception, detoxification, methylation, and gene regulation (supplementary tables S6 and S7, Supplementary Material online).

Although it is clear that the predominant mode of selection on amino-acid sequences in this species is purifying in nature, our results are in contrast to those of a recent study of Daphnia magna (another temporary-pond dweller), which found little compelling evidence for species-wide adaptive fixation of amino-acid substitutions for any gene (Fields et al. 2022). Although the authors suggest, without explanation, that this unexpected result may be a consequence of the cyclically parthenogenetic life cycle of Daphnia, the average amount of recombination/generation in temporary-pond Daphnia is comparable to, if not higher, than that in other sexual species such as Drosophila melanogaster (Lynch et al. 2017). An alternative interpretation is that reduced statistical power is involved here, as the latter study involved only 36 clones ($\simeq$4% of the sample size in the current study), and relied on quite distantly related outgroup species (with up to $60\text{\%}$ silent-site divergence), which can magnify uncertainty in $d_N/d_S$ ratios.

Only $2\text{\%}$ (14) of the between-species outlier genes were highlighted in any of the among-population analyses, and in no case with more than one of the latter methods, illustrating that even with data from >800 genotypes and 10 populations, within-species measures of differentiation among subpopulations provide little insight into issues of longer-term divergence, at least in this species. Even if measures of among-population divergence are reliably flagging genes undergoing the most extreme levels of local adaptation (which is contradicted by the internal inconsistency of the three methods), adaptive divergence at the interspecific level appears to involve dramatically different cellular components and biological processes than that at the level of population differentiation. A similar conclusion was reached in a study with D. melanogaster (Langley et al. 2012), although in this case genes highlighted at the level of between-species divergence had functions associated with reproduction, neuromuscular activity, and small-molecule binding, a very different constellation of functions than observed here, although gene regulation is highlighted in both Daphnia and Drosophila.

Our more general estimates of the fraction of amino-acid substitution sites under positive selection (α) in different functional gene categories may be downwardly biased by as much as 0.13 by the presence of segregating deleterious mutations within populations, but nonetheless reveal a consistent picture of the primary targets of long-term directional selection in D. pulex, highlighting in particular genes associated with ribosome structure (for both cytosolic and mitochondrial proteins), mitochondrial bioenergetics, environmental sensing and response (including light and gustatory reception, and detoxification), and growth regulation. Notably, a very substantial fraction of the protein products of these nuclear-encoded genes function within mitochondria, the key locale of energy production by oxidative phosphorylation. For example, ∼75% of the ribosomal protein-coding genes designated as NI${}_B$ outliers for positive selection are addressed to mitochondrial ribosomes, and a number of components of the complexes for ATP synthase, electron-transport chain proteins, inner- and outer-membrane translocases (TIM and TOM), ATP transporters, and superoxide dismutase have ${\mathrm{NI}}_B\le 0.4$, far below the proteome-wide mode.

Of the 618 protein-coding genes designated as candidates for positive selection based on NI${}_B$ estimates, 48 (∼8%) encode for products designated to the mitochondrion, and of these 18 are ribosomal proteins, 11 are membrane proteins, and 10 are associated with ATP production. Taken together this group of 48 mitochondrial protein outliers has a mean ${\mathrm{NI}}_B=0.30(0.13)$, which implies $\alpha =0.70$ (or 0.83 if the expected bias is applied). Of course, by their very nature outlier-analyses will always identify some extreme values, as the cutoff values for significance are arbitrary, but these exploratory analyses suggest that the mitochondrial proteome has been undergoing substantial remodeling in D. pulex, D. obtusa, or both species. These observations are concordant with prior work implying elevated rates of evolution in nuclear-encoded mitochondrial proteins (Pietromonaco et al. 1986; Barreto and Burton Barreto and Burton 2013; Barreto et al. 2018), putatively resulting from coevolutionary pressure induced by elevated rates of mutation in the mitochondrion. Estimates of the base-substitution rate in Daphnia mitochondrial genomes are 40–$100\times$ higher than those in the nuclear genome (Xu et al. 2012; Keith et al. 2016; Ho et al. 2020), consistent with this possibility.

Taken together, these results suggest that energy generation, protein assembly, and environmental sensing are among the strongest targets for long-term positive selection in Daphnia genomes. This is not too surprising, given that Daphnia populations are almost always food limited to some extent, filter-feed 24 h per day, even undergoing vertical diel migration in search of food in predator-free environments, and are well known for their phenotypic, behavioral, and life-history plasticity responses to environmental cues (Lampert 2011). Most Daphnia populations undergo annual numerical boom-and-bust cycles, and experience substantial short-term changes in the qualitative composition of the food supply, the presence of size-selective predators, and alterations in chemical and physical factors (including oxygen concentration, pH, and temperature). Less clear, however, is why the sets of genes associated with these presumably conserved functions are under relatively strong positive selection for amino-acid sequence changes, as opposed to being under strong purifying selection for pre-existing refinements.

Materials and Methods

Sample Preparation and Sequencing

We randomly collected D. pulex individuals from 10 temporary ponds that had refilled in early 2013 or 2014. The locations are distributed across the midwestern United States into southern Canada (supplementary table S1, Supplementary Material online). As in Lynch et al. (2017), to maximize the likelihood that each individual would originate from a unique resting egg, we collected hatchlings in the early spring before the occurrence of subsequent reproduction. Individual isolates were clonally isolated in the laboratory for two to three generations, and from these pools, DNA was extracted from 96 isolates per population, with each prepared into a library using a Bioo or Nextera kit, followed by tagging with unique oligomer barcodes. Pooled sequencing then involved paired-end short (100 or 150 bp) reads using the Illumina NextSeq 500 or HighSeq 2500 platform as previously described (Lynch et al. 2017).

Data Preparation

From the FASTQ files of sequence reads, we prepared nucleotide-read quartets (counts of A, C, G, and T) necessary for the population-genomic analyses, taking various filtering steps to process high-quality data. After trimming adapter sequences from the reads with Trimmomatic (version 0.36) (Bolger et al. 2014), the reads were mapped to the PA42 reference genome (version 3.0) (Ye et al. 2017), derived from one of the study populations (PA). Novoalign (version 3.02.11) (http://www.novocraft.com/) was applied with the “-r None” option to exclude reads mapping to more than one location. To reduce the mapping time, we split the FASTQ files using NGSUtils (version 0.5.9) (Breese and Liu 2013), mapped them separately to PA42, and combined the resulting SAM files using Picard (version 2.8.1) (http://broadinstitute.github.io/picard/). The SAM files of the mapped reads were converted to BAM files using Samtools (version 1.3.1) (Li et al. 2009). Marked duplicates and locally realigned indels in the sequence reads were stored in the BAM files using GATK (version 3.4-0) (McKenna et al. 2010; DePristo et al. 2011; Van der Auwera et al. 2013) and Picard. In addition, we clipped overlapping read pairs by applying BamUtil (version 1.0.13) (http://genome.sph.umich.edu/wiki/BamUtil), and made mpileup files from the processed BAM files using Samtools. The final file of nucleotide-read quartets for all individuals, called a pro file, was obtained using the proview command of MAPGD (version 0.4.26) (https://github.com/LynchLab/MAPGD).

Even after all of the above filtering steps, numerous sources of errors may remain in population-genomic data sets. For example, poor fits of data at a site can result when some sequence reads mapping to a site are actually derived from paralogs not found in the genome assembly. Thus, to minimize the use of potentially mismapped reads, we eliminated sites with nonbinomial deviations in read distributions using a goodness-of-fit test (Ackerman et al. 2017), when the latter identified $\ge$4 deviant individuals. To further refine the data, we removed also clones with mean coverage over sites $<3\times$, and clones with a sum of the goodness-of-fit values across the genome $<-0.4$, which can happen, for example, if a clone is contaminated with another clone. In addition, to avoid the chance inclusion of closely related individuals (e.g., pairs of full sibs that might have hatched from a single resting egg), we estimated the pairwise relatedness of clones using the relatedness command of MAPGD (Ackerman et al. 2017; supplementary text S1, Supplementary Material online) and kept only the clone with the highest coverage in any cluster with relatedness estimate $\ge$0.125. Furthermore, to avoid including obligately asexual clones that can sporadically appear in some populations, we searched for diagnostic asexual-specific alleles (Tucker et al. 2013; Xu, Spitze et al. (2015)), and excluded clones in which this fraction $\ge$0.03. Moreover, we screened clones using a set of Daphnia pulicaria-specific markers generated by Ye, Williams, et al. (2021) to identify clones with this potential ancestry, but this led to no further clone removal. The resulting total numbers of analyzed clones for each population are shown in supplementary table S1, Supplementary Material online.

Prior to final analyses, we further refined the data by removing sites associated with putatively repetitive regions identified by RepeatMasker (version 4.0.5) (www.repeatmasker.org/) using the library (Jurka et al. 2005) made on August 7, 2015. In addition, we set population-coverage (sum of depths of coverage over the clones) cutoffs to avoid analyzing problematic sites (supplementary table S1, Supplementary Material online). Finally, to remove false-positive gene models, we used Orthofinder (Emms and Kelly 2019) to determine orthologous genes between PA42 v4.2 and the latest D. pulex annotation from NCBI (https://www.ncbi.nlm.nih.gov/genome/annotationeuk/Daphniapulex/100/), only retaining gene models contained within the NCBI annotation in downstream analyses. After the completion of all of these filtering steps, allele and genotype frequencies in each population were estimated with the maximum-likelihood (ML) method of Maruki and Lynch (2015) using the allele command of MAPGD, and as a final precaution, sites with ML error-rate estimates >0.01 were removed.

In summary, the data preparation and utilization (supplementary text S1, Supplementary Material online) are conservative with respect to both individuals and sites. We removed individuals that were potentially contaminated in the lab, had close relatives in the population sample, or were obligately asexual. Sites that were associated with paralogous sequences and/or recent mobile-element insertions or were revealed by read distributions to have mapping issues were removed as well. In the end, 17–28% of the genomic sites were removed by these filters in each population.

Private Alleles

We identified the total subset of private alleles (Slatkin 1985) unique to single populations, as well as those that had higher frequencies than expected by chance conditional on the total frequency in the metapopulation. Letting $p_M$ denote the minor-allele frequency for a particular SNP over the total metapopulation, then assuming that alleles are randomly and independently drawn from the metapopulation with no structure, the probability of obtaining a private allele in a sample by chance is

$$P_p=\{1-(1-p_M{)}^{n_f}\}\cdot (1-p_M{)}^{n_o},$$

where $n_f$ and $n_o$ are numbers of the allele sampled in the focal population and the other populations, respectively. This analysis was performed for each of the 10 focal populations. The sample sizes were calculated as the effective numbers of sampled chromosomes to account for variation in read numbers in different individuals (Maruki and Lynch 2015); specifically, the effective number in each individual was calculated as $2-(1/2{)}^{x-1}$, where x is the depth of coverage in the individual. We further restricted this analysis to sites for which the effective number of sampled chromosomes was at least 20 for each population. To take the multiple-testing problem into account, we partitioned the analyses into bins of $p_M$ with $\mathrm{width}=0.01$, and attempted to eliminate false positives by Bonferroni correction such that the critical 0.05 probability cutoff was diminished by dividing by the total observed number of private alleles in the bin. To infer the contribution of introgression from closely related species to the observed private alleles in genes significantly enriched with private alleles, we aligned reference sequences of D. pulicaria (LK16) and D. obtusa to PA42.4.2 using LAST (version 1066) (Kielbasa et al. 2011) and examined the fractions of private alleles matching reference nucleotides for D. pulicaria (LK16), D. obtusa, or both of these species.

Estimation of Wright’s Fixation Indices

Wright’s (1951) fixation indices were estimated from the genotype-frequency estimates at SNP sites derived with the method of Maruki and Lynch (2015), restricting analyses to sites that were significantly polymorphic in at least one of the populations at the 5% level. The framework of Weir and Cockerham (1984) was used to obtain site-specific estimates of $F_{IT}$ (inbreeding coefficient in the metapopulation), $F_{ST}$ (genetic differentiation among populations), and $F_{IS}$ (mean inbreeding coefficient within populations), as described in Weir (1996).

The method of Weir and Cockerham was designed for estimating fixation indices from accurate genotypes with no missing data. However, for data generated by high-throughput sequencing, depths of coverage vary among sites, individuals, and chromosomes within diploid individuals, so adjustments are needed to account for variability of sample sizes. We did so by estimating the effective number of sampled individuals ($n_{ei}$) for which both chromosomes are sequenced at least once (Maruki and Lynch 2015) at each site within each deme. For deme $i,$

$$n_{ei}={\displaystyle \sum _{j=1}^{n_i}}\{1-(1/2{)}^{X_j}\},$$

where $n_i$ and $X_j$ are the number of sampled individuals in deme i and depth of coverage in individual j, respectively. We required that $n_{ei}$ be at least 10 in each deme. Letting $r_e$ denote the number of demes that satisfied this condition, the fixation indices were estimated by substituting $n_{ei}$ and $r_e$ for the numbers of sampled individuals in deme i and the number of demes, respectively, in the Weir and Cockerham equations.

Estimation of $X^{T}X$

Because we analyze multiple populations with different degrees of genetic differentiation among different population pairs, we also estimated $X^{T}X$ (Günther and Coop 2013) at the SNP sites. This $F_{ST}$ analog quantifies the genetic differentiation among populations taking its heterogeneity among different population pairs into account. We used Bayenv2.0 (Günther and Coop 2013) to estimate $X^{T}X$. We prepared the input file of allele counts using the method of Maruki and Lynch (2015). Because the software requires the allele-count data in all of the analyzed populations with two segregating alleles in the metapopulation, we analyzed only sites with such data. We estimated the covariance matrix of the allele-frequency estimates based on 100,000 Markov chain Monte Carlo (MCMC) iterations. We ran 10,000 MCMC iterations to estimate $X^{T}X$ at each site, which we found to yield estimates very similar to those based on 100,000 iterations on the largest scaffold (results not shown).

Analyses of Pairwise $F_{ST}$ Estimates

To examine the relationship between geography and genetic differentiation between populations, we built a neighbor-joining tree (Saitou and Nei 1987) based on the mean pairwise $F_{ST}$ estimates, using the MEGA X package (Kumar et al. 2018). Physical distances between populations were inferred from the geographic coordinates of the sampling sites using the R package geosphere (version 1.5-7) (Hijmans 2017). Statistical significance of the association of geographic and genetic distances was evaluated by distance-based Moran’s eigenvector map analysis of the relationship between the sampling locations and mean pairwise $F_{ST}$ estimates (Legendre et al. 2015; Borcard et al. 2018) using the R packages adespatial (version 0.3-14) (Dray et al. 2021) and vegan (version 2.5-7) (Oksanen et al. 2020).

Sliding-window Analyses of the $F_{ST}$ Estimates

Because the $F_{ST}$ estimates measured at individual SNP sites are highly variable (Weir and Hill 2002), we carried out sliding-window analyses of the estimates to examine their spatial patterns along the scaffolds. Each of the nonoverlapping windows contained a fixed number of 101 consecutive SNPs with minor-allele frequency estimates in the metapopulation $\ge$0.1 to avoid bias (as described in the text). To minimize the sampling variance, the window-specific means used as weights the reciprocal of the sampling variance of $F_{ST}$ estimates at each site (Weir and Hill 2002). In the very rare event of an $F_{ST}$ estimate being equal to 1.0, we used the sum of the effective number of sampled individuals over populations as the weight, as the sampling variance is otherwise equal to zero at such sites.

To identify the most statistically significant outliers among the window-specific $F_{ST}$ estimates, we used the actual empirical distribution of the window-specific $F_{ST}$ values to set cutoff values for significance. Here, we reasoned that windows with different $F_{ST}$ values may derive from different subdistributions, and then evaluated the degree to which their $F_{ST}$ estimate exceeded the mean of the overall distribution in units of standard deviations, using a t-like statistic,

$$t=\frac{{\hat{F}}_{ST}-{\overline{F}}_{ST,n}}{\sqrt{\text{Var}(F_{ST,n})+\text{Var}({\hat{F}}_{ST})}},$$ (1)

where ${\overline{F}}_{ST,n}$ and $\text{Var}(F_{ST,n})$ are the mean and the variance of the overall distribution of window-specific $F_{ST}$ estimates, and ${\hat{F}}_{ST}$ and $\text{Var}({\hat{F}}_{ST})$ denote an estimated window-specific $F_{ST}$ and its sampling variance (the squared standard error). To account for multiple comparisons, we binned the window-specific $F_{ST}$ estimates in categories of width 0.05, for example, ${\hat{F}}_{ST}=0.50$–$0.55$, and then used a right-tailed t distribution cutoff consistent with probability level $0.05/N$, where N is the number of windows in the bin (N typically being on the order of 100 in this study). With this method, windows with higher mean $F_{ST}$ estimates are more likely to be accepted as outliers, but only to an extent that depends on their sampling error.

Analysis of Selection on Coding-region DNA

To infer the form of natural selection operating on the amino-acid sequences of protein-coding genes, we estimated diversity at synonymous and nonsynonymous sites, ${\pi }_S$ and ${\pi }_N$, for each gene within each population, as well as the ratio ${\pi }_N/{\pi }_S$. For any particular site in a particular population, $\pi$ is simply estimated as $2\hat{p}(1-\hat{p})$, where $\hat{p}$ is the minor-allele frequency estimate. To minimize spurious behavior of ratios of estimates, the final gene-specific estimates of ${\pi }_N/{\pi }_S$ were obtained using metapopulation-wide means in the numerator and denominator. The sampling variances of gene-specific mean ${\pi }_S$ and ${\pi }_N$ were obtained by dividing the variance of population-specific estimates by the number of populations, and the sampling variance of ${\pi }_N/{\pi }_S$ was then obtained by use of the Delta-method equation for the variance of a ratio [A1.19b, in Lynch and Walsh (1998)]. In addition, the framework of Weir and Cockerham (1984) provided the difference between diversity estimates at the metapopulation level and the averages within populations, yielding estimates of among-population diversities for each site in each gene, which we denote as ${\varphi }_N$ and ${\varphi }_S$. Gene-specific estimates of ${\varphi }_N$ and ${\varphi }_S$ estimates were calculated by averaging over all sites within genes, and their standard errors were again estimated with the Delta-method formulation.

To estimate between-species divergence, we estimated for each protein-coding gene $d_N$ and $d_S$, respectively the mean numbers of nucleotide substitutions per nonsynonymous and synonymous sites, by drawing comparisons with orthologous genes contained within the closely related outgroup species Daphnia obtusa. We mapped sequence reads of D. obtusa to PA42 (version 4.2) using BWA-MEM (version 0.7.17) (https://arxiv.org/abs/1303.3997) and called genotypes using HGC (Maruki and Lynch 2017), setting the minimum and maximum coverage cutoff values at 6 and 100, respectively, and requiring the error-rate estimate $\le 0.01$. To avoid analyzing sites with mismapped nucleotide reads, we again excluded sites involved in putatively repetitive regions identified by RepeatMasker, and also made further restrictions on the use of D. pulex genome sites as noted above. Codons containing undetermined nucleotides, gaps, and more than one nucleotide difference between species and stop codons were removed from the alignments. $d_N$ and $d_S$ estimation was then restricted to genes with alignments consisting of at least 300 sites, using an algorithm that calculates potential numbers of replacement and silent sites (Hedrick 2005) in units of codons weighted by allele frequencies in the D. pulex population, yielding divergence estimates similar to those by PAML (Yang 2007). For each gene, $d_N$ and $d_S$ were estimated as the mean divergence estimates across all populations, applying Jukes and Cantor’s (1969) method. Then, gene-specific $d_N/d_S$ estimates were obtained as the ratio of mean $d_N$ and $d_S$ estimates over populations, and the variance of the ratio was again calculated using the delta method. Further information on statistical procedures associated with nucleotide-sequence variation and divergence are provided in the supplementary text S2, Supplementary Material online. Note that for these analyses, we relied upon sequences mapped to a more recently refined assembly of the PA42 genome (version 4.0; Ye, Jiang, et al. 2021).

Estimation of Mean α per Gene-Ontology Term

To identify candidate GO terms under positive selection, we estimated the fraction of substitutions at nonsynonymous sites that have been adaptive, α (Smith and Eyre-Walker 2002), for each of the GO terms in PA42.4.2 that are at category levels 4–7, where the categories were assigned to the GO terms in the ascending order starting from 1 for the three basic terms (biological process, cellular component, and molecular function) by a custom script. Equation (3) in Stoletzki and Eyre-Walker (2011), which is shown as equation (10.9c) in Walsh and Lynch (2018), was used to estimate the neutrality index (NI) (Rand and Kann 1996) and $\alpha (1-\mathrm{NI})$ for a GO term using divergence and metapopulation-wide heterozygosity estimates in genes associated with the GO term, excluding GO terms associated with fewer than 30 genes in PA42.4.2. Category-specific α and its sampling variance were estimated by a custom program with 1,000 bootstrap replications.

Enrichment Analysis of Gene-Ontology Terms in the Outlier Genes

To infer the functions of outlier genes, we found GO terms (Ashburner et al. 2000) associated with each of the genes in PA42.4.2, using a procedure analogous to that described in Ye et al. (2017). To find GO terms enriched in each type of outlier genes, we carried out enrichment analysis of the GO terms by a ${\chi }^2$-test using the Perl module Statistics::ChisqIndep (https://metacpan.org/pod/Statistics::ChisqIndep). To reduce redundancy among GO terms enriched in outlier genes, we removed GO terms when at least 80% of the associated genes are also found to be associated with another GO term with a larger number of associated genes.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.

Data Availability

The FASTQ files of the raw sequencing data are available at the NCBI Sequence Read Archive (accession numbers PRJNA351263 and SRP155055). FASTQ files of the D. obtusa sequence reads are available at the NCBI SRA (accession number SAMN12816670), and the D. obtusa genome assembly is available at the NCBI GenBank (accession number JAACYE000000000). The D. pulex genome assembly PA42 v4.2 is available at GenBank under accession GCA_911175335.1. The D. pulicaria genome assembly LK16 is available at the NCBI GenBank (accession number SAMN17106781). C++ programs for analyzing population structure (PSA) and finding private alleles (FPA) are available at https://github.com/Takahiro-Maruki/PSA and https://github.com/Takahiro-Maruki/FPA, respectively. The input files for these programs can be made using GFE_v3.0, available at https://github.com/Takahiro-Maruki/Package-GFE.