Using a novel two-stage strategy to characterize the spatial distribution of associations between temperature and COVID-19: A case study in the continental United States

Abstract

Background

Numerous studies have studied the association between daily average temperature (DAT) and daily COVID-19 confirmed cases, which show considerable heterogeneity, even opposite results, among different regions. Such heterogeneity suggests that characterizing the association on a large area scale would ignore the local variation, even obtain false results in some local regions. So, characterizing the spatial distribution of heterogeneous DAT-COVID-19 associations and exploring the causes plays an important role on making temperature-related region-specific intervention measures and early-warning systems.

Methods

Aiming to characterize the spatial distribution of associations between DAT and COVID-19 confirmed cases in the continental United States, we proposed a novel two-stage strategy. In the first stage, we used the common stratified distributed lag nonlinear model to obtain the rough state-specific associations. In the second stage, conditional autoregression was used to spatially smooth the rough estimations. Furtherly, based on the idea, two modified strategies were used to investigate the time-varying associations and the modification effects derived from the vaccination campaign.

Results

Around one-third of states exhibit no significant association between DAT and daily confirmed COVID-19 cases. Most of the remaining states present a low risk at low DAT and a high risk at high DAT, but several states present opposite associations. The average association curve presents a ‘S’ shape with positive association between −8 – 18 °C and keeping flat out of the range. An increased vaccination coverage rate will increase the risk when DAT < 12 °C, but slightly affect the risk when DAT > 12 °C.

Conclusion

A considerable spatial heterogeneity of DAT-COVID-19 associations exists in America and the average association curve presents a ‘S’ shape. The vaccination campaign significantly modifies the association when DAT is low, but only make a slight modification when DAT is high.

Graphical abstract

1. Introduction

Coronavirus disease 2019 (COVID-19), caused by severe acute respiratory syndrome coronavirus 2 (SARS-COV-2), is a novel contagious disease transmitted through droplets or direct contact (Fwca et al., 2020; Lai et al., 2020). Since the first case was discovered in Wuhan, China in December 2019 (WHO, 2020), it has spread across >200 countries and regions. As of March 8, 2022, the worldwide prevalence of COVID-19 epidemic had been more than two years, then almost all countries and regions had experienced two complete seasonal cycles, with a total of 447,149,230 confirmed cases and 6,025,164 deaths reported worldwide (WHO, 2022). At present, the cumulative number of confirmed cases is still increasing at a rate of >1,000,000 each day. Due to the strong infectivity (Lotfi and Rezaei, 2020), COVID-19 has brought and is bringing heavy burdens in terms of physical and mental health as well as economics.

It is well-acknowledged that temperature is one of the key factors affecting the spread of infectious diseases (Chan et al., 2011a; Bi et al., 2010). For example, high temperature can increase or decrease the survival time of viruses on the surface (Casanova et al., 2010; Chan et al., 2011b; Doremalen et al., 2013), and also can change human behaviors which may accelerate or inhibit the person-to-person spread of viruses (Bélanger et al., 2009). Therefore, exploring the association between temperature and the spread of COVID-19 will assist to understand the regularity of the epidemic, develop early warning systems, and make appropriate public health intervention measures according to the change of temperature. Currently, based on the daily confirmed cases, many researchers have adopted the commonly used time-series regression to characterize this association, but the results are distinctive in different countries and regions. A study across 279 prefecture-level cities in China (Lin et al., 2022) shows that a high daily average temperature (DAT) is associated with an increased number of daily confirmed cases when DAT is above −7 °C. A study across 153 countries (Liu et al., 2022) shows a positive relationship at low DAT, but a negative relationship at high DAT. A study in Brazil (Prata et al., 2020) shows an approximately negative linear association in the range from 16.8 to 25.8 °C, and then the association becomes positive or flat when DAT is above 25.8 °C. A study across 188 countries (Yuan et al., 2021) shows a negative association. Ai et al.'s study (Ai et al., 2022) shows that the infection risk of COVID is highest at DAT below 5 °C in the Northern Hemisphere and at around 15 °C in the Southern Hemisphere, respectively. As such, different studies show different, even completely opposite, results. In Table 1 , we summarized some representative related studies including the studied methods, results, and the length of time series. Getting insight into the reason for heterogeneity, most studies utilized time-series data with short length of less than one year, which may lead to an unstable estimate. The more likely reason is that the associations between DAT and COVID-19 are different in themselves across different countries and regions, since the region-specific factors, such as economic level, health condition, humidity, and rainfall, may modify the association, which has been shown in many previous studies (Qi et al., 2020a; Sarmadi et al., 2021; Khan et al., 2022; Ym and Il, 2021). Besides, since the outbreak of COVID-19, some intervening measures, e.g., the vaccination campaign and social restrictions, are gradually imposed by the government, which may also give rise to the heterogeneity not only in spatial dimension, but also in temporal dimension.

Table 1.

The associations between DAT and daily confirmed COVID-19 cases showed by some previous studies.

Studied regions	Length	Methods	Association
9 counties and cities (He et al., 2021)	< 6 months	Stratified GAM	Positive in most countries and regions
Brazil (Prata et al., 2020)	< 3 months	GAM	Negative when 16.8 < DAT < 25.8 °C; Positive or flatten when DAT > 25.8 °C
279 cities China (Lin et al., 2022)	< 3 months	GAM	Positive when DAT > −7 °C
153 countries (Liu et al., 2022)	< 6 months	GAM + Meta	Positive at low DAT. Negative at high DAT
188 countries (Yuan et al., 2021)	1 year	GAM/DLNM	Negative
Mainland China (Qi et al., 2020b)	< 3 months	GAM	Negative
122 cities in China (Xie and Zhu, 2020)	< 3 months	GAM	Positive when DAT < 3 °C; Flatten when DAT > 3 °C
8 counties (Ai et al., 2022)	1 year	DLNM	Highest risk at DAT < 5 °C in the Northern Hemisphere. Highest risk at around 15 °C in the Southern hemisphere. High temperature does not reduce risk in most countries.
4 states in America (Zhou et al., 2022)	6 months	DLNM	No significant association is found
Worldwide (Yan et al., 2022)	1 year	GAM	U-shaped association
12 cities in Italian (Fong and Smith, 2022)	2 years	DLNM + Meta	Inverted U-shaped association with peak risk at 15.1 °C
England (Nottmeyer and Sera, 2021)	9 months	DLNM + Meta	A curve with two stationary points, which are at 11.9 °C for high risk and 21.8 °C for low risk
Italy and Spain (Donzelli et al., 2022)	9 months	DLNM + Meta	Low temperature is associated with high COVID-19 risk

Such spatially heterogeneous associations, found in previous studies, suggest that using the total case data across a large area, such as a country or even several countries, cannot reflect the real region-specific associations between DAT and COVID-19, which may provide a false implication for public health intervention in some specific regions. Therefore, it is necessary to study the DAT-COVID-19 relationship at a relatively high spatial resolution. The commonly used method is to adopt a stratified analysis for a specific city as in Zhou et al.'s study (Zhou et al., 2022) and He et al.'s study (He et al., 2021), i.e., the model is independently constructed for each city, which may give unstable estimation and not achieve enough power, especially for the COVID-19 data with short-length time series. The two-stage analytical process (Gasparrini et al., 2012) may be an alternative solution, as in Fang et al.'s study (Fong and Smith, 2022). Specifically, in the first stage, a stratified analysis is used to obtain the region-specific associations. In the second stage, a multivariate meta-analysis is used to pool the estimations. However, such a two-stage strategy assumes an identical strength of autocorrelation among all the regions, which violates the intuitive first law of geography (Tobler, 1970), i.e., two regions closer together have a stronger correlation. Another limitation is that, because spline functions are frequently used to characterize the complex association due to their flexibility in permitting locally different association forms at different spans of temperature, in such case, to make multivariate meta-analysis available, the two-stage strategy is asked to utilize a relative DAT, such as the percentile, to characterize the association when the ranges of DAT vary widely across different regions. Otherwise, the GAMs in some regions will obtain missing estimations (Gasparrini et al., 2012). Such association between relative DAT and COVID-19 will lead to a loss of epidemiological value. In addition, due to the large number of parameters in GAM, the ideal Bayesian spatiotemporal model will cost much computing time, which is usually unacceptable in practical studies. Therefore, it would be of an important academic and epidemiological value to develop an appropriate analytical strategy to characterize the spatial distribution of associations between DAT and COVID-19.

The United States, as the most developed country, is the country with the largest number of accumulative COVID-19 cases worldwide. As of March 8, 2022, a total of 78,634,998 COVID-19 cases have been confirmed and 955, 296 deaths have been reported (WHO, 2022). The COVID-19 epidemic has caused a heavy burden in the United States. With a wide territory around 9.37 million square kilometers and the founding history based on the Federal Republic system, the United States exhibits considerably different natural conditions, culture, economic levels, religious believes, and intervention measures among different states. Therefore, the spatial heterogeneity of the DAT-COVID-19 association may present more intensity.

In this work, aiming to characterize the spatial distribution of associations between daily average temperature and COVID-19 in the continental United States, we proposed a novel two-stage strategy to obtain the state-specific DAT-COVID-19 associations, which may provide an implication for the state-specific public health intervention of COVID-19 in the Unites States. In the first stage, we used a common stratified DLNM to obtain the state-specific associations. In the second stage, the conditional autoregression based on Leroux prior was used to pool the estimates for more stable results. Furtherly, based on the novel two-stage strategy, we introduced the time-varying vaccination-related variables to investigate if (or how) the vaccination campaign modulates the DAT-COVID-19 association. This novel two-stage strategy can also be used for other research regarding characterizing the spatial distribution of exposure-response associations.

2. Data

A total of 49 regions, including 48 native American states and a special district, i.e., District of Columbia, are included in this study. For more clarity in writing and presenting, District of Columbia is deemed as a special state and each state is abbreviated as two capital letters from its full name. The detailed match table and the map location for each state can be seen in Table S1 and Fig. S1, respectively.

2.1. Data collection

From the date when the first case was confirmed until March 8, 2022, the daily number of COVID cases for each state was acquired. The data came from the National Centers for Disease Control and Prevention, retrieved from https://covid.cdc.gov/covid-data-tracker/#trends_dailycases. The daily case data was averaged with a 7-day moving average to lessen the fluctuation of report date. The meteorological variables, including daily average temperature and daily rainfall, were collected from 64,346 monitoring stations, retrieved from https://doi.org/10.7289/V5D21VHZ (Menne et al., 2012). The state-level vaccination-related data, including the percentage of people vaccinated at least one dose (PP1V) and the percentage of people with full vaccination (PPFV), were collected from https://covid.cdc.gov/covid-data-tracker/#vaccination-trends. The county-level population data came from the America's 24th census in 2021, retrieved from https://www.census.gov/.

2.2. Data processing

Because the spatial distributions of population and meteorological monitoring stations are uneven, we adopted a three-step process, based on kriging interpolation and population weights, to obtain a more accurate daily exposure dataset. Specifically, first, we used the ordinary kriging to acquire a high-resolution daily meteorological dataset with 1 km × 1 km grids. Then, the grid values in each county were respectively averaged to obtain county-level daily meteorological datasets. Finally, based on the county-level meteorological values and population, we took a population-weighting average to calculate the daily average meteorological values for each state, as such, the formula can be written as

$$m_{\mathit{i}\mathit{t}}=\frac{{\sum }_{j\mathit{=}\mathit{1}}^{n_{\mathit{i}}}{p}_{\mathit{i}\mathit{j}}{v}_{\mathit{i}\mathit{j}\mathit{t}}}{{\sum }_{\mathit{j}\mathit{=}\mathit{1}}^{{\mathit{n}}_{\mathit{i}}}{p}_{\mathit{i}\mathit{j}}},$$

where m _it is the meteorological value, i.e., DAT or rainfall, for state i at time t. n _i is the number of counties in state i and p _ij is the population in count j in state i. v _ijt is the corresponding meteorological value in count j in state i at time t.

Some other data processing details, e.g., the distribution of meteorological monitoring stations and handling the missing values and unqualified values, can be seen in the supplementary material.

3. Methods

A descriptive analysis, in terms of DAT, vaccination variables, COVID-19 case numbers, was performed. Then a two-stage analytical process was developed to characterize the spatial distribution of associations between DAT and COVID-19. Finally, referring to the idea of the developed two-stage strategy, a time-varying two-stage strategy was used to investigate the modification effect of vaccination on the DAT-COVID-19 association.

3.1. DLNM-LCAR strategy: characterizing the spatial distribution of association

3.1.1. The first stage: DLNM

Firstly, we used a common stratified time-series analysis to obtain the state-specific associations between DAT and daily confirmed COVID-19 cases. Due to the complex non-linear association and considerable lag effects, the commonly used distributed lag non-linear model (DLNM) was selected, which is able to characterize the complex exposure-lag-response relationship by a cross basis constructed by the multiplication of two groups of spline bases in terms of the exposure-response and lag-response relationship, respectively. Considering that the numbers of newly confirmed daily cases usually present a nonlinear tendency over time, a natural cubic spline with respect to time was used to adjust the long-term trend. Besides, the weekend and holidays may affect the public's behaviors, such as the frequency of nucleic acid testing and the intensity of crowd gathering, which will affect the newly confirmed daily cases, so the weekend and holiday effects were adjusted through the form of dummy variables. Due to the strong infectivity of COVID-19, an autoregression term was included in the model to reclaim the independence among errors. The daily rainfall was also included in the model as a confounder. The quasi-Poisson distribution was used to characterize the overdispersion.

For each state, the DLNM is defined as:

$$Y_{\mathit{t}}~\text{quasi}-\text{Poisson}\left(u_{\mathit{t}}\right),$$

$$\mathit{ln}\left(u_t\right)=\alpha +s_1\left({\mathrm{DAT}}_t\right)+s_2\left({\text{rainfall}}_t\right)+s_3\left({\text{time}}_t\right)+\text{Auto}.{\text{term}}_t+{\mathrm{DOW}}_t+{\text{Holiday}}_t,$$ (1)

where Y _t is the number of daily cases at time t for a specific state, with E(Y _t) ≡ u _t. α is the intercept, s ₁(DAT_t), s ₂(rainfall_t), s ₃(time_t), Auto. term_t, DOW_t, and Holiday_t indicate the effects from DAT, rainfall, long-term trend, autoregression term, weekend, and holiday, respectively. For s ₁(DAT_t), s ₂(rainfall_t), s ₃(time_t), and Auto. term_t, a series of various candidate function forms were set, the details can be seen in Tables S2–S5. Previous studies showed that COVID-19 usually has a 0–14 day incubation (Backer et al., 2020; Zaki and Mohamed, 2021), so we selected 14 days as the max lag time. For each candidate function form, we constructed a DLNM and calculate the Bayesian Information Criterion (BIC) for each state. Then the sum of BIC across 49 states was obtained. The final function forms were determined based on a thumb rule that an increased model complexity, measured by df, cannot considerably reduce the value of BIC. Based on the final model, for each state, taking a DAT, such as 12 °C in this study, as reference, we calculated the logarithm of relative risks (log-RRs) and their variances in terms of a series of representative DATs.

3.1.2. The second stage: LCAR

Due to not considering spatial autocorrelation, the state-specific log-RRs estimated in the first stage may not be unstable and present a loss of statistical power, especially for the state with a small population size. Since the work by Besag et al. (1991), the conditional autoregression (CAR) model has been the rule of smoothing risk in disease mapping. To obtain a more accurate state-specific association, i.e., the spatial distribution of associations between DAT and COVID-19 in America, we adopted the CAR model to spatially smooth the estimations in the first stage.

Specifically, for each pre-selected representative DAT, set ${\widehat{\theta }}_i$ as the estimated log-RR referring to the reference DAT in state i, and ${\widehat{\sigma }}_i^2$ as its variance. θ _i is the unknown real value. The CAR model can be written as

$${\widehat{\theta }}_i~N\left({\theta }_i,{\widehat{\sigma }}_i^2\right),$$

$${\theta }_i=\eta +{\xi }_i,$$ (2)

$$\mathit{\xi }~\mathit{MN}\left(\mathbf{0},{\left[\tau \mathbf{W}\right]}^{-\mathbf{1}}\right),$$

where η reflects the average association across all states. ξ _i is the ith element of ξ which measures the spatial heterogeneity. N(.) and MN(.) are the normal distribution and multivariate normal distribution, respectively. τ is the precision parameter. W is a square matrix which reflects the pattern of spatial autocorrelation. By selecting different Ws, different types of CAR model can be specified. In this study, a Leroux-prior-based CAR model, hereafter LCAR model, was used due to its flexibility of considering both the spatial autocorrelation random effect and independent random effect. As such, W in the LCAR model is defined as

$$\mathbf{W}\mathbf{=}\rho \mathbf{R}+\left(1-\rho \right){\mathbf{I}}_{n\times n},$$ (3)

where ρ makes an intensity balance between the spatial autocorrelation random effect and independent random effect. I _n×n is the identity matrix with dimension of n = 49. R is a n × n symmetric matrix with the diagonal elements equal to the number of neighbors around the ith state. For the off-diagonal elements, (R)_ij = − 1 if state i and j are neighbors, (R)_ij = 0 otherwise. The commonly used Integrated Nested Laplace Approximations (INLA) (Lindgren and Rue, 2015; Rue et al., 2009) was used to obtain the smoothed estimation of θ _i.

Note that, for each state, if the objective temperature was outside the range of DAT, the estimated log-RR in the first stage was set as missing due to the lack of extrapolation for the natural cubic spline function. For simplification, this two-stage analytic process was labelled as DLNM-LCAR hereafter.

3.2. Time-varying DLNM-LCAR and spatiotemporal LCAR

Because the association may vary over time, it is also meaningful to characterize the time-varying average associations. Based on the idea of DLNM-LCAR, we introduced the time-varying DLNM to construct a time-varying two-stage strategy, labelled as time-varying DLNM-LCAR. Specifically, in the first stage, for each states, we constructed a time-varying DLNM (Gasparrini et al., 2015) by including a linear interaction between time and the cross-basis variables into Model (1). As such, the time-varying DLNM can be written as

$$\mathit{ln}\left(u_t\right)=\alpha +s_1\left({\mathrm{DAT}}_t\right)+s_2\left({\text{rainfall}}_t\right)+s_3\left({\text{time}}_t\right)+\text{Auto}.{\text{term}}_t+{\mathrm{DOW}}_t+{\text{Holiday}}_t+\left({\text{time}}_t-\mathit{reftime}\right):s_1\left({\mathrm{DAT}}_t\right),$$

where reftime is the objective time at which we want to get the association. By ranging reftime, the associations at different time points are obtained, each of which is defined by the log-RRs at a series of selected representative DATs. In the second stage, for each time point, a LCAR model, like in Section 3.1.2, was be used to pool the log-RRs across states to obtain the time-specific average associations.

Furtherly, to investigate how a predictor modifies the effect, for each level of DAT, a spatiotemporal LCAR with a state-level time-varying vaccination predictor was constructed. Specifically, ${\widehat{\theta }}_{\mathit{it}}$, estimated from the time-varying DLNM, is the log-RR of a certain DAT at time t in state i and ${\widehat{\sigma }}_{\mathit{it}}^2$ is its estimated variance. θ _it is the unknown true value. Then spatiotemporal LCAR can be written as

$${\widehat{\theta }}_{\mathit{it}}~N\left({\theta }_{\mathit{it}},{\widehat{\sigma }}_{\mathit{it}}^2\right),$$

$${\theta }_{\mathit{it}}=\eta +\beta x_{\mathit{it}}+{\xi }_i+{\gamma }_t,$$ (4)

$$\mathit{\xi }~\mathit{MN}\left(\mathbf{0},{\left[\tau \mathbf{W}\right]}^{-1}\right)\mathit{,}$$

$${\gamma }_t\mid {\gamma }_{t-1}~N\left({\gamma }_{t-1},{\sigma }_{\gamma }^2\right),$$

where Leroux prior was also used to characterize the spatial autocorrelation as in Eq. (3) and the random walk prior was selected to characterize the temporal autocorrelation. x _it is a vaccination-related predictor and β measures the strength that the predictor modifies the effect. When the nonlinear modification effect is of interest, Eq. (4) can be extended to

$${\theta }_{\mathit{it}}=\eta +s\left(x_{\mathit{it}}\right)+{\xi }_i+{\gamma }_t,$$ (5)

where s(.) is a nonlinear function, such as the natural cubic spline function. The INLA method can also be used to obtain the parameter estimations. The implementing R codes are available at https://github.com/winkey1230/DLNM-LCAR.

4. Results

4.1. Descriptive analysis

As of March 8, 2022, a total of 75,433,589 COVID-19 cases were confirmed in the 49 states. The length of time series in the first-stage hierarchical analysis varies from 718 days to 749 days, considerably longer than that in previous studies, which may provide a more convincing result. The spatial distribution of accumulated cases is presented in Fig. 1A. Excluding three states with the largest three numbers of cases, i.e., CA (California), TX (Texas) and FL (Florida), most of cases concentrate on eastern America. But for the incidence, seen in Fig. 1B, almost all states have a high incidence and the average incidence is around 22.9 %.

Fig. 1.

The descriptive analyses for the COVID-19 cases, daily average temperatures and vaccination-related variables.

Fig. 1C shows that the vaccination coverage rate in the population increases over time since its introduction. As of March 8, 2022, the average coverage rates are up to 74.96 % and 64.10 % in terms of PP1V and PPFV, respectively, but they are much unevenly distributed across the America, shown in Fig. 1D and E. A large spatial and temporal variation of vaccination coverage rates brings an interest and assistance in investigating its modification effect on the association between DAT and COVID-19.

The boxplot in Fig. 1G shows that the variation ranges of DAT are much different between states, and even the ranges of quartile DAT do not intersect between some states, e.g., FL (Florida) and CO (Colorado), which suggests that the spline-function-based two-stage strategy may not be appropriate for the DAT on its original scale. The average DAT increases gradually from north to south, shown in Fig. 1F.

4.2. Spatially smoothed associations

For the optimal model in the first stage, the effect of DAT was characterized by a cross basis with 5-df natural cubic splines for the exposure dimension and 3-df natural cubic splines for the lag dimension. The effect of autoregression term was characterized by a cross basis with df = 4 for both dimensions. The effect of rainfall was characterized using 5-df natural cubic splines on the moving average. The df was selected as 11 for the long-term trend. The detailed information for selection can be seen in Fig. S1.

In the second stage, taking the 50 % percentile, 12 °C, as reference, we used LCAR model to smooth the relative risks of DATs ranging from −20 to 30 °C with a separate of 1 °C, which covers the most of DATs. Seen in Fig. 2 A, the smoothed state-specific association curves show a considerably heterogeneity among 49 states. The average exposure-response curve shows that an increased DAT is associated with an increased risk of COVID-19 when DAT is between −8 °C and 18 °C. When DAT is below −8 °C or above 18 °C, the risk seems not to further increase or decrease. Fig. 2B presents the lag-response curves at a low DAT −3 °C and a high DAT 24 °C, which show that the effects of DAT keep stable at lag 0–6 days, then start to decrease until at around lag 12 days.

Fig. 2.

The smoothed average exposure-response curves and lag-response curves. The shadow areas indicate 95 % confidence interval. In subfigure A, dot gray curves show the state-specific exposure-response relationships and the red solid curve shows average exposure-response relationship. In subfigure B, two lag-response relationships for a low and high DATs, respectively, are presented.

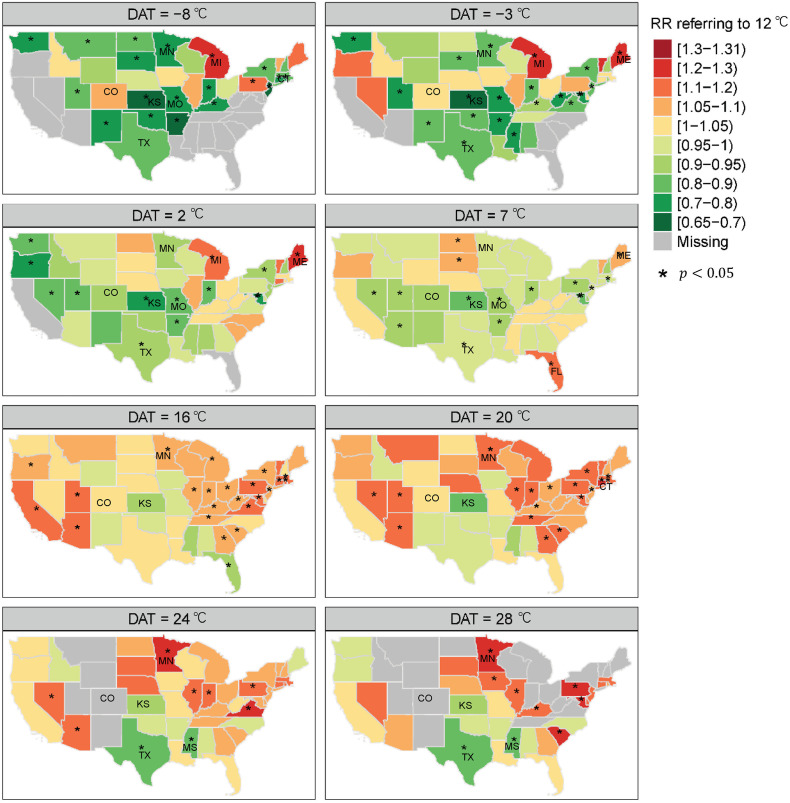
To exhibit the spatial distribution of the DAT-COVID-19 relationships more clearly in America, several representative DATs, i.e., −8, −3, 2, 7, 16, 20, 24, and 28 °C, were selected to present the relative risks, seen in Fig. 3 . Generally, the relationships between DAT and COVID-19 present a spatial correlation, i.e., adjacent states tend to have similar RRs. But more notably, different states also show distinct associations, even opposite ones. Specifically, when DAT is above 12 °C, a decreased DAT is significantly associated with a decreased risk of COVID-19 in around one-third of states, and more than half of states present no significant association. But three states, i.e., MI (Michigan), ME (Maine), and FL (Florida), present a significantly high risk when DAT decreases. When DAT is above 12 °C, around half of the states also exhibit no significant association, and most of the remaining states, mainly located in eastern America, show a positive association. However, two states, i.e., TX (Texas) and MS (Mississippi), show a significantly negative association.

Fig. 3.

The spatial distribution of smoothed relative risks for some DATs. When the specific DAT is outside the range of DAT in a state, the corresponding RR is set as missing. * indicates that the 95 % confidence interval does not contain 1.

4.3. Time-varying associations and the modification effect of vaccination

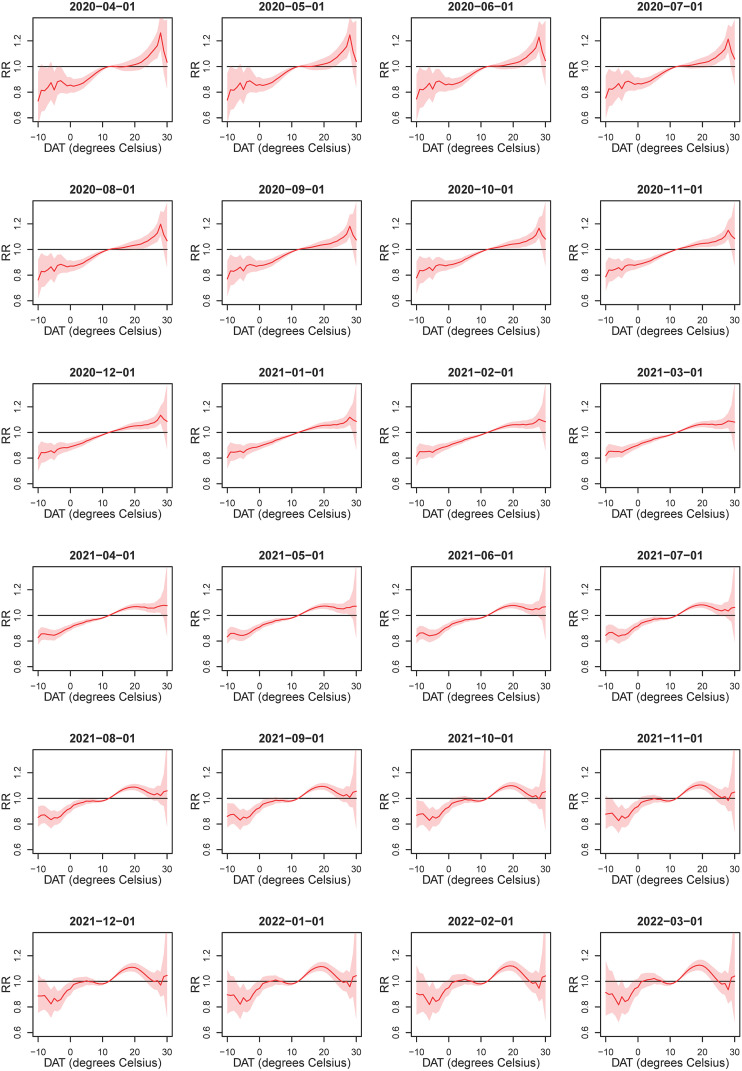
Using the time-varying DLNM-LCAR strategy, we obtained the pooled time-varying average associations across states. For presentation clarity, the associations at a series of representative times ranging from 2020-04-01 to 2022-03-01 with a separate of a month were given, shown in Fig. 4 . Before the introduction of COVID-19 vaccination (i.e., before 2021) and in the early stage of vaccination, DAT and COVID-19 presents a stable association, i.e., an increased DAT is associated with an increased COVID-19 risk. As the vaccination coverage rate increases (the variation tendency over time can be seen in Fig. 1C), the association curve gradually changes. When the vaccination coverage rate is high in 2022, the low DAT does not present a significantly low RR, especially at 0–12 °C. When DAT is at 12–20 °C, a positive association is still presented, but after 20 °C, the RR starts to decrease.

Fig. 4.

The time-varying average associations across states between DAT and COVID-19 risk.

To further investigate if the vaccination contributed to the heterogeneity of associations and how to modify the association, a spatiotemporal LCAR, with state-level time-varying PP1V or PPFV as a predictor, was constructed. The modification effects of vaccination at different DATs are shown in Fig. 5 . The result shows that when DAT is low (< 12 °C), the vaccination significantly changes the association, i.e., increases the RR referring to 12 °C. When DAT is around −5 °C, the modification effect is the strongest. When DAT is high (> 12 °C), the vaccination slightly affects the associations. Comparing PP1V with PPFV, PPFV exhibits a slightly stronger modification effect than PP1V. We also used a natural cubic spline function with df = 3 to explore the nonlinear modification effects. Shown in Fig. 6 , two representative DATs, i.e., a low DAT −3 °C and a high DAT 24 °C, were selected to present the results. The modification effects of vaccination are, as expected, not significant at the high DAT of 24 °C. When DAT = − 3 °C, the modification effects are significant, but not linearly correlated with vaccination rates (both PP1V and PPFV). When the vaccination rate is high, the modification curve is steeper rather than flatter, which suggests that increasing the vaccination still modifies the effect even though the current vaccination is at a high level. The results remain stable by changing the df to 4 and 5 for s(x) in Eq. (5).

Fig. 5.

The modification effects of vaccination variables on the associations between DAT and COVID-19 risk. For a given DAT, β measures the quantity that a percentage increase of vaccination will increase or minus the log-RR at this DAT.

Fig. 6.

The nonlinear modification effects of PP1V and PPFV when DAT = −3 and 24 °C. The observed maximum PP1V and PPFV are 95 % and 81 %, respectively.

4.4. Model performance

Under the condition that using spline functions to characterize the nonlinear associations, the commonly used multivariate-meta-analysis-based two-stage strategy may not be appropriate for the original scale of DAT due to the large variation of ranges, so we constructed a DLNM-Meta strategy as a comparison by simply replacing the LCAR model with the univariate meta-analysis model in the second stage. In addition, the naive stratified analysis from the first stage, labelled as Stratified DLNM, was also used as a reference. Compared with the DLNM-Meta and DLNM-LCAR, the Stratified DLNM assumes the associations to be independent among regions and does not borrow any information from each other.

Due to the real associations being unavailable, the common model selection criteria, such as deviance information criterion (Spiegelhalter et al., 2002) (DIC) and logarithmic score (Gneiting and Raftery, 2007) (LS), were used to evaluate the model performance in the second stage. For the Stratified DLNM, the second-stage model can be deemed as a special LCAR with τ → 0⁺ to reclaim the independence among states. For the two performance measures, a smaller value means a better model performance. LS, a cross validation measure based on conditional predictive ordinate (Pettit, 1990), can be used to evaluate the model's predictive ability. The results show that the values of DIC for DLNM-LCAR, DLNM-Meta, and Stratified DLNM, are −4013.84, −3993.16, and − 3707.60, respectively, as well as the values of LS are −1272.47, −1231.49, and − 460.74, respectively, which suggest that DLNM-LCAR strategy can achieve a better result by incorporating the spatial autocorrelation.

We also compared the average association curves and the spatial distributions obtained by DLNM-LCAR, DLNM-Meta, and Stratified DLNM. Seen in Fig. 7 , the results show that the point estimations of average associations are similar, but the 95 % CI are considerably different. In terms of the widths of CIs, Stratified DLNM < DLNM-Meta < DLNM-LCAR, which conforms to the statistical knowledge that ignoring the dependence between variables will underestimate the variance. Underestimated variance may increase the false positive error and also lead to inaccurate predictive results (Anselin, 1988; Zadnik and Reich, 2006). More detailly, Stratified DLNM completely ignore the dependence between regions. DLNM-Meta partly ignores the dependence, i.e., referring to Formula (2), the dependence between ξ _i’s is not considered. The comparison of the spatial distributions is detailed in Fig. S4. Generally, DLNM-LCAR obtains a smoother result than the other two, i.e., closer two states are more likely to have similar associations, which may be more reasonable.

Fig. 7.

The comparison of the average association curves estimated using Stratified DLNM, DLNM-Meta, and DLNM-LCAR.

4.5. Sensitivity analysis

The lag-response curves reminded that a max lag of 12 days may be an alternative selection. So we carried out a sensitivity analysis with the max lag of 12 days. This sensitivity analysis presents a similar result, seen in the supplementary materials.

5. Discussion

With considerable spatial heterogeneity between the DAT and COVID-19 daily confirmed cases shown by many previous studies, it is essential to characterize the spatial distribution of such heterogeneous associations for making reasonable region-specific health intervention measures and early-warning systems. In this work, aiming to characterize the spatial distribution of the DAT-COVID-19 association in the continental United States, we developed a novel two-stage strategy, called DLNM-LCAR. In the first stage, we used the common stratified DLNM to obtain a rough state-specific association estimation. In the second stage, a LCAR model was used to spatially smooth the associations across all the states. Compared with the naive stratified DLNM and the commonly used meta-based two-stage strategy, the DLNM-LCAR strategy is able to sufficiently employ spatial autocorrelation to achieve a more reasonable and stable spatial distribution. Based on the idea of DLNM-LCAR strategy, the time-varying DLNM-LCAR and spatiotemporal LCAR can be easily constructed to investigate the variation tendency of association over time and to investigate if (or how) a predictor modifies the association, respectively.

Using the DLNM-LCAR strategy, we found that around one-third of states exhibit no significant association between DAT and COVID-19 confirmed cases. As for the remaining states with significant association, when DAT is low, i.e., below 12 °C, most of them present a low risk, but two states, i.e., MI (Michigan) and ME (Maine), present a significantly high risk. When DAT is above 12 °C, most of them present a high risk, and these states are mainly clustered in eastern America, but two states, i.e., TX (Texas) and MS (Mississippi), present a significantly low risk. Such significantly heterogeneous, even opposite, associations suggest that temperature-related intervention measures and warning systems should be state-specific, especially for the states, TX, MI, ME and MS. Combining the epidemic prevention policies in America, we found that TX, ME, and MI are the three of four states that canceled the requirement of wearing masks at the earliest time, especially for TX as the first state of canceling the mask requirement. This finding may suggest that the intervention policy may affect the association between DAT and daily COVID-19 confirmed cases. A previous study (Smith et al., 2021) based on the SARS-COV-2 reproduction number in America shows that a high temperature will inhibit the transmission of COVID-19 or a cold temperature is conducive to the transmission in the absence of lockdown, and the lockdown intervention policy will significantly modify the association between temperature and reproduction number, which partially conforms to the finding in our study.

By spatially averaging the associations across 49 states, a S-shaped curve is overall presented. When DAT is between around −8 °C and 18 °C, an increased DAT is overall associated with an increased COVID-confirmed cases, but when DAT is below −8 °C or above 18 °C, the COVID-19 risk seems not to further decrease or increase, but keep flat. Such variation tendency conforms to that most of states with significant association present a low risk at low DAT and a high risk at high DAT. With saturate (or flat) effect at cold and hot temperature, we reasonably guess that the extreme temperature may change human's behaviors, such as reducing outdoor and social activities and increasing the time of turning on air conditioning and heating, which may bound the affection of atmospheric temperature on the spread of COVID-19.

We musk acknowledged that our analysis does not consider the real pictures of the pandemic that the hospital and medical system perceive due to the data availability, which may result in a loss of convincing, however, our analysis may provide a clue about how to conduct a validate analysis based the hospital and medical system-perceived pandemic in the future.

Since the outbreak of COVID-19 epidemic, several intervention measures, especially the vaccination campaign and social restrictions, have been adopted, which may also change the association in temporal dimension. We used the time-varying DLNM-LCAR to characterize the associations at different times. The result shows that the association exhibits a significant change over time, which roughly conforms to the vaccination campaign. So, we further constructed a spatiotemporal LCAR, with a vaccination-related predictor, to validate the guess. The result shows that the vaccination campaign significantly modifies the association when DAT < 12 °C, i.e., a high vaccination coverage rate will increase the RR at low DAT. When DAT > 12 °C, the vaccination campaign only makes a slight modification. These modification effects support the variation tendency of associations over time. For the social restrictions and other intervention measures, due to the data availability, they are not studied in our research.

Paying further attention to the average association curve in Fig. 2A, we found that the curve is not smooth at low and high DAT, which may violate the intuition. The reason is that a specific low or high DAT is outside the range of DAT in some states, which leads to an emergency missing association estimate in these states. Due to a wide 95 % confidence interval at low and high DAT, such an unsmooth association does not violate the common knowledge of epidemiology.

Another notable thing is that we did not consider the multivariate structure in the LCAR models, i.e., the correlation structure between the log-RRs at the selected representative DATs. The reason is that the large dimension of correlation structure will result in much intensive use of computing resources. More reasonably, previous study (Boca et al., 2017) has demonstrated that the effectiveness benefit of considering the correlation structure is slight when the dimension of multivariate structure is high due to the need to estimate a large between-location covariance matrix. On the other hand, if only a few exposure values are focused on or selecting the same knots for spline functions in all the regions is available, considering the correlation structure may be beneficial. So, we also give the methodology about the DLNM-LCAR with a multivariate structure in the supplementary materials.

In addition, to objectively verify the advantage of our proposed strategy, we also compared the DLNM-LCAR strategy with two intuitive strategies, i.e., the Stratified DLNM and DLNM-Meta, in terms of two objective model performance measures, i.e., DIC and LS. The results show that the DLNM-LCAR achieves the best performance, which suggests that incorporating an appropriate spatial autocorrelation pattern will obtain a more stable and accurate association estimation. As the factors affecting the association may present a complex spatial distribution, such as present clustering or spatial discontinuity, the first-law-of-geography spatial autocorrelation based on Leroux prior in LCAR model may not be an optimal choice. An alternative spatial prior which considers both the spatial discontinuity (or clustering) and the first-law-of-geography spatial correlation, such as DBSC-based (Santafe et al., 2021) and DDW-based (Wang et al., 2022) priors, may have the potential to further elevate the accuracy of estimation.

Although LCAR is a mature and widely-used method, but LCAR is only frequently used for the raw (first-hand) datasets, i.e., the observed data without estimation error, and is rarely used for the second-hand datasets which meta-analysis focuses on. So, our study may also provide a novel application situation about how to use the LCAR model in the second-hand datasets with estimation error.

6. Conclusion

The proposed two-stage strategy, DLNM-LCAR, is an efficient tool of characterizing the spatial distribution of heterogeneous associations. Using the DLNM-LCAR strategy, a considerable spatial heterogeneity of association between DAT and daily confirmed COVID-19 cases was found in America, which suggests that state-specific temperature-related public health intervention measures and early-warning systems should be designed. The further research suggested that the vaccination campaign significantly modifies the association when DAT is low, but only make a slight modification when DAT is high. In a multi-region study, the proposed strategy is an efficient method to characterize the short-term associations by considering the spatial autocorrelation.

CRediT authorship contribution statement

Wei Wang: Conceptualization, Formal analysis, Investigation, Methodology, Software, Writing – original draft. Shuming Ji: Data curation, Formal analysis, Software, Writing – review & editing. Jinyu Wang: Supervision, Writing – review & editing. Fang Liao: Conceptualization, Methodology, Writing – review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Editor: Anastasia Paschalidou

Appendix A. Supplementary data

Supplementary material

Data availability

I have shared the links to my data and code in the main text.