A Power-Efficient Brain-Machine Interface System with a Sub-mW Feature Extraction and Decoding ASIC Demonstrated in Nonhuman Primates

Abstract

Intracortical brain-machine interfaces have shown promise for restoring function to people with paralysis, but their translation to portable and implantable devices is hindered by their high power consumption. Recent devices have drastically reduced power consumption compared to standard experimental brain-machine interfaces, but still require wired or wireless connections to computing hardware for feature extraction and inference. Here, we introduce a Neural Recording And Decoding (NeuRAD) application specific integrated circuit (ASIC) in 180 nm CMOS that can extract neural spiking features and predict two-dimensional behaviors in real-time. To reduce amplifier and feature extraction power consumption, the NeuRAD has a hardware accelerator for extracting spiking band power (SBP) from intracortical spiking signals and includes an M0 processor with a fixed-point Matrix Acceleration Unit (MAU) for efficient and flexible decoding. We validated device functionality by recording SBP from a nonhuman primate implanted with a Utah microelectrode array and predicting the one- and two-dimensional finger movements the monkey was attempting to execute in closed-loop using a steady-state Kalman filter (SSKF). Using the NeuRAD’s real-time predictions, the monkey achieved 100% success rate and 0.82 s mean target acquisition time to control one-dimensional finger movements using just 581 μW. To predict two-dimensional finger movements, the NeuRAD consumed 588 μW to enable the monkey to achieve a 96% success rate and 2.4 s mean acquisition time. By employing SBP, ASIC brain-machine interfaces can close the gap to enable fully implantable therapies for people with paralysis.

I. Introduction

Brain-Machine interfaces (BMIs) have shown promise towards restoring motor function to people with spinal cord injury [1], [2]. Extracting intention information from brain activity can provide more accurate and natural control of hands and fingers than conventional methods, such as muscle-controlled prostheses and exoskeletons. An increasing number of studies have demonstrated that BMIs have these advantages through experiments with both non-human primates (NHP) [3]–[5] and humans [6], [7].

However, high power consumption has been a major obstacle for out-of-laboratory usage of BMI-based neural prostheses. To decode brain activity accurately, conventional approaches extracted features from high-bandwidth neural signals, inevitably consuming high amounts of electrical power [4], [8]. Such power-hungry systems are difficult to use as portable devices, since they require wired connections to computing racks to process the neural activity, nor as implantable devices, due to the high-power (i.e. hundreds of mW) that could result in unsafe tissue temperatures or large battery sizes [9], [10].

To resolve the power consumption issue, many research groups have developed application-specific integrated circuits (ASICs) to perform the necessary computations in place of general-purpose computers [11]–[13]. Several groups have presented spike-sorting accelerators [14]–[20] to compress the data for wireless transmission or devices that perform local decoding [21], [22]. Although promising for data acquisition purposes, these devices are often untested in vitro or in vivo, so their usability in a brain-machine interface environment is yet undetermined. Of those devices that have been tested in vitro or in vivo [23]–[31], all would still require wireless transmission of the neural data to external processing hardware to provide the full functionality of a brain-machine interface. The wireless link may potentially add substantial power consumption and may also limit the usable environment of the brain-machine interface to locations where wireless communication to external hardware is achievable. These works demonstrate that application-specific hardware can cut power, but none have addressed all of the end-to-end issues of implantable brain-machine interfaces.

Many research groups have also taken a signal processing approach towards reducing the power consumption of BMIs. Electroencephalography (EEG) and electrocorticography (ECoG) has been shown to well-represent hand postures [32], [33]. However, discrete classification of hand postures restricts the natural capabilities of BMIs, and long integration times can make usage feel sluggish and unnatural. Other groups have attempted continuous decoding from ECoG signals, but the efficacy of these signals in complex, multi-dimensional, non-oscillatory tasks is yet unknown [34], [35]. Intracortical neural features have shown specificity to individual neurons that enable high performance decoding for a variety of applications. Sorting spikes isolates the activity of individual neurons and creates strong discrete and continuous decoding [36]–[40]. This has motivated a number of the ASICs mentioned above, but the spike sorting procedure is inherently of the most computationally expensive neural features to extract. As such, the field has primarily shifted to counts of thresholded neural spikes in time bins to estimate the underlying firing rate of recorded multiunit neurons [41]. This technique has maintained the decoding performance of sorted units [8], [42] while eliminating much of the post-processing for real-time tasks, even functioning offline with lower bandwidths to reduce power consumption [43].

To address these issues in an alternative way, we and others have proposed the use of spiking band power (SBP), or the averaged intracortical signal in the 300–1,000 Hz frequency band. Previously we found that SBP lowers power due to its low-bandwidth, can detect firing rates of low amplitude units that would be invisible to threshold detectors, is more single unit specific than threshold detectors, and outperforms threshold detectors in prediction performance due to its specificity [44]–[46]. We recently demonstrated the simplicity of SBP on an embedded platform, requiring 33.6 mW to extract SBP from 96 channels [47]. Unfortunately, despite the cut in power consumption relative to high-bandwidth systems, the requirement to recharge a medical-grade 200 mAh battery daily is still a hindrance to implantability, even as a research tool. Furthermore, with processing consuming over 50% of that power consumption, it remains unknown how hardware acceleration can reduce processing consumption via clock speed reductions and offloading computations.

In this paper, we propose a Neural Recording And Decoding ASIC (NeuRAD) that better fits the requirements of an implantable device. By adopting SBP and developing optimized feature extraction hardware for it, the NeuRAD alone required 581 μW to extract 93 channels of SBP, predict finger movements in real-time with NHP, and interface with commercial bioelectrical Analog Front End (AFE) chips (Intan RHD series, Intan Technologies LLC., Los Angeles, CA, USA). By including both feature extraction and kinematics prediction on a single chip, the data rate could be reduced by a factor of 4,800× or 2,325× for one- or two-dimensional predictions, respectively, compared to the transmission of raw neural signals. This device is a fully integrated brain-machine interface relevant to a wide variety of neuroprosthetic applications, such as for the control of functional electrical stimulation [1], [2], computers [48], or exoskeletons [49] (Fig. 1). To our knowledge, this is the first ASIC capable of extracting SBP and decoding it into finger movements in real-time, validated in vivo with NHP, with a power consumption low enough for relevance to implantable brain-machine interfaces.

Fig. 1.

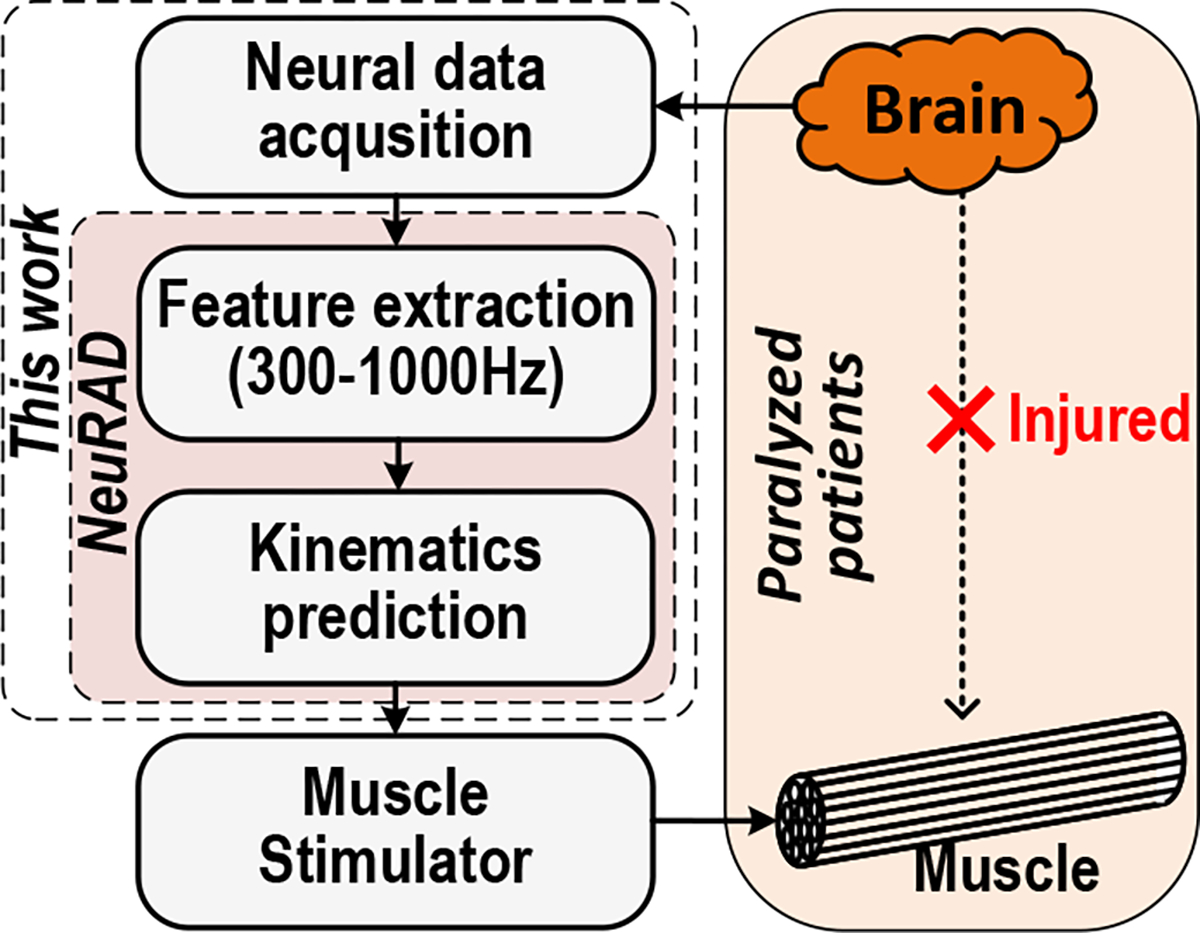
Usage Scenario. This work enables low-power intracortical signal processing and decoding for embedded neural prostheses.

II. Method

A. Hardware Design

1). Architecture of Neural Processor:

Fig. 2 presents the top-level architecture of the NeuRAD, supporting on-chip feature extraction and general processing. It has a fixed-point Signal Band Power Unit (SBPU), a fixed-point Matrix Acceleration Unit (MAU), and an ARM Cortex M0, interconnected by the AMBA High-performance Bus (AHB) lite. Using the neural signal data sampled from the AFE chips, Intan RHD2132s in this case, the SBPU calculates the SBP in customized signal bands on-the-fly, which can be referenced to a Common Average Reference (CAR), if enabled [50]. The MAU executes fixed-point matrix calculations to further process the SBP from the SBPU, which will be described in the following sections. The Cortex M0 core orchestrates all the blocks via the AHB lite. Interfaces such as Serial Peripheral Interface (SPI), Controller Area Network (CAN), and a proprietary serial interface are controlled through the bus. SPI is used to interface with the AFE chips and any other auxiliary chips, such as an Atmel AT32UC3C2256C (Microchip Technology Inc., Chandler, AZ, USA) included in our testing environment. CAN can be used to transmit relevant neural information or post-processed data to external devices, such as functional electrical stimulation systems or exoskeletons. Through the proprietary serial interface, the processor is fully programmable in C using an ARM compiler.

Fig. 2.

Architecture of the NeuRAD. *The device can work with auxiliary prosthetic hardware, which is not included in this work.

We implemented multiple voltage and clock domains to minimize power consumption. The voltage level of the system was set to 0.625 V except for chip’s interfaces at 3.3 V, and clock generators at 1.21 V. There are four clock domains for the various components, and their frequencies can be tuned separately to meet required usage conditions. The SBPU uses a neural clock and a sampling clock, and their frequencies decide the sampling rate of the AFEs. The system clock controls the processing time of the MAU and M0 core. The CAN clock determines the speed of the CAN interface, which needs to be tuned according to the baudrate of the CAN bus for valid communication. Additionally, clock gating is extensively used across the chip to further eliminate unnecessary power consumption.

2). Scalable Signal Band Power Unit:

SBPU is a dedicated hardware block to extract SBP features for reducing power consumption. In our case, we configured the SBPU to extract SBP from the 300–1,000 Hz signals provided by the AFE chips at 2 kSps. Channel usage and precision can be fully customized, enabling power saving opportunities that can be fit to the user without losing accuracy when post-processing the neural signals.

Fig. 3 shows the functional block diagram of the SBPU while Fig. 4 presents its processing pipeline. The SBPU samples the filtered and absolute-valued neural signal (a feature included in the RHD2132) of the enabled channels (maximum 93) from the AFE chips via SPI. This is executed in a single sampling time step of 0.5 ms, corresponding to a 2 kSps sampling rate. If enabled for some subset of channels, the data of the configured channels is used to simultaneously compute a common average reference. While the sampled neural signals are temporarily stored in the 3-lane FIFO (93 × 16 bits), the data of the configured channels for CAR are accumulated and multiplied by 1/(number of referenced channels) for each sampling time step, yielding the CAR value for that time step. CAR has been shown to reduce noise by >30% compared to standard types of electrical referencing [50]. The sampled neural signals are then digitally referenced to the calculated common average, if enabled, and accumulated per-channel to meet the binning period (100 samples for the closed-loop experiments conducted here). Finally, when the desired quantity of samples per accumulation period has been reached, the accumulated values per channel are multiplied by 1/(number of samples), resulting in SBP.

Fig. 3.

Signal Band Power Unit. The SBPU samples neural signals from off-chip biomedical amplifiers and computes the SBP feature. The maximum number of channels is constrained to 93 by the number of accumulators in the SBPU.

Fig. 4.

Processing pipeline of SBPU. The binning period n is configurable. The channels which are sampled are configurable, so the processing time for the data from each AFE can vary.

The list of channels which are sampled by the SBPU and the list of channels used to calculate the CAR are independently and fully configurable to reduce power consumption. Not all channels are informative and a particular channel may not remain representative of task-relevant information from day-to-day. Therefore, by disabling uninformative channels used for recording or for computation of the common average reference, the chip can reduce unnecessary data transfer and the corresponding operations, slowing down operation frequency and cutting power consumption.

The SBPU also supports scalable fixed-point precision to reduce power consumption. Every arithmetic operation and sampled datum from the AFEs is followed by a configurable shifting operation, which allows the precision to be optimized based on the incoming data. When scaled precision is used, only the MSBs are used for computation while the LSBs are zeroed, thereby reducing switching activity and saving electrical power.

The SBPU reduces power consumption by 44× compared to the baseline M0 core system without the SBPU, as illustrated in Fig. 11. The SBPU consumes only 0.34 mW to extract SBP from 2 kSps neural signals of 93 channels with CAR calculated across all 93 channels, while the consumption of the M0 core to perform the same calculations was 15.08 mW. In terms of memory usage, 186 bytes are persistently used and overwritten to store SBP measurements (93 channels with two bytes per channel) and two bytes are persistently used and overwritten to store the current sample’s common average reference, if enabled.

Fig. 11.

Power consumption comparison for the two hardware accelerators. (Left) SBP feature extraction with CAR from 93 channels at 2kSps. M0 controls the three SPI blocks and calculates referenced SBP with a 31.5 MHz clock at 1.35 V, while the SBPU requires a 2.9 MHz clock at 0.63 V. (Right) Continuous SSKF inference from 93 channels of SBP data every 50 ms. M0 calculates SSKF updates with a 240 kHz clock at 0.63 V or a 484 kHz clock at 0.63 V for 1D or 2D, respectively. MAU requires a 67.8 kHz clock at 0.63 V.

3). Matrix Acceleration Unit for Neural Signal Processing:

The MAU (Fig. 5) enables efficient processing of 16-bit fixed-point matrix-vector multiplication, which is required to implement decoding algorithms with high quantities of matrix operations. Although the steady-state Kalman filter implemented here (see subsequent Methods sections) is computationally efficient and would not take substantial advantage of a matrix accelerator, the MAU allows for more complex decoding algorithms (such as [51]) to be implemented while keeping computation latency and power consumption lower than if using the M0 core.

Fig. 5.

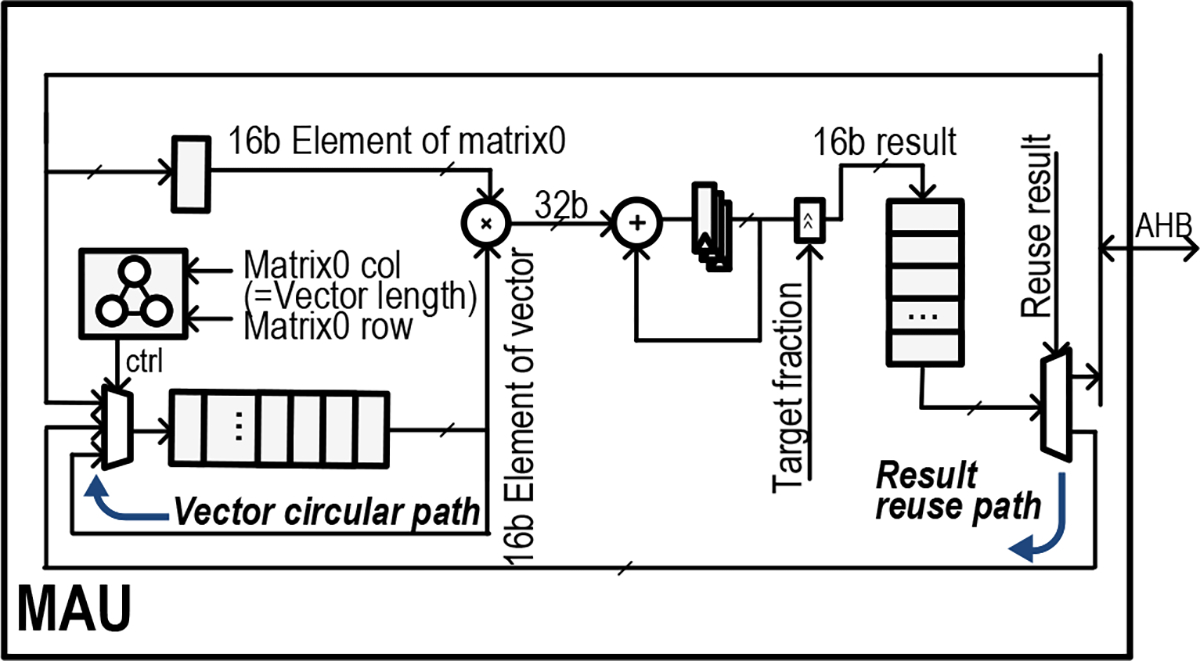
Matrix Acceleration Unit. The MAU performs matrix-vector multiplication and accumulation for efficient decoder processing.

The multiplication-accumulation (MAC) unit has a vector operand, which is stored in a FIFO, to calculate the matrix-vector product as the matrix data is streamed in. During the matrix-vector multiplication, the vector data is reused via a circular path. If the product vector is needed for the next operation, it can be automatically routed back into the FIFO through a result-reuse path, making it immediately ready for the subsequent calculation. This eliminates any processor intervention to queue intermediate calculations and improves the efficiency of the computation.

The MAU includes configurable precision in the MAC unit to reduce excessive signal toggling, like the SBPU. As different intermediate data may not necessarily share the same dynamic range, being able to configure the fractional bit widths for each recording channel allows maximum precision in 16-bit while maintaining the power savings of fixed-point.

The MAU reduces power consumption by 1.6× and 2.6× for 1D and 2D inference, respectively, compared to the baseline M0 core system without the accelerator, as illustrated in Fig. 11. The MAU consumes only 15.6 μW and 17.4 μW to predict 1D and 2D kinematics, respectively, from 93 channels of SBP. A single M0 core consumes 25.1 μW and 45.4 μW for the same 1D or 2D predictions, respectively.

B. Operating Modes

The device was tested in two operating regimes: a training mode and an inference mode. In both modes, the NeuRAD used the SBPU, MAU, and M0 in the same fashion to execute all computations. In inference mode, the NeuRAD exported only the predicted positions and velocities. In training mode, the NeuRAD additionally exported the 93 channels of neural data to support decoders requiring second-stage training, such as the ReFIT Kalman filter (see subsequent sections). Exporting the additional data requires higher M0 clock speeds, increasing power consumption. Training modes were always used when testing with the NHP to minimize code swapping, just requiring updates to the decoder’s parameters. We attempted to minimize downtime of the task to keep monkey motivation high. Functionality and consumption during inference modes were benchtop tested offline.

C. System Evaluation

We validated the chip’s proper functionality through online neural decoding experiments, as detailed below. All procedures were approved by the University of Michigan Institutional Animal Care and Use Committee.

1). Behavioral task:

We trained one adult male rhesus macaque, Monkey N, to perform movements of the index and middle-ring-small fingers (MRS) as a group to hit fingertip position targets in a virtual hand simulator, as illustrated in Fig. 6 and as described previously [46], [52]–[54]. Briefly, the NHP subject sat in a shielded chamber with its left arm flexed 90 degrees and resting on a table. The monkey’s palm was lightly constrained facing inward, with the fingers available to move a manipulandum. A flex sensor (FS-L-0073–103-ST, Spectra Symbol) was fastened to each door of the manipulandum (one for each finger group), measuring its position. Position data were recorded by a computer running xPC Target (Mathworks, Natick, MA, USA). A screen in front of the subject displayed a virtual model of a monkey hand (MusculoSkeletal Modeling Software [55]), which was controlled by either physical position data (sensor value) or the predicted position data from the NeuRAD.

Fig. 6.

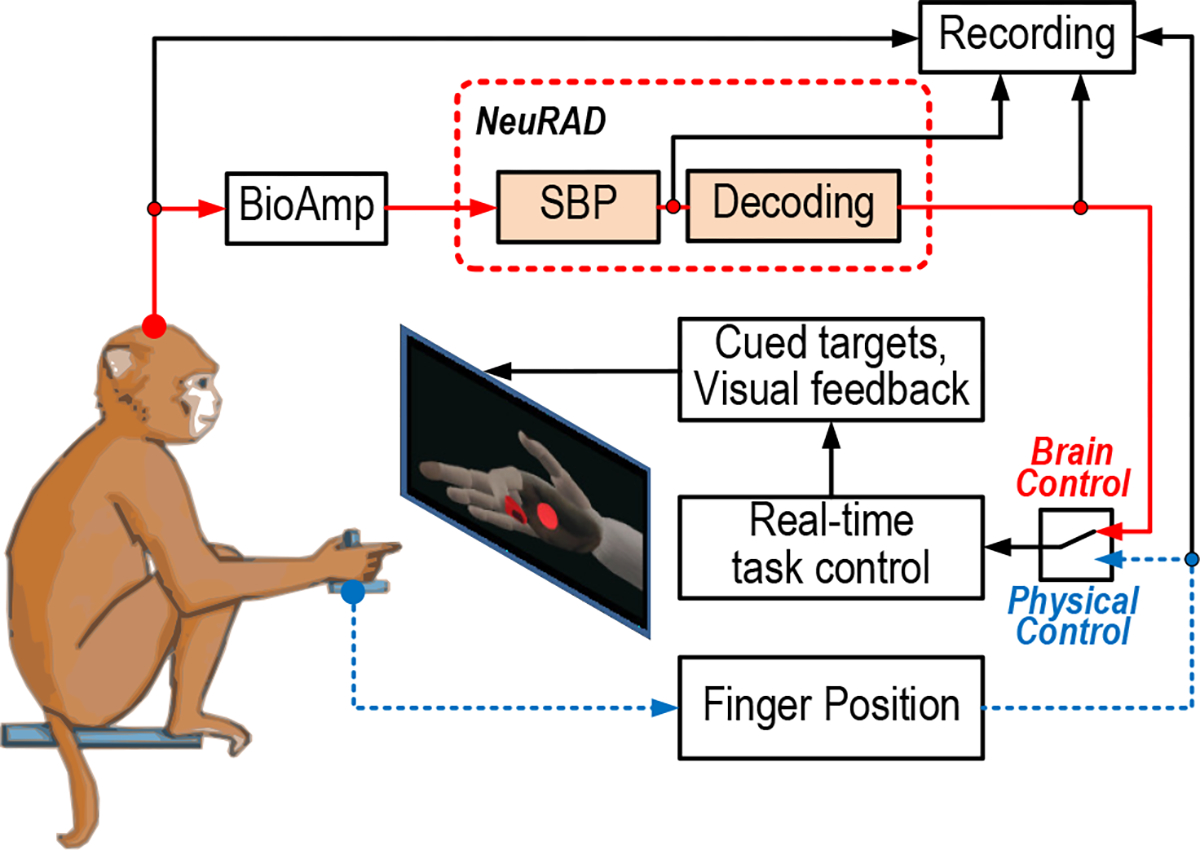
In-vivo experiment setup. The monkey moved his fingers together or his index finger individually separated from the middle-ring-small (MRS) fingers as a group to hit virtual targets presented on a computer screen. The virtual fingers were controlled by the monkey’s physical finger movements or the NeuRAD’s decode of the brain activity.

At the start of each trial, a spherical target appeared in the path of the virtual finger(s) of interest, and the monkey was required to move the virtual finger(s) to hit the target(s) and hold for a set period (500–750 ms, depending on the stage of training). Targets were presented in a center-out pattern. Initially, a target is shown in the neutral position, half-way between flexed and extended. Once the monkey successfully hit and held the target, the next one was generated randomly from a few set positions in the finger movement path. After the target(s) was successfully acquired or the trial timed out, the neutral target was again presented until success. The monkey was motivated with apple juice for reward following success.

2). Electrophysiology:

We implanted Monkey N with two 64-channel Utah arrays (Blackrock Microsystems LLC, Salt Lake City, UT, USA) in primary motor cortex using the arcuate sulcus as an anatomic landmark for hand area (see [52] for more details). Only 93 of the 128 total channels were used in this study. During some experiments, broadband neural signal data was recorded at 30 kSps using a Cerebus neural signal processor (Blackrock Microsystems) for later offline analysis. During online NeuRAD testing, the CerePort breakout (Blackrock Microsystems) was connected directly to the pedestal mounted to the monkey’s skull and to the connectors included on the NeuRAD’s testing board (see Fig. 8). Fig. 7 shows the array implants.

Fig. 8.

Experimental testing board. The NeuRAD ASIC was tested on the printed circuit board. The neural signal simulator (Blackrock Microsystems) was connected directly to the AFE chips, Intan RHD2132s, for offline system evaluation. The simulator’s reference was connected to the board’s ground plane. For closed-loop testing, the simulator was replaced with the connections to Monkey N’s implants. The AFE chips were connected to the NeuRAD for data extraction, and the extracted SBP and predicted kinematics were transferred to the Atmel microcontroller for transmission to the xPC Target computer. The NeuRAD is also capable of exporting predicted kinematics via the CAN transceiver, which was not investigated in this study.

Fig. 7.

Surgical photographs of Monkey N’s microelectrode array implants. Asterisked arrays were used in this study. A means anterior, L means lateral, CS means central sulcus.

Since the Cerebus is the state-of-the-art recording system for brain-machine interfaces in people, we wanted to compare its recording quality to that of the RHD2132s. On two consecutive days, we recorded from one of Monkey N’s electrodes that showed the highest amplitude spike according to the Cerebus, with the Cerebus recording on the first day and the RHD2132s recording on the second day. The Cerebus recorded the raw signal at 30 kSps with a 0.3 to 7,500 Hz bandwidth, and the RHD2132s were configured to record at 10 kSps with a 0.1 to 5,000 Hz bandwidth. The DSP filters in the RHD2132s were also configured to high-pass filter above 0.19 Hz. Then, we used a 2^nd-order Butterworth high-pass filter to filter each signal above 250 Hz, with an additional 2^nd-order Butterworth low-pass filter to filter the Cerebus signal below 5,000 Hz so that the pass-bands matched. Then, we set a −6.4×RMS threshold to extract just the largest amplitude unit’s spikes and calculated each system’s signal-to-noise ratio. Signal-to-noise ratio was calculated as the ratio between the magnitude of the mean spike waveform’s negative peak and the root-mean-square of the recording.

3). System Incorporation:

To test the NeuRAD in application, we switched control of the virtual hand from the manipulandum to the predictions made by the NeuRAD (Fig. 6). First, the monkey performed at least 350 trials using the manipulandum to control the virtual hand while the finger positions and the SBP activity were synchronously recorded in real-time. The SBP activity was calculated using the NeuRAD, which transmitted one averaged 16-bit value for each of the 93 channels to the attached Atmel AT32UC3C2256C via the SPI interface at the completion of each integration bin. The Atmel processor then exported the measurements to the xPC Target computer for real-time synchronization over a 230,400 baud UART connection. A MAX3222E (Maxim Integrated, San Jose, CA, USA) was powered by the NeuRAD’s testing board to convert the UART signal to RS232 for compatibility with the xPC Target computer.

Then, we trained a steady-state position/velocity Kalman filter (SSKF; described in the subsequent section) from the manipulandum control trials using Matlab R2019b (Mathworks, Natick, MA, USA) on an external computer. These parameters were programmed to the NeuRAD [52], [56]. Finally, we used the predictions calculated by the NeuRAD using the SSKF to control the virtual hand in real-time. The NeuRAD computed the 16-bit fixed-point values for each degree-of-freedom’s predicted positions and velocities using the SBP values computed by the SBPU in real-time. It then transmitted these predictions to the Atmel processor. The Atmel processor converted the fixed-point values to floating-point (for compatibility with the existing xPC Target software) then exported the floating-point predictions alongside the SBP measurements to the xPC Target computer via RS232.

4). Feature Extraction and Decoding:

We extracted SBP by first configuring the RHD2132s to filter incoming signals from 300–1,000 Hz (with an additional 220.6 Hz DSP high-pass filter) and absolute value the samples. Then, the SBPU coordinated sampling of the data from each RHD2132 at 2,000 samples per second per channel, and averaged the samples in 50 ms bins. The vector of 93 SBP measurements for each 50 ms bin was transferred to the decoding pipeline.

For decoding, we implemented the SSKF because it offers lower computational complexity and fewer stored parameters in comparison to the standard Kalman Filter (Table I). Importantly, SSKF shows comparable accuracy to the standard Kalman filter as the Kalman gain converges to a steady-state value within a few seconds of use [57]. Thus, calculation of the Kalman gain, which involves a computationally expensive matrix inversion, can be pre-computed during training and does not have to be executed in real-time.

TABLE I.

Computational Complexity

Algorithm	Computational Complexity	Size of parameters
KF	$\mathcal{O}\left(s^3+s^2+s{n}^2+n^3\right)$	2s2 + sn + n2
SSKF	$\mathcal{O}\left(s^2+sn\right)$	s2 + sn
velocity SSKF	$\mathcal{O}\left(v^2+vn\right)$	v2 + vn

s: number of states, n: number of channels, v: number of velocity states

Training was performed in Matlab R2019b with 10-fold cross validation at a variety of open-loop lags from zero to five, inclusive. The Kalman filter parameters were computed via least squares regression as described previously [52]. The steady-state Kalman gain was computed by making five seconds worth of predictions [58]. The parameters of the lag which produced the highest cross-validated velocity correlation were used for online control. No manual lag was added during online control, meaning once a prediction was computed, it was immediately transmitted to be displayed as feedback.

We additionally optimized parameter storage and operations by pre-computing matrix products. The original SSKF decoder computes updates via the following equation 1:

$${\widehat{x}}_t=A{\widehat{x}}_{t-1}+K\left(y_t-CA{\widehat{x}}_{t-1}\right)$$ (1)

where x is the state, i.e. position, velocity, etc.; A is the state transition matrix; y is the observation vector, i.e. SBP; K is the Kalman gain; C is the observation matrix; and subscript t is the time step. The number of MAC operations and the storage of parameters can be reduced by grouping and computing parameter products as in equation 2:

$${\widehat{x}}_t=(I-KC)A{\widehat{x}}_{t-1}+K{y}_t$$ (2)

In our case, training of the Kalman filter parameters assumed a three dimensional state space [p, v, 1] for 1D and a five dimensional state space [p_I, p_MRS, v_I ,v_MRS, 1] for 2D with a 93-dimensional observational space. The optimizations from the steady-state Kalman filter, as detailed above, enable us to compress the position-velocity Kalman filter we have previously published [52] to a velocity Kalman filter without change in functionality, with the initial position set to 0.5 (halfway between full flexion and full extension). In our implementation, the 1s state estimate was replaced with a 1, eliminating excess calculations. This further reduces the required stored parameters to 1×3 for the (I − KC)A matrix and 1 × 93 for the Kalman gain for 1D or 2 × 3 and 2 × 93, respectively, for 2D. The complexity is additionally reduced by integrating velocity to predict position, which overall results in 2, 883× lower computational complexity and 31× fewer stored parameters. In terms of storage, the velocity SSKF stores only the previous time step’s kinematic predictions (four bytes for a 1D, eight bytes for 2D Kalman filter) and trained parameters (188 bytes for 1D, 380 bytes for 2D Kalman filter).

In our circuit implementation, we used the MAU to conserve power during computation of the predicted state. First, at the conclusion of a 50 ms accumulation bin, the M0 streamed the measured SBP values y_t to the MAU followed by the trained K matrix. This yields a kinematic state prediction from the neural state. The result of this operation is fed to the MAU’s result-reuse path and is summed with the $(I-KC)A{\widehat{x}}_{t-1}$ computed during the previous time step. This yields the current time step’s velocity prediction, which is added to the previous time step’s position and displayed on the screen. Then, the state prediction is sent to the result-reuse path to compute the $(I-KC)A{\widehat{x}}_t$ product for the subsequent prediction. Finally, the MAU awaits the next set of SBP measurements.

For optimal SSKF performance, we performed a second stage of training for the Kalman filter parameters known as recalibrated feedback intention-training (ReFIT) in Matlab R2019b [59]. To adapt the ReFIT method to control multiple one-dimensional fingers, we rotated the net velocities of the fingers in two-dimensional space towards the net two-dimensional target (where applicable), and back-calculated each finger’s individual velocity prior to retraining, as was done previously [54]. While the ReFIT Kalman filter requires an additional training step, the retrained parameters fit into the same SSKF framework discussed in the prior paragraph. All closed-loop results presented in this manuscript represent control using the ReFIT Kalman filter with the NeuRAD operating in training mode.

To compare performance to the state-of-the-art finger decoding rig, we performed the same task with the monkey using the ReFIT Kalman filter and SBP but with the high-powered brain-machine interface rig. For these control experiments, the Cerebus acquired the neural activity, which was processed into SBP by the xPC Target computer. Then, the xPC Target computer predicted the finger movements from the SBP to control the virtual hand, as described previously [46], [52]–[54]. Control experiments were performed within one month of the corresponding NeuRAD test (i.e. one-dimensional or two-dimensional) to minimize the effects of signal quality over time.

III. Results

A. Chip Analysis

The NeuRAD was implemented in TSMC 180 nm CMOS technology as summarized in Fig. 9. The area of the ASIC was 9 mm². Core voltage was reduced to 0.625 V to achieve low power consumption while meeting required constraints for in-vivo testing, such as the neural signal sampling rate. Fig. 10 shows the shmoo plot of the chip’s overall function, overlaying the required constraints for sampling neural activity. I/O voltage was set to 3.3 V for communication with the other components such as the Intan RHD2132s.

Fig. 9.

Die photo of the NeuRAD (left). Summary of the chip (right).

Fig. 10.

Measured shmoo plot. The dashed line shows the minimum NCLK frequency for sampling neural signal data from 93 channels at 2 kSps.

Fig. 9 shows a photograph of the die for the ASIC. The chip included customized low-leakage SRAM. Other functional components such as SBPU, MAU, M0, and interface blocks were organized via automatic placement and routing (APR). Additional interfaces, including GPIOs, a CAN controller, and an MBUS interface [60] were included to assist with debugging and communication with other equipment as needed.

To estimate the power savings resulting from using hardware accelerators over using a general purpose microprocessor, we measured the power consumption of the system when the actions of the two accelerators, the SBPU and the MAU, were instead performed by the M0 core. Fig. 11 compares these measurements to the levels of power consumption when using each accelerator. The SBPU reduces power consumption by 44×, cutting the 15.08 mW required by the M0 core down to 0.34 mW to extract 93 channels of SBP features at 2 kSps with CAR of the entire 93 channels. To accomplish this functionality of the SBPU, the M0 operating frequency and voltage had to be boosted to 31.5 MHz and 1.36 V. For decoding, the MAU reduces power consumption by 1.6× for 1D (from 25.1 μW to 15.6 μW) and 2.6× for 2D (from 45.4 μW to 17.4 μW). To execute these computations, the M0 clock frequency had to be boosted to 240 kHz for 1D and to 484 kHz for 2D.

The NeuRAD substantially cut data rate by integrating feature extraction and inference in a single device, thereby reducing throughput and the corresponding transmission power. The collected signals from AFEs were processed by the SBPU into SBP via a mean-absolute value computation every 50 ms, then decoded into kinematic predictions of finger movements. Transmitting mean-absolute value computations across integration bins instead of raw recordings results in a data rate reduction corresponding to the number of samples accumulated. In this specific case of a 50 ms integration period, data reduction was 100× showing that the data rate can be reduced substantially during the decoder training period. Furthermore, in application, when only the predicted positions require transmission and not the SBP measurements, the data rate is reduced to a factor of the number of degrees-of-freedom. In the case of two-degrees of freedom, which is popular in the literature for controlling computer cursors, the data rate reduction is 2, 325× for our 50 ms update period. The data rate reduction saves 174 μW compared to the case of transferring sampled neural signal in-order.

Table II compares power consumption of the NeuRAD across various configurations. As a base configuration demonstrating 1 degree-of-freedom (DoF) kinematics inference, the NeuRAD was configured to sample 93 channels, calculate mean absolute-value in 100 sample bins with a 2.9 MHz clock frequency (neural clock) using SBPU, and compute KF updates with a 67.8 kHz clock frequency (system clock) using MAU. To do so, the NeuRAD consumed 581 μW. In a heavily optimized case, where we reduce the channel quantity to the 8 most-informative channels with a corresponding reduction in the sampling clock frequency to 1.18 MHz, the NeuRAD consumed only 200 μW. When adding CAR to this base configuration, the power consumption increased by just 5 μW, where this 0.86 % increase is easily justified by the improved SNR. When lowering the mean absolute-value and KF update periods from 50 ms to 30 ms (which may improve performance [54]), an additional 15 μW of power is consumed on top of the base configuration. 2-DoF kinematics inference consumes an additional 7 μW over the 1-DoF baseline configuration.

TABLE II.

Power measurement of NeuRAD in various configurations

Number of Sampling Channels (EA)	Number of Reference Channels (EA)	SSKF Update Period (ms)	Degrees of Freedom	Frequency (Neural / System Clock*)	No. Transmitted Bytes	NeuRAD Power (μW)
8	0	50	1	1.18 MHz / 67.8 kHz	2	200
93 [Fig. 12]	0	50	1	2.9 MHz / 67.8 kHz	2	581
93	0	30	1	2.9 MHz / 67.8 kHz	2	596
93 [training mode]	0	50	1	2.9 MHz / 500 kHz	194	644
93	93 (CAR)	50	1	2.9 MHz / 67.8 kHz	2	586
93	93 (CAR)	50	2	2.9 MHz / 67.8 kHz	4	588
93 [training mode]	93 (CAR)	50	2	2.9 MHz / 500 kHz	196	650

Gray rows were used for in vivo testing, with results displayed in Fig. 13

^*67.8 kHz is the slowest system clock can be achieved by the internal clock generator.

The power consumed by various device components in the demonstration scenario with the NHP using the NeuRAD to control one-dimensional finger movements (see subsequent section) is broken down in Fig. 12. The power for each component was measured by switching off the other active components and observing the change in power consumption. The total power consumption of the NeuRAD was 581 μW. SBPU consumed 59% (342 μW) of the total, collecting and processing SBP with a 2.9 MHz clock frequency. The MAU’s power consumption was 2.6% (15.6 μW) of the total, processing a 1D SSKF with a 67.8 KHz clock frequency. Raising the voltage level and driving external I/O signals at 3.3 V took 30% (174 μW) of the total. The remaining chip components, including the two clock generators for the system and neural clocks, consumed the remaining 8.4% (49 μW).

Fig. 12.

Power break down of the NeuRAD in the demonstrated one-dimensional prediction configuration. 93 sampled channels at 2 KSps with a 100-sample SBP bin size, resulting in a 50 ms inference period. Total power of the NeuRAD is 581 μW in this configuration.

A comparison between the NeuRAD in the in-vivo testing configuration and other state-of-the-art systems is shown in table III. The NeuRAD system consumes only 12.58 mW (12 mW from three Intan RHD2132s) for the complete BMI chain from recording to decoding. Our former work [47], which only extracts SBP features from three Intan RHD2132s, consumes 3× more power than the NeuRAD system. Comparing just processor consumption, the NeuRAD consumes 37× less power by avoiding an off-the-shelf microcontroller (MCU). The other neural recording devices [10], [61]–[64] consume 51 mW or 90.6 mW each for recording the neural signal wirelessly, which are 4× and 7× higher than the NeuRAD, respectively. In [21], [31], the mixed signal computing array chips consumed 0.4 μW and 4 mW, respectively, though the power overhead of the MCU, AFE, and TX/RX interfaces was not included and the devices were not tested in-vivo.

TABLE III.

Comparision with Previous Work

References	Tdis work	[47]	[61] [62] [63]	[10] [64]	[21]	[31]
Type	ASIC external wired	MCU external wired	ASIC external wireless	ASIC implanted wireless	ASIC implanted wireless	ASIC implanted wired
Amplifier Bandwidth	300–1000 Hz	300–1000 Hz	100–7800 Hz	500–5000 Hz	N/A	300–7000 Hz
Number of Channels	93	96	97	100	128	15
Sampling Frequency	2 kSps	2 kSps	20 kSps	20 kSps	20 kSps	25 kSps
Feature Extraction	SBP(CAR)	SBP	N/A	N/A	Spike firing rate*	Spike firing rate*
Decoding	SSKF continuous	N/A	N/A	N/A	Extreme Learning Machine (ELM) discrete (13 classes)	Spiking neural network discrete (63 classes)
Subject model	NHP	NHP	Human & NHP	NHP	NHP (No in-vivo)	Rodent (No in-vivo)
Data-Rate Reduction	4,800× (1D) 2,325× (2D)	100×	1× (recording only)	1× (recording only)	1000×	768×
Data Format	16b fixed-point	32b floating point	12b fixed-point	12b fixed-point	7b fixed-point	8b fixed-point
Process	180 nm	-	500,180 nm	600 nm	350 nm	180 nm
Power	0.581 mW (1D) / 0.588 mW (2D) RHD2132s: 12 mW	33.6 mW	51 mW	90.6 mW	Mixed-signal computing array: 0.4 μW**	Mixed-signal computing array: 4 mW**

^*Off-chip feature extraction used.

^**Power of MCU, AFE, TX/RX not included.

B. Closed-Loop Decoding

Offline testing of the NeuRAD enabled validation of the components with rapid timelines. However, there are a number of real-time variables that can impact the NeuRAD’s capabilities of accurately predicting a user’s intentions online, such as reduced SNRs due to higher electrode impedance compared to the amplifier input impedance, the presence of visual feedback, and the impact of the prediction latency on the BMI feedback loop. We validated functionality of the NeuRAD by directly recording from Monkey N’s Utah arrays using the RHD2132 bioamplifiers and predicting his intended finger movements in real-time using 1D and 2D SSKFs.

Fig. 13 illustrates 1D and 2D closed-loop prediction capabilities. In a one-dimensional task, Monkey N could use the NeuRAD to acquire targets with a 100% success rate with a mean acquisition time of 0.82 s, which was comparable to the best performance we previously presented using our high-powered brain-machine interface rig (99% success rate with a 1.3 s mean acquisition time) [46]. Cross-validated training correlation for velocity during the manipulandum control trials was 0.49. In the control experiment collected four days later, Monkey N acquired 100% of the targets with a mean acquisition time of 0.55 s using the high-power brain-machine interface, which exceeds but is comparable to the NeuRAD’s performance.

Fig. 13.

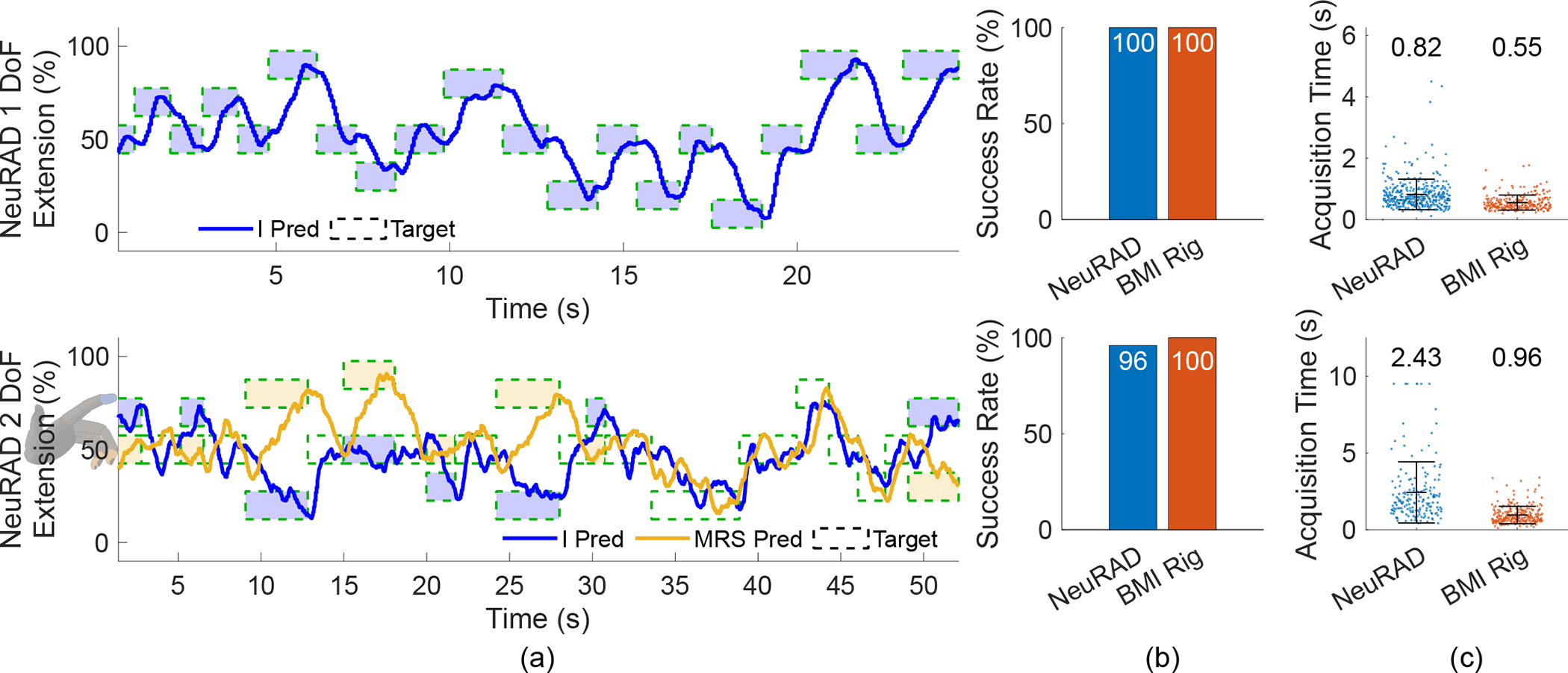
In vivo closed-loop decoding experiment results with the NeuRAD. The top row represents one-dimensional control, and the bottom row represents two-dimensional control. Asterisks indicate significant difference by a two-tailed two-sample t-test, p < 0.001. (a) The traces of the virtual finger positions as predicted by NeuRAD. (b) The success rates of target acquisition for each control system. (c) Target acquisition times for each control system. Each dot represents one trial.

In a two-dimensional task, Monkey N could acquire 96% of the targets with a 2.4 s mean acquisition time, which is lower but comparable to the best performance we previously presented (99% success rate with a 1.01 s mean acquisition time) [54]. Cross-validated training correlation for velocity during the manipulandum control trials was 0.29. In the control experiment collected 20 days prior, Monkey N could acquire 100% of the targets with a 0.96 s mean acquisition time. Supplementary Video 1 illustrates Monkey N’s usage of the NeuRAD to control the 1D and 2D movements of the virtual hand in real-time with comparison to the control sessions using the high-powered brain-machine interface rig. Fig. 15 shows the quality of spiking activity the day following the two-dimensional decoding experiment.

Fig. 15.

Snapshot of Monkey N’s array the day after the two-dimensional decoding experiment. Each square shows time-aligned threshold crossings of a −4.5 RMS voltage level for each electrode sampled at 30 kSps by the Cerebus.

Although the performance is adequate for a closed-loop BMI, we hypothesized that the reduction in performance was either due to lower fixed-point precision when computing SSKF predictions or worse signal-to-noise ratios when recording with the RHD2132s instead of the Cerebus. First, we took the same SBP measurements recorded during Monkey N’s usage of the 1D closed-loop ReFIT Kalman filter and predicted behavior with a double-precision SSKF (not in closed-loop, but using SBP measured during closed-loop control). The correlation between the two sets of predictions was 0.9997, suggesting precision did not substantially impact performance. To validate the impact of recording quality, we recorded a high-signal-to-noise ratio unit from Monkey N’s array at a high sampling rate using both recording systems. Fig. 14 shows example snippets from each recording as well as the sorted units overlaid as recorded by each system. We found that the RHD2132s recorded the unit with a 8.09 signal-to-noise ratio, approximately 8.6% smaller than the 8.85 signal-to-noise ratio with which the Cerebus recorded.

Fig. 14.

Comparison between the recording qualities of the RHD2132 and the Cerebus. (a) Example recordings from each system acquired on two consecutive days. (b) Comparison between spike waveform signal-to-noise ratios (SNRs).

To achieve this level of performance, the NeuRAD consumed just 581 μW for 1-DoF inference task and 588 μW for 2-DoF task with the bioamplifiers consuming a total 12 mW.

IV. Conclusion

Here, we have presented NeuRAD, a neural recording and decoding ASIC capable of real-time feature extraction and two degree-of-freedom predictions. Utilizing the Intan RHD2132s for power-efficient digital conversion of neural activity enabled low-power data acquisition and processing within the NeuRAD. The optimized SBPU hardware accelerator off-loaded the power-hungry SBP computations from the M0 processing core, leaving the M0 and the MAU to make intention predictions with the flexibility to choose the decoding algorithm. The NeuRAD also demonstrates that low-power, closed-loop, intracortical brain-machine interfaces are feasible in just 13 mW with off-the-shelf amplifiers, drastically reducing the power consumption compared to our previously published device and others while simultaneously incorporating additional functionality (on-chip feature extraction and decoding).

The power consumption of the Intan RHD2132 bioamplifiers was optimized by taking advantage of the 300–1,000 Hz spiking band power as a neural feature. Such a low-bandwidth setting brought the consumption of the amplifiers to 4 mW per chip, or 12 mW total. While this is substantially low-power for 32 low-noise, high-gain neural amplifiers, the RHD2132s support flexible filter cutoffs, sampling rates, and other features that make them the primary dominating component of the BMI compared to the processing hardware. The AFE could be made even more efficient by customizing the amplifiers to the spiking band, as we have shown previously [65], [66], or by developing the device with a more advanced process node. Additionally, by integrating the AFE into the NeuRAD, an additional 30% power savings could be achieved in the digital domain by eliminating the integrated level-shifter the NeuRAD requires to communicate with the Intan RHD2132s. We previously presented such an advantage [66] in a device which integrates an AFE and an SBP calculation unit in a single chip to save power for a free-floating mote application. In the device, pulse-interval modulated SBP was calculated by accumulating pulses, which were generated from the neural signal, and it was transmitted accordingly [67]. The scheme reduces power consumption for a free-floating mote application at the cost of measurement quality of the signal and off-chip demodulation overhead. Despite these potential power-saving customizations, using an off-the-shelf AFE provided its own set of advantages. Computation in the analog domain can have reliability and scalability issues, so we could avoid a potentially iterative process and focus on a rapid digital circuit prototype by using the established RHD2132s. Moreover, with devices like those we previously presented [65], [66], SBP output needs to be demodulated for inference calculation. Additionally, with the devices, implementing a common average referencing scheme would be challenging, something relatively trivial with raw samples in the digital domain, as was done in the NeuRAD. Lastly, using a validated, commercial AFE as the interface to the electrodes, device safety validation for human use might be accelerated, as the RHD2132 has already been used with humans [68].

Although the Kalman filter has been established in the literature as a high-performance control algorithm for brain-machine interfaces, many groups are investigating the use of more complex prediction algorithms to achieve higher levels of performance and longer decoder stability. For example, the shallow-layer, feed-forward neural network we recently presented that may improve performance over standard linear algorithms [51] might also be supported by this architecture. Unfortunately, in cases of greater computational complexity, the SRAM capacity incorporated in the NeuRAD quickly becomes a limiting factor in the number of learned parameters that can be stored. However, the architecture demonstrated here could support additional SRAM units for increased algorithmic complexity, replacement of the M0 core with a more powerful processing unit, or replacement of the M0 core with a customized integrated processing unit, such as a neural network accelerator [69], [70]. We have previously shown that brain-machine interface power consumption is heavily dominated by the AFE [46], indicating the possibility of incorporating even more complex processing hardware than what we have implemented here without drastically increasing power consumption.

In terms of closed-loop feedback control, the NeuRAD demonstrated it could predict one- and two-dimensional hand movements in real-time with high accuracy and reasonable acquisition times compared to our high-powered BMI rig. We hypothesize that the performance losses are direct results of worse SNRs when using the RHD2132s, which have amplifiers with substantially lower input impedances compared to the Cerebus (13 MΩ vs. >1 TΩ, respectively). From the perspective of functional restoration, however, the capability to control multiple dimensions simultaneously opens a realm of tasks that cannot be accomplished with one-dimensional control. In addition to the restoration of multiple-degree-of-freedom finger and arm function through functional electrical stimulation [71], controlling just two-dimensions enables the usage of computers, which have become central to modern livelihood. Several studies have investigated the use of high-powered BMIs to control computer cursors for typing [48], [72], [73] and tablet control [74]. The work presented here demonstrates that the same functional restoration can be achieved with a low-power BMI in a package suitable for portability and implantability.

The investigation of brain-machine interfaces in people with paralysis has grown drastically over the past two decades, with landmark accomplishments in the use of prostheses, development of novel techniques, and improvements in performance [1], [2], [6], [75]–[77]. These impressive outcomes from laboratory research reinforce the necessity of portable, clinically-viable brain-machine interfaces to translate these accomplishments to use in everyday life. The NeuRAD presented here and the work of others [10], [28], [61], [63] demonstrate that BMI technology has advanced far enough to be simultaneously optimized for power consumption, portability, implantability, and performance, in one complete package. However, only one such device has translated to use with humans [63], with a few more in the development stages at various venture interests [28]. There remain many improvements to BMIs that can be validated without incorporation into a monolothic device and instead can take advantage of existing off-the-shelf components. It still remains unclear what characteristics of these devices people with paralysis will find most important, motivating a need to safely and rapidly test modular solutions, which can be accomplished with off-the-shelf devices.

Biographies

Hyochan An (Student Member, IEEE) received the B.S. degree in electrical and computer engineering from Sungkyunkwan University, Seoul, South Korea, in 2014. He is currently pursuing the Ph.D. degree at the University of Michigan, Ann Arbor, MI, USA. He is a recipient of the Doctoral Fellowship from the Kwanjeong Educational Foundation in Korea. Between 2014 and 2017 he had worked as an Engineer for Samsung Electronics, Hwasung, Korea. His current research interests are energy-efficient accelerator design and system.

Samuel R. Nason-Tomaszewski received his B.S. degree in Electrical Engineering at the University of Florida with summa cum laude honors in 2016. Then, he proceeded to obtain his M.S. degree in 2018 followed by his Ph.D. degree in Biomedical Engineering in 2022 with Dr. Cindy Chestek at the University of Michigan. His dissertation focused on low-power brain-machine interface technologies for restoring function to paralyzed fingers through functional electrical stimulation. He is now a post-doctoral fellow with Dr. Chethan Pandarinath at Emory University. Sam was awarded an F31 predoctoral fellowship from the National Institutes of Health and won the 2021 Towner Prize for Outstanding PhD Research at the University of Michigan College of Engineering for his dissertation work.

Jongyup Lim (Member, IEEE) received the B.S. degree (summa cum laude) in electrical and computer engineering from Seoul National University, Seoul, South Korea, in 2016, and the M.S. and Ph.D. degrees in electrical and computer engineering from the University of Michigan, Ann Arbor, MI, USA, in 2018 and 2021, respectively. During his Ph.D. degree, he interned at Apple, Cupertino, CA, USA. His research interests include wireless neural recording systems, energy-efficient deep learning hardware, clock generation, and ultralow-power sensor node design. Dr. Lim was a recipient of the Doctoral Fellowship from the Kwanjeong Educational Foundation in South Korea.

Kyumin Kwon received the B.S. degree in electrical and electronic engineering from Yonsei University, Seoul, South Korea, in 2017. He is currently pursuing M.S. and Ph.D. degree in electrical and computer engineering from the University of Michigan, Ann Arbor, MI, USA. During his M.S. degree, he interned at Texas Instruments, Santa Clara, CA, USA. During his Ph.D. degree, he interned at Intel, Hillsboro, OR, USA. His research interests include phase locked loops, synthesizable analog blocks and design automation.

Matthew S. Willsey grew up in Indiana. He attended MIT, where he received B.S. and M.Eng degrees in Electrical Engineering with a research focus in digital signal processing. He completed medical school at Baylor College of Medicine and began his neurosurgery residency at the University of Michigan in 2014. He completed a PhD in Biomedical Engineering at the University of Michigan in 2020 under Drs. Parag Patil and Cynthia Chestek with a dissertation focused on neuromodulation and brain-machine interfaces. He will complete his residency in June of 2022.

Parag G. Patil, MD PhD joined the faculty at the University of Michigan in 2005. A native of Pennsylvania, he attended MIT, where he received a BS in electrical engineering in 1989. After graduation, he was awarded a Marshall Scholarship to study Philosophy and Economics at Magdalen College, Oxford University in the UK. On returning to the US, Dr. Patil pursued combined medical and doctoral studies in biomedical engineering at Johns Hopkins University (MD/PhD 1999), followed by neurosurgery residency at Duke University and fellowship at the University of Toronto.

Dr. Patil is currently Associate Professor of Neurosurgery, Neurology, Anesthesiology, and Biomedical Engineering. In addition, he serves as Associate Chair for Clinical and Translational Research, Co-Director of the Neuroscience and Sensory Clinical Trial Support Unit (CTSU), and in a leadership role in diverse multi-disciplinary, multi-investigator research efforts. His academic goal is to utilize engineering and mathematical techniques, along with interdisciplinary collaboration, to improve neuroprosthetics and to perform translational neuroscience research.

Hun-seok Kim (Member, IEEE) received the B.S. degree in electrical engineering from Seoul National University, Seoul, South Korea, in 2001, and the Ph.D. degree in electrical engineering from the University of California at Los Angeles (UCLA), Los Angeles, CA, USA, in 2010. He is currently an Assistant Professor with the University of Michigan, Ann Arbor, MI, USA. His research focuses on system analysis, novel algorithms, and VLSI architectures for low-power/high-performance wireless communications, signal processing, computer vision, and machine learning systems. Dr. Kim is the recipient of the DARPA Young Faculty Award (2018), and NSF CAREER Award (2019). He is an Associate Editor of IEEE Transactions on Mobile Computing, IEEE Transactions on Green Communications and Networking, and the IEEE Solid State Circuits Letters.

Dennis Sylvester (S’95—M’00—SM’04—F’11) is the Edward S. Davidson Collegiate Professor of Electrical and Computer Engineering at the University of Michigan, Ann Arbor. His main research interests are in the design of miniaturized ultra-low power microsystems, touching on analog, mixed-signal, and digital circuits. He has published over 500 articles and holds more than 50 US patents in these areas. His research has been commercialized via three major venture capital funded startup companies; Ambiq Micro, Cubeworks, and Mythic. He has received eleven best paper awards and nominations and was named a Top Contributing Author at ISSCC and most prolific author at IEEE Symposium on VLSI Circuits. He is currently a member of the Administrative Committee for IEEE Solid-State Circuits Society, an Associate Editor for IEEE Journal of Solid-State Circuits, and was an IEEE Solid-State Circuits Society Distinguished Lecturer for 2016–2017. He received his PhD in Electrical Engineering from UC-Berkeley, and held research staff positions at Synopsys and Hewlett-Packard Laboratories as well as visiting professorships at the National University of Singapore and Nanyang Technological University.

Cynthia A. Chestek received the B.S. and M.S. degrees in electrical engineering from Case Western Reserve University in 2005 and the Ph.D. degree in electrical engineering from Stanford University in 2010. From 2010 to 2012, she was a Research Associate at the Stanford Department of Neurosurgery with the Braingate 2 clinical trial. In 2012 she became an assistant professor of Biomedical Engineering at the University of Michigan, Ann Arbor, MI, where she runs the Cortical Neural Prosthetics Lab. She is the author of 58 full-length scientific articles. Her research interests include high-density interfaces to the nervous system for the control of multiple degree of freedom hand and finger movements.

David Blaauw received his B.S. in physics and computer science from Duke University in 1986 and his Ph.D. in computer science from the University of Illinois at Urbana-Champaign in 1991. Until August 2001, he worked for Motorola, Inc. in Austin, TX, and since August 2001, he has been on the faculty of the University of Michigan, where he is the Kensall D. Wise Collegiate Professor of EECS. He has published over 600 papers, has received numerous best paper awards and nominations, and holds 65 patents. His research has coverved ultra-low-power computing for mm-sensors, hardware for neural networks in edge devices and genomics acceleration. He serves on the IEEE International Solid-State Circuits Conference’s technical program committee. He is an IEEE Fellow and the director of the Michigan Integrated Circuits Lab.