LYMESIM 2.0: An Updated Simulation of Blacklegged Tick (Acari: Ixodidae) Population Dynamics and Enzootic Transmission of Borrelia burgdorferi (Spirochaetales: Spirochaetaceae)

Abstract

Lyme disease is the most commonly reported vector-borne disease in the United States, and the number of cases reported each year continues to rise. The complex nature of the relationships between the pathogen (Borrelia burgdorferi sensu stricto), the tick vector (Ixodes scapularis Say), multiple vertebrate hosts, and numerous environmental factors creates challenges for understanding and predicting tick population and pathogen transmission dynamics. LYMESIM is a mechanistic model developed in the late 1990s to simulate the life-history of I. scapularis and transmission dynamics of B. burgdorferi s.s. Here we present LYMESIM 2.0, a modernized version of LYMESIM, that includes several modifications to enhance the biological realism of the model and to generate outcomes that are more readily measured under field conditions. The model is tested for three geographically distinct locations in New York, Minnesota, and Virginia. Model-simulated timing and densities of questing nymphs, infected nymphs, and abundances of nymphs feeding on hosts are consistent with field observations and reports for these locations. Sensitivity analysis highlighted the importance of temperature in host finding for the density of nymphs, the importance of transmission from small mammals to ticks on the density of infected nymphs, and temperature-related tick survival for both density of nymphs and infected nymphs. A key challenge for accurate modeling of these metrics is the need for regionally representative inputs for host populations and their fluctuations. LYMESIM 2.0 is a useful public health tool that downstream can be used to evaluate tick control interventions and can be adapted for other ticks and pathogens.

Lyme disease is the most commonly reported vector-borne disease in the United States with ≥30,000 infections reported each year (Schwartz et al. 2017). The majority of cases are reported from 14 high incidence states in the Northeast, mid-Atlantic, and upper Midwest where Ixodes scapularis Say is the primary vector of Borrelia burgdorferi sensu stricto (s.s.), the primary etiological agent of Lyme disease in the United States. Since 1991 when Lyme disease became a notifiable condition, the number of cases reported annually has nearly tripled (Mead 2015), the number of counties in the eastern United States where I. scapularis is considered established has more than doubled (Eisen et al. 2016), and the number of counties identified as reporting high incidence of Lyme disease cases has increased by more than 320% (Kugeler et al. 2015). This disturbing trend underscores a need for tick bite prevention and tick control strategies that are proven to prevent Lyme disease cases. Several strategies have been shown in small-scale field trials to yield promising results for reducing the abundance of questing ticks or ticks on hosts or disrupting B. burgdorferi s.s. transmission (Eisen and Dolan 2016). However, very few approaches have been tested, either singly or as integrated tick management strategies, in large-scale trials with epidemiological outcomes; this is in large part because such studies are very costly and time-consuming (Eisen and Eisen 2018)

Simulation models can be used to inexpensively screen in silico various intervention methods, alone or in combination, and can therefore be useful for prioritizing prevention strategies to test in large-scale, costly field trials. To enable such exploration, we have updated LYMESIM, a mechanistic model developed in the late 1990s that simulates the life-history of I. scapularis and transmission dynamics of B. burgdorferi s.s. (Mount et al. 1997b). The original LYMESIM model was used to evaluate selected management strategies, including those that aim to reduce questing ticks, ticks on hosts, or abundance of key hosts for adult ticks (Mount et al. 1997a, Hayes et al.1999). Over the past two decades, support of the LYMESIM code waned such that the original code is no longer available to would-be users, and the model executable (designed for mid-1990s Windows operating systems) does not function in modern computing environments. To reinvigorate the use of this simulation model as a decision support tool, and to set the groundwork for using LYMESIM to prioritize the most promising prevention strategies for costly large-scale trials, we have recoded the original LYMESIM in a modern coding language. In addition, we have made several modifications to increase the biological realism of the models and to generate outcomes that are more easily measured under field conditions (i.e., density of questing nymphs and density of questing infected nymphs).

Other mathematical and simulation models have been created to explore tick and tick-borne pathogen systems using a variety of techniques for analyzing the Lyme disease spirochete transmission system. As a simplified calculation for assessing acarological risk for exposure to Lyme disease spirochetes, a number of ecological approaches provided methods for estimating the density of infected nymphs given some basic information (LoGiudice et al. 2003). A small number of models were explored to look at the extension of Leslie matrix models to tick life history, and these models were used to calculate the predicted relative abundances of the life stages (Sandberg et al. 1992). More complex population models have also been tested to look at the potential role of long-distance dispersal of ticks by birds in the spread of Lyme disease (Heffernan et al. 2014). With the advancement of computation, a number of agent-based models were developed to explore highly localized population dynamics of ticks (Li et al. 2012, Halsey and Miller 2018). Ogden et al. (2005, 2006) created a similar complex simulation model focused on the range expansion of I. scapularis populations into Canada. Each model type and implementation has strengths and weaknesses.

The goal of the recreation of LYMESIM is to provide an explicit model for testing interventions at a community scale. This type of testing is not possible with large-scale population level models because most interventions affect only ticks on certain hosts or in a specific activity state, and the population models do not usually divide the population up by these factors. Additionally, previous agent-based models have been limited to small spatial scales because of the computational time required to simulate each individual tick. LYMESIM is a complex set of dynamic difference equations that explicitly model the weather and habitat conditions of a specific location. The model tracks the tick populations in a manner that will allow for assessment of explicit interventions, but the model is simpler than a full agent-based model, and thus will run very quickly. For example, the model tracks the specific density of ticks on a given host type, and so, a host-targeted intervention could be tested with the model explicitly removing only the ticks on the host at the time of the intervention. Finally, updating a previously published complex simulation such as LYMESIM allows us to leverage all the research that was used to develop the original model, update it with more recent findings, and then use it to test interventions as well as identify critical parameters that will inform future field and laboratory research.

Here we present the updated version of the LYMESIM model with a full description of the new simulation model. We also present the results of testing the model on three geographically distinct locations.

Methods

Overview of Changes to the Original LYMESIM Model

Overall, the structure and parameter values of the original LYMESIM model (Mount et al. 1997b) were maintained in this recoding. However, we made several modifications that fall into three broad categories: 1) modernization and simplification, 2) integration of updated data related to the tick-pathogen system, and 3) changes to increase ease of field evaluation of model outcomes.

Specifically, the updated model was implemented in R statistical software (R Development Core Team 2008), and weather inputs were updated to span the years 2007–2016. LYMESIM was the last in a series of tick life history models and was built heavily upon the previously published models for the lone star tick, Amblyomma americanum (L.) (Acari: Ixodidae) (Haile and Mount 1987, Mount et al. 1993), the American dog tick, Dermacentor variabilis (Say) (Acari: Ixodidae) (Cooksey et al. 1990), and the cattle ticks, Rhipicephalus (Boophilus) microplus (Canestrini) (Acari: Ixodidae) and Rhipicephalus annulatus (Say) (Acari: Ixodidae) (Mount et al. 1991). Consequently, much of the simulation description in the original LYMESIM publication (Mount et al. 1997a) simply referenced these previous papers. There were a few places where the exact implementation was unclear in either LYMESIM or the previous models. For example, there is no mention of any nonlinearities or density-dependent feedback, but the original model does not exhibit the expected exponential growth or exponential decay that would be expected from the described linear matrix model.

Additionally, there were no statements in the original descriptions of LYMESIM about limits to the number of ticks that can feed simultaneously on a host, without which the model would allow thousands of ticks to feed on a single mouse, for example. Also, there was no input data file or parameter screen to modify day length, which should vary depending on time of year and geographic location and would likely affect timing of diapause (Belozerov et al. 2002, Randolph 2004, Ogden et al. 2005). For these missing pieces, we relied on standard modeling techniques such as adding a limit to the number of ticks that can feed on an animal at one time. We also expanded the input data file to include day length as well as the weather variables for each specific location.

We also updated some aspects of this model based on current knowledge of the tick and the pathogen. For example, we set the transovarial transmission rate for B. burgdorferi s.s. to zero based on the recent realization that early reports of B. burgdorferi s.s. infection in unfed field-collected larvae most likely failed to distinguish this spirochete from the relapsing fever spirochete Borrelia miyamotoi, which is passed transovarially in I. scapularis (Scoles et al. 2001, Rollend et al. 2013, Lynn et al. 2019). Several other parameter values were updated using subject matter expert opinion based on studies that have been published since the release of the original LYMESIM (see Supp Tables 1–7 [online only]). Additionally, we used five of the six original host types, but we replaced the large mammals host type—which referred to domestic livestock—with a more biologically meaningful host type comprising insectivores and other B. burgdorferi s.s.-reservoirs separate from the host type represented by the white-footed mouse (Peromyscus leucopus Rafinesque [Rodentia: Cricetidae]). A final model modification was the changed implementation of the survival for ticks of different life stages in the host-seeking category. We updated the survival function using simplified mathematics and modified assumptions about the physiological cost of questing to yield more realistic phenology curves across different regions of the United States. In addition to the simple percent survival based on weather conditions, each age class has a maximum number of weeks in that life stage, and that maximum is reduced for each week spent questing as a representation of the loss of fat reserves resulting from the energy required for that activity (Randolph 2004).

Finally, the original model did not include commonly measured field outcomes, such as the density of questing nymphs (DON) and the density of B. burgdorferi s.s.-infected questing nymphs (DIN); therefore, proxies of these measures were included in the updated model to enable evaluation of the model outputs using field data. Because DON and DIN are typically measured in forested areas, we restricted this model to 95% forest and 5% ecotone habitat, although other vegetation types (i.e., meadows) were included in the code for the model and could be used in future realizations of the model.

Model Structure: Life Cycle

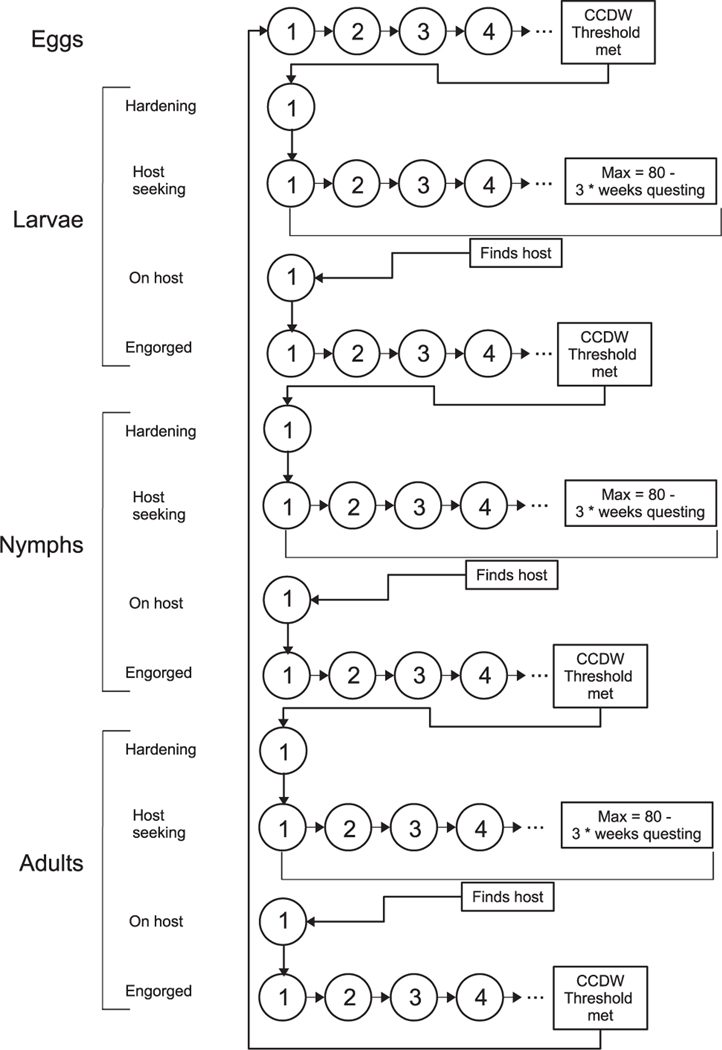
The tick portion of the updated model uses a series of cohort-based, discrete-time, age-structured equations with a 1-wk time step as shown in Fig. 1. All eggs laid in the same week are assigned to a single cohort, and that cohort moves through sequential age classes subjected to mortality from environmental and biological factors. That egg cohort tracks its own cumulative cohort degree week (explained below) until the total is more than the threshold required to progress to the next life stage, and then the entire cohort emerges as a larval cohort. All three blood-feeding life stages are broken into four activity stages: hardening, host-seeking, on-host, and engorged off-host. All cohorts of all life stages and activity age-classes are subjected to mortality from environmental and biological factors specifically calculated for that age-class. The first age-class after emergence for all life stages is assumed to be a hardening week after which the entire cohort is moved into the host-seeking activity age-classes. Each host-seeking cohort starts with the maximum of 80 wk for survival, and this maximum is reduced by 3 wk for each week the cohort is actively questing. Each week, as determined by host availability, a portion of the host-seeking cohort moves out of that activity age-class and into the on-host age class while the remainder less than age-class mortality move to the next host-seeking age-class unless the cohort has reached the maximum survival week, in which case that cohort is removed. The ticks that found a host are moved into the single week on-host age-class with a host-based mortality while on-host (calculation given below). All ticks surviving the on-host age-class are moved into an engorged cohort that moves through the age-classes much like the egg cohorts. Larval- and nymphal-engorged tick cohorts track their own cumulative cohort degree weeks. When the threshold is met, the tick cohort molts to the next life stage and moves into the hardening age-class. Engorged adult cohorts also track the cumulative cohort degree week, but after meeting the threshold, the females, which are assumed to be half of the adult cohort total, lay eggs to start the cycle again with a new cohort of eggs.

Fig. 1.

Life cycle model for Ixodes scapularis. Each circle is a 1-wk age-class and is subjected to an appropriate mortality rate depending on the stage, activity, weather conditions, and host availability. Cohort cumulative degree week (CCDW) is a variable assigned to each cohort that tracks the cumulative number of degrees that the weekly average temperature is above 6, the development threshold temperature. An egg cohort will transition to larvae when its CCDW is greater than 110. Similarly, an engorged larval cohort will emerge as nymphs when its CCDW is greater than 58, and an engorged nymphal cohort will emerge as adults when its CCDW is greater than 81. Finally, the engorged adult female cohort will lay eggs when the CCDW is greater than 28. Each host-seeking stage cohort is limited to a maximum of 80 wk less three times the number of weeks that cohort has been questing but unable to find a host.

Hosts relevant to the I. scapularis life cycle or enzootic maintenance of B. burgdorferi s.s. are modeled using six host types. Four of these host types are identical to those from the original model: the single species classes of white-footed mice (WFM) and white-tailed deer (WTD), and the multi-species classes of medium-sized mammals (MSM) and reptiles (REP). A fifth, changed host type from the original model is labeled (SHREW) and comprised of insectivores and other highly reservoir competent small mammals, separate from white-footed mice, as these have been shown to potentially play a large role for enzootic maintenance of B. burgdorferi s.s. (Brisson et al. 2008). The sixth and final host type—all other small mammals and birds (SMB)—is similar to the original model with the exception that some species were moved from this host type to the new host type called SHREW. The large mammals host type from the original model was omitted since it represented cattle and other large livestock, which play little role for either population dynamics of I. scapularis or enzootic maintenance of B. burgdorferi s.s. Each host type has an upper limit, i.e., carrying capacity, for the number of larvae, nymphs, and adults that can be feeding at one time on an animal of that type. Host-finding rates and habitat preferences vary by host type, and each host type is held at a constant density with equal birth and death rates equal to the inverse of the average life expectancy.

Model Structure: Weather Inputs

The original weather data input files for LYMESIM contained four input variables including weekly averages for temperature (degrees Celsius), saturation deficit (millibars), and relative humidity (percentage) plus the total weekly rainfall (cm), but the humidity data were never used in the model. Following the original model, we converted R(t), the total rainfall amount in week t, into a precipitation index, PI(t). The precipitation index was defined as follows: $PI(t)=R(t)/10+PI(t-1)\ast 0.65$. In addition, the model as described in (Mount et al. 1997a,b) used day length, but this value was not in any input file or input screen for LYMESIM, so it is unclear if the original model allowed this to vary between geographic locations. Day length is included in this simulation as an input parameter that depends on the exact hours of daylight for each specific location. The new LYMESIM input files require the same four weather variables using the same units as well as a new column to calculate the precipitation index plus another new column for weekly averaged day length in hours specific to the location of interest.

Model Structure: Temperature-Dependent Development and Fecundity Rates

As in the original model, hatching and molting rates are temperature-dependent. Because cohorts of eggs, larvae, nymphs, or adults could emerge in any given week and cross over from 1 yr to the next, each cohort has its own cohort-cumulative degree week (CCDW) total rather than the more commonly used calendar-year–based cumulative degree week total. The development thresholds and CCDW totals were taken directly from the original LYMESIM. All CCDW calculations use the same development threshold of 6°C, i.e., for a given cohort, CCDW are only accumulated when the temperature exceeds this threshold. The work of Ogden et al. (2004) showed that eggs can develop at temperatures as low as 4°C but at such a slow rate that it is unlikely to contribute to long-term dynamcis. The number of degree weeks for a week above the threshold is equal to the average weekly temperature minus 6°C and that difference is added to the total for each individual CCDW total. One assumption in the current version of the model is that there are no differences in the time required to accumulate the degree weeks, i.e., there is no difference if the CCDW is accumulated slowly over many weeks or quickly in a single week.

As in the original model, for a given cohort of eggs, once the CCDW totals more than 110, the eggs are moved into the larval life-stage (see Supp Fig. 1 [online only]). For an engorged larval cohort, a CCDW total of more than 58 would move that cohort to the first stage of nymphs. Similarly, for an engorged cohort of nymphs, a total of more than 81 would move the cohort to the first stage of adults. Finally, for engorged females, which is assumed to be half of all adults, a total CCDW greater than 28 would produce a cohort of eggs. Although there is limited evidence to support temperature-dependent fecundity, we kept the function in this version to remain true to the original model and for a more flexible model in the future. The model output is nearly identical when this function is replaced with a constant. The number of eggs laid per female is modeled to be temperature-dependent (Fish 1993), and for a temperature of T is given by

$$F=-24.58678T^2+835.9505T-4105.579,6<T<28,$$

$$F=0\text{, otherwise}.$$

This equation only gives positive numbers for weekly average temperatures between 6 and 28°C and has a maximum of approximately 3000 eggs at 17°C.

Model Structure: Survival Rates Off-Host

Each life stage and activity category has a maximum survival rate given in Supp Table 3 (online only) as a function of habitat type. Although the meadow habitat is not used for the current scenario evaluations, it was kept in the model for future scenarios to compare with field data that included meadow habitat. Each survival rate is then calculated weekly based on a complex combination of this maximum and quadratic and hyperbolic functions of precipitation index, temperature, and saturation deficits. Part of the original initialization of LYMESIM is to declare the division of the area being modeled by habitat type to give the proportion that is meadow, ecotone, and forest (M, E, and F, respectively; Supp Table 1 [online only]). Ticks are assumed to only move meaningful distances horizontally while on host, and so these habitat proportions are combined with the habitat preferences for each host type (H_M, H_E, H_F) to calculate the relative proportions of ticks expected to be found in each habitat type. These proportions are a weighted average of the habitat proportions and the relative preferences for each habitat type for each host type as well as the percent of blood meals that came from that host type. This calculation is done for each life stage, and then the relative expected percentage of ticks in each habitat type is given for the engorged off-host age classes of that life stage through the next bloodmeal. Of note, this implies that the expected location of eggs and unfed larval age classes will follow the adjusted habitat proportions for engorged adults since that is where the eggs are laid.

This survival factor is calculated as follows. First, an estimate of the total number of blood meals available for a given life stage will be a sum of the carrying capacity for each host type (K_H) times the density of that host type (H_T). The percent of blood meals from that host type, B_H, is then given by

$$B_H=\frac{K_H{H}_T}{{\sum }_X{K}_X{X}_T}.$$

Then the adjusted habitat proportions would be

$$F_A=\sum _{HostTypes}\frac{B_{H}F{H}_F}{F{H}_F+E{H}_E+M{H}_M},$$

$$E_A=\sum _{HostTypes}\frac{B_{H}E{H}_E}{F{H}_F+E{H}_E+M{H}_M},$$

$$M_A=\sum _{HostTypes}\frac{B_{H}M{H}_M}{F{H}_F+E{H}_E+M{H}_M}.$$

Based on the adjusted habitat proportions (F_A,E_A,M_A) for a given geographic location, the maximum survival for each age class, X, can be calculated as a weighted average of the values in Supp Table 3 (online only):

$$S_X=S_E(forest)\ast F_A+S_E(ecotone)\ast E_A+S_E(meadow)\ast M_A.$$

Using the parameters given in Supp Table 4 (online only), the total weekly survival rates are calculated by

$$Total=\frac{S_X\left(a_{sd}S{D}^2+b_{sd}SD+c_{sd}\right)\left(a_{pi}P{I}^2+b_{pi}PI+c_{pi}\right)\left(a_t+c_{t}T+e_t{T}^2\right)}{1+b_{t}T+d_t{T}^2},$$

where S_X is the maximum survival rate for age class X in an area with a given habitat vector, SD is the weekly saturation deficit, PI is the weekly precipitation index, T is the weekly temperature, and all parameters are taken from the appropriate row in Supp Table 4 (online only).

Model Structure: Activity-Dependent Maximum Survival

The original LYMESIM model had two survival rates for each life stage according to the age of the cohort with survival after 40 wk. To add the flexibility to LYMESIM for the variations in longevity found in the upper Midwestern United States (Hamer et al. 2012), we have modeled survival slightly differently. With the original environmentally driven mortality, which results in an exponential decay in the size of the population, we found that there were still ticks that could survive essentially forever. To replace that with a more realistic scenario, all three life stages are assumed to be able to survive up to a maximum of 80 wk, but for each cohort of ticks, this maximum is reduced by 3 wk for each week spend actively questing, e.g., $H{F}_X>0$. This survival assumes that a tick has a fixed amount of energy reserves that would allow for survival up to 80 wk with no activity and assumes that actively questing costs three times the energy that is spent inactive. The exact amount of energy used and the maximum survival times need to be evaluated with field and laboratory data.

Model Structure: Host-Finding Rates

Contrary to the name from the original model, not all ticks in the host-finding stages are actively host-seeking, but rather a specific host-finding rate is calculated for each week to determine the exact number that are actively host-seeking while the rest remain quiescent. Host-finding rates depend on both day length and temperature as well as the presumed amount of the area that a specific host type would cover within a week. Each host type had a base host-finding rate (BHRF) derived from an allometric relationship with host density (HD). For all host types and life stages, b = 0.515, and the values for a are given in Supp Table 5 (online only). The environmental parameters of weekly average day length (DL) and weekly average temperature (T) are used to calculate the adjusted host finding rates for larval and nymphal life stages while only weekly average temperature was used for the adjustments to adult rates,

$$\begin{array}{c}H{F}_{L,N}=a{(HD)}^b\left(-0.0105T^2+0.4316T-3.424\right)\times \\ \frac{\left(0.03116-0.007615DL+0.00004469D{L}^2\right)}{1-0.1374DL+0.004788D{L}^2},10.8<T<30.2,\end{array}$$

$$H{F}_A=a{(HD)}^b\left(-0.0095T^2+0.19T+0.05\right),0<T<\mathrm{20.2.}$$

The original equation in the description of LYMESIM (Mount et al. 1997b) has an error in the denominator of the day length calculation with positive linear term instead of the corrected negative shown above. Additionally, it is unclear the exact relationship between day length and activity of I. scapularis (Goddard 1992). These host finding rates were set to zero outside of the ranges listed above as otherwise the rates are calculated to be negative values. Within the hosts for a given life stage, there are no explicit host preference as there are no known experiments that have explicitly compared these host types, and so ticks are scaled across all available hosts if there are more hosts than needed.

Model Structure: Density-Dependent Survival on Hosts

The original LYMESIM model as described (Mount et al. 1997a,b) indicates only a decreased survival on-host from an exposure index. This index presupposes that the animals will develop resistance to ticks over time through exposure, but this resistance is short-lived and will wane within approximately 8 wk without tick exposure. Although it is unclear that hosts can develop this type of immunological resistance to I. scapularis (Levin and Fish 1998), there is evidence of mortality on host from host grooming behavior (Shaw et al. 2003). Although mortality from immunological response and from grooming behavior is very different biologically, the same mathematical formula can be used for both with increased mortality based on increased density on-host within a short period of time, and this mortality would be applied to all ticks including adult males.

The first step to calculation of the exposure index is to scale the immature life stages to the adult stage. The original LYMESIM model used the equivalent factors from A. americanum as they found no other reports of engorged I. scapularis immatures. In a study to assess the effects of a fungus on I. scapularis, the average engorged weights for the life stages of the control groups now give us this relationship for I. scapularis (Hornbostel et al. 2004). Average total weights of engorged ticks were 204 mg for females, 2.8 mg for nymphs, and 0.43 mg for larvae. This gives an equivalent factor relative to females of 0.014 for nymphs and 0.0021 for larvae. These factors are then applied to the tick burden on each host type to calculate the total engorgement index (EI). The tick burden for each host type is then combined with the tick burden from the previous weeks, with a weekly loss rate of 0.44. As this reduces the contribution of tick burdens by more than 99% after 8 wk, the simulation only calculates the contribution for the previous 8 wk,

$$EI(X,t)=\sum _{i=1}^9{0.44}^{i-1}\left[0.0021L_X(t-i)+0.014N_X(t-i)+A_X(t-i)\right],$$

where X is the host type, t is the simulation week, A_X(t) is the adult tick burden on host type X in week t, N_X(t) is the nymphal tick burden on host type X in week t, and L_X(t) is the larval tick burden on host type X in week t. Then for each host type, there is a given relationship between EI and the on-host survival. The original relationships were used and are shown in Supp Fig. 2 (online only).

Model Structure: Infection Dynamics

The simulation uses a standard susceptible-infected transmission model for the dynamics of B. burgdorferi s.s. Most key assumptions used in the original LYMESIM model remain in the current simulation along with a few changes. Shrews and other reservoir competent small mammals (SHREW) along with white-footed mice (WFM) host types are considered highly competent reservoirs for B. burgdorferi s.s., and ticks feeding on infected individuals are considered highly likely to acquire the pathogen, whereas other small mammals and birds (SMB) or medium-sized mammals (MSM) are assumed to be less effective reservoirs, resulting in pathogen acquisition by a lower proportion of feeding ticks (Supp Table 7 [online only]; Donahue et al. 1987, Ginsberg et al. 2005, Brunner et al. 2008). Reptiles (REP) and white-tailed deer (WTD) host types are assumed to be unable to serve as reservoirs, thus producing no infected fed ticks, but can serve as a source for blood meals (Telford III et al. 1988, Rulison et al. 2014). Assumptions in the current simulation include: 1) only the host types WFM, SHREW, SMB, and MSM can be infected, 2) all infected hosts are equally infectious to feeding ticks, and all infected ticks are equally likely to transmit the pathogen, 3) once a host is infected, it remains infected for life, 4) infected ticks and hosts have the same survival or reproduction rates as uninfected ticks and hosts, and 5) there is only one strain of B. burgdorferi s.s. in the system. Additionally, one key change from the original model is that transovarial transmission within the tick population is set to zero.

All transmission involves a tick vector: susceptible hosts can be infected through serving as a host for an infected tick, and susceptible ticks can be infected through feeding on an infectious host. Hosts have a constant population, but there is turnover through constant and equal birth and death rates. This turnover creates a constant pool of susceptible hosts as all hosts are born susceptible. Turnover rates are based on the average lifespan of the hosts for each host type, and the values used are given in Supp Table 6 (online only).

In the updated LYMESIM, it is assumed that the proportion of previously uninfected ticks that acquire infection during the week while feeding on an infected host, regardless of tick life stage, is 70% for WFM, 50% for SHREW, 5–10% for SMB and MSM, and 0% for REP and WTD (see Supp Table 7 [online only]). Susceptible hosts can similarly acquire the pathogen when an infected tick feeds on them. It is assumed, based on published information, that the probability of a susceptible host becoming infected with B. burgdorferi s.s. from the bite of a single infected I. scapularis nymph is extremely high to nearly 100% (Goddard et al. 2015, Eisen 2018). This parameter was called the tick infectivity factor (TIF) in the original model, and we set this parameter value to 90% for transmission from infectious nymphs and adults to hosts. Because a single host can be infested by multiple ticks, this simulation used the same approach as the original LYMESIM to scale the percent of hosts that get infected in a given week by the ratio of infectious ticks per host in that week. To calculate this percentage, a Monte Carlo simulation is used to combine the abundance of infectious ticks on a host, host density, and the infectiousness of the pathogen (Cooksey et al. 1990). For each host type, the TIF is then combined with the total abundance of infectious ticks (ITD) and the host density (HD) to get the average number of infected ticks per host (ITH) by

$$ITH=(ITD/HD)\ast TIF.$$

In addition, a separate Monte Carlo simulation was used to create the most likely percentage of hosts infected for a given ITH. To create this relationship, the simulation assigned ticks to a set of 100 hosts for a variety of levels of ITH from 0.01 to 7.5 in increments of 0.01. For each increment, the simulation used a random sample procedure to assign each tick to a host with replacement (see Supp Fig. 3 [online only]). This sampling creates a look up table that can be used for each host type each time step based on the calculated ITH.

Output Variables

To summarize the results of each model, we used a variety of outputs. The original LYMESIM model used two basic output measures: abundance of ticks on mice and abundance of ticks on all host types. Although these data are useful for comparison with ticks from hosts, they are not equivalent to what is expected for data for questing ticks based on drag sampling. For the comparisons with the original LYMESIM model, we used the abundance of ticks on host for each life stage as was done in the original software. To compare the new location scenarios with field data, we needed to calculate the model predictions of density of questing nymphal ticks to compare with the standard density of nymphs (DON) and density of B. burgdorferi s.s.-infected nymphs (DIN) measures generated by drag sampling. Because of how the model is set up, not all ticks in the host-seeking age-classes are truly actively questing in the traditional field use of the term. For each time step, there is a calculation based on weather conditions to estimate the percent of the host-seeking age-class that would be questing, called host-finding in the model. The remaining percent of the host-seeking age-class ticks are assumed to be quiescent. Because of the limitations of the carrying capacity on the hosts present, not all ticks who quest are successful, and there is often a ‘surplus’ of ticks that would feed on hosts, if carrying capacity were increased, but are returned in the model to the host-seeking age-class to try again in the following week. This ‘surplus’ of ticks ready to find a host are assumed to be the questing ones that would be collected if one were out dragging for ticks. Thus, in the model, we track the density of surplus nymphs in a given week, which is equivalent to DON, and the density of infected surplus nymphs, which is equivalent to DIN. We also report the ticks on hosts for comparison with the original LYMESIM and call them nymphs on hosts (NOH) and infected nymphs on hosts (INOH).

Model Scenarios

The new LYMESIM model was run using the input weather data and most of the original parameter values from the original software. Notably the weather data for the original software were from NOAA’s Comparative Climate Data Center, whereas for the updated model, we obtained weekly weather data for 2007–2016, as well as an average for that time frame, derived from the forcing data set (version 2) of the North American Land Data Assimilation System (NLDAS; Cosgrove et al. 2003). NLDAS was chosen because it provides a continuous spatiotemporal record of meteorological conditions over the United States and southern Canada for recent decades, and because it yielded realistic results in a study of the seasonality of Lyme disease (Moore et al. 2014). To explore the new LYMESIM 2.0 model, we chose three locations based on availability of published and unpublished DON and DIN data for comparison to model output. These locations were Norfolk, VA; Cary Institute near Millbrook, NY (here called Cary, NY); and Hinckley/Itasca, MN. The simulation runs for the three new locations used the NLDAS long-term average weather information to explore the phenology results of this new model and compare that with known variations in tick emergence patterns for these regions.

The data for Cary, NY, were taken from the supplemental materials from Ostfeld et al. (2018). Specifically, the reported densities of questing nymphs and densities of mice were averaged across the six field sites for each year from 2007 to 2016. A combination of multiple sources were used for the data for Minnesota, weather data were used from Itasca, and drag sampling was conducted by Bjork and her team in Hinckley from 2015 to 2017. The second tick data source was from the passive submission of Minnesota human-biting I. scapularis ticks from 2007 to 2016 to the collections of Nadolny through the Tick-Borne Disease Laboratory of the U.S. Army Public Health Center. The data for the final site in Virginia were collected by Gaff and her team through an ongoing active surveillance project in the Hampton Roads region of Virginia. Owing to the variation in the collection methods for each of these data sets, a relative ranking of reported tick collections was used rather than the absolute data. For each time series, the data are scaled by the highest value, resulting in a percent of highest reported tick collections for each data set. These values were then scaled to values between zero and ten for ease of graphing.

Sensitivity Analysis

Parameter estimations were taken from the original LYMESIM model, and then these values were updated based on published information, expert opinions, and model calibration. A full sensitivity analysis was completed to assess the relative significance of all model parameters. This analysis was completed using a Latin hypercube analysis, which allows all parameters to vary simultaneously (Marino et al. 2008, Alden et al. 2013). Each parameter was varied across a uniform range of approximately 10% above to 10% below the default value. The model for each location was run for 1000 scenarios using the average weather data for each location. The model results were summarized into two metrics: average ratio of DIN to DON and maximum DON. The average ratio of DIN to DON was calculated as the average over the entire year of the ratio of infected surplus nymphs to total surplus nymphs after the model run reached equilibrium. For simplicity, this is called simply average DIN, but it is the average prevalence. The maximum DON was calculated as the maximum surplus nymphs during the same year. The partial rank correlation coefficient was then calculated for each parameter, and those with a P-value of less than 0.05 were considered as significant.

Results

Model Phenology for Constant Hosts and Weather

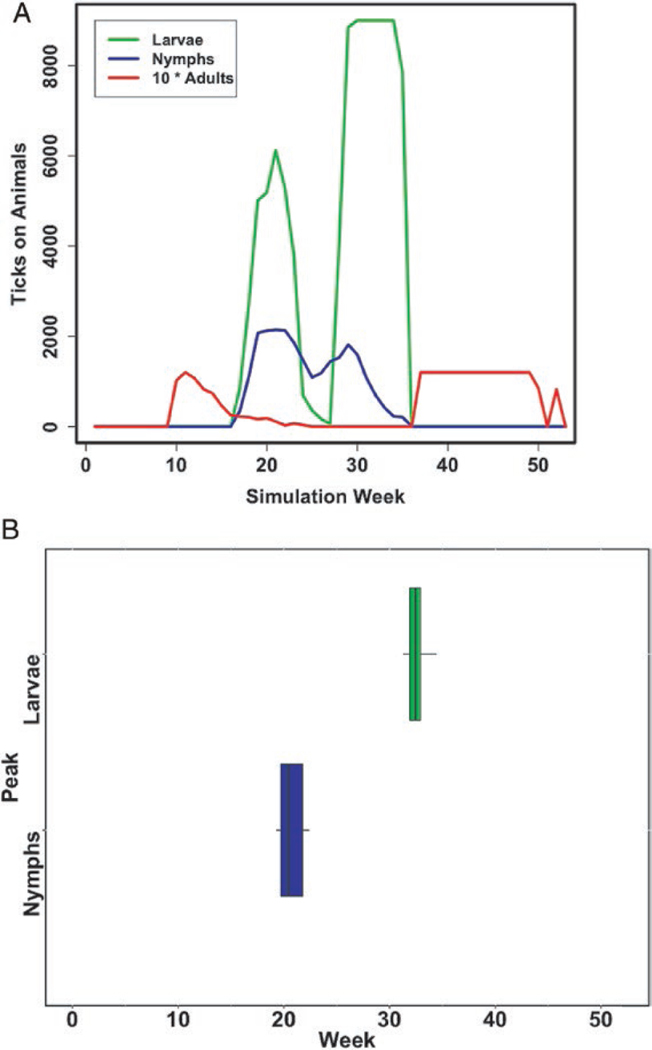
To assess the performance of the model, the first sets of runs used the ‘long-term average’ weather files, which were calculated by averaging the values from 2007 to 2016 for each site. Additionally, all runs for all sites used a constant host density for all years. To evaluate biological realism, we compared model predictions with field-collected data for timing and abundance of peak for each life stage. The model results for these constant-host, long-term average weather data show the expected relative abundance and timing of each life stage (Figs. 2a–4a). Our model predicts that New York has the highest peak for total I. scapularis nymphs on all hosts in late spring followed by the peak for total larvae on all hosts later in summer months with some overlap in timing with the additional peaks for these two life stages (Fig. 2a). Also, for New York as expected, the model predicts that the adults will be found on hosts throughout the fall and again briefly in the spring. Model results for Minnesota, by comparison, show a nearly complete overlap in the timing of the peaks of nymphs and larvae on hosts with a shorter time in fall and spring for the adult activity (Fig. 3a). The Virginia model results show a much longer pulse of larvae in late summer with adults active all winter (Fig. 4a).

Fig. 2.

Long-term average phenology for Cary, New York from (a) model prediction and (b) field data. The graph shows the total number of larval, nymphal, and adult (multiplied by 10) ticks on all host types predicted for each week. This model scenario is based on the average of weather conditions from 2007 to 2016. The field data show the timing of the peak for larval (right) and nymphal (left) ticks for 1994–2012 as reported by Levi et al. (2015). The field data are offset by life stage simply for readability. The timing of the nymphs and larvae for New York for the long-term data fall within the ranges expected, and the overlap of the life stages is similar to that found in many years in the data from Levi et al. (2015).

Fig. 4.

Long-term average phenology for Norfolk, Virginia, from (a) model predictions and (b) field data. The graph shows the total number of larval, nymphal, and adult (multiplied by 10) ticks on all host types predicted for each week. The model scenario is based on the average of weather conditions from 2007 to 2016. The field data were collected from ten sites in the Norfolk area from 2009 to 2018 using standard flagging techniques (Gaff, unpublished data). Both the field data and model results show a much smaller overlap in the activity of the immature stages, and the model results also agree with the field data in the activity of the adults during the entire winter.

Fig. 3.

Long-term average phenology for Minnesota, from (a) model predictions and (b) field data. The graph shows the total number of larval, nymphal, and adult (multiplied by 10) ticks on all host types predicted for each week. The model scenario is based on the average of weather conditions from 2007 to 2016 in Itasca, Minnesota. The field data were collected in 2015–2017 in Hinckley, Minnesota. Both the model results and field data show the nearly simultaneous peaks for nymphs and larvae, but the model results show a slightly earlier timing for the emergence of the immature life stages. The model results also do not have adults active during the summer months as was found in the field during those years. These differences are likely a reflection of the wide variability in the data for this region as can be seen in model results below using annual data rather than this long-term average.

Model Predicted DON and DIN For Constant Hosts and Yearly Variation in Weather

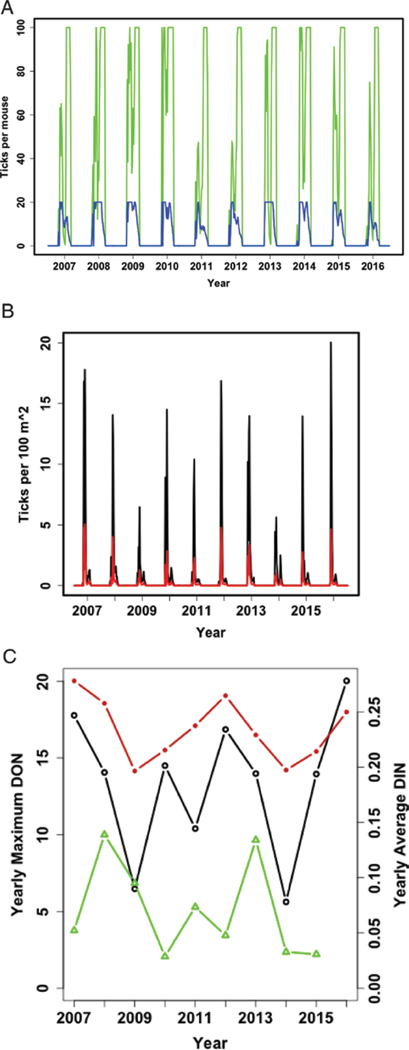
The second set of model results shows the model findings when the actual weekly weather data from 2007 to 2016 are used. For this analysis, the data are restricted to just I. scapularis nymphs on white-footed mice (NOH and INOH) and the numbers of total and infected questing (‘surplus’) ticks (DON and DIN) per hectare. Model results indicate that the peak of timing for nymphs feeding on white-footed mice precedes that of the larvae in both New York and Virginia (Fig. 5a and 5e), but larval and nymphal infestation peaks are synchronous in Minnesota (Fig. 5c). Among localities, there is considerable variation in DON (black lines) and DIN (red lines) such that predicted peak years are not consistent among sites. Among the three localities, Minnesota has the greatest fluctuations in DON and DIN (Fig. 5d).

Fig. 5.

These model results show the year-to-year variation in tick densities based on the actual weather for 2007–2016 for each location. Plots on the left show the model results for the predicted tick burden on white-footed mice (higher numbers are larvae per mouse, smaller numbers are nymphs per mouse) in New York (A, B), Minnesota (C, D), and Virginia (E, F). The burden spikes to the maximum number of ticks per host every summer in all locations and years except Minnesota in 2008. The plots on the right show the DON and DIN, which are the ticks that were questing but unable to find a host that week and could pose a risk to humans Minnesota has the greatest variability in predicted DON, and Virginia has lower expected DON with a maximum in 2007 of only about half the DON found at the maximum in Minnesota in 2011 or New York in 2016.

To assess the model outputs, we compared the maximum annual DON for each location with rank field data. The model results agree in general trends with the scale-ranked field data for Minnesota (Fig. 6b) and Virginia (Fig. 6c). The results for New York (Fig. 6a) did not show a similar matched trend. For all locations, we also calculated the average percentage of nymphs that were infected (NIP; calculated as DIN/DON*100) for each year, and these values were consistently between 25 and 30% for all years in these three locations. So although the absolute density of infected nymphs varies widely from year to year, the prevalence of infection does not vary substantially for any location.

Fig. 6.

Validation comparing DON and field data. The maximum DON for each year is shown for both model predictions (open circles) and field data (triangles), and the model values generally match the trends in the rank-scaled passively collected samples submitted to the Army Public Health Center from Camp Ripley field data for Minnesota and the rank-scaled active surveillance data for Virginia (Gaff, unpublished data). Additionally, the average prevalence (DIN/DON) is shown with closed circles (on the secondary, right-hand axis) and remains fairly consistent between 25 and 30% for all years in all locations.

Model Predicted DON, DIN, and NOH For Varying Host Density and Yearly Variation in Weather

As a further exploration of cause for the variability in year-to-year questing nymphal densities particularly in the New York simulation, we used the variations in white-footed mice density reported (Ostfeld et al. 2018) rather than the standard constant population along with the actual weekly weather data. Figure 7 shows the model results for NOH, DON, and DIN using the average rodent densities reported by Ostfeld et al. (2018) with all other host types held constant at the default values. The variation in mouse densities changed little in the predicted abundance of larvae or nymphs on white-footed mice (Fig. 7a) compared with the previous constant mouse density (Fig. 6a). The model produces different predictions for DON and DIN (Fig. 7b) than was found in the previous constant host scenario (Fig. 5a), and these results are a better match to the field data (Fig. 7c). More work remains to be done to investigate if including additional host density information could improve the match of the model results to the field data.

Fig. 7.

Addition of variation in white-footed mice density for NY. The plot in (a) shows the model results for the predicted tick burden on white-footed mice (larger numbers are larvae per mouse, and smaller numbers are nymphs per mouse). The plot in (b) shows the model predicted DON and DIN for NY, and the plot in (c) shows model predicted maximum DON for each year with open circles, the field data with triangles, and the average prevalence (DIN/DON) with closed circles (on the secondary, right-hand axis). Using only variations in weather data as shown in Fig. 6, model results for New York did not match with the trends seen in field collections. However, when the model used field data for white-footed mice populations, the results are shown in (a) and (b). The comparison to field data, while still not exact, is markedly improved. This highlights the need to understand all of the potential ecological drivers for tick densities.

Sensitivity Analysis Results

The key parameters for both maximum DON and average DIN were related to survival as a function of temperature (see Supp Tables 8 and 9 [online only] for full sensitivity results). In addition, both metrics were correlated with the parameters that drive the host finding rates related to day length for immature ticks. Average DIN was also correlated positively with densities of WFM and negatively with densities of MSM and WTD. Average DIN was also positively correlated with the infection rate from both WFM and SHREWS to ticks.

Discussion

Mathematical models provide valuable tools to explore the complex dynamics of biological systems. The original LYMESIM model was developed in the 1990s at the very beginning of the Lyme disease epidemic in the United States. To incorporate more recent knowledge of I. scapularis host-seeking phenology, host-tick associations, and pathogen persistence, we built upon the original LYMESIM model to develop LYMESIM 2.0. The revised model simulates the I. scapularis life cycle and enzootic transmission of B. burgdorferi s.s. and yields estimates of densities of questing nymphs and infected nymphs (DON and DIN) as well as abundances of nymphs infesting hosts (NOH) that are consistent with field-derived data.

DON and DIN are often significantly and positively correlated with human Lyme disease incidence at the town, city, or county scales, particularly in areas with high incidence of disease (Mather et al. 1996, Kitron and Kazmierczak 1997, Stafford et al. 1998, Diuk-Wasser et al. 2010, Pepin et al. 2012). The original LYMESIM model lacked outputs that estimated these two variables. Because these measures are commonly reported in field studies as estimates of acarological risk for exposure to I. scapularis nymphs and B. burgdorferi s.s., they were added to the updated model to enable comparisons with epidemiologically meaningful field derived metrics. Estimates of DON and DIN derived from LYMESIM 2.0 provided estimates of DON and DIN that were consistent with field observations in Minnesota, New York, and Virginia. Nymphal infection prevalence was found to be in the 25–30% range for all years and locations, which is consistent with commonly reported values (Connally et al. 2006, Pepin et al. 2012, Stromdahl et al. 2014, Feldman et al. 2015, Johnson et al. 2018).

One of the key challenges in modeling the life history of I. scapularis is simulating the variation in questing tick phenology observed across geographic regions (Yuval and Spielman 1990, Hamer et al. 2012). Since the original LYMESIM was published, Lyme disease incidence has increased substantially in the upper Midwest (Bacon et al. 2008, Mead 2015). Consequently, studies focusing on I. scapularis and B. burgdorferi s.s. in this region have increased and differences in host-seeking phenology of the tick in the upper Midwest compared with the Northeast have been elucidated (Hamer et al. 2012, Stromdahl et al. 2014). Most notably, in contrast to the Northeast where nymphal questing precedes larval activity, questing by immature life stages is synchronized in the upper Midwest. These differences have been postulated to contribute to geographic differences in the frequencies of B. burgdorferi s.s. genotypes, which might affect morbidity and incidence of Lyme disease (Gatewood et al. 2009, Pepin et al. 2012).

In the original LYMESIM, phenology was similar across regions. To more accurately simulate differences in host-seeking phenology across regions, in LYMESIM 2.0, we expanded the way survival is calculated to include both an environmentally driven mortality and an energy-reserves loss driven mortality. With only the original environmentally driven mortality, the model results for all areas had the phenology of New York. By teasing apart these two different causes of mortality, the model produces the expected varying phenological results by region. Ticks have limited fat reserves and cannot survive indefinitely in the environment (Randolph 2004, Sonenshine and Roe 2013). The original LYMESIM model reported having a reduced survival rate after 40 wk for any life stage, but this linear reduction did not have finite limits for survival. The new model uses a finite energy reserve that is depleted by questing activities. This allows for the somewhat counter-intuitive result that ticks will live longer in colder and drier climates simply because they can go into quiescence and diapause to conserve energy until weather conditions improve. There is little specific research on the complexities of weather-dependent inactivity of ticks, but there is general agreement that this is a response to adverse conditions such as cold weather or low humidity that allows I. scapularis to survive in a wide variety of areas (Eisen et al. 2016). Additional research is needed to pinpoint the cost to a tick in energy reserves for time spent questing, but the inclusion of this cost allows for the same biological assumptions in all regions.

When the original LYMESIM model was published, there was also limited knowledge of the diversity of hosts that are highly competent reservoirs of B. burgdorferi s.s. This led to including only one class of highly competent reservoir hosts, the white-footed mouse. With more recent research demonstrating the importance of the shrews (Blarina spp.) and other small mammals (Brisson et al. 2008), we added an additional class of highly competent reservoir hosts. Shrews and other small mammals are not as well studied as the white-footed mouse, but Brisson et al. (2008) found that locally up to half of all ticks infected with B. burgdorferi s.s. had fed on shrews. Within the updated model, while this modification increases the number of ticks feeding on highly competent hosts, the adjustments to include a maximum number of ticks per host kept the overall abundance of the ticks from growing exponentially. This new class of hosts will allow for testing of interventions that only target white-footed mice and not shrews or other reservoir hosts, such as mouse-targeted vaccines (Tsao et al. 2004).

Another important lesson learned in the testing of LYMESIM 2.0 is that while the biology of the tick is modeled the same across geographic regions, there appear to be differences in the inputs needed to accurately model annual DON and DIN so that they match field-derived data. In regions with widely fluctuating host populations such as those seen with the white-footed mice in New England resulting from synchronized oak masting events, inclusion of fluctuating host density is needed in these areas in order to accurately capture observed trends. Ostfeld et al. (2018) showed the relationship between the oak masting and tick abundance through the complex ecological web of the tick-host system. Additional surveillance for host density data is needed to parameterize nonconstant host populations in other geographic areas to gain a better understanding of the complex interplay between tick abundance, weather patterns, and host abundance over time. Finally, while it is clear that these masting effects that result in host variation are needed to understand the year-to-year variation, it is less clear how this variability affects interventions. Future model scenarios will explore the implications of this variability. Other factors may also be playing a role with the fluctuations of host densities as well as the seasonality of births for hosts, which is not included in the current model. These and many additional ecological factors can be explored with this model.

The results of the sensitivity analysis highlight the parameters that would be predicted to have the most influence on the average DIN or maximum DON. This information can be used to help apply existing tick control methods as well as to develop and target new control methods. For example, the nearly equal influence of WFM-to-tick and SHREW-to-tick transmission rates predicts that while a rodent vaccine or treatment might work, a better option might try to target both WFM and shrews. This model will be used in future analysis to test existing interventions as well as to identify potential yet-to-be developed interventions.

LYMESIM 2.0 is a useful tool in the public health efforts to better understand and hope fully help control the continuing challenge of Lyme disease. Overall, the lessons learned in the process of developing the model and the final model itself both help advance the understanding of the complexities of acarological risk for exposure to vector ticks and Lyme disease spirochetes. The underlying model structure also can be extended to other tick-borne pathogens and to other tick-pathogen systems.