Abstract
As the fourth most populous country in the world, Indonesia must increase the annual rice production rate to achieve national food security by 2050. One possible solution comes from the nanoscopic level: a genetic variant called Single Nucleotide Polymorphism (SNP), which can express significant yield-associated genes. The prior benchmark of this study utilized a statistical genetics model where no SNP position information and attention mechanism were involved. Hence, we developed a novel deep polygenic neural network, named the NucleoNet model, to address these obstacles. The NucleoNets were constructed with the combination of prominent components that include positional SNP encoding, the context vector, wide models, Elastic Net, and Shannon’s entropy loss. This polygenic modeling obtained up to 2.779 of Mean Squared Error (MSE) with 47.156% of Symmetric Mean Absolute Percentage Error (SMAPE), while revealing 15 new important SNPs. Furthermore, the NucleoNets reduced the MSE score up to 32.28% compared to the Ordinary Least Squares (OLS) model. Through the ablation study, we learned that the combination of Xavier distribution for weights initialization and Normal distribution for biases initialization sparked more various important SNPs throughout 12 chromosomes. Our findings confirmed that the NucleoNet model was successfully outperformed the OLS model and identified important SNPs to Indonesian rice yields.
Subject terms: DNA, Computational science, Computer science, Information technology, Scientific data, Statistics, Computer science, Plant genetics
Introduction
Yield is one of the superior rice traits which is controlled by multiple genes (called polygenic). Through a Genome-wide Association Study (GWAS), its genetic makeups can be discovered and perceived1–4, while still considering any covariates such as climatic conditions5,6, field factors6, intentional or unintentional environmental damages7, and even the dispensable genomes8. Rice, as a staple food for over half of the worldwide population, becomes an ideal species model within the monocots plant genomic research community8,9 due to its genome’s smallest size (of major cereals), relative simplicity and completeness, dense map, and also ease of manipulation7,10. Recall that the Food and Agricultural Organization of the United Nations estimated that by 2050 the worldwide population will increase 32% to 9.1 billion11. Particularly, Indonesia had a 1.09% increase in population growth rate by 202012,13 and thus has to increase the annual rice production to feed its entire population and achieve national food security.
GWAS that has been deployed for indica and japonica subspecies genome sequences database7,14,15 in many former studies manifests a remarkable improvement to break the conundrum of identifying what genes influence such traits. By delving deeper to the nanoscopic level, Single Nucleotide Polymorphism (SNP) has been widely applied to predict plant traits16–23. In recent years, the yield prediction-related tasks for rice genomic data have been completed using statistical genetic models to machine learning-based open frameworks24–26.
Rice yield predictive models should consider confounding variables27–32. In Indonesia, a Genetic Generalized Double Pareto Regression (GGDPR)6 model incorporates the 1232 Indonesian rice SNPs from 467 accessions with two field indicators and plant varieties as confounding variables. The same dataset is used for this research. GGDPR could control the covariate and allow the repeated measurements for the same rice species in a distinct environment. The algorithm itself, through its shrinkage prior ability, was claimed to successfully handle a condition where the number of the predictors is greater than the number of samples , 33,34, as usually happens in GWAS. With a 0.3% of false discovery rate, GGDPR revealed nine significant SNPs to Indonesian rice yields. One of the SNPs, TBGI050092 (Minor Allele Frequency/MAF = 3%, GGDPR β = − 0.186) resides within a gene responsible for rice growth35,36. Another intronic SNP, id10003620 (MAF = 5%, GGDPR β = 0.515) produces a pentatricopeptide protein, which plays role in stress and developmental response in rice37. Meanwhile, the protein product of TBGI272457 (MAF = 12%, GGDPR β = − 0.285) equipped rice plants with pathogenic resistance38,39. This study uncovers more important SNPs to Indonesian rice yields by constructing a novel deep polygenic neural network model, named the NucleoNets.
In this paper, we present several contributions as follows. First, we designed NucleoNets as the first Artificial Intelligence (AI) based predictive model for the Indonesian rice genomics data. Second, since SNP is scattered in chromosomes with a distinct position index, the learnable SNP positional embedding40 was involved in the NucleoNets. Third, we kept covariates (i.e., sample location and variety) in the NucleoNet’s wide model compartement41 as proportional memorization against the primary deep model. Fourth, the ablation study was conducted to witness the impact of different parameters initialization against the SNP importance results. Lastly, as the AI-based polygenic modeling for GWAS was completed, we revealed 15 novel important yield-associated SNPs through the NucleoNet’s attention mechanism42. Our research offers the availability of the new state-of-the-art with deep learning methods as a stepping-stone to answer the problem of crop yield predictions.
Methods
Research workflow
The research problem comprises the development of a deep polygenic neural network to predict Indonesian rice yields and reveal new important yield-associated SNPs. The developed hypothesis is that the Indonesian rice yields prediction performance of the NucleoNet model can outperform the basic linear regression model, i.e. Ordinary Least Squares (OLS) and OLS with an Elastic Net (ENET). To achieve these goals, there are five phases of the methodology.
First, both phenotype and genotype datasets were preprocessed. Second, basic regression modeling was developed to assess the dataset feasibility. Regression is also required for comparison, which is much more commonly used in GWAS. Third, the NucleoNet model was constructed, inspired by the Wide and Deep model. Next, the evaluation phase was done with various metrics to measure the model performance. Lastly, the t-test was conducted to test the hypothesis.
Data collections
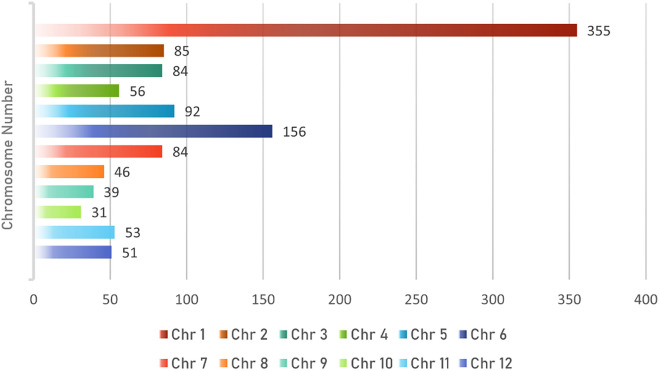
The dataset used for this research was originally curated by the Indonesian Center for Agricultural Biotechnology and Genetic Resources Research and Development (ICABIOGRAD). The database collection consists of 467 rice germplasm samples, 467 × 1536 genotypes (SNPs), and 467 × 4 locations × 12 phenotypes. In detail, the germplasm sample consists of 136 local varieties, 162 improved lines, 11 wild species, 34 near-isogenic lines, 29 released varieties, and 95 newly identified varieties. These samples contain 77 Japonica, 108 Tropical Japonica, and 249 Indica subspecies, leaving the remaining 33 samples with unlabelled subspecies. The Indonesian rice genome consists of 12 chromosomes, which each has different numbers of SNP. The proportion is depicted in Fig. 1. Both sample and phenotype data are in Comma-separated Values (CSV) format files, while genotype data is provided in CSV and PLINK format files.
Figure 1.
Number of SNPs for each chromosome.
The basic attributes in the genotype file are chromosome number (chr), SNP ID (snp), SNP position in DNA sequence (pos), reference allele (ref), alternative or mutated allele (alt), and genotype data/SNP (gt) itself. Meanwhile, the phenotype file describes 12 available rice traits (see Table 1 in the Supplementary Information). The rice planting location includes Subang, Citayam, Kuningan, and Greenhouse (a controlled environment). The incomplete rainy season climatic data such as temperature, humidity, wind speed, precipitation, and irradiance were excluded. The other exclusion reason is that the climatic data was reported to be practically identical throughout the locations6,43.
SNP validation
We validated our Indonesian rice SNPs data to the 18,128,777 Rice Genome Project (RGP) and found that only 57 Indonesian rice SNPs (4.63%) were registered in the International Rice Research Institute (IRRI) database (see Table 2 in the Supplementary Information).
Data preprocessing
This preprocessing phase aims to create a Genotype–Phenotype (GP) table consisting of the following columns: sample ID, sample name, sample location, sample variety, SNP, SNP position, and yield. Note that samples from the Greenhouse were excluded since all yields are unreported (thus, the total sample location is = 3).
The previous work6 reported that the raw genotype data consists of 1536 SNPs with approximately 389 megabases. After the genotype dosage imputation by the Bayesian Imputation Based Association Mapping (BIMBAM) software for SNPs with call rate beyond 25% and removal of monomorphic SNP, 697 rice samples × 1232 SNPs were obtained. The alternative imputation services are Online Plant-ImputeDB or Rice Imputation Server44 which utilized cloud computational offloading technology45. Note that before the imputation, referring to the raw data we received, the call rate of 9 significant SNPs is 0.222% for TBGI036687, 1.774% for TBGI050092, 0.665% for id4009920, 1.109% for id5014338, 1.330% for both TBGI272457 and id8000244, 20.843% for id7002427, 2.217% for id10003620, and 0% for id12006560. The call rate is calculated by dividing the number of samples that have a null value in their related SNP by the total number of samples.
Next, from the 697 samples, mild and extreme outliers in the yield data were detected by using the Interquartile Range (IQR) method. From here 10 missing yields were dropped and the outliers were imputed with the global mean. Therefore, the final Genotype–Phenotype table has 687 rice samples, with each has 1232 SNPs (genotypes) and 1 yield rate (phenotype to predict). See Fig. 2 for details.
Figure 2.
Data preprocessing step.
Note that in the genotype dataset, all SNPs were encoded based on the additive model46. The scheme encodes SNP according to the total of its alternative allele, as it represents a mutation in one locus (see Table 3 in the Supplementary Information). Genotype dosage, which is implanted within the BIMBAM tool, is a linear transformation technique used to fill the missing genotypes in SNP. It is based on the posterior genotype probabilities47,48. Most of the imputed SNPs are in real numbers. To adapt them with the SNP encodings, all real numbers were half-rounded to even (also known as a Banker’s rounding behavior, as applied in Python 3.x).
Regression modeling
The GP Table data frame was shuffled and 85% of the total data was then reserved for train data. After this splitting, the t rain data has a coefficient of variation (CV) of 1.878, and the test data has a CV of 1.798, which still showed the fair dispersion of yield data. In this regression section, we rendered three experiments. First, all SNPs were included in the Ordinary Least Squares (OLS) as a part of polygenic modeling (Experiment 1). Second, each SNP was regressed to yield as a part of an independent association test or marginal regression (Experiment 2), as commonly found when dealing with GWAS. Third, the Elastic Net (ENET) regression was conducted to see the results under the coefficients penalty (Experiment 3). All SNPs were included when the ENET was performed. Its results were plotted into the correlation heatmap to scrutinize the effects of the alpha constant (used to multiply the penalty term) and L1 ratio tuning. This ratio works by 0 < L1 ratio < 1. Both alpha and L1 ratio spaces follow the arithmetic sequence of , where and . All significant SNPs from Experiment 1, Experiment 2, and previous research6 were gathered and compared. These SNPs were then retrained in the OLS model to seek the best prediction score against the rice yield. The trial was also intended to meticulously examine whether there are beneficial insights and impacts of using only the partial SNP data.
The NucleoNet modeling
The GP table was loaded and shuffled. A tensor object was then created for SNP data (), SNP position data (), sample location data (), sample variety data (), and yield data (). The complete dataset has a format: [[tensor (), tensor (), tensor (), tensor ()], tensor ()]. We split the dataset into 70% of training data, 15% of validation data, and 15% of testing data. The fivefold cross-validation was conducted using the training and validation data. We utilized the Hyperopt library which has a Tree-structured Parzen Estimator (TPE) algorithm49. Given a search space, Hyperopt returned the best hyperparameters for the model, and hence the validation accuracy can be optimal50.
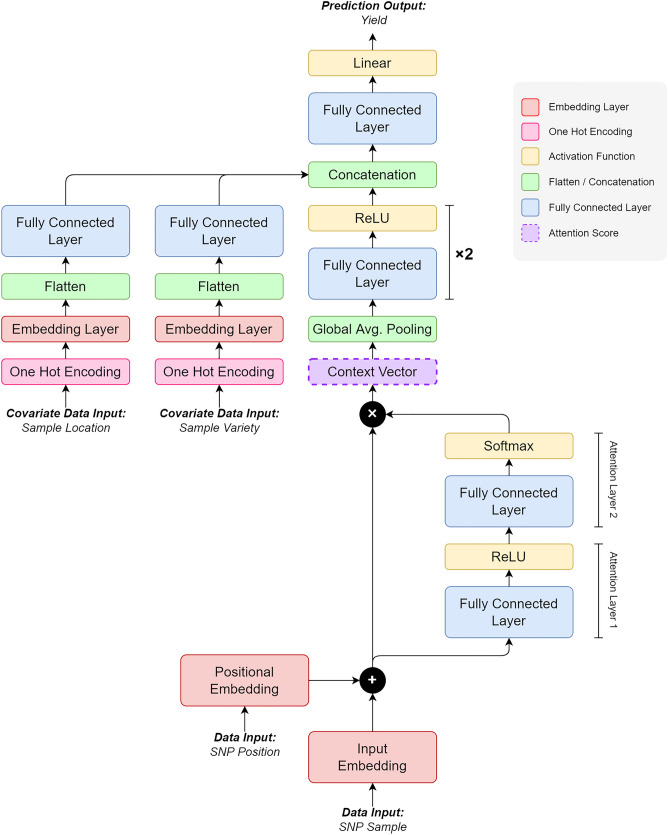
The design of the NucleoNet model is depicted in Fig. 3. Generally, it consists of a deep model which starts from SNP sample data () and SNP position data () inputs, and a wide model which starts from covariate data ( and ) inputs. In the deep model, embedding results from both and were added up; we called it . This was then fed into the attention layers before the attention score (context vector) was obtained. The context vector acts as an encoder map to the SNP input sequence, formulated as
| 1 |
Figure 3.
The NucleoNet model.
is the alignment model as a multi-layer neural network with Softmax activation function (from attention layers). The probability of reflects the importance of , thus it will be used as a measure of the SNP feature importance. While was retrieved in the testing stage, the context vector result was passed to the next layer, i.e., Global Average Pooling (GAP), in the training stage. GAP was used to reduce the spatial dimension of the Tensor data with less parameters. Outputs from GAP were then fed to the fully connected layers (FC1 and FC2). The output from FC2 marked the final result from the deep model.
Both covariates were encoded using a one-hot vector before being fed to the embedding layer. The one-hot vector size for the sample location data input () is = 3, while for the sample variety data input () is = 467. The flattened output from each layer was then concatenated with FC2 to form the Wide and Deep model. The fully connected layer (FC3) with linear activation function was added in the final layer and hence the NucleoNet model was completed. The prominent NucleoNet compartments are listed in Table 1. Meanwhile, Table 2 describes the detailed Tensor size of each layer in the model. Notice that the final output from Wide Model 1 and Wide Model 2 was reduced to suppress the effect of the covariate against the primary deep model.
Table 1.
The prominent parts of the NucleoNet model.
| No. | Component in model | Purpose |
|---|---|---|
| 1 | Positional encoding40 | Add SNP position information to the primary SNP data |
| 2 | The context vector42 | As the attention mechanism, to emit the SNP importance value |
| 3 | Wide model41 | Accommodate all covariates |
| 4 | Elastic net51–53 | Penalize all parameters in all layers |
| 5 | Entropy loss54,55 | Control the distribution of attention scores across all SNPs |
Table 2.
Tensor size for each layer in the NucleoNets. In this table, indicates the batch size, indicates the length of SNP, indicates the embedding size, indicates the number of attention hidden layers, indicates the number of sample locations, indicates the number of sample varieties, means the MLP hidden layer of the deep model, means the MLP hidden layer of the wide model, and FC means the Fully Connected layer.
| Deep model | Size | Wide model | Size | Wide deep model | Size |
|---|---|---|---|---|---|
| SNP data input () | Sample location data input () | Concat | |||
| SNP data embedding | Sample location one hot encoding | FC3 | |||
| SNP position input () | Sample location embedding | Output () | |||
| SNP position embedding | Sample location flatten | ||||
| SNP data + position () | Wide model 1 () | ||||
| Attention layer 1 () | Sample variety data input () | ||||
| Attention layer 2 () | Sample variety one hot encoding | ||||
| Context vector () | Sample variety embedding | ||||
| Concatenation (GAP) | Sample variety flatten | ||||
| FC1 | Wide model 2 () | ||||
| FC2 () |
We designed three experiments. Experiment 1 is the NucleoNet model with Mean Squared Error (MSE) loss function (called NucleoNetV1). Experiment 2 is the same except there is an additional modified ENET penalty in the loss function (called NucleoNetV2). Note that both ENET and Generalized Double Pareto (GDP) which was implemented in previous research6 have the same role in coefficients shrinkage33,34. The selection of ENET as shrinkage prior was due to simpler implementation and more commonly used in genomics studies to solve problems, such as selection method to eliminate trivial genes53, dense SNPs pre-selection56, genomic estimated breeding value (GEBV) prediction57, pharmacogenetics58, and even the epistasis analysis59. Equation (1) describes one of the ENET conventions which are used for the glmnet package in R and Scikit-learn in Python51,52, overriding the original naïve ENET. The advent of in Eq. (1) is considered to cancel the exponent 2 (from ) after derivative. For the NucleoNet, which is not a generalized linear model, this modified ENET is more suitable. The term implies the regularization weight to control this penalty against MSE loss, while denotes the coefficients and denotes the penalty term. The convex combination is no longer used, so .
| 2 |
| 3 |
Experiment 3 is the same as Experiment 2 except there is another additional Shannon’s entropy value54,55 in the loss function (called NucleoNetV3). This entropy acts as a control for the dispersion of attention scores across all SNPs. In other words, we prevent the attention score from collapsing to only one SNP. Equation (2) shows the Shannon’s entropy formula used in Experiment 3, where denotes the Shannon’s entropy value, denotes the probability value of , and denotes the entropy weight to control against the loss.
Hyperopt was executed for each designed experiment. Due to limited computational resources, Hyperopt parameters were set to 20 of training epoch, 10 of maximum evaluation, and 43 of initial seed. All the best hyperparameters found were retrieved and used for the NucleoNet model mini-batch training in 1000 epochs. We also set 15 as a number of patience, which is a maximum epoch number of tolerance when there is no further improvement in the training.
Ablation study
Seven ablation studies (ABSTs) in terms of weight initialization were also conducted, as summarized in Table 4 in the Supplementary Information. In the first attempt (ABST-1), we let weights and biases initialization by default in PyTorch, i.e., within the Kaiming Uniform distribution. For all ABSTs, weights and biases in the SNP data embedding, SNP position data embedding, sample location data embedding, sample variety data embedding, and fully connected layer in the deep model were initialized within the , which denotes the Normal distribution. In contrast, denotes the Uniform distribution, as used in ABST-5. From ABST-2 to ABST-7, we modified weights and biases initialization in the attention layer to examine the variability in the SNP importance measures.
Inspired from the previous study6 where it was considered , we also tried to varied the within the Normal and Uniform distribution. The Xavier Initialization is used to determine in the Normal distribution by taking as the gain value for the linear layer with the ReLU activation function. Meanwhile, the Kaiming Initialization is used to determine the lower and upper bound in the Uniform distribution by taking as the gain value for the linear layer. To your preference, and in Table 4 in the Supplementary Information means the number of the input and output nodes, respectively.
Evaluation metrics
Due to the prediction task, the best possible way to measure the model performance on the test dataset is by using or L2 Loss, Root MSE (), Mean Bias Error (), Mean Absolute Error () or L1 Loss, Mean Squared Logarithmic Error (), and Symmetric Mean Absolute Percentage Error (). These metrics are currently the most widely used in the agroindustry field, especially for yield forecasting with machine learning approaches60,61. See the Supplementary Information about the selection reason for these metrics. Note that due to the nonlinearity of the dataset, the Coefficient of Determination or R-squared () is unsuitable for the evaluation measurement32,62. The , , and inequality are defined as 63. A total of 104 testing data were used in both regression and deep learning approaches. The prediction evaluation is based on all these metrics. In addition, the paired t-test (or dependent t-test) was performed for hypothesis testing.
Hardware, software, and libraries
The research was executed in hardware with specifications of Intel® CoreTM i5-8250U @1.60 GHz (8 CPUs) ~ 1.8 GHz processor, X442UQR/X442UQR.308 system model, 16,384 MB RAM, and Windows 10 (64-bit) operating system. Developer software includes Jupyter Notebook 6.0.1, Rstudio 1.1.463, Preferred Installer Program/PIP 21.2.4, and PLINK 1.9. The main programming language is Python 3.7.1. Python libraries used are Torch 1.9.0, Pandas 1.3.3, Scikit-allel 1.3.5, Scikit-learn 0.24.2, Hyperopt 0.2.5, Statsmodels 0.12.2, Statistics 1.0.3.5, Matplotlib 3.4.3, Seaborn 0.11.2, and Numpy 1.19.5. All libraries may have the alternative and can be installed through the Python package manager (i.e., PIP).
Results
Statistical analysis
The same 467 species were grown in three distinct locations, i.e., Kuningan (2010–2011), Subang (2011–2012), and Citayam (2012–2013). Referred from the previous research6, the total data used is 697 samples. All 10 missing yields from Citayam were dropped, leaving 687 samples. The outliers were detected using the Interquartile Range (IQR) method, with Lower Outer Fence (LOF) of − 6.38, Lower Inner Fence (LIF) of − 2.19, Upper Inner Fence (UIF) of 8.98, and Upper Outer Fence (UOF) of 13.17. Precisely, 27 mild outliers were appeared and then imputed by 3.449 as the global mean of rice yield. No extreme outlier was found.
As we plotted the density distribution of rice yields in each location, 150 samples from Kuningan (5.01 ± 1.98) has the Skewness coefficient of 0.14 and the Kurtosis coefficient of − 0.86, 124 samples from Subang (3.62 ± 1.82) has of 0.08 and of − 0.85, and 413 samples from Citayam (2.83 ± 1.43) has of 0.19 and of − 0.61. Samples in Citayam have the largest , which means mostly the yield . However, the samples in Kuningan and Subang have the lowest , which means the yield is more varied than the rest. Higher from both supports the statement. Overall, all 687 data (3.44 ± 1.85, = 0.53, = − 0.06) is close to the normal distribution (since ), but still positively skewed (since ). See the distribution histograms in Table 5 in the Supplementary Information.
Ordinary least squares results
From the OLS, which is part of Experiment 1, we obtained 16 significant SNPs. From Experiment 2, where we regressed each SNP to yield, we obtained 36 significant SNPs. See the results in Table 3. All significant SNPs found in Experiment 1, Experiment 2, and previous research were once again regressed with the normal OLS and OLS + ENET models. Unfortunately, it seems that there is no prominent result by using only the partial SNP data. Nevertheless, the OLS + ENET model still outperformed the normal OLS results. Compare them in Tables 6 and 7 in the Supplementary Information. To these findings, we chose to utilize all SNPs in the deep learning model training instead. In Experiment 3, we conducted a simulation to scrutinize the effects of alpha constant (used to multiply the penalty term) and L1 ratio tuning in the ENET. Throughout these simulations, we can perceive that the L2 penalty domineeringly affects the outcome. To grasp the full impact of this ENET hyperparameter configuration in six different prediction measures, please refer to Fig. 2 in Supplementary Information. This trial consumed about 30 min 40 s of execution time (ET).
Table 3.
NucleoNets model comparison with other models. ✓: This symbol means the related part is available in the model. ✖: This symbol means the related part is unavailable in the model. *Not mentioned in the original paper6. **The Scikit-learn library does not support the p-value calculation. On the contrary, the Stasmodels library does not have an ENET function. ***NucleoNets results from ABST-6.
| Polygenic model | GGDPR | OLS | OLS + ENET | NucleoNetV1 | NucleoNetV2 | NucleoNetV3 | Wide and deep model |
|---|---|---|---|---|---|---|---|
| Total Indonesian rice SNPs | 1232 | 1232 | 1232 | 1232 | 1232 | 1232 | 1232 |
| SNP data | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| SNP position data | ✖ | ✖ | ✖ | ✖ | ✖ | ✖ | ✓ |
| Covariate: sample location | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Covariate: sample variety | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Shrinkage prior/regularization | Generalized double pareto | ✖ | ENET | ✖ | Modified ENET |
Modified ENET |
Modified ENET |
| Shannon’s entropy | ✖ | ✖ | ✖ | ✖ | ✖ | ✓ | ✓ |
| Evaluation: MSE | N/A* | 4.104 | 2.517 | 2.779*** | 2.799*** | 2.863*** | 8.535 |
| Evaluation: RMSE | N/A* | 2.026 | 1.587 | 1.667 | 1.673 | 1.692 | 2.921 |
| Evaluation: MBE | N/A* | − 0.236 | − 0.404 | 0.099 | 0.015 | − 0.074 | − 2.148 |
| Evaluation: MAE | N/A* | 1.673 | 1.321 | 1.407 | 1.412 | 1.433 | 2.497 |
| Evaluation: MSLE | N/A* | 0.286 | 0.185 | 0.184 | 0.191 | 0.197 | 0.468 |
| Evaluation: SMAPE | N/A* | 64.843% | 45.432% | 47.156% | 47.960% | 47.481% | 63.668% |
| Significance/importance level | N/A* | N/A** | N/A | ||||
| Number of significant/important SNP | 9 | 16 | N/A** | 29 | 35 | 23 | N/A |
| Execution time | N/A* | < 2 s | < 2 s | 1630 s | 5120 s | 4910 s | 6070 s |
The NucleoNets results
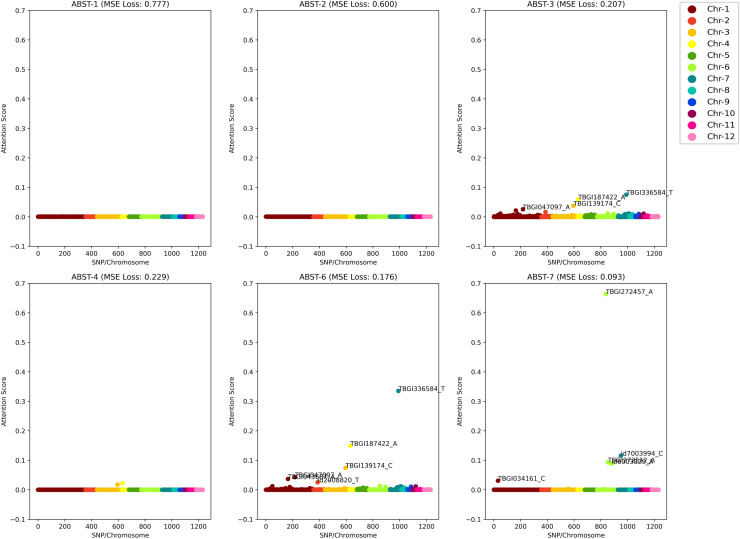
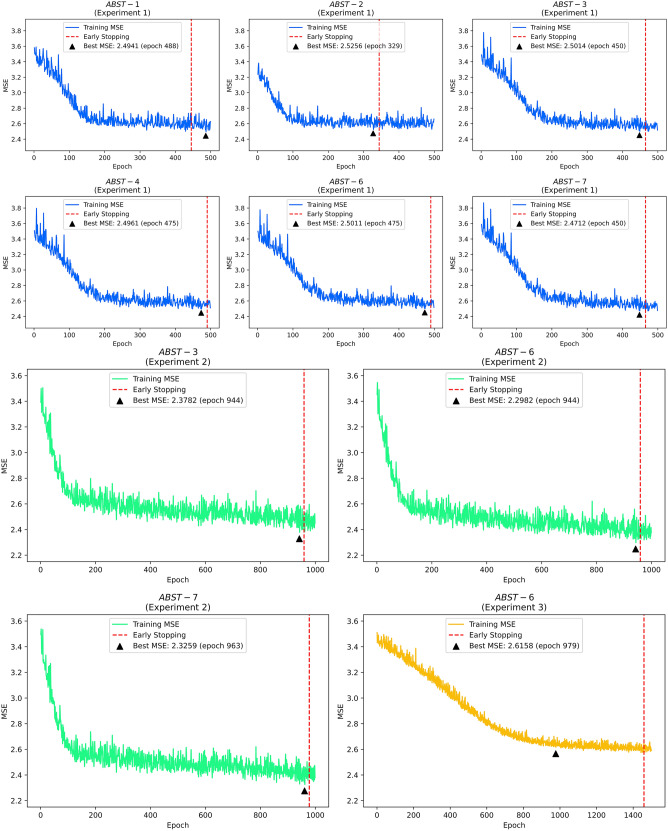
In Experiment 1, we performed 7 ablation studies (ABSTs) with distinct weights and biases initialization. Each of the ABSTs used hyperparameters found by Hyperopt, as inscribes in Table 8 in the Supplementary Information. This validation scheme gave an MSE of 3.032 and consumed about 1 h of ET. In contrast, the training time took approximately 1600 s for 500 epochs. As we can scrutinize in Table 9—Experiment 1 (Supplementary Information), there is only a slightly different result between each ABST. Referring to the MSE measurement, NucleoNetV1 gave testing scores of 2.890, 2.843, 2.785, 2.813, 2.779, and 2.794 for ABST-1, ABST-2, ABST-3, ABST-4, ABST-6, and ABST-7, respectively. The key to interpreting these results resided in their Manhattan plot, as depicted in Fig. 4. Note that for all plots, we utilized the same one random sample for uniform comparison. Since we discovered that ABST-3, ABST-6, and ABST-7 sparked more various important SNPs, the mixed-use of Xavier Initialization in attention layers was maintained throughout the rest of the experiments. All training plots for NucleoNetV1 are diagrammed in Fig. 5 (marked in blue).
Figure 4.
Ablation study results testing for one random sample.
Figure 5.
The NucleoNets training plots.
Experiment 2 was run in 1000 epochs with approximately 5000 s of ET. The validation scheme for NucleoNetV2 obtained an MSE of 3.097 and consumed about 1 h 16 min of ET. Referring to the MSE measurement, NucleoNetV2 gave testing scores of 2.782, 2.799, and 3.035 for ABST-3, ABST-6, and ABST-7. See Table 9—Experiment 2 (Supplementary Information) for results from other metrics. In ABST-3, both attention layers used Xavier Normal distribution to initiate weights and biases. Meanwhile, in ABST-6, the Xavier Normal distribution was initialized in the first attention layer and in ABST-7 the same distribution was initialized in the second attention layer. Training plots for NucleoNetV2 are diagrammed in Fig. 5 (marked in green).
In Experiment 3, we only reported the NucleoNetV3 testing results on ABST-6 since the SNP importance occurrence variation in the Manhattan plot is much higher than ABST-3 or ABST-7. The validation scheme for NucleoNetV3 obtained an MSE of 3.233 and consumed about 1 h 35 min of ET. NucleoNetV3 gave an MSE of 2.863, trained within 1,000 epochs and consumed approximately 4900 s of ET. See Table 9—Experiment 3 (Supplementary Information) for results from other metrics. For uniformity purposes in all NucleoNets, we determined the result from ABST-6 as primary and therefore are used as comparisons with other models. Training plots for NucleoNetV2 and NucleoNetV3 are diagrammed in Fig. 5 (marked in gold).
In addition, to compare with other deep neural network model and to show the advantage of the NucleoNets, wide and deep model was trained with the same hyperparameters setting of NucleoNetV3. As shown in Table 3, the absence of an attention mechanism reduced the performance. Hence, it is proved that NucleoNets not only obtained superior testing results by using the attention layer but also can emit important SNPs to rice yield.
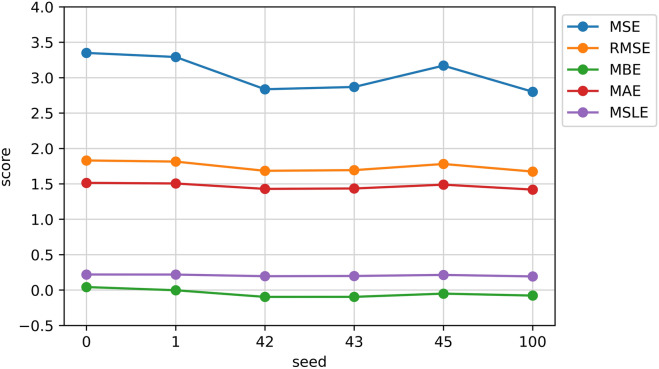
The use of seed = 43 is to let this experiment reproducible. However, Fig. 6 depicts the testing results from NucleoNetV3 under different seeds but in the same hyperparameters setting. Since the deep neural network follows the stochastic process while training, it is prevalent to get a slightly different result for different seeds.
Figure 6.
NucleoNetV3 testing results under different seeds.
Discussions
Comparison with GGDPR
We presented the performance comparison between the GGDPR model, polygenic OLS regression models, and deep polygenic NucleoNet models, as shown in Table 3. In the OLS model, ENET brought a notable improvement where the MSE score was reduced by 38.67%. However, in NucleoNets, each configuration brought a slight decline in MSE score. With additional modified ENET, the performance of NucleoNetV2 was reduced by 0.07% compared to NucleoNetV1. With additional entropy, the performance of NucleoNetV3 was reduced by 2.24% compared to NucleoNetV2. Nevertheless, the NucleoNets performances resulted in more varied and more numbers of important SNP in exchange. As we can scrutinize in Table 3, the best of NucleoNets, i.e., NucleoNetV1, has an MSE score close to the OLS + ENET model. The NucleoNetV1 reduced an MSE score by 32.28% compared to the basic OLS model.
Let the NucleoNet stands for an average attention score emerged from 104 testing samples. We found two same important SNPs as the previous research6, namely TBGI272457 (NucleoNetV1/ABST-7, GGDP β = N/A, OLS -value = 0.728, OLS β = − 0.025, =0.319) and id4009920 (NucleoNetV2/ABST-7, GGDP β = − 0.265, OLS -value = 0.952, OLS β = − 0.003, =0.407). The former resided on rice chromosome 6 and position 2,991,002, while the latter resided on rice chromosome 4 and position 30,174,569. id4009920 is a seed-specific protein Bn15D1B64,65. TBGI272457 acts as a transporter for anthocyanins vacuolar uptake in rice66. Anthocyanins, as members of flavonoid groups, play a role in reproduction and growth, and offer a protection mechanism against biotic or abiotic stress and plaques67,68. TBGI272457 is also classified as the NB-ARC domain-containing protein69, or resistance proteins (R) which are involved in pathogen recognition and activation of fundamental and innate plant immune system70,71. The presence of these genes brings disease resistance capabilities in rice72 and hence supports the sustainability of rice yields.
Indonesian rice yield-associated genes
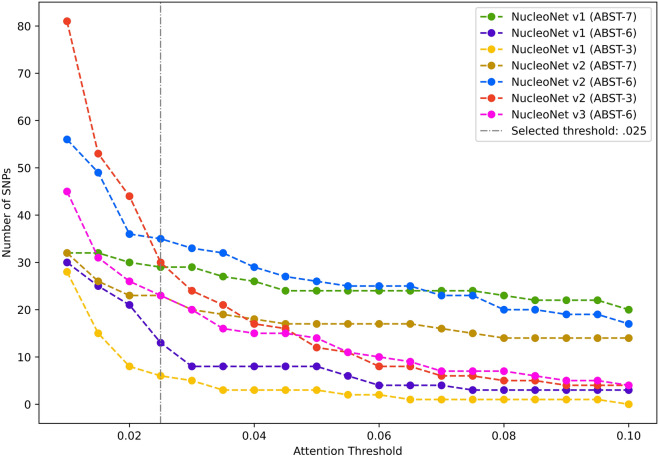
To the day this research is written, there is no prior use of attention score as a fundamental threshold to select important SNPs like -value usually did in GWAS. Therefore, we conducted trials with in all NucleoNets to see numbers of SNP revealed for each . Based on the results presented in Fig. 7, we decided to pick as an ideal and stable threshold since the value beyond it runs into stagnancies and the value behind it provides too diverse numbers of SNP for each NucleoNet model.
Figure 7.
Important SNPs emitted per attention score.
Based on this threshold, we summarized the top five important SNPs found by each NucleoNet model, as shown in Table 4. Some of their roles in rice plants were identified and discussed in many studies. For instance, TBGI133263 has a role in rice drought tolerance and photosynthesis mechanism73. Its existence was also proved to protect rice seed germination74. Its enzyme product, β-Glucosidase, has an impact on the rice root75,76. TBGI272488 was discovered as a rice yield-associated gene77. The SNP also controls the ATP-binding cassette (ABC) transporters78–80 which contributes to multidrug resistance in plants, including rice81,82. TBGI336599 was reported to have an impact on rice growth83. TBGI130922 controls the metabolism, including the cytokinin metabolism75, to support rice coleoptile growth84. One product of this gene is flavonoid-biosynthesis networks85,86. These flavonoid compounds have many roles in plants, including the reproduction process87 and specialized metabolite pathways88 in rice. The rest of the SNPs have no further description since they have not been mapped in the rice DNA strand. The other reason is their protein products are still hypothetical. Please refer to Tables 10 and 11 in the Supplementary Information to learn more about these SNPs with their respective genetic details.
Table 4.
Important SNPs found in the NucleoNets. Chr:Pos means Chromosome:Position. Suffix in each SNP denotes its alternate allele. *Intronic. **Intergenic.
| Model | SNP name | Chr:Pos | NucleoNets | Marginal regression | Full regression | |||
|---|---|---|---|---|---|---|---|---|
| Count | -value | -value | ||||||
| NucleoNetV1 | TBGI336584_T* | 7:28,902,549 | 104 | 0.349702 | 0.692976 | 0.367086 | 0.613405 | − 0.00464 |
| TBGI139174_C* | 3:10,546,292 | 100 | 0.078781 | 0.501128 | 0.118872 | 0.258786 | − 0.05250 | |
| TBGI043687_A* | 1:27,033,613 | 98 | 0.039402 | 0.461979 | 0.092519 | 0.749955 | 0.018242 | |
| TBGI047097_A* | 1:29,101,182 | 87 | 0.043968 | 0.245114 | 0.146880 | 0.731616 | − 0.00822 | |
| id2008820_T* | 2:23,034,401 | 48 | 0.028928 | 0.293053 | 0.133663 | 0.487864 | − 0.15724 | |
| NucleoNetV2 | id4010708_C | 4:31,871,929 | 76 | 0.334360 | 0.023139 | 0.178155 | 0.181538 | 0.092289 |
| TBGI133654_T* | 3:6,221,117 | 71 | 0.073753 | 0.981030 | − 0.00224 | 0.051080 | − 0.11139 | |
| TBGI133263_A** | 3:5,884,040 | 64 | 0.057674 | 0.554272 | 0.060059 | 0.616267 | 0.035691 | |
| id1010403_T* | 1:16,716,706 | 53 | 0.040871 | 0.275980 | 0.377068 | 0.725071 | 0.007040 | |
| TBGI272488_T* | 6:3,001,902 | 34 | 0.363929 | 0.451712 | 0.057712 | 0.725524 | 0.014053 | |
| NucleoNetV3 | id10004275_C | 10:16,252,942 | 102 | 0.050838 | 0.523674 | − 0.37561 | 0.373641 | 0.050556 |
| TBGI264076_A* | 5:27,953,016 | 91 | 0.125639 | 0.90349 | 0.018688 | 0.611320 | − 0.01367 | |
| TBGI130922_G** | 3:4,441,747 | 75 | 0.032907 | 0.356457 | − 0.07551 | 0.933317 | − 0.00536 | |
| TBGI038001_C* | 1:23,689,014 | 73 | 0.133440 | 0.564393 | − 0.04618 | 0.195798 | − 0.06157 | |
| TBGI336599_C* | 7:28,905,733 | 73 | 0.043163 | 0.930258 | − 0.00685 | 0.535020 | − 0.03080 | |
The null hypothesis significance testing
The hypothesis testing (known as NHST) was performed using 38 out of 104 testing data, and thus the degree of freedom is 37. The rest data were excluded due to data distinctions at the time of shuffling the test data for OLS and NucleoNet models. The population to be tested is squared error results from NucleoNetV1 (= 2.679, = 7.886), NucleoNetV2 ( = 2.642, = 8.166), NucleoNetV3 ( = 2.818, = 8.184), OLS ( = 4.758, = 29.383), and OLS + ENET ( = 3.121, = 8.166). See the full data description in Tables 12, 13, and 14 in the Supplementary Information.
The hypothesis to be tested is as follows. First, for each NucleoNet model , a two-tailed t-test (significance level, ) is performed to check whether there is a non-zero mean squared error difference compared to the OLS and OLS + ENET models. Statistically, the hypothesis to be tested (two-tailed) between NucleoNets and OLS is defined as : , : , while the hypothesis to be tested (two-tailed) between NucleoNets and OLS + ENET is defined as : , : . The decision rule, if |t-stat|> t-table or -value < , then we should reject and proceed to the one-tailed t-test for further investigation.
In a one-tailed t-test scenario (significance level, ), we checked whether the mean squared error from each NucleoNet model is less than or greater than the mean squared error from the OLS and OLS + ENET models. Statistically, the hypothesis to be tested (lower one-tailed) between NucleoNets and OLS is defined as : , : , while the hypothesis to be tested (lower one-tailed) between NucleoNets and OLS + ENET is defined as : , : . On the contrary, the hypothesis to be tested (upper one-tailed) between NucleoNets and OLS is defined as : , : , while the hypothesis to be tested (upper one-tailed) between NucleoNets and OLS + ENET is defined as : , : . The decision rule for lower one-tailed t-test, if |t-stat|< t-table and -value < , then we should reject . Meanwhile, the decision rule for upper one-tailed t-test, if |t-stat|> t-table and -value < , then we should reject . By these settings, NHST results are parsed down in Table 5.
Table 5.
The NHST results.
| Main model | Comparison model | t-test | Validation | Conclusion | Description | |
|---|---|---|---|---|---|---|
| NucleoNetV1 | OLS | Two-tailed | Reject , accept | Proceed to a one-tailed t-test | ||
| 1. |t-stat|> t-table | Is |− 2.998|> 2.026? | TRUE | ||||
| 2. -value < | Is 0.003 < 0.025? | TRUE | ||||
| One-tailed (less than) | Reject , accept | The Indonesian rice yields prediction performance of the NucleoNetV1 model outperformed the OLS model | ||||
| 1. t-stat < t-table | Is − 2.998 < − 1.687? | TRUE | ||||
| 2. -value < | Is 0.002 < 0.05? | TRUE | ||||
| One-tailed (greater than) | Reject , accept | |||||
| 1. t-stat > t-table | Is − 2.998 > 1.687? | FALSE | ||||
| 2. -value < | Is 0.998 < 0.05? | FALSE | ||||
| OLS + ENET | Two-tailed | Reject , accept | The Indonesian rice yields prediction performance of the NucleoNetV1 model has no difference from the OLS + ENET model | |||
| 1. |t-stat|> t-table | Is |− 1.028|> 2.026? | FALSE | ||||
| 2. -value < | Is 0.311 < 0.025? | FALSE | ||||
| One-tailed (less than) | – | |||||
| – | – | – | ||||
| One-tailed (greater than) | – | |||||
| – | – | – | ||||
| NucleoNetV2 | OLS | Two-tailed | Reject , accept | Proceed to a one-tailed t-test | ||
| 1. |t-stat|> t-table | Is |− 2.753|> 2.026? | TRUE | ||||
| 2. -value < | Is 0.091 < 0.025? | FALSE | ||||
| One-tailed (less than) | Reject , accept | The Indonesian rice yields prediction performance of the NucleoNetV2 model outperformed the OLS model | ||||
| 1. t-stat < t-table | Is − 2.753 < − 1.687? | TRUE | ||||
| 2. -value < | Is 0.005 < 0.05? | TRUE | ||||
| One-tailed (greater than) | Reject , accept | |||||
| 1. t-stat > t-table | Is − 2.753 > 1.687? | FALSE | ||||
| 2. -value < | Is 0.995 < 0.05? | FALSE | ||||
| OLS + ENET | Two-tailed | Reject , accept | The Indonesian rice yields prediction performance of the NucleoNetV2 model has no difference from the OLS + ENET model | |||
| 1. |t-stat|> t-table | Is |− 1.027|> 2.026? | FALSE | ||||
| 2. -value < | Is 0.311 < 0.025? | FALSE | ||||
| One-tailed (less than) | – | |||||
| – | – | – | ||||
| One-tailed (greater than) | – | |||||
| – | – | – | ||||
| NucleoNetV3 | OLS | Two-tailed | Reject , accept | Proceed to a one-tailed t-test | ||
| 1. |t-stat|> t-table | Is |− 2.937|> 2.026? | TRUE | ||||
| 2. -value < | Is 0.006 < 0.025? | TRUE | ||||
| One-tailed (less than) | Reject , accept | The Indonesian rice yields prediction performance of the NucleoNetV3 model outperformed the OLS model | ||||
| 1. t-stat < t-table | Is − 2.937 < − 1.687? | TRUE | ||||
| 2. -value < | Is 0.003 < 0.05? | TRUE | ||||
| One-tailed (greater than) | Reject , accept | |||||
| 1. t-stat > t-table | Is − 2.937 > 1.687? | FALSE | ||||
| 2. -value < | Is 0.997 < 0.05? | FALSE | ||||
| OLS + ENET | Two-tailed | Reject , accept | The Indonesian rice yields prediction performance of the NucleoNetV3 model has no difference from the OLS + ENET model | |||
| 1. t-stat < t-table | Is |− 0.743|> 2.026? | FALSE | ||||
| 2. -value < | Is 0.462 < 0.025? | FALSE | ||||
| One-tailed (less than) | – | |||||
| – | – | – | ||||
| One-tailed (greater than) | – | |||||
| – | – | - | ||||
Conclusions
In this study, a novel deep polygenic neural network named the NucleoNet model was constructed to accurately predict and identify important yield-associated SNPs in Indonesian rice accessions while controlling two major covariates, i.e., location and variety of the samples. The main results and findings are recapitulated as follows: (1) The Indonesian rice yields prediction performance of NucleoNetV1, NucleoNetV2, and NucleoNetV3 outperformed the OLS model. (2) The Indonesian rice yields prediction performance of NucleoNetV1, NucleoNetV2, and NucleoNetV3 has no difference with the OLS + ENET model. (3) Additional entropy penalty in the NucleoNet model brought a more diverse distribution of attention score across SNPs, at the expense of prediction accuracy as a cost. (4) Ablation study showed that the combination of Xavier distribution for weights initialization and Normal distribution for biases initialization sparked more various important SNPs. (5) Two significant SNPs discovered in the prior research, TBGI272457 and id4009920, were also discovered using the NucleoNets.
Since this research is still in its early stages, our future works in the Indonesian rice genomics field will focus on the following things: (1) Extend the covariates, including the influence of pests, pesticides, and climatic information in the year where the rice was planted. (2) Develop a particular deep learning model to impute missing SNPs. (3) Try various attention mechanisms such as self-attention or multi-head attention to improve the SNP significance measurement. (4) Implement the Deep Learning Important Features (DeepLIFT) model to handle SNP significance. (5) Reinforce the deep learning model by instilling it with a novel inductive bias for genomics data. (6) Compare deep learning results with broader common GWAS methods such as LASSO or Bayesian approaches. (7) Develop a biological-based method to validate that important SNPs found in the NucleoNets are useful to increase the annual rice production rate.
Supplementary Information
Acknowledgements
We would like to thank Stefanus Bernard, S.B io.Inf. from Genomik Solidaritas Indonesia Laboratorium (GSI Lab) and Natasya, S.Ked. from Faculty of Medicine, Tarumanegara University, Jakarta, Indonesia, who gave suggestions and comprehensions regarding the biological terms in this research project.
Author contributions
N.D.: Conceptualization, methodology, software, formal analysis, visualization, writing original draft, and project administration. T.J.W.: Conceptualization, methodology, resources, review and editing, and supervision. A.B.: Data curation, resources, review and editing, and supervision. B.P.: Validation, review and editing, project administration, and supervision. All authors reviewed the manuscript and agree on publication.
Code availability
All codes for this research are available at www.github.com/NicholasDominic/The-NucleoNets.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Nicholas Dominic, Email: nicholas.dominic@binus.ac.id.
Bens Pardamean, Email: bpardamean@binus.edu.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-022-16075-9.
References
- 1.Lee S, Lozano A, Kambadur P, Xing EP. An efficient nonlinear regression approach for genome-wide detection of marginal and interacting genetic variations. J. Comput. Biol. 2016;23:372–389. doi: 10.1089/cmb.2015.0202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Banerjee S, Zeng L, Schunkert H, Söding J. Bayesian multiple logistic regression for case-control GWAS. PLoS Genet. 2018;14:1–27. doi: 10.1371/journal.pgen.1007856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yoo YJ, Sun L, Bull SB. Gene-based multiple regression association testing for combined examination of common and low frequency variants in quantitative trait analysis. Front. Genet. 2013;4:1–17. doi: 10.3389/fgene.2013.00233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yoo YJ, Sun L, Poirier JG, Paterson AD, Bull SB. Multiple linear combination (MLC) regression tests for common variants adapted to linkage disequilibrium structure. Genet. Epidemiol. 2017;41:108–121. doi: 10.1002/gepi.22024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li X, et al. Genetic control of the root system in rice under normal and drought stress conditions by genome-wide association study. PLoS Genet. 2017;13:1–24. doi: 10.1371/journal.pgen.1006889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McMahan C, et al. A Bayesian hierarchical model for identifying significant polygenic effects while controlling for confounding and repeated measures. Stat. Appl. Genet. Mol. Biol. 2017;16:407–419. doi: 10.1515/sagmb-2017-0044. [DOI] [PubMed] [Google Scholar]
- 7.International Rice Genome Sequencing Project The map-based sequence of the rice genome. Nature. 2005;436:793–800. doi: 10.1038/nature03895. [DOI] [PubMed] [Google Scholar]
- 8.Yao W, et al. Exploring the rice dispensable genome using a metagenome-like assembly strategy. Genome Biol. 2015;16:1–20. doi: 10.1186/s13059-014-0572-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhao H, et al. RiceVarMap: A comprehensive database of rice genomic variations. Nucleic Acids Res. 2015;43:D1018–D1022. doi: 10.1093/nar/gku894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen H, et al. A high-density SNP genotyping array for rice biology and molecular breeding. Mol. Plant. 2014;7:541–553. doi: 10.1093/mp/sst135. [DOI] [PubMed] [Google Scholar]
- 11.Food and Agriculture Organization of the United Nations FAO’s Director-general on how to feed the world in 2050. Popul. Dev. Rev. 2009;35:837–839. doi: 10.1111/j.1728-4457.2009.00312.x. [DOI] [Google Scholar]
- 12.World Population Review. Megadiverse Countries 2020. https://worldpopulationreview.com/country-rankings/megadiverse-countries (2020).
- 13.UN DESA. World Population Prospects. https://population.un.org/wpp/Graphs/Probabilistic/POP/TOT/360 (2019).
- 14.Goff SA, et al. A draft sequence of the rice genome (Oryza sativa L. ssp. japonica) Science (80-). 2002;296:92–100. doi: 10.1126/science.1068275. [DOI] [PubMed] [Google Scholar]
- 15.Yu J, et al. A draft sequence of the rice genome (Oryza sativa L. ssp. indica) Science (80-). 2002;296:79–92. doi: 10.1126/science.1068037. [DOI] [PubMed] [Google Scholar]
- 16.Jiang CK, et al. Identification and distribution of a single nucleotide polymorphism responsible for the catechin content in tea plants. Hortic. Res. 2020;7:1–9. doi: 10.1038/s41438-019-0222-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sapkota S, Boatwright JL, Jordan K, Boyles R, Kresovich S. Identification of novel genomic associations and gene candidates for grain starch content in sorghum. Genes (Basel). 2020;11:1–15. doi: 10.3390/genes11121448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wu D, et al. Identification of a candidate gene associated with isoflavone content in soybean seeds using genome-wide association and linkage mapping. Plant J. 2020;104:950–963. doi: 10.1111/tpj.14972. [DOI] [PubMed] [Google Scholar]
- 19.Sun L, et al. New quantitative trait locus (QTLs) and candidate genes associated with the grape berry color trait identified based on a high-density genetic map. BMC Plant Biol. 2020;20:1–13. doi: 10.1186/s12870-019-2170-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.To HTM, et al. A genome-wide association study reveals the quantitative trait locus and candidate genes that regulate phosphate efficiency in a Vietnamese rice collection. Physiol. Mol. Biol. Plants. 2020;26:2267–2281. doi: 10.1007/s12298-020-00902-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lin Y, et al. Phenotypic and genetic variation in phosphorus-deficiency-tolerance traits in Chinese wheat landraces. BMC Plant Biol. 2020;20:1–9. doi: 10.1186/s12870-019-2170-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu W, et al. Genome-wide association study reveals the genetic basis of fiber quality traits in upland cotton (Gossypium hirsutum L.) BMC Plant Biol. 2020;20:1–13. doi: 10.1186/s12870-019-2170-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thabet SG, Moursi YS, Karam MA, Börner A, Alqudah AM. Natural variation uncovers candidate genes for barley spikelet number and grain yield under drought stress. Multidiscip. Digit. Publ. Inst. 2020;11:1–23. doi: 10.3390/genes11050533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Su Y, Xu H, Yan L. Support vector machine-based open crop model (SBOCM): Case of rice production in China. Saudi J. Biol. Sci. 2017;24:537–547. doi: 10.1016/j.sjbs.2017.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Basith S, Manavalan B, Shin TH, Lee G. SDM6A: A web-based integrative machine-learning framework for predicting 6mA sites in the rice genome. Mol. Ther. Nucleic Acids. 2019;18:131–141. doi: 10.1016/j.omtn.2019.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yu H, Dai Z. SNNRice6mA: A deep learning method for predicting DNA N6-methyladenine sites in rice genome. Front. Genet. 2019;10:1–6. doi: 10.3389/fgene.2019.00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Putri RE, Yahya A, Adam NM, Abd Aziz S. Rice yield prediction model with respect to crop healthiness and soil fertility. Food Res. 2019;3:171–176. doi: 10.26656/fr.2017.3(2).117. [DOI] [Google Scholar]
- 28.Supro IA, Mahar JA, Mahar SA. Rice yield prediction and optimization using association rules and neural network methods to enhance agribusiness. Indian J. Sci. Technol. 2020;13:1367–1379. doi: 10.17485/IJST/v13i13.79. [DOI] [Google Scholar]
- 29.Maeda, Y., Goyodani, T., Nishiuchi, S. & Kita, E. Yield prediction of paddy rice with machine learning. In Proc. 2018 Int. Conf. Parallel Distrib. Process. Tech. Appl. 361–365 (2018).
- 30.Das B, Nair B, Reddy VK, Venkatesh P. Evaluation of multiple linear, neural network and penalised regression models for prediction of rice yield based on weather parameters for west coast of India. Int. J. Biometeorol. 2018;62:1809–1822. doi: 10.1007/s00484-018-1583-6. [DOI] [PubMed] [Google Scholar]
- 31.Amaratunga, V. et al. Artificial neural network to estimate the paddy yield prediction using climatic data. Math. Probl. Eng.2020, (2020).
- 32.Chu Z, Yu J. An end-to-end model for rice yield prediction using deep learning fusion. Comput. Electron. Agric. 2020;174:105471. doi: 10.1016/j.compag.2020.105471. [DOI] [Google Scholar]
- 33.Armagan A, Dunson DB, Lee J. Generalized double pareto shrinkage. Stat. Sin. 2013;23:119–143. [PMC free article] [PubMed] [Google Scholar]
- 34.van Erp S, Oberski DL, Mulder J. Shrinkage priors for Bayesian penalized regression. J. Math. Psychol. 2019;89:31–50. doi: 10.1016/j.jmp.2018.12.004. [DOI] [Google Scholar]
- 35.Huang S, Shingaki-Wells RN, Taylor NL, Millar AH. The rice mitochondria proteome and its response during development and to the environment. Front. Plant Sci. 2013;4:1–6. doi: 10.3389/fpls.2013.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Teixeira PF, Glaser E. Processing peptidases in mitochondria and chloroplasts. Biochim. Biophys. Acta Mol. Cell Res. 2013;1833:360–370. doi: 10.1016/j.bbamcr.2012.03.012. [DOI] [PubMed] [Google Scholar]
- 37.Sharma M, Pandey GK. Expansion and function of repeat domain proteins during stress and development in plants. Front. Plant Sci. 2016;6:1–15. doi: 10.3389/fpls.2015.01218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sheikh AH, et al. Interaction between two rice mitogen activated protein kinases and its possible role in plant defense. BMC Plant Biol. 2013;13:1–11. doi: 10.1186/1471-2229-13-121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang Z, et al. Transcriptome-based analysis of mitogen-activated protein kinase cascades in the rice response to Xanthomonas oryzae infection. Rice. 2015;8:1–13. doi: 10.1186/s12284-014-0038-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vaswani A, et al. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017;30:5999–6009. [Google Scholar]
- 41.Cheng, H. T. et al. Wide & deep learning for recommender systems. In ACM Int. Conf. Proceeding Ser. 7–10 (2016) 10.1145/2988450.2988454.
- 42.Bahdanau, D., Cho, K. H. & Bengio, Y. Neural machine translation by jointly learning to align and translate. In 3rd Int. Conf. Learn. Represent. ICLR 2015—Conf. Track Proc. 1–15 (2015).
- 43.Baurley JW, Budiarto A, Kacamarga MF, Pardamean B. A web portal for rice crop improvements. Int. J. Web Portals. 2018;10:15–31. doi: 10.4018/IJWP.2018070102. [DOI] [Google Scholar]
- 44.Wang DR, et al. An imputation platform to enhance integration of rice genetic resources. Nat. Commun. 2018;9:1–10. doi: 10.1038/s41467-017-02088-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dominic N, Prayoga JS, Kumala D, Surantha N, Soewito B. The comparative study of algorithms in building the green mobile cloud computing environment. Springer B. Lect. Notes Netw. Syst. 2021;343:43–54. doi: 10.1007/978-3-030-89899-1_5. [DOI] [Google Scholar]
- 46.Mittag F, Römer M, Zell A. Influence of feature encoding and choice of classifier on disease risk prediction in genome-wide association studies. PLoS One. 2015;10:e0135832. doi: 10.1371/journal.pone.0135832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Song M, Wheeler W, Caporaso NE, Landi MT, Chatterjee N. Using imputed genotype data in the joint score tests for genetic association and gene–environment interactions in case-control studies. Genet. Epidemiol. 2018;42:146–155. doi: 10.1002/gepi.22093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yusuf I, et al. Genetic risk factors for colorectal cancer in multiethnic Indonesians. Sci. Rep. 2021;11:1–9. doi: 10.1038/s41598-020-79139-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Probst P, Boulesteix AL, Bischl B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019;20:1–32. [Google Scholar]
- 50.Dominic N, Daniel Cenggoro TW, Budiarto A, Pardamean B. Transfer learning using inception-resnet-v2 model to the augmented neuroimages data for autism spectrum disorder classification. Commun. Math. Biol. Neurosci. 2021;2021:1–21. [Google Scholar]
- 51.Lattes MB. Report: Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005;67:301–320. doi: 10.1111/j.1467-9868.2005.00503.x. [DOI] [Google Scholar]
- 52.Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010;33:1–22. doi: 10.18637/jss.v033.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zou H, Hastie T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005;67:301–320. doi: 10.1111/j.1467-9868.2005.00503.x. [DOI] [Google Scholar]
- 54.Shannon CE. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- 55.Shannon CE. A mathematical theory of communication part III: Mathematical preliminaries. Bell Syst. Tech. J. 1948;27:623–656. doi: 10.1002/j.1538-7305.1948.tb00917.x. [DOI] [Google Scholar]
- 56.Croiseau P, et al. Fine tuning genomic evaluations in dairy cattle through SNP pre-selection with the Elastic-Net algorithm. Genet. Res. (Camb) 2011;93:409–417. doi: 10.1017/S0016672311000358. [DOI] [PubMed] [Google Scholar]
- 57.Sarkar RK, Rao AR, Meher PK, Nepolean T, Mohaparta T. Evaluation of random forest regression for prediction of breeding value from genomewide SNPs. J. Genet. 2015;94:187–192. doi: 10.1007/s12041-015-0501-5. [DOI] [PubMed] [Google Scholar]
- 58.Rashkin SR, et al. A pharmacogenetic prediction model of progression-free survival in breast cancer using genome-wide genotyping data from CALGB 40502 (Alliance) Clin. Pharmacol. Ther. 2019;105:738–745. doi: 10.1002/cpt.1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wen J, Ford CT, Janies D, Shi X. A parallelized strategy for epistasis analysis based on Empirical Bayesian Elastic Net models. Bioinformatics. 2020;36:3803–3810. doi: 10.1093/bioinformatics/btaa216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Chen C, Twycross J, Garibaldi JM. A new accuracy measure based on bounded relative error for time series forecasting. PLoS One. 2017;12:1–23. doi: 10.1371/journal.pone.0174202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Elavarasan D, Vincent DR, Sharma V, Zomaya AY, Srinivasan K. Forecasting yield by integrating agrarian factors and machine learning models: A survey. Comput. Electron. Agric. 2018;155:257–282. doi: 10.1016/j.compag.2018.10.024. [DOI] [Google Scholar]
- 62.Spiess AN, Neumeyer N. An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010;10:1–11. doi: 10.1186/1471-2210-10-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pal R. Chapter 4: Validation methodologies. Predict. Model. Drug Sensit. 2017 doi: 10.1016/b978-0-12-805274-7.00004-x. [DOI] [Google Scholar]
- 64.Nallamilli BRR, et al. Polycomb group gene OsFIE2 regulates rice (Oryza sativa) seed development and grain filling via a mechanism distinct from Arabidopsis. PLoS Genet. 2013;9:e1003322. doi: 10.1371/journal.pgen.1003322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Jeong K, et al. Phosphorus remobilization from rice flag leaves during grain filling: an RNA-seq study. Plant Biotechnol. J. 2017;15:15–26. doi: 10.1111/pbi.12586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zhu Q-L, et al. In silico analysis of a MRP transporter gene reveals its possible role in anthocyanins or flavonoids transport in Oryze sativa. Am. J. Plant Sci. 2013;04:555–560. doi: 10.4236/ajps.2013.43072. [DOI] [Google Scholar]
- 67.Liu Y, et al. Anthocyanin biosynthesis and degradation mechanisms in Solanaceous vegetables: A review. Front. Chem. 2018;6:52. doi: 10.3389/fchem.2018.00052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Panche, A. N., Diwan, A. D. & Chandra, S. R. Flavonoids: An overview. J. Nutr. Sci.5, (2016). [DOI] [PMC free article] [PubMed]
- 69.Singh V, Sharma V, Katara P. Comparative transcriptomics of rice and exploitation of target genes for blast infection. Agric. Gene. 2016;1:143–150. doi: 10.1016/j.aggene.2016.08.004. [DOI] [Google Scholar]
- 70.van Ooijen G, et al. Structure-function analysis of the NB-ARC domain of plant disease resistance proteins. J. Exp. Bot. 2008;59:1383–1397. doi: 10.1093/jxb/ern045. [DOI] [PubMed] [Google Scholar]
- 71.Głowacki S, Macioszek VK, Kononowicz AK. R proteins as fundamentals of plant innate immunity. Cell. Mol. Biol. Lett. 2011;16:1–24. doi: 10.2478/s11658-010-0024-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Tian L, et al. Rna-binding protein RBP-P is required for glutelin and prolamine mRNA localization in rice endosperm cells. Plant Cell. 2018;30:2529–2552. doi: 10.1105/tpc.18.00321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Wang C, et al. Chloroplastic Os3BGlu6 contributes significantly to cellular ABA pools and impacts drought tolerance and photosynthesis in rice. New Phytol. 2020;226:1042–1054. doi: 10.1111/nph.16416. [DOI] [PubMed] [Google Scholar]
- 74.Sun L, et al. Carbon Starved Anther modulates sugar and ABA metabolism to protect rice seed germination and seedling fitness. Plant Physiol. 2021 doi: 10.1093/plphys/kiab391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Talla SK, et al. Cytokinin delays dark-induced senescence in rice by maintaining the chlorophyll cycle and photosynthetic complexes. J. Exp. Bot. 2016;67:1839–1851. doi: 10.1093/jxb/erv575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Chandran AKN, Jeong HY, Jung KH, Lee C. Development of functional modules based on co-expression patterns for cell-wall biosynthesis related genes in rice. J. Plant Biol. 2016;59:1–15. doi: 10.1007/s12374-016-0461-1. [DOI] [Google Scholar]
- 77.Wang Y, et al. Genetic bases of source-, sink-, and yield-related traits revealed by genome-wide association study in Xian rice. Crop J. 2020;8:119–131. doi: 10.1016/j.cj.2019.05.001. [DOI] [Google Scholar]
- 78.Patishtan J, Hartley TN, Fonseca de Carvalho R, Maathuis FJM. Genome-wide association studies to identify rice salt-tolerance markers. Plant Cell Environ. 2018;41:970–982. doi: 10.1111/pce.12975. [DOI] [PubMed] [Google Scholar]
- 79.Saha J, Sengupta A, Gupta K, Gupta B. Molecular phylogenetic study and expression analysis of ATP-binding cassette transporter gene family in Oryza sativa in response to salt stress. Comput. Biol. Chem. 2015;54:18–32. doi: 10.1016/j.compbiolchem.2014.11.005. [DOI] [PubMed] [Google Scholar]
- 80.Leonard GD, Fojo T, Bates SE. The role of ABC transporters in clinical practice. Oncologist. 2003;8:411–424. doi: 10.1634/theoncologist.8-5-411. [DOI] [PubMed] [Google Scholar]
- 81.Mackon E, et al. Recent insights into anthocyanin pigmentation, synthesis, trafficking, and regulatory mechanisms in rice (Oryza sativa L.) caryopsis. Biomolecules. 2021;11:1–26. doi: 10.3390/biom11030394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Nguyen Q-TT, Huang T-L, Huang H-J. Identification of genes related to arsenic detoxification in rice roots using microarray analysis. Int. J. Biosci. Biochem. Bioinform. 2014;4:22–27. [Google Scholar]
- 83.Narsai R, et al. Mechanisms of growth and patterns of gene expression in oxygen-deprived rice coleoptiles. Plant J. 2015;82:25–40. doi: 10.1111/tpj.12786. [DOI] [PubMed] [Google Scholar]
- 84.Wu YS, Yang CY. Comprehensive transcriptomic analysis of auxin responses in submerged rice coleoptile growth. Int. J. Mol. Sci. 2020;21:1292. doi: 10.3390/ijms21041292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Chen X, et al. Transcriptome and proteome profiling of different colored rice reveals physiological dynamics involved in the flavonoid pathway. Int. J. Mol. Sci. 2019;20:2463. doi: 10.3390/ijms20102463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Kim CK, et al. Multi-layered screening method identification of flavonoid-specific genes, using transgenic rice. Biotechnol. Biotechnol. Equip. 2013;27:3944–3951. doi: 10.5504/BBEQ.2013.0037. [DOI] [Google Scholar]
- 87.Koes RE, Quattrocchio F, Mol JNM. The flavonoid biosynthetic pathway in plants: Function and evolution. BioEssays. 1993;16:123–132. doi: 10.1002/bies.950160209. [DOI] [Google Scholar]
- 88.Davies KM, et al. The evolution of flavonoid biosynthesis: A bryophyte perspective. Front. Plant Sci. 2020;11:1–21. doi: 10.3389/fpls.2020.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All codes for this research are available at www.github.com/NicholasDominic/The-NucleoNets.