Comparison of Accuracy in Calculation of Absorbed Dose to the Kidneys Following Radioligand Therapy with ¹⁷⁷Lu-DKFZ-PSMA-617 by Two Different Background Correction Methods

Abstract

Background:

To improve the accuracy of activity image quality, scatter correction is a critical method. The aim of this study is to compare the accuracy in calculation of absorbed dose to patients following radioligand therapy (RLT) with ¹⁷⁷Lu-DKFZ-PSMA-617 by two different methods of background correction in the conjugate view method.

Materials and Methods:

This study involved 10 patients. The individualized patient dosimetry calculations were based on whole-body planar scintigraphy images acquired in 10 patients with a mean age of 71.4 ± 6.07 years (range 63–85 years) at approximately 0–2 h, 4–6 h, 18–24 h, and 36–48 h after administration of the mean 6253 ± 826.4 MBq (range 5500–7400 MBq) of ¹⁷⁷Lu-DKFZ-PSMA-617. Organ activities were calculated using the conjugate view method by Buijs and conventional background correction. Eventually, the absorbed dose of radiation was calculated using Medical Internal Radiation Dose formalism.

Results:

The dose per unit of injected activity (mGy/MBq) ± standard deviation for kidney using Buijs and conventional methods was 1.05 ± 0.11 and 0.63 ± 0.14, respectively.

Conclusion:

The Buijs background correction method was more accurate than the conventional method.

Introduction

Many cancer patients are successfully treated due to the improvement of old treatment techniques such as surgery, external beam radiotherapy, chemotherapy, and biotherapy. Unfortunately, for some patients, the treatment fails. This can be due to the extent of cancer spreading to multiple sites of the body.[1] To solve this problem, new treatments are being developed, including radioligand therapy (RLT).[2] Reliable estimates of the radiation dose from diagnostic or therapeutic radiopharmaceutical agents in nuclear medicine to assess the risks and benefits of using them are essential.[3,4,5] Once the RLT therapy has been decided on, several methods can be applied to estimate the amount of activity required for planned dose delivery to organs. The radiation dose estimation is the basis for the use of radiopharmaceuticals in nuclear medicine and it is also the first step in protection against radiation. For example, in therapeutic applications of radiopharmaceuticals, it is necessary to assess the absorbed dose in the tumor and normal tissues to choose the most appropriate treatment protocol, maintaining doses to vital organs at safe levels. It is important to state that the organ dose evaluation deeply depends on the activity quantification of that organ. The Committee on Medical Internal Radiation Dose (MIRD) is credited with developing a standardized data framework to establish correlations between delivered activity and radiation dose.[6,7,8] These studies showed that the absorbed dose in the target organs is estimated as a function of the accumulated activity in the source organs and generally provides the correct mathematically estimated dose.[9,10] The conjugate view method was used for the quantification of organ activities. The standard method for quantifying activity in an organ is a connection method in which, in general, an anterior image and a posterior image are obtained, and the regions of interest area (ROI) are drawn manually on the organs of interest.[11,12,13] Accurate estimation of activity from the measured count requires some modifications to the physical factors, such as attenuation, scattering, patient thickness, and the physical decay of the radionuclide used.[14] Several types of research were performed to study the activity evaluation using planar images, mainly investigating the attenuation and scatter corrections.[15] However, evaluation of different methods has been studied to improve the background, but still need to find an accurate way, especially in the evaluation of content in the parts with low absorption there. The accuracy of various background correction methods is required for optimizing the methods of activity quantification to calculated internal dose estimations for nuclear medicine diagnostic and therapeutic.[11,12,14] The main goal of this study was to compare accuracy in calculation of absorbed dose to kidneys in patients following peptide receptor radionuclide therapy with ¹⁷⁷Lu-DKFZ-PSMA-617 by two different methods of background in conjugate view method of Buijs and conventional.

Materials and Methods

Data analysis was performed on ten patients with distant metastases and progressive disease, aged 36–65 years (mean: 51.4 ± 60.7 years) and adequate hematological, liver, and renal function, who were treated with ¹⁷⁷Lu-DKFZ-PSMA-617 between April 2019 and September 2019 in Shohada-e Tajrish Hospital, Tehran, Iran. The physician determined the specific activity to be administered, according to the dosimetric results and the patient's clinical conditions. During the first cycle, patients were evaluated for dosimetry with ¹⁷⁷Lu-DKFZ-PSMA-617. The mean activity of 6253 ± 826.4 (range: 5500–7400 MBq) was used in this study. A summary of the treatment history for patients is shown in Table 1. The study was approved by the Hospital Ethics Committee, informed consent was obtained from all patients and it was carried out according to the provisions of the Declaration of Helsinki. Following injection of ¹⁷⁷Lu-DKFZ-PSMA-617, patients underwent imaging at 0–2, 4–6, 18–20, and 36–48 h in the form of whole-body planar acquisition. Planar imaging was used to measure the whole body and organs' activity over a number of days. All data were acquired on a dual-head gamma-camera (Symbia Evo Excel SIEMENS) equipped with low-energy high-resolution collimators and with 3/8” thick NaI crystals. Anterior and posterior views were acquired with a 16 cm/min scan speed, an energy window of 20% for a double peak at 113, and 208 keV. The first whole-body image was performed before voiding. A ¹⁷⁷Lu source was positioned. Static images were acquired for 300 s, using the same matrix, pixel size, and energy setting as for the whole-body images. The number of counts in a region of interest around the source in the images was determined and divided by scanning time. The system calibration factor for ¹⁷⁷Lu was determined in counts per second per MBq (cps/MBq) using Equation No. 1.[10]

Table 1.

Patient demographic baseline information

Number of patients	Age (year)	BMI (kg/cm2)	Activity (MBq)	PSA (ng/ml)	Gleason score	Cr	Platelets (103/µl)	Site of metastases
1	70	24	5920	40	5+5	1.08	198	Skeletal
2	63	21	6290	35.6	5+5	0.90	234	Skeletal, lymph node
3	77	23	5550	10	4+4	0. 81	158	Skeletal
4	72	24	7400	94	4+3	1.0	165	Skeletal, lymph node
5	72	25	5550	18.6	4+3	0.88	200	Skeletal, lymph node
6	85	24	5920	25	4+3	1.16	221	Skeletal
7	78	25	5550	55.8	5+3	2.02	199	Skeletal, lung
8	68	23	5550	74.4	4+3	1.23	256	Skeletal, pelvic
9	67	28	7400	7.6	4+4	1.09	217	Skeletal, lymph node
10	65	24	7400	31.2	5+5	1.12	323	Skeletal, lung
Mean±SD	71.4±6.07	24.01±1.79	6253±826.4	39.2±28.03	8.2±1.31	1.04±0.48	217±47

SD: Standard deviation, BMI: Body mass index, PSA: Prostate-specific antigen

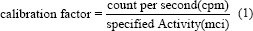
The organ in the body may receive radiation directly from the injected radionuclide or from other organs around them. For activity quantification, the conjugated view method was used. The count rates were measured by drawn ROI for kidneys. The activity was calculated for the kidneys at each time point, using Equations No. 2 and No. 3.[10]

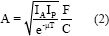
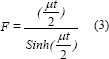
where I_A and I_p are background-corrected numbers of counts (cps) within specified ROI in each organ from anterior and posterior images, respectively. T is the anterior-posterior body thickness, t is the organ thickness, F is the gamma-camera calibration factor, and μ is the attenuation coefficient for ¹⁷⁷Lu. The thickness of the body and kidney organs was measured separately using side images (spectra and computerized tomography scan) as well as gamma-camera software for each patient. For paired organs (kidneys), the value was calculated and a single time-activity curve was obtained. For each ROI, the geometric mean of two conjugate views was calculated. The curve of activity as a function of the time was drawn for kidneys and fitted to bi-exponential function. The cumulative activity was calculated in each organ, separately using the MATLAB program. Each organ residence time (h) was calculated by cumulative activity per administered activity. By two different Buijs and conventional background correction methods, a counting rate was obtained.

Buijs method

According to the Buijs equation No. 4, the counting rate in a neighboring ROI is subtracted from the counting rate in the organs ROI.

I_A = I'_A − I_BGA × F

I_P = I'_P − I_BGP × F (4)

where I_A (I_P) is the background corrected counting rate in the anterior (posterior), I'_A (I'_P) is the measured counting rate in the anterior (posterior) ROI, and I_BGA (I_BGP) is the counting rate in the anterior (posterior) background ROI. F is the fraction of the total background activity I_BGA to be subtracted from the measured activity in the source organ's ROI, I_A (I_P). F is defined as Equation No. 5:

F = 1 – (t/T) (5)

where t is the organ thickness and T is the body thickness (cm) at the source organ.

Conventional background subtraction

The counting rate was measured in an adjacent ROI subtracted from the counting rate in the ROI, using Equation No. 6:

I_A = I'_A – I”_A × S_A

I_P = I'_P – I”_P × S_P (6)

The counts per pixel (count/pix) rate in the anterior (posterior) background ROI and the number of pixels in the anterior (posterior) source ROI region is defined by IA (IP) and I'A (I'P) SA (SP) the number of pixels in the anterior (posterior) source ROI region.

MIRD scheme provides a conventional method for estimating absorbed doses of radionuclides in internal organs. The mean absorbed dose for each organ was determined with Equation No. 7.

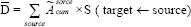
where D¯ is the absorbed dose of each target, 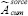is cumulative activity of each source, and the S-value is absorbed dose per cumulative activity for each pair source target. Dosimetry values were computed with an S-value value for Lu-177 derived from the Radiation Dose Assessment Resource website.[16,17,18] The dose evaluation was performed according to IDIAC-DOSE 2.1 software. An internal dosimetry computer program, IDAC-Dose 2.1, was developed based on the International Commission on Radiological Protection (ICRP) absorbed fractions and computational framework of internal dose assessment given for reference adults in ICRP Publication 133. The IDIAC-DOSE 2.1 software calculates absorbed doses to all 47 target regions defined in ICRP Publication 133. The results are presented in terms of absorbed dose per administered activity (mGy/MBq). All results were expressed as mean ± standard deviation (SD). The complete data analysis was done using Microsoft Excel (Microsoft office professional plus 2013) and MATLAB (R2011a; The MathWorks, Inc., Natick, MA) software.

Results

Table 2 shows that the kidney uptake was calculated using conventional, Buijs subtraction methods for background correction. The current study presents the absorbed per unit of injected activity (mGy/MBq) ± SD for kidneys after different background correction methods in the conjugate view method. Calculations were in accordance with MIRD recommendations. These values for kidney by Buijs method were 1.05 ± 0.11 and by the conventional method were 0.63 ± 0.14 mGy/MBq. The percentage difference between the absorbed doses in this study (Buijs and conventional) with MIRD software (IDIAC-DOSE 2.1) was 13% and 28%, respectively.

Table 2.

Mean uptake in the kidneys during radioligand therapy using two methods of background correction at different times

Time	0-2 h	4-6 h	18-24 h	36-48 h
Mean uptake activity [%IA] Buijs	2.1±0.7 (P<0.05)	1.7±0.6 (P<0.05)	1.3±0.5 (P<0.05)	0.8±0.3 (P<0.05)
	A range of: 1.3-2.6	A range of: 1.0-2.1	A range of: 0.9-1.6	A range of: 0.4-1.2
Mean uptake activity [%IA] conventional method	1.25±0.5 (P<0.05)	0.95±0.4 (P<0.05)	0.78±0.6 (P<0.05)	0.54±0.2 (P<0.05)
	A range of: 0.9-1.9	A range of: 0.7-1.7	A range of: 0.4-1.4	A range of: 0.3-0.9

P value obtained from one-sample t-test

Discussion

Biodistribution data for radiopharmaceuticals within the body and specific organs may be obtained from planar gamma-camera views using the conjugate view geometric mean method. The accuracy of this method will be greatest for radiopharmaceuticals distributed in a single organ or isolated organs that do not overlap in the planar projection.

For planar gamma-camera imaging, subtraction of background activity present in surrounding tissue from activity measured in the organ of interest is routinely performed. Background subtraction is required to allow accurate estimation of the organ activity or for comparisons of relative activity uptakes or retentions between tissues. Many studies have shown that factors such as effective attenuation coefficient, body thickness, device sensitivity, background activity, and overlap of tissue influence the accuracy of activity quantification. Current methods for quantifying organ activity are accurate enough for single or detached organs that do not sufficiently overlap with others in the planar project.[11,19,20] However, in most common clinical cases, the organs overlap and the uptake of activity in the background is such that a kind of background modification is needed to improve the accuracy of quantifying activity in the target organ.[20] Norrgren et al.[21] noted that background activity correction was the factor that had the greatest impact on the results. The main source of uncertainty in quantifying organ or tumor activity from planar images is the activity in the tissue around the source. The present study showed that the Buijs background correction method was more accurate than the conventional method on estimated absorbed dose for kidneys [Table 2]. As the results in Table 3 represents, the absorbed dose within the kidneys shows its agreement with the data of IDAC-DOSE 2.1 software. Buijs et al.[14] reported that the conventional method leads to excessive correction of background activity, because the organ volume is not considered.[14] The conventional method, which is the simplest method of background correction, is based on the use of ROI, which is conveniently adjacent to the organ's ROI. The number of counts per pixel in that background ROI is subtracted from the counts per pixel in the ROI. Another method simplified by Buijs et al.[14] is proposed, in which the thickness of the organ and the body is required. This method is used to avoid over subtraction of background activity due to the volume occupied by the organ. The present study showed that the Buijs background correction method is more accurate than the conventional method in estimating the absorbed dose. The conventional method for background correction does not correct for source volume in contrast to the Buijs methods. The accuracy of the activity quantification was evaluated using two different methods of background correction in ¹⁷⁷Lu-DKFZ-PSMA-617 scans. The choice of background correction method is even more important in order to determine the amount of activity absorption in the organ of interest at an acceptable level of accuracy.[20] Concerns about the safe and effective use of radiation in medicine led to the development of standard methods and methods for calibrating the amount of activity prescribed to patients. The comparison between two different methods of background activity correction applied in the present study showed that the Buijs method was the most appropriate method for background correction in ¹⁷⁷Lu-DKFZ-PSMA-617 scans. It should be noted that a less accurate estimation of the activity concentration may be due to background activity in the vicinity of the target organ. It is also affected by the size of the ROI which is used in data analysis. Incorrect estimates of body and organ thickness can also affect results. Using reference values can also be a source of error, as absorption dose values can vary somewhat in patients. Some of the items listed above, such as lack of precision in the thickness of the body and organs, and changes in the activity of background, to perform the measurement of a phantom can be resolved to decide which method to correct background for the organ to be most suitable. However, studies based on the phantom as well as it is a limitation, including the inability to accurately simulate irregularities and nonuniform background activity.[10] The method current study is a simple method that is easily implemented in any clinic with a gamma camera.

Table 3.

Result of absorbed dose per unit of injected activity (mGy/mBq)±standard deviation after administration of ¹⁷⁷Lu-DKFZ-PSMA-617 intravenously between two background correction methods (n=10)

Organ	Conventional method	Buijs	P
Kidneys	0.63±0.14 (a range of: 0.43-0.79)	1.05±0.11 (a range of: 0.8-1.34)	<0.05

Conclusion

One of the major sources of uncertainty in quantifying organ or tumor activity from planar images is the activity in the tissue around the source. Assessment of absorbed dose to kidney plays a vital role in maintaining safe delivery of RLT therapy to patients suffering from prostate cancer. The mean absorbed dose of ¹⁷⁷Lu-DKFZ-PSMA-617 was estimated in kidneys using two different methods of background correction showed Buijs method for background correction will provide the most accurate results.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.