Abstract
Pharmacokinetic/pharmacodynamic (PK/PD) indices making use of area under the curve, maximum concentration, and the duration that in vivo drug concentration is maintained above a critical level are commonly applied to clinical dose prediction from animal efficacy experiments in the infectious disease arena. These indices make suboptimal use of the nonclinical data, and the prediction depends on the shape of the PK profiles in the animals, determined by the species‐specific absorption, distribution, metabolism, and elimination properties, and the dosing regimen used in the efficacy experiments. Motivated by the principle that efficacy is driven by pharmacology, we conducted simulations using a generalized pathogen dynamic model, to assess the properties of an alternative efficacy predictor: the area under the effect curve (AUEC), computed using in vitro PD and in vivo PK. Across a wide range of hypothetical scenarios, the AUEC consistently showed regimen‐independent strong correlation (R 2 0.76–0.98) with in vivo efficacy, superior to all other indices. These findings serve as proof of concept that AUEC should be considered in practice as a translation tool for cross‐species dose prediction. Using AUEC for clinical dose prediction could also potentially cut down animal use by reducing or avoiding dose fractionation experiments.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
Several pharmacokinetic/pharmacodynamic (PK/PD) indices are commonly used in predicting efficacy for anti‐infectives.
WHAT QUESTION DID THIS STUDY ADDRESS?
The area under the effect curve (AUEC) was assessed as a novel index potentially overcoming some of the limitations of the conventional PK/PD indices.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
Simulations using a generalized disease‐drug model under a range of experimental conditions suggest that the AUEC could be a more reliable predictor than the conventional indices, while being a simpler approach compared with more mechanistic ones.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
Situational use of AUEC as a cross‐species translational tool for dose prediction is warranted. It has the potential to cut down animal use by reducing or avoiding dose fractionation experiments.
INTRODUCTION
Infectious diseases represent a major global health burden, affecting hundreds of millions of people every year. Drug development success rates for infectious diseases are relatively high compared with other therapeutic areas, 1 however, the return of investment is low. 2 , 3 For cost‐effective drug development, it is imperative to appropriately leverage the data made available during the discovery phase, in order to: identify clinical dosing regimens likely to be effective and safe, encourage compliance, and counter the development of drug‐resistance.
Conventionally, drug‐caused pathogen reduction for any given mechanism is thought to be time‐dependent or concentration‐dependent. In the former case, the so‐called pharmacokinetic/pharmacodynamic (PK/PD) indices considered as potential predictors of drug effect are usually the time that the concentration remains above the minimum inhibitory concentration (T MIC), the time the concentration remains above the level that causes 50% of maximum effect (T EC50), or the time the concentration remains above the level that causes 90% of maximum effect (T EC90). In the latter case, indices that reflect drug concentrations, like area under the curve (AUC) or maximum concentration (C max), can be related to anti‐pathogen effect. 4 , 5 , 6
Clinical dose prediction from animal experiments often relies on PK/PD indices. 7 Typically, efficacy experiments with dose‐fractionation design are conducted in rodents. Correlation between each of the PK/PD indices with in vivo efficacy is estimated; the index with the strongest correlation (highest R 2) is deemed as the optimal predictor and is used to identify the clinical dose, aided by observed or predicted human PK. 8 , 9
Despite their wide use, these PK/PD indices have limitations. Indeed, as PK drives efficacy through PD, and the PK‐PD relationship is a continuous one, we must acknowledge that (i) all in vivo drug concentrations on the PK curve contribute to PD and therefore to efficacy; and (ii) dosing interval (hence the shape of the PK curve) has an impact on PD and potentially on efficacy by extension. The indices T MIC, T EC50, and T EC90 dichotomize the drug concentration and hence the drug effect. Both C max and AUC are PK endpoints which are missing direct PD meaning. Furthermore, using C max implies only the peak of the PK profile affects efficacy, whereas using AUC overlooks the effect of dosing interval (or the shape of the PK curve), which varies greatly among species and hence is highly relevant in cross‐species dose prediction.
More sophisticated methods for dose prediction have been extensively discussed in recent literature. 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 These approaches rely on mathematical description of experimental data conducted in vitro or in animals to project the drug effect on pathogen dynamics in patients. They have the appeal of mechanistical reflection of the drug‐disease interaction and the ability of situational predictions, at the cost of more extensive laboratory experimentation and the need for sometimes unverifiable assumptions.
We propose the area under the effect over time curve (AUEC), which accounts for the collective pharmacological contribution of all in vivo drug concentrations over a dosing interval and is conditioned on the shape of the PK curve, as a “middle‐ground” approach between the simpler, mostly PK‐based, approaches and the more complex mechanistic approaches. It simplifies the translation and avoids the need to identify an anti‐pathogen breakpoint, hence, it has the potential to enable efficient fit‐for‐purpose dose prediction on a large scale for early‐stage drug candidates. The purpose of this work was to systematically evaluate the performance of AUEC as an alternative PK/PD index correlating with in vivo efficacy of anti‐infectives, using simulations in a wide range of scenarios.
METHODS
PK/PD simulations and fittings were carried out in NONMEM (version 7.3.0 and higher; see Supplementary Material S1). Post‐processing of simulation and fitting outputs (such as exploratory plots, goodness of fit plots, and derivation of R 2 values) was performed in R (version 3.5.2 and higher).
In vitro PD model
In vitro drug effect (E vitro) was simulated according to Equation 1, as a function of in vitro drug concentration (C vitro).
| (1) |
Interpretation of E vitro depends on the in vitro experiment performed: pathogen reduction, growth inhibition, kill percentage, or kill rate.
A range of EC50vitro and γ vitro values were tested (Table 1). EC90vitro was derived as 91/γvitro × EC50vitro.
TABLE 1.
Simulated scenarios and R 2 for the evaluation of the predictivity of PK/PD indices for in vivo efficacy
| Purposes of the scenarios | Scenario | In vitro and in vivo parameters | R 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| γ vitro | γ vivo | EC50vitro (ng/mL) | EC50vivo (ng/mL) | Emaxvivo (1/h) | Therapy duration (days) | Start of treatment (day) a | AUC24 | C max | T EC50 | T EC90 | AUEC24 | ||
| Base scenario and its variations | |||||||||||||
| Base scenario | 1 | 1 | 1 | 24 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | 0.22 | <0 | 0.96 |
| Importance of appropriate dose range | 2 | 1 | 1 | 2.4 | 2.4 | 1.5 | 10 | 7 | 0.36 | <0 | 0.79 | <0 | 0.76 |
| 3 | 1 | 1 | 7.2 | 7.2 | 1.5 | 10 | 7 | 0.64 | 0.06 | <0 | <0 | 0.89 | |
| 4 | 1 | 1 | 72 | 72 | 1.5 | 10 | 7 | 0.87 | 0.65 | 0.34 | <0 | 0.92 | |
| 5 | 1 | 1 | 240 | 240 | 1.5 | 10 | 7 | 0.70 | 0.46 | <0 | <0 | 0.83 | |
| Mismatch between in vitro/in vivo drug potency | 6 | 1 | 1 | 2.4 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | 0.34 | 0.19 | 0.84 |
| 7 | 1 | 1 | 7.2 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | 0.92 | <0 | 0.92 | |
| 8 | 1 | 1 | 72 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | <0 | <0 | 0.93 | |
| 9 | 1 | 1 | 240 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | <0 | <0 | 0.90 | |
| Impact of steepness of concentration‐effect curve | 10 | 0.5 | 0.5 | 24 | 24 | 1.5 | 10 | 7 | 0.75 | 0.29 | <0 | <0 | 0.93 |
| 11 | 0.7 | 0.7 | 24 | 24 | 1.5 | 10 | 7 | 0.89 | 0.54 | <0 | <0 | 0.97 | |
| 12 | 1.5 | 1.5 | 24 | 24 | 1.5 | 10 | 7 | 0.89 | 0.66 | 0.18 | <0 | 0.91 | |
| 13 | 2 | 2 | 24 | 24 | 1.5 | 10 | 7 | 0.91 | 0.71 | 0.61 | <0 | 0.90 | |
| Mismatch between in vitro/in vivo steepness of concentration‐effect curve | 14 | 0.5 | 1 | 24 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | 0.22 | <0 | 0.94 |
| 15 | 0.7 | 1 | 24 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | 0.22 | <0 | 0.91 | |
| 16 | 1.5 | 1 | 24 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | 0.22 | <0 | 0.91 | |
| 17 | 2 | 1 | 24 | 24 | 1.5 | 10 | 7 | 0.88 | 0.49 | 0.22 | <0 | 0.87 | |
| Additional conditions | |||||||||||||
| Impact of degree of in vivo drug efficacy | – | 1 | 1 | 24 | 24 | 1 | 10 | 7 | 0.85 | 0.55 | 0.84 | <0 | 0.91 |
| – | 1 | 1 | 24 | 24 | 0.6 | 10 | 7 | 0.81 | 0.46 | 0.78 | <0 | 0.88 | |
| – | 1 | 1 | 24 | 24 | 0.45 | 10 | 7 | 0.71 | 0.03 | 0.09 | <0 | 0.78 | |
| Early stage vs. late stage of infection | – | 1 | 1 | 24 | 24 | 1.5 | 10 | 3 | 0.93 | 0.54 | <0 | <0 | 0.98 |
| Evaluation of shorter treatment duration | – | 1 | 1 | 24 | 24 | 1.5 | 6 | 7 | 0.89 | 0.53 | 0.53 | <0 | 0.96 |
| – | 1 | 1 | 24 | 24 | 1.5 | 4 | 7 | 0.89 | 0.67 | 0.75 | <0 | 0.95 | |
| – | 1 | 1 | 24 | 24 | 1.5 | 2 | 7 | 0.85 | 0.63 | 0.83 | <0 | 0.95 | |
Abbreviations: AUC, area under the curve; AUEC, area under the effect curve; EC50, concentration leading to half of the maximum effect; EC90, concentration leading to 90% of maximum effect; Emax, maximum effect; PK/PD, pharmacokinetic/pharmacodynamic.
Day after inoculum.
In vivo efficacy model
In vivo pathogen dynamics and drug effect were described via a growth‐kill model with a maximum pathogen carrying capacity of the host system 10 :
| (2) |
In Equation 2, P(t) is the pathogen load at time t, k net is the net growth rate, P max is the maximum pathogen carrying capacity, Emaxvivo is the drug's maximum pathogen depletion rate, C(t)vivo is the drug concentration at time t (derived from the in vivo PK model), EC50vivo is the concentration required in vivo to elicit 50% of Emaxvivo, and γ vivo describes the steepness of the concentration‐response curve. The initial and maximum pathogen load on the logarithmic scale were assumed to be 6 and 20, respectively. Intersubject variability of 20% was included on EC50vivo. Net growth rate (k net) was assumed to be 0.3 h−1; Emaxvivo was assumed to be five times k net to reflect high efficacy.
In vivo PK model
The PK was simulated in mice weighing 0.025 kg, using a one‐compartmental model with parameters consistent with those commonly observed for anti‐infectives: absorption rate constant (k a) 1 h−1, apparent clearance (CL/F) 1.28 L/h/kg and apparent volume (V/F) 5.6 L/kg, resulting in a half‐life of ~ 3 h. The 3‐h half‐life in mice would allometrically scale to a 20‐h half‐life in humans, consistent with drug candidates selected for once daily administration. Low‐to‐moderate intersubject variability was included on CL/F, V/F, and k a, with percent coefficient of variation ~ 20%.
Animal experiment
Dose fractionation was implemented with dosing intervals of 3, 6, 12, or 24 h at total daily doses of 0.12, 0.36, 1.08, and 3.24 mg/kg. Doses were selected based on simulated in vivo exposure and drug potency, and they were reasonably consistent with actual in vivo experiments. A total of 160 animals were used (10 per dosing regimen). The therapy was initiated at the steady‐state of pathogen replication (day 7) to reflect a late/chronic stage of the infection, and the treatment duration was relatively long (10 days).
Derivation of PK/PD indices
Five PK/PD indices were considered as potential predictors of in vivo pathogen load at the end of treatment: area under concentration‐time curve over 24 h at steady‐state (AUC24), maximum concentration at steady‐state (C max), time above EC50vitro (T EC50) and EC90vitro (T EC90; expressed as percentage of time over the dosing interval), and area under the effect, E, over 24 h at steady‐state (AUEC24), which was derived as the integral of Equation 3:
| (3) |
Equation 3 is as Equation 1 where in vitro concentration is substituted with C(t)vivo, i.e., predicted in vivo concentration over time, and Emaxvitro is assumed equal to Emaxvivo (as it is only a proportionality constant not impacting PK/PD index correlation with in vivo efficacy).
Evaluation of the PK/PD indices’ performance
The correlation of each PK/PD index with in vivo efficacy was evaluated in a wide range of scenarios (Table 1).
For each scenario, in vivo efficacy was defined as (P max − P end)/P max × 100, where P end is the pathogen load at the end of the treatment. A sigmoidal Emax relationship between efficacy and each PK/PD index was estimated:
| (4) |
In Equation 4, Index is the value of the PK/PD index, Index50 is the index value corresponding to 50% reduction in pathogen load, and γ_index is the shape parameter specific to the PK/PD index (AUC24, C max, T EC50, T EC90, or AUEC24). To compare the quality of the fittings among the indices, R 2 was used as per common practice. Goodness of fit was also graphically assessed via plotting observed data and predicted curve of efficacy versus PK/PD index.
First, the base scenario (Table 1, scenario 1) and its variations (Table 1, scenarios 2–17) were explored, where different PD parameters (EC50 and γ) were considered, assuming in vitro/in vivo concordance or mismatch.
Second, the dependency of the PK/PD indices on the PK curve shape was assessed in the base scenario and its variations via the estimation of the covariate effect of dosing interval on the key parameter for the relationship between each PK/PD index and efficacy (i.e., Index50). A drop of 10.83 points (p < 0.001) in the log‐likelihood objective function was considered statistically significant. This was motivated by the observation that drugs tend to have shorter half‐lives in smaller animals, and the shape difference in the PK curve could be a major contributor to mis‐prediction of clinical dose from animal models. Less frequent dosing produces more fluctuating PK profiles, resembling shorter half‐lives. A PK/PD index less dependent on this shape would have higher cross‐species translation reliability.
Last, additional conditions were explored, challenging the hypotheses applied for the base scenario and its variations regarding the degree of in vivo drug efficacy (Emaxvivo 5 times k net vs. 3.3, 2.0, or 1.5 times k net), treatment start (on day 7 for late‐stage infection versus on day 3 for early‐stage infection), and treatment duration (10 days vs shorter duration of 6, 4, or 2 days), to “stress‐test” the dependency of our results on the base scenario (see Table 1).
RESULTS
Under the condition of a highly efficacious drug treating the disease at the steady‐state, a relatively simple base scenario (scenario 1) served as a starting point, from which groups of other scenarios (scenarios 2–17) were explored. Further conditions of lower efficacy drugs, pre‐steady‐state treatment, or shorter treatment duration were also explored. Table 1 shows the R 2 for the estimated relationship between in vivo efficacy and each PK/PD index in all conditions. The efficacy versus PK/PD index correlation plots of the base scenario are reported as a reference for the other scenarios in Figures 1, 2, and 4.
FIGURE 1.
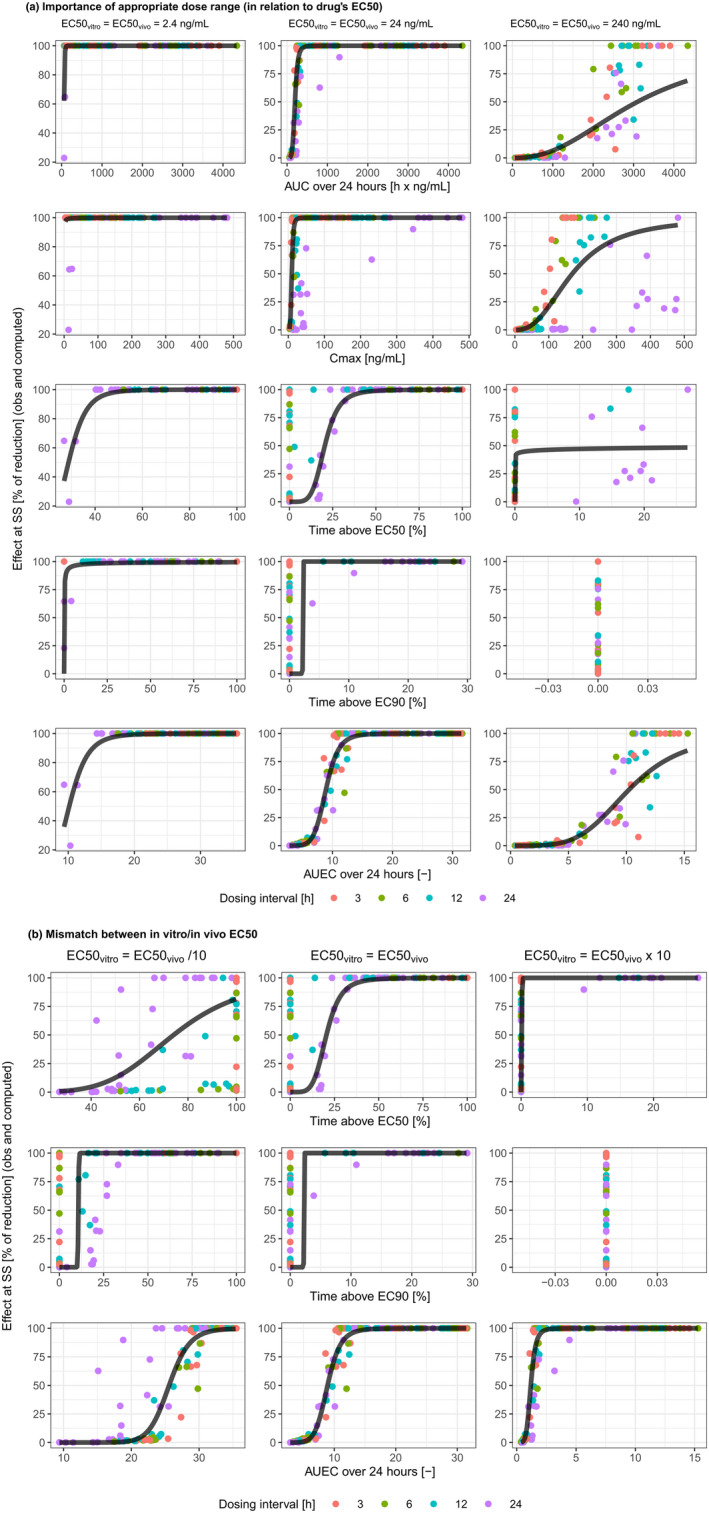
The importance of adequate dose range in relation to the drug's potency (a), and of matching in vitro/in vivo drug's potency (b). AUC, area under the curve; C max, maximum concentration; EC50, concentration leading to half of the maximum effect; EC90, concentration leading to 90% of maximum effect; obs, observed; SS, steady‐state.
FIGURE 2.
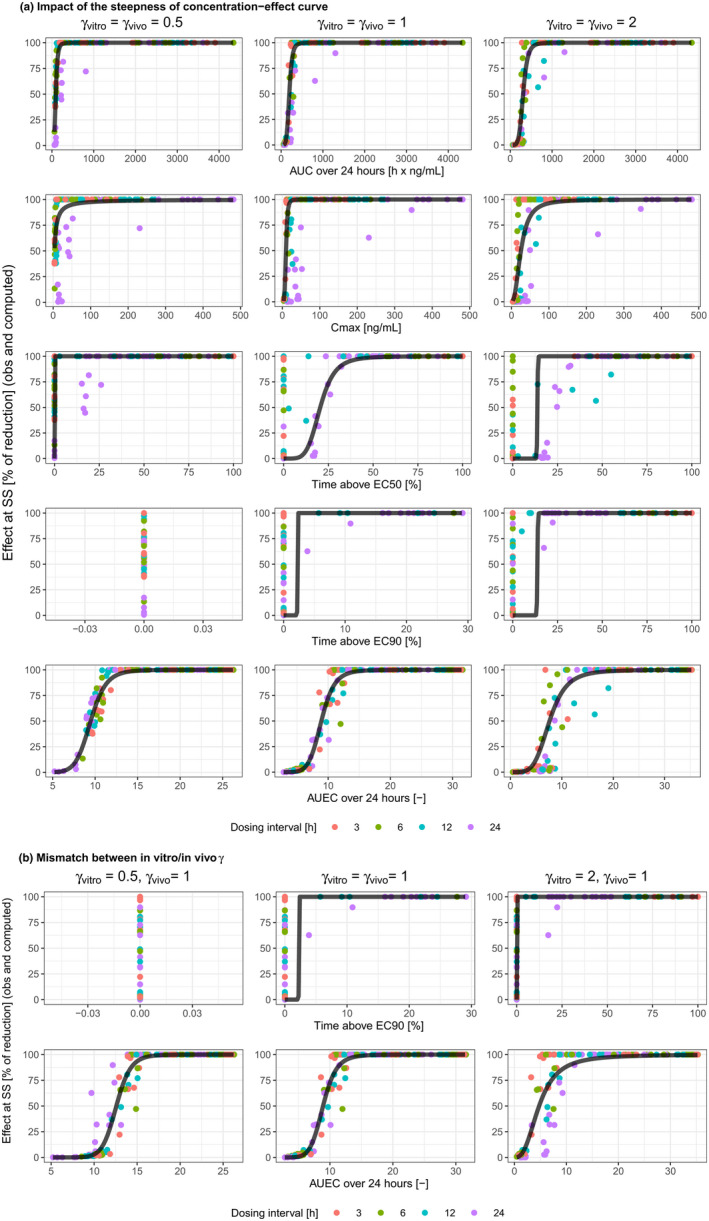
Impact of the steepness of concentration‐effect curve (a), and of its mismatch between in vitro and in vivo experiments (b). AUC, area under the curve; AUEC, area under the effect curve; C max, maximum concentration; EC50, concentration leading to half of the maximum effect; EC90, concentration leading to 90% of maximum effect; obs, observed; SS, steady‐state.
FIGURE 4.
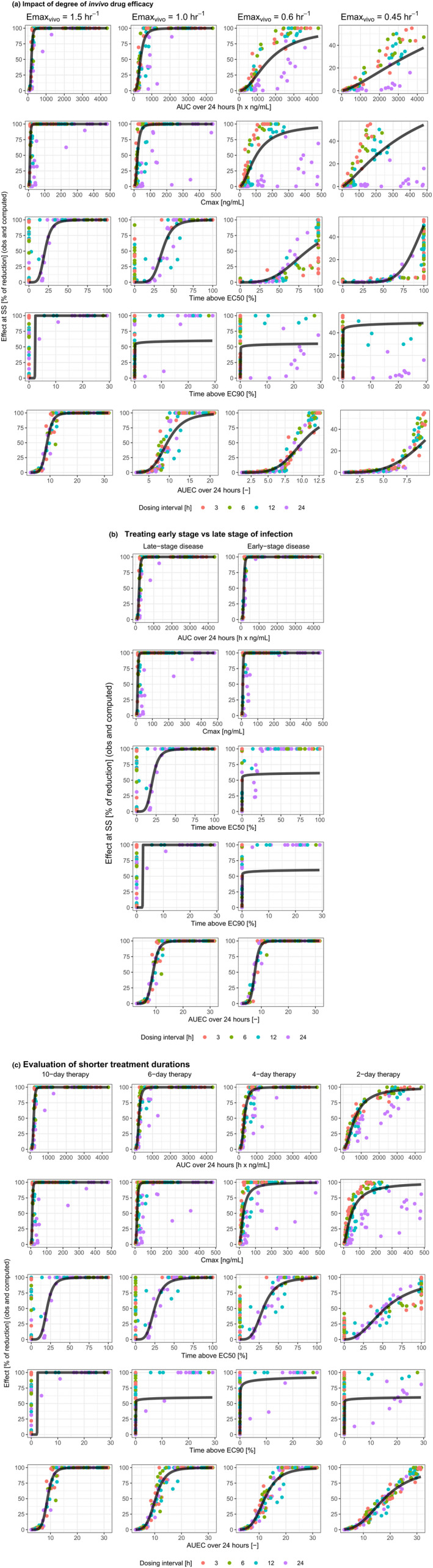
Performance of PK/PD indices for drugs with varying degrees of in vivo efficacy (a), treating different stages of infection (b), or with various treatment durations (c). AUC, area under the curve; AUEC, area under the effect curve; C max, maximum concentration; EC50, concentration leading to half of the maximum effect; EC90, concentration leading to 90% of maximum effect; Emax, maximum effect; obs, observed; PD, pharmacodynamic; PK, pharmacokinetic; SS, steady‐state.
Base scenario
In the base scenario (scenario 1), where there was no in vitro versus in vivo discrepancy for EC50 or γ and the doses for the animal experiment adequately covered the entire effect curve, a reasonable fit (i.e., a fitted curve well representing the overall trend) was obtained only for AUC24 and AUEC24 (Figure 1a, center column). The AUEC24 performed better than AUC24, with R 2 > 0.9 (Table 1). Other PK/PD indices, most notably T EC50, showed data clustering, suggesting regimen‐dependent relationship between the PK/PD index and efficacy.
Appropriate dose range for the drug's potency
In reality, the dose range of in vivo experiment does not always cover the full range of drug efficacy. Table 1 scenarios 2–5 and Figure 1a show how this would impact the performance of various PK/PD indices by using the same dosing regimens as for the base scenario but changing drug potency. When both EC50vitro and EC50vivo went from high to low, lower dose levels were more likely to show efficacy. This was reflected by better efficacy at lower AUC24 and C max, as well as at lower T EC50 and T EC90. In scenarios 2–5, the data of AUC24 and AUEC24 were far less dispersed around the fitting curve compared to the data of other PK/PD indices (Figure 1a). The R 2 remained high and relatively stable for AUEC24 and was generally lower for all other PK/PD indices (Table 1).
Mismatch between in vitro/in vivo drug potency
The in vivo and in vitro potencies of a drug are likely to be different. Although this discrepancy will not affect the strength of correlation (R 2) for AUC24 and C max, its implication for the other PK/PD indices is shown in Table 1 scenarios 6–9 and Figure 1b. Under the tested conditions, AUEC24 was usually the best predictor, with R 2 higher or comparable to that of AUC24 (Table 1). Both T EC50 and T EC90 performed poorly, except for T EC50 when EC50vitro was approximately one‐third of EC50vivo (scenario 7). In this case, the R 2 of T EC50 was like that of AUEC24, however, data appeared more dispersed around the fitted curve. When there was in vitro/in vivo potency mismatch, AUEC24 was the only endpoint that maintained consistent relationship with efficacy.
Steepness of concentration‐effect curves
AUEC24 was a reliable predictor with high R 2 (>0.9) and good fit, regardless of the steepness of the concentration‐effect curve (Table 1 scenarios 10–13 and Figure 2a). When both γ vitro and γ vivo went from low to high, there was slight improvement in predictivity for AUC24 and notable improvement for C max. The dosing‐interval dependency of the data pattern for T EC50 remained evident, irrespective of the steepness of the concentration‐effect curve. As γ increased, EC90 would become closer to EC50; this could explain the more similar data distribution for T EC90 and T EC50 at higher γ vitro and γ vivo. As γ decreased, EC90 would become higher, leading to TEC90 approaching zero within the dose range tested.
Mismatch between in vitro/in vivo steepness of concentration‐effect curve
It is also conceivable that the in vitro concentration‐effect curve has a different steepness than the in vivo curve (γ vitro ≠ γ vivo). This should have no impact on the relationship with efficacy for AUC24, C max, and T EC50 (Table 1 scenarios 14–17, Figure 2b). As a driver of in vivo efficacy, AUEC24 was better than or comparable to AUC24 (when γ vitro went from low to high, scenario 17), and superior to all other PK/PD indices.
Dosing interval as a covariate for the relationship between a PK/PD index and in vivo efficacy
Although statistical significance of dosing interval as a covariate for the efficacy versus PK/PD index relationship reflects the improvement of the fitting, the variation of the Index50 across dosing intervals is more important. Indeed, this variation reflects the pharmacological dependency of Index50 on dosing regimen.
For AUC50, dosing interval was a statistically significant covariate across all scenarios 1–17, based on objective function value drop. However, AUC50 estimates varied in most cases by less than two‐fold across dosing intervals (Figure 3a).
FIGURE 3.
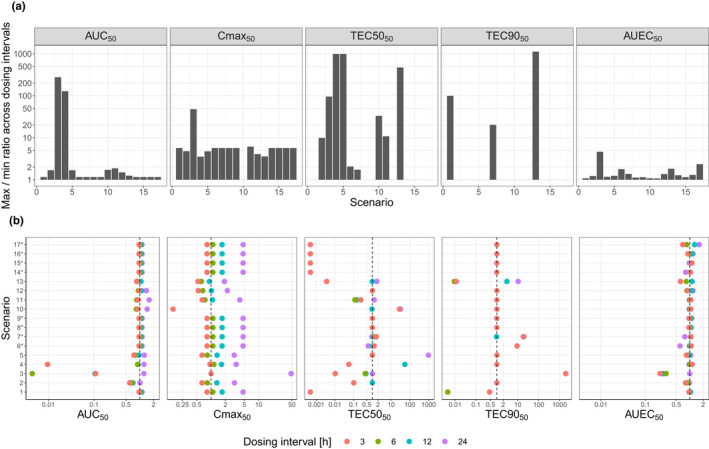
Dispersion of Index50 across the range of dosing intervals, represented as: the maximum‐to‐minimum ratio for Index50s across all dosing intervals (a), the dosing‐interval‐specific Index50 normalized to Index50 estimated in base model (b)
*For AUC24 and C max, fittings for scenarios 6–9 and 14–17 are the same as for scenario 1. For T EC50, fittings for scenarios 14–17 are the same as for scenario 1. AUC, area under the curve; C max, maximum concentration; EC50, concentration leading to half of the maximum effect; EC90, concentration leading to 90% of maximum effect.
The effect of dosing interval on Cmax50 was statistically significant in all scenarios except scenario 2. The estimated Cmax50 generally had approximately a five‐fold variation across dosing intervals (Figure 3a), mainly due to higher estimates obtained for 24‐h dosing interval (Figure 3b).
In most scenarios, TEC5050 and TEC9050 were not statistically significantly impacted by dosing interval, except for scenarios 5, 7, 10, and 11 for TEC5050 and scenario 11 for TEC9050. Estimates for TEC5050 and TEC9050 varied up to ~ 1000‐fold across dosing intervals (Figure 3a).
For AUEC50, dosing interval was a statistically significant covariate in all scenarios 1–17 except scenarios 6, 10, 11, and 14. However, AUEC50 estimates were highly consistent across all dosing intervals, with less than two‐fold difference in most cases, and less than five‐fold differences in all scenarios (Figure 3a).
For both AUC24 and C max, generally a longer dosing interval was associated with a lower potency. No clear trend between dosing interval and potency was observed for T EC50, T EC90, and AUEC24 (Figure 3b).
Drugs with varying degrees of in vivo efficacy
When Emaxvivo was reduced from five times k net to 3.3, 2.0 or 1.5 times, the R 2 values remained high for AUC24 (0.71–0.85) and AUEC24 (0.78–0.91), but were variable for C max (0.03–0.55) and T EC50 (0.09–0.84) and always negative for T EC90 (Table 1, “Impact of degree of in vivo drug efficacy”, and Figure 4a).
Timing of treatment initiation
When treatment was started at an early disease stage (day 3), instead of late stage (day 7), the R 2 values for AUC24, C max, and AUEC24 were slightly higher than in the base scenario, but were negative for T EC50 and T EC90 (Table 1, “Early stage versus late stage of infection at start of therapy”, and Figure 4b).
Duration of the therapy
When the duration of the therapy was reduced from 10 days to 6, 4, or 2 days, the R 2 values again remained high for AUC24 (0.85–0.89) and AUEC24 (0.95–0.96), were moderate‐to‐high for C max (0.53–0.67) and T EC50 (0.53–0.83), whereas they remained negative for T EC90 (Table 1, “Evaluation of shorter treatment duration”, and Figure 4c).
DISCUSSION
For any given dosing regimen, the three conventional PK/PD indices, using AUC, C max, and time above a critical concentration cutoff, are all closely correlated. This is the reason that dose‐fractionation experiments are necessary for differentiating these indices for their correlation to efficacy. But this reveals a problem with all conventional PK/PD indices.
Dosing interval is a major driver for the shape of the PK profile, which has an impact on pharmacology and, by extension, efficacy. 21 It affects the correlation between a conventional PK/PD index and in vivo efficacy and consequentially, clinical dose prediction. This has been supported by our recent unpublished observations: predicted clinical dose varied significantly depending on the dosing interval applied in animal experiments. In clinical therapeutics, there are also reports that the required level of a PK/PD index depends on the dosing regimen. 22 Furthermore, there are situations where different PK/PD indices are suitable for different patient populations, for the same drug in the same indication 23 , 24 : if efficacy is driven by different PK/PD indices for older and younger patients or for patients with better and worse kidney function, at what age or creatine clearance value should one draw the line?
Therefore, it was not surprising that our simulations showed that the Index50 of the conventional PK/PD indices all depended on dosing interval (Figure 3). On the other hand, the Index50 for AUEC was largely independent of dosing interval, suggesting that AUEC offers the potential for more robust dose prediction. In addition, it also promises an important additional benefit of reducing or avoiding dose fractionation in animal experiments, leading to lower animal numbers.
There are ways to conduct preclinical experiments to mimic the predicted PK profile in patients. One way is to dose animals more frequently to compensate for the shorter half‐life of the drug, so the PK fluctuation over time reflects what is predicted for humans, however, this is logistically challenging. 21 Another way is to design highly sophisticated dynamic in vitro systems, such as the hollow‐fiber models, which mimic both pathogen dynamics and predicted drug kinetics in patients 25 ; but they can be costly for early candidate screening on a large scale. In addition, both these approaches depend on the predicted shape of the PK profile in patients; and such prediction is often not reliable.
Here, we introduce the use of AUEC to predict in vivo efficacy, as a middle ground between the use of the conventional (mostly PK‐based) PK/PD indices in standard animal experiments and the more logistically challenging and/or expensive in vivo/in vitro approaches. This is underpinned by the principle that efficacy is driven by collective pharmacology, which is in turn influenced by the shape of the PK curve. Our simulations were designed in a generalized setting, so the principal findings could be broadly relevant: a generic pathogen dynamic model where the drug reduced pathogen load via a sigmoidal PD effect counteracting the saturable net pathogen growth in vivo; a sigmoidal in vitro dose–response relationship; and a one‐compartment linear in vivo PK model with first‐order absorption and elimination. Notably, our simulated in vivo dataset was more extensive than the usual animal experiments; it was designed to stress‐test the conventional and newly proposed PK/PD indices. Within this setting, we explored a broad range of scenarios for a relatively long duration of treatment with a highly efficacious drug at disease steady‐state. The scenarios were designed to test the impact of the choice of dose range in relation to potency (by simultaneously changing the drug's potency both in vitro and in vivo to the same extent), the mismatch between in vitro/in vivo potency, and the shape variation of in vitro and in vivo potency curves. Some of these variations were aimed to reflect in vitro versus in vivo differences in measured efficacy endpoint, pathogen vitality or fertility, treatment sensitivity or resistance, drug penetration to infection site, in vivo host immunity, and/or nonspecific binding to proteins or laboratory ware. 11 , 26 Additional conditions for drugs with lower degrees of efficacy, therapies at different stages of infection, or various treatment durations were also tested, to assess the robustness of the comparison of the PK/PD indices.
The AUEC24 showed strong correlation with in vivo efficacy in all conditions, comparable or better than other PK/PD indices in each scenario. The performance of AUC24 was worse (R 2 ≤ 0.7) when the dose range was suboptimal in relation to the drug's potency (Table 1, scenarios 2, 3, and 5). For T EC50 and T EC90, there was a tendency of data clustering around shorter (3, 6, and 12 h) or longer (24 h) dosing intervals (Figures 1, 2, and 4). Generally, C max showed moderate or poor correlation with in vivo efficacy.
Among the conventional indices, T EC50 appeared to be the strongest efficacy driver in scenario 2, whereas AUC24 appeared to be the strongest driver for the other scenarios. This observation highlighted an issue with reliance on R 2 to determine the optimal efficacy predictor and presents another reason for avoiding the need to class a drug as being time‐ or concentration‐dependent (at least not by R 2). The R 2 measures the relative dispersion of the data around the regression line: the higher this dispersion, the lower its value. As such, it is partly an artifact of the experimental condition, such as the chosen dose range: it tends to penalize the index whose dynamic range (the middle part of the sigmoidal Emax curve) is best covered by the experimental data.
Both T EC50 and T EC90 showed weak correlation to efficacy across most scenarios (Table 1). To better understand this, we estimated the strength of regimen‐specific correlation by including dosing interval as a covariate on both Index50 and γ_index for T EC50 and T EC90 (data not shown). The R 2 turned out to be quite different across dosing intervals, with higher values for 24‐h and/or 12‐h dosing intervals, which are more commonly applied in practice in animal experiments despite not providing PK profile shapes comparable to those in humans (animals tend to have much shorter half‐lives than humans). This observation highlighted the apparent utility of the time‐dependent PK/PD indices in clinical therapeutics, where only a single dosing interval is used. It explained not only how the critical value for the time above a cutoff threshold could depend on the dosing interval, 22 but also how different efficacy drivers were required for different dosing intervals. 23 It revealed a paradox: less extensive or less robust dose fractionation experiments (unlike the one we simulated) are more likely to establish a correlation, which might actually be an experimental artifact.
Our simulations were aimed to reflect drug discovery settings, where the duration of both in vitro and in vivo experiments is too short for resistance to develop. Therefore, resistance development was not included in our assessment. However, we evaluated scenarios where in vivo EC50 could be much higher than in vitro EC50, as well as varying degrees of Emaxvivo approaching k net. Collectively, these scenarios may somewhat reflect in vivo resistance not being anticipated during the in vitro stage.
Mechanistic modeling of greater sophistication has been proposed for pharmacotherapies treating bacterial, 10 , 12 , 13 viral, 14 , 15 , 16 , 17 and parasitic infections. 11 , 18 , 19 These more resource‐demanding approaches offer the appeal of closer reflection of the mechanism of the disease‐drug systems. Supported by more extensive experimental data, such as in vitro time‐kill curves to characterize the pathogen dynamics as a function of drug concentration, they are more versatile in their predictivity. Under explicit assumptions, they have the potential to address multiple pathogen populations with different susceptibility to drug intervention, adjust for tissue penetration, incorporate host immunity, describe drug combinations, and predict the outcome of prolonged treatments. On the other hand, using PK/PD indices for clinical dose prediction of anti‐infectives is a relatively simple, empirical, and economical approach, suitable for large‐scale screening and ranking of compounds.
Simulated with a generalized pathogen‐drug model in a range of scenarios, our findings serve as proof of concept that AUEC could be an alternative efficacy determinant for cross‐species dose prediction. It has the potential to be more robust than the conventional indices, with further benefit of reducing or avoiding animal dose‐fractionation experiments.
For anti‐infectives, the end point for both in vitro and in vivo experiments is often the same—pathogen count. This may have contributed to the strong correlation between AUEC (largely driven by in vitro pharmacology) and efficacy (in vivo). However, fundamentally the AUEC approach is aimed to directly establish the link between pharmacology and efficacy, instead of relying on drug concentration as a surrogate of pharmacology. The foundation for pharmacotherapy, that pharmacology drives efficacy, is not limited to infectious diseases. Conceivably, the shape of the PK profile matters more when pharmacology is more directly linked to drug concentration; hence, this is where AUEC's ability to reconcile species difference in PK profile matters more. Regardless of the indication or the dose predictor, the reliability of the therapeutic dose predicted from preclinical efficacy model depends to a great extent on the relevance of the model. The applicability and predictivity of this relatively simple approach of replacing PK AUC with PD AUEC as a translational tool for dose prediction, underpinned by the pharmacological basis of clinical efficacy, should be broadly tested in different types of infections alongside the conventional PK/PD indices and could also be explored in areas beyond infectious disease.
AUTHOR CONTRIBUTIONS
C.C. and S.M.L. wrote the manuscript. C.C. and L.I. designed the research. S.M.L. and L.I. performed the research. C.C., S.M.L., and L.I. analyzed the data.
CONFLICT OF INTEREST
The authors declared no competing interests for this work.
Supporting information
Supplementary Material S1
ACKNOWLEDGMENTS
The authors thank Dr. Raman Sharma (Clinical Pharmacology Modelling and Simulation, GSK) and Dr. Pablo Gamallo (Global Health Research, GSK) for providing their thoughtful comments on the manuscript.
Chen C, Lavezzi SM, Iavarone L. The area under the effect curve as an efficacy determinant for anti‐infectives. CPT Pharmacometrics Syst Pharmacol. 2022;11:1029‐1044. doi: 10.1002/psp4.12811
Chao Chen and Silvia Maria Lavezzi made equal contributions to this work.
Funding information
This work was funded by GlaxoSmithKline.
REFERENCES
- 1. DiMasi JA, Florez MI, Stergiopoulos S, et al. Development times and approval success rates for drugs to treat infectious diseases. Clin Pharmacol Ther. 2020;107(2):324‐332. [DOI] [PubMed] [Google Scholar]
- 2. Lo AW, Siah KW, Wong AW. Estimating probabilities of success of vaccine and other anti‐infective therapeutic development programs. National Bureau of Economic Research; 2020. Accessed March 10, 2021. http://www.nber.org/papers/w27176 [Google Scholar]
- 3. Dunne M. Antiretroviral drug development: the challenge of cost and access. AIDS. 2007;21:S73‐S79. [DOI] [PubMed] [Google Scholar]
- 4. Drusano GL. Antimicrobial pharmacodynamics: critical interactions of 'bug and drug'. Nat Rev Microbiol. 2004;2(4):289‐300. [DOI] [PubMed] [Google Scholar]
- 5. Mueller M, de la Peña A, Derendorf H. Issues in pharmacokinetics and pharmacodynamics of anti‐infective agents: kill curves versus MIC. Antimicrob Agents Chemother. 2004;48(2):369‐377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Ambrose PG, Bhavnani SM, Rubino CM, et al. Pharmacokinetics‐pharmacodynamics of antimicrobial therapy: it's not just for mice anymore. Clin Infect Dis. 2007;44(1):79‐86. [DOI] [PubMed] [Google Scholar]
- 7. European Medicines Agency . Guideline on the use of pharmacokinetics and pharmacodynamics in the development of antimicrobial medicinal products; 2016. Accessed March 09, 2021. https://www.ema.europa.eu/en/documents/scientific‐guideline/guideline‐use‐pharmacokinetics‐pharmacodynamics‐development‐antimicrobial‐medicinal‐products_en.pdf.
- 8. Turnidge J, Paterson DL. Setting and revising antibacterial susceptibility breakpoints. Clin Microbiol Rev. 2007;20(3):391‐408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Cadwell JJS. The hollow fiber infection model for antimicrobial pharmacodynamics and pharmacokinetics. Adv Pharmacoepidem Drug Safety S. 2012;1:2167‐1052. [Google Scholar]
- 10. Nielsen EI, Friberg LE. Pharmacokinetic‐pharmacodynamic modeling of antibacterial drugs. Pharmacol Rev. 2013;65(3):1053‐1090. [DOI] [PubMed] [Google Scholar]
- 11. Rayner CR, Smith PF, Andes D, et al. Model‐informed drug development for anti‐infectives: state of the art and future. Clin Pharmacol Ther. 2021;109(4):867‐891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Landersdorfer CB, Ly NS, Xu H, Tsuji BT, Bulitta JB. Quantifying subpopulation synergy for antibiotic combinations via mechanism‐based modeling and a sequential dosing design. Antimicrob Agents Chemother. 2013;57(5):2343‐2351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Clewe O, Wicha SG, de Vogel CP, de Steenwinkel JEM, Simonsson USH. A model‐informed preclinical approach for prediction of clinical pharmacodynamic interactions of anti‐TB drug combinations. J Antimicrob Chemother. 2018;73(2):437‐447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV‐1 dynamics in vivo: virion clearance rate, infected cell life‐span, and viral generation time. Science. 1996;271(5255):1582‐1586. [DOI] [PubMed] [Google Scholar]
- 15. Best K, Guedj J, Madelain V, et al. Zika plasma viral dynamics in nonhuman primates provides insights into early infection and antiviral strategies. Proc Natl Acad Sci. 2017;114(33):8847‐8852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Madelain V, Baize S, Jacquot F, et al. Ebola viral dynamics in nonhuman primates provides insights into virus immuno‐pathogenesis and antiviral strategies. Nat Commun. 2018;9(1):1‐11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Gonçalves A, Maisonnasse P, Donati F, et al. SARS‐CoV‐2 viral dynamics in non‐human primates. PLoS Comput Biol. 2021;17(3):e1008785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zaloumis S, Humberstone A, Charman SA, et al. Assessing the utility of an anti‐malarial pharmacokinetic‐pharmacodynamic model for aiding drug clinical development. Malar J. 2012;11(1):1‐14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Patel K, Batty KT, Moore BR, Gibbons PL, Bulitta JB, Kirkpatrick CM. Mechanism‐based model of parasite growth and dihydroartemisinin pharmacodynamics in murine malaria. Antimicrob Agents Chemoter. 2013;57(1):508‐516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bulitta JB. Informing and validating translational mechanism‐based models for antibiotics by experimental and computational approaches. Clin Pharmacol Ther. 2021;110:1426‐1428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Chen C. Impact of dosing schedule in animal experiments on compound progression decisions. Drug Discov Today. 2019;24(2):371‐376. [DOI] [PubMed] [Google Scholar]
- 22. Sturkenboom MGG, Märtson AG, Svensson EM, et al. Population pharmacokinetics and Bayesian dose adjustment to advance TDM of anti‐TB drugs. Clin Pharmacokinet. 2021;60:685‐710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Kristoffersson AN, David‐Pierson P, Parrott NJ, et al. Simulation‐based evaluation of PK/PD indices for meropenem across patient groups and experimental designs. Pharm Res. 2016;33(5):1115‐1125. [DOI] [PubMed] [Google Scholar]
- 24. Nielsen EI, Cars O, Friberg LE. Pharmacokinetic/pharmacodynamic (PK/PD) indices of antibiotics predicted by a semimechanistic PKPD model: a step toward model‐based dose optimization. Antimicrob Agents Chemother. 2011;55(10):4619‐4630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Nuermberger EL. Preclinical efficacy testing of new drug candidates. Microbiol Spectr. 2017;5(3). doi: 10.1128/microbiolspec.TBTB2-0034-2017 [DOI] [PubMed] [Google Scholar]
- 26. Simpson JA, Watkins ER, Price RN, Aarons L, Kyle DE, White NJ. Mefloquine pharmacokinetic‐pharmacodynamic models: implications for dosing and resistance. Antimicrob Agents Chemother. 2000;44(12):3414‐3424. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material S1


