Doppelgänger spotting in biomedical gene expression data

Summary

Doppelgänger effects (DEs) occur when samples exhibit chance similarities such that, when split across training and validation sets, inflates the trained machine learning (ML) model performance. This inflationary effect causes misleading confidence on the deployability of the model. Thus, so far, there are no tools for doppelgänger identification or standard practices to manage their confounding implications. We present doppelgangerIdentifier, a software suite for doppelgänger identification and verification. Applying doppelgangerIdentifier across a multitude of diseases and data types, we show the pervasive nature of DEs in biomedical gene expression data. We also provide guidelines toward proper doppelgänger identification by exploring the ramifications of lingering batch effects from batch imbalances on the sensitivity of our doppelgänger identification algorithm. We suggest doppelgänger verification as a useful procedure to establish baselines for model evaluation that may inform on whether feature selection and ML on the data set may yield meaningful insights.

Graphical abstract

Highlights

• •Doppelgänger effects inflate the machine learning performance
• •Doppelgänger effects exist in RNA-Seq and microarray gene expression data
• •Developed doppelgangerIdentifier, a software to identify and verify doppelgängers
• •Provide guidelines for proper doppelgänger identification

Bioinformatics; Genomics; Human Genetics.

Introduction

The doppelgänger effect (DE) describes the situation when a machine learning (ML) model performs well on a validation set regardless of how it has been trained. DE is problematic as it could exaggerate the performance of the ML model on real-world data and potentially complicate model selection processes that are solely based on validation accuracy. Hence, it is crucial for ML practitioners to be aware of the presence of any doppelgängers before model validation.

ML has been increasingly adopted in biology. Some notable examples include models predicting enhancer-promoter interactions, RNA secondary structure, and protein structure. Across these applications, several independent studies have noted the presence of confounding similarities [similar chromosomes (Cao and Fullwood, 2019), RNA families (Szikszai et al., 2022), or shared ancestry (Greener et al., 2022)]) between training and validation sets resulting in overinflated validation performances. Extrapolating from the above-cited studies, we conjecture that chance similarities between training and validation sets (causing DEs) would have similar consequences on ML models trained across a wide variety of biological data. Indeed, in this paper, we also show that DEs are prevalent in several examples of gene expression data. Hence, it is crucial to address DEs in biological data to train better models that can explain biology.

Previously. we introduced the phenomenon of DE in biomedical data set and broadly suggested a technique for identifying (or “spotting”) potential doppelgängers between and within data sets (Wang et al., 2021). There are two key definitions – data doppelgängers (DDs) and functional doppelgängers (FDs). DDs are sample pairs that exhibit very high mutual correlations or similarities. For example, we may use pairwise Pearson’s correlation coefficient (PPCC) to identify DDs such that sample pairs with high PPCCs are also referred to as PPCC DDs. On the other hand, FDs are sample pairs that, when split across training and validation data, results in inflated ML performance, i.e., the ML will be accurate regardless of how it was trained (It can be assumed that such models have not truly “learnt”). In our previous finding, PPCC DDs also act as FDs, although we suspect, under certain conditions, that it is also possible for non-PPCC DDs to act as FDs. To the best of our knowledge, there has been limited literature on how FDs could be readily identified or any publicly available software for the expressed purpose of FD identification. As of now, we were only aware of an R package, doppelgangR. However, this package aims to identify duplicate samples between and within data sets, and does not actually deal with doppelgängers (which are not technical duplicates but rather independent data that somehow resembled each other).

In this descriptor paper, we address the following gaps from our previous feature paper regarding DEs: first, the identification method utilized in the feature paper was only mentioned briefly. Hence, there may be insufficient details for successful adoption of this practice. Secondly, the feature paper only demonstrates the existence of DE within a single proteomics data set; hence, it does not show the pervasiveness of the DE across other data modalities such as high-throughput gene expression (genomics). Lastly, the feature paper does not explore possible limitations of the current approach and possible methods of mitigating such limitations.

To address the first research gap, we have developed a new R package, doppelgangerIdentifier, with user-friendly functions for PPCC DD identification and DD inflationary effect verification, in hopes that this would lead toward better data science practices in the community. The doppelgangerIdentifier package is currently available at https://github.com/lr98769/doppelgangerIdentifier together with a step-by-step guide on how PPCC DDs can be identified and verified within and between microarray and RNA-Seq data sets.

The second limitation was scope: We previously concentrated our descriptions on a single renal cell carcinoma (RCC) protein expression (proteomics) data set because RCC has well-defined meta-data, allowing us to construct a variety of positive and negative evaluation scenarios demonstrating clearly the additive inflationary effects of DDs. However, RCC is only a single data set representing a single disease type. It is also derived from mass spectrometry, which is not the most common platform used in the biomedical or life science community. To address this limitation, we aim to demonstrate the wider implications of DEs across a wider variety of diseases and biomedical comparisons (i.e., What is the generalizability of DEs?). We would also like to show that DEs are also present in widely-used gene expression profiling technologies. Hence, we intend to explore DE in two types of gene expression data sets, namely a well-studied microarray gene expression data from the study of Belorka and Wong (Belorkar and Wong, 2016) and a widely available RNA-Seq gene expression data from the Cancer Cell Line Encyclopedia (CCLE) project (Broad, 2018; Ghandi et al., 2019). This allows us to corroborate our DE studies against prior analyses.

Previously, DDs were identified within a single data set between two even-sized batches. However, this experimental setup does not account for other compositions of data sets. For instance, a common practice for ML practitioners in the biomedical field is to utilize multiple data sets from different sources in order to increase statistical power and reduce uncertainty. This process is referred to as data integration or mega analysis (Eisenhauer, 2021), which, unfortunately, produces a multitude of problems, the most prominent of which is known as batch effects (BEs) (Goh et al., 2017). BEs are technical sources of variation that can confound statistical feature selection, and mislead ML model training. The most common BE correction method, ComBat, is very widely used (Zhang et al., 2020) and usually assumed to work correctly. However, ComBat should not be applied carelessly as its efficiency relies on the balance of class distributions across batches (Li et al., 2021). Moreover, if the new source of data is used as a form of external validation (Ho et al., 2020a) i.e., the ML model is trained on a data set and evaluated on another independently-derived data set, the DE may overstate the ML model’s performance (Wang et al., 2021). We expect batch effects may confound DEs, especially when not removed properly. Recently, the effects of batch imbalance on proper batch effect removal are becoming a serious concern. We believe it may also affect the sensitivity of our doppelgänger identification algorithm. Thus, our final aim is to see how doppelgänger “spotting” is impacted when BEs are inadequately dealt with (i.e., what are the technical barriers that prevent us from correctly estimating and observing DEs?).

Results

Software and code

The doppelgangerIdentifier R package allows users to easily identify PPCC DDs between and within data sets and verify the impacts of these detected PPCC DDs on ML model validation accuracy. It provides four functions for computation and visualization:

In Table 1, functions are sequenced (top to bottom) in the order they are usually invoked in: first, PPCC DDs are identified with getPPCCDoppelgangers and visualized with visualisePPCCDoppelgangers. Using the PPCC DDs found in getPPCCDoppelgangers, we may construct a CSV file describing the samples in each training-validation pair. Training-validation pairs should be chosen strategically to have incrementally increasing numbers of PPCC DDs between the training and validation sets. This allows us to observe the inflationary effects of the PPCC DDs easily. Next, we may use verifyDoppelgangers to execute the experiment plan in the CSV file and generate the validation accuracies of all KNN models. Finally, we may use visualiseVerificationResults to plot the validation accuracies on a scatter-violin plot. If we observe a positive relationship between the number of PPCC DDs and validation accuracies in the scatter-violin plot, we can conclude that the detected PPCC DDs (included in the test) are in fact FDs.

Table 1.

List of functions in the doppelgangerIdentifier R package

Function Name	Role	Used In
getPPCCDoppelgangers	Detects PPCC DDs between two batches or within a batch	“PPCC DD identification” sections
visualisePPCCDoppelgangers	Plot PPCCs from getPPCCDoppelgangers in a univariate scatterplot	“PPCC DD identification” sections
verifyDoppelgangers	Trains random KNN models according to a user-defined experiment plan (CSV file describing samples in each training-validation set) to verify the confounding effects of PPCC DDs identified by getPPCCDoppelgangers	“Functional doppelgänger testing” sections
visualiseVerificationResults	Plots validation accuracies of KNN models from verifyDoppelgangers in scatter-violin plots	“Functional doppelgänger testing” sections

Each row describes the name (Function Name), role (Role), and sections of the paper where it is utilized (Used In) of each function in the doppelgangerIdentifer package. The algorithms for getPPCCDoppelgangers and verifyDoppelgangers were described in greater detail in Methods.

To cater to both microarray and RNA-Seq data, we provided an option in the getPPCCDoppelgangers and verifyDoppelgangers functions to choose between two batch correction methods: (1) ComBat for microarray data and (2) ComBat-Seq for RNA-Seq data sets. We also allow users to use other batch correction methods by providing a button to toggle the batch correction step in both functions; users can carry out batch correction with their preferred method before the invocation of both functions and disable batch correction when using the functions. We recognize that users may want to utilize different similarity metrics for the identification of DDs, hence, we also provide a parameter to pass in a user-defined correlation function in the getPPCCDoppelgangers function.

The doppelgangerIdentifier R package also includes four ready-to-use data sets (gene expression count matrix and meta data in the appropriate formats for all functions in doppelgangerIdentifier). The details of the data sets are described in Table 2.

Table 2.

List of ready-to-use data sets in the doppelgangerIdentifier R package

Name	Description	Citation
Rc	Renal Cell Carcinoma Proteomics DataSet	Guo et al
Dmd	Duchenne Muscular Dystrophy (DMD) Microarray DataSet	Haslett et al., Pescatori et al
Leuk	Leukemia Microarray DataSet	Golub et al., Armstrong et al
All	Acute Lymphoblastic Leukemia (ALL) Microarray DataSet	Ross et al., Yeoh et al

The first column, “Name,” gives the variable names of each data set; the second column, “Description” describes the type of data set; and the last column, “Citation,” cites the original paper the data sets were retrieved from. The meta data of each data set are also available in the package with the variables name in the format of “datasetName_metadata.” For instance, the meta data for the “rc” data set have the variable name “rc_metadata.”

The doppelgangerIdentifier R package is available on GitHub (https://github.com/lr98769/doppelgangerIdentifier) with instructions for installation and a complete documentation. We also included a step-by-step tutorial of the package on the renal cell carcinoma proteomics data from our seminal paper (Wang et al., 2021) and on a breast cancer RNA-Seq data set in the README R Markdown file. All R code used to generate results and graphs in this paper can be found at https://github.com/lr98769/doppelgangerSpotting.

Demonstration of DD identification with other correlation metrics

Other than Pearson’s correlation coefficient, other correlation metrics such as the Spearman Rank correlation coefficient and Kendall Rank correlation coefficient can also be used to identify DDs. Spearman Rank correlation coefficient is calculated by first ranking the values in each sample, then Pearson’s correlation coefficient is applied to the ranked variables. Spearman Rank correlation coefficient measures the monotonic relationship between samples, and is more general than Pearson’s correlation coefficient that only measures the linear relationship. Using a similar identification method as that of PPCC, Pairwise Spearman Rank correlation coefficients (PSRCC) are calculated between sample pairs for lymph_lung and large_upper data sets. The results are illustrated in Figure 1. On the other hand, the Kendall Rank correlation coefficient is based on the order of the rankings of the variables in each sample. Like the Spearman Rank correlation coefficient, the Kendall Rank correlation coefficient also measures the monotonic relationship between samples and is more general than PPCC. Using a similar identification method as that of PPCC, Pairwise Kendall Rank Correlation Coefficients (PKRCC) are calculated between sample pairs for lymph_lung and large_upper data sets. The results are illustrated in Figure 2. Though there are some differences, it is difficult to say which correlation measure is best. This may depend on the required sensitivity and precision of the analysis. It may also depend on the data distributions. This warrants deeper analysis. For the remainder of this paper, we will stick to the use of the PPCC (although users can also switch to their preferred correlation measures in doppelgangerIdentifier).

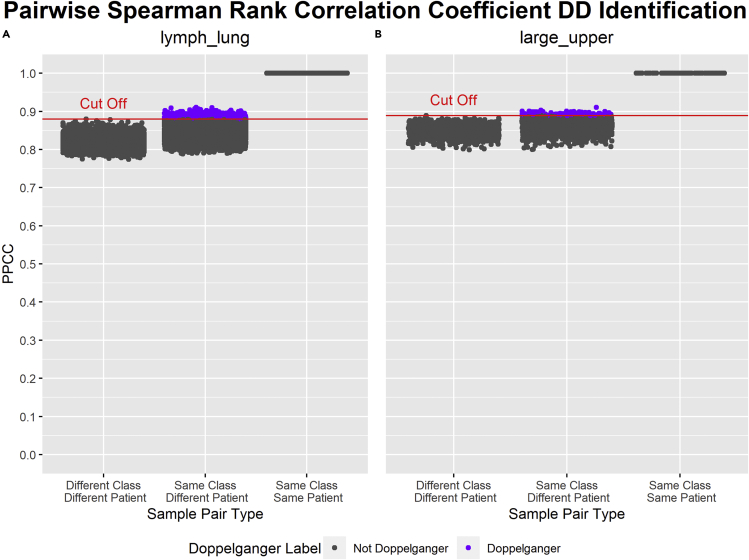
Figure 1.

Results of PSRCC DD Identification on lymph_lung and large_upper data sets

x-=axis: types of sample pairs based on the similarities of their class and patient. y-axis: PSRCC (Pairwise Spearman Rank Correlation Coefficient) values of each sample pair. Dots labeled in gray are not PSRCC DDs (data doppelgängers), whereas dots labeled in purple are PSRCC DDs. PSRCC DDs are sample pairs in “Same Class Different Patient” with a PSRCC value greater than the cut-off. The cut-off is the maximum PSRCC of any sample pair in “Different Class Different Patient.” The cut-off PSRCC is higher in large_upper (B) than in lymph_lung (A). In sum, 1,034 PSRCC DDs were identified within lymph_lung (A), whereas 144 PSRCC DDs were identified within large_upper (B).

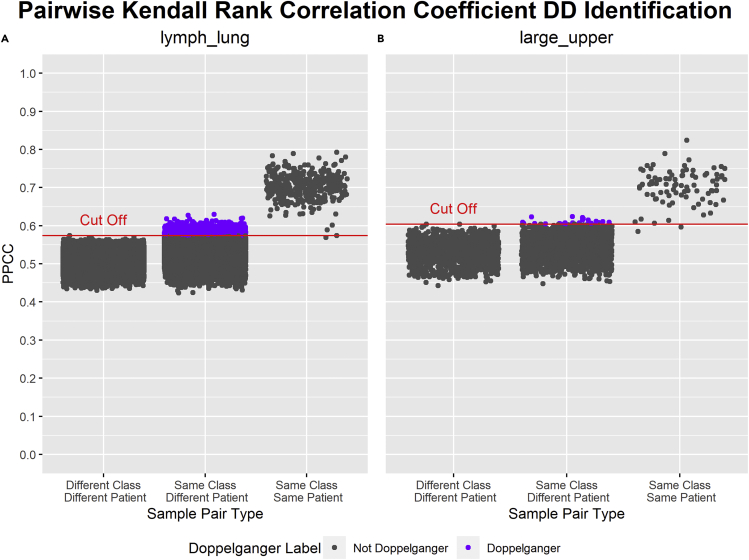
Figure 2.

Results of PKRCC DD Identification on lymph_lung and large_upper data sets

x-axis: types of sample pairs based on the similarities of their class and patient. y-axis: PKRCC (Pairwise Kendall Rank Correlation Coefficient) values of each sample pair. Dots labeled in gray are not PKRCC DDs (data doppelgängers), whereas dots labeled in purple are PKRCC DDs. PKRCC DDs are sample pairs in “Same Class Different Patient” with a PKRCC value greater than the cut-off. The cut-off is the maximum PKRCC of any sample pair in “Different Class Different Patient.” The cut-off PKRCC is higher in large_upper (B) than in lymph_lung (A). In sum, 1,719 PKRCC DDs were identified within lymph_lung (A), whereas 17 PKRCC DDs were identified within large_upper (B).

FDs in RNA-Seq data

PPCC DD identification

To evaluate the prevalence of the DEs in gene expression data, we explore DEs in other data set types with different sizes, assay platforms, and disease types. In this section, we focus on identifying PPCC DDs in two RNA-Seq data sets, lymph_lung and large_upper. Both data sets were named after the two cancer cell lines present within each subset (cf. Table 3 for meta data of both data sets). PPCC DDs were recognized using the procedure described in “data doppelgänger identification with PPCC” with each sample assumed to be taken from different patients and each sample pair defined to have different classes if they are of different cancer types. The DD identification procedure can be summarized as the calculation of PPCC values of all sample pairs after batch correction and the spotting of PPCC DDs with a dynamically calculated PPCC threshold and rules based on sample pair types. The results from applying the PPCC DD identification procedure on both lymph_lung and large_upper data sets are illustrated in Figure 3.

Table 3.

Explored RNA-Seq data set (obtained from the CCLE website)

DataSet Name	Tumor Class Distribution	ENSEMBL IDs (Genes)
lymph_lung	173 Haematopoietic and Lymphoid Tissue	57,820
lymph_lung	188 Lung	57,820
large_upper	56 Large Intestine	57,820
large_upper	31 Upper Aerodigestive Tract	57,820

We created two data sets from the CCLE data set each with two tumor cell lines: Haematopoietic and Lymphoid Tissue-Lung (lymph_lung) tumors and Large Intestine-Upper Aerodigestive Tract (large_upper) tumors. The lymph_lung tumor pair was chosen as both classes had the greatest number of samples in the CCLE data set and we intended to explore the prevalence of DE in a larger data set. The large_upper tumor pair was chosen as both tumors affect the digestive system.

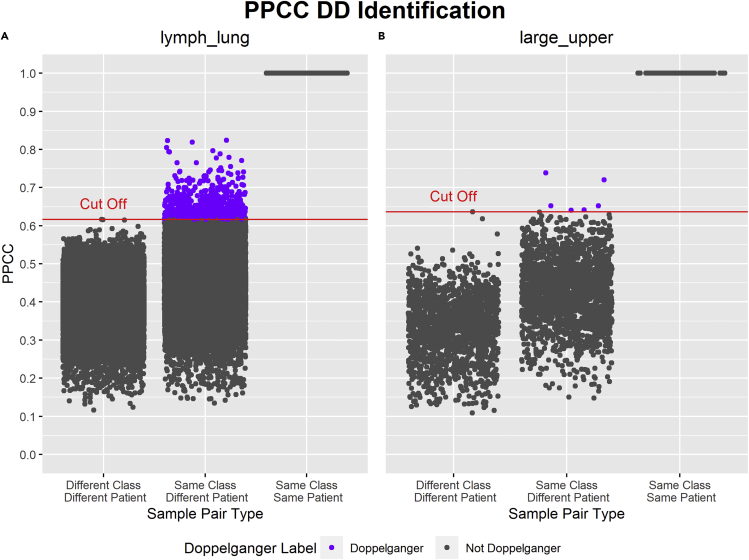
Figure 3.

Results of PPCC DD Identification on lymph_lung and large_upper data sets

x-axis: types of sample pairs based on the similarities of their class and patient. y-axis: PPCC (Pairwise Pearson’s correlation coefficient) values of each sample pair. Dots labeled in gray are not PPCC DDs (data doppelgängers), whereas dots labeled in purple are PPCC DDs. PPCC DDs are sample pairs in “Same Class Different Patient” with a PPCC greater than the cut-off. The cut-off is the maximum PPCC of any sample pair in “Different Class Different Patient.” The cut-off PPCC is higher in large_upper (B) than in lymph_lung (A). There is a wider distribution of PPCCs in lymph_lung compared with large_upper. In sum, 692 PPCC DDs were identified within lymph_lung (A), whereas six PPCC DDs were identified within large_upper (B).

Based on the PPCC strip plots in Figure 3, we observe higher PPCC values in lymph_lung for both “Different Class Different Patient” and “Same Class Different Patient” sample pairs compared with large_upper. This indicates higher mutual correlations within lymph_lung compared with large_upper.

Comparing the PPCC DDs identified for both large_upper and lymph_lung, we observed higher numbers and proportions of PPCC DDs in lymph_lung (692; 1.06% of all sample pairs) compared with large_upper (6; 0.157% of all sample pairs). We noticed a similar trend when comparing the number of PPCC DD samples (samples that are PPCC DDs with at least one other sample). There were higher numbers and proportions of PPCC DD samples in lymph_lung (181; 50.1% of all samples in lymph_lung) compared with large_upper (9; 10.3% of all samples in large_upper). The higher proportions of PPCC DDs and PPCC DD samples in lymph_lung compared with large_upper were most likely owing to the presence of stronger outliers in large_upper for “Different Class Different Patient” samples pairs (large_upper: Outlier Z score = 3.82448; lymph_lung: Outlier Z score = 3.80650; evident in Figure 3). These stronger outliers resulted in greater inflation in the PPCC cut-off, which, in turn, resulted in a greater decrease in DD identification sensitivity.

Comparing the proportions of PPCC DDs and PPCC DD samples in both data sets with proportions from our feature paper (8.02% of all sample pairs; 50% of all samples), we observed great variations in the proportions of PPCC DDs in data sets of different biological contexts. This establishes the absence of a universal estimate for PPCC DD proportions for all data sets, further emphasizing the importance of the PPCC DD identification step.

FD testing

We have identified PPCC DDs in lymph_lung and large_upper data sets. In this section, we verify if these PPCC DDs have an inflationary effect on the accuracies of trained ML models (Verify that PPCC DDs are FDs). We apply the verification steps detailed in “Functional Doppelgänger Testing” with the experimental setup described in Table 4. The verification steps mainly comprise the training of multiple random ML models and their subsequent evaluation on validation sets with incrementally increasing numbers of PPCC DD samples (Validation samples that are PPCC DDs with at least one sample in the training set). We expect a positive relationship between the number of PPCC DD samples and the validation accuracies of the random ML models if most of the identified PPCC DDs are FDs. The results of FD testing in both data sets are presented in Figure 4.

Table 4.

Experiment set up for functional doppelgänger testing for both lymph_lung and large_upper RNA-Seq data sets

DataSet Name	Training	Validation	Positive Control	Training-Validation Sets
lymph_lung	148 Haematopoietic and Lymphoid Tissue, 163 Lung	25 Haematopoietic and Lymphoid Tissue, 25 Lung	25 Haematopoietic and Lymphoid Tissue, 25 Lung duplicates from the training set	0 Doppel, 10 Doppel, 20 Doppel, 30 Doppel, 40 Doppel, 50 Doppel and 50 Pos Con
large_upper	51 Large Intestine, 26 Upper Aerodigestive Tract	5 Large Intestine, 5 Upper Aerodigestive Tract	5 Large Intestine duplicates from the training set, 5 Upper Aerodigestive Tract	0 Doppel, 1 Doppel, 2 Doppel, 3 Doppel, 4 Doppel, 5 Doppel and 5 Pos Con

The “DataSet Name” column states the given name of the data set. The “Training,” “Validation,” and “Positive Control” columns show the class distribution of the training data, validation data in “i Doppel” cases, and the validation data in the “Pos Con” cases, respectively. The “Training-Validation Sets” column lists the names of the training-validation sets in the experiment set-up. “i Doppel” training-validation sets have validation sets with i number of PPCC DD samples (Validation samples that are PPCC DDs with at least one sample in the training set). “i Pos Con” training-validation sets have validation sets with i number of duplicates from the training set

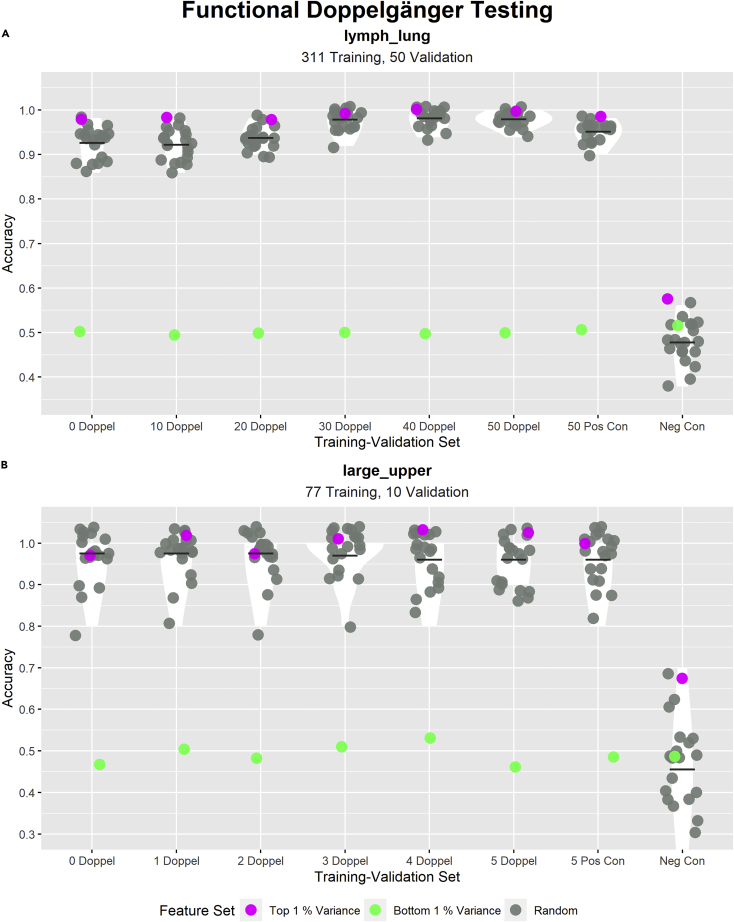
Figure 4.

Testing inflationary effects of identified PPCC DDs (Pairwise Pearson’s correlation coefficient data doppelgängers) in both lymph_lung and large_upper data sets

In each subplot, the title describes the data set used, whereas the subtitle states the sizes of the training and validation sets. Each subplot shows the distributions of model accuracies across different training-validation sets. The x-axis indicates the characteristics of the validation set: “i Doppel” (where i = 0, 10, 20, 30, 40, 50 or 0, 1, 2, 3, 4, 5) refers to a validation set with i number of PPCC DD samples (Validation samples that are PPCC DDs with at least one training sample). “i Pos Con” (where i = 50, 5) refers to the validation set with i samples duplicated from the training set. “Neg Con” refers to the accuracies produced by 22 binomial distributions (In A, n = 50 and p = 0.5; in B, n = 10 and p = 0.5). The performance of 22 models with different feature sets (20 models with random feature sets (gray), one model with features of highest variance (pink) and one model with features of lowest variance (green)) were evaluated on each validation set. The y-axis indicates the validation accuracies of all models (1 indicates all validation samples were correctly classified) (cf. Table 4 for experiment set up). The scatterplot shows the accuracies of each model, the violin plot shows the distribution of random model accuracies and the cross bar highlights the mean random model accuracy. Accuracies of all models in (A) and (B) appear to be near 1 ((A) displayed higher model accuracies than (B)), regardless of the number of PPCC DD samples in the validation set. We observed increasing mean random model accuracy with increasing numbers of PPCC DD samples in (A). We also noted a slight decreasing trend in mean random model accuracy with increasing numbers of PPCC DD samples in (B).

In Figure 4A, despite the overall high random model validation accuracies, we still observed a positive relationship between the number of PPCC DD samples and random model validation accuracy; this indicates that most of the detected PPCC DDs were FDs, capable of inflating model accuracies. Most interestingly, “50 Doppel” (validation set with 50 PPCC DD samples) had higher random model validation accuracies compared with “50 Pos Con” (validation set with 50 duplicates from the training set). This could suggest that in some cases, DEs may have stronger inflationary effects compared with leakage. In Figure 4B, we noted a consistently high random model validation accuracy across all training-validation pairs with a slight decrease in accuracy as the number of PPCC DD samples increased. This peculiar trend suggests two possible scenarios: (1) The identified PPCC DDs are not FDs but the sample pairs that were removed from the training-validation set as PPCC DD samples were added were true FDs. (2) The identified PPCC DDs are FDs; however, they have smaller inflationary effects than the non-PPCC DD FDs they were replacing.

Analyzing PPCC DD identification outcomes in both data sets, we can conclude that PPCC DD identification was more precise in lymph_lung since most of lymph_lung’s detected PPCC DDs were FDs whereas none of the PPCC DDs in large_upper were obvious FDs. The disparity in PPCC DD identification success could be attributed to the presence of stronger outliers in large_upper that strongly impacts PPCC DD recovery (as pointed out in the previous section). Comparing random model accuracies across both data sets, we observed higher model accuracies in (A; lymph_lung). A possible explanation for this observation would be the existence of greater data correlations in lymph_lung (as suggested in the previous section), which further inflates model accuracy or owing to the larger validation set size in lymph_lung.

Across data sets, the random model accuracies remain close to 1 regardless of the training-validation set. This may point to the presence of many non-PPCC DD FDs even in the “0 Doppel” cases where no PPCC DDs exist between the training and validation sets. A reason for the existence of many non-PPCC DD FDs would be poor FD recovery during PPCC DD identification. Some reasons for poor FD recovery include (1) limitations of PPCC as a measure of a sample pair’s ability to confound or (2) owing to the identification method’s susceptibility to outliers (overly strict thresholds owing to “Different Class Different Patient” sample pairs with anomalously high PPCCs; as observed in the previous section).

How batch imbalance affects DD identification

PPCC DD identification

As all of our input microarray data sets are imbalanced between batches, this needs to be addressed early in the analysis. Batch imbalances, i.e. different numbers of samples in both batches, have been shown to worsen the performance of two-step batch correction algorithms like ComBat (Li et al., 2021; Zhou et al., 2019). Our doppelgänger identification method relies on ComBat to first reduce the impact of batch effects before PPCC values are calculated (This is a critical step. To see the drastic reductions in PPCC should no batch correction be performed, please refer to the R Markdown at https://github.com/lr98769/doppelgangerSpotting/blob/master/rmarkdowns/DMD_no_combat.Rmd). Batch correction can be tricky: incomplete or inefficient batch correction may leave lingering batch effects that confound sample similarities. We expect that it will lead to reduced sensitivity in DD identification.

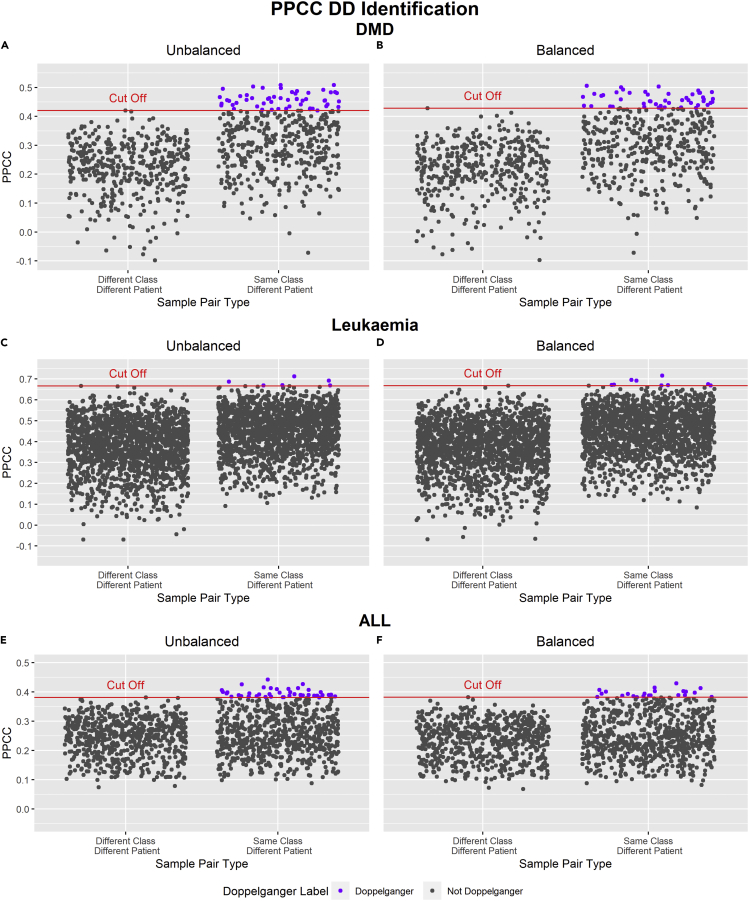
Hence, it is of interest to study the impact of batch imbalances on the performance of our doppelgänger identification algorithm. In this experiment, we observed the PPCC distributions, PPCC cut-off points, and the number of identified PPCC DDs of each data set pair (DMD, leukemia, and ALL) with and without batch balancing (Haslett et al., 2002).

Figure 5 and Table 5 depict how the presence of batch imbalance in data sets affects PPCC DD identification outcomes. In Figure 5, we observed a slight increase in the PPCC cut-off, whereas the overall PPCC distribution showed the opposite trend for all three data sets after batch balancing; Comparing the median PPCC values before and after batch balancing, we noted a decrease in PPCC values after batch balancing. Analyzing the PPCC disparity between sample pairs of different types (“Different Class Different Patient” and “Same Class Different Patient”) across all three data sets, we noticed significant differences in DMD and very subtle differences in leukemia and ALL. The absence of significant differences in PPCC values between the two sample types diminishes the sensitivity of the doppelgänger identification procedure in leukemia and ALL (inferred from the lower PPCC DD proportions in Table 5). This may suggest that in leukemia and ALL, Pearson’s correlation coefficient is an inadequate metric for the differentiation of FD sample pairs.

Figure 5.

PPCC distributions sample pairs between DMD, leukemia, and ALL data sets with and without batch imbalance

x-axis: types of sample pairs based on the similarities of their class and patient. y-axis: PPCC values of each sample pair

(A–F) In (A) and (B), sample pairs containing sample NOR_12 from Haslett et al. (2002) were removed from both scatterplots as they yielded highly negative correlations with all samples of Pescatori et al. (2007), which suggests the sample is likely an outlier or anomaly. Comparing the PPCC cut-offs before and after batch correction, we observed that the PPCC cut-off increased slightly for all three data sets

Table 5.

Summary of identified PPCC DDs (Pairwise Pearson’s correlation coefficient data doppelgängers) before and after balancing

DataSet	Number of PPCC DDs in Unbalanced	Number of PPCC DDs in Balanced	Batch Imbalance Ratio	Description of PPCC DDs
DMD	54 (6.25%)	47 (5.44%)	1.5	2 additional PPCC DDs in the balanced case, 9 additional PPCC DDs in the unbalanced case
Leukemia	6 (0.174%)	9 (0.260%)	1.5	3 additional PPCC DDs in the balanced case
ALL	41 (2.96%)	22 (1.59%)	1.27	9 additional PPCC DDs in the unbalanced case

The first column “DataSet” contains the names of the data sets described in each row. The next two columns contain the number of PPCC DDs and the proportion of PPCC DDs (percentage of all sample pairs that are PPCC DDs) in brackets in both balanced and unbalanced cases. The “Batch Imbalance Ratio” column denotes the extent of batch imbalance in each data set; it is calculated by dividing the batch size of the larger batch by the batch size of the smaller batch. The final column, “Description of PPCC DDs,” mentions notable observations of PPCC DDs in both cases.

Examining the results in Table 5, we noted significant changes in the number of identified PPCC DDs after batch balancing; the number of PPCC DDs decreased in the DMD and ALL data sets and increased in the leukemia data set. From trends discussed in Figure 5 (increasing cut-offs and decreasing PPCC values after batch balancing), we would expect the number of PPCC DDs to decrease (as seen in DMD and ALL); potentially reducing the number of false positive PPCC DDs (PPCC DDs that do not function as FDs). Surprisingly, we also noted additional PPCC DDs identified after batch balancing in DMD and leukemia. This increase in detected PPCC DDs could suggest that balancing our batches before doppelgänger identification may in some cases lead to a slightly better recovery of PPCC DDs.

While testing for PPCC DDs in the DMD data set, we also detected an outlier in the Haslett et al., 2002) data set (NOR_12) that produced highly negative PPCC values with all other samples of Pescatori et al., 2007). A PCA (Principal Component Analysis) plot of the DMD data set paints a similar picture; NOR_12 was isolated from all other samples in PC2. This finding proposes another benefit to performing PPCC DD identification; the ability to identify anomalies in the data set through studying the PPCC distributions of individual samples. This makes doppelgangerIdentifier very useful for exploratory data analysis as well.

FD testing

In the previous section, we have detected PPCC DDs in DMD, leukemia, and ALL data sets. To determine if these PPCC DDs could induce FD effects, we incrementally added DDs into the training-validation sets and observed changes in the validation accuracy (see STAR Methods). If we observe an increase in validation accuracy after adding PPCC DDs to the training-validation set, we can verify that these PPCC DDs are FDs. We illustrate the results of this procedure on all three data sets in Figure 6.

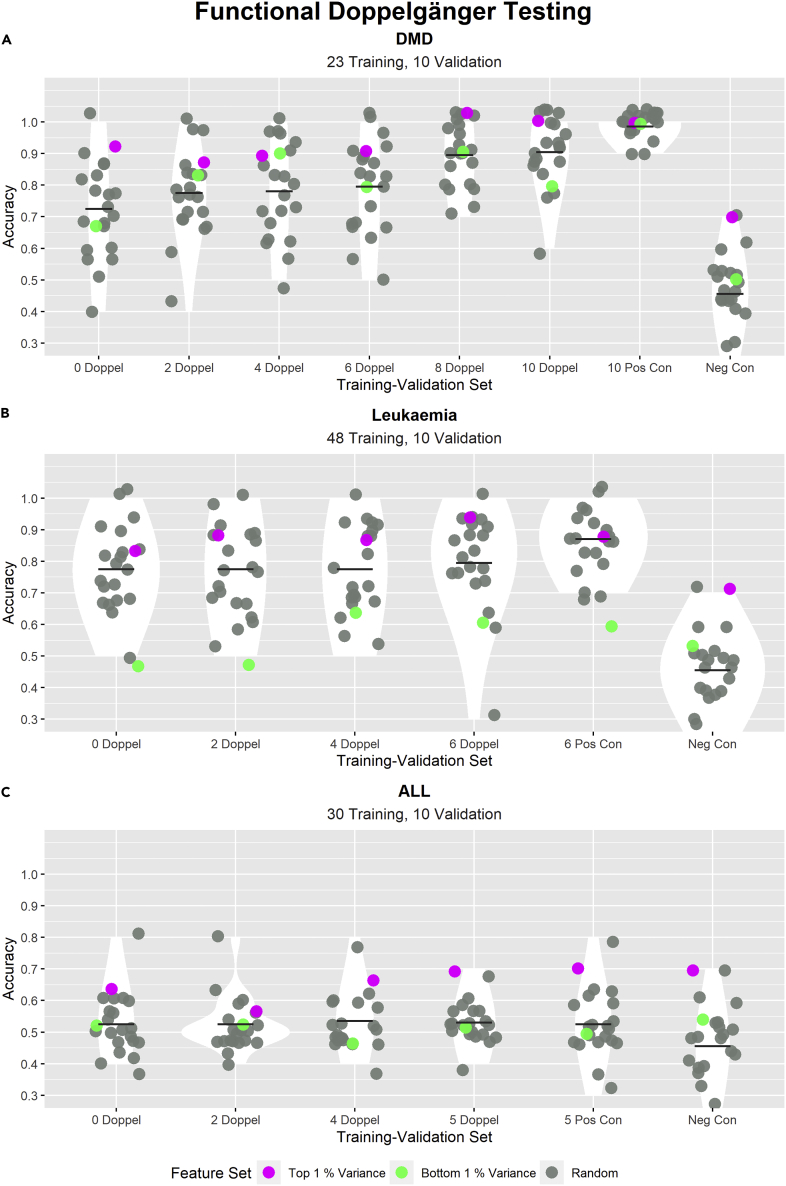
Figure 6.

Testing the inflationary effects of the detected PPCC DDs in the batch balanced case of DMD, leukemia, and ALL data sets

In each subplot, the title describes the data set used, whereas the subtitle states the sizes of the training and validation sets. Each subplot shows the distributions of model accuracies across different training-validation sets. The x-axis labels describe the characteristics of each training-validation set: “i Doppel” (where i = 0, 2, 4, 6, 8, 10 or 0, 2, 4, 6 or 0, 2, 2, 4, 5) refers to a training-validation set where there are i numbers of PPCC DD samples in the validation set; PPCC DD samples are samples in the validation set that are PPCC DDs with at least one sample in the training set. “i Pos Con” (where i = 10, 6, 5) refers to training-validation sets with i samples duplicated from the training set. “Neg Con” refers to the accuracies produced by 22 binomial distributions (n = 10, p = 0.5). The y-axis indicates the validation accuracies of all models (1 indicates all validation samples were correctly classified). The performance of 22 models with different feature sets (20 models with random feature sets (gray), one model with features of highest variance (pink) and one model with features of lowest variance (green)) were evaluated for each training-validation set. The scatterplot shows the accuracies of each model, the violin plot shows the distribution of random model accuracies, and the cross bar highlights the mean random model accuracy

(A–C) High random model accuracies can be observed for (A) and (B), whereas for (C), random model accuracies remained close to 0.5 across all training-validation sets. In (A), a positive relationship between the number of PPCC DD samples and random model validation accuracies is evident. This suggests that most of the tested PPCC DDs are functional doppelgängers (FDs). In (B), we observed a more gradual increasing trend between “4 Doppel” and “6 Doppel.” This suggests that only PPCC DDs added between “4 Doppel” and “6 Doppel” training-validation sets are FDs.

FD testing aims to verify if identified DDs (This manuscript focuses on PPCC DDs in particular) are true FDs that are capable of inflating random model accuracies. The results of FD testing on the three data sets describe three possible outcomes of FD testing: (1) most of the tested PPCC DDs are FDs; (2) some of the tested PPCC DDs are FDs; and (3) none of the tested PPCC DDs are FDs.

In DMD (Figure 6A), we observed a strong positive relationship between the number of PPCC DD samples (Validation samples that are PPCC DDs with at least one sample in the training set) and the validation accuracies of random KNN models. The presence of such a strong positive trend demonstrates that most of the tested PPCC DDs are true FDs. In leukemia (Figure 6B), we only observed a slight increase in random model validation accuracies from “4 Doppel” to “6 Doppel.” This observation suggests that not all of the tested PPCC DDs are true FDs; PPCC DDs added between the “4 Doppel” to “6 Doppel” training-validation sets show inflationary effects and are hence FDs, whereas the PPCC DDs added between “0 Doppel” and “4 Doppel” are not FDs. In ALL (Figure 6C), there were no changes in mean random model validation accuracies across all training-validation sets, which suggests that none of the added PPCC DDs were FDs.

The presence of FDs in both DMD and leukemia demonstrates that DEs are also present in other biomedical data. The differences in the extent of validation accuracy inflation in DMD and leukemia show that the strength of the DE varies across data sets of different disease contexts. We also observed in both data sets high random model validation accuracies in “0 Doppel” (where no PPCC DDs exist between training and validation sets). This observation hints at the presence of non-PPCC DD FDs. Future work could focus on methods to identify these non-PPCC DD FDs. Ideally, with the exclusion of both non-PPCC DD FDs and PPCC DD FDs from the training-validation set, the “0 Doppel” case would then show similar accuracy distributions with the negative control. We also observed that random feature sets could perform as well or better than the feature set consisting of variables with the highest variance.

In the previous section, we mentioned that the detected PPCC DDs changed after batch balancing. To determine if these additionally identified PPCC DDs have an inflationary effect on random model accuracy, we carried out FD testing on these PPCC DDs in a separate experiment set-up described in Table 6. The results of these tests are depicted in Figure 7.

Table 6.

Experiment set up for functional doppelgänger testing for all microarray data sets

Disease	Training	Validation	Positive Control	Training-Validation Sets
DMD	12 DMD and 11 NOR from Haslett et al. (2002)	5 DMD and 5 NOR from Pescatori et al. (2007)	5 DMD and 5 NOR duplicates from Haslett et al. (2002)	0 Doppel, 2 Doppel, 4 Doppel, 6 Doppel, 8 Doppel, 10 Doppel and 10 Pos Con
Leukemia	24 ALL and 24 AML from Armstrong et al. (2002)	5 ALL and 5 AML from Golub et al. (1999)	5 ALL and 1 AML duplicates from Armstrong et al. (2002) and 4 AML non-doppelgänger samples from Golub et al. (1999)	0 Doppel, 2 Doppel, 4 Doppel, 6 Doppel and 6 Pos Con
ALL	15 BCR and 15 E2A from Yeoh et al. (2002)	5 BCR and 5 E2A from Ross et al. (2004)	5 E2A duplicates from Yeoh et al. (2002) and 5 BCR non-doppelgänger samples from Ross et al. (2004)	0 Doppel, 2 Doppel, 4 Doppel, 5 Doppel and 5 Pos Con
DMD (Additional)	12 DMD and 11 NOR from Haslett et al. (2002)	5 DMD and 5 NOR from Haslett et al. (2002)	1 DMD and 2 NOR duplicate from Haslett et al. (2002), 4 DMD and 3 NOR non-doppelgänger samples from Haslett et al. (2002); (Pescatori et al., 2007)	0 Doppel, DMD_13_P (Unbalanced)b, NOR_2_P (Unbalanced)b, NOR_7_P (Unbalanced)b and 3 Pos Con
Leukemia (Additional)	24 ALL and 24 AML from Armstrong et al. (2002)	5 ALL and 5 AML from Golub et al. (1999)	2 ALL duplicate from Armstrong et al. (2002), 3 ALL and 5 AML non- doppelgänger samples from Golub et al. (1999)	0 Doppel, ALL_22_G (Balanced)a, ALL_19_G (Balanced)a and 2 Pos Con
ALL (Additional)	15 BCR and 15 E2A from Yeoh et al. (2002)	5 BCR and 5 E2A from Ross et al. (2004)	2 E2A duplicates from Yeoh et al. (2002), 3 E2A and 5 BCR non-doppelgänger samples from Ross et al. (2004)	0 Doppel, E2A_2_R (Unbalanced)b, E2A_13_R (Unbalanced)b and 2 Pos Con

The “Disease” column states the disease type of the data set. Disease types labeled with the “(Additional)” label describes the set up for testing the functionality of PPCC DD samples identified in the unbalanced case but not in the balanced case and vice versa. The “Training,” “Validation,” and “Positive Control” columns show the class distribution and source of the training data, validation data in “i Doppel” cases, and the validation data in the “Pos Con” cases, respectively. The “Training-Validation Sets” column lists the names of the training-validation sets in the experiment set-up. “i Doppel” training-validation sets have validation sets with i number of PPCC DD samples (validation samples that are PPCC DDs with at least one sample in the training set). “i Pos Con” training-validation sets have validation sets with i number of duplicates from the training set (cf. Table 7 for abbreviations).

^aAdditional doppelgängers were identified in the balanced batches case but not in the unbalanced batches case.

^bAdditional doppelgängers were identified in the unbalanced batches case but not in the balanced batches case.

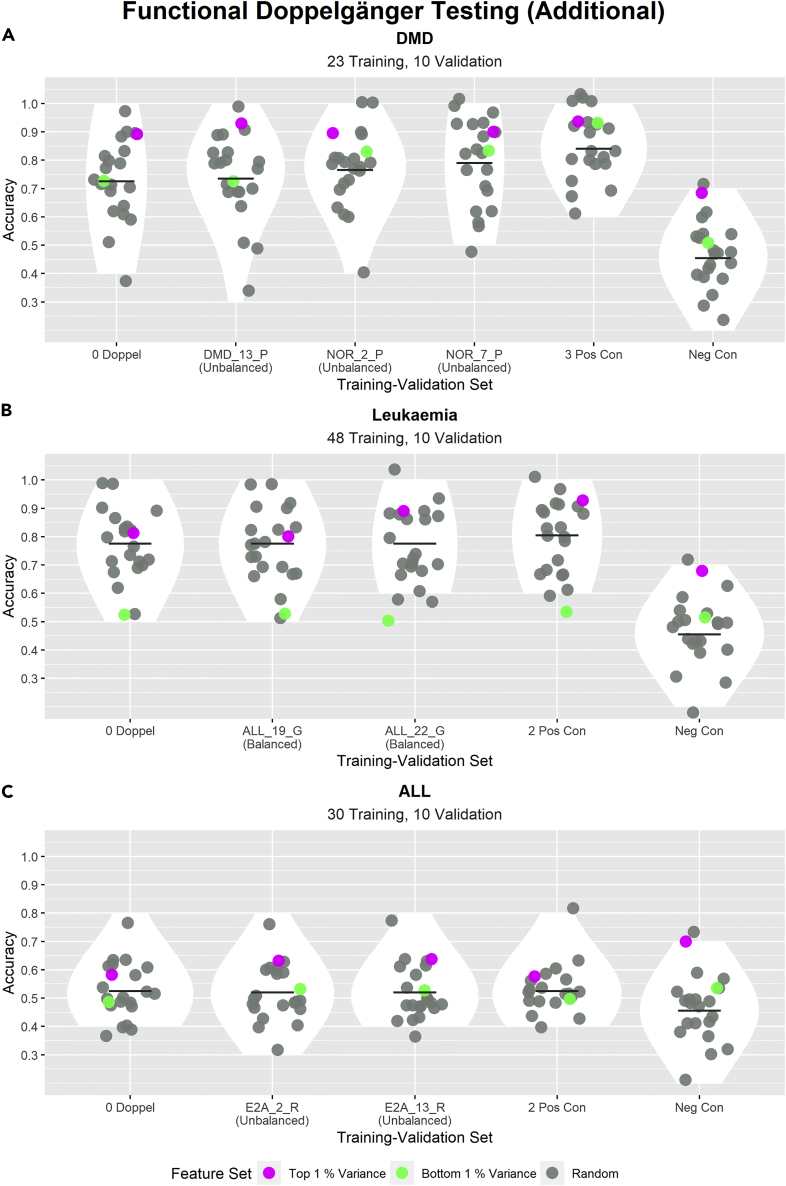
Figure 7.

Testing the inflationary effects of the additionally detected PPCC DDs in both batch balanced and imbalanced cases of DMD, leukemia and ALL data sets

In each subplot, the title describes the data set used, whereas the subtitle states the sizes of the training and validation sets. Each subplot shows the distributions of model accuracies across different training-validation sets. The “0 Doppel” training-validation set describes a training-validation set with no PPCC DD samples between the training and validation sets; PPCC DD samples are samples in the validation set that are PPCC DDs with at least one sample in the training set. Subsequent training-validation sets are named after the PPCC DD sample added to the previous validation set (e.g., “NOR_2_P” was added to the validation set of “DMD_13_P,” the validation set of “NOR_2_P″ has two PPCC DD samples). Each PPCC DD sample is named according to this convention: Class_SampleNumber_FirstLetterOfDataSetSource. For example, “DMD_13_P″ is the 13th sample having the class “DMD” and originates from the Pescatori data set. The bracketed words “Balanced” and “Unbalanced” written under the PPCC DD sample names inform us in which case they were identified in. For instance, “DMD_13_P (Unbalanced)” was identified in the unbalanced case but not in the balanced case. “i Pos Con” refers to training-validation sets with i samples duplicated from the training set (where i = 3 or 2). “Neg Con” refers to the accuracies produced by 22 binomial distributions (n = 10, p = 0.5). The y-axis indicates the validation accuracies of all models (1 indicates all validation samples were correctly classified). The performance of 22 models with different feature sets (20 models with random feature sets (gray), one model with features of highest variance (pink), and one model with features of lowest variance (green)) were evaluated for each training-validation set. The scatterplot shows the accuracies of each model, the violin plot shows the distribution of random model accuracies, and the cross bar highlights the mean random model accuracy.

(A–C) In (A), a positive trend between the random model accuracy and the number of PPCC DD samples can be observed. This suggests that the identified PPCC DDs are true FDs. This trend was not observed in (B) or (C).

From the positive trend observed in Figure 7A, we can conclude that the additional PPCC DDs identified before batch correction were FDs. However, we did not observe any inflation in model accuracies for leukemia or ALL. This result suggests that batch imbalance could influence the identification of PPCC DDs, resulting in a reduction or increase in the number of identified PPCC DDs. However, these additional PPCC DDs (in either balanced or imbalanced cases) may not necessarily be FDs (leukemia and ALL data set). This highlights the importance of the FD testing procedure for the verification of DDs as well as the importance of the correct treatment of batch effects.

Discussion

DEs are prevalent in a wide variety of biological data. They may disrupt analytical practices centered around selecting feature sets with the highest validation accuracy (with the expectation that the most accurate model yields the most correct explanation). Observations of DEs and random feature set superiority in DMD and leukemia further emphasize how we should not naively trust any feature selection processes or ML outcomes purely based on validation accuracy since high accuracies could be achieved by any feature set and a good feature set could perform just as well as a random feature set in the presence of DEs. Such phenomenon is not unheard of: In biology, random signature superiority effects and irrelevant signature superiority effects have been observed in breast cancer (Goh and Wong, 2018, 2019; Ho et al., 2020a; Venet et al., 2011) and are owing to a variety of confounding factors, the most prominent of which is high class-effect proportion (CEP) (Ho et al., 2020b). For data with high CEP, good accuracy is assured regardless of feature selection or identification of DDs. This approach is also largely problematic and untrue given what we know about Rashomon Sets (Rudin, 2019) and “No Free Lunch” theorem (Wolpert, 1996).

Our results also highlight the importance of checking for DEs before model validation so as to be cognizant of patterns of mutual correlations present in data. We may exploit these patterns not only to improve model explainability but also ensure models are minimally biased. As DDs act mostly as FDs, identified doppelgänger pairs should not be split across training-validation sets.

In addition, the identification of PPCC pairs also allows us to identify anomalous data or outliers, acting as a data quality assurance check. The validation series comprising increasing doppelgänger loads can also educate us on the nature of the data well. For example, the performance of random models in the “0 Doppel” case could serve as a baseline. If we see high model accuracies, given random signatures in spite of DDs already being dealt with, it will probably be difficult to extract explainable models from this disease. In stark contrast, such as in the ALL data, we observed the accuracies of all random KNN models clustered around 0.5 even as the number of PPCC DDs increased. This observation may suggest little class effects present in the ALL data set (Figure 6C), which makes it difficult for randomly trained KNN classifiers to distinguish between classes (BCR-ABL and E2A-PBX1). Indeed, checking for DDs can also help us develop deeper insight.

While checking for PPCC DDs, it is important for users to be conscious of the impacts of batch imbalance on the performance of the identification algorithm, especially if data integration is part of the analysis pipeline. As illustrated by the leukemia data set, the batch imbalance could reduce the number of PPCC DDs, potentially allowing some FDs to remain undetected. Allowing undetected FDs in the validation set could result in lingering DEs during model testing. Whereas our evaluations only revealed subtle differences between balanced and unbalanced cases, it is not known how badly data integrity is affected should batch imbalances be very extreme and/or batch effects are large and heterogeneous. Such work warrants an extensive investigation and goes beyond the scope of this paper. We can only advise that when batch effects and batch imbalances warrant concern, it is useful to model data with and without balancing to evaluate the difference. It is also useful to try to model and visualize the batch effect (Čuklina et al., 2021).

Limitations of the study

Though the PPCC DD identification method has been proven to be able to identify FDs, there is still room for improvement as seen from the elevated performance in lymph_lung, large_upper, DMD, and leukemia data sets. In all the above cases, some DEs persist even where no PPCC DDs should exist between training and validation sets. This may suggest that FDs still exist between the training and validation sets but are undetectable by PPCC. This could be the result of the shortcomings of Pearson’s correlation (Clark, 2013). The Pearson’s correlation may perform poorly in the presence of outlier values and non-normal data. Observing the distributions of values in each sample shows that the distribution of signals is far from normal. Hence, it is possible that non-normality may have reduced the effectiveness of Pearson’s correlation in detecting DDs. Another possible hypothesis is Pearson’s correlation’s inability to capture non-linear relationships and therefore, it is unable to identify more complex FDs that are linearly dissimilar but non-linearly associated. Future work could perhaps focus on incorporating other similarity metrics robust to non-normal data like Spearman’s measure or metrics capable of detecting non-linear relationships like dCor (Székely and Rizzo, 2009) into the DD identification procedure. We would also explore synergies between these correlation measures and high-dimensional data normalization methods. Another possible reason for poor FD recovery could be attributed to the presence of anomalously high “Different Class Different Patient” PPCC values (observed in all data sets); this would inflate the PPCC cut-off reducing the number of detected PPCC DDs. Perhaps future work could attempt to alter the definition of the PPCC cut-off to be more robust to outliers. We expect that as more in the community become interested in DEs, more FD identification methods will be developed.

Currently, there are no established methods to remove DEs from a data set without compromising its statistical power. Possible approaches to neutralizing DEs in data sets include experimenting with different data transformation techniques like Gene Fuzzy Score (GFS) (Belorkar and Wong, 2016) or feature generation. A temporary solution to mitigate DEs is to identify FDs before data splitting and to avoid assorting FDs across training and validation sets. During the model evaluation, we suggest comparing the accuracies of fine-tuned ML models with randomly trained models for an unbiased assessment of its performance on unseen data.

Prevailing data science practices propose the use of non-overlapping data subsets for training, validation, and testing (Chicco, 2017; Wujek et al., 2016). However, it is becoming increasingly apparent that such practices are insufficient for a fair assessment of ML models since high associations between training and validation sets could overexaggerate model performance (Cao and Fullwood, 2019; Greener et al., 2022). Hence, we recommend doppelgangerIdentifier as a tool to construct training-validation sets with a low propensity to overstate the model accuracy. We suggest ML practitioners to check for PPCC DDs before the training-validation split with getPPCCDoppelgangers. With the detected PPCC DDs, assort samples into training and validation sets with increasing numbers of PPCC DDs and execute the functionality test with verifyDoppelgangers. With this functionality test, we can check if the identified PPCC DDs are FDs (if an increase in validation accuracy is observed) and if all FDs have been identified in the 0 PPCC DDs case. If the validation accuracies of random models in the 0 PPCC DDs case centered around 0.5 (consistent with the accuracy of a randomly trained model; seen in the ALL data set), the validation set would be deemed suitable for model evaluation (free from DEs). Should an elevated accuracy be observed in the 0 PPCC DDs case (seen in the leukemia data set), the test would inform us of the intensity of the DEs between the training and validation set even in the absence of PPCC DDs. This could serve as a baseline for feature selection.

Conclusion

We have shown that the DE is widely observed across a multitude of diseases and high-throughput assay platforms capturing gene expression. We present doppelgangerIdentifier, a software suite that eases doppelgänger identification. Our results showed that DEs may be confounded by batch effects such that when improperly dealt with, lingering batch effects may lead to underestimation of DDs. As the performance of batch correction algorithms drops when batch size imbalances are present in data, we advise caution. Techniques such as oversampling may be useful, but still requires careful post-hoc analysis. Examining DEs across a multitude of diseases and phenotype comparisons, the exact presentation of DEs in each data set and context is unique, and must be interpreted carefully with domain knowledge. We show that checking for DDs can also serve as robust data quality procedures, useful for assaying data outliers and anomalies. In addition, the validation series sets allow us to establish baselines that also inform on whether feature selection and ML, in general, may yield meaningful insights. Finally, we noted that the use of Pearson’s correlation may not be sufficiently robust for more complex associations, leading to an underestimation of DEs. As DEs are still being investigated, we will devise and evaluate additional approaches, including combinatorial approaches between batch correction, data normalization, and doppelgänger detection in future works.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
3 Preprocessed Microarray DataSets	Belorkar and Wong, 2016	https://github.com/lr98769/doppelgangerIdentifier
CCLE RNA-Seq Data Set	Cancer Cell Line Encyclopedia, 2018	https://depmap.org/portal/download/api/download?file_name=ccle%2Fccle_2019%2FCCLE_RNAseq_rsem_genes_tpm_20180929.txt.gz&bucket=depmap-external-downloads
Software and algorithms
doppelgangerIdentifier R Package	This paper	https://github.com/lr98769/doppelgangerIdentifier
R Version 4.0.3	R Foundation for Statistical Computing	https://cran.r-project.org/bin/windows/base/
Other
Original code used for result generation in this paper	This paper	https://github.com/lr98769/doppelgangerSpotting

Resource availability

Lead contact

Further information should be directed to the lead contact, Wilson Wen Bin Goh, (wilsongoh@ntu.edu.sg).

Materials availability

This study did not generate new reagents.

Method details

Data sets

To demonstrate the prevalence and platform/disease independence of DEs, we applied our PPCC DD identification method (doppelgangerIdentifier) on two gene expression RNA-Seq data sets (Broad, 2018; Ghandi et al., 2019) and three pairs of gene expression microarray data sets (Belorkar and Wong, 2016). The details of each data set are summarised in the following two sections:

Gene expression RNA-Seq data sets

The CCLE RNA-Seq gene expression data set is a publicly available data set comprising 1019 cell lines. According to Ghandi et al. (2019), the data set was generated with the following steps: First, RNA-Seq reads were produced by following the Illumina TruSeq RNA Sample Preparation protocol (for non-strand specific RNA sequencing). Next, the RNA-Seq reads were aligned with STAR 2.4.2a58. Finally, gene expression levels were estimated with RSEM v.1.2.22 from the RNA-Seq reads. In this manuscript, we only utilised 448 cell lines out of the 1019 cell lines in the CCLE data set. Table 3 summarizes how the CCLE RNA-Seq data was divided into two cross-class data sets.

The two above RNA-Seq data sets contain samples bearing different diseases and were obtained using a different gene expression profiling technology from the renal cell carcinoma microarray gene expression data set evaluated in our seminal paper. Owing to the larger size of the lymph_lung data set, we can observe the impacts of DE on a larger RNA-Seq data set. However, since both data sets were obtained from the same source, we assume no batch effects exist within the data set and hence will not be performing any batch correction. As a result, we will not be exploring the effects of batch imbalance on batch correction efficacy with these data sets.

Gene expression microarray data sets

The gene expression microarray data sets were derived from 6 independently-derived microarray data sets (Armstrong et al., 2002; Golub et al., 1999; Haslett et al., 2002; Pescatori et al., 2007; Ross et al., 2004; Yeoh et al., 2002) each with different data generation methods. Refer to see Table for a summary of the data generation methods for each data set. see Table summarizes how pairs of gene expression microarray datasets sharing the same class labels were merged with reference to the original data table published by Belorkar and Wong (Belorkar and Wong, 2016).

Table of explored microarray data sets

Disease	Source	Affy GeneChip	Class Distribution	DataSet Size	Probes Before Mapping	ENSEMBL IDs Before Merging	ENSEMBL IDs After Merging
DMD	Haslett et al. (2002)	HG-U95Av2	12 DMD, 12 Control	24	12,600	8,987	8,813
DMD	Pescatori et al. (2007)	HG-U133A	22 DMD, 14 Control	36	22,283	13,077	8,813
Leukemia	Golub et al. (1999)	HU-6800	47 ALL, 25 AML	72	7,129	5,472	5,145
Leukemia	Armstrong et al. (2002)	HG-U95Av2	24 ALL, 24 AML	48	12,564	8,967	5,145
ALL	Yeoh et al. (2002)	HG-U95Av2	15 BCR-ABL, 27 E2A-PBX1	42	12,625	8,987	8,813
ALL	Ross et al. (2004)	HG-U133A	15 BCR-ABL, 18 E2A-PBX1	33	22,283	13,077	8,813

We explore data sets of the following two diseases: Duchenne muscular dystrophy (DMD) and leukemia. The DMD data set comprises normal and DMD samples. The leukemia data set comprises two different types of leukemia: acute lymphocytic leukemia (ALL) and acute myeloid leukemia (AML). The ALL data set comprises Acute lymphocytic leukemia samples with two different mutations: BCR-ABL and E2A-PBX1 (refer to Table 8 for the data processing methods of each data set).

Table 8.

Summary of microarray data generation methods. The following table was compiled with reference to the sources of each microarray data set

DataSet Name	Description of Data Generation Method
Haslett et al. (2002)	24 quadriceps biopsies (12 from DMD patients, 12 from controls). RNA extraction with Trizol, Hybridized to HG-U95Av2 GeneChips. GeneChip scanning with Affymetrix/Hewlett–Packard G2500A Gene Array Scanner. Expression values calculated with Affymetrix GeneChip Ver. 5.0 software
Pescatori et al. (2007)	36 quadriceps biopsies (24 from DMD patients, 12 from controls). RNA extraction with Trizol, Hybridized to HG-U133A GeneChips, GeneChip scanning with Affymetrix G2500 GeneChip scanner. Raw data processed with the log scale robust multiarray analysis (rma) procedure by Irizarry et al. (2003), then normalized and background-corrected. Genes with little variation (having less than 20% of arrays having variation greater than 1.5 times the median) across arrays were excluded from the data set
Golub et al. (1999)	38 leukemia samples from bone marrow aspirates (27 childhood ALL, 11 adult AML) and 34 independent leukemia samples (24 bone marrow, 10 peripheral blood; 20 childhood ALL, 4 adult AML, 10 childhood AML). Extracted with Trizol (Gibco/BRL), RNAqueous reagents (Ambion) or aqueous extraction (Qiagen). Hybridized to HU-6800 GeneChips. No mention of data processing methods
Armstrong et al. (2002)	48 leukemia samples from peripheral blood or bone marrow (24 ALL, 24 AML). Extracted with Trizol. Hybridized to HG-U95Av2 GeneChips. Expression values calculated with Affymetrix GeneChip software. Raw data normalized with a linear scaling method
Yeoh et al. (2002)	42 bone marrow samples (15 BCR-ABL, 27 E2A-PBX1). Extracted with Trizol. Hybridized to HG-U95Av2 GeneChips. GeneChip scanning with a laser confocal scanner (Agilent). Expression values calculated with Affymetrix Microarray software v.4.0. Average intensity difference (AID) values of each sample were normalized
Ross et al. (2004)	33 bone marrow (BM) aspirates or peripheral blood (PB) samples (15 BCR-ABL, 18 E2A-PBX1). Hybridized to HG-U133A GeneChips. Expression values calculated with Affymetrix Microarray Suite 5.0 (MAS 5.0). Raw data scaled to 500 with global methods. Parameters for the determination of detection values (present, marginal, or absent) were set to default values

These three data sets in Table explore different diseases beyond the proteomics renal cell carcinoma (RCC) data set we used previously (Wang et al., 2021). Since all three data set pairs were independently-derived using different microarrays, substantial batch effects are expected to exist once integrated or merged. In addition, all data set pairs have different sample sizes which allows us to explore the effects of such batch size differences on the subsequently identified PPCC DDs. Before the following experiments were carried out, the pairs of data sets were combined into a single data set with the following procedure:

• 1.All probes of both data sets were converted to ENSEMBL IDs using biomaRt (Except GolubData since the hu6800 chip was not found in biomaRt, instead the library hu6800.db was utilized).
• 2.To ensure a one-to-one mapping between the probes and ENSEMBL IDs in both data sets, all probes with no ENSEMBL ID were removed. Probes with multiple ENSEMBL IDs were replaced by the ENSEMBL ID with the smallest value (ENSEMBL IDs were ordered using the default R order function and all ENSEMBL IDs after the first ENSEMBL ID were removed). We took the median values of probes sharing the same ENSEMBL ID. After this procedure, both data sets would consist of unique ENSEMBL ID variables.
• 3.To join both data sets without any null values or data imputation (since both data sets may not have the same number and type of ENSEMBL IDs), we took the intersection of ENSEMBL IDs between both data sets. This set of ENSEMBL IDs would be the ENSEMBL IDs of the joined data set.
• 4.Both data sets were joined along the shared set of ENSEMBL IDs.

Methods

Data doppelgänger identification with PPCC

In our feature paper, we used a simple method for identifying PPCC DDs (Wang et al., 2021). Like Waldron et al. (Waldron et al., 2016), we define similarity based on Pearson’s Correlation Coefficient (PCC) across sample pairs. This is known as the pairwise PCC or PPCC. PPCC is meaningless if calculated for all sample pairs without context. For example, PPCC calculated for technical replicates of the same sample will always be high. But these are not true doppelgängers as they are merely repeated measures of the same sample. Replicates of the same sample accidentally split into training and validation data in ML will cause “leakage” issues (Kaufman et al., 2012). DDs are similar to data leakage, but covers the scenario of non-replicate samples being too similar (by chance) or broadly dissimilar except in a few critical ways (e.g., decision rules used by the ML). Waldron et al. (Waldron et al., 2016) looked for duplicates based on the highest PPCCs. However, if they have checked the meta-data, then they would have realized these were technical replicates of the same sample being used across a multitude of studies. The PPCC technique in itself cannot differentiate leakage and DDs, and so devising context based on meta-data is necessary.

The contextual rules we set are as follows: In clinical data comprising samples taken from multiple patients, we first calculate PPCCs between sample pairs of the same class that must come from different individuals (P1). Next, we calculate PPCCs between sample pairs of different classes (P2). If replicate information is present, then we may calculate PPCCs between sample pairs of the same class which come from the same individual (P3). P3 is optional, and can only be performed if technical replicates (batches) are present. Comparing P1 against P2, we may spot DDs for pairs in P1 where PPCC is greater than the maximal of P2. If P3 is present (the PPCC distribution of technical replicates), then we may better define DDs, by stating that DDs should be between minimum PPCC of P3 and above the maximum of P2. Also, any sample in P1 with PPCCs within the PPCC-distribution ranges of P3 would mean the samples are so similar they look like technical replicates. If the majority of samples behaved like this, one must exercise great caution when attempting ML model development.

Before PPCC DD identification, we may employ data preprocessing methods like batch-correction and min-max normalisation. If batch effects exist in the data set, apply batch correction methods like ComBat or ComBat-Seq (sva implementation is included in doppelgangerIdentifier). If the data set requires data realignment after batch correction, the data can be transformed with min-max normalisation (this step can be toggled in doppelgangerIdentifier) prior to the PPCC DD identification steps detailed below:

• 1.Pearson’s correlation coefficients were calculated between samples. This value is defined as the pairwise Pearson’s correlation coefficient (PPCC).
• 2.Sample pairs are labelled and split based on the previously-described contextual rules.
• 3.A threshold for identifying PPCC data doppelgängers is defined based on the previously-described contextual rules.
• 4.Sample pairs in P1 with a PPCC value greater than the calculated threshold are identified as PPCC DDs.

ComBat was chosen as the default batch correction method for PPCC DD identification as it has been highlighted as the standard for batch correction in numerous academic papers for proteomic studies, gene expression microarray data and high-throughput data (Chen et al., 2011; Čuklina et al., 2021; Leek et al., 2010). In addition, ComBat (and its subsequent refinements such as ComBat-Seq) is the only batch correction method which caters to both microarray and RNA-seq gene expression data sets.

The above procedure can be easily applied to any gene expression data set with the getPPCCDoppelgangers function from the doppelgangerIdentifier package. The user need only provide the gene expression count matrix and the meta data (containing the patient id, batch and class of each sample in table form). For a step-by-step guide on how to identify PPCC DDs, please refer to the R Markdown tutorial at https://github.com/lr98769/doppelgangerIdentifier/blob/main/README.Rmd.

Functional doppelgänger testing

To test if the PPCC DDs identified using the above protocol have an inflationary effect on validation accuracy (and are therefore FDs), we may use doppelgangerIdentifier to perform the following procedure:

• 1.The data set is first batch-corrected with ComBat (if data integration is required) and then min-max normalized to avoid scaling issues.
• 2.
  22 feature sets were generated: (Each feature set comprises 1% of the total number of features for all data sets):

  • a.
    20 randomly generated feature sets (These simulated non-meaningful “random” learning. The distribution of random models can inform how inflated ML models become when spiked with increasing numbers of DDs).
  • b.
    1 feature set containing features of the highest variance (These simulate deliberate feature selection based on features which exhibited the greatest changes. To avoid class bias, we do not select based on methods such as the t-test or other similar statistical tests. We expect this to form the upper bound of ML model performance).
  • c.
    1 feature set containing features of the lowest variance (This is a negative control, where we purposely select features which hardly changed in the data set. We expect this to form the lower bound of ML model performance).

In summary, the purpose of the randomly generated feature sets is to show doppelgängers’ ability to overexaggerate the performance of a randomly trained model. Feature sets selected with reference to variance (top 1%, and bottom 1%) allow us to observe how PPCC data doppelgängers affect properly and poorly trained models.

• 3.The data was partitioned to form a series of training-validation sets. Each consecutive training-validation set contains increasing proportions of PPCC data doppelgängers (e.g. from 0 to 100%). If replicates exist, then we may construct a positive control (Pos Con) to demonstrate inflated accuracies due to leakage.

The number of correctly classified validation samples for each feature set (22 feature sets in total) was modelled with a binomial distribution with n = number of samples in validation and p = 0.5 (probability of randomly guessing the labels of a validation sample). This serves as a null model for the experiment since a binary model trained on random signatures is expected to be equal in performance to a series of random coin tosses (Ho et al., 2020a).

• 4.For each training-validation set and feature set, a K-Nearest Neighbours (KNN) model from the class package was independently trained and validated.

The KNN is a useful and powerful model highly suitable for biomedical data modelling. Previously, we have also evaluated DEs using Naïve Bayes (NB), Decision Tree (DT) and Logistic Regression (Logit) models. The KNN provided the best performance overall. This was not surprising, as KNN is suited for analyzing high-dimensional data, and is quick to train. Moreover, DT cannot deal well with high dimensional data while NB and Logit makes certain assumptions, which may not be valid for biomedical data. For NB, it assumes variable independence while for Logit, it assumes linearity between dependent and independent variables. All KNN models were trained with the hyperparameter k equals to the square root of n (the sample size of the training set). The following are the k values for each of the data sets: lymph_lung-k = 17, large_upper-k = 9, DMD-k = 5, ALL-k = 5, Leukaemia-k = 7.

This procedure can be easily applied to any gene expression data set with the verifyDoppelgangers function from the doppelgangerIdentifier package. The user only has to prepare the list of samples in each training-validation set, the gene expression count matrix and the meta data (containing the patient id, batch and class of each sample in table form). For a step-by-step guide on how to verify the functionality of PPCC DDs, please refer to the R Markdown tutorial at https://github.com/lr98769/doppelgangerIdentifier/blob/main/README.Rmd.

Functional doppelgängers in RNA-Seq data

In this section, we demonstrate how doppelgangerIdentifier can be utilised to identify FDs within an RNA-Seq data set. First, we identify PPCC DDs in both lymph_lung and large_upper RNA-Seq data sets (see Error! Not a valid bookmark self-reference. section) with the protocol described in “data doppelgänger identification with PPCC” (Data was min-max normalised prior to the identification procedure). Next, with the procedure mentioned in “Functional Doppelgänger Testing”, we validate the inflationary effects of all identified PPCC DDs in both data sets. The experimental set up for functional doppelgänger testing is described in Table 4.

How batch imbalance affects DD identification

To investigate the effects of batch imbalance on PPCC data doppelgänger identification, we compare two cases: (1) imbalanced batches and (2) balanced batches. In the balanced batches case, we over sample the smaller batch to match the sample size of the larger batch prior to doppelgänger identification (and batch correction). This over sampling results in many duplicate sample pairs after doppelgänger identification. Since we will be comparing the number of detected PPCC DDs in both cases, we have to ensure both cases result in the same total number of sample pairs. Hence, we removed duplicate sample pairs after doppelgänger identification in the balanced batches case. The steps below illustrate the two cases in greater detail:

• 1)
  Imbalanced Batches

  • 1.
    Batch-correct and min-max normalise the data set.
  • 2.
    PPCC data doppelgängers were identified in the imbalanced data sets with getPPCCDoppelgangers (see data Doppelgänger identification with PPCC).
• 2)
  Balanced Batches

  • 1.
    The datasets with a smaller sample size were randomly oversampled with replacement.
  • 2.
    Batch-correct and min-max normalise the dataset.
  • 3.
    PPCC data doppelgängers were identified in the oversampled datasets with getPPCCDoppelgangers (see PPCC Doppelgänger identification method).
  • 4.
    Duplicate samples and sample pairs added in step 1 were removed.

We compared the PPCC distributions, identified PPCC cut-offs and the number of identified PPCC data doppelgängers between the imbalanced and balanced cases. see Table shows the class distribution of datasets after over sampling.

Class distribution of microarray data sets after over sampling

Disease	Source	Before Over Sampling	After Over Sampling
DMD	Haslett et al. (2002)	12 DMD, 12 Control	17 DMD, 19 Control
DMD	Pescatori et al. (2007)	22 DMD, 14 Control	22 DMD, 14 Control
Leukemia	Golub et al. (1999)	47 ALL, 25 AML	47 ALL, 25 AML
Leukemia	Armstrong et al. (2002)	24 ALL, 24 AML	37 ALL, 35 AML
ALL	Yeoh et al. (2002)	15 BCR-ABL, 27 E2A-PBX1	15 BCR-ABL, 27 E2A-PBX1
ALL	Ross et al. (2004)	15 BCR-ABL, 18 E2A-PBX1	19 BCR-ABL, 23 E2A-PBX1

The “Disease” column states the disease type of the data set pairs, the “Source” column denotes the source of each data set, the “Before Over Sampling” column shows the class distribution of the data sets before oversampling, the “After Over Sampling” column shows the class distribution of the data sets after over sampling the smaller data set in the pair (cf. for Table 7 abbreviations).

PPCC DDs identified in the batch-balanced case were tested for inflationary effects through functional doppelgänger testing (see functional Doppelgänger Testing). When more PPCC DDs were found in the balanced case or the imbalanced case, the additional PPCC DDs were tested to see if they acted as FDs (These PPCC DDs were tested in a separate experimental set up). Table 6 describes the experimental set up for the three pairs of datasets.

Quantification and statistical analysis

Some statistical analysis methods were utilized during functional doppelgänger (FD) testing.

• •Binomial distributions, with n = number of samples in the validation set and p = 0.5, were used in the negative control to simulate the validation accuracies of random feature sets. This serves as a null model for the experiment since a binary model trained on random signatures is expected to be equal in performance to a series of random coin tosses (Ho et al., 2020a).
• •During data analysis, for each training-validation set, we calculate the mean validation accuracies for models with random feature sets. This statistic aids in the analysis of the relationship between random model validation accuracy and the number of DDs (between the training and validation sets).

The statistical details of each FD testing experiment can be found in the figure legends of Figures 4, 6 and 7. No statistical tests were used in this study.

Published: August 19, 2022

Data and code availability

• •The CCLE RNA-Seq data set used was an existing, publicly available data. The data set (CCLE_RNAseq_rsem_genes_tpm_20180929.txt.gz) can be downloaded from the CCLE (Broad, 2018) DepMap portal. All 3 preprocessed microarray data sets derived from (Belorkar and Wong, 2016) have been added to the doppelgangerIdentifier package (which is available at https://github.com/lr98769/doppelgangerIdentifier) and are publicly available as of the date of publication.
• •All original code used to generate the results in this manuscript have been deposited at https://github.com/lr98769/doppelgangerSpotting and is publicly available as of the date of publication. The doppelgangerIdentifier package is publicly available as of the date of publication at https://github.com/lr98769/doppelgangerIdentifier.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.