Analysis of measured high-resolution doublet rovibronic spectra and related line lists of ¹²CH and ¹⁶OH

Abstract

Detailed understanding of the energy-level structure of the quantum states as well as of the rovibronic spectra of the ethylidyne (CH) and the hydroxyl (OH) radicals is mandatory for a multitude of modelling efforts within multiple chemical, combustion, astrophysical, and atmospheric environments. Accurate empirical rovibronic energy levels, with associated uncertainties, are reported for the low-lying doublet electronic states of ¹²CH and ¹⁶OH, using the Measured Active Rotational-Vibrational Energy Levels (Marvel) algorithm. For ¹²CH, a total of 1521 empirical energy levels are determined in the primary spectroscopic network (SN) of the radical, corresponding to the following seven electronic states: X ²Π, A ²Δ, B ²Σ⁻, C² Σ⁺, D ²Π, E ²Σ⁺, and F ²Σ⁺. The energy levels are derived from 6348 experimentally measured and validated transitions, collected from 29 sources. For ¹⁶OH, the lowest four doublet electronic states, X ²Π, A ²Σ⁺, B ²Σ⁺, and C ²Σ⁺, are considered, and a careful analysis and validation of 15 938 rovibronic transitions, collected from 45 sources, results in 1624 empirical rovibronic energy levels. The large set of spectroscopic data presented should facilitate the refinement of line lists for the ¹²CH and ¹⁶OH radicals. For both molecules hyperfine-resolved experimental transitions have also been considered, forming SNs independent from the primary SNs.

Understanding the energy-levels and rovibronic spectra of the ethylidyne (CH) and the hydroxyl (OH) radicals is mandatory for a multitude of modelling efforts within multiple chemical, combustion, astrophysical, and atmospheric environments.

1. Introduction

The free radicals methylidyne (CH) and hydroxyl (OH) play central roles in multiple chemical, combustion, astronomical, and atmospheric environments exhibiting a wide range of thermochemical properties. Therefore, their rovibronic spectra have been studied in considerable detail by methods of high-resolution molecular spectroscopy. Here we collect and analyze these data using the Measured Active Rotational-Vibrational Energy Levels (Marvel) procedure.^1–5

The CH radical has played a fundamental role in the furtherance of our scientific understanding during the last century. The radical's spectrum was identified in 1918.⁶ In 1937,⁷ methylidyne became the first molecule detected in interstellar space, prior to the proliferation of radio spectroscopy in the post-WWII period. The assignment of the broad 429.5–431.5 nm band, the so-called G-band of Fraunhofer, containing transitions corresponding to ¹²CH, was made 26 years before ¹⁶OH was detected using radio astronomy.⁸ Beyond its original discovery in the interstellar medium, CH has been detected in stellar atmospheres,⁹ including the Sun,^10,11 in comets,¹² in protostellar accretion disks,¹³ in planetary nebula,¹⁴ and in extragalactic sources.¹⁵ CH is used as a tracer for molecular hydrogen in the interstellar medium due to its origin being predominantly from the radiative association and recombination of C⁺ and H.¹⁶ It is also used as part of the classification of carbon giants.^17,18 CH is important in further chemical and physical environments. For example, during combustion of hydrocarbons it is an important intermediate giving the flame its characteristic blue color.¹⁹ The ubiquity of CH across multiple environments, with a broad range of thermodynamic conditions, is why CH is one of the spectroscopically most studied diatomic molecules. Furthermore, this is why the proposed analysis of the rovibronic spectra of CH is so pertinent and broadly beneficial for future studies, both in helping to interpret observations and to improve astronomical, chemical, and physical models. Note in this respect that several hyperfine transitions of ¹²CH have been measured with an accuracy of a few Hz, providing a convenient way to put limits on the possible variation of the fine-structure constant and the electron-proton mass ratio with respect to time and local densities.²⁰

OH is arguably the most important free radical in the Earth's atmosphere,^21,22 governing atmospheric chemistry during the day. The OH radical is responsible for airglow^23,24 and it is, together with HO₂, one of the most dominant oxidizing agents of organic molecules in the troposphere.²⁵ The hydroxyl radical is highly relevant for chemists as it has a significant role in the reactions characterizing combustion systems and flames^26,27 and even in heterogeneous catalysis.²⁸ OH is also of significant astrophysical interest, since it can be found in comets,²⁹ stellar atmospheres,³⁰ including the solar photosphere³¹ and sunspots,³² interstellar clouds,³³ exoplanets,²⁷ and planetary atmospheres.^34–36 Accordingly, a large number of transitions of OH have been detected, the assigned spectra extend from resolved Λ-doubling and hyperfine transitions³⁷ in the microwave (MW) to rotation (the “pure rotation” and the “spin-flip” branches), vibration–rotation, and rovibronic transitions.

Both OH and CH have key transitions at THz frequencies which have been studied from space using observatories such as the Kuiper Airborne Observatory,³⁸ the ISO (Infrared Space Observatory),³⁹ and Herschel,^40–42 provoking dedicated laboratory studies.⁴³ More recently, similar studies have been performed with the airborne SOFIA (Stratospheric Observatory for Far-Infrared Astronomy) observatory.^44–47 These studies often investigate hyperfine-resolved transitions.

Spectroscopic parameters and line lists have been published for both radicals. There are no CH data reported in the spectroscopic database and information system HITRAN,⁴⁸ while ¹⁶OH is molecule #13 in there and HITRAN2020⁴⁹ lists altogether 55 698 lines in the range of 0–43 408 cm⁻¹ for ¹⁶OH. The GEISA-2020 database⁵⁰ is based on effective Hamiltonian (EH) calculations and contains a large number of data for OH. The most recent line list⁹ among those available,^9,51 created for ¹²CH and ¹³CH, covers rovibronic transitions X–X, A–X, B–X, and C–X. As for OH, the available CH line lists cover transitions within the ground state⁵² as well as A–X electronic transitions.⁵³ The ground-state transitions form the so-called Meinel bands,⁵⁴ used, for example, to estimate OH rotational temperatures. The line lists of ref. 9, 52 and 53 were created as part of the MoLLIST project.⁵⁵ The Jet Propulsion Laboratory (JPL) catalog⁵⁶ contains data for both CH and OH.

A motivation for performing Marvel analyses of high-resolution spectra is the construction of high-accuracy line lists. Given that first-principles theoretical procedures can predict transition intensities with an accuracy competitive with state-of-the-art experiments,^57,58 use of empirical energy levels, such as those determined by the Marvel procedure, to determine transition frequencies provides a route to constructing line lists of experimental quality. This is a major current objective of the ExoMol project.⁵⁹ Note that similar Marvel-based studies have already been performed on second-row hydride radicals, like⁹ BeH,⁶⁰ a radical important for fusion studies, and ¹⁴NH.⁶¹

In this paper we undertake Marvel studies for the lowest seven doublet electronic states of CH and the lowest four doublet electronic states of OH (see Fig. 1 for the states covered in this study). To do this we analyze the experimental spectroscopic data available for the parent ¹²CH^{6,9–15,20,40,51,62–105} and ¹⁶OH^{8,21,31,38,41,43–47,52,53,106–158} isotopologues, using the Hamiltonian-free Marvel procedure,^1–5 and obtain high-accuracy empirical rovibronic energy levels with well-defined uncertainties. The empirical energy levels obtained allow the critical assessment of line lists^9,51–53 created previously for the two radicals. The principal aim of this study is to provide a set of validated experimental rovibronic transitions as well as a large number of empirical rovibronic energy levels, facilitating the construction of the next generation of line lists for ¹²CH and ¹⁶OH.

Fig. 1. Schematic representation of rovibronic band systems for the radicals CH (top) and OH (bottom) considered in this study; the wavenumber scale of the term values is approximate. While high-quality spectroscopic data are available which involve the low-lying a ⁴Σ⁻ state of ¹²CH, there are no observed intercombination transitions connecting this state to the doublet states; therefore, these transitions are not treated here.

2. Methodological details

2.1. Marvel

The Marvel approach^1–5 converts a set of assigned experimental transitions into empirical energy levels with associated uncertainties that are propagated from the input transitions to the output energy levels. This conversion relies on the construction of a spectroscopic network (SN),^3,159–161 built upon the measured and assigned transitions.

2.2. Quantum numbers

Marvel requires that all transitions are assigned with a unique set of descriptors, usually quantum numbers, which are self-consistent across the entire dataset. A brief discussion of the labels we use is especially important as over time spectroscopists adopted different rules to assign the spectral lines of CH and OH, causing considerable confusion and making a global spectroscopic analysis error prone.

The electronic ground state of CH, X ²Π, has the following electron configuration: (1σ)² (2σ)² (3σ)² (1π)¹. The four lowest-energy electronic states of CH (see the top panel of Fig. 1), a ⁴Σ⁻ (T_e = 6024.40 cm⁻¹), A ²Δ (T_e = 23148.7375 cm⁻¹), B ²Σ⁻ (T_e = 24642.425 cm⁻¹), and C ²Σ⁺ (T_e = 31809.6428 cm⁻¹), all arise from a 1π ← 3σ excitation. In this list T_e is the electronic term and all T_e values are taken from ref. 9. During the present SN-based study, we only consider doublet states. There are three more doublet states of ¹²CH besides X, A, B, and C, all above 50 000 cm⁻¹, which we considered: D ²Π, E ²Σ⁺, and F ²Σ⁺ (see the top panel of Fig. 1). In the literature, there has been some valid debate about the designation of the higher-lying Σ and Π electronic states of CH.^{66,84,162,163} While technically this may not be correct, we keep the traditional spectroscopic designation of the electronic states of CH, and, for example, denote the second ²Π state as D ²Π, with clear consequences for the designation of the higher ²Σ⁺ states.

It is most appropriate to treat the high-resolution spectra of ¹²CH as a diatomic having Hund's case (b) coupling.³⁷ This means that Ω (= Λ + Σ) is not a good quantum number (Λ and Σ are the quantum numbers for the projection of the electronic orbital angular momentum L and the electron spin angular momentum S onto the internuclear axis, respectively). Furthermore, L is coupled to the overall rotational angular momentum R to form N, and N is then coupled to S to form the angular momentum J (N = L + R and J = N + S). Thus, to label the rovibronic states of ¹²CH within Marvel we use the following descriptors: the electronic state called state, e.g., X2Pi, the vibrational quantum number (v), the total angular momentum quantum number (J), the rotationless parity (e/f),¹⁶⁴ and values of F₁ and F₂ to label the spin components. We denote the F₁ and F₂ spin components by 1 and 2 in the Marvel transition file, respectively. Many CH spectra are assigned using the quantum number N, this can be used to give the spin components J = N + 1/2 and J = N − 1/2 corresponding to F₁ and F₂, respectively.⁵¹

The electronic ground state of OH, X ²Π, corresponds to the following electron configuration: (1σ)² (2σ)² (3σ)² (1π)³. In this study, the rovibronic energy levels of the following four doublet states are considered: X ²Π, A ²Σ⁺, B ²Σ⁺, and C ²Σ⁺ (see the bottom panel of Fig. 1). The lower levels of ¹⁶OH are well represented by a Hund's case (a) coupling.³⁷ The following descriptors were employed to label the rovibronic states of ¹⁶OH: state, Ω, v, J, and the rotationless parity¹⁶⁴ (e/f). State designates the electronic state, Ω is the projection of the total angular momentum along the internuclear axis, and J is the total angular momentum quantum number without the nuclear spin. Regarding these descriptors we need to note the following: (1) in the case of ¹⁶OH, Ω can be either 1/2 or 3/2. The ground electronic state of ¹⁶OH is inverted (the spin-rotation constant of OH is negative); thus, the ²Π_3/2 (F₁) component lies below the ²Π_1/2 (F₂) component. (2) We follow the e/f scheme advocated in 78BrKaKeMi.¹⁶⁵ This means that in the case of ²Π_1/2 the order of parity (e/f) changes when J > 7/2. (3) In the case of ²Σ⁺ electronic states the Ω = 1/2 energy levels belong to the f parity (F₁) and the Ω = 3/2 levels have e parity (F₂).

3. Compilation of experimental sources

Our intention was to consider and analyse all literature sources of experimentally measured and assigned high-resolution ¹²CH and ¹⁶OH spectra. How far this was achieved is discussed separately for the two radicals.

3.1. ¹²CH

The structure of the CH band system treated in this study is displayed in Fig. 1 (see the top panel). The seven electronic states considered, X ²Π, A ²Δ, B ²Σ⁻, C ²Σ⁺, D ²Π, E ²Σ⁺, and F ²Σ⁺, are linked by a series of transitions, part of high-resolution, rotationally-resolved spectra. The lowest quartet state is the a ⁴Σ⁻ state, whose term value is only about T_e = 6024 cm⁻¹.^9,163 Nelis et al.⁸⁶ recorded a far-infrared laser magnetic resonance spectrum containing 558 transitions within this state. Unfortunately, there are no reported intercombination transitions for CH linking the doublet and quartet manifolds. Thus, here we are concentrating on the SN formed by the seven doublet electronic states.

The full list of data sources employed in the final Marvel analysis^{9,10,20,62,63,66,73,74,76–79,81,83,84,87,89–97,99,101,102,105} of ¹²CH is given in Table 1, which also provides details of the range of wavenumbers and the number of transitions measured and validated for each vibronic band, with some statistical analysis of the uncertainties characterizing the source segments. After careful analysis, altogether 29 sources could be utilized, covering a total of 6348 transitions.

Experimental sources, denoted with unique tags, used to construct the spectroscopic network of the hyperfine-unresolved rovibronic transitions of ¹²CH. Given are the wavenumber range (Range), in cm⁻¹, of each source, the number actual (A) and validated (V) transitions, plus uncertainty (unc.) statistics, in cm⁻¹, with Avg. = average and Max. = maximum.

Taga	Range	A/V	Avg. unc.	Max. unc.
13TrHeHiTa102	0.02–0.11	2/2	2.96 × 10−9	4.92 × 10−9
06McMoBrTh99	0.11–0.49	3/3	7.04 × 10−7	1.00 × 10−6
85StWoBr79	0.11–0.11	1/1	1.69 × 10−4	1.69 × 10−4
83BrBr74	0.16–0.81	4/4	2.01 × 10−4	5.98 × 10−4
84BrBr76	0.24–23529.83	82/81	5.59 × 10−3	2.80 × 10−2
83BoDeDe73	1.46–2.54	5/5	9.34 × 10−6	1.33 × 10−5
95Zachwiej_C91	14.27–15781.09	138/138	5.58 × 10−3	1.58 × 10−2
00Amano96	17.77–17.91	2/2	8.56 × 10−5	1.50 × 10−4
13TrHeToLe20	17.77–17.91	2/1	3.50 × 10−7	3.50 × 10−7
01DaEvBr97	67.07–141.78	8/8	5.78 × 10−5	1.33 × 10−4
10CoBe101	2093.93–3036.75	205/204	2.04 × 10−2	5.26 × 10−2
91BeBrOlHa89	2162.60–27561.99	572/570	9.84 × 10−3	7.36 × 10−2
87Bernath83	2309.84–2953.36	183/183	5.52 × 10−3	1.46 × 10−2
89MeGrSaFa10	2332.12–3037.34	378/378	5.38 × 10−3	3.50 × 10−2
84LuAm77	2580.65–2937.06	54/54	1.15 × 10−3	3.28 × 10−3
96KePaRyZa92	20202.55–27562.00	231/228	1.73 × 10−2	1.33 × 10−1
95Zachwiej91	20232.36–24007.21	1015/974	1.36 × 10−2	2.80 × 10−1
14MaPlVaCo9	21842.11–31628.30	679/535	5.11 × 10−1	2.04
41Gero63	22372.25–27561.60	1108/1091	1.29 × 10−1	1.59
90BeKePaRy87	23037.98–23878.85	557/498	6.14 × 10−2	4.58 × 10−1
98KuHsHuLe94	24475.90–27548.20	111/93	2.23 × 10−1	5.78 × 10−1
91Para90	25348.38–25823.34	59/50	8.45 × 10−3	2.28 × 10−2
99LiKuHsLe95	30980.42–32048.74	124/116	2.00 × 10−1	2.00 × 10−1
19MeLiUb105	31002.32–32269.09	213/212	6.85 × 10−2	5.00 × 10−1
32Heimer62	31049.00–32388.47	159/133	2.00 × 10−1	2.00 × 10−1
69HeJo66	31226.14–64621.60	150/115	3.78 × 10−1	4.14
97BeKeRy93	31387.80–32202.22	63/50	3.55 × 10−2	8.50 × 10−2
86UbMeTeDy81	31677.57–31908.06	35/32	3.17 × 10−3	8.25 × 10−3
85ChChCo78	63685.00–64155.00	48/46	4.568	8.87
87ChPaChCo84	63686.10–69110.30	157/149	2.04	7.99

^aTags denote experimental data-source segments employed during this study. The column ‘Range’ indicates the range (in cm⁻¹) corresponding to validated wavenumber entries within the experimental transitions list. ‘A/V’ is an ordered pair, where A and V are the number of assigned and validated transitions related to a given source segment, respectively, obtained at the end of the Marvel analysis.

Some of the available sources had to be excluded from our final Marvel analysis. Table 2 lists these sources and gives a brief explanation for their exclusion. In a number of cases, like 65BlNi,⁶⁵ the exclusion is due to the fact that the transitions reported are simply not available in the source. Other sources claimed to have measured highly-accurate and well-resolved transitions, but the accuracy of the transition data provided is not even close to the claimed uncertainty. Another case is the example of 88LyWo,⁸⁵ who report successful measurement of the A ²Δ–X ²Π R1(5.5) transition with an uncertainty of 0.0002 cm⁻¹ but with no actual transition wavenumber given.

Details about the experimental sources on ¹²CH spectroscopy excluded during this study, with reason given for the exclusion.

Source	Reason for exclusion
00Amano96	Criticised by 13TrHeHiTa102 as having large systematic errors.
08JaZiMcPe100	No extractable data; focuses on magnetic resonance.
14TrHeToHi103	Data provided by 13TrHeToLe.20
19MaRoBrMu104	Modelling/experimental study with no extractable data.
56KiBr64	Data are superceded with those from more accurate sources.
65BlNi65	No extractable data available from this source.
71BaBr67	Data are superceded with those from more accurate sources.
74RyElIrSu69	Astronomical measurement of lower accuracy than laboratory determinations.
78HoMuHeEv70	Data are superceded with those from more accurate sources.
83BrEv75	Only Hamiltonian parameters are provided.
83BrBr74	Calculated data only.
88LyWo85	No transitions data provided.
88NeBrEv86	Only Hamiltonian parameters are provided.
90NeBrEv88	Only Hamiltonian parameters are provided.
91GrLaSaVa11	No transitions data provided.

In addition to the observed sources provided in Table 1, additional ground-state transitions were incorporated into the final input transitions file, calculated from the effective Hamiltonian (EH) term values provided by Zachwieja.⁹¹ In the input transitions file, these lines are tagged as 95Zachwiej_C.xx and they are useful for two reasons. First, they help to fix the values of the ground-state energies, which is particularly important for ¹²CH, as it lacks a substantial list of MW transitions. An accurate set of ground-state energies helps determining whether a rovibronic transition is an outlier and therefore improves the self-consistency of the SN. Second, use of EH values allows two or more components of the SN to be unified, as they provide linking transitions that are otherwise not present among the observed ones. Utilization of EH energies does, however, have a drawback: we do not know the accuracy of the individual energy levels. In general, the energies of lower-J states are more accurately determined by the EH method than those of states with higher J values. When experimental results conflicted with an EH value, the effective Hamiltonian value was deleted. Our final list of transitions contains 138 transitions determined using the EH approach. It is the duty of future accurate measurements to replace as many of these artificial transitions as feasible.

3.2. ¹⁶OH

The full list of ¹⁶OH data sources used in the final Marvel analysis,^{21,31,43,52,53,116,121,131,133,137–141,143–145,147,150,151,154} along with some characteristics, is given in Table 3. Although we aim to process all experimentally measured transitions, sometimes the earlier experimental studies are just too inaccurate to justify their inclusion into the Marvel input transitions file. For example, in the case of the A²Σ⁺–X²Π band, the average uncertainty of the 9200 lines of 18YoBeHoMa⁵³ is about 5 × 10⁻⁴ cm⁻¹, while the accuracy of earlier works, for example, 34TaKo¹⁶⁶ and 62DiCr,¹⁶⁷ is significantly worse, only about 0.01−0.1 cm⁻¹. Consequently, we decided to exclude these sources from our analysis. For similar reasons, we excluded the airglow^168–171 and night-sky^{23,54,172,173} spectra of ¹⁶OH from our analysis, as well. Some papers recorded spectra but do not provide any line positions.^114,174

Experimental sources, denoted with unique tags, used to construct the spectroscopic network of hyperfine-unresolved rovibronic transitions of ¹⁶OH. Given are the wavenumber range (Range) of each source, the number actual (A) and validated (V) transitions, plus uncertainty (unc.) statistics, with Avg. = average and Max. = maximum, in cm⁻¹.

Source tag	Range/cm−1	A/V	Avg. unc.	Max. unc.
09BeCo_C154	0.06–36721.34	197/197	3.07 × 10−3	2.63 × 10−2
79KeCl21	51.40–147.85	41/41	9.45 × 10−2	2.10 × 10−1
11MaPiBaBr43	101.28–942.57	215/215	5.16 × 10−4	5.00 × 10−3
91HaWh140	101.30–330.30	28/28	2.96 × 10−2	7.00 × 10−2
95MeSaGrFa145	361.05–3407.62	620/620	3.61 × 10−3	6.20 × 10−2
97PoZoViTe147	396.57–563.87	19/19	5.00 × 10−3	5.00 × 10−3
09BeCo154	640.95–791.94	31/31	2.00 × 10−3	2.00 × 10−3
83GoMuLaDo31	814.32–961.66	31/31	8.55 × 10−3	1.05 × 10−1
85LeBoDe133	918.81–1095.03	38/38	2.66 × 10−3	3.05 × 10−2
94AbDaRaEn143	2066.66–8666.48	1925/1912	2.31 × 10−3	3.01 × 10−1
90AbDaRaEn137	2211.70–3922.00	295/286	5.00 × 10−3	5.11 × 10−2
76MaChMa121	2696.00–10358.28	1117/1057	1.05 × 10−2	1.13 × 10−1
84Amano131	3280.04–3767.76	38/38	5.55 × 10−3	1.50 × 10−2
01NiHaNe150	3558.07–3855.04	23/23	1.27 × 10−2	4.14 × 10−2
16BrBeWeSn52	4308.76–7154.83	351/351	8.00 × 10−4	2.61 × 10−3
02TeBeZoSh151	5540.67–6866.25	300/289	6.25 × 10−3	4.39 × 10−2
90SaCo138	7657.31–36730.42	75/65	2.93 × 10−1	4.00 × 10−1
18YoBeHoMa53	15702.77–43408.75	9257/9257	8.01 × 10−4	2.10 × 10−2
91CoSaCo139	17898.38–39286.60	328/320	4.79 × 10−1	5.50 × 10−1
94StBrAb144	29998.33–33059.25	562/562	1.42 × 10−2	7.00 × 10−2
72Engleman116	32122.39–35560.02	107/107	1.02 × 10−1	3.00 × 10−1
93CoChCo141	34993.51–46930.92	340/340	1.55 × 10−2	2.55 × 10−1

For a successful Marvel analysis of transitions data one needs to construct a well-connected SN. It is essential to know the rotational energy levels of the vibrational ground state. Since there are no high-accuracy pure rotational measurements for ¹⁶OH, we had to rely on calculated energy levels, based on the EH results of 09BeCo.¹⁵⁴ The calculated lines included are denoted by ‘_C’ in the database.

4. Marvel results

4.1. ¹²CH

A total of 6348 assigned transitions from 29 distinct data sources were included in our final Marvel analysis of the measured spectra of ¹²CH. From these transitions 5906 lines belong to the principal component, determining 1521 empirical (Marvel) energy levels. Our database contains 49 floating transitions (transitions which could not be linked to the principal component), as well, linking 82 rovibronic energy levels. These floating transitions are retained in the dataset as they might be linked easily to the principal component when new experimental data become available.

After the necessary reassignments, only 393 transitions had to be removed from the dataset considered by the final Marvel analysis, as they are not consistent with the validated transitions. These transitions are retained in the final list of transitions but are given as negative wavenumber entries. Table 4 gives a brief summary of the characteristics of the Marvel results obtained for the seven doublet electronic states studied. The transitions file and the energy levels are given in the ESI.†

A brief summary of the ¹²CH Marvel results for the different electronic states, the energy and uncertainty ranges are given in cm⁻¹. Unc. = uncertainty, Avg. = average.

State	v range	Levels	Unc. range	Avg. unc.	Range of energy levels
X2Π	0–5	711	0.0000–1.3510	0.0252	0.0000–21277.3362
A2Δ	0–5	514	0.0051–1.0013	0.1910	23260.1771–39244.0815
B2Σ−	0–1	109	0.0071–0.5001	0.1026	25712.5053–31474.7352
C2Σ+	0–2	141	0.0054–0.5001	0.0736	31791.6558–43701.3123
D2Π	0–2	58	0.1000–4.1430	0.7270	58999.2647–65867.9341
E2Σ+	2–2	25	0.5000–2.7250	0.9777	68793.1355–70652.4969
F2Σ+	0–0	15	0.5000–1.0000	0.7539	64531.9000–64793.2681

4.2. ¹⁶OH

Employing 15 938 measured transitions, we could determine 1624 empirical rovibronic energy levels for ¹⁶OH. The detailed validation process resulted in the deletion of 119 transitions. The present Marvel database contains 72 floating transitions including 81 rovibronic energy levels. Future high-resolution studies may connect these floating components to the principal one.

Table 5 provides information about four experimentally measured electronic states. It is interesting to note that there are more A ²Σ⁺–X ²Π than X ²Π–X ²Π transitions measured (not seen in Table 5). This is solely due to the source 18YoBeHoMa,⁵³ in which more than 9200 assigned A ²Σ⁺–X ²Π lines are given. The transitions file and the energy levels of this study are available in the ESI.†

A brief summary of the ¹⁶OH Marvel results for the different electronic states, the energy and uncertainty ranges are given in cm⁻¹. Unc. = uncertainty, Avg. = average.

State	v Range	Levels	Unc. range	Avg. unc.	Range of energy levels
X2Π	0–13	1204	0.0000–0.3005	0.0035	0.0000–36721.3447
A2Σ	0–9	350	0.0011–0.5000	0.1209	32440.5786–52482.2452
B2Σ+	0–1	40	0.0051–0.7071	0.0527	68406.2992–69409.1102
C2Σ+	0–1	30	0.6103–0.7071	0.6845	88261.1865–89690.2761

5. Comparison with existing datasets

The Cologne Database for Molecular Spectroscopy (CDMS),¹⁷⁵ one of the standard spectroscopic databases, contains data neither for CH nor for OH. There are, however, several other spectroscopic datasets assembled for CH and/or OH. Comparisons of these literature datasets with the results of the present study are given next.

The source 96JoLaIwYu⁵¹ supposedly contains 112 821 calculated lines for ¹²CH, involving the lowest four doublet electronic states. At the time of the writing of this paper, these data are simply unavailable; thus, no comparison could be performed.

5.1. MoLLIST⁵⁵ for ¹²CH

We used the term values of the CH dataset of 14MaPlVaCo,⁹ downloaded from the VizieR website,¹⁷⁶ to compare with our final empirical (Marvel) energy levels. Fig. 2 shows the differences between the empirical energy levels of this study and the results of 14MaPlVaCo⁹ for the X ²Π, A ²Δ, and B ²Σ⁻ electronic states.

Fig. 2. Differences between the Marvel energy levels of this study and the empirical results of 14MaPlVaCo,⁹ concerning the X²Π, A²Σ⁺, and B²Σ⁻ electronic states of the ¹²CH radical.

Unfortunately, we found several conflicts between the positions of newly identified lines, Tables A.2–A.4 of ref. 9, and the official ESI of that study (and the latest version of this database downloaded from the VizieR website¹⁷⁶). There are conflicts, for example, concerning the labels. To wit, according to Table A.2 of ref. 9, the transition at 22440.19 cm⁻¹ is P22ff(17.5), but in the ESI it is designated as P22ee(17.5), i.e., there is a conflict in the rotationless parity. We found several similar cases and we used the labels found in the ESI during this analysis. Furthermore, Table A.3 of ref. 9 contains several non-existent rovibrational energy levels in the B ²Σ⁻ state. For example, this table contains P22ff transitions, but in the ²Σ⁻ state the parity of an F = 2 level is ‘e’.

As seen in Fig. 2, there are a few energies where the deviations are larger than 1 cm⁻¹. The reason for these large differences is also the conflict between the 14MaPlVaCo article and its ESI. For example, the difference between the Marvel and the 14MaPlVaCo values for the (A2Delta 3 11.5 e 2) level is more than 6.0 cm⁻¹. In Table A.2 of ref. 9, the wavenumber of the P22ee(12.5) line is 22606.47 cm⁻¹, but the wavenumber of this line in the ESI is 22612.49 cm⁻¹.

5.2. MoLLIST⁵⁵ for ¹⁶OH

We used the term values of the MoLLIST⁵⁵ OH dataset downloaded from the ExoMol website,^177,178 to compare with our final empirical energy levels. Fig. 3 shows the deviations between the empirical energy levels of this study and the results of the MoLLIST OH dataset for the X ²Π and A ²Σ⁺ electronic states.

Fig. 3. Differences between the Marvel energy levels of this study and the empirical results of MoLLIST,⁵⁵ concerning the X²Π and A²Σ⁺ electronic states of the ¹⁶OH radical.

Fig. 3 shows that between 20 000 and 40 000 cm⁻¹ there are several energies where the deviations are larger than 0.01 cm⁻¹. It seems that there are conflicts between the measured transitions of 94AbDaRaEn¹⁴³ and 95MeSaGrFa¹⁴⁵ and the fitted MoLLIST⁵⁵ results.

Furthermore, we compared the term values of 09BeCo¹⁵⁴ to the Marvel energy levels of the B ²Σ⁺ electronic state. Fig. 4 shows the deviations between the Marvel energy levels and the results of 09BeCo¹⁵⁴ for the B ²Σ⁺ electronic state. The Marvel energy levels are determined by the measured transitions of 91CoSaCo¹³⁹ and it is important to note that the authors of 91CoSaCo excluded from the fitting the last two transitions (clear outliers in Fig. 4). This explains why the differences between the Marvel and the 09BeCo¹⁵⁴ results are much larger in the case of the last two energy levels.

Fig. 4. Differences between the Marvel energy levels and the earlier results of 09BeCo¹⁵⁴ concerning the B²Σ⁺ state of the ¹⁶OH radical.

5.3. HITRAN and GEISA databases of ¹⁶OH

The canonical spectroscopic database and information system HITRAN2020⁴⁹ contains 55 698 rovibronic transitions for the ¹⁶OH radical, involving the X ²Π and A ²Σ⁺ electronic states and the transitions go all the way up to 43408.75 cm⁻¹. Therefore, it can be used to check the completeness of our empirical Marvel dataset. Most of the line positions of the X ²Π–X ²Π and A ²Σ⁺–X ²Π bands have been updated in HITRAN2020, using the calculated parameters of 16BrBeWeSn.⁵²

Since the line positions of HITRAN2020 are based on effective Hamiltonian calculations, it is not surprising that there are about 43 000 lines that are not available in our Marvel database, which contains almost exclusively experimental information. Of the transitions common to both HITRAN and Marvel, we could reproduce about 13 000 lines within 0.05 cm⁻¹. There are 370 HITRAN transitions where the differences between the HITRAN and the Marvel lines are larger than 0.05 cm⁻¹.

Similar to the HITRAN2020 database, the recent version of GEISA-2020⁵⁰ is based on EH calculations. This database contains 42 866 rovibronic transitions in the X ²Π–X ²Π and A ²Σ⁺–X ²Π band systems up to 35877.03 cm⁻¹. The GEISA-2020 database also contains about 25 000 lines that are not part of our experimental database. Since the GEISA database does not contain exact information about the e/f parity, we could not perform a line-by-line comparison.

6. Hyperfine transitions

Although Marvel has been used for the analysis of the spectra of a number of two- to five-atomic species, thus far networks of hyperfine-resolved transitions have not been considered. In those cases where hyperfine-resolved measured lines were available, only their average was utilized.^61,179 For the radicals ¹²CH and ¹⁶OH, we decided to retain at least some of the experimental information about the hyperfine lines in the Marvel transitions input file. Most of the published measured transitions are given in MHz; therefore, we keep this unit in our Marvel database.

Note that there are several outstanding papers which report highly accurate spin-rotation splittings within the A and C states of ¹²CH^81,82 and the A ²Σ⁺ state of ¹⁶OH.^{71,72,122,127,130,136} For example, 86MeUbDy¹³⁶ contains hyperfine-resolved transitions between e/f doublets in the v = 0 vibrational state, 83MeMaMeDy¹³⁰ contains similar data for both the v = 0 and v = 1 vibrational states of ¹⁶OH, and 18FaFuMe¹⁵⁷ provides 12 highly accurate hyperfine-resolved transitions connecting the X and A states of ¹⁶OH.

None of the hyperfine lines discussed here were employed during the Marvel analysis of the large amount of hyperfine-unresolved data. The issue of how to combine a mixture of hyperfine resolved and unresolved transitions within a Marvel procedure is a subject of active study¹⁸⁰ and one we plan to address elsewhere.

6.1. ¹²CH

To construct the spectroscopic network of the hyperfine-resolved transitions for the ¹²CH radical we collected all available measured transitions belonging to the ground (v = 0) vibrational state. The full list of data sources employed in the final hyperfine Marvel analysis of ¹²CH is given in Table 6, which also provides details on the range of frequencies and the number of transitions measured and validated, along with some statistical data about the uncertainties of the sources. This table also shows that we collected 73 transitions from 9 sources. In order to get a complete energy value set up to J = 9/2, we had to add 6 calculated lines (published in 01DaEvBr⁹⁷) to the database.

Experimental sources used to construct the ¹²CH hyperfine spectroscopic network. Given are the frequency range of the validated transitions of each source, the number of actual (A) and validated (V) transitions, and selected uncertainty statistics. Avg. = average, unc. = uncertainty, and max. = maximum.

Source tag	Range/MHz	A/V	Avg. unc./MHz	Max. unc./MHz
85ZiTu80	701.68–724.79	2/2	1.00 × 10−2	1.00 × 10−2
13TrHeToLe20	701.68–3349.19	7/7	9.71 × 10−6	2.10 × 10−5
73RyElIr68	3263.79–3349.19	3/3	3.00 × 10−3	3.00 × 10−3
06CaMoBrTh98	3263.80–14778.96	9/9	2.00 × 10−3	3.00 × 10−3
83BrBr74	4847.84–24482.10	14/14	4.61 × 10−1	1.00 × 10−0
84BrBr76	7274.78–7398.38	4/4	2.63 × 10−1	4.50 × 10−1
00Amano96	532721.33–536795.68	6/6	2.90 × 10−1	8.50 × 10−1
13TrHeHiTa102	532721.59–536795.57	6/6	6.00 × 10−4	6.00 × 10−4
01DaEvBr97	2010810.46–4250352.95	16/15	1.53 × 10−1	6.50 × 10−1
01DaEvBr_C97	3376791.22–4238488.08	6/6	1.37 × 10−1	1.60 × 10−1

Fig. 5 shows the SN of the hyperfine transitions measured for the ¹²CH radical. As also seen there, we cannot reach the f and e levels of J = 9/2 energy states of F₁ and F₂, respectively, without the calculated transitions (red lines). Since this Marvel database contains only the hyperfine transitions of the ground (v = 0) vibrational and electronic state, the following four descriptors were employed to label the rotational levels: Ω (1 for the F₁ and 2 for the F₂ component), J, the rotationless parity (e/f), and the total angular momentum F. Table 7 contains the first 36 Marvel -determined hyperfine energy levels up to J = 9/2. As seen there, there are three hyperfine energy levels within the F₂ component which are known with an outstanding accuracy of just a few (3–6) Hz.

Fig. 5. Spectroscopic-network representation of the Λ-doublet and proton hyperfine splittings and the electric-dipole- and magnetic-dipole-allowed transitions measured for the ground electronic (X ²Π) and vibrational (v = 0) state of the ¹²CH radical. The blue arrows depict the experimentally measured transitions, while the red arrows correspond to calculated ones. See the text for the definition of the labels denoting the states.

Energy values and the corresponding uncertainties of hyperfine-resolved levels of the ¹²CH radical based on transitions data reported in Table 6. Unc. = uncertainty. See the text for the meaning of the J, F, F₁, and F₂ descriptors.

J	F1				F2
	Parity	F	Energy/MHz	Unc./MHz	Parity	F	Energy/MHz	Unc./MHz
1/2					e	0	0.000	0.000
1/2					e	1	13.713200	4.24 × 10−6
1/2					f	0	3277.506647	5.20 × 10−6
1/2					f	1	3349.192556	3.00 × 10−6
3/2	f	1	536070.7812	6.00 × 10−4	e	1	2006762.629	2.00 × 10−1
3/2	f	2	536073.0819	6.00 × 10−4	e	2	2006812.83	2.00 × 10−1
3/2	e	2	536774.7595	6.00 × 10−4	f	1	2014087.83	2.00 × 10−1
3/2	e	1	536795.5695	6.00 × 10−4	f	2	2014161.25	2.00 × 10−1
5/2	f	3	2193034.61	4.58 × 10−1	e	2	4592650.00	2.24 × 10−1
5/2	f	2	2193043.82	4.96 × 10−1	e	3	4592693.00	2.24 × 10−1
5/2	e	2	2197913.93	6.38 × 10−1	f	2	4607406.67	2.24 × 10−1
5/2	e	3	2197882.44	6.08 × 10−1	f	3	4607471.96	2.24 × 10−1
7/2	f	4	4718557.56	4.47 × 10−1	e	3	7999837.21	2.69 × 10−1
7/2	f	3	4718571.82	4.86 × 10−1	e	4	7999876.51	2.45 × 10−1
7/2	e	4	4729822.75	3.32 × 10−1	f	3	8024257.39	2.45 × 10−1
7/2	e	3	4729858.84	5.71 × 10−1	f	4	8024319.08	2.45 × 10−1
9/2	f	5	8095348.78	4.66 × 10−1	e	4	12238325.35	2.93 × 10−1
9/2	f	4	8095365.91	4.69 × 10−1	e	5	12238362.39	2.77 × 10−1
9/2	e	5	8115282.26	3.46 × 10−1	f	4	12274610.34	2.65 × 10−1
9/2	e	4	8115321.04	5.80 × 10−1	f	5	12274669.61	3.32 × 10−1

6.2. ¹⁶OH

The SN of hyperfine-resolved transitions of ¹⁶OH is considerably larger than that of ¹²CH, containing more than 200 experimentally-measured hyperfine transitions, collected from 27 sources. Marvel can only determine the absolute energy of a quantum state if, within the SN, there is a path leading from the given level to the lowest energy level. There are no hyperfine-resolved transitions connecting the different vibrational states of ¹⁶OH; thus, only the ground (v = 0) vibrational state is investigated here.

We used the same four descriptors to label the rotational levels of ¹⁶OH hyperfine energies as in the case of ¹²CH: Ω (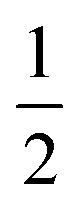 for the F₂ and for the F₁ component), J, the rotationless parity (e/f), and the total angular momentum F. As mentioned earlier, we followed the e/f scheme and the order of the F numbers advocated in 78BrKaKeMi (see Fig. 3 of 78BrKaKeMi¹⁶⁵). This means that in the ²Π_3/2 component the order of the quantum number F inverts above with larger F values belonging to lower energies. For the ²Π_1/2 case the order of (e/f) parity components swaps for 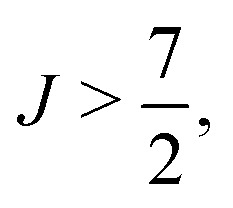with the f states lying at lower energy. The full list of data sources employed in the final Marvel analysis of the hyperfine lines of ¹⁶OH is given in Table 8. This table also provides details on the range of frequencies and the number of transitions measured and validated, along with some statistical data about the uncertainties of the sources.

Experimental sources used to construct the spectroscopic network of ¹⁶OH hyperfine lines. Given are the frequency range of the validated transitions of each source, the number of actual (A) and validated (V) transitions, and selected uncertainty statistics. Avg. = average, unc. = uncertainty, and max. = maximum.

Source tag	Range/MHz	A/V	Avg. unc./MHz	Max. unc./MHz
75DeMa119	7.43–23838.93	11/11	2.50 × 10−2	5.23 × 10−2
75MeDy120	88.95–23826.62	17/17	5.88 × 10−3	1.00 × 10−2
73MeDy118	88.95–193.00	4/4	5.00 × 10−4	5.00 × 10−4
76MeMeMiDy122	1171.49–13441.42	11/11	1.82 × 10−3	5.00 × 10−3
06LeMeHuSa153	1612.23–1720.53	2/2	4.75 × 10−5	8.50 × 10−5
64Radford109	1612.23–1720.53	4/4	2.33 × 10−3	3.30 × 10−3
72MeDy117	1612.23–1720.53	4/4	1.25 × 10−4	2.00 × 10−4
79CoSaAuLe125	1612.23–66133.35	12/12	2.55 × 10−2	5.00 × 10−2
06HuLeSaYe152	1665.40–1667.36	2/2	8.00 × 10−6	1.20 × 10−5
59EhToSt108	1665.46–1667.34	2/2	6.50 × 10−2	1.00 × 10−1
68Goss111	1720.53–1720.53	1/1	3.00 × 10−3	3.00 × 10−3
68Radford113	4660.24–6049.08	7/7	6.56 × 10−3	1.10 × 10−2
70BaDiGoRa115	7749.91–7831.96	4/4	5.00 × 10−3	5.00 × 10−3
55DoSaTo107	7760.36–36994.43	12/12	6.31	35.75
77DeMaBaBr123	8534.86–70858.93	20/20	3.11 × 10−2	1.20 × 10−1
80SaVa128	13433.96–13442.13	4/4	2.64 × 10−2	5.35 × 10−2
99ThWuSpMe148	13434.00–13442.08	4/4	9.92 × 10−3	2.47 × 10−2
68PoBe112	13434.62–36994.43	8/8	1.15 × 10−1	4.78 × 10−1
96WuSpMeAn146	13434.64–13441.42	2/2	5.00 × 10−4	5.00 × 10−4
65PoLi110	13434.65–13441.41	2/2	2.00 × 10−2	2.00 × 10−2
53SaScDoTo106	23818.16–36994.43	4/4	3.01 × 10−1	5.99 × 10−1
81KoZoLe129	66094.85–70887.99	6/6	3.33 × 10−2	5.00 × 10−2
93VaEv_C142	1834735.02–4602881.87	35/35	7.90 × 10−2	1.56 × 10−1
13Drouin156	1834735.06–2603427.29	17/17	5.34 × 10−1	2.37
86BlFaPi134	1834735.51–3036645.05	17/17	9.37 × 10−1	2.47
86BrZiJeEv135	1837816.39–3789214.99	22/22	7.79 × 10−1	4.74
93VaEv142	1837816.39–4209632.49	13/13	1.20 × 10−1	4.00 × 10−1
85FaBlPi132	2509935.44–2509988.61	3/3	8.04 × 10−1	8.08 × 10−1

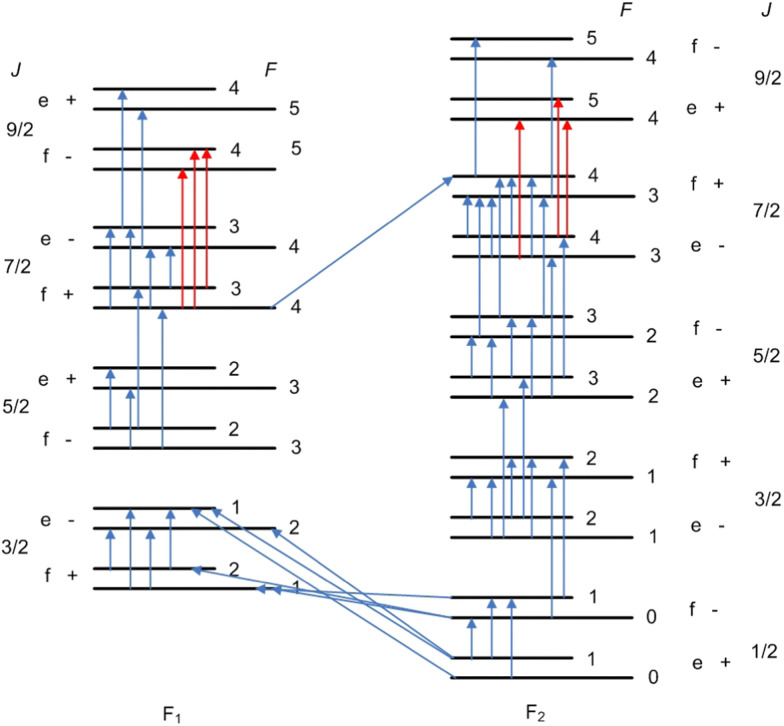
Fig. 6 shows the SN representation of the hyperfine transitions of the ¹⁶OH radical on its ground electronic and vibrational state. As seen there, we can reach the J = 9/2 and 7/2 energy levels of the F₂ and F₁ components, respectively, if we use the calculated hyperfine transitions of 93VaEv¹⁴² (red lines).

Fig. 6. Spectroscopic-network representation of the Λ-doublet and proton hyperfine splittings and the electric-dipole- and magnetic-dipole-allowed transitions measured for the ground electronic (X ²Π) and vibrational (v = 0) state of the ¹⁶OH radical. The blue arrows depict the experimentally measured transitions, while the red arrows correspond to calculated ones. See the text for the definition of the labels denoting the states.

Table 9 contains the first 32 Marvel-determined hyperfine energy levels. It is interesting to note that the most accurate transition, provided by 06HuLeSaYe,¹⁵² is 1 667 358 996 ± 4 Hz; therefore, the uncertainty of the (X2Pi 1.5 0 1.5 e 2) level is an outstanding 10⁻¹⁰ cm⁻¹ (i.e., better than 10⁻⁵ MHz, see Table 9). There are three hyperfine energy levels in the F₁ component which have remarkable, about 10 Hz accuracy.

Energy values and the corresponding uncertainties of hyperfine-resolved levels of the ¹⁶OH radical based on transitions data reported in Table 8. Unc. = uncertainty. See the text for the meaning of the J, F, F₁, and F₂ descriptors.

J	F1				F2
	Parity	F	Energy/MHz	Unc./MHz	Parity	F	Energy/MHz	Unc./MHz
1/2					e	0	3786170.1	1.56 × 10−1
1/2					e	1	3786185.0	1.56 × 10−1
1/2					f	0	3790845.3	1.56 × 10−1
1/2					f	1	3790935.7	1.56 × 10−1
3/2	e	1	0.000	0.000	e	1	5620920.0	1.56 × 10−1
3/2	e	2	53.170893	1.08 × 10−5	e	2	5620931.9	1.56 × 10−1
3/2	f	1	1665.40180	1.20 × 10−5	f	1	5628681.8	1.56 × 10−1
3/2	f	2	1720.52989	1.00 × 10−5	f	2	5628752.0	1.56 × 10−1
5/2	e	2	2509987.83	2.84 × 10−2	e	2	8657190.1	1.57 × 10−1
5/2	e	3	2510001.83	2.80 × 10−2	e	3	8657207.9	1.57 × 10−1
5/2	f	2	2516018.58	2.84 × 10−2	f	2	8665326.0	1.57 × 10−1
5/2	f	3	2516036.92	2.80 × 10−2	f	3	8665397.5	1.57 × 10−1
7/2	e	4	6053780.92	3.21 × 10−2	e	3	12869482.9	1.89 × 10−1
7/2	e	3	6053788.36	3.17 × 10−2	e	4	12869506.5	1.89 × 10−1
7/2	f	4	6067222.34	3.21 × 10−2	f	3	12874956.0	1.89 × 10−1
7/2	f	3	6067223.00	3.17 × 10−2	f	4	12875030.0	1.89 × 10−1
9/2	e	5	10646265.25	8.34 × 10−2	f	4
9/2	e	4	10646286.57	8.33 × 10−2	f	5
9/2	f	5	10670091.87	8.34 × 10−2	e	4
9/2	f	4	10670104.18	8.33 × 10−2	e	5

6.3. Comparison with the JPL catalog for ¹²CH and ¹⁶OH

The Jet Propulsion Laboratory (JPL) catalog⁵⁶ contains submillimeter, millimeter, and microwave spectral lines in the frequency range between 0 and 10 000 GHz for more than 300 atomic and molecular species. Since the JPL catalog contains both calculated and experimental lines, with the corresponding ‘experimental’ energy levels, it was an obvious choice to use this database to check the quality of the empirical (Marvel) results of this study. Fig. 7 shows the differences between the Marvel and the JPL energy levels, both for ¹²CH and ¹⁶OH.

Fig. 7. Comparison of the empirical (Marvel) energy levels of this study with those of the JPL dataset for ¹²CH (blue circles) and ¹⁶OH (red triangles).

For ¹²CH, the JPL catalog lists 58 experimentally measured hyperfine transitions and this dataset was extended with 67 lines of FT-IR measurements,⁸³ which are not hyperfine resolved. The accuracy of the lines in the emission spectrum of 87Bernath⁸³ is significantly worse than that of the hyperfine measurements; therefore, we decided to consider only the 58 hyperfine lines during the comparison. As Fig. 7 shows (see the empty blue circles), most of the differences between the empirical energy levels of this study and those of the JPL database are less than 200 kHz.

For the OH radical, the JPL catalog lists 3153 experimentally measured transitions, which belong to six isotopologues. From the transitions listed, 739 lines belong to the vibrational ground state of ¹⁶OH. It is important to note that the JPL database contains results from a far-infrared spectrum (11MaPiBaBr,⁴³ with 0.0002 cm⁻¹ average uncertainty), an IR spectrum (85LeBoDe,¹³³ with 0.001 cm⁻¹ average uncertainty), and a solar spectrum (95MeSaGrFa,¹⁴⁵ with 0.001 cm⁻¹ average uncertainty). As seen in Fig. 7, the differences between the Marvel and the JPL energy levels (red triangles) are less than 200 kHz, mutually confirming the data contained.

7. Conclusions

Accurate empirical rovibronic energy levels, with dependable, statistically significant, individual uncertainties, are reported for the following seven and four doublet electronic states of ¹²CH and ¹⁶OH: (X ²Π, A ²Δ, B ²Σ⁻, C ²Σ⁺, D ²Π, E ²Σ⁺, and F ²Σ⁺) and (X ²Π, A ²Σ⁺, B ²Σ⁺, and C ²Σ⁺), respectively. For ¹²CH, a total of 1521 rovibronic energy levels are determined in the principal component of its measured spectroscopic network (SN), utilizing 6348 experimentally measured and validated transitions. For ¹⁶OH, after a careful analysis and validation of 15 938 rovibronic transitions, collected from 45 sources, 1624 empirical rovibronic energy levels are determined. Determination of the empirical energy levels is based on the Measured Active Rotational-Vibrational Energy Levels (Marvel) algorithm.

The hyperfine lines measured for the two radicals are included in the Marvel analysis. These accurately measured transitions form floating components within the SN; thus, at the moment, they do not contribute toward improving the overall accuracy of the experimental SNs of ¹²CH and ¹⁶OH. Nevertheless, in the near future it might become possible to connect the hyperfine-resolved and-unresolved components, see, for example, Bowesman et al.¹⁸⁰ The most accurate line is provided by 06HuLeSaYe¹⁵² at 1 667 358 996 ± 4 Hz which allows the (X2Pi 1.5 0 1.5 e 2) level to be determined with an uncertainty of only 10⁻¹⁰ cm⁻¹.

The present database of ¹²CH and ¹⁶OH transitions and energy levels are compared to several line lists, including the HITRAN2020,⁴⁹ GEISA,⁵⁰ MoLLIST,⁹ and JPL⁵⁶ datasets. This comparison shows an overall satisfactory agreement and also points toward the inaccuracy of a small subset of effective Hamiltonian energies.

The large set of data presented should serve as a starting point to refine the line lists of these radicals. Such attempts have been made by us before, see the case of ¹²C₂.¹⁸¹ We note that the determination of accurate energy levels will allow a large number of new transitions to be predicted with experimental accuracy; in the case of our recent study of formaldehyde (H₂CO) this gearing led to a more than a twenty-fold increase in the number of predicted transitions relative to the number of unique measured transitions.¹⁸²

Conflicts of interest

There are no conflicts to declare.