A single early introduction governed viral diversity in the second wave of SARS-CoV-2 epidemic in Hungary

Abstract

Retrospective evaluation of past waves of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) epidemic is key for designing optimal interventions against future waves and novel pandemics. Here, we report on analysing genome sequences of SARS-CoV-2 from the first two waves of the epidemic in 2020 in Hungary, mirroring a suppression and a mitigation strategy, respectively. Our analysis reveals that the two waves markedly differed in viral diversity and transmission patterns. Specifically, unlike in several European areas or in the USA, we have found no evidence for early introduction and cryptic transmission of the virus in the first wave of the pandemic in Hungary. Despite the introduction of multiple viral lineages, extensive community spread was prevented by a timely national lockdown in March 2020. In sharp contrast, the majority of the cases in the much larger second wave can be linked to a single transmission lineage of the pan-European B.1.160 variant. This lineage was introduced unexpectedly early, followed by a 2-month-long cryptic transmission before a soar of detected cases in September 2020. Epidemic analysis has revealed that the dominance of this lineage in the second wave was not associated with an intrinsic transmission advantage. This finding is further supported by the rapid replacement of B.1.160 by the alpha variant (B.1.1.7) that launched the third wave of the epidemic in February 2021. Overall, these results illustrate how the founder effect in combination with the cryptic transmission, instead of repeated international introductions or higher transmissibility, can govern viral diversity.

Introduction

In Europe, the first outbreak of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections was detected at the beginning of 2020, soon after the first reports on the epidemic emerged from Wuhan, China (Gorbalenya et al. 2020; Wu et al. 2020; Zhou et al. 2020). Following the rapid establishment of community transmission in most European countries (Nadeau et al. 2021), the World Health Organization (WHO) declared a coronavirus disease 2019 (COVID-19) pandemic on 11 March 2020 (Cucinotta and Vanelli 2020). As a response to the daily rise of new cases, most European countries introduced non-pharmaceutical public health interventions in mid-March, such as international and domestic travel restrictions, social distancing, as well as school and workplace closures, aiming to prevent or slow down the transmission of the SARS-CoV-2 virus (Flaxman et al. 2020). However, due to significant differences in international travel patterns and the timing of implementing adequate preventive measures, the intensity of the first wave of the pandemic extensively differed across European countries (Plümper and Neumayer 2020).

In Hungary, the first SARS-CoV-2 cases were detected at the beginning of March 2020: more than a month later than in many Western European countries. The national strategy involved a fast implementation of strict suppressive measures, right after the WHO had declared the pandemic, aiming at lowering the effective reproduction number (R_t) below 1 to stop the circulation of the virus in the community (see Fig. 1A; Röst et al. 2020; Hale et al. 2021). As a consequence, the first wave was largely suppressed in Hungary (Fig. 1B; Supplementary Table ST1). The total case count of 3,921 in the first wave (407 cases per million inhabitants) is 9-fold lower than the average for Western European countries (Ritchie et al. 2020). This figure is supported by a representative country-wide seroconversion study (Merkely et al. 2020), as well as by the relatively low death toll (55 deaths per million inhabitants in total, Fig. 1B).

Figure 1.

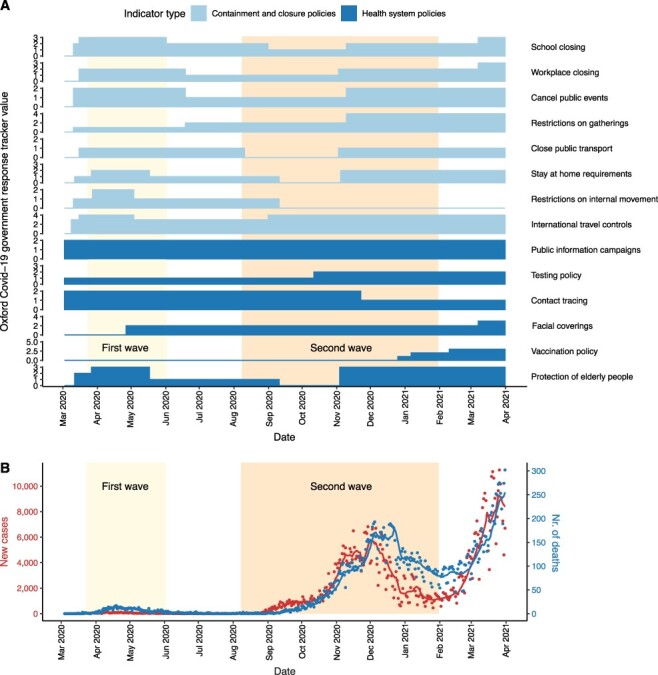
Public health interventions and case counts for the first two waves in Hungary. (A) Timeline of public health interventions as measured by the Oxford COVID-19 government response tracker values based on data related to Hungary in the global panel database of pandemic policies (Hale et al. 2021). ‘Containment and closure policy’ values and selected ‘health system policy’ values quantify non-pharmaceutical interventions from the date of the first SARS-CoV-2 genome sampled in Hungary (3 March 2020) until the date of the last genome sample included in the analysis (31 March 2021). Scales of the y-axes correspond to the number of categories that a given type of intervention variable can take (between 0–2 and 0–5). For further information on the dataset, see Supplementary Table ST2. (B) Number of new confirmed COVID-19 cases and deaths caused by COVID-19 per day between the date of the first case and the last available SARS-CoV-2 genome sequence sampled in Hungary. Dots represent actual data (Ritchie et al. 2020), while lines represent 7-day moving average values. The first and last dates of the waves were defined based on the 7-day moving average of confirmed COVID-19 cases in Hungary: the first wave (light yellow background) lasted from 3 March 2020 (first confirmed case) to 2 June 2020 (i.e. when the rolling mean dropped to less than 20). The second wave lasted from 8 August 2020 (i.e. when the 7-day moving average increased above 20) to 31 January 2021, when the third wave started.

Along with the gradual lifting of COVID-19 restrictions in numerous European countries after the first wave, Hungary also started to loosen the previously established suppressive restrictions to implement a reopening strategy in early May (Fig. 1A; Supplementary Table ST2). Specifically, while international movements were still controlled until mid-June 2020 by demanding SARS-CoV-2 testing upon entry into the country, most domestic measures were relaxed between May and September when case counts reached an alarmingly increasing trend again, similarly to other European countries (Plümper and Neumayer 2020). Only milder interventions were in place that did not completely stop viral circulation but aimed to avoid the overload of the healthcare system (mitigation strategy). By early November, when strict non-pharmaceutical interventions were introduced again, case counts reached thousands on a daily basis, which is in sharp contrast to the first wave (Fig. 1B). By the end of the second wave (February 2021), the death toll was ∼20-fold higher (1,239 deaths per million inhabitants in total, Fig. 1B) than it was during the first wave (Ritchie et al. 2020; Oroszi et al. 2021). Therefore, the question emerges: can the investigation of viral dynamics shed light on the sequence of events underlying the marked difference in the two waves of the SARS-CoV-2 epidemic in Hungary?

In general, daily case counts based on diagnostic SARS-CoV-2 testing serve as a measure, indicating the intensity of community transmission. Besides, viral genome sequencing has emerged as a crucial tool to gain further insights into viral transmission patterns and hence the dynamics of the pandemic (Moreno et al. 2020; Washington et al. 2021). The main advantage of these tools is that they monitor both the evolutionary changes and the associated transmission patterns of the virus. The retrospective reconstruction of these events is of paramount importance to learn from past experience and thereby to prepare for future critical public health situations (Alm et al. 2020). Global efforts to sequence SARS-CoV-2 genomes have yielded more than 7 million sequences collected from over 200 countries (until 14 January 2022), shared publicly on repositories like the Global Initiative on Sharing All Influenza Data (GISAID; Shu and McCauley 2017), and analysed by many research groups using, for example, the Nextstrain pipeline (Hadfield et al. 2018). By enabling real-time phylogenetic analyses, such initiatives offer an unprecedented opportunity to understand viral transmission patterns and guide public health interventions to mitigate the pandemic (Meredith et al. 2020; Oude Munnink et al. 2020).

Here, we report on sequencing 221 SARS-CoV-2 samples and analysing an additional pool of 131 sequence data from Hungary, deposited in GISAID. We have found evidence for introductions of multiple viral lineages in the first wave. Importantly, these introductions did not result in widespread community spread due to a strict and timely national lockdown. In contrast, the much more extensive second wave of the epidemic in Hungary displayed a much lower viral diversity and was dominated by the European variant B.1.160. Remarkably, the majority of sequences in the second wave can be linked to a single importation of the B.1.160 variant at the beginning of the summer in 2020, followed by a 2-month long, unexpected cryptic transmission before inducing a massive surge of cases and hospitalisations. Genomic and epidemiologic analyses indicate that the dominance of B.1.160 was not driven by an intrinsic transmission advantage or by repeated introductions, but rather by chance founder events (founder effect), that is the loss of genetic variation that occurs when a new population is established by a very small number of individuals (Provine 2004; Rambaut et al. 2004). This likely happened through a single establishment of the B.1.160 lineage followed by possible circulation in a subpopulation with higher contact rates or superspreading events during the cryptic transmission period.

Results

Different patterns of viral diversity in the first and second waves in Hungary

We analysed 352 genomes from Hungary, deposited in GISAID, including 221 genomes sequenced as part of the present study using the Artic Network protocol (see Materials and Methods). The genomes were obtained from samples collected between 29 April 2020 and 23 February 2021, mostly covering the first and second waves of the SARS-CoV-2 epidemics in Hungary (105 and 219 genomes, respectively, metadata are available in Supplementary Tables ST3 and ST4). The samples originated across the country, including fifteen out of the nineteen counties plus the capital (Budapest) in the first wave and sixteen counties plus the capital in the second wave (metadata is available in Supplementary Table ST5). To explore the differences between the two waves, we first compared the diversities of circulating variants as defined by the Pangolin lineage assignments (Rambaut et al. 2020).

Overall, we identified twenty-five distinct viral variants in the two waves of Hungary, the vast majority (98.46 per cent) belonging to the large European parent lineage B.1 which emerged in early 2020 (Fig. 2A; Supplementary Tables ST3, ST4, and ST6). Note that except for four sequences, all Hungarian genomes contain the D614G substitution in the spike protein (Supplementary Table ST4), which has rapidly replaced the ancestral variant due to its increased transmissibility (Korber et al. 2020). These patterns are consistent with multiple introductions from other European countries. While the first wave was driven by multiple variants circulating at low to intermediate frequencies, the second wave showed a markedly different pattern: it was dominated by a single, high-frequency variant, B.1.160 (20A.EU2 Nextstrain clade), suggesting a lower genetic diversity. Indeed, the second wave shows a significantly lower Shannon diversity of variants than the first wave, despite the larger number of sequenced samples (Fig. 2B; P = 2.55 × 10⁻⁶; two-sided Hutcheson t-test). Importantly, this pattern cannot be explained by among-region sampling differences between the two waves as the conclusion holds when comparing the two waves within the same densely populated region (Pest county and the capital, Budapest; see Supplementary Fig. S1). Interestingly, while the B.1.160 variant exhibits a relatively low average prevalence in other countries (5.88 per cent in non-Hungary countries from Fig. 2C), this variant plus a second one (B.1.177 or 20E.EU1) accounted for the majority of sequences in Europe in autumn 2020 (Hodcroft et al. 2021). While B.1.160 was highly overrepresented in specific Western and Central European countries during this period (Fig. 2C), it reached the highest frequency in Hungary among all countries (12-fold and 10-fold higher than the average prevalence in other countries globally and in neighbouring countries of Hungary, respectively, Supplementary Table ST7).

Figure 2.

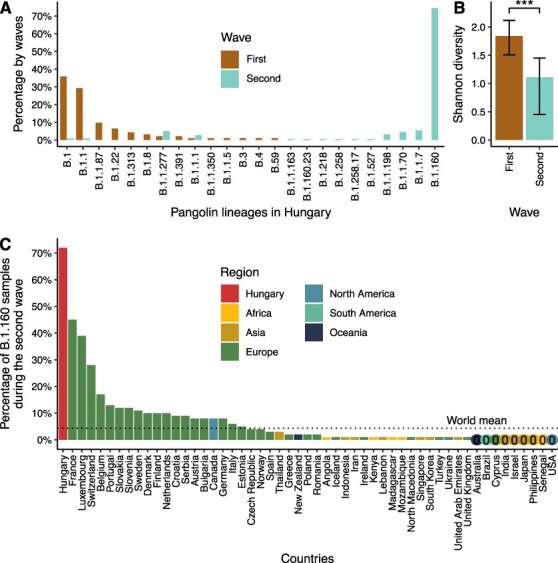
Different viral diversity patterns in the first and second waves of the pandemic in Hungary. (A) Prevalence of circulating SARS-CoV-2 Pangolin lineages in the first two waves shown as percentages of genome sequences in each wave. Waves are colour-coded. The lineages shown on the x-axis are ordered by decreasing percentages in the first wave and increasing percentages in the second wave. (B) Shannon diversity indices based on Pangolin lineage distributions for the two waves (1.84 and 1.11 for the first and second waves, respectively). The confidence intervals (based on the bias-corrected and accelerated bootstrap method by using 10,000 bootstrap replicates) are shown as error bars. *** represents a significant difference, two-tailed Hutcheson t-tests: P = 2.55 × 10⁻⁶. (C) Prevalence of the B.1.160 Pangolin lineage in countries with more than 100 sequenced SARS-CoV-2 genomes during the second wave in Hungary. The numbers are based on metadata downloaded from GISAID on 9 December 2021. Bars are coloured by regions. Countries with less than 0.5 per cent of the B.1.160 Pangolin lineage are indicated with 0 and coloured by regions.

In sum, these results show that the genetic diversity of SARS-CoV-2 greatly differed between the first and second waves of the epidemic in Hungary, implying distinct transmission dynamics.

Different transmission dynamics in the first and second waves

To gain insights into the dynamics of viral transmission during the two waves, we inferred distinct introductions of SARS-CoV-2 to Hungary by phylogenetic analysis (see Methods). In brief, we reconstructed a time-scaled Bayesian tree of the 352 Hungarian sequences, along with 1,311 sequences representing the global diversity of the virus during the investigated period (Fig. 3A; Supplementary Fig. 2; Methods). The Bayesian analysis allows us to infer the posterior probabilities and time of internal nodes (Methods). Based on these analyses, we identified clades that contain mostly Hungarian sequences and have a high phylogenetic support (Methods). Each of these clades likely represents transmission lineages that were independently established in Hungary. This analysis also identified singleton sequences, potentially representing introduction events that did not lead to widespread community transmission. Finally, we analysed the relative prevalence and size distributions of the transmission lineages in the two waves to gain further insight into the transmission dynamics of the virus.

Figure 3.

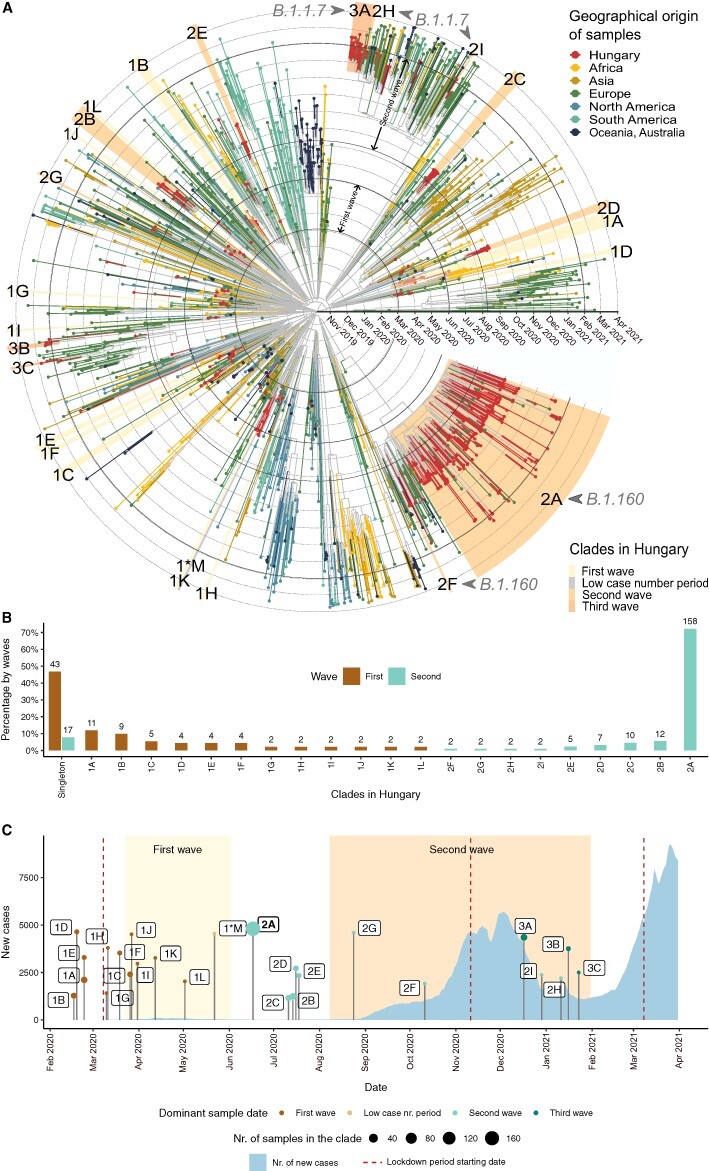
Transmission dynamics in the first and second waves. (A) Time-scaled phylogeny of SARS-CoV-2 genomes sampled in Hungary and globally. Tips and tip branches are coloured based on the geographical origin of the samples—Hungarian samples are shown in red. Concentric circles indicate the first day of each month. The start and end dates of the two waves are indicated with bolder circles. Hungarian clades are highlighted according to the time period when most of the samples were taken. The names of the clades start with 1, 2, or 3 for the clades in the first, second, and third waves, respectively, and are ranked using the alphabet based on their sizes (no. of samples in the clade). Sample ‘1*M’ represents the only clade from the low case number period. (B) Relative sizes of the Hungarian transmission lineages are shown as a percentage of genomes belonging to each transmission lineage (with absolute numbers shown above each bar). Coloured bars represent the first and second waves, respectively. The clades shown on the x-axis are ordered by decreasing percentages in the first wave and increasing percentages in the second wave. Percentages of singletons are shown on the left. (C) Timeline showing the number of new COVID-19 cases in Hungary (light blue area) and the TMRCA of each Hungarian clade. The size of TMRCA dots shows the number of Hungarian genome samples in each clade. Dots are coloured according to the time period (first wave, low case number period, and second and third waves) dominant in the clade (see Supplementary Table ST6). Periods of the first and second waves are highlighted with a light and dark yellow background. The start date of lockdown periods is indicated with vertical dark red-dashed lines.

We found two major differences in the transmission patterns of the first and second waves. First, the two waves dramatically differ in their prevalence of singleton sequences (Fig. 3B; P = 3.41 × 10⁻¹⁴; Fisher’s exact test). In particular, while almost half (46.74 per cent) of the sequences in the first wave are singletons, the same figure is only 7.76 per cent in the second wave (43 out of 92, and 17 out of 219 singleton sequences, respectively). This pattern suggests several introductions in the first wave that did not result in community transmission. In contrast, the vast majority of sequences isolated during the second wave are part of Hungarian transmission lineages (92.24 per cent of the sequences belong to nine clades in the second wave, while 53.26 per cent of the sequences belong to twelve clades in the first wave, see Fig. 3B). Second, while the size range of the transmission lineages in the first wave is between 2.17 per cent and 14.13 per cent of sampled sequences, we inferred a massive transmission lineage of the B.1.160 variant in the second wave, which gave rise to 75.8 per cent of sampled sequences (i.e. clade 2A in Figs 3A and 4). The presence of a single giant clade suggests that a small number of introductions led to community spread in the second wave. We provide further evidence for this scenario below. Notably, while an overdispersed size distribution of transmission lineages has been reported by previous works, the extent of overdispersion observed in the Hungarian second wave appears to be more extreme (du Plessis et al. 2021; Lemieux et al. 2021; Murall et al. 2021).

Figure 4.

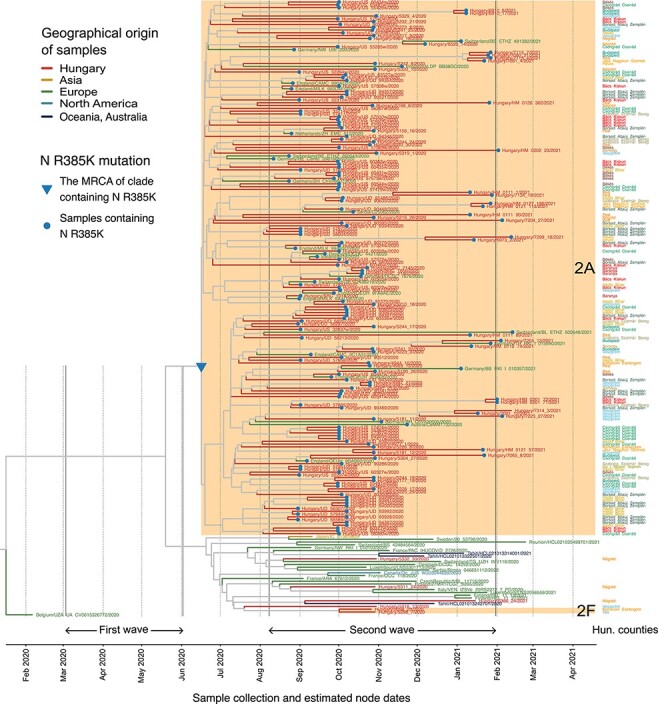
A shared mutation defines the large B.1.160 transmission lineage. The close-up view of the B.1.160 branch on the phylogenetic tree shows all viral sequences of the B.1.160 lineage that have been included in the phylogenetic analysis (Fig. 3). Tips and tip branches are coloured based on the broad geographic origin of the samples. The two monophyletic Hungarian clades (2A and 2F, highlighted with an orange background) and the four Hungarian singletons are shown as red branches. Counties of origin of the Hungarian samples are indicated on the right side of the figure and are colour-coded. Dotted vertical lines indicate the first day of each month. The start and end dates of the two waves are indicated with solid vertical lines. Samples carrying the R385K mutation are marked with a blue dot. The blue triangle marks the MRCA of the clade 2A carrying the R385K mutation in the nucleocapsid gene.

Finally, we analysed the geographic distribution of the large transmission lineage identified in the second wave (i.e. clade 2A in Fig. 3A). Consistent with its extensive community transmission, this lineage was found to display an unusually wide geographic spread across the country as demonstrated by its detection in sixteen out of nineteen counties in Hungary (including Budapest) (Fig. 4; Supplementary Table ST4). This is in contrast to other transmission lineages that spanned between 1 and 5 counties only.

In sum, the first two waves of the epidemic markedly differed in their viral transmission patterns. While community spread was largely absent in the first wave, the B.1.160 variant led to extensive community spread that was responsible for the majority of cases in the second wave.

Cryptic community transmission in the summer of 2020

We next investigated the timing of viral introductions by inferring the time to the most recent common ancestor (TMRCA) of each Hungarian transmission lineage (Fig. 3C; Supplementary Tables ST4 and ST6M). Note that due to incomplete viral sampling, TMRCA is not necessarily the time when the transmission lineage was introduced but rather represents the date of the first inferred transmission event of a lineage (du Plessis et al. 2021). The first reported case of COVID-19 was detected on 3 March 2020 in Hungary, but it was unclear whether earlier introductions had led to cryptic transmission in the community before this date. Our analysis revealed that the earliest lineages were most likely introduced in mid-February 2020 (Fig. 3C; Supplementary Tables ST4 and ST6; Supplementary Fig. S2), indicating no prolonged cryptic transmission in the first wave. Together with the high frequency of singletons, this finding suggests that public health interventions were introduced before widespread community transmission could have occurred in the first wave. In contrast, the large B.1.160 transmission lineage of the second wave was established around 17 June 2020, well before case numbers in the second wave soared in September 2020. This pattern indicates cryptic community transmission of the B.1.160 lineage during a 2-month-long period, as official case numbers were extremely low until the second half of August (see Fig. 3C).

An alternative scenario to the prolonged cryptic transmission of the virus is the possibility of a large number of repeated cross-border introductions of the B.1.160 variant at the end of summer. There are two circumstances that would make repeated introductions a plausible alternative. First, not only domestic public health interventions were substantially relaxed during the summer, but also summer travels were resumed throughout Europe in general (Hodcroft et al. 2021). Second, the B.1.160 variant was among the most widespread lineages in Europe in the fall of 2020 (Hodcroft et al. 2021). Therefore, to test whether cryptic transmission or repeated introduction governed transmission patterns of B.1.160 in Hungary, we examined marker mutations that are unique to the large transmission lineage.

In the large Hungarian transmission lineage, 98.2 per cent of the B.1.160 genomes contain the R385K mutation in the nucleocapsid protein. Remarkably, this mutation is completely absent in the sampled Hungarian B.1.160 genomes outside of the large transmission lineage. Specifically, beyond the large transmission lineage, we have identified four singletons and one small transmission lineage of two sequences belonging to the B.1.160 Pangolin lineage, and none of them contain the R385K mutation (Fig. 4; Supplementary Tables ST4 and ST6). Next, we checked the presence of the R385K mutation in all available B.1.160 samples worldwide. The B.1.160 variant harbouring the R385K mutation was present in many European countries in general, including four neighbouring countries of Hungary (Austria, Croatia, Slovakia, and Slovenia). However, its frequency was substantially lower in these countries than in Hungary (Supplementary Table ST8). Even in countries where the B.1.160 lineage was dominant, such as France and Belgium (Fig. 2C; Supplementary Table ST7), the R385K mutation was present only in a minority of sequenced B.1.160 samples (Supplementary Table ST8). As a consequence, if the high prevalence of the B.1.160 lineage in Hungary was driven by repeated imports, it would have been unlikely to result in the dominance of the R385K variant. Taken together, the presence of the R385K mutation, along with the results of the Bayesian phylogenetic analysis (Fig. 4), indicates that the large B.1.160 transmission lineage is likely attributable to a single early introduction event (Fig. 3C).

All the above analyses rely on a phylogenetic analysis that involves only forty-eight non-Hungarian sequences from the B.1.160 lineage, potentially underestimating the number of importations into Hungary. To investigate whether our conclusions hold when including a much larger sample of international B.1.160 sequences, we performed a complementary analysis. Specifically, we built a maximum likelihood phylogenetic tree of 172 Hungarian and 1,993 representative international B.1.160 sequences that capture well the global diversity of this Pangolin lineage. Then, we used a likelihood-based ancestral state reconstruction method to infer distinct introduction events into Hungary (Methods, see also Michaelsen et al. 2022). This phylogeographic analysis infers two distinct introductions into Hungary, giving rise to two separate clades on the tree with one of them containing the majority (57 per cent) of the Hungarian B.1.160 sequences (Supplementary Fig. S3). Both clades contain numerous sequences from other countries as well, including the UK, Germany, Austria, and Slovenia, indicating repeated migration events from Hungary into these regions (Supplementary Fig. S3). Importantly, both Hungarian and non-Hungarian genomes in these two clades carry almost exclusively the R385K mutation, while this mutation is extremely rare outside the two clades (Supplementary Fig. S3). Collectively, these patterns could be consistent with two alternative scenarios. First, the R385K mutation might have arisen on two independent occasions and specifically in those ancestors that established the two Hungarian B.1.160 clades. Note that this scenario assumes the repeated coincidence of importation and mutation events. Second, the B.1.160 was successfully established in Hungary on a single occasion only, but the phylogenetic analysis does not have sufficient power to resolve this event due to the low number of mutations that distinguish the sequences (Morel et al. 2021). We consider the latter scenario more plausible as it does not assume the repeated coincidence of rare events and is also consistent with the Bayesian phylogenetic analysis.

In conclusion, the totality of evidence supports the scenario that a single introduction dominated the spread of the B.1.160 variant in Hungary. Specifically, the early introduction of a single B.1.160 variant has likely established a massive, 2-month-long cryptic community transmission, eventually being responsible for over 75 per cent of the sequenced cases in Hungary during the second wave.

No evidence for increased transmissibility of B.1.160

The dominance of the B.1.160 variant during the second wave can be explained by two mutually non-exclusive scenarios. The B.1.160 lineage might have become dominant due to local epidemiological factors. Specifically, a marked shift in variant frequencies is plausible in low-incidence settings where a large fraction of cases may emerge from a single introduction and subsequent superspreading events (Hodcroft et al. 2021). Alternatively, the B.1.160 lineage might have displayed an increased intrinsic transmission advantage over other D614G lineages. Indeed, earlier studies have suggested that the B.1.160 variant may have higher transmissibility for two reasons. First, the mutation​​ S477N in the spike protein results in stronger Ace2 receptor binding, and mutations with such an effect have been shown to mediate increased transmissibility (Barton et al. 2021). Second, the B.1.160 variant quickly became dominant in France during the summer of 2020 (Fournier et al. 2021).

To test whether the rise in the frequency of B.1.160 is attributable to its increased transmissibility, we analysed the dynamics of epidemic growth during the period when the B.1.160 variant became dominant (i.e. in September and October 2020). Specifically, genomic data indicate that the B.1.160 variant increased in frequency from 40 per cent to 95 per cent between 1 September and 28 October (Fig. 5A). Assuming that this rise in the frequency of B.1.160 is solely explained by its transmission advantage over other lineages, we inferred a net growth rate advantage of 0.0773 using a transmission dynamics model (Althaus et al. 2021) (Fig. 5A; see Supplementary Notes for details). Note that this growth advantage corresponds to an estimated ∼44 per cent increase in the basic reproduction number (R₀) (Supplementary Notes). Next, we examined whether the observed epidemic growth is better explained by a model with a constant growth rate (i.e. considering that B.1.160 has no transmission advantage) or by another model in which two lineages with different growth rates compete (i.e. considering that B.1.160 has a net growth rate advantage of 0.0773). Importantly, the second model uniquely predicts an increase in the epidemic growth rate as B.1.160 becomes dominant in the population (Fig. 5B). To estimate epidemic growth, we used reported daily death counts rather than lab-confirmed positive cases, as the latter was presumably saturated at that time due to limited testing capacities in Hungary. Fitting the two models to mortality data revealed that the model with a constant growth rate agrees well with daily death counts (Fig. 5B; Supplementary Notes). In contrast, assuming a transmission advantage yields a poorer fit as it overestimates the number of fatalities in late September 2020 (Fig. 5B). Furthermore, the assumed transmission advantage implies a marked shift in the effective reproduction number (R_t) during the investigated period (from 1.135 to 1.365; see Supplementary Notes), which is inconsistent both with other epidemiological observations (e.g. hospitalisation data; Oroszi et al. 2021) and with the lack of changes in public health measures (Figs 1A, 3C).

Figure 5.

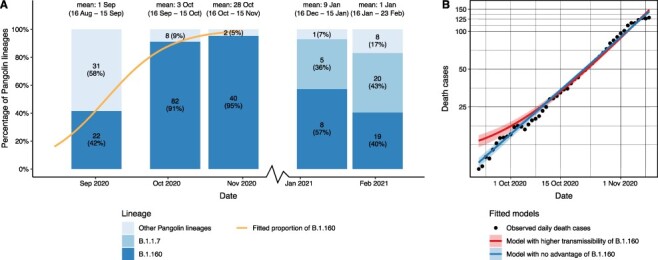
No evidence for increased transmissibility of the B.1.160 variant. (A) The relative prevalence of the B.1.160, the B.1.1.7 (alpha), and all other Pangolin lineages in Hungary between 16 August and 23 February 2021. The genome sequences were grouped for each month from Day 16 to Day 15 of the next month (dates are shown above the bars), using available genome sequences for each month. Note that only a single sequence was available for December 2020, hence it was omitted from the plot. Each barplot was positioned along the x-axis at the mean of the corresponding sample collection dates. Numbers in bars indicate the actual numbers and percentages of sequenced genomes belonging to a particular Pangolin lineage. The orange line represents a logistic growth model fitted on the proportion of the B.1.160 lineage between 16 August 2020 and 15 November 2020—when the lineage B.1.160 became dominant in the country. The model assumes competition between B.1.160 and other circulating lineages (see Supplementary Notes). A net growth rate difference of 0.0773 provides the best fit to the observed proportion of B.1.160. (B) Two models were fitted to observed daily death cases (black dots): an exponential model where the B.1.160 lineage has no selective advantage, and a competition model where the B.1.160 Pangolin lineage has a net growth rate advantage of 0.0773 over other lineages.

Finally, we reasoned that the rapid spread of the alpha variant of concern (B.1.1.7 lineage), which caused the third wave in Hungary in February 2021, also refutes a large transmission advantage of the B.1.160 variant. Specifically, the alpha variant is estimated to be 40–60 per cent more transmissible than prior lineages and, therefore, has the potential to spread even in the presence of public health interventions that suppress other circulating lineages (Davies et al. 2021; Volz et al. 2021). To estimate the time of introduction of the alpha variant to Hungary, we analysed twenty-five Hungarian sequences assigned to the B.1.1.7 Pangolin lineage that were sampled between 6 January and 22 February 2021. Phylogenetic analysis revealed at least three independent introductions of the alpha variant that led to onward transmission (Supplementary Tables ST4 and ST6). We estimate that the earliest introduction likely occurred in mid-December 2020, i.e. at the same time when specific interventions successfully suppressed the spread of the B.1.160 variant which was dominant at that time. Collectively, these observations suggest that the alpha variant had substantially higher transmissibility over the B.1.160 variant, leading to immediate community transmission that rendered the alpha variant dominant despite public health measures in place.

Overall, these results indicate that the B.1.160 variant did not have a substantial transmission advantage over the then-circulating D614G variants; thus, it likely became dominant due to chance events under favourable epidemiological conditions.

Discussion

Viral genome sequencing has emerged as a crucial tool for the retrospective reconstruction of past waves of the pandemic (Moreno et al. 2020; du Plessis et al. 2021; Washington et al. 2021; Wilkinson et al. 2021). These data provide insights into the characteristics of viral transmission, which is of paramount importance to prepare for future pandemic situations (Alm et al. 2020). The present genomic surveillance analysis compares viral transmission patterns across the first two waves of the SARS-CoV-2 epidemic in Hungary. Comparing these waves is especially instructive because they had markedly different outcomes. While the first wave in the spring of 2020 was successfully suppressed in its early phase, the second wave (fall and winter of 2020) was much more intense. Here, we have reconstructed the viral dynamics underlying such a striking difference.

The first wave is characterised by multiple viral introductions that did not result in widespread community spread due to a timely national lockdown. We estimate that the first successful introductions occurred in mid-February 2020 (Fig. 3A, 3C; Supplementary Fig. S2; Supplementary Table ST4), implying no or negligible cryptic phase in the first wave. Remarkably, this estimate coincides with that derived from a global metapopulation epidemic model (i.e. 16 February 2020; Davis et al. 2021), which did not leverage genomic information. In sharp contrast, the majority of the cases in the second wave in the fall of 2020 can be linked to a single and unexpectedly early introduction of the B.1.160 variant, at the beginning of the summer. Due to relaxed domestic public health interventions, this introduction was followed by extensive community transmission. As a consequence, the time elapsed between the introduction of the virus and the imposition of strict public health measures largely differed between the two waves. Specifically, while this period merely spanned 3 weeks during the first wave, it was approximately 4 months during the second wave, partly due to a 2-month period of cryptic transmission. Indeed, consistent with these findings, prior studies showed that the timing of lockdown strongly impacts viral transmission (Moreno et al. 2020; Ragonnet-Cronin et al. 2021) and is a major determinant of COVID-19 mortality across countries (Dye et al. 2020; Islam et al. 2020; Loewenthal et al. 2020). We note that seasonal factors also likely contributed to the large case numbers in the second wave, which occurred during the autumn and winter periods (Neher et al. 2020).

The B.1.160 variant, as well as another one called B.1.177 (20E.EU1), accounted for most sequenced samples in the autumn of 2020 in Europe (Hodcroft et al. 2021). In principle, the high prevalence of these lineages might have been explained by their intrinsic advantages over prior variants (Fournier et al. 2021). However, a study has found no evidence for a transmission advantage of B.1.177 (Hodcroft et al. 2021). Here, we have coupled genome analysis with epidemic modelling to demonstrate that the B.1.160 variant is also unlikely to be more transmissible than prior variants (Fig. 5A, 5B). Then what could explain the high prevalence of these lineages? Hodcroft et al. explained the extreme rise of the B.1.177 variant in Spain (80 per cent prevalence by September 2020 with a gradual rise from early June) by chance events under favourable epidemiological conditions (Hodcroft et al. 2021). At the beginning of the summer of 2020, when lockdowns of the first wave were released, SARS-CoV-2 had low incidences in most European countries (Ritchie et al. 2020). It has been suggested that in such low-incidence settings, stochastic superspreading events or circulation in a subpopulation with higher contact rates may contribute to a large fraction of cases, making large shifts in variant frequencies without a significant transmission advantage (i.e. founder effect; Hodcroft et al. 2021; Lauring and Hodcroft 2021). Our findings that B.1.160 was introduced shortly after the release of restrictions and was spreading cryptically for a prolonged period, possibly due to transmission in specific age groups or areas that are not well surveyed, are consistent with this scenario. More broadly, our study indicates that early introductions followed by cryptic community transmission in the presence of relaxed domestic public health interventions can have a marked impact on the genetic diversity of circulating lineages even without a transmission advantage.

In sum, tracking viral transmission dynamics within and between communities is key to design optimal mitigation strategies and effective public health interventions aiming to prevent the emergence and spread of future pandemics. National policies should endorse thorough genomic surveillance to quickly identify the emergence or introduction of potentially dangerous new variants and help rapid decision-making.

Materials and methods

Sequencing data

Nucleic acid samples were extracted from oro-pharyngeal swab samples using a Direct-zol™ RNA MiniPrep Plus extraction kit (Zymo Research, Irvine, CA, USA). Reverse transcription and multiplex polymerase chain reaction (PCR) were performed on the basis of information provided by the Artic Network initiative (Quick, 2020), using the V3 primer set. Both the concentration and the quality of the polymerase chain reaction (PCR) products were measured and checked using the Agilent 4200 TapeStation System (Agilent Technologies, Santa Clara, CA, USA) and a ThermoFisher Scientific Qubit 4 Fluorometer (Thermo Fisher Scientific, Waltham, MA, USA). The sequencing libraries were prepared using ninety-eight overlapping amplicons covering the whole viral genome. The libraries were then quantitatively checked, barcoded, and sequenced using the Oxford Nanopore MinION Flow Cells (R9.4.1) (Oxford Nanopore Technologies, Littlemore, Oxford, UK).

During primary data analysis, we used RAMPART (Mapleson et al. 2015) to track the sequencing process in ‘real-time’ in order to acquire instant information regarding the quality of samples and the coverage of the amplicons. Sequencing reads of samples with sufficient amplicon coverage were mapped, and consensus sequences were generated by the bioinformatics pipeline included in the Artic Network protocol. The minimum supported consensus calling was twenty reads per site. The mean genome coverage values and the coverage of site 385 in the nucleocapsid gene are listed in Supplementary Table ST9.

SARS-CoV-2 genome sequences and their metadata were downloaded from GISAID (Shu and McCauley 2017) on 5 April 2021, containing 984,282 samples from all over the world and 434 samples from Hungary. Except for the analysis of the N R385K mutation, the variant surveillance metadata for that part were downloaded from GISAID on 9 December 2021. We note that no additional Hungarian samples have been uploaded to GISAID since 2 April 2021 (as of 26 January 2022). We removed samples from non-human specimens, as well as those with incomplete or invalid sampling dates (before December 2019 and after 5 April 2021), samples with missing Pangolin lineage classification, sequences shorter than 28 KB or with more than 1,000 ambiguities (De Maio et al. 2021), and duplicated sequences. We also excluded sequences from CMBG FN Brno, since these contained an unusually large amount of single nucleotide polymorphysms (SNPs). After these steps, 352 Hungarian and 870,787 non-Hungarian samples remained.

Analysis of viral diversity

We used the Pangolin lineage assignments (Rambaut et al. 2020) provided in the GISAID metadata table (Supplementary Table ST3) to calculate Shannon diversity indices and to perform Hutcheson t-tests. The Shannon diversity indices, Hutcheson t-tests, and bias-corrected and accelerated bootstrap confidence intervals (Davison and Hinkley 1997) for the Shannon diversity indices were calculated using the vegan v2.5-7 (Oksanen et al. 2020), the ecolTest v0.0.1 (Salinas and Ramirez-Delgado 2021), and the boot v1.3-28 (Canty and Ripley 2021) R libraries, respectively. The number of bootstrap replicates was 10,000.

Bayesian phylogenetic analysis of all Hungarian sequences

Next, we used these 352 Hungarian sequences and a subsample of non-Hungarian sequences to calculate a time-scaled phylogenetic tree. Subsampling was performed as follows. First, neighbouring sequences for the Hungarian samples were identified using vsearch v2.17.0 (Rognes et al. 2016) with a minimum of 95 per cent identity. Duplicate sequences were dropped. Then we added randomly selected samples, resulting in at least one sample per each European country per every 2 weeks, and one sample per each non-European region per every 2 weeks. Overall, this procedure yielded 1,311 non-Hungarian sequences representing the global diversity of SARS-CoV-2.

We aligned the sequences using MAFFT v7.475 (Nakamura et al. 2018). To filter out exceedingly divergent sequences, likely representing low-quality sequences or poor alignment, we built a phylogenetic tree using RapidNJ v2.3.2 (Simonsen et al. 2008) and applied TreeShrink v1.3.9 (Mai and Mirarab 2018). Then the remaining 352 Hungarian and 1,315 non-Hungarian sequences were realigned with MAFFT. Certain sequence sites were masked as suggested by De Maio et al. (2021) using a vcf file they provided. Finally, we removed sites with at least N-2 gaps or ambiguous nucleotides, where N is the number of genomes.

We inferred a time-scaled coalescent tree with BEAST v1.10.5 (Suchard et al. 2018), using the GTR+Γ4 nucleotide substitution model, uncorrelated relaxed clock with lognormal distribution, exponential population growth tree prior to parametrisation for growth rate and exponential population size (Nie et al. 2020; Pipes et al. 2021). Four independent chains were run for 100 million states and parameters, and trees were sampled at every 10,000 states. All of the other BEAST parameters not mentioned here were set for the default values. Based on the log files that we inspected with Tracer v1.7.2 (Rambaut et al. 2018), burnin was set to 80 million (see Supplementary Fig. 4). Chains were combined using LogCombiner v.1.10.5. The maximum clade credibility tree was inferred from the timed Bayesian posterior tree distribution using TreeAnnotator v.1.10.5 and visualised with ggtree v3.1.4 (Yu 2020) R library.

Descending clades that likely represent Hungarian transmission lineages (i.e. Hungarian clades) were defined by the following criteria: (1) the clade should contain at least two Hungarian samples, (2) the clade should have a posterior probability for the MRCA node higher than 0.7, and (3) the percentage of Hungarian sequences should be at least 75 per cent within the clade. In addition to the clades defined by the above criteria, we also included clade 2A based on the unique presence of the N R385K mutation despite having a slightly lower (0.63) posterior probability. Note that out of the twenty-five Hungarian clades, twenty-one have a posterior probability above 0.97.

The most recent common ancestor (MRCA) of each clade was identified using the phylobase v0.8.10 (Hackathon et al. 2020) R library.

Phylogenetic analysis of the B.1.160 lineage

Here, we estimated the number of independent introductions of Pangolin lineage B.1.160 into Hungary using many more global B.1.160 sequences and an orthogonal methodology than shown in Fig. 3. We downloaded all SARS-CoV-2 genomes and variant surveillance metadata belonging to the Pangolin lineage B.1.160 (and its sublineages) from GISAID on 24 March 2022. After removing samples from non-human specimens, as well as those with incomplete or invalid sampling dates, samples with missing Pangolin lineage classification, sequences shorter than 28 KB or with more than 1,000 ambiguities (De Maio et al. 2021), and duplicated sequences, 26,653 genomes remained. Next, we selected a subsample of ∼2,000 sequences that represent the phylogenetic diversity of the B.1.160 lineage. Specifically, we calculated a distance matrix using the RapidNJ v2.3.2 (Simonsen et al. 2008) and applied the partitioning around medoids (pam, cluster v2.1.3 R library; Maechler et al. 2022) algorithm to group the genomes into 2,000 distinct clusters to retain the maximum sequence diversity. Then, we kept all samples from Hungary and a single randomly chosen sample from each cluster, yielding 172 Hungarian and 1,993 non-Hungarian genome sequences for further analyses. Note that the 172 Hungarian sequences fall into thirty-eight sequence clusters. After sequence alignment with MAFFT v7.503 (Nakamura et al. 2018), we removed all sites containing Ns or gaps only and calculated a maximum likelihood phylogenetic tree using the iqtree v2.2.1-beta software (Minh et al. 2020) with the GTR+Γ4 nucleotide substitution model. The resulting phylogenetic tree was rooted using the midpoint rooting method of the phytools v1.0-3 (Revell 2012) R library. Next, we performed ancestral state reconstruction on the tree to infer likely viral introductions into Hungary. Specifically, the tree, the sampling dates of the genomes, and the geographical origin of the samples (Hungarian or not) served as inputs for the ancestral state reconstruction calculated with maximum likelihood and MPPA algorithms using the PastML v1.9.34 software (Ishikawa et al. 2019) with F81 model.

Epidemic analysis of the potential transmission advantage of the B.1.160 variant

To test the hypothesis that the B.1.160 variant has an intrinsic competitive advantage by enhanced transmissibility, we used a transmission dynamics model within the susceptible-infected-removed framework (Althaus et al. 2021). In brief, we used variant frequency data from available genome sequences to infer a net growth rate advantage of 0.0773 by assuming that the observed rise in the frequency of the B.1.160 variant is solely explained by its transmission advantage (see Fig. 5A). Next, we fitted two models to the observed epidemic growth based on daily death counts as follows: one model with a constant growth rate (i.e. considering that B.1.160 has no transmission advantage) and a second one in which the B.1.160 lineage has the above-inferred growth advantage over other variants (see Fig. 5B). The full analysis and its methodological details are presented as a Supplementary Note.

Supplementary data

Supplementary data are available at Virus Evolution online.

Funding

This work was supported by the National Laboratory of Biotechnology grant NKFIH-871-3/2020 (B.K.), the National Laboratory for Health Security, RRF-2.3.1-21-2022-00006 (G.R. and B.P.), the National Laboratory of Virology, RRF-2.3.1-21-2022-00010 (G.K., F.J., G.E.T, B.Z., B.S., and Z.L.), the European Union’s Horizon 2020 research and innova-tion programme under grant agreement (grant no. 739593 to B.P. and B.K.), the National Research, Development and Innovation Office, Hungary (NKFIH) grant PD 131839 (E.A.), NKFIH ‘Frontline’ KKP 129814 (B.P.) and KKP 129877 (G.R.), János Bolyai Research Fellowship from the Hungarian Academy of Sciences BO/352/20 (B.K.), and the New National Excellence Program of the Ministry of Human Capacities UNKP-20-5-SZTE-654 and UNKP-21-5-SZTE-579 (B.K.).

Conflict of interest:

None declared.

Author contributions

G.K., G.E.T., B.Z., B.S., Zs.L., and F.J., collected and sequenced samples, processed sequencing data. E.A., B.M.V., B.P. and B.K. designed data analyses. E.A. and B.M.V. carried out all bioinformatic analyses. B.P. and B.K. wrote the manuscript with input from all co-authors.