Artificial Intelligence in Radiation Therapy

Abstract

Artificial intelligence (AI) has great potential to transform the clinical workflow of radiotherapy. Since the introduction of deep neural networks, many AI-based methods have been proposed to address challenges in different aspects of radiotherapy. Commercial vendors have started to release AI-based tools that can be readily integrated to the established clinical workflow. To show the recent progress in AI-aided radiotherapy, we have reviewed AI-based studies in five major aspects of radiotherapy including image reconstruction, image registration, image segmentation, image synthesis, and automatic treatment planning. In each section, we summarized and categorized the recently published methods, followed by a discussion of the challenges, concerns, and future development. Given the rapid development of AI-aided radiotherapy, the efficiency and effectiveness of radiotherapy in the future could be substantially improved through intelligent automation of various aspects of radiotherapy.

I. Introduction

ARTIFICIAL intelligence (AI) is a data-driven agent that is designed to imitate human intelligence. The concept of AI is believed to be originated from the idea of robots, which can help human perform laborious and time-consuming tasks. In recent years, the advancements of both computer hardware and software have enabled the development of more and more sophisticated AI agents that can excel certain complex tasks without human input. Meanwhile, the growth and sharing of data has powered the continuous evolvement of AI by machine learning (ML) and deep learning (DL).

ML, a subset of AI, enables machines to achieve artificial intelligence through algorithms and statistical techniques trained with data where the training process informs decisions made by the machine learning framework, thus improving the end result as experience is gained[14]. Supervised ML methods for the automatic segmentation of images involves training and tuning a predictive model, often integrating prior knowledge about an image via training samples (i.e., other similarly annotated images to inform the current segmentation task). ML employs statistical tools to explore and analyze previously labeled data with image representations being built from pre-specified filters tuned to a specific segmentation task. Although ML techniques are more efficient with image samples and have a less complicated structure, they are often not as accurate when compared to DL techniques [23]. DL is a subset of ML that was originally designed to mimic the learning style of the human brain using neurons. Unlike ML where the “useful” features for the segmentation process must be decided by the user, with DL, the “useful” features are decided by the network without human intervention.

Radiation oncology is a type of cancer treatment that requires multidisciplinary expertise including medicine, biology, physics, and engineering. The workflow of typical radiotherapy consists of medical imaging, diagnosis, prescription, CT simulation, target registration/contouring, treatment planning, treatment quality assurance and treatment delivery. Owing to the technological advances in the past few decades, the workflow of radiotherapy has become increasingly complex, resulting in heavy reliance on human-machine interactions. Each step in the clinical workflow is highly specialized and standardized with its own technical challenges. Meanwhile, the requirement of manual input from a diverse team of healthcare professionals including a radiation oncologist, medical physicist, medical dosimetrist, and radiation therapist has resulted in a sub-optimal treatment process that prevents patients’ wider access to the scarce treatment infrastructures. The wide adoption of image guided radiotherapy has created a massive amount of imaging data that needs to be analyzed in a short period of time. However, humans are limited in reviewing and analyzing large amounts of data due to time constraints. Machines, on the other hand, can be trained to share many repetitive workloads with humans and therefore boosting the capacity of quality healthcare. Since the introduction of deep neural networks, many AI-based methods have been proposed to address challenges in different aspects of radiotherapy. Given the rapid development of AI-aided radiotherapy, the efficiency and effectiveness of radiotherapy in the future could be substantially improved through intelligent automation in various aspects of radiotherapy.

Several articles have been published regarding artificial intelligence in radiation oncology[30-32]. Huynh et al. provided a high level general description of AI methods, reviewed its impact on each step of the radiation therapy workflow and discussed how AI might change the roles of radiotherapy medical professionals[32]. Siddique et al. provided a review of AI in radiotherapy, including diagnostic processes, medical imaging, treatment planning, patient simulation, and quality assurance[31]. Vandewinckele et al. published an overview of AI based applications in radiotherapy, focusing on the implementation and quality assurance of AI models[30]. In this study, to show the recent progress in AI-aided radiotherapy, we have reviewed AI-based studies in five major aspects of radiotherapy including image reconstruction, image registration, image segmentation, image synthesis, and automatic treatment planning. In each section, we summarized and categorized the recently published methods, followed by a discussion of the challenges, concerns and future development. Specifically,H. Zhang contributed to the image reconstruction section; Y. Fu, T. Liu and X. Yang contributed to the image registration section; E. D. Morris and C. K. Glide-Hurst contributed to the image segmentation section; S. Pai, A. Traverso, L. Wee and I. Hadzic contributed to the image synthesis section; P. Lønne and C. Shen contributed to the automatic treatment planning section.

II. Image Reconstruction

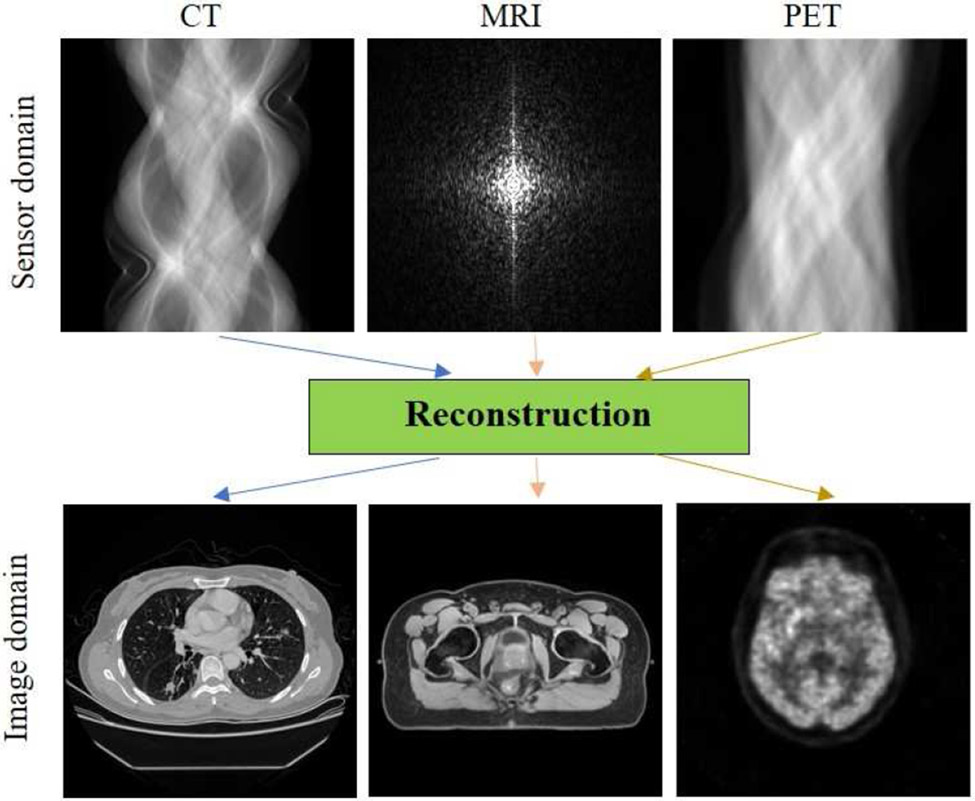
Tomographic imaging plays an important role in external-beam radiation therapy for simulation and treatment planning, pre-treatment and intrafractional image guidance, as well as follow-up care. Before treatment, the patient usually undergoes a computed tomography (CT) simulation to acquire images of the area of body to be treated with radiation. The acquired CT images are used to delineate the tumors and surrounding critical structures, and then to design an optimal treatment plan for the patient. For tumors around the diaphragm, such as those in the liver and lower lung lobe, 4D CT scans may also be performed to capture the motion of tumors in respiration. Due to the advantage of superior soft tissue contrast, magnetic resonance imaging (MRI) scans are also prescribed for some patients with brain tumors, paraspinal tumors, head and neck cancer, prostate cancer, and extremity sarcoma. The MRI scans are fused to simulation CT images to facilitate tumor delineation and organs at risk (OAR) contouring, or in MRI-only simulation to synthesize CT images for treatment planning and dose calculation[43]. Different from anatomical imaging such as CT and MRI, positron emission tomography (PET) provides information on tumor metabolism and is used for visualization of tumor extent and delineation of volume in need of dose-escalation, e.g., in head and neck cancers[45]. In addition, cone-beam CT (CBCT) is equipped on most C-arm linear accelerators (LINACs) and widely used in daily procedures for verifying the position of the patient and treatment target. Gated CBCT or 4D-CBCT is sometimes utilized for positioning patient with moving tumors, such as in lung stereotactic ablative radiotherapy (SABR). Furthermore, CT, megavoltage CT (MV-CT), MV-CBCT are also integrated in some radiotherapy machines for image guidance. MRI-LINAC systems have also been developed in the past decade[48], in which MRI helps to improve patient setup and target localization, and enables interfraction and intrafraction radiotherapy adaptation[50]. Very recently, PET-guided radiation therapy is also ready for clinical adoption to treat advanced-stage and metastatic cancers[53]. Finally, after completing their radiation treatment course, patients may have another scan (CT, MRI, or PET) before a follow-up appointment with radiation oncologist.

In the clinic, tomographic images are displayed on the console soon after a patient scan. Thus, making it easy to be unaware of the crucial reconstruction step which is performed in the background by dedicated reconstruction computers. In fact, reconstruction is at the heart of tomographic imaging modalities, because many clinical tasks in the radiation therapy workflow are highly dependent on the reconstruction quality, including target delineation, OARs segmentation, image registration or fusion, image synthesis, treatment planning, dose calculation, patient positioning, image guidance, and radiation therapy response assessment. Poor reconstruction quality would inevitably jeopardize the accuracy of the clinical tasks mentioned above and eventually the outcome for cancer patients. Thus, tomographic image reconstruction has always been an active area of research, with the aim of reducing radiation exposure and/or scan time, suppressing noise and artifacts, and improving image quality.

After data acquisition, the detector measurements are usually preprocessed/calibrated by vendors for various degrading factors. Then, the sensor domain measurements $y\in {\mathbb{R}}^{I\times 1}$ and the desired image $x\in {\mathbb{R}}^{J\times 1}$ can be expressed as[55]:

$$y=\mathit{A}x\oplus \epsilon$$ (1)

where $\mathit{A}\in {\mathbb{R}}^{I\times J}$ is the system matrix for CT and PET and encoding matrix for MRI, I is the number of sensor measurements, J is the number of image voxels, ε is the noise intrinsic to the data acquisition, and the operator ⊕ denotes the interaction between signal and noise. The operator ⊕ becomes + when additive Gaussian noise is assumed for CT and MRI measurements, and becomes a nonlinear operator when Poisson noise is assumed for PET measurements. Essentially, image reconstruction is an inverse problem where we reconstruct the unknow image x from the measurements y.

Various image reconstruction methods have been proposed in the past few decades. Analytical reconstruction methods, such as filtered back-projection (FBP) for CT, Feldkamp-Davis-Kress (FDK) for CBCT, and inverse fast Fourier transform for MRI, are based on the mathematical inverse of the forward model. Because of their high efficiency and stability, they are still employed by most commercial scanners. However, the reconstructed images may suffer from excessive noise and streak artifacts when the sensor measurements are noisy and undersampled. Iterative reconstruction methods[56-61], including algebraic reconstruction technique, statistical image reconstruction, compressed sensing, and prior-image-based reconstruction, are based on sophisticated system modeling of data acquisition and prior knowledge. They have shown advantages of reducing radiation dose or data acquisition time and improving image quality over analytical methods. One example of these iterative methods is the penalized weighted least square (PWLS) reconstruction which is widely used for CT/CBCT, MRI and PET:

$$\widehat{x}=argmin\Vert y-\mathit{A}x{\Vert }_W^2+\beta R(x)$$ (2)

where W is a weighting matrix accounting for reliability of each sensor measurement, R(x) is a regularization term incorporating prior knowledge or expectations of image characteristics, and β > 0 is a scalar control parameter to balance data fidelity and regularization. Commonly used regularizations are based on the Markov random field (MRF) or total variation (TV), while a comprehensive review of the regularization strategies can be found in[58].

Inspired by the successes of AI in many other fields, researchers have investigated to leverage AI, especially DL for tomographic image reconstruction[62]. Numerous papers have been published on this topic, and image reconstruction has become a new frontier of DL[63]. It is noted that many DL-based reconstruction methods can be shared by CT, MRI and PET, thus we focus on reviewing them for CT and CBCT since they are most widely used in radiation therapy. Interested readers can refer to these review articles [64-68] on DL for PET and MRI reconstruction.

Patients for radiation therapy receive multiple CT and CBCT scans, and the accumulated imaging dose could be significant. Considering the harmful effects of X-ray radiation including secondary malignancies, low-dose imaging with satisfactory image quality for clinical tasks are desirable. Aside from hardware improvements, two other strategies have been investigated to achieve low-dose imaging for CT and CBCT, reducing the X-ray tube current and exposure time (low-flux acquisition) or the angular sampling per rotation (sparse-view acquisition)[58]. However, these strategies would increase noise and streak artifacts in the FBP or FDK reconstructed images. 4D-CBCT has the potential to reduce motion artifacts and improve patient setup and treatment accuracy, but the scan takes 2-4 minutes to acquire enough projections at each respiratory phase to achieve acceptable image quality. The long scan time leads to increased patient discomfort, intraimaging patient motion, and additional imaging radiation dose. An accelerated scan is desirable in the clinic but the FDK reconstructed images from the sparse-view acquisition are also degraded with severe streak artifacts[69]. While iterative reconstruction can tackle these challenges to some extent, the reconstruction time might be too long. Therefore, many DL-based reconstruction methods have been developed to further improve image quality and/or substantially reduce reconstruction time, which can be grouped into the following five categories.

A. Image Domain Methods

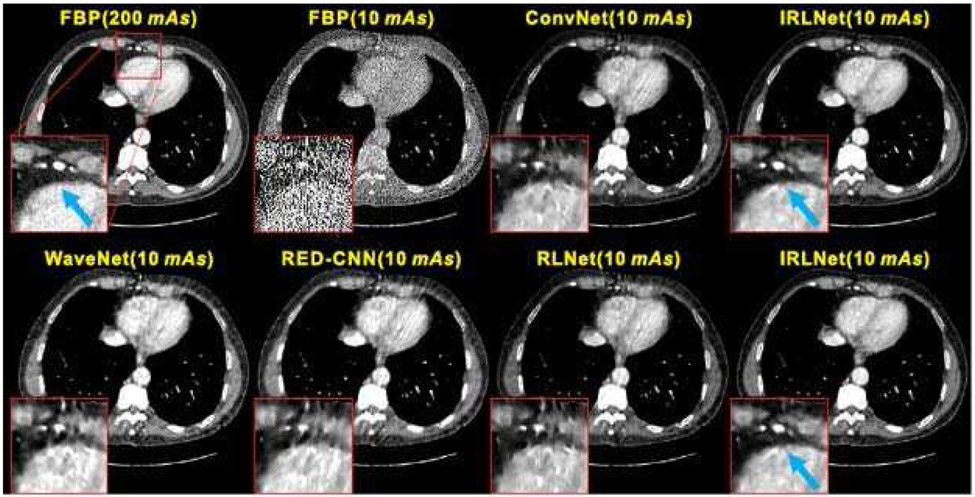
One simple approach to improve low-dose CT image quality is post-reconstruction denoising, and researchers have applied many different filters to the FBP reconstructed low-dose CT images to suppress noise and streak artifacts. Similarly, the FBP reconstructed low-dose images can be fed into a DL neural network to learn a mapping between the low-dose image and its high-quality counterpart. For example, Kang et al. [70] applied a deep convolutional neural network (CNN) to the wavelet transform coefficients of low-dose CT images, which can effectively suppress noise in the wavelet domain. Chen et al. [71] proposed using overlapped patches from low-dose and corresponding high-quality CT images to boost the number of samples, and then employed a residual encoder–decoder CNN (RED-CNN) to improve low-dose image quality. Yang et al. [72] explored a generative adversarial network (GAN) based denoising method with Wasserstein distance and perceptual similarity to improve the GAN performance. Wang et al. [73] argues that these image-to-image mapping approaches have some limitations for ultralow-dose CT images. They proposed an iterative residual-artifact learning CNN (called IRLnet) which estimates the high-frequency details within the noise and then removes them iteratively while the residual low-frequency details can be processed through the conventional network.

The streak artifacts in FBP reconstructed images from sparse-view acquisition are difficult to remove by conventional CNNs. Han and Ye [74] found that the existing U-Net architecture resulted in image blurring and false features for sparse-view CT reconstruction, and proposed a dual frame U-Net and tight frame U-Net to overcome limitations. Zhang et al. [75] investigated a method based on a combination of DenseNet and deconvolution for sparse-view CT, which employs the advantages of both and greatly increases the depth of the network to improve image quality. Alternatively, Jiang et al. [76] used TV-based iterative reconstruction to obtain sparse-view CBCT images (which are superior to FDK reconstructed images), and then fed them into a symmetric residual CNN to learn the mapping between TV-reconstructed images and ground truth. Then, for new sparse-view CBCT acquisitions, one can use the network to boost TV-reconstructed images.

It is noted above that DL methods are based on a supervised learning framework, which requires both the low-dose CT images and corresponding high-quality counterparts. However, these image pairs may not be available in many clinical scenarios. Wolterink et al. [77] explored a GAN consists of a generator CNN and a discriminator CNN to reduce image noise, which showed a generator CNN trained with only adversarial feedback can learn the appearance of high-quality images. Li et al. [78] investigated a cycle-consistent GAN (CycleGAN) based method which does not require low-dose and reference full-dose images from the same patient. In the near future, more unsupervised learning approaches which require no reference ground truth, or semi-supervised learning requiring limited reference data, may be explored for low-dose CT and CBCT.

B. Sensor Domain Methods

It is advantageous to remove noise in the CT sinogram or projection data to prevent its propagation into the reconstruction process, but the edges in sensor domain are usually not well defined as those in the image domain, resulting in edge blurring in the final reconstructed images[79]. Thus, DL-based denoising methods are rarely applied to the sensor domain directly. Instead, efforts [80-82] were dedicated to sparse-view CT reconstruction, which utilize DL to interpolate or synthesize unmeasured projection views. Then, the FBP method is used to reconstruct images with substantially reduced streaking artifacts. Additionally, Beaudry et al. [83] proposed a DL method to reconstruct high-quality 4D-CBCT images from sparse-view acquisitions. They estimated projection data for each respiratory bin by taking projections from adjacent bins and linear interpolation, and then trained a CNN model to predict full projection data which are reconstructed with the FDK method.

C. DL for FBP

DL methods can also be combined with the FBP reconstruction. In 2016, Wurfl et al. [84] demonstrated that FBP reconstruction can be mapped onto a deep neural network architecture, in which the projection filtering is reformed as a convolution layer and the back-projection is formed with a fully connected layer. They showed the advantage of learning projection-domain weights for the limited angle CT reconstruction problem. He et al. [85] further proposed an inverse Radon transform approximation framework which resembles the FBP reconstruction steps. They constructed a neural network with three dedicated components (a fully connected filtering layer, a sinusoidal back-projection layer, and a residual CNN) corresponding to projection filtering, back-projection, and postprocessing. They demonstrated that the approach outperforms TV-based iterative reconstruction for low-flux and sparse-view CT. Li et al. [86] also proposed an iCT-Net which consists of four major cascaded components that are also analogous to the FBP reconstruction. This approach can achieve accurate reconstructions under various data acquisition conditions such as sparse-view and truncated data.

D. DL for Iterative Reconstruction

DL is also applied to iterative reconstruction methods for different purposes including regularization design, parameter tuning, optimization algorithms, and reconstruction results improvement. Wu et al. [87] proposed regularizations trained by artificial neural network for PWLS reconstruction of low-dose CT, which can learn more complex image features and thus outperform the TV and dictionary learning regularizations. Chen et al. [88] learned a CNN-based regularization for PWLS reconstruction and found it can preserve both edges and regions with smooth intensity transition without staircase artifacts. Gao et al. [89] constructed a CNN texture prior from previous full-dose scan for PWLS reconstruction of current ultralow-dose CT images. One drawback of the conventional model based iterative reconstruction is manual tuning of the hyperparameter which controls tradeoff between data fidelity and regularization. Shen et al. [90] used deep reinforcement learning to train a system which can automatically adjust the parameter, and demonstrated that the parameter-tuning policy network is equivalent or superior to manual tuning. Chen et al. [91] proposed a Learned Experts’ Assessment-based Reconstruction Network (LEARN) for sparse-data CT that learns both regularization and parameters in the model. He et al. [92] also proposed a DL-based strategy for PWLS to simultaneously address regularization design and parameter selection in one optimization framework. DL can also be used to modify optimization algorithms for iterative reconstruction. Kelly et al. [93] incorporated DL within an iterative reconstruction framework, which utilizes a CNN as a quasi-projection operator within a least-squares minimization procedure for limited-view CT reconstruction. Gupta et al. [94] presented an iterative reconstruction method that replaces the projector in a projected gradient descent algorithm with a CNN, which is guaranteed to converge and under certain conditions converging to a local minimum for the non-convex inverse problem. They also showed improved reconstruction over TV or dictionary learning based reconstruction for sparse-view CT. Adler and Oktem [95] proposed learned Primal-Dual algorithm for CT iterative reconstruction which replaces the proximal operators with CNNs. They demonstrated this DL-based iterative reconstruction is superior to TV regularized reconstruction and DL-based denoising methods.

E. Domain Transformation Methods

Researchers have also leveraged DL to map sensor domain measurements to image domain reconstruction directly. For example, Zhu et al. [96] proposed an automated transform by manifold approximation (AUTOMAP) approach to achieve end-to-end image reconstruction. But the approach requires high memory for storing the fully connected layer and thus, limits this approach to small size image reconstruction. Fu and De Man [97] recursively decomposed the reconstruction problem into hierarchical sub problems and each can be solved by a neural network. Shen et al. [98] proposed a deep-learning model trained to map a single 2D projection to 3D CBCT images by using patient-specific prior information. They introduced a feature-space transformation between a single projection and 3D volumetric images within a representation- generation framework. Inspired by this work, Lei et al. [99] investigated a GAN-based approach with perceptual supervision to generate instantaneous volumetric images from a single 2D projection for real time imaging in lung SABR.

It should be noted that many reconstruction methods mentioned above are generic and may be used for both diagnostic imaging and image-guided radiotherapy. We are expecting to see more evaluations and validations of these techniques on specific applications in radiotherapy. By now, there are still many concerns on stability and reliability of the DL-based reconstruction methods because of their black-box nature. More research efforts are needed to interpret these DL models and improve robustness and accuracy of DL-based reconstruction.

Although with great potential, we have not seen reports of using DL-based reconstruction algorithms for radiotherapy applications in clinic. The DL-based reconstruction algorithms from GE Healthcare and Canon Medical Systems have received FDA 510(k) clearance. Solomon et al. [100] studied the noise and spatial resolution properties of DL-based reconstruction from GE, and found it can substantially reduce noise compared to FBP while maintaining similar noise texture and high-contrast spatial resolution but also with degraded low-contrast spatial resolution. since the quality of reconstructed image is so crucial in radiotherapy, more clinical assessments and comparisons are needed before we can confidently adopt them in clinic.

III. Image Registration

Image registration is an important component for many medical applications such as motion tracking [101], segmentation [101-103], image guided radiotherapy [104, 105] and so on. Image registration is to seek an optimal spatial transformation which aligns the anatomical structures of two or more images based on its appearances. Traditional image registration methods include optical flow [106], demons [107], ANTs [108], HAMMER [109], ELASTIX [110] and so on. Recently, many DL (DL)-based methods have been published and achieved state-of-art performances in many applications[111]. cNN uses multiple learnable convolutional operation to extract features from the images. Many types of architectures exist for CNN, including the AlexNet, U-Net, ResNet, DenseNet and so on. Due to its excellent feature extraction ability, cNN has become one of the most successful models in DL-based image processing, such as image segmentation and registration. Early works that utilized CNN for image registration attempted to train a network to predict the multi-modal deep similarity metric to replace the traditional image similarity metrics such as mutual information in the iterative registration framework [112, 113]. It is important to ensure the smoothness of the first order derivative of the learnt deep similarity metrics in order to fit them into traditional iterative registration frameworks. The gradient of the deep similarity metric with respect to the transformation can be calculated using the chain rule. The major drawback of this method is that it inherits the iterative nature of the traditional registration frameworks. To enable fast registration, many CNN-based image registration methods have been proposed to directly infer the final DVF in a single/few forward predictions. In this section, we focus on this type of registration method since there is a clear trend towards direct DVF inference for DL-based fast image registration.

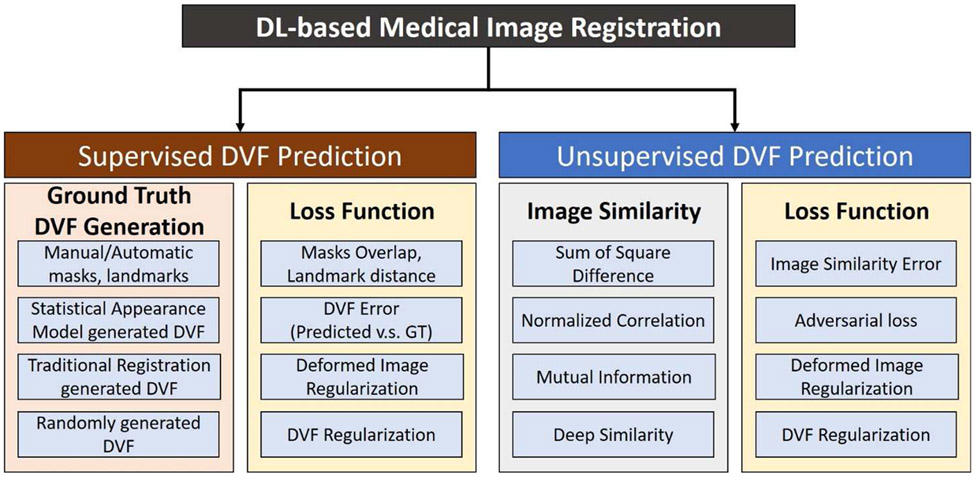
According to the network training strategy, this type of CNN-based image registration method can be grouped into two broad categories which are supervised DVF prediction and unsupervised DVF prediction, as shown in Fig. 3. supervised DVF prediction refers to DL models that are trained with known ground truth transformation between the moving and the fixed images. on the contrary, unsupervised DVF prediction does not need the ground truth transformation for network training. For supervised DVF prediction, the ground truth DVF can be generated artificially using mathematical models or by traditional registration algorithms. The DVF error between the predicted and ground truth DVFs can be minimized to train the network. For unsupervised DVF prediction, ground truth DVF is not needed, however, robust image similarity metrics are necessary to train the network to maximize the image similarity between the deformed images and the fixed images. Over the last several years, there has been an increasing number of publications on CNN-based direct DVF inference methods.

Fig. 3.

Supervised and unsupervised deformation vector field (DVF) prediction methods.

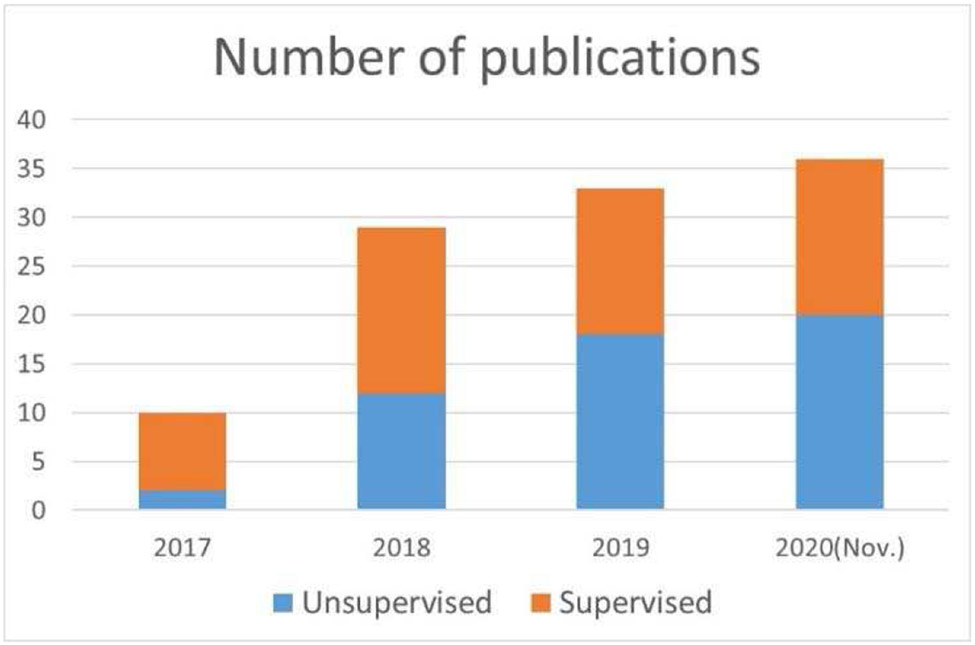
To investigate the trend of the number of publications that used supervised and unsupervised learning methods for image registration, we have collected 100+ publications from various databases, including Google Scholar, PubMed, Web of Science, Semantic Scholar and so on. Keywords including but not limited to machine learning, deep learning, learning-based, convolutional neural network, image registration, image fusion, image alignment were used. Fig. 4 shows the number of publications from the year of 2017 through November of 2020. In 2017 and 2018, the supervised methods are clearly more prevalent. From 2019, the unsupervised methods have become slightly more popular than the supervised methods.

Fig. 4.

Overview of number of publications in DL-based medical image registration.

A. Supervised Transformation Prediction

Supervised transformation prediction aims to train the network with ground truth transformations. However, the ground truth transformation is usually unavailable in practice. Various methods have been proposed to generate/estimate the ground truth transformation, including manual/automatic masks contouring, landmark detection/selection, artificial transformation generation, traditional registration-calculated transformation, and model-based transformation generation. Table I shows a list of selected references that used supervised transformation prediction. Salehi et al. trained a CNN-based rigid image registration for fetal brain MR scans [114]. The network was trained to predict both rotation and translation parameters using datasets generated by randomly rotating and translating the original 3D images. Eppenhof et al. trained a CNN to perform 3D Lung deformable image registration using synthetic transformations [20]. The network was trained by minimizing the mean square error (MSE) between the predicted DVF and the ground truth DVF. A target registration error (TRE) of 4.02±3.08 mm was achieved on DIRLAB [115], which was worse than 1.36±0.99 mm [116] that was achieved when using the traditional DIR method. The TRE was later reduced from 4.02±3.08 mm to 2.17±1.89 mm on DIRLAB datasets using a U-Net architecture [21].

TABLE I.

Selected supervised transformation prediction methods

References	ROI	Patch- based	Modality	Transformation
[8]	Cardiac	No	MR	Deformable
[13]	Brain	Yes	MR	Deformable
[15]	Brain	Yes	MR	Deformable
[16]	Pelvic	Yes	MR-CT	Deformable
[17, 18]	Prostate	No	MR-US	Deformable
[19]	Lung	Yes	CT	Deformable
[20, 21]	Lung	No	CT	Deformable
[12]	Brain	Yes	MR	Deformable
[24]	Brain	No	T1, T2, Flair	Affine
[25-27]	Lung	Yes	CT	Deformable
[29]	Prostate	No	MR-TRUS	Affine + Deformable
[33]	Pelvis	No	CT-CBCT	Deformable
[35]	Cardiac	No	MRI	Deformable

Instead of using artificially generated transformation as ground truth, Sentker et al. proposed generating the DVF using PlastiMatch [117], NiftyReg [118], and VarReg [119] as ground truth [19]. The authors showed that the network trained using VarReg had better performance than those trained using PlastiMatch and NiftyReg on DIRLAB [115] datasets. The best TRE values they achieved on DIRLAB was 2.50±1.16 mm, which was not better than the network trained using artificially generated transformations. statistical appearance models (SAM) have also been used by Uzunova et al. to generate a large and diverse set of training image pairs with known transformations from a few sample images [120]. They showed that CNNs learnt from the SAM-generated transformation outperformed cNNs learnt from artificially generated and affine registration-generated transformations. sokooti et al. used a model of respiratory motion to simulate ground truth DVF for 3D-CT lung image registration [26]. They have outperformed models that were trained using artificially generated transformations. They achieved a TRE of 1.86 mm for the DIRLAB datasets. Instead of using the artificially-generated dense DVF, higher-level correspondence information such as masks of anatomical organs were also used for network training [18, 121]. Networks trained using higher-level of correspondences such as organ masks or landmarks are often called weakly supervised methods since the exact dense voxel-level transformation was unknown during the training. It is called weakly supervised also because the higher-level of correspondence was not required in inference stage to facilitate fast registration.

one major limitation of supervised transformation prediction is that the generated transformation may not reflect the true physiological motion, resulting in a biased model towards the artificially generated transformation prediction. It is possible to mitigate this problem using better transformation models to generate various training image pairs which simulate realistic transformations.

B. Unsupervised Transformation Prediction

The loss function definition in supervised transformation prediction methods was straightforward. However, for unsupervised transformation prediction, it was not so straightforward to define a proper loss function without knowing the ground truth transformations. Fortunately, the spatial transformer network (STN) which allows spatial manipulation of data during training was proposed [122]. The STN can be readily plugged into existing CNN architectures. The STN was used to deform the moving image based on the current predicted DVF to generate the deformed images which were compared to the fixed image to calculate image similarity loss. Table II shows a list of selected references that used unsupervised transformation predictions with their respective similarity metrics. SSD stands for sum of squared difference, MI stands for mutual information, MSE stands for mean squared error, CC stands for cross correlation.

TABLE II.

Selected unsupervised transformation prediction methods

References	ROI	Patch- based	Modality	Transform	Similarity
[9]	Brain	No	MR	Deformable	SSD
[10]	Brain	No	MR	Affine	MI
[11, 12]	Brain	Yes	MR	Deformable	Intensity & gradient difference
[22]	HN	Yes	CT	Deformable	MSE
[28]	Cardiac	No	MR	Deformable	CC
[34]	Lung	No	MR	Deformable	MSE
[36]	Brain	No	MR-US	Deformable	MSE after intensity mapping
[37]	Cardiac, Lung	Yes	MR, CT	Affine and Deformable	MSE
[38, 39]	Brain	No	MR	Deformable	CC
[40]	Liver	No	CT	Deformable	CC
[41, 42]	Brain	No	MR	Deformable	CC
[44]	Liver	No	CT	Deformable	CC
[46]	Abdomen	Yes	CT	Deformable	CC
[47]	Abdomen	Yes	CT	Deformable	CC
[49]	Lung	Yes	CT	Deformable	CC
[51, 52]	Prostate	No	MR-TRUS/CBCT	Deformable	None
[54]	Lung, Cardiac	Yes	CT, MRI	Deformable	CC

An unsupervised CNN-based registration method, called VoxelMorph was proposed for MR brain atlas-based registration [38, 39]. The VoxelMorph has a U-Net like architecture. With STN, the image similarity between the deformed images and the fixed images were maximized during training. The predicted transformation was regularized to have low local spatial variations. They have achieved comparable performance to the ANT [108] registration method in terms of the Dice similarity coefficient (DSC) score of multiple anatomical structures. Zhang et al. proposed a network to predict diffeomorphic transformation using trans-convolutional layers for end-to-end MRI brain DVF prediction [123]. An inverse-consistent regularization term was used to penalize the difference between two transformations from the respective inverse mappings. The network was trained using a combination of an image similarity loss, a transformation smoothness loss, an inverse consistent loss, and an anti-folding loss.

Lei et al. used an unsupervised CNN to perform 3D CT abdominal image registration [46]. A dilated inception module was used to extract multi-scale motion features for robust DVF prediction. Besides the image similarity loss and DVF regularization loss, an adversarial loss term was added by training a discriminator. Vos et al. proposed a fast unsupervised registration framework by stacking multiple CNNS into a larger network for cardiac cine MRI and 3D CT lung image registration [37]. They showed their method was comparable to conventional DIR methods while being several orders of magnitude faster. Jiang et al. proposed a multi-scale framework with unsupervised CNN for 3D CT lung DIR [124]. They cascaded three CNN models with each model focusing on its own scale level. The network was trained using image patches to optimize an image similarity loss and a DVF smoothness loss. They demonstrated that the network trained on SPARE datasets has good performance on the DIRLAB datasets. The same trained network could also be generalized to CT-CBCT and CBCT-CBCT registration without re-training or fine-tuning. Jiang et al. achieved an average TRE of 1.66±1.44 mm on DIRLAB datasets. Fu et al. proposed an unsupervised whole-image registration for 3D-CT lung DIR [49]. The network adopted a multi-scale approach where the CoarseNet was first trained using down-sampled images for global registration. Secondly, local image patches were registered to the image patches of the fixed image using a patch-based FineNet. A discriminator was trained to provide adversarial loss to penalize unrealistic warped images. They have outperformed some traditional registration methods with an average TRE of 1.59±1.58 mm on DIRLAB datasets.

Compared to supervised transformation prediction, unsupervised methods could alleviate the problem of lack of training datasets since ground truth transformation is not needed. However, without direct transformation supervision, DVF regularization terms have become more important to ensure plausible transformation prediction. So far, most of the unsupervised methods focused on unimodality registration since it is relatively easy to define image similarity metrics for unimodal registration than multi-modal image registration.

Supervised transformation prediction methods are limited by the lack of known transformations in the training datasets. Artificial transformations could introduce errors due to the inherent differences between the artificial and realistic transformations. Model-based transformation generation which could simulate highly realistic transformation has been shown to alleviate the lack of realistic ground truth transformation. On the other hand, unsupervised methods need extensive transformation regularization terms to constrain the predicted transformation since ground truth transformation is not available for supervision. One challenge is to efficiently determine the relative importance of each regularization term. Repeated trial and evaluation were often performed to find an optimal set of transformation regularization terms that could help generate not only physically plausible but also a physiologically realistic deformation field for a certain registration task. Another limitation for unsupervised transformation prediction is that it relies on effective and accurate image similarity metrics to calculate similarity loss and train the network. However, multi-modal image similarity metrics are usually more difficult to define and calculate than unimodal image similarity metrics. Therefore, there is a lack of multi-modal unsupervised image registration methods as compared to unimodal image registration methods. Deep similarity metrics could be trained for multimodal image registration tasks and used in unsupervised transformation prediction. However, the training of deep similarity metrics often requires pre-aligned training image pairs which are difficult to obtain.

IV. Image segmentation

In radiation therapy, image segmentation can be described as the process where each pixel in an image is assigned a label, and pixels with similar labels are linked such that a visual or logical property is realized()[125]. Resultant groupings of pixels with the same label are called delineations (i.e., segmentations). Once RT images are acquired, tumors and OARs are delineated, often by a physician or dosimetrist, to be incorporated into the treatment planning process. Manual segmentation has been reported to be the most time consuming process of radiation therapy, introducing substantial inter- and intra-observer variability[126], and dependent on image acquisition and display settings[127]. To address these limitations, auto-segmentation is often employed. Auto-segmentation may be unsupervised, where only the image itself is considered and image intensity/gradient analyses are implemented, performing best with distinct boundaries[23]. Supervised segmentation, on the other hand, integrates prior knowledge about the image often in the form of other similarly annotated images to inform the current segmentation task (i.e., training samples).

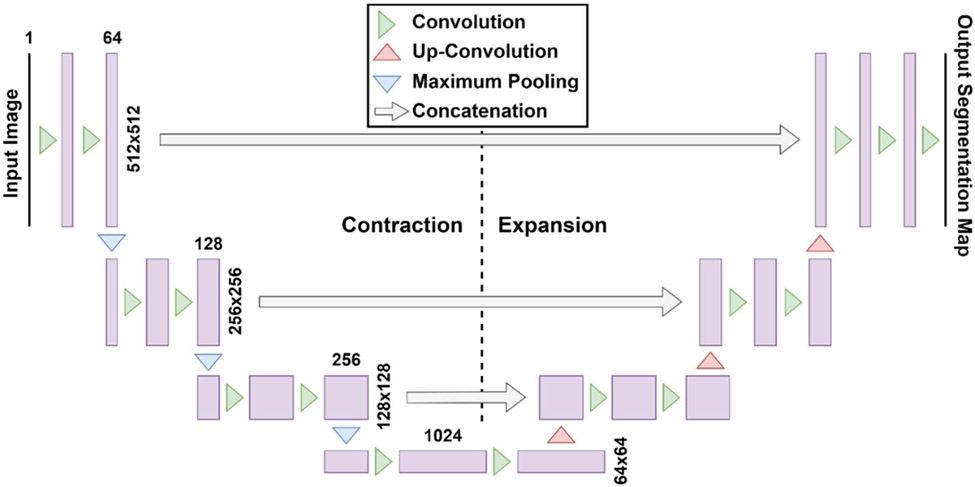
Recent DL techniques[128, 129] are well poised for the task of accurate automatic segmentation with less reliance on organ contrast[130-132] as the algorithm is designed to acquire higher order features from raw data[128]. Deep neural networks (DNNs) learn a mapping function between an image and a corresponding feature map (i.e. segmented ground-truth) by incorporating multiple hidden layers between the input and output layer. The U-Net[5] is a DNN architecture that has shown great promise for generating accurate and rapid delineations for applications in RT[133]. The U-Net “U-shaped” architecture shown in Fig. 5 was inspired by the original fully convolutional network from Long et al. [134] and was initially implemented by Ronneberger et al. [5] in 2015 to segment biomedical image data using 30 annotated image sets. The U-Net has an additional expansion pathway that replaces the maximum pooling operations with up-convolutions to increase the resolution of the feature maps, a desirable feature for medical image segmentation. The original 2D U-NET was quickly implemented into 3D volumetric inputs to train using the entire dataset and annotations simultaneously to improve segmentation continuity, including multi-channel inputs of different image types[135] (i.e., MRI, CT, etc.). Overall, the U-Net is an end-to-end solution has shown remarkable potential to segment medical images, even when the amount of training data is scarce[136]. Various deep neural networks have also been applied to medical image segmentation[133] including deep CNNs with adaptive fusion[137] or multi-stage[138] strategies, as well as generative adversarial networks (GANs)[139].

Fig. 5.

Architecture for original U-Net by Ronneberger et al. [5] with the contraction path shown on the left and the expansion path shown on the right. The original input image has a size of 512 x 512. Feature maps are represented by purple rectangles with the number of feature maps on top of the rectangle.

Data scarcity may be a challenge in radiation therapy. Publicly available annotated “ground truth data” for training and validation are available through The Cancer Imaging Archive[140]. Several other strategies are employed to improve the variability and diversity of available data—without new unique samples—which is referred to as data augmentation. Data augmentation has been shown to improve auto-segmentation accuracy and prevent model overfitting[135, 137, 141]. Examples of augmentation include image flipping, rotation, scaling, and translation (pixels/axis). other emerging areas of data augmentation include integrating inter-fractional data such as incorporating daily cone-beam CTs for patients to increase segmentation accuracy in radiation therapy[142] and using transfer learning to generate new training imagesets from other modalities. Typical endpoints of AI segmentation include qualitative review or comparison with ground truth labels using overlap metrics such as the DSC or distance metrics such as the Hausdorff distance or mean distance to agreement.

Applications of AI for segmentation in RT planning typically fall into two main classes: organs at risk and lesions. Table III outlines a few state-of-the-art examples of each with key findings, with a comprehensive list available in other references[143].

TABLE III.

Example applications of DL into medical image segmentation for radiation therapy planning purposes

Author	Disease Site	Image Type, Number of cases	Algorithm	Outcome
Zhu et al.[1]	Head and Neck	Planning CT, 261	3D U-Net, whole image	-9 OAR contours generated in ~0.12 seconds -Increased DSC ~3%
Lei et al.[2]	Male Pelvis	Cone-beam with synthetic MRI, 100	CycleGAN	-DSC >0.9 and MDA <1.0 mm for bladder, prostate, rectum from ground truth delineations
Dong et al.[3]	Thorax	CT, 35	U-Net GAN	-DSC>0.87 and MDA <1.5 mm for lungs, cord, heart -DSC esophagus ~0.75 -Negligible dosimetric differences
van der Heyden et al.[4]	Brain	Dual-energy CT, 14	2-step 3D U-Net	-Quantitatively and qualitatively outperformed atlas method for all organs at risk but optic nerves
Chen et al.[6]	Abdomen	3T MRI, 102	2D U-Net	-9/10 OARs had DSC 0.87-0.96 -Duodenum DSC ~0.8
Fu et al.[7]	Abdomen	0.35 T, MR-linac, 120	CNN with correction method	-4/5 OARs had DSC >0.85 (liver, kidneys, stomach, bowel) -Duodenum DSC ~0.65

Emerging areas of interest include segmenting substructures of organs at risk including the cardiac substructures[135], applications for adaptive radiation therapy[7], and longitudinal response assessment. other areas under development include optimizing loss functions, such as integrating DSC less, unweighted DSC loss, or focal DSC loss, with tunable hyperparameters[144] to better address segmentation accuracy for small structures[145].

V. Image synthesis

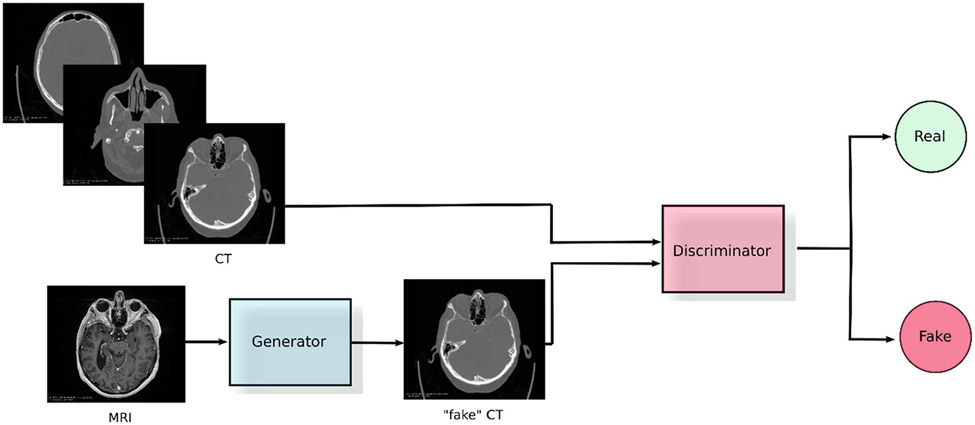
In this section, we focus on generative modelling of information content across imaging modalities relevant to the radiotherapy workflow. Generative modelling, in this context, refers to capturing information about the data distribution associated with each modality thus enabling translation across different modalities. Within generative modelling, we limit our review to techniques that are most suitable to represent unpaired data obtained in real clinical settings where obtaining one-to-one correspondences between modalities may not be feasible. Among these techniques, GANs have proven to be very successful. GANs are a framework that optimize an objective by running a min-max two player game between two networks. One of the networks, called the generator, tries to learn the data distribution by trying to fool the other network, called the discriminator, which simultaneously tries to differentiate between real images and fake images created by the generator.

GAN-based approaches have also shown to be superior when paired data is available where they eliminate the need to design hand-crafted losses in the image-space[146]. We present methods proposed to aid different stages of the workflow ranging from image acquisition to treatment delivery. Specifically, we discuss MRI to CT, CBCT to CT and CT to PET translation. We focus our review on techniques aimed [?]at inter-modality translation due to the large variation in content representation across these modalities. For example, CT images capture electron densities through Hounsfield units whereas MRI images are generated based on the excitation and relaxation of hydrogen protons. These differences in representation allow for effective demonstration of the capacity of GAN-based image translation approaches to learn complex mappings.

A. MRI to CT Translation

MRI-only radiotherapy can provide multiple benefits to the patient and clinic due to its immense flexibility in imaging physiological and functional characteristics of tissue, combined with much superior soft-tissue differentiation. It also avoids additional risk induced by subjecting the patient to ionizing radiation via CT. However, MRI lacks the ability to provide electron densities which is explicitly needed in radiation dosimetry transport calculations. Generative modelling of information content between MRI to CT modalities can allow for obtaining electron densities from MRI. This is done by translating it into a synthetic CT while retaining structural information present within the original MRI scan itself. In order to effectively translate between the modalities, suitable input-output representations need to be determined, and this is done as follows: 1) constructing a mapping between paired MRI-CT data from the same patient (registered to ensure correspondence) or 2) unpaired MRI-CT data from the same patient or across patients. For MRI-to-CT translation in nasopharyngeal cancer treatment planning – Peng et al. [147] use conditional GANs for paired data and CycleGANs for unpaired data. CycleGANs ensure reliable translation by enforcing cycle-consistency in the MRI-to-CT translation[148]. They use 2D U-Net based generators that operate on a slice-by-slice basis and 6-layered convolutional discriminators. Wolterink et al. [149] and Lei et al. [150, 151] use paired data from the same patients for MRI-to-CT translation for treatment planning of brain tumors and brain /pelvic tumors, respectively. Although they use registered MRI-CT data from the same patient, they employed Cycle-GANs to account for local differences between the spatial representation across these modalities. Wolterink et al. used data from sagittal slices on a slice-by-slice basis and used the default CycleGAN setup including a patch-based discriminator to preserve high frequency features. Lei et al. operated on 3D patches of smaller sizes (32³) and implemented dense blocks[152] in the generator to capture multiscale information. They also proposed the use of novel mean P-distance (l_p norm) and spatial gradient differences as cycle-consistency losses to avoid blurriness and promote sharpness respectively.

In terms of results, Peng et al. reported mean absolute Hausdorff Unit (HU) differences (MAE) within the body of 69.6±9.27 for the paired approach and 100.6±27.39 for the unpaired approach. Wolterink et al. reported 73.7±2.3 HU MAE and Lei et al. reported 57.5±4.7 HU MAE for the brain.

These methods are not directly comparable since they use different data, but they do represent an estimate of their quantitative performance. However, it is difficult to ascertain clear clinical applicability based solely on these metrics. Consider a case where the average HU values are biased by strong deviations in areas belonging to the tumor where other areas are quite accurate. If this is placed in comparison to another case where smaller but uniform deviations are present across the entire scan, which scenario would be more clinically relevant? These metrics fail to answer these questions in entirety. Peng et al. provided additional metrics such as comparing dose distributions of translated CT with the reference CT with 2%/2-mm gamma passing rates of (98.68%±0.94%) and (98.52%±1.13%) for the paired and unpaired approaches, respectively. This gives a better idea of dosimetric accuracy of implementing their methods in a treatment planning system.

B. CT to PET translation

PET/CT scans can play a crucial role in combining anatomical and functional information to pinpoint metabolic activity and may provide better information in the contouring process for treatment planning. Synthesizing virtual PET from CT-only workflows can eliminate the need for the more costly PET/CT scan. Additionally, this reduces cost and complexities such as storage of radiotracers associated with PET imaging. Ben-Cohen et al. proposed a conditional-GAN (cGAN) [146] based method to generate PET from contrast enhanced CT-scans for false positive reduction in lesion detection within the liver. They used paired PET/CT data and performed a transformation to align and interpolate the PET to the CT. A first synthesized estimate of PET is performed using a fully convolutional variant of VGG [153] followed by a cGAN applied on channel concatenated input comprising of CT and the previous PET estimate. In this two-stage network, while optimizing over the image-losses, SUV-based weighting is applied to provide better results in PET regions with high-SUVs. The proposed method obtains a mean absolute SUV difference of 0.73±0.35 across all regions and 1.33±0.65 in high-SUV regions. Finally, false positives are shown to be reduced from 2.9% to 2.1% in liver lesion detection when using the generated PET information for detection. Bi et al. [154] explored synthesis of PET image from paired PET/CT data for lung cancer patients and propose three different methods exploiting varied input representations. All three methods apply a U-Net based cGAN but vary in terms of input provided to the model: (1) binary label-map of the tumor annotations, (2) CT image, and (3) channel-combined CT with binary label-map. The last method provided the results closest to the real-PET image with a SUV MAE of 4.60. The authors suggested that this synthesized PET can be used to form training data for PET/CT based prediction models. Further, they formulated a potential extension of their work to combine both real and synthetic PET to boost the training samples in an attempt to boost generalization.

C. CBCT to CT Translation

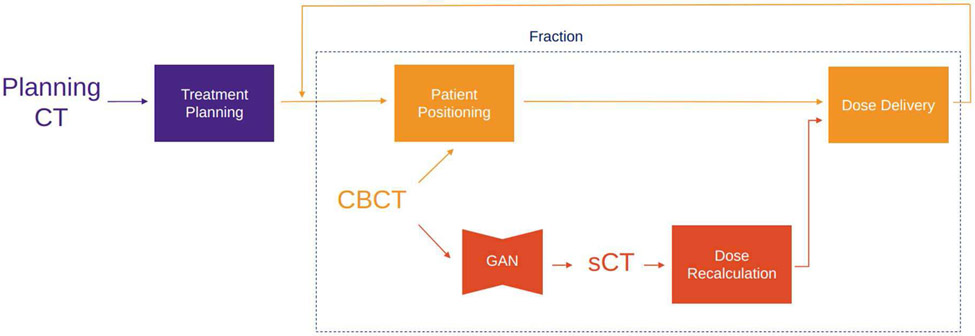
Radiotherapy treatment planning starts with acquiring a CT scan of the patient, usually denoted as a planning CT (pCT). Dose calculation as well as beam energy and arrangement are derived from the pCT, comprising a treatment plan. Commonly, in order to correctly position the patient at each fraction of the dose delivery, a CBCT scan is obtained. However, CBCT can potentially provide insight into the anatomical changes that occurred over the course of the treatment and could enable adaptive radiotherapy by leveraging that information to adjust the treatment plan. Unfortunately, treatment re-planning is not possible with CBCT scans as they are noisier, contain more artifacts and have inferior soft-tissue contrast compared to fan-beam CT. One way to make use of the information in a CBCT scan is by using deformable image registration (DIR) to map pCT to the anatomy of CBCT [155], producing a scan with HU values of the pCT with the latest anatomy, in literature referred as deformed planning CT (dpCT) or virtual CT (vCT). On the other hand, generative DL methods may provide a faster and potentially superior alternative to treatment re-planning based on dpCT or other techniques (look-up table [156], Monte Carlo[157], scatter correction with pCT prior [158]) by synthesizing a CT scan from an input CBCT scan. Such synthetic CT (sCT) should have all the characteristics of a CT scan while preserving the anatomy from the CBCT. Maspero et al. [159] trained 4 standard CycleGAN [148] models on lung, breast, and head-and-neck scans – three for each anatomical site separately and one model on all sites jointly. They showed that a single model for all three anatomical sites performs comparably against models trained per anatomical site, which would simplify its possible clinical adoption. The results are evaluated using rescanned CT (rCT) as ground truth, where rCT is a CT scan that is acquired at the same fraction as the CBCT in question. The reported HU MAE for sCT are 5312, 6618, 8310 for head-and-neck, lung and breast, respectively. Liang et al. ()[160] used a standard CycleGAN model, but evaluate the HU accuracy and dose calculations against dpCT instead of rCT. Furthermore, they performed an evaluation of anatomical accuracy of sCT using deformable head-and-neck phantoms. The phantom allows for a simulation of the patient at the beginning of the treatment and after a few fractions of the treatment, where the tumor shrinkage is observed. This provides a CBCT and rCT scan with identical anatomy, which can be used to assess if and how translation of CBCT to sCT affects the representation of the anatomy. They concluded that the CycleGAN model has higher anatomical accuracy than DIR methods.

D. Clinical Perspective and Future Applications of Synthetic Imaging

In the radiotherapy workflow, medical images are one of the most important sources of data used in decision-making. Imaging is used in all the steps of patient care in oncology: diagnosis, staging, treatment planning, treatment delivery, and disease follow-up. Based on the anatomical site of a tumor and the specific properties we want to investigate, some imaging modalities might be more appropriate than others. For example, an MRI scan is suggested for malignancies located in the pelvic region, due to the large presence of soft tissues compared to bone structures. This allows an improved ability to contour lesions and surrounding organs. CT is the predominant modality for staging lung tumors, but recently MRI scans, and more specifically Diffusion Weighted Imaging (DWI) sequences, are used to evaluate the involvement of mediastinal lymph nodes with higher sensitivity than CT, with implications on better staging and treatment decisions. Finally, it is well established that treatment planning always requires the acquisition of a CT scan, while PET imaging is often used prior to treatment planning to evaluate the presence of metastasis and the degree of suspicion of the identified lesions, and within/after treatment fractions to quantify treatment response[161]. Such examples highlight the need for multiple modalities of imaging to fully capture the complexity of human anatomy and tumor tissues in tandem with the specific tasks that we want to accomplish. This would eventually improve the decision-making process. In an ideal scenario, all modalities of imaging for the patient would be available, but that is far from being an achievable or practical solution.

Several reasons stand behind this evidence:

1). Cost-effectiveness:

Scanning patients costs both hospitals and the patients themselves. These costs may be reimbursed by healthcare providers or insurance companies. With an increasing number of new and diverse imaging technologies a growing demand for cost-effectiveness analysis (CEA) in imaging technology assessment is induced. As pointed out by Sailer et al. [162], when assessing the cost-effectiveness of diagnostic imaging, the initial question is whether adding an imaging test in a medical pathway does indeed lead to improved medical decision-making. One of the most significant examples was the lung cancer screening trial entitled NLST[163], which showed that participants who received low-dose helical CT scans had a 15 to 20 percent lower risk of dying from lung cancer than participants who received standard chest X-rays. In radiotherapy, a study [164] highlighted the costs related to various radiological imaging procedures in image-guided radiotherapy of cancers, based on standard billing procedures. The median imaging cost per patients was $6197, $6183, $6358, $6428, $6535 and $6092 from 2009 to 2014, respectively. This seems to highlight an upcoming trend of reducing costs related to imaging. Unfortunately, it is not clear if this reduction in costs was associated with an optimization of the diagnostic imaging.

2). Patient safety and comfort:

Recent studies indicated that repetitive imaging scans can deposit considerable radiation doses to some radiosensitive organs (e.g. heart) and could cause higher radiogenic cancer risks to the patients, with children being more impacted by this issue[165]. In a very utilitarian way, we might want to have an image with the highest possible contrast to be able to better identify suspicious structures, and to possibly obtain images of our patients within short intervals of time. This would allow using these images, for example, to perform a better evaluation of treatment response. Unfortunately, due to the physics of imaging, ionizing imaging methods give a signal to noise ratio proportional to the released dose to the body[166]. More dose leads to better contrast, but also increases the probability of radiation-induced effects to the patient. Another point is represented by images acquired with the injection of an intravenous (IV) contrast medium. IV contrast media are usually toxic substances that need to be expelled by our body. If it is true that images acquired with IV contrast media (e.g., contrast enhanced CT) provide better resolution for specific anatomic regions compared to images without them (e.g., conventional CT); it also stands that many patients might not be eligible for the injection of a contrast media, because of poor performance status, presence of comorbidities, or poor renal function [167]. Finally, some imaging modalities such as DWI require longer acquisition times compared to T1 and T2 sequences [168], with an impact on costs and also on patients’ comfort.

3). Differences in imaging acquisition protocols and interoperability:

Despite the presence of specific guidelines and recommendations for diagnostic imaging, each institution might adopt not only different image acquisition protocols, but might also be missing specific imaging modalities (or sequences), which might be the standard of care in another institution. This evidence has an impact when performing or designing multicenter institutional studies, especially if retrospective and with the aim of the development of image-derived biomarkers. For example, if a center has developed a prognostic model based on an image-derived biomarker obtained by processing a specific imaging modality, a large external validation of this biomarker might not be possible because this imaging modality may not be available in many institutions. Additionally, when considering quantitative imaging analysis via machine learning and more specifically radiomics[169], a recent review pointed how different acquisition settings (e.g., slice thickness, tube current, reconstruction kernels) should be preferrable with respect to others, since they increase the reproducibility of the biomarkers[170]. It is, as mentioned before, not obvious that these acquisition settings are the same across all clinics. One possible solution, which is close to utopia, is to force each institution to acquire images with the same acquisition protocols. However, even if this was accomplished, the variability of scanner manufacturers, a well-known factor that impacts the stability of image-derived biomarkers, would still be difficult to tackle.

All the points presented above show that there is an open space for the application of DL based synthetic imaging. Without going into details, applications can include the generation of multi-modalities from a starting image (as explained in the case of the section MRI to CT of this paper), augmentation of image quality without exposing the patient to additional dose (as explained in the case of the section CBCT to CT translation), but also the recent work that introduces fast DL reconstruction for DWI images [171-173]. Synthetic imaging is taking a prominent role in oncology. We refer the reader to the following publications as proof of some interesting clinical applications that DL for image generation can offer[174, 175], and to these more general reviews[176, 177].

VI. Automatic treatment planning

In radiotherapy planning, a main objective is to deliver the prescribed dose accurately to the target, keeping the dose to OAR below acceptable limits and minimizing dose to surrounding, healthy tissue. The treatment planning process begins with delineation of target volumes and OARs on a planning CT. A set of dose-constraints are defined for targets, OARs and other regions of interest, typically dose-volume relations, stating the minimum or maximum dose that can be allowed to a given region. Intensity Modulated Radiation Therapy (IMRT) and Volumetric Modulated Arc Therapy (VMAT) are modern techniques that allow the treatment planner to create complex treatment plans by providing a set of such objectives that an optimizer algorithm will attempt to fulfill by inverse optimization, as illustrated by the workflow in Fig. 8. The optimizer often fails to achieve all the desired objectives, due to complicated patient geometry, limitations of the treatment modality or machine, etc. To improve the plan, the planner and physician discuss available options and clinical preference before adjusting the objectives for a new iteration of optimization. In recent years, automated treatment planning techniques have been developed, that aim to provide vastly improved starting points for the treatment planner, and even produce clinically acceptable treatment plans without human interaction.

Fig. 8.

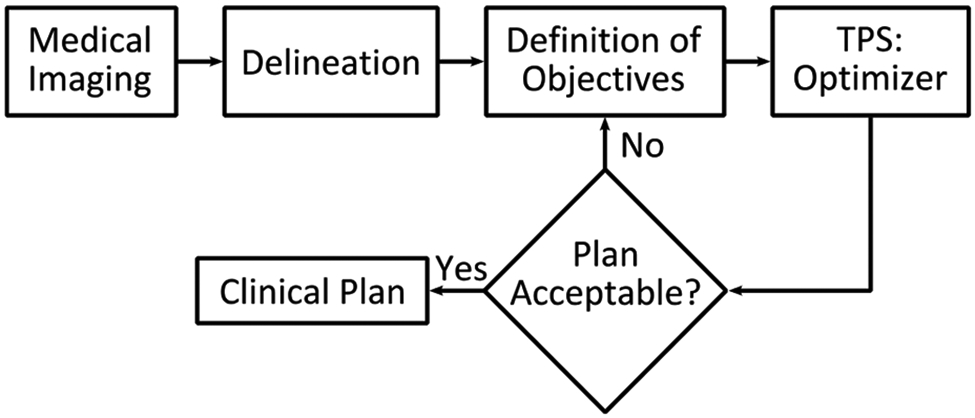
The inverse treatment planning process begins with delineation of target volumes and OARs on medical images. Optimization objectives are defined and passed to the optimizer algorithm of the TPS. If the resulting plan is not acceptable, trade-off evaluation is performed to define new targets iteratively until a clinical plan is accepted.

The current planning workflow apparently relies heavily on humans (planner and physician). The reason for this workflow is twofold. First, there is no clear metrics to mathematically quantify plan quality. Although there are some plan quality scoring systems defined over the years [178], they might not necessarily reflect the most stringent clinical requirement for each patient. Second, for a specific patient, the best plan is unknown. The planning process has to explore the very high-dimensional solution space in a trial-and-error process to find out the optimal solution [179, 180]. This complex and cumbersome process poses substantial hurdles to plan quality and planning efficiency.

Due to extensive human involvement, the plan quality heavily depends on a number of human factors, such as the planner’s experience, the planner-physician communications, the amount of effort and available time for treatment planning, and the rate of human errors etc. [181-183]. Suboptimal plans are often unwittingly accepted [183-185], deteriorating treatment outcomes [186].

Moreover, while modern computers can solve the optimization problem rapidly, the trial-and-error iterative planning process yields hours of planning time for a typical planner to generate a plan for the physician to review [187-189]. Multiple iterations between physician and planner are often needed, which extends the overall planning time up to one week in some challenging tumor sites. This lengthy process strongly contributes to the delay between diagnosis and start of RT, which has been shown to adversely affect treatment outcome. Moreover, patient’s anatomy may change during the time waiting for treatment planning [190, 191], making the plan carefully designed based on the initial patient anatomy sub-optimal for the changed anatomy [192, 193]. Additionally, the delayed treatment will increase the anxiety of patients who have already been overwhelmed by cancer diagnosis and are eager to start treatment. Such delays can be particularly severe in low- and middle-income countries, with limited resources, capacity, staff and expertise [194].

The problem of sub-optimal plan quality and planning efficiency are indeed intertwined. Due to the low planning efficiency, the optimality of a plan is hard to guarantee for every patient in current practice given the strict time constraints. Heavy time pressure also increases human error rate and may limit availability of advanced treatment techniques. Auto-planning (AP) techniques are urgently needed to tackle these problems in the current planning process.

AP has already been around for some time and is rapidly improving. There are several research projects and in-house solutions being developed worldwide, and most commercial vendors of treatment planning systems (TPS) have implemented some variety of AP tools. Studies show promising results for AP, but large-scale clinical implementation is not yet seen.

A. Classical Auto-planning Strategies

Classical AP tools can be divided into three categories: treatment planner mimicking (TPM), multi-criteria optimization (MCO) and knowledge-based planning (KBP).

1). Treatment Planner Mimicking:

In treatment planner mimicking (TPM), the behavior and choices of the treatment planner are analyzed over time and converted into computer logic. Such logic can be a series of IF/THEN statements of decision making. Provided with a prioritized list of objectives the TPM follows its logic to create optimizer objectives that it tunes iteratively while steering the optimizer, in the same way that a human treatment planner would, pushing each objective as far as it can without degrading objectives of higher priority. The TPM is not as limited by time as a human planner, allowing it to perform more iterations, potentially leading to higher plan quality. Tol et al. designed a system that automatically scans DVH lines in the Eclipse TPS (Varian Medical Systems, Palo Alto, USA) optimization window, and moved the mouse cursor to adjust on-screen optimization objectives. In a blinded test, automated head-and-neck cancer (HNC) plans were preferred over MP by a HNC radiation oncologist in 19/20 cases, and the method is now in clinical use [195]. Several modern TPSs include possibilities for scripting, which have been used to develop in-house TPM by extracting DVH parameters directly from the TPS and automatically adjusting optimization objectives iteratively until the optimal solution is found [196-202]. A commercial TPM solution is available in Philips Pinnacle TPS (Philips Radiation Oncology Systems, Fitchburg, WI, US) Auto-Planning. Pinnacle Auto-Planning works by defining a template, called a technique, consisting of parameters, e.g., beam setup, dose prescriptions and objectives for each disease site [203]. When the technique is applied to a new patient, the AP will iteratively optimize a treatment plan, add helper volumes with new objectives to control the dose in the same fashion as a human planner might do, lower dose to OARs and reduce hot and cold spots in the dose distribution. The use of this system has been reported in several studies [198, 203-214], creating APs of comparable or higher quality, reduced planning times and improved OAR sparing in comparison to MPs. In a study by Cilla et al. Pinnacle Auto-Planning produced high-quality plans for HNC and high-risk prostate and endometrial cancer while reducing planning time by 60-80 minutes, corresponding to 1/3 of the MP time [203]. However, Zhang et al. found that for nasopharyngeal carcinoma some automated plans did not fully meet dose objectives for the planning target volumes (PTV) and cautioned that AP cannot be fully trusted, and a manual selection between MP and AP should be performed for each patient [213].

2). Multi Criteria Optimization:

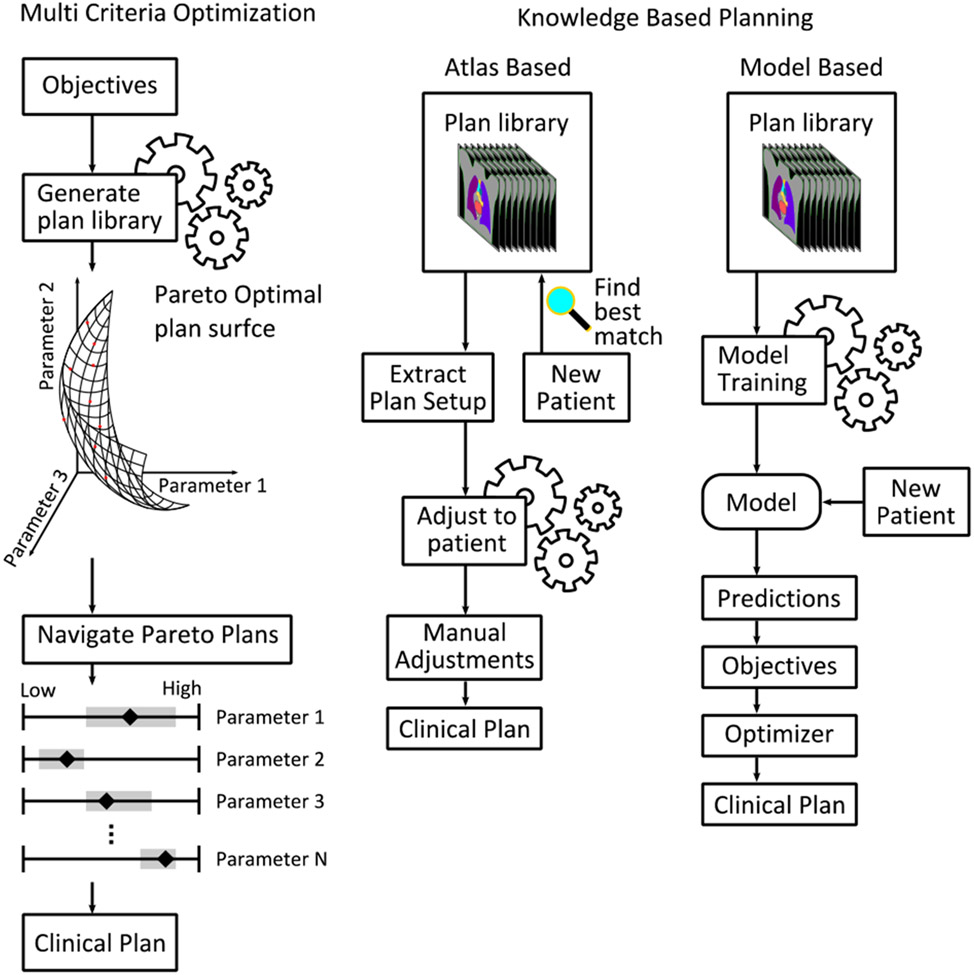
MCO is a method for AP that explores so-called Pareto-optimal (PO) plans. In a space spanned by assigning a dimension to each optimization parameter, the PO surface consists of plans that cannot be further optimized without degrading the performance of another objective. A schematic view of the MCO planning process is presented in Fig. 9. The PO surface is populated by several plans with various objective prioritizations, and while the clinically ideal plan is always on the PO surface, not all plans at the PO surface will be clinically acceptable or desirable. Hussein et al. describes two approaches for AP with MCO, a priori and a posteriori. In the case of a priori, only a single pareto-optimal plan is fully generated and presented to the treatment planner, while for a posteriori MCO, multiple plans are automatically generated, and the treatment planner can perform trade-off navigation using e.g., a navigation star [215] or sliders RayStation MCO (RaySearch Laboratories, Stockholm, Sweden), Varian Eclipse MCO) representing the objectives [216]. A posteriori MCO offers a convenient method to efficiently find an optimal treatment plan, while the treatment planner takes active choices in the process, and has been subject to several studies [217-229]. Kierkels et al. found that MCO plans had similar performance to MP, but allowed inexperienced planners to make high quality plans [224]. Creating a large number of plans is computationally intensive, but can be done in the background while the planner attends to other tasks. Furthermore, estimations made by Bortfield and Craft suggests that as few as N+1 plans are needed to populate the PO surface, where N is the number of objectives [230]. The Erasmus-iCycle software [217] presents a solution for a priori MCO, where a disease-site-specific wish-list is defined with absolute and desired constraints, used for iterative optimization by the software. The software has been used in several studies, yielding clinically acceptable plans of similar or higher quality when compared to manually created plans [231-236].

Fig. 9.

Schematic view of some classical auto-planning workflows. Left: Multi criteria optimization generates a library of pareto optimal plans from a set of objectives. In the schematic, the user navigates the plans a posteriori by use of sliders for each parameter. Right: Knowledge based planning relies on a set of high-quality clinical plans. Atlas based methods finds the best matching patient in the library when introduced to a new patient, extracts the plan and adjusts it to the new patient. Model based approaches train a predictive model on the library plans. The model is used to predict parameters for new patients, which are used to generate objectives for the optimizer.

3). Knowledge Based Planning:

KBP exploits the knowledge and expertise of treatment planners to aid the planning process for new patients, through a library of high-quality clinical treatment plans. When a new patient is presented to the system, it will be characterized based on anatomical and geometrical features. There are two branches of KBP. In atlas-based systems, the closest matching patient in the library is chosen, and the plan setup belonging to that patient will be duplicated to the new patient and recalculated on its planning-CT. In model-based systems a predictive model is trained from the plan library, to predict parameters used for creating automated plans for new patients. The workflow for these approaches is illustrated in Fig. 9.

4). Atlas-based KBP:

Atlas based KBP [237-246] searches a library (i.e. atlas) of clinical plans to find the plan most similar in geometry to the new patient. The library plan setup is copied to the new patient, and the dose is calculated on the CT of the new patient. A general approach is to copy the plan setup and position the isocenter centered in the target volume of the new patient. The original plan can be adapted further, as demonstrated for HNC patients by Schmidt et al. where the atlas plan was adapted to the new patient by deforming the atlas plan beam fluences to suit the target volume in the new patient and warping the atlas primary/boost dose distribution to the new anatomy. The warped dose distribution was then used to generate dose-volume constraints as optimization constraints. In this study it was found that AP had similar or better quality compared to MP for all objectives. The extra steps to deform and warp the plan led to improved performance compared to simply using the atlas plan directly [244]. Atlas-based KBP can either be used to provide a starting point for further optimization, or fully automate planning. Schreibmann et al. demonstrated the use of atlas-based KBP for whole brain radiotherapy, generating high quality treatment plans in 3-4 minutes, with reduced doses to OARs [245], thus reducing the clinical workload.

5). Model-based KBP:

Model based KBP [194, 202, 210, 214, 226, 229, 237, 238, 247-282] trains a model on the plan library to predict parameters for a new patient introduced to the system. Such parameters can be e.g., beam settings, DVHs for target volumes and OARs, or full 3D dose distributions. DVH prediction has been widely studied in recent years for most disease sites, e.g., head and neck [214, 226, 258, 272, 274, 281], prostate [210, 238, 251, 255, 264, 266-268, 270, 276, 281], upper GI [259, 265, 273, 280], lower GI [229, 254, 269, 277, 278] and breast [259, 262, 275]. A commercial software for DVH prediction is Varian RapidPlan. RapidPlan examines geometric and dosimetric properties of structures in each library plan and uses these to calculate a set of features. The calculated data of each plan is included in model training, where principal component analysis (PCA) is used to identify the 2-3 most important features, which are used as input for a regression model [283]. The final model is then used for DVH prediction. DVHs can be converted to objectives for the inverse planning optimizer by sampling the predicted DVH curve and creating corresponding dose-volume objectives. The majority of studies demonstrate that the dose distribution to target volumes of the APs are equally good or better than that of MPs, with no human planner interaction, while the time it takes to generate a plan is drastically reduced. Several studies also demonstrate reduced dose to OARs for APs compared to MPs, possibly due to manual planners not having sufficient time to make further improvements once a clinically acceptable plan is found. One major limitation of DVH prediction models is that they only consider dose-volume relations for delineated structures, and not spatial distributions, thus the planner must be aware of issues such as where excess dose in healthy tissue is placed.

KBP models can be trained by relatively few patients, as demonstrated by Boutillier et al., who successfully trained a model for rectum DVH estimation using 20 library plans [284]. In a recent review of KBP methods by Ge and Wu, it is suggested that more complex plans will require larger plan libraries. Development of larger training databases, e.g., by multi-institution collaborations, is recommended [261]. Another option to increase plan library size is to include plans from other techniques, e.g., 3D-CRT and IMRT plans for training a VMAT model [285], or plans from a different TPS [273]. However, as demonstrated by Ueda et al., models may perform differently when used under other conditions than those of library plans [273], thus proper QA during commissioning is important.

B. Modern AI in Radiation Therapy Treatment Planning

Modern AI, in particular the recent advancement in DL techniques, have achieved great success in a wide range of different disciplines, including medicine and healthcare. In the regime of RT treatment planning, a number of DL-driven AP methods have been developed recently in literature to address the remaining challenges in classical AP approaches. These novel methods can be roughly categorized into three groups: DL-based dose prediction; DL-based fluence map/aperture prediction; and DL-based intelligent treatment planner.

1). DL based Dose Prediction:

The DL dose prediction AP workflow is depicted in Fig. 10. A key step in this type of approaches is to build a DL-based dose prediction agent. Constructed by a carefully designed deep neural network (DNN), the dose prediction agent directly derives the dose distribution of a clinically acceptable plan based on the patient anatomical information (e.g. organ contours and/or CT image) and planning configurations (e.g. prescription dose, treatment beam/arc setups). Pioneer study [286] was firstly performed to investigate the feasibility of DL-based dose prediction using the treatment planning task of prostate cancer IMRT as a testbed. As a proof-of-principle study, a simplified 2D dose prediction was considered. The prediction accuracy was validated on a set of dosimetric quantities of clinical interest. With feasibility well justified, DL-based dose prediction was then successfully extended to other modalities (e.g. VMAT and helical tomotherapy) [287-291], and more complicated treatment sites (e.g. HNC and lung cancer) [287-290, 292], as well as to the direct 3D dose distribution prediction [291-293], which all are of more clinical and practical values. Later on, Pareto optimal dose prediction models [228, 293, 294], which can generate multiple plans reflecting different trade-offs among critical organs, were also developed to better address the diverse clinical needs. The clinical application of DL-based prediction methods is analogue to the classical KBP methods while the major difference is that DL-based dose prediction derives dose distributions directly in contrast to the DVHs generated in KBP. Despite the great success achieved, DL-based dose prediction also suffers from the similar hurdle as KBP, i.e. the predicted dose may be dosimetrically attractive, but not be physically achievable.

Fig. 10.

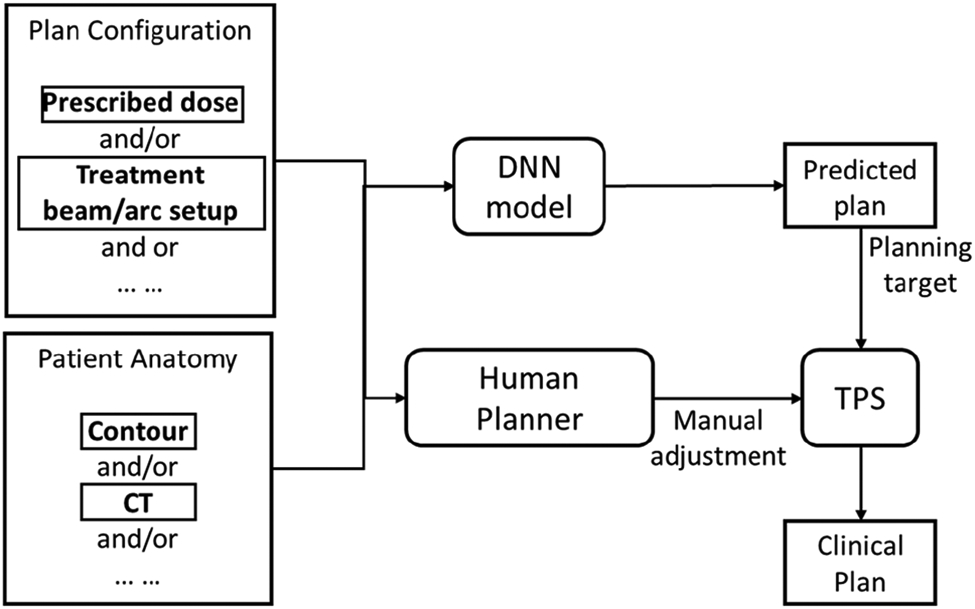
General workflow of DL dose prediction based auto-planning.

2). DL based Fluence Map Prediction:

As shown in Fig. 11, the second type of approaches predicts the fluence map of an optimal plan from patient anatomy using DNN [196, 295-297], bypassing the plan optimization process in inverse treatment planning. More specifically, Lee et al.[295] developed a DNN model to derive the optimal fluence map of IMRT in a beam-by-beam-fashion using the beam’s eye view of PTV/organ contours, and the predicted optimal dose distribution for each beam as input. Li et al. [296] proposed a Dense-Res Hybrid Network (DRHN) to take a series of projections characterizing patient anatomy and treatment geometry as input and output the fluence intensity maps for the nine-field beam prostate cancer IMRT. Wang et al. [297] proposed two-stage strategy with each stage accomplished by a dedicated DNN. In the first stage, the dose of a beam is predicted from the contours and CT image of a patient, and the fluence map is then obtained based on the predicted dose of beam in the second stage. Note that these algorithms were all developed specifically for IMRT, which typically involves only a very limited number of treatment beams (≤9). Lin et al. [196] proposed a DL-based fluence map prediction approach that can handle the more general VMAT planning in which fluence map of 64 treatment beams at different angles needs to be determined. By assuming the dose of an optimal plan already known, the projected dose was employed as input of the established DNN model to predict the fluence map. All these studies have shown DL as a promising tool for fluence map prediction. However, the physical achievability and deliverability of the predicted fluence map is again not guaranteed.

Fig. 11.

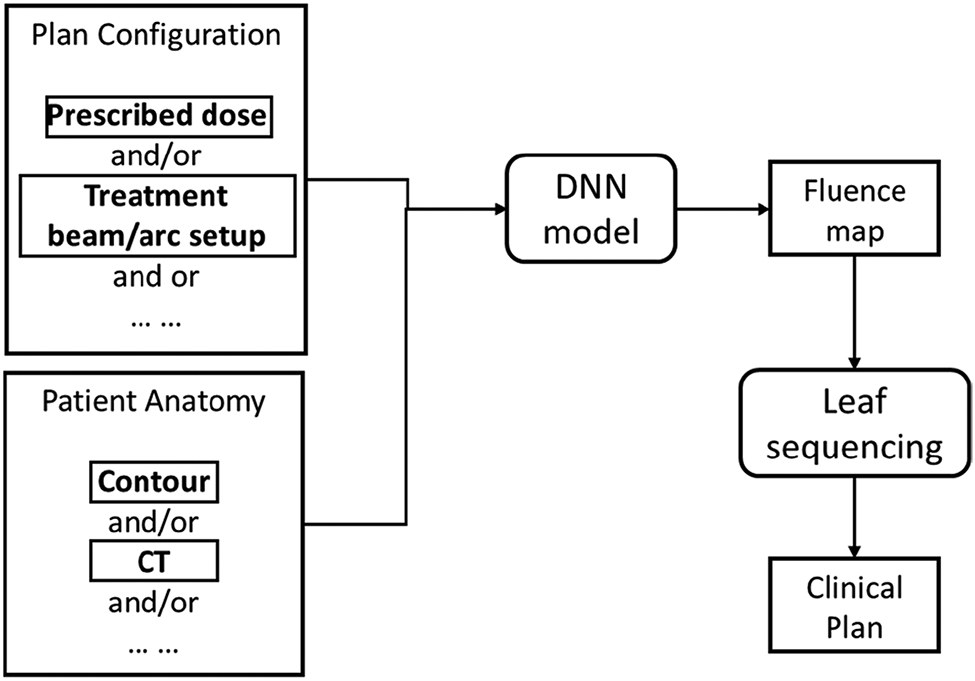
General workflow of DL fluence map prediction based auto-planning.

3). DL based Virtual Treatment Planner:

Motivated by the tremendous success of reinforcement learning (RL) in achieving human-level intelligence in decision-making process, the third group of methods focuses on developing RL-based virtual treatment planners (VPNs) to automatically adjust treatment planning setups or machine parameters [298-302] for high-quality treatment plans (Fig. 12). The idea of training a VPN is similar to the trial-and-error learning process of human beings. It allows the VPN to explore different ways of adjusting treatment planning setups/machine parameters and observe the impacts of these adjustments to the plan quality. VPN will gradually learn the consequences of applying different adjustments to a given plan from a wide spectrum of scenarios encountered in the training process, such that it can pick the adjustment leading to optimal plan quality. The feasibility of RL-based VPN has been demonstrated in both a proof-of-principle context of high-dose-rate brachytherapy [300] and more complicated cases of external beam radiotherapy [298, 299, 301, 302], showing that intelligent behaviors of operating a TPS can be spontaneously generated via an end-to-end RL. Unlike the dose prediction and fluence map prediction methods, RL-based approaches naturally guarantee the achievability and deliverability since the final plans are generated by a TPS. However, the low training efficiency and poor scalability of VPN have limited its applications to only simple treatment planning problems. Although recent studies have shown that the training efficiency and model scalability can be substantially improved by incorporating human knowledge [299], and DNN of hierarchical architecture ()[298], respectively, the feasibility of VPN on a commercial TPS for complex clinical treatment planning tasks still needs to be further investigated. Moreover, the VPNs in existing studies are trained under the guidance of simple plan evaluation quantities, such as ProKnow score (ProKnow Systems, Sanford, FL, USA), which does not necessarily reflect the real planning objectives in clinic. Better metrics of more clinical relevance, e.g. physicians’ preference on plan quality, need to be quantified, and incorporated to guide the training process of a VPN.

Fig. 12.

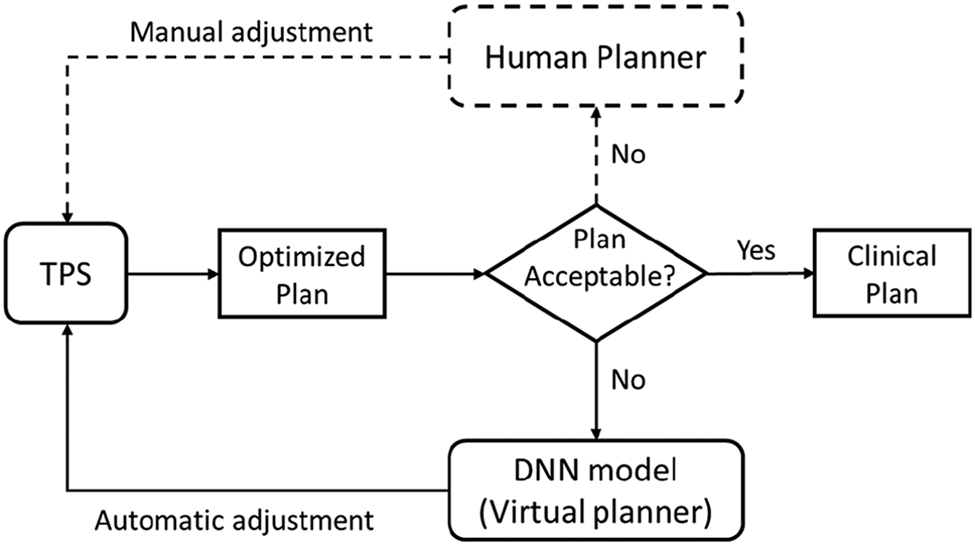
General workflow of virtual treatment planner based auto-planning, analog to conventional human planning process (dashed route).

C. Challenges of Auto-planning

Although classical/DL based AP methods have achieved great success in many aspects, a number of technical or practical challenges remain unsolved. The first major challenge is the data size problem. Training effective AP models often requires a large cohort of data of sufficient diversity to cover the variations among different patients. However, such datasets are non-trivial to collect, and their accessibility is very limited due to many concerns, such as privacy issues. This is indeed more of a concern for DL-based algorithm since it typically requires huge amount of data to optimize DNNs with respect to the large number of learnable parameters. Lack of data often leads to severe overfitting, which may substantially deteriorate the performance of models on new patient cases never observed in model training. Second, despite their encouraging performance, most of the AP models, especially the DL-based ones, are difficult to interpret. To confidently deploy a model to automate the treatment planning process of patients, it is essential to have a good understanding about the reason behind the plan generation process. Such interpretability of a model is necessary to ensure its generality and robustness on different patients. Lack of interpretability may lead to unexpected model failure in clinical deployment stage, posing serious risk to patients. In addition, there is also arising worries de-staffing/deskilling of human planners. However, in a study by Speer et al., it was found that experienced planners outperform AP systems in complex cases [23]. In this regard, AP will be helpful to reduce the workload from simple cases and enable human planners to spend more time on complex cases, thereby further improving plan quality. To implement AP in most clinics, commonly accepted guidelines on implementation and quality assurance of AI models will play an important role, as discussed thoroughly in a recent review article by Vandewinckele et al. [303].

D. Outlooks/Future Directions

AP has a great potential to automate and accelerate the tedious and time-consuming treatment planning process of RT. It is expected to improve the quality of treatment plans to a better level consistently, allowing to deliver the best of care to each patient. AP would also release human planners from simple cases, whose efforts can be focused on more challenging cases. The urgent need AP is further amplified in the regime of adaptive RT where planning efficiency critically affects the success of adaptation. Furthermore, moving towards the era of personalized care, AP permits quick generation of treatment plans of different treatment techniques, e.g. IMRT vs. VMAT, standard fractionation vs. SBRT, and photon vs. proton treatment, etc., from which the best treatment plan can be chosen for optimal treatment outcome.

The remaining challenges of AP approaches, such as data size and interpretability, need to be addressed for the development of effective and reliable models. Collecting a large inter-institutional dataset is attractive, but less practical due to privacy and regulation concerns. One potential solution might be federated learning [304-306], which allows each institution to keep their own data while having the model be trained on all data. In addition, interpretable machine learning/DL [307, 308] has become a central topic recently due to the increasing need of model expainability and reliability in many applications including RT. More efforts are definitely needed along these directions to fulfill the urgent, but unmet need of AP.

Fig. 1.

Illustration of image reconstruction from sensor domain.

Fig. 2.

Comparison of ultralow-dose CT images (120 kVp, 10 mAs) reconstructed by six different approaches. All the images are displayed in the same window of [−160, 240] HU. Figure reprinted from Wang et al. with permission.

Fig. 6.

GAN Framework showing MRI to CT image translation. The generator tries to learn the data distribution of MRI and CT images and uses this learnt representation to convert an MRI image to a fake CT image. The generator learns this representation by trying to fool the discriminator while it is comparing real and fake CTs and learning to differentiate between them.

Fig. 7.

Workflow for adaptive radiotherapy enabled by dose calculation from CBCT images. Prior to dose recalculation, a CBCT image is converted to a synthetic CT (sCT), providing correct HU values and removing artifacts, while preserving the anatomy.