Water filling of microcavities

Abstract

Cavity-filling is a common phenomenon whereby a fluid fills all or part of a cavity, displacing another immiscible fluid. In this study, we experimentally and theoretically investigate the effects of the cavity aspect ratio, channel width, tilting angle of the cavity leading wall, and inlet flow rate on the morphology of the water-air interface and the filling fraction of various cavities. Considering the influencing factors, we derive two formulas for predicting the filling fraction, and verify these expressions against experimental results. The findings of this study provide theoretical guidance for applications related to pressure-driven filling of cavity structures.

I. INTRODUCTION

In recent years, the filling of cavities (gaps, holes, grooves, pores, and wells) by fluids in microscale channels or textured surfaces has received significant research attention.^1–3 Cavity-filling driven by inlet pressure or capillary force is a common phenomenon in engineering and nature,^4–6 such as in the cases of gravure printing with grooves,^7,8 embossing lithography with pits,^9–12 superhydrophobic and/or self-cleaning surfaces,^13–15 enhanced oil recovery from shales,^16–20 surface coating with notches,^21,22 drag reduction with infused-phase fluid in textured or patterned surfaces,^23–26 and liquid infusion into microfluidic chips with wells.^27,28 Depending on the application, it may be desirable to either fill or empty the cavity. In the case of self-cleaning^13–15 and drag reduction,^23–26 no cavity-filling is expected, whereas in many other cases, it is desirable to fill the cavity, e.g., surface coating and gravure printing. When the filling liquid reaches the leading edge of the cavity, the sudden change of the contact angle pins the three-phase contact line (e.g., air-liquid-solid wall), and this plays an important role in the cavity-filling process.^14–27 Understanding the background physics of the cavity-filling process provides theoretical guidance for the design of patterned surfaces with cavities in practical applications.

The factors that influence the filling fraction include the cavity geometry and inlet flow rate of the filling fluid, which have been investigated in many studies.^28–34 Li et al.²⁸ experimentally and theoretically investigated the effect of the cavity width on the filling or cleaning fraction, finding that the filling fluid can completely fill cavities with widths above a critical value, whereas the Cassie status²⁹ will be maintained when some pre-infused fluid is sealed in a narrow cavity. Sun et al.³⁰ simulated the effect of the cavity width/length ratio on the filling fraction, and found that this determines the performance of drag reduction on cavity-patterned surfaces. To guide oil recovery, Ankur et al.^31,32 studied the effects of the cavity configuration (triangular or wavy) on oil displacement efficiency. Gao et al.³³ investigated the effect of the inlet flow rate on the morphology of the gas-liquid interface and the pinning phenomenon during the cavity-filling process, while Reddy et al.³⁴ simulated the evolution of the interface during the cavity-filling process and found that the filling fraction is greatly affected by the cavity size.

The advancing contact angle (θ_a) of the two-phase interface on the channel wall also has a significant effect on the interface morphology and the cavity-filling fraction.³⁴ At the leading cavity edge, the sudden decrease in the θ_a pins the contact point until θ_a increases to a certain threshold, whereupon the depinning phenomenon occurs.³⁵ To optimize the surface conditions for good imprinting results, Kim et al.³⁶ simulated the effects of the θ_a and aspect ratio of recessed features on the flow behavior during the filling process. Quere et al.³⁷ reported that the wettability and roughness of the wall can affect the θ_a significantly, with the contact line first maintaining the pinning state and then suddenly moving when θ_a exceeds a critical value. Alizadeh et al.³⁸ numerically investigated the effects of wettability and interfacial tension on the redistribution and transport of oil in pore models. Sharma et al.³⁹ performed an experimental and modeling study to investigate brine-rock interactions during low-salinity-water flooding in carbonates, finding that θ_a plays an important role in oil recovery.

Although many studies have attempted to reveal the effects of various factors on the cavity-filling fraction, more effects should be devoted to explore the influence of the geometrical factors on the dynamic evolution of the interface morphology and the cavity-filling fraction. In this study, using high-speed microphotography, we carried out experiments to systematically investigate the effects of the cavity aspect ratio, channel width, and inlet flow rate on the morphological evolution of the air-water interface and filling fraction. Moreover, considering the influencing factors, we theoretically derived two formulas to predict the filling fraction, and found these to be consistent with experimental results.

The current paper is structured as follows. Details of the materials and methods are provided in Sec. II. Experimental results for the air-water interface morphology are presented in Secs. III A–III D. Two theoretical formulas for predicting the filling fraction in rectangular and other-shaped cavities are derived and verified against the experimental results in Secs. III E and III F. Finally, the conclusions to this study are presented in Sec. IV.

II. MATERIALS AND METHODS

A. Microfluidic device

The microfluidic chip used in this study consists of a straight microchannel with several rectangular cavities located on one side [Fig. 1(a)]. The total length of the microchannel is 18.8 mm. The width of the microchannel (W) takes one of three values (50 μm, 100 μm, or 200 μm). The length of the cavity takes two values (L_c = 100 μm or 200 μm), whereas the cavity width (W_c) varies from 0.2L_c–2.0L_c at fixed intervals of 0.2L_c. The depth of the microchannel and the cavities is 100 μm. The cavity width/length ratio is defined as $e=W_c/L_c$ and the channel width ratio is defined as $W/L_c=\lambda$. Cavities with triangular and trapezoid shapes are also examined. The microfluidic chip was made of polydimethylsiloxane (PDMS) using soft photolithography methods.⁴⁰

FIG. 1.

Microfluidic chip and experimental setup. (a) Microfluidic chip consisting of a straight channel and many cavities. (b) Snapshot of the morphology of the water-air interface in a rectangular cavity. (c) Experimental system.

B. Experimental setup

To visualize the evolution of the water-air interface during the filling process [Fig. 1(b)], a microscope imaging system was employed [Fig. 1(c)], which consists of an inverted microscope (IX73, Olympus), a high-speed camera (VEO340L, Phantom), and a syringe pump (Harvard Apparatus, PHD2000). The high-speed camera was set to capture images with a resolution of 1280 × 800 pixels at 1,000 frames per second (fps). ImageJ and MATLAB software were used to measure and analyze the angle and interface morphology. All experiments were conducted at 25 ± 0.5°C.

In the experiments, deionized water (density ρ₁ = 997 kg/m³, dynamic viscosity μ = 0.903 mPa s, and surface tension σ = 71.97 mN/m) was used as the filling fluid. The inlet flow rate Q varied from 1–200 μl/min. Theoretically, the inlet Reynolds number of the channel is Re = 2Qρ/μ (W + H), which is less than 49.1 under our conditions. The maximum value of the capillary number Ca = Qμ/WHσ is 8.4 × 10⁻⁴, and the maximum value of the Weber number We = 2ρQ²/WH (W + H) σ is 0.41. Therefore, the surface tension and the fluid pressure dominate the evolution of interface morphology in the process.

C. Theoretical formula of the filling fraction

To analyze the filling fraction theoretically, we consider a simplified two-dimensional model. As the interface morphology is dominated by the interfacial tension and fluid pressure (the effects of gravity, fluid inertia, and flow shear stress are neglected), it can be assumed that the water-air interface maintains an arc shape during the filling process. Therefore, according to the interface morphology at the second pinning stage [Fig. 2], the filling fraction can be calculated as:

$$\begin{array}{r}\mathrm{\Delta }={\displaystyle \frac{{\displaystyle \frac{\pi ({90}^{°}-\theta +\beta )}{{180}^{°}}+\sin \theta \cos \theta -2\cos \theta \cos \beta -\sin \beta \cos \beta }}{2e{(\cos \theta +\sin \beta )}^2}\times 100\text{\%},}\end{array}$$ (1)

where β is the angle between the interface and the channel wall at the trailing edge. The derivation of Eq. (1) is explained in Appendix A. The value of β can be theoretically derived as

$$\beta =\arcsin {\displaystyle \frac{(1-\lambda )\cos \theta }{\sqrt{1+{\lambda }^2}}+\phi (0<\beta <\pi ),}$$ (2)

$$\phi =\arctan \left({\displaystyle \frac{1}{\lambda }}\right),$$ (3)

where λ is the aspect ratio of W/L_c and $\phi$ is a phase angle used to determine β. Therefore, for a given value of λ, it is possible to calculate the β value. Detail of the derivation of is provided in Appendix B.

FIG. 2.

Schematic diagram of the geometric relationship between the interface and cavity.

III. RESULTS AND DISCUSSION

A. Evolution of water-air interface morphology

The dynamic evolution of the water-air interface morphology in a 200 × 200 μm² cavity is divided into five stages [Fig. 3]. In the microchannel, a stable water-air interface is formed. The acute angle (θ) between the interface and channel wall is 70°. Please note that we used the acute angle, in this study, to make the explanations and formulas more convenient. The conventional advancing contact angle is θ_a = 180°–θ = 110°. When arriving at the leading cavity wall (t₁ = 0 ms), the contact point of the interface on the upper wall of the channel is pinned at the edge, and the pinning phenomenon of the interface occurs, as commonly observed in microscale flows.⁴¹

FIG. 3.

Morphologies of water-air interface during filling process in a 200 × 200 μm² cavity (W = 50 μm, Q = 1 μl/min). (a) Start-up stage; (b) first pinning stage; (c) and (d) interface rising stage; (e) second pinning stage; (f) final stage.

In the pinning process, the interface changes its morphology continuously under the combined effects of the Laplace pressure and driving fluid pressure. As the interface deforms, its tangent line rotates slowly around the leading edge, forming a new acute angle (α) between the interface and leading wall at t₂ = 99 ms. When α is almost equal to θ, the interface starts to slip along the leading wall (depinning), and the slip distance (d) increases with time. The interface contact point on the lower channel wall continues slipping with the same θ_a of 110°.

As water continues to be injected, the interface deforms and stretches continuously, leading to the displacement of air, until the interface is pinned at the cavity trailing edge at t₅ = 149 ms. Finally, the interface splits into two parts, one of which shrinks and traps some air in the cavity at t₆ = 164 ms.

B. Effect of cavity size on final interface morphology

The cavity size has a significant influence on the filling fraction and final interface morphology. Figure 4(a) shows that the shallow cavity with e = 0.2 is almost filled with water (only a very small amount of air remains at the bottom), while there are two small air bubbles trapped in the farthest corners of the cavity with e = 0.4. When e ≥ 0.6, the interface cannot reach the cavity bottom. As e increases from 0.6 to 2.0, the volume of air trapped in the cavity increases. Moreover, the interface becomes curved in cavities with e = 0.6, 0.8, and 1.0, whereas it remains almost straight with a nearly fixed position in cavities with e ≥ 1.2.

FIG. 4.

Final interface morphology in different cavities: (a) L_c = 100 μm; (b) L_c = 200 μm (W = 50 μm, Q = 1 μl/min).

Figure 4(b) shows two air bubbles trapped in the farthest corners of cavities with e = 0.2, 0.4, and 0.6. When e ≥ 0.8, the interface cannot reach the cavity bottom and the filling volume of water remains almost unchanged. Moreover, all the interfaces become visibly curved in cavities with e ≥ 0.8, which indicates that the interface morphology is more susceptible to deformation in large cavities. The final morphology of the interface is determined by the complex interaction of the two-phase interfacial tension, fluid pressure, flow shear stress, and surface tension on the walls.

Figure 5 shows the slippage distance (d) of the interface along the leading cavity wall. With L_c = 200 μm, d increases from 40 μm to 120 μm as e increases from 0.2 to 0.6, and then fluctuates around a high plateau when e ≥ 0.8. The average value of this plateau is 128 μm. Similarly, with L_c = 100 μm, d increases and then remains almost unchanged. However, the maximum value of d is only 41 μm in this case, much lower than that with L_c = 200 μm. Thus, the maximum slippage distances with L_c = 100 μm and 200 μm are 41 μm and 128 μm, respectively, and the filling fraction in wide cavities is greater than that in narrow cavities.

FIG. 5.

Slippage distances in cavities with different aspect ratios (W = 50 μm, Q = 1 μl/min).

C. Effect of channel width on filling fraction

The effect of the microchannel width (W) on the filling fraction is now investigated. Figure 6 shows the interface morphologies in channels with different widths at the second pinning stage. The slippage of the interface on the leading wall in the 100 × 100 μm² cavity (left) is less pronounced than in the 200 × 200 μm² cavity (right). The slippage of the interface decreases as the channel width increases from 50 μm to 100 μm and 200 μm. Moreover, in the 100 × 100 μm² cavity with W = 200 μm [Fig. 6(c)], as α is always less than θ, the interface is still pinned by the leading edge when it becomes pinned by the trailing edge, and so there is no slippage of the interface and no filling of water.

FIG. 6.

Interface morphology at the second pinning stage in cavities. (a) W = 50 μm, (b) W = 100 μm, and (c) W = 200 μm at Q = 1.0 μl/min. Left column: L_c = W_c = 100 μm; right column: L_c = W_c = 200 μm.

Furthermore, as the channel width increases, the radius of curvature of the arc interface increases with the stretching length. In addition, for both cavities, the water filling time (the time from the water reaching the leading edge to the moment of the second pinning stage) increases with increasing channel width. The reasons include the low average flow velocity in wider channels and the interface expansion. The slippage and morphology of the interface are determined by a complex relationship between the surface tension, θ_a, fluid pressure, and filling time.

The relationship of the geometry parameters with the cavity-filling fraction (Δ), defined as the ratio of water area to cavity area, is characterized in Fig. 7. Basically, the filling fractions gradually decrease with increasing cavity aspect ratio. The maximum filling fraction is nearly 100% for shallow cavities. For W = 200 μm and L_c = 100 μm, the filling fraction is always less than 1%. Moreover, for cavities with the same aspect ratio, the filling fraction decreases with increasing channel width. Furthermore, due to the long filling time, the filling fraction in cavities with L_c = 200 μm is higher than that in cavities with L_c = 100 μm.

FIG. 7.

Filling fractions under different geometry factors (Q = 1.0 μl/min).

D. Effect of inlet flow rate on filling fraction and contact angle

The relationships between the inlet flow rate (Q = 1.0–200 μl/min) and the filling fraction (Δ) in cavities with different widths (L_c = 200 μm, W = 50 μm) are shown in Fig. 8(a). With W_c ≤ 120 μm, Δ is close to 100%, regardless of the flow rate. The reason is that the cavity is so shallow that the interface can slip to the cavity bottom and drive the air out of the cavity before the occurrence of the second pinning stage. With W_c = 160 μm, Δ first decreases from 78.5% to 50.4% at Q = 50 μl/min, then increases to 82.7% at Q = 200 μl/min. In cavities with W_c = 200 μm, 240 μm, and 280 μm, the average filling fractions are 61.3%, 50.3%, and 44.1%, respectively, and these are almost independent of the flow rate. In deep cavities with W_c = 320 μm, 360 μm, and 400 μm, the filling fractions are uniformly low, decreasing slightly at first and then increasing to about 51% at Q = 200 μl/min. We speculate that this is because a vortex may occur in the cavity at Q = 200 μl/min,^42–44 driving the interface to move towards the cavity bottom.

FIG. 8.

Effects of inlet flow rate on (a) filling fractions and (b) advancing contact angles on the walls (W = 50 μm, L_c = 200 μm).

The effects of the inlet flow rate on the θ_a at the channel wall (180°−θ) and leading cavity wall (180°−α) are shown in Fig. 8(b). It can be found that as Q increases, the θ_a increases slightly from 109.3° to 111.8°, while θ and α decrease from 70.7° to 68.2°. The acute angle is determined by the interfacial tension and fluid pressure drop across the interface, which can be described using the force analysis equilibrium equation as

$$P_{drop}={\displaystyle \frac{2(W+H)\sigma \cos \theta }{W\times H},}$$ (4)

E. Comparison of theoretical and experimental results

Figure 9 show that the experimental and theoretical results of the β values are in good agreement. As λ increases from 0.25 to 2.0, β gradually decreases from 90.5° to 17.2°. The results indicate that, for a certain cavity with known geometrical factors (e and λ), the filling fraction in Eq. (1) is only dependent on the acute angle θ, which can be adjusted by controlling the inlet flow rate.

FIG. 9.

Comparison of theoretical and experimental results for the angle β.

For example, with λ = 1, Eqs. (2) and (3) yield $\beta ={45}^{°}$, which agrees well with the observations of Chen et al.,²⁸ who found that the fluid-fluid interfaces are circular and approximately symmetrical to a 45° line in cavities with W = L_c = 100 μm.

We can rewrite Eq. (1) as

$$\mathrm{\Delta }={\displaystyle \frac{{\displaystyle \frac{\pi ({135}^{°}-\theta )}{{180}^{°}}+\sin \theta \cos \theta -\sqrt{2}\cos \theta -{\displaystyle \frac{1}{2}}}}{2e{\left(\cos \theta +{\displaystyle \frac{\sqrt{2}}{2}}\right)}^2}\times 100\text{\%}.}$$ (5)

Using Eq. (5) and the measured value of θ = 70° at Q = 1.0 μl/min in a cavity with W = L_c = 200 μm, the filling fraction can be calculated. The theoretical and experimental results for the filling fraction with different aspect ratios are consistent, as shown in Fig. 10, where both decline exponentially as e increases. For shallow cavities (e = 0.2), Δ is close to 99%, whereas for deep cavities (e = 2.0), Δ is about 8.8%. Moreover, for a more specific cavity (square) with W = L_c = W_c (e = λ = 1), Δ is around 19.6%.

FIG. 10.

Comparison of theoretical and experimental results for the filling fraction (W = L_c = 200 μm, Q = 1.0 μl/min, θ = 70°).

For the purpose of drag reduction using a stable air-water interface, the slippage distance should be d = 0. According to the derivation in the Appendix A, the equation $\sin \theta -\cos \beta =0$ must be satisfied, whereby the critical width of the cavity can be derived as

$$L_c^{\ast }={\displaystyle \frac{2W}{1+\tan \theta }.}$$ (6)

Equation (6) is in good agreement with the result of Chen et al.²⁸ According to Eq. (6), when $L_c<L_c^{\ast }$, the interface will always be pinned at the leading edge.

F. Effects of cavity shape on filling fraction

The effects of the tilting angle (θ_L) between the leading cavity wall and the main flow direction on the filling fraction are now investigated. Figure 11 shows the interface morphology at the second pinning stage in cavities with different shapes (triangle, quadrilateral, and trapezoid). It can be found that, as θ_L increases from 30°–105° [Figs. 11(a)–11(h)], the slippage distance of the interface along the leading wall (d/sin θ_L) decreases, leading to a reduction of the filling fraction. During the depinning stage, the angle α between the interface and leading wall must decrease from θ + θ_L to θ. Thus, the time needed for depinning is longer in the case of large values of θ_L than with small θ_L.

FIG. 11.

Interface morphology in cavities with different tilting angles (W = 100 μm, L_c = 200 μm, Q = 1 μl/min). (a) θ_L = 30°, (b) θ_L = 45°, (c) θ_L = 60°, (d) θ_L = 75°, (e) θ_L = 105°, (f) θ_L = 120°, (g) θ_L = 135° and (h) θ_L = 150°.

When θ_L ≥ 120°, the interface is pinned at the leading edge in Figs. 11(f)–11(h). The α is still above the angle of θ = 70° when the interface is pinned at the trailing wall. It can be found that only the entrance region is filled with water, which leads to a low filling fraction. The calculated absolute filling volumes in Figs. 11(f)–11(h) are 2.38 nl, 2.36 nl and 2.04, respectively. Moreover, as the interface is always pinned at the trailing wall (θ_L ≥ 120°), the absolute filling volume is mainly determined by the interface morphology in the entrance region, and the W_c become irrelevant in deep cavities. The results indicate that the tilting angle has a significant effect on the pinning effect and the filling fraction.

To predict the filling fraction of cavities, we modify Eq. (5) to the following form:

$$\mathrm{\Delta }={\displaystyle \frac{{\displaystyle \frac{\pi ({\theta }_L-\theta +\beta )}{{180}^{°}}-\sin ({\theta }_L-\theta +\beta )+{\displaystyle \frac{\sin \theta -\cos ({\theta }_L+\beta )}{\sin {\theta }_L}\times [\sin ({90}^{°}-\theta +{\theta }_L)-\cos \beta ]}}}{(1+K_1)K_2{\left({\displaystyle \frac{\sin \theta -\cos ({\theta }_L+\beta )}{\sin {\theta }_L}}\right)}^2}\times 100\text{\%},}$$ (7)

where the length of the cavity bottom is K₁ × L_c and W_c = K₂ × L_c (in which K₁ and K₁ are length coefficients). The derivation of Eq. (7) is explained in Appendix C.

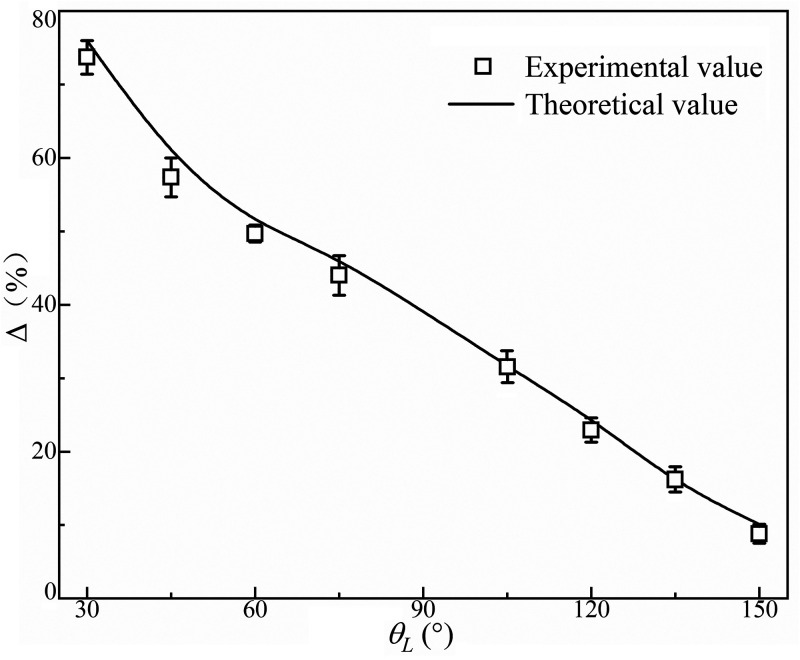
Based on Eq. (7), the calculated filling fractions and experimental results for cavities with different values of θ_L are shown in Fig. 12. Both sets of results decline linearly as θ_L increases. The maximum filling fraction is about 75.9% when θ_L = 30°. For θ_L ≥ 120°, the filling fraction is less than 22.9%. The minimum filling fraction is about 8.8% with θ_L = 150°. The theoretical results are in good agreement with the experimental results.

FIG. 12.

Comparison between the theoretical and experimental results for the filling fraction of cavities with different shapes (W = 100 μm, L_c = 200 μm, Q = 1.0 μl/min, θ = 70°, β = 72°).

IV. CONCLUSIONS

In this study, using microfluidics and high-speed microphotography, we carried out experiments and theoretical analysis to investigate systematically the effects of various influencing factors on the filling fraction of cavities. During the filling process, the interface morphology evolves dynamically, as determined by the combined effects of the cavity size, acute angle, fluid pressure, and so on. The final interface morphology and location determines the filling fraction, which decreases as the aspect ratio increase from e = 0.2 to e = 2.0. As the channel width increases, the filling fraction decreases. In shallow cavities (e < 0.8, W = 50 μm, and L_c = 50 μm), the filling fraction can reach Δ = 100%. As the flow rate increases from 1.0 μl/min to 200 μl/min, the θ_a increases slightly from 109.3° to 111.8°, while the filling fraction changes in a complex manner that is affected by the pinning and depinning effects.

To predict the filling fraction in rectangular cavities, considering various influencing factors, we derived a theoretical formula that is consistent with our experimental results. We extended this formula to a new form for predicting the filling fraction of cavities with other shapes (triangle, quadrilateral, and trapezoid), and again verified its accuracy against our experimental results. To the best of our knowledge, these two prediction formulas are the first such universal expressions to be proposed, which could provide theoretical guidance for related applications.

APPENDIX A: CALCULATION OF THE FILLING FRACTION AND ANGLE β

In Fig. 13, the contact points of the interface on the leading cavity wall, the trailing edge, and the channel wall are denoted as A, B, and C, respectively. The angles between the tangent lines of the interface and the walls at the three points are α, β, and θ, respectively. The center of the circular interface is O. The radius is R, the angles ∠AOE = α, ∠OBF = β, ∠OCG = θ, and ∠AOB =  ${90}^{°}-\alpha +\beta$. According to the geometric relationship, W = CG + BF = R(cos θ+cos β), L_c = OE + OF = R (cos α + sin β), and the slippage distance d = AE–BF = R (sin α−cos β). Thus, the filling area of water in the cavity can calculated as

$$S_{\mathrm{filling}}=S_{\mathrm{\Delta }\mathrm{ABD}}+(S_{\mathrm{Sector}\mathrm{OAB}}-S_{\mathrm{\Delta }\mathrm{OAB}}),$$ (A1)

where the sector area (OAB) and the triangle areas (AOB) and (ABD) are as follows:

$${\mathrm{S}}_{\mathrm{\Delta }\mathrm{ABD}}={\displaystyle \frac{1}{2}(d\times L_c)={\displaystyle \frac{1}{2}{R}^2(\sin \alpha -\cos \beta )(\cos \alpha +\sin \beta ),}}$$ (A2)

$${\mathrm{S}}_{\mathrm{Sector}\mathrm{OAB}}={\displaystyle \frac{({90}^{°}-\alpha +\beta )\pi R^2}{{360}^{°}},}$$ (A3)

$${\mathrm{S}}_{\mathrm{\Delta }\mathrm{OAB}}={\displaystyle \frac{1}{2}{R}^2\sin {90}^{°}-\alpha +\beta ={\displaystyle \frac{1}{2}{R}^2\cos (\alpha -\beta ).}}$$ (A4)

FIG. 13.

Schematic diagram of the geometric relationship between the interface and rectangular cavity.

Therefore, considering $\theta =\alpha$ and W_c = e × L_c, the filling fraction Δ is derived as

$$\mathrm{\Delta }={\displaystyle \frac{S_{\mathrm{filling}}}{W_c{L}_c}={\displaystyle \frac{{\displaystyle \frac{\pi ({90}^{°}-\theta +\beta )}{{180}^{°}}+\sin \theta \cos \theta -2\cos \theta \cos \beta -\sin \beta \cos \beta }}{2e{(\cos \theta +\sin \beta )}^2}\times 100\text{\%}.}}$$ (A5)

APPENDIX B: CALCULATION OF THE ANGLE OF THE INTERFACE ON THE TRAILING EDGE β

Setting $W/L_c=\lambda$, we can write

$${\displaystyle \frac{W}{L_c}={\displaystyle \frac{\cos \theta +\cos \beta }{\cos \theta +\sin \beta },}}$$ (B6)

$$\lambda \sin \beta -\cos \beta =(1-\lambda )\cos \theta \equiv \sqrt{(1+{\lambda }^2)}\sin (\beta -\phi )=(1-\lambda )\cos \theta ,$$ (B7)

where φ is the phase angle, namely an adjustment angle for the calculation of β:

$$\beta =\arcsin {\displaystyle \frac{(1-\lambda )\cos \theta }{\sqrt{1+{\lambda }^2}}+\phi ,}$$ (B8)

$$\phi =\arctan \left({\displaystyle \frac{1}{\lambda }}\right).$$ (B9)

APPENDIX C: CALCULATION OF THE FILLING FRACTION IN CAVITIES WITH DIFFERENT TILTING ANGLES θ_L

In Fig. 14, the radius of the interface is R, the angles ∠ADB = θ_L, ∠AOE =  ${90}^{°}-\theta +{\theta }_L$, ∠OBF = β, α = θ, and ∠AOB =  ${\theta }_L-\theta +\beta$. According to the geometric relationship, W = CG + BF = R (cos θ + cos β), L_c = OE + OF = R $[\sin \beta +\cos ({90}^{°}-\theta +{\theta }_L)+d/\tan {\theta }_L]$, and the slippage distance d = AD × sin θ_L = R $[\sin ({90}^{°}-\theta +{\theta }_L)-\cos \beta ]$. Thus, the areas of the sector (OAB) and the triangles (AOB) and (ABD) are as follows:

$${\mathrm{S}}_{\mathrm{Sector}\mathrm{OAB}}={\displaystyle \frac{({\theta }_L-\theta +\beta )\pi R^2}{{360}^{°}},}$$ (C10)

$${\mathrm{S}}_{\mathrm{\Delta }\mathrm{OAB}}={\displaystyle \frac{1}{2}{R}^2(\sin {\theta }_L-\theta +\beta ),}$$ (C11)

$$\begin{array}{rl}{\mathrm{S}}_{\mathrm{\Delta }\mathrm{ABD}}& ={\displaystyle \frac{1}{2}(d\times L_c)={\displaystyle \frac{R^2[\sin \theta -\cos ({\theta }_L+\beta )]}{2\sin {\theta }_L}}}\\ & \times [\sin ({90}^{°}-\theta +{\theta }_L)-\cos \beta ].\end{array}$$ (C12)

FIG. 14.

Schematic of geometrical relationships between the interface and cavity with a tilting angle.

Therefore, using Eq. (A5), the filling fraction can be derived as

$$\mathrm{\Delta }={\displaystyle \frac{{\mathrm{S}}_{\mathrm{filling}}}{S_{\mathrm{cavity}}}={\displaystyle \frac{{\displaystyle \frac{\pi ({\theta }_L-\theta +\beta )}{{180}^{°}}-\sin ({\theta }_L-\theta +\beta )+{\displaystyle \frac{\sin \theta -\cos ({\theta }_L+\beta )}{\sin {\theta }_L}\times [\sin ({90}^{°}-\theta +{\theta }_L)-\cos \beta ]}}}{(1+K_1)K_2{\left({\displaystyle \frac{\sin \theta -\cos ({\theta }_L+\beta )}{\sin {\theta }_L}}\right)}^2}\times 100\text{\%},}}$$ (C13)

where the length of the cavity bottom is K₁ × L_c and W_c = K₂ × L_c (in which K₁ and K₁ are the length coefficients).

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

Feng Shen: Conceptualization (lead); Methodology (lead); Writing – review & editing (lead). Lin Zhu: Formal analysis (lead); Visualization (lead). Jie Chen: Validation (equal); Writing – review & editing (equal). Zhaomiao Liu: Investigation (equal); Supervision (lead).

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.