On a global continuum model for COVID-19 virus in the presence of vaccine and induced immunity. Stability and initial states control

Abstract

The dynamics of COVID-19 virus were investigated in the literature via mathematical models. These models take into account the action of the suspected-exposed-infected-recovered people (SEIR). Also, among them, those which account for quarantined, social distancing functions or health isolation, were presented. In the absence of effective vaccines or therapies, prevention and treatment strategies for COVID-19 infections can not issue to non-epidemic state. Over the world, vaccination against the virus is set on. This motivated us to develop a model for inspecting if this treatment will issue to non endemic state. To this end, a global continuum model for the dynamics of this virus in the presence of vaccine and stimulated immunity is constructed. The present model deals with EIR - deceased individuals (EIRD) together with action of the health isolation and travelers (HIT). Which is described by nonlinear dynamical system (NLDS). Our aim here is to reduce the problem of solving this system to the case of solving LDS. This is carried by introducing the unified method (UM) via an approach present by the authors. By the UM, the solutions of a NLDS are recast to solutions of LDS via auxiliary equations. Numerical results of the exact solutions are evaluated, with initial data for the EIRD together with the number of vaccinated people. Real data are taken from Egypt (can be from elsewhere) at the end of the first wave, and they are considered as the initial conditions. These results are compared with a previous work by the authors in the absence of vaccination. The results of exposed, infected, recovered and deceased people are computed. It is found that the number of infected people decays to zero asymptotically, while, the number of infected people decays to an asymptotic value. This is in contrast to the results found previously in the case of absence of vaccination, where, these numbers grow monotonically. This is completely new. It is shown that locking-down has a remarkable effect in diminishing the number of infected people. The region of initial conditions for I-E people, that guarantee non-epidemic, non-endemic states, is determined via initial states control analysis. A software tool, based on this model, for simplifying the utilization of various data of different countries is developed. It is worth to mention that, the exact solutions of nonlinear dynamical equations, found here, are novel.

1. Introduction

In the last two years, COVID-19 pandemic acted as global health and economic crisis. An important role in the management and control of the crisis is handled by mathematical models which can help for developing a strategy to overcome the spreading of COVID-19 [1]. A mathematical model with input parameters based on actual data from the European Center for Disease was presented in [2]. COVID-19 virus is transmitted among people through respiratory droplets [3], [4], [5], [6]. The asymptomatic ratio estimate may lead to understanding the virus transmission [7]. All relative effect on infections accompanied by various interventions are subject to uncertainty and anxiety. Mathematical models are needed to predict future health care requirement [8]. Some mathematical models for the outbreak of COVID-19 were presented in [9]. The dynamical behavior of COVID-19 infection by incorporating isolation class was studied in [10]. In this work, the most suitable values of its parameters are inspected. Due to Egypt’s high population density, the control of the pandemic COVID-19 is too necessary in the premier stage and it is a duty problem. Reducing the outbreak size due to the influential parameter was proposed to study the COVID-19 dynamics via many mathematical models [11]. By introducing a quarantine class and intervention rules, to slow down disease transmission, a mathematical model was formulated in [12]. In [13], a mathematical model for inspecting the spread of covid-19 epidemic, with implementation of the population intervention, in Italy was proposed. Also, a discrete and continuum model for COVID-19 by accounting for health isolation and travelers effects was constructed, by the authors, in the absence of vaccination [14]. While, this work takes into account of the effects of vaccination and induced immunity. In [14], it was found that the numbers of infected and exposed (IE) people are strictly increasing with time. While in the present work, it will be shown that, the numbers of IE people decrease asymptotically to zero with time. These results are completely novel.

Recently, the role of the cellular immune response has an evidence in defense against viral infections, and tumor progression [15], [16], [17]. Some relevant works were carried in the literature [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29].Vaccines that induce large quantities of high affinity virus-neutralizing antibodies may globally prevent infection. Vaccination requires a precise clinical management, followed by detailed evaluation of safety and immune responses [30], [31], [32], [33]. Also, it leads to neutralizing antibodies, protection and no undesirable disease elevation. For safe immunization of the population against COVID-19, there is an urgent need to accelerate vaccination.

2. Global continuum model

We propose a EIRD-HIT model in the presence of vaccine and induced immunity by,

$$\begin{array}{c}\hfill \frac{dE(t)}{\mathit{dt}}=-\sigma E(t)-\frac{\alpha E(t)I(t)}{N}+k_1-{\delta }_1-{\mu }_{1}E(t)\mathit{Im}(t),\hfill \\ \hfill \frac{I(t)}{\mathit{dt}}=-\sigma I(t)+\frac{\alpha E(t)I(t)}{N}+k_2-{\delta }_2-{\mu }_{2}I(t)\mathit{Im}(t),\hfill \\ \hfill \frac{\mathit{dIm}(t))}{\mathit{dt}}={\mu }_{1}E(t)\mathit{Im}(t)+{\mu }_{2}I(t)\mathit{Im}(t),\hfill \\ \hfill \frac{\mathit{dR}(t)}{\mathit{dt}}=\beta I(t)+{\mu }_{2}I(t)\mathit{Im}(t),\hfill \\ \hfill \frac{\mathit{dD}(t)}{\mathit{dt}}=\gamma I(t)-{\mu }_{2}I(t)\mathit{Im}(t),t⩾0,\hfill \end{array}$$ (1)

where

$\alpha$	Exposed to infection rate
$\beta$	Interaction of recovered with infected rate
$\gamma$	Interaction of deceased with deceased rate
$\sigma$	Isolated rate
$k_1$	Exposed travelers pumping rate
$k_2$	Infected travelers pumping rate
${\delta }_1$	Exposed vaccinated pumping rate
${\delta }_2$	Infected vaccinated pumping rate
${\mu }_1$	Induced immunity rate in exposed
${\mu }_2$	Induced immunity rate in infected
N	Population number in a country

Indeed, in (3), it is plausible to take into consideration that there is a time lag between infection and decease or recovered, that is diseased or recovered people were antecedent infected. Thus, a time delay should be in (3), in $I(t)$.

That is by accounting for the laps of time required for an infected individual to be recovered or diseased, are taken ${\tau }_1$and ${\tau }_2$ respectively. Eq. (1) becomes,

$$\begin{array}{c}\hfill \frac{dE(t)}{\mathit{dt}}=-\sigma E(t)-\frac{\alpha E(t)I(t)}{N}+k_1-{\delta }_1-{\mu }_{1}E(t)\mathit{Im}(t),\hfill \\ \hfill \frac{I(t)}{\mathit{dt}}=-\sigma I(t)+\frac{\alpha E(t)I(t)}{N}+k_2-{\delta }_2-{\mu }_{2}I(t)\mathit{Im}(t),\hfill \\ \hfill \frac{\mathit{dIm}(t))}{\mathit{dt}}={\mu }_{1}E(t)\mathit{Im}(t)+{\mu }_{2}I(t)\mathit{Im}(t)\hfill \\ \hfill \frac{\mathit{dR}(t)}{\mathit{dt}}=\beta I(t-{\tau }_1)+{\mu }_{2}I(t-{\tau }_1)\mathit{Im}(t),\hfill \\ \hfill \frac{\mathit{dD}(t)}{\mathit{dt}}=\gamma I(t-{\tau }_2)-{\mu }_{2}I(t-{\tau }_1)\mathit{Im}(t),t⩾0,\hfill \end{array}$$ (2)

where ${\tau }_1$ and ${\tau }_2$are the measure of time lags which are estimated from the real data. It is worth noticing that the first three equations are closed. When the solutions $I(t)$ and $\mathit{Im}(t)$ are known, then $R(t)$ and $D(t)$ are obtained by direct integrals.

It is worthy to mention that, in the present work, the initial state-real data for exposed, infected, and diseased people are taken here, when $t=t_0$ where $0⩽t<t_0$ is the period of the first wave of COVID-19 in the absence of vaccination. Consequently, $t>t_0$ stands to the second and later waves. Thus, we bear this in mind, when interpreting the results found later on. As COVID-19 may lead to different symptoms in different local spaces, so the model presented here holds in the case when the vaccine is designed appropriately with relevance to the specific space.

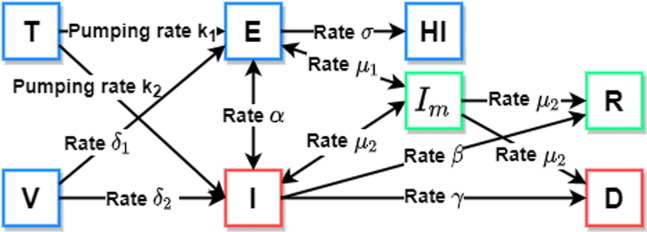
The scheme of the model is shown in Fig. 1 .

Fig. 1.

Proposed model.

3. The approach and exact solutions of (2)

3.1. The approach

We consider the NLDS,

$$\begin{array}{c}\hfill \dot{u}=f_1(u,v,w),\dot{v}=f_2(u,v,w),\dot{w}=f_3(u,y,z),\hfill \end{array}$$ (3)

where $f_i,i=1,2,3$ are of quadratic nonlinearity.

The approach is based on recasting the problem of solving (3) to solve coupled linear ODEs (or LDS) via implementing the unified method for rational solutions, as in what follows.

We write the solutions of (3) in the forms,

$$\begin{array}{c}\hfill u(t)=\frac{1}{Q}(a_0+a_1{g}_1(t)+a_2{g}_{2(}t)),v(t)=\frac{1}{Q}(b_0+b_1{g}_1(t)+b_2{g}_2(t))\hfill \\ \hfill w(t)=\frac{1}{Q}(d_0+d_1{g}_1(t)+d_2{g}_2(t)),Q=s_0+s_1{g}_1(t)+s_2{g}_{2(}t),\hfill \end{array}$$ (4)

where $g_i(t),i=1,2$ are auxiliary functions that satisfy the auxiliary equations,

$$\begin{array}{c}\hfill g_1^{\prime }(t)={\alpha }_0+{\alpha }_1{g}_1(t)+{\alpha }_2{g}_2(t),\hfill \\ \hfill g_2^{\prime }(t)={\beta }_0+{\beta }_1{g}_1(t)+{\beta }_2{g}_2(t)\text{.}\hfill \end{array}$$ (5)

By substituting (4) and (5) into (3) and by setting the coefficients of $g_i^j,i=1,2,j=0,1,2,\dots$equal to zero gives rise to a set of nonlinear algebraic equations, which are then solved.

3.2. Exact solutions of (2)

In (2), we remark that the first three equations are in a closed form. Thus, we find the solutions of these equations. To this end, we write,

$$\begin{array}{c}\hfill E(t)=\frac{1}{P}(a_0+a_1{g}_1(t)+a_2{g}_2(t)),I(t)=\frac{1}{P}(b_0+b_1{g}_1(t)+b_2{g}_2(t))\hfill \\ \hfill \mathit{Im}(t)=\frac{1}{P}(d_0+d_1{g}_1(t)+d_2{g}_2(t)),P=s_0+s_1{g}_1(t)+s_2{g}_2(t),\hfill \\ \hfill g_1^{\prime }(t)={\alpha }_0+{\alpha }_1{g}_1(t)+{\alpha }_2{g}_2(t),\hfill \\ \hfill g_2^{\prime }(t)={\beta }_0+{\beta }_1{g}_1(t)+{\beta }_2{g}_2(t),t⩾0\text{.}\hfill \end{array}$$ (6)

By substituting from (6) into (2) and by using Section 3.1, the solutions of the third, second and first equations give rise, respectively, to,

$$\begin{array}{c}\hfill a_1=\frac{1}{d_1{\mu }_1}({\beta }_1{d}_2{s}_1-d_1(b_1{\mu }_2+{\beta }_1{\mu }_2)),\hfill \\ \hfill a_2=\frac{1}{d_1^2{\mu }_1}(d_1^2(s_2({\alpha }_1-{\beta }_2)-b_2{\mu }_2)+d_1{d}_2(\mathrm{s}1({\beta }_2-{\alpha }_1)+{\beta }_1{s}_2)-{\beta }_1{d}_2^2{s}_1),\hfill \\ \hfill a_0=\frac{1}{d_1^2{\mu }_1}(d_1^2(-b_0{\mu }_2-{\beta }_0{s}_1+{\alpha }_1{s}_0)+d_1({\beta }_0{d}_2{s}_1+{\beta }_1{d}_2{s}_0-d_0{\alpha }_1{s}_1)\hfill \\ \hfill -{\beta }_1{d}_2{d}_0{s}_1),\hfill \\ \hfill {\alpha }_2=\frac{1}{d_1^2}{d}_2(\mathrm{d}1({\alpha }_1-{\beta }_1)+{\beta }_1{d}_2),\hfill \\ \hfill {\alpha }_1=\frac{d_1{\alpha }_0}{d_0}-\frac{d_2{\beta }_1}{d_1}+\frac{d_2{\beta }_0}{d_0},\hfill \end{array}$$ (7)

$$\begin{array}{c}\hfill d_2=\frac{1}{b_1{s}_1\alpha {\beta }_1}{d}_1({\mu }_1\mathrm{N}{s}_1({\beta }_1{b}_2-k_2{s}_1+{\delta }_2{s}_1)+b_1{\beta }_1{s}_2(\alpha -{\mu }_{1}N)\hfill \\ \hfill \left(\alpha +b_1^2{\mu }_2+b_1{\mu }_{1}N(d_1{\mu }_2+s_1(\beta +\gamma ))\right),\hfill \\ \hfill b_0=\frac{b_1{d}_0}{d_1},{\delta }_2=\frac{1}{d_1^2{\mu }_1{\mathit{Ns}}_1{s}_0({\beta }_0{s}_1-{\beta }_1{s}_0)}(\left(d_1^2{k}_2{\mu }_1{\mathit{Ns}}_1{s}_0({\beta }_0{s}_1-{\beta }_1{s}_0)\right)\hfill \\ \hfill \alpha +b_1^2{\mu }_2\left({\beta }_1{d}_0^2{s}_1-\beta \mathrm{o}{d}_1^2\mathrm{so}\right)+b_1{d}_1(d_0{s}_1{\beta }_1({\mu }_1{s}_{0}N(\beta +\gamma )\hfill \\ \hfill {\alpha }_0+s_1(\alpha -{\mu }_{1}N)+{\beta }_0{s}_2(\alpha -{\mu }_{1}N)){\beta }_1+d_0^2{\mu }_1{\mu }_2{\mathit{Ns}}_0-d_1{s}_0(\alpha {\alpha }_0{\beta }_1{s}_1\hfill \\ \hfill {\beta }_0{d}_1{\mu }_1{\mu }_2\mathrm{N}+{\mu }_1+\mathrm{N}{s}_1(\beta \mathrm{o}(\beta +\gamma )-{\alpha }_0{\beta }_1)+{\beta }_1{\beta }_0{s}_2(\alpha -{\mu }_1\mathrm{N})))),\hfill \\ \hfill {\beta }_0=\frac{1}{d_1{\mu }_1{s}_1\mathrm{N}}(\alpha {\beta }_1{d}_1{s}_0+{\beta }_1{\mu }_1{s}_1{d}_0\mathrm{N}+\alpha -{\beta }_1{d}_0{s}_1),\hfill \\ \hfill \gamma =\frac{1}{b_1{\mu }_1{s}_1\mathrm{N}}({\beta }_1{s}_1{b}_2(\alpha -{\mu }_{1}N)-b_1(\alpha \mathrm{b}1\mu 2+d_1{\mu }_1{\mu }_2\mathrm{N}+\beta {\mu }_1{s}_1\mathrm{N}\hfill \\ \hfill +{\beta }_1{s}_2(\alpha -{\mu }_{1}N))),\hfill \\ \hfill {\alpha }_0=\frac{1}{(b_1{d}_1{\mathit{Ns}}_1^2{\mu }_1(-\alpha +N{\mu }_1)}\left({\alpha }^2{b}_1{d}_1{\beta }_1{s}_2{s}_0+2\alpha b_1{\beta }_1{d}_0{\mu }_1\mathrm{N}{s}_2{s}_0+{\alpha }^2(-b_1{\beta }_1{d}_0{s}_1{s}_2\right)\hfill \\ \hfill -2\alpha b_1{d}_1{\beta }_1{\mu }_1\mathrm{N}{s}_2{s}_0--b_1{\beta }_1{d}_0{\mu }_1^2{\mathrm{N}}^2{s}_1{s}_2+\alpha {\beta }_1+b_2{d}_1{\mu }_1\mathrm{N}{s}_1{s}_0\left(\alpha b_1^2{d}_0{\mu }_1{\mu }_2\mathrm{N}{s}_1+b_1{d}_1{d}_0{\mu }_1^2{\mu }_2{\mathrm{N}}^2{s}_1+{\beta }_1{b}_1{d}_1{\mu }_1^2{\mathrm{N}}^2{s}_2{s}_0-b_2{d}_1{\beta }_1{\mu }_1^2{\mathrm{N}}^2{s}_1{s}_0\right),\hfill \\ \hfill d_1=\frac{1}{b_1{\mu }_1^2{\mu }_2{\mathrm{N}}^2}(b_1\left({\beta }_1{s}_2{(\alpha -{\mu }_1\mathrm{N})}^2-{\alpha }^2{b}_1{\mu }_2\right)-{\beta }_1{s}_1{b}_2{(\alpha -{\mu }_1\mathrm{N})}^2),\hfill \\ \hfill b_2=\frac{1}{{\beta }_1{\mu }_1\mathrm{N}{s}_1(\alpha -{\mu }_1\mathrm{No})}({\alpha }^2{b}_1^2{\mu }_2-b_1{\beta }_1{\mu }_1^2{\mathrm{N}}^2{s}_2-\alpha {\beta }_2{\mu }_1{b}_1\mathrm{No}{s}_1+2\alpha {\mu }_1{\beta }_1{b}_1\mathrm{No}{s}_2),\hfill \end{array}$$ (8)

$$\begin{array}{c}\hfill {\delta }_1=\frac{1}{{\mu }_1^3{\mu }_2{\mathrm{N}}^2{s}_1^2({\mu }_1\mathrm{No}-\alpha )}\left(-{\alpha }^3{b}_1{\mu }_2(b_1{\mu }_2({\mu }_1+{\mu }_2)-{\beta }_2{\mu }_1{s}_1+{\beta }_1{\mu }_1{s}_2)\right)\hfill \\ \hfill +{\mathrm{N}}^2\alpha \mu 1^2\left(b_1^2{\mu }_1{\mu }_2^2+b_1{\beta }_2{\mu }_2{s}_1({\mu }_2-2{\mu }_1)+{\beta }_1^2{s}_2^2({\mu }_1-{\mu }_2)\right)\hfill \\ \hfill \left({\beta }_1{s}_2(b_1{\mu }_2(2{\mu }_1-{\mu }_2)+2{\beta }_2{s}_1(-{\mu }_1+{\mu }_2))++s_1^2\left({\beta }_2^2({\mu }_1-{\mu }_2)-k_1{\mu }_1{\mu }_2\right)\right)\hfill \\ \hfill -\mathrm{N}{\alpha }^2{\mu }_1\left(b_1^2{\mu }_2^3-b_1{s}_1{\beta }_2{\mu }_2({\mu }_1+2{\mu }_2)+{\beta }_2^2{\mu }_1{s}_1^2+{\beta }_1^2{\mu }_1{s}_2^2\right)\hfill \\ \hfill \left(+s_2{\beta }_1(b_1{\mu }_2({\mu }_1+2{\mu }_2)-2{\beta }_2{\mu }_1{s}_1)+{\mu }_1^3{\mu }_2{\mathrm{N}}^3{s}_1(\sigma (b_1{\mu }_2-{\beta }_2{s}_1+{\beta }_1{s}_2)+k_1{\mu }_1{s}_1)\right),\hfill \\ \hfill b_1=\frac{1}{\alpha {\mu }_2}{\mu }_1\mathrm{N}({\beta }_2{s}_1-{\beta }_1{s}_2),\hfill \\ \hfill {\beta }_1=\frac{s_1}{\mathrm{s}2\left({\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)}\left({\alpha }^2{\beta }_2+{\mu }_1{\mathrm{N}}^2({\beta }_2(\mu 2-2\mu 1)-{\mu }_2\sigma )+\alpha \mathrm{N}(\beta 2({\mu }_1+{\mu }_2)-{\mu }_2\sigma )\right)\text{.}\hfill \end{array}$$ (9)

By substituting (7)-(9) into (6), we find the solutions,

$$\begin{array}{c}\hfill E(t)=\frac{1}{{\alpha }^2{\mu }_{1}H}(\mathrm{N}(\alpha +{\mu }_1\mathrm{N}){\mu }_2\left({\alpha }^2{d}_0{\mu }_1-2d_0{\mu }_1^3{\mathrm{N}}^2+\alpha d_0{\mu }_1^2\mathrm{N}+\alpha d_0\mathrm{N}{\mu }_1{\mu }_2\right)\hfill \\ \hfill \left(+d_0{\mu }_1^2{\mu }_2{\mathrm{N}}^2-\alpha {\mu }_1\mathrm{N}\sigma s_1{g}_1(t)-\alpha {\mu }_1\mathrm{N}\sigma s_2{g}_2(t)+{\alpha }^2\sigma s_0\right),\hfill \\ \hfill I(t)=\frac{1}{{\alpha }^{2}H}{\mathrm{N}}^2{\mu }_1\left(d_0{\mu }_1\left(-{\alpha }^2+{\mu }_1{\mathrm{N}}^2(2{\mu }_1-{\mu }_2)-\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)\right)\hfill \\ \hfill \alpha \sigma +s_1{g}_1(t)(\alpha +{\mu }_1\mathrm{N})+\alpha \sigma s_2{g}_2(t)(\alpha +{\mu }_1\mathrm{N})),\hfill \\ \hfill \mathit{Im}(t)=-\frac{1}{{\mu }_{1}H}(d_0{\mu }_1\left(-{\alpha }^2+{\mu }_1{\mathrm{N}}^2(2{\mu }_1-{\mu }_2)-\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)\hfill \\ \hfill \alpha \sigma +s_1(\alpha +{\mu }_1\mathrm{N})g_1(t))+\alpha \sigma (\alpha +{\mu }_1\mathrm{N})s_2{g}_2(t)),\hfill \\ \hfill H={\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)(s_0+s_1{g}_1(t)+s_2{g}_2(t))\text{.}\hfill \end{array}$$ (10)

The solutions of the auxiliary equations are,

$$\begin{array}{c}\hfill g_1(t)=\frac{1}{s_{1}Q}(k_1+\alpha {\mu }_1{\mu }_2{\mathrm{N}}^2{\sigma }^2{s}_1{(\alpha +{\mu }_1\mathrm{N})}^2\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right)\hfill \\ \hfill \left(\alpha \mathrm{N}({\mu }_1+{\mu }_2+{\beta }_2{\mu }_1(-t)+\mu 2t(\sigma -{\beta }_2))+{\alpha }^2(1-{\beta }_{2}t)\right)\hfill \\ \hfill \left(+{\mu }_1{\mathrm{N}}^2({\mu }_2+2{\mu }_1({\beta }_{2}t-1)+{\mu }_{2}t(\sigma -{\beta }_2))\right)g_1(0)\hfill \\ \hfill -\alpha {\mu }_1{\mu }_2{\mathrm{N}}^2{\sigma }^2{s}_{2}t{(\alpha +{\mu }_1\mathrm{N})}^2\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right)\hfill \\ \hfill \left(\left({\alpha }^2{\beta }_2+{\mu }_1{\mathrm{N}}^2({\beta }_2(-2{\mu }_1+{\mu }_2)-{\mu }_2\sigma )+\alpha \mathrm{N}(\beta 2({\mu }_1+{\mu }_2)-{\mu }_2\sigma )\right)g_2(0)\right),\hfill \\ \hfill g_2(t)=\frac{1}{s_{2}Q}\left(k_2+\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right){\mathrm{N}}^2{s}_{1}t\alpha {\mu }_1{(\alpha +{\mu }_1\mathrm{N})}^2{\mu }_2{\sigma }^2\right)\hfill \\ \hfill ({\alpha }^2{\beta }_2+{\mu }_1{\mathrm{N}}^2({\beta }_2(-2{\mu }_1+{\mu }_2)-{\mu }_2\sigma )\alpha +\mathrm{N}(\beta 2({\mu }_1+{\mu }_2)-\mu 2\sigma )g_1(0)\hfill \\ \hfill +\alpha {\mu }_1{\mu }_2{\mathrm{N}}^2{s}_2{(\alpha +{\mu }_1\mathrm{N})}^2\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right)\hfill \\ \hfill \left(\alpha \mathrm{N}({\mu }_1+{\mu }_2+{\beta }_2{\mu }_{1}t+\mu 2t({\beta }_2-\sigma ))+{\alpha }^2({\beta }_{2}t+1)\right)\hfill \\ \hfill \left(\left({\mu }_1+{\mathrm{N}}^2({\mu }_2-2{\mu }_1({\beta }_{2}t+1)+{\mu }_{2}t({\beta }_2-\sigma ))\right){\sigma }^2{g}_2(0)\right),\hfill \\ \hfill Q=\alpha {\mu }_1{\mu }_2{\mathrm{N}}^2{\sigma }^2{\left(\alpha +{\mu }_1\mathrm{N}\right)}^2\left({\alpha }^2+\mu 1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right),\hfill \\ \hfill k_1=\frac{1}{{\beta }_0^2{\mu }_1^3{\mathrm{N}}^2(2{\mu }_1\mathrm{N}-\alpha )}\left(2{\alpha }^3{\left({\alpha }_0{\beta }_1+{\beta }_0{\beta }_2\right)}^2-5{\alpha }^2{\mu }_1\mathrm{N}{\left({\alpha }_0{\beta }_1+{\beta }_0{\beta }_2\right)}^2\right)\hfill \\ \hfill {\mu }_1^3+{\mathrm{N}}^3\left(-{\alpha }_0^2{\beta }_1^2-2{\alpha }_0{\beta }_0{\beta }_1{\beta }_2-{\beta }_0^2\left({\beta }_2^2-2{\delta }_1{\mu }_1\right)\right)\hfill \\ \hfill \left(\alpha {\mu }_1^2+{\mathrm{N}}^2\left(3{\alpha }_0^2{\beta }_1^2+6{\alpha }_0{\beta }_0{\beta }_1{\beta }_2+{\beta }_0^2\left(3{\beta }_2^2-2\delta {\mu }_1\right)\right)\right),\hfill \\ \hfill k_2=-\frac{1}{{\beta }_0^2{\mu }_1^2\mu 2{\mathrm{No}}^2(\alpha -2{\mu }_1\mathrm{N})}{\left(3{\alpha }^2{\mu }_1\mathrm{N}{\left({\alpha }_0{\beta }_1+{\beta }_0{\beta }_2\right)}^2\right)}^2\hfill \\ \hfill {\left(-{\alpha }^3{\left({\alpha }_0{\beta }_1+{\beta }_0{\beta }_2\right)}^2\right)}^2\alpha {\mu }_1^2-{\mathrm{N}}^2\left(3{\alpha }_0^2{\beta }_1^2+6{\alpha }_0{\beta }_0{\beta }_1{\beta }_2+\right)\hfill \\ \hfill \left(\left({\beta }_0^2\left(3{\beta }_2^2+{\delta }_2{\mu }_2\right)\right){\mu }_1^3+{\mathrm{N}}^3\left(\alpha {\mathrm{o}}^2\beta 1^2+2{\alpha }_0{\beta }_0{\beta }_1{\beta }_2+\beta {\mathrm{o}}^2\left({\beta }_2^2+2{\delta }_2{\mu }_2\right)\right)\right)\text{.}\hfill \end{array}$$ (11)

The values of $g_i(0),i=1,2$ are determined from the initial conditions $I(0),E(0)$ and $\mathit{Im}(0)$.We have

$$\begin{array}{c}\hfill g_1(0)=\frac{1}{H_1}\left(d_0{\mu }_1{\mu }_2\mathrm{N}(\alpha +{\mu }_{1}N)\left({\alpha }^2+{\mu }_1{\mathrm{N}}^2({\mu }_2-2{\mu }_1)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)\right)\hfill \\ \hfill -\alpha \left({\alpha }^{3}E(0){\mu }_1(g_2(0)s_2+s_0)+g_2(0){\mu }_1^2{\mu }_2{\mathrm{N}}^3\sigma s_2\right)\hfill \\ \hfill {\alpha }^2+\mathrm{N}\left(\mathrm{E}(0)g_2(0){\mu }_1{s}_2({\mu }_1+{\mu }_2)+s_0\left(\mathrm{E}(0){\mu }_1^2+\mathrm{E}(0){\mu }_1{\mu }_2-{\mu }_2\sigma \right)\right)\hfill \\ \hfill \left(\left(\alpha {\mu }_1{\mathrm{N}}^2\left(g_2(0)s_2\left(-2\mathrm{E}(0){\mu }_1^2+\mathrm{E}(0){\mu }_1{\mu }_2+{\mu }_2\sigma \right)+s_0\left(-2\mathrm{E}(0){\mu }_1^2+\mathrm{E}(0){\mu }_1{\mu }_2-{\mu }_2\sigma \right)\right)\right)\right),\hfill \\ \hfill \hfill \\ \hfill H_1=\alpha {\mu }_1{s}_1\left({\alpha }^3\mathrm{E}(0)+\alpha {\mathrm{N}}^2\left({\mu }_2(\mathrm{E}(0){\mu }_1+\sigma )-2\mathrm{E}(0){\mu }_1^2\right)+{\alpha }^2\mathrm{E}(0)\mathrm{N}({\mu }_1+{\mu }_2)+{\mu }_1{\mu }_2{\mathrm{N}}^3\right)\hfill \\ \hfill \hfill \\ \hfill E(0)=\frac{1}{{\mu }_1^2\mathrm{No}\left(-{\alpha }^2+2{\mu }_1^2{\mathrm{N}}^2-{\mu }_1{\mu }_2{\mathrm{N}}^2-\alpha {\mu }_1\mathrm{No}-\alpha {\mu }_2\mathrm{No}\right)}\hfill \\ \hfill \left({\alpha }^3\mathrm{I}(0){\mu }_2-\alpha \mathrm{I}(0){\mu }_1^2{\mu }_2{\mathrm{N}}^2-2\mathrm{I}(0){\mu }_1^3{\mu }_2{\mathrm{N}}^3+2{\alpha }^2\mathrm{I}(0){\mu }_1{\mu }_2\mathrm{N}\right)\hfill \\ \hfill +{\alpha }^2\mathrm{I}(0{\mu }_2^2\mathrm{N}-\alpha {\mu }_1{\mu }_2{\mathrm{N}}^2\sigma -{\mu }_1^2{\mu }_2{\mathrm{N}}^3\sigma \hfill \\ \hfill \left(+2\alpha \mathrm{I}(0){\mu }_1{\mu }_2^2{\mathrm{N}}^2+\mathrm{I}(0){\mu }_1^2{\mu }_2^2{\mathrm{N}}^3\right),\hfill \\ \hfill \mathit{Im}(0)=\frac{{\alpha }^{2}I(0)/}{N^2{\mu }_1^2},\hfill \\ \hfill \mathit{Im}(0)=\frac{1}{b_2^2{s}_1^2-3b_1^2{s}_2^2}3b_1{s}_2(-2b_1{b}_2+b_2{s}_{1}I(0)+b_1{s}_{2}I(0)),\hfill \end{array}$$ (12)

where $g_2(0)$ and $s_i,i=0,1,2$ are arbitrary. When substituting from (11) and (12) into (10), we get the final solutions,

$$\begin{array}{c}\hfill E(t)=\frac{P_1}{\mu Q_0},P_1=-\left(\mathrm{N}\alpha +{\mu }_1\mathrm{N}\mu 2\sigma \left(-d_0{\mu }_1\left({\alpha }^2+{\mu }_1{\mathrm{N}}^2({\mu }_2-2{\mu }_1)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)\right)\right)\hfill \\ \hfill \hfill \\ \hfill \left(\sigma (-(\alpha +\mu 1\mathrm{N}))\left(\alpha s_0-{\mu }_1\mathrm{N}(g_1(0)s_1+g_2(0)s_2)\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right)\right)\right),\hfill \\ \hfill \hfill \\ \hfill I(t)=\frac{P_2}{Q_0},P_2={\mu }_1{\mathrm{N}}^2{\sigma }^2{(\alpha +{\mu }_1\mathrm{N})}^2(g_1(0)s_1+g_2(0)s_2)\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right),\hfill \\ \hfill \hfill \\ \hfill \mathit{Im}(t)=\frac{P_3}{{\mu }_1{Q}_0},P_3=-\left({\alpha }^2{\sigma }^2{(\alpha +{\mu }_1\mathrm{N})}^2(g_1(0)s_1+g_2(0)s_2)\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right),\right)\hfill \\ \hfill \hfill \\ \hfill Q_0={\alpha }^2+{\mu }_1{\mathrm{N}}^2({\mu }_2-2{\mu }_1)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\left(d_0\mu 1\left({\alpha }^2+{\mu }_1{\mathrm{N}}^2({\mu }_2-2{\mu }_1)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)\right)\hfill \\ \hfill \hfill \\ \hfill \left(+\alpha \sigma (\alpha +{\mu }_1\mathrm{N})\left((g_1(0)s_1+g_2(0)s_2)\exp \left(\frac{{\mu }_2\mathrm{N}\sigma t(\alpha +{\mu }_1\mathrm{N})}{{\alpha }^2+{\mu }_1{\mathrm{N}}^2(-2{\mu }_1+{\mu }_2)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)}\right)+s_0\right)\right),\hfill \end{array}$$ (13)

together with the equations,

$$\begin{array}{c}\hfill {\delta }_1=\mathrm{k}1+\frac{{\mu }_2{\mathrm{N}}^3{\sigma }^2(\alpha +{\mu }_{1}N)(\alpha ({\mu }_1+{\mu }_2)+{\mu }_1\mathrm{N}({\mu }_2-\mu 1))}{\alpha {\left({\alpha }^2+{\mu }_1{\mathrm{N}}^2({\mu }_2-2{\mu }_1)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)}^2},\hfill \\ \hfill \hfill \\ \hfill \sigma =\frac{{\mu }_1(\beta +\gamma )\left({\alpha }^2+{\mu }_1{\mathrm{N}}^2({\mu }_2-2{\mu }_1)+\alpha \mathrm{N}({\mu }_1+{\mu }_2)\right)}{{\mu }_2\left({\alpha }^2-{\mu }_1^2{\mathrm{N}}^2\right)}\text{.}\hfill \end{array}$$ (14)

4. Numerical results

The solutions in (13) are evaluated numerically and they are displayed in in the following figures. Here, it is assumed that the vaccine is applied at May 1st, 2021 and the real data are taken in Egypt at this date [34].

In Fig. 2 (i)-(iii) for the exposed, infected and immunity are displayed against t (in days).

Fig. 2.

(i)-(iii) are displayed when $\mathrm{N}=100000000$, ${\delta }_1=193782,{\delta }_2=10000,\sigma =0.0028,\gamma =0.00001,\mathrm{I}(0)=228584,R(0)=103913$, $\alpha =0.0045,\beta =0.003,s_0=0.002,k_1=500,k_2=100,s_1=0.5,s_2=0.6,{\mu }_1=0.4,{\mu }_2=0.1,{\beta }_2=0.3,g_2(0)=3\times {10}^4$, $d_0=0.0001$.

These figures show that the number of exposed decreases with time and it attains an asymptotic value. While the number of infected people decreases to an asymptotic value.

In Fig. 3 (i) and (ii), the numbers of deceased with time and recovered people are shown respectively.

Fig. 3.

(i) and (ii). By using the caption in Figs. 2 (i)-(iii), the numbers of deceased and recovered people are displayed for when $D(0)=43640,R(0)=171542,{\tau }_1=10,{\tau }_2=15$.

These figures show that the numbers of deceased and recovered people increase and attain a steady state. We observe that these calculated numbers are highly oscillatory, and we estimate that they are determined up to uncertain range.

A MATLAB software application is developed based on the final equations (9) and (10) to permit researchers to employ this model for various real data of different countries up to parameters and real data adaptation. See [34]. Fig. 4 shows a screenshot for the tool.

Fig. 4.

Screenshot for the MATLAB software application.

5. Stability and initial states control

5.1. Stability

Here we consider the closed equations in (2) for $E(t),I(t)$ and $\mathit{Im}(t)$. The equilibrium states are

$$\begin{array}{c}\hfill \mathit{Ee}=\frac{(-k_1-k_2+{\delta }_1+{\delta }_2){\mu }_2}{-{\mu }_1(\beta +\gamma )+{\mu }_2\sigma },\mathit{Ie}=\frac{(-k_1-k_2+{\delta }_1+{\delta }_2){\mu }_1}{{\mu }_1(\beta +\gamma )-{\mu }_2\sigma },\hfill \\ \hfill \hfill \\ \hfill \mathit{Ime}=\frac{P_1}{Q_1},P_1=(-k_1^2\alpha {\mu }_1{\mu }_2-\alpha {(-k_2+{\delta }_1+{\delta }_2)}^2{\mu }_1{\mu }_2\hfill \\ \hfill +N({\mu }_1(\beta +\gamma )-{\mu }_2\sigma )((\beta +\gamma ){\delta }_1{\mu }_1+(-k_2+{\delta }_2{\mu }_2\sigma )\hfill \\ \hfill +k_1{\mu }_1(2\alpha (-k_2+{\delta }_1+{\delta }_2){\mu }_2-N(\beta +\gamma )({\mu }_1(\beta +\gamma )-{\mu }_2\sigma ))),\hfill \\ \hfill \hfill \\ \hfill Q_1=N{\mu }_1{\mu }_2(k_1+k_2-{\delta }_1-{\delta }_2)({\mu }_1(\beta +\gamma )-{\mu }_2\sigma )\text{.}\hfill \end{array}$$ (15)

We mention that there exist two other equilibrium states,

$$\begin{array}{c}\hfill \mathit{Ee}=\frac{H_1\mp \sqrt{H_2}}{2\alpha \sigma },\mathit{Ie}=\frac{H_1\pm \sqrt{H_2}}{2\alpha \sigma (\beta +\gamma )},\mathit{Ime}=0,\hfill \\ \hfill H_1=(k_1+k_2)\alpha -\alpha ({\delta }_1+{\delta }_2)-(\beta +\gamma )N\sigma ,\hfill \\ \hfill H_2=4N\alpha (\beta +\gamma ){(k_2-\sigma {\delta }_2-\alpha (k_1+k_2)+\alpha ({\delta }_1+{\delta }_2)+N\beta \sigma +N\gamma \sigma )}^2\text{.}\hfill \end{array}$$ (16)

The results in (16) are not realistic and will not be considered here.

Now, we write

$$E(t)=\mathit{Ee}+{\epsilon }_1{e}^{\lambda t},I(t)=\mathit{Ie}+{\epsilon }_2{e}^{\lambda t},\mathit{Im}(t)=\mathit{Ime}+{\epsilon }_3{e}^{\lambda t}\text{.}$$ (17)

By substituting (16) into (2), the eigenvalues are determined by the equation

$$\begin{array}{c}\hfill \mathit{Det}M=0,\hfill \\ \hfill M=\left(\begin{array}{ccc}\hfill m_{11}\hfill & \hfill m_{12}\hfill & \hfill m_{13}\hfill \\ \hfill m_{21}\hfill & \hfill m_{22}\hfill & \hfill m_{23}\hfill \\ \hfill m_{31}\hfill & \hfill m_{32}\hfill & \hfill m_{33}\hfill \end{array}\right)\hfill \\ \hfill \hfill \\ \hfill m_{11}=\frac{\mathit{Ie}\alpha }{N}+\lambda +\mathit{Ime}{\mu }_1+\sigma ,m_{12}=\frac{\mathit{Ee}\alpha }{N},m_{13}=\mathit{Ee}{\mu }_1,\hfill \\ \hfill \hfill \\ \hfill m_{21}=-\frac{\mathit{Ie}\alpha }{N},m_{22}=-\frac{\mathit{Ee}\alpha }{N}+\beta +\gamma +\lambda +\mathit{Ime}{\mu }_2,m_{23}=\mathit{Ie}{\mu }_2,\hfill \\ \hfill \hfill \\ \hfill m_{31}=-\mathit{Ime}{\mu }_1,m_{32}=\mathit{Ime}{\mu }_2,m_{33}=\lambda -\mathit{Ee}{\mu }_1-\mathit{Ie}{\mu }_2\text{.}\hfill \end{array}$$ (18)

The Eq. (18) gives rise to

$$\begin{array}{c}\hfill -\mathit{Ime}{\mu }_1(\frac{{(\mathit{Ee})}^2\alpha {\mu }_1}{N}-\mathit{Ee}{\mu }_1(\beta +\gamma )-\mathit{Ee}\lambda {\mu }_1+\frac{\mathit{EeIe}\alpha {\mu }_2}{N}-\mathit{EeIme}{\mu }_1{\mu }_2)\hfill \\ \hfill \hfill \\ \hfill -\mathit{Ime}{\mu }_2(\frac{\mathit{EeIe}\alpha {\mu }_1}{N}+\frac{{(\mathit{Ie})}^2\alpha {\mu }_2}{N}+\mathit{Ie}\lambda {\mu }_2+\mathit{IeIme}{\mu }_1{\mu }_2+\mathit{Ie}{\mu }_2\sigma )+(\lambda -\mathit{Ee}{\mu }_1\hfill \\ \hfill \hfill \\ \hfill -\mathit{Ie}{\mu }_2)(\frac{\mathit{Ee}\mathit{Ie}{\alpha }^2}{N^2}+(-(\frac{\mathit{Ee}\alpha )}{N}+\beta +\gamma +\lambda +\mathit{Ime}{\mu }_2)(\frac{\mathit{Ie}\alpha }{N}+\lambda +\mathit{Ime}{\mu }_1+\sigma ))=0\text{.}\hfill \end{array}$$ (19)

When eliminating $\mathit{Ee},\mathit{Ie}$ and Ime in(19), by using (15) we get the equation that determines the eigenvalues. It is very lengthy and will not produced here. Instead, we show this by carrying the contour plot of the final equation in Fig. 5 .

Fig. 5.

When $N=100000000,\beta =0.04,\sigma =0.45,k_1=500,k_2=100,{\mu }_1=0.02,\gamma =0.0001,{\mu }_2=0.209,\alpha =0.1$.

This figure shows that $\lambda <0$ so that the NLDS is asymptotically stable.

5.2. Initial states control

To analyze the initial states control, we impose the conditions, $\frac{\mathit{dE}(t)}{\mathit{dt}}{\mid }_{t=0}<0,\frac{\mathit{dI}(t)}{\mathit{dt}}{\mid }_{t=0}<0$, and $\frac{\mathit{dD}(t)}{\mathit{dt}}{\mid }_{t=0}<0$. These equations give rise to

$$\begin{array}{c}\hfill {\delta }_1>k_1-\alpha \frac{E(0)I(0)}{N}+\sigma E(0)-{\mu }_{1}I(0)\mathit{Im}(0),\hfill \\ \hfill \hfill \\ \hfill {\delta }_2>k_2+\alpha \frac{E(0)I(0)}{N}-\sigma I(0)-{\mu }_{2}I(0)\mathit{Im}(0),\mathit{Im}(0)>\frac{\gamma }{{\mu }_2}\text{.}\hfill \end{array}$$ (20)

Eq. (20) reveals that the number of vaccinated peoples, among infected and exposed, should have a lower bound. to inspect the domain of controlled states, we rewrite (18) in the form,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathit{Im}(0)>\frac{1}{{\mu }_{1}E(0)}(k_1-\alpha \frac{E(0)I(0)}{N}+\sigma E(0)-{\delta }_1),\hfill \end{array}\hfill \\ \hfill \hfill \\ \hfill \mathit{Im}(0)>\frac{1}{{\mu }_{2}I(0)}(k_2+\alpha \frac{E(0)I(0)}{N}-\sigma I(0)-{\delta }_2)\mathit{Im}(0)>\frac{\gamma }{{\mu }_2}\text{.}\hfill \end{array}$$ (21)

The results in (21) are displayed in Fig. 6 .

Fig. 6.

When ${\delta }_1=2000,\delta 2=10000,\gamma =0.00001,N=100000000,k_1=500,k_2=100,{\mu }_1=0.2,{\mu }_2=0.02,\alpha =0.00000045$.

According to Fig. 6, the filling region is controlled which diminishes with increasing the number of exposed peoples.

6. Conclusions

In this work, a global continuum model that accounts for the exposed, infected, recovered, deceased, locked-down and travelers, EIRD-HIT and in the presence of vaccine and induced immunity is presented. This is with relevance to the second and later waves of COVID-19. The exact solutions of the model equations are found via a novel approach where the unified method, with coupled linear auxiliary equations, is used. Numerical evaluation of the solutions are done by assuming that the vaccine is applied at May 1st, 2021, so that the real data in Egypt, at this date, are taken into consideration. It is found that the numbers of exposed and infected people decrease to zero asymptotically. This in contrast to the results found when studying the dynamics of COVID-19 in the absence of vaccination. In the later case, it was found that the numbers of exposed and infected people increase strictly. These results are new. Furthermore, the stability of the dynamic system of COVID-19 is studied. It is found that the dynamical system of the second and later waves of COVID-19 is asymptotically stable which has an impact on the dynamic of the virus, that is, it will not be endemic. Further, the conditions for save initial states, non epidemic, are inspected and it is found that the initial states control domain diminishes with increasing the initial umber of exposed peoples, which is realistic.

7. Data Statement

The data used throughout the paper are the public numbers of reported cases by the Ministry of Health and Population in Egypt available for download through [23].

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.