Developmental trajectories of cortical thickness by functional brain network: The roles of pubertal timing and socioeconomic status

Abstract

The human cerebral cortex undergoes considerable changes during development, with cortical maturation patterns reflecting regional heterogeneity that generally progresses in a posterior-to-anterior fashion. However, the organizing principles that govern cortical development remain unclear. In the current study, we characterized age-related differences in cortical thickness (CT) as a function of sex, pubertal timing, and two dissociable indices of socioeconomic status (i.e., income-to-needs and maternal education) in the context of functional brain network organization, using a cross-sectional sample (n = 789) diverse in race, ethnicity, and socioeconomic status from the Lifespan Human Connectome Project in Development (HCP-D). We found that CT generally followed a linear decline from 5 to 21 years of age, except for three functional networks that displayed nonlinear trajectories. We found no main effect of sex or age by sex interaction for any network. Earlier pubertal timing was associated with reduced mean CT and CT in seven networks. We also found a significant age by maternal education interaction for mean CT across cortex and CT in the dorsal attention network, where higher levels of maternal education were associated with steeper age-related decreases in CT. Taken together, our results suggest that these biological and environmental variations may impact the emerging functional connectome.

1. Introduction

The human cerebral cortex undergoes a profoundly complex set of developmental changes that begin early in gestation, are far from complete at birth, and extend through adulthood. These patterns are highly influenced by environmental, genetic, and hormonal factors. Prior studies on macroscale organization and cortical thickness (CT) development have suggested a posterior-to-anterior gradient, where earliest maturation occurs in occipital regions and latest in superior frontal regions (Gogtay et al., 2004, Valk et al., 2020, Westlye et al., 2010). Recent studies, however, suggest that some structural changes during maturation occur at a large-scale, network level (Oldham and Fornito, 2019). For example, Krongold et al. (2017) modeled cortical changes in youth aged 5–22 years and found that while surface area maturation exhibited a posterior-anterior gradient, CT development distinguished primary sensorimotor from association regions. They concluded that these maturational distinctions support a functionally driven basis for CT development. Incongruencies in reported CT trajectories highlight another aspect of neurodevelopment that requires further study. Walhovd et al. (2017) described contrasts between early-emerging and late-emerging views of CT development, where early researchers reported increases in CT that peaked in early school age (Shaw et al., 2006, Sowell et al., 2004) whereas more recent reports describe monotonic thinning from early childhood (Brown et al., 2012, Mutlu et al., 2013). Still, reports of nonlinear CT trajectories suggest that some regions do not thin monotonically (Shaw et al., 2008, Vijayakumar et al., 2016, Zhou et al., 2015) which may point to developmental periods that may differ in their degree of age-related functional maturation (e.g., school age versus early adolescence versus late adolescence). These periods of structural fine-tuning require further investigation to better understand network-based organization that may reflect normative cognitive and behavioral changes (Gur et al., 2021).

Sexual dimorphism and pubertal processes are also suspected to affect the organization of the developing brain (Dima et al., 2021, Frangou et al., 2021, Juraska and Willing, 2017). While some studies find little or no sex differences in CT (Vijayakumar et al., 2016, Wierenga et al., 2014), others report significant variation in temporal and parietal regions by sex (Gennatas et al., 2017, Mutlu et al., 2013). In addition, the onset of puberty may mark a period of brain reorganization (Juraska and Willing, 2017). Puberty presents a significant biological event during the developmental period requiring investigation to distinguish its potential effects on neural circuitry. This is particularly important in the context of the brain’s functional organization, given evidence suggesting that puberty is associated with one’s socioemotional development and psychopathology risk over and above age (Ullsperger and Nikolas, 2017). In addition to pubertal stage, pubertal timing (i.e., pubertal stage relative to one’s age- and sex-matched peers) imparts hormonal and psychosocial changes that can result in significant individual differences (Graber, 2013). The onset of puberty, where sex hormones elicit the process of sexual maturation, has activation and organizational effects on the brain that may impactbrain structure dissociable from the effects of chronological age. During sensitive periods of development, organizational effects of gonadal hormones permanently set developmental trajectories (Schulz and Sisk, 2016; Sisk, 2017; Sisk and Zehr, 2005). The timing of these effects, in turn, has significant implications for neural plasticity. For example, Piekarski et al. (2017) found that early exposure to ovarian hormones has lasting effects on neocortex activity in female mice and suggested that early pubertal timing may prematurely open a sensitive developmental window. Thus, there is evidence that pubertal timing effects persist far beyond adolescence and alter the course of brain maturation.

The developing brain is also highly sensitive to environmental factors, such as socioeconomic status (SES). It is difficult to know what normative development truly looks like without considering the large environmental differences that characterize an increasingly diverse population and shape human neural development. The influence of SES inequalities is pervasive, affecting both brain development and neurocognition (Jednoróg et al., 2012; Judd et al., 2020; Taylor et al., 2020) and has significant implications for how neuroscience informs policy. Therefore, we capitalized on the HCP-D’s diverse sample to investigate how SES impacts cortical development. SES is a multidimensional construct (Hackman and Farah, 2009), with parental education (PE) and family income operationalized as two dissociable indices of SES. Both components may contribute to developmental outcomes (Duncan and Magnuson, 2012). Much like the impact of puberty, SES has been implicated in socioemotional development throughout childhood and adolescence. Variations in early experience may influence brain development as a means of adapting to environment-specific needs, raising the question of how SES differences alter the structure of functional brain networks. Piccolo et al. (2016) reported a steeper rate of cortical thinning in children from lower compared to higher PE backgrounds. By adolescence, however, CT maturation in low PE children plateaued, whereas cortical thinning in high PE children continued. Parker et al. (2017) reported that female adolescents from low income-to-needs (INR) households had greater rates of CT decline compared to their peers. However, little is known about how either family INR or PE interact with structural maturation within functionally defined brain networks.

The current cross-sectional study aimed to characterize age-related changes in CT as a function of age, sex, pubertal timing, and SES in the context of functional brain network organization using a sample diverse in race, ethnicity, and SES from the Lifespan Human Connectome Project in Development (HCP-D). Previous research examining developmental differences in CT has largely relied on gyral and sulcal based atlases. Here, we used the Cole-Anticevic Brain Network Parcellation (Ji et al., 2019), where network labels were assigned to the Glasser et al. (2016) multimodal parcellation using community detection based on resting-state functional connectivity which identified twelve functional brain networks. While most recent studies have found that CT follows a linear monotonic decline with age for most cortical regions (Ducharme et al., 2016, Raznahan et al., 2011, Tamnes et al., 2010, Wierenga et al., 2014), other, typically older, studies have noted that regional CT trajectories displayed cubic and quadratic patterns (Shaw et al., 2008, Sowell et al., 2007). These differences in CT across regions might reflect larger, network-based variation. He et al. (2007) argued that CT networks contain small-world properties (i.e., high clustering coefficient and short path length) that provide the structural substrates for the functional organization of complex networks. Therefore, investigating CT by functional network may provide a more nuanced context of brain maturation than examining changes by individual structure alone. We hypothesized that primary sensory networks would reach asymptote earlier than association networks. While we did not expect sex differences in CT, we hypothesized that earlier pubertal timing would be associated with cortical thinning and that SES would be positively associated with CT by functional brain network. However, given that current evidence is less clear concerning how these factors affect CT trajectories, we made no a priori hypotheses about how age, puberty, or SES would impact curve shape.

2. Methods

2.1. Participants

The present study included 789 typically developing children, adolescents, and young adults aged 5–21 years from the HCP-D (Harms et al., 2018, Somerville et al., 2018) (see Table 1 for participant characteristics). Participants were recruited across four sites: Harvard University, University of California-Los Angeles, University of Minnesota, and Washington University in St. Louis. Exclusion criteria for recruitment included (i) premature birth (< 37 weeks gestation); (ii) serious neurological condition (e.g., stroke, cerebral palsy); (iii) serious endocrine condition (e.g., precocious puberty, untreated growth hormone deficiency); (iv) long term use of immunosuppressants or steroids; (v) any history of serious head injury; (vi) hospitalization > 2 days for certain physical or psychiatric conditions or substance use; (vii) treatment > 12 months for psychiatric conditions; (viii) claustrophobia; or (ix) pregnancy. Participants provided written informed consent and assent, and parents of participants under 18 years provided written informed consent for their child’s participation. All methods were approved by the Institutional Review Board at Washington University in St. Louis (IRB #201603135).

Table 1.

Demographic and acquisition site characteristics of the sample. SD, standard deviation; IQR, interquartile range; SES, socioeconomic status; UCLA, University of California Los Angeles; UMinn, University of Minnesota; WUSTL, Washington University in St. Louis.

	Participants
	(n = 789)
Mean Age in Years (SD)	13.9 (4.1)
Range (Years)	5.4–21.9
Sex (% Female)	51.1
% Female	51.1
Race (%)
Native American/Alaska Native	1.5
Asian	10.4
Black/African American	16.7
Native Hawaiian/Pacific Islander	0.04
White	59.4
More than one race	8.5
Unknown	3.1
Median Income ($)	110,000
IQR ($)	100,000
SES Bracket (%)
Low	25.7
Medium	34.3
High	40.0
Acquisition Site (%)
Harvard	28.4
UCLA	25.1
UMinn	23.9
WUSTL	22.6

2.2. Pubertal development scale

The Pubertal Development Scale (PDS; Petersen et al., 1988) is a self-report measure of secondary sexual characteristics and was used to assess pubertal status. The PDS is a five-item measure with responses coded on a four-point scale (1 = ‘not yet started’ to 4 = ‘seems complete’). The last two items are sex-specific: males answered questions about facial hair and voice change, while females answered questions about breast development and onset of menarche. Sex was defined as the sex assigned at birth. Ratings were averaged across items to create a dimensional PDS score, consistent with methods described in Petersen et al. (1988). An index of pubertal timing was computed by regressing the youth’s biological age from their PDS score. As such, higher residual scores represent earlier timing in the present study.

For this study, parents completed the PDS on behalf of any children 5–13 years of age. Adolescents and young adults aged 9–21 years completed the PDS on their own. Since both parent and child-report data were collected for adolescents aged 9–13 years and responses were well correlated (r = 0.72), parent and child reports were averaged for youth ages 9–13.

2.3. Socioeconomic status

We measured two indices of SES – maternal education (ME) and income-to-needs (INR) ratio. ME was defined as the highest educational level achieved by the child’s mother (Lawson et al., 2013, Leonard et al., 2019). INR was defined as the total family income divided by a computed estimate of the state-specific poverty level based on total household size. A state poverty level was used to address cost of living differences between states. As the median income levels in St. Louis are relatively similar to the national levels, the national poverty line was used for St. Louis. Then, for each of the three other cities (Boston, Los Angeles, Minneapolis), the percent difference in costs of living from St. Louis were used to adjust the state poverty line (increases of 17 %, 56 %, and 62 % for Minneapolis, Los Angeles and Boston, respectively). Thus, for example, while the poverty line for a family of 4 in St. Louis was $24,600 (the national poverty line), it was $28,896 for Minneapolis, $38,337 for Los Angeles, and $39,951 for Boston. The INR distribution in our sample displayed extreme positive skew (Skew=8.41), and the range spanned from 0.16 to 26.62 (M = 4.22, SD = 4.62) with 75% of the sample having an INR below 5.18. Therefore, we Winsorized INR to minimize extreme outliers and avoid spurious effects due to their influence. This was accomplished with the function “Winsorize” from the R package “DescTools” (Signorell et al., 2022).

2.4. Image acquisition

Structural T1w MRI images were acquired on a 3 T Siemens Prisma with a 32 channel head coil using a multi-echo 3D MPRAGE sequence (Mugler and Brookeman, 1990; van der Kouwe et al., 2008) (0.8 mm isotropic voxels, TR/TI = 2500/1000 ms, TE = 1.8/3.6/5.4/7.2 ms, flip angle = 8°, FOV = 256 ×240×166 mm, matrix size = 320 ×300, 208 sagittal slices, in-plane (iPAT) acceleration factor of 2). T2w volumes were also acquired at the same spatial resolution using the variable-flip-angle turbo-spin-echo 3D SPACE sequence (Mugler et al., 2000) (TR/TE=3200/564 ms; same FOV, matrix and in-plane acceleration). Both the T1w and T2w acquisitions included volumetric navigators for motion detection and selective reacquisition of the lines in k-space that are corrupted by motion, which together help to reduce the incidence of poor-quality structural data (Harms et al., 2018, Tisdall et al., 2012) (see Harms et al., 2018 for detailed protocol description). If the T1w or T2w structural scans were nonetheless deemed at the time of acquisition to be of poor quality, they were reacquired (typically immediately in the same imaging session, although sometimes in a different session). Only the single pair of T1w/T2w scans rated the highest in quality were used in subsequent processing. Both ‘PreScan Normalized’ (Siemen’s approach for removing the receive coil intensity profile) and non-normalized reconstructions were generated at the scanner. The former were used for image quality review at the scanner, while the latter were as the inputs for subsequent processing (consistent with the use of non-normalized reconstructions as the input for the processing of the HCP Young Adult acquisitions).

2.5. Image processing

The structural MRI data were analyzed using the HCP Pipelines (Glasser et al., 2013) version 4.0.0, instantiated into the QuNex container environment (qunex.yale.edu), using the same processing as the Lifespan HCP Release 2.0 in the NIMH Data Archive (nda.nih.gov). Briefly, the T1w and T2w volumes were processed through the PreFreeSurfer pipeline, which included gradient nonlinearity distortion correction, registration of the T2w volume to the T1w volume, correction for the receive coil bias field, brain-extraction, and rigid registration into an anterior/posterior-commissure aligned ‘native’ space. Next, a version of FreeSurfer (v6.0.0; Dale et al., 1999; Fischl and Dale, 2000) optimized for use with high-spatial resolution structurals was used for computing the ‘white’ and ‘pial’ surfaces, including use of the T2w volume to optimize the pial surface placement. Last, the PostFreeSurfer pipeline produced cortical surface models in GIFTI format and surface-related data in CIFTI format, with each subject’s cortical surface registered to a common 32k_FS_LR mesh using ‘MSMAll’ areal-feature-based cortical surface registration, which is a multimodal registration constrained by cortical myelin maps and resting-state network maps (Glasser et al., 2016, Robinson et al., 2014).

Following cortical surface reconstruction, a single experienced individual performed a manual ‘SurfaceQC’ review of the accuracy of the white and gray matter surface placement, including checking for dural inclusions and incomplete capture of the cortical ribbon. This practice included examination of T1w/T2w ratio “myelin maps” (Elam et al., 2021, Glasser and Van Essen, 2011), which are sensitive to errors in the surface placement, and thus a valuable tool for promoting efficient QC of the FreeSurfer surfaces. Participants with more than just minor (focal) issues were flagged for possible future editing and excluded from the cohort analyzed for the current study (n = 32). This ‘SurfaceQC’ review of the HCP-D data revealed some degradation of the accuracy of surface placement relative to expectations established by the HCP Young Adult project, which we subsequently traced to artifacts in the longer echos. The only tractable solution was to use the mean of just the shortest two echos (i.e., exclude the longest two of four echos) as the T1w input to the HCP Pipelines (Elam et al., 2021).

Here, we focus on network-level cortical thickness, acknowledging that the trajectories of network-level surface area also warrant further investigation. Cortical thickness values were extracted using the Cole-Anticevic Brain Network Parcellation (CAB-NP; Ji et al., 2019). The CAB-NP utilized the Human Connectome Project Multi-Modal Parcellation version 1.0 (HCP MMP1.0; Glasser et al., 2016) areas to identify resting-state network communities. The HCP MMP1.0 atlas divides each hemisphere into 180 areas based on spatial ‘gradient ridges’ that overlap for at least two group-average areal features (myelin, thickness, resting-state, task-fMRI, and visuotopic maps). The CAB-NP parcellation was generated using data from 337 HCP Young Adult (Van Essen et al., 2013) subjects by first calculating functional connectivity between each region of the HCP MMP1.0. Next, the Louvain community detection algorithm was used to assign parcellated cortical regions to functional networks. From the 360 MMP1.0 areas, 12 functionally defined networks were identified in previous work by the CAB-NP (Ji et al., 2019): primary visual (VIS1), secondary visual (VIS2), somatomotor (SMN), cingulo-opercular (CON), dorsal attention (DAN), language (LAN), frontoparietal (FPN), auditory (AUD), default-mode (DMN), posterior multimodal (PMM), ventral multimodal (VMM), and orbito-affective (ORA) networks. Besides somatomotor and cognitive networks similar to those reported by Power et al. (2011) and Yeo et al. (2011), three novel networks (posterior multimodal, ventral multimodal, and orbito-affective) were identified. Follow-up analyses of robustness (i.e., split-half replication, network confidence scores, inter-subject variability) were conducted to confirm the consistency of the novel networks. Of the 12 networks, parcel-level network assignment confidence scores were lowest for the orbito-affective network. This network also exhibited a low signal-to-noise ratio and included only three cortical areas per hemisphere.

Visualization of cortical thickness data overlaid on surface models was performed in Connectome Workbench v1.4.2 (Marcus et al., 2011). Two dense label (.dlabel.nii) files for parcellation were downloaded from https://github.com/ColeLab/ColeAnticevicNetPartition, one organized by cortical parcels and the other organized by network assignment. As inputs for computing CT, we used the ‘MSMAll’ registered corrected cortical thickness dense scalar (corrThickness.dscalar.nii) files, given that the Glasser parcellation was derived on ‘MSMAll’ registered data (Glasser et al., 2016). The corrected cortical thickness values had the FreeSurfer ‘curv’ (mean curvature, a signed measure of cortical folding) regressed from the maps of uncorrected thickness. This compensates for the fact that cortical folding induces systematic biases in cortical thickness, with gyral crowns thicker than regions within sulcal banks and sulcal fundi thinner than these flat regions (Glasser et al., 2016). Data were parcellated (i.e., mean thickness computed within each parcel) using Connectome workbench’s (v1.4.1) ‘-cifti-parcellate’ function.

2.6. Statistical analyses

Our general analysis approach is overviewed here first, followed by more detailed descriptions. First, all CAB-NP network CT trajectories were modeled using Generalized Additive Models (GAM) based on our assumption that trajectories may be nonlinear. Next, the smooth terms from the GAMs were tested for nonlinearity. Trajectories that were determined to be linear were subsequently also fit using linear modeling. For nonlinear trajectories, periods of significant changes in CT slope were identified. For linear trajectories, relative rates of linear decline were determined by comparing correlated correlation coefficients. Finally, the effects of sex, pubertal timing, and SES on CT trajectories were evaluated. Effect sizes are reported as standardized beta values (“β”) or partial eta squared (η²p) for main effects of the five-level ME factor. Post-hoc comparisons of significant age by ME interactions were accomplished by changing the reference ME level to test contrasts with the “relevel” function in the R package “stats” (R Development Core Team, 2020). All analyses were conducted in R version 3.6.2 (R Development Core Team, 2020).

2.6.1. Network CT trajectories using GAMs

First, to evaluate the potential presence of nonlinear trajectories, the data were modeled using GAMs in the R package “mgcv”. With the use of penalized splines, GAMs can flexibly model nonlinear relationships. Nonlinearities are estimated using restricted maximum likelihood (REML), where smooth terms are penalized for increasing complexity (Wood, 2001). Age-related differences in CT were examined for each of the 12 networks, and corrections for multiple comparisons were performed at the network level. Age was entered into the GAM as a smooth factor to capture any important nonlinear patterns over development. Covariates included acquisition site, surface holes from FreeSurfer, and number of volumetric navigators (NumNavs) for the T1w scan. “Surface holes” refers to the number of topological defects prior to FreeSurfer’s automated topology correction (Rosen et al., 2018) on the brain’s surface, which increases for poorer quality structural data. “NumNavs” is a proxy for the amount of head movement during the scan (Klapwijk et al., 2019). The reacquisition threshold parameter used to compute motion scores was 0.4, computed as the maximum displacement within a head sized sphere (64 mm).

Other variables of interest that were modeled linearly included sex, PDS scores, ME, and INR. The best-fit model was selected using Akaike information criterion (AIC; Bozdogan, 1987). For each model, we compared AIC scores for a full model containing both main effects and an interaction vs. a simpler model containing only main effects. If the two models had similar AIC scores, we selected the full model if the interaction term was significant at p < 0.05. If the interaction term was not significant, we selected the simpler model. The initial full models examining the effects of age and each variable of interest on nonlinear trajectories of cortical thickness are as follows (in R syntax):

Age: Network ~ s(Age) + Sex + Covariates

Sex: Network ~ s(Age) + Sex + Age*Sex + Covariates

Pubertal Timing: Network ~ s(Age) + Sex + PDS + Age*PDS + Covariates

Maternal Education: Network ~ s(Age) + Sex + ME + Age*ME + Covariates

Income-to-Needs Ratio: Network ~ s(Age) + Sex + INR + Age*INR + Covariates

2.6.2. Test for nonlinearity

Next, a restricted likelihood ratio test was used to determine whether the nonlinearity of the GAMs was a significantly better fit than a linear model. This was accomplished with the R package “RLRsim” (Scheipl et al., 2008). Using the function “exactRLRT”, nonlinearity was determined by examining if the variance of the random effect was equal to zero. If the test for nonlinearity returned a value of p < 0.05, the nonlinear GAM was determined to be the appropriate fit.

2.6.3. Nonlinear CT trajectories

For models where the smooth term was nonlinear, periods of change in the slope between age and CT were identified by generating posterior simulations of the first derivative of the spline term in the model (e.g., where new data is simulated from the fitted model and compared to the observed data, taking into account smoothing parameter estimation uncertainty; (Simpson, 2018). This was accomplished with the R function “derivSimulCI” (www.gist.github.com/gavinsimpson). This function produces plots of the first derivative of the splines (slopes) along with the 95% point-wise confidence intervals. Periods where the confidence interval around the first derivative excludes 0 represent the developmental periods with the strongest evidence for an age-related difference in cortical thickness (i.e., increasing or decreasing slope).

2.6.4. Linear CT trajectories

Linear models examining age-related differences in CT were fit using the “lm” function in the R package “stats” (R Development Core Team, 2020) if the GAM model was rejected by the test for nonlinearity. Standardized beta values were used to examine the rate of change in cortical thickness over our age span. To formally compare the relative rates of linear decline for each of these networks, we implemented the Meng et al. (1992) method for comparing correlated coefficients (relations of age and thickness for each network). This method produces a Z score to determine if there is a significant difference between the magnitudes of the age-related decline in CT (see Meng et al., 1992 for an in-depth review).

To determine if starting and ending thickness values predicted network CT trajectories, we calculated the correlation between mean network CT in early childhood (i.e., ages 5–8 years) and in early adulthood (i.e., ages 19–21 years) and network slopes.

2.6.5. CT variability between sexes

To investigate if there were differences in network CT variability between males and females, we estimated a variance ratio (Wierenga et al., 2022). Random forest analysis was used to calculate predicted outcomes with residuals for each model, both linear and nonlinear, using the R package “randomForest” (Breiman, 2001). Accounting for age, volumetric navigators, and surface holes, the residual variances for males and females were calculated separately to create the test statistic. Next, random permutations of sex among the residuals were performed using 10,000 permutations, and p-values were calculated as the proportion of the permutated t-statistic greater than the observed t-statistic. Finally, p-values were FDR corrected for multiple comparisons.

2.6.6. Hemispheric symmetry

We compared left and right hemisphere network slopes to evaluate stability in hemispheric patterns of cortical thinning. To assess concordance between hemispheres by network, we extracted the linear slopes for each of the 360 areas that compose the 12 Cole-Anticevic networks. All 180 HCP_MMP1.0 areas have a corresponding area in the opposite hemisphere, reflecting a high degree of bilateral symmetry in many areal features. However, there are some genuine asymmetries, and some area pairs have different CAB-NP network assignments in the left vs right hemispheres. Since we were interested in comparing slopes within networks by hemisphere, only the 167 corresponding area pairs that belonged to the same networks were analyzed. Correlations between left and right hemisphere slopes were examined across areas within each network.

2.6.7. Outlier screening and other details

After screening all variables for outliers, between 1.01 % and 2.28 % of observations were noted as extreme values. These values were Winsorized using the function “Winsorize” in the R package “DescTools” (Signorell et al., 2022) to limit the effects of extreme values on our results.

All q-values reflect a false discovery rate (FDR) correction for multiple comparisons. Corrections were based on the number of CT comparisons made, totaling 13 (12 CAB-NP networks and mean CT). Adjustments were calculated using the R function “p.adjust” in the R package “stats” (R Development Core Team, 2020) specifying the FDR method.

Significant interactions were decomposed using the “emtrends” function from the “emmeans” package in R (Lenth et al., 2018) to perform pairwise contrasts using the Tukey HSD method. Effect sizes for pairwise contrasts were calculated using the “eff_size” function from the “emmeans” package.

3. Results

We examined age-related differences in CT by functional network in a sample diverse in race, ethnicity, and socioeconomic status. Supplementary Figure 1 shows a simple trajectory of mean cortical thickness (both hemispheres, all areas), binned into 1 year age bins.

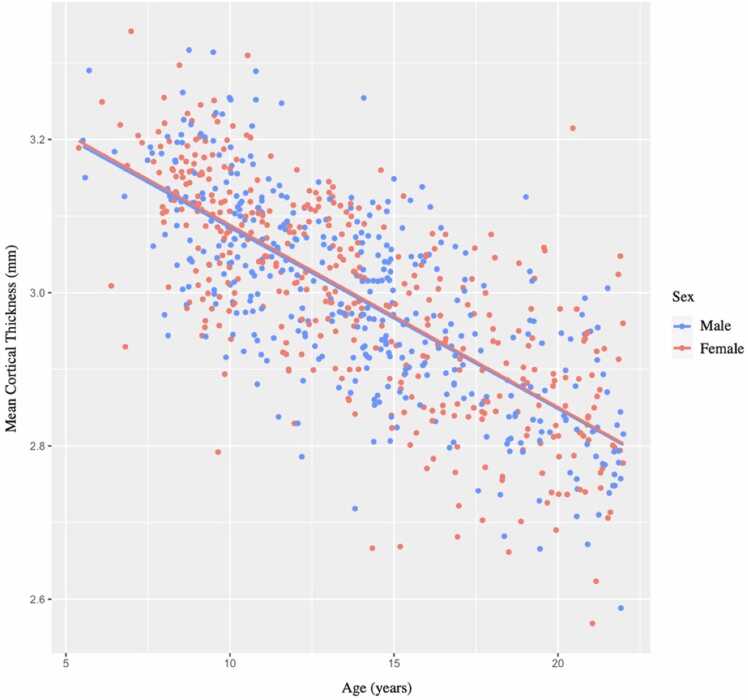
In magnitude, mean thickness declined from 3.2 mm to 2.8 mm on average, i.e., 10% over 16 years (0.6%/year or 0.025 mm/year). This is similar to previous reports (Ducharme et al., 2016). In a more formal GAM, the test for nonlinearity in mean CT was rejected (p = 1.00). In the “Age” model, mean CT displayed a significant linear decline across the age span (β = −0.70, q < 0.001), with no main effect of sex (β = 0.02, q = 0.77) or age by sex interaction (β = 0.03, q = 0.97), controlling for acquisition site, surface holes, and NumNavs (Fig. 1).

Fig. 1.

Scatterplot simple linear regression showing mean cortical thickness (mm) by age in years. Regression lines reflect age-related changes in mean cortical thickness for each sex. mm, millimeters.

3.1. Developmental trajectories by functional networks

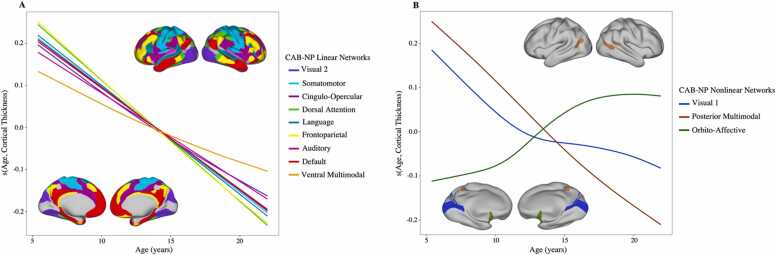
Developmental curves for CT were estimated for the 12 CAB-NP networks. First, all GAM models were tested for nonlinearity using a restricted likelihood ratio test (RLRT). Of the 12 networks, three (ORA, VIS1, and PMM) displayed significantly nonlinear trajectories (Fig. 2), although the RLRT for the PMM was very close (p = 0.04) to rejecting the hypothesis of a nonlinear trajectory.

Fig. 2.

A. Linear cortical thickness trajectories over the developmental age span by Cole-Anticevic functional network. B. Nonlinear cortical thickness trajectories over the developmental age span by Cole-Anticevic functional network. Cole-Anticevic network surface plots shows network location.

The RLRT of the remaining nine networks rejected the hypothesis of nonlinearity, and thus were deemed to have linear CT trajectories (see Table 2 for statistics).

Table 2.

Nonlinearity test, linear model statistics, and generalized additive model statistics for each network across the developmental age span. RLRT test for nonlinearity examines if the variance of the random effect is equal to zero. If p < 0.05, the trajectory was deemed to follow a nonlinear pattern and was modeled using a generalized additive model. Generalized additive model and linear model statistics are shown for each network trajectory. All effects of age were significant at the p < 0.001 level. RLRT, restricted likelihood ratio test; Adj. R², adjusted R²; edf, effective degrees of freedom for the smooth term 'age'; B, unstandardized beta; β, standardized beta.

	Generalized Additive Model		Test for Nonlinearity		Linear Model
	edf	Adj. R2	RLRT	p-value	B	β	Adj. R2
Mean	0.01	0.53	0	1	-0.02	-0.71	0.53
VIS1	3.92	0.23	23.76	< 0.001	-0.01	-0.43	0.20
VIS2	1.99	0.48	1.32	0.07	-0.02	-0.68	0.48
SMN	1.00	0.45	0	1	-0.02	-0.67	0.45
CON	1.00	0.52	0	1	-0.02	-0.70	0.51
DAN	1.00	0.57	0	1	-0.03	-0.74	0.57
LAN	1.00	0.50	0	1	-0.03	-0.72	0.51
FPN	1.53	0.60	0.16	0.21	-0.03	-0.75	0.60
AUD	1.00	0.30	0	1	-0.02	-0.55	0.30
DMN	1.00	0.55	0	1	-0.02	-0.72	0.55
PMM	2.38	0.49	1.80	0.04	-0.03	-0.68	0.48
VMM	1.76	0.14	0.50	0.14	-0.01	-0.40	0.14
ORA	3.23	0.14	3.47	0.01	-0.02	-0.28	0.14

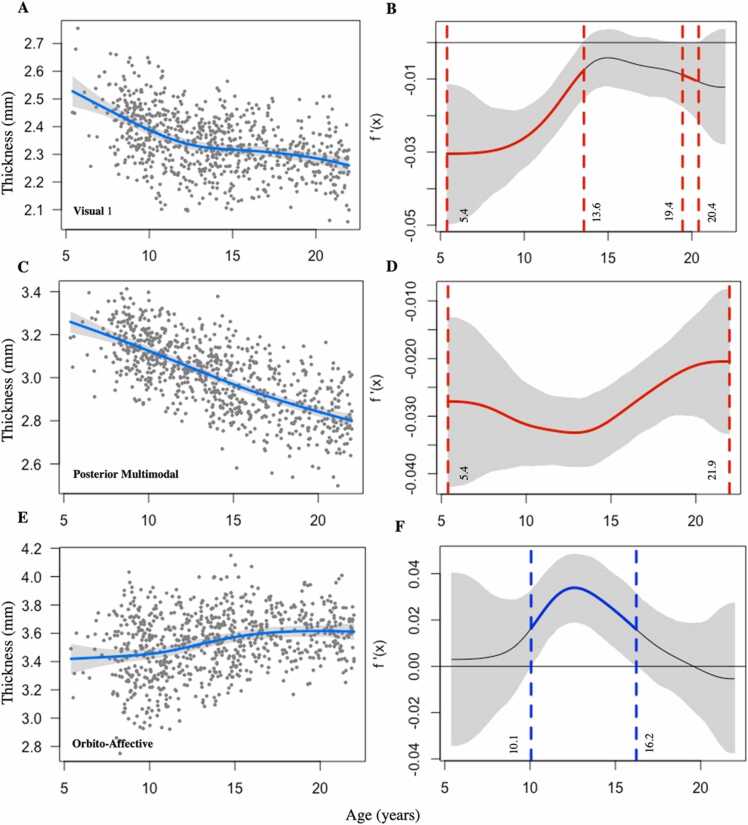
To further characterize the nonlinear trajectories for these three networks, we performed posterior simulations of the first derivative of the spline term “age”. This allowed us to identify periods of significant change in the slope of the relationship of CT to age. For each of the three networks with a nonlinear trajectory, the left panels of Fig. 3 display the GAM estimate of the cortical thickness trajectory over the age span, whereas the right panels display periods of significant change in slope denoted by colorized line segments.

Fig. 3.

A, Scatterplot of VIS1 network cortical thickness trajectory. B, First derivative plot of VIS1 network trajectory. There were two periods of significant variance in the rate of change in cortical thickness across the age span: from ages 5.4–13.6 years and from ages 19.4–20.4 years. C, Scatterplot of PMM network cortical thickness trajectory. D, First derivative plot of PMM network trajectory. Cortical thickness significantly decreased over the age span (5.4–21.9 years of age), with varying instantaneous rates of change. E, Scatterplot of ORA network cortical thickness trajectory. F, First derivative plot of ORA network trajectory. Cortical thickness significantly increased from ages 10.1–16.2 years. For first derivative plots, periods of significant change are denoted by colorized line segments. Grey bands show a 95 % point-wise confidence interval, and segments of the spline where the confidence interval does not include zero are denoted by either red (significant decrease) or blue lines (significant increase). VIS1, visual 1; PMM, posterior multimodal; ORA, orbito-affective; f′(x), first derivative. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

For the VIS1 network (Fig. 3B), there were two periods of significant decline in slope for cortical thickness over development: (1) from ages 5–14 years and (2) from ages 19–20 years; in the intervening period (ages 14–19) the slope did not differ significantly from zero. Cortical thickness in the PMM network decreased over the entire available age span (ages 5–22 years), but the rate of change in CT varied, as demonstrated by the varying slope of the spline fit (see Fig. 3C and D). The ORA was the only network where a significant increase in cortical thickness was noted (Figs. 2 and 3 E). This occurred between ages 10–16 years (Fig. 3F). However, given the small size of the ORA network, wide dispersion of age-related cortical thickness data in this region, and other methodological considerations, these observations for the ORA network should be interpreted cautiously (see Section 4.1).

The remaining nine Cole-Anticevic networks exhibited linear trajectories over the available age span. We found that the network slopes were ordered as follows from steepest to most shallow: DAN, FPN, DMN, SMN, VIS2, LAN, CON, AUD, and VMM. To examine the relative rates of linear decline for each of these networks, we used the Meng et al. (1992) method for comparing correlated correlation coefficients. After all correlation coefficients were compared, the DAN, FPN, and DMN networks exhibited the steepest slopes, respectively, over the age span and were not significantly different from one another. However, all three of these network slopes significantly differed from the VIS2, CON, LAN, AUD, and VMM networks. Additionally, DAN and FPN network slopes significantly differed from the SMN slope, though there were no significant differences between DMN and SMN slopes. Next, the SMN, VIS2, LAN, and CON networks displayed slopes that were not different from one another. The AUD network slope was significantly shallower than all other network slopes, with the exception of the DMN and VMM networks. Lastly, the VMM network, which displayed the shallowest slope, differed from all other linear networks (Figs. 4 and 5; see Supplementary Table 1 for statistics).

Fig. 4.

Heatmap displaying Z-score values obtained from Meng test conducted to identify significant differences between the two correlated coefficients. The correlation coefficients are the association between age and mean thickness for a network. VIS2, visual 2; SMN, somatomotor; CON, cingulo-opercular; DAN, dorsal attention; LAN, language; FPN, frontoparietal; AUD, auditory; DMN, default mode; VMM, ventral multimodal; * , significant differences between network correlation coefficients.

Fig. 5.

Cortical surfaces illustrating standardized beta values for age in linear network trajectories. Magnitude of age effect on thickness from steepest to shallowest is: DAN, FPN, DMN, SMN, VIS2, LAN, CON, AUD, and VMM. Functional networks that are nonlinear are shown in grey.

To investigate if starting or ending CT values significantly impacted observed network slopes, we calculated the correlation between mean CT in early childhood and early adulthood in relation to each network’s slope. We found that neither early childhood (p = 0.63) nor early adulthood (p = 0.06) CT predicted network CT trajectories. These relationships, however, were largely driven by ORA slope, which was an outlier. Therefore, we conducted follow-up analyses where ORA slope was excluded. Still, there was no significant association between early childhood (p = 0.50) or early adulthood (p = 0.93) and network CT trajectories.

To evaluate stability in hemispheric patterns of cortical thinning, correlations between left and right hemisphere slopes were examined across areas (167 areas) within each network (12 networks). Results indicated that the slopes of homologous areas for most networks were significantly correlated, suggesting stability in the patterns across hemispheres. However, model slopes for homologous areas that comprise the ORA network were only moderately correlated (Fig. 6 & Supplementary Table 2).

Fig. 6.

Cortical surfaces illustrating Pearson correlation between left and right hemisphere area slopes. Slopes of homologous areas for most networks were significantly correlated, with the exception of the areas that comprise the orbito-affective network which were only moderately correlated.

3.2. Sex effects

The best-fitting "sex" model for each network was the simpler model examining the main effect of sex, with no age by sex interaction term. There was no significant main effect of sex for any network. Additionally, there were no sex differences in CT variability for any network (see Supplementary Table 3 for AIC values, Supplementary Table 4 for full statistics, and Supplementary Table 5 for Fisher’s variance ratio statistics).

3.3. Pubertal timing effects

The best-fitting "pubertal timing" model for each network was the simpler model examining the main effect of pubertal timing, where biological age was regressed from PDS scores. Age and PDS scores were strongly correlated (r = 0.78). Earlier pubertal timing was associated with reduced mean CT (β = −0.21, q < 0.001), as well as with reduced CT in the following seven networks: VIS2 (β = −0.18, q = 0.002), SOM (β = −0.14, q = 0.02), CON (β = −0.12, q = 0.03), DAN (β = −0.16, q = 0.002), FPN (β = −0.19, q < 0.001), DMN (β = −0.12, q = 0.02), and PMM (β = −0.23, q < 0.001) (see Supplementary Table 6 for full statistics).

3.4. ME and INR effects

To investigate if either indicator of SES was associated with network cortical thickness, maternal education (ME) and income-related (INR) were examined in two separate models. ME and INR were themselves only modestly correlated (r = 0.36, p < 0.001), consistent with those two measures capturing dissociable information about SES.

The best-fitting "ME" model was the full model including an age by ME interaction for mean CT and CT in the VIS2, CON, DAN, and LAN. The remaining networks were best fit by the simpler model examining only the main effect of ME. Slopes significantly differed between individuals whose mothers achieved a bachelor’s degree and those whose mothers achieved a master’s degree for both mean CT (β = −0.29, q = 0.03) and DAN CT (β = −0.28, q = 0.03) (Fig. 7).

Fig. 7.

Age by maternal education interaction effects on Cole-Anticevic network and mean cortical thickness. Beta values represent the age trend (i.e., slope) for cortical thickness across maternal education levels. For both mean cortical thickness and cortical thickness in the dorsal attention network, those whose mothers achieved a master’s degree displayed a steeper cortical thinning slope than those whose mothers achieved a bachelor’s degree. * , significant difference of maternal education level in cortical thickness slopes over the age span.

However, there were no other significant contrasts by ME level for any other network. Thus, main effects were examined. There was a main effect of ME on CON (η²p = 0.02, q = 0.026), DMN (η²p = 0.02, q = 0.015), and VMM (η²p = 0.03, q = 0.004) CT. For these networks, higher levels of maternal education were associated with greater CT. The best-fitting "INR" model for each network was the simpler model examining the main effect of INR on CT. There was a main effect of INR on VMM CT (β = 0.11, q = 0.033), where higher INR was associated with greater CT. There were no other main effects of INR on network CT (see Supplementary Tables 7 & 8 for full statistics).

4. Discussion

The current study examined developmental trajectories of curvature-corrected cortical thickness by functional network in terms of age, sex, pubertal timing, and two indices of SES in a diverse sample of children and adolescents. Examining cortical maturation at the network level provides a large-scale spatial framework for understanding how functionally connected areas that contribute to many different facets of cognition, emotion, and behavior develop. Four main observations emerged from this study: 1) CT largely followed a linear decline from our earliest measured age (5 years), except for three networks that contained a statistically significant nonlinear component; 2) there was no effect of sex for any network CT; 3) earlier pubertal timing was associated with reduced mean CT and reduced CT in seven networks; 4) ME was positively associated with CT in three networks, with observed ME by age interactions for mean CT and CT in the DAN, while INR was positively associated with VMM CT.

4.1. Nonlinear trajectories

We found that VIS1, PMM, and ORA network CT followed a nonlinear trajectory over the investigated age span, whereas CT decline was linear in the remaining nine networks. In an MR study, primary visual cortical thinning was reported to follow a cubic trajectory over the developmental period (Shaw et al., 2008). We found a significant decrease in VIS1 network CT from early childhood to early adolescence and again for a brief period in late adolescence. While the PMM followed a nonlinear trajectory, the test for nonlinearity was close to being rejected (p = 0.04). Regions in the PMM are involved in spatial navigation and identifying event structures in narratives (Ji et al., 2019). These cognitive functions develop at varying times from early childhood to early adulthood, with abilities increasing and plateauing at different stages (Genereux and McKeough, 2007, Pine et al., 2002). This begs the question of if and how maturational patterns of associated networks map on to the development of these skills. Our results suggests that the rate of cortical thinning in the PMM is not consistent across the age span and may quicken during early adolescence.

In stark contrast to all other network trajectories, ORA network CT appeared to increase from early to middle childhood. These results should be interpreted with caution, however, as the ORA network exhibited a low signal-to-noise ratio and had the lowest parcel-level network assignment confidence scores (Ji et al., 2019). Additionally, the VIS1 and PMM are among the smaller networks, which might influence our results. Acknowledging these caveats, the nonlinear changesin VIS1, PMM, and ORA CT may reflect more complex age-related periods of large-scale brain network fine tuning, such as a succession from a less organized brain early in life to a more mature reorganization (Dosenbach et al., 2010, Fair et al., 2009).

4.2. Linear trajectories

Consistent with many previous studies, we found that CT trajectories for most networks followed a monotonic linear decline (Ducharme et al., 2016, Koolschijn and Crone, 2013). Network CT slopes were not predicted by network mean CT in early childhood or in early adulthood, suggesting that these values did not significantly impact our results. Thus, networks that started out with greater thickness did not have systematically different slopes. Of the networks that followed linear trajectories, the DAN, FPN, and DMN exhibited the fastest rates of cortical thinning and did not statistically differ by trajectory slopes. The FPN can flexibly couple with either the DAN or DMN, depending on task requirements (Buckner et al.,2008; Dosenbach et al., 2007). Specifically, tasks that require externally oriented, goal-directed cognition elicit increased functional connectivity between the FPN and DAN, whereas internally motivated cognition is associated with increased connectivity between the FPN and DMN (Spreng et al., 2013, Vincent et al., 2008). Additionally, the FPN, DAN, and DMN are implicated in what Menon (2011) referred to as the “triple network theory of psychopathology”, as abnormal intrinsic organization and interconnectivity of these networks are commonly seen in many psychiatric disorders. In turn, the normative development of these networks is important for actively maintaining and manipulating information to effectively judge and select appropriate action (Koechlin and Summerfield, 2007). Given the functional relationship and orientation of the DAN, FPN, and DMN networks, our finding of similar trajectories of CT across these networks adds further developmental insight into how these networks are intimately linked.

Structural imaging studies have found that gray matter loss occurs earliest in primary sensorimotor areas and later in association areas (Paus, 2005, Sowell et al., 2004). Here, we found that networks associated with higher order executive functioning (e.g., DAN, FPN, and DMN, but not CON and LAN) exhibited steeper slopes of cortical thinning than did primary sensorimotor regions (e.g., SMN, VIS2, and AUD). It is well-established that sensory and motor brain regions reach maturity early in life and by two years of age resemble adult-like morphology (Gao et al., 2019, Lyall et al., 2015). Our finding of shallower CT slopes in the SMN, VIS2, and AUD compared to other association networks may be reflective of that early maturation that is not captured within our sampled age range.

Similarly, cortical thinning in the LAN network followed a relatively shallow trajectory. Early research into language development suggested that the most dramatic changes in language ability occur during the first two years of life (Bates et al., 1992), yet we did not examine children younger than 5 years of age. The CON network, which is involved in the task-positive system (Dosenbach et al., 2006), displayed a significantly shallower slope than other task-positive networks (i.e., FPN and DAN). Previous functional imaging studies observed increased cross-network integration between the CON and SMN from late childhood into adulthood (Fair et al., 2012, Grayson et al., 2014), which moderated age-related increases in cognitive control (Marek et al., 2015). In the current study, CT trajectories in the CON and SMN networks did not significantly differ, suggesting similar thinning patterns from early childhood into adulthood. This gradual structural maturation may reflect the previously reported functional integration between the CON and SMN that is implicated in the development of adult-like cognitive control.

The VMM exhibited the slowest rate of cortical thinning. The VMM is one of the three novel networks identified by the CAB-NP, consisting of four cortical regions on the ventral surface of the temporal lobe (Ji et al., 2019). Due to its novelty, specific functionality of this network is currently unknown, though Ji and colleagues propose that it may be involved in higher-order semantic processing. Given that semantic cognition has been shown to improve into late adulthood (Hoffman, 2018), the relatively slow rate of cortical thinning in the VMM may mirror this developmental course.

4.3. Sex and pubertal timing effects

While growth trajectories are highly influenced by age, sex differences and pubertal maturation may also account for variations in cortical maturation. Though we found no network CT differences by sex, we did find that earlier pubertal timing was associated with reduced mean CT and reduced CT in seven of the twelve functional networks. Our findings expand on the current literature suggesting that puberty may represent a critical period of brain organization (Goddings et al., 2019) by providing evidence that accelerated puberty is associated with large-scale network CT. Pubertal timing-related cortical thinning was found in most networks associated with higher-order cognition. Specifically, those who reported a more advanced pubertal stage displayed reduced CT compared to their age-mates. The role of puberty in the brain’s functional network organization has been largely unexplored. A recent graph theory study examining the development of the functional connectome in relation to pubertal stage reported greater efficiency in the DMN, DAN, FPN, VIS, among others, with higher pubertal stage. While functional connectivity is a very different measure than CT, our findings point to accelerated puberty effects in similar networks, providing important morphological information about how advanced pubertal processes relative to one’s age impact cortical thinning in the context of functional network membership.

4.4. ME and INR effects

While accelerated pubertal timing represents a potentially negative biological factor in the current study, as evidenced by its association with lower average CT, high SES represents a positive environmental factor. Given the brain’s sensitivity to environmental factors, we capitalized on the diverse socioeconomics in the HCP-D data by examining how SES indices relate to cortical development. Generally, studies investigating the effects of SES on neural structure have found that higher SES is associated with greater CT in children and adolescents (Mackey et al., 2015). In the current study, ME was positively associated with CON, DMN, and VMM network CT, with a significant ME by age interaction for mean CT and DAN CT. This is in line with previous research showing that higher maternal education is associated with greater CT (Lawson et al., 2013). In an observational study, Rosen et al. (2020) found that a child’s access to enriching materials and complex stimuli, language used in the home, and caregiver involvement in the child’s learning was positively associated with parental education. Thus, the cognitive stimulation associated with higher parental education (Chou et al., 2010, Duncan et al., 2014) may influence the CT differences we observed.

While maternal education represents a non-material component of a child’s SES, INR reflects a material resource that can have a substantial impact on a child’s access to nutritious foods, high-quality childcare, and safe neighborhoods (Duncan and Magnuson, 2012). We observed a main effect of INR on VMM CT, where higher INR was associated with greater CT in this network. As noted in Section 4.2, the VMM is proposed to be associated with higher-order semantic processing. Though the VMM’s novelty precludes specific conclusions based on its functionality, our results suggest that its age-related changes in thickness are similarly affected by both indices of SES. However, unlike ME, no other effects of INR were found. Higher levels of maternal education exhibited effects on CT in higher order association networks that are critical to goal-directed cognition (Dosenbach et al., 2006, Spreng et al., 2013). These functions are integral to adult-like cognitive control, and the differential impact of ME compared to INR that we observed in the current study suggests that the cognitively enriching environment associated with higher parental education might have a more extensive impact on cortical development. Taken together, these results build upon the literature showing that SES indices uniquely contribute to brain maturation.

4.5. A comment on diversity in the lifespan human connectome project in development

An important facet of the present study that is unfortunately overlooked in many investigations of brain development is the use of a sample rich in diversity. A recent review published in a special issue of the Annals of the New York Academy of Sciences in (2020) by Dotson and Duarte outlined a lack of demographic representation in research investigating neural and cognitive development. This has significant implications for how neuroscientific and developmental research ultimately informs policy and clinical care. It may also partially explain problems with reproducibility, beyond what is accounted for by other methodological considerations. Outlined in Table 1, the demographic makeup of our sample is closely representative of the current United States population. We therefore argue that, though cross-sectional, our results provide relatively generalizable information about cortical maturation.

4.6. Limitations

The main limitation of this study is its cross-sectional design. This prevents us from analyzing within-subject changes in CT trajectories, which is necessary for capturing true developmental change. However, longitudinal data collection is now complete in the HCP-D. Second, we did not sample for individuals younger than 5 years of age. Third, we used an income-to-needs ratio and maternal education as our measures of SES, acknowledging that SES is a multifaceted construct that encompasses factors beyond these measures (e.g., occupation, neighborhood disparity, etc.). We chose to focus on INR and ME due to their robust and dissociable associations with child development (Brito et al., 2018, Johnson et al., 2021, Olson et al., 2021) but contend that future work should incorporate additional SES components into their investigations of brain development. Fourth, we used the Pubertal Development Scale as our sole measure of pubertal timing. However, HCP-D saliva assays measuring puberty-related hormones (e.g., testosterone, progesterone, and DHEA) are currently underway.

Our results should also be interpreted in the context of microstructural mechanisms that may confound apparent changes in CT. The neurobiological mechanisms underlying age-related changes in CT are complex and are subject to bias relating to the pattern of myelination. Voxel intensity in T1w MR images is affected by myelin content, whereby higher myelin content increases voxel intensity. Thus, heavily myelinated areas, such as the visual cortex, are particularly subject to alterations in the gray-white matter boundary contrast, potentially resulting in artificially thin estimates of CT (Glasser and Van Essen, 2011). This ultimately presents a potential confound in our results, as apparent changes in CT may actually reflect changes in myelination.

5. Conclusions

The results presented here provide unique insights into the structural basis of large-scale functional brain networks. Previous studies examining cortical thickness trajectories laid the foundation for our understanding of structural development. However, prior work largely did not focus on functionally defined networks. Structure and function are intimately linked and should be considered together when assessing brain maturation. We found evidence for age, puberty, and SES-related differences in CT in the context of functional network organization, suggesting that these biological and environmental variations may impact the emerging functional connectome. Importantly, the role these functional networks play in cognition, emotion, and behavior may be impacted by their structural organization during sensitive periods of development. Characterizing these processes in the context of typical development not only elucidates normative cortical maturation but also provides a foundation for investigating aberrant deviations that contribute to psychopathology. Future work using longitudinal data should investigate how trajectories of psychopathology are associated with functional network CT maturation, and if maturational patterns of CT (e.g., timing, curve shape) are related to specific disorders or their symptoms. Furthermore, examining if these relationships differ by SES could help inform how environmental factors, particularly those associated with early life stress, contribute to psychopathology risk and alter brain maturation patterns. For example, a number of factors often correlated with SES (poor nutrition, disrupted sleep, exposure to toxins) may be part of a pathway by which low SES relates to brain development. Interventions that improve such factors could help decouple the association between SES and brain development. 5.1 A mechanistic perspective on CT.

It is instructive to view our findings through the lens of developmental mechanisms that may regulate CT and surface area. Why is the cortex markedly thinner in some areas vs others (e.g., primary sensory vs. motor), and why do nearly all areas get progressively thinner from early childhood through adolescence, whereas surface area increases until approximately the beginning of adolescence, then progressively decreases (Piccolo et al., 2016, Tamnes et al., 2017)? One plausible general mechanism posits that increases or decreases in cortical volume reflect a net increase or decrease, respectively, in the aggregate cellular and extracellular components in a given local region, but that net growth or shrinkage is manifested as a change in thickness and/or surface area according to the distribution of mechanical tension along anisotropically oriented cellular components, particularly axons, dendrites, and glial processes (Van Essen, 2020). By this hypothesis, cortex tends to be relatively thin in regions dominated by radially oriented processes (e.g., the apical dendrites of pyramidal cells, ascending/descending axons, and radial glial cells) and relatively thick in regions containing a higher proportion of tangentially and/or obliquely oriented processes. When a given patch of cortex increases or decreases in volume during development (including postnatal), changes in cellular composition leading to an increased or decreased radial bias would tend to make cortex thinner or thicker, respectively, and no change in the radial bias would lead to similar percentage-wise effects on thickness and surface area. While this tension-based hypothesis may be difficult to evaluate experimentally during normal postnatal maturation, it nonetheless provides a useful conceptual framework for relating the distribution of microscopic cellular components to macroscopic measures of thickness and surface area.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary Figure 1

Supplementary material

.

Data Availability

The HCP-Development Lifespan 2.0 Release is available for download from the HCP website at: https://www.humanconnectome.org/study/hcp-lifespan-development/data-releases. This website also contains detailed release notes: https://www.humanconnectome.org/study/hcp-lifespan-development/document/hcp-development-20-release. This release includes cross-sectional visit 1 (V1) preprocessed structural and functional imaging data, unprocessed V1 imaging data for all included modalities (structural, resting state fMRI, task fMRI, diffusion, and ASL), and non-imaging demographic and behavioral assessment data from 652 HCP-Development (HCP-D, ages 5–21) healthy participants. This manuscript used data from 789 HCP-D, some of which are not currently available for download.