GPCR homomers and heteromers: A better choice as targets for drug development than GPCR monomers?

Abstract

G protein-coupled receptors (GPCR) are targeted by many therapeutic drugs marketed to fight against a variety of diseases. Selection of novel lead compounds are based on pharmacological parameters obtained assuming that GPCR are monomers. However, many GPCR are expressed as dimers/oligomers. Therefore, drug development may consider GPCR as homo- and hetero-oligomers. A two-state dimer receptor model is now available to understand GPCR operation and to interpret data obtained from drugs interacting with dimers, and even from mixtures of monomers and dimers. Heteromers are distinct entities and therefore a given drug is expected to have different affinities and different efficacies depending on the heteromer. All these concepts would lead to broaden the therapeutic potential of drugs targeting GPCRs, including receptor heteromer-selective drugs with a lower incidence of side effects, or to identify novel pharmacological profiles using cell models expressing receptor heteromers

1. Introduction

1.1. Receptor monomers, dimers and higher-order oligomers

G protein-coupled receptor (GPCR) homo and heteromerization open a completely new therapeutic potential for drugs targeting GPCRs. Although the phenomenon of GPCR homo and heteromerization is becoming accepted (Bouvier, 2001, Rios et al., 2001, George et al., 2002, Franco et al., 2003, Agnati et al., 2003, Terrillon and Bouvier, 2004, Agnati et al., 2005, Franco et al., 2005, Prinster et al., 2005, Milligan, 2006, Maggio et al., 2007, Franco et al., 2008, Maurel et al., 2008, Franco, in press), there is controversy concerning the percentage of receptor monomers, dimers and oligomers existing in the plasma membrane of cells. At least for non-peptide neurotransmitter and hormone receptors there are data indicating that these receptors do not occur as monomers in the plasma membrane, i.e. dimer and oligomer assembly occur already in the endoplasmic reticulum (Bouvier, 2001, Terrillon and Bouvier, 2004). On the other hand, some recent studies suggest that the neurotransmitter/hormone encounters the receptor as a mixture of monomers, dimers and oligomers (Gurevich & Gurevich, 2008). To provide evidence supporting one or another view is out of the scope of this short review. The aim of this review is to present receptor dimer-based new approaches that may be instrumental for drug discovery. If one considers that the main GPCR target is a monomer, the classical monomer-based approaches are the models of choice. If one considers that the main targets are constituted by receptor homodimers (or receptor heteromers, see below), the classical approaches are not longer appropriate. Furthermore, in the case of complex pharmacological data, even assuming the occurrence of a mixture of monomers, dimers and oligomers, the dimer-based procedures give more answers and meaningful parameter values than the classical models.

We are just contemplating the tip of the iceberg in what concerns receptor dimer/oligomerization. There are physiological, biochemical, and pharmacological consequences that are starting to be known for a bunch of receptors but that are completely unknown for the majority. For instance, the proportion of monomers versus dimers or oligomers or the proportion of homodimers/homooligomers versus heterodimers/heterooligomers is unknown for the majority of the receptors. Apart from technical problems, which are quite often insurmountable even in transfected cells (expressing one or two receptors to form homo and heterodimers and, eventually, monomers), the possibilities for receptor heteromer formation in a real neuron and for a given receptor is likely to be quite high. For instance, in the GABAergic striatopallidal neuron, D₂ receptors can potentially heteromerize with adenosine A_2A, glutamate metabotropic mGlu₅, cannabinoid CB₁, histamine H₃ and somatostatin SST₅ receptors (Agnati et al., 2003, Carriba et al., 2007, Durán-Prado et al., 2008, Ferrada et al., 2008). Even accepting that constitutive receptor homodimers are already assembled in the endoplasmic reticulum and the same is assumed to be the case for receptor heterodimers (Bouvier, 2001, Vidi et al., 2008), it is entirely speculative what may happen in cases of multiple heteromerization and/or homo and heterooligomerization. The cell membrane is plastic and therefore changes in the nature and degree of receptor homo and/or heterooligomerization are likely to occur. There are few cases in which the agonist induces receptor dimerization, but there are more examples indicating that there is not short-term regulation of preassembled constitutive receptor dimers (Agnati et al., 2003, Ferré et al., 2007). We have some evidence that long term regulation may happen involving internalization, degradation, synthesis of molecules and trafficking (see for instance Hillion et al., 2002). A recent study by Vidi et al. (2008) elegantly addresses the question of the role of ligand-dependent homo- and heteromerization of adenosine A_2A and dopamine D₂ receptors. Thus, prolonged stimulation of D₂ receptors leads to internalization of D₂–D₂ and A_2A–D₂ receptor oligomers and results in a decreased A_2A–D₂ relative to A_2A–A_2A receptor oligomer formation (Vidi et al., 2008). Future studies will decipher the mechanisms involved in the long-term putative changes in receptor oligomerization. Again the mechanisms may vary from receptor to receptor and/or from a receptor heteromer to another and/or from one cell to another. The sunken part of the iceberg is still waiting to be explored.

1.2. Looking for receptor homo- and heteromers

Coimmunoprecipitation followed by immunoblotting has been widely used to study physical protein–protein interactions. However, coimmunoprecipitation of amphiphilic protein membrane molecules, such as GPCRs, requires membrane solubilisation (Miller and Lefkowitz, 2001, Hall and Lefkowitz, 2002), thus raising the possibility that the observed complexes are solubilisation artefacts. To overcome this technical limitation, powerful biophysical techniques, such as bioluminescence and fluorescence resonance energy transfer (BRET and FRET, respectively) have been implemented, which has allowed the demonstration of receptor oligomerization in the natural environment of the living cell. BRET and FRET techniques have been widely used to prove the occurrence of a variety of homo- and heteromers of GPCRs in living cells (Milligan and Bouvier, 2005, Pfleger and Eidne, 2005, Pfleger and Eidne, 2006, Pfleger et al., 2006). Quite recent data have given rise to the idea that, even at physiological expression levels, GPCRs in the plasma membrane are forming a variety of structures such as homotetramers and possible higher-order homo-structures as described for dopamine D₂ or adenosine A_2A receptors (Guo et al., 2008, Gandia et al., 2008), heterotrimers as recently described for adenosine A_2A, dopamine D₂ and cannabinoid CB₁ receptors and for adenosine A_2A, dopamine D₂ and metabotropic mGlu₅ receptors (Cabello et al., 2009, Carriba et al., 2008) and dimers of heterodimers as described for GABA receptors (Maurel et al., 2008). Ma et al. (2007) have even been able to recover oligomers (tetramers) of M₂ muscarinic cholinergic receptors when detergent-isolated monomers are reconstituted into lipid vesicles; importantly, reconstituted homooligomers display binding properties closely resembling those of muscarinic receptors in myocardial preparations. Collectively, these reports suggest that oligomers of receptors are formed in such a way that non-interacting homodimers may co-exist with homodimers interacting with other receptor to form heterooligomers. As mentioned above monomers may also be coexisting with dimers/oligomers. Occurrence of receptor heteromers opens new challenges such as identification of their presence and quaternary structure in native tissues. Commenting on these issues is out of the scope of this review (see Pin et al., 2007, Ferré et al., 2009, for recent recommendations about the recognition of receptor heteromers).

1.3. Receptor heteromers are distinct functional entities

Studies performed by Maggio et al. (1999) showed that M₂ and M₃ muscarinic receptor subtypes could cross-interact with each other and form a new pharmacological receptor heteromer, with distinctive ligand binding profile. Actually there is consensus in considering that a receptor heteromer is an entity with a different pharmacology and a different functionality (Ferré et al., 2009). Therefore, distinctive pharmacological and functional characteristics (a kind of “heteromer fingerprint”) are indeed invaluable to detect receptor heteromers in native tissues and we would predict to be invaluable for drug development.

At the ligand binding level, a common biochemical fingerprint of a receptor heteromer is found when occupying one receptor by an agonist or an antagonist modulates binding of agonists to the partner receptor; for instance, the ability of adenosine A_2A receptor agonists to change the affinity of dopamine D₂ agonists in the A_2A–D₂ receptor heteromer (Ferré et al., 1991, Ferré et al., 2007). Evidence of receptor heteromers by means of ligand binding experiments was recently provided for instance for serotonin 5-HT_2A-metabotropic glutamate mGlu₂ receptor complex, which is probably involved in psychosis (González-Maeso et al., 2008). Not only the metabotropic glutamate agonist LY379268 increases the affinity of different hallucinogens for the 5-HT_2A receptor-binding site but also, a selective 5-HT_2A receptor agonist decreases the affinity of different agonists for the mGlu₂ receptor binding site. All of these results constitute solid evidence for hetero-oligomerization of GPCR receptors at the cell surface. For 5-HT_2A-mGlu₂ receptor heteromers (González-Maeso et al., 2008), both the ligand binding modulation and heteromerization is altered with specific mutated or chimeric receptors.

Reports are starting to appear that link heteromers to a distinct signalling machinery. In fact, there is a selective G_q-protein coupling of the D₁–D₂ receptor heteromer whereas D₁ and D₂ receptor expressed as homomers are coupled to G_s and G_i proteins, respectively (George and O’Dowd, 2007, Rashid et al., 2007). Dopamine receptor-mediated calcium signalling in the central nervous system was assumed to be due to an interaction between dopamine D₁ receptors and calcyon (Lezcano et al., 2000). Six years later co-authors retracted the report (Lezcano et al., 2006) and consequently, the only evidence to our knowledge correlating dopamine neurotransmission and calcium signalling is through the D₁–D₂ receptor heteromer. Shift in coupling is not a particular characteristic of dopamine receptor heteromers and the opioid receptor system has also provided examples of such versatility (Fan et al., 2005, George et al., 2000). Taken all the evidence it seems that receptor heteromers in neurons are instrumental to provide versatility in neurotransmission (Franco, in press). In fact a given neurotransmitter is sensed differently by a given neuron depending on the receptor heteromers being expressed. To exemplify this Ciruela et al. (2006) have reported that adenosine A₁–A_2A receptor heteromers are sensors of adenosine concentration leading to negative regulation of striatal glutamate release at low adenosine concentrations and to positive regulation of striatal glutamate release at higher adenosine concentrations.

2. Screening drugs targeting G protein-coupled receptors

2.1. General considerations

As of today there are multiple choice options for screening depending on the nature of the therapeutic target and on the strategy of the laboratory or company involved in drug discovery. The existence of receptor dimers, especially of receptor heterodimers, arise concerns about the use of monomer-based strategies but open exciting new possibilities for drug development. Therefore, the first choice consists of deciding whether the real target is a receptor monomer, a homodimer or a heterodimer. If receptor monomers are assumed to be the target no modifications in the current approaches are required. If receptor homodimers are assumed to be the target, no modifications are required if screening is based in second-messenger readouts. If binding is used in screening of drugs targeting receptor homodimers, dimer-based mechanistic approaches are more suitable to fit binding data than monomer-based models (see below). Finally, and more interestingly, drug discovery may consider that the real target is a receptor heteromer.

When deciding that the therapeutic target is a receptor heteromer, a suitable cell model is needed to perform the screening of drugs under development. If screening is based on competition assays of radioligand binding to each receptor a drug discovery team may consider performing binding either in a natural receptor heteromer-containing source or in a heterologous cell system expressing receptor heteromers. A different approach would be to order drugs according to the efficacy, taking profit of the fact that receptor heteromers may couple to distinct signalling machinery. An appropriate example is provided by the discovery of D₁–D₂ receptor heteromers (George and O’Dowd, 2007, Rashid et al., 2007). Drugs acting on dopamine D₁ or D₂ receptors may be selected by assays of cAMP in cells expressing either D₁ or D₂ receptors; in contrast, these assays are inappropriate for selecting drugs acting on D₁–D₂ receptor heteromers. This is due to the coupling of these heteromers to G_q (see above). The screening of D₁–D₂ receptor–heteromer-selective compounds cannot be based on cAMP but on Ca²⁺ readouts.

2.2. Screening drugs targeting receptor heteromers: receptor–heteromer-selective drugs

Receptor–heteromer-selective drugs are considered to be compounds with higher affinity for a given receptor when forming heteromers with a partner receptor. As mentioned above the early studies of Maggio et al. (1999) suggested that receptor heteromers may display different pharmacology than the individual receptors. Some examples of natural or synthetic receptor heteromer-selective compounds are given below. Antagonists are more often than agonists the compounds being developed for therapeutic purposes. Testing an adenosine receptor antagonist, caffeine, Ciruela et al. (2006) demonstrated that the affinity of the compound for the A_2A receptor was one order of magnitude lower when the A_2A receptor is forming heteromers with A₁ receptors. Therefore, when developing compounds (agonists or antagonists) targeting receptor heteromers, one has to assume that the affinity may be different when assays are performed in cells expressing one of the receptors or in cells (natural or transfected) expressing the two heteromer-forming receptors. Upon deciding to perform binding assays a novel approach is needed since procedures of screening based on competition curves using membranes from cells transfected with the cDNA encoding for one receptor might miss compounds more selective for receptor heteromers. It is likely that compounds discarded as having low affinity for a given receptor may be re-evaluated and found to display higher affinity for receptor heteromers, i.e. receptor heteromer-selective behaviour. Compared to the classical GPCR targets, receptor–heteromer-selective drugs can potentially target more efficiently a specific receptor in a particular cellular type and cellular domain, which selectively expresses the receptor heteromer, and convey fewer side effects than other non-heteromer-selective drugs.

Exciting possibilities for receptor heteromer selective compounds have been deduced upon identification of heteromers of opioid receptors. Morphine functions primarily by activating μ opioid receptors (Law et al., 2000). Several interactions between μ and δ opioid receptors have been described (Abdelhamid et al., 1991, Zhu et al., 1999, Morinville et al., 2003, Guan et al., 2005) and, for instance, the μ–δ opioid receptor heteromer represents a functional unit distinct from μ or δ opioid receptors. This possibility would be supported by the fact that μ opioid receptor agonist-induced signalling can be enhanced by co-treatment with δ opioid receptor selective ligands, including δ opioid receptors selective antagonists (that do not elicit a signal when administered alone) (Gomes et al., 2000). The “novel” pharmacology of opioid–receptor heteromers has been instrumental to detect heteromer-selective drugs. In fact, Waldhoer et al. (2005) reported that the κ-opioid-selective agonist, U69593, exhibits as potent and efficacious activities at κ-δ receptor heteromers, whereas 6’-guanidinonaltrindole, a less selective κ-opioid receptor agonist, is 6-fold more potent as agonist for the receptor heteromer than for the κ-opioid receptor homomer, and has the unique property of selectively activating only opioid receptor heteromers but not homomers.

The D₁–D₂ receptor heteromers possesses a unique pharmacology, such that a specific subset of D₁ receptor agonists can activate the heteromer by acting concurrently on both the D₁ receptor and a distinct conformation of the D₂ receptor that depends upon the presence of the D₁ receptor. These drugs are more efficient in engaging the receptor–heteromer-mediated signalling pathway (Ca²⁺-mediated signalling in this case, see above). Although several different D₁ receptor agonists have equivalent ability to bind with high affinity to the D₁ receptor, only SKF81297 or SKF83959, but not SKF83822, could activate G_q/11 through D₁ receptors in conjunction with D₂ receptor activation by quinpirole. In the absence of quinpirole, SKF81297 or SKF83959 could activate the complex by acting as full agonists for the D₁ receptor and partial agonists for the D₂ receptor. The “special” D₂ receptor pharmacology was induced by the presence of D₁ receptors and was independent of D₁ receptor activation. Strikingly, the ability of the agonists SKF81297 and SKF83959 but not SKF83822 to activate D₁–D₂ receptor heteromer correlates with their specificity in stimulating phosphoinositide turnover in the brain. Because SKF83959 does not activate adenyl cyclase-coupled D₁ or D₂ receptors or G_q/11 through D₁ receptor homomers, it has been proposed that this D₁-like receptor agonist is in fact a selective agonist for the G_q/11-coupled D₁–D₂ receptor heteromer (Rashid et al., 2007).

3. Tools to fit binding data

3.1. Receptor monomer-based tools to fit binding data

Sooner or later drug discovery needs equations to fit complex binding data and these equations are often derived from a mechanistic model. Colquhoun (1973) and Thron (1973) pioneered theoretical analysis that led to the subsequent development of models for neurotransmitter/hormone receptors (see Franco et al., 1996, Franco et al., 2005, Franco et al., 2008, Casadó et al., 2007). All these models considered receptors as monomers. The most cited model of GPCR operation is the ternary complex model (De Lean et al., 1980), which also considers receptors as monomers. Scientists have widely used the ternary complex model to explain how agonists, neutral antagonists, inverse agonists, etc. exert their function. But a relevant question is whether this model allows devising an equation useful to fit radioligand binding data. Initially De Lean et al. (1980) proposed the ternary complex model and an elaborated strategy to fit agonist binding data to the ternary complex model which led to the estimation of the concentration of a factor interacting with the receptor (“X”, X may be a G protein) that was needed to explain any complex binding data. Assuming that the equilibrium constant for the binding of X to the receptor did not change with the different agonists used and by means of an estimation of such a constant the proportion of receptor versus X was determined and was found to be variable depending on the agonist used. Apart from other considerations, it should be noted that the strategy was not user-friendly due to the fact that the authors did not provide equations useful for fitting data (of saturation or competition assays) by non-linear regression. In the presentation of the extended ternary complex model the same laboratory (Samama et al., 1993) did not attempt to use the model to fit complex binding data but used instead the strategy of considering one (if simple binding data) or two (for complex binding data) non-interconvertible affinity states of a monomeric receptor. The ternary complex model include equilibria between the receptor and other proteins (“X”) that may likely occur in the living cells. In membranes it would be reasonable to assume that ligands bind to two different and independent (i.e. not connected by any equilibrium) species, R and RX. If R and RX display the same affinity for a given radioligand (simple binding data) data can be fitted assuming one single affinity state, and this is enough to handle non-complex binding data. In the classical and most used version of this approach the two affinity states are assumed to correspond to G protein-coupled and uncoupled forms of the receptors. For complex data equations derived from the so-called two-independent-site model allow calculating two parameters, which correspond to the dissociation equilibrium binding of the ligand to the high affinity (coupled) state (K_DH) and to the dissociation equilibrium binding of the ligand to the low affinity (uncoupled) state (K_DL). This approach has been instrumental for the past 25 years and is still used to fit data from non-hyperbolic (complex) saturation curves or biphasic competition curves.

3.2. Dimer-based tools to fit binding data

Given the predominance of GPCR as dimers, dimer receptor models have been developed as a natural outcome (Franco et al., 2005, Franco et al., 2006, Albizu et al., 2006, Casadó et al., 2007). Dimer models are for example able to explain both concave upward and concave downward Scatchard plots. One of those, the two-state dimer receptor model, has two important characteristics: i) it is as useful as the ternary complex model to explain constitutive activity, the mechanism of activation by agonists (full or inverse), etc. and ii) allows a suitable development to fit binding data without the need of considering proteins interacting with the receptor. Therefore, this novel model allows both, to understand receptor operation and to fit simple or complex binding data.

Taking into account the dimeric structure of GPCR, the interpretation of the biphasic binding isotherms is relatively easy. In fact, positive or negative cooperativity may occur by assuming, like in the case of dimeric enzymes or other dimeric proteins, that binding of the first ligand to the dimer modifies the equilibrium parameters of binding of the second ligand molecule to the dimer. Like enzymes with two or more subunits, receptor dimer cooperativity arises from ligand-driven intradimeric (interprotomer) conformational changes. Some studies have provided a direct link between agonist-driven conformational changes in the dimer and cooperativity on ligand binding (Galvez et al., 2001, Suzuki et al., 2004, Urizar et al., 2005, Springael et al., 2006, Albizu et al., 2006). Another difference with respect to the ternary-complex model is that there is no need to take into account G proteins or any other “X” interacting protein able to modulate ligand affinity and/or receptor function (Saura et al., 1996, Sarrió et al., 2000, Pacheco et al., 2005). For all practical purposes this indicates that the dimer-model is useful for understanding GPCR operation in living cells, where G protein may be in dynamic equilibrium with receptors, or in isolated membranes, where the G protein–GPCR interaction may not be as dynamic as in living cells.

Dimer models as originally described (Franco et al., 2005, Franco et al., 2006, Albizu et al., 2006) were defined by equations that include microscopic kinetic constants, which do not give practical information about how to determine the macroscopic constants values. More recently, Casadó et al. (2007) have reported a macroscopic analysis for the two-state dimer receptor model that is readily applicable in receptor pharmacology data management, i.e. in competition experiments using a radiolabelled ligand and a drug as displacer (very common experiments in drug screening). It should be noted that from such a mechanistic development the equations are useful even assuming binding to a preparation containing multiple conformations of the receptors. This means that equations derived from the two-state dimer receptor model can fit data even if compounds are binding to hundreds of different conformations. In fact, the obtained parameters for compound “A” (K_DA1 and K_DA2) must be interpreted as reflecting the macroscopic equilibrium constants for the binding of the first and second molecule of A to, respectively, all the conformational states of unoccupied dimers and all the conformational states of semi-occupied dimers.

4. Practicalities on how to perform screening using saturation assays

4.1. Practicalities in determining affinities from saturation data

With a few exceptions, if a neutral antagonist is used as radioligand, simple binding data (hyperbolic saturation isotherms) are expected and, therefore, the choice of the model is irrelevant and data may just be fitted to a model for the binding of ligands to one affinity state. This means that irrespective of the actual (mechanistic) working model, particular parameter values allow reducing any model-derived equation to the equation of a hyperbola. For many agonists and for some antagonists complex binding may occur. In those cases one may use the two-independent-site model to obtain K_DH and K_DL values or the two-state dimer receptor model to obtain (for ligand A) K_DA1 and K_DA2 values, (see Casadó et al., 2007 and Eq. (1) in Appendix A) i.e. the putative equilibrium dissociation constants for the binding of, respectively, the first and the second molecule of A to the dimer. As to what concerns saturation curves, and aiming at determining equilibrium constants one may choose any of these two models. Nonetheless, the election may not be so easy if one needs the model for further purposes, as those described below.

4.2. Practicalities in determining homotropic cooperativity

As negative cooperativity cannot be distinguished from binding site heterogeneity by equilibrium binding alone, Springael et al. (2006) used infinite tracer dilution conditions to demonstrate that negative cooperativity is established between chemokine CCR2/CCR5 receptor heteromers and that G proteins may modulate the inter-protomer heteromeric cross-talk. Once cooperativity is demonstrated for GPCRs, a possibility to explain it was to assume that there is communication between receptor protomers. Cooperative agonist binding likely results from conformational changes transmitted from one protomer to the second (in a dimer). Mesnier and Banères (2004) using a spectroscopy approach were able to show intradimer (i.e. inter-protomer) cross-talk in the leukotriene BLT1 receptor dimer. Although less frequent (or less reported) than “negative cooperativity” binding data consistent with positive cooperativity have been reported (Lazareno et al., 1998, Albizu et al., 2006, White et al., 2007). These and other complementary evidence, whose detailed description is out of the scope of the present article, suggest that cooperativity (negative and positive) occurs in GPCRs; since GPCRs are often expressed as dimers, complex binding data may likely result from cooperativity in ligand binding to dimers.

Monomer-based models do not provide specific tools to handle and quantify cooperativity. Moreover, monomer-based models are unable to explain the occurrence of positive cooperativity. In contrast dimer-based models handle cooperativity in an easy way. One relevant difference between protein monomers and dimers/oligomers is the possibility of cooperativity; in fact, in dimer/oligomers, one protomer can communicate to another protomer in the molecule by transmitting conformational changes. For the specific purpose of quantitating cooperativity, the two-state dimer model provides a newly defined parameter, the dimer cooperativity index (D_C), which for ligand A is defined as D_CA = log (4 K_DA1/K_DA2) (Casadó et al., 2007, Eq. (6) in Appendix A). Dc is conceptually similar to the Hill index, i.e. D_C < 0 indicates negative cooperativity, D_C > 0 indicates positive cooperativity and D_C = 0 denotes absence of cooperativity.

4.3. Comparing the performance of monomer- and dimer-based models on fitting saturation data

Casadó et al. (2007) have reported a macroscopic analysis for the two-state dimer receptor model that is readily applicable in receptor pharmacology data management. This approach gives useful parameters values for qualitatively different data, i.e. from simple or complex data and for negative or positive cooperativity. It is well known that the occurrence of two independent affinity states of a monomeric receptor in a membrane cannot explain data such as that displayed in Fig. 1 corresponding to positive cooperativity. None of the available monomeric models is able to fit data corresponding to positive cooperativity. In contrast, the equations derived from the dimer-model (Eq. (1) in Appendix A) are useful to fit such data of specific [³H]estradiol binding to dimeric estrogen receptor from calf uteri (Notides et al., 1981). From nonlinear regression the derived pharmacological parameters values (K_DA1, K_DA2 and D_C) are obtained (Table 1). The value of D_C of 1.8 is a measure of the positive cooperativity of estradiol binding.

Fig. 1.

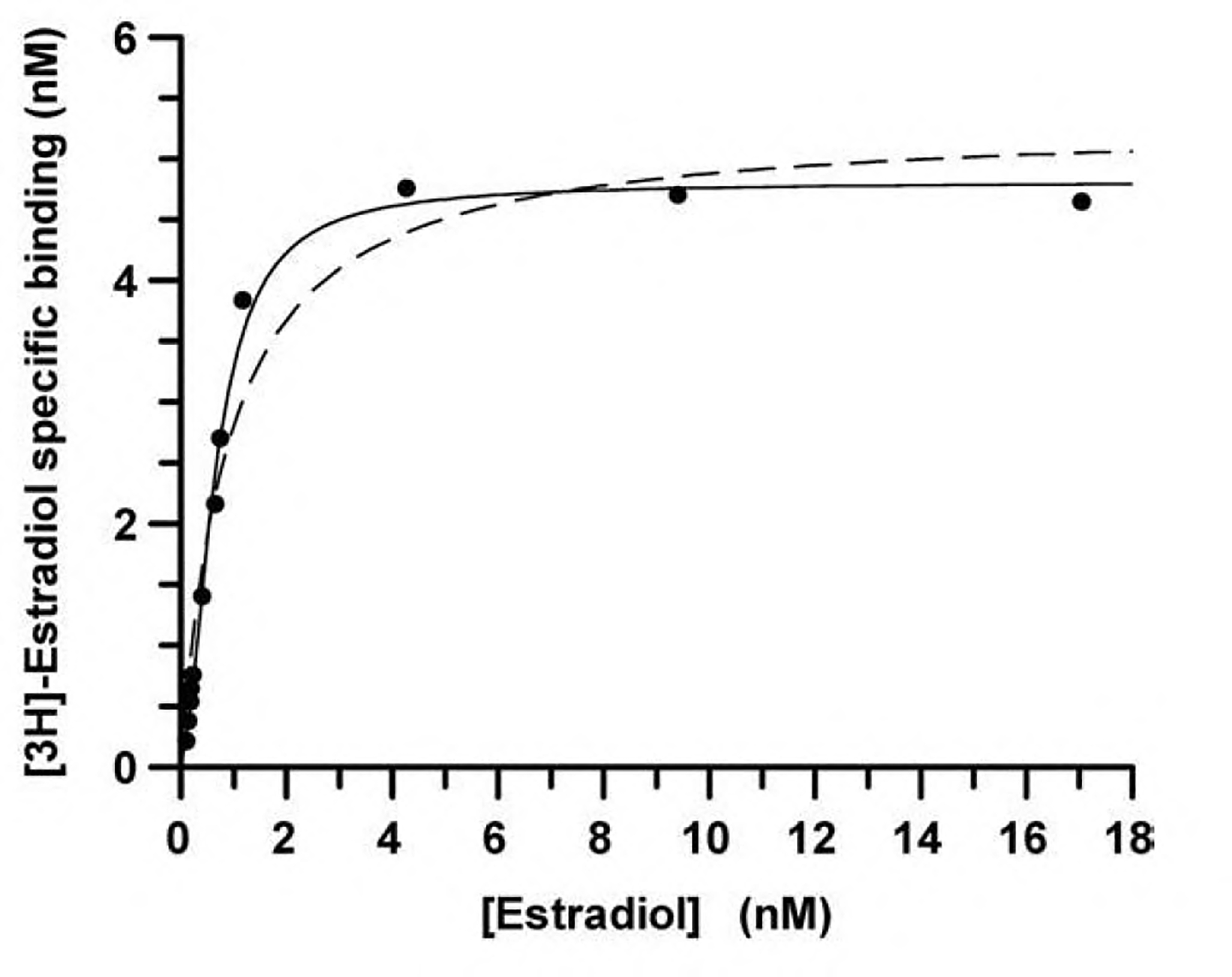
Saturation data for the [³H]estradiol binding to estrogen receptors from calf uteri. Data points obtained from Fig. 2 in Notides et al. (1981) were fitted assuming one or two affinity states (dashed line) or a two-state dimer. F test indicated that a significant improvement is obtained by assuming the two-state dimer receptor model; thus, in Table 1, only the parameter values obtained assuming dimers are shown.

Table 1.

Parameter values of agonist estradiol binding to estrogen receptors.

Model	Parameters	Values
Two-state dimer	RT (nM)	2.4 ± 0.1
	KDA1 (nM)	3 ± 1
	KDA2 (nM)	0.2 ± 0.1
	D C	1.8

Data for non-linear regression were taken from Fig. 1 and fitted assuming the two-state dimer receptor model. R_T is the total amount of receptor dimers, K_DA1 and KDA2 are, respectively, the equilibrium dissociation constants of the first and second binding of [³H]estradiol to a dimer. D_C is the dimer cooperativity index for [³H]estradiol binding. Parameter values are mean ± s.e.m.

5. Practicalities on how to perform screening using competition assays

5.1. General considerations

For drug screening, scientists usually use radioligand (antagonist)/drug competition curves. Also the agonist affinity constants for many GPCRs are usually determined from radioligand (antagonist)/agonist competition curves. If monomers are assumed to be the target receptor, monomeric models can be used, but if homodimers have been described for the receptor, as it occurs for many GPCRs, it seems more reasonably to use dimer-based models. On deciding which model to use a sensible approach would be to try a dimer-based and a monomer-based model and compare results (preferably using a statistical test). It is important to note that on selecting a monomer-based model one is not eliminating the possible occurrence of dimers. Analogously, on considering a dimer-model one is not automatically discarding the possibility that mixtures of monomers and dimers/oligomers exist. In the first case one will end up with parameters assumed to be dissociation constants of equilibrium involving monomers and in the second case one will end up with parameters assumed to be dissociation constants of equilibrium involving dimers. On having this in mind one will use the calculated parameters (from one or another model) for comparison and use the resulting information to select drugs for further development.

5.2. Practicalities in comparing affinities of compounds from competition data

As stated above, irrespective of the actual mechanistic model, particular parameter values can lead to reduce any-model derived equation to the equation of a hyperbola; thus, data may be fitted to one affinity state if the competition curve is monophasic. However, quite often competition curves are biphasic and in these cases data should be fitted to equations derived from suitable monomer- or dimer-based models. For instance, one may use the two-independent-site/state model and Eq. (8) (see Appendix A) to calculate two IC₅₀ values (one for the displacement of the binding to the high-affinity state, IC_50H, and another for the displacement of the binding to the low-affinity state, IC_50L). These values are related with the respective equilibrium dissociation constants K_DHA and K_DLA according with the Cheng–Prusoff equation (Cheng & Prusoff, 1973; Eq. (9) in Appendix A). From these values one can calculate the actual concentration of B providing half saturation (B₅₀) using Eq. (10) (see Appendix A). To our knowledge, this truly complex equation is not used in drug screening. Therefore, in the case of biphasic curves the most convenient value for comparing between the different drugs, B₅₀, is not used when considering a monomer based model.

Alternatively, the handling of competition curves by means of equations derived from two-state dimer receptor model is very straightforward. Using the “dimer” approach, fitting data to the suitable equations (Eqs. (2), (3), (4) in Appendix A) provides the equilibrium dissociation constants of the first (K_DB1) and second (K_DB2) binding of the competitor to the receptor dimer. B₅₀ is easily obtainable from these two parameters (Eq. (7) in Appendix A). This results in an easy calculation of a robust parameter, B₅₀, useful to order different drugs irrespective of whether competition curves are monophasic or biphasic, something that is not collectively correct using IC₅₀ values.

5.3. Comparing the performance of monomer and dimer-based models fitting competition data

Equations corresponding to the binding to one affinity state or to two affinity states for monomeric receptor models and to a two-state dimer receptor model were used to fit by nonlinear regression two sets of actual data (Fig. 2, Fig. 3; see details in the legend), one corresponding to simple (monophasic) and one to complex (biphasic) binding data. The values of the parameters obtained by using either of the approaches have been compared (Table 2, Table 3). According to a previous report (Casadó et al., 2007), binding of a selective antagonist SCH 23390 to dopamine D₁ receptor is non-cooperative. Thus, although these receptors form dimers (Ng et al., 1994), binding of [³H]SCH 23390 in the presence of increasing concentrations of non-radiolabelled SCH 23390 gives a monophasic competition curve (Fig. 2). The resulting data can be satisfactorily handled by assuming one affinity monomeric specie or by assuming a dimer without SCH 23390 binding cooperativity (data fit to Eq. (5) in Appendix A). By using the suitable equation on performing non-linear regression, one may then decide to calculate parameters specific for the monomer-based model or for the dimer-based model (see Table 2).

Fig. 2.

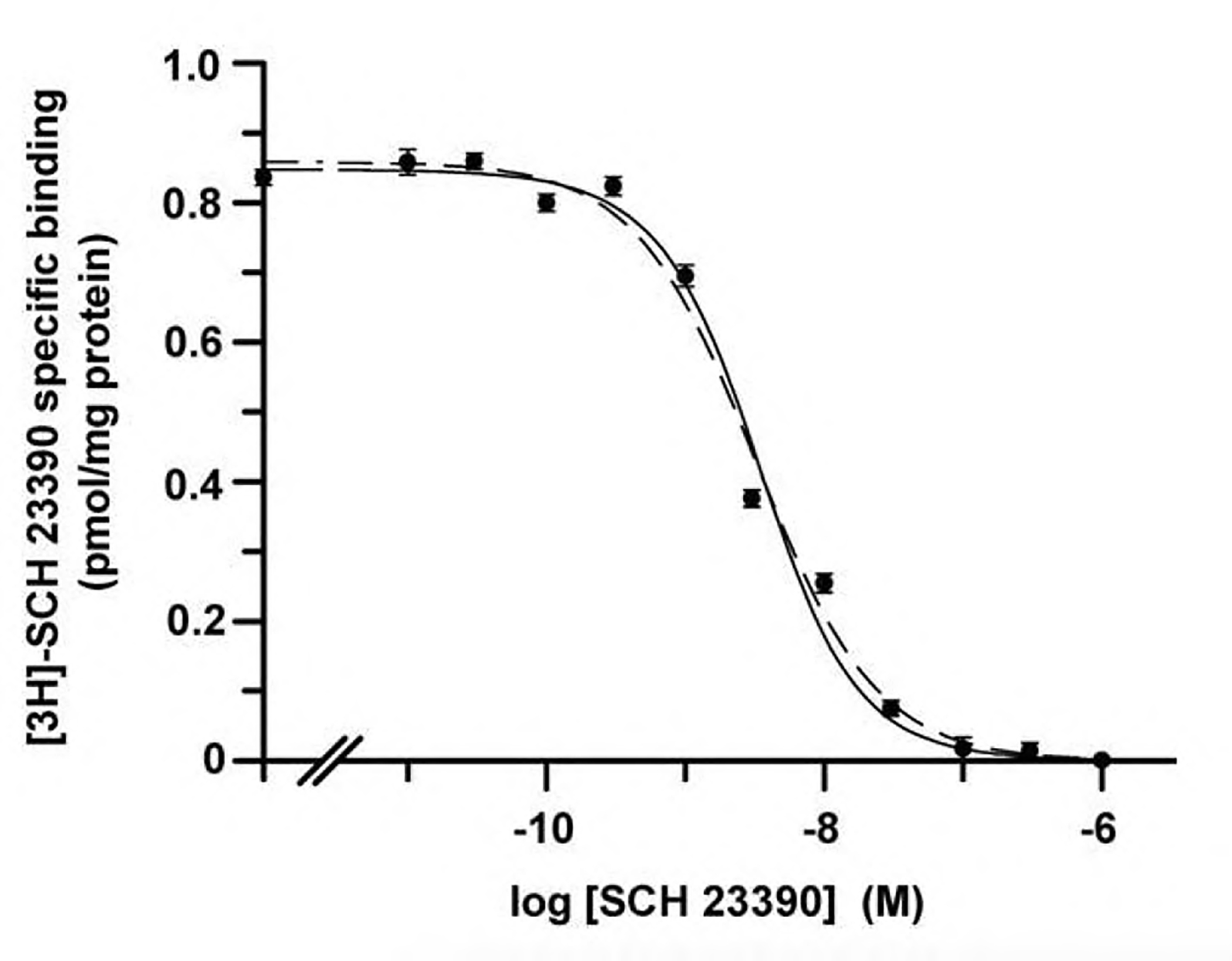
Monophasic competition data for antagonist binding to dopamine D₁ receptors. Competition was performed using variable concentrations of non-radiolabeled SCH 23390 and 2.7 nM [³H]SCH 23390 in lamb brain striatal membranes (0.5 mg protein/ml) using the protocol described in Ferrada et al., 2009. Data were fitted using equations derived from the two-state dimer receptor model (solid line) or derived from the assumption of one-affinity (monomeric) state (dashed line). The parameter values obtained by non-linear regression are indicated in Table 2.

Fig. 3.

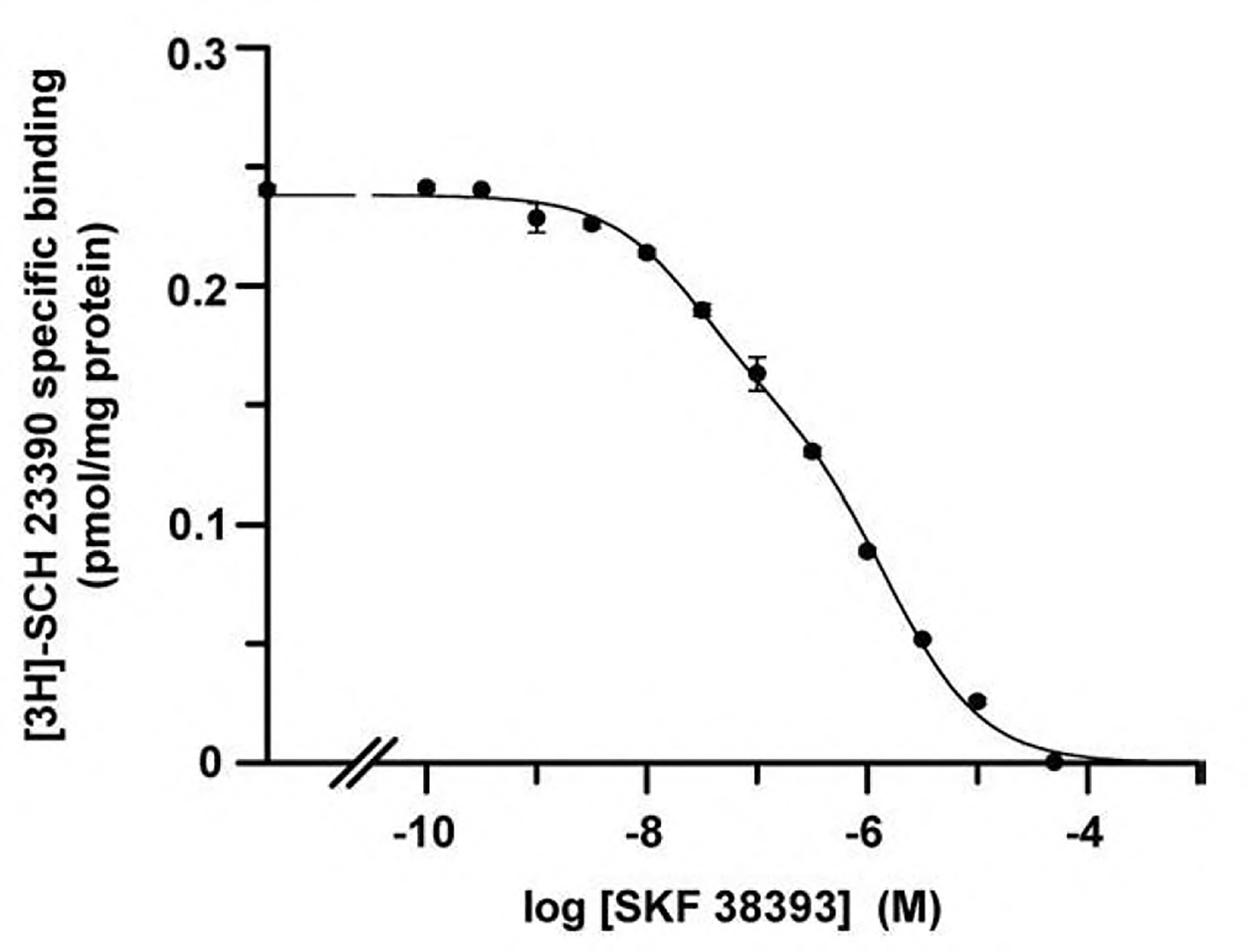
Biphasic competition curves for antagonist versus agonist binding to dopamine D₁ receptors. Competition was performed using variable concentrations of non-radiolabeled SKF 38393 (agonist) and 1.2 nM [³H]SCH 23390 (antagonist) in lamb brain striatal membranes (0.5 mg protein/ml) using the protocol described in Ferrada et al., 2009. Data were fitted using equations derived from the two-state dimer receptor model or derived from the assumption of two-affinity (monomeric) states. The two fittings led to indistinguishable curves. The parameter values obtained by non-linear regression are indicated in Table 3.

Table 2.

Parameter values of the antagonist SCH 23390 binding to dopamine D1 receptors obtained by fitting data to different models.

Model	Parameters	Values
One-affinity statea	R (pmol/mg protein)	0.86 ± 0.01
	KD (nM)	0.5 ± 0.4
Two state dimer	RT (pmol/mg protein)	0.61 ± 0.09
	KD1 (nM)	0.6 ± 0.3
	KD2 (nM)	2.4 ± 1.2
	D C	0
	B50 (nM)	1.2

Competition experiments were performed using variable concentrations of nonr-adiolabeled SCH 23390 and 2.7 nM [³H]SCH 23390. Data for non-linear regression were taken from Fig. 2. R is the maximum specific binding and K_D is the equilibrium dissociation constants of the competing ligand (SCH 23390). R_T is the total amount of receptor dimers, K_D1 and K_D2 are, respectively, the equilibrium dissociation constants ofvthe first and second binding of SCH 23390 to the dimer. D_C is the “dimer cooperativity” index for the binding of SCH 23390 and B₅₀ is the concentration of the competitor (SCH 23390) providing half saturation. Parameter values are mean ± s.e.m.

^aF test indicated that no significant improvement is obtained by assuming two-affinity states.

Table 3.

Parameter values of the antagonist SCH 23390 binding to dopamine D₁ receptors obtained by fitting data to different models.

Model	Parameters	Values
Two-affinity statesa	RH (%)	38 ± 2
	KDH (nM)	12 ± 2
	RL (%)	62 ± 4
	KDL (nM)	610 ± 80
Two state dimer	RT (pmol/mg protein)	0.196 ± 0.001
	KDB1 (nM)	18 ± 2
	KDB2 (nM)	390 ± 80
	KDAB (nM)	18 ± 4
	D C	−0.74
	B50 (nM)	84

Competition was performed using variable concentrations of non-radiolabeled SKF 38393 (agonist, B) and 1.2 nM [³H]SCH 23390 (antagonist, A). Data for non-linear regression were taken from Fig. 3. R_H and R_L are, respectively, the % of maximum specific binding corresponding to high and low affinity sites and K_DH and K_DL are the equilibrium dissociation constants of the competing ligand B (SKF 38393) for, respectively, high and low affinity sites. R_T is the total amount of receptor dimers, KD_B1 and KD_B2 are, respectively, the equilibrium dissociation constants of the first and second binding of SKF 38393 to a dimer. K_DAB is the hybrid equilibrium dissociation constant of SKF 38393 binding to a receptor dimer semi-occupied by [³HSCH 23390. D_CB is the “dimer cooperativity” index for the binding of SKF 38393 and B₅₀ is the concentration providing half saturation. Parameter values are mean ± s.e.m.

^aF test indicated that a significant improvement is obtained by assuming two-affinity states (compared to one-affinity state).

Biphasic competition curves have been described for the binding of [³H]SCH 23390 to dopamine D₁ receptor in the presence of variable concentrations of the agonist SKF 38393 (Fig. 3; Casadó et al., 2007). Data points in Fig. 3 can be satisfactorily handled by the two-independent site model or the two-state dimer receptor model but not by assuming one affinity state. The parameter values obtained appear in Table 3. By the two-independent-site model R_H (high affinity equilibrium binding) and R_L (low affinity equilibrium binding) were calculated, being ~38:62 the proportion of receptors in high affinity (usually considered coupled to G proteins) versus those in low affinity (usually considered uncoupled to G proteins). Using the two-state dimer receptor model the number of receptor dimers (R_T), which correspond to half of maximum binding, are directly obtained without any a priori assumption about coupling or uncoupling to G proteins or else. The two macroscopic constants (K_DB1 and K_DB2) correspond to the SKF 38393 binding to an empty dimer and to a semi-occupied dimer, respectively. Comparison of values in Table 3 shows that the values of macroscopic constants, K_DB1 and K_DB2, are different from the K_DH and K_DL values obtained assuming the classical two-independent-site model. Moreover, one of the main advantages provided by the two-state dimer receptor model is the quantification of cooperativity by calculation of a cooperative index (D_C). For the agonist SKF 38393 D_C measures the affinity modifications occurring when a protomer senses the binding of the same ligand molecule to the partner protomer (in a dimer). The D_C value was − 0.74, which indicates negative cooperativity for agonist SKF 38393 binding.

5.4. Practicalities when the use of monomeric-models does not provide robust parameters

Recently we have provided evidence that the shape of competition curves may change depending on the concentration of the radioligand (Casadó et al., in press). In this circumstance competitor IC₅₀ values deduced from different competition curves using the classical equations (Eqs. (8), (9) in Appendix A) of the two-independent-site model, will be different; therefore, the different values will have limited utility in drug screening. To prove that a dimer-model can handle this situation better than the classically-used monomeric model, a simulation experiment was performed taking in consideration the kinetic parameters (Table 3) obtained for the D₁ receptor antagonist [³H]SCH 23390 binding in the presence of a competing D₁ receptor agonist, SKF 38393. The selected concentrations were from 0.05 to 10 nM in the case of the radioligand and from 0.001 nM to 1 mM in the case of the competitor. Although curves in Fig. 4 are the result of simulation, it should be noted that variation from monophasic to biphasic curves may be obtained from actual data (Casadó et al., in press). Data points were generated assuming a random error similar to that expected in competition assays. Data sets were fitted to the two-state dimer receptor model (Eq. (3) in Appendix A) and to the two-independent-site model using Eq. (8) in Appendix A. In the latter case the affinity constants were calculated using Eq. (9) (see Appendix A). Considering the two-state dimer receptor model, comparable parameters are obtained irrespective of the shape of the competition curve (Table 4). In contrast, parameter values obtained when fitting data to equations derived from a monomer-based models are very different. For each simulated experimental condition, fitting data to the two-independent-site model gives different percentages of high and low affinity sites and significantly different affinities (Table 4). None of available monomer-based models are able to explain this behaviour and one may doubt about the usefulness of the different affinity constants resulting from non-linear regression. In contrast, the two-state dimer model gives robust affinity constant values irrespective of the concentration of the radioligand. It is true that on fitting a particular set of data the monomer-based equation may slightly improve the fit respect to using the dimer-based equation. This is expected since binding to two (monomeric) affinity states is represented by more parameters than binding to a receptor dimer; however, statistical tests select the two-state dimer receptor model as the simplest to explain the biphasic curves of Fig. 4. Taken together the results summarized in Table 4 show that the dimer-based model is very reliable and do not depend on the experimental condition used in competition assays. The ability of a dimer-model to explain different shapes in competition curves using the same competitor and different concentrations of the radioligand is explained by a parameter, K_DAB. Mechanistically, this equilibrium constant is defining the extent of radioligand/competitor modulation, i.e. how binding of the radioligand to one protomer is affecting the binding of the competitor to the second protomer in the dimer (Casadó et al., in press). It should be stressed that the selection of a model able to provide robust parameter values is very important when one suspects that a given drug may display different affinities for a given receptor but in different heteromeric contexts (as in the above-commented example of caffeine acting on adenosine receptors). On using IC₅₀ value(s) derived from the use of monomer-based models one may end misplacing one or more of the drugs in the multiple lists reflecting the order of affinities of the different drugs when assayed in cells expressing different heteromers.

Fig. 4.

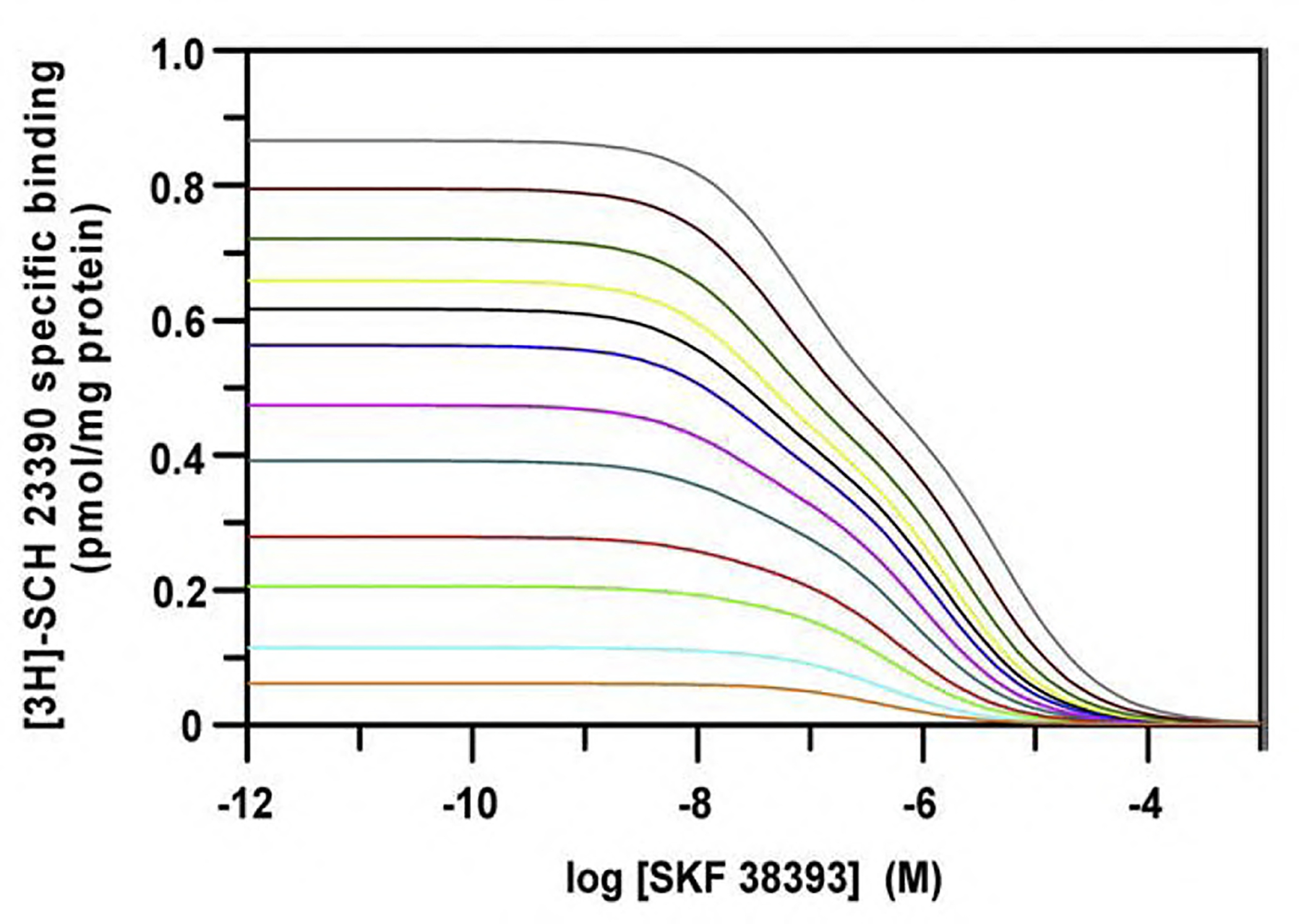
Competition assays simulation. Simulation was performed considering Eq. (3) (see Appendix A), 1 pmol/mg protein of maximum binding (RT=0.50 pmol/mg protein), the values of K_DA1, K_DB1, K_DB2 and K_DAB from Tables 2 and 3, different radioligand concentrations (A in Eq. (3); 0.05, 0.1, 0,2, 0.3, 0.5, 0.7, 1.0, 1.25, 1.5, 2.0, 3.0, 5.0 and 10 nM bottom to top) and different competitor concentrations (0.001 nM to 1 mM as for the D1 receptor agonist SKF 38393, B, in Eq. (3)).

Table 4.

Parameter values of the antagonist SCH 23390 binding to dopamine D₁ receptors obtained by fitting data to different models.

		5.0 nM [3H] SCH 23390	0.5 nM [3H] SCH 23390	0.1 nM [3H] SCH 23390
Model	Parameters	Values
Two-affinity statesa	RH (%)	46 ± 1	28b ± 1	0
	KDH (nM)	6 ± 1	11b ± 2	-
	RL (%)	54 ± 1	72b ± 2	100c
	KDL (nM)	460 ± 20	440 ± 10	320c ± 10
Two state dimer	RT (pmol/mg protein)	0.499 ± 0.001	0.499 ± 0.001	0.501 ± 0.001
	KDB1 (nM)	21 ± 5	18 ± 2	22 ± 4
	KDB2 (nM)	390 ± 30	410 ± 30	420 ± 20
	KDAB (nM)	18 ± 1	19 ± 3	23 ± 5
	D C	−0.67	−0.75	−0.68
	B50 (nM)	90	86	96

Competition curves were simulated as indicated in the legend of Fig. 4. Parameter values were obtained by fitting three data point sets simulated considering a random experimental error in the range of ± 2.5%. R_H and R_L are, respectively, the % of maximum specific binding corresponding to high and low affinity sites and K_DH and K_DL are the equilibrium dissociation constants of the competing ligand (SKF 38393) for, respectively, high and low affinity sites. R_T is the total amount of receptor dimers, K_DB1 and K_DB2 are, respectively, the equilibrium dissociation constants of the first and second binding of SKF 38393 to a dimer. K_DAB is the hybrid equilibrium dissociation constant of SKF 38393 binding to a receptor dimer semi-occupied by [³H]SCH 23390. DCB is the “dimer cooperativity” index for the binding of ligand SKF 38393 and B₅₀ is the concentration providing half saturation. Parameter values are mean ± s.e.m.

^aF test indicated that a significant improvement is obtained by assuming two-affinity states (compared to one-affinity state) except at 0.1 nM [³H]SCH 23390.

^bp<0.05 compared with values obtained at 5 nM [3H]SCH 23390 concentration.

^cp<0.05 compared with values obtained at 5 and 0.5 nM [3H]SCH 23390 concentration.

6. Conclusions and perspectives

As well as being conceptually coherent with the existence of homodimers of GPCR, the recently devised two-state dimer receptor model exhaustively described elsewhere (Casadó et al., 2007, Franco et al., 2005, Franco et al., 2007), can easily be used to fit binding data. This is now possible after the development made by Casadó et al. (2007) from which pharmacologists can take advantage. Saturation and competition data fitted using the tools derived from receptor-dimer models may give information not only of maximum binding (2 R_T) or macroscopic dissociation constants values for the competitor but about the existence and the extent of cooperativity (D_C) in radioligand and/or competitor binding and provide a meaningful parameter (B₅₀) for ordering the compounds according to their actual binding potency. There is of great interest in developing drugs acting as allosteric modulators of GPCRs (Raddatz et al., 2007, Schwartz and Holst, 2006). Taking advantage from receptor dimer models, it is now possible to have more tools to measure the effect of an allosteric effector by assuming that it may modify the affinity for the binding of the agonists/antagonists to the receptor (the macroscopic equilibrium dissociation constants) and/or the cooperativity in ligand binding (D_C value) and/or radioligand-competitor modulation (K_DAB). Therefore allosteric modulation can be dissected much more than previously by still using the usual ligand binding assays. Allosteric effectors may offer an additional dimension of selectivity for GPCRs since allosteric sites are not under the same evolutionary pressure as the orthosteric site (Kenakin et al., 2006, Soudijn et al., 2004). When dealing with receptor heteromers, we can conceive allosteric sites, which mediate physiological and pharmacological regulation, located in any of the protomers of the heteromer. Specific allosteric centers may also be created after heteromerization; to illustrate this one heterotrimeric G protein may behave as allosteric effector by interacting with one given heterodimer not only to make possible signaling but also to regulate agonist binding.

Appendix A. Fitting complex binding data assuming G protein-coupled receptor dimers or G protein-coupled receptor monomers

A. Fitting data from saturation experiments

A.1. Equations derived from the two-state dimer receptor model

In saturation experiments the following equation deduced by Casadó et al. (2007) may be used:

$$A_{\text{bound}}=\left(K_{\text{DA}2}A+2A^2\right)R_{\text{T}}/\left(K_{\text{DA}1}{K}_{\text{DA}2}+K_{\text{DA}2}+A^2\right)$$ (1)

A represents the radioligand concentration, R_T is the total amount of receptor dimers and K_DA1 and K_DA2 are the macroscopic dissociation constants describing the binding of the first and the second radioligand molecule (A) to the dimeric receptor.

B. Fitting data from competition experiments

B.1. Equations derived from the two-state dimer receptor model

In competition experiments the following equation deduced by Casadó et al. (2007) may be used:

$$A_{bound}=\left(K_{\text{DA}2}A+2A^2+K_{\text{DA}2}AB/K_{\text{DAB}}\right)\text{RT}/(K_{\text{DA}1}{K}_{\text{DA}2}+K\text{DA}2A+A^2+K_{\text{DA}2}AB/K_{\text{DAB}}+K_{\text{DA}1}{K}_{\text{DA}2}B/K_{\text{DB}1}+K_{\text{DA}1}{K}_{\text{DA}2}{B}^2/\left(K_{\text{DB}1}{K}_{\text{DB}2}\right))$$ (2)

A represents the radioligand concentration, R_T is the total amount of receptor dimers and K_DA1 and K_DA2 are the macroscopic dissociation constants describing the binding of the first and the second radioligand molecule (A) to the dimeric receptor. K_DA1 and K_DA2 are already known (obtained from saturation assays using Eq. (1)). B represents the competing compound (variable) concentration and K_DB1 and K_DB2 are, respectively, the equilibrium dissociation constants of the first and second binding of B; K_DAB may be considered as a hybrid equilibrium dissociation constant, which is the dissociation constant of B binding to a receptor dimer semi-occupied by A.

A simpler equation may be used when radioligands used in competition experiments are antagonists displaying non-cooperative binding (K_DA2 = 4K_DA1). Then Eq. (2) simplifies to:

$$A_{\text{bound}}=\left(4K_{\text{DA}1}A+2A^2+4K_{DA1}AB/K_{\text{DAB}}\right)RT/(4{K_{\text{DA}1}}^2+4K_{\text{DA}1}A+A^2+4K_{\text{DA}1}AB/K_{\text{DAB}}+4{K_{\text{DA}1}}^{2}B/K_{\text{DB}1}+4K_{\text{DA1}}^2{B}^2/\left(K_{\text{DB}1}{K}_{\text{DB}2}B\right))$$ (3)

Eq. (3) is a simple and instrumental equation to fit data from assays of competition to a receptor dimer.

When both the radioligand A and the competitor B show non-cooperative binding, it results that K_DA2 = 4K_DA1 and K_DB2 = 4K_DB1, and Eq. (2) simplifies to:

$$A_{\text{bound}}=\left(4K_{\text{DA}1}A+2A^2+4K_{\text{DA}1}AB/K_{\text{DAB}}\right)R_{\text{T}}/(4{K_{\text{DA1}}}^2+4K_{\text{DA}1}A+A^2+4K_{\text{DA}1}AB/K_{\text{DAB}}+4K_{\text{DA}1}^{2}B/K_{\text{DB}1}+{K_{\text{DA}1}}^2{B}^2/\left({K_{\text{DB}1}}^2\right)$$ (4)

When both the radioligand and competitor are the same molecule and binding is non-cooperative, Eq. (4) simplifies to:

$$A_{\text{bound}}=\left(4K_{\text{DA}1}A+2A^2+AB\right)R_{\text{T}}/\left(4K_{\text{DA}1}^2+4K_{\text{DA}1}A+A^2+AB+4K_{\text{DA}1}B+B^2\right)$$ (5)

On the other hand, to quantify cooperativity, the dimer cooperativity index for the competing ligand B is defined by Casadó et al. (2007) as:

$$D_{\text{C}}=\log \left(4K_{\text{DB}1}{K}_{\text{DB}2}\right)$$ (6)

A direct calculation of the concentration of competitor (B) providing half saturation, i.e. a 50% decrease in the binding of the radioligand, is possible (see Casadó et al., 2007):

$$D_{50}={\left(K_{\text{DB}1}{K}_{\text{DB}2}\right)}^{1/2}$$ (7)

B.2. Equations derived from the two-affinity states (monomeric) model

For biphasic (complex) competition assays the following equation (for a fixed radioligand A concentration being competed by variable B concentrations) may be used:

$$A_{\text{bound}}=\left(R_{\text{H}}\cdot \mid {\text{C}}_{50\text{H}}/\left({\text{IC}}_{50\text{H}}+B\right)\right)+\left(\text{RL}\cdot {\text{IC}}_{50\text{L}}/\left(\mid {\text{C}}_{50\text{L}}+B\right)\right)$$ (8)

where R_H and R_L are the specific binding for, respectively, high and low affinity species in the absence of competing ligand. IC_50H and IC_50L (for the competitor, B) values are related with the respective equilibrium dissociation constants K_DHA and K_DLA according to the Cheng–Prusoff equation (Cheng & Prusoff, 1973) as:

$${\text{IC}}_{50\text{H}}=K_{\text{DHB}}\cdot \left(1+\left(A/K_{\text{DHA}}\right)\right){\text{IC}}_{50\text{L}}={\text{K}}_{\text{DLB}}\cdot \left(1+\left(A/K_{\text{DLA}}\right)\right)$$ (9)

Assuming two affinity states the actual concentration of B providing half saturation (B₅₀) could be calculated using the following equation:

$$B_{50}=\frac{\left(K_{\text{DHB}}+K_{\text{DLB}}-2\right)\cdot \sqrt{K_{\text{DHB}}+K_{\text{DLB}}}+\sqrt{K_{\text{DHB}}^2\cdot \left(R_{\text{H}}+R_{\text{L}}\right)-2\cdot K_{\text{DHB}}\left[K_{\text{DHB}}\cdot \left(R_{\text{H}}+R_{\text{L}}\right)+2\cdot \left(R_{\text{H}}-R_{\text{L}}\right)\right]+K_{\text{DLB}}^2\cdot \left(R_{\text{H}}+R_{\text{L}}\right)+4\cdot K_{\text{DLB}}\cdot \left(R_{\text{H}}-R_{\text{L}}\right)+4\cdot \left(R_{\text{H}}+R_{\text{L}}\right)}}{2\cdot \sqrt{R_{\text{H}}+R_{\text{L}}}}$$ (10)

To our knowledge this truly complex equation has never been used in drug screening.