Hydrated Anions: From Clusters to Bulk Solution with Quasi-Chemical Theory

Conspectus

The interactions of hydrated ions with molecular and macromolecular solution and interface partners are strong on a chemical energy scale. Here, we recount the foremost ab initio theory for the evaluation of the hydration free energies of ions, namely, quasi-chemical theory (QCT). We focus on anions, particularly halides but also the hydroxide anion, because they have been outstanding challenges for all theories. For example, this work supports understanding the high selectivity for F^– over Cl^– in fluoride-selective ion channels despite the identical charge and the size similarity of these ions. QCT is built by the identification of inner-shell clusters, separate treatment of those clusters, and then the integration of those results into the broader-scale solution environment. Recent work has focused on a close comparison with mass-spectrometric measurements of ion-hydration equilibria. We delineate how ab initio molecular dynamics (AIMD) calculations on ion-hydration clusters, elementary statistical thermodynamics, and electronic structure calculations on cluster structures sampled from the AIMD calculations obtain just the free energies extracted from the cluster experiments. That theory–experiment comparison has not been attempted before the work discussed here, but the agreement is excellent with moderate computational effort. This agreement reinforces both theory and experiment and provides a numerically accurate inner-shell contribution to QCT. The inner-shell complexes involving heavier halides display strikingly asymmetric hydration clusters. Asymmetric hydration structures can be problematic for the evaluation of the QCT outer-shell contribution with the polarizable continuum model (PCM). Nevertheless, QCT provides a favorable setting for the exploitation of PCM when the inner-shell material shields the ion from the outer solution environment. For the more asymmetrically hydrated, and thus less effectively shielded, heavier halide ions clustered with waters, the PCM is less satisfactory. We therefore investigate an inverse procedure in which the inner-shell structures are sampled from readily available AIMD calculations on the bulk solutions. This inverse procedure is a remarkable improvement; our final results are in close agreement with a standard tabulation of hydration free energies, and the final composite results are independent of the coordination number on the chemical energy scale of relevance, as they should be. Finally, a comparison of anion hydration structure in clusters and bulk solutions from AIMD simulations emphasize some differences: the asymmetries of bulk solution inner-shell structures are moderated compared with clusters but are still present, and inner hydration shells fill to slightly higher average coordination numbers in bulk solution than in clusters.

Key References

• Asthagiri D.; Dixit P. D.; Merchant S.; Paulaitis M. E.; Pratt L. R.; Rempe S. B.; Varma S.. Ion selectivity from local configurations of ligands in solutions and ion channels. Chem. Phys. Lett. 2010, 485, 1–7 10.1016/j.cplett.2009.12.013.¹ This article gives a basic discussion of quasi-chemical theory (QCT), including some history, physical motivation, and the connection between direct and cluster QCT.

• Gomez D. T.; Pratt L. R.; Rogers D. M.; Rempe S. B.. Free Energies of Hydrated Halide Anions: High Through-Put Computations on Clusters to Treat Rough Energy-Landscapes. Molecules 2021, 26, 3087. 10.3390/molecules26113087.² This paper details the theory and calculation of the QCT inner-shell contributions, which lay the basis for testing against the cluster–experimental association free energies.

• Muralidharan A.; Pratt L. R.; Chaudhari M. I.; Rempe S. B.. Quasi-chemical theory for anion hydration and specific ion effects: Cl^–(aq) vs. F^–(aq). Chem. Phys. Lett. 2019, 737, 100037. 10.1016/j.cpletx.2019.100037.³ This paper shows how to approximate the outer-shell contribution by combining the PCM model with structure sampling from dynamical cluster simulations.

• Chaudhari M. I.; Vanegas J. M.; Pratt L.; Muralidharan A.; Rempe S. B.. Hydration mimicry by membrane ion channels. Annu. Rev. Phys. Chem. 2020, 71, 461–484 10.1146/annurev-physchem-012320-015457.⁴ This paper reviews local hydration structures of mono- and divalent cations and assesses the concept of hydration mimicry for the rapid transport of specific ions through ion channels. Cluster QCT and surface potentials that provide hydration free energies are also reviewed.

1. Introduction

This Account describes recent research at the intersection of the topics of ion–water clusters,^5,6 the theory of solutions,^1,7,8 specific ion effects,⁹⁻¹¹ and the selectivity of membrane ion channels.⁴ We focus on anions in water because of their central position in classic specific ion effects, so-called Hofmeister effects.¹⁰ The anions considered here have been challenges for the molecular quasi-chemical theory (QCT),^1,7,8,12 which is the most advanced theory available to address hydration while accounting for chemical-level interactions and because recent theoretical progress on those challenges seems decisive.^2,3,13,14 We include HO^–(aq) in this discussion because of its centrality in aqueous solution chemistry and the continued theory and simulation interest in this ion¹⁵⁻¹⁷ and because the new results sharpen our understanding of the hydration of that ion.

1.1. Context: Selectivity of Membrane Ion Channels

As active components of nearly half of all proteins,^18,19 ions can bind to proteins and stabilize conformational states required for biological function and can participate in enzyme catalysis.²⁰ As an example, K⁺ ions bind to membrane channel proteins and stabilize functional conformations, thereby catalyzing the permeation of K⁺ across cellular membranes while also rejecting other ions such as Na⁺.²¹

Selective ion transport plays an important role in numerous physiological functions, including electrical signaling and cell volume control. Loss of ion selectivity, or blocking of ion transport, can have either catastrophic or beneficial effects. For example, the loss of selective conduction of K⁺ over Na⁺ by potassium channels in cardiac muscle interferes with the termination of action potentials, which can lead to life-threatening heart arrhythmia.²¹ In beneficial cases of blocked ion transport, drugs that block specific channels hold promise for treating neurological disorders, autoimmune diseases, and cancers.^22,23 Peptide toxins from several poisonous animals exemplify detrimental possibilities of blocked ion transport.²⁴ Indeed, simple divalent metal ions can be potent channel blockers by getting trapped in the channel, and both monovalent and divalent ions permeate selectively. Thus, understanding the mechanisms of specific ion binding and transport in proteins is important for understanding protein function critical to health, disease, and therapeutic development.²⁰

For anions such as Cl^–, the regulation of ion concentration is achieved through membrane transport proteins of the CLC family and others, including channelrhodopsins, which facilitate the passage of Cl^– through electrochemical potential gradients.²⁵⁻²⁷ While those structurally diverse proteins select for Cl^–, other channel proteins discriminate against Cl^–. An interesting example is FLUC, a family of fluoride-specific ion channels with dual-topology architecture.²⁸ These channels display an astonishingly high selectivity of 10⁴ for F^– over Cl^– despite their identical charge and their size similarity. Understanding such mechanisms for selectivity in ion transport has been a target for many modeling and simulation studies of high variety, emphasizing the K⁺/Na⁺ selectivity of potassium ion channels; for example, see refs (29−38). However, computational studies of anion transport mechanisms demonstrated by chloride-selective channels³⁹⁻⁴² that address comparisons to alternatives such as FLUC are less mature.^3,43

A conceptually natural strategy for addressing ion selectivity with computation would be direct simulations controlling for the contrasting cases or perhaps a clear, quantitative theory that permits controlling for mechanistic features of the ion binding or transport. Both of these requests are difficult. Here, we work toward the second of these alternatives by building a statistical molecular theory of ion binding thermodynamics.

1.2. Free Energies of Binding of Hydrated Ions Span a Chemical Scale of Energies

QCT^1,7,47 aims to evaluate interaction free energies of ions in solution⁴⁸ (Figure 1) and protein binding sites.^{1,4,29,30,32,33,35,46,47,49−55} That interaction free energy, or excess chemical potential,

1

is obtained from the full chemical potential μ_X less the indicated ideal contribution. Here, T is the temperature, R is the molar gas constant, ρ_X is the number density of the ion of interest, and 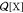is the canonical partition function of a molecule X in volume V.^4,56

Figure 1.

QCT hydration free energies, μ_X^(ex), for several aqueous ions. Values for anions are shown by open circles. The computed value for Ni²⁺(aq) is taken from the reevaluation of ref (44). Results for H⁺(aq) are from refs (45) and (46). The following discussion unpacks the QCT theory that is applied. These results are the most deliberate attempt at an ab initio evaluation of these free energies. The values shown are all much larger in magnitude than RT.

These free energies—single-ion activities when X is an ion—are knowable and appropriate targets for computation, but they are not measured solely on the basis of classic thermodynamics. Thus, widely available tabulations—Figure 1 utilizes one such tabulation—adopt extrathermodynamic assumptions.

Observe (Figure 1) that the free energies span a chemical energy scale much larger than RT ≈ 0.6 kcal/mol at room temperature. For example, the hydration free energy of Be²⁺ is about 1000RT. Clustered below −400 kcal/mol are values for divalent transition-metal ions.^44,51 Including the aqueous ferric ion, Fe³⁺(aq), for which QCT performs satisfactorily,⁵⁷ would require expanding the range of Figure 1 by another factor 2. Thus, though the now-canonical van der Waals perspective on liquids is an appropriate definition of the statistical mechanical problem for treating liquids generically, it immediately emphasizes <1%-magnitude free-energy effects. In contrast, the basic concept of QCT is to treat an ion together with inner-shell partners as an individual molecular species.^{1,7,12,57−59} Interactions of typical ions with inner-shell partners are chemical in nature, molecularly intricate, and intense on a thermal scale. The concept of “inner-shell” partners is central to QCT. It identifies near neighbors of a targeted species and will be discussed later for the present applications.

Molecular quasi-chemical theory (QCT)^1,7,8,59 was developed with the explicit goal of including chemical-level interactions within a molecular statistical thermodynamic theory. Initial applications were simple and remarkably accurate.⁵⁸ That success obviates a canonical “molecular force-field fitting → molecular simulation” workflow in the study of liquids.

1.2.1. Direct QCT

The basic status of QCT may be supported by the fact that QCT itself can be implemented through molecular simulation calculations.⁸ That approach is termed “direct” QCT.⁶⁰ In the direct approach, we acknowledge and exploit the spatial dependence of solute–solvent interaction strengths. The short-range interactions can be chemically involved, and for a suitable choice of the inner shell, the long-range interactions admit a Gaussian statistical model. This direct QCT approach parses the hydration free energy into physically meaningful and computationally well-defined chemical, packing, and long-range nonspecific contributions, thereby becoming a framework for conceptualizing molecular solutions.¹²

Direct QCT works naturally with common simulation packages based on either empirical classical or ab initio force fields.⁸ On that simulation basis, QCT provides a compelling molecular theory of liquid water itself.⁶¹⁻⁶³ The direct QCT approach enabled the first direct calculation of the hydration free energy of a protein.⁶⁴ Subsequent studies have highlighted the limitations of additive models of free energies that are de rigueur in biophysical speculation and recently led to transformative insights into decades-old assumptions about hydrophobic hydration in proteins.⁶⁵

Nevertheless, the initial motivation was the exploitation of molecular electronic structure calculations within statistical thermodynamic modeling.⁵⁷ That approach is called “cluster” QCT, wherein the chemical contribution noted above is related to physical solute–solvent clusters. The connection between direct and cluster approaches has been deliberately discussed elsewhere.^1,8,12,66

1.2.2. Cluster QCT

Cluster QCT provides a concise format,

2

for the free energies that we seek. This is exact statistical thermodynamics¹ and provides a foundation for mixed-resolution approaches, such as QM/MM. We will discuss these three terms in turn. The first term on the right of eq 2 is the inner-shell contribution. It is obtained by studying n water molecules clustering with the X species of interest² but without the exterior solution. This contribution involves the equilibrium constant, K_n⁽⁰⁾, discussed in section 2.1 below. 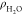By utilizing the solution density of the ligands, , this term properly assesses the availability of the water molecule ligands.

The rightmost term of eq 2 is the outer-shell contribution. This term involves the hydration of the identified (H₂O)_nX cluster, addressing interactions of the cluster with the exterior solution environment. Previous applications of QCT have utilized the polarizable continuum model (PCM)⁶⁷ for this task. (See refs (68) and (69) as examples.) PCM has been incorporated into standard electronic structure codes and focuses on the interactions with the solution at long range. Nevertheless, it is approximate on a molecular scale, and a symptom of that approximate character is the sensitivity of PCM results to radii parameters that are required. We will discuss that issue further below.

The remaining term in eq 2 involves the probability p_X(n) that n water molecules contact a distinguished X during its physical motion in solution. This term describes the polydispersity of the populations of an X inner shell; if only one size, say n, were possible, then ln p_X(n) = 0. The determination of p_X(n) requires the adoption of a proximity criterion describing how a water molecule contacts an X.^3,13,14,70 That polydispersity contribution is typically the smallest of these three and is conceptually the simplest, and here we utilize the AIMD simulation of the solution of interest to compute this term.

1.2.3. Anion Hydration

QCT applies to both cation and anion hydration cases. In contrast to cations, however, anion hydration clusters often exhibit H-bond donation to the ion (Figure 2; see also ref (70).). Anion-hydration clusters can be structurally delicate, specifically involving ligand–ligand hydrogen bonds, and that can make hydrated anions more challenging cases.

Figure 2.

Structure sampled from the AIMD trajectory for the isolated (H₂O)₅F^– cluster.

Initial QCT applications to hydrated anions worked simply with reasonable accuracy^3,13,14,46 compared with experiments.⁷¹ Nevertheless, specifics of the technical ingredients can be perplexing (Figure 3). The refinement of those initial applications has led to the further considerations discussed here, specifically, treatment of anharmonic effects on free energies of ion hydration clusters and the status of the polarizable continuum model⁶⁷ (PCM) for the hydration free energy of those clusters.

Figure 3.

Cluster free energies using the harmonic approximation compared with experimental values for (H₂O)_nHO^– and 1 ≤ n ≤ 4. The implicit density is ρ₀ = p/RT with p = 1 atm and T = 300 K. The molecular graphic insets show optimized structures for each n. The legend indicates electron density functional and basis sets, thus demonstrating the sensitivity to those aspects of these calculations. K_n⁽⁰⁾ is the traditional equilibrium constant, introduced with eq 3 below.

1.3. Theory Implemented with Simulation Data

We implement QCT here by bringing together quantities available from several different standard computations. The simulation work here thus contrasts with “let’s take a look” direct numerical simulations. Indeed, QCT seeks to define minimal clusters that provide the information necessary for the statistical thermodynamic theory; thus, we explicitly do not attempt to construct observational dynamical simulations, nor do we seek a large cluster-size limit in our simulation calculations.⁷² Before returning to discuss the theory, we note the details required for the computational procedures in the following. In addition, AIMD simulations of these systems are indeed readily available, and those observational calculations help to secure details that fill-out our understanding of these systems. Here, we note some of that previous work.

The extended work of Heuft and Meijer⁷³⁻⁷⁵ initiated AIMD calculations on halide anions in water. They noted that residence times of water ligands in a halide inner shell spanned approximately 8, 12, and 17 ps for I^–, Cl^–, and F^–, respectively. Those time scales are readily accessible by current AIMD calculations.

The interesting work of Wiktor et al.⁷⁶ focused on a basic thermodynamic quantity, the partial molar volumes of ions in water. Such studies are likely to provide fruitful next steps in the understanding of these systems.

The AIMD of Duignan and co-workers^77,78 on F^–(aq) also focused on a basic thermodynamic characteristic of simple ions in water, namely, hydration free energies. They made a case for the application of ultrahigh accuracy electronic structure calculations to these problems. Our discussion below will identify aspects of the present efforts that overlap with that previous work but support a different conclusion: specifically, standard electronic structure calculations, properly integrated into statistical thermodynamic theory, are sufficient for experimental accuracy.

Finally, for this section, we note the extensive AIMD work on HO^–(aq) that has been exhaustively reviewed.^16,17 Though that work did not proceed to the evaluation of standard thermodynamic characteristics, the discussions below will elaborate on specific points of comparison.

1.3.1. Procedures for Bulk X(aq) Solutions

The data utilized here for F^–(aq) and Cl^–(aq) was obtained from previous work^3,14 that treated a single ion and 64 water molecules using the VASP simulation package.⁷⁹ The system was a cubic cell of edge 1.24 nm with periodic boundary conditions. The PW91 generalized gradient approximation described the core–valence interactions using the projector augmented wave (PAW) method. Plane waves with a kinetic energy cutoff of 400 eV and a time step of 0.5 fs were used for the simulation in the NVE ensemble. A temperature of 350 K was targeted for the simulation to avoid glassy behavior that can result at lower T.^3,14 After discarding 50 ps of trajectory as aging, our analysis was based on a 50 ps production trajectory.

For HO^–(aq), Br^–(aq), and I^–(aq), the AIMD calculations are new here and used the CP2K simulation package⁸⁰ to treat a single ion and 64 water molecules under periodic boundary conditions. We adopted the PBE functional with Goedecker, Teter, and Hutter⁸¹ (GTH) pseudopotentials in the GPW schemes,⁸² as broadly used and consistent with our previous cluster results.⁷⁰ Molecularly optimized DZVPMOLOPT-SR-GTH basis sets were obtained from the CP2K website. Plane waves with a kinetic energy cutoff of 400 eV and a time step of 0.5 fs were used for the simulation in the NVT ensemble. The cubic cell with edge 1.27 nm reasonably matches the experimental density of water under our standard conditions. T = 300 K was selected⁸³ through the Nosé–Hoover thermostat. Our analysis was based on 50 ps of production trajectory after 50 ps of aging. Figure 4 provides a standard overview of the bulk solution structures observed.

Figure 4.

Radial distributions of H₂O molecule H atoms relative to the X anion from the AIMD trajectory, with the left panel for the isolated (H₂O)₃X cluster and the right panel for X(aq) with periodic boundary conditions corresponding to our thermodynamic state. The neighborship-ordered distributions on the left panel are normalized to 1/ϱ_H, with ϱ_H being the number density of solvent H atoms for the right panel. These distributions are thus directly comparable. The red dashed curves (right-side axes) give the running H-atom coordination number, n_H|X(r). For the (H₂O)₃HO^– cluster, n_H|O(r) plateaus near 3, indicating simple H-bond donation. For the bulk solution, n_H|O(r) plateaus at about 3.8.

1.3.2. Procedures for Isolated (H₂O)_nX

Molecular dynamics trajectories of the isolated (H₂O)_nX clusters for 2 ≤ n ≤ 5 and X = F^–, HO^–, Cl^–, Br^–, and I^– were obtained using CP2K, just as for the HO^–, Br^–, and I^– bulk solution calculations specified above. The pseudopotentials, functionals, and basis sets were the same. These simulations set the temperature at 300 K with the Nosé–Hoover thermostat, using the GPW basis with default settings and a kinetic energy cutoff of 400 eV. Five picoseconds of the production trajectory, with a time step of 1 fs, was analyzed after 5 ps of aging.

For our statistical, or rough landscape, analysis of those trajectories, cluster structures were screened for consistency with our clustering definition (Figure 5). Each clustered configuration is analyzed, according to the right-hand side of eq 5, and the separate structures are subjected to single-point calculations using the Gaussian⁸⁴ electronic structure software with the PBE functional and the DEF2TZVP basis set for F^–, HO^–, Cl^–, Br^–, and I^– configurations. Using the resulting thermal averaging in eq 5 and K₁⁽⁰⁾ from experiment, the resulting stepwise K_n (Figure 6) produce the accurate results used below.^2,70

Figure 5.

Clustering of inner-shell water molecules with the central anion. (Top panel): Primitive clustering criterion requiring a clustered water molecule to donate an H atom to the sphere within radius r of the ion. The rightmost water molecule is a member of this cluster, but the leftmost is not. The bottom water molecule donates two H atoms though counts only one ligand. (Middle panel): Clustered configuration chosen arbitrarily from the AIMD trajectory for an isolated (H₂O)₄I^–. (Bottom panel): Clustered configuration selected arbitrarily from the AIMD simulation of I^–(aq) solution. These graphics illustrate asymmetric anion hydration that is moderated in the bulk solution (bottom) compared with clusters (middle).

Figure 6.

For HO^–, free energies for the inner-shell contributions (eq 2). The implicit density is ρ₀ = p/RT with p = 1 atm and T = 300 K. The embedded graphics depict structures sampled from the AIMD trajectory.

2. Discussion and Results

2.1. Inner-Shell Contributions

The study of the associative equilibria

3

is a basic feature of QCT. Here X ≡ F^–, HO^–, Cl^–, Br^–, or I^–. Equation 3 directs attention to

4

where is the number density of (H₂O)_nX species. K_n⁽⁰⁾ requires the definition of formed (H₂O)_nX clusters for the evaluation of actual densities. Such definitions amount to defining the proximity of an H₂O ligand to an X ion. Although judgment might be required for a natural proximity definition, here we defer the discussion of that definition until after subsequent QCT developments.

Our scheme for evaluating K_n⁽⁰⁾ is anchored in classic statistical thermodynamics^3,7,56 and proceeds incrementally following

5

This formulation introduces the energy differences

6

The brackets in eq 5, ⟨···|n⟩, indicate the thermal average utilizing the canonical simulation stream for the (H₂O)_nX cluster.³ The symbol β stands for 1/RT.

The evaluation of the energy combination ΔU_n, eq 6, starts with the sampled configuration of the (H₂O)_nX cluster. Each ligand in turn serves to compose the energy difference suggested by the exchange

7

Geometries of species on the right of eq 7 conform to the sampled (H₂O)_nX structure on the left. To appreciate ΔU_n, we use the following accounting. Consider first the contribution {U[(H₂O)_nX] – U[(H₂O)_n−1X]}. This is the energy change for introducing an additional H₂O ligand into an (H₂O)_n−1X complex. The remaining combination {U[(H₂O)X] – U[X]} is the energy change for introducing one H₂O ligand to a bare X ion. The difference ΔU_n thus reflects the crowding of the nth H₂O ligand, including any degradation of binding of the nth H₂O ligand to the X ion (Figure 7).

Figure 7.

Distribution of βΔU₃ (eq 6). The solid line is the Gaussian model distribution with the sample mean and variance. Positive values of βΔU₃ reflect the unfavorable crowding of ligands. The required single-point calculations used the PBE functional and the DEF2TZVP basis.

Charge is balanced in eq 3, and the energy combination of eq 6 is not affected by the electrostatic potential of the phase.⁴

For n = 1, eq 5 correctly reduces to the trivial case of K₀⁽⁰⁾ = 1. In evaluating K_n for n ≥ 2, the value of K₁⁽⁰⁾ can be supplied from experiment⁷¹ or alternative theory. This term incorporates the interaction strength between X and one H₂O molecule. Carrying out subsequent steps in this scheme then addresses the issues that make anion hydration more challenging, i.e., competing interactions of neighboring H₂O molecules in those clusters.

Figure 3 shows that a modest vertical shift of those harmonic approximation values substantially improves the agreement between harmonic approximation computations and experimental results throughout. Since the approach from eq 5 takes K₁⁽⁰⁾ as input, the present more detailed development should benefit similarly. This approach does not directly address issues of quantum mechanical zero-point motion, except to the extent that a pragmatic inclusion of an external K₁ incorporates zero-point motion empirically. The empirical grounding of this procedure might be particularly relevant to the multimodal possibilities of the H atom that is interior to (HO)HOH^–,¹⁶ similar to the Zundel cation (H₂O)H(OH₂)⁺. This inner-shell evaluation can use electronic-structure methods of arbitrary sophistication since the calculations need be carried out only for modest-sized clusters. These results reexamine a previous application of QCT to HO^–(aq) that was strikingly accurate for the dissociation thermodynamics.⁴⁶

2.1.1. Specific Definition of Clustering

In the discussion above, we did not address the consequences of any specific clustering proximity definition. That delinquency amounts to the assumption that complexes encountered in our cluster simulations, i.e., at moderate temperatures, are typically well clustered. Going further, we consider how a specific treatment might be built from here. A simple clustering criterion is that a clustered water molecule should donate at least one H atom within an assigned radius of the ion (Figure 5).

We introduce a geometric indicator

8

of a clustered configuration. b_X(k) indicates whether molecule k is clustered (value 1) with the ion X or not (value 0). χ_n takes a value of 1 if the n molecules are clustered with the ion and zero otherwise. Thus, χ_n is indeed an indicator function.

We will denote by K̅_n⁽⁰⁾ as the equilibrium constant obtained by our scheme above without the definition of a restrictive inner-shell region. Then

9

where ⟨χ_n⟩ indicates the statistical average evaluated as above, without a specific definition of clustered.

Note that 0 ≤ χ_n ≤ 1 and thus ln[K_n⁽⁰⁾/K̅_n] ≤ 0. This result makes physical sense because matching the natural clustering should not increase the free energy.

An interesting physical consideration is that the experimental results implicitly describe some specific physical clustering. Poorly formed physical clusters, not conforming to our mathematically defined cluster, might lose a weakly bound ligand, which would then populate the outer shell, perhaps to be pumped away in the experiment. These considerations raise the question, what clustering definition is most appropriate for the experiments?

The estimated average, ln⟨χ_n⟩, sampled from AIMD dynamics of (H₂O)_nX for 2 ≤ n ≤ 5 clusters (Table 1) shows that, generally, as n increases, ⟨χ_n⟩ decreases as repulsive interactions between water molecules force ligands to the outer shell. This behavior is especially evident for (H₂O)₅I^– on the one hand, where none of the sampled configurations had all five water molecules within the defined inner shell. On the other hand, ln⟨χ_n⟩ ≈ 0 for (H₂O)₃HO^– (Table 1), which indicates that the present clustering definition effectively encompasses the region of physical clustering for that case.

Table 1. Estimated ln⟨χ_n⟩ from AIMD Calculations of (H₂O)_nX Defined Above^a.

	n
ion (X)	2	3	4	5
F– (0.27 nm)	0.00	–0.21 ± 0.07	–1.61 ± 0.28	– 1.05 ± 0.19
HO– (0.25 nm)	–0.02 ± 0.02	0.00	–2.83 ± 0.56
Cl– (0.29 nm)	0.00	–0.06 ± 0.03	–0.42 ± 0.10	–2.21 ± 0.40
Br– (0.31 nm)	–0.13 ± 0.05	–0.22 ± 0.07	–0.42 ± 0.10	–1.61 ± 0.28
I– (0.34 nm)	–0.13 ± 0.05	–0.36 ± 0.09	–0.20 ± 0.07

^aProduction trajectories were sampled at 10/ps so that the sample sizes were m = 51. The indicated uncertainties approximate one standard error according to the formula , which assumes independence of the observations. The radius parameters r (Figure 5) are noted in parentheses. This parameter was chosen to match approximately the first minimum of the observed g_H|X; see Figure 4.

2.2. Outer Shell and PCM

The outer-shell cluster contribution of eq 2 to the hydration free energy can be treated³ using the polarizable continuum model⁶⁷ (PCM) in the Gaussian suite of electronic structure programs.⁸⁴ The geometrical structures sampled from the AIMD trajectory for (H₂O)_nX were subjected to two single-point electronic calculations separately: one for the isolated cluster and a second with the external (dielectric) medium described by the PCM tool. The difference, ε̅_j, is employed in computing

10

where m is the number of configurations from the simulation stream that satisfies the clustering definition. Equation 10 corresponds to the potential distribution theorem (PDT) approach,^1,56 recognizing that thermal fluctuations implicit in the PCM⁶⁷ approach complete the PDT averaging.

PCM is an approximate description of molecular-scale aspects of hydration.⁸⁵ PCM does include approximate accounts of packing effects and dispersion interactions, secondary to long-range electrostatic interactions.⁶⁷ Our discussion has emphasized that QCT is built by the identification of inner-shell clusters, the separate treatment of those clusters, and the integration of those results into the broader-scale solution environment. Inevitably, approximations are required to describe the outer-shell effects, and here those approximations are bundled in the PCM model.

The approximate character of the PCM model is signaled by the sensitive dependence on radii parameters that locate jumps in dielectric responses used in defining the model. It is reassuring that empirical values of those parameters are of reasonable magnitude. Still, the results are sensitive to those radii parameters, and they are not determined by theory⁸⁶ or experiment separate from the model. It is striking and important that QCT moderates that sensitivity by the subtraction of the ligand free energies in the formulation of that outer-shell contribution.^1,58 That insensitivity is achieved operationally by the boundaries of X being somewhat buried by the ligands and the ligand boundaries being unchanged in the subtraction (eq 2). The indicated subtraction reflects the appearance of the factors together with K_n⁽⁰⁾ of eq 2.

For the cases of F^–(aq) and Cl^–(aq), we know already that this PCM-assisted application of QCT works satisfactorily³ and similarly for HO^–(aq).^46,70,87 For the cases of Br^–(aq) and I^–(aq), that procedure is somewhat degraded,⁷⁰ which we surmise as being due to the asymmetric hydration (Figure 5) of those ions that leaves the central ion more exposed comparatively. Therefore, we tried the alternative approach,

11

where the M clustered structures are sampled from the trajectory of the X(aq) AIMD simulations. This strategy is the well-known inverse formula of the standard potential distribution theorem,⁵⁶ but is implemented with the PCM tool. Our physical argument is that clustered (H₂O)_nX structures obtained with this inverse procedure ought to relieve intracluster hydrogen bonding and bury the X ion from contact with the water comparatively better (see also refs (88) and (69)); therefore, the severe PCM approximation might perform better. Indeed, that was found to be the case, and the results discussed below (Figure 8) for the cases of Br^–(aq) and I^–(aq) were obtained with this inverse procedure.

Figure 8.

(Black) Excess hydration free energy of X(aq). (Red) Outer-shell contribution evaluated using the PCM⁶⁷ with cluster configurations sampled from AIMD. (Green) Inner-shell free energies.⁷⁰ (Blue) Polydispersity contribution obtained from the Gaussian model for p(n) from AIMD data. In the cases of Br^–(aq) and I^–(aq), these results used the PCM in the inverse procedure of eq 11. Otherwise, results were obtained with direct eq 10.

The treatment of long-range electrostatic interactions in this implementation of QCT is worth emphasizing. Though the sampling of the bulk solution structures uses the preferred and commonplace periodic boundary conditions in treating long-rang interactions, i.e., Ewald electrostatics, the energetics that enter into the free-energy computations reported do not use Ewald electrostatics.

2.3. Polydispersity and Net Hydration Free Energies

We have noted above that the polydispersity contribution is the smallest of the three contributions to cluster QCT. It is conceptually simplest and utilizes direct AIMD simulation in order to estimate p_X(n). Thus, at this stage, we display all three contributions and their combination (Table 2, then Figures 8 and 9) and then proceed to their physical discussion.

Table 2. Hydration Free Energies of Anions under Standard Conditions^a.

X	μX(ex) (kcal/mol)	experiment* (kcal/mol)89
F–	–112	–111.1
HO–	–101	–102.8
Cl–	–82	–81.3
Br–	–73	–75.3
I–	–64	–65.7

^aThese results are obtained from exp(−βμ_X^(ex)) = ∑_np_X(n)exp[K_nρ_H2Oⁿ − ln p_X (n), − β(μ_(H2OnX − nμ_H2O^(ex))] which rearranges eq 2 and then acknowledges the normalization of p_X(n). The root mean-squared difference of these two columns is approximately 1.6 kcal/mol.

Figure 9.

QCT evaluation of the hydration free energy for HO^–(aq), labeled as for Figure 8.

Note again that these free energies span a chemical scale of energies. For the least strongly bound case (I^–), the magnitudes of the net free energies are in excess of 60 kcal/mol, roughly 100RT here. The net quantities (eq 2, then Figure 8 and 9) are independent of n on that chemical energy scale. The agreement with the experimental tabulation (Table 2) is excellent and consistent across the anions treated. The latter point shows that the agreement is not affected by an assignment of a free-energy value for H⁺(aq) in the experimental tabulation.

2.4. Some Structural Observations

Though this work has explicitly marshalled simulation calculations toward evaluating QCT free energies, some structural observations are also available.

The cluster definition (Figure 5 and Table 1) based on H-atom donation, either singly or doubly, works satisfactorily: small values estimated for ln⟨χ_n⟩ indicate that the defined clustering volumes encompass the clustering observed from the AIMD for (H₂O)_nX cases, especially for the smaller values of n. For example, we see ln⟨χ₃⟩ ≈ 0 with (H₂O)₃HO^– (Table 1). This result suggests simple H-bond donation, and that is supported by the radial distribution functions in the (H₂O)₃HO^– case (Figure 4). This observation provides a simple rationale for the remarkable success of QCT free-energy calculations for HO^–(aq).^15,46,87 Thus, QCT for hydrated anions works better if the anion inner shell is characterized by H-bond donation. This conclusion is consistent with previous work^3,13,14 but focuses attention specifically on the XH radial distribution functions (Figure 4).

Nevertheless, the structures of the clusters are different from the bulk aqueous solution case, as depicted by the XH rdfs (Figure 4). For the clusters, setting aside F^– and HO^–, asymmetric hydration structures prevail (Figure 5). Asymmetric inner-shell structures are moderated in the bulk hydration environment but still evident.⁹³ For the bulk hydration cases overall, the XH rdfs suggest the filling of inner shells to slightly higher average coordination numbers than for the clusters. Using HO^– again as an example, the expected coordination number is about 3.8 (Figure 4), which may be compared to the work of ref (15) that estimated 3.7. The predictions of hydration structure agree well with experimental estimates based on X-ray and neutron diffraction and X-ray absorption fine structure studies (Table 3). Additional information, including traditional XO radial distribution functions, and further discussion can be found in the Ph.D. thesis of Diego T. Gomez.⁷⁰

Table 3. Hydration Structure of Anions from the Peak of the Radial Distribution Function.

X	rO|X (nm)	exp
F–	0.268	0.262–0.26990
HO–	0.260	0.265–0.27091
Cl–	0.324	0.310–0.32090
Br–	0.327	0.329–0.34090
I–	0.352	0.350–0.37090,92

3. Conclusions

The final free energies (Figures 8 and 9 and Table 2) are accurate in comparison with the standard tabulation in ref (89), and the final composite results of Figures 8 and 9 are independent of n on the chemical energy scale of relevance. Evaluations of the inner-shell and polydispersity contributions of eq 2 are key to the demonstration of this theoretical accuracy. Structural information obtained by simulations shows that the distinctive asymmetry of anion clusters is moderated in bulk aqueous solution.

The inner-shell free-energy contribution directly tracks available experimental information on gas-phase cluster hydration equilibria, and the polydispersity contribution is a direct structural observation from the AIMD trajectory. Neither of those contributions is expected to be sensitive to the potential of the phase.

The excellent theory–experiment agreement observed for those inner-shell cluster contributions is a breakthrough that supports the approximate remainder of the theory. The n-dependent balance of the PCM-approximated, outer-shell contribution with the remaining numerically exact contributions suggests that the PCM approximation performs satisfactorily in these applications.

The implementation of this PCM-approximate outer-shell contribution requires statistical thermodynamic processing for the AIMD results, involving single-point electronic structure calculations of cluster structures sampled from the AIMD trajectory. Since the required electronic structure calculations treat only inner-shell clusters, this electronic structure effort could employ arbitrarily accurate numerical theory. In contrast to earlier recommendations, further effort in that direction is not warranted here because of the observed excellent theory–experiment agreement for the inner-shell cluster contribution.

In summary, the excellent agreement of anion hydration free energies is due to quantum computations accurately checked with experiment, together with the physical statistical thermodynamic theory that enables these computations. Furthermore, the AIMD simulations reveal differences in anion cluster structures compared with structures found in bulk aqueous solution, with the latter having less asymmetry and higher average coordination numbers. Finally, the ability to predict both an accurate solvation free energy and an accurate solvation structure of anions supports future work using QCT to understand the mechanisms of ion transport and selectivity for the large diversity of anion-selective transport proteins.

Biographies

Diego T. Gomez was born in Albuquerque, New Mexico. He holds chemical engineering degrees from New Mexico State University (B.S., 2017) and Tulane University (Ph.D., 2021). His contributions include quasi-chemical theory for aqueous halide solutions and theoretical studies of capillary bridges.

Lawrence R. Pratt was born in Flint, Michigan. He is professor emeritus of chemical engineering at Tulane University. He holds chemistry degrees from Michigan State University (B.S., 1972) and the University of Illinois (M.S., 1974 and Ph.D., 1977). Prior to Tulane, he spent 23 years as a technical staff member at Los Alamos National Laboratory. He has contributed to the theory of the hydrophobic effect, the development of transition path sampling, orbital free density functional theory, and the theory of liquids and solutions.

Dilipkumar N. Asthagiri was born in Trichy, India. He is an associate research professor of chemical engineering at Rice University. He holds degrees in chemical engineering from the University of Delaware (Ph.D., 1999), University of Michigan (M.S., 1994), and the Indian Institute of Technology-Madras (BTech, 1992). His contributions include those in the molecular statistical thermodynamics of hydration and its role in biomolecular structure and assembly and the NMR relaxation of confined fluids and MRI contrast agents.

Susan B. Rempe was born in Spokane, Washington and grew up in Kalispell, Montana. She is a senior scientist at Sandia National Laboratories, an affiliate scientist at the Center for Integrated Nanotechnologies, and a research professor at the University of New Mexico. She holds degrees in chemistry from the University of Washington (Ph.D., 1998; M.S., 1993) and the University of Montana (B.A., 1989) and a degree in pre-medical sciences from Columbia University (B.A., 1987). She has contributed to the theory of liquids and condensed matter, selective ion binding and transport, hydrophobic effects, and the design of separation membranes.

The authors declare no competing financial interest.