SUMMARY
Cortical processing of task-relevant information enables recognition of behaviorally meaningful sensory events. It is unclear how task-related information is represented within cortical networks by the activity of individual neurons and their functional interactions. Here, we use two-photon imaging to record neuronal activity from the primary auditory cortex of mice during a pure-tone discrimination task. We find that a subset of neurons transiently encode sensory information used to inform behavioral choice. Using Granger causality analysis, we show that these neurons form functional networks in which information transmits sequentially. Network structures differ for target versus non-target tones, encode behavioral choice, and differ between correct versus incorrect behavioral choices. Correct behavioral choices are associated with shorter communication timescales, larger functional correlations, and greater information redundancy. In summary, specialized neurons in primary auditory cortex integrate task-related information and form functional networks whose structures encode both sensory input and behavioral choice.
Graphical Abstract
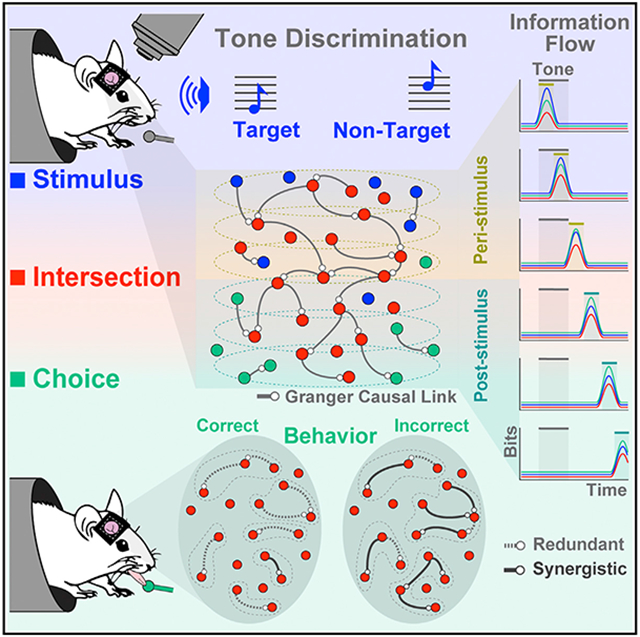
In brief
Francis et al. find that, as mice perform an auditory discrimination task, cortical neurons form functional networks in which task-relevant information transmits sequentially between neurons. Network structures encode behavioral choice, and correct behavioral choices are associated with shorter communication timescales, larger functional correlations, and greater information redundancy between neurons.
INTRODUCTION
Cortical processing of task-relevant information enables mammals to recognize behaviorally meaningful stimuli while navigating the sensory environment. Performance of an auditory task modulates neural representations of task-related sounds at the level of single neurons or small populations, already in the primary auditory cortex (A1) (Kuchibhotla et al., 2017; Kato et al., 2015; David et al., 2012; Francis et al., 2018a, 2018b; Tsunada et al., 2016; Brosch et al., 2011; Carcea et al., 2017; Fritz et al., 2003; Insanally et al., 2019; Schwartz and David, 2018; Yin et al., 2020; Bagur et al., 2018; Mcginley et al., 2015; Guo et al., 2019; Rodgers and Deweese, 2014; Niwa et al., 2013; Christison-Lagay and Cohen, 2018). We recently showed that performing a pure-tone detection task increases neuronal responses to target tones in A1 layer 2/3 (L2/3) and changes functional connectivity by forming small strongly linked neuronal networks that encode behavioral choice (Francis et al., 2018b). However, natural auditory scenes typically include both target and non-target sounds that require discrimination. The effect of discrimination on the functional networking of neurons and how target versus non-target information propagates through the population are poorly understood.
Given the diversity of neuronal connectivity and stimulus selectivity in A1 L2/3 (Atencio and Schreiner, 2010; Atzori et al., 2001; Oviedo et al., 2010; Meng et al., 2017; Bandyopadhyay et al., 2010; Rothschild et al., 2010; Kanold et al., 2014; Maor et al., 2016; Winkowski and Kanold, 2013; Sakata and Harris, 2009; Yang et al., 2008; Sadagopan and Wang, 2009; Liu and Kanold, 2021), we hypothesized that there may exist specialized neurons in A1 L2/3 that represent varying amounts of sensory or choice information and that a subset of these neurons, which carry sensory information used to inform behavioral choice, form functionally connected networks whose structural properties encode behavioral choice during task performance.
To investigate our hypotheses, we trained mice to behaviorally discriminate target versus non-target pure tones while we recorded neuronal activity in A1 L2/3 using two-photon (2P) Ca2+ imaging. We then quantified how much stimulus information (SI), behavioral choice information (CI), and intersection information (II), i.e., sensory information that is used to inform behavioral choice, was carried by individual neurons (Runyan et al., 2017; Panzeri et al., 2017). We used Granger causality (GC) analysis to study how these neurons were organized into functional networks (Kim et al., 2011; Sheikhattar et al., 2018; Francis et al., 2018b; Seth et al., 2015; Kaminski et al., 2001; Bresslerand Seth, 2011; Quinn et al., 2015), and compiled network statistics to quantitatively compare key aspects of network structure. Here, we extended GC analysis to not only study functional network structure, but also the timescales of network interactions. Finally, to study how task-related information is transmitted and shared within functional networks, we computed information redundancy between pairs of neurons (Schneidman et al., 2003; Pola et al., 2003).
We found that task performance modulated neuronal response amplitudes, network structures, and information transmission in A1 L2/3. Individual neurons encoded II at different peak times which, across the population, tiled the duration of a trial. Networked neurons encoding II exhibited sparse connectivity and shared redundant stimulus information relevant for behavioral choice. Network structures differed for target versus non-target tones, encoded behavioral choice, and differed between correct and incorrect behavioral choices. Moreover, choice-dependent functional networks also showed different communication timescales. Together, our results describe how networked neurons in A1 L2/3 that integrate sensory and behavioral information during auditory task performance sequentially transmit task-related information.
RESULTS
To study how task-relevant information is transmitted within neuronal networks, we trained nine transgenic CBA × Thy1-GCaMP6s F1 mice (Frisina et al., 2011; Dana et al., 2014) to perform a pure-tone frequency discrimination task (Kuchibhotla et al., 2017; Pi et al., 2013) while we imaged neuronal responses in A1 L2/3 using in vivo 2P Ca2+ imaging (Figure 1).
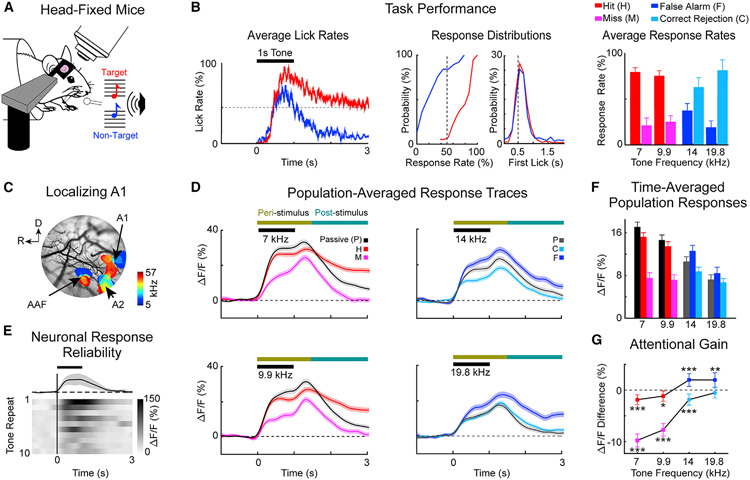
Figure 1. Two-photon imaging in awake-behaving mice shows neural responses modulated by behavioral choice.
(A) Head-fixed mice were trained to discriminate low-frequency target tones (red) versus high-frequency non-target tones (blue).
(B) Average lick rates within a trial during task performance (left panel). The horizontal black bar shows the tone presentation. The red trace and blue traces show the lick rate for hits (H) and false alarms (F), respectively. The dotted line illustrates chance performance, where licking is not timed to tone presentation, but rather it is evenly distributed across a given trial. Cumulative distribution functions across experiments for hit (red) and false alarm (blue) response rates and latencies (middle panels). Average behavioral choice rates, i.e., hit (red), miss (pink), false alarm (blue), and correct rejection (cyan), for each presented tone (right panel). Error bars show 2 SEM (n = 34 experiments).
(C) Primary auditory cortex (A1) was localized within a craniotomy by using widefield imaging to visualize tonotopy in auditory cortex.
(D) Average neuronal population response traces in A1 layer 2/3 (L2/3) (n = 2,792 neurons) color coded for behavioral choice as in (B). Each trace shows the response to the indicated tone. Shading shows 2 SEM. The horizontal colored bars show the peri- and post-stimulus windows, respectively, used for later analyses.
(E) Neurons in A1 L2/3 responded transiently, with jittered amplitude and timing in response to repeated identical tones.
(F) Neuronal response amplitude varied with both task performance and tone frequency. Error bars show 2 SEM.
(G) Attentional gain was defined as the difference between neural responses during behavioral versus passive trials for the same tone. Error bars show 2 SEM, and asterisks indicate statistically significant differences based on bootstrap t test (*p < 0.05, **p < 0.01, ***p < 0.001).
Head-fixed mice learned to perform an auditory tone discrimination task
Head-fixed mice were trained to lick a waterspout in response to hearing a low-frequency target tone (Figure 1A; 7 or 9.9 kHz, red), and to avoid licking the waterspout after hearing a high-frequency non-target tone (14 or 19.8 kHz, blue). The four frequencies were randomly interleaved across trials. Figure 1B shows that the mice learned to behaviorally discriminate targets versus non-targets. Each trial’s behavioral response was categorized into four groups, based on the first lick on each trial: hit (H: licking after target onset), miss (M: no licking after a target), false alarm (F: licking after non-target onset), or correct rejection (C: no licking after a non-target). The middle panel of Figure 1B shows the distribution of H and F behavioral response times (i.e., the time of the first lick in a trial). The average H and F response latencies relative to stimulus onset were 0.64 ± 0.02 and 0.75 ± 0.04 s, respectively. Across the 34 experiments, the hit rate (78.8% ± 5.1%) was significantly higher than the false alarm rate (F = 27.1% ± 7.3%; p < 0.001, t test) and the correct rejection rate (74.3% ± 6.9%) was significantly higher (p < 0.001, t test) than both the F and M rate (20.8% ± 5.2%). Thus, the mice were able to discriminate between target versus non-target tones (d’ = 1.4 ± 0.4).
Decision making modulated neuronal response amplitude in A1 L2/3
To characterize neural responses during behavior, we imaged Ca2+-dependent fluorescence in the auditory cortex. To localize 2P imaging fields for each experiment to A1, we first mapped the tonotopy of the auditory cortex in each mouse using widefield imaging (Figure 1C) (Liu et al., 2019; Francis et al., 2018b).
We performed 2P imaging (Figures 1D-1G) at a depth of 150–250 μm from the cortical surface in each mouse (34 experiments, 9 mice, 2,792 neurons). We observed fluorescence (ΔF/F) responses to all 4 tones with response dynamics typical of GCaMP6s (Chen et al., 2013; Dana et al., 2014). Similar to previous studies, neural traces showed a complex pattern of task-dependent changes in response amplitude (Bagur et al., 2018; Brosch et al., 2011; Carcea et al., 2017; David et al., 2012; Francis et al., 2018a, 2018b; Guo et al., 2019; Kato et al., 2015; Kuchibhotla et al., 2017; Rodgers and Deweese, 2014; Schwartz and David, 2018; Tsunada et al., 2016; Yin et al., 2020).
To make sure our results do not reflect neural coding of task-related movement (i.e., licking/behavioral choice) or reward, we first quantified how neuronal response amplitude varied with task performance and pure-tone frequency during passive trials, in which the mouse sat quiescently hearing tones without doing an auditory task, and then during behavioral task performance. To make a fair comparison, we averaged neural traces only during the first 0.5 s after tone onset for the trials with behavioral response latencies greater than 0.5 s after stimulus onset. This accounted for 74% of H trials. While licking has been shown to impact activity in the auditory cortex (Nelson and Mooney, 2016), we previously showed that it did not drive neural activity in A1 L2/3 during a go/no-go task (Francis et al., 2018b).
As shown in Figure 1F, we found significant neural responses (p < 0.001) at all frequencies in both passive and behavior conditions, indicating that the mice could hear the tones. This result, in combination with our finding that behavioral responses were similarly time locked to both low- and high-frequency tone presentations in our go/no-go task (Figure 1B) provides compelling evidence that the mice were in fact doing a target versus non-target discrimination task, and not simply target detection. Overall, responses to non-target tones were smaller than those to target tones (p < 0.001). In contrast, trials without behavioral responses (M and C) had the lowest average response amplitudes and there were no significant differences in neuronal responses to target versus non-target frequencies (p > 0.05, Kruskal-Wallis test). Thus, the amplitude of pure-tone responses in A1 during task performance was strongly modulated not only by acoustic stimulation but also by behavioral choice.
Aberrant attentional gain in A1 L2/3 reflects incorrect decision making
The change in neuronal response amplitude to the same sound for passive versus behavior trials quantifies attentional gain in A1. As shown in Figure 1G, correct behavioral choices (i.e., hits and correct rejections) had a small, but significant negative gain (7 kHz, H: −1.9% ± 0.97%, p < 0.001; 9.9 kHz, H: −1.2% ± 1.01%, p < 0.05; 14 kHz, C: −1.85% ± 1.08%, p < 0.001; 19.8 kHz, C: −0.5% ± 1.02%, p > 0.05). In contrast, attentional gain for incorrect behavioral choices was more varied. False alarms occurred when neuronal responses had a small positive gain (14 kHz, F: 1.97% ± 1.23%, p <0.001; 19.8 kHz, F: 1.96% ± 1.42%, p < 0.01), whereas misses occurred when responses had a large negative attentional gain (7 kHz, M: −9.76% ± 1.25%, p < 0.001; 9.9 kHz, M: −7.7% ± 1.24%, p < 0.001). Thus, incorrect decision making was associated with aberrant attentional gain, i.e., deviations from the slight negativity observed during correct decision making.
Task-relevant information is transiently encoded by individual neurons in A1 L2/3
We hypothesized that single neurons in A1 might represent varying amounts of sensory or choice information. We first performed spike inference, as summarized in Figure 2A and described in detail in STAR Methods, followed by quantifying the task-relevant information carried by each neuron in single trials using information theory (Shannon, 1948; Quian Quiroga and Panzeri, 2009). For each neuron, we quantified how much information was present about the acoustic stimulus (SI; i.e., target versus non-target tone; Figure 2B, left) and about the behavioral choice (CI; i.e., lick versus no-lick; Figure 2B, right). We also computed intersection information (II; Figure 2B, middle) (Panzeri et al., 2017; Pica et al., 2017), which quantifies how much of the sensory information encoded by the neurons is used to inform behavioral choices, and is thus a direct measure of task-relevant information. We found that 1,183/2,792 neurons (42%) carried either significant SI or CI (permutation test, p < 0.1, corrected for comparisons across multiple time windows, see STAR Methods). A total of 708/1,183 neurons did not carry significant II (permutation test, p > 0.1); i.e., they either had stimulus information that did not inform choice (e.g., stimulus response was not causal to formation of the choice), or choice information not related to the stimulus (e.g., internal choice bias). The remaining 475/1,183 neurons carried significant II, SI, and CI (permutation test, p < 0.1), and thus integrate both sensory and behavioral information that is directly relevant for the decision-making task (Panzeri et al., 2017).
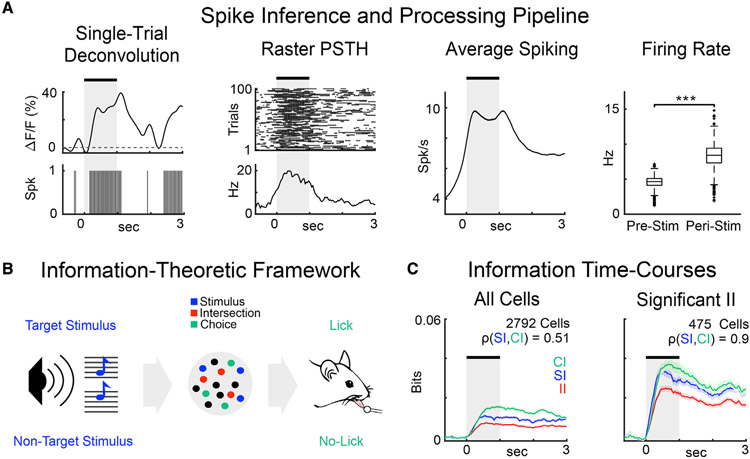
Figure 2. Processing pipeline and information-theoretic framework.
(A) Examples of deconvolution of the ΔF/F response traces (first panel); trial-by-trial spiking activity and peri-stimulus time histogram for a single neuron (second panel); average firing rate across neurons is higher in the post-stimulus interval than pre-stimulus (rightmost panel; p < 0.001, Wilcoxon rank-sum test).
(B) Stimulus encoding and behavioral readout during auditory task performance. Blue, green, and red circles, respectively, represent neurons with stimulus information (SI) only, choice information (CI) only, and intersection information (II). II accounts for the part of sensory and choice information used to perform the task.
(C) Time courses of information types (SI, CI, and II) in different groups of neurons. Solid lines represent the mean and shaded areas represent the SEM across all neurons in each group.
To better illustrate the dynamics of the information carried by either the whole population or by the neurons with significant II, SI, and CI (shortened to “II neurons” hereafter), we computed the average II, SI, and CI time courses. II neurons carried the largest amounts of II, SI, and CI throughout the trial (Figure 2C). Moreover, CI was highly correlated to SI (Pearson correlation = 0.9) for II neurons, while this correlation was smaller across the entire population (Pearson correlation = 0.51), suggesting that similar levels of CI and SI are present across II neurons (Figure 2C). At the time of peak information, each neuron carried 0.117 ± 0.003 bits of SI, 0.121 ± 0.004 bits of CI, and 0.085 ± 0.002 bits of II, respectively (mean ± SEM across the 475 II neurons).
We restricted our further analyses to 12 out of 34 sessions with at least 20 II neurons due to our interest in subsequent network analyses for which, given the number of experimental trials, up to 20 neurons could be analyzed with statistical confidence. This left us with 375/475 II neurons for subsequent analyses (see STAR Methods). Figure 3A shows the peak-normalized information time courses for each II neuron, sorted by the peak latency of the respective information (SI, CI, or II) across neurons. Qualitative inspection showed that neurons transiently encoded SI, CI, or II, tiling the trial duration. The SI, CI, and II time courses of II neurons showed similar average trends, while neurons that carried either significant SI or CI, but not II, showed more heterogeneous trends (Figure S1).
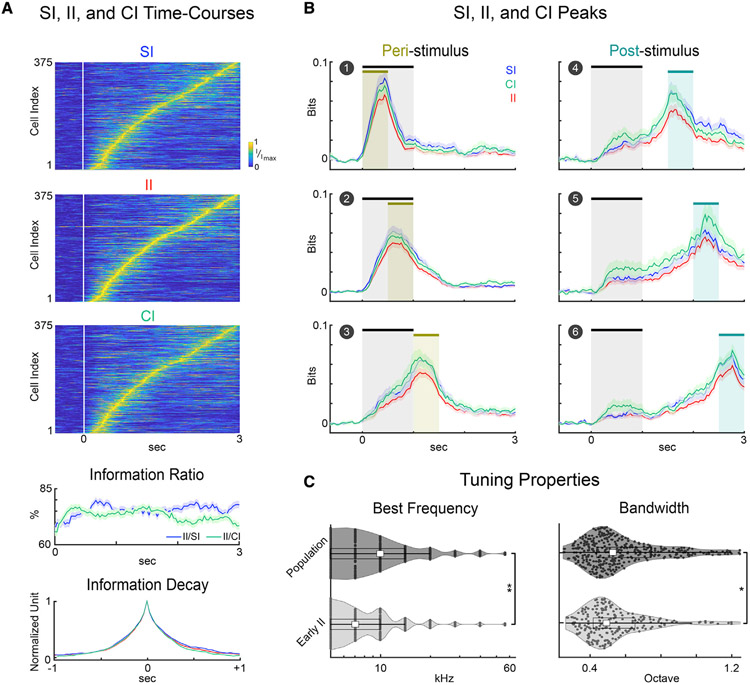
Figure 3. A1 L2/3 neurons transiently carried SI, CI, and II.
(A) Information time courses were normalized to the peak of each neuron’s information and sorted by peak time of II. Information ratio was first computed for each neuron and then averaged across neurons. Transiency of SI, CI, and II shown by the peak-aligned information decay within ±1 s from the peak (bottom panel). Error bars show 1 SEM.
(B) Time course of SI, CI, and II averaged over neurons. We quantified the SI, CI, and II in six separate stages of the behavioral task, which account for the peri-stimulus (0–1.5 s) and the post-stimulus intervals (1.5–3 s) shown by the shaded regions. Error bars show 1 SEM.
(C) Violin plots of the estimated best frequency (BF) (left) and tuning bandwidth (BW) (right) of neurons with early II versus overall population. Early II neurons had significantly lower BFs (p < 0.01, Wilcoxon rank-sum test) and narrower BWs (p < 0.05, Wilcoxon rank-sum test) compared with the overall population.
We next computed the II/SI and II/CI ratios to identify how much of the stimulus and choice information was used for informing behavioral choice. The average II/SI and II/CI ratio was high (>70%) for II neurons throughout the trial, meaning that most of the SI was used for informing choice and most of the CI reflected stimulus discrimination rather than a stimulus-unrelated choice bias (Figure 3A). Conversely, neurons with significant SI or CI, but not II, showed an overall decrease of information within the 500 ms waiting period after tone onset (Figure S1). In addition, they showed lower II/SI or II/CI ratios down to ~30%, especially at the peak times, meaning that SI and CI are not optimally used to perform the task. These results indicate that we identified neurons in A1 L2/3 that transiently carry significant stimulus information used to inform behavioral choice. To quantify this transiency, we aligned information peaks across neurons and analyzed the peak-aligned traces within ±1 s of the peak (Figure 3A), which could be fit with an exponential with time constant . Thus, individual neurons transiently carried SI, CI, and II for an effective duration of ~250 ms.
To inspect the dynamics of information carried across the trial duration, we clustered the neurons based on their II-peak latencies. We labeled neurons that peaked in the first 1.5 s after stimulus onset as peri-stimulus II, and the remainder as post-stimulus II (Figure 3B). We subdivided the peri-stimulus II neurons into three sequential task-related periods within a trial: (1) the 500-ms waiting period just after tone onset, (2) the 500-ms interval after the waiting period, and (3) the 500 ms after tone offset (labeled respectively in Figure 3B, left column). We found that 52/375, 85/375, and 60/375 neurons had II that peaked in the first, second, and third peri-stimulus periods, respectively (Figure 3B, left column), adding up to 197/375 neurons. Furthermore, 45/375, 40/375, and 48/375 neurons had II that peaked in the fourth, fifth, and sixth post-stimulus periods (1.5–3 s), respectively (labeled respectively in Figure 3B, right column). The remaining 45/375 neurons peaked after 3 s. Although the values of SI, CI, and II remained comparable throughout the trial, neurons with earlier responses carried slightly more SI than CI (Figure 3B, left column, blue versus green traces) and neurons with later responses carried slightly higher CI than SI (Figure 3B, right column, green versus blue traces).
Given that II neurons carried SI, we next examined their tuning properties (Figure 3C). We found that the best frequencies (BFs) (the frequency values eliciting the highest response during passive tone presentation) of II neurons were lower (p < 0.01, Wilcoxon rank-sum test) than the average BF of the overall population. II neurons also had narrower bandwidth (BW) (p < 0.05, Wilcoxon rank-sum test) than the overall population. Our results show that task-relevant information was transiently encoded by individual neurons, yet sustained throughout the trial by sequential encoding across a population of neurons in A1 L2/3.
Neurons with intersection information form sparse timescale-invariant functional networks
Since individual neurons had low information content and only transiently encoded II (Figures 2B, 2C, and 3A), we hypothesized that II neurons might form functional networks to more robustly encode task-relevant information. We previously used GC analysis to identify small functional networks of interacting neurons whose network structure depended on behavioral choice (Francis et al., 2018b), but did not study how network structure might vary with integration timescales, i.e., the duration over which neurons might interact. Our finding that II was transiently encoded by individual neurons, but sustained across time by the population, necessitated the examination of relevant timescales of interactions between II neurons. Hence, we extended our previous GC analysis by considering the interaction timescales.
GC analysis uses multivariate statistics to infer causal influences within a population of neurons by testing if the recent history of a neuron can improve the prediction of another neuron’s activity. The duration of the recent history over which interactions are quantified, referred to as the “integration window,” is a hyperparameter of GC analysis, whose value, w, sets the longest interaction window considered (Figure 4A, left schematic). Short (S; w = 233 ms) integration windows quantify dynamics that are more likely to reflect local neuronal interactions. Long (L; w = 1033 ms) integration windows would additionally capture the effects of potentially slower and indirectly mediated interactions that may involve distant neurons. The specific values of w we used were integer multiples of the imaging frame rate. Importantly, the S-timescale interactions are a subset of the L-timescale interactions (see STAR Methods). For each experiment (n = 12), we performed GC analysis on the 20 neurons with the lowest, i.e., “shortest,” II-peak latencies to identify the contribution of neurons whose activity carried task-relevant information during stimulus presentation. We used 20 neurons per experiment to avoid overfitting the data, given the limited number of experimental trials (see STAR Methods). GC networks were estimated individually for each behavioral choice category (H, M, C, and F) in the discrimination task, importantly contrasting previous work (Francis et al., 2018b) in which we could only analyze networks corresponding to H and M categories in a detection task.
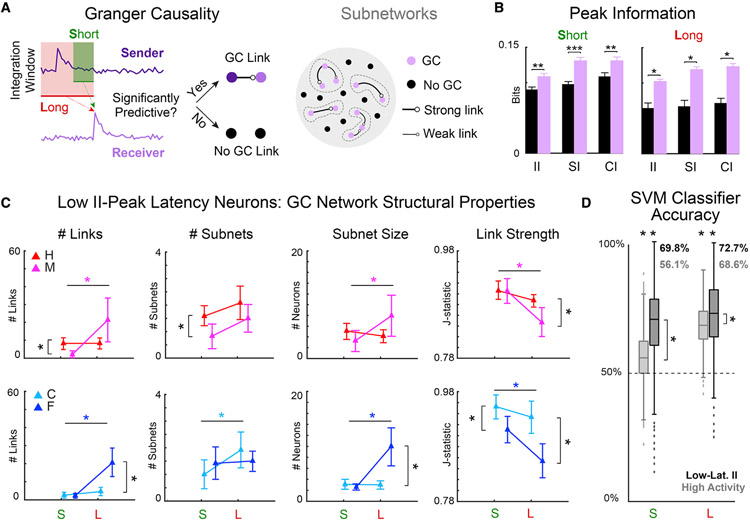
Figure 4. Behavioral choice was encoded in the network structure of low II-peak latency neurons.
(A) Functional networks of short (S)- and long (L)-timescale interactions among low II-peak latency neurons were estimated using Granger causality (GC) analysis for each behavioral choice: hit (H), miss (M), correct rejection (C), and false alarm (F). Disjoint sets of interlinked neurons constituted subnetworks (dashed gray boundaries).
(B) GC-linked neurons, for both S- and L-timescales, had more information than GC-unlinked neurons (*p < 0.05, **p < 0.01, ***p < 0.001).
(C) Four GC network statistics were analyzed: number of links, number of subnetworks, size of subnetworks, and statistical strength of links. Error bars show 2 SEM. Statistically significant differences, indicated by asterisks, were identified by Wilcoxon’s signed rank test (p < 0.05). See also Table S1.
(D) Network statistics were used to train a support vector machine (SVM) to classify behavioral responses into correct or incorrect decisions. Across timescale and selection of neurons, decisions were predicted significantly better than chance (p < 0.001). S-timescale network structure of low II-peak latency neurons was better decoded than highly responsive neurons (p < 0.001). L-timescale network structures had high decoding accuracy, but low II-peak latency networks were better decoded than highly responsive neurons (p < 0.001). Two-sample t tests (p < 0.05) were used to compare distributions and a one-sample t test (p < 0.05) to compare with chance performance.
We found that across all trials GC networks were sparse: only 1% of possible links connecting 21.98% of the selected II neurons were detected in S-timescale networks, while 3.61% were detected in L-timescale networks connecting 51.67% of the selected II neurons. Unlike simpler measures, such as Pearson correlation, GC is a directed measure of communication, which can distinguish senders from receivers (Figure 4A). This allowed us to investigate the proportion of senders and receivers within the network. For the S-timescale networks, 10.10% of neurons were senders, 9.06% were receivers, and 2.81% were GC-linked neurons that had net degree of zero. For the L-timescale networks, however, 24.58% of the neurons were senders, 19.79% were receivers, and 7.29% had a net degree of zero. This indicates that an additional 29.69% of the selected II neurons were recruited over the longer integration window.
Speculating that the information content of GC-linked neurons differed from GC-unlinked neurons, we compared SI, CI, and II at the II-peak time. We found that SI, CI, and II were higher in GC-linked than in GC-unlinked neurons, in both S- and L-timescale networks (Figure 4B). These results suggest that GC-linked neurons form networks carrying signals of greater relevance for performing the auditory discrimination task. Given that neurons carry information over a wide range of timescales (Figure 4B), we tested whether neurons’ II-peak latencies depended on their membership in S- or L-timescale networks. We compared the distributions of II-peak latencies of neurons in S- versus L-timescale networks and found no significant difference (Wilcoxon rank-sum test, p = 0.5847). Furthermore, we compared the II-peak latency for pairs of GC-linked neurons and found that the II-peak of receiver neurons follows that of sender neurons by 2.07 time bins (69 ms) on average; however, this difference was not statistically significant (Wilcoxon signed rank test, p = 0.1743). As such, we found no evidence to support that II-peak latency correlates with membership of the linked neurons in S- versus L-timescale networks or the direction of the GC links.
To characterize how the structure of the GC networks depends on the timescale of interactions and on behavioral choice, we analyzed four network statistics separately for H, M, C, and F trials: number of links, number of subnetworks (isolated subsets of neurons), subnetwork size (number of member neurons), and statistical strength of links (Youden’s J statistic) (Francis et al., 2018b) (shown from left to right in Figure 4C; see also Table S1). We focused on neurons with low II-peak latency, as they are more likely to be causally related to choice. For both M and F networks (incorrect behavior), the number of links and the size of subnetworks were greater for L- than S-timescale networks, while link strength was smaller for L-than S-timescale networks. In contrast, we found no differences for L- versus S-timescale networks in H or C trials (correct behavior) for the number of links, size of subnetworks, and link strengths. In C trials, the number of subnetworks increased with integration window length. Together, our results show that incorrect decision (M and F) L-timescale networks are larger but connected less strongly than their S-timescale counterparts. In contrast, the structure of correct decision networks (H and C) was invariant across timescales. Noting that S-timescale interactions are a subset of the L-timescale interactions in our model, the invariance of the correct decision network structure between S- and L-timescales may suggest the involvement of a network of local cortical interactions, rather than of interactions mediated by wider loops involving farther neurons.
For S-timescale, comparison of H and M networks showed that the former had more links and larger subnetworks, suggesting that larger networks are beneficial for encoding correct discrimination of the target. The average link strength was greater in C than in F networks, suggesting that stronger links are beneficial for encoding correct rejection of the non-target. In contrast, for L-timescale, both the number of links and the sizes of subnetworks were smaller for correct than incorrect categories, while links remained stronger for the correct category.
Neuronal network structure encodes behavioral choice
Since the GC network structures for neurons with low II-peak latency strongly depended on behavioral choice, we sought to directly test if the network structures encode behavioral choice. Thus, we used the four network statistics as features for a support vector machine trained to distinguish between correct (H and C) and incorrect (M and F) decisions. For comparison, we trained a similar classifier for networks of neurons with high response rates, chosen regardless of the information content they carry. The comparison between the network structure of II neurons and responsive neurons is non-trivial because a pair of neurons both carrying II is neither necessary nor sufficient for there to be a GC link between them (see Figure S2 for counterexamples). The GC network statistics of highly responsive neurons are reported in Table S2. Of all low II-peak latency neurons, 30.21% were also identified as highly responsive neurons (see STAR Methods for selection criterion). The network structure of S-timescale networks for low II-peak latency neurons classified behavioral choice much more accurately than that of highly responsive neurons (Figure 4D, left bar plots). In contrast, the features of L-timescale networks classified behavioral choice well for both low II-peak latency and highly responsive neurons, although more accurately for the former (Figure 4D, right bar plots). These results show that S-timescale networks of low II-peak latency neurons better encode behavioral choice than those of highly responsive neurons and suggest that low II-peak latency neurons form a specialized group of neurons in A1.
One possibility is that strong choice predictivity from network interactions is not a special property of networks formed by II neurons but is also present in networks of neurons with either SI not used for choice or CI not related to the stimulus. To test this possibility, we compared the predictivity of low II-peak latency neurons with that of SI and CI neurons that did not have significant II (Figures S3A and S3B; Table S3). While seven sessions had a sufficient number of exclusively CI neurons, only one session had a sufficient number of exclusively SI neurons for GC network analysis; hence, we focused on the networks of exclusively CI neurons to contrast with the low-latency II neurons analyzed in Figure 4. Network structures of low II-peak latency neurons were more predictive than CI neurons (Figure S3B). Furthermore, the network structures of neurons with the greatest II-peak magnitudes (Figures S3C and S3D; Table S4) were also more predictive of behavioral choice than highly responsive neurons (Figure S3D). Our results suggest that the encoding of behavioral choice in the S-timescale network structure is specific to II neurons, and it is not found as much in groups of neurons with choice information not related to the stimulus.
The spatial extent of neuronal subnetworks varies less by timescale during correct behavioral choices
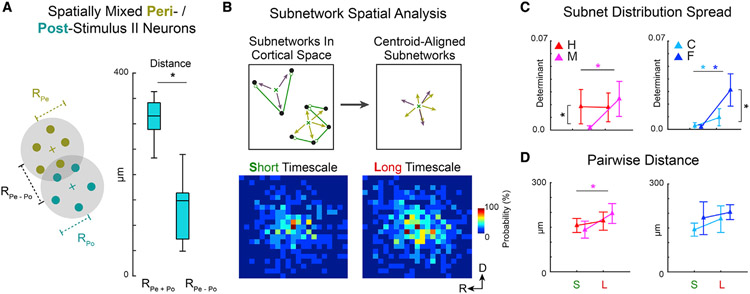
Since 2P imaging gives the exact spatial location of each neuron in a field of view, we sought to characterize how II neurons and their functional networks were distributed spatially. We first studied if neurons with II peaks in peri- versus post-stimulus intervals were in different regions or if they were intermingled. We calculated the sum of the average distances of peri- (Pe) and post-stimulus (Po) neurons to their centroids (RPe and RPo, respectively) and compared the sum with the distance between the centroids (RPe – Po). The distance between centroids was smaller than the spread of each set of neurons (Figure 5A). Thus, Pe and Po neurons were heterogeneously distributed within the field of view, suggesting that information flow did not have intrinsic spatial directionality from one subarea to another during task performance.
Figure 5. Subnetwork dispersion varied less by timescale during correct behavioral choices.
(A) Neurons with peri- (Pe) and post-stimulus (Po) II peaks were spatially intermingled. The sum of average distances of Pe neurons to their centroid (RPe) and of Po neurons to theirs (RPo), denoted as RPe + Po, was smaller than the distance between centroids (RPe − Po) (p < 0.001, two-sample t test).
(B) Subnetwork spatial distributions. Low II-peak latency neurons (black) that are linked (green) in groups isolated from others constitute subnetworks (top left). Relative locations of subnetworked neurons were aggregated over all subnetworks (top right). The distributions of relative locations are shown as 2D histograms (25 × 25 μm bins) for S- and L-timescales (bottom left and right).
(C) Determinant of spatial distribution covariance matrix. L-timescale C, M, and F subnetworks were more spatially dispersed than S-timescale subnetworks (M: p < 0.001; F: p = 0.002; C: p = 0.014). For S-timescales, H versus M subnetworks were more dispersed (p = 0.002), as were F versus C subnetworks for L-timescales (p = 0.003).
(D) Pairwise distances between linked neurons remained similar for S- versus L-timescales, except for M trials (p = 0.047). (C) and (D) show mean ±2 SEM. Asterisks indicate statistically significant differences based on Wilcoxon’s signed rank test (p < 0.05).
We next analyzed how subnetworks were dispersed by computing the vector distances of subnetworked neurons to the subnetwork centroid (Figure 5B, top schematic; see also STAR Methods). Subnetworks of L-timescale interactions tended to be more spatially dispersed than the S-timescale ones (Figure 5B, bottom subpanels), as indicated by the determinant of the distance vector covariance matrix (Figure 5C). The dispersion of M, F, and C subnetworks were larger for L- than S-timescales. Differences in dispersion were also observed between H and M trials for S-timescale subnetworks and between C and F trials for L-timescale subnetworks. To see if differences in the dispersion of subnetworks across timescales were due to greater distances between linked neurons, rather than the inclusion of additional neurons, we computed the average pairwise distance between linked neurons, i.e., the average link length (Figure 5D). Except for M networks, GC link lengths were stable across timescales, indicating that the greater subnetwork spatial dispersion for L-timescale interactions was more likely due to the inclusion of additional neurons than an increased distance between linked neurons. These results suggest that correct choices are associated with spatially stable compact subnetworks while incorrect choices involve activity spread to additional neurons.
Networked neurons communicate task-relevant stimulus information that reverberates redundantly
A functional link between neurons suggests that task-relevant information is transmitted from one neuron to another. This would create a population code whose information content is reverberated redundantly across neurons because the same information is shared by different neurons.
To investigate the nature of information present in the functional networks, we measured information redundancy (Schneidman et al., 2003; Pola et al., 2003) between GC-linked neurons (Figure 6A). We used a normalized redundancy index defined as the information carried jointly by two neurons minus the sum of the information that each carried independently, normalized with respect to the total information carried by the two neurons jointly. The value of the normalized redundancy index indicates the fraction of total joint information that is shared by two neurons. Neurons share redundant information when the redundancy index is negative, i.e., together they carry less information than the sum of the information they carry separately. Positive values of the redundancy index are associated to synergy, i.e., the contribution from the interaction between the neurons to the joint information cannot be inferred by considering each neuron individually.
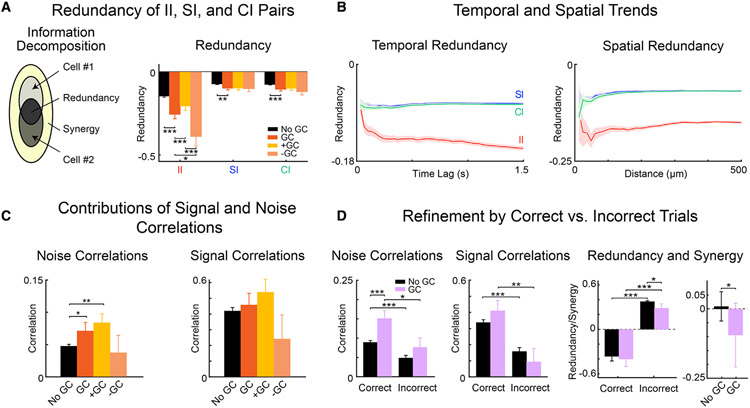
Figure 6. Redundancy and correlations increase during correct behavioral choice.
(A) Left panel: decomposition of joint information of pairs of neurons into synergistic, cell-unique, and redundant components. Right panel: normalized time-lagged redundancy computed for GC-linked neurons (red), either positive (orange) or negative (salmon), and GC-unlinked pairs of neurons (black). GC-linked neurons carried more redundant information than GC-unlinked neurons (II, SI, CI). Pairs of neurons connected with negative GC links carried more redundant information related to II.
(B) Normalized redundancy across time-lagged neuronal activity (left panel), and versus the Euclidean distance (right panel) between pairs of both GC-linked and GC-unlinked neurons.
(C) Pairwise time-lagged signal and noise correlations between pairs of neurons at the peak of intersection information. Noise correlations were higher in GC-linked than GC-unlinked neurons, while signal correlations are distributed similarly.
(D) Noise and signal correlations in correct versus incorrect trials (two leftmost panels); normalized time-lagged redundancy in correct versus incorrect trials (center-right panel); difference between the redundancy in correct versus incorrect trials for GC-linked and GC-unlinked neurons (rightmost panel). Statistical comparisons were made with a two-sample t test (*p < 0.05, **p < 0.01, ***p < 0.001).
For SI, CI, and II, we computed redundancy at the peak time of II, for each pair of neurons used in GC analysis. Normalized redundancy between pairs of neurons with a S-timescale GC link was compared with those with no GC link (Figure 6A). For S-timescales, we found that information shared by pairs of neurons was redundant. This implies that neurons shared part of the information they transiently carried at different times. Normalized redundancy was much larger for II than CI and SI (Figure 6A, left bar plots versus middle and right bar plots). For L-timescales, we found similar trends but proportionally smaller variations between GC-linked and GC-unlinked neurons (Figure S4). This means that neurons shared more of the behaviorally relevant, than behaviorally irrelevant, portion of the SI they carried. Importantly, the difference between normalized redundancy for GC-linked versus GC-unlinked neurons was much larger for II than for SI or CI (Figure 6A, red versus black bar plots), reinforcing the interpretation that S-timescale GC links mediate the exchange of behaviorally relevant sensory information.
GC links can be positive or negative valued, reflecting functionally facilitative or suppressive interactions, respectively (Francis et al., 2018b; Sheikhattar et al., 2018). We found that negative GC links had a much larger effect on redundancy, suggesting that they mediate more II exchange than positive links (Figure 6A, orange versus yellow bar plots). These results might indicate a mediating role of inhibitory circuits in task-related network activity (Kuchibhotla et al., 2017). Sorting the normalized redundancy with respect to the II-peak time lags (Figure 6B, left panel) revealed that II redundancy varies across time lags with an overall increasing trend (from −0.1 to −0.15). This indicates that redundant information persists during the trial.
Previous studies showed that nearby cells typically interact redundantly (Nirenberg et al., 2001; Reich et al., 2001; Chechik et al., 2006). We thus investigated how redundant information spreads spatially for II, SI, and, CI by plotting the time-lagged redundancy as a function of the Euclidean distance between pairs of neurons (Figure 6B, right panel). We found a peak of redundant interaction for II at a distance of ~50 μm (II = − 0.1971 ± 0.0187), which then reached a plateau at ~320 μm (II = − 0.1499 ± 0.0039), followed by a distance-independent trend. SI and CI were similarly redundant and reached a plateau at ~208 mm (SI = − 0.0691 ± 0.0019, CI = − 0.0709 ± 0.0019. Together, these results suggest that GC links indicate redundant communication of behaviorally relevant stimulus information, and that redundant neurons are located in close proximity of each other.
Signal correlations, noise correlations, and redundancy in correct versus incorrect trials
Redundancy is critically shaped by signal and noise correlation (Schneidman et al., 2003; Pola et al., 2003). To gain more insights into the origin of redundancy, we quantified noise correlations, i.e., the single-trial covariations of activity that are unrelated to stimulus signals, and signal correlations, i.e., the covariations of activity that reflect similarity in trial-averaged stimulus tuning (see STAR Methods).
Figure 6C shows the signal and noise correlations for GC-linked and GC-unlinked pairs of neurons computed at the II-peak times using all available trials. Noise correlations reduce population information (and thus contribute to redundancy) when they have the same sign as the signal correlations (Schneidman et al., 2003; Pola et al., 2003). In our analysis, both signal and noise correlations were, on average, positive (Figure 6C). Thus, the observed redundancy reflects the matching positive signs of both signal and noise correlations. GC-linked pairs of neurons exhibited higher noise correlations than GC-unlinked pairs of neurons, consistent with the view that trial-to-trial correlations should be stronger for neurons that are functionally linked. Signal correlations did not vary (p > 0.05, t test) between GC-linked and GC-unlinked pairs of neurons.
To examine the possible advantages of the observed correlations and redundancy values for task performance and behavioral accuracy, we next refined them by separating correct (H or C) and incorrect (M or F) trials (Figure 6D). We found several results of interest. First, in correct trials, noise correlations were stronger and had the same sign as the signal correlations (Figure 6D, two leftmost subplots), leading to a strong redundancy of information in correct trials (Figure 6D, third subplot).
Second, neurons did not exhibit redundancy in incorrect trials, and were indeed synergistic, i.e., with positive redundancy index (Figure 6D, third subplot). This property held for both pairs that were or were not GC linked. It is important here to note that GC-linked neurons had stronger noise correlations in correct trials (Figure 6D, leftmost subplot), suggesting stronger noise correlations during correct behavior results, at least in part, from network communication as revealed by GC analysis. The source of the synergy between neurons during incorrect trials, despite having positive signal and noise correlations, is further examined in Figure S5.
Third, when computing the difference between the normalized redundancy index in correct and incorrect trials, we observed that there was more redundancy in correct trials for GC-linked pairs (Figure 6D, rightmost panel). Together, these results suggest that redundancy and noise correlations may provide advantages for task performance. In addition, greater redundancy during correct behavior choices may partly result from increased within-network communication.
DISCUSSION
In this study we found that, during the performance of an auditory discrimination task, individual neurons in A1 L2/3 transiently carried information about the stimulus (SI), behavioral choice (CI), or both (II) for hundreds of milliseconds, and that task-relevant information was sustained across the duration of a 3-s trial by sequential propagation of SI, CI, and II in functionally connected neuronal populations. Furthermore, we identified a subpopulation of low II-peak latency neurons, which formed functionally connected networks whose structure could reliably predict behavioral choice. Our findings suggest that the spatiotemporal structure of functional connectivity between low II-peak latency neurons in A1 L2/3 may form a neural population base for sustained representation of task-relevant information.
A1 L2/3 contains a diverse population of neurons with differing functional connectivity (Meng et al., 2017; Liu and Kanold, 2021). Here, we find that the bandwidth of II neurons is lower than that of other neurons. This suggests that these neurons might be part of a class of A1 L2/3 neurons that receive L4 inputs and have limited integration across the tonotopic axis (Meng et al., 2017).
Task relevance of S- versus L-timescale neuronal interactions
The nested parameterization of L- and S-timescale interactions allowed us to differentiate between solely S-timescale versus additional L-timescale interactions in functional networks. Comparing L- versus S-timescale networks showed that correct choice L-timescale networks consisted of fewer but stronger links that were mostly S-timescale influences. In contrast, incorrect choice networks are characterized by a mixture of both S- and L-timescale links, and by an increased network size due to recruitment of additional spatially distant neurons nearby (within a 2P field of view). These additional L-timescale links likely reflect the local effects of slower interactions with distant neurons, perhaps reflecting non-sensory task-related interaction, such as error signaling or deviance detection (Parras et al., 2021; Steinmetz et al., 2019; Stringer et al., 2019; Chen et al., 2015; Khouri and Nelken, 2015). Since subnetworks during correct trials varied less by timescale, this suggests that the influence of more distant neurons is suppressed when correct decisions are made, leaving predominantly S-timescale interactions. Such suppression could be mediated by inputs to A1 that can activate inhibitory circuits (Fritz et al., 2010; Winkowski et al., 2013, 2018; Liu et al., 2021).
Magnitude of stimulus, choice, and intersection information in A1 L2/3 neurons
We used information theory to characterize neural selectivity to the task variables, and quantify, as function of trial time, the amount of SI, CI, and II. Our non-parametric approach for establishing neural selectivity (Quian Quiroga and Panzeri, 2009) is relatively assumption-free and can capture linear dependencies on stimulus and choice (which are commonly captured using parametric approaches, such as generalized linear models) as well as possible non-linear interactions between stimulus and choice. The latter non-linearities are expected to exist under general conditions (Chicharro et al., 2021) and are difficult to reveal with parametric approaches unless one introduces strong model assumptions.
The amount of SI and CI per neuron were both approximately 0.1 bits at the information peak. Given that 1 bit of information is needed to solve the binary discrimination task, and that neurons were found to carry partly redundant information, a first implication of these values is that task performance must rely on networks of at least tens of neurons. This consideration is compatible with the high behavioral choice prediction afforded by networks of 20 functionally connected neurons. Previous studies of A1 L2/3 reported much higher values of SI than CI (Runyan et al., 2017; Pica et al., 2017). We interpret these dissimilarities as largely influenced by task design, which is distinct from the one used in Runyan et al. (2017), rather than a difference of computations. In contrast to our use of a go/no-go task in tone discrimination, these previous studies involved discrimination of the location of broad-band sounds during spatial navigation in a virtual reality setting, with large delays between stimulus and reward, as well as using a forced-choice task, in which all stimuli could be associated with a reward. Here, we found values of II to be close to those of SI, suggesting that most of the auditory information carried by the neurons we identified was used to inform choice, supporting the assumption that the identified functional networks are important for the execution of the task.
Population coding via reverberation of redundant information in networks
We found high redundancy between the behaviorally relevant stimulus information carried at the time of information peaks between pairs of low II-peak latency neurons. The redundancy was higher between pairs of neurons that were GC linked based on S-timescale interactions, suggesting that the GC link may reflect the transfer of behaviorally relevant information from one neuron to another. Redundancy has been traditionally viewed as a negative feature of population coding that should be reduced, based on theories of efficient coding (Attneave, 1954; Barlow, 1961; Nigam et al., 2019), and on the often implicit assumption of optimal information readout, implying that higher neural information corresponds to better performance (Gold and Shadlen, 2001). However, other studies have proposed that high values of spatiotemporal redundancy might facilitate biophysical signal propagation (Valente et al., 2021; Salinas and Sejnowski, 2001; Alonso et al., 1996).
Recent studies have proposed that the benefits of redundancy may outweigh its disadvantages by making task-related signals available for longer timescales (Runyan et al., 2017) and facilitating the behavioral readout of the sensory signal (Valente et al., 2021). Here, our results of higher redundancy and stronger noise correlations during correct behavior, especially for GC-linked neurons, confirm the prediction of these previous works and add the insight that stronger noise correlations and higher redundancy during correct behavior may partly originate from increased within-network communication as revealed by GC analysis.
Importantly, previous studies highlighting the role of redundancy in behavioral readout (Runyan et al., 2017; Valente et al., 2021) concentrated only on the average strength of pairwise noise correlations. In contrast, we characterized the network-level structure of behaviorally relevant information sharing and of correct perceptual decisions. We found that higher redundancy in GC-linked neurons was accompanied by a higher number of links, larger subnetworks in correct target detection, and stronger links in correct rejection of non-targets. Together, redundancy and GC analyses suggest that correct decisions in an auditory discrimination task may require temporary reverberation of information in the spatiotemporal structure of neuronal networks. This might explain larger redundancy for behaviorally relevant than behaviorally irrelevant sensory information.
In summary, our results show that, during behavioral discrimination of pure-tone frequencies, task-relevant information is transmitted sequentially across individual neurons in A1 and is sustained for long periods of time within compact neuronal networks.
Limitations of the study
Our study demonstrates a statistical relationship between the considered features of neural activity and behavior but does not causally demonstrate the role of these features in generating correct and incorrect perceptions. Only perturbations of, and observation of, the behavioral changes that manipulations of such features (e.g., using holographic 2P optogenetics) induce could establish causality. Furthermore, we found similarities and differences with previous studies of the behavioral relevance of emergent features (e.g., correlations, redundancy, GC networks) of population codes in the auditory cortex. We speculate that some of these differences may be due to task differences. Since neither previous studies nor ours systematically manipulated the behavioral task design, we could not establish how our conclusions would vary in different task conditions.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Patrick O. Kanold (pkanold@jhu.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
Imaging data have been deposited in the Digital Repository at the University of Maryland and are publicly available as of the date of publication. DOIs are listed in the key resources table.
All original code has been deposited at Zenodo and the Digital Repository at the University of Maryland and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| 2-photon dataset | This paper | https://doi.org/10.13016/m2yt-mfxk |
| Experimental models: Organisms/strains | ||
| Mouse: CBA/CaJ | The Jackson Laboratory | JAX: 000654 |
| Mouse: C57BL/6J-Tg(Thy1-GCaMP6s)GP4.3Dkim/J | The Jackson Laboratory | JAX: 024275 |
| Software and algorithms | ||
| MATLAB | MathWorks | https://www.mathworks.com |
| Granger Causality Analysis | This paper | https://doi.org/10.13016/ebv5-yzqy |
| Intersection Information Analysis | This paper | https://doi.org/10.5281/zenodo.850362 |
| Other | ||
| Bergamo II series multiphoton microscope | ThorLabs | Cat# B248; Serial# 1 |
| Pulsed femtosecond Ti:Sapphire 2-photon laser | Coherent | Vision S |
| CMOS camera | ThorLabs | Cat# DCC3240M |
| 470nm bandpass filter for blue wide-field LED | Chroma | Cat# ET470/40x |
| 495nm longpass filter for CMOS camera | Chroma | Cat# Q495lp |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
All procedures were approved by the University of Maryland Institutional Animal Care and Use Committee. We used n = 9 mice (3 female, 6 male) F1 offspring of CBA/CaJ strain (The Jackson Laboratory; stock #000654) crossed with transgenic C57BL/6J-Tg(thy1-GCaMP6s)GP4.3Dkim/J mice (Dana et al., 2014) (The Jackson Laboratory; stock #024275) (CBAxThyl), 8–24 weeks old, in 34 total experiments. We used the F1 generation of the crossed mice because they have good hearing into adulthood (Frisina et al., 2011). Each mouse was tested once per day over multiple days. The mice were trained to perform the task before collecting 2P data during task performance. Mice were housed under a reversed 12 h-light/12 h-dark light cycle and trained during the dark cycle.
METHOD DETAILS
Auditory task
We designed a pure-tone frequency discrimination task that used behavioral response-timing rules to induce well controlled behavioral responses in mice. Each mouse was first trained on a positive reinforcement tone detection task, with water used as a rewarding stimulus, as done previously (Francis et al., 2018b). We then trained the mice on the frequency discrimination task. Each trial began with 1 s of silence, followed by a 55 dB SPL amplitude modulated (8 Hz) tone presented for 1 s. The target tone frequencies were 7 and 9.9 kHz. The non-target frequencies were 14 and 19.8 kHz. The tone frequency was randomized across trials. The tone was followed by 2 s of silence, and a random 5–9 s inter-trial interval (ITI). The tone was presented during every trial of task-performance, and the mice were trained to lick a waterspout after the onset of a target tone and to avoid licking the waterspout after a non-target tone. Each trial’s behavioral response was categorized as a hit (licking after target onset), miss (no licking after a target), false alarm (licking after non-target onset), or correct rejection (no licking in response to a non-target). Incorrect behavioral responses were punished with an 8 s time-out added to the ITI. The mice were trained to delay behavioral responses until 0.5 s after the onset of a target tone in order to be rewarded with a water droplet. While licking has been shown to impact activity in auditory cortex (Nelson and Mooney, 2016), we have previously shown that licking in the absence of perceptual decision making does not drive neural activity in A1 L2/3 during a go/no-go task (Francis et al., 2018b). Here, our use of a behavioral delay was primarily for improving task performance, since behavioral delays in a go/no-go task design reduces impulsive licking. Mice were trained on the task until hit rates were consistently above 70%, and then imaged during behavior. Mouse health was monitored daily by a skin turgor test and checking that body weight remained above 80% of the initial off-study weight.
Imaging
Chronic window implantation, widefield imaging, and 2-photon (2P) imaging, were performed as previously (Francis et al., 2018b). In brief, a chronic imaging window was implanted over a 3 mm craniotomy over auditory cortex. For widefield imaging, neuronal activity was quantified by comparing fluorescence during the stimulus versus the silent pre-stimulus baseline, resulting in a response amplitude (ΔF/F). After visualizing wide-field tonotopic maps, a site was selected for 2P imaging in primary auditory cortex (A1) for each mouse. For each 2P imaging site, we determined the frequency selectivity (best frequency [BF]) of individual neurons during passive trials, i.e., trials when the mouse sat quiescently hearing tones without doing an auditory task. BFs were determined from neuronal responses to 55 dB SPL pure tones ranging f–om 4–56.6 kHz. We used a scanning microscope (Bergamo II series, B248, Thorlabs) coupled to a pulsed femtosecond Ti:Sapphire 2-photon laser with dispersion compensation (Vision S, Coherent). The microscope was controlled by ThorImageLS software. The laser was tuned to λ = 940 nm. The field of view was 370 × 370 μm. Imaging frames of 512 × 512 pixels (pixel size 0.72 μm) were acquired at 30 Hz by bidirectional scanning of an 8 KHz resonant scanner.
A different set of neurons was imaged for each experiment. Using an average field of view from each experiment, the somatic centers of putative neurons were manually localized and stored. A ring-like region of interest (ROI) was cropped around the cell center using the method described in Chen et al. (2013). Overlapping ROI pixels (due to closely juxtaposed neurons) were excluded from analysis. For each labeled neuron, a raw fluorescence signal over time was extracted from somatic ROIs. Pixels within the ROI were averaged to create individual neuron fluorescence traces, FC(t), for each trial of the experiment. Neuropil fluorescence was estimated for each cellular ROI using an additional ring-shaped ROI, which began 3 pixels from the somatic ROI. Pixels from the new ROI were averaged to obtain neuropil fluorescence traces, FN(t), for the same time-period as the individual neuron fluorescence traces. Pixels from regions with overlapping neuropil and cellular ROIs were removed from neuropil ROIs. Neuropil-corrected cellular fluorescence was calculated as . Only cells with positive values obtained from averaging across time were kept for analysis, since negative values may indicate the dominance of neuropil contamination. ΔF/F was calculated from , for each neuron, by finding the average F taken from the silent baseline period, subtracting that value from subsequent time-points, then dividing all time-points by the baseline F. All images were processed using MATLAB (The Mathworks) using our prior methods (Francis et al., 2018b).
Computation of stimulus and choice information
We first deconvolved the single-trial fluorescence traces into spike rates, obtained with a sliding window approach across the entire duration of a trial (Figure 2A). We inferred the relative spiking activity from the fluorescence traces with a first-order autoregressive model using the CaImAn algorithm (Giovannucci et al., 2019; Vogelstein et al., 2010) and binarized the deconvolved traces into 0, when there was no activity at all, and 1, if the spiking activity was above 0 (Figure 2A). To validate our deconvolution, we computed the averaged spiking activity time course of the whole population. In accordance with previous studies (Forli et al., 2018; Petrus et al., 2014), we found the firing rates in the pre-/peri-stimulus intervals were 4.4 ± 0.7 and 8.2 ± 1.6 Hz (mean ± s.d. across cells) respectively (Figure 2A). We computed mutual information carried by neurons at a given time either about stimulus category S (low vs high frequency tones), and about the behavioral choices C (lick vs. no-lick), defined as follows (Quian Quiroga and Panzeri, 2009; Cover and Thomas, 1991):
| (Equation 1) |
where X = S, C denotes the set of task variables, either stimuli S or choices C. Rt is the set of responses of the neuron measured at a given time t. p(x, rt) denotes the joint probability of observing in a given trial a value x for the stimulus or choice variable and a value rt for the activity of the neuron at time , and , are the marginal probabilities.
To compute the time dependent spike rates rt, we first inferred the relative spiking activity from the fluorescence traces with the CalmAn first-order autoregressive model (Giovannucci et al., 2019; Vogelstein et al., 2010). We then averaged the spiking activities with a sliding window of 10 imaging frames, in time-steps of 1 imaging frame, and the resulting activity was binarized as 0/1 (occurrence or not of at least 1 spike in each window). We then computed information in these spike rates from Equation (1) with the Information Breakdown Toolbox (Magri et al., 2009). We then subtracted for each neuron the average information computed in the pre-stimulus interval. This procedure insures the removal of the limited sampling bias, as well as the removal of possible contributions of pre-stimulus choice signals (Niwa et al., 2013) reflecting e.g. stimulus-unrelated internal bias.
Computation of intersection information
We computed intersection information II(S,R,C), following exactly the procedure published in (Pica et al., 2017), to which we refer for full details. II(S, R, C) builds on the mathematical and numerical techniques of Partial Information Decomposition (Bertschinger et al., 2014; Makkeh et al., 2018; Williams and Beer, 2010), and it quantifies the part of sensory information that is is used to inform behavioral readout and is bounded by both I(S;R) and choice I(S;C) (Pica et al., 2017). As for stimulus and choice information, we subtracted the average intersection information evaluated in the pre-stimulus interval to remove limited sampling biases.
Computation of information significance
To select individual neurons with significant information of each type, we used a non-parametric permutation test (creating a null hypothesis distribution of information values obtained randomly shuffling across trials the stimulus-response or choice-response associations), and we set a threshold of p < 0.1. Note that we constructed the null hypothesis distribution selecting for each random permutation the maximum information over all time windows of the permuted values. The so obtained p values are already corrected for multiple comparisons across time bins. Because having significant II also requires having significant CI and SI, when selecting neurons with significant II we required that those neurons have also significant SI, CI and II at p < 0.1. Given that these three tests are not independent, we could not evaluate the expected number of falsely labeled II neurons simply by taking the product of the three p value thresholds. To empirically estimate the rate of falsely labeled II neurons, we repeated our selection procedure using surrogate data in which for each neuron we randomly permuted the trials at the outset. The fraction of surrogate neurons that exhibit significance at p < 0.1 simultaneously for CI, SI and II provides an empirical estimate of the false positive rate in our selection procedure. We found that only 1% (31 out of 2,792 neurons) of the surrogate neurons were classified as significant. Thus, our set of II-selected neurons contains 1% of falsely labeled II neurons, which corresponds effectively to a p < 0.01 selection p value.
We further checked how our results generalize when requiring at same time significant SI, CI and II with a more stringent threshold at p < 0.05. In this case, we could only select 7 (rather than 12) experimental sessions with at least 20 II neurons for GC analysis. We repeated our analysis for II neurons chosen with threshold p < 0.05 (See Figures S3E-S3F and Table S5), finding the same qualitative trends of Figure 4 but with fewer significant differences due to fewer number of sessions (n = 7 in Figures S3E-S3F vs. n = 12 in Figure 3). Notably, we were able to decode correct vs. incorrect choice more accurately (Figure S3F) with this even more stringent threshold.
Granger Causality Analysis
Granger causality (GC) analysis evaluates the predictive influence of the past activity of one neural process on present activity of another. GC analysis was performed similarly as in our previous work (Francis et al., 2018b) by fitting sparse vector autoregressive (VAR) models to the ensemble neural responses (ΔF/F), calculating an unbiased GC measure for each potential link, and characterizing the GC link strengths using Youden’s J-statistics following false discovery rate control at a rate of 0.001. We highlight here three key differences from previous analysis regarding model estimation, modeling history-dependency, and neuron selection, and refer the reader to (Francis et al., 2018b) for a recapitulation of the remaining details.
In order to estimate GC network connectivity amongst larger networks, the maximum likelihood problem in (Francis et al., 2018b) is solved, employing the Orthogonal Matching Pursuit (OMP) algorithm (Zhang, 2011; Cai and Wang, 2011) to fit sparse VAR models rather than ℓ1-regularisation. OMP enables the sparsity of the estimated parameter vector—i.e. the number of non-zero parameters—to be controlled, thus mitigating model overfitting more robustly. The sparsity level of each VAR model is obtained by cross-validation. The set of non-zero parameters, called the model support set, is iteratively selected: at each iteration, a new parameter with the greatest contribution to the residual estimation error is added to the support and maximum likelihood estimation is performed over the updated support set.
The neural responses of a set of C neurons, indexed by c = 1,…,C, are denoted by , where tt = 1,…,T and r = 1,…,R index time bins and trial repetitions, respectively. The covariates of the VAR model of each neural response incorporate the self- and cross-histories of activity over an integration window of L samples within which neuronal interactions are assumed to occur. The integration window is subdivided into M non-overlapping windows of lengths {Wm}m = 1:M. The average activity of neuron (c) in the m-th window lag with respect to time bin t and trial r is given by
| (Equation 2) |
where and b0 = 0. The collection of history covariates comprises the regressors of . Note that the conditional independence of responses given the collection of history covariates allows to estimate the VAR parameters at the single-trial level by maximizing the joint likelihood of the within-trial responses via OMP (Francis et al., 2018b).
Interactions between neurons over short timescales (S) are modeled with an integration window of L = 7 lags with M = 3 subdivisions with window lengths {Wm}m = 1:M = {2m–1}m = 1:M lags. Long timescale (L) interactions are modeled by instead using a cross-history integration window of length L = 31 lags with M = 5 subdivisions whose window lengths are similarly defined. S and L timescale interactions thus respectively correspond to 233 ms and 1033 ms windows of effective history. It is clear from the parameterization that the S and L interactions are modeled in a nested fashion. We validate this approach by simulating a 10 neuron network consisting of both S- and L-timescale links (see Figure S6). Employing the L integration window for GC analysis, we are able to correctly identify all L- and S-timescale interactions; however, using the S integration window, while the S-timescale links are correctly identified, the L-timescale links are expectedly discarded, thus corroborating the sensitivity and specificity of our proposed inference framework.
Twenty neurons were analyzed from each 2P experiment. Analyzing a subset of fixed size avoids intersession variations in the number of recorded neurons that could affect analyses. The total number of model parameters, M•C, needs to be much smaller than the total number of samples, R•T, for reliable model estimation. We use at most M = 5 subintervals and per trial used the T = 105 time samples of the response after stimulus onset; we calculated C = 20 to be the maximum number of neurons that satisfies this condition, conservatively assuming at minimum R = 10 trials per session of each behavioral choice category. In our main results, 20 II neurons with the lowest II-peak latency in each experiment (n = 12) in which at least as many II neurons were identified. For consistency, 20 exclusively CI neurons were similarly selected in the analyses presented in Figures S3A-S3B. Highly active neurons in each 2P experiment (n = 34) were selected per behavioral choice category. The neural response of the cth neuron at the tth time index of the rth repeated trial of a behavioral category, , is normalized . The 20 neurons with the smallest trial-averaged variances of the normalized responses, , were selected.
Decoding behavioral choice from network structure
To test if network structures encode behavioral choice, we trained classifiers on four GC network statistics — number of links, number of subnetworks, size of subnetworks, and statistical strength of links — to distinguish correct (Hit or Correct Rejection) and incorrect (Miss or False Alarm) decisions. Feature vectors consisting of these statistics were compiled for each behavioral choice network from the VAR parameters estimated at the single-trial level. We then trained a linear support vector machine (SVM) at the single-trial level to predict behavioral choice using a randomly selected 75% of the feature vectors, with the remaining 25% used to evaluate prediction accuracy. This procedure was repeated 2000 times, each with a new randomized partition of feature vectors, to characterize the distribution of average classification accuracy.
Spatial distribution of GC subnetworks
To investigate the spatial scales over which functionally linked neurons interact, we leveraged the spatial location of individual neurons available in 2P imaging to analyze how subnetworks were distributed across the imaged cortical area. To this end, the locations of subnetworked neurons relative to their centroid were obtained as follows. For a subnetwork of R neurons with positions , we compute their locations relative to the subnetwork centroid, , where , and . The relative locations are compiled over all subnetworks to yield an empirical distribution. The covariance matrix of the distribution describes the spatial spread of subnetworks. Its determinant – which accounts for both the covariance between x and y as well as their respective variances – is used as a comparative statistic to quantify differences in the spatial dispersion of subnetworks across conditions.
Computation of information redundancy
We used a normalized redundancy index defined as the information carried jointly by two neurons minus the sum of the information that each carried independently, normalized with respect to the total information carried by the two neurons jointly (Pola et al., 2003; Schneidman et al., 2003):
| (Equation 3) |
For each of the two neurons, we selected activity at the time t1,t2 of their peak information. The single neuron information was computed as in section “Definition of stimulus, choice and intersection information for single neurons”. The joint time-lagged stimulus and choice information was computed as follows:
| (Equation 4) |
Notations are as in Equation (1), with now p(X, r1,t1, r2,t2) denoting the probability of observing in a given trial a value x of the behavioral variable (stimulus category or choice) and a joint response r1,t1 , r2,t2 of the two neurons at times t1,t2 respectively. Intersection information was computed with the methods detailed in (Pica et al., 2017), using the joint response r1,t1, r2,t2 as the neural response variable.
Computation of signal and noise correlations
We computed noise correlations as across-trials Pearson correlations of the activity of pairs of neurons at fixed stimulus (then averaged over stimuli), whereas signal correlations were computed as Pearson correlations across stimuli of the trial-averaged responses to each of the two stimuli (high vs low frequency tones). Given the imbalance in the number of correct and incorrect trials, we equalized the sample sizes by randomly subsampling the correct trials, to avoid systematic errors in the comparisons between correct and incorrect trials (see Figure 6D).
QUANTIFICATION AND STATISTICAL ANALYSIS
Unless noted otherwise, statistical comparisons were performed using a bootstrap t test with 10,000 iterations or a Kolmogorov–Smirnov test (KS-test), for both one- and paired-sample tests. Kruskal-Wallis tests were used when there were >2 groups being compared. We used a Bonferroni correction for multiple comparisons. All mean values are reported with 2 standard errors of the mean, unless noted differently.
Supplementary Material
Highlights.
Aberrant attentional gain in auditory cortex reflects incorrect decision making
Task-relevant information is transiently encoded by individual neurons
Neuronal network structures with task-relevant information encode behavioral choice
Networked neurons communicate task-relevant information redundantly
ACKNOWLEDGMENTS
The authors thank Menatallah Mohamed for surgical assistance and Marco Celotto for providing software. Supported by NIH RO1DC9607 (to P.O.K.), U01NS90569 (to P.O.K.), P01AG55365 (to P.O.K.), U19NS107474 (to P.O.K., B.B., and S.P.), R01DC17785 (to P.O.K.), R21DC017829 (to N.A.F.), NSF ECCS1807216 and ECCS2032649 (to B.B.).
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2022.110878.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Alonso J-M, Usrey WM, and Reid RC (1996). Precisely correlated firing in cells of the lateral geniculate nucleus. Nature 383, 815–819. 10.1038/383815a0. [DOI] [PubMed] [Google Scholar]
- Atencio CA, and Schreiner CE (2010). Columnar connectivity and laminar processing in cat primary auditory cortex. PLoS One 5, e9521. 10.1371/journal.pone.0009521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attneave F (1954). Some informational aspects ofvisual perception. Psychol. Rev 61, 183–193. 10.1037/h0054663. [DOI] [PubMed] [Google Scholar]
- Atzori M, Lei S, Evans DIP, Kanold PO, Phillips-Tansey E, Mcintyre O, and Mcbain CJ (2001). Differential synaptic processing separates stationary from transient inputs to the auditory cortex. Nat. Neurosci 4, 1230–1237. 10.1038/nn760. [DOI] [PubMed] [Google Scholar]
- Bagur S, Averseng M, Elgueda D, David S, Fritz J, Yin P, Shamma S, Boubenec Y, and Ostojic S (2018). Go/No-Go task engagement enhances population representation of target stimuli in primary auditory cortex. Nat. Commun 3, 2529. 10.1038/s41467-018-04839-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandyopadhyay S, Shamma SA, and Kanold PO (2010). Dichotomy of functional organization in the mouse auditory cortex. Nat. Neurosci 13, 361–368. 10.1038/nn.2490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow HB (1961). Possible principles underlying the transformations of sensory messages. Sens. Commun, 217–234. [Google Scholar]
- Bertschinger N, Rauh J, Olbrich E, Jost J, and Ay N (2014). Quantifying unique information. Entropy 16, 2161–2183. 10.3390/e16042161. [DOI] [Google Scholar]
- Bressler SL, and Seth AK (2011). Wiener-Granger causality: a well established methodology. Neuroimage 58, 323–329. 10.1016/j.neuroimage.2010.02.059. [DOI] [PubMed] [Google Scholar]
- Brosch M, Selezneva E, and Scheich H (2011). Representation of reward feedback in primate auditory cortex. Front. Syst. Neurosci 5, 5. 10.3389/fnsys.2011.00005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai TT, and Wang L (2011). Orthogonal matching Pursuit for sparse signal recovery with noise. IEEE Trans. Inf. Theor 57, 4680–4688. 10.1109/tit.2011.2146090. [DOI] [Google Scholar]
- Carcea I, Insanally MN, and Froemke RC (2017). Dynamics of auditory cortical activity during behavioural engagement and auditory perception. Nat. Commun 8, 14412. 10.1038/ncomms14412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chechik G, Anderson MJ, Bar-Yosef O, Young ED, Tishby N, and Nelken I (2006). Reduction of information redundancy in the ascending auditory pathway. Neuron 51, 359–368. 10.1016/j.neuron.2006.06.030. [DOI] [PubMed] [Google Scholar]
- Chen IW, Helmchen F, and Lutcke H (2015). Specific early and late oddball-evoked responses in excitatory and inhibitory neurons of mouse auditory cortex. J. Neurosci 35, 12560–12573. 10.1523/jneurosci.2240-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen TW, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chicharro D, Panzeri S, and Haefner RM (2021). Stimulus-dependent relationships between behavioral choice and sensory neural responses. Elife 10, e54858. 10.7554/elife.54858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christison-Lagay KL, and Cohen YE (2018). The contribution of primary auditory cortex to auditory categorization in behaving monkeys. Front. Neurosci 12, 601. 10.3389/fnins.2018.00601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover TM, and Thomas JA (1991). Elements of Information Theory (Wiley; ). [Google Scholar]
- Dana H, Chen TW, Hu A, Shields BC, Guo C, Looger LL, Kim DS, and Svoboda K (2014). Thy1-GCaMP6 transgenic mice for neuronal population imaging in vivo. PLoS One 9, e108697. 10.1371/journal.pone.0108697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David SV, Fritz JB, and Shamma SA (2012). Task reward structure shapes rapid receptive field plasticity in auditory cortex. Proc. Natl. Acad. Sci. U S A 109, 2144–2149. 10.1073/pnas.1117717109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forli A, Vecchia D, Binini N, Succol F, Bovetti S, Moretti C, Nespoli F, Mahn M, Baker CA, Bolton MM, et al. (2018). Two-photon bidirectional control and imaging of neuronal excitability with high spatial resolution in vivo. Cell Rep. 22, 3087–3098. 10.1016/j.celrep.2018.02.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis NA, Elgueda D, Englitz B, Fritz JB, and Shamma SA (2018a). Laminar profile of task-related plasticity in ferret primary auditory cortex. Sci. Rep 8, 16375. 10.1038/s41598-018-34739-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis NA, Winkowski DE, Sheikhattar A, Armengol K, Babadi B, and Kanold PO (2018b). Small networks encode decision-making in primary auditory cortex. Neuron 97, 885–897.e6. 10.1016/j.neuron.2018.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisina RD, Singh A, Bak M, Bozorg S, Seth R, and Zhu X (2011). F1 (CBAxC57) mice show superior hearing in old age relative to their parental strains: hybrid vigor or a new animal model for "golden ears"? Neurobiol. Aging 32, 1716–1724. 10.1016/j.neurobiolaging.2009.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz JB, David SV, Radtke-Schuller S, Yin P, and Shamma SA (2010). Adaptive, behaviorally gated, persistent encoding of task-relevant auditory information in ferret frontal cortex. Nat. Neurosci 13, 1011–1019. 10.1038/nn.2598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz J, Shamma S, Elhilali M, and Klein D (2003). Rapid task-related plasticity of spectrotemporal receptive fields in primary auditory cortex. Nat. Neurosci 6, 1216–1223. 10.1038/nn1141. [DOI] [PubMed] [Google Scholar]
- Giovannucci A, Friedrich J, Gunn P, Kalfon J, Brown BL, Koay SA, Taxidis J, Najafi F, Gauthier JL, Zhou P, et al. (2019). CalmAn an open source tool for scalable calcium imaging data analysis. Elife 8, e38173. 10.7554/elife.38173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold J.l., and Shadlen MN (2001). Neural computations that underlie decisions about sensory stimuli. Trends Cogn. Sci 5, 10–16. 10.1016/s1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
- Guo L, Weems JT, Walker WI, Levichev A, and Jaramillo S (2019). Choice-selective neurons in the auditory cortex and in its striatal target encode reward expectation. J. Neurosci 39, 3687–3697. 10.1523/jneurosci.2585-18.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Insanally MN, Carcea I, Field RE, Rodgers CC, Depasquale B, Rajan K, Deweese MR, Albanna BF, and Froemke RC (2019). Spike-timing-dependent ensemble encoding by non-classically responsive cortical neurons. Elife 8, e42409. 10.7554/elife.42409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaminski M, Ding M, Truccolo WA, and Bressler SL (2001). Evaluating causal relations in neural systems: granger causality, directed transfer function and statistical assessment of significance. Biol. Cybern 85, 145–157. 10.1007/s004220000235. [DOI] [PubMed] [Google Scholar]
- Kanold PO, Nelken I, and Polley DB (2014). Local versus global scales of organization in auditory cortex. Trends Neurosci. 37, 502–510. 10.1016/j.tins.2014.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato HK, Gillet SN, and Isaacson JS (2015). Flexible sensory representations in auditory cortex driven by behavioral relevance. Neuron 88, 1027–1039. 10.1016/j.neuron.2015.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khouri L, and Nelken I (2015). Detecting the unexpected. Curr. Opin. Neurobiol 35, 142–147. 10.1016/j.conb.2015.08.003. [DOI] [PubMed] [Google Scholar]
- Kim S, Putrino D, Ghosh S, and Brown EN (2011). A Granger causality measure for point process models of ensemble neural spiking activity. Plos Comput. Biol 7, e1001110. 10.1371/journal.pcbi.1001110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuchibhotla KV, Gill JV, Lindsay GW, Papadoyannis ES, Field RE, Sten TAH, Miller KD, and Froemke RC (2017). Parallel processing by cortical inhibition enables context-dependent behavior. Nat. Neurosci 20, 62–71. 10.1038/nn.4436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, and Kanold PO (2021). Diversity of receptive fields and sideband inhibition with complex thalamocortical and intracortical origin in L2/3 of mouse primary auditory cortex. J. Neurosci 41, 3142–3162. 10.1523/jneurosci.1732-20.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Whiteway MR, Sheikhattar A, Butts DA, Babadi B, and Kanold PO (2019). Parallel processing of sound dynamics across mouse auditory cortex via spatially patterned thalamic inputs and distinct areal intracortical circuits. Cell Rep. 27, 872–885.e7. 10.1016/j.celrep.2019.03.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Xin Y, and Xu NL (2021). A cortical circuit mechanism for structural knowledge-based flexible sensorimotor decision-making. Neuron 109, 2009–2024.e6. 10.1016/j.neuron.2021.04.014. [DOI] [PubMed] [Google Scholar]
- Magri C, Whittingstall K, Singh V, Logothetis NK, and Panzeri S (2009). A toolbox for the fast information analysis of multiple-site LFP, EEG and spike train recordings. BMC Neurosci. 10, 81. 10.1186/1471-2202-10-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makkeh A, Theis D, and Vicente R (2018). BROJA-2PID: a robust estimator for bivariate partial information decomposition. Entropy 20, 271. 10.3390/e20040271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maor I, Shalev A, and Mizrahi A (2016). Distinct spatiotemporal response properties of excitatory versus inhibitory neurons in the mouse auditory cortex. Cereb. Cortex 26, 4242–4252. 10.1093/cercor/bhw266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mcginley MJ, David SV, and Mccormick DA (2015). Cortical membrane potential signature of optimal states for sensory signal detection. Neuron 87, 179–192. 10.1016/j.neuron.2015.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng X, Winkowski DE, Kao JPY, and Kanold PO (2017). Sublaminar subdivision of mouse auditory cortex layer 2/3 based on functional translaminar connections. J. Neurosci 37, 10200–10214. 10.1523/jneur-osci.1361-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson A, and Mooney R (2016). The basal forebrain and motor cortex provide convergent yet distinct movement-related inputs to the auditory cortex. Neuron 90, 635–648. 10.1016/j.neuron.2016.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nigam S, Pojoga S, and Dragoi V (2019). Synergistic coding of visual information in columnar networks. Neuron 104, 402–411.e4. 10.1016/j.neuron.2019.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nirenberg S, Carcieri SM, Jacobs AL, and Latham PE (2001). Retinal ganglion cells act largely as independent encoders. Nature 411, 698–701. 10.1038/35079612. [DOI] [PubMed] [Google Scholar]
- Niwa M, Johnson JS, O’connor KN, and Sutter ML (2013). Differences between primary auditory cortex and auditory belt related to encoding and choice for AM sounds. J. Neurosci 33, 8378–8395. 10.1523/jneurosci.2672-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oviedo HV, Bureau I, Svoboda K, and Zador AM (2010). The functional asymmetry of auditory cortex is reflected in the organization of local cortical circuits. Nat. Neurosci 13, 1413–1420. 10.1038/nn.2659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panzeri S, Harvey CD, Piasini E, Latham PE, and Fellin T (2017). Cracking the neural code for sensory perception by combining statistics, intervention, and behavior. Neuron 93, 491–507. 10.1016/j.neuron.2016.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parras GG, Casado-Roman L, Schroger E, and Malmierca MS (2021). The posterior auditory field is the chief generator of prediction error signals in the auditory cortex. Neuroimage 242, 118446. 10.1016/j.neuroimage.2021.118446. [DOI] [PubMed] [Google Scholar]
- Petrus E, Isaiah A, Jones A, Li D, Wang H, Lee H, and Kanold P (2014). Crossmodal induction of thalamocortical potentiation leads to enhanced information processing in the auditory cortex. Neuron 81, 664–673. 10.1016/j.neuron.2013.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pi HJ, Hangya B, Kvitsiani D, Sanders JI, Huang ZJ, and Kepecs A (2013). Cortical interneurons that specialize in disinhibitory control. Nature 503, 521–524. 10.1038/nature12676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pica G, Piasini E, Safaai H, Runyan C, Diamond M, Fellin T, Kayser C, Harvey C, and Panzeri S (2017). Quantifying how much sensory information in a neural code is relevant for behavior. Adv. Neural Inf. Process. Syst 30, 3686–3696. [Google Scholar]
- Pola G, Thiele A, Hoffmann KP, and Panzeri S (2003). An exact method to quantify the information transmitted by different mechanisms of correlational coding. Network 14, 35–60. 10.1088/0954-898x/14/1/303. [DOI] [PubMed] [Google Scholar]
- Quian Quiroga R, and Panzeri S (2009). Extracting information from neuronal populations: information theory and decoding approaches. Nat. Rev. Neurosci 10, 173–185. 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- Quinn CJ, Kiyavash N, and Coleman TP (2015). Directed information graphs. IEEE Trans. Inf. Theor 61, 6887–6909. 10.1109/tit.2015.2478440. [DOI] [Google Scholar]
- Reich DS, Mechler F, and Victor JD (2001). Independent and redundant information in nearby cortical neurons. Science 294, 2566–2568. 10.1126/science.1065839. [DOI] [PubMed] [Google Scholar]
- Rodgers CC, and Deweese MR (2014). Neural correlates of task switching in prefrontal cortex and primary auditory cortex in a novel stimulus selection task for rodents. Neuron 82, 1157–1170. 10.1016/j.neuron.2014.04.031. [DOI] [PubMed] [Google Scholar]
- Rothschild G, Nelken I, and Mizrahi A (2010). Functional organization and population dynamics in the mouse primary auditory cortex. Nat. Neurosci 13, 353–360. 10.1038/nn.2484. [DOI] [PubMed] [Google Scholar]
- Runyan CA, Piasini E, Panzeri S, and Harvey CD (2017). Distinct timescales of population coding across cortex. Nature 548, 92–96. 10.1038/nature23020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadagopan S, and Wang X (2009). Nonlinear spectrotemporal interactions underlying selectivity for complex sounds in auditory cortex. J. Neurosci 29, 11192–11202. 10.1523/jneurosci.1286-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakata S, and Harris KD (2009). Laminar structure of spontaneous and sensory-evoked population activity in auditory cortex. Neuron 64, 404–418. 10.1016/j.neuron.2009.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E, and Sejnowski TJ (2001). Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci 2, 539–550. 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneidman E, Bialek W, and Berry MJ (2003). Synergy, redundancy, and independence in population codes. J. Neurosci 23, 11539–11553. 10.1523/jneurosci.23-37-11539.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz ZP, and David SV (2018). Focal suppression of distractor sounds by selective attention in auditory cortex. Cereb. Cortex 28, 323–339. 10.1093/cercor/bhx288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seth AK, Barrett AB, and Barnett L (2015). Granger causality analysis in neuroscience and neuroimaging. J. Neurosci 35, 3293–3297. 10.1523/jneurosci.4399-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon CE (1948). A mathematical theory of communication. Bell Syst. Tech. J 27, 379–423. 10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- Sheikhattar A, Miran S, Liu J, Fritz JB, Shamma SA, Kanold PO, and Babadi B (2018). Extracting neuronal functional network dynamics via adaptive Granger causality analysis. Proc. Natl. Acad. Sci. U S A 115, E3869–E3878. 10.1073/pnas.1718154115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz NA, Zatka-Haas P, Carandini M, and Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273. 10.1038/s41586-019-1787-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255. 10.1126/science.aav7893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsunada J, Liu ASK, Gold JI, and Cohen YE (2016). Erratum: causal contribution of primate auditory cortex to auditory perceptual decision-making. Nat. Neurosci 19, 642. 10.1038/nn0416-642b. [DOI] [PubMed] [Google Scholar]
- Valente M, Pica G, Bondanelli G, Moroni M, Runyan CA, Morcos AS, Harvey CD, and Panzeri S (2021). Correlations enhance the behavioral readout of neural population activity in association cortex. Nat. Neurosci 24, 975–986. 10.1038/s41593-021-00845-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogelstein JT, Packer AM, Machado TA, Sippy T, Babadi B, Yuste R, and Paninski L (2010). Fast nonnegative deconvolution for spike train inference from population calcium imaging. J. Neurophysiol 104, 3691–3704. 10.1152/jn.01073.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams PL, and Beer RD (2010). Nonnegative decomposition of multivariate information. preprint at arXiv, arXiv:1004.2515 10.48550/arXiv.1004.2515. [DOI] [Google Scholar]
- Winkowski DE, and Kanold PO (2013). Laminar transformation of frequency organization in auditory cortex. J. Neurosci 33, 1498–1508. 10.1523/jneurosci.3101-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkowski DE, Bandyopadhyay S, Shamma SA, and Kanold PO (2013). Frontal cortex activation causes rapid plasticity of auditory cortical processing. J. Neurosci 33, 18134–18148. 10.1523/jneurosci.0180-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkowski DE, Nagode DA, Donaldson KJ, Yin P, Shamma SA, Fritz JB, and Kanold PO (2018). Orbitofrontal cortex neurons respond to sound and activate primary auditory cortex neurons. Cereb. Cortex 28, 868–879. 10.1093/cercor/bhw409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Deweese MR, Otazu GH, and Zador AM (2008). Millisecond-scale differences in neural activity in auditory cortex can drive decisions. Nat. Neurosci 11, 1262–1263. 10.1038/npre.2008.2280.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin P, Strait DL, Radtke-Schuller S, Fritz JB, and Shamma SA (2020). Dynamics and hierarchical encoding of non-compact acoustic categories in auditory and frontal cortex. Curr. Biol 30, 1649–1663.e5. 10.1016/j.cub.2020.02.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang T (2011). Sparse recovery with orthogonal matching Pursuit under RIP. IEEE Trans. Inf. Theor 57, 6215–6221. 10.1109/tit.2011.2162263. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Imaging data have been deposited in the Digital Repository at the University of Maryland and are publicly available as of the date of publication. DOIs are listed in the key resources table.
All original code has been deposited at Zenodo and the Digital Repository at the University of Maryland and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| 2-photon dataset | This paper | https://doi.org/10.13016/m2yt-mfxk |
| Experimental models: Organisms/strains | ||
| Mouse: CBA/CaJ | The Jackson Laboratory | JAX: 000654 |
| Mouse: C57BL/6J-Tg(Thy1-GCaMP6s)GP4.3Dkim/J | The Jackson Laboratory | JAX: 024275 |
| Software and algorithms | ||
| MATLAB | MathWorks | https://www.mathworks.com |
| Granger Causality Analysis | This paper | https://doi.org/10.13016/ebv5-yzqy |
| Intersection Information Analysis | This paper | https://doi.org/10.5281/zenodo.850362 |
| Other | ||
| Bergamo II series multiphoton microscope | ThorLabs | Cat# B248; Serial# 1 |
| Pulsed femtosecond Ti:Sapphire 2-photon laser | Coherent | Vision S |
| CMOS camera | ThorLabs | Cat# DCC3240M |
| 470nm bandpass filter for blue wide-field LED | Chroma | Cat# ET470/40x |
| 495nm longpass filter for CMOS camera | Chroma | Cat# Q495lp |