Winning and losing in online gambling: Effects on within-session chasing

Zhang Chen; Roos Arwen Doekemeijer; Xavier Noël; Frederick Verbruggen

doi:10.1371/journal.pone.0273359

. 2022 Aug 18;17(8):e0273359. doi: 10.1371/journal.pone.0273359

Winning and losing in online gambling: Effects on within-session chasing

Zhang Chen ^1,^*, Roos Arwen Doekemeijer ¹, Xavier Noël ², Frederick Verbruggen ¹

Editor: Gaëtan Merlhiot³

PMCID: PMC9387854 PMID: 35981088

Abstract

The tendency to continue or intensify gambling after losing (loss-chasing) is widely regarded as a defining feature of gambling disorder. However, loss-chasing in real gambling contexts is multifaceted, and some aspects are better understood than others. Gamblers may chase losses between multiple sessions or within a single session. Furthermore, within a session, loss-chasing can be expressed in the decision of (1) when to stop, (2) how much stake to bet, and (3) the speed of play after winning and losing. Using a large player-tracking data set (>2500 players, >10 million rounds) collected from the online commercial game Mystery Arena, we examined these three behavioral expressions of within-session loss-chasing. While the first two aspects (when to stop and how much stake to bet) have been examined previously, the current research is the first large-scale study to examine the effects of wins and losses on the speed of play in real gambling. The players were additionally assigned different involvement levels by the operator based on their gambling behavior on the operator’s own platform, which further allowed us to examine group differences in loss-chasing. We found that after winning, both the high- and low-involvement groups were less likely to stop, and increased the stake amount, thus showing win-chasing instead of loss-chasing in these two facets. After losing, both groups played more quickly though, which may reflect an urge to continue gambling (as an expression of loss-chasing). Wins and losses had a smaller influence on the speed of play for the high-involvement players, suggesting that they might have reduced sensitivity to wins and/or losses. Future work can further examine chasing in different gambling products and in people with gambling problems to assess the generalizability of these findings.

Introduction

Gambling is a popular activity worldwide. While most people gamble within their means, for a small yet significant proportion of the population, it may spiral out of control and develop into problem gambling [1, 2] (the past-year problem gambling rates vary between 0.1% and 5.8% worldwide [3]). Excessive gambling can lead to adverse consequences for the people with gambling problems, those around them, and the society at large [4].

One important behavioral phenomenon that is generally considered to mark the transition from non-problem to problem gambling is chasing [5]. ‘Chasing’, or more commonly loss-chasing, describes a gambler’s tendency to continue or intensify gambling to recoup previous losses. Loss-chasing is widely regarded as a defining feature of gambling disorder [6, 7]. Further understanding of whether and how gamblers chase losses (across the whole spectrum of gambling involvement) will therefore provide important insights into the development of gambling problems. Such knowledge will also be crucial in developing tools that can effectively detect and reduce problem gambling.

Loss-chasing can be expressed in multiple aspects of gambling behavior. Players may chase losses between sessions, such as returning another time to recover previous losses, or within sessions, by continuing or intensifying gambling after losses within a session [8]. In this paper, we focus on within-session loss-chasing in an online commercial gambling product (with behavioral tracking data from >2500 players and >10 million rounds). We examined three purported behavioral expressions of within-session chasing, namely (1) when players decided to end a session, (2) how much stake they placed in each round, and (3) how quickly they played. Most previous studies on chasing have focused on the first two aspects, while the speed of play as a potential expression of chasing has received less attention (certainly in real gambling games). The current research is the first large-scale study to examine the effects of wins and losses on the speed of play in real gambling. Below we introduce the three facets of within-session loss-chasing in turn.

Three expressions of within-session loss-chasing

Gamblers may chase losses by continuing a gambling session after a loss. To test how wins and losses influence the decision of when to stop, Leino and colleagues examined when players ended a session when playing real electronic gaming machines (EGMs) [9]. They found that EGM players were more likely to end a session after losing than after winning, thus showing no loss-chasing in this facet. One explanation may be that the EGM players in Leino et al.’s study were mostly people without gambling problems, who were able to stop after losing to avoid further losses. Interestingly though, some work has shown that people with gambling problems also did not show loss-chasing in this aspect. For instance, three studies found that participants with greater problem gambling severity were more likely to play beyond a required number of rounds, and played more rounds in total in simulated gambling, compared to those without gambling problems [10–12]. Intriguingly, in all three studies, the nominal win or loss in the preceding 30 rounds did not influence participants’ decision of when to stop. In other words, people with gambling problems played longer sessions in general, but the decision of when to end a session was not influenced by wins or losses per se.

People may also chase losses by placing a higher stake, sometimes beyond the amount they initially intended to spend [8, 13]. While some previous work has indeed found increased stakes after a loss [14–16], others have observed the opposite [17, 18]. Whether people bet larger or smaller amounts after losing may depend on many factors, such as whether the gamble provides the opportunity to offset prior losses (i.e., the break-even effect [17]), the presentation format of the gamble [19], and whether the losses are realized or not [20]. The last finding, namely the realization effect, may be especially relevant here. Imas [20] showed in a lab-based study that when losses were realized, such as when money was transferred between accounts after losing, people took less ‘risk’ by making a smaller bet after a loss; in contrast, when losses were unrealized, such as when the loss was not converted into real money yet, people took more ‘risk’ by making a larger bet after losing. In real online gambling, whether players will place a higher or a lower stake after losing may depend on whether they perceive the loss to be ‘realized’ or not. On the one hand, the loss may be seen as ‘realized’, as money is taken away from players’ accounts. On the other hand, the loss may still be ‘unrealized’, because the money on the gambling platform may be perceived as game token (i.e., play money) rather than real money. We will therefore examine this facet in the current study.

Most previous research has focused on the decision of when to stop or how much money to bet as expressions of chasing. Here we argue that the speed of play might also be a crucial aspect of chasing. Previous work has shown that in simulated gambling or gambling-like tasks in the laboratory, participants initiated a new game more quickly after a loss than after a win [21–24] and a non-gamble trial [25, 26]. The faster initiation of a new gamble after a loss (the so-called post-loss speeding effect [25]) may reflect a stronger urge to continue playing after losing, and can therefore be seen as an expression of loss-chasing [13]. Speeding up after losing may lead to a vicious circle between continued gambling and losing, as games of faster speed of play are generally experienced as more exciting and harder to stop, especially for people with gambling problems [27–29]. It is therefore important to examine how wins and losses may influence the speed of play in real (online) gambling.

The current research

With regards to the three behavioral expressions of within-session loss-chasing discussed above, people seemed to chase losses in the speed of play, but not in the decision of when to end a session. In terms of how much money to bet, inconsistent findings have been reported. However, it is important to note that loss-chasing is a multifaceted and highly dynamic construct. The behavioral expressions of loss-chasing may vary across different gambling contexts (e.g., simulated gambling in the lab vs. real gambling), different types of gambling games (e.g., casino games vs. poker games [30]), and different subgroups of gamblers (e.g., people with different levels of gambling involvement). Much previous work on loss-chasing is conducted in laboratory contexts. While such studies have provided valuable insights into loss-chasing, it is also important to systematically characterize whether and how gamblers may chase losses in real gambling contexts.

In the current research, we examined how wins and losses might influence the three expressions of within-session chasing in an online commercial gambling product Mystery Arena, with a large behavioral tracking data set. Given the multifaceted and dynamic nature of loss-chasing and some inconsistent findings in the literature, a priori we did not have strong predictions for whether loss-chasing would occur in each facet or not. This study was therefore exploratory in nature, and mainly aimed at characterizing loss-chasing (i.e., its presence or absence in each facet) in real online gambling. Note though that we selected a gambling product that seemed most suitable for examining the speed of play, as this aspect of gambling behavior is often ignored.

The large number of players additionally allowed us to explore how loss-chasing may vary as a function of gambling involvement. People differ in how involved they are in gambling, with those with gambling problems constituting a subgroup that has a very high level of involvement. Examining loss-chasing across the whole spectrum will provide insights into the role of loss-chasing in the progression of gambling involvement. The gambling operator gathered data on each player’s gambling involvement on their platform (across all games), based on the players’ money and time expenditure. We therefore used this data to examine how the three expressions of loss-chasing may differ between gamblers with high versus low levels of involvement.

Materials and methods

Participants

We analyzed data from Mystery Arena, developed by Gaming1. In total, 2713 players were randomly selected by the operator and data on their play behavior were retrieved in March 2020. The retrieved data covered a period since 2014.

Procedure

Below we first describe the general rules of the game, and then explain how players interacted with the game interface in more detail.

General rules of the game

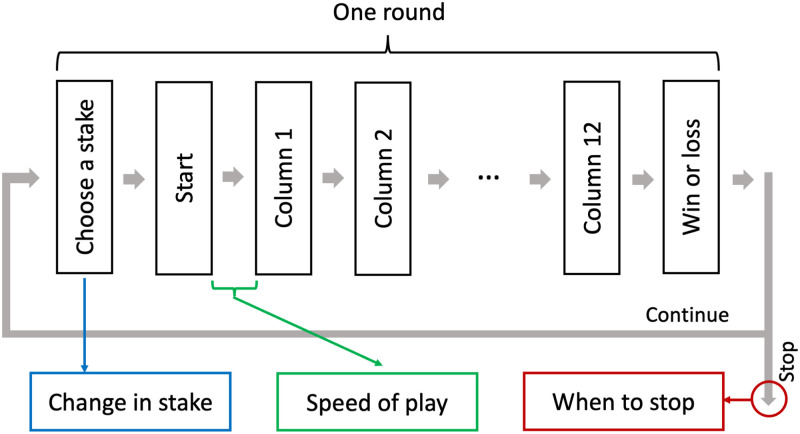
Before starting a round, players needed to place a stake (Fig 1). The stake was for the whole round, and could not be changed after pressing start. Twelve columns of dice (three dice per column) then appeared one by one. Players needed to put these 12 columns into 4 slots, with 3 columns in each slot. They won points in a slot when a horizontal or a diagonal line of the slot contained the same dice. After all 12 columns had been placed, the points from all 4 slots were added up and converted into monetary prizes (win or loss). After finishing a round, players could continue or end the session.

Gambling products are often categorized into two broad types, chance-based games that involve little deliberation or skill (e.g., slot machines, lotteries), and skill-based games in which players can exert some influence over the outcome (e.g., Blackjack, sports betting) [31]. On the continuum from chance-based to skill-based games, Mystery Arena sits between the two endpoints, but probably somewhere closer to the endpoint of chance-based games. That is, the dice are randomly generated, which largely determines the outcome (i.e., the chance component). However, players can decide in which slot to place each column, which also influences the outcome (i.e., the skill component).

The game interface

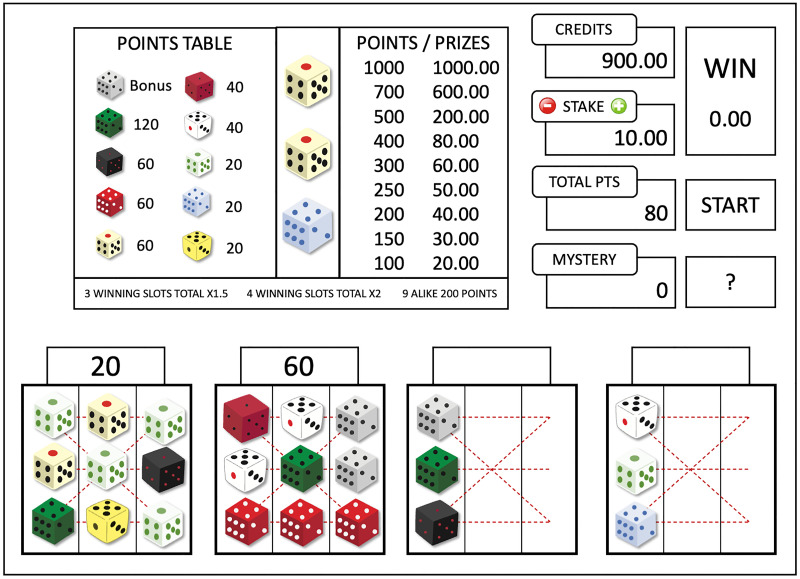
Fig 2 provides a schematic illustration of the game interface. Before starting a round, players could adjust the stake (from 0.25 euro to 20 euro, ten levels in total) by clicking on the plus and the minus button on the “STAKE” panel. As they adjusted the stake, the monetary prizes were adjusted accordingly in the “POINTS / PRIZES” panel. The stake acted as a multiplier, changing the monetary prizes paired with the points. After choosing a stake, players started the game by clicking on the “START” button, or anywhere except the “STAKE” panel.

A column of three dice was then shown (between the “POINTS TABLE” panel and the “POINTS / PRIZES” panel, see Fig 2). There were 10 different dice, with each dice worth a certain amount of points or a bonus play. Each dice was randomly drawn with equal probabilities. Four slots were displayed on the lower half of the interface. Players could place the column of dice into one of the four slots by clicking on the slot. After a column was placed, a new column of three dice was shown. Each slot was filled from left to right. If any of the three horizontal lines or the two diagonal lines in a slot contained the same dice, participants received corresponding points. After all twelve columns were placed, the points won from all four slots were summed up. The sum was multiplied by 1.5 if players won points in 3 slots, multiplied by 2 if they won points in all 4 slots, and players received an extra 200 points if the 9 dices in any slot were the same. In case of a win (≥ 100 points), the points were converted to a monetary prize, and displayed in the ‘WIN’ panel. The monetary prize was then reduced to 0 in the ‘WIN’ panel while the available credits increased (i.e., ‘transferring’ money into players’ accounts), along with an animation and sounds of pouring golden coins. At the end of the animation, the message ‘PLAY AGAIN’ appeared. In case of a loss (< 100 points), players directly got the message ‘PLAY AGAIN’. Wins and losses thus differed in their visual and auditory feedback events. In both cases, players could advance to the next round by clicking on the ‘START’ button or anywhere except the ‘STAKE’ panel. Note that players could also start a new round before the ‘PLAY AGAIN’ message appeared. Due to the differences in the feedback after wins and losses, and the flexibility in when to start a new round, we did not use the speed of starting a new round as the indicator for the speed of play. Instead, we used the interval between starting a new round till placing the first column in the new round (see Fig 1), which is not confounded by the factors discussed above.

If a certain slot contained three dice for a bonus play (on a horizontal or a diagonal line), the main game would pause and players would play a bonus game to win extra rewards. After the bonus game, the main game resumed. The bonus game occurred in 1.47% of the rounds in the current data. We do not have data on players’ responses in these bonus games. In the analysis, we included all rounds both with and without bonus games. In other words, we analyzed the effects of winning and losing on chasing behavior, regardless of whether players won from the main game or the bonus game. Furthermore, in the main game (with the 4 slots), instead of using the computer mouse, players could use the space bar or the Enter key on the keyboard to play. In that case, the program automatically determined the best location to place each column. This would presumably allow players to play at a higher speed than using the computer mouse. Players may also use mobile devices instead of desktops to play [32]. We do not have data on whether players used desktops or mobile devices, and whether they used the computer mouse or the keyboard to play.

Measures

Behavioral tracking data

Table 1 provides an overview of the variables in the behavioral tracking data, and the explanation for each variable.

Table 1. An overview of the variables in the behavioral tracking data.

Variable	Explanation
Player ID	A unique, deidentified ID for each player.
Session ID	A unique, deidentified ID for each session. One session consists of all rounds from when a player logged into the game, till when they disconnected.
Round ID	A unique, deidentified ID for each round. One round consists of placing all 12 columns of dice into the 4 slots.
Stake amount	The stake amount in each round, in euro.
Win amount	The amount of money a player won in a round, in euro. In case of a loss, the win amount is 0.
Speed of starting a round	The duration from when players placed the last column in the previous round, till when they started the current round, in milliseconds.
Speed of placing the columns	How quickly players placed each of the 12 columns into the slots, in milliseconds. Note that we used the speed of placing the first column as the behavioral indicator of speed of play.
Bonus game	Whether a bonus game occurred or not in a round.

Open in a new tab

Defining the low- and high-involvement groups

The operator also tracks each player’s overall monetary and time expenditure on their platform (see S1 File for a detailed description of the indicators). Based on these indicators, each player is assigned a level of gambling involvement from the operator, from 0 to 5, with a higher level standing for higher involvement. Gaming1 provided us with data from players with levels 0, 3, 4, and 5, but no data from players with levels 1 and 2. Since the indicators that players exhibit may vary over time, the involvement level of a player can accordingly also change. This is the case for some level 3/4/5 players in the data, where one player had different involvement levels across time. All level 0 players in the data had consistently level 0. Because the involvement level varied within some players, and that we do not have data on which indicators each player exhibited (i.e., Gaming1 only provided us general scores), we therefore focused on the comparison between the level 0 players and the level 3/4/5 players, without making further distinctions among levels 3, 4 and 5. We will refer to the level 0 players as the low-involvement group, and the level 3/4/5 players as the high-involvement group.

Statistical analysis

Data analyses were conducted in R (4.0.2) [33], using R packages afex (0.27–2) [34], BayesFactor (0.9.12–4.2) [35], bookdown (0.21) [36], ggplot2 (3.3.2) [37], ggpubr (0.4.0) [38], kableExtra (1.2.1) [39], knitr (1.29) [40], Rmisc (1.5) [41], and tidyverse (1.3.0) [42].

Players and play behavior

To examine whether and to what extent the two groups differed in their gambling involvement, we conducted a series of comparisons between the high- and low-involvement groups (see the ‘Defining the low- and high-involvement groups’ section above for how the two groups are defined). We used both the frequentist Welch’s t-tests [43] and Bayesian t-tests. For all Bayesian t-tests, a Cauchy distribution with a scale parameter of 0.707 (the default in the BayesFactor package) was used as the prior. Bayesian t-tests provide Bayes factors, which indicate the relative likelihood of obtaining the observed data under the alternative hypothesis versus the null hypothesis [44]. We reported the natural logarithm of Bayes factors (lnBF), as some Bayes factors were large. To interpret the Bayes factors, we used the widely adopted verbal labels [45]. For instance, a lnBF above 3.40 (i.e., a BF above 30) is considered ‘very strong’ evidence for the alternative hypothesis. P values were corrected for multiple comparisons using the Holm-Bonferroni method. Hedges’ g was reported as effect sizes for t tests [46].

Overview of the analyses on loss-chasing

We conducted three sets of analyses, each focusing on one facet of loss-chasing. Table 2 provides an overview of the behavioral indicator used, the main analysis, the expression of loss-chasing, and (as a preview of the results) whether loss-chasing was observed or not for each facet. In the sections that follow, we explain each set of analyses in detail.

Table 2. An overview of the behavioral indicator, main analysis, loss-chasing expression and whether it was observed in the current study for each facet.

Facet	Behavioral indicator	Main analysis	Loss-chasing expression	Observed?
When to stop	The probabilities of ending a session after winning and losing, while controlling for the overall probability of stopping.	Mixed ANOVA on the relative likelihoods of stopping, with the prior outcome (loss vs. win, within-subjects) and involvement level (high vs. low, between-subjects) as factors.	The probability of ending a session will be lower after a loss than after a win.	No
Change in stake	The probability of changing the stake, and the average change in stake amount after winning and losing.	Mixed ANOVA on the probability of changing stake and the average change in stake amount, with the prior outcome (loss vs. win, within-subjects) and involvement level (high vs. low, between-subjects) as factors.	Players will increase the stake amount more after a loss than after a win.	No
Speed of play	How quickly players place the first column of dice after starting a round (z score) after winning and losing.	Mixed ANOVA on the mean RT z scores, with the prior outcome (loss vs. win, within-subjects) and involvement level (high vs. low, between-subjects) as factors.	Players will place the first column of a round more quickly after a loss than after a win.	Yes

Open in a new tab

When to stop

Aim of analyses. The first set of analyses focused on whether winning and losing would influence the probability of ending a session, as an expression of loss-chasing.

Behavioral indicator. We used the probabilities of ending a session after a win and after a loss as the behavioral indicators of when to stop. More concretely, for each player, we computed the total number of winning rounds (all sessions combined), and the number of winning rounds that were at the end of a session (i.e., players decided to stop after these rounds). Dividing the latter by the former resulted in the probability of stopping after winning (i.e., p(stop|win)). The probability of stopping after losing (i.e., p(stop|loss)) was then similarly computed. If players chased losses by continuing playing, p(stop|loss) would be lower than p(stop|win). Note that this analysis is conceptually similar to the logistic regression used by Leino et al. [9], who examined the effects of gambling outcomes on the decision to continue vs. stop as a binary variable.

Importantly though, since the high-involvement players on average had longer sessions (as a criterion to create the two groups), the overall probability of ending a session was lower for the high-involvement players than for the low-involvement players (see S1 File). We therefore had to control for the overall probability of stopping in the analyses. For each player, we computed the total number of rounds (all sessions combined, regardless of the outcome) and the number of rounds at the end of a session. Dividing the latter by the former resulted in the overall probability of stopping (i.e., p(stop − overall)). For each player, we then divided both p(stop|win) and p(stop|loss) by p(stop − overall). The resulting values indicated the relative likelihoods of stopping after winning and losing, controlling for each player’s general probability of stopping.

Analysis methods. To achieve reliable estimates of p(stop|win) and p(stop|loss), players needed to have at least 5 wins and 5 losses in the data. For the included players, the relative likelihoods of stopping were computed as outlined above, and analyzed using a mixed ANOVA with prior outcome (loss vs. win, within-subjects) and involvement level (high vs. low, between-subjects) as independent variables. We then conducted a series of within-group and between-group pairwise comparisons to break down the effects from ANOVA.

Change in stake

Aim of analyses. The second set of analyses examined whether players would chase losses within a session by increasing the stake amount more after losing than after winning.

Behavioral indicator. We used two behavioral indicators, namely the probability of changing the stake, and the average change in stake amount, for after winning and losing respectively. High-involvement players overall placed higher stakes than low-involvement players (again, as a criterion to create the two groups). We therefore used the change in stake rather than the absolute stake amount as the behavioral indicator. More concretely, for each round, we computed the difference between the current stake amount and the previous stake amount. Average changes in stake amount were then computed for after a win and after a loss, separately.

Analysis methods. The first round of each session was excluded, as it did not have a previous round. To achieve reliable estimates, players needed to have at least 5 rounds following a win and 5 rounds following a loss. For each player, we calculated the probability of changing stake and the average change in stake amount (in euro cents) after a win and a loss. A positive (negative) change in stake amount means players increased (decreased) the stake in the current round. The probability of changing stake and the change in stake amount (euro cents) were submitted to a mixed ANOVA, with prior outcome (loss vs. win, within-subjects) and involvement level (high vs. low, between-subjects) as independent variables.

Speed of play

Aim of analyses. The last set of analyses examined whether players would chase losses by playing more quickly after losing than after winning.

Behavioral indicator. The speed of starting a round in the behavioral tracking data is the duration from when players placed the last column in the previous round till when they started the current round (Table 1). This duration included the different feedback events after winning and losing, and the time spent on adjusting the stake. Due to these confounding factors, we used the response time (RT) of placing the first column as the behavioral indicator of speed of play instead. This RT is from when players started the current round till when they put the first column in one of the 4 slots, and thus is not confounded by the factors mentioned above.

The high-involvement players overall played more quickly than the low-involvement players (see the Supplemental Materials), which might attenuate the influence of wins and losses on the speed of play. To control for the general playing speed, we therefore standardized the RTs within each player (i.e., RT z scores = (RT—mean RT of each player) / standard deviation of RTs for each player), and used the RT z scores in the analyses.

Analysis methods. We used the same RT exclusion criteria as in previous work [25, 26]. The first round of each session (i.e., no prior outcome) and rounds where the RT was above 5000 milliseconds were excluded. Players needed to have at least 5 rounds after a loss and 5 rounds after a win to be included in the analysis. The RT data were then standardized within each player. The mean RT z scores were calculated for each player, for rounds after a win and after a loss, respectively. We again used a mixed ANOVA, with prior outcome (loss vs. win, within-subjects) and involvement level (high vs. low, between-subjects) as independent variables.

Ethics

The study procedures were carried out in accordance with the Declaration of Helsinki. When creating an account on the operator’s platform, players confirmed (by clicking on a checkbox) that they had read the terms and conditions and the privacy policy, and thus provided consent for the use of their data for research purposes. Gaming1 provided the deidentified data to the researchers for statistical analysis. The current project was approved by the ethics committee of the faculty of psychology at the Université Libre de Bruxelles. Gaming1 does not allow the round-level raw data to be shared. However, the anonymized per player summary data and the analysis code are publicly available at https://osf.io/vuy5d/. All reported results can be reproduced with the summary data.

Results

Players and play behavior

Players

In total, the sample consisted of 2713 players, with 910 players in the low-involvement group (i.e., level 0; 409 females, 501 males, M_age = 37.7, SD_age = 12.7) and 1803 players in the high-involvement group (i.e., levels 3, 4, or 5; 800 females, 1003 males, M_age = 40.2, SD_age = 10.9). See S1 File for distributions of age and gender, and the total number of sessions and rounds played for both groups.

Play behavior

In total, players played 120,863 sessions and 10,370,013 rounds. We compared the following parameters between the two groups (see Table 3): (1) the total number of sessions played per player, (2) the total number of rounds played per player, (3) the mean number of rounds per session, (4) the median number of rounds per session, (5) the mean stake (in euro) in each round, (6) the median stake (in euro) in each round, (7) the probability of winning in all rounds combined, (8) the mean win amount (the presented win amount minus the stake, in euro) per round, in the rounds where players won, (9) the median win amount (in euro) per round, in the rounds where players won, (10) the mean loss amount (the loss amount equals the stake, in euro), in the rounds where players lost, (11) the median loss amount (in euro), in the rounds where players lost, and (12) the total amount of money spent per player (in euro; a positive value indicates that they overall lost money).

Table 3. Comparing play behavior between the two groups.

Parameter	High (N = 1803)	Low (N = 910)	diff	lowerCI	upperCI	df	t	p	lnBF	g
(1) Session number	64.2 (162.8)	5.6 (12.2)	58.6	51.1	66.2	1842.2	15.2	<.001	54.3	0.618
(2) Round number	5590.3 (13764)	319.5 (833.7)	5270.7	4632.6	5908.8	1828.1	16.2	<.001	61.6	0.659
(3) Mean round number	82.1 (78.3)	51.3 (63.3)	30.8	25.4	36.3	2195.6	11.0	<.001	48.7	0.449
(4) Median round number	60.6 (65.4)	45.9 (60.2)	14.8	9.8	19.7	1963.6	5.8	<.001	12.9	0.238
(5) Mean stake (Euro)	2.2 (3.2)	0.7 (0.9)	1.5	1.3	1.6	2344.2	18.2	<.001	87.0	0.738
(6) Median stake (Euro)	1.9 (3.3)	0.7 (0.9)	1.3	1.1	1.4	2283.0	15.1	<.001	58.8	0.613
(7) Win probability (%)	21.8 (4.8)	18.7 (8.4)	3.1	2.5	3.7	1214.3	10.4	<.001	70.8	0.424
(8) Mean win (Euro)	6.2 (10)	1.8 (2.7)	4.5	4.0	5.0	2262.4	17.5	<.001	74.3	0.734
(9) Median win (Euro)	3 (5)	1 (1.3)	1.9	1.7	2.2	2248.0	15.2	<.001	55.4	0.637
(10) Mean loss (Euro)	2.2 (3.2)	0.7 (0.9)	1.5	1.3	1.6	2345.8	18.2	<.001	86.9	0.738
(11) Median loss (Euro)	1.9 (3.3)	0.7 (0.8)	1.3	1.1	1.4	2222.7	15.3	<.001	59.2	0.620
(12) Total spent (Euro)	520.1 (2687.3)	38.7 (152.5)	481.4	356.9	605.9	1824.9	7.6	<.001	11.3	0.308

Open in a new tab

Note: Parameter = behavioral indicators compared between the two groups. See the text for an explanation for each parameter. High, Low = means of parameters for the high- and low-involvement groups, with standard deviations in parentheses. diff = difference between the high-involvement group and the low-involvement group. lowerCI, upperCI = lower and upper boundary of 95% confidence intervals of the difference. df, t, p = degrees of freedom, t value and p value from the Welch’s t-tests. P values were corrected for multiple comparisons using the Holm-Bonferroni method. lnBF = the natural logarithm of Bayes factors. g = Hedges’s average g.

The high-involvement players played more sessions and rounds in total. Their sessions were longer (i.e., contained more rounds) on average. The high-involvement players bet more, and as a result won more money when they won a game and lost more money when they lost a game. The overall probability of winning was higher in the high- than the low-involvement group. Two not mutually exclusive explanations exist for the latter finding. First, some players might play relatively few games, and decide to stop after experiencing a low winning probability. These players were more likely to be classified into the low-involvement group. Second, the game involved a skill component, as players needed to decide where to place each column. The high-involvement players might have a better knowledge of how to place the columns, and therefore achieved higher winning probabilities. Due to the negative expected value of the game, both groups lost money though (i.e., the total money spent was positive). Furthermore, the high-involvement players in total lost more money.

Most of the behavioral indicators we examined here overlapped with the ones used by Gaming1 to assign involvement levels to the players. These results thus served as ‘manipulation checks’, to show that the high-involvement group was indeed more involved in Mystery Arena than the low-involvement group. Next, we examined the influence of gambling outcomes and players’ involvement level on (1) when to stop, (2) change in stake, and (3) the speed of play.

When to stop

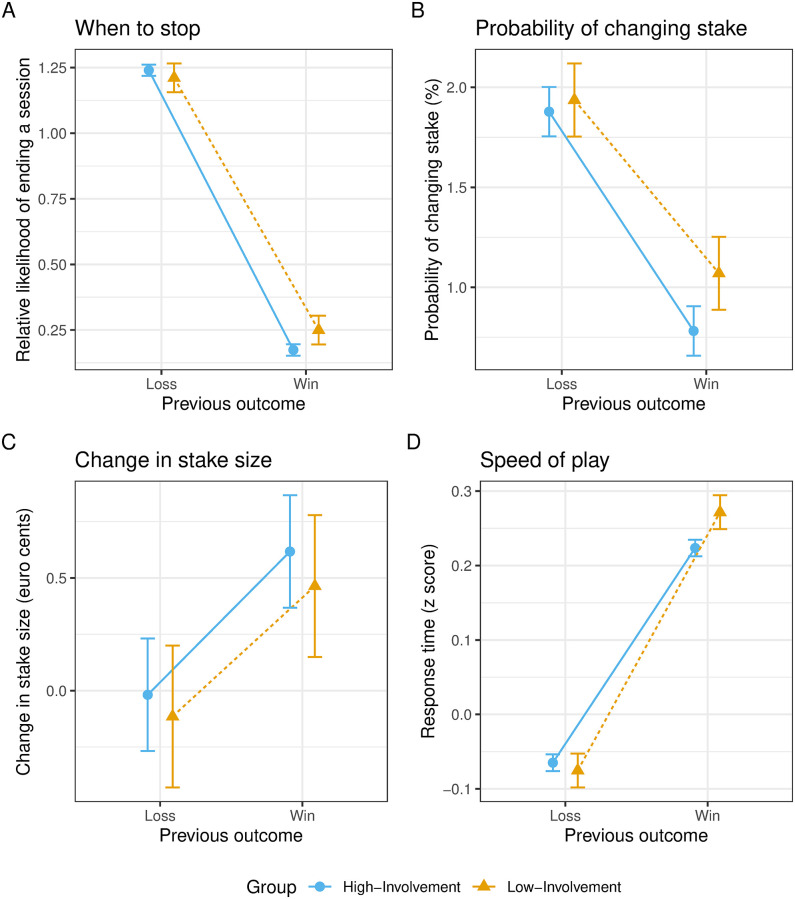
The ANOVA on the likelihoods of stopping after winning and losing (controlling for the overall probability of ending a session) revealed a significant main effect of prior outcome (Table 4). Players were more likely to stop after a loss than after a win (Fig 3, Panel (A)). This result is thus opposite to the prediction of loss-chasing (Table 2), but consistent with the results by Leino and colleagues on EGMs players [9]. Players in the current data set thus did not seem to chase losses; instead, they chased wins, by being more likely to continue playing after winning.

Table 4. Statistical analyses on when to stop.

Number of players and rounds included in the analyses in each group
Group	Player		Round (Mean)		Round (SD)		Round (Min)		Round (Max)
High-Involvement	1679		6001.9		14176.8		12		200706
Low-Involvement	651		440.9		959.3		13		13114
ANOVA
Effect	df		MSE		F		ges		p
Involvement Level (High vs. Low)	1, 2328		0.09		5.36		<.001		.021
Prior Outcome (Loss vs. Win)	1, 2328		0.29		3353.74		.520		<.001
Interaction	1, 2328		0.29		8.95		.003		.003
Pairwise comparisons
Comparison (A vs. B)	A-mean	B-mean	diff	lowerCI	upperCI	df	t	p	lnBF	g
High-Loss vs. High-Win	1.24 (0.15)	0.17 (0.49)	1.07	1.04	1.10	1678.0	68.5	<.001	1115.02	3.297
Low-Loss vs. Low-Win	1.21 (0.22)	0.25 (0.79)	0.96	0.88	1.04	650.0	24.4	<.001	207.52	1.884
High-Loss vs. Low-Loss	1.24 (0.15)	1.21 (0.22)	0.03	0.01	0.05	898.1	3.0	.007	3.33	0.140
High-Win vs. Low-Win	0.17 (0.49)	0.25 (0.79)	-0.08	-0.14	-0.01	850.1	-2.3	0.027	0.83	0.105
(High-Loss—High-Win) vs. (Low-Loss—Low-Win)	1.07 (0.64)	0.96 (1.01)	0.10	0.02	0.19	860.4	2.5	0.027	1.47	0.114

Open in a new tab

Note: ANOVA: df = degrees of freedom. In a 2 by 2 ANOVA, the dfs for all effects are the same. MSE = mean square of the error. ges = generalized eta squared. Pairwise comparisons: Comparison (A vs. B) = the two variables compared in each comparison. A-mean, B-mean = means of the left (A) and the right (B) variable in a comparison, with standard deviations in parentheses. diff = difference between A and B. lowerCI, upperCI = lower and upper boundary of 95% confidence intervals of the difference. df, t, p = degrees of freedom, t value and p value from the Welch’s t tests (between-subjects comparisons) or paired-samples t tests (within-subjects comparisons). P values were corrected for multiple comparisons using the Holm-Bonferroni method. lnBF = the natural logarithm of Bayes factors. g = Hedges’s average g.

Fig 3 — (A) when to stop, (B) probability of changing stake, (C) change in stake size, and (D) speed of play. For panel (A), relative likelihoods are the conditional probabilities of stopping after a loss and after a win, normalized per player by the overall probability to stop, e.g. p(*stop*|*loss*)/p(*stop* − *overall*) and p(*stop*|*win*)/p(*stop* − *overall*). Error bars stand for 95% within-subject confidence intervals.

Both the main effect of involvement level and the interaction effect were statistically significant. To break down these effects, we conducted pairwise comparisons. First, we compared the likelihood of stopping after losing versus winning for the two groups separately. Both groups were more likely to stop after a loss than after a win (High-Loss vs. High-Win and Low-Loss vs. Low-Win in Table 4), thus showing win-chasing in both groups. To examine if the extent of win-chasing differed between groups, for each player, we calculated a difference score between the likelihood of stopping after a loss and after a win. A positive difference score indicates win-chasing, with a larger value for a stronger tendency to chase wins. A direct between-group comparison showed larger difference scores for the high-involvement players ((High-Loss—High-Win) vs. (Low-Loss—Low-Win) in Table 4). The high-involvement players thus showed a stronger tendency to chase wins. Note though that the between-group difference is small (Hedges’s g = 0.114), and the Bayes factor (lnBF = 1.47; BF = 4.35) only provided anecdotal evidence for the alternative hypothesis.

In this analysis, we relied on the operator data to define one session of play, which was from when gamblers logged into the platform till when they logged off. However, players may also take a break without logging off. In an extra analysis, we assumed that players had taken a break when they took more than 10 minutes to respond, and that a new session started after they took a break. Both groups were still more likely to stop after a loss than after a win. The tendency to chase wins was descriptively larger in the high-involvement group, but the effect size was again quite small (Hedges’s g = 0.100) and the Bayes factor was inconclusive (lnBF = 0.39, BF = 1.48; see the Supplemental Materials). The between-group difference in the extent of win-chasing thus does not seem robust, and is at best small.

Change in stake

Players overall changed stake very infrequently (Fig 3, Panel (B)). Only the main effect of prior outcome was statistically significant (Table 5). Players were more likely to change stake after a loss than after a win, similar to the win-stay, lose-shift strategy often observed in competitive games [47]. This effect was observed in both groups (High-Loss vs. High-Win and Low-Loss vs. Low-Win for probability of changing stakes in Table 5). For the between-group comparisons, no statistically significant effects were found, and the BFs all provided moderate to strong support for the null effect (Table 5).

Table 5. Statistical analyses on change in stake.

Number of players and rounds included in the analyses in each group
Group	Player		Round (Mean)		Round (SD)		Round (Min)		Round (Max)
High-Involvement	1678		5936.6		14046.5		11		197613
Low-Involvement	648		435.5		949.0		13		12959
Probability of changing stakes (%)—ANOVA
Effect	df		MSE		F		ges		p
Involvement Level (High vs. Low)	1, 2324		17.85		1.57		<.001		.210
Prior Outcome (Loss vs. Win)	1, 2324		6.35		141.80		.016		<.001
Interaction	1, 2324		6.35		1.95		<.001		.163
Probability of changing stakes (%)—Pairwise comparisons
Comparison (A vs. B)	A-mean	B-mean	diff	lowerCI	upperCI	df	t	p	lnBF	g
High-Loss vs. High-Win	1.88 (3.09)	0.78 (3.96)	1.10	0.92	1.27	1677.0	12.3	<.001	68.96	0.311
Low-Loss vs. Low-Win	1.94 (3.15)	1.07 (3.40)	0.87	0.61	1.12	647.0	6.6	<.001	17.83	0.264
High-Loss vs. Low-Loss	1.88 (3.09)	1.94 (3.15)	-0.06	-0.34	0.23	1154.7	-0.4	1.000	-2.88	0.019
High-Win vs. Low-Win	0.78 (3.96)	1.07 (3.40)	-0.29	-0.61	0.04	1359.3	-1.7	0.726	-1.63	0.081
(High-Loss—High-Win) vs. (Low-Loss—Low-Win)	1.10 (3.65)	0.87 (3.35)	0.23	-0.08	0.54	1273.0	1.4	1.000	-1.99	0.067
Change in stake amount (euro cents)—ANOVA
Effect	df		MSE		F		ges		p
Involvement Level (High vs. Low)	1, 2324		11.23		1.30		<.001		.255
Prior Outcome (Loss vs. Win)	1, 2324		24.22		14.21		.004		<.001
Interaction	1, 2324		24.22		0.03		<.001		.858
Change in stake amount (euro cents)—Pairwise comparisons
Comparison (A vs. B)	A-mean	B-mean	diff	lowerCI	upperCI	df	t	p	lnBF	g
High-Loss vs. High-Win	-0.02 (3.76)	0.62 (5.09)	-0.64	-0.99	-0.28	1677.0	-3.5	<.001	2.61	0.144
Low-Loss vs. Low-Win	-0.12 (2.47)	0.46 (4.17)	-0.58	-1.02	-0.13	647.0	-2.6	0.110	0.10	0.174
High-Loss vs. Low-Loss	-0.02 (3.76)	-0.12 (2.47)	0.10	-0.17	0.36	1770.6	0.7	1.000	-2.78	0.033
High-Win vs. Low-Win	0.62 (5.09)	0.46 (4.17)	0.15	-0.25	0.56	1424.3	0.7	1.000	-2.72	0.035
(High-Loss—High-Win) vs. (Low-Loss—Low-Win)	-0.64 (7.37)	-0.58 (5.77)	-0.06	-0.62	0.51	1490.7	-0.2	1.000	-2.94	0.009

Open in a new tab

For the change in stake amount (in euro cents), again only the main effect of prior outcome was statistically significant (Table 5). Players on average increased their stake after a win, but not after a loss (Fig 3, Panel (C)). As a result, the increase in stake amount was larger after a win than after a loss. Players were thus less likely to change stake after winning, but when they did, they tended to increase the stake. The same pattern was observed for both groups. However, the effect was not statistically significant for the low-involvement group after correcting for multiple comparisons, and the BF was inconclusive (Low-Loss vs. Low-Win in Table 5 for change in stake amount; lnBF = 0.10, BF = 1.11). The between-group comparisons all yielded strong support for the null effect. Overall, players did not chase losses in stake amount. If anything, they showed a small tendency to chase wins, by betting a slightly larger stake after winning.

Speed of play

As mentioned above, the high-involvement players overall played more quickly than low-involvement players (see the Supplemental Materials for an analysis on raw RTs). We therefore focused on the RT z scores here. The main effect of involvement level, the main effect of prior outcome and their interaction effect were all statistically significant (Table 6). Players played more quickly after a loss than after a win (Fig 3, Panel (D)), and this effect was observed for both high- and low-involvement players (High-Loss vs. High-Win and Low-Loss vs. Low-Win in Table 6). Both groups thus showed loss-chasing in their speed of play. To examine whether the extent of loss-chasing differed between the two groups, for each player, we calculated a difference score between RT z scores after a loss and after a win (i.e., RT_diff = RT_loss—RT_win). A negative difference score indicates a tendency to chase losses, with more negative values for stronger tendencies to chase losses. These difference scores were then compared between the two groups. We found that the difference scores were less negative in the high-involvement group than in the low-involvement group ((High-Loss—High-Win) vs. (Low-Loss—Low-Win) in Table 6), suggesting that gambling outcomes had a smaller influence on the speed of play for high-involvement players. In other words, the high-involvement players showed a smaller loss-chasing effect in their speed of play.

Table 6. Statistical analyses on speed of play.

Number of players and rounds included in the analyses in each group
Group	Player		Round (Mean)		Round (SD)		Round (Min)		Round (Max)
High-Involvement	1678		5914.4		13975.3		11		196747
Low-Involvement	646		433.3		943.7		16		12856
ANOVA
Effect	df		MSE		F		ges		p
Involvement Level (High vs. Low)	1, 2322		0.02		15.22		.002		<.001
Prior Outcome (Loss vs. Win)	1, 2322		0.06		1483.85		.322		<.001
Interaction	1, 2322		0.06		12.55		.004		<.001
Pairwise comparisons
Comparison (A vs. B)	A-mean	B-mean	diff	lowerCI	upperCI	df	t	p	lnBF	g
High-Loss vs. High-Win	-0.065 (0.074)	0.224 (0.259)	-0.288	-0.304	-0.273	1677.0	-35.8	<.001	472.22	1.732
Low-Loss vs. Low-Win	-0.075 (0.090)	0.272 (0.331)	-0.347	-0.379	-0.315	645.0	-21.1	<.001	166.10	1.643
High-Loss vs. Low-Loss	-0.065 (0.074)	-0.075 (0.090)	0.010	0.003	0.018	994.0	2.6	0.009	1.04	0.120
High-Win vs. Low-Win	0.224 (0.259)	0.272 (0.331)	-0.048	-0.076	-0.020	963.6	-3.3	0.003	3.79	0.153
(High-Loss—High-Win) vs. (Low-Loss—Low-Win)	-0.288 (0.330)	-0.347 (0.417)	0.058	0.023	0.094	971.5	3.2	0.003	3.25	0.148

Open in a new tab

Discussion

Using data unobtrusively recorded while players played the online gambling product Mystery Area, we examined three behavioral expressions of within-session loss-chasing. Overall, both high- and low-involvement players were less likely to stop after a win than after a loss (i.e., win-chasing in when to stop). Furthermore, both groups increased the stake amount more after a win than after a loss (i.e., win-chasing in stake amount). For the speed of play, both groups responded more quickly after a loss than after a win (i.e., loss-chasing in speed of play), with a smaller effect in high-involvement players. Below we first discuss each behavioral expression of chasing in turn, and then discuss what these results imply for chasing in real gambling more generally.

When to stop

To examine when players ended a session, we compared the probability of stopping after a win and after a loss, while controlling for the overall stopping probability for each player. In line with the finding by Leino et al. [9], we found no loss chasing in this facet. Players were more likely to continue playing after winning, thus showing win-chasing instead. Whether players can continue a gambling session or not is necessarily limited by the amount of money available. Winning provides gamblers with extra funds to continue, while after losing, they may have to stop due to insufficient funds. In other words, the fact that gamblers were more likely to stop after a loss does not necessarily mean that they voluntarily decided to stop. Instead, sometimes they might have had to stop because they ran out of money after losing. However, since we do not have data on the amount of money available in players’ accounts, this hypothesis cannot be directly tested. This possibility nevertheless suggests that chasing losses by continuing playing may be constrained by available funds in real gambling, and future work can consider this constraint, by for instance recording funds available in gamblers’ accounts.

Change in stake

Players were more likely to change stakes after a loss than after a win (although the overall probability of changing stakes was quite low), in line with the win-stay, lose-shift strategy [47]. Moreover, they increased the stake amount more after winning than losing. No loss-chasing was therefore observed in stake change. Multiple explanations may explain the absence of loss-chasing here. First, gambling funds may constrain how much money gamblers can bet. Winning may provide players with more funds to place a larger bet, whereas after losing, players might not have sufficient funds to increase the stake. Second, players might become more risk-taking after winning (e.g., the house money effect [17]), thus showing win-chasing in stake amount. Note that in this game, gamblers seemed to pick a certain amount and rarely changed the stake when playing. This game and the way it was played by most gamblers may hence not be ideal for assessing how gamblers adjust stakes after wins and losses.

Speed of play

Gamblers played more quickly after a loss than after a win, thus showing loss-chasing in the speed of play. This finding is consistent with previous findings from laboratory tasks and simulated gambling [23, 25, 26], and serves as the first demonstration of this effect in real gambling in a large-scale study. Surprisingly, the highly involved players showed a smaller effect. They bet more money on average, and consequently won more money when they won a gamble, and lost more money when they lost a gamble. Previous work has shown that individuals tended to pause longer when the size of obtained reward increased [22]. Furthermore, it has been speculated that the omission of larger wins (i.e. larger losses in our study) may be more frustrating [25]. Based on this, one would predict a larger difference between wins and losses for high-involvement players (larger win/loss amounts) compared with low-involvement players (smaller win/loss amounts). However, we observed the opposite. The difference in the speed of play after a win versus a loss consists of two effects: slowing down after winning (the post-reinforcement pause effect [48]), and speeding up after losing (the post-loss speeding effect [25]). Due to the lack of a neutral baseline, we cannot distinguish between these two effects here. Accordingly, two explanations (not mutually exclusive) may account for the smaller effect for highly involved gamblers: the high-involvement group may be less sensitive to wins, and/or they may be less sensitive to losses (e.g., [49, 50]). Future research may utilize simulated gambling tasks that include neutral outcomes (e.g., [25]), and examine how the two effects may be related to gamblers’ level of involvement.

Chasing: A multifaceted phenomenon

One strength of the current work is the simultaneous examination of three behavioral expressions of within-session loss-chasing. Among the three facets examined, we observed win-chasing in (1) when to stop and (2) change in stake amount, and loss-chasing in (3) the speed of play. Instead of chasing wins or losses in all aspects of gambling behavior, gamblers seemed to intensify some facets after winning, and other facets after losing. This finding highlights the multifaceted and dynamic nature of chasing. To understand chasing, it is therefore necessary to simultaneously characterize multiple aspects of gambling behavior. We note that the speed of play may be an important facet via which chasing can be expressed. As discussed above, after losing, gamblers may not have enough money to place a larger stake, and might even be forced to stop. These factors may contribute to the observed win-chasing in the first two facets. By contrast, as long as gamblers have sufficient funds to continue playing, the speed of play is not limited by prior outcomes. As such, the speed of play may serve as a ‘pure’ measure of gambler’s urge to continue playing, since it is not constrained by available funds. The speed of play has received less attention than the other two facets so far. Our results suggest that it might be fruitful to consider the speed of play when examining chasing in real gambling.

Wins and losses had comparable effects in both the low- and high-involvement groups. Overall, we did not observe a stronger tendency to chase losses in players who were more involved in gambling. This finding seems to run counter to the idea that loss-chasing is a defining feature of problem gambling [6], and may thus be more pronounced as people become more involved in gambling. One possibility is that gambling involvement based on operator tracking data may not correlate with problem gambling severity (see below). Second, the clinical diagnosis of gambling disorder (e.g., DSM-5 [4]) uses between-session chasing as a criterion, while we examined within-session chasing here. On the one hand, within-session chasing can be a building block for between-session chasing [8]. For instance, extensive and intensified gambling within a session may be more likely to lead to substantial financial losses (due to the negative expected value of most gambling products), which may lead gamblers to come back another time to try to recoup previous losses (i.e., between-session chasing). On the other hand, between-session chasing does not necessarily mean that loss-chasing is also intensified within a session. Indeed, although the highly involved players gambled more intensively, wins and losses in the previous round had a smaller influence on their speed of play. This potential dissociation between within- and between-session chasing again highlights the multifaceted nature of loss-chasing, and the necessity of carefully delineating different facets of chasing in real gambling.

Limitations and future directions

One important limitation of the current research is that we analyzed data from one specific gambling product, Mystery Arena. The fast-paced nature of Mystery Arena may make it especially suitable for assessing certain aspects of loss-chasing (e.g., the speed of play) but less so for other aspects (e.g., the change in stake, as discussed above). In other gambling products, loss-chasing may be expressed differently. Moreover, different gambling products may attract different types of gamblers, who may differ in their chasing behavior (e.g., online poker vs. casino [30]). Further examining loss-chasing in other gambling products will illuminate the generalizability of the current findings.

Second, the gamblers in the current sample were assigned different involvement levels based on player tracking data, using a proprietary algorithm by Gaming1. Although some indicators used by Gaming1 showed some overlap with the clinical criteria for gambling disorder in DSM-5 (see the Supplemental Materials), it is unclear to what extent the involvement levels indeed correlate with (the risk levels of) problem gambling. One fruitful avenue for future research is to use more validated measures of problem gambling, and examine the correlations between problem gambling severity and behaviors tracked by the operators. Such information will allow for a more systematic examination of loss-chasing behavior across the whole spectrum of gambling involvement, from infrequent social gamblers to those who have problems with their gambling.

Conclusion

To conclude, using a large data set collected from an online commercial gambling product Mystery Arena, we examined three behavioral expressions of within-session loss-chasing for gamblers with high and low levels of gambling involvement. Overall, players were less likely to stop and tended to increase the stake after a win (i.e., win-chasing). However, after a loss, they played the game more quickly, which may reflect an urge to continue gambling (loss-chasing in the speed of play). Furthermore, wins and losses had a smaller influence on the speed of play for highly involved gamblers, which might reflect their reduced sensitivity to wins and/or losses. These findings highlight the multifaceted and dynamic nature of chasing in real gambling. Future studies may examine loss-chasing in other gambling products and in people with gambling problems to evaluate the generalizability of the current findings.

Supporting information

S1 File. Online supplemental materials.

(PDF)

Click here for additional data file.^{(253KB, pdf)}

Acknowledgments

We thank Olivier Massiot and Florian Merchie from Gaming1 for their invaluable assistance with the current project.

Data Availability

The anonymized per player summary data and the analysis code are publicly available at https://osf.io/vuy5d/. All reported results can be reproduced with the summary data.

Funding Statement

This work was supported by an ERC Consolidator grant (European Union’s Horizon 2020 research and innovation programme, grant agreement No 769595; https://erc.europa.eu/) and Methusalem Project 01M00221 (Ghent University; https://www.ugent.be/en/research/funding/bof/methusalem) awarded to Frederick Verbruggen. Zhang Chen is supported by a Postdoctoral fellowship of the Scientific Research Foundation, Flanders (FWO-Vlaanderen; https://www.fwo.be/ Xavier Noël is supported by the Fonds de la Recherche Scientifique (F.R.S.-FNRS; https://www.frs-fnrs.be/en/), Belgium and research funding from BAGO (Belgian Association of Gaming Operators; https://bago.be/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1. Clark L, Limbrick-Oldfield EH. Disordered Gambling: A Behavioral Addiction. Current Opinion in Neurobiology. 2013;23(4):655–659. doi: 10.1016/j.conb.2013.01.004 [DOI] [PubMed] [Google Scholar]
2. Potenza MN. The Neural Bases of Cognitive Processes in Gambling Disorder. Trends in Cognitive Sciences. 2014;18(8):429–438. doi: 10.1016/j.tics.2014.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Calado F, Griffiths MD. Problem Gambling Worldwide: An update and Systematic Review of Empirical Research (2000–2015). Journal of Behavioral Addictions. 2016;5(4):592–613. doi: 10.1556/2006.5.2016.073 [DOI] [PMC free article] [PubMed] [Google Scholar]
4. American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders. Fifth edition ed. American Psychiatric Association; 2013. [Google Scholar]
5. Blaszczynski A, Nower L. A Pathways Model of Problem and Pathological Gambling: Pathways Model of Gambling. Addiction. 2002;97(5):487–499. doi: 10.1046/j.1360-0443.2002.00015.x [DOI] [PubMed] [Google Scholar]
6. Zhang K, Clark L. Loss-Chasing in Gambling Behaviour: Neurocognitive and Behavioural Economic Perspectives. Current Opinion in Behavioral Sciences. 2020;31:1–7. doi: 10.1016/j.cobeha.2019.10.006 [DOI] [Google Scholar]
7. Toce-Gerstein M, Gerstein DR, Volberg RA. A Hierarchy of Gambling Disorders in the Community: Gambling Disorders. Addiction. 2003;98(12):1661–1672. doi: 10.1111/j.1360-0443.2003.00545.x [DOI] [PubMed] [Google Scholar]
8. Breen RB, Zuckerman M. ‘Chasing’ in Gambling Behavior: Personality and Cognitive Determinants. Personality and Individual Differences. 1999;27(6):1097–1111. doi: 10.1016/S0191-8869(99)00052-5 [DOI] [Google Scholar]
9. Leino T, Torsheim T, Pallesen S, Blaszczynski A, Sagoe D, Molde H. An Empirical Real-World Study of Losses Disguised as Wins in Electronic Gaming Machines. International Gambling Studies. 2016;16(3):470–480. doi: 10.1080/14459795.2016.1232433 [DOI] [Google Scholar]
10. Lister JJ, Nower L, Wohl MJA. Gambling Goals Predict Chasing Behavior during Slot Machine Play. Addictive Behaviors. 2016;62:129–134. doi: 10.1016/j.addbeh.2016.06.018 [DOI] [PubMed] [Google Scholar]
11. Nigro G, Ciccarelli M, Cosenza M. The Illusion of Handy Wins: Problem Gambling, Chasing, and Affective Decision-Making. Journal of Affective Disorders. 2018;225:256–259. doi: 10.1016/j.jad.2017.08.010 [DOI] [PubMed] [Google Scholar]
12. Ciccarelli M, Cosenza M, Griffiths MD, D’Olimpio F, Nigro G. The Interplay between Chasing Behavior, Time Perspective, and Gambling Severity: An Experimental Study. Journal of Behavioral Addictions. 2019;8(2):259–267. doi: 10.1556/2006.8.2019.29 [DOI] [PMC free article] [PubMed] [Google Scholar]
13. O’Connor J, Dickerson M. Definition and Measurement of Chasing in Off-Course Betting and Gaming Machine Play. Journal of Gambling Studies. 2003;19:359–386. doi: 10.1023/A:1026375809186 [DOI] [PubMed] [Google Scholar]
14. Gehring WJ, Willoughby AR. The Medial Frontal Cortex and the Rapid Processing of Monetary Gains and Losses. Science. 2002;295(5563):2279–2282. doi: 10.1126/science.1066893 [DOI] [PubMed] [Google Scholar]
15. Smith G, Levere M, Kurtzman R. Poker Player Behavior After Big Wins and Big Losses. Management Science. 2009;55(9):1547–1555. doi: 10.1287/mnsc.1090.1044 [DOI] [Google Scholar]
16. Studer B, Limbrick-Oldfield EH, Clark L. ‘Put Your Money Where Your Mouth Is!’: Effects of Streaks on Confidence and Betting in a Binary Choice Task. Journal of Behavioral Decision Making. 2015;28(3):239–249. doi: 10.1002/bdm.1844 [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Thaler RH, Johnson EJ. Gambling with the House Money and Trying to Break Even: The Effects of Prior Outcomes on Risky Choice. Management Science. 1990;36(6):643–660. doi: 10.1287/mnsc.36.6.643 [DOI] [Google Scholar]
18. Demaree HA, Burns KJ, DeDonno MA, Agarwala EK, Everhart DE. Risk Dishabituation: In Repeated Gambling, Risk Is Reduced Following Low-Probability “Surprising” Events (Wins or Losses). Emotion. 2012;12(3):495–502. doi: 10.1037/a0025780 [DOI] [PubMed] [Google Scholar]
19. Weber M, Zuchel H. How Do Prior Outcomes Affect Risk Attitude? Comparing Escalation of Commitment and the House-Money Effect. Decision Analysis. 2005;2(1):30–43. doi: 10.1287/deca.1050.0034 [DOI] [Google Scholar]
20. Imas A. The Realization Effect: Risk-Taking After Realized Versus Paper Losses. American Economic Review. 2016;106(8):2086–2109. doi: 10.1257/aer.20140386 [DOI] [Google Scholar]
21. Corr PJ, Thompson SJ. Pause for Thought: Response Perseveration and Personality in Gambling. Journal of Gambling Studies. 2014;30(4):889–900. doi: 10.1007/s10899-013-9395-4 [DOI] [PubMed] [Google Scholar]
22. Dixon MJ, MacLaren V, Jarick M, Fugelsang JA, Harrigan KA. The Frustrating Effects of Just Missing the Jackpot: Slot Machine Near-Misses Trigger Large Skin Conductance Responses, But No Post-Reinforcement Pauses. Journal of Gambling Studies. 2013;29(4):661–674. doi: 10.1007/s10899-012-9333-x [DOI] [PubMed] [Google Scholar]
23. Stange M, Graydon C, Dixon MJ. “I Was That Close”: Investigating Players’ Reactions to Losses, Wins, and Near-Misses on Scratch Cards. Journal of Gambling Studies. 2016;32(1):187–203. doi: 10.1007/s10899-015-9538-x [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Chen Z, Reimer CB, Verbruggen F. Proximity and Expectancy Modulate Response Vigor After Reward Omission. Collabra: Psychology. 2020;6(1):18184. doi: 10.1525/collabra.18184 [DOI] [Google Scholar]
25. Verbruggen F, Chambers CD, Lawrence NS, McLaren IPL. Winning and Losing: Effects on Impulsive Action. Journal of Experimental Psychology: Human Perception and Performance. 2017;43(1):147–168. doi: 10.1037/xhp0000284 [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Eben C, Chen Z, Vermeylen L, Billieux J, Verbruggen F. A Direct and Conceptual Replication of Post-Loss Speeding When Gambling. Royal Society Open Science. 2020;7(5):200090. doi: 10.1098/rsos.200090 [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Loba P, Stewart SH, Klein RM, Blackburn JR. Manipulations of the Features of Standard Video Lottery Terminal (VLT) Games: Effects in Pathological and Non-Pathological Gamblers. Journal of Gambling Studies. 2001;17(4):297–320. doi: 10.1023/A:1013639729908 [DOI] [PubMed] [Google Scholar]
28. Blaszczynski A, Sharpe L, Walker M, Shannon K, Coughlan MJ. Structural Characteristics of Electronic Gaming Machines and Satisfaction of Play Among Recreational and Problem Gamblers. International Gambling Studies. 2005;5(2):187–198. doi: 10.1080/14459790500303378 [DOI] [Google Scholar]
29. Linnet J, Rømer Thomsen K, Møller A, Callesen MB. Event Frequency, Excitement and Desire to Gamble, among Pathological Gamblers. International Gambling Studies. 2010;10(2):177–188. doi: 10.1080/14459795.2010.502181 [DOI] [Google Scholar]
30. Gainsbury SM, Suhonen N, Saastamoinen J. Chasing Losses in Online Poker and Casino Games: Characteristics and Game Play of Internet Gamblers at Risk of Disordered Gambling. Psychiatry Research. 2014;217(3):220–225. doi: 10.1016/j.psychres.2014.03.033 [DOI] [PubMed] [Google Scholar]
31. Jiménez-Murcia S, Granero R, Fernández-Aranda F, Menchón JM. Comparison of Gambling Profiles Based on Strategic versus Non-Strategic Preferences. Current Opinion in Behavioral Sciences. 2020;31:13–20. doi: 10.1016/j.cobeha.2019.09.001 [DOI] [Google Scholar]
32. M Gainsbury S, Liu Y, Russell AMT, Teichert T. Is All Internet Gambling Equally Problematic? Considering the Relationship between Mode of Access and Gambling Problems. Computers in Human Behavior. 2016;55:717–728. doi: 10.1016/j.chb.2015.10.006 [DOI] [Google Scholar]
33.R Core Team. R: A Language and Environment for Statistical Computing; 2020. Available from: https://www.R-project.org/.
34.Singmann H, Bolker B, Westfall J, Aust F, Ben-Shachar MS. afex: Analysis of Factorial Experiments; 2020. Available from: https://CRAN.R-project.org/package=afex.
35.Morey RD, Rouder JN. BayesFactor: Computation of Bayes Factors for Common Designs; 2018. Available from: https://CRAN.R-project.org/package=BayesFactor.
36.Xie Y. bookdown: Authoring Books and Technical Documents with R Markdown; 2020. Available from: https://CRAN.R-project.org/package=bookdown.
37.Wickham H, Chang W, Henry L, Pedersen TL, Takahashi K, Wilke C, et al.. ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics; 2020. Available from: https://CRAN.R-project.org/package=ggplot2.
38.Kassambara A. ggpubr:’ggplot2’ Based Publication Ready Plots; 2020. Available from: https://CRAN.R-project.org/package=ggpubr.
39.Zhu H. kableExtra: Construct Complex Table with’kable’ and Pipe Syntax; 2020. Available from: https://CRAN.R-project.org/package=kableExtra.
40.Xie Y. knitr: A General-Purpose Package for Dynamic Report Generation in R; 2020. Available from: https://CRAN.R-project.org/package=knitr.
41.Hope RM. Rmisc: Ryan Miscellaneous; 2013. Available from: https://CRAN.R-project.org/package=Rmisc.
42.Wickham H. tidyverse: Easily Install and Load the’Tidyverse’; 2019. Available from: https://CRAN.R-project.org/package=tidyverse.
43. Delacre M, Lakens D, Leys C. Why Psychologists Should by Default Use Welch’s t-Test Instead of Student’s t-Test. International Review of Social Psychology. 2017;30(1):92–101. doi: 10.5334/irsp.82 [DOI] [Google Scholar]
44. Dienes Z. Using Bayes to Get the Most out of Non-Significant Results. Frontiers in Psychology. 2014;5. doi: 10.3389/fpsyg.2014.00781 [DOI] [PMC free article] [PubMed] [Google Scholar]
45. Wagenmakers EJ, Love J, Marsman M, Jamil T, Ly A, Verhagen J, et al. Bayesian Inference for Psychology. Part II: Example Applications with JASP. Psychonomic Bulletin & Review. 2018;25(1):58–76. doi: 10.3758/s13423-017-1323-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Lakens D. Calculating and Reporting Effect Sizes to Facilitate Cumulative Science: A Practical Primer for t-Tests and ANOVAs. Frontiers in Psychology. 2013;4. doi: 10.3389/fpsyg.2013.00863 [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Dyson BJ, Wilbiks JMP, Sandhu R, Papanicolaou G, Lintag J. Negative Outcomes Evoke Cyclic Irrational Decisions in Rock, Paper, Scissors. Scientific Reports. 2016;6(1):20479. doi: 10.1038/srep20479 [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Felton M, Lyon DO. The Post-Reinforcement Pause. Journal of the Experimental Analysis of Behavior. 1966;9(2):131–134. doi: 10.1901/jeab.1966.9-131 [DOI] [PMC free article] [PubMed] [Google Scholar]
49. Campbell-Meiklejohn DK, Woolrich MW, Passingham RE, Rogers RD. Knowing When to Stop: The Brain Mechanisms of Chasing Losses. Biological Psychiatry. 2008;63(3):293–300. doi: 10.1016/j.biopsych.2007.05.014 [DOI] [PubMed] [Google Scholar]
50. Raimo S, Cropano M, Trojano L, Santangelo G. The Neural Basis of Gambling Disorder: An Activation Likelihood Estimation Meta-Analysis. Neuroscience & Biobehavioral Reviews. 2021;120:279–302. doi: 10.1016/j.neubiorev.2020.11.027 [DOI] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0273359.r001

Decision Letter 0

Gaëtan Merlhiot

2 Mar 2022

PONE-D-21-35671Winning and losing in online gambling: Effects on within-session chasingPLOS ONE

Dear Dr. Chen,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Thank you for your patience, I had issues to secure enough reviewers. I could receive reviews of the manuscript and read the manuscript before reading the reviews. I share reviewers opinions and I have additional comments. I would appreciate if the authors could address all the reviewers' comments and mine :

On the overall, the introduction and discussion are well written, but the material and statistical analysis need to be reworked. That’s one of the main issues of this article. The methods and statistical analysis seem to have been correctly done but the way it is explained is far too complex. In addition, the discussion lacks perspective and there is no clear message regarding the results of this study under the scope of the current literature.

Introduction:

Hypothesis: It seems there was no clear hypothesis, and it was more an exploratory study. I would appreciate further explanation on this matter.

Material and methods:

The game is extremely simple but when referring to the figure and the explanation of the game gave by the authors, this game seemed too complex. I think the authors need to improve the figure 1 (also please place figure 1 under the figure), and the game explanation. Figure 1 should allow reader to understand how the game works at first sight. Essential information could be provided first, followed by the additional information for further details

Measures:

Same as previous comments, please provide essential information first and then provide details. A summarizing table with measures, tests and associated hypothesis would be appreciated.

Statistical analysis:

The presentation of the statistical analysis is too complex, and readers will get lost very quickly. The authors need to provide the purpose of each of the analyses so the readers will understand easily. There are several other issues such as: Line 235, nothing is specified about the two groups; Line 250 how the High-involvement and low-involvement players group are defined? I couldn’t find anything in the method.

Results

Figure 3 is misleading with the shifted lines between groups and the vertical reading arrangement. In addition, I do not understand why the three behavioral expressions are presented within the same figure. The arrangement of the figure should be based on a horizontal reading pattern with A and B as the top left and top right sub figure and the C as the bottom left and bottom right sub figure.

Please submit your revised manuscript by Apr 16 2022 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: https://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.

We look forward to receiving your revised manuscript.

Kind regards,

Gaëtan Merlhiot

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Please provide additional details regarding participant consent. In the ethics statement in the Methods and online submission information, please ensure that you have specified what type you obtained (for instance, written or verbal, and if verbal, how it was documented and witnessed). If your study included minors, state whether you obtained consent from parents or guardians. If the need for consent was waived by the ethics committee, please include this information.

3. Thank you for stating the following in the Acknowledgments Section of your manuscript:

We thank Olivier Massiot and Florian Merchie from Gaming1 for their invaluable 554

assistance with the current project. This work was supported by an ERC Consolidator 555

grant (European Union’s Horizon 2020 research and innovation programme, grant 556

agreement No 769595) and Methusalem Project 01M00221 (Ghent University) awarded 557

to Frederick Verbruggen. Xavier No¨el is supported by the Fonds de la Recherche 558

Scientifique (F.R.S.-FNRS), Belgium

Please note that funding information should not appear in the Acknowledgments section or other areas of your manuscript. We will only publish funding information present in the Funding Statement section of the online submission form.

Please remove any funding-related text from the manuscript and let us know how you would like to update your Funding Statement. Currently, your Funding Statement reads as follows:

This work was supported by an ERC Consolidator grant (European Union’s Horizon 2020 research and innovation programme, grant agreement No 769595; https://erc.europa.eu/) and Methusalem Project 01M00221 (Ghent University; https://www.ugent.be/en/research/funding/bof/methusalem) awarded to Frederick Verbruggen. Xavier Noël is supported by the Fonds de la Recherche Scientifique (F.R.S.-FNRS; https://www.frs-fnrs.be/en/), Belgium and research funding from BAGO (Belgian Association of Gaming Operators; https://bago.be/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Please include your amended statements within your cover letter; we will change the online submission form on your behalf.

4. Thank you for stating the following in the Competing Interests section:

I have read the journal's policy and the authors of this manuscript have the following competing interests: XN received research funding from BAGO (Belgian Association of Gaming Operators) of which Gaming1 is affiliated. No honorarium was received. There was no editorial direction or censorship from Gaming1. ZC, RD, and FV declare that no competing interests exist.

Please confirm that this does not alter your adherence to all PLOS ONE policies on sharing data and materials, by including the following statement: "This does not alter our adherence to PLOS ONE policies on sharing data and materials.” (as detailed online in our guide for authors http://journals.plos.org/plosone/s/competing-interests). If there are restrictions on sharing of data and/or materials, please state these. Please note that we cannot proceed with consideration of your article until this information has been declared.

Please include your updated Competing Interests statement in your cover letter; we will change the online submission form on your behalf.

5. In your Data Availability statement, you have not specified where the minimal data set underlying the results described in your manuscript can be found. PLOS defines a study's minimal data set as the underlying data used to reach the conclusions drawn in the manuscript and any additional data required to replicate the reported study findings in their entirety. All PLOS journals require that the minimal data set be made fully available. For more information about our data policy, please see http://journals.plos.org/plosone/s/data-availability.

Upon re-submitting your revised manuscript, please upload your study’s minimal underlying data set as either Supporting Information files or to a stable, public repository and include the relevant URLs, DOIs, or accession numbers within your revised cover letter. For a list of acceptable repositories, please see http://journals.plos.org/plosone/s/data-availability#loc-recommended-repositories. Any potentially identifying patient information must be fully anonymized.

Important: If there are ethical or legal restrictions to sharing your data publicly, please explain these restrictions in detail. Please see our guidelines for more information on what we consider unacceptable restrictions to publicly sharing data: http://journals.plos.org/plosone/s/data-availability#loc-unacceptable-data-access-restrictions. Note that it is not acceptable for the authors to be the sole named individuals responsible for ensuring data access.

We will update your Data Availability statement to reflect the information you provide in your cover letter.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: No

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: No

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: I have reviewed this manuscript previously – and positively – for a different journal, and I would like to say what a pleasant surprise it is to see that most of my previous concerns have been addressed in this new submission.

This is an unusual and sophisticated piece of research using naturalistic gambling data from a specific online gambling game (‘Mystery Arena’) in a large sample (over 2500 gamblers making over 10 million bets). The paper provides a detailed behavioural analysis of ‘loss chasing’, a key feature of problematic gambling. An important contribution is the description of 3 distinct expressions of loss chasing: ‘when to stop’ (linked to persistence), the amount bet, and the speed of play. They compare these variables between winning and losing gambles, and between groups classified by the gambling operator as higher or lower risk, using their own (proprietary) algorithm. The indicators used by the gambling operator are shown in the Supp material, and while this classification is a little opaque (given the proprietary aspect), there is certainly useful information in these analyses, and I thought the authors handled its (limited) validity very appropriately. The groups differ primarily on the stopping variable (although not in the conventional ‘loss’ chasing direction) and on the speed of play variable.

As with much research, a key strength is also a key weakness: the authors focus on Mystery Arena as one specific gambling product, because chasing may be expressed differently on different kinds of gambling (e.g. slot machine gamblers may persist whereas sports bettors may escalate their stake size). The authors also note that it is better suited to the speed of play analysis that a conventional slots game. I fully agree on both accounts, but I might add as a limitation that it seems a slightly unorthodox game. The authors refer on pg 16 that it is ‘chance based’ and compare on pg 4 to a ‘conventional slot machine’. I would say that the behavioural requirements per bet (‘skill’, in a colloquial sense) are greater than a slot machine, and in the manipulation checks, the high involvement do seem to win more than the low involvement groups. To what extent do the motor requirements of the game actually afford experienced players control over the return to player? Could the authors add a clear statement (perhaps in the task methods) as to where this game falls on the skill /chance continuum? Later on in the manuscript, they also refer to the game as a “gamble” e.g. Discussion line 1. I would suggest term ‘gambling product’.

Of the 3 definitions of chasing, I feel the ‘when to stop’ analysis is the most challenging; for the change in stake and speed of play analyses, I feel there would be much agreement among researchers about how to operationalize those variables. For ‘when to stop’, the authors approach this in an interesting way, by looking at the probability of winning for that player’s overall ‘session’, and the pwin on their last trial (i.e. before they stop). As p(win-end) is less than p(win-overall), they conclude that players stop when they are losing, i.e. the opposite of loss ‘chasing’. This is the first paper that I have seen operationalize chasing in this way, and it’s an interesting way of simplifying a very complex variable. At the same time, it loses some of the dynamics of chasing, by ignoring the length of the session, and it doesn’t seem to adequately orthogonalize the responses to winning and losing. For example, the authors acknowledge that their effect (the low pwin-end) could reflect stopping after a losing streak, or bigger wins early in the session, and/or exhausting funds. The secondary analysis excluding breaks over 10 minutes does not really shed any light on these ambiguities. Overall, I think the authors could stick with this analysis, but I would encourage them to note that there are other ways to operationalize this variable, e.g. the logistic regression by Leino.

Minor

P2 please use ‘person first language’ i.e. people with gambling problems, not ‘problem gamblers’

Pg 6 line 218 – 230. Rather than endorsing or rejecting the terminology from the gambling operator (‘pathological addictive gambler’ etc), I think this section could be shortened just by introducing the five levels and the binarization.

Table 1 please add units to the parameters, e.g. is the mean and median win in Euros?

Not a huge problem but printed in black and white, the two lines in Fig 3 and elsewhere are indistinguishable.

Reviewer #2: In this manuscript the authors study the phenomenon of “loss chasing” in gambling data from a large dataset obtained from an online gambling company. The experimental setting describe an agent engaged with a repeated decision-making task, where in each trial the agent may choose to continue or halt participation in a gamble that may result a win or a loss. If the agent decides to continue gambling, they also choose whether to change the previous gambled amount (the “stake”). In this framework, loss chasing is the tendency to increase the stakes and probability of choosing to continue gambling specifically in trials that follow losses. In terms of the probability to continue gambling, the authors identify the opposite of loss chasing with an increased likelihood to stop gambling after losing compared to after winning (Fig 3.a). In changing gambled stakes, participants were more likely to change their stake after a loss compared to a win. However, stake change after loss and win were both very rare (2% and 1% to change stake respectively), and the amount of stake changing after loss was centered around zero (Fig 3.b). In testing reaction times, the authors found that participants made quicker decisions following a loss compared to wins. Across these behavioral features, the authors compare the behavior of light and heavy gamblers.

The manuscript seems methodologically sound. Given the importance of better understanding gambling behavior, and the limitation in studying such behavior in the lab setting, the extensive ecological dataset analyzed here is valuable in unveiling the underlying mechanisms of gambling in its common and pathological forms. My main concern in reviewing the manuscript is a lack of clear message. Having studied the data, what new insights did we gain about gambling behavior? Does the evidence support the notion of loss chasing or does it not? What do the findings suggest on the decision-making mechanisms of gamblers? What do they imply to the vulnerability of gamblers to specific types of games? How would these vulnerabilities be expressed in different types of gambling games? How could the novel understanding from the present study be utilized for the design of interventions in gambling disorders? It is not necessary to address all these questions. Rather, a better distilling of a main message and its implications in some broader context could strengthen the manuscript and its impact, and make it easier to follow. Minor refinements or a reframing of the introduction, and some expansion of the discussion may accomplish this goal.

Major comments

-------------------

* The main effect of loss chasing is implicated in the tendency to chase, namely continue gambling (possibly with greater stakes), after a loss. As the authors suggest, comparing the groups of high- and low-involvement gamblers should consider each group’s winning base-rate, which is higher for the high-involvement groups. This is equivalent to the comparison of two geometrical distributions with a different p (“The probability distribution of the number X of Bernoulli [with probability p] trials needed to get one success” [Wikipedia]). The question of whether participants engage in loss chasing is equivalent to asking what is the probability, given the data, that participants do not in fact have a fixed probability p for stopping, but that p is conditioned on the outcome of the previous trial. Figure 3.a greatly demonstrate this effect. Still, because it was unintuitive for me to mentally compare two geometrical distributions with different p’s, it was difficult for me to appreciate the magnitude of this effect in light of a null model which assumes that participants chose to stop gambling regardless of the last outcome. One way to help the reader could be to simulate the null model and position the present data within this simulation. One way to approach this is to simulate a vector of wins and losses according to the empirical distribution of probabilities to win or lose in the studied game. With this simulated vector of wins and losses, consider the probabilities pStop_loss^high, pStop_win^high, pStop_loss^low, pStop_win^low as the simulated probability to stop after a loss or a win in the high and low involvement groups. A null model would assume that pStop_win=pStop_loss= the empirical probability to stop. The distribution of probability of to stop for each of the groups may serve as the null hypothesis which by comparison would allow to appreciate the current data. After simulating this null hypothesis, subsequent simulations may push pStop_win and pStop_loss gradually apart (pStop_loss-pStop_win=0.01, 0.02,…). The resulting sequence of distributions (per each [pStop_loss-pStop_win] difference) may allow the estimation of: a. what is the most probable p_win and p_loss given the data, b. how likely it is that they are different within each group and c. between groups.

Minor comments

-------------------

* The introduction is somewhat repetitive and could be edited to be shorter and more concise. In general, I could easily understand the text, but the manuscript could benefit from further editing and proofreading.

* It might not be my place to comment on this, but it stood out - Given that one of the perspectives of the manuscript is gambling disorder, it is slightly odd that the first sentence of the introduction frame gambling as a recreational activity that people engage with for pleasure and fun (in the same way that a paper on endangered species may choose to refrain from framing sports hunting as a recreational activity that people engage with for pleasure; even if evidently both claims are true).

* “The influential pathways model proposed three distinct pathways from initial 8 gambling exposure to problem gambling [5] While different psychological and biological 9 processes are involved in the distinct pathways, all three …” It is not clear to the reader who is unfamiliar with the pathway model that problem gambling is one type of a pathway. More broadly, if the three different paths are of interest (it seems they are), it would assist the reader if they would be clearly defined here.

* line 14: “It is also one of the only signs of disordered gambling that can be directly captured in gambling behavior… The decision to continue gambling despite substantial financial losses is arguably the 38 most prototypical behavioral manifestation of loss-chasing” It is not essentials to your claims, but the reader remains wondering – why is this true? Is this a clinical, mechanistic, or other type of argument?

* Figure 1 has no caption, and I think a caption would assist the reader.

* Figure 1 shows the conversion between points and prizes which for most of the table has a conversion factor of 50 (100 points equal a prize of 20.0), but for the higher amounts of 600 and 1000 the conversions rate changes. I couldn’t understand if this is on purpose and of importance (it may be addressed in the text and I just missed it).

* It would assist the understanding of the game if several game-strategies could be explained or demonstrated. It seems there are a few degrees of freedom to participants of the game – where to place the columns, when to stop. Is the game based purely on luck (e.g. like a roulette) or does it have some elements of competency (like black jack)? Namely, could the game be played better by a competent player?

* Also, it wasn’t completely clear how are the cost of participating in a game calculated – are they determined per new draw of a dice-column? If so, could the stakes be modified between draws of dices? Does it mean that costs increased with each decision to draw a new column? Or, was participation cost a single amount set prior to a session? If so, why would it be beneficial to stop before the end of a session (before filling all the columns)?

* A related question is how did the game itself operate – were dices randomly drawn at each round with uniform distribution? Or by a different distribution? Was the game reactive (changed dice allocation based on the user choices)?

* This is a matter of taste: Figures 2 displays the distribution of age and gender across the two groups. This figure does not, of course, hinder understanding, but age and gender statistics seem like the least interesting aspect of the data; visualizing any of the rows of table 1 would be, subjectively for me, more relevant to the substance of the manuscript.

* Although it appears elsewhere, it would be helpful to add the number of participants per group to table 1 (e.g., to remind the reader that there were many more “High” participants compared to “low” ones; thus, explaining how come their “Round number” is so much higher).

* In table 2, 3, 4 the ANOVA’s df are identical to the main effects and interaction. I guess this is by design, but it is unintuitive (ANOVA tables for factors A and B are often presented with df |A|-1, |B|-1, (|A|-1)(|B|-1)). A comment addressing this would have helped me understanding the tables.

* Table 2 – I couldn’t understand the label of the last row. Is it “High- vs. Low-Involvement (Difference[Session End, session Overall])” what is “left” and what is “right” here?

* The Introduction is somewhat confusing in that when I approached the results, I was under the impression that the authors are about to demonstrate loss chasing in its most intuitive form – that gamblers tend to chase (continue gambling) after losses. The fact that the data suggests the opposite is important and interesting; but the expectations build up I had given previous sections left my quite confused. The way I read it, I was expecting to find that losses were followed by increased tendency to stop, and then the respective result is just glossed over (“Overall, p(win-end) was significantly lower than p(win-overall) 350 (Fig 3, Panel (A)). Players were thus more likely to stop after losing than after winning”).

In short, the way the introduction is written I was expecting to find that participants have greater likelihood to gamble after losses and it took me some time to understand that what the authors find is the opposite. It would have been easier for me to comprehend the text if the introduction would “prepare” me to this result, or be more clear about the fact that this result is surprising; or more explicit that this findings is inconsistent with loss chasing.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: Yes: Luke Clark

Reviewer #2: Yes: Ohad Dan, Ph.D.

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2022 Aug 18;17(8):e0273359. doi: 10.1371/journal.pone.0273359.r002

Author response to Decision Letter 0

11 May 2022

Please see the attached response to reviewers letter to find our responses to the comments by the editor and the reviewers.

Attachment

Submitted filename: Plos-One-Revision.pdf

Click here for additional data file.^{(1.6MB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0273359.r003

Decision Letter 1

Gaëtan Merlhiot

13 Jul 2022

PONE-D-21-35671R1Winning and losing in online gambling: Effects on within-session chasingPLOS ONE

Dear Dr. Chen,

I am glad to see that all reviewers’ comments were considered. Please revise the manuscript to address the remaining minor concerns according to reviewers’ suggestions.

Please ensure that your decision is justified on PLOS ONE’s publication criteria and not, for example, on novelty or perceived impact.

For Lab, Study and Registered Report Protocols: These article types are not expected to include results but may include pilot data. Please submit your revised manuscript by Aug 27 2022 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Gaëtan Merlhiot

Academic Editor

PLOS ONE

Journal Requirements:

Please review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript. If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: The authors have been very attentive to the referee comments. This is a sophisticated piece of research: they are using high-resolution behavioural gambling data from a real online gambling platform, in a large dataset (10 million bets), looking at three distinct behavioural expressions that each require careful operationalizing. The value of the paper is in the contrast of the three expressions of chasing. They have done an excellent job of conveying their objectives and analysis pipeline as clearly as possible.

Reviewer #2: I was very happy to receive the updated manuscript. The revised version substantially improves on its previous. The Introduction is more concise, the Methods easier to follow, and the discussion better explains the multifaceted nature of loss chasing. In particular, I found table 1 to be helpful in shaping the reader’s expectations from the findings. Similarly, the grouping of all findings into a single figure (Fig. 3) is helpful. I thank the authors for the comprehensive point-by-point responses to my previous comments.

I have only minor comments:

1. Line 153 - “Note that players could also start a new round before the ’PLAY AGAIN’ message appeared” – I wasn’t sure what to make of this comment. If I understand correctly, games that concluded in a win were followed by a pleasant animation that participants may have chosen to savor. Games that were concluded by a loss were not. The comparison of timing between [win, something nice, continue?] and [lose, continue?] suggests then that the choice to continue to an additional game would be – by the construction of the game – quicker after losses, as indeed indicated by the results (e.g., Fig 3.D). Is this comment offered as a limitation to the finding of quicker RT after a loss? If so, it can potentially be framed as such more explicitly. Also, a comparison of the animation time and the difference between wins and losses reaction time may shed light on the role of the animation in generating this effect (if the animation is 1 second and the mean difference between wins and losses RT is 5 seconds then the effects of the animation are potentially of lesser concern). Alternatively, does this comment just explains the actual structure of the game and has no relation to RT?

2. I do not understand participants inclusion criterion. Line (236): “players needed to have at least 5 wins and 5 losses in the data”, line (255) “players again needed to have at least 5 rounds following a win and 5 rounds following a loss” – the ‘again’ seems to imply this is the same criterion but I’m not sure that it is: a player may have a single loss followed by 6 wins, satisfying the second condition but not the first.

3. Fig 3.a axis labels – The use of relative likelihoods of ending a session is well explained. However, I don’t know “relative likelihood” as a standard term. Due to the importance of the panel, and the possibly not so intuitive units of that panel, it would have been easier for me if “relative likelihood” was also described in the figure caption. Something like “relative likelihoods are the conditional stopping probabilities given a win or a loss, normalized per-participant by the overall probability to stop, e.g. for losses P(stop|loss)/P(stop-overall)”.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: Yes: Luke Clark

Reviewer #2: Yes: Ohad Dan

**********

PLoS One. 2022 Aug 18;17(8):e0273359. doi: 10.1371/journal.pone.0273359.r004

Author response to Decision Letter 1

14 Jul 2022

Dear editor,

Thank you again for the opportunity to revise our manuscript. In this letter, we list the comments by the two reviewers in bold, and explain how we have addressed each comment by Reviewer #2. Texts from the revised manuscript are shown in green. In the pdf file of the revised manuscript, we have highlighted the changes.

Kind regards,

Zhang Chen

We would like to thank Reviewer #1 for these encouraging words, and for his constructive comments on our manuscript.

We would also like to thank Reviewer #2 for the constructive comments, which have greatly improved the quality and clarity of our manuscript.

I have only minor comments:

The feedback event is indeed generally longer after a win than after a loss. For this reason, we did not use the speed of initiating a new game as the indicator for the speed of play, but rather the interval between starting a new game till inserting the first column in a new game. The RT that we used is therefore not confounded by the factors mentioned by the reviewer, as we described in the data analysis section (line 271):

The speed of starting a round in the behavioral tracking data is the duration from when players placed the last column in the previous round till when they started the current round (Table 1). This duration included the different feedback events after winning and losing, and the time spent on adjusting the stake. Due to these confounding factors, we used the response time (RT) of placing the first column as the behavioral indicator of speed of play instead. This RT is from when players started the current round till when they put the first column in one of the 4 slots, and thus is not confounded by the factors mentioned above.

To make sure that readers clearly understand which RT indicator was used, when explaining the general procedure, we now immediately add a clarification in the revised manuscript (line 153):

Due to the differences in the feedback after wins and losses, and the flexibility in when to start a new round, we did not use the speed of starting a new round as the indicator for the speed of play. Instead, we used the interval between starting a new round till placing the first column in the new round (see Fig 1), which is not confounded by the factors discussed above.

The reviewer is correct in noting that these two inclusion criteria are not the same. To avoid misunderstanding, we have deleted the word ‘again’ on line 255.

Thank you for this suggestion. We have now added an explanation on relative likelihoods in the caption of Figure 3.

For panel (A), relative likelihoods are the conditional probabilities of stopping after a loss and

after a win, normalized per player by the overall probability to stop, e.g. p(stop|loss)/p(stop − overall) and p(stop|win)/p(stop − overall).

Attachment

Submitted filename: responses.pdf

Click here for additional data file.^{(60.1KB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0273359.r005

Decision Letter 2

Gaëtan Merlhiot

8 Aug 2022

Winning and losing in online gambling: Effects on within-session chasing

PONE-D-21-35671R2

Dear Dr. Chen,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Gaëtan Merlhiot

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

PLoS One. doi: 10.1371/journal.pone.0273359.r006

Acceptance letter

Gaëtan Merlhiot

10 Aug 2022

PONE-D-21-35671R2

Winning and losing in online gambling: Effects on within-session chasing

Dear Dr. Chen:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Gaëtan Merlhiot

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 File. Online supplemental materials.

(PDF)

Click here for additional data file.^{(253KB, pdf)}

Attachment

Submitted filename: Plos-One-Revision.pdf

Click here for additional data file.^{(1.6MB, pdf)}

Attachment

Submitted filename: responses.pdf

Click here for additional data file.^{(60.1KB, pdf)}

Data Availability Statement

The anonymized per player summary data and the analysis code are publicly available at https://osf.io/vuy5d/. All reported results can be reproduced with the summary data.

[pone.0273359.ref001] 1. Clark L, Limbrick-Oldfield EH. Disordered Gambling: A Behavioral Addiction. Current Opinion in Neurobiology. 2013;23(4):655–659. doi: 10.1016/j.conb.2013.01.004 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref002] 2. Potenza MN. The Neural Bases of Cognitive Processes in Gambling Disorder. Trends in Cognitive Sciences. 2014;18(8):429–438. doi: 10.1016/j.tics.2014.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref003] 3. Calado F, Griffiths MD. Problem Gambling Worldwide: An update and Systematic Review of Empirical Research (2000–2015). Journal of Behavioral Addictions. 2016;5(4):592–613. doi: 10.1556/2006.5.2016.073 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref004] 4. American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders. Fifth edition ed. American Psychiatric Association; 2013. [Google Scholar]

[pone.0273359.ref005] 5. Blaszczynski A, Nower L. A Pathways Model of Problem and Pathological Gambling: Pathways Model of Gambling. Addiction. 2002;97(5):487–499. doi: 10.1046/j.1360-0443.2002.00015.x [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref006] 6. Zhang K, Clark L. Loss-Chasing in Gambling Behaviour: Neurocognitive and Behavioural Economic Perspectives. Current Opinion in Behavioral Sciences. 2020;31:1–7. doi: 10.1016/j.cobeha.2019.10.006 [DOI] [Google Scholar]

[pone.0273359.ref007] 7. Toce-Gerstein M, Gerstein DR, Volberg RA. A Hierarchy of Gambling Disorders in the Community: Gambling Disorders. Addiction. 2003;98(12):1661–1672. doi: 10.1111/j.1360-0443.2003.00545.x [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref008] 8. Breen RB, Zuckerman M. ‘Chasing’ in Gambling Behavior: Personality and Cognitive Determinants. Personality and Individual Differences. 1999;27(6):1097–1111. doi: 10.1016/S0191-8869(99)00052-5 [DOI] [Google Scholar]

[pone.0273359.ref009] 9. Leino T, Torsheim T, Pallesen S, Blaszczynski A, Sagoe D, Molde H. An Empirical Real-World Study of Losses Disguised as Wins in Electronic Gaming Machines. International Gambling Studies. 2016;16(3):470–480. doi: 10.1080/14459795.2016.1232433 [DOI] [Google Scholar]

[pone.0273359.ref010] 10. Lister JJ, Nower L, Wohl MJA. Gambling Goals Predict Chasing Behavior during Slot Machine Play. Addictive Behaviors. 2016;62:129–134. doi: 10.1016/j.addbeh.2016.06.018 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref011] 11. Nigro G, Ciccarelli M, Cosenza M. The Illusion of Handy Wins: Problem Gambling, Chasing, and Affective Decision-Making. Journal of Affective Disorders. 2018;225:256–259. doi: 10.1016/j.jad.2017.08.010 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref012] 12. Ciccarelli M, Cosenza M, Griffiths MD, D’Olimpio F, Nigro G. The Interplay between Chasing Behavior, Time Perspective, and Gambling Severity: An Experimental Study. Journal of Behavioral Addictions. 2019;8(2):259–267. doi: 10.1556/2006.8.2019.29 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref013] 13. O’Connor J, Dickerson M. Definition and Measurement of Chasing in Off-Course Betting and Gaming Machine Play. Journal of Gambling Studies. 2003;19:359–386. doi: 10.1023/A:1026375809186 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref014] 14. Gehring WJ, Willoughby AR. The Medial Frontal Cortex and the Rapid Processing of Monetary Gains and Losses. Science. 2002;295(5563):2279–2282. doi: 10.1126/science.1066893 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref015] 15. Smith G, Levere M, Kurtzman R. Poker Player Behavior After Big Wins and Big Losses. Management Science. 2009;55(9):1547–1555. doi: 10.1287/mnsc.1090.1044 [DOI] [Google Scholar]

[pone.0273359.ref016] 16. Studer B, Limbrick-Oldfield EH, Clark L. ‘Put Your Money Where Your Mouth Is!’: Effects of Streaks on Confidence and Betting in a Binary Choice Task. Journal of Behavioral Decision Making. 2015;28(3):239–249. doi: 10.1002/bdm.1844 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref017] 17. Thaler RH, Johnson EJ. Gambling with the House Money and Trying to Break Even: The Effects of Prior Outcomes on Risky Choice. Management Science. 1990;36(6):643–660. doi: 10.1287/mnsc.36.6.643 [DOI] [Google Scholar]

[pone.0273359.ref018] 18. Demaree HA, Burns KJ, DeDonno MA, Agarwala EK, Everhart DE. Risk Dishabituation: In Repeated Gambling, Risk Is Reduced Following Low-Probability “Surprising” Events (Wins or Losses). Emotion. 2012;12(3):495–502. doi: 10.1037/a0025780 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref019] 19. Weber M, Zuchel H. How Do Prior Outcomes Affect Risk Attitude? Comparing Escalation of Commitment and the House-Money Effect. Decision Analysis. 2005;2(1):30–43. doi: 10.1287/deca.1050.0034 [DOI] [Google Scholar]

[pone.0273359.ref020] 20. Imas A. The Realization Effect: Risk-Taking After Realized Versus Paper Losses. American Economic Review. 2016;106(8):2086–2109. doi: 10.1257/aer.20140386 [DOI] [Google Scholar]

[pone.0273359.ref021] 21. Corr PJ, Thompson SJ. Pause for Thought: Response Perseveration and Personality in Gambling. Journal of Gambling Studies. 2014;30(4):889–900. doi: 10.1007/s10899-013-9395-4 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref022] 22. Dixon MJ, MacLaren V, Jarick M, Fugelsang JA, Harrigan KA. The Frustrating Effects of Just Missing the Jackpot: Slot Machine Near-Misses Trigger Large Skin Conductance Responses, But No Post-Reinforcement Pauses. Journal of Gambling Studies. 2013;29(4):661–674. doi: 10.1007/s10899-012-9333-x [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref023] 23. Stange M, Graydon C, Dixon MJ. “I Was That Close”: Investigating Players’ Reactions to Losses, Wins, and Near-Misses on Scratch Cards. Journal of Gambling Studies. 2016;32(1):187–203. doi: 10.1007/s10899-015-9538-x [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref024] 24. Chen Z, Reimer CB, Verbruggen F. Proximity and Expectancy Modulate Response Vigor After Reward Omission. Collabra: Psychology. 2020;6(1):18184. doi: 10.1525/collabra.18184 [DOI] [Google Scholar]

[pone.0273359.ref025] 25. Verbruggen F, Chambers CD, Lawrence NS, McLaren IPL. Winning and Losing: Effects on Impulsive Action. Journal of Experimental Psychology: Human Perception and Performance. 2017;43(1):147–168. doi: 10.1037/xhp0000284 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref026] 26. Eben C, Chen Z, Vermeylen L, Billieux J, Verbruggen F. A Direct and Conceptual Replication of Post-Loss Speeding When Gambling. Royal Society Open Science. 2020;7(5):200090. doi: 10.1098/rsos.200090 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref027] 27. Loba P, Stewart SH, Klein RM, Blackburn JR. Manipulations of the Features of Standard Video Lottery Terminal (VLT) Games: Effects in Pathological and Non-Pathological Gamblers. Journal of Gambling Studies. 2001;17(4):297–320. doi: 10.1023/A:1013639729908 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref028] 28. Blaszczynski A, Sharpe L, Walker M, Shannon K, Coughlan MJ. Structural Characteristics of Electronic Gaming Machines and Satisfaction of Play Among Recreational and Problem Gamblers. International Gambling Studies. 2005;5(2):187–198. doi: 10.1080/14459790500303378 [DOI] [Google Scholar]

[pone.0273359.ref029] 29. Linnet J, Rømer Thomsen K, Møller A, Callesen MB. Event Frequency, Excitement and Desire to Gamble, among Pathological Gamblers. International Gambling Studies. 2010;10(2):177–188. doi: 10.1080/14459795.2010.502181 [DOI] [Google Scholar]

[pone.0273359.ref030] 30. Gainsbury SM, Suhonen N, Saastamoinen J. Chasing Losses in Online Poker and Casino Games: Characteristics and Game Play of Internet Gamblers at Risk of Disordered Gambling. Psychiatry Research. 2014;217(3):220–225. doi: 10.1016/j.psychres.2014.03.033 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref031] 31. Jiménez-Murcia S, Granero R, Fernández-Aranda F, Menchón JM. Comparison of Gambling Profiles Based on Strategic versus Non-Strategic Preferences. Current Opinion in Behavioral Sciences. 2020;31:13–20. doi: 10.1016/j.cobeha.2019.09.001 [DOI] [Google Scholar]

[pone.0273359.ref032] 32. M Gainsbury S, Liu Y, Russell AMT, Teichert T. Is All Internet Gambling Equally Problematic? Considering the Relationship between Mode of Access and Gambling Problems. Computers in Human Behavior. 2016;55:717–728. doi: 10.1016/j.chb.2015.10.006 [DOI] [Google Scholar]

[pone.0273359.ref033] 33.R Core Team. R: A Language and Environment for Statistical Computing; 2020. Available from: https://www.R-project.org/.

[pone.0273359.ref034] 34.Singmann H, Bolker B, Westfall J, Aust F, Ben-Shachar MS. afex: Analysis of Factorial Experiments; 2020. Available from: https://CRAN.R-project.org/package=afex.

[pone.0273359.ref035] 35.Morey RD, Rouder JN. BayesFactor: Computation of Bayes Factors for Common Designs; 2018. Available from: https://CRAN.R-project.org/package=BayesFactor.

[pone.0273359.ref036] 36.Xie Y. bookdown: Authoring Books and Technical Documents with R Markdown; 2020. Available from: https://CRAN.R-project.org/package=bookdown.

[pone.0273359.ref037] 37.Wickham H, Chang W, Henry L, Pedersen TL, Takahashi K, Wilke C, et al.. ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics; 2020. Available from: https://CRAN.R-project.org/package=ggplot2.

[pone.0273359.ref038] 38.Kassambara A. ggpubr:’ggplot2’ Based Publication Ready Plots; 2020. Available from: https://CRAN.R-project.org/package=ggpubr.

[pone.0273359.ref039] 39.Zhu H. kableExtra: Construct Complex Table with’kable’ and Pipe Syntax; 2020. Available from: https://CRAN.R-project.org/package=kableExtra.

[pone.0273359.ref040] 40.Xie Y. knitr: A General-Purpose Package for Dynamic Report Generation in R; 2020. Available from: https://CRAN.R-project.org/package=knitr.

[pone.0273359.ref041] 41.Hope RM. Rmisc: Ryan Miscellaneous; 2013. Available from: https://CRAN.R-project.org/package=Rmisc.

[pone.0273359.ref042] 42.Wickham H. tidyverse: Easily Install and Load the’Tidyverse’; 2019. Available from: https://CRAN.R-project.org/package=tidyverse.

[pone.0273359.ref043] 43. Delacre M, Lakens D, Leys C. Why Psychologists Should by Default Use Welch’s t-Test Instead of Student’s t-Test. International Review of Social Psychology. 2017;30(1):92–101. doi: 10.5334/irsp.82 [DOI] [Google Scholar]

[pone.0273359.ref044] 44. Dienes Z. Using Bayes to Get the Most out of Non-Significant Results. Frontiers in Psychology. 2014;5. doi: 10.3389/fpsyg.2014.00781 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref045] 45. Wagenmakers EJ, Love J, Marsman M, Jamil T, Ly A, Verhagen J, et al. Bayesian Inference for Psychology. Part II: Example Applications with JASP. Psychonomic Bulletin & Review. 2018;25(1):58–76. doi: 10.3758/s13423-017-1323-7 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref046] 46. Lakens D. Calculating and Reporting Effect Sizes to Facilitate Cumulative Science: A Practical Primer for t-Tests and ANOVAs. Frontiers in Psychology. 2013;4. doi: 10.3389/fpsyg.2013.00863 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref047] 47. Dyson BJ, Wilbiks JMP, Sandhu R, Papanicolaou G, Lintag J. Negative Outcomes Evoke Cyclic Irrational Decisions in Rock, Paper, Scissors. Scientific Reports. 2016;6(1):20479. doi: 10.1038/srep20479 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref048] 48. Felton M, Lyon DO. The Post-Reinforcement Pause. Journal of the Experimental Analysis of Behavior. 1966;9(2):131–134. doi: 10.1901/jeab.1966.9-131 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0273359.ref049] 49. Campbell-Meiklejohn DK, Woolrich MW, Passingham RE, Rogers RD. Knowing When to Stop: The Brain Mechanisms of Chasing Losses. Biological Psychiatry. 2008;63(3):293–300. doi: 10.1016/j.biopsych.2007.05.014 [DOI] [PubMed] [Google Scholar]

[pone.0273359.ref050] 50. Raimo S, Cropano M, Trojano L, Santangelo G. The Neural Basis of Gambling Disorder: An Activation Likelihood Estimation Meta-Analysis. Neuroscience & Biobehavioral Reviews. 2021;120:279–302. doi: 10.1016/j.neubiorev.2020.11.027 [DOI] [PubMed] [Google Scholar]

PERMALINK

Winning and losing in online gambling: Effects on within-session chasing

Zhang Chen

Roos Arwen Doekemeijer

Xavier Noël

Frederick Verbruggen

Roles

Abstract

Introduction

Three expressions of within-session loss-chasing

The current research

Materials and methods

Participants

Procedure

General rules of the game

Fig 1. A flowchart showing the events within one round, and on which event each expression of loss-chasing is based.

The game interface

Fig 2. A schematic illustration of the game interface.

Measures

Behavioral tracking data

Table 1. An overview of the variables in the behavioral tracking data.

Defining the low- and high-involvement groups

Statistical analysis

Players and play behavior

Overview of the analyses on loss-chasing

Table 2. An overview of the behavioral indicator, main analysis, loss-chasing expression and whether it was observed in the current study for each facet.

When to stop

Change in stake

Speed of play

Ethics

Results

Players and play behavior

Players

Play behavior

Table 3. Comparing play behavior between the two groups.

When to stop

Table 4. Statistical analyses on when to stop.

Fig 3. Behavioral expressions of within-session chasing.

Change in stake

Table 5. Statistical analyses on change in stake.

Speed of play

Table 6. Statistical analyses on speed of play.

Discussion

When to stop

Change in stake

Speed of play

Chasing: A multifaceted phenomenon

Limitations and future directions

Conclusion

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Gaëtan Merlhiot

Roles

Author response to Decision Letter 0

Decision Letter 1

Gaëtan Merlhiot

Roles

Author response to Decision Letter 1

Decision Letter 2

Gaëtan Merlhiot

Roles

Acceptance letter

Gaëtan Merlhiot

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases