Summary
Population genetic analyses of local ancestry tracts routinely assume that the ancestral admixture process is identical for both parents of an individual, an assumption that may be invalid when considering recent admixture. Here, we present Parental Admixture Proportion Inference (PAPI), a Bayesian tool for inferring the admixture proportions and admixture times for each parent of a single admixed individual. PAPI analyzes unphased local ancestry tracts and has two components: a binomial model that leverages genome-wide ancestry fractions to infer parental admixture proportions and a hidden Markov model (HMM) that infers admixture times from tract lengths. Crucially, the HMM accounts for unobserved within-ancestry recombination by approximating the pedigree crossover dynamics, enabling inference of parental admixture times. In simulations, we find that PAPI’s admixture proportion estimates deviate from the truth by 0.047 on average, outperforming ANCESTOR and PedMix by 46.0% and 57.6%, respectively. Moreover, PAPI’s admixture time estimates were strongly correlated with the truth () but have an average downward bias of 1.01 generations that is partly attributable to inaccuracies in local ancestry inference. As an illustration of its utility, we ran PAPI on African American genotypes from the PAGE study (N = 5,786) and found strong evidence of assortative mating by ancestry proportion: couples’ ancestry proportions are highly correlated (R = 0.87) and are closer to each other than expected under random mating (p < 10−6). We anticipate that PAPI will be useful in studying the population dynamics of admixture and will also be of interest to individuals seeking to learn about their personal genealogies.
Keywords: local ancestry, assortative mating, admixture
Introduction
Widespread consumer interest in one’s personal genetic ancestry and genealogy has fueled the rise of direct-to-consumer genetic testing companies,1,2 enabling high resolution studies of population structure, admixture, and migration patterns.3, 4, 5 One of the most popular features these companies provide is ancestry estimation: the geographic locations of the populations from which customers inherited their DNA. The techniques for such estimation, first developed by academic researchers,6, 7, 8 have applications both to demographic inference9, 10, 11 as well as to disease association mapping.12,13
Inferring an individual’s genome-wide and locus-specific ancestry—i.e., local ancestry6—reveals not only that person’s genetic heritage but also information about the genetic ancestry of his or her parents.14,15 Indeed, each parent transmits half of his or her genome to a child, so in principle, one can recover half the DNA of each parent by analyzing data from a single individual. In practice however, phasing errors and uncertain interchromosomal phase pose substantial challenges to reconstructing the parents’ genomes, although methods that analyze multiple siblings and/or use population allele frequencies can be effective.16, 17, 18
Many past studies of admixed individuals have focused on population-level ancestry questions, including migration times,5,9,19 yet analyzing data from couples has the power to provide refined information about demographic patterns. For example, it makes possible studies of assortative mating by ancestry,20, 21, 22 could help identify subgroups with different admixture histories, and may detect outlier individuals with patterns distinct from the bulk of the population.
The features derivable from local ancestry signals include population ancestry proportions and estimated times since admixture based on tract lengths.9,23 Individual-level ancestry proportions are generally reliable to infer, depending on the ancestral populations,6,24,25 yet computing admixture times for an individual (or his/her parents) from only one genome has not received careful attention and may be difficult. In particular, high variance in tract lengths9 and the finite genome size can lead to noisy admixture times estimates.26 Even so, noisy estimates may still be useful when analyzed in aggregate across many samples.
Although phase accuracy remains an issue in the context of local ancestry inference,13 homozygous ancestry regions provide unambiguous information about the ancestry of the two parents at that locus. As such, even when analyzing unphased local ancestry tracts,6,25 one can leverage these homozygous regions (as well as the lack thereof) to estimate the parental ancestry fractions. Analyzing unphased local ancestry tracts also helps prevent biases due to phase inaccuracy, both in estimating the parental ancestry proportions and the time since admixture (see subjects and methods).
We developed Parental Ancestry Proportion Inference (PAPI), a tool that provides estimates of both the admixture proportions and times since admixture of both parents of two-way admixed individuals. PAPI uses both a binomial model and a hidden Markov model (HMM) to infer these parental values, and, by default, combines these two models into a composite likelihood. We validated PAPI by using both simulated African Americans and trios from the HapMap African ancestry in Southwest USA (ASW) population.27 PAPI’s parental ancestry estimates are highly accurate, its time since admixture estimates are well correlated with the ground truth, and it can determine when the two parents have different times since admixture. We applied PAPI to African Americans from the PAGE study28 and find strong evidence for ancestry-based assortative mating (results).
Subjects and methods
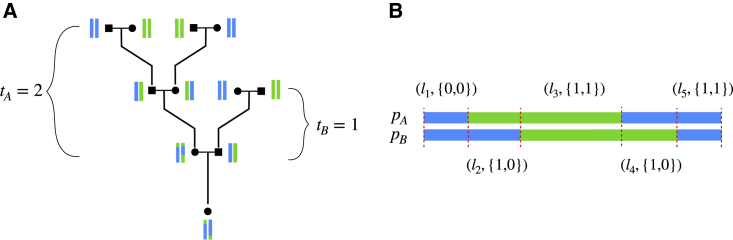
PAPI is designed to infer the ancestry proportions (pA,pB) and the average number of generations to unadmixed ancestors (tA,tB) for the unsexed parents A and B of a single admixed individual (Figure 1). It takes unphased diploid local ancestry tracts for focal admixed individuals as input and works on two-way admixed samples, but the approach can be extended to handle multi-way admixture. Throughout this paper, we label the two populations being analyzed arbitrarily as 0 and 1.
Figure 1.
Example pedigree and local ancestry data
(A) Pedigree with vertical bars next to each individual representing two of their chromosomes, each colored to represent local ancestry from two populations, blue and green. tA and tB are the number of generations to the unadmixed ancestors for parents A and B, respectively; this is the generation in which at least one couple contains individuals of different ancestries.
(B) PAPI takes in unphased local ancestry tracts denoted by xi = (li, ai). The image depicts a particular phasing of the data with labels that correspond to the observed unphased data.
The advantage of using unphased local ancestry calls is that they are immune to switch errors that affect the phased input to (and therefore output of) haplotype-based local ancestry methods. PAPI makes inferences of times since admixture (tA,tB) based on local ancestry tract lengths, and switch errors can create artificially short or long ancestry tracts that would bias this approach if it relied on phased input. Additionally, switch errors in phased input can put an ancestry tract on an incorrect haplotype, which would lead to incorrect (pA,pB) estimates.
PAPI employs a composite likelihood built from two component models: a binomial model that infers (pA,pB) and a hidden Markov model (HMM) that jointly infers all parameters . The binomial model uses genome-wide diploid ancestry proportions to infer (pA,pB). In turn, the HMM estimates by integrating over all possible phasings of the input local ancestry tracts using the forward algorithm. Our empirical findings indicate that forming a composite likelihood from these two models provides more accurate estimates of than those of each component alone (results).
A key challenge in inferring (tA,tB) is that a subset of the crossovers the ancestors transmitted typically occurs between haplotypes of the same ancestry and, as a result, are not observable in local ancestry calls. The HMM accounts for this by approximating the rate of these hidden crossovers from the parental ancestry proportions (pA,pB) as described below. This approximation relies on a population genetic model of ancestry tract length distributions following a pulse migration,9 which serves here as a simplified model of the complex dynamics of the meioses in the focal individual’s pedigree.
A binomial model to infer parent ancestry proportions
The binomial model for estimating (pA,pB) operates on genome-wide diploid ancestry fractions. As a motivating example, consider a locus in the focal individual that is homozygous for ancestry. This locus carries unambiguous information about both parents’ ancestries—it is certain that each parent carries at least one copy of the given ancestry in that region. Furthermore, low proportions of homozygous ancestry regions indicate that the parents most likely differ in their ancestry at most loci. For example, a child that is heterozygous for ancestry at every position most likely has two parents with very high levels of ancestry from distinct populations. An alternative but unlikely explanation of such data is that the parents have ancestries that alternate between the two populations across chromosomes. Thus, considering the genome-wide fraction of each type of unphased local ancestry call in the focal sample (i.e., homozygous for population 0 or 1 or heterozygous for ancestry) allows us to formulate a parsimonious model of the parents’ ancestry fractions. These observations, which may not be fully captured in some other models of parental ancestry, are the key motivation behind PAPI’s binomial model. We note that the approach described below is equivalent to that adopted in another recently developed method to model parental ancestry.29
PAPI’s binomial model treats the DNA transmitted by a given parent as a sequence of Bernoulli trials parameterized by the parent’s ancestry proportion—i.e., by the target of inference pj. We calculate pj as the fraction of parent j’s genome contained in tracts of ancestry 0, calculated with Morgan units. Note that PAPI only has access to the ancestry proportion of the haplotype the parent transmitted. This proportion will in general differ from because of recombination and random assortment of alleles to gametes and is only equal to pj in expectation. The difference between the transmitted and true parent proportions most likely accounts for some of the variance in estimation accuracy we observe in practice (results).
Formally, let be the input unphased diploid local ancestry tracts of a focal sample. Each of these tracts is a tuple xi = (li,ai) for where li represents the tract length in Morgans and is its unphased local ancestry (Figure 1B). Curly braces in the ancestry component indicate that these values are unordered, since the data are unphased, so the class is consistent with the phased, ordered states (in square brackets) and .
The likelihood of the binomial model is:
| (Equation 1) |
where is the fraction of parent j’s genome contained in tracts of ancestry 1, , and , with I being the indicator function. That is, is the total Morgan length of the genome contained in tracts of ancestry type a, scaled by a hyperparameter τ that accounts for the effective number of independent markers. This hyperparameter is necessary because the segment lengths are in Morgan units, and the effective number of independent loci in a tract of length 1 Morgan is the number of crossovers that have occurred in that interval since admixture began. In expectation, this number is exactly tj for the haplotype parent j transmitted. Following this reasoning, we set τ to a rough population averaged number of generations since admixture. For all the analyses presented in results, we set , consistent with average estimates of the time since admixture from previous studies in African Americans,6,30,31 and with PAPI’s own estimates in the HapMap ASW population of African American samples27 (results). PAPI is strongly robust to even large variations in τ: considering versus , the accuracy of its admixture proportion estimates decreases by only 1.32% (in relative terms and measured with ; see “computing measures of accuracy and bias”) and that of its admixture time estimates by 0.621% (measured with Pearson correlation; Figures S2 and S3).
Modeling the relationship between admixture time and ancestry switch rates
Crossover placement along a haplotype that was subject to m meioses can be modeled as a Poisson process with rate m per Morgan. If , this model provides a good fit to intercrossover distances generated under a crossover interference model.26 However, applying the Poisson model to local ancestry segments is complicated by the presence of within-population hidden crossovers. These are historical crossovers that occur at homozygous ancestry positions and, as a result, are not directly observed in local ancestry tracts. Their presence requires an adjustment to the ancestry switch rate parameter—i.e., this rate is not a direct measure of the number of meioses since admixture.
In this subsection we assume that for each parent , all the ancestors tj generations ago are unadmixed and that at least one couple in that generation includes individuals of both ancestries, while the other individuals have the same ancestry (Figure 1A). We refer to this form of pedigree throughout as the “base case,” and it corresponds to a single pulse of admixture, with migrants entering only tj generations ago. This means that at least one of the ancestors generations ago is entirely heterozygous for ancestry. We do this to defer consideration of the crossover rate parameter in more complex admixture scenarios—those with multiple pulses of admixture—to later in the text (see “simulating multiple pulses of admixture on a pedigree”).
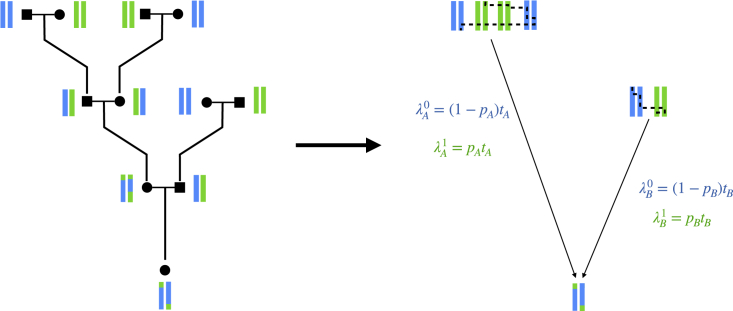
The model we adopt approximates pedigree-generated crossovers as Markovian transitions within a pool of haplotypes (Figure 2). The proportion of haplotypes in the pool from population 0 is pj, the parental ancestry proportion. Gravel proposed a population genetic model of this form in the context of pulse admixture events,9 and noted that the probability of transitioning to a haplotype of a different ancestry is simply the proportion of haplotypes of that ancestry in the population. In particular, the Poisson rates for switching from ancestry 0 to 1 and for switching from 1 to 0, are as follows:
| (Equation 2) |
Figure 2.
Markovian approximation to an individual’s full pedigree
Example pedigree for an admixed individual (left). Viewing the unadmixed ancestors as a pool of founder haplotypes (right), one for each parent, and further viewing recombinations as a Markovian switching process in this pool motivates the use of a single-pulse migration model to capture the effect of tj and pj on the observed between-ancestry Poisson switch rates and .
Thus, to obtain the switch rate out of a given ancestry, the adjustment to the crossover rate is the proportion of haplotypes of the opposite ancestry. Intuitively, one can view these rate parameters ( and ) as the expected count of crossovers per Morgan that result in an ancestry switch.
Note the nature of the approximation made here, which is 2-fold: first, crossovers in the model are no longer constrained to occur within an individual, which ignores long-range correlations caused by within-individual meioses.32 Second, pj is used to represent the proportion of founder haplotypes of ancestry 0 even though this value—parent j’s ancestry proportion—may differ from the fraction of founders that have this ancestry. Despite these caveats, our empirical results suggest that this is an effective approximation (results).
An important limitation in applying the formulas in Equation 2 is that they incorrectly account for the crossovers transmitted by an individual that is entirely heterozygous for ancestry. To illustrate this, consider such a parent j, who will have pj = 0.5. Equation 2 implies that , and because every locus in parent j’s genome is heterozygous for ancestry, all of j’s crossovers will produce ancestry switches. This makes the rate of switches per Morgan, and so, despite including only one meiosis, the equations will suggest that tj = 2. The issue is that the model implicitly assumes that the ancestry proportions of parent j’s two chromosomes are both 0.5 when in fact one is entirely composed of ancestry 0 and the other of ancestry 1. This scenario arises for all ancestors with entirely heterozygous ancestry, and we have found that subtracting 1 from the raw estimates is an effective fix no matter how large tj is26 (data not shown). PAPI applies this correction internally by subtracting 1 from the tj point estimates and from each Markov chain Monte Carlo (MCMC) sample followed by rounding up negative values to 0.
A hidden Markov model to jointly infer admixture times and ancestry proportions
PAPI computes the likelihood of the observed unphased local ancestry tracts given assignments of the parameters , and uses either an MCMC or gradient descent (GD) method to estimate these parameters (below). The hidden states of the HMM encode phased local ancestry assignments , where , and the two elements of correspond to a transmitted chromosome by a given parent; as a matter of convention, we let the first element be the chromosome transmitted by parent A. Because the phase is unknown, the HMM integrates over all possible phase assignments to compute the likelihood of the unphased data. In order to model the relationship of and to the observed data while accounting for hidden recombinations (above), PAPI internally reparameterizes as by applying Equation 2 for , and the method therefore calculates the likelihood . Below, we treat the conditioning on parameters as implicit and omit them from the probabilities.
The HMM models the local ancestry tract lengths as exponentially distributed, as follows from a Poisson crossover model. More specifically, the initial probability is a product of the probabilities of the first observed tracts (for haplotypes A and B) in , both of which have length : . We define the transition probabilities to ensure that tracts that extend beyond the interval they start in have a total probability consistent with their full length. That is, the transition probability depends on whether the ancestry of a haplotype changes between adjacent intervals and only includes the leading term in the first interval where haplotype j has switched ancestries. We express these as follows:
| (Equation 3) |
For example, in the first case in Equation 3, parent B’s transmitted chromosome does not change ancestry (), and the transition probability incorporates the term to reflect this. The total probability of this tract from its origin in a given interval k to its termination at the end of some interval then is —which is identical to the probability of observing a tract of length . By contrast, for this case to apply, haplotype A would have changed ancestries, and the formula includes a leading term here where the tract begins. Other cases follow this same pattern, but the final case (in Equation 3) requires two crossovers to occur at the same position (one on each haplotype). This is prohibited by the model, and the corresponding transition probability is set to 0. If the observed data implies such a transition and PAPI is run without an error model (below), it will throw an error. Although in our analyses such transitions never occurred in the HAPMIX local ancestry tracts, a user can address any such cases by pre-processing them to introduce a small tract that switches the ancestry of only one haplotype between the two disallowed tracts.
The above formulation is somewhat non-standard in that the initial and transition probabilities depend on the tract lengths, which are part of the observed data. An alternative might put the exponential terms—which are calculated from the tract lengths—into the emission probabilities, leaving only the leading λ terms in the transition probabilities. However, doing this yields transition probabilities that are typically greater than one and obscures the conceptual underpinnings of the model—that of Poisson processes. The current formulation can be thought of as implicitly combining more standard transition and emission terms in the transition probabilities. We therefore set the emission probabilities in this formulation to 1 if the hidden state is a phased version of the observed local ancestry and 0 if not. We describe an optional error model that allows for mismatched hidden and observed ancestry states in the next subsection.
We treat the final tract of a chromosome as partially observed, as the position of the next crossover is unknown and would land somewhere beyond the chromosome endpoint. Such tracts should contribute only an exponential term to the likelihood, with the leading term omitted—corresponding to the probability of a tract of length greater than that observed. PAPI accomplishes this by setting the probability of transitioning from the final tract to a special end state as follows: . These inverse terms act to cancel out the and terms that were introduced when the tracts with ancestry and were first transitioned to, leaving only exponential terms as desired.
With the HMM’s initial, transition, and emission probabilities specified, PAPI computes the likelihood of the observed data given by marginalizing over all possible hidden state paths with the forward algorithm. The model treats each chromosome as independent given , so the total likelihood is the product of each chromosome’s likelihood. Note that the fact that parent labels are arbitrary and interchangeable introduces non-identifiability into the model. In particular, and have the same likelihood and only produce swapped parent labels. When run in the MCMC inference mode (see below), PAPI handles this non-identifiability by restricting the parameter space to points such that . When run in the GD inference mode (below), there is no need to restrict the space, as PAPI will find a mode of the posterior distribution, and the presence of more than one equivalent mode does not hamper the inference.
The above HMM is similar to that of ANCESTOR,14 another approach for inferring parent ancestry proportions. Both methods apply to unphased local ancestry calls and model the phase of those calls in the hidden states. A point of departure is that PAPI parameterizes the model explicitly in terms of (although it still performs the underlying calculations in terms of ), which affords it two advantages. First, by modeling hidden crossovers (above), PAPI can produce direct estimates of and rather than only and . Second, PAPI’s HMM uses more of the available information for inferring by incorporating these parameters into the transition probabilities (via and ), thus producing more accurate estimates of across a range of scenarios (results). While the estimates from PAPI’s HMM are in general more accurate than those of ANCESTOR, for the most accurate estimates, PAPI’s binomial component is important, and PAPI performs best when run with the HMM and binomial component together with the full model (results).
Handling erroneous tracts
Despite being immune to switch errors, unphased local ancestry segments are still subject to erroneous calls that have the potential to bias the inference of . We address this by providing an optional error model that has a non-zero probability of emitting unphased local ancestry tracts with a different ancestry than that of the hidden state. Using the congruence operator, we say if the ordered hidden state z has the same ancestry values as those in the unordered observed local ancestry a; e.g., and . Using this notation, the emission probabilities of the error model are as follows:
| (Equation 4) |
Here, φ is a hyperparameter that we set heuristically so that when , decreases by a factor of for every centiMorgan unit increase in , so . We divide the first case in Equation 4 by 1/2 because there are three unordered local ancestry calls and therefore two ways to select such that . The exponential form of these equations leads to higher emission probabilities for incongruous tracts that are small. Another way to think about this is that the model applies a penalty for treating larger tracts as erroneous and that the penalty decreases exponentially with decreasing tract size. So if the HMM encounters a sufficiently small tract where differs from both and , it may favor the incongruous hidden state (i.e., where but ) in order to avoid ancestry state switches over a small distance (see Equation 3) while incurring the incongruous tract penalty from Equation 4.
Combining component models and performing inference
As noted earlier, PAPI can combine the output signals from its two component models—the binomial model and the HMM—which improves its inference of compared to either model alone (results). Notably, both models operate on the same data , which renders their likelihoods non-independent, but the HMM analyzes the unphased local ancestry calls directly, while the binomial model considers the summary statistics in . Despite this non-independence, PAPI’s default setting combines them to form a composite likelihood, treating . Furthermore, PAPI uses a Bayesian model, computing the following posterior based on the composite likelihood (which we refer to as the full model):
| (Equation 5) |
Here, we make explicit the assumption that all the model parameters (in ) are independent, and note that the binomial likelihood since that model only considers . We use uniform priors on the parameters, with and . The full model can be thought of as treating the posterior distribution on from the binomial model as a prior to the HMM. This may explain the improved accuracy (and speed) of the full model when compared to either the binomial or HMM alone (results); i.e., the genome-wide information from the binomial likelihood shapes the overall distribution, making it more strongly peaked near the true and .
PAPI uses one of two methods to perform inference, as specified by the user. By default, it performs gradient descent (GD) with the constrained optimization algorithm L-BFGS-B (implemented in the scipy-optimize33 Python package). This yields a point estimate corresponding to a local maximum of the likelihood function. The empirical results suggest that these estimates, despite being local maxima, are reliable in practice. The second inference method uses MCMC in order to draw from the posterior distribution—specifically performing slice sampling (via the PyMC3 package34). In this setting, PAPI performs 500 burn-in iterations followed by 1,000 MCMC draws across four independent chains per individual (6,000 samples total) and outputs a 90% credible interval for each of the parameters.
The GD inference method is quite fast, whereas the MCMC approach requires larger compute times. In light of timing and performance (see results), we recommend running PAPI with the full model (Equation 5) in the GD inference mode. It is also possible to run the HMM or binomial model alone, i.e., to analyze or , respectively. (In these settings, PAPI does not leverage a composite likelihood.) Note that all three models supply estimates, and a user can run the binomial model in MCMC mode if posterior distributions of alone are required (which we recommend, as the MCMC runs are much faster with the binomial model alone [results]).
Simulating realistic admixed genotypes
Perhaps the most realistic way to simulate genetic data for an admixed individual is to explicitly model their pedigree and simulate a meiosis for each of their ancestors. This would appropriately constrain crossovers to occur only between the two haplotypes of each ancestor and can incorporate crossover interference modeling.26 However, doing this requires the use of data from founders, where T is the number of ancestral generations in the pedigree, thus consuming large data resources from unadmixed individuals to simulate only a single admixed individual. Furthermore, some unadmixed samples must be held out of the simulation for use in the panels required by the local ancestry inference software.
We adopted a three-step hybrid simulation scheme that explicitly accounts for pedigree-based transmissions while using far fewer unadmixed samples (Figure S1). First, we ran Ped-sim26 to simulate individuals from a specified pedigree structure, similar to the above approach, but without providing input genetic data, and thus obtained no output genotypes at this stage. We used a sex-specific genetic map,35 a Poisson crossover model, and ran Ped-sim in a mode (using the –bp option) that outputs the founder haplotype ID that the focal admixed individual carries at each position, with crossover break points indicated. Rather than using the resulting break point file as is, with its unique haplotypes, in step two we modified it by mapping each founder haplotype to one of the two ancestral population labels according to the desired value of as well as (see below). Finally, we used this population-only break point file as input to admix-simu,36 which also takes in genetic data corresponding to unadmixed founder haplotypes from each population. Admix-simu treats the founder haplotypes as a pool and samples haplotype segments on the basis of the population labels and break points contained in the break point file. More specifically, at each break point, the method randomly samples a new haplotype (of the appropriate population) from the pool, creating non-overlapping sampling paths (Figure S1). This interrupts the linkage disequilibrium (LD) on either side of a break point as in a real crossover and approximates the full pedigree model. After sampling all segments of the target admixed individuals’ haplotypes, admix-simu outputs the final haplotypes, which we then grouped in pairs to form individual diploid genotypes.
We simulated pedigrees of the base case form introduced earlier (see “modeling the relationship between admixture time and ancestry switch rates”), assigning the founders in generations to different populations according to the proportions given by the expectation . This expectation will in general differ from the realized values (in the parents of the focal individual) that we used to calculate deviation statistics (see “computing measures of accuracy and bias”). Further, the range of values is constrained by the number of founder individuals in the pedigree, which depends on (e.g., it is impossible to simulate when , as the number of founder haplotypes is too small). Therefore, we assigned the founder ancestries to approximate the expected proportions as closely as possible.
We used data from the HapMap CEU and YRI populations as the input unadmixed founder haplotypes for simulating. In order to provide large unadmixed panels to the local ancestry inference software and ensure these are unrelated to the target simulated individuals, we first excluded children from the HapMap CEU and YRI populations and split the remaining individuals (trio parents, duo parents, and unrelated samples) into four sets of 22 individuals for the two populations. We then used the pipeline described above to simulate admixed individuals in four separate runs, each using one of the four sets of simulation founders as input to admix-simu and with each assigned a different value: or . We repeated this procedure (with the same four founder datasets) for each of the desired settings of (tA,tB) (see results for these values). This produces four sets of simulated samples for every (tA,tB) that are unrelated to the other three sets of unadmixed samples. Doing this allows us to utilize the three sets of unadmixed samples (66 individuals in total) as panels in HAPMIX when analyzing the corresponding simulated individuals, thus leveraging all the available data for simulating while still maintaining sizeable panels for local ancestry inference.
To phase the HapMap samples, we first downloaded the Phase III genotypes (see data and code availability) and performed a lift over to GRCh37 coordinates.37 We then removed all markers that were unmapped by the lift over and, for positions typed on both the Affymetrix and Illumina arrays, removed the Affymetrix genotypes. A few positions remained duplicated, and we retained one random genotype for each such site. Following this, we used the reported relationships to identify trios and duos and used PLINK 1.938 to set sites with Mendelian errors to missing (using the –set-me-missing option). Finally, we phased the data by running Beagle 3.3.2 (October 31, 2011)39 on all the samples, supplying the labeled trios and duos as well as all unrelated individuals. (Notably this phasing run included all HapMap populations, not just the YRI and CEU samples.)
Simulating multiple pulses of admixture on a pedigree
The base case pedigree only includes a subset of the admixture histories that are possible, as unadmixed ancestors from distinct populations will in general appear at more than one generation in an admixed individual’s pedigree. We sought to ask what value of tj our pulse-migration model (Equation 2) will estimate in more general cases.
To characterize this, we simulated admixed haplotypes that have two admixture time parameters, and , which are, respectively, the earlier and later generations in which couples containing unadmixed individuals of different ancestries occur (all other individuals are unadmixed of the majority ancestry). To perform these simulations, we used a base case pedigree for with a desired setting of and generated new pedigrees by replacing lineages—starting from the left-most lineage and working to the right—by lineages with a time since admixture of and with the same . We use a parameter q to define the proportion of all the couples in the generation composed of individuals of different ancestries. By this definition, the range of q depends on , as the maximum fraction of couples containing unadmixed individuals of different ancestries is , so when , q ranges between 0 and 1 and when , q’s maximum value is 0.5.
Note that for this analysis we used only the exact local ancestry tracts derived from the Ped-sim break point positions. We represent the tracts lengths from population 0 as for and from population 1 as for . From these, we estimated the Poisson rates by using the maximum likelihood estimator for the 22 finite autosomes26 as and . Finally, from these same data, we also estimated .
In order to calculate the value of the model in Equation 2 infers, we reasoned that and each give a measure of , and we compute a weighted average of these two estimators. Specifically, because our estimates of the total Morgan fraction of the genome that fall in tracts of ancestry 0 and 1 are and respectively, we calculated this as a weighted average:
| (Equation 6) |
Here, as in PAPI, we subtract 1 for reasons described earlier (see “modeling the relationship between admixture time and ancestry switch rates”).
Handling local ancestry calls as input to PAPI
PAPI reads local ancestry calls produced by either HAPMIX or LAMP-LD. (Note that methods such as RFMix24 that require phased haplotypes and produce phased local ancestry calls are unsuitable for input to PAPI.) HAPMIX outputs posterior probabilities of the three possible unphased diploid local ancestry states at every marker, which PAPI converts into an internal representation of fixed (i.e., non-probabilistic) local ancestry calls. This conversion works by taking the maximally probable state at each marker. In contrast, LAMP-LD outputs fixed local ancestry calls and PAPI converts them directly into an internal representation. In simulated data, we found that LAMP-LD is prone to producing erroneous short segments, leading to an upward bias in admixture time inference. To address this, we filtered out LAMP-LD tracts shorter than 1 cM, which helps correct this bias (results not shown). Note that filtering out tracts can introduce state transitions prohibited by the HMM (see “a hidden Markov model to jointly infer admixture times and ancestry proportions”). In order to avoid this, we filtered out only those tracts that are flanked by tracts of identical ancestry state. The filtering process consists of deleting the target tract and merging the flanking tracts to fill in the missing space. We applied this filter in all the LAMP-LD-based analyses.
Data processing for ANCESTOR and PedMix
We formed the input to ANCESTOR by converting the non-probabilistic local ancestry calls that PAPI uses into the format expected by ANCESTOR. In order to run PedMix, we followed the authors recommendations and applied (1) a 0.05 minor allele frequency filter, (2) LD pruning (removing SNPS with ) by using overlapping blocks of 1,000 SNPs and a sliding window increment of 25 SNPs (with the PLINK option –indep-pairwise 1000 25 0.25), and (3) a switch-error correction tool provided by the authors. An additional utility for filtering SNPs on the basis of allele frequency differences between the ancestral populations reduced PedMix’s performance, and we thus omitted this step.
Computing measures of accuracy and bias
The A and B parent labels in PAPI’s estimates separate the inferred time and ancestry proportions of one parent from the other. However, PAPI does not infer the sexes of these parents, and in order to compute measures of accuracy and bias in our simulations, it is necessary to map these labels to specific parents. To do this, we choose the assignment that minimizes the sum of squared errors. Let and be the ancestry proportions of the parent with the larger and smaller estimates, respectively. Then, representing the estimated labels by an ordered vector , we minimize and use as the mapping between estimated and true parent labels.
In results, we report the mean absolute deviation of the estimated parameters from the truth, which serves as a measure of accuracy, computing this as
| (Equation 7) |
We also report a measure that uses exact rather than absolute differences, which serves as a measure of bias. This statistic is a vector of two numbers corresponding to the bias of each parent’s ancestry proportion individually:
| (Equation 8) |
We also compute analogous metrics for the estimates, denoted and .
Filtering and processing the PAGE data
We used PAPI to analyze African American individuals from the BioMe Biobank subset of the Population Architecture using Genomics and Epidemiology (PAGE II; dbGaP: phs000925.v1.p1) study.28 In order to identify admixed individuals with African and European ancestry, we merged all the individuals (N = 12,754) with the HapMap CEU and YRI trio parents—the latter providing known population labels—and ran ADMIXTURE v1.340 with . We analyzed the estimated ancestry proportions for the HapMap individuals to determine which of the K populations corresponded to African and European ancestry. We then selected PAGE individuals that met each of the following three criteria as subjects for our study: (1) has 5% African ancestry, (2) has 5% European ancestry, and (3) the sum of these two ancestries is 99.5%. This identified a total of 5,786 subjects for our analysis.
Because the number of SNPs that intersect between the PAGE and HapMap III datasets is small, we used 107 YRI and 95 CEU unrelated individuals from the 1,000 Genomes Project41 (1000G) data as panels for performing local ancestry inference in the PAGE subjects. To get a common set of SNPs between 1000G and PAGE, we first filtered out multiallelic and indel variants from both datasets. Next, in order to prevent any strand inconsistencies in the allele encodings of the two datasets, we ran PLINK v2.00a2.3LM with the –ref-from-fa option to recode the PAGE alleles to the forward strand of the GRCh37 reference genome (the 1000G data are already encoded in this manner). This may not correctly assign alleles at A/T and C/G SNPs, and we filtered these SNPs later (below). Next, we applied the “composite filter” provided in the quality control report distributed with the PAGE data, which includes filters for Hardy-Weinberg equilibrium, discordant calls in duplicated samples, and Mendelian errors, among others. In order to identify any remaining incorrectly coded alleles, we applied a chi-squared test for allele frequency differences between two groups of subjects—the 5,786 PAGE individuals and a subset of 1000G composed of 80 YRI and 20 CEU individuals. Markers in the PAGE data and the 1000G subset are expected to have similar allele frequencies, and those with statistically significant differences indicate a potential mismatch in the strand encoding. We filtered all markers with from both datasets. Finally, we removed all A/T and C/G SNPs, as allele-encoding mismatches in these markers (e.g., at high minor allele frequency variants) may not be detected by any of the analyses above. All of these steps left 409,095 markers that overlapped between PAGE and the 1000G data, and we used these to perform local ancestry inference via HAPMIX on each PAGE sample with the 1000G data as panels.
Results
We validated PAPI’s approach to deconvolving parental transmissions within unphased diploid local ancestry tracts of a given individual by using simulated and real data. Our first analysis contrasts the accuracy of PAPI’s estimates with each of its models and inference modes. Following this, we compare PAPI’s parameter estimates of (pA,pB) with those of ANCESTOR and PedMix (which do not estimate (tA,tB)) under a number of simulated scenarios, finding that PAPI reliably infers these parent ancestry fractions. We then turn to an examination of the quality of PAPI’s (tA,tB) estimates by using both inferred local ancestry tracts and exact tracts from our simulation pipeline. For these analyses, we considered a range of admixture histories, including the base case and more complex pedigrees (subjects and methods).
Following these efforts, we applied PAPI to a large dataset of African Americans from the PAGE study. By leveraging PAPI’s power to accurately infer parental ancestry proportions, we examined the relationship of couples’ ancestries to one another and find strong evidence of non-random mating, as described below.
Evaluating the performance of PAPI’s component models
We simulated the genotypes of admixed individuals under three scenarios: (1) , with and ; (2) ; and (3) (Table S1; see subjects and methods for simulation details). For every in scenarios 1 and 2, we simulated 22 admixed individuals for each of for a total of 88 individuals per scenario. In scenario 3, the small numbers of generations correspond to limited ranges of parent ancestry proportions; as such, when , we simulated a total of 88 admixed individuals for (22 individuals for each of and 44 individuals for ) and when , we simulated 22 admixed individuals for each of for a total of 132 individuals. Note that here and elsewhere in results, corresponds to African ancestry proportions. As described in subjects and methods, our simulation pipeline assigns population labels to unadmixed founders while matching as closely as possible the desired parent ancestry proportions. Because of random assortment and recombination, the realized (pA,pB) vary, and in general these founder ancestry assignments only give the expectation (or more precisely, the closest possible values to this expectation). However, we used the realized values of (pA,pB) for computing deviation metrics and .
PAPI can estimate (pA,pB) by using any of its three models: the binomial, the HMM, or the full model (a composite of the binomial and the HMM; subjects and methods). We ran all three models on the scenario 1 simulated individuals (Figure S4), and, averaged across all data points taken together, the GD estimates of (pA,pB) under the full model are quite reliable with . This is the best performing GD-based model overall with an absolute deviance 6.52% and 14.0% smaller than those of the HMM () and binomial model (), respectively. The same trend holds for the MCMC estimates, albeit with lower relative differences among the models: averaged across all scenario 1 data points, the full, HMM, and binomial models achieve values of 0.040, 0.041, and 0.042, respectively. The differences between the models are most pronounced when ; in particular, using the GD inference mode for this setting, the statistics for the binomial, HMM, and full models are, respectively, 0.061, 0.054, and 0.053; in turn, using MCMC inference, the corresponding measures are 0.061, 0.054, and 0.049, respectively. Note that while the MCMC (pA,pB) estimates under the full model are more accurate than the corresponding GD estimates overall, this method’s increased runtime and loss of accuracy in (tA,tB) estimation (below) make the MCMC estimates less effective when a user also seeks admixture time estimates.
Considering PAPI’s (tA,tB) estimates, we measured the Pearson correlation R of the inferred estimates with the true simulated tB values in scenario 1 data (tA = 9 is held fixed in scenario 1, and we ignore it in the correlation analysis). Here, PAPI’s GD estimates under the full model yield R = 0.761, representing a modest improvement compared to the HMM (R = 0.713). By contrast, the MCMC results in this case show weaker performance, with the full model yielding R = 0.678 and the HMM model alone obtaining R = 0.681.
We also benchmarked PAPI’s runtime for every combination of options (inference mode and model) on compute nodes with Intel Xeon E5 4620 processors, utilizing 4 GB of RAM (Table S2). We analyzed the 88 individuals simulated under scenario 2 with , one individual per PAPI run. The average wall clock time for the full model using the MCMC mode is 8.97 h per individual compared to 23.9 s using the GD mode, making the GD mode 1,346 faster than MCMC. The MCMC and GD runtimes for the full model are, somewhat counter-intuitively, slightly shorter than those for the HMM model (6.00% and 9.20% shorter, respectively), while runtimes for the HMM with the error model option turned on are slightly longer (3.29% and 8.75% longer for the MCMC and GD options, respectively). Finally, the binomial model runtimes are quite fast, with the MCMC mode completing in 5.38 min and GD mode requiring only 7.3 s.
In light of these results, we recommend running PAPI with the full model and using the GD inference option in most cases. These are PAPI’s default settings, and unless otherwise stated, we used these options to produce the rest of the results. A notable exception to this recommendation is when a user seeks only estimates; in this case the MCMC runtimes for the binomial model are relatively fast, and while this mode provides the least accurate estimates of all MCMC-based models, they are more accurate than the best GD estimates, making the speed and accuracy trade-off worthwhile.
Accuracy of parent ancestry estimates across admixture scenarios
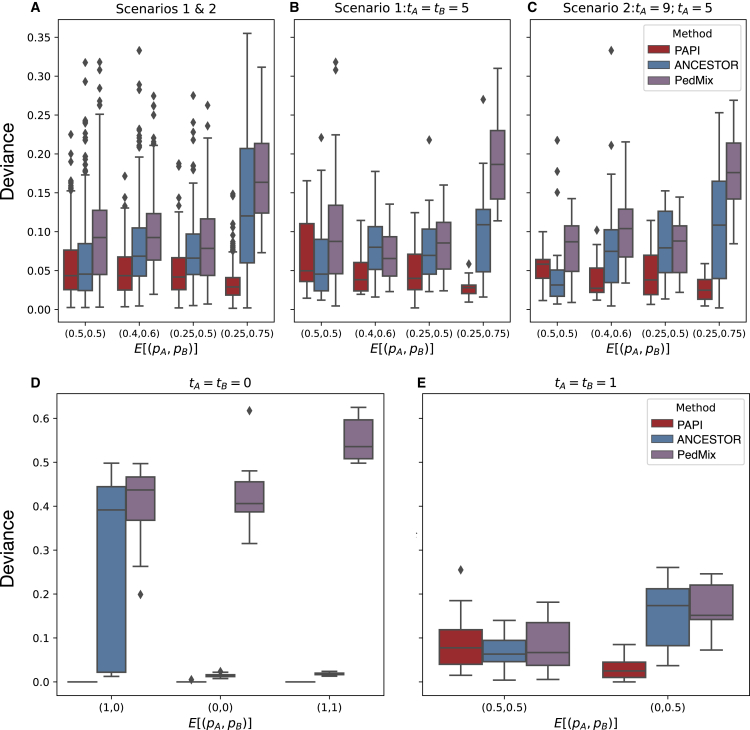
To evaluate PAPI’s performance in the context of other methods, we compared its inferred parental ancestry proportions with those of ANCESTOR and PedMix across all three simulation scenarios described above. Figure 3A shows for the three methods considering all scenario 1 and 2 data points, and Figures 3B and 3C show representative cases from each scenario. Overall, PAPI achieves on average for all scenario 1 and 2 cases compared to and from ANCESTOR and PedMix (representing improvements of 45.9% and 57.6%), respectively. PAPI’s performance improves with increasing ; for example, when , PAPI’s absolute deviance (averaged over admixture times) is 0.032, which is 75.6% and 81.1% lower than ANCESTOR and PedMix’s corresponding values of and . In fact, this setting yields PAPI’s lowest mean deviance and ANCESTOR and PedMix’s highest. This trend is recapitulated when using PAPI’s HMM alone compared to ANCESTOR (Figure S5). While the exact explanation of these results is likely multi-factorial, it seems that the PAPI HMM is better equipped to exploit the strictly less informative heterozygous ancestry regions as well as those with homozygous ancestry (see discussion). We examined the relative performance of PAPI, ANCESTOR, and PedMix in every setting of (tA,tB) from scenarios 1 and 2 and find that PAPI outperforms both ANCESTOR and PedMix in the majority of cases, with a handful of exceptions when (see Figures S6 and S7).
Figure 3.
Deviance statistics in simulated data for inferred parent ancestry proportions from PedMix, ANCESTOR, and PAPI
(A) Average absolute deviances (dabs,p) on all scenario 1 and 2 data.
(B and C) Absolute deviances for data points where (B) tA = tB = 5 and (C) tA = 9 and tB = 5.
(D and E) Average absolute deviance on all scenario 3 data.
(D) PAPI estimates the ground truth near perfectly when and (E) ANCESTOR and PedMix outperform PAPI when but PAPI’s deviance is low when .
PAPI’s parent ancestry estimates have little bias, with average in scenario 1 samples and in scenario 2 samples. The corresponding biases for ANCESTOR are higher at and in scenarios 1 and 2, respectively. Those of PedMix are also higher than PAPI with in scenario 1 and in scenario 2. Furthermore, the standard deviations of PAPI’s estimates are low at 0.035 in scenario 1 and 0.029 in scenario 2 samples, with corresponding values for ANCESTOR being 0.064 and 0.065 and for PedMix being 0.059 and 0.062.
Turning to the scenario 3 simulated data, in cases where both parents of the focal sample are unadmixed and from different populations (, so the focal sample is heterozygous for ancestry genome-wide), PAPI infers the ground truth with near-perfect accuracy (). In turn, ANCESTOR and PedMix have fairly high deviances in this case with average and 0.416, respectively (Figure 3D). When all four grandparents are unadmixed with each couple containing individuals of each ancestry ( and ), PAPI is less accurate than both ANCESTOR and PedMix, with the three methods having values of 0.089, 0.067, and 0.087, respectively (Figure 3E). Even so, when exactly one parent is unadmixed ( and ), PAPI achieves , which is considerably better than ANCESTOR’s and PedMix’s 0.176 (Figure 3E).
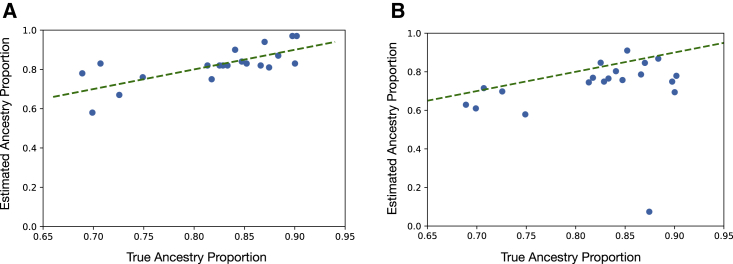
Finally, we validated PAPI’s parent ancestry estimates in real data by running it on the offspring of all ten African American trios in the HapMap ASW population. The availability of parental data provides a direct measure of the ground truth via those parents’ local ancestries (which we inferred with HAPMIX). As in the simulated data, we assigned the estimated parent labels to the real parents by minimizing the sum of squared deviances (subjects and methods). Figure 4 shows the estimated and true parent ancestry proportions of the trio children for PAPI and ANCESTOR. In these real samples, PAPI achieves and , which is more accurate and less biased compared to ANCESTOR’s values of and . PAPI’s parental ancestry proportion estimates with the binomial and HMM models alone achieve similar but slightly reduced performance compared to these full model results (binomial model mean and ; HMM mean and ; Figure S8).
Figure 4.
PAPI and ANCESTOR’s parent ancestry proportion estimates for the HapMap ASW trio children
Scatter plots of estimated versus true parent ancestry proportions for (A) PAPI’s full model and (B) ANCESTOR.
Accuracy of time since admixture estimates
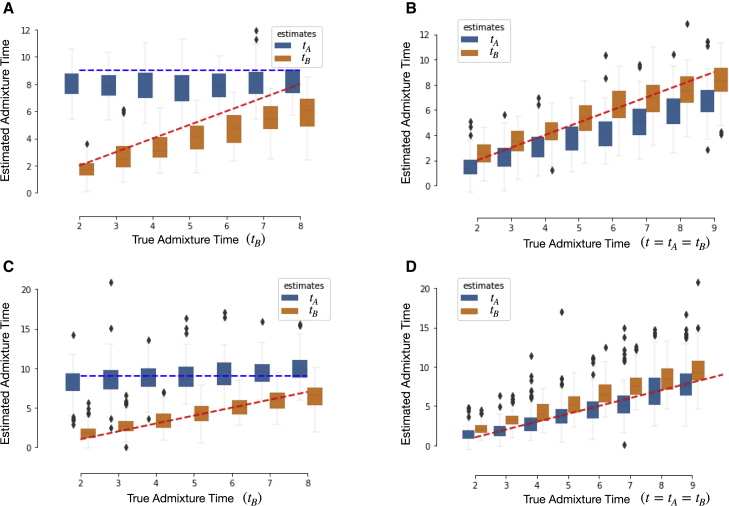
We used PAPI to estimate (tA,tB) in data simulated under scenarios 1 and 2 (above) and found that it reliably recovers the truth under both scenarios (Figures 5A and 5B). In scenario 1 data, the PAPI estimates for the two parents are well separated, with the difference between the two estimates proportional to the true difference. More specifically, there is a high correlation between and the corresponding PAPI estimate (R = 0.76), and a more moderate one between the inferred branch differences and the truth (R = 0.53). PAPI achieves similar quantitative results in the scenario 2 data, where the correlation between its estimates and the truth is R = 0.79 (calculated with both the tA and tB data points).
Figure 5.
PAPI’s estimated time since admixture in simulated individuals
(A and B) Box plots of estimated times based on HAPMIX local ancestry tracts for (A) scenario 1 samples (where ) and (B) scenario 2 data (where tA = tB).
(C and D) Estimated times based on exact local ancestry tracts for (C) scenario 1 and (D) scenario 2 individuals. In (A) and (C), the x-axis gives the true tB since tA is held fixed in these cases. Blue and orange dashed lines represent the simulation ground truths for tA and tB, respectively in (A) and (C), while the red dashed lines in (B) and (D) represent the simulation ground truths for tA and tB.
PAPI’s estimates in these simulated data have an overall downward bias, with mean for scenario 1 and for scenario 2 data points. In order to understand the source of these biases, we ran PAPI on the exact ancestry tracts output by the simulator for data from both scenarios. This analysis yields reduced bias measures of mean for scenario 1 and for scenario 2 samples (Figures 5C and 5D), suggesting that some of the downward bias can be explained by errors in local ancestry inference. The larger number of outliers in Figures 5C and 5D may be due to the presence of small tracts in the exact simulated data, which may go undetected by HAPMIX.
We contrasted these HAPMIX-based results with those obtained with tracts inferred by LAMP-LD (after filtering out tracts smaller than 1 cM; subjects and methods). As shown in Figure S9, the LAMP-LD-based estimates are biased upwards on average for both scenarios, with mean for scenario 1 and for scenario 2 data points. The LAMP-LD-based estimates also show weaker correlations with the truth compared to the HAPMIX-based estimates with R = 0.59 for scenario 1 (considering only values) and for scenario 2 data points. Given these results, and the fact that HAPMIX further classifies ≥98.5% of SNPs correctly for all three diploid ancestry states (see Figure S10), we conducted all further analyses with HAPMIX local ancestry tracts.
The above results consider the estimates in aggregate across simulated individuals, but PAPI is designed to be applied to individual samples as well. We plotted sample-specific point estimates of (obtained with the MCMC inference mode) in the scenario 2 data along with their 90% Bayesian credible intervals (CIs) in Figure S11. The 90% CIs overlap true values in 86% of data points and have a mean range of 4.99. Notably, when the true , the 90% CIs of the model (in this case run with the error model option) have very large mean range of 16.5 and are strongly biased (; Figure S12). This is due to the fact that when , both and must be either 0 or 1, and hence the inferred values in are each close to one of these extremes. Equation 2 implies that when this happens, either or , and therefore relatively small changes in can lead to large changes in tj; thus small erroneous tracts can readily bias the results. Note that PAPI performs better in GD inference mode when using the error model (see “effectiveness of PAPI’s error model”); this may be because GD identifies a local maximum while the MCMC calculation integrates error and non-error state assignments for short, erroneous tracts. Still, as noted below in the discussion of the error model, we advise caution in interpreting the tj estimates when or .
We further validated PAPI’s tj estimates in real data by again analyzing the ten ASW trio offspring. Here, the parents’ true time since admixture cannot be directly ascertained, so we first ran PAPI on each trio parent and computed the truth as an average of that parent’s time since admixture estimates, adding one for the meiosis to the trio offspring: and , where for , and represent PAPI’s estimates on the trio father and trio mother, respectively. We then assigned the trio children’s estimates to parent labels by minimizing the sum of squared differences (subjects and methods). PAPI’s estimates in these data have a strong correlation with the truth of R = 0.77, in line with that observed in the simulated data (Figure S13). These estimates are somewhat biased with .
Interpreting time since admixture estimates
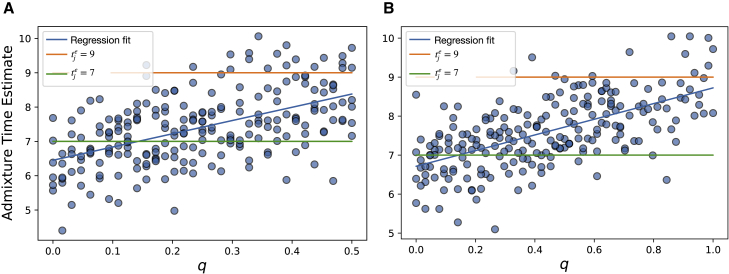
As described in subjects and methods, we simulated single haplotypes under a larger class of pedigree structures defined by four parameters—, , , and q. We carried out these simulations with for each of , where, when , q varied between in increments of , and when , q varied between in the same increments (q’s maximum value is 0.5 for ). We further simulated structures with for , varying q between in increments of .
Given the exact local ancestry segments output by the simulation pipeline, we applied Equation 6 to estimate and then empirically examined the relationship between and the simulation parameters , , , and q. Our results suggest that linearly increases from to as q increases from 0 to its maximum value (Figures 6 and S14), but notably, the estimates are downwardly biased from the weighted average over all N simulated datapoints. In particular, when , this weighted average is , where i indexes individual datapoints. When , we use and as the weights on and , respectively, with the factor of 2 accounting for q’s smaller range in this case. We measured the bias as when and when . Similar biases arise in PAPI’s estimates when using both simulated exact ancestry tracts and tracts inferred by HAPMIX (see the previous subsection).
Figure 6.
PAPI’s estimated time since admixture with two migrant pulses
Plots show estimated time since admixture versus q (the proportion of couples in the generation with unadmixed individuals of different ancestries) when and for (A) and (B) . The blue lines depict the least-squares regressions on the plotted data points.
While these results indicate that the estimated times since admixture may generally be a weighted average of the times in which individuals of a given ancestry entered an individual’s pedigree, a full understanding of the quantitative relationship requires more detailed analyses that are beyond the scope of this work. Instead we note simply that PAPI’s admixture time estimates potentially represent inputs from several generations and should not be interpreted as the generation in which admixture occurred.
Effectiveness of PAPI’s error model
While generally reliable, local ancestry inference methods do produce erroneous tracts, which can lead to biased estimates (see “accuracy of time since admixture estimates”). These biases are most pronounced when the true and values are close to 0 or 1, such as in a subset of the scenario 3 simulated data (where and ). In these cases, PAPI’s error model helps account for any erroneous tracts, leading to improved estimates of ( with the error model as opposed to without) and ( with the error model and without). Despite these improvements when the true , note that in practice a few small tracts in real data that this model considers to be erroneous may in fact be real and reflect old admixture. As such, by default, PAPI runs without the error model, and we advise caution in interpreting its estimates when or . If a user is confident that the population under study is only recently admixed, using the error model can improve the results. In either case, it may be prudent to re-run PAPI in MCMC mode and examine the posterior distribution of for samples with or or to simply avoid consideration of results from such parents.
Ancestry proportions of parental couples are strongly correlated with each other in PAGE African Americans
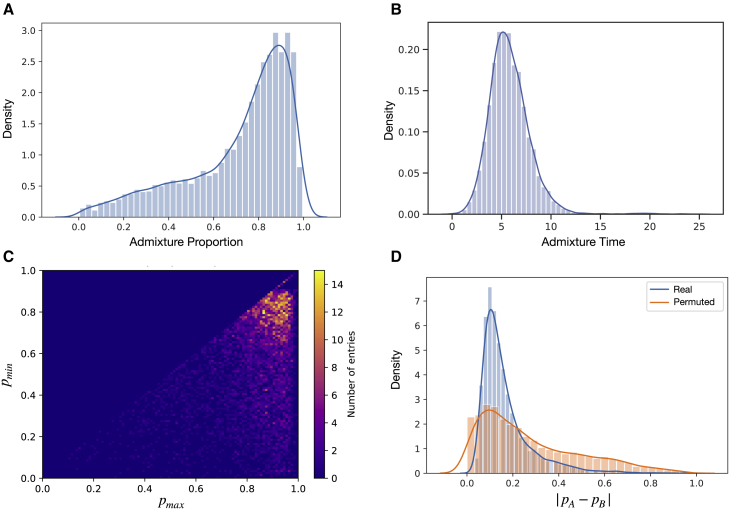
We ran PAPI on detected African Americans from the BioMe Biobank subset of the PAGE study,28 considering a total of 5,786 individuals that met our ancestry-based criteria for inclusion (subjects and methods). Here, we initially examined the parental ancestry proportion estimates from PAPI’s binomial model run in MCMC inference mode—the recommended mode when only pj estimates are required (see “evaluating the performance of PAPI’s component models”). The average African ancestry proportion in the parents is pj = 0.71, which is roughly consistent with previous estimates in African Americans.6,30,31 The majority of parents have proportions between 0.8 and 1.0, corresponding to high African ancestry, but a heavy left tail in the distribution drives down the mean (Figure 7A). Figure 7B plots the estimated time since admixture—obtained by running PAPI with the default options—considering all parents that have for . This distribution has an overall Gaussian-like shape, which may suggest random mating with respect to the time since admixture among the ancestors of these African Americans. The population mean of estimates is 6.10, again roughly consistent with previous estimates in African Americans.6,30,31 We infer a small set of individuals (0.04% of the dataset) with , but since the simulated data also contain some overestimated extreme values, we assumed that these estimates are inflated.
Figure 7.
PAPI analyses from African Americans in the BioMe Biobank subset of PAGE
(A) Distribution of the parent ancestry estimates (both pA and pB plotted separately) in these African Americans.
(B) Distribution of time since admixture estimates (tA and tB plotted separately).
(C) Heatmap of the ancestry proportions of couples (pA, pB) ordered as (pmax, pmin).
(D) Distribution of estimates from the real couples along with a permuted distribution.
We analyzed PAPI's parental admixture proportion estimates within all parent pairs—all couples—from these African Americans. Figure 7C depicts a heatmap of (since the A and B labels are arbitrary) where one salient feature is a strong cluster of points centered roughly at that spreads diffusely outward. This cluster is consistent with a pattern of assortative mating between individuals with high African ancestry, and includes a meaningful fraction of the couples (25.2% of individuals in the dataset have and ). Furthermore, the Pearson correlation coefficient between and is R = 0.871, also indicating assortative mating by ancestry.
To more precisely characterize the strength of the signal for non-random mating in these couples, we examined the per-individual distribution of (Figure 7D). This density is roughly Gaussian with a heavy right tail and has a mean of 0.169, largely driven by the high density of couples noted above. This real data distribution is visibly distinct from what would arise under random mating, as randomly shuffling the members of the couples creates a much more dispersed, thick-tailed density (Figure 7D). Indeed, the mean across permutations is 0.272, and no permutation mean reached as small a value as in the real data (minimum permutation mean 0.264; ). Notably the real data distribution has a depletion of mass near , which could be due to PAPI being biased when . Consistent with this, PAPI shows slightly reduced performance in simulated data when (see Figure 3).
In order to ensure that the assortative mating signal is not being driven by this bias (or other biases in PAPI’s inference), we simulated genotypes for 176 admixed African Americans in the same manner as before (subjects and methods) but with and with the (pA,pB) pairs randomly sampled from the parental admixture proportion distribution depicted in Figure 7A. As we sampled pA and pB independently, this produces a null (random mating) distribution akin to the shuffled distribution above. The results from running PAPI on these simulated individuals (see Figure S15) are remarkably similar to the permuted distribution in Figure 7D, and the mean in these simulated individuals is 0.261. This indicates that potential bias in PAPI’s inference is not driving the assortative mating signal. Moreover, the simulated data distribution also lacks mass near , suggesting that, while PAPI is somewhat biased in this region of the parameter space, this bias alone does not drive the assortative mating signal. Taken together, these observations provide strong evidence for assortative mating by ancestry proportion in the parents of these African American individuals.
Discussion
In this paper, we described and evaluated PAPI, a novel approach to inferring the admixture proportions and times since admixture for each parent of an extant individual that combines two models. The first is a binomial model that takes a global view of the ancestry of an individual, considering the overall proportions of homozygous and heterozygous ancestry in their genome. As noted earlier, this model is equivalent to that described in a recent paper.29 PAPI employs a Bayesian framework and combines this binomial model with a second HMM that leverages the information present in the length distribution of local ancestry tracts. The HMM incorporates a population genetic model9—but uses parameters specific to the individual’s pedigree—to capture the hidden recombinations within these tracts (i.e., those that do not switch the ancestry of the haplotype).
To characterize PAPI’s accuracy, we simulated African Americans under various pedigree topologies and distributions of parent ancestry proportions and also used the real HapMap ASW trios. Our results show that PAPI is more accurate than ANCESTOR and PedMix at inferring parent ancestry proportions in many settings (Figure 4) and can detect when (Figure 5). In simulations that rely on inferred local ancestry tracts, PAPI is able to recover tj estimates highly correlated with the truth, albeit with a downward bias when using HAPMIX local ancestry tracts and an upward bias when using tracts from LAMP-LD (Figure 5).
PAPI’s approach models historical crossovers with a Markovian approximation to the more elaborate dynamics of crossover transmissions in a pedigree. The transition probabilities of PAPI's HMM are otherwise similar to those of ANCESTOR, although ANCESTOR also supports non-exponential tract length distributions by using a stochastic expectation maximization technique for inference. In contrast, PedMix15 parameterizes the full pedigree up to the grandparental generation by using an ancestral configuration vector (which captures grandparental ancestry states, phase error, and all transmitted recombinations) while treating older recombinations as Markovian. Despite only approximating pedigree-based crossovers, and through its two component models, PAPI produces highly accurate estimates of parental ancestry proportions without relying on phased input. Note that neither PedMix nor ANCESTOR estimate parental admixture times (ANCESTOR instead provides estimates of average ancestry tract lengths for each parent).
As noted earlier, ANCESTOR and PedMix’s performance decline as the difference increases, while PAPI maintains strong performance throughout the (pA, pB) settings we considered. By using a pulse-migration model for local ancestry, PAPI’s HMM embeds the parent ancestry proportions pj in its transition probabilities, enabling it to derive signal from all tracts, including those of heterozygous ancestry that are phase-uncertain. Compared to ANCESTOR, this change in the likelihood function shifts probability mass to regions of parameter space with divergent pA and pB when the focal individual has high heterozygous ancestry. ANCESTOR’s model, on the other hand, seems to derive signal for (pA, pB) by using the HMM initial probabilities, i.e., from the first tract on each chromosome, rather than from all tracts (see section 2.3 in the ANCESTOR paper for its transition probabilities14). In turn, PedMix’s performance is affected by phase errors that its model partially addresses15—an issue that both PAPI and ANCESTOR avoid. Another factor in PAPI’s improved performance when is large may be that the difference between the true parent ancestry and that transmitted to the focal individual has lower variance when and/or are near either end of the range.
PAPI’s ancestry estimates in the PAGE dataset add to a growing body of evidence for assortative mating by ancestry proportion in African Americans.22 Others have noted these signals in Latinos21 and found that they frequently cannot be explained by socioeconomic factors alone and are important to take into account when designing genetic studies. For example, using Wright-Fisher simulations that allow for ancestry-based assortative mating, Zaitlen et al.22 showed that assuming random-mating leads to significant underestimates of population-scale admixture times.
Overall, PAPI’s applications include both the study of the population genetics of mating in African Americans and the potential to provide individual-level information to study subjects. Given this ability to infer parental ancestry proportions for individual samples, we expect PAPI to be of interest to direct-to-consumer genetic testing companies and to consumers themselves who wish to better understand their genetic heritage.
Acknowledgments
We thank the two anonymous reviewers for their valuable feedback that improved this paper. Funding for this work was provided by NIH grant R35 GM133805. Computing was performed on a cluster administered by the Biotechnology Resource Center at Cornell University.
Declaration of interests
A.L.W. is an employee of and holds stock in 23andMe and is the owner of HAPI-DNA LLC.
Published: July 26, 2022
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.ajhg.2022.06.016.
Supplemental information
Data and code availability
The PAPI code is available at https://github.com/williamslab/papi. Genotype data for BioMe Biobank subset of the PAGE II dataset are available (dbGaP: phs000925.v1.p1), and the phased 1000 Genomes data used for local ancestry inference are publicly available at ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/release/20130502/. The simulated genotype data supporting the current study have not been deposited in a public repository but can be reproduced using Ped-sim (https://github.com/williamslab/ped-sim), admix-simu (https://github.com/williamslab/admix-simu), scripts distributed with PAPI, and the publicly available HapMap CEU and YRI data (https://ftp.ncbi.nlm.nih.gov/hapmap/genotypes/2009-01_phaseIII/plink_format/).
References
- 1.Ruhl G.L., Hazel J.W., Wright Clayton E., Malin B.A. Public attitudes toward direct to consumer genetic testing. AMIA Annu. Symp. Proc. 2019;2019:774. [PMC free article] [PubMed] [Google Scholar]
- 2.Regalado A. More than 26 million people have taken an at-home ancestry test. MIT Tech. Rev. 2019;11:2019. [Google Scholar]
- 3.Bryc K., Durand E.Y., Macpherson J.M., Reich D., Mountain J.L. The genetic ancestry of African Americans, Latinos, and European Americans across the United States. Am. J. Hum. Genet. 2015;96:37–53. doi: 10.1016/j.ajhg.2014.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Han E., Carbonetto P., Curtis R.E., Wang Y., Granka J.M., Byrnes J., Noto K., Kermany A.R., Myres N.M., Barber M.J., et al. Clustering of 770, 000 genomes reveals post-colonial population structure of North America. Nat. Commun. 2017;8:14238. doi: 10.1038/ncomms14238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Micheletti S.J., Bryc K., Ancona Esselmann S.G., Freyman W.A., Moreno M.E., Poznik G.D., Shastri A.J., 23andMe Research Team. Mountain J.L., et al. Genetic consequences of the transatlantic slave trade in the Americas. Am. J. Hum. Genet. 2020;107:265–277. doi: 10.1016/j.ajhg.2020.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pritchard J.K., Stephens M., Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Price A.L., Patterson N.J., Plenge R.M., Weinblatt M.E., Shadick N.A., Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 8.Price A.L., Tandon A., Patterson N., Barnes K.C., Rafaels N., Ruczinski I., Beaty T.H., Mathias R., Reich D., Myers S. Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 2009;5:e1000519. doi: 10.1371/journal.pgen.1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gravel S. Population genetics models of local ancestry. Genetics. 2012;191:607–619. doi: 10.1534/genetics.112.139808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Novembre J., Johnson T., Bryc K., Kutalik Z., Boyko A.R., Auton A., Indap A., King K.S., Bergmann S., Nelson M.R., et al. Genes mirror geography within Europe. Nature. 2008;456:98–101. doi: 10.1038/nature07331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Waples R.K., Hauptmann A.L., Seiding I., Jørsboe E., Jørgensen M.E., Grarup N., Andersen M.K., Larsen C.V.L., Bjerregaard P., Hellenthal G., et al. The genetic history of Greenlandic-European contact. Curr. Biol. 2021;31:2214–2219.e4. doi: 10.1016/j.cub.2021.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Seldin M.F., Pasaniuc B., Price A.L. New approaches to disease mapping in admixed populations. Nat. Rev. Genet. 2011;12:523–528. doi: 10.1038/nrg3002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Atkinson E.G., Maihofer A.X., Kanai M., Martin A.R., Karczewski K.J., Santoro M.L., Ulirsch J.C., Kamatani Y., Okada Y., Finucane H.K., et al. Tractor uses local ancestry to enable the inclusion of admixed individuals in GWAS and to boost power. Nat. Genet. 2021;53:195–204. doi: 10.1038/s41588-020-00766-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zou J.Y., Halperin E., Burchard E., Sankararaman S. Inferring parental genomic ancestries using pooled semi-Markov processes. Bioinformatics. 2015;31:i190–i196. doi: 10.1093/bioinformatics/btv239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pei J., Zhang Y., Nielsen R., Wu Y. Inferring the ancestry of parents and grandparents from genetic data. PLoS Comput. Biol. 2020;16:e1008065. doi: 10.1371/journal.pcbi.1008065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nettelblad C. Inferring haplotypes and parental genotypes in larger full sib-ships and other pedigrees with missing or erroneous genotype data. BMC Genet. 2012;13:85. doi: 10.1186/1471-2156-13-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Young A.I., Moeen Nehzati S., Lee C., Benonisdottir S., Cesarini D., Benjamin D.J., Turley P., Kong A. Mendelian Imputation of Parental Genotypes for Genome-wide Estimation of Direct and Indirect Genetic Effects. bioRxiv. 2020 doi: 10.1101/2020.07.02.185199. Preprint at. [DOI] [Google Scholar]
- 18.Hwang L.-D., Tubbs J.D., Luong J., Lundberg M., Moen G.-H., Wang G., Warrington N.M., Sham P.C., Cuellar-Partida G., Evans D.M. Estimating indirect parental genetic effects on offspring phenotypes using virtual parental genotypes derived from sibling and half sibling pairs. PLoS Genet. 2020;16:e1009154. doi: 10.1371/journal.pgen.1009154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johnson N.A., Coram M.A., Shriver M.D., Romieu I., Barsh G.S., London S.J., Tang H. Ancestral components of admixed genomes in a Mexican cohort. PLoS Genet. 2011;7:e1002410. doi: 10.1371/journal.pgen.1002410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Howe L.J., Battram T., Morris T.T., Hartwig F.P., Hemani G., Davies N.M., Smith G.D. Assortative mating and within-spouse pair comparisons. PLoS Genet. 2021;17:e1009883. doi: 10.1371/journal.pgen.1009883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zou J.Y., Park D.S., Burchard E.G., Torgerson D.G., Pino-Yanes M., Song Y.S., Sankararaman S., Halperin E., Zaitlen N. Genetic and socioeconomic study of mate choice in Latinos reveals novel assortment patterns. Proc. Natl. Acad. Sci. USA. 2015;112:13621–13626. doi: 10.1073/pnas.1501741112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zaitlen N., Huntsman S., Hu D., Spear M., Eng C., Oh S.S., White M.J., Mak A., Davis A., Meade K., et al. The effects of migration and assortative mating on admixture linkage disequilibrium. Genetics. 2017;205:375–383. doi: 10.1534/genetics.116.192138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liang M., Nielsen R. The lengths of admixture tracts. Genetics. 2014;197:953–967. doi: 10.1534/genetics.114.162362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Maples B.K., Gravel S., Kenny E.E., Bustamante C.D. A discriminative modeling approach for rapid and robust local-ancestry inference. Am. J. Hum. Genet. 2013;93:278–288. doi: 10.1016/j.ajhg.2013.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Baran Y., Pasaniuc B., Sankararaman S., Torgerson D.G., Gignoux C., Eng C., Rodriguez-Cintron W., Chapela R., Ford J.G., Avila P.C., et al. Fast and accurate inference of local ancestry in Latino populations. Bioinformatics. 2012;28:1359–1367. doi: 10.1093/bioinformatics/bts144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Caballero M., Seidman D.N., Qiao Y., Sannerud J., Dyer T.D., Lehman D.M., Curran J.E., Duggirala R., Blangero J., Carmi S., Williams A.L. Crossover interference and sex-specific genetic maps shape identical by descent sharing in close relatives. PLoS Genet. 2019;15:e1007979. doi: 10.1371/journal.pgen.1007979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.International HapMap Consortium A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wojcik G.L., Graff M., Nishimura K.K., Tao R., Haessler J., Gignoux C.R., Highland H.M., Patel Y.M., Sorokin E.P., Avery C.L., et al. Genetic analyses of diverse populations improves discovery for complex traits. Nature. 2019;570:514–518. doi: 10.1038/s41586-019-1310-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pfaffelhuber P., Sester-Huss E., Baumdicker F., Naue J., Lutz-Bonengel S., Staubach F. Inference of recent admixture using genotype data. Forensic Sci. Int. Genet. 2022;56:102593. doi: 10.1016/j.fsigen.2021.102593. [DOI] [PubMed] [Google Scholar]
- 30.Smith M.W., Patterson N., Lautenberger J.A., Truelove A.L., McDonald G.J., Waliszewska A., Kessing B.D., Malasky M.J., Scafe C., Le E., et al. A high-density admixture map for disease gene discovery in African Americans. Am. J. Hum. Genet. 2004;74:1001–1013. doi: 10.1086/420856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Moorjani P., Patterson N., Hirschhorn J.N., Keinan A., Hao L., Atzmon G., Burns E., Ostrer H., Price A.L., Reich D. The history of African gene flow into Southern Europeans, Levantines, and Jews. PLoS Genet. 2011;7:e1001373. doi: 10.1371/journal.pgen.1001373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nelson D., Kelleher J., Ragsdale A.P., Moreau C., McVean G., Gravel S. Accounting for long-range correlations in genome-wide simulations of large cohorts. PLoS Genet. 2020;16:e1008619. doi: 10.1371/journal.pgen.1008619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Virtanen P., Gommers R., Oliphant T.E., Haberland M., Reddy T., Cournapeau D., Burovski E., Peterson P., Weckesser W., Bright J., et al. SciPy 1.0 Contributors SciPy 1.0: fundamental algorithms for scientific computing in python. Nat. Methods. 2020;17:261–272. doi: 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Salvatier J., Wiecki T.V., Fonnesbeck C. Probabilistic programming in Python using PyMC3. PeerJ Comp. Sci., 2016;2:e55. [Google Scholar]
- 35.Bhérer C., Campbell C.L., Auton A. Refined genetic maps reveal sexual dimorphism in human meiotic recombination at multiple scales. Nat. Commun. 2017;8:14994. doi: 10.1038/ncomms14994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Williams A. 2016. Admix-Simu: Program To Simulate Admixture Between Multiple Populations.https://github.com/williamslab/admix-simu.git [Google Scholar]
- 37.Hinrichs A.S., Karolchik D., Baertsch R., Barber G.P., Bejerano G., Clawson H., Diekhans M., Furey T.S., Harte R.A., Hsu F., et al. The UCSC genome Browser Database: update 2006. Nucleic Acids Res. 2006;34:D590–D598. doi: 10.1093/nar/gkj144. Database issue):D590–D598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chang C.C., Chow C.C., Tellier L.C., Vattikuti S., Purcell S.M., Lee J.J. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience. 2015;4:7. doi: 10.1186/s13742-015-0047-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Browning S.R., Browning B.L. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. Am. J. Hum. Genet. 2007;81:1084–1097. doi: 10.1086/521987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Alexander D.H., Novembre J., Lange K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 2009;19:1655–1664. doi: 10.1101/gr.094052.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.1000 Genomes Project Consortium. Brooks L.D., Durbin R.M., Garrison E.P., Kang H.M., Korbel J.O., Marchini J.L., McCarthy S., McVean G.A., Abecasis G.R. A global reference for human genetic variation. Nature. 2015;526:68–74. doi: 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The PAPI code is available at https://github.com/williamslab/papi. Genotype data for BioMe Biobank subset of the PAGE II dataset are available (dbGaP: phs000925.v1.p1), and the phased 1000 Genomes data used for local ancestry inference are publicly available at ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/release/20130502/. The simulated genotype data supporting the current study have not been deposited in a public repository but can be reproduced using Ped-sim (https://github.com/williamslab/ped-sim), admix-simu (https://github.com/williamslab/admix-simu), scripts distributed with PAPI, and the publicly available HapMap CEU and YRI data (https://ftp.ncbi.nlm.nih.gov/hapmap/genotypes/2009-01_phaseIII/plink_format/).